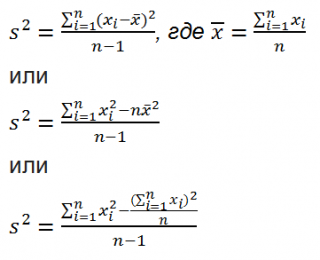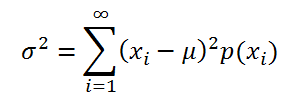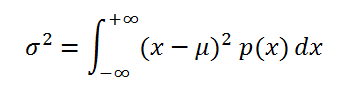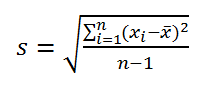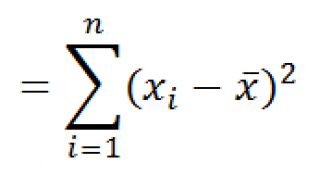Приветствую посетителей блога statanaliz.info. В данной статье рассмотрим, что такое «выборочная несмещенная дисперсия».
Тема не нова, так как с таким показателями как размах значений, среднее линейное отклонение, дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации мы уже знакомы.
Понятие о сплошном и выборочном наблюдении
С точки зрения охвата объекта исследования, статистический анализ можно разделить на два вида: сплошной и выборочный. Сплошной статанализ предполагает изучение генеральной совокупности данных, то есть всего явления во всем его многообразии без распространения выводов на другие элементы, не входящие в анализируемую совокупность. Из названия данного типа явствует, что наблюдению подвергаются тотально все элементы. Результат анализа распространяется на всю генеральную совокупность без каких-либо допущений и поправок на ошибку. Данный тип статистического исследования является наиболее полным и точным, так как дополнительные знания почерпнуть уже неоткуда – информация собрана со всех элементов объекта исследования. Это бесспорный плюс.
Отличным примером сплошного наблюдения является перепись населения. «Всесоюзная перепись населения» — красиво звучало! Кстати, советская статистика, как и наука в целом, была одной из самых лучших в мире. Денег на проведение сплошных обследований не жалели, так как при СССР статистика выполняла свою прямую функцию – исследовала реальность, без чего невозможно было строить «светлое будущее». При этом советские ученые-статистики справедливо критиковали буржуазную статистику за то, что те скрывают от народа реальное положение дел и используют статистику для промывки мозгов. Об этом, кстати, писали и сами буржуи. Более практичный пример сплошного наблюдения – опрос жителей многоэтажного дома на предмет заваривания мусоропровода. Опрашиваются все, результат дает вполне однозначный ответ об отношении жителей к мусоропроводу. Ошибки в выводах маловероятны.
Как бы там ни было, у сплошного наблюдения есть отрицательное качество: на организацию и проведение исследования могут потребоваться значительные ресурсы. Одно дело взять пробу из партии товаров, другое – проверять всю партию. Одно дело опросить тысячу прохожих на улице, совсем другое – организовать перепись населения.
В противовес сплошному придумали выборочное наблюдение. Название метода точно отражает его суть: из генеральной совокупности отбирается и анализируется только часть данных, а выводы распространяют на всю генеральную совокупность. Отбор данных происходит таким образом, чтобы выборка была репрезентативной, то есть, сохранила внутреннюю структуру и закономерности генеральной совокупности. Если это условие не соблюдено, то дальнейший анализ во многом теряет смысл.
Сам анализ выборочных данных происходит так же, как и при сплошном наблюдении (рассчитываются различные показатели, делаются прогнозы и т.д.), только с поправкой на ошибку. Это значит, что рассчитывая тот или иной показатель, мы понимаем, что при повторной выборке его значение будет другим. К примеру, провели опрос общественного мнения. Опрос показал, что за кандидата N желают проголосовать 60% опрошенных. Если провести еще один такой же опрос, даже в том же месте, то результат будет отличаться. То есть, взяв первое значение 60%, следует понимать, что с той или иной вероятностью оно могло быть, скажем, и 58%, и 62%. Точность и разброс выборочных показателей зависят от характера данных и их количества.
У выборочного наблюдения есть один существенный плюс и один минус, однако по сравнению со сплошным наблюдением крайности меняются местами. Плюс заключается в том, что для проведения выборочного обследования требуется гораздо меньше ресурсов. Минус – в том, что выборочное наблюдение всегда ошибочно. Поэтому основная задача проведения выборочного наблюдения – добиться максимальной точности при приемлемых затратах на его проведение.
Выборочная несмещенная дисперсия
И вот, стало быть, дисперсия. Дисперсия, как и доля или средняя арифметическая, также меняет свое значение от выборки к выборке, но здесь есть интересная особенность. Дисперсия ведь рассчитывается от средней величины, а она в свою очередь, тоже рассчитывается по выборке, то есть является ошибочной. Как же это обстоятельство влияет на саму дисперсию?
Если бы мы знали истинную среднюю величину (по генеральной совокупности), то ошибка дисперсии была бы связана только с нерепрезентативностью, то есть с тем, что данные в выборке оказались бы ближе или дальше от средней, чем в целом по генеральной совокупности. При этом при многократном повторении данные стремились бы к своему реальному расположению относительно средней.
Выборочный показатель, который при многократном повторении выборки стремится к своему теоретическому значению, называется несмещенной оценкой. Почему оценкой? Потому что мы не знаем реальное значение показателя (по генеральной совокупности), и с помощью выборочного наблюдения пытаемся его оценить. Оценка показателя – это есть его характеристика, рассчитанная по выборке.
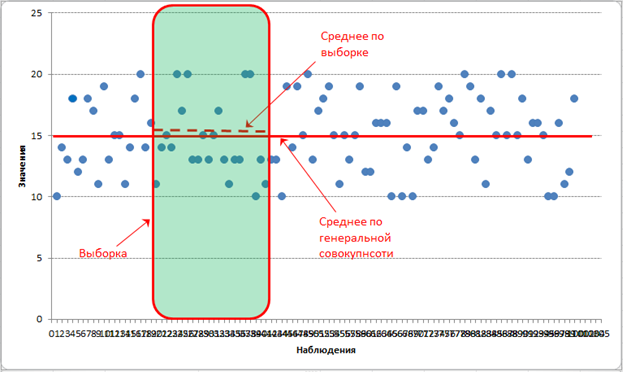
Теперь смотрим внимательно на выборочную среднюю. Выборочная средняя – это несмещенная оценка математического ожидания, так как средняя из выборочных средних стремится к своему теоретическому значению по генеральной совокупности. Где она расположена? Правильно, в центре выборки! Средняя всегда находится в центре значений, по которым рассчитана – на то она и средняя. А раз выборочная средняя находится в центре выборки, то из этого следует, что сумма квадратов расстояний от каждого значения выборки до выборочной средней всегда меньше, чем до любой другой точки, в том числе и до генеральной средней. Это ключевой момент. А раз так, то дисперсия в каждой выборке будет занижена. Средняя из заниженных дисперсий также даст заниженное значение. То есть при многократном повторении эксперимента выборочная дисперсия не будет стремиться к своему истинному значению (как выборочная средняя), а будет смещена относительно истинного значения по генеральной совокупности.
Отклонение выборочной средней от генеральной показано на рисунке.
Несмещенность оценки – одна из важных характеристик статистического показателя. Смещенная оценка показателя заранее говорит о тенденции к ошибке. Поэтому показатели стараются оценивать таким образом, чтобы их оценки были несмещенными (как у средней арифметической). Чтобы решить проблему смещенности выборочной дисперсии, в ее расчет вносят корректировку – умножают на n/(n-1), либо сразу при расчете в знаменатель ставят не n, а n-1. Получается так.
Выборочная смещенная дисперсия:
Выборочная несмещенная дисперсия:
Под выборочной дисперсией понимают, как правило, именно несмещенный вариант.
Теперь посмотрим на практическую сторону отличия смещенной и несмещенной дисперсии. Соотношение между выборочной и генеральной дисперсией составляет n/n-1. Несложно догадаться, что с ростом n (объема выборки) данное выражение стремится к 1, то есть разница между значениями выборочной и генеральной дисперсиями уменьшается.
Так, в выборке из 11 наблюдений относительная разница составляет 11/10 = 10%. При 21 наблюдениях, отличие сокращается до 5%, при 31 наблюдении – до 3,3%, при 51 – до 2%, при 101 – до 1%. Короче, при достаточно большой выборке данных (50 и выше наблюдений) относительная разница между смещенной и несмещенной дисперсией практически исчезает. Оценка параметра, когда с ростом выборки его отклонение от теоретического значения уменьшается, называется асимптотически несмещенной оценкой.
При переходе к среднеквадратичном отклонению по выборке (корень из выборочной дисперсии) разница становится еще меньше.
Таким образом, эффект смещенной дисперсии проявляется в небольших выборках. В больших выборках можно использовать генеральную дисперсию, что как бы не усложняет и не упрощает жизнь. Вручную сейчас никто не считает. Все легко посчитать в Excel. Но понимать различие в терминологии и в сути показателей все же следует.
Из данной статьи неплохо бы усвоить следующее.
1. Формула генеральной дисперсии в выборке дает смещенную оценку.
2. В знаменателе несмещенной оценки n-1 вместо n.
3. При большом объеме выборки (от 100 наблюдений) разница между смещенной и несмещенной дисперсиями практически исчезает.
4. Стандартное отклонение по выборке – это корень из выборочной дисперсии.
До новых встреч на блоге statanaliz.info.
Поделиться в социальных сетях:
Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Еще…Меньше
Для агрегирования (суммы) значений в сводной таблице можно использовать сводные функции, такие как Sum, Count и Average.
Функция Sum используется по умолчанию для полей числовых значений, размещаемых в сводной таблице, но вот как выбрать другую суммарную функцию:
-
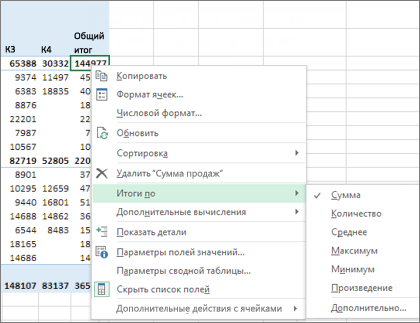
В сводной таблице щелкните правой кнопкой мыши поле значения, которое нужно изменить, и выберите команду «Суммировать значения по».
-
Щелкните функцию сводки.
Примечание: Функции сведения недоступны в сводных таблицах на базе источников данных OLAP.
Используйте эту функцию сводки:
Чтобы вычислить
:Сумма
Сумма значений. Используется по умолчанию для полей с числовыми значениями. Если поле содержит пустые или нечисловые (текстовые, даты или логические) значения при его добавлении в область «Значения» списка полей, сводная таблица использует для этого поля функцию Count.
После того как поле будет помещено в область значений, можно изменить суммарную функцию на Сумму, а пустые или нечисловые значения в сводной таблице будут изменены на 0, чтобы их можно было суммировать.
СЧЁТ
Количество заполненных полей. Функция сведения данных СЧЁТ работает так же, как СЧЁТЗ. СЧЁТ по умолчанию используется для пустых полей и полей с нечисловыми значениями.
Среднее
Среднее арифметическое.
Максимум
Наибольшее значение.
Минимум
Наименьшее значение.
Произведение
Произведение значений.
Смещенное отклонение
Оценка стандартного отклонения генеральной совокупности, где выборка является подмножеством всей генеральной совокупности.
СТАНДОТКЛОНП
Стандартное отклонение генеральной совокупности, которая содержит все сводимые данные.
ДИСП
Оценка дисперсии генеральной совокупности, где выборка является подмножеством всей генеральной совокупности.
Несмещенная дисперсия
Дисперсия генеральной совокупности, которая содержит все сводимые данные.
Число разных элементов
Число уникальных значений. Эта сводная функция работает только при использовании модели данных в Excel.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Нужна дополнительная помощь?
Программа Excel предлагает пользователям 6 итоговых функций, отображаемых в списке Итоги по, и 5 дополнительных итоговых функций, доступ к которым открывается после выбора параметра Дополнительно (More Options) в списке Итоги по. Эти функции описаны в следующем списке.
- Сумма (Sum). Суммирует все числовые данные.
- Количество (Count). Подсчитывает количество всех ячеек, включая ячейки с числами, текстом и ошибками. Операция эквивалентна функции Excel СЧЁТЗ ().
- Среднее (Average). Вычисляет среднее значение.
- Максимум (Мах). Выводит максимальное значение.
- Минимум (Min). Выводит минимальное значение.
- Произведение (Product). Перемножает все ячейки. Например, если ваш набор данных содержал ячейки с числами 3, 4 и 5, то в результате будет выведено значение 60.
- Количество чисел (Count Nums). Подсчитывает только числовые ячейки. Операция эквивалентна функции Excel СЧЁТ ().
- Смещенное, несмещенное отклонение (StdDev, StdDevP). Подсчитывает стандартное отклонение. Используйте операцию Несмещенное отклонение, если набор данных содержит генеральную совокупность. Если набор данных содержит выборку из генеральной совокупности, используйте операцию Смещенное отклонение.
- Смещенная, несмещенная дисперсия (Var, VarP). Подсчитывает статистическую дисперсию. Если ваши данные содержат только выборку из генеральной совокупности, используйте операцию Смешенная дисперсия для поиска расхождений в данных.
Стандартное отклонение позволяет выяснить, насколько тесно группируются результаты вокруг среднего значения.
1
Выборочная оценка математического
ожидания – выборочное среднее
в Excel
вычисляется с помощью
функция СРЗНАЧ,
при этом
реализуется формула

2
Оценка дисперсии – несмещенная
(исправленная) выборочная дисперсияможет быть получена с помощью функцииДИСП.
В Excel
реализована формула

3.
Несмещенное выборочное средние
квадратические отклонения (стандартное
отклонение)
вычисляется
с помощью функции
СТАНДОТКЛОН.
Вычисления
в Excel
выполнены по формуле

4
Выборочная (смещенная) оценка дисперсии
вычисляется с помощью
функция ДИСПР.
Результат
вычисления выборочных оценок
,
,
и
показан на рис.1.
… … … …
… … …
Рис.
1. Фрагмент листа Excel
с исходными данными и выборочными
оценками параметров.
2. Описательная статистика.
Выполните
процедуру Описательная
статистика.
В
главном меню Excel
выбрать: Данные
→ Анализ данных → Описательная статистика
→ ОК.
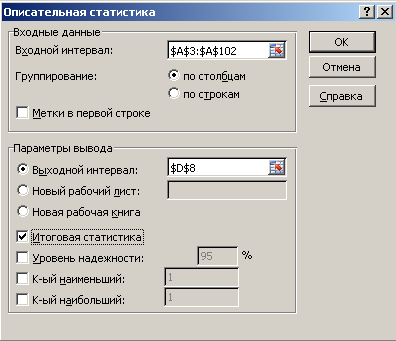
В
появившемся окне Описательная
статистика
ввести:
Входной
интервал –
100 случайных чисел в ячейках $A$3:
$A$102;
Группирование
— по столбцам;
Выходной
интервал –
адрес ячейки, с которой начинается
таблица Описательная
статистика – например,
$D$8;
Итоговая
статистика
– поставить галочку. ОК.
Рис.
2. Диалоговое окно Описательная
статистика
с заполненными полями ввода.
На
листе Excel
появится таблица – Столбец
1. В
таблице даются все необходимые параметры,
кроме моды Mo(X).
Рис.
3. Таблица Описательная
статистика
Таблица содержит
описательные статистики, в частности:
Среднее
– оценка математического ожидания
;
Стандартное
отклонение
– оценка среднего квадратического
отклонения;
Дисперсия
– выборочная исправленная дисперсия
;
Эксцесс
и Асимметричность
– оценки эксцесса и асимметрии;
Медиана
– оценка
медианы;
Мода
– оценка
моды, #Н/Д – нет данных (наиболее часто
встречающееся значение случайной
величины в выборке).
Приблизительное
равенство нулю оценок эксцесса и
асимметрии, и приблизительное равенство
оценки среднего оценке медианы дает
предварительное основание выбрать в
качестве основной гипотезы H0
распределения элементов генеральной
совокупности — нормальный закон.
Интервал
– размах выборки;
Минимум
– минимальное значение случайной
величины в выборке ;
Максимум
– максимальное значение случайной
величины в выборке .
Результаты
процедуры Описательная
статистика
потребуются в дальнейшем при построении
теоретического закона распределения.
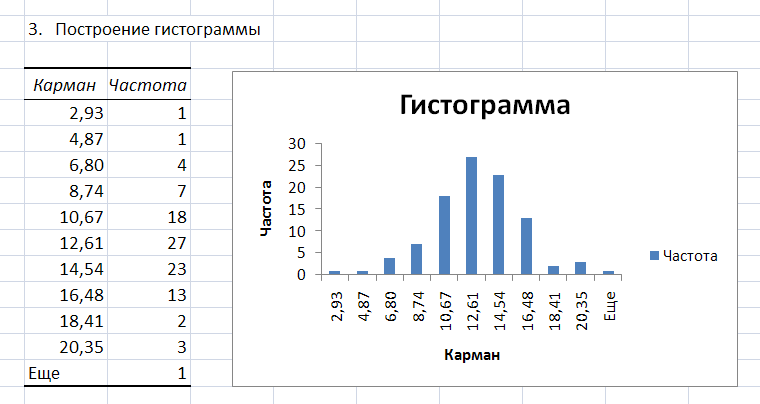
3. Построение гистограммы
В
главном меню Excel
выбрать Данные
→ Анализ данных → Гистограмма → ОК.
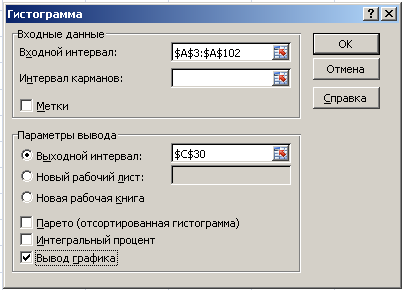
Далее
необходимо заполнить поля ввода в
диалоговом окне Гистограмма.
Входной
интервал:
100 случайных чисел в ячейках $A$3:
$A$102;
Интервал
карманов:
не
заполнять;
Выходной
интервал:
адрес ячейки, с которой начинается вывод
результатов процедуры Гистограмма;
Вывод
графика –
поставьте галочку.
Если
поле ввода Интервал
карманов не
заполняется, то процедура вычисляет
число интервалов группировки k
и границы интервалов автоматически по
формуле.
,
где,
скобки
означают – округление до целой части
числа в меньшую сторону.
В
рассматриваемом варианте n
= 100,
следовательно, k
= 11.
Действительно:
Рис.
4. Диалоговое окно Гистограмма.
В
результате выполнения процедуры
Гистограмма
появляется таблица, содержащая границы
xi
интервалов
группировки (столбец – Карман)
и частоту попадания случайных величин
выборки mi
в i–ый
интервал (столбец
–
Частота).
Справа от таблицы
– график гистограммы.
Рис.
5. Фрагмент листа Excel
с результатами процедуры Гистограмма.
По
виду гистограммы можно предположить
(принять гипотезу) о том, что выборка
случайных чисел подчиняется нормальному
закону распределения.
Далее,
для того чтобы убедиться в правильности
выбранной гипотезы (по крайней мере
визуально) надо, первое – построить
график гипотетического нормального
закона распределения, выбрав в качестве
параметров (математического ожидания
и среднего квадратического отклонении)
их оценки (среднее и стандартное
отклонение), и совместить график
гипотетического распределения с графиком
гистограммы.
И,
второе – используя критерий согласия
Пирсона установить справедливость
выбранной гипотезы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В Excel имеются функции, отдельно вычисляющие исправленную дисперсию s 2 по формуле (2.6) и исправленное стандартное отклонение s по формуле (2.8), генеральные и выборочные дисперсию Dг и 
Использование стандартных функций Excel возможно только при обработке несгруппированных данных. Если исходные данные уже сгруппированы, то вычисление дисперсий и стандартных отклонений следует производить по указанным выше формулам, используя функции суммирования и извлечения корня.
Для вычисления исправленной дисперсии s 2 по формуле (2.6) и исправленного стандартного отклонения s по формуле (2.8) имеются функции ДИСП (или VAR) и СТАНДОТКЛОН (или STDEV). Аргументом этих функций является набор чисел, как правило, заданный диапазоном ячеек, например, =ДИСП(В1:В48), если данные содержатся в интервале ячеек от В1 до В48.
Для вычисления выборочной (или генеральной) дисперсии по формуле (2.3) и стандартного отклонения по формуле (2.7) имеются функции ДИСПР (или VARP) и СТАНДОТКЛОНП (или STDEVP), соответственно.
Аргументы этих функций такие же как и для исправленной дисперсии.
Воспользуйтесь поиском по сайту:

Источник
Дисперсия и стандартное отклонение в EXCEL
history 4 октября 2016 г.
Вычислим в MS EXCEL дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.
Сначала рассмотрим дисперсию , затем стандартное отклонение .
Дисперсия выборки
Дисперсия выборки ( выборочная дисперсия, sample variance ) характеризует разброс значений в массиве относительно среднего .
Все 3 формулы математически эквивалентны.
Из первой формулы видно, что дисперсия выборки это сумма квадратов отклонений каждого значения в массиве от среднего , деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления дисперсии выборки используется функция ДИСП() , англ. название VAR, т.е. VARiance. С версии MS EXCEL 2010 рекомендуется использовать ее аналог ДИСП.В() , англ. название VARS, т.е. Sample VARiance. Кроме того, начиная с версии MS EXCEL 2010 присутствует функция ДИСП.Г(), англ. название VARP, т.е. Population VARiance, которая вычисляет дисперсию для генеральной совокупности . Все отличие сводится к знаменателю: вместо n-1 как у ДИСП.В() , у ДИСП.Г() в знаменателе просто n. До MS EXCEL 2010 для вычисления дисперсии генеральной совокупности использовалась функция ДИСПР() .
Дисперсию выборки можно также вычислить непосредственно по нижеуказанным формулам (см. файл примера ) =КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1) – обычная формула =СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1 ) – формула массива
Дисперсия выборки равна 0, только в том случае, если все значения равны между собой и, соответственно, равны среднему значению . Обычно, чем больше величина дисперсии , тем больше разброс значений в массиве.
Дисперсия выборки является точечной оценкой дисперсии распределения случайной величины, из которой была сделана выборка . О построении доверительных интервалов при оценке дисперсии можно прочитать в статье Доверительный интервал для оценки дисперсии в MS EXCEL .
Дисперсия случайной величины
Чтобы вычислить дисперсию случайной величины, необходимо знать ее функцию распределения .
Для дисперсии случайной величины Х часто используют обозначение Var(Х). Дисперсия равна математическому ожиданию квадрата отклонения от среднего E(X): Var(Х)=E[(X-E(X)) 2 ]
Если случайная величина имеет дискретное распределение , то дисперсия вычисляется по формуле:
где x i – значение, которое может принимать случайная величина, а μ – среднее значение ( математическое ожидание случайной величины ), р(x) – вероятность, что случайная величина примет значение х.
Если случайная величина имеет непрерывное распределение , то дисперсия вычисляется по формуле:
Для распределений, представленных в MS EXCEL , дисперсию можно вычислить аналитически, как функцию от параметров распределения. Например, для Биномиального распределения дисперсия равна произведению его параметров: n*p*q.
Примечание : Дисперсия, является вторым центральным моментом , обозначается D[X], VAR(х), V(x). Второй центральный момент — числовая характеристика распределения случайной величины, которая является мерой разброса случайной величины относительно математического ожидания .
Примечание : О распределениях в MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
Размерность дисперсии соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг 2 . Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из дисперсии – стандартное отклонение .
Некоторые свойства дисперсии :
Var(Х+a)=Var(Х), где Х — случайная величина, а — константа.
Var(Х)=E[(X-E(X)) 2 ]=E[X 2 -2*X*E(X)+(E(X)) 2 ]=E(X 2 )-E(2*X*E(X))+(E(X)) 2 =E(X 2 )-2*E(X)*E(X)+(E(X)) 2 =E(X 2 )-(E(X)) 2
Это свойство дисперсии используется в статье про линейную регрессию .
Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y — случайные величины, Cov(Х;Y) — ковариация этих случайных величин.
Если случайные величины независимы (independent), то их ковариация равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе стандартной ошибки среднего .
Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1) 2 Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения доверительного интервала для разницы 2х средних .
Примечание : квадратный корень из дисперсии случайной величины называется Среднеквадратическое отклонение (или другие названия — среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение, стандартное отклонение, стандартный разброс).
Стандартное отклонение выборки
Стандартное отклонение выборки — это мера того, насколько широко разбросаны значения в выборке относительно их среднего .
По определению, стандартное отклонение равно квадратному корню из дисперсии :
Стандартное отклонение не учитывает величину значений в выборке , а только степень рассеивания значений вокруг их среднего . Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х выборок: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается. Для таких случаев используется Коэффициент вариации (Coefficient of Variation, CV) — отношение Стандартного отклонения к среднему арифметическому , выраженного в процентах.
В MS EXCEL 2007 и более ранних версиях для вычисления Стандартного отклонения выборки используется функция =СТАНДОТКЛОН() , англ. название STDEV, т.е. STandard DEViation. С версии MS EXCEL 2010 рекомендуется использовать ее аналог =СТАНДОТКЛОН.В() , англ. название STDEV.S, т.е. Sample STandard DEViation.
Кроме того, начиная с версии MS EXCEL 2010 присутствует функция СТАНДОТКЛОН.Г() , англ. название STDEV.P, т.е. Population STandard DEViation, которая вычисляет стандартное отклонение для генеральной совокупности . Все отличие сводится к знаменателю: вместо n-1 как у СТАНДОТКЛОН.В() , у СТАНДОТКЛОН.Г() в знаменателе просто n.
Стандартное отклонение можно также вычислить непосредственно по нижеуказанным формулам (см. файл примера ) =КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Другие меры разброса
Функция КВАДРОТКЛ() вычисляет с умму квадратов отклонений значений от их среднего . Эта функция вернет тот же результат, что и формула =ДИСП.Г( Выборка )*СЧЁТ( Выборка ) , где Выборка — ссылка на диапазон, содержащий массив значений выборки ( именованный диапазон ). Вычисления в функции КВАДРОТКЛ() производятся по формуле:
Функция СРОТКЛ() является также мерой разброса множества данных. Функция СРОТКЛ() вычисляет среднее абсолютных значений отклонений значений от среднего . Эта функция вернет тот же результат, что и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка) , где Выборка — ссылка на диапазон, содержащий массив значений выборки.
Вычисления в функции СРОТКЛ () производятся по формуле:
Источник
Выборочная дисперсия. Исправленная дисперсия
Оценка параметров генеральной совокупности
Выборочное среднее
Пусть имеется случайная выборка объема n, представленная вариационным рядом <(xj, nj)>, где xj — варианты, nj — частоты, j = 1, 2, …, m. Если мы имеем дело с интервальным вариационным рядом, то xj — середины интервалов.
Выборочное среднее значение определяется по формуле

Если выборка не сгруппирована, то выборочная средняя определяется по формуле
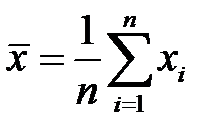
Выборочное среднее 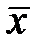
Если у генеральной совокупности генеральная средняя равна a и среднеквадратическое отклонение равно σ, то среднеквадратическое отклонение выборочной средней 

Среднеквадратическое отклонение выборочной средней 

где N — объем генеральной совокупности.
Для вычисления выборочной средней для не сгруппированной выборки в программе Excel можно воспользоваться следующей функцией (которая вычисляет среднее арифметическое):
Число1, число2, . — это от 1 до 30 аргументов, для которых вычисляется среднее.
- Аргументы должны быть либо числами, либо именами, массивами или ссылками, содержащими числа.
- Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.
Если выборка представлена вариационным рядом, то для вычисления выборочного среднего можно воспользоваться функцией СУММПРОИЗВЕД(массив1;массив2;…), которая вычисляет сумму произведений соответствующих элементов массивов массив1, массив2 и т.д.
Пример 3.1. Найти выборочное среднее для выборки из 10 числовых значений, записанных в ячейках А2:А11 (см. рис. 3.1).
Решение. Введите в ячейку А12 формулу =СРЗНАЧ(А2:А11). Получим значение 1,9.
Пример 3.2. Найти выборочное среднее для выборки, представленной вариационным рядом из 10 числовых значений вариант, записанных в ячейках С2:С11, и 10 значений частот, записанных в ячейках D2:D11 .
Решение. Введите в ячейку C12 формулу
Получим значение 3,571429.
Выборочная дисперсия. Исправленная дисперсия
Выборочная дисперсия s 2 для сгруппированной в вариационный ряд выборки определяется по формуле
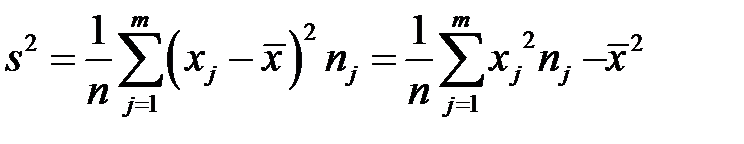
Исправленная дисперсия 

Если выборка не сгруппирована, то выборочная дисперсия s 2 определяется по формуле

а исправленная дисперсия 

Исправленная дисперсия является несмещенной оценкой генеральной дисперсии, т.е. математическое ожидание исправленной дисперсии равно генеральной дисперсии.
В программе Excel для вычисления выборочной дисперсии для выборки, не сгруппированной в вариационный ряд, предназначена функция
Число1, число2. — от 1 до 30 числовых аргументов, соответствующих выборке (числа или диапазоны ячеек).
ДИСПР предполагает, что аргументы представляют всю генеральную совокупность. Если данные представляют только выборку из генеральной совокупности, то дисперсию следует вычислять, используя функцию ДИСП.
Формула для ДИСПР имеет вид (3.7).
Для вычисления исправленной дисперсии предназначена функция
Формула для ДИСП имеет вид (3.8).
Обратите внимание на имена этих функций, можно подумать, что ДИСПР() вычисляет исправленную дисперсию, а ДИСП() — выборочную, тогда как на самом деле функция ДИСП() вычисляет исправленную дисперсию, а ДИСПР() — выборочную.
Источник
Adblock
detector