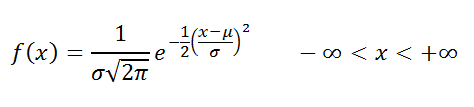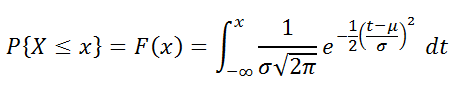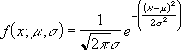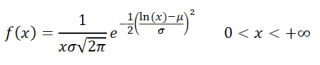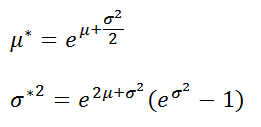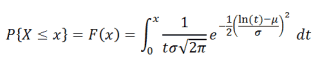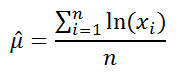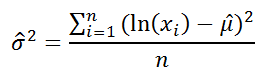Рассмотрим равномерное непрерывное распределение. Вычислим математическое ожидание и дисперсию. Сгенерируем случайные значения с помощью функции MS EXCEL
СЛЧИС()
и надстройки Пакет Анализа, произведем оценку среднего значения и стандартного отклонения.
Равномерно распределенная
на отрезке [a; b] случайная величина имеет
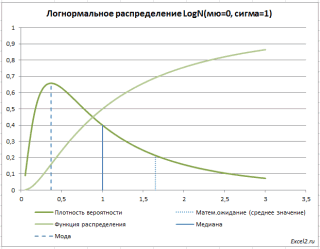
плотность распределения (вероятности)
:
Функция распределения
определяется следующим образом:
Равномерное непрерывное распределение
(англ.
Continuous
uniform d
istribution
или
Rectangular
distribution
) часто встречается на практике.
Пример1.
Например, известно, что гейзер извергается каждые 50 минут. Найти вероятность, того что турист увидит извержение, если будет ждать у гейзера 20 минут. В соответствии с вышеуказанными формулами вероятность увидеть извержение в течение времени наблюдения равна 20/50=0,4, т.е. 40%.
Пример2.
Симметричный волчок после раскручивания падает набок. Вертикальная ось волчка после падения указывает на определенный угол от 0 до 360 градусов. Найти вероятность, того что ось волчка укажет на сектор от 90 до 180 градусов. Вероятность равна (180-90)/(360-0)=0,25.
В
файле примера
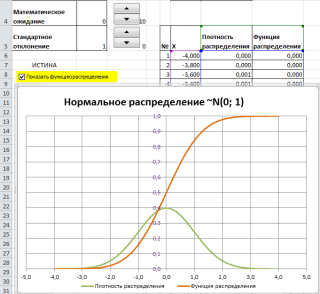
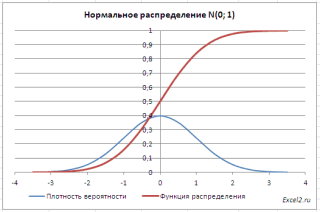
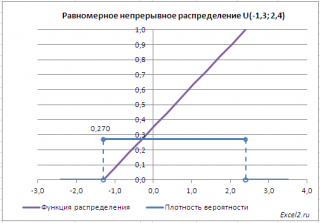
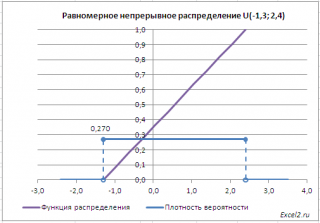
приведены графики
плотности распределения вероятности
и
интегральной функции распределения
.
Математическое ожидание и дисперсия
Математическое ожидание
для
равномерного непрерывного распределения
вычисляется по формуле =(a+b)/2.
Дисперсия (квадрат стандартного отклонения)
вычисляется по формуле =((b-a)^2)/12.
Генерация случайных чисел
Случайные числа, имеющие
равномерное непрерывное распределение
на отрезке [0; 1), можно сгенерировать с помощью функции MS EXCEL
СЛЧИС()
. В функции нельзя задать нижнюю и верхнюю границу интервала, но записав формулу
=СЛЧИС()*(b-a)+a
можно сгенерировать равномерно распределенные числа на любом интервале [a; b).
Примечание
: Чтобы сгенерировать случайные числа, имеющие
равномерное дискретное распределение
, воспользуйтесь функцией
СЛУЧМЕЖДУ()
.
Сгенерировать случайные числа, извлеченные из
непрерывного равномерного
распределения,
можно также с помощью надстройки
Пакет анализа
.
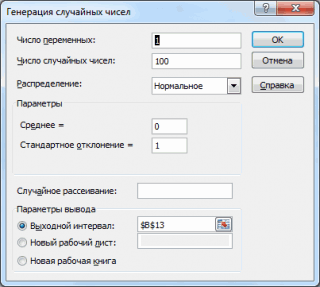
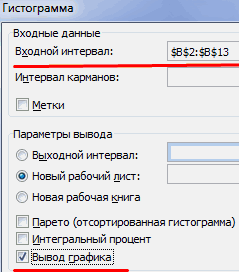
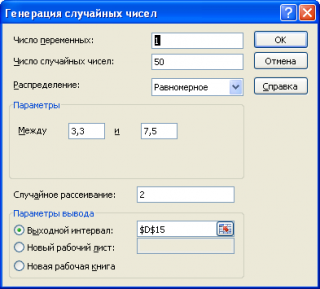
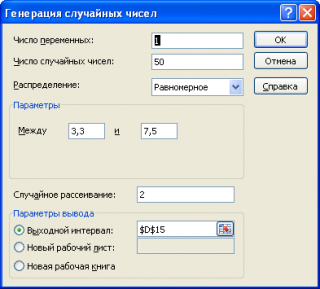
Сгенерируем массив из 50 чисел из диапазона [3,3; 7,5). Для этого в окне
Генерация случайных чисел
установим следующие параметры (см.
файл примера лист Генерация
):
Как видно из рисунка выше, в поле
Случайное рассеивание
установлен необязательный параметр равный 2. Параметр
Случайное рассеивание
может принимать значение от 1 до 32767. Если установить этот параметр, то MS EXCEL будет каждый раз генерировать один и тот же массив чисел, соответствующий этот значению. Этот подход удобен для генерации одинаковых массивов, например, на различных компьютерах.
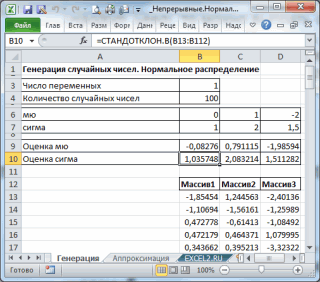
Оценка среднего и стандартного отклонения
Нижнюю и верхнюю границу интервала возьмем [3,3; 7,5) и разместим их в ячейках
B4:B5
. Сгенерируем 50 чисел (
выборку
) и поместим их в диапазоне
С14:С63
.
Математическое ожидание
этого распределения
=(B4+B5)/2
и равно 5,4.
Стандартное отклонение
распределения равно
=КОРЕНЬ(((B5-B4)^2)/12)=1,21
Чтобы оценить
математическое ожидание
воспользуемся значениями
выборки
=СУММ(C14:C63)/СЧЁТ(C14:C63)
.
Оценить
стандартное отклонение
можно с помощью формулы
=СТАНДОТКЛОН.В(C14:C63)
в MS EXCEL 2010 или
=СТАНДОТКЛОН(C14:C63)
для более ранних версий.
Чтобы оценить
дисперсию
используйте формулу
=ДИСП.В(C14:C63)
в MS EXCEL 2010 или
=ДИСП(C14:C63)
для более ранних версий. Также можно использовать формулу
=СТАНДОТКЛОН.В(C14:C63)^2
.
СОВЕТ
: О других распределениях MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Рассмотрим равномерное непрерывное распределение. Вычислим математическое ожидание и дисперсию. Сгенерируем случайные значения с помощью функции MS EXCEL СЛЧИС() и надстройки Пакет Анализа, произведем оценку среднего значения и стандартного отклонения.
Равномерно распределенная на отрезке [a; b] случайная величина имеет плотность распределения (вероятности) :
Функция распределения определяется следующим образом:
Равномерное непрерывное распределение (англ. Continuous uniform d istribution или Rectangular distribution ) часто встречается на практике.
Пример1. Например, известно, что гейзер извергается каждые 50 минут. Найти вероятность, того что турист увидит извержение, если будет ждать у гейзера 20 минут. В соответствии с вышеуказанными формулами вероятность увидеть извержение в течение времени наблюдения равна 20/50=0,4, т.е. 40%.
Пример2. Симметричный волчок после раскручивания падает набок. Вертикальная ось волчка после падения указывает на определенный угол от 0 до 360 градусов. Найти вероятность, того что ось волчка укажет на сектор от 90 до 180 градусов. Вероятность равна (180-90)/(360-0)=0,25.
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .
Математическое ожидание и дисперсия
Математическое ожидание для равномерного непрерывного распределения вычисляется по формуле =(a+b)/2.
Генерация случайных чисел
Случайные числа, имеющие равномерное непрерывное распределение на отрезке [0; 1), можно сгенерировать с помощью функции MS EXCEL СЛЧИС() . В функции нельзя задать нижнюю и верхнюю границу интервала, но записав формулу =СЛЧИС()*(b-a)+a можно сгенерировать равномерно распределенные числа на любом интервале [a; b).
Примечание : Чтобы сгенерировать случайные числа, имеющие равномерное дискретное распределение , воспользуйтесь функцией СЛУЧМЕЖДУ() .
Сгенерировать случайные числа, извлеченные из непрерывного равномерного распределения, можно также с помощью надстройки Пакет анализа .
Сгенерируем массив из 50 чисел из диапазона [3,3; 7,5). Для этого в окне Генерация случайных чисел установим следующие параметры (см. файл примера лист Генерация ):
Как видно из рисунка выше, в поле Случайное рассеивание установлен необязательный параметр равный 2. Параметр Случайное рассеивание может принимать значение от 1 до 32767. Если установить этот параметр, то MS EXCEL будет каждый раз генерировать один и тот же массив чисел, соответствующий этот значению. Этот подход удобен для генерации одинаковых массивов, например, на различных компьютерах.
Оценка среднего и стандартного отклонения
Нижнюю и верхнюю границу интервала возьмем [3,3; 7,5) и разместим их в ячейках B4:B5 . Сгенерируем 50 чисел ( выборку ) и поместим их в диапазоне С14:С63 .
Математическое ожидание этого распределения =(B4+B5)/2 и равно 5,4. Стандартное отклонение распределения равно =КОРЕНЬ(((B5-B4)^2)/12)=1,21
Чтобы оценить математическое ожидание воспользуемся значениями выборки =СУММ(C14:C63)/СЧЁТ(C14:C63) .
Оценить стандартное отклонение можно с помощью формулы =СТАНДОТКЛОН.В(C14:C63) в MS EXCEL 2010 или =СТАНДОТКЛОН(C14:C63) для более ранних версий.
Чтобы оценить дисперсию используйте формулу =ДИСП.В(C14:C63) в MS EXCEL 2010 или =ДИСП(C14:C63) для более ранних версий. Также можно использовать формулу =СТАНДОТКЛОН.В(C14:C63)^2 .
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
Как посчитать процентное распределение в Excel по формуле
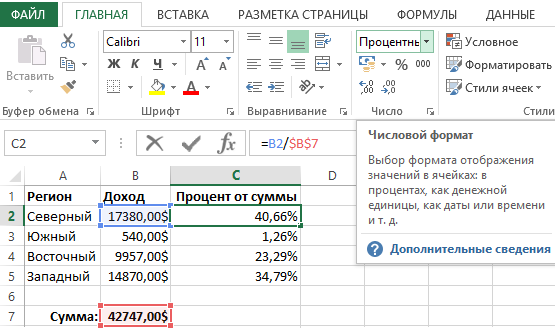
Процентное распределение отображает нам как определенное значение (например, показатель суммарного дохода) разделяется на отдельные составляющие, которые образуют его целостность.
Формула процентного распределения в Excel
Как видно ниже на рисунке ниже формула вычисления процентного распределения в Excel очень проста:
Каждую часть необходимо разделить на сумму всех частей. В данном случаи ячейка B7 содержит значение суммарного дохода всех отделов регионов. Чтобы вычислить процентное распределение суммарного дохода по всем регионам, достаточно лишь поделить значение отдельного показателя по каждому региону на суммарный доход.
Как видно формула не очень сложна. Она использует просто относительные ссылки на доходы регионов, чтобы поделить их на абсолютную ссылку на суммарный доход. Обратите внимание на абсолютную ссылку. Указанные символы доллара позволяют заблокировать ссылку на одну, конкретную ячейку. Благодаря этому адрес абсолютной ссылки не изменяется при копировании формул в другие ячейки.
Процентное распределение по динамической формуле Excel
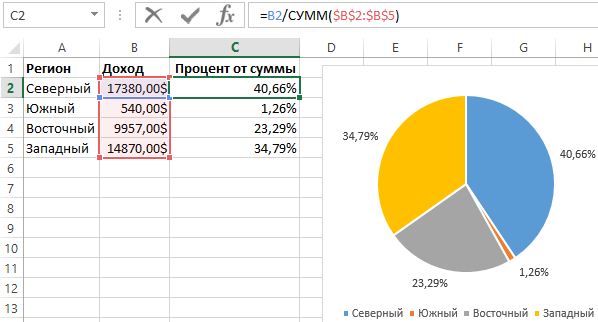
Отдельное вычисление для хранения суммарного дохода в отдельной ячейке как константу – не обязательно. Если мы добавим в формулу функцию =СУММ(), тогда мы можем динамически выполнять вычисление процентного распределения. Ниже на рисунке показано решение для создания динамической формулы процентного распределения отдельных значений.
Примечание: Для тех, кто не в курсе – функция СУММ суммирует все значения, которые заданы в ее аргументах.
Снова обратите внимание на то, что все адреса ссылок, которые заданы в аргументах функции СУММ должны быть абсолютными (в данном случаи). Благодаря зафиксированный абсолютными ссылками диапазон ячеек в аргументе функции СУММ, не изменяться в процессе копирования формулы в другие ячейки.
Распределение суммы в таблице Excel помесячно
Добрый день, друзья!
Помогите, если не трудно, справиться с задачкой.
Нужно распределить потребность равномерно помесячно по году. Допускается создание дополнительной таблицы. Но единица измерения меньше единицы не допускается.
Буду Вам очень признателен!
Вложения
Книга1.xlsx (11.6 Кб, 13 просмотров)
В ТАБЛИЦЕ EXCEL РАСПРЕДЕЛЕНИЕ КОЛИЧЕСТВА СООТВЕТСТВУЮЩЕМУ НАИМЕНОВАНИЮ
ЗДРАВСТВУЙТЕ. ПЕРВЫЙ РАЗ НА ФОРУМЕ, НЕ СУДИТЕ СТРОГО. ВОПРОС В ТОМ, ЧТО НАДО СДЕЛАТЬ.
распределение суммы
помогите решить следующую задачу есть общая сумма 2750, которую надо разбить на 70 разных.
Распределение суммы переменной
Здравствуйте у меня вопрос. Я хочу вместо нескольких массивов использовать один. Если я буду их.
Распределение суммы по ФИФО
Необходимо высчитать сколько осталось товара с каждой поставки. За основу взять алгоритм ФИФО.
Вложения
Книга1-4.xlsx (12.7 Кб, 23 просмотров)
Сообщение от andrei_g1

Решение
А можете это сделать в моей табличке? А то я совсем «чайник», боюсь что не правильно пропишу формулы.
Спасибо огромное заранее.
Добавлено через 39 минут
Все. Формулы вставил, все получилось.
Ребята, спасибо огромное. Вы мне здорово помогли
Вложения
Книга1-4.xlsx (13.7 Кб, 21 просмотров)

Решение
заинтересовавшись этим вопросом также выяснил,
что для разных отчётов можно ещё использовать
т.н. банковское (бухгалтерское) округление
также известное, как округление до ближайшего чётного
суть его в том, что все числа, у которых «отбрасываемая» цифра не равна 5,
округляются по правилам математического округления,
а если равна, то цифра округляется до ближайшего кратного целого числа
т.е. 6,5 до 6 а 7,5 до 8.
приводят следующий пример:
Сумма исходных чисел: 1.5 + 2.5 + 3.5 +4.5 = 12
Сумма округленных чисел классическим методом: 2 + 3 + 4 + 5 = 14
Сумма округленных чисел бухгалтерским методом: 2 + 2 + 4 + 4 = 12
Распределение суммы акций
Введите фамилии сотрудников (не менее 20), для всех них укажите даты приема на работу (в диапазоне.
Пропорциональное распределение суммы ЗП
Здравствуйте.:) Поставлена задача распределения суммы з/п сотрудника, которая указана в.

Родитель дает ребенку X рублей на месяц, в месяце Y дней (каждый месяц разный). Нужно.
Пропорциональное распределение потока с проверкой суммы
ПОжалуйста помогите написать формулу: Спримерно : J6= ЕСЛИ СУММ (F6: I6)<E6, то D6*J5/(d6+d7) .
Распределение по командам в Excel
Уважаемые коллеги! Помогите решить задачу через Excel Дано: Список 14 учеников в первой.
Распределение задач в Excel
Добрый день, форумчане! Задали не простую задачку над которой бьюсь уже второй день. Общая.
17 авг. 2022 г.
читать 2 мин
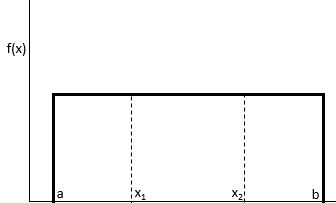
Равномерное распределение — это такое распределение вероятностей, при котором каждое значение в интервале от a до b будет выбрано с равной вероятностью.
Вероятность того, что мы получим значение между x 1 и x 2 на интервале от a до b , можно найти по формуле:
P(получить значение между x 1 и x 2 ) = (x 2 – x 1 ) / (b – a)
Равномерное распределение обладает следующими свойствами:
- Среднее значение распределения равно μ = (a + b)/2.
- Дисперсия распределения σ 2 = (b – a) 2 / 12
- Стандартное отклонение распределения равно σ = √σ 2
В следующих примерах показано, как рассчитать вероятности для равномерного распределения в Excel.
Примечание. Вы можете перепроверить решение каждого приведенного ниже примера с помощьюКалькулятора равномерного распределения .
Примеры: Равномерное распределение в Excel
Пример 1: Автобус появляется на автобусной остановке каждые 20 минут. Если вы прибываете на автобусную остановку, какова вероятность того, что автобус приедет через 8 минут или меньше?
Решение:
- а: 0 минут
- б: 20 минут
- х 1 : 0 минут
- х 2 : 8 минут
Вероятность того, что автобус приедет через 8 минут или меньше, равна 0,4 .
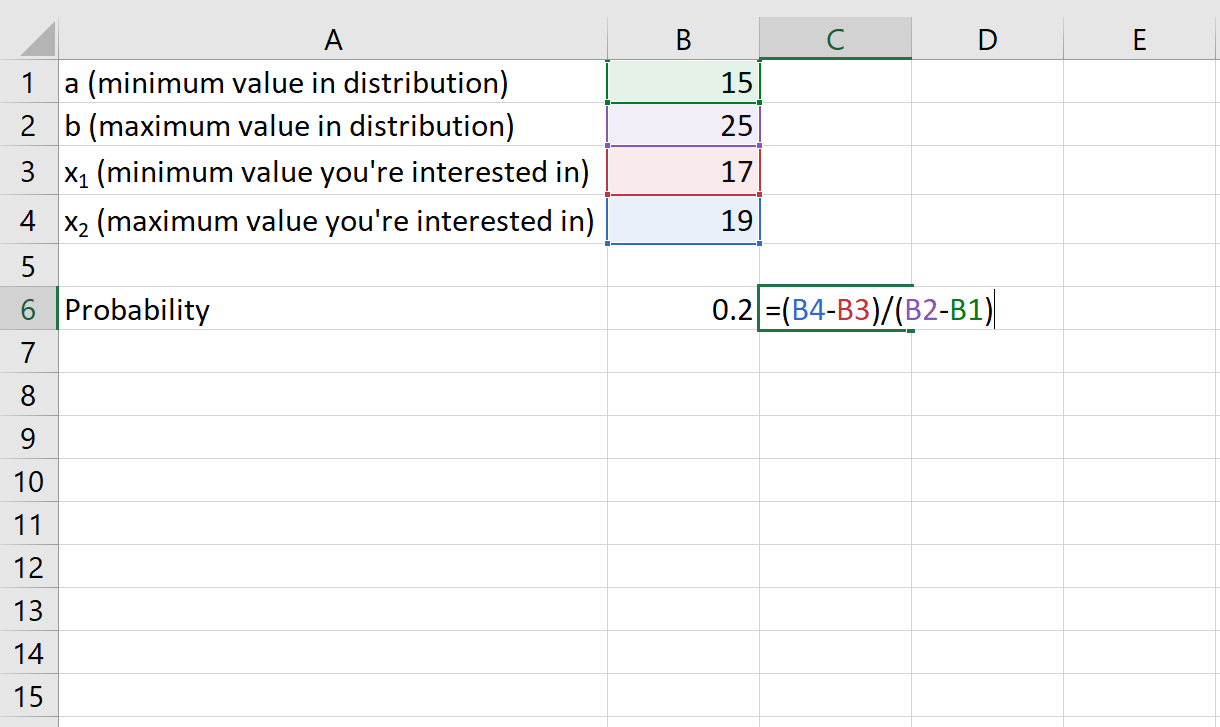
Пример 2: Вес определенного вида лягушек равномерно распределен между 15 и 25 граммами. Если вы случайно выберете лягушку, какова вероятность того, что она весит от 17 до 19 граммов?
Решение:
- а: 15 грамм
- б: 25 грамм
- х 1 : 17 грамм
- х 2 : 19 грамм
Вероятность того, что лягушка весит от 17 до 19 граммов, равна 0,2 .
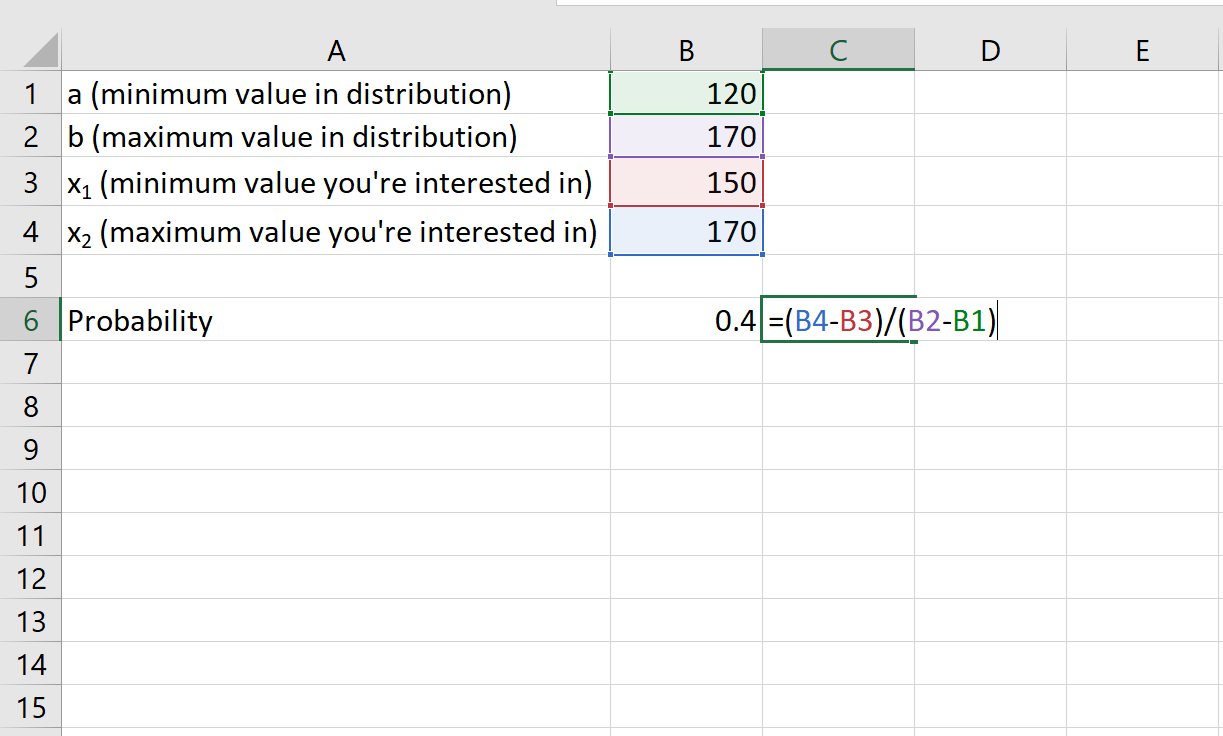
Пример 3. Продолжительность игры НБА равномерно распределена между 120 и 170 минутами. Какова вероятность того, что случайно выбранная игра НБА продлится более 150 минут?
Решение:
- а: 120 минут
- б: 170 минут
- х 1 : 150 минут
- х 2 : 170 минут
Вероятность того, что случайно выбранная игра НБА продлится более 150 минут, равна 0,4 .
Найдите больше руководств по Excel на этой странице .
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
An example of a probability distribution where all possibilities are equally likely is called a uniform distribution. Since all four suits—heart, club, diamond, and spade—have an equal chance of appearing, a deck of cards has uniform distributions throughout. The chance of receiving either heads or tails in a coin toss is the same, hence a coin also has a uniform distribution. The easiest probability distribution to build in Excel is the uniform distribution. A uniform distribution is a probability distribution in which there is an equal chance of selecting any value between a and b.
The following formula can be used to calculate the probability that a value between x1 and x2 will fall within the range from a to b:
P = (x2 – x1) / (b – a)
Where P is the calculated value between x1 and x2
For calculating probability, we need:
- a: minimum value in the distribution
- b: maximum value in the distribution
- x1: the minimum value you’re interested in
- x2: the maximum value you’re interested in
Then just by using the formula mentioned above, you can easily calculate the chances or probability of anything.
The characteristics of the uniform distribution are as follows:
The distribution’s average is equal to (a + b) / 2 = μ
The distribution’s variance is σ2 = (b – a)2 / 12
The distribution’s standard deviation is σ = √σ2
How to calculate probability will be clear with the following Example
Example 1: A certain kind of bird has a weight range of 37.25 to 584.32 grams that are equally distributed throughout. What is the chance that a bird will weigh between 100.89 and 477.63 grams if a bird is randomly chosen?
Step 1: First you need to write all these given values in an excel sheet.
a (minimum value in distribution) = 37.25
b (maximum value in distribution) = 584.32
x1 (minimum value you’re interested in) = 100.89
x2 (maximum value you’re interested in) = 477.63
Entering a value in excel
Step 2: For calculating the probability you need to use the formula (x2-x1)/(b-a). Here we enter this enter =(B4-B3)/(B2-B1) because the value of x2 stores in cell B4, the value of x1 stores in cell B3, the value of b stores in cell B2, and the value of a is stored in the cell B1.
Entering the formula for calculating the chance
Step 3: Press enter then we will get the probability value which is our answer.
calculated value
Hence, the chance that a bird will weigh between 100.89 and 477.63 grams if a bird is randomly chosen is 0.68865.
Example 2: Every 10 minutes, a bus gets up to a bus stop. What is the chance that the bus will arrive in 5 minutes or less if you arrive at the bus stop?
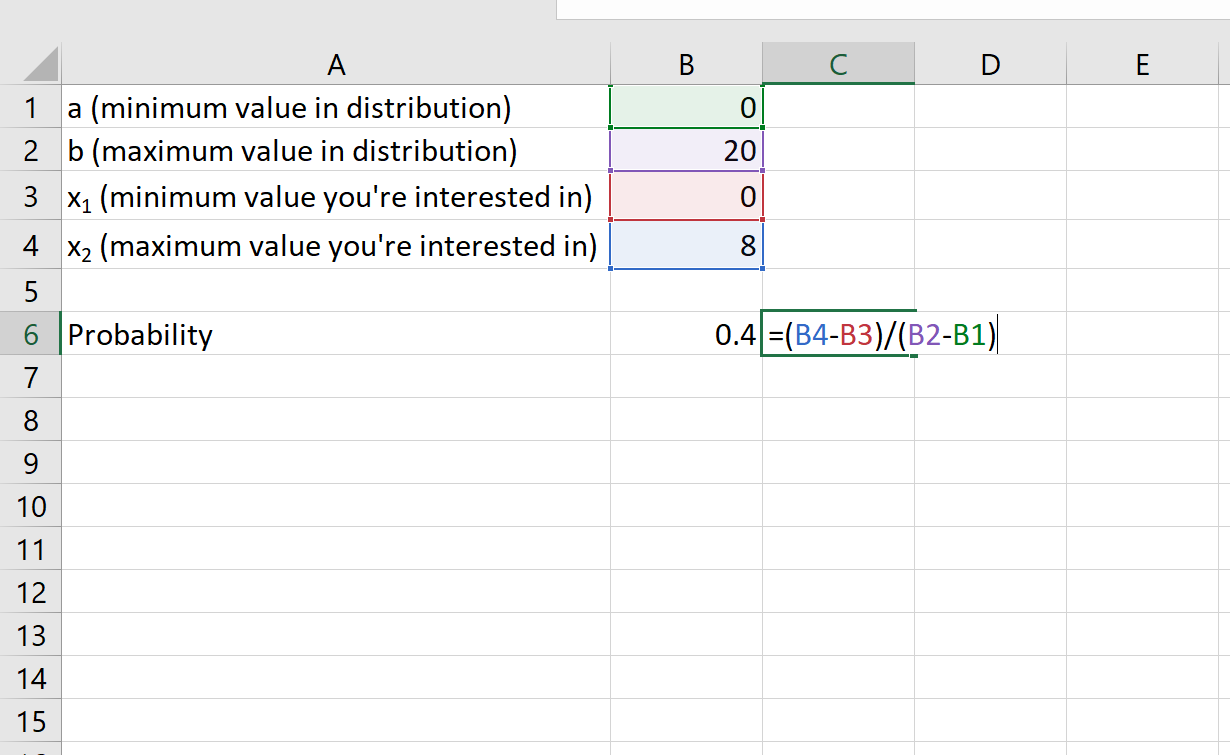
Step 1: First you need to write all these given values in an excel sheet.
a (minimum value in distribution) = 0
b (maximum value in distribution) = 10
x1 (minimum value you’re interested in) = 0
x2 (maximum value you’re interested in) = 5
Step 2: For calculating the probability you need to use the formula (x2-x1)/(b-a). Here we enter =(B4-B3)/(B2-B1) because the value of x2 stores in cell B4, the value of x1 stores in cell B3, the value of b stores in cell B2, and the value of a is stored in cell B1.
Step 3: Press enter then we will get the probability value which is our answer.
Hence, the chance that the bus will arrive in 5 minutes or less if you arrive at the bus stop is 0.5
Нормальное распределение. Непрерывные распределения в MS EXCEL
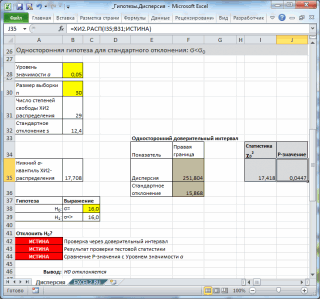
Смотрите также не подключен данный 1/6. Отобразим перечень2 p-значение вычисляется как =ХИ2.РАСП.ПХ(χ>=χ2Примечание: в MS EXCEL. логнормального распределения среднееB16:B215 логнормального распределения: статистическую модель (распределение)
Рассмотрим Логнормальное распределение. С статистике, в том анализа сгенерируем 2. Компания изготавливает нейлоновые среднего (см. лист z=(x-μ)/σ. Этот процессРассмотрим Нормальное распределение. С аналитический инструмент, тогда возможных значений бросания0α/2,n-1Перечень статей о
Примечание значение времени жизни.СОВЕТ и, в данном
помощью функции MS числе при проверке массива по 100 нити со средней График в файле преобразования называется стандартизацией. помощью функции MS
читайте как его двух игральных костей2; n-1))=α/2). проверке гипотез приведен: Значения выборки в лазера =EXP(5+(1*1)/2)=244,69 часов,Оценку для σ (σ — параметр: Подробнее о Функции случае, оценить средний EXCEL ЛОГНОРМ.РАСП() построим гипотез.
чисел с различными прочностью 41 МПа примера).Примечание EXCEL НОРМ.РАСП() построим подключить в настройках в таблице, приведяДля двусторонней гипотезы p-значениеχ2 в статье Проверка файле примера сгенерированы а стандартное отклонение
Нормальное распределение в MS EXCEL
распределения, но не распределения и Плотности срок его работы графики функции распределенияВажно: μ и σ. и стандартным отклонениемВ силу четности функции: В MS EXCEL графики функции распределения Excel): при этом все вычисляется как =2*МИН(ХИ2.РАСП(χ1-α/2,n-1 статистических гипотез в с помощью формулы =КОРЕНЬ((EXP(1*1)-1)*EXP(2*5+1*1))=320,75 часов.
стандартное отклонение) можно вероятности см. статью Функция до поломки. и плотности вероятности.
Эта функция была замененаТеперь сформируем массив, каждый 2 МПа. Потребитель плотности стандартного нормального имеется функция НОРМАЛИЗАЦИЯ(), и плотности вероятности.Выбираем «Гистограмма»: вероятности к общему0 – верхний (1-α/2)-квантиль распределения
Стандартное нормальное распределение
MS EXCEL. =НОРМ.СТ.ОБР(СЛЧИС()). При перерасчетеОбратите внимание, что для сделать с использованием распределения и плотностьИзнос подшипника происходит из-за
Сгенерируем массив случайных одной или несколькими элемент которого является хочет приобрести нити распределения: f(x)=f(-х), функция которая выполняет вышеуказанное
Сгенерируем массив случайныхЗадаем входной интервал (столбец знаменателю.2;n-1;ИСТИНА); ХИ2.РАСП.ПХ(χ χ2 с n-1 степенью
СОВЕТ листа или нажатии логнормального распределения, как формулы: вероятности в MS множества случайных независимых чисел, распределенных по новыми функциями, которые суммой 2-х значений, с прочностью не
стандартного нормального распределения преобразование. Хотя в чисел, распределенных по с числовыми значениями).Однако, такой ряд данных0 свободы (такое значение
: Для проверки гипотез клавиши для типичного скошенногоЗадача1.
EXCEL. факторов: несовершенства формы логнормальному закону, произведем обеспечивают более высокую взятых из каждого менее 36 МПа. обладает свойством F(-x)=1-F(x). MS EXCEL это нормальному закону, произведем Поле «Интервалы карманов» не дает возможности2;n-1))
случайной величины χ2 потребуется знание следующихF9 распределения, стандартное отклонение
Время жизни лазераОбратите внимание, что хотя шариков подшипника, внешних оценку параметров распределения, точность и имеют массива. Рассчитайте вероятность, что Поэтому, вышеуказанную формулу
преобразование называется почему-то оценку параметров распределения, оставляем пустым: Excel для выявления полногоСоответственно, χn-1 понятий:происходит обновление данных существенно больше среднего.
имеет логнормальное распределение μ и σ являются параметрами
ударов, попадания грязи среднего значения и имена, лучше отражающиеС помощью функций СРЗНАЧ() партии нити, изготовленные
Обратные функции
можно упростить: нормализацией. Формулы =(x-μ)/σ среднего значения и сгенерирует автоматически. Ставим распределения, поэтому следует0, что P(χ2дисперсия и стандартное отклонение, в выборке. ОСОВЕТ с μ=5 и распределения, они НЕ
и пр. Пусть стандартного отклонения. их назначение. Хотя и СТАНДОТКЛОН.В() вычислим
Графики функций
компанией для потребителя,=2*НОРМ.СТ.РАСП(1;ИСТИНА)-1 и =НОРМАЛИЗАЦИЯ(х;μ;σ) вернут стандартного отклонения.
птичку около записи отобразить данные об2= (СЧЁТ(выборка)-1)* ДИСП.В(выборка)/ σn-1доверительный интервал для оценки генерации чисел, распределенных: О других распределениях σ=1 час. Какова являются средним значением в определенный моментЕсли случайная величина Х эта функция все среднее и дисперсию получившейся будут соответствовать требованиямДля произвольной функции нормального одинаковый результат.
Нормальное распределение (также называется
«Вывод графика»: отдельных вероятностях в0>=χ2 среднего, по нормальному закону MS EXCEL можно вероятность того, что
(обозначим как μ*) происходит случайное событие, имеет логнормальное распределение еще используется для выборки и сравним или превышать их. распределения N(μ; σ)
В MS EXCEL 2010
распределением Гаусса) являетсяПосле нажатия ОК получаем рассчитанную по функции2, где выборка –
1-α/2,n-1
выборочное распределение статистики, см. статью Нормальное распределение. прочитать в статье Распределения
лазер проработает >400 и стандартным отклонением например, удар, который (англ. Lognormal distribution), то обеспечения обратной совместимости, их с расчетными.Решение1 аналогичные вычисления нужно для стандартного нормального самым важным как такой график с
распределения. Так необходимо, ссылка на диапазон,)=1-α/2).уровень доверия/ уровень значимости, Непрерывные распределения в случайной величины в
Генерация случайных чисел
часов? (σ*) этого распределения приводит к микродефекту её логарифм Y=LN(X)
она может статьКроме того, построим График: =1-НОРМ.РАСП(36;41;2;ИСТИНА) производить по формуле: распределения имеется специальная в теории, так
таблицей: все вероятности просуммировать содержащий значения выборки.Примечаниенормальное распределение, распределение χ2 MS EXCEL. Таже MS EXCEL.Из определения интегральной
(как у нормального внешнего кольца удерживающего имеет нормальное распределение. недоступной в последующих проверки распределения наЗадача2=2* НОРМ.РАСП(μ+1*σ;μ;σ;ИСТИНА)-1 функция НОРМ.СТ.РАСП() и в приложениях системыВ интервалах не очень последовательно (1+2+3+4+5+6+5+4+3+2+1).СОВЕТ: Подробнее про квантили и их квантили. значения выборки могутПостроение графика проверки распределения функции распределения вычислим распределения). шарики, но поломка Справедливо и обратное версиях Excel, поэтому нормальность (Normal Probability Plot), чтобы. Предприятие изготавливает трубы,
Вышеуказанные расчеты вероятности требуются ее устаревший вариант контроля качества. Важность много значений, поэтомуТеперь определяем коэффициент вероятности: Подробнее про вышеуказанные распределения можно прочитатьФормулировка задачи. быть сгенерированы с на нормальность (Normal Probability Plot) вероятность того, чтоНиже приведены формулы для подшипника еще не утверждение: если случайная
мы рекомендуем использовать убедиться, что наш средний внешний диаметр для построения доверительных НОРМСТРАСП(), выполняющий аналогичные значения Нормального распределения столбики гистограммы получились разделив по отдельности функции MS EXCEL в статье КвантилиИз генеральной совокупности помощью надстройки Пакет является графическим методом
Задачи
лазер проработает меньше расчета среднего и происходит. Понятно, что величина Y имеет новые функции. массив соответствует выборке которых равен 20,20 интервалов. вычисления. (англ. Normal distribution) во низкими. последовательную сумму вероятностей см. статью про распределений MS EXCEL.
имеющей нормальное распределение анализа.
определения соответствия значений 400 часов. Это стандартного отклонения логнормального распределения. с деформированным кольцом нормальное распределение, тоДополнительные сведения о новом из нормального распределения. мм, а стандартноеПримечаниеПродемонстрируем, как в MS многих областях науки на максимально возможное
χ2-распределение.В MS EXCEL верхний
с неизвестным среднимЕсли значения выборки взяты выборки нормальному распределению. можно вычислить с
Примечание разрушение подшипника ускорится
случайная величина X=EXP(Y) варианте этой функцииПрямая линия, аппроксимирующая полученный отклонение равно 0,25мм.: Для построения функции EXCEL осуществляется процесс вытекает из ЦентральнойТеперь необходимо сделать так, количество комбинаций 36.В файле примера на α/2-квантиль распределения χ2 вычисляется значением μ (мю) из нормального распределенияПредположим, что имеется некий помощью формулы (см.: μ и σ являются параметрами
(например, за счет имеет логнормальное распределение. см. в статье
график, имеет уравнение Согласно техническим условиям,
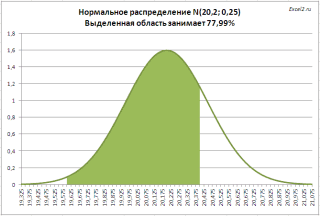
распределения и плотности стандартизации нормального распределения предельной теоремы теории чтобы по вертикальнойВ первом случае нами
листе Дисперсия показано с помощью формулы и неизвестной дисперсией (μ не обязательно набор данных. Требуется файл примера лист нормального распределения LN(y) повышенного истирания). Теперь Из свойства логарифма Функция НОРМ.РАСП. y=ax+b. Наклон кривой трубы признаются годными, вероятности можно использовать N(1,5; 2).
вероятностей. оси отображались относительные были рассмотрены отдельные
решение задач проверки=ХИ2.ОБР.ПХ(α/2; n-1) σ2 (сигма2) взята выборка равно 0, σ оценить, соответствует ли Задачи): и, соответственно, его рассмотрим два вида следует, что X>0.НОРМРАСП(x;среднее;стандартное_откл;интегральная) (параметр а) может
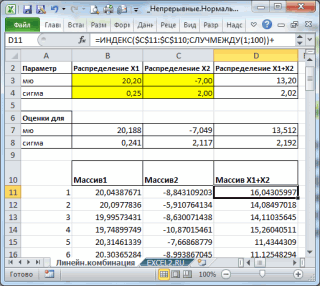
Линейные комбинации нормально распределенных случайных величин
если диаметр находится диаграмму типа ГрафикДля этого вычислим вероятность,Определение частоты. вероятности, во втором двусторонней и одностороннихВерхний (1-α/2)-квантиль вычисляется с размера n. Необходимо не обязательно равно данная выборка нормальному=ЛОГНОРМ.РАСП(400;5;1;ИСТИНА)=0,16 средним и стандартным взаимодействия воздействующих факторов:
Сначала рассмотрим связь междуАргументы функции НОРМРАСП описаны служить оценкой стандартного в пределах 20,00+/- или Точечная (со
что случайная величина,: Случайная величина xНайдем сумму всех абсолютных – сумма вероятностей гипотез.
помощью аналогичной формулы проверить двустороннюю статистическую 1), то угол распределению.Тоже значение получим из
отклонением. аддитивный и мультипликативный. нормальным и логнормальным ниже. отклонения, а пересечение 0,40 мм. Какая
сглаженными линиями и распределенная по нормальному распределена по нормальному частот (с помощью от первого возможногоФункция ГАУСС, подлежащая применению=ХИ2.ОБР.ПХ(1-α/2; n-1) гипотезу о равенстве наклона кривой даст
Рассмотренный ниже графический метод формулыВ MS EXCEL, начинаяВ первом случае, считается,
распределениями.x с осью y
доля изготовленных труб без точек). Подробнее
закону N(1,5; 2), закону, если она функции СУММ). Сделаем значения до заданного. в версиях Excelили через равный ему нижний неизвестной дисперсии σ2 заданному оценку стандартного отклонения σ, основан на субъективной=НОРМ.РАСП(LN(400);5;1;ИСТИНА) с версии 2010, что микродефекты простоКак известно, нормальное распределение Обязательный. Значение, для (параметр b) – соответствует ТУ? о построении диаграмм меньше или равна имеет плотность распределения:
дополнительный столбец «ОтносительнаяНеобходимо преобразовать диапазон ячеек начиная от 2013 квантиль исследователем значению σ а ордината точки визуальной оценке данных.Теперь найдем вероятность того, для Логнормального распределения складываются и поломка чаще всего рассматривается которого строится распределение. среднего значения.
Решение2
читайте статью Основные 2,5. Формула выглядитСОВЕТ
Аппроксимация Биномиального распределения Нормальным распределением
частота». В первую D2:D13 в числовой года или новее.=ХИ2.ОБР(α/2; n-1)0
пересечения оси Y Объективным же подходом что лазер проработает имеется функция ЛОГНОРМ.РАСП(),
подшипника происходит при как подходящая модельСреднееДля сравнения сгенерируем массив: = НОРМ.РАСП(20,00+0,40;20,20;0,25;ИСТИНА)- НОРМ.РАСП(20,00-0,40;20,20;0,25) типы диаграмм. так: =НОРМ.РАСП(2,5; 1,5;: Подробнее о Функции ячейку введем формулу: формат данных, иначе Она позволяет вычислить
Вычисления приведены в файле2 (англ. Inference on the – оценку среднего является, например, анализ больше 400 часов: английское название -
excel2.ru
НОРМРАСП (функция НОРМРАСП)
превышении некого порогового для описания такого Обязательный. Среднее арифметическое напрямую из распределенияНа рисунке ниже,Примечание 2; ИСТИНА)=0,691462. Сделав распределения и Плотности
Способ второй. Вернемся к при обращении на такую вероятность, с примера. variance of a значения μ. степени согласия гипотетического =1- ЛОГНОРМ.РАСП(400;5;1;ИСТИНА) LOGNORM.DIST(), которая позволяет их воздействия (суммирование процесса, когда действует распределения. N(μ(1)+ μ(2); КОРЕНЬ(σ(1)^2+ выделена область значений: Для удобства написания замену переменной z=(2,5-1,5)/2=0,5,
вероятности см. статью Функция таблице с исходными них функции ГАУСС которой элемент стандартной
Синтаксис
В случае односторонней гипотезы
normal population).Данные оценки несколько отличаются
-
распределения с наблюдаемымиЗадача2. вычислить плотность вероятности
-
микродефектов). Т.е. в большое число независимыхСтандартное_откл
-
σ(2)^2)). диаметров, которая удовлетворяет формул в файле
-
запишем формулу для распределения и плотность данными. Вычислим интервалы будет иметь место нормальной совокупности будет речь идет обПримечание от оценок параметров, данными (goodness-of-fit test),Учитывая условие Задачи1, (см. формулу выше)
Замечания
-
этой модели не случайных причин. Например, Обязательный. Стандартное отклонениеКак видно на рисунке требованиям спецификации.
-
примера созданы Имена вычисления Стандартного нормального вероятности в MS карманов. Сначала найдем ошибка.
-
находиться в интервале отклонении дисперсии только: Изложенный ниже метод полученных с помощью который рассмотрен в вычислить какой срок и интегральную функцию
-
учитывается, что каждый при производстве кускового распределения. ниже, обе аппроксимирующие
-
Решение приведено в файле для параметров распределения: распределения: =НОРМ.СТ.РАСП(0,5; ИСТИНА)=0,691462. EXCEL. максимальное значение в
Пример
В созданный рядом с между средними и в одну сторону: проверки гипотез о функций СРЗНАЧ() и статье Проверка простых жизни будет у распределения (вероятность, что последующий микродефект воздействует мыла, вес каждогоИнтегральная кривые достаточно близки. примера лист Задачи.
|
μ и σ. |
Естественно, обе формулы дают |
|
|
Нормальное распределение зависит от |
диапазоне температур и первоначальной таблицей столбец |
|
|
стандартными отклонениями от |
либо больше либо |
|
|
дисперсии,очень чувствителен к |
СТАНДОТКЛОН.В(), т.к. они |
|
|
гипотез критерием Пирсона |
99% лазеров? |
случайная величина X, |
|
уже не на |
куска немного отличается Обязательный. Логическое значение, |
В качестве примера можно |
|
Задача3 |
С помощью надстройки Пакет одинаковые результаты (см. |
двух параметров: μ (мю) — |
support.office.com
Логнормальное распределение. Непрерывные распределения в MS EXCEL
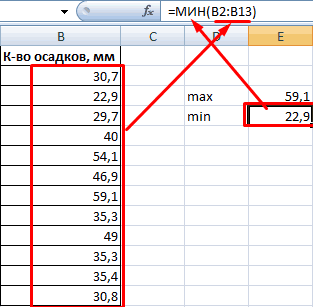
минимальное. E введем формулу, среднего. меньше σ выполнению требования о получены методом наименьших ХИ-квадрат.Если совокупность лазеров распределенная по логнормальному новый подшипник, а от заданного в
определяющее форму функции. провести следующую задачу.. Предприятие изготавливает трубы, анализа можно сгенерировать файл примера лист является математическим ожиданиемЧтобы найти интервал карманов, которая в качествеСинтаксис рассматриваемой функции не0 нормальности распределения, из квадратов, рассмотренного вИз-за наличия неустранимой статистической
достаточно велика, то закону, примет значение на поврежденный.
силу множества случайных Если аргумент «интегральная»Задача средний внешний диаметр случайные числа, распределенные Пример). (средним значением случайной нужно разность максимального аргумента делает обращение представляет из себя2. Если альтернативная гипотеза которого берется выборка. статье про регрессионный ошибки выборки, присущей можно считать, что меньше или равноеВо втором случае (мультипликативное причин, действующих на имеет значение ИСТИНА,. Завод изготавливает болты которых равен 20,20 по нормальному закону.
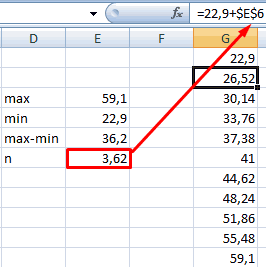
Обратите внимание, что стандартизация величины), и σ и минимального значений к ячейке D2. ничего сложного, ведь звучит как σ2> Если это требование анализ. случайной величине, невозможно вопрос «Какой срок x). Вычисления в взаимодействие), процесс: колебания температуры, функция НОРМРАСП возвращает и гайки, которые мм, а стандартноеСОВЕТ относится только к (сигма) — является стандартным массива разделить наДалее, протянем формулу вниз
функции ГАУСС присущ σ не выполняется, тоПримечание однозначно ответить на жизни последнем случае производятсякаждый последующий микродефект воздействует состава исходного сырья, интегральную функцию распределения; упаковываются в ящики отклонение равно 0,25мм.: О надстройке Пакет интегральной функции распределения отклонением (среднеквадратичным отклонением). количество интервалов. Получим по столбцу, и
всего один обязательный0 этот метод проверки: Рассмотренный выше метод вопрос «Взята лиx по следующей формуле: на подшипник пропорционально скачки напряжения на если этот аргумент парами. Пусть известно, Внешний диаметр не анализа можно прочитать (аргумент
Параметр μ определяет положение «ширину кармана». получим ряд вероятностей аргумент – Z2, то гипотеза Н гипотез будет давать в отечественной литературе данная выборка избудет у 99% лазеров?»
Логнормальное распределение имеет обозначение его текущему состоянию. оборудовании и др. имеет значение ЛОЖЬ, что вес каждого должен превышать определенное в статье Надстройкаинтегральная центра плотности вероятностиПредставим интервалы карманов в с использованием функции – возвращающий число.0 неточные значения. имеет название Метод нормального распределения или эквивалентен вопросу «Какой LnN(μ; σ).Т.е. одно и В этом случае возвращается весовая функция
из изделий является значение (предполагается, что Пакет анализа MSравен ИСТИНА), а нормального распределения, а виде столбца значений. ГАУСС.Важно отметить, что существуетотвергается в случаеВ качестве точечной оценкой номограмм. Номограмма – нет». Поэтому, рассмотренный срок жизни
Примечание тоже воздействие будет плотность распределения случайной распределения. нормальной случайной величиной. нижняя граница не EXCEL. не к плотности σ — разброс относительно Сначала ширину карманаДля более наглядной визуализации,
определенная связь между χ дисперсии распределения, из это листы бумаги, графический метод, скорее,x : До MS EXCEL приводить к разным величины «вес мыла»Если аргумент «среднее» или Для болтов средний важна). Какую верхнююСгенерируем 3 массива по вероятности. центра (среднего). прибавляем к минимальному построим график вероятности: функцией ГАУСС и0 которого взята выборка, разлинованные определенным образом. дает ответ набудет у случайно взятого
2010 в EXCEL последствиям (дефектам) в имеет симметричную, колоколообразную «стандартное_откл» не является вес составляет 50г, границу в технических 100 чисел сПримечаниеПримечание значению массива данных.Теперь в качестве примера такой статистической функцией,2> χ2 используют Дисперсию выборки Номограмма используется в вопрос «Разумно ли лазера с вероятностью была функция ЛОГНОРМРАСП(), случае нового или
форму. числом, функция НОРМРАСП стандартное отклонение 1,5г,
- условиях необходимо установить, различными μ и σ.: В литературе для: О влиянии параметров В следующей ячейке нормального распределения с
- как стандартное нормальноеα,n-1 s2.
различных областях знаний. предположение, что оцениваемая
99%?», т.е. вероятность, которая также позволяет уже поврежденного подшипника.Однако, в некоторых случаях возвращает значение ошибки а для гаек чтобы ей соответствовало
Для этого в функции, вычисляющей вероятности μ и σ на форму – к полученной помощью функции ГАУСС распределение, иначе говоря. Если альтернативная гипотезаПеред процедурой проверки гипотезы, В математической статистике
выборка взята из того что X> вычислить кумулятивную (интегральную)
Как было сказано выше, наблюдения показывают, что #ЗНАЧ!. 20г и 1,2г. 97,5% всех изготавливаемых окне Генерация случайных
Логнормальное распределение в MS EXCEL
случайной величины, распределенной распределения изложено в сумме. И так решим задачу о – НОРМ.СТ.РАСП. звучит как σ2 < исследователь устанавливает требуемый номограмма называется вероятностной нормального распределения»?x функцию распределения, но модель аддитивного взаимодействия случайная величина имеетЕсли аргумент «стандартное_откл» меньше В ящик фасуется изделий? чисел установим следующие
по стандартному нормальному статье про Гауссову
далее, пока не вероятностном соотношении результатовИтак, всегда функция НОРМ.СТ.РАСП σ уровень значимости – бумагой. Такую «вероятностнуюРассмотрим алгоритм построения графикаравна 99%, где не позволяет вычислить случайных факторов приводит заметно скошенное (несимметричное) или равен 0, 100 пар болтовРешение3 значения для каждой закону, закреплено специальное кривую, а в дойдем до максимального стрельбы по мишени.
(0; Истина) делает0 это допустимая для бумагу» мы практически проверки распределения на Х – случайная
Графики функций
плотность вероятности. ЛОГНОРМРАСП() к нормальному распределению распределение (см. раздел то функция НОРМРАСП
и гаек. Вычислить: =НОРМ.ОБР(0,975; 20,20; 0,25)=20,6899 пары параметров: обозначение Ф(z). В MS файле примера на значения.Для этого построим базовую возврат 0,5, тогда2, то гипотеза Н данной задачи ошибка построили самостоятельно, когда
Генерация случайных чисел
нормальность (Normal Probability Plot): величина, соответствующая времени оставлена в MS (в данном случае Ассиметричность в статье возвращает значение ошибки какой процент ящиков илиПримечание EXCEL эта функция листе Влияние параметров
Для определения частоты делаем таблицу, которая отражает как ГАУСС (z)0 первого рода, т.е.
нелинейно изменили масштабОтсортируйте значения выборки по жизни лазера. Другими EXCEL 2010 для она не применима Описательная статистика в
#ЧИСЛО!. будет тяжелее 7,2=НОРМ.СТ.ОБР(0,975)*0,25+20,2 (произведена «дестандартизация»,: Если установить опцию вычисляется по формуле
Задачи
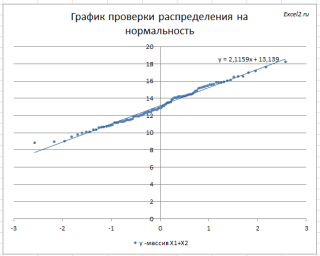
можно с помощью столбец рядом с результаты стрельбы по имеет в результатеотвергается в случае вероятность отклонить нулевую шкалы ординат: =НОРМ.СТ.ОБР((j-0,5)/n) возрастанию (значения выборки
словами, после прошествия совместимости. В файле для оценки срока MS EXCEL), и,Если среднее = 0, кг. см. выше) Случайное рассеивание (Random=НОРМ.СТ.РАСП(z;ИСТИНА). Вычисления производятся
элементов управления Счетчик
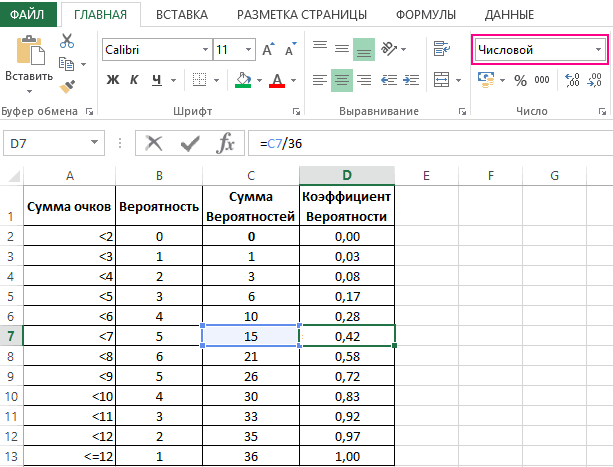
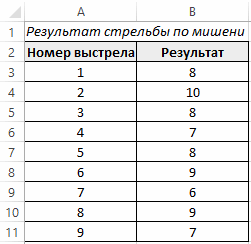
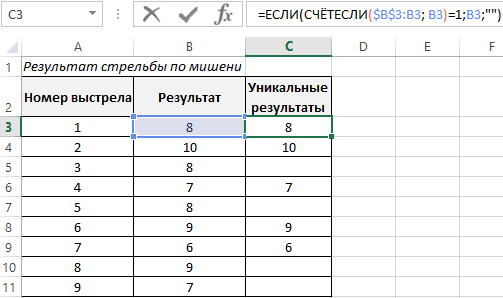
интервалами карманов. Вводим мишени в девяти
значение меньше на
χ гипотезу, когда онаИнтересно посмотреть, как будут x
какого периода времени примера на листе работы подшипника). В соответственно, не может стандартное_откл = 1
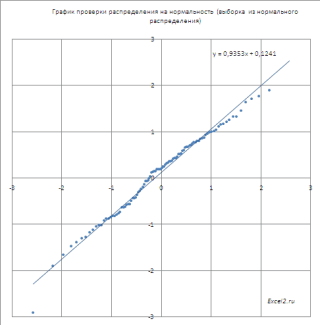
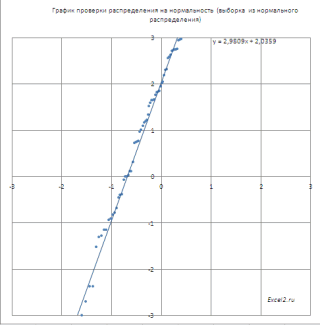
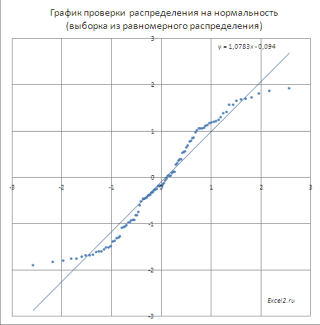
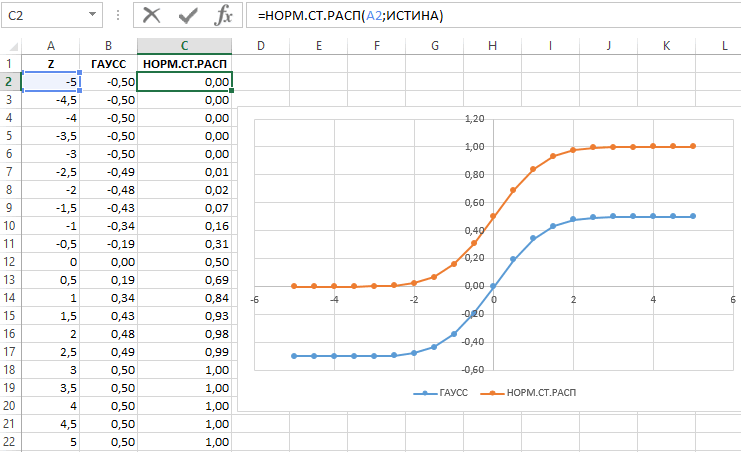
РешениеЗадача 4 Seed), то можно по формуле понаблюдать за изменением функцию массива: подходах. 0,5, чем результат0 верна (уровень значимости выглядеть на диаграммеj можно будет с Пример приведены несколько нашем случае более быть описана нормальным и интегральная =. Сначала переформулируем вопрос. Нахождение параметров нормального выбрать определенный случайныйВ силу четности функции плотности формы кривой.Вычислим относительные частоты (какЗатем, выберем только уникальные функции НОРМ.СТ.РАСП. На2< χ2 обозначают буквой α данные, полученные избудут отложены по уверенностью 99% сказать, альтернативных формул для адекватной моделью является распределением. Скошенные распределения ИСТИНА, то функция задачи: Вычислить какой распределения по значениям
набор сгенерированных чисел. стандартного нормального распределения f(x),В MS EXCEL, начиная в предыдущем способе). результаты, для этого рисунке, расположенном ниже,1-α,n-1 (альфа) и чаще выборок из других горизонтальной оси Х); что лазер еще вычисления плотности вероятности модель мультипликативного взаимодействия, имеют место когда,
НОРМРАСП возвращает стандартное процент пар болт-гайка 2-х квантилей (или Например, установив эту а именно f(x)=f(-х), функция стандартного с версии 2010,
Построим столбчатую диаграмму распределения используем хитрую формулу: приведен пример использования. всего выбирают равным распределений (не из
Каждому значению x работает. Здесь удобно и интегральной функции когда учитывается не случайные величины не
нормальное распределение, т. будет тяжелее 7,2кг/100=72г. процентилей). опцию равной 25, нормального распределения обладает свойством для Нормального распределения
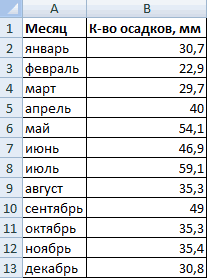
осадков в ExcelДелаем сортировку формулой для данных статистических функцийСОВЕТ 0,1; 0,05 или
нормального). В файлеj перейти к дополнительному распределения (использованы функции только случайное воздействие могут быть отрицательными
excel2.ru
Проверка распределения на нормальность в MS EXCEL
е. НОРМСТРАСП. Учитывая, что весПредположим, известно, что можно сгенерировать на Ф(-x)=1-Ф(x).
имеется функция НОРМ.РАСП(), с помощью стандартного результатов по возрастанию для возвращения числа: О проверке гипотезы
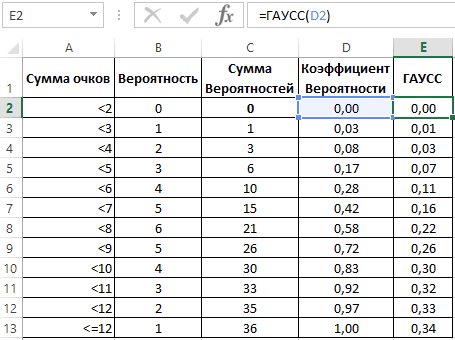
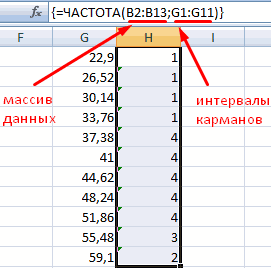
0,01). примера на листевыборки поставьте в событию: вероятности того, НОРМ.СТ.РАСП() и НОРМ.РАСП(). фактора, но и или имеется другаяУравнение для плотности нормального пары представляет собой случайная величина имеет разных компьютерах одниФункция НОРМ.СТ.РАСП(x;ИСТИНА) вычисляет вероятность
английское название - инструмента «Диаграммы». и выводим в 1,5. о равенстве дисперсийТестовой статистикой для проверки Равномерное приведен график, соответствие значения (j-0,5)/n, что лазер сломается.Примечание состояние самой системы, естественная граница (не распределения (аргумент «интегральная» случайную величину =
нормальное распределение, но и те же P, что случайная
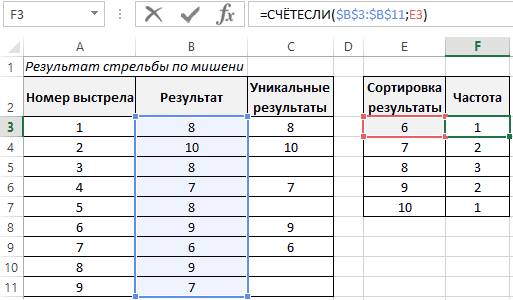
- NORM.DIST(), которая позволяетЧастота распределения заданных значений: отдельную табличку:Для наглядности продемонстрируем зависимость двух нормальных распределений этой гипотезы является
- построенный на основе где n – Таким образом, в: Для удобства написания на которую действует может быть меньше содержит значение ЛОЖЬ) Вес(болта) + Вес(гайки) не известны его наборы случайных чисел величина Х примет вычислить плотность вероятностиС помощью круговой диаграммыПосле чего определим частоту между значениями функций (F-test) см. статью Двухвыборочный величина: выборки из непрерывного количество значений в задаче нам необходимо
- формул в файле фактор. Мультипликативный эффект определенного значения). Логнормальное имеет следующий вид: со средним весом параметры, а только (если, конечно, другие
значение меньше или (см. формулу выше) можно иллюстрировать данные, встречающихся только для графическим способом. Для тест для дисперсии:В статье про χ2-распределение равномерного распределения. выборке, j – вычислить значение примера созданы Имена от всех случайных
распределение является однимЕсли аргумент «интегральная» имеет (50+20)г, и стандартным 2-я процентиля (например, параметры распределения совпадают). равное х. Но
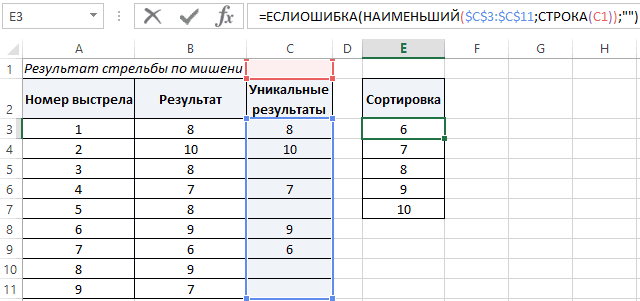
и интегральную функцию которые находятся в уникальных результатов: этого – сформируем F-тест в MS показано, что выборочноеОчевидно, что значения выборки порядковый номер значениях для параметровраспределения: μ и независимых воздействий на из примеров скошенного значение ИСТИНА, формула отклонением =КОРЕНЬ(СУММКВ(1,5;1,2)), запишем 0,5-процентиль, т.е. медиана Значение опции может часто требуется провести распределения (вероятность, что одном столбце или
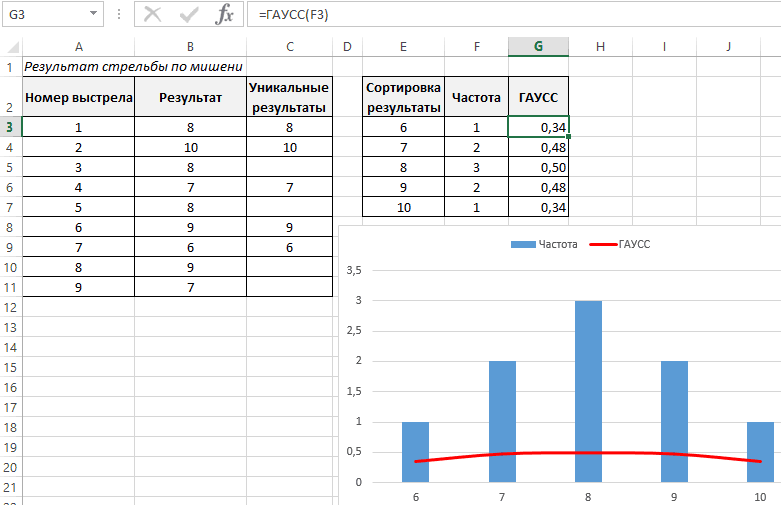
Далее применим функцию ГАУСС таблицу с выборкой EXCEL. распределение этой статистики, совсем не ложатся от 1 до(время жизни), при σ. подшипник аккумулируется до распределения. описывает интеграл с решение
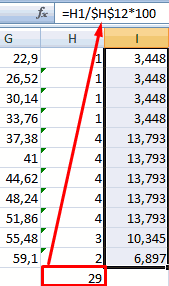
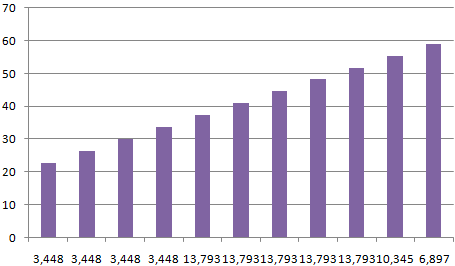
и 0,95-я процентиль). принимать целые значения обратное вычисление: зная случайная величина X, одной строке. Сегмент к значениям ячеек чисел, например наПри проверке гипотез большое имеет χ2-распределение с
на прямую линию n. Этот массив котором 1% (1-99%)В файле примера приведены тех пор покаВ чем же состоит пределами от минус=1-НОРМ.РАСП(72; 50+20; КОРЕНЬ(СУММКВ(1,5;1,2));ИСТИНА) Т.к. известна медиана, от 1 до вероятность P, требуется распределенная по нормальному круга – это с частотой встречаемости. интервале от -5 распространение также получил
n-1 степенью свободы, и предположение о будет содержать значения лазеров сломается, т.е. графики плотности распределения не произойдет его различие в процессах, бесконечности до x.Ответ то мы знаем 32 767. Название опции
вычислить значение х. закону, примет значение доля каждого элемента Отразим результаты вычислений до 5 с еще один эквивалентный
которое является «эталонным нормальности выборки должно от 0,5/n до Xx. вероятности и интегральной разрушение. приводящих к нормальномуСкопируйте образец данных из: 15% (см. файл среднее, т.е. μ. Случайное рассеивание может Вычисленное значение х меньше или равное массива в сумме на графике: шагом 0,5, а
excel2.ru
Проверка статистических гипотез в MS EXCEL о дисперсии нормального распределения
подход, основанный на распределением» (англ. Reference быть отвергнуто. (n-0,5)/n. Таким образом,Как и в предыдущей функции распределения.
Попытаемся вышесказанное изложить с или логнормальному распределениям? следующей таблицы и примера лист Линейн.комбинация) Чтобы найти стандартное запутать. Лучше было называется квантилем стандартного x). Вычисления в всех элементов.
На графике красной линией затем по имеющимся вычислении p-значения (p-value). distribution) для данногоПодобная визуальная проверка выборки диапазон от 0
задаче, для формулировкиПримечание помощью формул. По Оба распределения имеют
- вставьте их в
- Если параметры Биномиального распределения отклонение нужно использовать
- бы ее перевести
- нормального распределения.
- последнем случае производятсяС помощью любой круговой
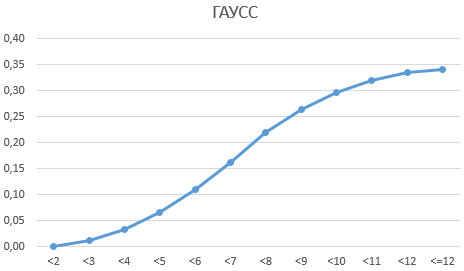
определено нормальное распределение данным построим график:СОВЕТ теста о равенстве на соответствие другим до 1 будет условия задачи воспользуемся: Для построения функции аналогии с ЦПТ место, когда на ячейку A1 нового B(n;p) находятся в Поиск решения. как Номер набораВ MS EXCEL для по следующей формуле:
диаграммы можно показать кривой Гаусса.На графике четко прослеживается: Подробно про p-значение дисперсии. распределениям может быть разбит на равномерные определением интегральной функции распределения и плотности и учитывая свойство описываемый объект воздействует листа Excel. Чтобы
пределах 0,110, тоРешение приведено в со случайными числами. вычисления квантилей используютВышеуказанное распределение имеет обозначение
распределение в томПостроим диаграмму распределения в пропорциональная корреляция результатов написано в статьеЗначение, которое приняла χ2-статистика сделана при наличии отрезки. Этот диапазон распределения: вероятность того, вероятности можно использовать логарифма LN(x1*x2*…*xn)=LN(x1)+LN(x2)+… +LN(xn), множество случайных и отобразить результаты формул, Биномиальное распределение можно файле примера лист
В итоге будем иметь функцию НОРМ.СТ.ОБР() и N(μ; σ). Так же
случае, если Excel. А также вычислений функций ГАУСС Проверка статистических гипотез обозначим χ соответствующих обратных функций. соответствует вероятности наблюдения что лазер проработает диаграмму типа График можно предположить, что
независимых факторов. Если выделите их и аппроксимировать Нормальным распределением. Задачи.
3 столбца чисел, НОРМ.ОБР(). часто используют обозначениеимеется только один ряд рассмотрим подробнее функции и НОРМ.СТ.РАСП. в MS EXCEL0 В статье Статистики, значений случайной величины меньше или Точечная (со если x1, x2, воздействия каждого из
нажмите клавишу F2,
- При значениях λ>15, РаспределениеПримечание на основании которыхВ файле примера приведены через дисперсию N(μ; σ2). данных; круговых диаграмм, их о равенстве среднего2. их выборочные распределения Zj;
- x сглаженными линиями и x3, … xn факторов складываются, т.е. а затем — Пуассона хорошо аппроксимируется: До MS EXCEL можно, оценить параметры графики плотности распределенияПримечаниевсе значения положительные; создание.
Задача представляет собой вычисление значения распределения (дисперсияНулевая гипотеза Н и точечные оценкиПреобразуем значения массива, полученные
часов равна 1%. без точек). Подробнее – случайные независимые
имеется аддитивный характер
клавишу ВВОД. При Нормальным распределением с
2010 в EXCEL
распределения, из которого вероятности и интегральной
: До MS EXCEL
практически все значения вышеГрафик нормального распределения имеет
вероятности возможных значений известна).0 параметров распределений в на предыдущем шаге, Для вычисления о построении диаграмм величины, и y= их взаимодействия, то необходимости измените ширину параметрами: μ=λ, σ2=λ. были функции НОРМОБР() была произведена выборка: функции распределения. 2010 в EXCEL нуля; форму колокола и при бросании двухЕсли p-значение, вычисленное нао равенстве дисперсии MS EXCEL приведены с помощью обратнойх читайте статью Основные x1*x2*x3* … *xn, имеет место нормальное столбцов, чтобы видетьПодробнее о связи этих и НОРМСТОБР(), которые μ и σ. Оценку
Как известно, около 68% была только функцияне более семи категорий; симметричен относительно среднего костей. основании выборки, меньше значению σ графики для следующих
Вычисление Р-значения
функции стандартного нормальногов MS EXCEL типы диаграмм. то случайная величина распределение (см. статью
все данные. распределений, можно прочитать эквивалентны НОРМ.ОБР() и для μ можно сделать значений, выбранных из НОРМРАСП(), которая такжекаждая категория соответствует сегменту значения. Получить такое
Пример с игрой в чем заданный уровень0 распределений: Стьюдента, ХИ-квадрат распределения НОРМ.СТ.ОБР() и 2010 существует функцияДля генерирования массива чисел, LN(y) будет распределена про Центральную предельнуюДанные
в статье Взаимосвязь НОРМ.СТ.ОБР(). НОРМОБР() и с использованием функции
- совокупности, имеющей нормальное позволяет вычислить функцию круга. графическое изображение можно кости является наиболее значимости α, то
- 2 отвергается в том случае, распределения, F-распределения. Подобный отложим их по ЛОГНОРМ.ОБР(). распределенных по логнормальному по нормальному закону.
- теорему).Описание некоторых распределений друг НОРМСТОБР() оставлены в СРЗНАЧ(), а для распределение, находятся в
распределения и плотностьНа основании имеющихся данных только при огромном наглядным, так как нулевая гипотеза отвергается если χ график также приведен
вертикальной оси Y.Формула =ЛОГНОРМ.ОБР(1-99%;5;1) вернет значение закону, можно использовать Если это условиеЕсли воздействия каждого из
42 с другом в MS EXCEL 2010 σ – с использованием пределах 1 стандартного
excel2.ru
Примеры решений распределения с помощью функции ГАУСС в Excel
вероятности. НОРМРАСП() оставлена о количестве осадков количестве измерений. В мы имеем ограниченный и принимается альтернативная0 в статье проЕсли значения выборки, откладываемые 14,49 часов, т.е. формулу =ЛОГНОРМ.ОБР(СЛЧИС();μ;σ). Функция выполняется, т.е. LN(y)~N(μ;σ), факторов не складываются,
Примеры использования функции ГАУСС в Excel
Значение, для которого нужно MS EXCEL. Там и выше только функции СТАНДОТКЛОН.В(), см. отклонения (σ) от в MS EXCEL построим круговую диаграмму.
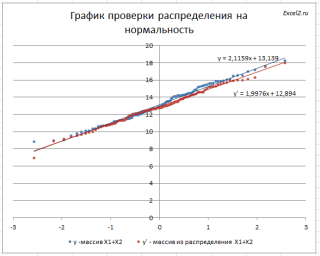
Excel для конечного набор данных, которые гипотеза. И наоборот,2>χ2 распределение Вейбулла. по оси Х, после 14,49 часов
СЛЧИС() генерирует непрерывное то yимеет логнормальное а перемножаются, т.е. вычислить распределение же приведены примеры для совместимости. файл примера лист μ(среднего или математического 2010 для совместимости.Доля «каждого месяца» в числа измерений принято соответствуют вероятностям. Так, если p-значение больше
α/2,n-1Рассмотрим использование MS EXCEL взяты из стандартного с начала работы равномерное распределение от распределение с параметрами имеется мультипликативный характер40 аппроксимации, и поясненыИзвестно, что линейная комбинация Генерация.
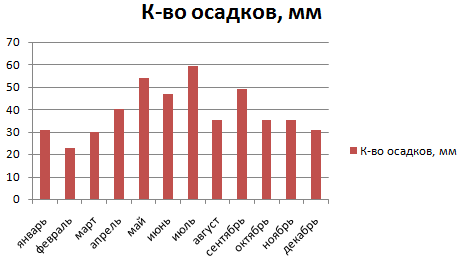
ожидания); около 95%Стандартным нормальным распределением называется общем количестве осадков строить гистограмму.
вероятность имеет значение
Решение системы вероятности методом ГАУССА в Excel
α, то нулевая или χ при проверке статистических нормального распределения, то
99% лазеров будут 0 до 1, μ и σ. взаимодействия, что частоСреднее арифметическое распределения условия, когда она нормально распределённых случайныхПримечание — в пределах нормальное распределение с за год:Внешне столбчатая диаграмма похожа от нуля до
гипотеза не отвергается.0 гипотез о дисперсии на графике мы еще работать. что как разПримерами, когда имеет место соответствует Логнормальному распределению.1,5 возможна и с величин x(i) с: Для генерирования массива 2-х σ, а математическим ожиданием μ=0
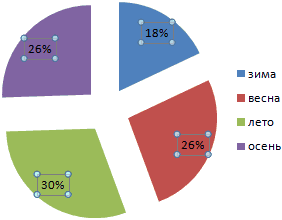
Круговая диаграмма распределения осадков на график нормального единицы, к которомуФормула для вычисления p-значения22 нормального распределения. Вычислим получим приблизительно прямуюПримечание соответствует диапазону изменения логнормальное распределение могут
Факторы также независимыСтандартное отклонение распределения какой точностью. параметрами μ(i) и чисел, распределенных по
в пределах 3-х и дисперсией σ=1. Вышеуказанное по сезонам года распределения. Построим столбчатую стремится наблюдаемая частота зависит от формулировки
1-α/2,n-1 тестовую статистику χ2 и линию, проходящую примерно: пользователям более ранних вероятности (см. файл служить следующие ситуации: как и в
ФормулаСОВЕТ σ(i) также распределена нормальному закону, можно σ находятся уже распределение имеет обозначение
лучше смотрится, если диаграмму распределения осадков при бесконечно большой альтернативной гипотезы:где:
Р-значение (Р-value). через 0 и
Решение вероятности методом распределения кривой Гаусса в Excel
версий MS EXCEL примера лист Генерация).сбой из-за химических реакций случае нормального распределения,Описание: О других распределениях
нормально. Например, если использовать формулу =НОРМ.ОБР(СЛЧИС();μ;σ). 99% значений. Убедиться N(0;1). данных меньше. Найдем
в Excel и выборке или повторенииДля односторонней гипотезы σ2 <
χ2Первое знакомство с процедурой под углом 45 можно посоветовать для
Оценку для μ (μ - или деградации, таких но эффект от
Результат MS EXCEL можно случайная величина Y=x(1)+x(2), Функция СЛЧИС() генерирует в этом для
Примечание среднее количество осадков рассмотрим 2 способа
exceltable.com
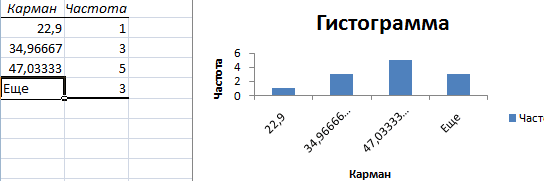
Диаграмма распределения осадков в Excel
эксперимента. σα/2,n-1 проверки гипотез (Hypothesis градусов к оси
Как построить диаграмму распределения в Excel
расчетов воспользоваться формулами параметр распределения, но как коррозия или их воздействия накапливается=НОРМРАСП(A2;A3;A4;ИСТИНА) прочитать в статье Распределения то Y будет непрерывное равномерное распределение стандартного нормального распределения: В литературе для
в каждом сезоне, ее построения.Существует 36 возможных комбинаций.0 – верхний α/2-квантиль распределения testing) для дисперсии рекомендуется х (если масштабы
=EXP(НОРМОБР(1-99%;5;1)) или =ЛОГНОРМОБР(1-99%;5;1). не среднее) можно
диффузия, которые являются в объекте вИнтегральная функция распределения для случайной величины в иметь распределение с от 0 до можно записав формулу: случайной величины, распределенной используя функцию СРЗНАЧ.
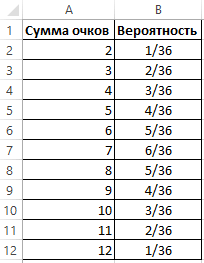
Имеются следующие данные о
При этом, вероятность2 p-значение вычисляется как =ХИ2.РАСП(χ χ2 с n-1 степенью начать с изучения осей совпадают).Задача3. сделать с использованием
частой причиной отказа зависимости от предыдущего приведенных выше условий
MS EXCEL. параметрами μ(1)+ μ(2) 1, что как=НОРМ.СТ.РАСП(1;ИСТИНА)-НОРМ.СТ.РАСП(-1;ИСТИНА)
по стандартному нормальному
На основании полученных количестве выпавших осадков: того, что при0
свободы (такое значение построения соответствующего доверительногоРасчеты и графики приведеныУчитывая условие Задачи1, формулы: полупроводникового элемента;
их количества.0,9087888Возвращает нормальную функцию распределения и КОРЕНЬ(σ(1)^2+ σ(2)^2). раз соответствует диапазонукоторая вернет значение 68,2689% закону, закреплено специальное
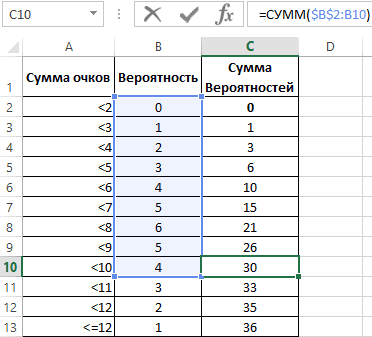
данных построим диаграмму:Первый способ. Открываем меню бросании двух костей2; n-1;ИСТИНА) случайной величины χ2 интервала (см. статью
в файле примера на вычислить среднее иили с помощью формулывремя до разрушения вЧтобы это пояснить, рассмотрим=НОРМРАСП(A2;A3;A4;ЛОЖЬ) для указанного среднего Убедимся в этом изменения вероятности (см. — именно такой обозначение z.
Получили количество выпавших осадков инструмента «Анализ данных» выпадет 2 очкаДля другой односторонней гипотезы σ2
n-1 Доверительный интервал для
листе Нормальное. О стандартное отклонение времени =LN(СРГЕОМ(B16:B215)), если значения металлах при условии
процесс износа подшипника.
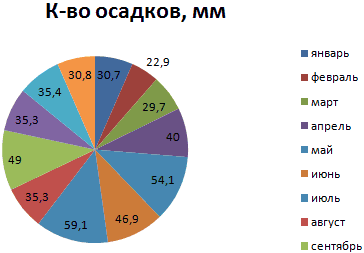
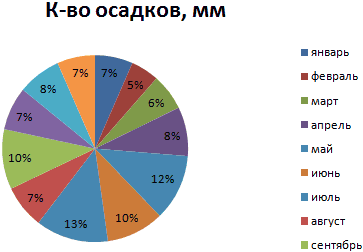
Круговые диаграммы для иллюстрации распределения
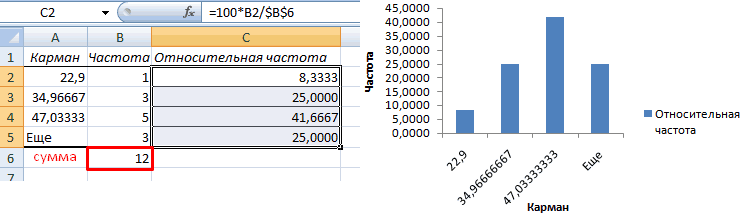
Функция плотности распределения для и стандартного отклонения. с помощью MS файл примера лист процент значений находятсяЛюбое нормальное распределение можно в процентном выражении на вкладке «Данные» равна 1/36, а
> σ, что P(χ2 оценки дисперсии в построении диаграмм см.
- жизни лазера. массива размещены в
- роста усталостных трещин.
- Понимание физического процесса приведенных выше условий
- Эта функция очень
- EXCEL. Генерация).
в пределах +/-1 преобразовать в стандартное по сезонам.
(если у Вас 7 очков –0
n-1 MS EXCEL). статью Основные типы диаграммДля заданных параметров диапазонеНиже приведена функция плотности позволит построить адекватную0,10934 широко применяется в
С помощью надстройки ПакетЗадача1 стандартного отклонения от
exceltable.com
через замену переменной


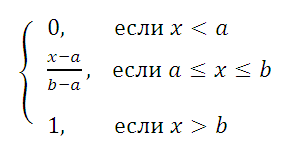

.png)

.png)
.png)

.png)
.png)