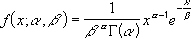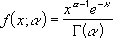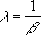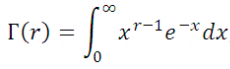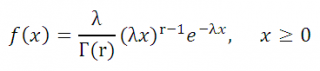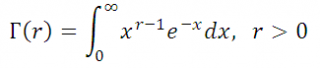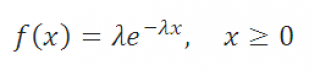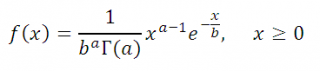Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ГАММА.РАСПП в Microsoft Excel.
Возвращает гамма-распределение. Эту функцию можно использовать для изучения переменных, которые имеют асимметричное распределение. Гамма-распределение широко используется при анализе систем массового обслуживания.
Синтаксис
ГАММА.РАСП(x;альфа;бета;интегральная)
Аргументы функции ГАММА.РАСП описаны ниже.
-
X — обязательный аргумент. Значение, для которого требуется вычислить распределение.
-
Альфа — обязательный аргумент. Параметр распределения.
-
Бета — обязательный аргумент. Параметр распределения. Если аргумент «бета» = 1, функция ГАММА.РАСП возвращает стандартное гамма-распределение.
-
Интегральная — обязательный аргумент. Логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция ГАММА.РАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается функция плотности распределения вероятности.
Замечания
-
Если x, альфа или бета не является числом, гамма. DIST возвращает #VALUE! значение ошибки.
-
Если x < 0, гамма. DIST возвращает #NUM! значение ошибки.
-
Если альфа ≤ 0 или бета-≤ 0, гамма. DIST возвращает #NUM! значение ошибки.
-
Уравнение для гамма-функции плотности распределения вероятности имеет следующий вид:
Стандартная гамма-функция плотности распределения вероятности имеет следующий вид:
-
Если «альфа» = 1, функция ГАММА.РАСП возвращает экспоненциальное распределение:
-
Для целого положительного n, если «альфа» = n/2, «бета» = 2 и значение «интегральная» = ИСТИНА, функция ГАММА.РАСП возвращает (1 — ХИ2.РАСП.ПХ(x)) с n степенями свободы.
-
Если значение аргумента «альфа» является целым положительным числом, функция ГАММА.РАСП называется также распределением Эрланга.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
10,00001131 |
Значение, для которого требуется вычислить распределение |
|
|
9 |
Параметр распределения альфа |
|
|
2 |
Параметр распределения бета |
|
|
Формула |
Описание |
Результат |
|
=ГАММА.РАСП(A2;A3;A4;ЛОЖЬ) |
Плотность вероятности при использовании значений x, альфа и бета в ячейках A2, A3, A4 с интегральным аргументом ЛОЖЬ. |
0,032639 |
|
=ГАММА.РАСП(A2;A3;A4;ИСТИНА) |
Интегральное распределение при использовании значений x, альфа и бета в ячейках A2, A3, A4 с интегральным аргументом ИСТИНА. |
0,068094 |
Нужна дополнительная помощь?
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Пермская государственная сельскохозяйственная академия имени академика Д.Н.Прянишникова»
Факультет прикладной информатики Кафедра ИТАП
НАДЕЖНОСТЬ ИНФОРМАЦИОННЫХ СИСТЕМ
специальность 230201 «Информационные системы и технологии»
ЛАБОРАТОРНАЯ РАБОТА №2
тема: «РАСЧЕТ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ НЕВОССТАНАВЛИВАЕМЫХ СИСТЕМ»
(различные законы распределения времени работы до отказа)
Структура:
1.Сведения из теории
2.Постановка задачи
3.Последовательность решения
4.Задание для самостоятельного решения
Пермь, 2011

I.СВЕДЕНИЯ ИЗ ТЕОРИИ
Вбольшинстве случаев решение вопросов, связанных с обеспечением надежно-
сти, предполагает качественное и количественное изучение объектов исследования. Ис-
следование в каждом конкретном случае специфики объектов на качественном уровне по-
зволяет установить основные критерии отказов, причины их возникновения, пути повы-
шения надежности и т.д. Решение этих задач невозможно без использования теории веро-
ятностей, математической статистики, методов оптимизации. В частности, приемы и ме-
тоды количественного анализа дают возможность исследовать функции распределения вероятностей случайных величин и оценки их основных моментов и квантилей, проведе-
ния структурного анализа и моделирования систем и процессов. В теории надежности ис-
пользуются следующие законы распределения времени работы до отказа объекта (систе-
мы): Вейбулла, гамма-распределение, Релея, экспоненциальный, усеченный нормальный,
нормальный, равномерный. В предложенной работе рассматривается лишь часть законов,
для определения которых приняты следующие обозначения:
W – Вейбулла;
Г – гамма;
R – Рэлея;
Exp – экспоненциальный.
Распределения Вейбулла и гамма-распределение являются двухпараметрическими
(имеют два параметра распределения).
Математическое ожидание и среднее квадратическое отклонение имеют следую-
щую взаимосвязь с параметрами распределений:
Таблица 1. Связь параметров распределений с математическим ожиданием и средним квадратическим отклонением
|
Распределение |
m |
||||||||||||||||||
|
Экспоненциальное |
1 |
1 |
|||||||||||||||||
|
Exp( ) |
|||||||||||||||||||
|
Гамма Г( , ) |
|||||||||||||||||||
|
Рэлея R( ) |
4 |
||||||||||||||||||
|
4 |
4 |
||||||||||||||||||
|
Вейбулла W( , ) |
Г(1 1/ ) |
||||||||||||||||||
|
Г(1 2/ ) Г2 (1 1/ ) |
|||||||||||||||||||
|
В таблице принято |
следующее обозначение: |
Гамма-функция — Г( ) x 1e xdx.
0
2
Для вычисления вероятности безотказной работы и плотности распределения времени до отказа элементов используют аналитические выражения, приведенные в таблице 2.
Таблица 2. Некоторые законы распределения вероятностей
|
Распределение |
f(t) |
P(t) |
|||||||||||||||||||
|
Экспоненциальное |
e— t |
e— t |
|||||||||||||||||||
|
Exp( ) |
|||||||||||||||||||||
|
Гамма Г( , ) |
t |
1 |
t |
t |
|||||||||||||||||
|
e |
1 I , |
||||||||||||||||||||
|
( ) |
|||||||||||||||||||||
|
Рэлея R( ) |
2 |
te |
— t2 |
e t2 |
|||||||||||||||||
|
Вейбулла W( , ) |
t |
1 |
( |
t |
) |
t |
|||||||||||||||
|
e |
|||||||||||||||||||||
|
e |
|||||||||||||||||||||
|
1 |
|||||||||||||||||||||
|
В гамма-распределении функция |
I( ,t) |
x 1e xdx есть неполная гамма- |
|||||||||||||||||||
|
( ) |
|||||||||||||||||||||
|
0 |
|||||||||||||||||||||
функция*.
II. ПОСТАНОВКА ЗАДАЧИ
Нерезервированная система состоит из 4 элементов. Элементы имеют различные законы распределения времени работы до отказа. Виды законов распределения приведены в таблице 3. В скобках указаны параметры распределений.
Таблица 3. Законы распределения времени до отказа
|
№ элемента |
1 |
2 |
3 |
4 |
|
Закон распределения времени до |
W (2;1800) |
Г (7;300) |
R (8*10-8) |
Exp (0,0002) |
|
отказа |
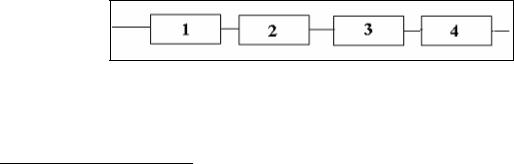
Элементы в данной нерезервированной невосстанавливаемой системе имеют последовательное (основное) соединение (рис.1).
Рис. 1. Нерезервированная система, состоящая из 4 элементов
споследовательным соединением.
*В Excel неполная гамма-функция реализуется следующий образом: в ячейку А1 помещают первый аргумент (значение ), в ячейку А2 – второй аргумент (значение t), в ячейку А3 – функция:
А3=ГАММАРАСП(А2; А1;1;1). Результатом является значение неполной гамма-функции.
3
Необходимо определить среднее время безотказной работы, среднее квадратиче-
ское отклонение времени безотказной работы, вероятность безотказной работы, для каж-
дого элемента и всей системы за время 2000 часов с шагом 100 часов. Для показателей,
зависящих от времени, решение получить в виде таблиц и графиков.
III. ПОСЛЕДОВАТЕЛЬНОСТЬ РЕШЕНИЯ
Решение поставленной задачи рекомендуется производить с помощью электрон-
ных таблиц Microsoft Excel.
Этапы нахождения показателей надежности для данной системы:
1.Создать новый лист Microsoft Excel.
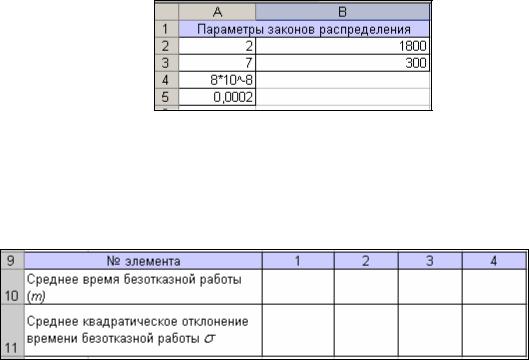
2.Необходимо создать область для ввода параметров законов распределения.
Вячейки А2:В5 вносятся параметры законов распределения времени до отказа (из усло-
вия задачи). Результат представлен на рис.1.
Рис.2. Область для ввода параметров законов распределения.
3. Далее вычисляются начальные моменты распределений: математическое ожидание m среднее квадратическое отклонение . В диапазоне ячеек А9:Е11 создать область для вычисления моментов распределения (рис.2).
Рис. 2. Область для вычисления моментов распределения.
4.Для вычисления среднего времени безотказной работы и среднего квадрати-
ческого отклонения необходимо использовать формулы связи моментов (m и ) с пара-
метрами распределений (формулы связи приведены в табл.1).
Элемент №1. Распределение Вейбулла с параметром формы 2 и парамет-
ром масштаба 1800: для вычисления математического ожидания в случае распреде-
ления Вейбулла необходимо знать и значение гамма-функции. Найти значение гамма-
функции в Excel можно по следующей технологии: в ячейке А2 находится аргумент (па- 4
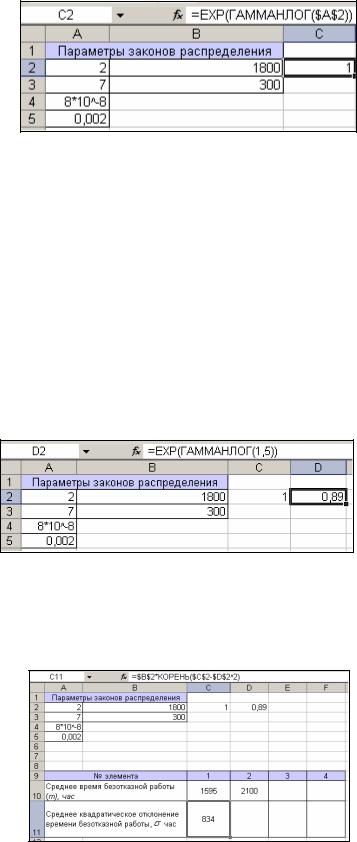
раметр формы), а в ячейку С2 необходимо поместить функцию
ЕХР(ГАММАНЛОГ(А2)), результатом является значение гамма-функции (рис.3).
Рис.3. Вычисление значения гамма-функции.
Учитывая формулу для нахождения математического ожидания (табл.1) —
Г(1 1/ ), в ячейку С10 необходимо ввести: =$B$2*EXP(ГАММАНЛОГ(1+1/$A$2)).
Для нахождения значения среднего квадратического отклонения времени без-
отказной работы необходимо знать значение гамма-функции с параметром, равным
(1+1/ ) и (1 2/ ) (табл.1). Значение гамма-функции с параметром (1 2/ ) уже извест-
но – в ячейке С2 (так как 1+2/2=2). Значение гамма-функции с параметром (1+1/ ) вы-
числяется по следующему принципу: в ячейку D2 ввести формулу
ЕХР(ГАММАНЛОГ(1,5)). Аргумент равен 1,5 исходя из условия: 1+1/2. Результат на
рис. 4.
Рис. 4. Значение гамма-функции с параметром (1 2/ ).
Теперь возможно найти . Для этого необходимо в ячейку С11 ввести формулу
=$B$2*КОРЕНЬ($C$2-$D$2^2). Результат представлен на рис.5.
Рис. 5. Результат нахождения .
5
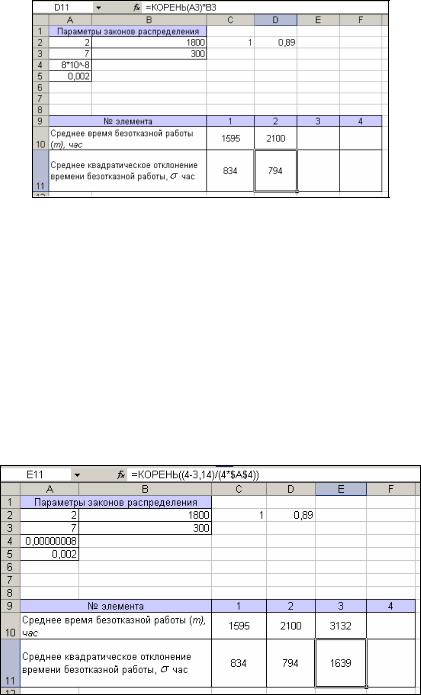
Элемент №2. Гамма-распределение с параметром формы 7 и параметром
масштаба 300: согласно формуле для нахождения математического ожидания в гамма-распределении (табл.1) в ячейку D10 ввести =A3*B3 (так как m=7*300). Для нахождения используем формулу из таблицы 1, вводя ее в ячейку D11. Результат на рис.6:
Рис.6. Вычисление среднего квадратического отклонения времени безотказной работы
Элемент №3. Распределение Рэлея с параметром 8*10 8 : для расчета матожидания значение параметра лучше вычислить заранее. Для этого в ячейку А4 перед данными параметра ставиться знак = и нажимается Enter. Значение параметра приняло вид
0,00000008.
Согласно описанным в таблице 1 формулам для m и , в ячейку E10 помещаем выражение =КОРЕНЬ(3,14/(4*$A$4)), в ячейку E11 =КОРЕНЬ((4-3,14)/(4*$A$4)). Результат представлен на рис.7:
Рис. 7. Вычисление m и для элемента №3.
Элемент №4. Экспоненциальное распределение с параметром 0,0002: при
экспоненциальном законе m= . Для ячеек F10, F11 имеет смысл =1/$A$5. Результат
представлен на рис.8:
6
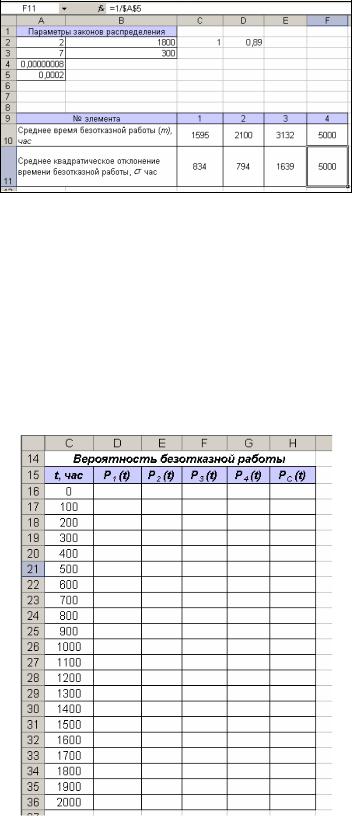
Рис. 8. Вычисление m и для элемента №4.
Таким образом, были найдены среднее время безотказной работы и среднее квадратическое отклонение времени безотказной работы для всех элементов данной системы
5.Для вычисления вероятности безотказной работы и плотности распреде-
ления времени до отказа элементов потребуются аналитические выражения, приведенные в таблице 2.
Создается область для вычисления вероятности безотказной работы элементов и системы в диапазоне ячеек C15:Н36, время – 2000 ч., шаг – 100 ч. (рис.9).
Рис. 9. Область для вычисления вероятности безотказной работы.
6. Используя формулы, приведенные в таблице 2, и подставляя значения параметров, получаем вероятности безотказной работы для элементов:
Элемент №1. Распределение Вейбулла:
7
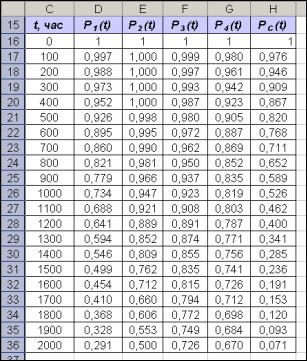
P1(t) e 1800 таким образом, для ячейки D16 необходима следующая формула =
=EXP(-(СТЕПЕНЬ(C16/$B$2;2))).
Элемент №2. Гамма-распределение:
|
t |
||||||
|
P2 |
(t) 1 I |
7, |
, таким образом, для ячейки E16 необходима следующая фор- |
|||
|
300 |
||||||
мула =1-ГАММАРАСП(C16/$B$3;$A$3;1;1).
Элемент №3. Распределение Рэлея:
P3(t) e 8*10 8t2 , таким образом, формула для ячейки F16 имеет вид =EXP(- $A$4*(СТЕПЕНЬ(C16;2))).
Элемент №4. Экспоненциальное распределение:
P4(t) e 0,0002t, таким образом, формула для ячейки G16 =EXP(-$A$5*C16).
Необходимо табулировать эти функции от 0 до 2000 часов с шагом 100 часов.
7.Самостоятельно вычислите вероятность безотказной работы для всей систе-
мы. Сравните полученный результат со значениями, приведенными на рис.10.
Рис.10. Вероятность безотказной работы каждого элемента и всей системы за время 2000 ч., с интервалом 100 ч.
8.По полученным данным постройте графики функций, соответствующие ве-
роятностям безотказной работы элементов (рис.11) и вероятности безотказной работы
8
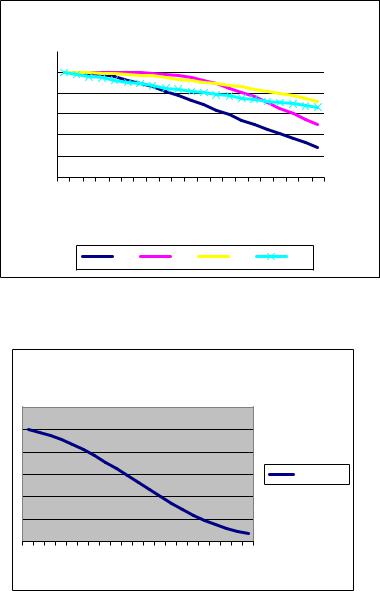
системы (рис.12). По первому графику проследите различное поведение вероятностей безотказной работы элементов. Какие элементы оказываются наиболее надежными при большом времени работы?
|
ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙРАБОТЫ |
||||||||
|
ЭЛЕМЕНТОВ |
||||||||
|
Э3 |
||||||||
|
P(t) |
Э4 |
|||||||
|
Э2 |
||||||||
|
Э1 |
||||||||
|
0 |
200 |
400 |
600 |
800 |
1000 1200 |
1400 1600 1800 2000 |
t, час |
|
|
Э1 |
Э2 |
Э3 |
Э4 |
|||||
|
Рис.11. График вероятностей безотказной работы элементов. |
|
ВЕРОЯТНОСТЬБЕЗОТКАЗНОЙРАБОТЫ |
||||||||||
|
СИСТЕМЫ |
||||||||||
|
Система |
||||||||||
|
0 |
200 |
400 |
600 |
800 |
1000 |
1200 |
1400 |
1600 |
1800 |
2000 |
|
Рис. 12. График вероятности безотказной работы системы. |
IV. ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Самостоятельное определение плотность распределения времени до отказа, ин-
тенсивность отказов каждого элемента. Решение необходимо получить в виде таблиц и графиков.
9
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Функция ГАММА в Excel используется для расчета значения, которое принимает гамма-функция для некоторого числа r, и возвращает соответствующее числовое значение.
Гамма-функция имеет следующий вид:
Здесь r является некоторым положительным числом, отличным от нуля.
Пример взаимосвязи функций ГАММА и ФАКТР в Excel
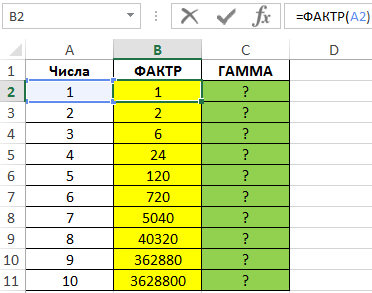
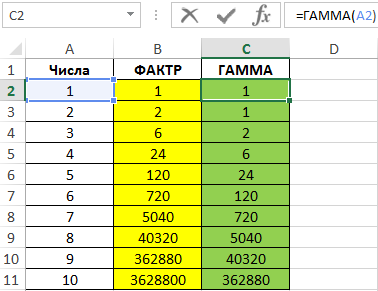
Пример 1. Согласно одному из свойства гамма-функции, между ней и факториалом чисел существует определенная взаимосвязь: ГАММА(x)=ФАКТР(x-1). Подтвердить справедливость этого равенства с помощью Excel.
Введем последовательный ряд чисел от 1 до 10 и ррассчитаем факториалы чисел с помощью формулы:
Для расчета значений гамма-функции используем следующую формулу и получаем результат:
Как видно, начиная с числа из ячейки A3, каждое текущее значение факториала соответствует последующему значению гамма-функции.
Вычисление гамма-функции и корня числа Пи в Excel
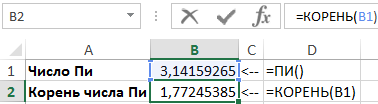
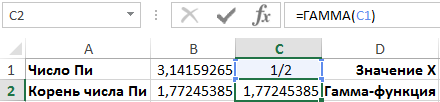
Пример 2. Известно, что значение гамма-функции при заданном параметре x равном ½ соответствует корню из константы Пи. Доказать справедливость этого суждения с помощью Excel. Для нахождения числа Пи используем функцию Excel: =ПИ(), а для корня с числа Пи воспользуемся формулой: =КОРЕНЬ(ПИ()), как показано ниже на рисунке:
Для решения используем следующее выражение формулой:
В ячейках B2 и C2 проверяем равенство результатов вычисления корня квадратного (функция КОРЕНЬ) из константы Пи (функция ПИ) и значения гамма-функции для числа ½.
Особенности синтаксиса функции ГАММА в Excel
Функция имеет следующую синтаксическую запись:
=ГАММА(x)
Единственным аргументом, обязательным для заполнения, является x – числовое значение, являющееся одним из параметров гамма-распределения.
Примечания:
- Аргумент x принимает числовые значения из диапазона от 0 (не включительно) до бесконечности со знаком плюс. Если аргумент указан отрицательным числом или нулем, функция вернет код ошибки #ЧИСЛО!
- Рассматриваемая функция выполняет промежуточные преобразования типов данных. Например, =ГАММА(ИСТИНА) вернет значение 1, =ГАММА(“4”) вернет значение 6.
- Если в качестве аргумента x было введено не преобразуемое к числовым данным значение, результатом выполнения функции будет код ошибки #ЗНАЧ!.
Рассмотрим Гамма распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL
ГАММА.РАСП()
построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметров распределения.
Гамма распределение
(англ.
Gamma
distribution
)
зависит от 2-х параметров:
r
(определяет форму распределения) и λ (определяет масштаб).
Плотность вероятности
этого распределения задается следующей формулой:
где Г(r) – гамма-функция:
если r – положительное целое, то Г(r)=(r-1)!
СОВЕТ
: Подробнее о
Функции распределения
и
Плотности вероятности
см. статью
Функция распределения и плотность вероятности в MS EXCEL
.
Вышеуказанная форма записи
плотности распределения
наглядно показывает его связь с
Экспоненциальным распределением
. При r=1
Гамма распределение
сводится к
Экспоненциальному распределению
с параметром λ.
Если параметр λ – целое число, то
Гамма распределение
является суммой
r
независимых и одинаково распределенных по
экспоненциальному закону
с параметром λ случайных величин
x
. Таким образом, случайная величина
y
=
x
1
+
x
2
+…
x
r
имеет
гамма распределение
с параметрами
r
и λ.
Экспоненциальное распределение
, в свою очередь, тесно связано с дискретным
распределением Пуассона
. Если
Распределение Пуассона
описывает число случайных событий, произошедших за определенный интервал времени, то
Экспоненциальное распределение,
в этом случае,описывает длину временного интервала между двумя последовательными событиями.
Из этого следует, что, например, если время до наступления первого события описывается
экспоненциальным распределением
с параметром λ, то время до наступления второго события описывается
гамма распределением
с r = 2 и тем же параметром λ.
Гамма распределение в MS EXCEL
В MS EXCEL принята эквивалентная, но отличающаяся параметрами форма записи
плотности
гамма распределения
.
Параметр α (
альфа
) эквивалентен параметру
r
, а параметр
b
(
бета
) – параметру
1/λ
. Ниже будем придерживаться именно такой записи, т.к. это облегчит написание формул.
В MS EXCEL, начиная с версии 2010, для
Гамма распределения
имеется функция
ГАММА.РАСП()
, английское название — GAMMA.DIST(), которая позволяет вычислить
плотность вероятности
(см. формулу выше) и
интегральную функцию распределения
(вероятность, что случайная величина X, имеющая
гамма распределение
, примет значение меньше или равное x).
Примечание
: До MS EXCEL 2010 в EXCEL была функция
ГАММАРАСП()
, которая позволяет вычислить
интегральную функцию распределения
и
плотность вероятности
.
ГАММАРАСП()
оставлена в MS EXCEL 2010 для совместимости.
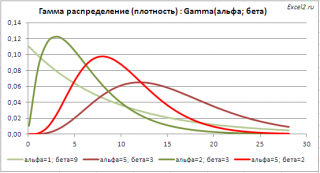
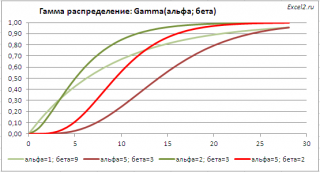
Графики функций
В
файле примера
приведены графики
плотности распределения вероятности
и
интегральной функции распределения
.
Гамма распределение
имеет обозначение Gamma
(альфа; бета).
Примечание
: Для построения
функции распределения
и
плотности вероятности
можно использовать диаграмму типа
График
или
Точечная
(со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью
Основные типы диаграмм
.
Примечание
: Для удобства написания формул в
файле примера
для параметров распределения
альфа и бета
созданы соответствующие
Имена
.
Примечание
: Зависимость от 2-х параметров позволяет построить распределения разнообразных форм, что расширяет применение этого распределения.
Гамма распределение
, как и
Экспоненциальное распределение
часто используется для расчета времени ожидания между случайными событиями. Кроме того, возможно использование применение этого распределения для моделирования уровня осадков и при проектировании дорог.
Как было показано выше, если параметр
альфа
= 1, то функция
ГАММА.РАСП()
возвращает
экспоненциальное распределение
с параметром
1/бета
. Если параметр
бета
= 1, функция
ГАММА.РАСП()
возвращает стандартное
гамма распределение
.
Примечание
: Т.к.
ХИ2-распределение
является частным случаем
гамма распределения
, то формула
=ГАММА.РАСП(x;n/2;2;ИСТИНА
) для целого положительного n возвращает тот же результат, что и формула
=ХИ2.РАСП(x;n; ИСТИНА)
или
=1-ХИ2.РАСП.ПХ(x;n)
. А формула
=ГАММА.РАСП(x;n/2;2;ЛОЖЬ)
возвращает тот же результат, что и формула
=ХИ2.РАСП(x;n; ЛОЖЬ)
, т.е.
плотность вероятности
ХИ2-распределения.
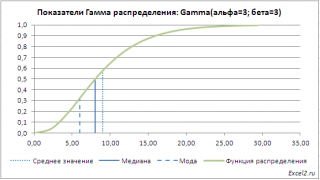
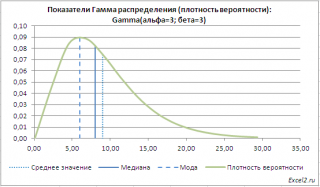
В
файле примера на листе Графики
приведен расчет
Среднего значения (математического ожидания)
гамма распределения
равного
альфа*бета
и
дисперсии (квадрата стандартного отклонения)
равного
альфа*бета
2
. Там же построены графики
функции распределения
и
плотности вероятности
с отмеченными значениями
среднего
,
медианы
и
моды
.
Генерация случайных чисел и оценка параметров
Для генерирования массива чисел, имеющих
гамма распределение
, можно использовать формулу
=ГАММА.ОБР(СЛЧИС(); альфа; бета)
Функция
СЛЧИС()
генерирует
непрерывное равномерное распределение
от 0 до 1, что как раз соответствует диапазону изменения вероятности (см.
файл примера лист Генерация
).
Если случайные числа содержатся в диапазоне
B15:B214
, то оценку параметра
альфа
можно сделать с использованием формулы
=СРЗНАЧ(B15:B214)^2/ДИСП.В(B15:B214)
Для оценки параметра
бета
используйте формулу
=ДИСП.В(B15:B214)/СРЗНАЧ(B15:B214)
СОВЕТ
: О других распределениях MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Функция ГАММА.РАСП возвращает гамма-распределение.
Описание функции ГАММА.РАСП
Возвращает гамма-распределение. Эту функцию можно использовать для изучения переменных, которые имеют асимметричное распределение. Гамма-распределение широко используется при анализе систем массового обслуживания.
Синтаксис
=ГАММА.РАСП(x; альфа; бета; интегральная)Аргументы
xальфабетаинтегральная
Обязательный аргумент. Значение, для которого требуется вычислить распределение.
Обязательный аргумент. Параметр распределения.
Обязательный аргумент. Параметр распределения. Если аргумент «бета» = 1, функция ГАММА.РАСП возвращает стандартное гамма-распределение.
Обязательный аргумент. Логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция ГАММА.РАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается функция плотности распределения.вероятности.
Замечания
- Если значение аргумента «x», «альфа» или «бета» не является числом, функция ГАММА.РАСП возвращает значение ошибки #ЗНАЧ!.
- Если x < 0, функция ГАММА.РАСП возвращает значение ошибки #ЧИСЛО!.
- Если «альфа» ≤ 0 или «бета» ≤ 0, функция ГАММА.РАСП возвращает значение ошибки #ЧИСЛО!.
- Уравнение для гамма-функции плотности вероятности имеет следующий вид:
$$f(x,alpha ,beta )=frac{1}{beta ^{alpha }Gamma (alpha )}x^{alpha -1}e^{-frac{x}{beta }}$$
- Стандартная гамма-функция плотности распределения вероятности имеет следующий вид:
- Если «альфа» = 1, функция ГАММА.РАСП возвращает экспоненциальное распределение:
- Для целого положительного n, если «альфа» = n/2, «бета» = 2 и значение «интегральная» = ИСТИНА, функция ГАММА.РАСП возвращает (1 — ХИ2.РАСП.ПХ(x)) с n степенями свободы.
- Если значение аргумента «альфа» является целым положительным числом, функция ГАММА.РАСП называется также распределением Эрланга.