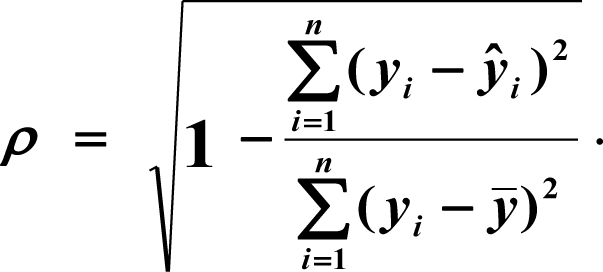Нелинейный график в excel - Word и Excel - помощь в работе с программами

Решение нелинейного уравнения в Excel

Разберём решение нелинейного уравнения в Excel вида:

y=4x 3 +2x–7

Ячейку A4 оставим пустой, а в ячейки B4 запишем формулу вида

Затем в Excel перейдём на вкладку Данные -> Поиск Решения

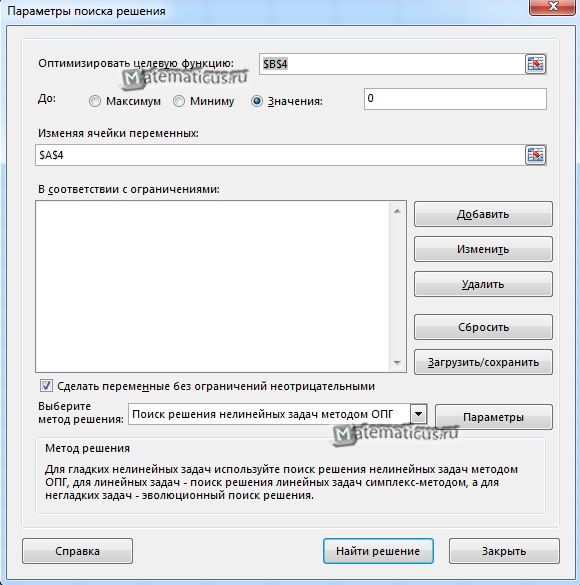
Открывается окно Параметры поиска решения. В поле оптимизировать целевую функцию выбираем ячейку B4, ставим Значения 0, ячейку переменной указываем A4, ставим галочку сделать переменные без ограничений неотрицательными, выбираем метод решения — поиск решения нелинейных задач методом ОПГ (обобщенного приведенного градиента) и жмем Найти решение

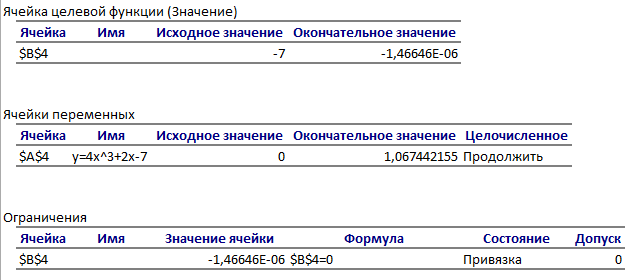
Получаем решение искомой задачи

x=1,06744215530327

Отчет результатов вычисления в Excel

Графический способ решения уравнений в среде Microsoft Excel 2007

Тип урока: Обобщение, закрепление пройденного материала и объяснение нового.

Цели и задачи урока:

повторение изученных графиков функций;
повторение и закрепление графического способа решения уравнений;
закрепление навыков записи и копирования формул, построения графиков функций в электронных таблицах Excel 2007;
формирование и первичное закрепление знаний о решении уравнений с использованием возможностей электронных таблиц Excel 2007;
формирование мышления, направленного на выбор оптимального решения;
формирование информационной культуры школьников.

Оборудование: персональные компьютеры, мультимедиапроектор, проекционный экран.

Материалы к уроку: презентация Power Point на компьютере учителя (Приложение 1).

Слайд 1 из Приложения1 ( далее ссылки на слайды идут без указания Приложения1).

Объявление темы урока.

1. Устная работа (актуализация знаний).

Слайд 2 — Соотнесите перечисленные ниже функции с графиками на чертеже (Рис. 1):

у = 6 — х; у = 2х + 3; у = (х + 3) 2 ; у = -(х — 4) 2 ; .

Слайд 3 Графический способ решения уравнений вида f(x)=0.

Корнями уравнения f(x)=0 являются значения х₁, х₂, … точек пересечения графика функции y=f(x) с осью абсцисс (Рис. 2).

Найдите корни уравнения х 2 -2х-3=0, используя графический способ решения уравнений (Рис.3).

Слайд 5 Графический способ решения уравнений вида f (x)=g (x).

Корнями уравнения f(x)=g(x) являются значения х₁, х₂, … точек пересечения графиков функций y=f(x) и у=g(x). (Рис. 4):

Слайд 6 Найдите корни уравнения , используя графический способ решения уравнений (Рис. 5).

2. Объяснение нового материала. Практическая работа.

Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае – Microsoft Excel 2007, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью (метод Подбор параметра).

I. Графический способ решения уравнений вида f(x)=0 в Excel.

Дальнейшая работа выполняется учителем в Excel одновременно с учениками с подробными (при необходимости) инструкциями и выводом результатов на проекционный экран. Слайды Приложения 1 используются для формулировки задач и подведения промежуточных итогов.

Пример1: Используя средства построения диаграмм в Excel, решить графическим способом уравнение —х 2 +5х-4=0.

Для этого: построить график функции у=-х 2 +5х-4 на промежутке [ 0; 5 ] с шагом 0,25; найти значения х точек пересечения графика функции с осью абсцисс.

Выполнение задания можно разбить на этапы:

1 этап: Представление функции в табличной форме (рис. 6):

в ячейку А1 ввести текст Х, в ячейку A2 — Y;

в ячейку В1 ввести число 0, в ячейку С1 – число 0,25;

выделить ячейки В1:С1, подвести указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму черного крестика, протянуть маркер выделения вправо до ячейки V1 (Рис. 7).

При вводе формулы можно вводить адрес ячейки с клавиатуры (не забыть переключиться на латиницу), а можно просто щелкнуть мышью на ячейке с нужным адресом.

После ввода формулы в ячейке окажется результат вычисления по формуле, а в поле ввода строки формул — сама формула (Рис. 8):

скопировать содержимое ячейки B2 в ячейки C2:V2 за маркер выделения. Весь ряд выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.

2 этап: Построение диаграммы типа График.

выделить диапазон ячеек B2:V2;

на вкладке Вставка|Диаграммы|График выбрать вид График;

на вкладке Конструктор|Выбрать данные (Рис. 9) в открывшемся окне «Выбор источника данных» щелкнуть по кнопке Изменить в поле Подписи горизонтальной оси — откроется окно «Подписи оси». Выделить в таблице диапазон ячеек B1:V1 (значения переменной х). В обоих окнах щелкнуть по кнопкам ОК;

на вкладке Макет|Оси|Основная горизонтальная ось|Дополнительные параметры основной горизонтальной оси выбрать:

Интервал между делениями: 4;

Интервал между подписями: Единица измерения интервала: 4;

Положение оси: по делениям;

Выбрать ширину и цвет линии (Вкладки Тип линии и Цвет линии);

самостоятельно изменить ширину и цвет линии для вертикальной оси;
на вкладке Макет|Сетка|Вертикальные линии сетки по основной оси выбрать Основные линии сетки.

Примерный результат работы приведен на рис. 10:

3 этап: Определение корней уравнения.

График функции у=-х 2 +5х-4 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня: х₁=1; х₂=4.

II. Графический способ решения уравнений вида f(x)=g(x) в Excel.

Пример 2: Решить графическим способом уравнение .

Для этого: в одной системе координат построить графики функций у₁= и у₂=1-х на промежутке [ -1; 4 ] с шагом 0,25; найти значение х точки пересечения графиков функций.

1 этап: Представление функций в табличной форме (рис. 1):

Перейти на Лист2.

Аналогично Примеру 1, применив приемы копирования, заполнить таблицу. При табулировании функции у₁=воспользоваться встроенной функцией Корень (Рис. 11).

2 этап: Построение диаграммы типа График.

Выделить диапазон ячеек (А2:V3);

Аналогично Примеру 1 вставить и отформатировать диаграмму типа График, выбрав дополнительно в настройках горизонтальной оси: вертикальная ось пересекает в категории с номером 5.

Примерный результат работы приведен на Рис. 12:

3 этап: Определение корней уравнения.

Графики функций у₁= и у₂=1-х пересекаются в одной точке (0;1) и, следовательно, уравнение имеет один корень – абсцисса этой точки: х=0.

III. Метод Подбор параметра.

Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в специально подобранных примерах 1 и 2.

Возможности электронных таблиц позволяют находить приближенные значения коней уравнения с заданной точностью. Для этого используется метод Подбор параметра.

Пример 3: Разберем метод Подбор параметра на примере решения уравнения —х 2 +5х-3=0.

1 этап: Построение диаграммы типа График для приближенного определения корней уравнения.

Построить график функции у=—х 2 +5х-3, отредактировав полученные в Примере 1 формулы.

выполнить двойной щелчок по ячейке B2, внести необходимые изменения;

с помощью маркера выделения скопировать формулу во все ячейки диапазона C2:V2.

Все изменения сразу отобразятся на графике.

Примерный результат работы приведен на Рис. 13:

2 этап: Определение приближенных значений корней уравнения.

График функции у=-х 2 +5х-3 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня.

По графику приближенно можно определить, что х₁≈0,7; х₂≈4,3.

3 этап: Поиск приближенного решения уравнения с заданной точностью методом Подбор параметра.

1) Начать с поиска более точного значения меньшего корня.

По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 0,75. В таблице значений функции этот аргумент размещается в ячейке E1.

Выделить ячейку Е2;

перейти на вкладку Данные|Анализ «что-если»|Подбор параметра…;

В открывшемся диалоговом окне Подбор параметра (Рис. 14) в поле Значение ввести требуемое значение функции: 0.

В поле Изменяя значение ячейки: ввести $E$1 (щелкнув по ячейке E1).

Щелкнуть по кнопке ОК.

В окне Результат подбора (Рис. 15) выводится информация о величине подбираемого и подобранного значения функции:

В ячейке E1 выводится подобранное значение аргумента 0,6972 с требуемой точностью (0,0001).

Установить точность можно путем установки в ячейках таблицы точности представления чисел – числа знаков после запятой (Формат ячеек|Число|Числовой).

Итак, первый корень уравнения определен с заданной точностью: х₁≈0,6972.

2) Самостоятельно найти значение большего корня с той же точностью. (х₂≈4,3029).

IV. Метод Подбор параметра для решения уравнений вида f(x)=g(x).

При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения х точек пересечения графика функции y(x) с осью абсцисс.

3. Закрепление изученного материала. Самостоятельная работа.

Задание: Используя метода Подбор параметров, найти корни уравнения с точностью до 0,001.

ввести функцию у=и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):

найти приближенное значение х точки пересечения графика функции с осью абсцисс (х≈1,4);

найти приближенное решение уравнения с точностью до 0,001 методом Подбор параметра (х≈1,438).

4. Итог урока.

Слайд 12 Проверка результатов самостоятельной работы.

Слайд 13 Повторение графического способа решения уравнения вида f(x)=0.

Слайд 14 Повторение графического способа решения уравнения вида f(x)=g(x).

5. Домашнее задание.

Используя средства построения диаграмм в Excel и метод Подбор параметра, определите корни уравнения х 2 -5х+2=0 с точностью до 0,01.

Решение нелинейных уравнений в Excel и Mathcad (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Кафедра прикладной математики и вычислительной техники

Решение нелинейных уравнений в Excel и Mathcad

к выполнению лабораторных работ

по дисциплине «Вычислительная математика»

Решение нелинейных уравнений в Excel и Mathcad: Метод. указ. / Сост. , — Самара: СГАСУ, 20с.

Методические указания разработаны в соответствии с Государственным образовательным стандартом изучения дисциплины «Вычислительная математика».

Рассмотрена реализация численных методов при решении нелинейных уравнений и систем уравнений в Excel и MathCad. Приведены варианты заданий для индивидуального выполнения и вопросы для самоконтроля и тестирования.

Предназначены для студентов специальности 230201 – «Информационные системы и технологии» всех форм обучения.

Рецензент к. ф-м. н.

Ó , составление, 2012

1 Решение нелинейного уравнения

1.1 Общие сведения о решении нелинейного уравнения

1.2 Отделение корней

1.3 Уточнение корней стандартными средствами Excel и Mathcad

1.4 Метод деления отрезка пополам

1.6 Метод Ньютона (касательных)

1.7 Комбинированный метод

1.8 Метод итераций

2 Решение систем нелинейных уравнений

2.1 Общие сведения о решении систем нелинейных уравнений

2.2 Решение систем нелинейных уравнений методом Ньютона

2.3 Решение систем нелинейных уравнений методами итераций

3 Задания к лабораторным работам

Лабораторная № 1. Отделение корней и стандартные инструменты решения нелинейного уравнения

Лабораторная № 2. Сравнение методов уточнения корней нелинейного уравнения

Лабораторная № 3. Решение систем нелинейных уравнений

Лабораторная № 4. Программирование методов решения нелинейных уравнений и систем

4 Вопросы и тесты для самоконтроля

Список рекомендуемой литературы

1 Решение нелинейного уравнения

1.1 Общие сведения о решении нелинейного уравнения

Как правило, нелинейное уравнения общего вида f(х)=0 невозможно решить аналитически. Для практических задач достаточно найти приближенное значение x, в определенном смысле близкое к точному решению уравнения хточн.

В большинстве случаев поиск приближенного решения включает два этапа. На первом этапе отделяют корни, т. е. находят такие отрезки, внутри которых находится строго один корень. На втором этапе уточняют корень на одном из таких отрезков, т. е. находят его значение с требуемой точностью.

Достигнутая точность может оцениваться либо «по функции» (в найденной точке x, функция достаточно близка к 0, т. е. выполняется условие |f(x)|≤ ef, где ef требуемая точность по оси ординат), либо «по аргументу» (найден достаточно маленький отрезок [a,b], внутри которого находится корень, т. е. |b–a|≤ ex, где ex требуемая точность по оси абсцисс).

1.2 Отделение корней

Отделение корней может производиться сочетанием графического и аналитического исследования функции. Такое исследование опирается на теорему Вейерштрасса, в соответствии с которой для непрерывной на отрезке [a,b] функции f(х) и любого числа y, отвечающего условию f(a)≤y≤f(b), существует на этом отрезке точка x, в которой функция равна y. Следовательно, для непрерывной функции достаточно найти отрезок, на концах которого функция имеет разные знаки, и можно быть уверенным, что на этом отрезке есть корень уравнения f(х)=0.

Для ряда методов уточнения желательно, чтобы найденный на первом этапе отрезок содержал только один корень уравнения. Это условие выполняется, если функция на отрезке монотонна. Монотонность, можно проверить либо по графику функции, либо по знаку производной.

Пример Найти с точностью до целых все корни нелинейного уравнения y(x)=x3 ‑ 10x + 7=0 а) построив таблицу и б) построив график. Найти корень уравнения на выделенном отрезке, используя опции «Подбор параметра» и «Поиск решения».

Решение Создадим в Excel таблицу, содержащую аргументы и значения функции и по ней построим точечную диаграмму. На рисунке 1 приведен снимок решения.

На графике видно, что уравнение имеет три корня, принадлежащие отрезкам [-4, -3], [0, 1] и [2, 3]. Эти отрезки можно выявить и наблюдая за сменой знаков функции в таблице. По построенному графику можно сделать вывод, что на указанных отрезках функция f(x) монотонна и, следовательно, на каждом из них содержится только по одному корню.

Такой же анализ может быть выполнен и в пакете Mathcad. Для этого достаточно набрать определение функции f(x), используя оператор присваивания (:=) и естественные общепринятые обозначения математических операций и стандартных функций, задать цикл для изменения аргумента, например, а затем вывести на экран таблицу значений функции (расположенными в одной строке командами x= f(x)=) и график. Цикл можно задать, например, командой x:=-5,-4.5…5. Шаг цикла формируется путем задания начального и следующего за ним значений переменной, а перед конечным значением переменной ставится точка с запятой, которая будет визуально отображена на экране в виде многоточия.

Рисунок 1 – Таблица и график для отделения корней нелинейного уравнения

1.3 Уточнение корней стандартными средствами Excel и Mathcad

Во всех методах уточнения корней необходимо задать начальное приближение, которое затем и будет уточняться. Если уравнение имеет несколько корней, в зависимости от выбранного начального приближения будет найден один из них. При неудачно выбранном начальном приближении решение может и не быть найдено. Если в результате первого этапа расчетов уже выделен отрезок, содержащий единственный корень уравнения, в качестве начального приближения можно взять любую точку этого отрезка.

В Excel для уточнения значений корней можно использовать опции «Подбор параметра» и «Поиск решения». Пример оформления решения приведен на рисунках 2 и 3.

Рисунок 2 – Ввод значений для использования средств решения уравнения в Excel

Рисунок 3 – Результаты использования средств решения уравнения в Excel

В Mathcad для уточнения корней уравнения можно использовать функцию root(….) или блок решения. Пример использования функции root(…) приведен на рисунке 4, а блока решения на рисунке 5. Следует обратить внимание, что в блоке решения (после заголовка блока Given) между левой и правой частями уравнения должен стоять жирный знак равенства (тождества), который можно получить выбором из соответствующей палитры инструментов, либо нажатием одновременно клавиши Ctrl и =.

Рисунок 4 – Решение уравнения с использованием функции root(…) в Mathcad

Рисунок 5 – Решение уравнения с использованием блока решения в Mathcad

Как видим, каждый стандартный инструмент находит решение уравнения с определенной точностью. Эта точность зависит от метода, используемого в пакете и, в определенной степени, настроек пакета. Управлять точностью результата здесь достаточно сложно, а часто и невозможно.

В то же время, очень просто построить собственную таблицу или написать программу, реализующие один из методов уточнения корней. Здесь можно использовать критерии точности расчета, задаваемые пользователем. При этом достигается и понимание процесса расчетов без опоры на принцип Митрофанушки: «Извозчик есть, довезет».

Далее рассмотрены несколько наиболее распространенных методов. Отметим очевидный момент: при прочих равных условиях тот метод уточнения корней будет более эффективен, в котором результат с той же погрешностью найден с меньшим числом вычислений функции f(x) (при этом достигается и максимальная точность при одинаковом числе вычислений функции).

1.4 Метод деления отрезка пополам

В этом методе на каждом шаге отрезок делится на две равные части. Затем сравнивают знаки функции на концах каждой из двух половинок (например, по знаку произведения значений функций на концах), определяют ту из них, в которой содержится решение (знаки функции на концах должны быть разные), и. сужают отрезок, перенося в найденную точку его границу (а или b). Условием окончания служит малость отрезка, где содержится корень («точность по x»), либо близость к 0 значения функции в средине отрезка («точность по y»). Решением уравнения считают середину отрезка, найденного на последнем шаге.

Пример. Построить таблицу для уточнения корня уравнения x3 –10x+7=0 на отрезке [-4, -3] методом деления отрезка пополам. Определить сколько шагов надо сделать методом деления отрезка пополам и какая при этом достигается точность по х, для достижения точности по y, равной 0,1; 0,01; 0, 001.

Решение Для решения можно использовать табличный процессор Excel, позволяющий автоматически продолжать строки. На первом шаге заносим в таблицу значения левого и правого концов выбранного начального отрезка и вычисляем значение середины отрезка с=(a+b)/2, а затем вводим формулу для вычисления функции в точке a (f(a)) и растягиваем (копируем) её для вычисления f(c) и f(b). В последнем столбца вычисляем выражение (b—a)/2, характеризующего степень точности вычислений. Все набранные формулы можно скопировать во вторую строку таблицы.

На втором шаге нужно автоматизировать процесс поиска той половины отрезка, где содержится корень. Для этого испльзуется логическая функция ЕСЛИ (Меню: ВставкаФункцияЛогические). Для нового левого края отрезка мы проверяем истинность условия f(a)*f(c)>0, если оно верно, то мы в качестве нового значения левого конца отрезка берем число c (т. к. это условие показывает, что корня на отрезке [a, c] нет), иначе оставляем значение a. Аналогично, для нового правого края отрезка мы проверяем истинность условия f(c)*f(b)>0, если оно верно, то мы в качестве нового значения правого конца отрезка берем число c (т. к. это условие показывает, что корня на отрезке [c, b] нет), иначе оставляем значение b.

Вторую строку таблицы можно продолжить (скопировать) на необходимое число последующих строк.

Итерационный процесс завершается, когда очередное значение в последнем столбце становится меньшим, чем заданный показатель точности ex. При этом, значение середины отрезка в последнем приближении, принимается в качестве приближенного значения искомого корня нелинейного уравнения. На рисунке 6 приведен снимок решения. Для построения аналогичного процесса в Mathcad можно использовать бланк, подобный приведенному на рисунке 7. Число шагов N может варьироваться до достижения в таблице результатов требуемой точности. При этом таблица будет автоматически удлиняться или укорачиваться.

Итак, одним из трех корней нелинейного уравнения x3 – 10x + 7=0, найденным с точностью e=0,0001, является x= — 3,46686. Как мы видим, он действительно принадлежит отрезку [-4; -3].

Рисунок 6 – Уточнение корня методом деления отрезка пополам в Excel

Рисунок 7 – Уточнение корня методом деления отрезка пополам в Mathcad

1.5 Метод хорд

В этом методе нелинейная функция f(x) на отделенном интервале [а, b] заменяется линейной – уравнением хорды, т. е. прямой соединяющей граничные точки графика на отрезке. Условие применимости метода – монотонность функции на начальном отрезке, обеспечивающая единственность корня на этом отрезке. Расчет по методу хорд аналогичен расчету методом деления отрезка пополам, но теперь на каждом шаге новая точка x внутри отрезка [a,b] рассчитывается по любой из следующих формул:

.

1.6 Метод Ньютона (касательных)

Идея, на которой основан метод, аналогична той, которая реализована в методе хорд, только на каждом шаге кривая f(x) заменяется касательной к ней, проведенной в предыдущей найденной точке. В качестве начальной точки в зависимости от свойств функции берется или левая граница отрезка, содержащего корень – x0 = а (если f(а) f»(х) > 0), или правая его граница: x0 = b (если f(b) f»(х)>0). Расчет нового приближения на следующем шаге i+1 производится по формуле:

.

Алгоритм применим для монотонных функций, сохраняющих выпуклость или вогнутость в промежутке между начальным приближением и корнем уравнения (т. е. должен сохраняться знак первой и второй производных функции f(x)). работоспособен при выпуклых и монотонных функциях f(x). В расчетах нет необходимости отслеживать две границы отрезка, поэтому достаточно на каждом шаге вычислять значения x, f(x) и f′(x). При этом легко оценить «точность по y», по значению левой части уравнения на очередном шаге. Для оценки «точности по x» нужно отслеживать разницу приближений на предыдущем и последующих шагах, которая связана с разницей между найденным приближением и точным значением корня.

Следует обратить внимание на следующую особенность метода: последовательность x1, x2, x3,… приближается к корню с другой стороны, в отличие от использования метода хорд при прочих равных условиях.

Главным достоинством метода касательных является квадратичная скорость сходимости, что во многих случаях может привести к сокращению числа вычислений функции.

Уточнить корень уравнения tg (0,55x+0,1) – x2=0 на отрезке [0.6, 0.8] методом касательных до точности 0,001.

Точность вычислений можно оценить из соотношения

2 Решение систем нелинейных уравнений

2.1 Общие сведения о решении систем нелинейных уравнений

Систему n нелинейных уравнений с n неизвестными x1, x2, . xn записывают в виде:

где F1, F2,…, Fn – функции независимых переменных, среди которых есть нелинейные.

Как и в случае систем линейных уравнений, решением системы является такой вектор X*, который при подстановке обращает одновременно все уравнения системы в тождества.

Система уравнений может не иметь решений, иметь единственное решение, конечное или бесконечное количество решений. Вопрос о количестве решений должен решаться для каждой конкретной задачи отдельно.

Численные методы решения системы уравнений носят итерационный характер и требуют задания начального приближения X0.

Рассмотрим две группы таких методов: метод Ньютона с различными его модификациями и методы итераций (простых итераций и Зейделя).

2.2 Решение систем нелинейных уравнений методом Ньютона

Будем рассматривать этот метод на примере системы двух нелинейных уравнений с двумя неизвестными:

Начальные значения x0 и y0 определяются графически. Для нахождения каждого последующего приближения (xi+1, yi+1) используют вектор значений функций и матрицу значений их первых производных, рассчитанные в предыдущей точке (xi, yi).

,

Для расчета новых приближений на шаге i+1 используется матричная формула

.

Следует обратить внимание, что в последней формуле используется вычисление матрицы, обратной к матрице первых производных.

Расчет останавливают при выполнении одного (а иногда и обоих) из двух условий. Первое из них заключается в том, что на очередном шаге максимальное по модулю из изменений аргументов x и y становится меньше заданная погрешность по аргументам. В соответствии со вторым из условий, на очередном шаге максимальное по модулю значение левых частей уравнений должно отличаться от нуля меньше, чем заданная погрешность по функциям.

В упрощенном методе Ньютона матрица производных и матрица, обратная к ней вычисляются только один раз (в начальной точке) и для расчетов используется матричная формула

.

Приведенные формулы особенно легко записать в Mathcad, где имеются операторы для вычисления производных и действий с матрицами. Однако при правильном использовании матричных операций эти формулы достаточно просто записываются и в Excel. Правда, здесь придется заранее получить формулы для вычисления производных. Для аналитического вычисления производных также может быть использован Mathcad.

2.3 Решение систем нелинейных уравнений методами итераций

Для реализации этих методов исходную систему уравнений необходимо путем алгебраических преобразований явно выразить каждую переменную через остальные. Для случая двух уравнений с двумя неизвестными новая система будет иметь вид

.

Для решения такой системы задаются начальным приближением x0, y0. Уточненные решения получают по шагам, подставляя в правые части уравнений значения, найденные на предыдущем шаге. В методе простых итераций для уточнения решения используют формулы:

.

Если одно из решений системы и начальные значения x0 и y0 лежат в области D, задаваемой неравенствами: a ≤ x ≤ b, c ≤ y ≤ d, то расчет по методу простых итераций сходится при выполнении в области D соотношений:

источники:

http://urok.1sept.ru/articles/564361

http://pandia.ru/text/78/157/38912.php

Источник

Nonlinear regression is a regression technique that is used when the relationship between a predictor variable and a response variable does not follow a linear pattern.

The following step-by-step example shows how to perform nonlinear regression in Excel.

Step 1: Create the Data

First, let’s create a dataset to work with:

Step 2: Create a Scatterplot

Next, let’s create a scatterplot to visualize the data.

First, highlight the cells in the range A1:B21. Next, click the Insert tab along the top ribbon, and then click the first plot option under Scatter:

The following scatterplot will appear:

Step 3: Add a Trendline

Next, click anywhere on the scatterplot. Then click the + sign in the top right corner. In the dropdown menu, click the arrow next to Trendline and then click More Options:

In the window that appears to the right, click the button next to Polynomial. Then check the boxes next to Display Equation on chart and Display R-squared value on chart.

This produces the following curve on the scatterplot:

Note that you may need to experiment with the value for the Order of the polynomial until you find the curve that best fits the data.

Step 4: Write the Regression Equation

From the plot we can see that the equation of the regression line is as follows:

y = -0.0048x⁴ + 0.2259x³ – 3.2132x² + 15.613x – 6.2654

The R-squared tells us the percentage of the variation in the response variable that can be explained by the predictor variables.

The R-squared for this particular curve is 0.9651. This means that 96.51% of the variation in the response variable can be explained by the predictor variables in the model.

Additional Resources

How to Perform Simple Linear Regression in Excel
How to Perform Multiple Linear Regression in Excel
How to Perform Logarithmic Regression in Excel
How to Perform Exponential Regression in Excel

Источник

Нелинейная регрессия в Excel

Добрый день, уважаемые читатели блога! Сегодня мы поговорим о нелинейных регрессиях. Решение линейных регрессий можно посмотреть по ССЫЛКЕ.

Данный способ применяется, в основном, в экономическом моделировании и прогнозировании. Его цель – пронаблюдать и выявить зависимости между двумя показателями.

Основными типами нелинейных регрессий являются:

полиномиальные (квадратичная, кубическая);
гиперболическая;
степенная;
показательная;
логарифмическая.

Также могут применяться различные комбинации. Например, для аналитики временных рядов в банковской сфере, страховании, демографических исследованиях используют кривую Гомпцера, которая является разновидностью логарифмической регрессии.

В прогнозировании с помощью нелинейных регрессий главное выяснить коэффициент корреляции, который покажет нам есть ли тесная взаимосвязь меду двумя параметрами или нет. Как правило, если коэффициент корреляции близок к 1, значит связь есть, и прогноз будет довольно точен. Ещё одним важным элементом нелинейных регрессий является средняя относительная ошибка (А), если она находится в промежутке <8…10%, значит модель достаточно точна.

На этом, пожалуй, теоретический блок мы закончим и перейдём к практическим вычислениям.

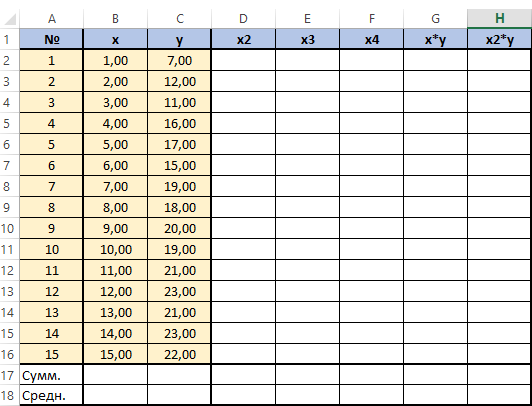
У нас имеется таблица продаж автомобилей за промежуток 15 лет (обозначим его X), количество шагов измерений будет аргумент n, также имеется выручка за эти периоды (обозначим её Y), нам нужно спрогнозировать какова будет выручка в дальнейшем. Построим следующую таблицу:

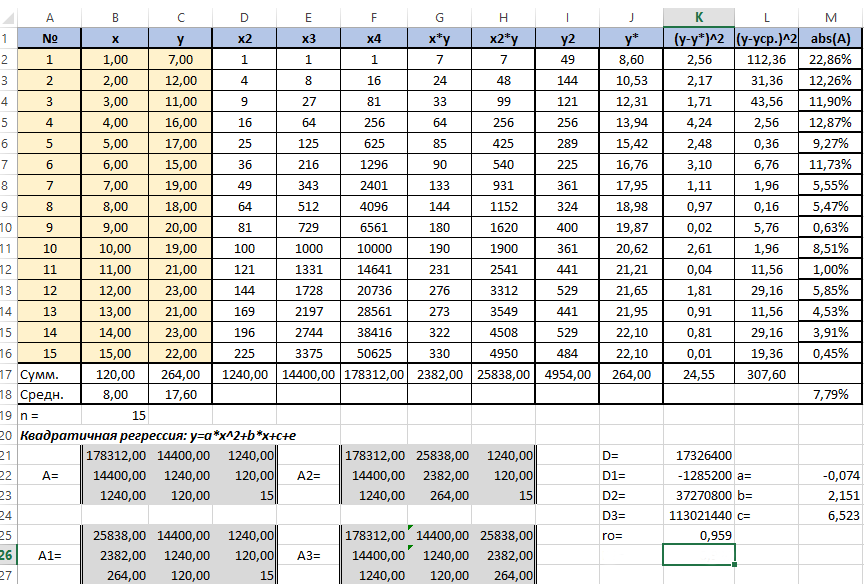
Для исследования нам потребуется решить уравнение (зависимости Y от X): y=ax²+bx+c+e. Это парная квадратичная регрессия. Применим в этом случае метод наименьших квадратов, для выяснения неизвестных аргументов — a, b, c. Он приведёт к системе алгебраических уравнений вида:

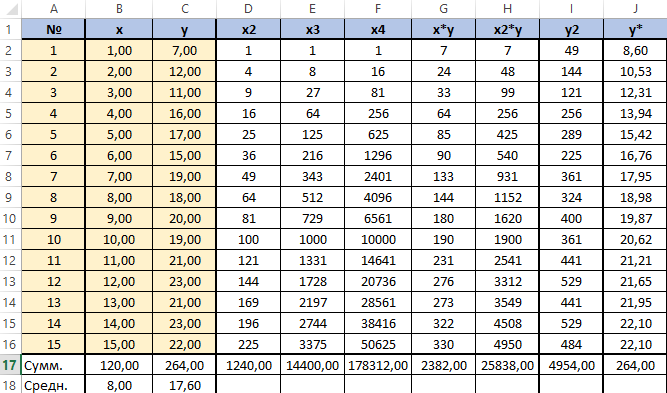
Для решения этой системы воспользуемся, к примеру, методом Крамера. Видим, что входящие в систему суммы являются коэффициентами при неизвестных. Для их вычисления добавим в таблицу несколько столбцов (D,E,F,G,H) и подпишем соответственно смыслу вычислений — в столбце D возведём x в квадрат, в E в куб, в F в 4 степень, в G перемножим показатели x и y, в H возведём x в квадрат и перемножим с y.

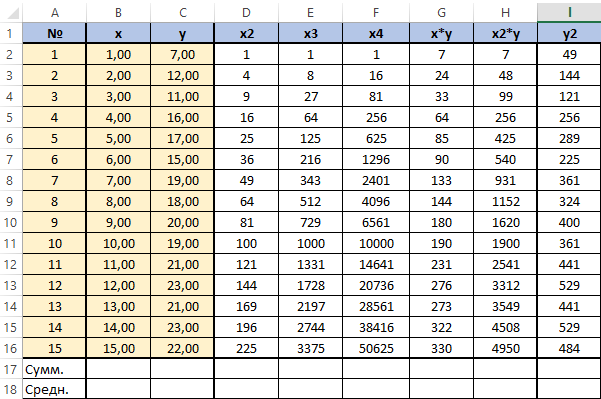
Получится заполненная нужными для решения уравнения таблица вида.

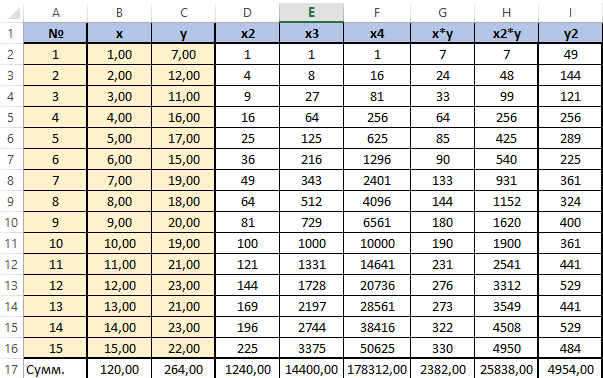
Далее посчитаем суммы по каждому столбцу — воспользуемся ∑ в программе Excel.

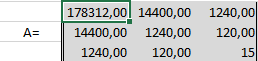
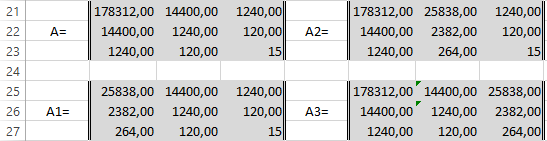
Сформируем матрицу A системы, состоящую из коэффициентов при неизвестных в левых частях уравнений. Поместим её в ячейку А22 и назовём «А=«. Следуем той системе уравнений, которую мы избрали для решения регрессии.

То есть, в ячейку B21 мы должны поместить сумму столбца, где возводили показатель X в четвёртую степень — F17. Просто сошлёмся на ячейку — «=F17». Далее нам необходима сумма столбца где возводили X в куб — E17, далее идём строго по системе. Таким образом, нам необходимо будет заполнить всю матрицу.

В соответствии с алгоритмом Крамера наберём матрицу А1, подобную А, в которой вместо элементов первого столбца должны размещаться элементы правых частей уравнений системы. То есть сумма столбца X в квадрате умноженная на Y, сумма столбца XY и сумма столбца Y.

Также нам понадобятся ещё две матрицы — назовём их А2 и А3 в которых второй и третий столбцы будут состоять из коэффициентов правых частей уравнений. Картина будет такова.

Следуя избранному алгоритму, нам нужно будет вычислить значения определителей (детерминантов, D) полученных матриц. Воспользуемся формулой МОПРЕД. Результаты разместим в ячейках J21:K24.

Расчёт коэффициентов уравнения по Крамеру будем производить в ячейках напротив соответствующих детерминантов по формуле: a (в ячейке M22) — «=K22/K21»; b (в ячейке M23) — «=K23/K21»; с (в ячейке M24) — «=K24/K21».

Получим наше искомое уравнение парной квадратичной регрессии:

y=-0,074x²+2,151x+6,523

Оценим тесноту линейной связи индексом корреляции.

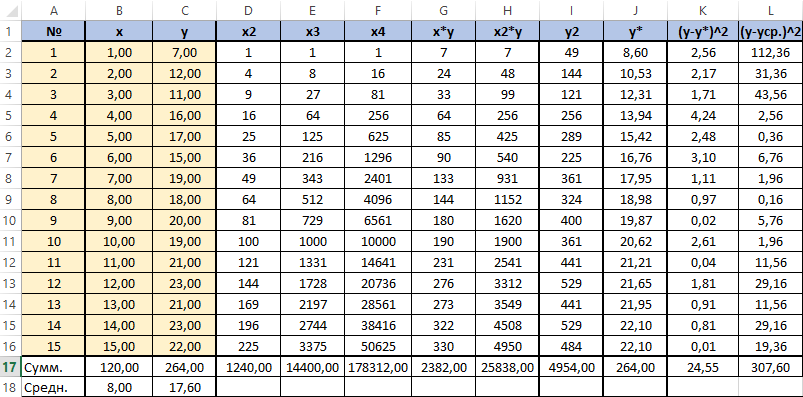
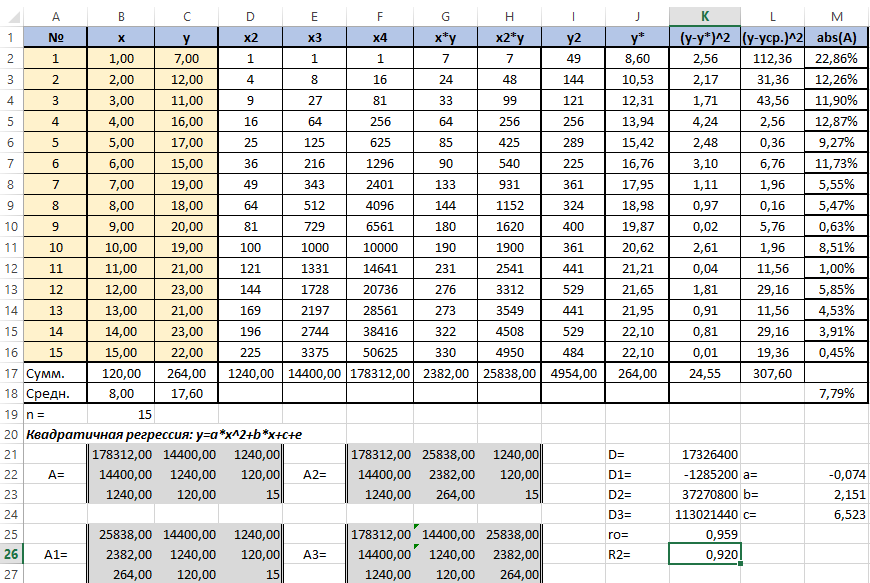
Для вычисления добавим в таблицу дополнительный столбец J (назовём его y*). Расчёта будет следующей (согласно полученному нами уравнению регрессии) — «=$m$22*B2*B2+$M$23*B2+$M$24». Поместим её в ячейку J2. Останется протянуть вниз маркер автозаполнения до ячейки J16.

Для вычисления сумм (Y-Y усредненное)² добавим в таблицу столбцы K и L с соответствующими формулами. Среднее по столбцу Y посчитаем с помощью функции СРЗНАЧ.

В ячейке K25 разместим формулу подсчёта индекса корреляции — «=КОРЕНЬ(1-(K17/L17))».

Видим, что значение 0,959 очень близко к 1, значит между продажами и годами есть тесная нелинейная связь.

Осталось оценить качество подгонки полученного квадратичного уравнения регрессии (индекс детерминации). Он рассчитывается по формуле квадрата индекса корреляции. То есть формула в ячейке K26 будет очень проста — «=K25*K25».

Коэффициент 0,920 близок к 1, что свидетельствует о высоком качестве подгонки.

Последним действием будет вычисление относительной ошибки. Добавим столбец и внесём туда формулу: «=ABS((C2-J2)/C2), ABS — модуль, абсолютное значение. Протянем маркером вниз и в ячейке M18 выведем среднее значение (СРЗНАЧ), назначим ячейкам процентный формат. Полученный результат — 7,79% находится в пределах допустимых значений ошибки <8…10%. Значит вычисления достаточно точны.

Если возникнет необходимость, по полученным значениям мы можем построить график.

Файл с примером прилагается — ССЫЛКА!

Источник

Для
построения графиков в MS
Excel
имеется
прекрасное средство – мастер диаграмм,
который предлагает пользователю большой
набор типов графиков и диаграмм,
позволяющих наглядно представить
данные, наиболее выгодном свете.

Даже
удивительно, как часто мы сталкиваемся
с необходимостью решить то или иное
уравнение, например, определить процентную
ставку, при которой предлагаемая сделка
выгодна, или вычислить скорость оборота
капиталовложений. Подбор параметра
(Goal
Seek)
как раз и является тем средством MS
Excel,
которое позволяет элементарно просто
решать подборные задачи.

Построение графика
функции.

Рассмотрим технологию
построение графика на примере функции

у=cos²(πx)
при х [0:
1]. Процесс построения графиков функции
состоит из двух этапов:
создание
таблицы значений функции
и непосредственного
построения её графика.
Эти два этапа последовательно будут
описаны в следующих двух разделах.

Таблица значений
функции.

Для
построения графика функции необходимо
первоначально построить таблицу и её
значений при различных значениях
аргумента, причем аргумент изменяют
обычно с фиксированным шагом. Шаг
выбирают небольшим, так чтобы таблица
значений функции отражала её поведение
на интервале табуляции. В нашем случае
возьмем в качестве шага изменения
аргумента, например, 0,1. Нам надо найти
у (0), у(0,1), у(0,2), …, у(1). С этой целью ячейки
диапазона А1:А11
последовательно введем 0, 0.1, …, 1, т. е.
значения переменной х. Отметим, что это
последовательность значений представляет
собой арифметическую прогрессию. Ввести
в ячейки диапазона ряд последовательных
значений, образующих арифметическую
прогрессию, можно двумя способами.

Первый
способ
заключается в следующем:

В ячейки А1 и А2
введите первый и второй члены
арифметической прогрессии.
Выделите
диапазон ячеек А1:А2.
Расположите
указатель мыши на маркере заполнения
выделенного диапазона и протяните его
вниз (в данном случае на диапазон А3:А11)
до тех пор, пока не получится числовой
ряд нужной длины.

Второй
способ
позволяет пользоваться диалоговым
окном Прогрессия.
Для этого:

В ячейку А1 введите
первый член арифметической прогрессии.
Выберите
команду Правка/
Заполнить/ Прогрессия.
Появившемся
диалоговом окне Прогрессия
в группе Расположение
выбираем переключатель по
столбцам, в
группе Тип
– переключатель арифметическая.
В поле Шаг
введите значение 0.1, а в поле Предельное
значение –
1.
Нажмите
кнопку ОК.

Диалоговое
окно Прогрессия
закроется, а на рабочем месте автоматически
будет построена требуемая прогрессия.

Диалоговое
окно Прогрессия,
отображаемое на экране выбором команды
Правка/
Заполнить/ Прогрессия,
также позволяется создавать геометрические
прогрессии.

Вернемся
к рассматриваемрму примеру построения
графика. В ячейку В1 введите формулу: =
COS(ПИ()*А1^2)

Ввод
формул в ячейку можно производить либо
с клавиатуры, либо с помощью диалогового
окна Мастер
функций,
которое отображается на экране либо
выбором команды Вставка
– Функция, либо
нажатием кнопки Вставка
функции
панели инструментов Стандартная.
Мастер
функций содержит список всех функций
рабочего листа, справки по их синтаксису
и примеры применения.

Продемонстрируем
работу функций на примере ввода упомянутой
выше формулы.

Выберите ячейку
В1.
Нажмите
кнопку Вставка
функции
панели инструментов Стандартная, либо
выберите команду Вставка
– функция.
На экране отобразится диалоговое окно
Мастер функций
– шаг 1 из 2.
Оно состоит из двух частей:

Левая
– Категория
со списком двенадцати категорий
функций;
Правая
– Функция
со списком имен функций, входящих в
выбранную категорию.

Категория
Полный
алфавитный перечень содержит
все встроенные функции и их имена
упорядочены в алфавитном порядке,
категория 10
недавно использовавшихся
содержит имена десяти последных
примененнных функций,. Эта
категория ускоряет вызов функций,
постоянно используемых пользователем.

Функция
COS
относится к категории Математические.
Выберите эту функцию и нажмите кнопку
OK.
На экране отобразится панель формул.

В
поле Число
вводится аргумент функции – в
рассматриваемом примере это ПИ () А1. С
помощью клавиатуры в это поле введите
только ПИ() , а ссылку на ячейку А1 в
формулу добавьте , щелкнув по ячейке А1
на рабочем листе. Конечно, ее можно было
также ввести с клавиатуры, но предложенный
способ дает дополнительную проверку
правильности ввода. После нажатия
кнопки OK
в ячейку В1 будет введена формула:

=
COS(ПИ()*А1)

4.
С помощью клавиатуры добавьте в формуле
=Cos(ПИ()*А1)
операцию возведения квадрат функции
Cos.
После всех описанных действий в ячейке
В1 должна появится формула:

=Cos(ПИ()*А1)^2

Таким
образом, пока найдено значение функции
Cos²(x)
для значения Х из ячейки А1. Теперь нам
осталось найти значение этой функции
для диапазона А2:А11. Для этого:

выберите ячейку
В1
расположите
указатель мыши на маркере заполнения
выделенной ячейки и пробуксируйте его
вниз на диапазон В2:В11

Для
того чтобы в ячейках рабочего листа
отображались не значения, а формулы,
надо выбрать команду Сервис
| Параметры
и на вкладке Вид
появившегося диалогового окна Параметры
в группе Параметры
окна установить
флажок формулы.

На
рисунке видно будет результат табуляции
функции. Выглядит он не очень презентабельно:
после десятичной точки отображается
различное количество десятичных знаков.
Кроме того, происходит перемешивание
числового экспоненциального форматов.
А именно, в ячейке В6 в место 0 отображается
3.75Е – 33, что приблизительно и равно
нулю. Поэтому форматы надо привести к
какому-то общему виду, например, как
показано на правом рабочем листе:
значение аргумента выводится в числовом
формате с точностью до одного знака
после десятичной точки, а значение
функции – с точностью до трех знаков
после десятичной точки. Отформатируем,
например, значения аргумента. Для этого
надо выбрать диапазон А1:А11. Это можно
сделать, например, следующим способом.
Выберите ячейку А1, а затем при нажатой
клавише <Shift>
выделить ячейку А11. Диапазон А1:А11 выбран.
Переходим к форматированию данных.
Выберите команду Формат | Ячейки. В
появившемся диалоговом окне Формат
ячеек на вкладке Число десятичных знаков
введите 1. Нажмите кнопку ОК.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Пакет MS Excel позволяет при построении уравнения линейной регрессии большую часть работы сделать очень быстро. Важно понять, как интерпретировать полученные результаты.

Для работы необходима надстройка Пакет анализа
, которую необходимо включить в пункте меню СервисНадстройки

В Excel 2007 для включения пакета анализа надо нажать перейти в блок Параметры Excel
, нажав кнопку в левом верхнем углу, а затем кнопку «Параметры Excel
» внизу окна:

Для построения модели регрессии необходимо выбрать пункт СервисАнализ данныхРегрессия
. (В Excel 2007 этот режим находится в блоке Данные/Анализ данных/ Регрессия
). Появится диалоговое окно, которое нужно заполнить:

1) Входной интервал Y
¾ содержит ссылку на ячейки, которые содержат значения результативного признака y
. Значения должны быть расположены в столбце;

2) Входной интервал X
¾ содержит ссылку на ячейки, которые содержат значения факторов . Значения должны быть расположены в столбцах;

3) Признак Метки
ставится, если первые ячейки содержат пояснительный текст (подписи данных);

4) Уровень надежности
¾ это доверительная вероятность, которая по умолчанию считается равной 95%. Если это значение не устраивает, то нужно включить этот признак и ввести требуемое значение;

5) Признак Константа-ноль
включается, если необходимо построить уравнение, в котором свободная переменная ;

6) Параметры вывода
определяют, куда должны быть помещены результаты. По умолчанию строит режим Новый рабочий лист
;

7) Блок Остатки
позволяет включать вывод остатков и построение их графиков.

В результате выводится информация, содержащая все необходимые сведения и сгруппированная в три блока: Регрессионная статистика
, Дисперсионный анализ
, Вывод остатка
. Рассмотрим их подробнее.

1. Регрессионная статистика
:

множественный R
определяется формулой (коэффициент корреляции Пирсона
);

R
(коэффициент детерминации
);

Нормированный R
-квадрат вычисляется по формуле (используется для множественной регрессии);

Стандартная ошибка S
вычисляется по формуле ;

Наблюдения ¾ это количество данных n
.

2. Дисперсионный анализ
, строка Регрессия
:

Параметр df
равен m
(количество наборов факторов x
);

Параметр SS
определяется формулой ;

Параметр MS
определяется формулой ;

Статистика F
определяется формулой ;

Значимость F
. Если полученное число превышает , то принимается гипотеза (нет линейной взаимосвязи), иначе принимается гипотеза (есть линейная взаимосвязь).

3. Дисперсионный анализ
, строка Остаток
:

Параметр df
равен ;

Параметр SS
определяется формулой ;

Параметр MS
определяется формулой .

4. Дисперсионный анализ
, строка Итого
содержит сумму первых двух столбцов.

5. Дисперсионный анализ
, строка Y-пересечение
содержит значение коэффициента , стандартной ошибки и t
-статистики .

P
-значение ¾ это значение уровней значимости, соответствующее вычисленным t
-статистикам. Определяется функцией СТЬЮДРАСП(t
-статистика; ). Если P
-значение превышает , то соответствующая переменная статистически незначима и ее можно исключить из модели.

Нижние 95%
и Верхние 95%
¾ это нижние и верхние границы 95-процентных доверительных интервалов для коэффициентов теоретического уравнения линейной регрессии. Если в блоке ввода данных значение доверительной вероятности было оставлено по умолчанию, то последние два столбца будут дублировать предыдущие. Если пользователь ввел свое значение доверительной вероятности, то последние два столбца содержат значения нижней и верхней границы для указанной доверительной вероятности.

6. Дисперсионный анализ
, строки содержат значения коэффициентов, стандартных ошибок, t
-статистик, P
-значений и доверительных интервалов для соответствующих .

7. Блок Вывод остатка
содержит значения предсказанного y
(в наших обозначениях это ) и остатки .

28 Окт

Основными типами нелинейных регрессий являются:

полиномиальные (квадратичная, кубическая);
гиперболическая;
степенная;
показательная;
логарифмическая.

В прогнозировании с помощью нелинейных регрессий главное выяснить коэффициент корреляции, который покажет нам есть ли тесная взаимосвязь меду двумя параметрами или нет. Как правило, если коэффициент корреляции близок к 1, значит связь есть, и прогноз будет довольно точен. Ещё одним важным элементом нелинейных регрессий является средняя относительная ошибка (А

), если она находится в промежутке <8…10%, значит модель достаточно точна.

На этом, пожалуй, теоретический блок мы закончим и перейдём к практическим вычислениям.

Для исследования нам потребуется решить уравнение (зависимости Y от X): y=ax 2 +bx+c+e. Это парная квадратичная регрессия. Применим в этом случае метод наименьших квадратов, для выяснения неизвестных аргументов — a, b, c. Он приведёт к системе алгебраических уравнений вида:

Получится заполненная нужными для решения уравнения таблица вида.

Сформируем матрицу A

системы, состоящую из коэффициентов при неизвестных в левых частях уравнений. Поместим её в ячейку А22 и назовём «А=
«. Следуем той системе уравнений, которую мы избрали для решения регрессии.

Расчёт коэффициентов уравнения по Крамеру будем производить в ячейках напротив соответствующих детерминантов по формуле: a
(в ячейке M22) — «=K22/K21»; b
(в ячейке M23) — «=K23/K21»; с
(в ячейке M24) — «=K24/K21».

Получим наше искомое уравнение парной квадратичной регрессии:

y=-0,074x 2 +2,151x+6,523

Оценим тесноту линейной связи индексом корреляции.

Для вычисления добавим в таблицу дополнительный столбец J (назовём его y*). Расчёта будет следующей (согласно полученному нами уравнению регрессии) — «=$m$22*B2*B2+$M$23*B2+$M$24».
Поместим её в ячейку J2. Останется протянуть вниз маркер автозаполнения до ячейки J16.

Для вычисления сумм (Y-Y усредненное) 2 добавим в таблицу столбцы K и L с соответствующими формулами. Среднее по столбцу Y посчитаем с помощью функции СРЗНАЧ.

В ячейке K25 разместим формулу подсчёта индекса корреляции — «=КОРЕНЬ(1-(K17/L17))».

Видим, что значение 0,959 очень близко к 1, значит между продажами и годами есть тесная нелинейная связь.

Коэффициент 0,920 близок к 1, что свидетельствует о высоком качестве подгонки.

Если возникнет необходимость, по полученным значениям мы можем построить график.

Файл с примером прилагается — ССЫЛКА !

Категории:

/

от
28.10.2017

Пакет MS Excel
позволяет при построении уравнения линейной регрессии большую часть работы сделать очень быстро. Важно понять, как интерпретировать полученные результаты.
Для построения модели регрессии необходимо выбрать пункт СервисАнализ данныхРегрессия (в Excel 2007
этот режим находится в блоке Данные/Анализ данных/Регрессия). Затем полученные результаты скопировать в блок для анализа.

В Excel
имеется еще более быстрый и удобный способ построить график линейной регрессии (и даже основных видов нелинейных регрессий, о чем см. далее). Это можно сделать следующим образом:

1) выделить столбцы с данными X
и Y
(они должны располагаться именно в таком порядке!);

2) вызвать Мастер диаграмм
и выбрать в группе Тип
– Точечная
и сразу нажать Готово
;

3) не сбрасывая выделения с диаграммы, выбрать появившейся пункт основного меню Диаграмма
, в котором следует выбрать пункт Добавить линию тренда
;

4) в появившемся диалоговом окне Линия тренда
во вкладке Тип
выбрать Линейная
;

5) во вкладке Параметры
можно активизировать переключатель Показывать уравнение на диаграмме
, что позволит увидеть уравнение линейной регрессии (4.4), в котором будут вычислены коэффициенты (4.5).

6) В этой же вкладке можно активизировать переключатель Поместить на диаграмму величину достоверности аппроксимации (R^2)
. Эта величина есть квадрат коэффициента корреляции (4.3) и она показывает, насколько хорошо рассчитанное уравнение описывает экспериментальную зависимость. Если R
2 близок к единице, то теоретическое уравнение регрессии хорошо описывает экспериментальную зависимость (теория хорошо согласуется с экспериментом), а если R
2 близок к нулю, то данное уравнение не пригодно для описания экспериментальной зависимости (теория не согласуется с экспериментом).

В результате выполнения описанных действий получится диаграмма с графиком регрессии и ее уравнением.

§4.3. Основные виды нелинейной регрессии

Параболическая и полиномиальная регрессии.

Параболической
зависимостью величины Y
от величины Х
называется зависимость, выраженная квадратичной функцией (параболой 2-ого порядка):

Это уравнение называется уравнением параболической регрессии Y
на Х
. Параметры а
, b
, с
называются коэффициентами параболической регрессии
. Вычисление коэффициентов параболической регрессии всегда громоздко, поэтому для расчетов рекомендуется использовать компьютер.

Уравнение (4.8) параболической регрессии является частным случаем более общей регрессии, называемой полиномиальной. Полиномиальной
зависимостью величины Y
от величины Х
называется зависимость, выраженная полиномом n
-ого порядка:

где числа а i
(i
=0,1,…, n
) называются коэффициентами полиномиальной регрессии
.

Степенная регрессия.

Степенной
зависимостью величины Y
от величины Х
называется зависимость вида:

Это уравнение называется уравнением степенной регрессии Y
на Х
. Параметры а
и b
называются коэффициентами степенной регрессии
.

ln =lna
+b·
lnx
. (4.11)

Это уравнение описывает прямую на плоскости с логарифмическими координатными осями lnx
и ln . Поэтому критерием применимости степенной регрессии служит требование того, чтобы точки логарифмов эмпирических данных lnx i
и lnу i
находились ближе всего к прямой (4.11).

Показательная регрессия.

Показательной
(или экспоненциальной
) зависимостью величины Y
от величины Х
называется зависимость вида:

(или ). (4.12)

Это уравнение называется уравнением показательной
(или экспоненциальной
) регрессии Y
на Х
. Параметры а
(или k
) и b
называются коэффициентами показательной
(или экспоненциальной
) регрессии
.

Если прологарифмировать обе части уравнения степенной регрессии, то получится уравнение

ln =x·
lna
+lnb
(или ln =k·x
+lnb
). (4.13)

Это уравнение описывает линейную зависимость логарифма одной величины ln от другой величины x
. Поэтому критерием применимости степенной регрессии служит требование того, чтобы точки эмпирических данных одной величины x i
и логарифмы другой величины lnу i
находились ближе всего к прямой (4.13).

Логарифмическая регрессия.

Логарифмической
зависимостью величины Y
от величины Х
называется зависимость вида:

=a
+b·
lnx
. (4.14)

Это уравнение называется уравнением логарифмической регрессии Y
на Х
. Параметры а
и b
называются коэффициентами логарифмической регрессии
.

Гиперболическая регрессия.

Гиперболической
зависимостью величины Y
от величины Х
называется зависимость вида:

Это уравнение называется уравнением гиперболической регрессии Y
на Х
. Параметры а
и b
называются коэффициентами гиперболической регрессии
и определяются методом наименьших квадратов. Применение этого метода приводит к формулам:

В формулах (4.16-4.17) суммирование проводится по индексу i
от единицы до количества наблюдений n
.

К сожалению, в Excel
нет функции, вычисляющих коэффициенты гиперболической регрессии. В тех случаях, когда заведомо не известно, что измеряемые величины связаны обратной пропорциональностью, рекомендуется вместо уравнения гиперболической регрессии искать уравнение степенной регрессии, так в Excel
имеется процедура ее нахождения. Если же между измеряемыми величинами предполагается гиперболическая зависимость, то коэффициенты ее регрессии придется вычислять с помощью вспомогательных расчетных таблиц и операций суммирования по формулам (4.16-4.17).

Статистическая обработка данных может также проводиться с помощью надстройки ПАКЕТ АНАЛИЗА
(рис. 62).

Из предложенных пунктов выбирает пункт «РЕГРЕССИЯ
» и щелкаем на нем левой кнопкой мыши. Далее нажимаем ОК.

Появится окно, показанное на рис. 63.

Инструмент анализа «РЕГРЕССИЯ
» применяется для подбора графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или нескольких независимых переменных. Например, на спортивные качества атлета влияют несколько факторов, включая возраст, рост и вес. Можно вычислить степень влияния каждого из этих трех факторов по результатам выступления спортсмена, а затем использовать полученные данные для предсказания выступления другого спортсмена.

Инструмент «Регрессия» использует функцию ЛИНЕЙН
.

Диалоговое окно «РЕГРЕССИЯ»

Метки Установите флажок, если первая строка или первый столбец входного диапазона содержит заголовки. Снимите этот флажок, если заголовки отсутствуют. В этом случае подходящие заголовки для данных выходной таблицы будут созданы автоматически.

Уровень надежности Установите флажок, чтобы включить в выходную таблицу итогов дополнительный уровень. В соответствующее поле введите уровень надежности, который следует применить, дополнительно к уровню 95%, применяемому по умолчанию.

Константа — ноль Установите флажок, чтобы линия регрессии прошла через начало координат.

Выходной интервал Введите ссылку на левую верхнюю ячейку выходного диапазона. Отведите как минимум семь столбцов для выходной таблицы итогов, которая будет включать в себя: результаты дисперсионного анализа, коэффициенты, стандартную погрешность вычисления Y, среднеквадратичные отклонения, число наблюдений, стандартные погрешности для коэффициентов.

Новый рабочий лист Установите переключатель в это положение, чтобы открыть новый лист в книге и вставить результаты анализа, начиная с ячейки A1. При необходимости введите имя для нового листа в поле, расположенном напротив соответствующего положения переключателя.

Новая рабочая книга Установите переключатель в это положение для создания новой книги, в которой результаты будут добавлены в новый лист.

Остатки Установите флажок для включения остатков в выходную таблицу.

Стандартизированные остатки Установите флажок для включения стандартизированных остатков в выходную таблицу.

График остатков Установите флажок для построения графика остатков для каждой независимой переменной.

График подбора Установите флажок для построения графика зависимости предсказанных значений от наблюдаемых.

График нормальной вероятности
Установите флажок, для построения графика нормальной вероятности.

Функция ЛИНЕЙН

Для проведения расчетов выделяем курсором ячейку, в которой хотим отобразить среднее значение и нажимаем на клавиатуре клавишу =. Далее в поле Имя указываем нужную функцию, например СРЗНАЧ
(рис. 22).

Функция ЛИНЕЙН
рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую. Можно также объединять функцию ЛИНЕЙН
с другими функциями для вычисления других видов моделей, являющихся линейными в неизвестных параметрах (неизвестные параметры которых являются линейными), включая полиномиальные, логарифмические, экспоненциальные и степенные ряды. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива.

Уравнение для прямой линии имеет следующий вид:

y=m 1 x 1 +m 2 x 2 +…+b (в случае нескольких диапазонов значений x),

где зависимое значение y — функция независимого значения x, значения m — коэффициенты, соответствующие каждой независимой переменной x, а b — постоянная. Обратите внимание, что y, x и m могут быть векторами. Функция ЛИНЕЙН
возвращает массив{mn;mn-1;…;m 1 ;b}. ЛИНЕЙН
может также возвращать дополнительную регрессионную статистику.

ЛИНЕЙН
(известные_значения_y; известные_значения_x; конст; статистика)

Известные_значения_y — множество значений y, которые уже известны для соотношения y=mx+b.

Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.

Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.

Известные_значения_x — необязательное множество значений x, которые уже известны для соотношения y=mx+b.

Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то массивы_известные_значения_y и известные_значения_x могут иметь любую форму — при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).

Если массив_известные_значения_x опущен, то предполагается, что этот массив {1;2;3;…} имеет такой же размер, как и массив_известные_значения_y.

Конст — логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.

Если аргумент «конст» имеет значение ИСТИНА или опущен, то константа b вычисляется обычным образом.

Если аргумент «конст» имеет значение ЛОЖЬ, то значение b полагается равным 0 и значения m подбираются таким образом, чтобы выполнялось соотношение y=mx.

Статистика — логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии.

Если аргумент «статистика» имеет значение ИСТИНА, функция ЛИНЕЙН возвращает дополнительную регрессионную статистику. Возвращаемый массив будет иметь следующий вид: {mn;mn-1;…;m1;b:sen;sen-1;…;se1;seb:r2;sey:F;df:ssreg;ssresid}.

Если аргумент «статистика» имеет значение ЛОЖЬ или опущен, функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.

Дополнительная регрессионная статистика.(табл.17)

Величина	Описание
se1,se2,…,sen	Стандартные значения ошибок для коэффициентов m1,m2,…,mn.
seb	Стандартное значение ошибки для постоянной b (seb = #Н/Д, если аргумент «конст» имеет значение ЛОЖЬ).
r2	Коэффициент детерминированности. Сравниваются фактические значения y и значения, получаемые из уравнения прямой; по результатам сравнения вычисляется коэффициент детерминированности, нормированный от 0 до 1. Если он равен 1, то имеет место полная корреляция с моделью, т. е. различия между фактическим и оценочным значениями y не существует. В противоположном случае, если коэффициент детерминированности равен 0, использовать уравнение регрессии для предсказания значений y не имеет смысла. Для получения дополнительных сведений о способах вычисления r2, см. «Замечания» в конце данного раздела.
sey	Стандартная ошибка для оценки y.
F	F-статистика или F-наблюдаемое значение. F-статистика используется для определения того, является ли случайной наблюдаемая взаимосвязь между зависимой и независимой переменными.
df	Степени свободы. Степени свободы полезны для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели необходимо сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН. Для получения дополнительных сведений о вычислении величины df см. «Замечания» в конце данного раздела. Далее в примере 4 показано использование величин F и df.
ssreg	Регрессионная сумма квадратов.
ssresid	Остаточная сумма квадратов. Для получения дополнительных сведений о расчете величин ssreg и ssresid см. «Замечания» в конце данного раздела.

На приведенном ниже рисунке показано, в каком порядке возвращается дополнительная регрессионная статистика (рис. 64).

Замечания:

Любую прямую можно описать ее наклоном и пересечением с осью y:

Наклон (m): чтобы определить наклон прямой, обычно обозначаемый через m, нужно взять две точки прямой (x 1 ,y 1) и(x 2 ,y 2); наклон будет равен (y 2 -y 1)/(x 2 -x 1).

Y-пересечение (b): Y-пересечением прямой, обычно обозначаемым через b, является значение y для точки, в которой прямая пересекает ось y.

Уравнение прямой имеет вид y=mx+b. Если известны значения m и b, то можно вычислить любую точку на прямой, подставляя значения y или x в уравнение. Можно также воспользоваться функцией ТЕНДЕНЦИЯ.

Если имеется только одна независимая переменная x, можно получить наклон и y-пересечение непосредственно, воспользовавшись следующими формулами:

Наклон: ИНДЕКС (ЛИНЕЙН(известные_значения_y; известные_значения_x); 1)

Y-пересечение: ИНДЕКС (ЛИНЕЙН (известные_значения_y; известные_значения_x); 2)

Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель, используемая функцией ЛИНЕЙН. Функция ЛИНЕЙН использует метод наименьших квадратов для определения наилучшей аппроксимации данных. Когда имеется только одна независимая переменная x, m и b вычисляются по следующим формулам:

где x и y – выборочные средние значения, например x = СРЗНАЧ (известные_значения_x), а y = СРЗНАЧ (известные_значения_y).

Функции аппроксимации ЛИНЕЙН и ЛГРФПРИБЛ могут вычислить прямую или экспоненциальную кривую, наилучшим образом описывающую данные. Однако они не дают ответа на вопрос, какой из двух результатов больше подходит для решения поставленной задачи. Можно также вычислить функцию ТЕНДЕНЦИЯ (известные_значения_y; известные_значения_x) для прямой или функцию РОСТ(известные_значения_y; известные_значения_x) для экспоненциальной кривой. Эти функции, если не задавать аргумент новые_значения_x, возвращают массив вычисленных значений y для фактических значений x в соответствии с прямой или кривой. После этого можно сравнить вычисленные значения с фактическими значениями. Можно также построить диаграммы для визуального сравнения.

Проводя регрессионный анализ, Microsoft Excel вычисляет для каждой точки квадрат разности между прогнозируемым значением y и фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов (ssresid). Затем Microsoft Excel подсчитывает общую сумму квадратов (sstotal). Если конст = ИСТИНА или значение этого аргумента не указано, общая сумма квадратов будет равна сумме квадратов разностей действительных значений y и средних значений y. При конст = ЛОЖЬ общая сумма квадратов будет равна сумме квадратов действительных значений y (без вычитания среднего значения y из частного значения y). После этого регрессионную сумму квадратов можно вычислить следующим образом: ssreg = sstotal — ssresid. Чем меньше остаточная сумма квадратов, тем больше значение коэффициента детерминированности r2, который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными. Коэффициент r2 равен ssreg/sstotal.

В некоторых случаях один или более столбцов X (пусть значения Y и X находятся в столбцах) не имеет дополнительного предикативного значения в других столбцах X. Другими словами, удаление одного или более столбцов X может привести к значениям Y, вычисленным с одинаковой точностью. В этом случае избыточные столбцы X будут исключены из модели регрессии. Этот феномен называется «коллинеарностью», поскольку избыточные столбцы X могут быть представлены в виде суммы нескольких неизбыточных столбцов. Функция ЛИНЕЙН проверяет на коллинеарность и удаляет из модели регрессии все избыточные столбцы X, если обнаруживает их. Удаленные столбцы X можно определить в выходных данных ЛИНЕЙН по коэффициенту, равному 0, и по значению se, равному 0. Удаление одного или более столбцов как избыточных изменяет величину df, поскольку она зависит от количества столбцов X, в действительности используемых для предикативных целей. Подробнее о вычислении величины df см. ниже в примере 4. При изменении df вследствие удаления избыточных столбцов значения sey и F также изменяются. Часто использовать коллинеарность не рекомендуется. Однако ее следует применять, если некоторые столбцы X содержат 0 или 1 в качестве индикатора указывающего, входит ли предмет эксперимента в отдельную группу. Если конст = ИСТИНА или значение этого аргумента не указано, функция ЛИНЕЙН вставляет дополнительный столбец X для моделирования точки пересечения. Если имеется столбец со значениями 1 для указания мужчин и 0 — для женщин, а также имеется столбец со значениями 1 для указания женщин и 0 — для мужчин, то последний столбец удаляется, поскольку его значения можно получить из столбца с «индикатором мужского пола».

Вычисление df для случаев, когда столбцы X не удаляются из модели вследствие коллинеарности происходит следующим образом: если существует k столбцов известных_значений_x и значение конст = ИСТИНА или не указано, то df = n – k – 1. Если конст = ЛОЖЬ, то df = n — k. В обоих случаях удаление столбцов X вследствие коллинеарности увеличивает значение df на 1.

Формулы, которые возвращают массивы, должны быть введены как формулы массива.

При вводе массива констант в качестве, например, аргумента известные_значения_x следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк. Знаки-разделители могут быть различными в зависимости от параметров, заданных в окне «Язык и стандарты» на панели управления.

Следует отметить, что значения y, предсказанные с помощью уравнения регрессии, возможно, не будут правильными, если они располагаются вне интервала значений y, которые использовались для определения уравнения.

Основной алгоритм, используемый в функции ЛИНЕЙН
, отличается от основного алгоритма функций НАКЛОН
и ОТРЕЗОК
. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных. Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то:

Функция ЛИНЕЙН
возвращает значение, равное 0. Алгоритм функции ЛИНЕЙН
используется для возвращения подходящих значений для коллинеарных данных, и в данном случае может быть найден по меньшей мере один ответ.

Функции НАКЛОН и ОТРЕЗОК возвращают ошибку #ДЕЛ/0!. Алгоритм функций НАКЛОН и ОТРЕЗОК используется для поиска только одного ответа, а в данном случае их может быть несколько.

Помимо вычисления статистики для других типов регрессии функцию ЛИНЕЙН можно использовать при вычислении диапазонов для других типов регрессии, вводя функции переменных x и y как ряды переменных х и у для ЛИНЕЙН. Например, следующая формула:

ЛИНЕЙН(значения_y, значения_x^СТОЛБЕЦ($A:$C))

работает при наличии одного столбца значений Y и одного столбца значений Х для вычисления аппроксимации куба (многочлен 3-й степени) следующей формы:

y=m 1 x+m 2 x 2 +m 3 x 3 +b

Формула может быть изменена для расчетов других типов регрессии, но в отдельных случаях требуется корректировка выходных значений и других статистических данных.

Источник