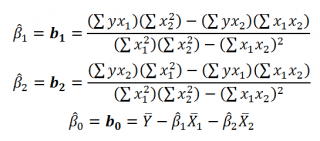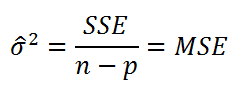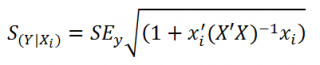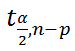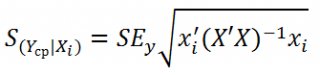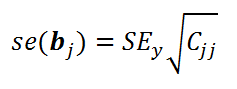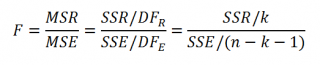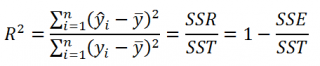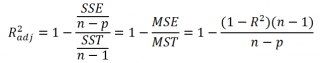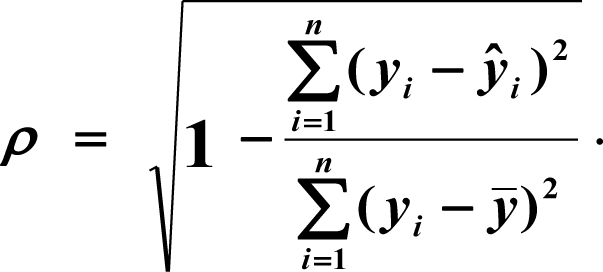Нелинейная множественная регрессия excel

Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.

Подключение пакета анализа

Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.

1. Перемещаемся во вкладку «Файл».



2. Переходим в раздел «Параметры».



3. Открывается окно параметров Excel. Переходим в подраздел «Надстройки».



4. В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».



5. Открывается окно доступных надстроек Эксель. Ставим галочку около пункта «Пакет анализа». Жмем на кнопку «OK».

Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».

Виды регрессионного анализа

Существует несколько видов регрессий:

• параболическая;
• степенная;
• логарифмическая;
• экспоненциальная;
• показательная;
• гиперболическая;
• линейная регрессия.

О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.

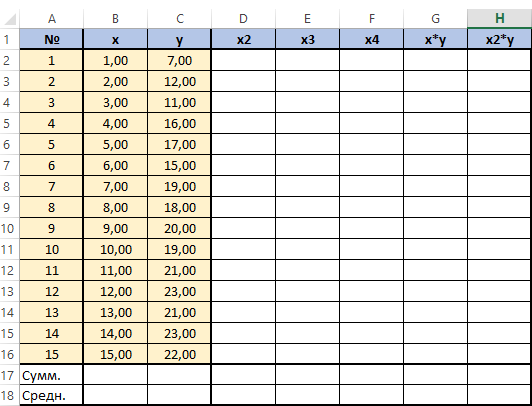
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.

Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.

1. Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».





2. Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».



3. Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.

   В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.

   В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».

   

   С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.

   

   После того, как все настройки установлены, жмем на кнопку «OK».

Разбор результатов анализа

Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.

Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.

Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.

Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.

Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.

Рассмотрим использование

MS

EXCEL

для прогнозирования переменной

Y

на основании нескольких переменных Х, т.е. множественную регрессию.

Перед прочтением этой статьи рекомендуется освежить в памяти

простую линейную регрессию

– прогнозирование на основе значений только одного фактора.

Disclaimer

: Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей

Множественного регрессионного анализа.

Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения

Регрессии

– плохая идея.

Статья про

Множественный регрессионный анализ

получилась большая, поэтому ниже для удобства приведены ее разделы:

• Оценка неизвестных параметров
• Диаграмма рассеяния
• Вычисление прогнозных значений Y

  (отдельное наблюдение и среднее значение) и построение доверительных интервалов

• Стандартные ошибки и доверительные интервалы для коэффициентов регрессии
• Проверка гипотез
• Генерация данных для множественной регрессии с помощью заданного тренда
• Коэффициент детерминации

Прогнозирование единственной переменной Y на основании значений 2-х или более переменных Х называется

множественной регрессией

.

Множественная линейная регрессионная модель

(Multiple Linear Regression Model)

имеет вид Y=β

₀

+β

₁

*X

₁

+β

₂

*X

₂

+…+β

_k

*X

_k

+ε. В этом случае переменная Y зависит от k поясняющих переменных Х, т.е.

регрессоров

. ε —

случайная ошибка

. Модель является линейной относительно неизвестных параметров β.

Оценка неизвестных параметров

В этой статье рассмотрим модель с 2-мя регрессорами. Сначала введем необходимые обозначения и понятия множественной регрессии.

Для описания зависимости Y от 2-х переменных

линейная модель

имеет вид:

Y=β

₀

+β

₁

*X

₁

+β

₂

*X

₂

+ε.

Параметры этой модели β

_i

нам неизвестны, но их можно оценить, используя случайную выборку (измеренные значения переменной Y от заданных Х). Оценки параметров модели (β

₀

, β

₁

, β

₂

) обычно вычисляются

методом наименьших квадратов (МНК)

, который минимизирует сумму квадратов ошибок прогнозирования (критерий минимизации в англоязычной литературе обозначают как SSE – Sum of Squared Errors).

Соответствующие оценки параметров будем обозначать как

b

₀

,

b

₁

и

b

₂

.

Ошибка ε имеет случайную природу и имеет свою функцию распределения со

средним значением

=0 и

дисперсией σ

²

.

Оценки

b

₁

и

b

₂

называются

коэффициентами регрессии

, они определяют влияние соответствующей переменной X, когда все остальные независимые переменные остаются

неизменными

.

Сдвиг (intercept)

или

постоянный

член

b

₀

, определяет прогнозируемое значение Y, когда все поясняющие переменные Х равны 0 (часто

сдвиг

не имеет физического смысла в рамках модели и обусловлен лишь математическими вычислениями

МНК

).

Вычислив оценки, полученные методом

МНК,

позволяют прогнозировать значения переменной Y:

Y=

b

₀

+

b

₁

*X

₁

+

b

₂

*X

₂

Примечание

: Для случая 2-х регрессоров, все спрогнозированные значения переменной Y будут лежать в плоскости (в

плоскости регрессии

).

В качестве примера рассмотрим технологический процесс изготовления нити:

Инженер, на основе имеющегося опыта, предположил, что

прочность нити

Y зависит от

концентрации исходного раствора

(Х

₁

) и

температуры реакции

(Х

₂

), и соответствует модели линейной регрессии. Для нахождения комбинации переменных Х, при которых Y принимает максимальное значение, необходимо определить коэффициенты регрессии, сделав выборку.

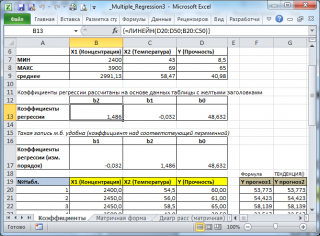
В MS EXCEL

коэффициенты множественной регрессии

удобнее всего вычислить с помощью функции

ЛИНЕЙН()

. Это сделано в

файле примера на листе Коэффициенты

. Чтобы вычислить оценки:

• выделите 3 ячейки в одной строке (т.к. мы рассматриваем случай 2-х регрессоров, то будут вычислены 2
  
  коэффициента регрессии
  
  +
  
  величина сдвига
  
  = 3 значения, для вывода которых понадобится 3 ячейки). Пусть это будет диапазон
  
  С8:Е8
  
  ;
• в

  Строке формул

  введите =
  
  ЛИНЕЙН(D20:D50;B20:C50)
  
  . Предполагается, что в столбце
  
  В
  
  содержатся прогнозируемые значения Y (в нашей модели это Прочность нити), в столбцах
  
  С
  
  и
  
  D
  
  содержатся значения контролируемых параметров Х (Х1 – Концентрация в столбце С и Х2 – Температура в столбце D).

• нажмите
  
  CTRL
  
  +
  
  SHIFT
  
  +
  
  ENTER
  
  (т.к. это

  формула массива

  ).

В левой ячейке будет рассчитано значение

коэффициента регрессии

b

2

для переменной Х2, в средней ячейке — значение

коэффициента регрессии

b

1

для переменной Х1, в правой –

сдвиг

. Обратите внимание, что порядок вывода

коэффициентов

регрессии

обратный по отношению к расположению столбцов с данными соответствующих переменных Х (вычисленный коэффициент

b

2

располагается

левее

по отношению к

b

1

, тогда как значения переменной Х2 располагаются

правее

значений переменной Х1). Это может привести к путанице, поэтому лучше разместить коэффициенты над соответствующими столбцами с данными, как это сделано в строке 17

файла примера

.

Примечание

: В принципе без функции

ЛИНЕЙН()

можно обойтись, записав альтернативные формулы. Для этого в

файле примера на листе Коэффициенты

в столбцах

I

:

K

вычислены отклонения значений переменных Х

_1i

, Х

_2i

, Y

_i

от их средних значений

, т.е.:

Далее коэффициенты регрессии рассчитываются по следующим формулам (эти формулы справедливы только при прогнозировании по 2-м независимым переменным Х):

При прогнозировании по 3-м и более независимым переменным Х формулы для вычисления

коэффициентов регрессии

значительно усложняются, поэтому следует использовать матричный подход.

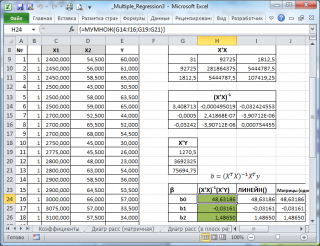
В

файле примера на листе Матричная форма

выполнены расчеты

коэффициентов регрессии

с помощью матричного подхода.

Расчет можно произвести как пошагово, так и одной

формулой массива

:

=МУМНОЖ(МОБР(МУМНОЖ(ТРАНСП(B9:D33);(B9:D33)));МУМНОЖ(ТРАНСП(B9:D33);(E9:E33)))

Коэффициенты регрессии

(вектор

b

)

в этом случае вычисляются по формуле

b

=(X

^T

X)

^-1

(X

^T

Y) или в другом виде записи

b

=(X

^’

X)

^-1

(X

^’

Y)

Под Х подразумевается матрица, состоящая из столбцов значений переменной Х с дополнительным столбцом единиц, а под Y – вектор-столбец значений Y.

Символ

^Т

или ‘ – это

транспонирование матрицы

, а обозначение

^-1

говорит о

вычислении обратной матрицы

.

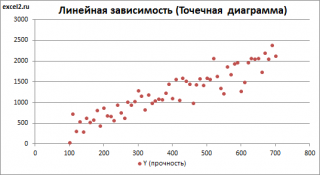
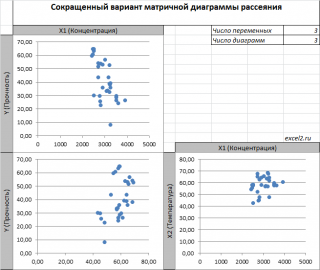
Диаграмма рассеяния

В случае

простой линейной регрессии

(один регрессор, т.е. одна переменная Х) для визуализации связи между прогнозируемым значением Y и переменной Х строят

диаграмму рассеяния

(двумерную).

В случае

множественной

линейной регрессии

двумерную диаграмму рассеяния можно построить только для анализа влияния каждого отдельного регрессора на Y (при этом остальные Х не меняются), т.е. так называемую Матричную диаграмму рассеивания (См.

файл примера лист Диагр расс (матричная)

).

К сожалению, такую диаграмму трудно интерпретировать.

Более того, матричная диаграмма может вводить в заблуждение (см.

Introduction

to

linear

regression

analysis

/

D

.

C

.

Montgomery

,

E

.

A

.

Peck

,

G

.

G

.

Vining

, раздел 3.2.5

), демонстрируя наличие или отсутствие линейной взаимосвязи между отдельным регрессором X

_i

и Y.

Для случая с 2-мя регрессорами можно предложить альтернативный вид матричной

диаграммы рассеяния

. В стандартной диаграмме рассеяния строятся проекции на координатные плоскости Х1;Х2, Y;X1 и Y;X2. Однако, если взглянуть на точки относительно

плоскости регрессии

, то картину, на мой взгляд, будет проще интерпретировать.

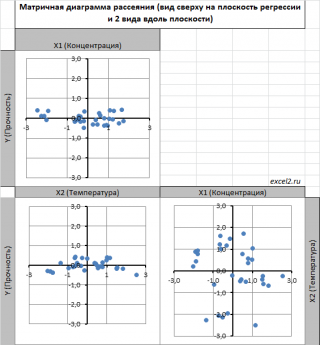
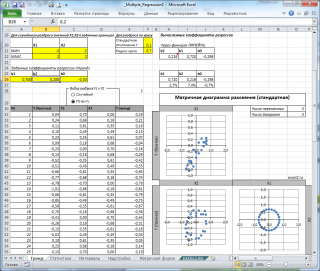
Сравним две матричные диаграммы рассеяния (см.

файл примера на листе «Диагр расс (в плоск регрессии)»

, построенные для одних и тех же наблюдений. Первая – стандартная,

вторая представляет собой вид сверху на плоскость регрессии и 2 вида вдоль плоскости.

На второй диаграмме становится очевидно, что разброс точек относительно плоскости регрессии совсем не большой и поэтому, скорее всего, построенная модель является полезной, а выбранные 2 переменные Х позволяют прогнозировать Y (конечно, для подтверждения этой гипотезы нужно

провести процедуру F-теста

).

Несколько слов о построении альтернативной матричной диаграммы рассеяния:

• Перед построением необходимо нормировать значения наблюдений (для каждой переменной вычесть

  среднее

  и разделить на

  стандартное отклонение

  ). В этом случае практически все точки на диаграммах будут находится в диапазоне +/-3 (по аналогии со

  стандартным нормальным распределением

  , 99% значений которого лежат в пределах +/-3 сигма). В этом случае, на диаграмме можно фиксировать мин/макс значений осей, чтобы EXCEL автоматически не модифицировал масштаб осей при изменении данных (это не всегда удобно);

• Теперь координаты точек необходимо рассчитать в системе отсчета относительно плоскости регрессии (в которой плоскость Оху’ совпадает с плоскостью регрессии). Для этого необходимо найти

  матрицу вращения

  , например, через вращение приводящее к совмещению нормали к плоскости регрессии и вектора оси Z (0;0;1);

• Новые координаты позволяют построить альтернативную матричную диаграмму. Кроме того, для удобства можно вращать систему координат вокруг новой оси Z, чтобы нагляднее представить себе распределение точек относительно плоскости регрессии (для этого использована Полоса прокрутки в ячейках
  
  Q
  
  31:
  
  S
  
  31
  
  ).

Вычисление прогнозных значений Y (отдельное наблюдение и среднее значение) и построение доверительных интервалов

После того, как нами были найдены тем или иным способом коэффициенты регрессии можно приступать к вычислению прогнозных значений Y на основе заданных значений переменных Х.

Уравнение прогнозирования или уравнение регрессии в случае 2-х независимых переменных (регрессоров) записывается в виде:

Y=

b

₀

+

b

₁

*

Х

₁

+

b

₂

*

Х

₂

Примечание:

В MS EXCEL

прогнозное значение Y для заданных Х

₁

и Х

₂

можно также предсказать с помощью функции

ТЕНДЕНЦИЯ()

. При этом 2-й аргумент будет ссылкой на столбцы, содержащие все значения переменных Х

₁

и Х

₂

, а 3-й аргумент функции должен быть ссылкой на диапазон ячеек, содержащий 2 значения Х (Х

_1i

и Х

_2i

) для выбранного наблюдения i (см.

файл примера, лист Коэффициенты, столбец G

). Функция

ПРЕДСКАЗ()

, использованная нами в простой регрессии, не работает в случае

множественной регрессии

.

Найдя прогнозное значение Y, мы, таким образом, вычислим его точечную оценку. Понятно, что фактическое значение Y, полученное при наблюдении, будет, скорее всего, отличаться от этой оценки. Чтобы ответить на вопрос о том, на сколько хорошо мы можем предсказывать новые значения Y, нам потребуется построить

доверительный интервал

этой оценки, т.е. диапазон в котором с определенной заданной вероятностью, скажем 95%, мы ожидаем новое значение Y.

Доверительные интервалы

построим при фиксированном Х для:

• нового наблюдения Y;
• среднего значения Y (интервал будет уже, чем для отдельного нового наблюдения)

Как и в случае

простой линейной регрессии

, для построения

доверительных интервалов

нам потребуется сначала вычислить

стандартную ошибку модели

(standard error of the model)

, которая приблизительно показывает насколько велика ошибка предсказания значений переменной Y на основании значений переменных Х.

Для вычисления

стандартной ошибки

оценивают

дисперсию

ошибки ε, т.е. сигма^2

(ее часто обозначают как

MS

Е либо

MSres

)

. Затем, вычислив из полученной оценки квадратный корень, получим

Стандартную ошибку регрессии (часто обозначают как

SEy

или

sey

).

где SSE – сумма квадратов значений ошибок модели ei=yi — ŷi (

Sum of Squared Errors

). MSE означает Mean Square of Errors (среднее квадратов ошибок, точнее остатков).

Величина n-p – это количество

степеней свободы

(

df

–

degrees

of

freedom

), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y, р – количество оцениваемых параметров модели). В случае

простой множественной регрессии

с 2-мя регрессорами

число степеней свободы

равно n-3, т.к. при построении

плоскости регрессии

было оценено 3 параметра модели

b

(т.е. на это было «потрачено» 3

степени свободы

).

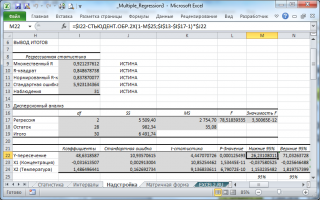
В MS EXCEL

стандартную ошибку

SEy можно вычислить формулы (см.

файл примера, лист Статистика

):

=

ИНДЕКС(ЛИНЕЙН($E$13:$E$43;$C$13:$D$43;;ИСТИНА);3;2)

Стандартная ошибка

нового наблюдения Y при заданных значениях Х (вектор Хi) вычисляется по формуле:

x

_i

— вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.

Соответствующий доверительный интервал вычисляется по формуле:

где α (альфа) –

уровень значимости

(обычно принимают равным 0,05=5%)

р – количество оцениваемых параметров модели (в нашем случае = 3)

n-p – число степеней свободы

–

квантиль

распределения Стьюдента

(задает количество

стандартных ошибок

, в +/- диапазоне которых вероятность обнаружить новое наблюдение равно 1-альфа). Т.е. если

квантиль

равен 2, то диапазон шириной +/- 2

стандартных ошибок

относительно прогнозного значения Y будет с вероятностью 95% содержать новое наблюдение Y (для каждого заданного Хi). В MS EXCEL вычисления квантиля производят по формуле =

СТЬЮДЕНТ.ОБР.2Х(0,05;n-p)

, подробнее см.

в статье про распределение Стьюдента

.

– прогнозное значение Yi вычисляемое по формуле Yi=

b

0+

b

1*

Х1i+

b

2*

Х2i (точечная оценка).

Стандартная ошибка

среднего значения Y при заданных значениях Х (вектор Хi) будет меньше, чем стандартная ошибка отдельного наблюдения. Вычисления производятся по формуле:

x

_i

— вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.

Соответствующий

доверительный интервал

вычисляется по формуле:

Прогнозное значение Yi (точечная оценка) используется тоже, что и для отдельного наблюдения.

Стандартные ошибки и доверительные интервалы для коэффициентов регрессии

В разделе

Оценка неизвестных параметров

мы получили точечные оценки

коэффициентов регрессии

. Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со

средним значением

и

дисперсией

. Но, чтобы перейти от

точечных оценок

к

интервальным

, необходимо вычислить соответствующие

стандартные ошибки

(т.е.

стандартные отклонения

)

коэффициентов регрессии

.

Стандартная ошибка коэффициента регрессии

b

_j

(обозначается

se

(

b

_j

)

) вычисляется на основании

стандартной ошибки

по следующей формуле:

где C

_jj

является диагональным элементом матрицы (X

^’

X)

^-1

. Для коэффициента сдвига

b

₀

индекс j=1 (верхний левый элемент), для

b

₁

индекс j=2,

b

₂

индекс j=3 (нижний правый элемент).

SEy –

стандартная ошибка регрессии

(см.

выше

).

В MS EXCEL

стандартные ошибки коэффициентов регрессии

можно вычислить с помощью функции

ЛИНЕЙН()

:

=

ИНДЕКС(ЛИНЕЙН($E$13:$E$43;$C$13:$D$43;;ИСТИНА);2;j)

Примечание

: Подробнее о функции

ЛИНЕЙН()

см. статью

Функция MS EXCEL ЛИНЕЙН()

.

Применяя матричный подход

стандартные ошибки

можно вычислить и через обычные формулы (точнее через

формулу массива

, см.

файл примера лист Статистика

):

=

КОРЕНЬ(СУММКВРАЗН(E13:E43;F13:F43) /(n-p)) *КОРЕНЬ (ИНДЕКС (МОБР (МУМНОЖ(ТРАНСП(B13:D43);(B13:D43)));j;j))

При построении

двухстороннего доверительного интервала

для

коэффициента регрессии

его границы определяются следующим образом:

b

_j

+/- t*Se(

b

_j

)

где t – это

t-значение

, которое можно вычислить с помощью формулы =

СТЬЮДЕНТ.ОБР.2Х(0,05;n-p)

для

уровня значимости

0,05.

В результате получим, что найденный

доверительный интервал

с вероятностью 95% (1-0,05) накроет истинное значение

коэффициента регрессии

b

_j

.

Здесь мы считаем, что

коэффициент регрессии

b

_j

имеет

распределение Стьюдента

с n-p

степенями свободы

(n – количество наблюдений, т.е. пар Х и Y).

Проверка гипотез

Когда мы строим модель, мы предполагаем, что между Y и переменными X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.

Единственный вариант, когда Y не зависит X, возможен, когда все

коэффициенты регрессии

β

равны 0.

Чтобы убедиться, что вычисленная нами оценка

коэффициентов регрессии

не обусловлена лишь случайностью (они не случайно отличны от 0), используют

проверку гипотез

. В качестве

нулевой гипотезы

Н

₀

принимают, что линейной связи нет, т.е. ВСЕ β=0. В качестве альтернативной гипотезы

Н

₁

принимают, что ХОТЯ БЫ ОДИН коэффициент β <>0.

Процедура проверки значимости множественной регрессии, приведенная ниже, является обобщением

дисперсионного анализа

, использованного нами в случае

простой линейной регрессии (F-тест)

.

Если нулевая гипотеза справедлива, то

тестовая

F

-статистика

имеет

F-распределение

со степенями свободы

k

и

n

—

k

-1

, т.е. F

_{k, n-k-1}

:

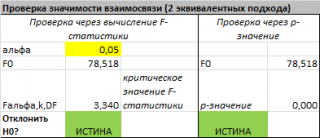
Проверку значимости регрессии можно также осуществить через вычисление

p

-значения

. В этом случае вычисляют вероятность того, что случайная величина F примет значение F

₀

(это и есть

p-значение

), затем сравнивают p-значение с заданным

уровнем значимости α (альфа)

. Если

p-значение

больше уровня значимости

,

то нулевую гипотезу нет оснований отклонить, и регрессия незначима.

В MS EXCEL значение F

₀

можно вычислить на основании значений выборки по вышеуказанной формуле или с помощью функции

ЛИНЕЙН()

:

=

ИНДЕКС(ЛИНЕЙН(E13:E43; C13:D43;;ИСТИНА);4;1)

В MS EXCEL для проверки гипотезы через

p

-значение

используйте формулу =F.РАСП.ПХ(F

₀

;k;n-k-1)<

альфа

Если формула вернет ИСТИНА, то регрессия значима. Если формула вернет ЛОЖЬ, то у нас нет оснований отклонить нулевую гипотезу, т.е. «скорее всего» все коэффициенты регрессии равны 0 (см.

файл примера лист Статистика

, где показано эквивалентность обоих подходов проверки значимости регрессии).

В MS EXCEL критическое значение для заданного

уровня значимости

F

_{1-альфа, k, n-k-1}

можно вычислить по формуле =

F.ОБР(1- альфа;k;n-k-1)

или =

F.ОБР.ПХ(альфа;k; n-k-1)

. Другими словами требуется вычислить

верхний альфа-

квантиль

F

-распределения

с соответствующими

степенями свободы

.

Таким образом, при значении статистики F

₀

> F

_{1-альфа, k, n-k-1}

мы имеем основание для отклонения нулевой гипотезы.

В программах статистики результаты процедуры

F

-теста

выводят с помощью стандартной таблицы

дисперсионного анализа

. В

файле примера такая таблица приведена на листе Надстройка

, которая построена на основе результатов, возвращаемых инструментом

Регрессия надстройки Пакета анализа MS EXCEL

.

Генерация данных для множественной регрессии с помощью заданного тренда

Иногда, бывает удобно сгенерировать значения наблюдений, имея заданный тренд.

Для решения этой задачи нам потребуется:

• задать значения регрессоров в нужном диапазоне (значения переменных Х);
• задать коэффициенты регрессии (
  
  b
  
  );
• задать тренд (вычислить значения Y=
  
  b
  
  ₀
  
  +
  
  b
  
  ₁
  
  *
  
  Х
  
  ₁
  
  +
  
  b
  
  ₂
  
  *
  
  Х
  
  ₂
  
  );
• задать величину разброса Y вокруг тренда (варианты: случайный разброс в заданных границах или заданная фигура, например, круг)

Все вычисления выполнены в

файле примера, лист Тренд

для случая 2-х регрессоров. Там же построены

диаграммы рассеяния

.

Коэффициент детерминации

Коэффициент детерминации

R

²

показывает насколько полезна построенная нами

линейная регрессионная модель

.

По определению

коэффициент детерминации

R

²

равен:

R

²

=

Изменчивость объясненная моделью (

SSR

) / Общая изменчивость (

SST

).

Этот показатель можно вычислить с помощью функции

ЛИНЕЙН()

:

=

ИНДЕКС(ЛИНЕЙН(E13:E43;C13:D43;;ИСТИНА);3)

При добавлении в модель новой объясняющей переменной Х,

коэффициент детерминации

будет всегда расти. Поэтому, рост

коэффициента детерминации

не может служить основанием для вывода о том, что новая модель (с дополнительным регрессором) лучше прежней.

Более подходящей статистикой, которая лишена указанного недостатка, является

нормированный

коэффициент детерминации

(Adjusted R-squared):

где p – число независимых

регрессоров

(вычисления см.

файл примера лист Статистика

).

Пакет MS Excel
позволяет при построении уравнения линейной регрессии большую часть работы сделать очень быстро. Важно понять, как интерпретировать полученные результаты.
Для построения модели регрессии необходимо выбрать пункт СервисАнализ данныхРегрессия (в Excel 2007
этот режим находится в блоке Данные/Анализ данных/Регрессия). Затем полученные результаты скопировать в блок для анализа.

В Excel
имеется еще более быстрый и удобный способ построить график линейной регрессии (и даже основных видов нелинейных регрессий, о чем см. далее). Это можно сделать следующим образом:

1) выделить столбцы с данными X
и Y
(они должны располагаться именно в таком порядке!);

2) вызвать Мастер диаграмм
и выбрать в группе Тип
– Точечная
и сразу нажать Готово
;

3) не сбрасывая выделения с диаграммы, выбрать появившейся пункт основного меню Диаграмма
, в котором следует выбрать пункт Добавить линию тренда
;

4) в появившемся диалоговом окне Линия тренда
во вкладке Тип
выбрать Линейная
;

5) во вкладке Параметры
можно активизировать переключатель Показывать уравнение на диаграмме
, что позволит увидеть уравнение линейной регрессии (4.4), в котором будут вычислены коэффициенты (4.5).

6) В этой же вкладке можно активизировать переключатель Поместить на диаграмму величину достоверности аппроксимации (R^2)
. Эта величина есть квадрат коэффициента корреляции (4.3) и она показывает, насколько хорошо рассчитанное уравнение описывает экспериментальную зависимость. Если R
2 близок к единице, то теоретическое уравнение регрессии хорошо описывает экспериментальную зависимость (теория хорошо согласуется с экспериментом), а если R
2 близок к нулю, то данное уравнение не пригодно для описания экспериментальной зависимости (теория не согласуется с экспериментом).

В результате выполнения описанных действий получится диаграмма с графиком регрессии и ее уравнением.

§4.3. Основные виды нелинейной регрессии

Параболическая и полиномиальная регрессии.

Параболической
зависимостью величины Y
от величины Х
называется зависимость, выраженная квадратичной функцией (параболой 2-ого порядка):

Это уравнение называется уравнением параболической регрессии Y
на Х
. Параметры а
, b
, с
называются коэффициентами параболической регрессии
. Вычисление коэффициентов параболической регрессии всегда громоздко, поэтому для расчетов рекомендуется использовать компьютер.

Уравнение (4.8) параболической регрессии является частным случаем более общей регрессии, называемой полиномиальной. Полиномиальной
зависимостью величины Y
от величины Х
называется зависимость, выраженная полиномом n
-ого порядка:

где числа а i
(i
=0,1,…, n
) называются коэффициентами полиномиальной регрессии
.

Степенная регрессия.

Степенной
зависимостью величины Y
от величины Х
называется зависимость вида:

Это уравнение называется уравнением степенной регрессии Y
на Х
. Параметры а
и b
называются коэффициентами степенной регрессии
.

ln =lna
+b·
lnx
. (4.11)

Это уравнение описывает прямую на плоскости с логарифмическими координатными осями lnx
и ln . Поэтому критерием применимости степенной регрессии служит требование того, чтобы точки логарифмов эмпирических данных lnx i
и lnу i
находились ближе всего к прямой (4.11).

Показательная регрессия.

Показательной
(или экспоненциальной
) зависимостью величины Y
от величины Х
называется зависимость вида:

(или ). (4.12)

Это уравнение называется уравнением показательной
(или экспоненциальной
) регрессии Y
на Х
. Параметры а
(или k
) и b
называются коэффициентами показательной
(или экспоненциальной
) регрессии
.

Если прологарифмировать обе части уравнения степенной регрессии, то получится уравнение

ln =x·
lna
+lnb
(или ln =k·x
+lnb
). (4.13)

Это уравнение описывает линейную зависимость логарифма одной величины ln от другой величины x
. Поэтому критерием применимости степенной регрессии служит требование того, чтобы точки эмпирических данных одной величины x i
и логарифмы другой величины lnу i
находились ближе всего к прямой (4.13).

Логарифмическая регрессия.

Логарифмической
зависимостью величины Y
от величины Х
называется зависимость вида:

=a
+b·
lnx
. (4.14)

Это уравнение называется уравнением логарифмической регрессии Y
на Х
. Параметры а
и b
называются коэффициентами логарифмической регрессии
.

Гиперболическая регрессия.

Гиперболической
зависимостью величины Y
от величины Х
называется зависимость вида:

Это уравнение называется уравнением гиперболической регрессии Y
на Х
. Параметры а
и b
называются коэффициентами гиперболической регрессии
и определяются методом наименьших квадратов. Применение этого метода приводит к формулам:

В формулах (4.16-4.17) суммирование проводится по индексу i
от единицы до количества наблюдений n
.

К сожалению, в Excel
нет функции, вычисляющих коэффициенты гиперболической регрессии. В тех случаях, когда заведомо не известно, что измеряемые величины связаны обратной пропорциональностью, рекомендуется вместо уравнения гиперболической регрессии искать уравнение степенной регрессии, так в Excel
имеется процедура ее нахождения. Если же между измеряемыми величинами предполагается гиперболическая зависимость, то коэффициенты ее регрессии придется вычислять с помощью вспомогательных расчетных таблиц и операций суммирования по формулам (4.16-4.17).

Регрессионный анализ — это статистический метод исследования, позволяющий показать зависимость того или иного параметра от одной либо нескольких независимых переменных. В докомпьютерную эру его применение было достаточно затруднительно, особенно если речь шла о больших объемах данных. Сегодня, узнав как построить регрессию в Excel, можно решать сложные статистические задачи буквально за пару минут. Ниже представлены конкретные примеры из области экономики.

Виды регрессии

Само это понятие было введено в математику в 1886 году. Регрессия бывает:

• линейной;
• параболической;
• степенной;
• экспоненциальной;
• гиперболической;
• показательной;
• логарифмической.

Пример 1

Рассмотрим задачу определения зависимости количества уволившихся членов коллектива от средней зарплаты на 6 промышленных предприятиях.

Задача. На шести предприятиях проанализировали среднемесячную заработную плату и количество сотрудников, которые уволились по собственному желанию. В табличной форме имеем:

		Количество уволившихся	Зарплата
		30000 рублей
			35000 рублей
			40000 рублей
			45000 рублей
			50000 рублей
			55000 рублей
			60000 рублей

Для задачи определения зависимости количества уволившихся работников от средней зарплаты на 6 предприятиях модель регрессии имеет вид уравнения Y = а 0 + а 1 x 1 +…+а k x k , где х i — влияющие переменные, a i — коэффициенты регрессии, a k — число факторов.

Для данной задачи Y — это показатель уволившихся сотрудников, а влияющий фактор — зарплата, которую обозначаем X.

Использование возможностей табличного процессора «Эксель»

Анализу регрессии в Excel должно предшествовать применение к имеющимся табличным данным встроенных функций. Однако для этих целей лучше воспользоваться очень полезной надстройкой «Пакет анализа». Для его активации нужно:

• с вкладки «Файл» перейти в раздел «Параметры»;
• в открывшемся окне выбрать строку «Надстройки»;
• щелкнуть по кнопке «Перейти», расположенной внизу, справа от строки «Управление»;
• поставить галочку рядом с названием «Пакет анализа» и подтвердить свои действия, нажав «Ок».

Если все сделано правильно, в правой части вкладки «Данные», расположенном над рабочим листом «Эксель», появится нужная кнопка.

в Excel

Теперь, когда под рукой есть все необходимые виртуальные инструменты для осуществления эконометрических расчетов, можем приступить к решению нашей задачи. Для этого:

• щелкаем по кнопке «Анализ данных»;
• в открывшемся окне нажимаем на кнопку «Регрессия»;
• в появившуюся вкладку вводим диапазон значений для Y (количество уволившихся работников) и для X (их зарплаты);
• подтверждаем свои действия нажатием кнопки «Ok».

В результате программа автоматически заполнит новый лист табличного процессора данными анализа регрессии. Обратите внимание! В Excel есть возможность самостоятельно задать место, которое вы предпочитаете для этой цели. Например, это может быть тот же лист, где находятся значения Y и X, или даже новая книга, специально предназначенная для хранения подобных данных.

Анализ результатов регрессии для R-квадрата

В Excel данные полученные в ходе обработки данных рассматриваемого примера имеют вид:

Прежде всего, следует обратить внимание на значение R-квадрата. Он представляет собой коэффициент детерминации. В данном примере R-квадрат = 0,755 (75,5%), т. е. расчетные параметры модели объясняют зависимость между рассматриваемыми параметрами на 75,5 %. Чем выше значение коэффициента детерминации, тем выбранная модель считается более применимой для конкретной задачи. Считается, что она корректно описывает реальную ситуацию при значении R-квадрата выше 0,8. Если R-квадрата<0,5, то такой анализа регрессии в Excel нельзя считать резонным.

Анализ коэффициентов

Число 64,1428 показывает, каким будет значение Y, если все переменные xi в рассматриваемой нами модели обнулятся. Иными словами можно утверждать, что на значение анализируемого параметра оказывают влияние и другие факторы, не описанные в конкретной модели.

Следующий коэффициент -0,16285, расположенный в ячейке B18, показывает весомость влияния переменной Х на Y. Это значит, что среднемесячная зарплата сотрудников в пределах рассматриваемой модели влияет на число уволившихся с весом -0,16285, т. е. степень ее влияния совсем небольшая. Знак «-» указывает на то, что коэффициент имеет отрицательное значение. Это очевидно, так как всем известно, что чем больше зарплата на предприятии, тем меньше людей выражают желание расторгнуть трудовой договор или увольняется.

Множественная регрессия

Под таким термином понимается уравнение связи с несколькими независимыми переменными вида:

y=f(x 1 +x 2 +…x m) + ε, где y — это результативный признак (зависимая переменная), а x 1 , x 2 , …x m — это признаки-факторы (независимые переменные).

Оценка параметров

Для множественной регрессии (МР) ее осуществляют, используя метод наименьших квадратов (МНК). Для линейных уравнений вида Y = a + b 1 x 1 +…+b m x m + ε строим систему нормальных уравнений (см. ниже)

Чтобы понять принцип метода, рассмотрим двухфакторный случай. Тогда имеем ситуацию, описываемую формулой

Отсюда получаем:

где σ — это дисперсия соответствующего признака, отраженного в индексе.

МНК применим к уравнению МР в стандартизируемом масштабе. В таком случае получаем уравнение:

в котором t y , t x 1, … t xm — стандартизируемые переменные, для которых средние значения равны 0; β i — стандартизированные коэффициенты регрессии, а среднеквадратическое отклонение — 1.

Обратите внимание, что все β i в данном случае заданы, как нормируемые и централизируемые, поэтому их сравнение между собой считается корректным и допустимым. Кроме того, принято осуществлять отсев факторов, отбрасывая те из них, у которых наименьшие значения βi.

Задача с использованием уравнения линейной регрессии

Предположим, имеется таблица динамики цены конкретного товара N в течение последних 8 месяцев. Необходимо принять решение о целесообразности приобретения его партии по цене 1850 руб./т.

	номер месяца	название месяца	цена товара N
			1750 рублей за тонну
			1755 рублей за тонну
			1767 рублей за тонну
			1760 рублей за тонну
			1770 рублей за тонну
			1790 рублей за тонну
			1810 рублей за тонну
			1840 рублей за тонну

Для решения этой задачи в табличном процессоре «Эксель» требуется задействовать уже известный по представленному выше примеру инструмент «Анализ данных». Далее выбирают раздел «Регрессия» и задают параметры. Нужно помнить, что в поле «Входной интервал Y» должен вводиться диапазон значений для зависимой переменной (в данном случае цены на товар в конкретные месяцы года), а в «Входной интервал X» — для независимой (номер месяца). Подтверждаем действия нажатием «Ok». На новом листе (если так было указано) получаем данные для регрессии.

Строим по ним линейное уравнение вида y=ax+b, где в качестве параметров a и b выступают коэффициенты строки с наименованием номера месяца и коэффициенты и строки «Y-пересечение» из листа с результатами регрессионного анализа. Таким образом, линейное уравнение регрессии (УР) для задачи 3 записывается в виде:

Цена на товар N = 11,714* номер месяца + 1727,54.

или в алгебраических обозначениях

y = 11,714 x + 1727,54

Анализ результатов

Чтобы решить, адекватно ли полученное уравнения линейной регрессии, используются коэффициенты множественной корреляции (КМК) и детерминации, а также критерий Фишера и критерий Стьюдента. В таблице «Эксель» с результатами регрессии они выступают под названиями множественный R, R-квадрат, F-статистика и t-статистика соответственно.

КМК R дает возможность оценить тесноту вероятностной связи между независимой и зависимой переменными. Ее высокое значение свидетельствует о достаточно сильной связи между переменными «Номер месяца» и «Цена товара N в рублях за 1 тонну». Однако, характер этой связи остается неизвестным.

Квадрат коэффициента детерминации R 2 (RI) представляет собой числовую характеристику доли общего разброса и показывает, разброс какой части экспериментальных данных, т.е. значений зависимой переменной соответствует уравнению линейной регрессии. В рассматриваемой задаче эта величина равна 84,8%, т. е. статистические данные с высокой степенью точности описываются полученным УР.

F-статистика, называемая также критерием Фишера, используется для оценки значимости линейной зависимости, опровергая или подтверждая гипотезу о ее существовании.

(критерий Стьюдента) помогает оценивать значимость коэффициента при неизвестной либо свободного члена линейной зависимости. Если значение t-критерия > t кр, то гипотеза о незначимости свободного члена линейного уравнения отвергается.

В рассматриваемой задаче для свободного члена посредством инструментов «Эксель» было получено, что t=169,20903, а p=2,89Е-12, т. е. имеем нулевую вероятность того, что будет отвергнута верная гипотеза о незначимости свободного члена. Для коэффициента при неизвестной t=5,79405, а p=0,001158. Иными словами вероятность того, что будет отвергнута верная гипотеза о незначимости коэффициента при неизвестной, равна 0,12%.

Таким образом, можно утверждать, что полученное уравнение линейной регрессии адекватно.

Задача о целесообразности покупки пакета акций

Множественная регрессия в Excel выполняется с использованием все того же инструмента «Анализ данных». Рассмотрим конкретную прикладную задачу.

Руководство компания «NNN» должно принять решение о целесообразности покупки 20 % пакета акций АО «MMM». Стоимость пакета (СП) составляет 70 млн американских долларов. Специалистами «NNN» собраны данные об аналогичных сделках. Было принято решение оценивать стоимость пакета акций по таким параметрам, выраженным в миллионах американских долларов, как:

• кредиторская задолженность (VK);
• объем годового оборота (VO);
• дебиторская задолженность (VD);
• стоимость основных фондов (СОФ).

Кроме того, используется параметр задолженность предприятия по зарплате (V3 П) в тысячах американских долларов.

Решение средствами табличного процессора Excel

Прежде всего, необходимо составить таблицу исходных данных. Она имеет следующий вид:

• вызывают окно «Анализ данных»;
• выбирают раздел «Регрессия»;
• в окошко «Входной интервал Y» вводят диапазон значений зависимых переменных из столбца G;
• щелкают по иконке с красной стрелкой справа от окна «Входной интервал X» и выделяют на листе диапазон всех значений из столбцов B,C, D, F.

Отмечают пункт «Новый рабочий лист» и нажимают «Ok».

Получают анализ регрессии для данной задачи.

Изучение результатов и выводы

«Собираем» из округленных данных, представленных выше на листе табличного процессора Excel, уравнение регрессии:

СП = 0,103*СОФ + 0,541*VO — 0,031*VK +0,405*VD +0,691*VZP — 265,844.

В более привычном математическом виде его можно записать, как:

y = 0,103*x1 + 0,541*x2 — 0,031*x3 +0,405*x4 +0,691*x5 — 265,844

Данные для АО «MMM» представлены в таблице:

Подставив их в уравнение регрессии, получают цифру в 64,72 млн американских долларов. Это значит, что акции АО «MMM» не стоит приобретать, так как их стоимость в 70 млн американских долларов достаточно завышена.

Как видим, использование табличного процессора «Эксель» и уравнения регрессии позволило принять обоснованное решение относительно целесообразности вполне конкретной сделки.

Теперь вы знаете, что такое регрессия. Примеры в Excel, рассмотренные выше, помогут вам в решение практических задач из области эконометрики.

Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.

Подключение пакета анализа

Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.

1. Перемещаемся во вкладку «Файл».
2. Переходим в раздел «Параметры».
3. Открывается окно параметров Excel. Переходим в подраздел «Надстройки».
4. В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
5. Открывается окно доступных надстроек Эксель. Ставим галочку около пункта «Пакет анализа». Жмем на кнопку «OK».

Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».

Виды регрессионного анализа

Существует несколько видов регрессий:

• параболическая;
• степенная;
• логарифмическая;
• экспоненциальная;
• показательная;
• гиперболическая;
• линейная регрессия.

О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.

Линейная регрессия в программе Excel

Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.

Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.

Разбор результатов анализа

Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.

Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.

Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.

Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.

Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.

Мы рады, что смогли помочь Вам в решении проблемы.

Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

Метод линейной регрессии позволяет нам описывать прямую линию, максимально соответствующую ряду упорядоченных пар (x, y). Уравнение для прямой линии, известное как линейное уравнение, представлено ниже:

ŷ — ожидаемое значение у при заданном значении х,

x — независимая переменная,

a — отрезок на оси y для прямой линии,

b — наклон прямой линии.

На рисунке ниже это понятие представлено графически:

На рисунке выше показана линия, описанная уравнением ŷ =2+0.5х. Отрезок на оси у — это точка пересечения линией оси у; в нашем случае а = 2. Наклон линии, b, отношение подъема линии к длине линии, имеет значение 0.5. Положительный наклон означает, что линия поднимается слева направо. Если b = 0, линия горизонтальна, а это значит, что между зависимой и независимой переменными нет никакой связи. Иными словами, изменение значения x не влияет на значение y.

Часто путают ŷ и у. На графике показаны 6 упорядоченных пар точек и линия, в соответствии с данным уравнением

На этом рисунке показана точка, соответствующая упорядоченной паре х = 2 и у = 4. Обратите внимание, что ожидаемое значение у в соответствии с линией при х
= 2 является ŷ. Мы можем подтвердить это с помощью следу­ющего уравнения:

ŷ = 2 + 0.5х =2 +0.5(2) =3.

Значение у представляет собой фактическую точку, а значение ŷ — это ожидаемое значение у с использованием линейного уравнения при заданном значении х.

Следующий шаг — определить линейное уравнение, максимально соответствующее набору упорядоченных пар, об этом мы говорили в предыдущей статье, где определяли вид уравнения по методу наименьших квадратов.

Использование Excel для определения линейной регрессии

Для того, чтобы воспользоваться инструментом регрессионного анализа встроенного в Excel, необходимо активировать надстройку Пакет анализа
. Найти ее можно, перейдя по вкладке Файл –> Параметры
(2007+), в появившемся диалоговом окне Параметры
Excel
переходим во вкладку Надстройки.
В поле Управление
выбираем Надстройки
Excel
и щелкаем Перейти.
В появившемся окне ставим галочку напротив Пакет анализа,
жмем ОК.

Во вкладке Данные
в группе Анализ
появится новая кнопка Анализ данных.

Чтобы продемонстрировать работу надстройки, воспользуемся данными с предыдущей статьи, где парень и девушка делят столик в ванной. Введите данные нашего примера с ванной в столбцы А и В чистого листа.

Перейдите во вкладку Данные,
в группе Анализ
щелкните Анализ данных.
В появившемся окне Анализ данных
выберите Регрессия
, как показано на рисунке, и щелкните ОК.

Установите необходимыe параметры регрессии в окне Рег­рессия
, как показано на рисунке:

Щелкните ОК.
На рисунке ниже показаны полученные результаты:

Эти результаты соответствуют тем, которые мы получили путем самостоя­тельных вычислений в предыдущей статье.

Регрессионный анализ — это статистический метод исследования, позволяющий показать зависимость того или иного параметра от одной либо нескольких независимых переменных. В докомпьютерную эру его применение было достаточно затруднительно, особенно если речь шла о больших объемах данных. Сегодня, узнав как построить регрессию в Excel, можно решать сложные статистические задачи буквально за пару минут. Ниже представлены конкретные примеры из области экономики.

Виды регрессии

Само это понятие было введено в математику Фрэнсисом Гальтоном в 1886 году. Регрессия бывает:

• линейной;
• параболической;
• степенной;
• экспоненциальной;
• гиперболической;
• показательной;
• логарифмической.

Пример 1

Рассмотрим задачу определения зависимости количества уволившихся членов коллектива от средней зарплаты на 6 промышленных предприятиях.

Задача. На шести предприятиях проанализировали среднемесячную заработную плату и количество сотрудников, которые уволились по собственному желанию. В табличной форме имеем:

Для задачи определения зависимости количества уволившихся работников от средней зарплаты на 6 предприятиях модель регрессии имеет вид уравнения Y = а0 + а1×1 +…+аkxk, где хi — влияющие переменные, ai — коэффициенты регрессии, a k — число факторов.

Для данной задачи Y — это показатель уволившихся сотрудников, а влияющий фактор — зарплата, которую обозначаем X.

Использование возможностей табличного процессора «Эксель»

Анализу регрессии в Excel должно предшествовать применение к имеющимся табличным данным встроенных функций. Однако для этих целей лучше воспользоваться очень полезной надстройкой «Пакет анализа». Для его активации нужно:

• с вкладки «Файл» перейти в раздел «Параметры»;
• в открывшемся окне выбрать строку «Надстройки»;
• щелкнуть по кнопке «Перейти», расположенной внизу, справа от строки «Управление»;
• поставить галочку рядом с названием «Пакет анализа» и подтвердить свои действия, нажав «Ок».

Если все сделано правильно, в правой части вкладки «Данные», расположенном над рабочим листом «Эксель», появится нужная кнопка.

Линейная регрессия в Excel

Теперь, когда под рукой есть все необходимые виртуальные инструменты для осуществления эконометрических расчетов, можем приступить к решению нашей задачи. Для этого:

• щелкаем по кнопке «Анализ данных»;
• в открывшемся окне нажимаем на кнопку «Регрессия»;
• в появившуюся вкладку вводим диапазон значений для Y (количество уволившихся работников) и для X (их зарплаты);
• подтверждаем свои действия нажатием кнопки «Ok».

В результате программа автоматически заполнит новый лист табличного процессора данными анализа регрессии. Обратите внимание! В Excel есть возможность самостоятельно задать место, которое вы предпочитаете для этой цели. Например, это может быть тот же лист, где находятся значения Y и X, или даже новая книга, специально предназначенная для хранения подобных данных.

Анализ результатов регрессии для R-квадрата

В Excel данные полученные в ходе обработки данных рассматриваемого примера имеют вид:

Прежде всего, следует обратить внимание на значение R-квадрата. Он представляет собой коэффициент детерминации. В данном примере R-квадрат = 0,755 (75,5%), т. е. расчетные параметры модели объясняют зависимость между рассматриваемыми параметрами на 75,5 %. Чем выше значение коэффициента детерминации, тем выбранная модель считается более применимой для конкретной задачи. Считается, что она корректно описывает реальную ситуацию при значении R-квадрата выше 0,8. Если R-квадрата tкр, то гипотеза о незначимости свободного члена линейного уравнения отвергается.

В рассматриваемой задаче для свободного члена посредством инструментов «Эксель» было получено, что t=169,20903, а p=2,89Е-12, т. е. имеем нулевую вероятность того, что будет отвергнута верная гипотеза о незначимости свободного члена. Для коэффициента при неизвестной t=5,79405, а p=0,001158. Иными словами вероятность того, что будет отвергнута верная гипотеза о незначимости коэффициента при неизвестной, равна 0,12%.

Таким образом, можно утверждать, что полученное уравнение линейной регрессии адекватно.

Задача о целесообразности покупки пакета акций

Множественная регрессия в Excel выполняется с использованием все того же инструмента «Анализ данных». Рассмотрим конкретную прикладную задачу.

Руководство компания «NNN» должно принять решение о целесообразности покупки 20 % пакета акций АО «MMM». Стоимость пакета (СП) составляет 70 млн американских долларов. Специалистами «NNN» собраны данные об аналогичных сделках. Было принято решение оценивать стоимость пакета акций по таким параметрам, выраженным в миллионах американских долларов, как:

• кредиторская задолженность (VK);
• объем годового оборота (VO);
• дебиторская задолженность (VD);
• стоимость основных фондов (СОФ).

Кроме того, используется параметр задолженность предприятия по зарплате (V3 П) в тысячах американских долларов.

Решение средствами табличного процессора Excel

Прежде всего, необходимо составить таблицу исходных данных. Она имеет следующий вид:

• вызывают окно «Анализ данных»;
• выбирают раздел «Регрессия»;
• в окошко «Входной интервал Y» вводят диапазон значений зависимых переменных из столбца G;
• щелкают по иконке с красной стрелкой справа от окна «Входной интервал X» и выделяют на листе диапазон всех значений из столбцов B,C, D, F.

Отмечают пункт «Новый рабочий лист» и нажимают «Ok».

Получают анализ регрессии для данной задачи.

Изучение результатов и выводы

«Собираем» из округленных данных, представленных выше на листе табличного процессора Excel, уравнение регрессии:

СП = 0,103*СОФ + 0,541*VO – 0,031*VK +0,405*VD +0,691*VZP – 265,844.

В более привычном математическом виде его можно записать, как:

y = 0,103*x1 + 0,541*x2 – 0,031*x3 +0,405*x4 +0,691*x5 – 265,844

Данные для АО «MMM» представлены в таблице:

Подставив их в уравнение регрессии, получают цифру в 64,72 млн американских долларов. Это значит, что акции АО «MMM» не стоит приобретать, так как их стоимость в 70 млн американских долларов достаточно завышена.

Как видим, использование табличного процессора «Эксель» и уравнения регрессии позволило принять обоснованное решение относительно целесообразности вполне конкретной сделки.

Теперь вы знаете, что такое регрессия. Примеры в Excel, рассмотренные выше, помогут вам в решение практических задач из области эконометрики.

Линия регрессии является графическим отражением взаимосвязи между явлениями. Очень наглядно можно построить линию регрессии в программе Excel.

Для этого необходимо:

1.Открыть программу Excel

2.Создать столбцы с данными. В нашем примере мы будем строить линию регрессии, или взаимосвязи, между агрессивностью и неуверенностью в себе у детей-первоклассников. В эксперименте участвовали 30 детей, данные представлены в таблице эксель:

1 столбик — № испытуемого

2 столбик — агрессивность
в баллах

3 столбик — неуверенность в себе
в баллах

3.Затем необходимо выделить оба столбика (без названия столбика), нажать вкладку вставка

,
выбрать точечная

, а из предложенных макетов выбрать самый первый точечная с маркерами

.

4.Итак у нас получилась заготовка для линии регрессии — так называемая — диаграмма рассеяния
. Для перехода к линии регрессии нужно щёлкнуть на получившийся рисунок, нажать вкладку конструктор,

найти на панели макеты диаграмм

и выбрать Ма
кет9

, на нем ещё написано f(x)

5.Итак, у нас получилась линия регрессии. На графике также указано её уравнение и квадрат коэффициента корреляции

6.Осталось добавить название графика, название осей. Также по желанию можно убрать легенду, уменьшить количество горизонтальных линий сетки (вкладка макет

, затем сетка

). Основные изменения и настройки производятся во вкладке Макет

Линия регрессии построена в MS Excel. Теперь её можно добавить в текст работы.

Нелинейная регрессия в Excel

Добрый день, уважаемые читатели блога! Сегодня мы поговорим о нелинейных регрессиях. Решение линейных регрессий можно посмотреть по ССЫЛКЕ.

Данный способ применяется, в основном, в экономическом моделировании и прогнозировании. Его цель – пронаблюдать и выявить зависимости между двумя показателями.

Основными типами нелинейных регрессий являются:

• полиномиальные (квадратичная, кубическая);
• гиперболическая;
• степенная;
• показательная;
• логарифмическая.

Также могут применяться различные комбинации. Например, для аналитики временных рядов в банковской сфере, страховании, демографических исследованиях используют кривую Гомпцера, которая является разновидностью логарифмической регрессии.

В прогнозировании с помощью нелинейных регрессий главное выяснить коэффициент корреляции, который покажет нам есть ли тесная взаимосвязь меду двумя параметрами или нет. Как правило, если коэффициент корреляции близок к 1, значит связь есть, и прогноз будет довольно точен. Ещё одним важным элементом нелинейных регрессий является средняя относительная ошибка (А), если она находится в промежутке <8…10%, значит модель достаточно точна.

На этом, пожалуй, теоретический блок мы закончим и перейдём к практическим вычислениям.

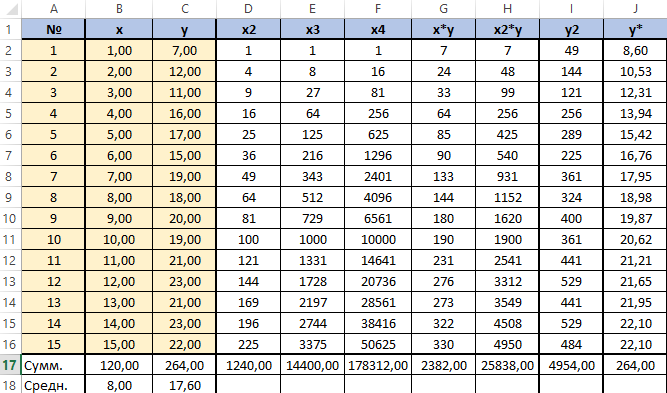
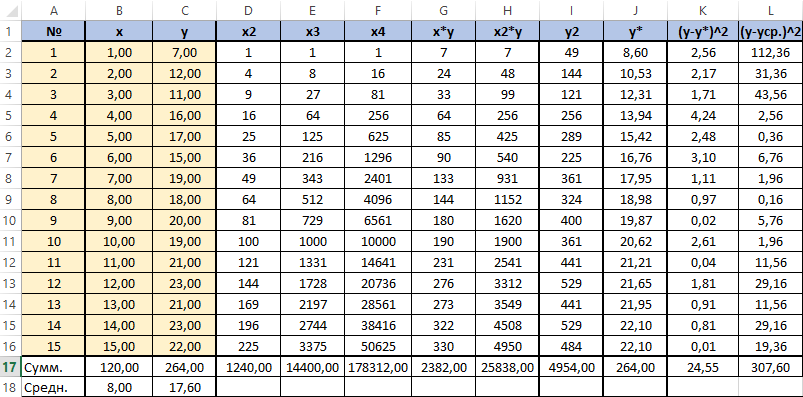
У нас имеется таблица продаж автомобилей за промежуток 15 лет (обозначим его X), количество шагов измерений будет аргумент n, также имеется выручка за эти периоды (обозначим её Y), нам нужно спрогнозировать какова будет выручка в дальнейшем. Построим следующую таблицу:

Для исследования нам потребуется решить уравнение (зависимости Y от X): y=ax²+bx+c+e. Это парная квадратичная регрессия. Применим в этом случае метод наименьших квадратов, для выяснения неизвестных аргументов — a, b, c. Он приведёт к системе алгебраических уравнений вида:

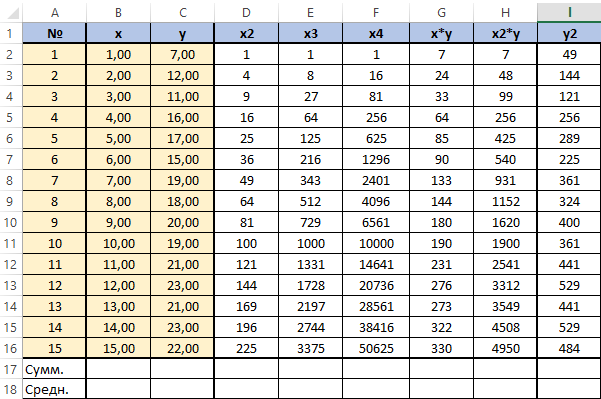
Для решения этой системы воспользуемся, к примеру, методом Крамера. Видим, что входящие в систему суммы являются коэффициентами при неизвестных. Для их вычисления добавим в таблицу несколько столбцов (D,E,F,G,H) и подпишем соответственно смыслу вычислений — в столбце D возведём x в квадрат, в E в куб, в F в 4 степень, в G перемножим показатели x и y, в H возведём x в квадрат и перемножим с y.

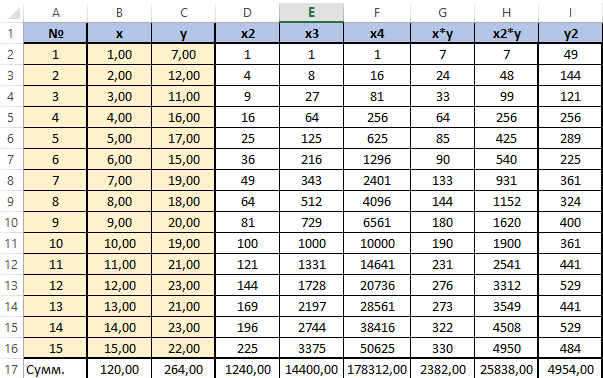
Получится заполненная нужными для решения уравнения таблица вида.

Далее посчитаем суммы по каждому столбцу — воспользуемся ∑ в программе Excel.

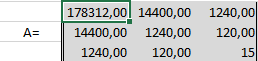
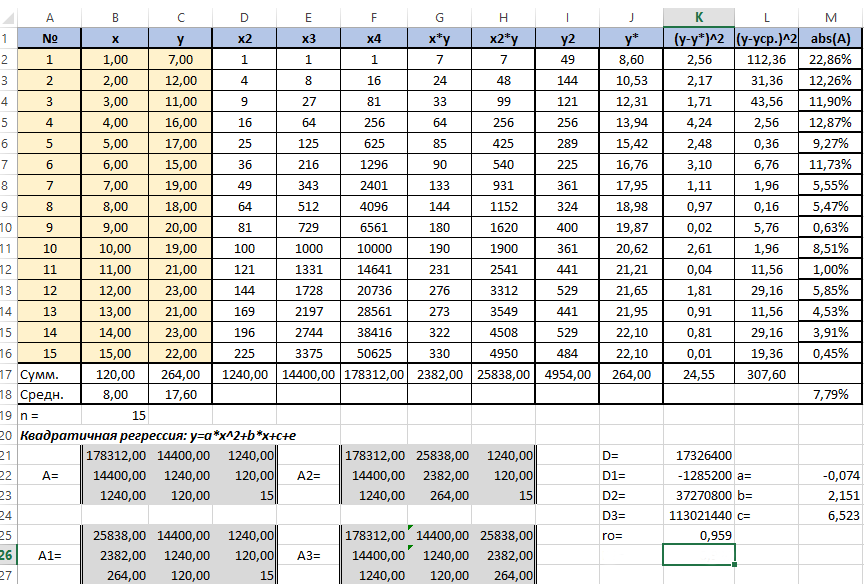
Сформируем матрицу A системы, состоящую из коэффициентов при неизвестных в левых частях уравнений. Поместим её в ячейку А22 и назовём «А=«. Следуем той системе уравнений, которую мы избрали для решения регрессии. 

То есть, в ячейку B21 мы должны поместить сумму столбца, где возводили показатель X  в четвёртую степень — F17. Просто сошлёмся на ячейку — «=F17». Далее нам необходима сумма столбца где возводили X в куб — E17, далее идём строго по системе. Таким образом, нам необходимо будет заполнить всю матрицу.

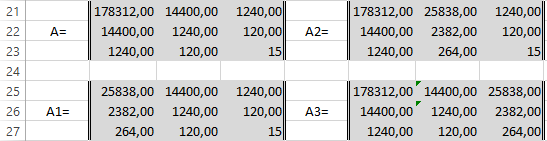
В соответствии с алгоритмом Крамера наберём матрицу А1, подобную А, в которой вместо элементов первого столбца должны размещаться элементы правых частей уравнений системы. То есть сумма столбца X в квадрате умноженная на Y, сумма столбца XY и сумма столбца Y. 

Также нам понадобятся ещё две матрицы — назовём их А2 и А3 в которых второй и третий столбцы будут состоять из коэффициентов правых частей уравнений. Картина будет такова.

Следуя избранному алгоритму, нам нужно будет вычислить значения определителей (детерминантов, D) полученных матриц. Воспользуемся формулой МОПРЕД. Результаты разместим в ячейках J21:K24.

Расчёт коэффициентов уравнения по Крамеру будем производить в ячейках напротив соответствующих детерминантов по формуле: a (в ячейке M22) — «=K22/K21»; b (в ячейке M23) — «=K23/K21»; с (в ячейке M24) — «=K24/K21».

Получим наше искомое уравнение парной квадратичной регрессии:

y=-0,074x²+2,151x+6,523

Оценим тесноту линейной связи индексом корреляции. 

Для вычисления добавим в таблицу дополнительный столбец J (назовём его y*). Расчёта будет следующей (согласно полученному нами уравнению регрессии) — «=$m$22*B2*B2+$M$23*B2+$M$24». Поместим её в ячейку J2. Останется протянуть вниз маркер автозаполнения до ячейки J16.

Для вычисления сумм (Y-Y усредненное)² добавим в таблицу столбцы K и L с соответствующими формулами. Среднее по столбцу Y посчитаем с помощью функции СРЗНАЧ.

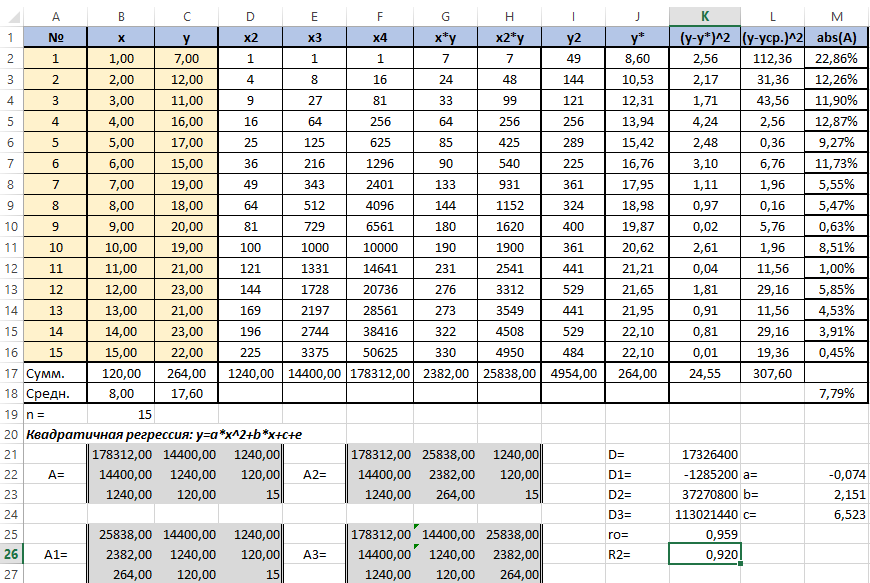
В ячейке K25 разместим формулу подсчёта индекса корреляции — «=КОРЕНЬ(1-(K17/L17))».

Видим, что значение 0,959 очень близко к 1, значит между продажами и годами есть тесная нелинейная связь. 

Осталось оценить качество подгонки полученного квадратичного уравнения регрессии (индекс детерминации). Он рассчитывается по формуле квадрата индекса корреляции. То есть формула в ячейке K26 будет очень проста — «=K25*K25».

Коэффициент 0,920 близок к 1, что свидетельствует о высоком качестве подгонки.

Последним действием будет вычисление относительной ошибки. Добавим столбец и внесём туда формулу: «=ABS((C2-J2)/C2), ABS — модуль, абсолютное значение. Протянем маркером вниз и в ячейке M18 выведем среднее значение (СРЗНАЧ), назначим ячейкам процентный формат. Полученный результат — 7,79% находится в пределах допустимых значений ошибки <8…10%. Значит вычисления достаточно точны.

Если возникнет необходимость, по полученным значениям мы можем построить график.

Файл с примером прилагается — ССЫЛКА!