Научная работа по excel

Иногда достаточно сложно радоваться изучению математики. Многие из нас считают, что это достаточно утомительное занятие и предпочитают избегать этого на протяжении всей жизни. Это ещë одна причина использовать программу Microsoft Excel для получения идеальных вычислений, наглядности решения некоторых задач. Я сейчас обращаюсь к девятиклассникам! Вы только  представьте, как эти формулы могут помочь вам облегчить  вашу жизнь, наглядно представить все этапы решения задач, увидеть закономерность в построении графиков функций и помочь при  подготовке к ОГЭ.  Эта тема достаточно актуальна в настоящее время, так как вам предстоит трудное испытание – сдача экзамена по математике.

Проблема. Как установить отношения между величинами с помощью прикладных программ? Как проявить творческие способности ? Как закрепить на практике теоретические знания по темам при решении  заданий ОГЭ?

Решение проблемы: опираясь на знания, полученные на уроках информатики, в ходе дополнительных занятий с учителем и в результате самообразования мною был разработан сборник  по теме «Возможности программы Excel при решении математических задач».

Цель исследовательской работы: изучить  возможности использования программного комплекса Еxcel для решения задач по математике и создать сборник  по теме «Возможности программы Excel при решении математических задач».

Задачи исследовательской работы:

• познакомить с возможностями программы Еxcel;
• познакомить с этапами создания сборника;
• освоить навыки работы в программе Еxcel.

 Материал сборника содержит разбор примеров, которые наиболее часто встречаются при решении задач прикладного характера. Это такие задачи как решение уравнений, систем уравнений, построение графиков функций. В данной работе описываются все этапы решения серии задач на функциональную зависимость,  работу с графиками, решение геометрических задач. Эти задачи занимают значительное место в заданиях ОГЭ.

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа села Синодское

Научно — исследовательская работа по математике

«Исследование графиков функций с помощью Excel»

Автор: учащийся 7 класса

МБОУ СОШ с.Синодское

Ворфоломеев Евгений Юрьевич

Научный руководитель:

учитель математики

МБОУ СОШ с.Синодское

Ромахина Каринэ Петросовна

2016 г.

Оглавление

1. Введение. Цели и задачи..………………………………………. 3

2. Теоретическая часть…………………………………………….. 4-5

3. Практическая часть……………………………………………… 6-8

а) Исследование графика линейной функции

б) Исследование системы линейных уравнений с двумя

переменными

1. Заключение ………………………………………………………….. 8

2. Список литературы ………………………………………………9

3. Приложение ……………………………………………………..10-17

Введение

На уроках алгебры мы изучаем функции и их свойства, строим графики функций, учимся решать уравнения и системы уравнений. В своей работе я показал способы построения графиков функций, исследовал свойства функций и графиков в зависимости от параметров, входящих в ее уравнение, графический способ решения уравнений и системы уравнений с двумя переменными – с помощью программы Microsoft Excel.

Программа MS Excel позволяет очень быстро создать любое количество графиков различных функций, а также рассмотреть большое количество примеров изменения графиков в зависимости от параметров.

Цели и задачи исследования:

исследовать изменение расположения графика линейной функции, в зависимости от параметров входящих в её уравнение; показать принцип построения графиков уравнений с помощью формул в электронных таблицах; ознакомиться с методами решения линейных уравнений с двумя переменными и систем уравнений с помощью электронной таблицы Microsoft Excel.

Выявить преимущества решения систем уравнений графическим способом.

Гипотеза:

Использование программы Microsoft Excel наглядно иллюстрирует построение графиков элементарных и более сложных функций, позволяет исследовать преобразование  графиков, изменение графика функции в зависимости от исходных данных.

1. Теоретическая часть

Линейной функцией называется функция, которую можно задать формулой вида y = kx + b, где x — независимая переменная, k и b — некоторые числа. Графиком линейной функции является прямая. Прямая определяется двумя точками. Значит, для построения графика линейной функции достаточно найти координаты двух точек графика, нанести полученные точки на координатную плоскость и через них провести прямую. Пусть в формуле у = kх + b число k равно нулю. Тогда формульное представление линейной функции получает вид у = 0 ∙ х + b, т. е. у = b. Функция, задаваемая формулой у = b, при любом значении аргумента принимает одно и то же значение b. Пусть в формуле у = kх + b число b это нуль. Тогда формульное представление линейной функции становится таким: у = kх. Прямой пропорциональностью называется функция, которую можно задать формулой вида y = kx, где x — независимая переменная, k — не равное нулю число. Графиком прямой пропорциональности является прямая, проходящая через начало координат. 
Для построения графика прямой пропорциональности достаточно отметить какую-либо точку графика, отличную от начала координат и провести через эту точку и начало координат прямую. Графики двух разных линейных функций вида у = kх + b: пересекаются, если коэффициенты k разные; параллельны, если коэффициенты k одинаковые.

Через свойства линейной функции можно решать системы линейных уравнений. Причем это решение изящно, а его графическая интерпретация помогает глубже вникнуть в смысл математических понятий.

Уравнение вида ах + ву = с — линейное уравнение с двумя переменным, где х и у переменные, а, в и с – некоторые числа. Если а = 0, то уравнение принимает вид 0· х + bу = с. Если b = 0, то уравнение принимает вид ах + 0· у = с.

Если a=0, b = 0, с = 0, то уравнение принимает вид 0· х+ 0·у= 0.

 Если а = 0, в = 0, с≠0, то уравнение принимает вид 0· х+ 0·у= с.

Графиком линейного уравнения с двумя переменными называется множество всевозможных точек координатной плоскости, координаты которых будут являться решениями этого линейного уравнения.  График представляет собой прямую линию. Поэтому такие уравнения и называются линейными.

Уравнение вида ах + ву = с — линейное уравнение с двумя переменным, где х и у переменные, а, в и с – некоторые числа. Если а = 0, то уравнение принимает вид 0· х + bу = с. Если b = 0, то уравнение принимает вид ах + 0· у = с.

Если a=0, b = 0, с = 0, то уравнение принимает вид 0· х+ 0·у= 0.

 Если а = 0, в = 0, с≠0, то уравнение принимает вид 0· х+ 0·у= с.

Графиком линейного уравнения с двумя переменными называется множество всевозможных точек координатной плоскости, координаты которых будут являться решениями этого линейного уравнения.  График представляет собой прямую линию. Поэтому такие уравнения и называются линейными.

Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. Решением системы уравнений с двумя переменными называется пара значений переменных, обращающих каждое уравнение системы в верное равенство. Решить систему уравнений – это означает найти их общие решения. Поиск общего решения нескольких уравнений называют решением системы уравнений.

II. Практическая часть

Исследование графика линейной функции.

1.Рассмотрим функцию y=kx+b такую, что k ≠ 0, b = 0.

Фyнкция вида y=kx (прямая пропорциональность).

В одной системе координат построим графики функций:

y=3x, y=x, y=-3x.
Вывод:
График линейной функции вида у=kх проходит через начало координат. (приложение 1)

2.Рассмотрим функцию y=kx+b такую, что k ≠ 0, b ≠ 0.

В одной системе координат построим графики функций:

y=2x+5, y=-2x+5
Вывод:
График линейной функции вида y = kx + b пересекает ось Оy в точке (0;b). (приложение 2)
3.Рассмотрим функцию y=kx+b, где k=0, b ≠ 0

y= b.

В одной системе координат построим графики функций: y=5, y=-5.
Вывод:
График линейной функции вида y = b проходит параллельно оси Оx и пересекает ось Оy в точке (0;b). (приложение 3)
4.В одной системе координат построим графики функций, где k – одно и то же число.

y=2x, y=2x+5, y=2x-5.
Вывод:
Графики линейных функций вида y=kx+b параллельны, если коэффициенты при х одинаковы.

(приложение 4)

5.В одной системе координат построим графики функций:

y=4x-5, y= -2x+7.
Вывод:
Графики двух линейных функций вида y=kx+b пересекаются, если коэффициенты при х различны. (приложение 5)
Коэффициент k называют угловым коэффициентом прямой – графика функции y=kx+ b.
Вывод:

Если kx тупой. Функция убывает.
Если k0 , то угол наклона графика к оси Оx острый. Функция возрастает. (приложение 6).

Итак, исследуя расположение прямой, в зависимости от изменения значения k можно сделать вывод, что внося изменения в одну ячейку электронной таблицы, не меняя более ничего, мы можем получать различные расположения прямой.

Исследование системы уравнений с двумя переменными.

1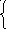.Решить систему уравнений y-2x=1

6x-y=7

В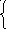ыразим y через x y=2x+1

y= 6x-7 и построим графики уравнений. (приложение 7)

Подводя курсор к точке пересечения линий легко можно увидеть решение уравнения (2;5).

2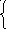.Решить систему уравнений

x-2y=6

3x+2y=-6

В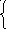ыразим y через x y=x/2-3

y=-1,5x-3

Подводя курсор к точке пересечения линий легко можно увидеть решение уравнения (3;-1,5).

Применяя известный алгоритм построения графиков, получаем график. (приложение

Вывод:

Имея один шаблон для решения систем уравнений, не применяя особых усилий можно за короткое время решить много систем уравнений, а также использовать этот метод решения использовал для проверки домашних заданий.

Заключение:

Проделав данную исследовательскую работу, я пришел к следующим выводам: используя программу MS Excel на уроках математики можно получить наглядное представление о свойствах функции, графиках функций, взаимном расположении графиков, а также закрепить навыки и умения построения графиков функций, проводить исследования.

Использование компьютерных программ для построения графиков функций, изучение их свойств и закономерностей, дает возможность рассмотреть большое количество примеров с минимальными усилиями.

Список литературы

1.Алгебра. Учебник для 7 класса средней школы, под редакцией Теляковского С.А.

2.Д.В. Беклемишев. Курс аналитической геометрии и линейной алгебры. Москва, Наука, 1980 г.

3.М.Я. Выгодский. Справочник по высшей математике. Москва, 1977 г.

4. Математика. Учебное пособие под редакцией Муравья Л.Я., г. Москва Бридж 1994г.

5.В.С. Шипачёв. Основы высшей математики. Москва, Высшая школа, 1989 г.

9

Цель работы: Исследовать возможность моделирования исследование математических функций, при помощи современных компьютерных средств. Методы проведенных исследований: математическое моделирование. Основные результаты научного исследования (научные, практические): разработана компьютерная модель для исследования  математических функций на основе программы Microsoft Excel .

актуальность темы работы – Microsoft Excel — одна из самых загадочных и интересных программ в пакете MS Office. Интересна она многочисленными средствами автоматизации работы, оформления документов и богатыми вычислительными возможностями. Загадочность ее состоит в том, что большинство пользователей применяют лишь малую толику того, что может дать им Excel. Это тем более удивительно, что спектр возможностей программы практически безграничен: от создания простых таблиц, построения диаграмм и графиков до решения сложных вычислительных задач и моделирования различных процессов.

постановка и формулировка проблемы – данная работа посвящена использованию электронных таблиц EXCEL в анализе функций. В ней, используя знания и навыки работы с мастером функций и диаграмм Excel, будет проведен анализ  функций с проведением расчетов по формулам и с построением графиков.
Для анализа элементарных функций необходимо уметь решать следующие задачи:

• определение возрастания или убывания функции на заданном интервале,
• определение максимума (минимума) данной функции на заданном интервале,
• нахождение точек пересечения функции с осью ОХ,
• нахождение производной функции

Применение Excel для решения исследовательских задач

Нижегородский институт менеджмента и
бизнеса

РЕФЕРАТ

по информатике

Выполнила:
Брянская Златаслава

студентка 2
курса, гр. 3 ФММ

Проверил: к.т.н., профессор,

Нижний Новгород 2013

Содержание

Введение

. Процессор электронных
таблиц Microsoft Excel

.1 Окно программы Microsoft
Excel

.2 Операции с листом

.3 Операции со строками,
столбцами, блоками

.4 Операции с ячейками

.5 Данные

.6 Функции

.7 Особенности использования
логических функций

.8 Графические возможности MS
Excel

.9 Работа со списками

.10 Применение Excel для
решения исследовательских задач

Заключение

Список литературы

Приложения

. Применение команд подбор
параметра и поиск решения

Введение

Электронные таблицы (табличный процессор) — прикладная программа,
позволяющая автоматизировать труд экономистов, бухгалтеров и других, которым
приходится работать с информацией, представленной в виде разнообразных таблиц.

Программа обеспечивает: оформление и вывод на экран заготовки (формы)
таблицы, состоящей из К строк и М столбцов; редактирование текстовых и числовых
значений в любых ячейках таблицы; вычисление по формулам; построение графиков и
диаграмм; статистическую обработку информации; печать на бумагу.

Рабочее поле программы — электронное окно, в котором видна часть таблицы.
Основным элементом электронных таблиц является ячейка, которая находится на
пересечении столбца и строки.

Структура электронной таблицы определяется количеством столбцов и типом
данных, находящихся в ячейках таблицы.

1. Процессор
электронных таблиц Microsoft Excel

.1 Окно
программы Microsoft Excel

Окно программы содержит все стандартные элементы Windows: зону заголовка, горизонтальное меню, панели
инструментов, полосы прокрутки, строку состояния. Элементы, специфичные для
таблицы MS Excel такие:

1
Вверху после
панелей инструментов имеется строка формул, в которой вводятся и редактируются
данные.

2
Ниже строки
расположены заголовки столбцов, слева — заголовки строк, На их пересечении
расположена кнопка, которая служит для выделения всей таблицы.

3
Внизу перед
строкой состояния размещена строка с ярлычками листов.

Основные
понятия

Объектом обработки в программе является документ, который хранится в
файле с расширением .xls. В
терминах таблицы Excel файл
называется рабочей книгой. В книге размещается от 1 до 155 электронных таблиц,
каждая из которых называется рабочим листом.

Лист состоит из 16384 строк и 256 столбцов. Строки пронумерованы целыми
числами от 1 до 16384, столбцы — буквами латинского алфавита: A, B, …, Z, AA, AB,… IV.

На пересечении строки и столбца находятся ячейки. В ячейку вводятся
числа, текст или формулы.

Ячейки имеют адреса, состоящие из обозначения столбца и номера строки: A1, B10. Текущая ячейка, в которую вводится информация, помечена
светящимся указателем. Смежные ячейки образуют блок: это либо прямоугольная
область, либо часть столбца, стоки, либо ячейка. Адрес блока состоит из
координат противоположных углов, разделенных двоеточием: B13:C19 (прямоугольная область), C1:C10 (столбец), D:F (строка).

1.2 Операции
с листом

Новая рабочая книга по умолчанию состоит из 16 листов. Это число можно
изменить на вкладке Основные команды Сервис/Параметры в поле списка Листов в
новой рабочей книге.

Для перемещения по листам служат четыре кнопки в левом нижнем углу листа.
Щелкнув правой кнопкой на одной из них, откроем контекстное меню для выбора
листа по его номеру.

Для удаления листа следует щелкнуть правой кнопкой на ярлычке листа,
выбрать команду Удалить или выбрать команду меню Правка/Удалить лист.

Для удаления нескольких подряд идущих листов необходимо щелкнуть мышью на
ярлычке первого из них, нажать клавишу [Shift], щелкнуть на ярлычке последнего, выделив группу
листов и воспользоваться контекстным меню.

Для выделения листов, идущих не подряд, нажать [Ctrl], щелкнуть на нужных ярлычках, затем воспользоваться
контекстным меню.

Переименование листов. Во вновь открываемых книгах листы имеют имена Лист
1, Лист 2 и т.д. Обычно им дают имена, отражающие их содержание. Это имя затем
выводится при печати как название таблицы. Для переименования листов выбираем
команду контекстного меню Переименовать или команду главного меню
Формат/Лист/Переименовать.

Для вставки нового листа служит команда главного меню Вставка/Рабочий
лист.

Перемещение листов производится командой меню Правка/Переместить
(копировать). В диалоговом окне команды в поле В книгу указывается имя книги,
куда перемещается лист. В поле Перед листом задается перед каким листом
вставляется новый лист. Копирование выполняется аналогично, но включается
флажок Создавать копию Перемещаемый (копируемый) лист выделяется. Можно также
для выполнения операции воспользоваться контекстным меню.

.3 Операции
со строками, столбцами, блоками

Выделение:

4
столбца —
щелкнуть мышью на букве с именем столбца;

5
нескольких
столбцов — щелкнуть мышью на букве первого столбца и потянуть;

6
строки — щелкнуть
мышью на имени строки;

7
нескольких строк
— щелкнуть мышью на имени первой строки и потянуть;

8
блока — щелкнуть
мышью на первой ячейке блока и потянуть до последней;

9
нескольких
несмежных блоков — выделить первую ячейку, нажать клавишу [Ctrl], выделить следующие.

Отмена выделения — щелкнуть мышью по любому невыделенному участку.

Перемещение блока: Выделить перемещаемый блок; поместить указатель мыши
на рамку выделения блока (указатель примет вид белой стрелки); потянуть мышь и
перетащить блок на новое место.

Копирование блока выполняется аналогично перемещению, но нажимается
клавиша [Ctrl].

Заполнение. Операция означает, что содержимое блока (строки, столбца,
ячейки) повторяется несколько раз. Операция выполняется аналогично перемещению,
но курсор мыши наводится на нижний правый угол блока и имеет форму черного
плюса.

Удаление (очистка) содержимого блока. Для удаления блок выделяется и
нажимается клавиша [Delete] или можно
воспользоваться командой Удалить контекстного меню. Для очистки содержимого
блока его следует выделить и вызвать команду Очистить контекстного меню.

Автозаполнение. Команда позволяет быстро вводить типовые
последовательности (дни недели, месяцы, годы, арифметические или геометрические
последовательности с любым шагом). Например, требуется заполнить ячейки G10 — M10 названиями месяцев. Для этого записываем в ячейку G10 название январь, в ячейку H10 пишем февраль; выделяем ячейки G10:H10, указываем на черный квадрат правом нижнем углу блока
(указатель должен выглядеть как черный плюс); щелкаем мышкой и, не отпуская
левой кнопки, растягиваем рамку до ячейки М10. Для указания шага арифметической
или геометрической прогрессии можно воспользоваться командами меню Для этого
вводим в первую ячейку блока начальное значение, выбираем команду меню Правка
/Заполнение/Прогрессия, Задаем значение Шаг и Предельное значение.

.4 Операции с
ячейками

Адресация ячеек. Обозначение ячейки, составленное из номера строки и
столбца, на пересечении которых она расположена, называется относительным
адресом ячейки. Например, A5, D15. При операциях копирования,
удаления, вставки этот адрес изменяется автоматически. Если в адресе ставится
знак $, адрес называется абсолютным. Этот адрес не из меняется при
использовании в операциях. Например,

$A$10 — не изменяется номер строки и
номер столбца;

$A10 — не изменяется номер строки;

A$10 —
не изменяется номер столбца.

Ячейки с абсолютными адресами используются для хранения констант,
коэффициентов, которые являются исходными данными; в ячейках с относительными
адресами хранятся переменные.

Выделение ячейки выполняется щелчком мыши на ее содержимом.

Удаление и очистка ячеек. Для удаления ячейки следует ее выделить,
выбрать команду Правка/Удалить. Затем нужно указать, каким способом следует
сомкнуть оставшиеся ячейки (со сдвигом влево или вправо). Кроме удаления ячейки
целиком со всем содержимом предусмотрена операция полной или частичной очистки
выделенной ячейки. Для этого выбираем команду Правка/Очистить. Появится
подменю:

Форматы — удаляются только форматы ячейки;

Содержимое — удаляются данные, занесенные в ячейку;

Примечания — удаляются только примечания, связанные с ячейкой.

Для того, чтобы удалить из выделенной ячейки все, проще всего нажать
клавишу [Delete].

Расположение содержимого ячейки в несколько строк. Длинный текст можно
расположить в несколько строк. Для этого установите ширину столбца так, чтобы
она удовлетворяла вас с точки зрения обозримости таблицы. Выберите команду меню
Формат/Ячейки. В диалоговом окне Формат ячеек раскройте вкладку Выравнивание,
установите флажок Переносить по словам.

Копирование. Выделите ячейку. В меню выберите пункт Правка /Копировать. Установите
курсор в ту ячейку, куда будете копировать содержимое и выберите команду
Правка/Вставить. Можно воспользоваться аналогичными командами контекстного
меню.

Заполнение ячеек. Сделайте заполняемую ячейку текущей и вводите данные с
клавиатуры обычным образом. Нажмите клавишу [Enter]. Будет активизирована следующая ячейка. Можно
указать, какая ячейка будет активной далее. Для этого раскройте вкладку Правка
команды Сервис/Параметры. Установите индикатор Переход к другой ячейке после
ввода и в поле списка В направлении выберите ячейку, которая будет
активизирована: справа, слева, сверху или снизу от исходной.

Изменение содержимого ячеек. Существует три способа редактирования
содержимого ячеек.

Первый способ предполагает использование режима редактирования в ячейке.
Для этого нажмите клавишу [F2],
установите курсор в нужную позиция ячейки, введите новое содержимое, нажмите
клавишу [Enter].

Второй способ. Установите курсор мыши в ячейке, после чего в строке
формул появится ее содержимое. Щелкните в строке формул и вводите данные.

Третий способ предполагает внесение изменений непосредственно в ячейку,
но переход в режим редактирования производится двойным щелчком правой кнопки
мыши внутри ячейки. На мой взгляд это наиболее удобный способ.

Отменить изменение и восстановить содержимое ячейки можно, нажав клавишу
[Esc].

.5 Данные

Существует три типа данных: текст, число, формула.

Если первый символ данных является буквой или символом ‘ (апострофом),
вводимые данные воспринимаются как текст. Если первый символ — число, то данные
являются числовыми. Формула или адрес ячейки начинаются со знака =.

Особенности задания числовых данных. Числа в ячейках можно задать в
разном формате: например, 100 000 р. — денежный формат; 100% — процентный
формат; 1,24У+2 — научный. Указать формат представления чисел можно командой
Формат/Ячейки/Число. В окне команды следует выбрать нужный формат.

Особенности задания формул. Формула определяет способ обработки данных и
хранится в ячейке. В этой же ячейке хранится и результат вычисления по формуле.
Обычно в строке формул видна формула, а в ячейке — результат. Для получения
формулы в ячейке надо дважды не ней щелкнуть мышкой. В формулах можно
использовать знаки арифметических операций + (сложение), — (вычитание), *
(умножение), / (деление) и ^ (возведение в степень). При записи формул следует
помнить о приоритетах операций и порядке их выполнения. Сменить порядок
выполнения операций можно с помощью круглых скобок. Их количество в формуле не
ограничено. Пример формулы:

= D4 + E4 — E5^2 *
(C2 + D4) / C3

Для редактирования формул нужно использовать клавишу [F2] или двойной щелчок мыши на ячейке
с формулой.

.6 Функции

В MS Exсel имеется около
200 встроенных функций. Их полный список можно получить командой
Вставка/Функция. Этот список разбит по категориям. Функция имеет следующий вид

= Имя функции (Список аргументов)

В качестве аргументов используются адреса ячеек или имена других функций.

Для построения формул с использованием функций следует выделить ячейку,
куда будет вставляться формула и вызвать Мастер функций, нажав клавишу f_x на панели инструментов или выбрать
команду Вставка/Функция. В списке Категория выбрать категорию функции (если
категория не известна, то для просмотра полного списка функций следует выбрать
пункт Все). В окне Функция можно выбрать нужное функции. Для перехода к заданию
аргументов функции надо нажать кнопку Далее. Мастер функций различает аргументы
обязательные и необязательные. В качестве аргументов можно использовать
константы (абсолютные адреса ячеек), переменные (относительные адреса ячеек) и
имена других функций.

Существует два способа ввода аргументов: 1) ввод адреса аргумента с
клавиатуры; 2) ввод адреса, выделяя ячейки мышью (этот способ, на мой взгляд,
предпочтительнее). После ввода обязательных аргументов следует нажать кнопку
Готово.

Для функции суммирования закреплена кнопка на Панели инструментов S. Для ее использования следует:

10  активизировать ячейку, в которой
должна размещаться сумма, щелкнуть на кнопке S и нажать клавишу [Enter];

или

11  выделить область, подлежащую
суммирования, нажать кнопку S и клавишу Enter].

Если суммируется содержимое несмежных ячеек, то активизируйте ячейку,
куда будет записана сумма, щелкните на кнопке S, затем щелкните на первой ячейке, которая включается
в сумму, нажмите клавишу [Ctrl]
и укажите остальные ячейки. Отпустите клавишу [Ctrl] и нажмите клавишу [Enter].

.7
Особенности использования логических функций

Способ вычисления значения в ячейке может зависеть от выполнения
какого-либо условия. Для организации таких вычислений используется условная
функция ЕСЛИ Ее общий вид:

ЕСЛИ(<логическое выражение>;<формула1>;<формула2>)

<логическое выражение> включает в себя адреса ячеек, числовые
значения, формулы и знаки операций отношения > (больше), >= (больше или
равно), < (меньше), <= (меньше или равно), = (равно), <> (не
равно). Если <логическое выражение> выполняется, то значение его равно
ИСТИНА, иначе его значение — ЛОЖЬ. Если <логическое выражение> имеет
значение истина, то выполняется <формула1>, иначе — <формула2>.

Пример 1. Пусть имеем цену (Ц) 1 кг продукта. Количество (Q) продукта задается в кг или т.
Требуется определить стоимость (С) некоторого количества продукта, которая
вычисляется следующим образом

если Ц руб/кг, Q кг, о С = Q * Ц

если Ц руб/кг, Q т, то С = Q * Ц * 1000

если Ц руб/кг, Q шт, то С = 0

Сформируем таблицу:

В столбце А записан код единицы измерения веса:

если Q измеряется в кг, то А1 = 1;

если Q измеряется в т, то А1 = 2;

если Q измеряется в шт., то А1 = 3;

В столбце B записан вес, а в
столбце C — цена продукта. В ячейке D1 записана формула

ЕСЛИ(А1=1; B1*C1; ЕСЛИ(А1=2;A1*B1*1000;0)).

Число вложенных функций ЕСЛИ не должно превышать 7.

Для объединения условий применяются функции И и ИЛИ. Их общий вид:

И(<логическое выражение1>;<логическое выражение1>;…)

ИЛИ(<логическое выражение1>;<логическое выражение;…>).

Значение функции И истинно, если истинны все логические выражения,
являющиеся ее аргументами. В остальных случаях значение функции И ложно.
Значение функции ИЛИ ложно, если ложны все логические выражения, являющиеся ее
аргументами, в остальных случаях значение функции ИЛИ ложно.

Функции могут содержать до 30 аргументов.

Пример 2. Пусть задана цена (Ц) 1 кг или 1 шт. продукта. Количество (Q) продукта задается в кг, шт. или т.
Требуется определить стоимость (С) некоторого количества продукта, которая
вычисляется следующим образом

если Ц руб/кг, Q кг, то С = Q * Ц

если Ц руб/кг, Q т, то С = Q * Ц * 1000

если Ц руб/кг, Q шт, то С = Q * Ц

Сформируем таблицу:

В столбце А записан код единицы измерения веса:

если Q измеряется в кг, то А1 = 1;

если Q измеряется в т, то А1 = 2;

если Q измеряется в шт., то А1 = 3;

В столбце B записан код
единицы измерения цены:

если Ц измеряется в руб/кг,то B1 = 1;

если Ц измеряется в руб/шт, то B1 = 2;

В столбце C записан вес, а в
столбце D — цена продукта. В ячейке F1 записана формула

ЕСЛИ(И(А1=1;B1=1); C1*D1;

ЕСЛИ(И(А1=2;D1=2); C1*D1*1000;0); C1*D1; 0))).

.8
Графические возможности MS Excel

Программа поддерживает 14 типов различных двух- и трехмерных диаграмм.

Определим некоторые понятия, связанные с диаграммами и графиками.
Диаграмма — это способ графического представления табличных данных. Программа
реализует несколько типовых способов представления диаграмм: плоское или
объемное, столбчатую, круговую или в виде графика. Серии данных — группа
данных, расположенных внутри одной строки или столбца. На диаграмме серия может
быть отображена набором полом (вертикальных или горизонтальных), секторов
круга, точками графика. Диаграмма включает одну или несколько серий данных.
Набор всех имен серий, представленных на диаграмме, называется легендой.

Вот некоторые из наиболее употребительных типов диаграмм и графиков:

1 Тип «С областями». Диаграмма
формируется как сумма соответствующих значений данных нескольких серий. На
диаграмме отмечаются области, соответствующие различным сериям. Это позволяет
отобразить не только динамику изменения значений каждой серии, но также их
взаимные пропорции и динамику изменения общей итоговой суммы. Диаграмма
используется для отображения динамических процессов с целью оценки влияния на
общий результат отдельных составляющих. Например: динамика выпуска продукции с
учетом работы отдельных цехов; годовая диаграмма роста денежных доходов
населения с учетом различных групп населения.

2 Тип «Линейчатая». В отличие
от первого типа диаграмм метки данных откладываются не по вертикали, а по
горизонтали.

4 Тип «График». Это один из
самых удобных способов представления данных, изменяющихся во времени. Если
гистограмма часто используется для представления структуры и взаимных пропорций
некоторого статичного набора данных, то график применяется для описания
характера динамически изменяющихся данных. Интересной модификацией графиков
являются биржевые или минимаксные графики. Они позволяют отобразить динамику
суточного изменения цен на бирже с четом цен открытия, минимальной и
максимальной цены и цен закрытия биржи.

5 Тип «Круговая диаграмма».
Назначение этого графика состоит в отображении структуры составляющих
некоторого набора данных и их взаимные пропорции. Может быть использована,
например, для отображения структуры затрат при производстве какой-либо
продукции.

6
Тип
«Точечная XY».
Диаграмма этого типа имеет принципиальное отличие от всех остальных. Во всех
рассматриваемых ранее диаграммах числовые значения отображаются по одной оси, а
метки результата — по другой. Значения диаграммы типа XY строятся одновременно по двум сериям. При этом значения
одной серии отсчитываются по оси X, а
другой серии — по оси Y.
Каждая пара значений образует одну точку диаграммы. Такой подход позволяет
использовать параметрическую зависимость нескольких числовых серий.

Диаграммы имеют модификации, которые мы не рассматриваем.

Для построения диаграмм используется Мастер построения диаграмм, который
с помощью 5 окон позволяет получить информацию для автоматического построения
диаграммы или графика и внедрения его в рабочий лист. microsoft excel
электронный таблица график

Правила построения диаграмм следующие:

1 Щелкните кнопкой Мастер диаграмм на
панели инструментов Стандартная и укажите место на листе для размещения
диаграммы.

2
Первый шаг. В
окне Шаг 1 из 5 выделите ячейки, содержимое которых будет представлено в диаграмме.
Нажмите кнопку Далее.

3
Второй шаг. В
окне Шаг 2 из 5 выберите тип диаграммы. Нажмите кнопку Далее.

4 Третий шаг. Содержимое окна Шаг 3 из
5 зависит от типа выбранной диаграммы на шаге 2. В этом окне выбирается формат
представления диаграммы. Нажмите кнопку Далее.

5
Четвертый шаг. В
окне 4 из 5 следует указать, где находятся данные — в столбцах или строках и
указать интервал, содержащий названия рядов данных для легенды. Нажмите кнопку
Далее.

6 Пятый шаг. На шаге 5 из 5 указываем,
следует ли добавить к тексту легенду с названиями маркеров данных и ввести
названия диаграммы, осей X и Y. Нажмите кнопку Готово.

На любом шаге построения диаграммы можно вернуться к предыдущему шагу,
нажав кнопку Назад или отменить построение диаграммы. Для редактирования диаграммы
используется двойной щелчок мыши.

.9 Работа со
списками

Создание списка начинается с формирования заголовков столбцов.

Все записи в списке должны быть оформлены одинаково. При вводе данных не
следует добавлять пустые строки, строки дефисов или символов подчеркивания,
поскольку это может затруднить в дальнейшем сортировку и фильтрацию
данных.распознает списки автоматически. Поэтому для сортировки его, например,
по определенному критерию, достаточно поместить указатель ячейки с ячейку
внутри списка. После активизации функции сортировки Excel автоматически выделит
весь список.

При автоматическом определении списка признаком его конца является первая
пустая строка.

В качестве примера используем список сотрудников предприятия «Роза
ветров», представленный в приложении.

В приложении описано, как создать список, как отфильтровать с помощью
Автофильтра или Расширенного фильтра, как отсортировать список по колонке, как
подвести промежуточные итоги, как составить сводную таблицу, как построить
диаграмму.

.10
Применение Excel для решения исследовательских задач

В Excel есть средства для решения
исследовательских задач, таких как поиск корня уравнения, решение
оптимизационных задач: линейное программирование, транспортная задача и др. с
помощью команд Поиск решение, статистическая обработка данных: задачи
корреляции, регрессии, вычисление коэффициентов достоверности (коэффициент
детерминации, критерии Фишера, Стьюдента и др.).

Заключение

В реферате рассмотрено применение Microsoft Excelдля решения задач, связанных с работой
менеджера-маркетолога, таких как построение таблиц и работа с ними: операции со
строками, столбцами, блоками и ячейками, операции с данными, автоматизация
работы с таблицами. Рассмотрено применение формул и функций для производства
расчетов. Подробно рассмотрен вопрос построения графиков. В приложении
рассмотрены вопросы применения Excel
для решения исследовательских задач и работа со списками.

Список
литературы

1. Симонович
С.В., Евсеев Г.А., Алексеев А.Г. Специальная информатика: Учебное пособие. —
М.: АСТ — ПРЕСС: Инфорком-Пресс, 2010. — 480 с.

2.      Р.
Персон. Microsoft Excel в подлиннике: В 2 т.: пер. с англ. — СПб.: BHV — Санкт-Петербург, 2002.

.        Данко
П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах в
двух частях. Учебное пособие для вузов. Издательский дом «ОНИКС 21 век»: Мир и
образование, 2007.

Приложения

1.      Применение команд подбор параметра и
поиск решения

Для иллюстрации этих команд взята задача поиска корней уравнения, а
именно, найти все корни, входящие в диапазон [2;3], уравнения

Решение.

При
решении задачи необходимо на листе Подбор параметра книги Исследовательская
работа Microsoft Excel построить таблицу
следующего содержания:

Ячейка	Величина	Значение или формула
А6	Нижняя граница диапазона х	2
А7	Следующее значение х по формуле	=А6+0,1
А8:А16	Значения переменной х на заданном диапазоне	Копия ячейки А7 на диапазон А8:А16
В6	Значение функции у в точке х=2	=3*sin(A6^(1/2))+0,35*A6-3,8
В7:В16	Значения функции у на заданном диапазоне	Копия ячейки В6 на В7:В16

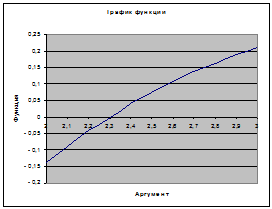
Далее с помощью мастера диаграмм строим диаграмму типа точечная «график»
(исходные данные — диапазон А6:В16). Результат показан на рис. 1.

Рис. 1. График функции

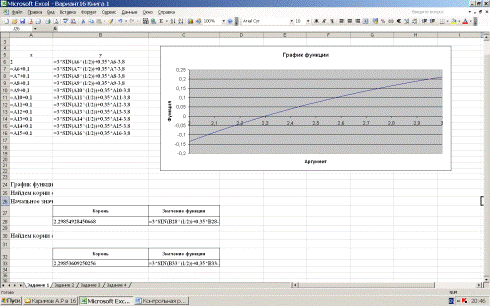
На рис. 2 приведены расчетные формулы

Рис. 2. Расчетные формулы к заданию 1

График функции пересекает ось ОХ в диапазоне [2,2;2,4]. Найдем корень с
помощью инструментов Подбор параметра и Поиск решения, взяв за приближенное
значение корня значение 2,3.

Для поиска корня подбором параметра копируем диапазон А6:В6 в диапазон
В28:С28 и заносим в В28 значение 2,3. Применим команду СервисПараметры. На
вкладке Вычисления устанавливаем количество итераций 1000 и точность вычислений
0,000001.

Применим команду СервисПодбор параметра. В появившемся окне заполняем:
установить в ячейке С28 значение 0, изменяя значение ячейки В28 и нажимаем ОК.

В ячейке В28 получим значение корня 2,298549285, а в ячейке С28 получаем
значение функции 0,0000053.

Для поиска корня с помощью инструмента Поиск решения вначале копируем
А6:В6 на диапазон В35:С35 и в В35 заносим 2,3. Затем воспользуемся командой
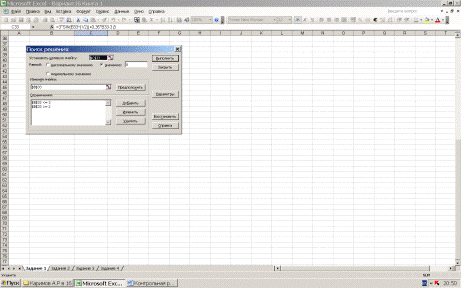
СервисПоиск решения. В появившемся окне, представленном на рис. 3

Рис. 3. Окно Поиск решения

Заполняем: установить целевую ячейку $C$35 равной значению 0, изменяя ячейки $B$35. При этом должны быть установлены
ограничения $B$35<=3 и $B$35>=2. Нажимаем кнопку Выполнить.

В ячейке В35 получим значение корня 2,298536093, а в ячейке С35 значение
функции -0,0000000317.

При решении этой задачи применена команда СервисСценарий, чтобы узнать,
что если корень уравнения взять 2,35. Результат сценария представлен ниже

. Применение
команд для работы со списками Фильтр, Итоги, Сводная таблица, Формы Книга,
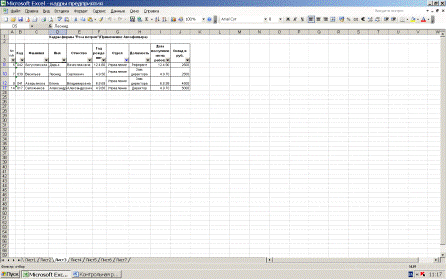
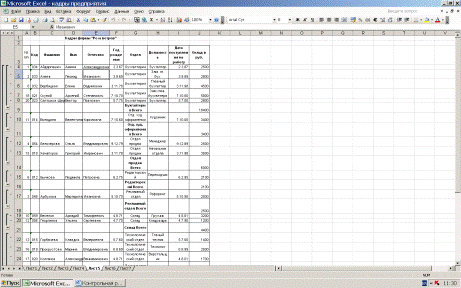
демонстрирующими технологию работы со списками, называется Кадры предприятия.

Решение. На Рис. 4 представлена таблица «Кадры фирмы «Роза ветров».С
помощью команды ДанныеФорма на листе появляется Форма, которая может оказаться
более удобной, чем таблица при просмотре данных или вводе их. Она же
представлена ни листе 1 книги Исследовательская работа.

Рис 4. Таблица «Кадры предприятия»

На рис. 5 показано окно сортировки таблицы по фамилии, имени, отчеству.

Рис. 5. Окно сортировки таблицы по фамилии, имени, отчеству

На Рис. 6. представлена таблица, отсортированная по фамилии, имени,
отчеству. Она же представлена на листе 2 книги Исследовательская работа.

Рис. 6. таблица, отсортированная по столбцам фамилия, имя, отчество

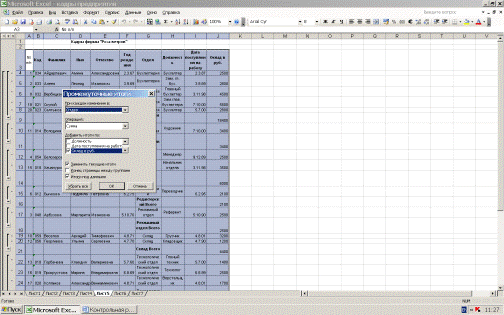
На рис. 7 представлено окно применения Автофильтра для отбора из таблицы
работников управления. Для вызова этого окна необходимо применить команду
Данные/Фильтр/Автофильтр и в строке кнопок выбора и столбце отдел щелкнуть по
строчке управление.

Рис. 7. Использование автофильтра для отбора работников управления

На рис. 8. представлена выбранная таблица. Она же представлена на листе3
книги Исследовательская работа.

Рис. 8. Таблица с работниками управления

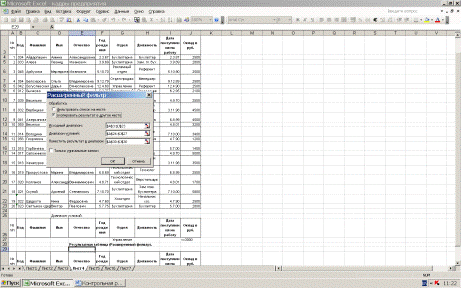
На рисунке 9. представлено окно усиленного (расширенного) фильтра для
выбора работников управления с окладами <=3000 руб.

Вызов окна производится командой Данные/Фильтр/Расширенный фильтр.

Рис. 9. Окно расширенного фильтра для выбора работников управления с
окладами <=3000 руб.

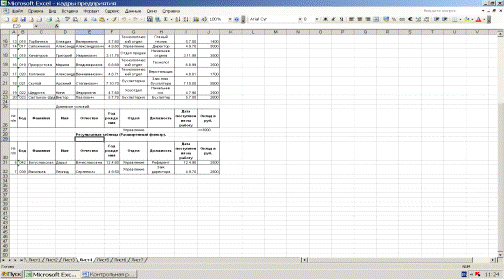
На рис.10. представлена выбранная таблица. Эта же таблица представлена на
листе 4 книги Исследовательская работа.

Рис.10. Таблица работники управления с окладами <= 3000 руб.

На рис. 11. представлено окно итогов зарплаты по отделам предприятия

Рис. 11. Окно промежуточных итогов зарплаты по отделам предприятия

Для расчета итогов необходимо отсортировать таблицу по отделам и
воспользоваться командой Данные/Итоги.

На рис.12. представлена итоговая таблица. Она же приведена на листе5
книги Исследовательская работа.

Рис. 12. Таблица с промежуточными итогами

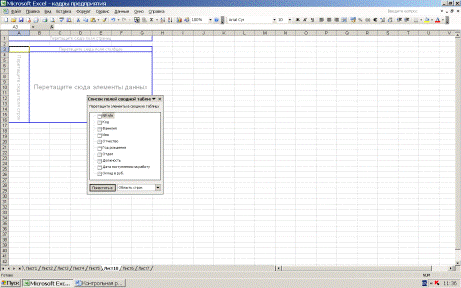
На рис.13. приведено окно сводной таблицы Оклады по отделам, которое
открывается по команде ДанныеСводная таблица.

Рис. 13. Окно сводной таблицы

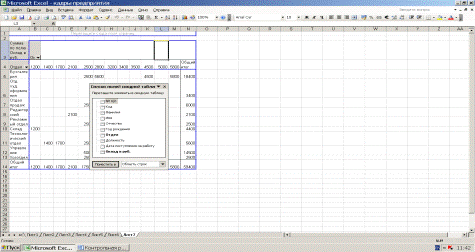
После перетаскивания показателей в строки, столбцы и в таблицу, получим
сводную таблицу Оклады по отделам.

На рис. 14. приведена сводная таблица. Она же приводится на листе 7 книги
Исследовательская работа.

Рис. 14. Сводная таблица Оклады по отделам

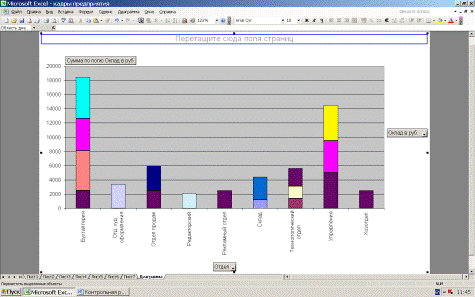
На рис. 15
приведена диаграмма, построенная на основании сводной таблицы

Рис. 15. Диаграмма Сумма окладов по отделам предприятия

Основные термины (генерируются автоматически): программный макрос, практическая задача, таблица умножения, интерактивная таблица умножения, созданная таблица, задача, таблица, домашнее задание, интерактивная электронная таблица, возможность программы.

Ключевые слова

диаграмма,

электронная таблица,

программный макрос

Похожие статьи