-
Выполните
ввод исходных данных по образцу. -
Введите
соответствующие смыслу формулы в ячейки
E4 и F4 (для вычисления налога используйте
абсолютную ссылку В$11). -
Скопируйте
вниз формулы: из ячейки E4 в блок ячеек
E5:E9;
из
ячейки F4 в блок ячеек F5:F9
(по стрелке). -
Введите
по смыслу формулы в ячейки F13, E16, E19. -
Отформатируйте
числа в столбце F, оставив две цифры в
дроби. (Формат, Ячейки, Числовой …) -
Постройте
диаграмму на отдельном листе для блока
F4:F9. -
Выполните
сортировку данных по столбцу F.
|
A |
B |
C |
D |
E |
F |
|
|
1 |
Прибыль |
|||||
|
2 |
Название предприятия |
Доход (р.) |
Налог |
|||
|
3 |
апрель |
май |
июнь |
квартал |
за квартал |
|
|
4 |
ОТЗ |
15000 |
12000 |
8400 |
||
|
5 |
Петрозаводскмаш |
24446 |
19800 |
15500 |
||
|
6 |
Северянка |
6380 |
4700 |
5200 |
||
|
7 |
БОП |
38000 |
34900 |
28000 |
||
|
8 |
Славмо |
14580 |
13800 |
15670 |
||
|
9 |
Хлебозавод |
12300 |
11700 |
13400 |
||
|
10 |
||||||
|
11 |
Налог (в %) |
13 |
||||
|
12 |
Сумма за квартал (р.) |
|||||
|
13 |
||||||
|
14 |
||||||
|
15 |
Максимальный ход за квартал (р.) |
|||||
|
16 |
||||||
|
17 |
||||||
|
18 |
Средний за квартал (р.) |
|||||
|
19 |
Задание 5.
Создайте ЭТ “Доставка
груза” по образцу:
|
A |
B |
C |
D |
E |
F |
|
|
1 |
НАРЯД-ЗАДАНИЕ |
|||||
|
2 |
Номер заявки |
Наименование груза |
Стоимость |
Расстояние км |
N этажа |
Доставка р. |
|
3 |
||||||
|
4 |
1 |
Диван |
4300 |
3 |
1 |
|
|
5 |
2 |
Книжный |
3750 |
6 |
4 |
|
|
6 |
3 |
Холодильник |
8500 |
10 |
5 |
|
|
7 |
4 |
Мягкая |
13200 |
5 |
8 |
|
|
8 |
5 |
Стол |
1500 |
5 |
8 |
|
|
9 |
ВСЕГО |
|||||
|
10 |
Наценка |
5 |
||||
|
11 |
Наценка |
3 |
||||
|
12 |
Наценка |
2,5 |
Пояснение.
Формула
в ячейке F4
вводится с учетом того, что стоимость
доставки груза складывается из следующих
трех величин (наценок):
а) 5% от стоимости груза,
б)
от расстояния (3 р./км),
в) номера этажа
(2,5 р./этаж).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.
Содержание
- Транспортная задача: описание
- Подготовительный этап: включение функции “Поиск решения”
- Пример задачи и ее решение
- Условия
- Алгоритм решения
- Заключение
Транспортная задача: описание
С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.
Транспортные задачи бывают двух типов:
- Закрытая – совокупное предложение продавца равняется общему спросу.
- Открытая – спрос и предложение не равны. Чтобы решить такую задачу, нужно сначала привести ее к закрытому типу. В этом случае добавляется условный покупатель или продавец с недостающим количеством спроса или предложения. Также в таблицу издержек следует внести соответствующую запись (с нулевыми значениями).
Подготовительный этап: включение функции “Поиск решения”
Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:
- Открываем меню “Файл”.
- В перечне слева выбираем пункт “Параметры”.
- В параметрах кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу, выбрав значение “Надстройки Excel” для параметра “Управление”, щелкаем по кнопке “Перейти”.
- В открывшемся окне ставим галочку напротив надстройки “Поиск решения” и жмем OK.
- В результате, если мы перейдем во вкладу “Данные”, то увидим здесь кнопку “Поиск решения” в группе инструментов “Анализ”.
Пример задачи и ее решение
Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.
Условия задачи
Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.
Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).
Алгоритм решения
Итак, приступи к решению нашей задачи:
- Для начала строим таблицу, количество строк и столбцов в которой соответствует числу продавцов и покупателей, соответственно.
- Перейдя в любую свободную ячейку щелкаем по кнопке “Вставить функцию” (fx).
- В открывшемся окне выбираем категорию “Математические”, в списке операторов отмечаем “СУММПРОИЗВ”, после чего щелкаем OK.
- На экране отобразится окно, в котором нужно заполнить аргументы:
- в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
- в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).
- по готовности жмем OK.
- Щелкаем по ячейке, расположенной слева от самого верхнего левого элемента новой таблицы, после чего снова жмем кнопку “Вставить функцию”.
- На этот раз нам нужна функция “СУММ”, которая также, находится в категории “Математические”.
- Теперь нужно заполнить аргументы. В качестве значения аргумента “Число1” указываем верхнюю строку созданной для расчетов таблицы (целиком) – вручную или методом выделения на листе. Жмем кнопку OK, когда все готово.
- В ячейке с функцией появится результат, равный нулю. Наводим указатель мыши на ее правый нижний угол, и когда появится Маркер заполнения в виде черного плюсика, зажав левую кнопку мыши тянем его до конца таблицы.
- Это позволит скопировать формулу и получить аналогичные результаты для остальных строк.
- Выбираем ячейку, которая находится сверху от самого верхнего левого элемента созданной таблицы. Аналогично описанным выше действиям вставляем в нее функцию “СУММ”.
- В значении аргумента “Число1” теперь указываем (вручную или с помощью выделения на листе) все ячейки первого столбца, после чего кликаем OK.
- С помощью Маркера заполнения выполняем копирование формулы на оставшиеся ячейки строки.
- Переключаемся во вкладку “Данные”, где жмем по кнопке функции “Поиск решения” (группа инструментов “Анализ”).
- Перед нами появится окно с параметрами функции:
- в качестве значения параметра “Оптимизировать целевую функцию” указываем координаты ячейки, в которую ранее была вставлена функция “СУММПРОИЗВ”.
- для параметра “До” выбираем вариант – “Минимум”.
- в области для ввода значений напротив параметра “Изменяя ячейки переменных” указываем диапазон ячеек новой таблицы (без суммирующей строки и столбца).
- нажимаем кнопку “Добавить” в блоке “В соответствии с ограничениями”.
- Откроется небольшое окошко, в котором мы можем добавить ограничение – сумма значений первых столбцов исходной и созданной таблицы должны быть равны.
- становимся в поле “Ссылка на ячейки”, после чего указываем нужный диапазон данных в таблице для расчетов.
- затем выбираем знак “равно”.
- в качестве значения для параметра “Ограничение” указываем координаты аналогичного столбца в исходной таблице.
- щелкаем OK по готовности.
- Таким же способом добавляем условие по равенству сумм верхних строк таблиц.
- Также добавляем следующие условия касательно суммы ячеек в таблице для расчетов (диапазон совпадает с тем, который мы указали для параметра “Изменяя ячейки переменных”):
- больше или равно нулю;
- целое число.
- В итоге получаем следующий список условий в поле “В соответствии с ограничениями”. Проверяем, чтобы обязательно была поставлена галочка напротив опции “Сделать переменные без ограничений неотрицательными”, а также, чтобы в качестве метода решения стояло значение “Поиск решения нелинейных задач методов ОПГ”. Когда все готово, нажимаем “Найти решение”.
- В результате будет выполнен расчет и отобразится окно с результатами поиска решения. Оцениваем их, и в случае, когда они нас устраивают, нажимаем OK.
- Все готово, мы получили таблицу с заполненными данными и транспортную задачу можно считать успешно решенной.
Заключение
Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой

Была в сети 27.02.2023 19:35

Лисицына Елена Владимировна
Учитель информатики
30 лет
2 784
13 711
Местоположение
Россия, Дзержинск, Нижегородская область
16.01.2022 22:28
Создайте электронную таблицу «Доставка груза» по образцу и вычислите стоимость доставки. Обратите внимание, что при копировании формул относительные ссылки изменяются, а абсолютные не изменяются.
Просмотр содержимого документа
«Практическая работа «Доставка груза» в MS Excel»
Рекомендуем курсы ПК и ППК для учителей
Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления.
Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект.
Виды транспортных задач
Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.
Условия транспортной задачи можно представить двумя способами:
- в виде схемы;
- в виде матрицы.
В процессе решения могут быть ограничения (либо задача решается без них).
По характеру условий различают следующие типы транспортных задач:
- открытые открытые транспортные задачи (запас товара у поставщика не совпадает с потребностью в товаре у потребителя);
- закрытые (суммарные запасы продукции у поставщиков и потребителей совпадают).
Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.
Пример решения транспортной задачи в Excel
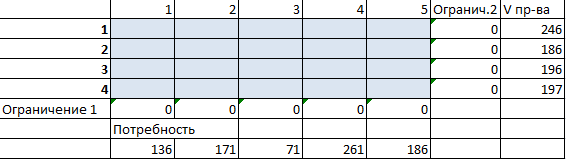
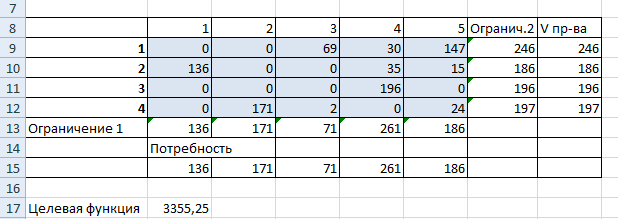
Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.
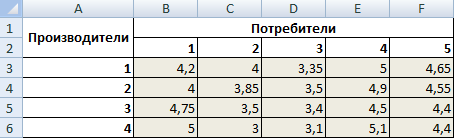
Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:
| Производители | Потребители | Объем производства | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | 4,2 | 4 | 3,35 | 5 | 4,65 | 246 |
| А2 | 4 | 3,85 | 3,5 | 4,9 | 4,55 | 186 |
| А3 | 4,75 | 3,5 | 3,4 | 4,5 | 4,4 | 196 |
| А4 | 5 | 3 | 3,1 | 5,1 | 4,4 | 197 |
| Объем потребления | 136 | 171 | 71 | 261 | 186 |
Задача: минимизировать транспортные расходы по перевозке продукции.
- Проверим, является ли модель транспортной задачи сбалансированной. Для этого все количество производимого товара сравним с суммарным объемом потребности в продукции: 246 + 186 + 196 + 197 = 136 + 171 + 71 + 261 + 186. Вывод – модель сбалансированная.
- Сформулируем ограничения: объем перевозимой продукции не может быть отрицательным и весь товар должен быть доставлен к пунктам назначения (т.к. модель сбалансированная).
- Введем стоимость перевозки единицы продукции в рабочие ячейки Excel.
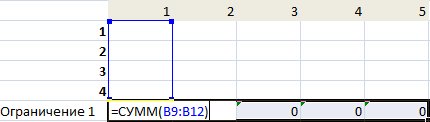
- Введем формулы для расчета суммарной потребности в товаре. Это будет первое ограничение.
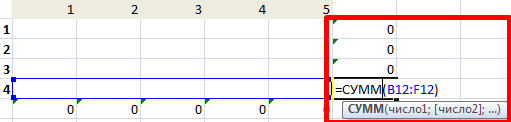
- Введем формулы для расчета суммарного объема производства. Это будет второе ограничение.
- Вносим известные значения потребности в товаре и объема производства.
- Вводим формулу целевой функции СУММПРОИЗВ(B3:F6; B9:F12), где первый массив (B3:F6) – стоимость единицы перевозки товаров. Второй (B9:F12) – искомые значения транспортных расходов.
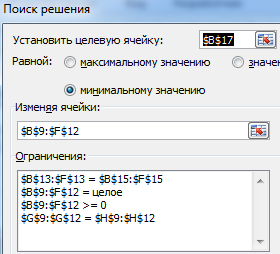
- Вызываем команду «Поиск решения» на закладке «Данные» (если там нет данного инструмента, то его нужно подключить в настройках Excel, а как это сделать описано в статье: расширенные возможности финансового анализа). Заполняем диалоговое окно. В графе «Установить целевую ячейку» — ссылка на целевую функцию. Ставим галочку «Равной минимальному значению». В поле «Изменяя ячейки» — массив искомых критериев. В поле «Ограничения»: искомый массив >=0, целые числа; «ограничение 1» = объему потребностей; «ограничение 2» = объему производства.
- Нажимаем «Выполнить». Команда подберет оптимальные переменные при заданных ограничениях.
Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.
Решение открытой транспортной задачи в Excel
При таком типе возможны два варианта развития событий:
- суммарный объем производства превышает суммарную потребность в товаре;
- суммарная потребность больше суммы запасов.
Открытую транспортную задачу приводят к закрытому типу. В первом случае вводят фиктивного потребителя. Его потребности равны разнице всего объема производства и суммы существующих потребностей.
Во втором случае вводят фиктивного поставщика. Объем его производства равен разнице суммарной потребности и суммарных запасов.
Единица перевозки груза для фиктивного участника равняется 0.
Когда все преобразования выполнены, транспортная задача становится закрытой и решается обычным способом.
Читайте также по теме: решение транспортной задачи методом потенциалов в Excel.
Лабораторная работа «Перевозка грузов»
Перед
диспетчером компании «Уралтранссибсервис» встала непростая задача. Три
грузовика компании должны забрать с разных предприятий Новосибирска следующий
груз (см. ниже таблицу) и доставить его в Омск.
Грузоподъемность каждой машины – 12
тонн, и хотелось бы распределить весь груз примерно поровну. Ну, может быть,
допустив 100 – 150 кг перегрузки какого-нибудь грузовика.
|
Наименование |
Количество |
Вес единицы груза (кг) |
1-й |
2-й |
3-й |
|
Станки (шт.) |
11 |
850 |
|||
|
Трубы |
4 |
1930 |
|||
|
Буровое |
2 |
1700 |
|||
|
Отделочный камень |
4 |
1250 |
|||
|
Промышленные |
7 |
730 |
|||
|
Кабель (бухты) |
5 |
1100 |
|||
|
Всего |
В этой задаче
есть отличие от предыдущего задания. Вовсе не обязательно грузить весь кабель
на одну машину. Поэтому в ячейках могут стоять не только 0 и 1. Связь
заключается в том, сколько единиц данного груза (ящиков, штук) берет конкретная
автомашина.
Есть еще одно
отличие. На складе было 11 станков. 4 увез первый грузовик, 3 – второй
грузовик, а остальное – третий. Спрашивается, ск5олько станков увез третий
грузовик? Решение этой задачи можно поручить компьютеру.
И еще нам
потребуется нижняя строка, которая контролирует загрузку каждого грузовика. Ее
формулы записываются аналогично, как в предыдущей работе.
Используя навыки
работы с электронными таблицами, выполните задания:
1.
Заполните таблицу.
|
A |
B |
C |
D |
E |
F |
|
|
1 |
Наименование |
Количество |
Вес единицы груза (кг) |
1-й |
2-й |
3-й |
|
2 |
Станки (шт.) |
11 |
850 |
|||
|
3 |
Трубы (упаковка) |
4 |
1930 |
|||
|
4 |
Буровое оборудование |
2 |
1700 |
|||
|
5 |
Отделочный камень |
4 |
1250 |
|||
|
6 |
Промышленные |
7 |
730 |
|||
|
7 |
Кабель (бухты) |
5 |
1100 |
|||
|
8 |
Всего груза |
2.
В столбцах D, E и F должны находиться числа, определяющие,
сколько единиц данного груза берет соответствующий грузовик.
3.
Перед тем как начинать распределение груза,
необходимо заполнить формулами нижнюю строку ячеек (D8,
E8 и F8). Так, в ячейке D8 должна стоять формула:
= D2*С2+ D3*С3+ D4*С4+
D5*С5+ D6*С6+ D7*С7
Это позволит в
дальнейшем контролировать загрузку машин.
4.
Необходимо заполнить формулами ячейки F2 – F7.
Предоставим компьютеру автоматически загружать третий грузовик теми товарами,
которые не взяли первые два. Так в ячейке F2 должна стоять формула: =B2 – D2 – E2.
Воспользуйтесь функцией автозаполнения, чтобы заполнить оставшиеся ячейки.
5.
Ваша задача – таким образом распределить товары,
чтобы загрузка каждой их автомашин не превышала 12 тонн более чем на 100-150
килограммов.