Решение уравнений методом итерации в экселе
Найдем корень нелинейного уравнения в табличном процессоре Excel методом итерации с использованием циклических ссылок. Для включения режима циклических вычислений в Excel 2003 в меню Сервис/Параметры/вкладка Вычисления следует поставить флажок Итерации и флажок выбора вида ведения вычислений: автоматически. В MS Excel 2010 следует зайти в меню Файл/Параметры/Формулы и поставить флажок в поле «Включить итеративные вычисления».
M – максимальное значение производной на промежутке (по модулю). Найдем М, для этого вычислим
Т. к. значение производных Меню сайта
Excel. Использование циклических ссылок для решения уравнений итерационным способом
Ранее я описал, как найти и исправить циклическую ссылку. Напомню, что циклическая ссылка появляется, если в ячейку Excel введена формула, содержащая ссылку на саму эту ячейку (напрямую или через цепочку других ссылок). Например (рис. 1), в ячейке С2 находится формула, ссылающаяся на саму ячейку С2.
Рис. 1. Пример циклической ссылки
Но. Не всегда циклическая ссылка является бедствием. Циклическую ссылку можно использовать для решения уравнений итерационным способом. Для начала нужно позволить Excel вести вычисления, даже при наличии циклической ссылки. В обычном режиме Excel, обнаружив циклическую ссылку, выдаст сообщение об ошибке, и потребует ее устранения. В обычном режиме Excel не может провести вычисления, так как циклическая ссылка порождает бесконечный цикл вычислений. Можно, либо устранить циклическую ссылку, либо допустить вычисления по формуле с циклической ссылкой, но ограничив число повторений цикла. Для реализации второй возможности щелкните на кнопке «Office» (в левом верхнем углу), а затем на «Параметры Excel» (рис. 2).
Скачать заметку в формате Word, примеры в формате Excel
Рис. 2. Параметры Excel
В открывшемся окне «Параметры Excel» перейдите на вкладку Формулы и отметьте «Включить итеративные вычисления» (рис. 3). Помните, что эта опция включается для приложения Excel в целом (а не для одного файла), и будет действовать, пока вы ее не отключите.
Рис. 3. Включить итеративные вычисления
На этой же вкладе, можно выбрать, как будут вестись вычисления: автоматически или вручную. При автоматическом вычислении Excel сразу рассчитает конечный результат, при вычислениях, вручную, можно будет наблюдать результат каждой итерации (простым нажатием F9 запуская каждый новый цикл вычисления).
Решим уравнение третьей степени: х 3 – 4х 2 – 4х + 5 = 0 (рис. 4). Для решения этого уравнения (и любого другого уравнения совершенно произвольного вида) понадобится всего одна ячейка Excel.
Рис. 4. График функции f(x)
Для решения уравнения нам понадобится рекуррентная формула (то есть, формула, выражающая каждый член последовательности через один или несколько предыдущих членов):
(1) x = x – f(x)/f’(x), где
f(x) – функция, задающая уравнение, корни которого мы ищем; f(x) = х 3 – 4х 2 – 4х + 5
f’(x) – производная нашей функции f(x); f’(x) = 3х 2 – 8х – 4; производные основных элементарных функций можно посмотреть здесь.
Если вы заинтересовались, откуда взялась формула (1), можете почитать, например, здесь.
Итоговая рекуррентная формула имеет вид:
(2) х = x – (х 3 – 4х 2 – 4х + 5)/(3х 2 – 8х – 4)
Выберем любую ячейку на листе Excel (рис. 5; в нашем примере это ячейка G19), присвоим ей имя х, и введем в нее формулу:
Можно вместо х использовать адрес ячейки… но согласитесь, что имя х, смотрится привлекательнее; следующую формулу я ввел в ячейку G20:
Рис. 5. Рекуррентная формула: (а) для поименованной ячейки; (б) для обычного адреса ячейки
Как только мы введем формулу и нажмем Enter, в ячейке сразу же появится ответ – значение 0,77. Это значение соответствует одному из корней уравнения, а именно второму (см. график функции f(x) на рис. 4). Поскольку начальное приближение не задавалось, итерационный вычислительный процесс начинался со значения, по умолчанию хранимого в ячейке х и равного нулю. Как же получить остальные корни уравнения?
Для изменения стартового значения, с которого рекуррентная формула начинает свои итерации, предлагается использовать функцию ЕСЛИ: [1]
Здесь значение «-5» – начальное значение для рекуррентной формулы. Изменяя его, можно выйти на все корни уравнения:
| Начальное значение | Корень уравнения |
| 1 | 0,77 |
| -5 | -1,40 |
| 8 | 4,63 |
[1] Идея подсмотрена здесь
7 комментариев для “Excel. Использование циклических ссылок для решения уравнений итерационным способом”
Офигенный сайт!
И как всегда когда не нужно все находишь!
Блин у меня по экономическому моделированию в Excell курсовик был в институте, вот время помню кучу потерял а тут все в одном флаконе:)
Все равно инфа пригодится, даже очень!
И нам зараза в этом гребанном институте мать их так этих учителей даже близко ничего подобного не рассказывали. Я не про этот пример говорю а про остальные..
«Вычисление стандартного отклонения для данных с тенденцией», «Нормальное распределение» и т.п.. даже объяснить не могли или не хотели как это все применять, а тут все наглядно и понятно! Огромное спасибо! Не зря я на этот сайт наткнулся, чую он мне еще окажет неплохую помощь))))
В упор не понимаю откуда берется предел для определения корней уравнения, если «Здесь значение «-5» – начальное значение для рекуррентной формулы. Изменяя его, можно выйти на все корни уравнения»
У меня график получается, который с осью Х не имеет вообще пересечений, мож где накосячила?
Пожалуйста подскажите, а то у меня взрыв мозга будет скоро…((((
Тамара, если Вы строите график на основе моих данных, откройте файл Excel; если Вы используете собственные данные, пришлите мне на mail Ваш файл, попробую помочь))
Спасибо заранее за беспокойство, вот такое уравнение у^3-20у^2-158у-420=0, если не трудно объясните пожалуйста как вы определяте предел в каких знчениях надо считать корни.
Решение уравнений в Excel методом итераций Крамера и Гаусса
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах -1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: <=B12:E12/D12>.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (<=(B11:E11-B16:E16*D11)/C11>). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (<=(B10:E10-B15:E15*C10-B16:E16*D10)/B10>). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х 3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
источники:
http://baguzin.ru/wp/excel-ispolzovanie-tsiklicheskih-ssylok-d/
http://exceltable.com/otchety/reshenie-uravneniy
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
Хn+1 = Xn– F (Xn) / M, n = 0, 1, 2, … .
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
Скачать решения уравнений в Excel
Корень на заданном промежутке один.
Метод итерации в excel для нелинейных уравнений
Найдем корень нелинейного уравнения в табличном процессоре Excel методом итерации с использованием циклических ссылок. Для включения режима циклических вычислений в Excel 2003 в меню Сервис/Параметры/вкладка Вычисления следует поставить флажок Итерации и флажок выбора вида ведения вычислений: автоматически. В MS Excel 2010 следует зайти в меню Файл/Параметры/Формулы и поставить флажок в поле «Включить итеративные вычисления».
M – максимальное значение производной на промежутке (по модулю). Найдем М, для этого вычислим
Т. к. значение производных Меню сайта
Решение нелинейных уравнений в Excel и Mathcad (стр. 1 )
 |
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 |
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Кафедра прикладной математики и вычислительной техники
Решение нелинейных уравнений в Excel и Mathcad
к выполнению лабораторных работ
по дисциплине «Вычислительная математика»
Решение нелинейных уравнений в Excel и Mathcad: Метод. указ. / Сост. , — Самара: СГАСУ, 20с.
Методические указания разработаны в соответствии с Государственным образовательным стандартом изучения дисциплины «Вычислительная математика».
Рассмотрена реализация численных методов при решении нелинейных уравнений и систем уравнений в Excel и MathCad. Приведены варианты заданий для индивидуального выполнения и вопросы для самоконтроля и тестирования.
Предназначены для студентов специальности 230201 – «Информационные системы и технологии» всех форм обучения.
Рецензент к. ф-м. н.
Ó , составление, 2012
1 Решение нелинейного уравнения
1.1 Общие сведения о решении нелинейного уравнения
1.2 Отделение корней
1.3 Уточнение корней стандартными средствами Excel и Mathcad
1.4 Метод деления отрезка пополам
1.6 Метод Ньютона (касательных)
1.7 Комбинированный метод
1.8 Метод итераций
2 Решение систем нелинейных уравнений
2.1 Общие сведения о решении систем нелинейных уравнений
2.2 Решение систем нелинейных уравнений методом Ньютона
2.3 Решение систем нелинейных уравнений методами итераций
3 Задания к лабораторным работам
Лабораторная № 1. Отделение корней и стандартные инструменты решения нелинейного уравнения
Лабораторная № 2. Сравнение методов уточнения корней нелинейного уравнения
Лабораторная № 3. Решение систем нелинейных уравнений
Лабораторная № 4. Программирование методов решения нелинейных уравнений и систем
4 Вопросы и тесты для самоконтроля
Список рекомендуемой литературы
1 Решение нелинейного уравнения
1.1 Общие сведения о решении нелинейного уравнения
Как правило, нелинейное уравнения общего вида f(х)=0 невозможно решить аналитически. Для практических задач достаточно найти приближенное значение x, в определенном смысле близкое к точному решению уравнения хточн.
В большинстве случаев поиск приближенного решения включает два этапа. На первом этапе отделяют корни, т. е. находят такие отрезки, внутри которых находится строго один корень. На втором этапе уточняют корень на одном из таких отрезков, т. е. находят его значение с требуемой точностью.
Достигнутая точность может оцениваться либо «по функции» (в найденной точке x, функция достаточно близка к 0, т. е. выполняется условие |f(x)|≤ ef, где ef требуемая точность по оси ординат), либо «по аргументу» (найден достаточно маленький отрезок [a,b], внутри которого находится корень, т. е. |b–a|≤ ex, где ex требуемая точность по оси абсцисс).
1.2 Отделение корней
Отделение корней может производиться сочетанием графического и аналитического исследования функции. Такое исследование опирается на теорему Вейерштрасса, в соответствии с которой для непрерывной на отрезке [a,b] функции f(х) и любого числа y, отвечающего условию f(a)≤y≤f(b), существует на этом отрезке точка x, в которой функция равна y. Следовательно, для непрерывной функции достаточно найти отрезок, на концах которого функция имеет разные знаки, и можно быть уверенным, что на этом отрезке есть корень уравнения f(х)=0.
Для ряда методов уточнения желательно, чтобы найденный на первом этапе отрезок содержал только один корень уравнения. Это условие выполняется, если функция на отрезке монотонна. Монотонность, можно проверить либо по графику функции, либо по знаку производной.
Пример Найти с точностью до целых все корни нелинейного уравнения y(x)=x3 ‑ 10x + 7=0 а) построив таблицу и б) построив график. Найти корень уравнения на выделенном отрезке, используя опции «Подбор параметра» и «Поиск решения».
Решение Создадим в Excel таблицу, содержащую аргументы и значения функции и по ней построим точечную диаграмму. На рисунке 1 приведен снимок решения.
На графике видно, что уравнение имеет три корня, принадлежащие отрезкам [-4, -3], [0, 1] и [2, 3]. Эти отрезки можно выявить и наблюдая за сменой знаков функции в таблице. По построенному графику можно сделать вывод, что на указанных отрезках функция f(x) монотонна и, следовательно, на каждом из них содержится только по одному корню.
Такой же анализ может быть выполнен и в пакете Mathcad. Для этого достаточно набрать определение функции f(x), используя оператор присваивания (:=) и естественные общепринятые обозначения математических операций и стандартных функций, задать цикл для изменения аргумента, например, а затем вывести на экран таблицу значений функции (расположенными в одной строке командами x= f(x)=) и график. Цикл можно задать, например, командой x:=-5,-4.5…5. Шаг цикла формируется путем задания начального и следующего за ним значений переменной, а перед конечным значением переменной ставится точка с запятой, которая будет визуально отображена на экране в виде многоточия.
Рисунок 1 – Таблица и график для отделения корней нелинейного уравнения
1.3 Уточнение корней стандартными средствами Excel и Mathcad
Во всех методах уточнения корней необходимо задать начальное приближение, которое затем и будет уточняться. Если уравнение имеет несколько корней, в зависимости от выбранного начального приближения будет найден один из них. При неудачно выбранном начальном приближении решение может и не быть найдено. Если в результате первого этапа расчетов уже выделен отрезок, содержащий единственный корень уравнения, в качестве начального приближения можно взять любую точку этого отрезка.
В Excel для уточнения значений корней можно использовать опции «Подбор параметра» и «Поиск решения». Пример оформления решения приведен на рисунках 2 и 3.
Рисунок 2 – Ввод значений для использования средств решения уравнения в Excel
Рисунок 3 – Результаты использования средств решения уравнения в Excel
В Mathcad для уточнения корней уравнения можно использовать функцию root(….) или блок решения. Пример использования функции root(…) приведен на рисунке 4, а блока решения на рисунке 5. Следует обратить внимание, что в блоке решения (после заголовка блока Given) между левой и правой частями уравнения должен стоять жирный знак равенства (тождества), который можно получить выбором из соответствующей палитры инструментов, либо нажатием одновременно клавиши Ctrl и =.

Рисунок 5 – Решение уравнения с использованием блока решения в Mathcad
Как видим, каждый стандартный инструмент находит решение уравнения с определенной точностью. Эта точность зависит от метода, используемого в пакете и, в определенной степени, настроек пакета. Управлять точностью результата здесь достаточно сложно, а часто и невозможно.
В то же время, очень просто построить собственную таблицу или написать программу, реализующие один из методов уточнения корней. Здесь можно использовать критерии точности расчета, задаваемые пользователем. При этом достигается и понимание процесса расчетов без опоры на принцип Митрофанушки: «Извозчик есть, довезет».
Далее рассмотрены несколько наиболее распространенных методов. Отметим очевидный момент: при прочих равных условиях тот метод уточнения корней будет более эффективен, в котором результат с той же погрешностью найден с меньшим числом вычислений функции f(x) (при этом достигается и максимальная точность при одинаковом числе вычислений функции).
1.4 Метод деления отрезка пополам
В этом методе на каждом шаге отрезок делится на две равные части. Затем сравнивают знаки функции на концах каждой из двух половинок (например, по знаку произведения значений функций на концах), определяют ту из них, в которой содержится решение (знаки функции на концах должны быть разные), и. сужают отрезок, перенося в найденную точку его границу (а или b). Условием окончания служит малость отрезка, где содержится корень («точность по x»), либо близость к 0 значения функции в средине отрезка («точность по y»). Решением уравнения считают середину отрезка, найденного на последнем шаге.
Пример. Построить таблицу для уточнения корня уравнения x3 –10x+7=0 на отрезке [-4, -3] методом деления отрезка пополам. Определить сколько шагов надо сделать методом деления отрезка пополам и какая при этом достигается точность по х, для достижения точности по y, равной 0,1; 0,01; 0, 001.
Решение Для решения можно использовать табличный процессор Excel, позволяющий автоматически продолжать строки. На первом шаге заносим в таблицу значения левого и правого концов выбранного начального отрезка и вычисляем значение середины отрезка с=(a+b)/2, а затем вводим формулу для вычисления функции в точке a (f(a)) и растягиваем (копируем) её для вычисления f(c) и f(b). В последнем столбца вычисляем выражение (b—a)/2, характеризующего степень точности вычислений. Все набранные формулы можно скопировать во вторую строку таблицы.
На втором шаге нужно автоматизировать процесс поиска той половины отрезка, где содержится корень. Для этого испльзуется логическая функция ЕСЛИ (Меню: Вставка

Вторую строку таблицы можно продолжить (скопировать) на необходимое число последующих строк.
Итерационный процесс завершается, когда очередное значение в последнем столбце становится меньшим, чем заданный показатель точности ex. При этом, значение середины отрезка в последнем приближении, принимается в качестве приближенного значения искомого корня нелинейного уравнения. На рисунке 6 приведен снимок решения. Для построения аналогичного процесса в Mathcad можно использовать бланк, подобный приведенному на рисунке 7. Число шагов N может варьироваться до достижения в таблице результатов требуемой точности. При этом таблица будет автоматически удлиняться или укорачиваться.
Итак, одним из трех корней нелинейного уравнения x3 – 10x + 7=0, найденным с точностью e=0,0001, является x= — 3,46686. Как мы видим, он действительно принадлежит отрезку [-4; -3].
Рисунок 6 – Уточнение корня методом деления отрезка пополам в Excel
Рисунок 7 – Уточнение корня методом деления отрезка пополам в Mathcad
1.5 Метод хорд
В этом методе нелинейная функция f(x) на отделенном интервале [а, b] заменяется линейной – уравнением хорды, т. е. прямой соединяющей граничные точки графика на отрезке. Условие применимости метода – монотонность функции на начальном отрезке, обеспечивающая единственность корня на этом отрезке. Расчет по методу хорд аналогичен расчету методом деления отрезка пополам, но теперь на каждом шаге новая точка x внутри отрезка [a,b] рассчитывается по любой из следующих формул:

1.6 Метод Ньютона (касательных)
Идея, на которой основан метод, аналогична той, которая реализована в методе хорд, только на каждом шаге кривая f(x) заменяется касательной к ней, проведенной в предыдущей найденной точке. В качестве начальной точки в зависимости от свойств функции берется или левая граница отрезка, содержащего корень – x0 = а (если f(а) f»(х) > 0), или правая его граница: x0 = b (если f(b) f»(х)>0). Расчет нового приближения на следующем шаге i+1 производится по формуле:

Алгоритм применим для монотонных функций, сохраняющих выпуклость или вогнутость в промежутке между начальным приближением и корнем уравнения (т. е. должен сохраняться знак первой и второй производных функции f(x)). работоспособен при выпуклых и монотонных функциях f(x). В расчетах нет необходимости отслеживать две границы отрезка, поэтому достаточно на каждом шаге вычислять значения x, f(x) и f′(x). При этом легко оценить «точность по y», по значению левой части уравнения на очередном шаге. Для оценки «точности по x» нужно отслеживать разницу приближений на предыдущем и последующих шагах, которая связана с разницей между найденным приближением и точным значением корня.
Следует обратить внимание на следующую особенность метода: последовательность x1, x2, x3,… приближается к корню с другой стороны, в отличие от использования метода хорд при прочих равных условиях.
Главным достоинством метода касательных является квадратичная скорость сходимости, что во многих случаях может привести к сокращению числа вычислений функции.
Уточнить корень уравнения tg (0,55x+0,1) – x2=0 на отрезке [0.6, 0.8] методом касательных до точности 0,001.
Точность вычислений можно оценить из соотношения
2 Решение систем нелинейных уравнений
2.1 Общие сведения о решении систем нелинейных уравнений
Систему n нелинейных уравнений с n неизвестными x1, x2, . xn записывают в виде:
где F1, F2,…, Fn – функции независимых переменных, среди которых есть нелинейные.
Как и в случае систем линейных уравнений, решением системы является такой вектор X*, который при подстановке обращает одновременно все уравнения системы в тождества.
Система уравнений может не иметь решений, иметь единственное решение, конечное или бесконечное количество решений. Вопрос о количестве решений должен решаться для каждой конкретной задачи отдельно.
Численные методы решения системы уравнений носят итерационный характер и требуют задания начального приближения X0.
Рассмотрим две группы таких методов: метод Ньютона с различными его модификациями и методы итераций (простых итераций и Зейделя).
2.2 Решение систем нелинейных уравнений методом Ньютона
Будем рассматривать этот метод на примере системы двух нелинейных уравнений с двумя неизвестными:
Начальные значения x0 и y0 определяются графически. Для нахождения каждого последующего приближения (xi+1, yi+1) используют вектор значений функций и матрицу значений их первых производных, рассчитанные в предыдущей точке (xi, yi).

Для расчета новых приближений на шаге i+1 используется матричная формула

Следует обратить внимание, что в последней формуле используется вычисление матрицы, обратной к матрице первых производных.
Расчет останавливают при выполнении одного (а иногда и обоих) из двух условий. Первое из них заключается в том, что на очередном шаге максимальное по модулю из изменений аргументов x и y становится меньше заданная погрешность по аргументам. В соответствии со вторым из условий, на очередном шаге максимальное по модулю значение левых частей уравнений должно отличаться от нуля меньше, чем заданная погрешность по функциям.
В упрощенном методе Ньютона матрица производных и матрица, обратная к ней вычисляются только один раз (в начальной точке) и для расчетов используется матричная формула

Приведенные формулы особенно легко записать в Mathcad, где имеются операторы для вычисления производных и действий с матрицами. Однако при правильном использовании матричных операций эти формулы достаточно просто записываются и в Excel. Правда, здесь придется заранее получить формулы для вычисления производных. Для аналитического вычисления производных также может быть использован Mathcad.
2.3 Решение систем нелинейных уравнений методами итераций
Для реализации этих методов исходную систему уравнений необходимо путем алгебраических преобразований явно выразить каждую переменную через остальные. Для случая двух уравнений с двумя неизвестными новая система будет иметь вид

Для решения такой системы задаются начальным приближением x0, y0. Уточненные решения получают по шагам, подставляя в правые части уравнений значения, найденные на предыдущем шаге. В методе простых итераций для уточнения решения используют формулы:

Если одно из решений системы и начальные значения x0 и y0 лежат в области D, задаваемой неравенствами: a ≤ x ≤ b, c ≤ y ≤ d, то расчет по методу простых итераций сходится при выполнении в области D соотношений:
1 Численный метод решения нелинейных уравнений
1.1 Область локализации корней
В общем виде любое уравнение одной переменной принято записывать так 

Например , для уравнения 

Рисунок 1. График функции 
Таким образом, можно приблизительно определять область локализации корней уравнения. Заметим, что отделить корень можно не единственным образом: если корень отделён на каком-либо отрезке, то годится и любой меньший отрезок, содержащий этот корень. Вообще говоря, чем меньше отрезок, тем лучше, но при этом не следует забывать о том, что на отделение корня на меньших отрезках также тратятся вычислительные усилия, и, быть может, весьма значительные. Таким образом, часто для начала довольствуются весьма широким отрезком, на котором корень отделён.
Некоторые виды уравнений допускают аналитическое решение. Например, степенные алгебраические уравнения степени n 

1.2 Критерии сходимости при решении уравнений
Ø Абсолютная погрешность — абсолютное изменение приближения на соседних шагах итерации
Ø Относительная погрешность — относительное изменение приближения на соседних шагах итерации
Ø Близость к нулю вычисленного значения левой части уравнения (иногда это значение называют невязкой уравнения, так как для корня невязка равна нулю)
1.3 Метод половинного деления (метод дихотомии)
Метод половинного деления основан на последовательном делении отрезка локализации корня пополам.
Для этого выбирается начальное приближение к отрезку [ a , b ], такое, что f ( a ) × f ( b ) 
Рисунок 2. Последовательное деление отрезка пополам и приближение к корню
Алгоритм метода дихотомии можно записать так:
1. представить решаемое уравнение в виде
2. выбрать a, b и вычислить
3. если f(a) × f( с ) то a=a; b = c иначе a = c; b=b
4. если критерий сходимости не выполнен, то перейти к п. 2
Пример решения уравнения методом дихотомии
Найти решение заданного уравнения методом дихотомии с точностью до 10 -5 .
Пример создания расчетной схемы на основе метода дихотомии на примере уравнения: 
Данный метод заключается в проверке на каждой итерации условия:
если f ( a ) × f (с) 
Рисунок 3. Последовательность итераций метода дихотомии при поиске корня уравнения 
a ) схема расчета (зависимые ячейки); b) режим отображения формул;
Для нашего примера итерационная последовательность для нахождения решения принимает вид:
Точность до пятой значащей цифры достигается за 20 итераций.
Скорость сходимости этого метода является линейной.
При выполнении начального условия он сходится к решению всегда.
Метод половинного деления удобен при решении физически реальных уравнений, когда заранее известен отрезок локализации решения уравнения.
2 Решение уравнений , используя “Подбор параметра ”
Используя возможности Excel можно находить корни нелинейного уравнения вида f(x)=0 в допустимой области определения переменной. Последовательность операций нахождения корней следующая:
1. Производится табулирование функции в диапазоне вероятного существования корней;
2. По таблице фиксируются ближайшие приближения к значениям корней;
3. Используя средство Excel Подбор параметра, вычисляются корни уравнения с заданной точностью.
При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность устанавливаются в меню Сервис/Параметры/вкладка Вычисления. Если Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы выполнить очередную итерацию и просмотреть результат. При решении задачи в пошаговом режиме появляется кнопка П родолжить — для возврата в обычный режим подбора параметра.
2.1 Пример решения уравнения, используя “Подбор параметра”
Например , найдем все корни уравнения 2x 3 -15sin(x)+0,5x-5=0 на отрезке [-3 ; 3].
Для локализации начальных приближений необходимо определить интервалы значений Х, внутри которых значение функции пересекает ось абсцисс, т.е. функция меняет знак. С этой целью табулируем функцию на отрезке [–3; 3] с шагом 0,2, получим табличные значения функции. Из полученной таблицы находим, что значение функции трижды пересекает ось Х, следовательно, исходное уравнение имеет на заданном отрезке все три корня.
Рисунок 4. Поиск приближенных значений корней уравнения
Выполните команду меню Сервис/Параметры, во вкладке Вычисления установите относительную погрешность вычислений E=0,00001, а число итераций N=1000, установите флажок Итерации.
Выполните команду меню Сервис/Подбор параметра. В диалоговом окне (рисунок 9) заполните следующие поля:
þ Установить в ячейке : в поле указывается адрес ячейки, в которой записана формула правой части функции;
þ Значение : в поле указывается значение, которое должен получить полином в результате вычислений, т.е. правая часть уравнения (в нашем случае 0);
þ Изменяя значение : в поле указывается адрес ячейки (где записано начальное приближение), в которой будет вычисляться корень уравнения и на которую ссылается формула.
Рисунок 5. Диалоговое окно Подбор параметра для поиска первого корня
После щелчка на ОК получим значение первого корня -1,65793685 .
Выполняя последовательно операции аналогичные предыдущим, вычислим значения остальных корней: -0,35913476 и 2,05170101 .
3 Решение уравнений и систем уравнений, используя надстройку “Поиск решения”
Для решения уравнений можно также использовать команду Поиск решения, доступ к которой реализуется через пункт меню Сервис/Поиск решения.
Последовательность операций нахождения корней следующая:
1. Найти приближенное значение корня уравнения
2. Открыть диалог Поиск решения и установить следующие параметры (рисунок 10):
þ в поле У становить целевую ячейку ввести адрес ячейки, содержащей формулу (левую часть уравнения);
þ установить переключатель в положение ‘ значению’ и ввести значение 0 (правая часть уравнения);
þ в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргумента x целевой функции,;
þ в поле Ограничения с помощью кнопки Д обавить ввести все ограничения, которым должен отвечать результат поиска (область поиска корня уравнения);
þ для запуска процесса поиска решения нажать кнопку В ыполнить.
þ Для сохранения полученного решения необходимо использовать переключатель С охранить найденное решение в открывшемся окне диалога Результаты поиска решения.

Рисунок 6. Диалоговое окно Поиск решения
Полученное решение зависит от выбора начального приближения. Поиск начальных приближений рассмотрен выше.
Рассмотрим некоторые Опции, управляющие работой Поиска решения, задаваемые в окне Параметры (окно появляется, если нажать на кнопку Параметры окна Поиск решения):
þ Максимальное время — ограничивает время, отведенное на процесс поиска решения (по умолчанию задано 100 секунд, что достаточно для задач, имеющих около 10 ограничений, если задача большой размерности, то время необходимо увеличить).
þ Относительная погрешность — задает точность, с которой определяется соответствие ячейки целевому значению или приближение к указанным ограничениям (десятичная дробь от 0 до 1).
þ Неотрицательные значения — этим флажком можно задать ограничения на переменные, что позволит искать решения в положительной области значений, не задавая специальных ограничений на их нижнюю границу.
þ Показывать результаты итераций — этот флажок позволяет включить пошаговый процесс поиска, показывая на экране результаты каждой итерации.
þ Метод поиска — служит для выбора алгоритма оптимизации. Метод Ньютона был рассмотрен ранее. В Методе сопряженных градиентов запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и если итерации дают слишком малое отличие в последовательных приближениях.
Рисунок 7. Вкладка Параметры окна Поиск решения
3.1 Пример решения уравнения, используя надстройку “Поиск решения”
Например , найдем все корни уравнения 2x 3 -15sin(x)+0,5x-5=0 на отрезке [-3 ; 3]. Для локализации начальных приближений необходимо определить интервалы значений Х, внутри которых значение функции пересекает ось абсцисс, т.е. функция меняет знак. С этой целью табулируем функцию на отрезке [–3;3] с шагом 0,2, получим табличные значения функции. Из полученной таблицы находим, что значение функции трижды пересекает ось Х, следовательно, исходное уравнение имеет на заданном отрезке все три корня. На рисунке 12 представлен пример заполнения окна Поиск решения для нахождения первого корня на отрезке [-2; -1].
Рисунок 8. Пример решения уравнения при помощи надстройки Поиск решения
Задание 1. Решение уравнений численным методом
На листе 1 (название листа: Численные методы) для заданного уравнения вида f(x)=0 (Таблица 1. Индивидуальные задания ) реализовать итерационные расчетные схемы методов, указанных в Таблице 1 для нахождения хотя бы одного корня на заданном интервале. Количество итераций просчитать, оценивая 

Задания 2. Решение уравнений встроенными средствами “Подбор параметра” и “Поиск решения”
На листе 2 (название листа: Подбор Поиск) для заданного уравнения вида f(x)=0 (Таблица 1. Индивидуальные задания) на заданном интервале и с некоторым шагом (шаг выбрать самостоятельно) построить таблицу значений функции f(x) и определить количество корней уравнения и выделить интервалы, на которых находятся корни. Построить график функции. Уточнить на заданных интервалах с точностью до 10 -6 корни уравнения с помощью встроенных средств: Подбор параметра, Поиск решения
источники:
http://pandia.ru/text/78/157/38912.php
http://zf.bsut.by/it/fbo/zda/t5.htm
Отметим, что у полинома третьей степени имеется не более трех вещественных корней. Для нахождения корней их предварительно надо локализовать. С этой целью необходимо полином протабулировать. Построим таблицу значений полинома на отрезке [—1,1] с шагом 0,2 и график полинома. Результат приведен на рис. 29, где в ячейку В2 введена формула
=A2^3 — 0,01*A2^2 — 0,7044*A2 + 0,139104.
На рис. 29 видно, что полином меняет знак на интервалах [—1,—0,8], [0,2, 0,4] и [0,6, 0,8]. Это означает, что на каждом из них имеется корень данного полинома. Поскольку полином третьей степени имеет не более трех действительных корней, мы локализовали все его корни.
Найдем корни полинома методом последовательных приближений с помощью команды Сервис / Подбор параметров. Относительная погрешность вычислений и предельное число итераций задаются на вкладке Вычисления диалогового окна Параметры, открываемого командой Сервис / Параметры (рис. 30).
Зададим относительную погрешность и предельное число итераций равными 0,00001 и 1000 соответственно. В качестве начальных приближений к корням можно взять любые точки из отрезков локализации корней. Возьмем в качестве начальных приближений их средние точки: —0.9, 0.3, 0,7 и введем их в диапазон ячеек С2:С4. В ячейку D2 введем формулу
=C2^3 — 0,01*C2^2 — 0,7044*C2 + 0,139104.
Выделим эту ячейку и с помощью маркера заполнения протащим введенную в нее формулу на диапазон D2:D4. В ячейках D2:D4 будут вычислены значения полинома при значениях аргумента, введенных в ячейки C2:C4.
Теперь выберем команду Сервис / Подбор параметров и заполним диалоговое окно Подбор параметров следующим образом (рис. 31).
В поле Установить в ячейке введем D2. В этом поле дается ссылка на ячейку, в которую введена формула, вычисляющая значение левой части уравнения. В поле Значение введем 0 (в этом поле указывается правая часть уравнения). В поле Изменяя значение ячейки введем С2 (в этом поле дается ссылка на ячейку, отведенную под переменную).
Вводить ссылки на ячейки в поля диалогового окна Подбор параметров удобнее не с клавиатуры, а щелчком на соответствующей ячейке. При этом Excel автоматически будет превращать их в абсолютные ссылки (в нашем примере в $D$2 и $C$2).
После нажатия кнопки ОК средство подбора параметров находит приближенное значение корня, которое помещается в ячейку С2. В данном случае оно равно —0,920. Аналогично в ячейках С3 и С4 находим два оставшихся корня. Они равны 0,210 и 0,720.
Решение уравнений в Excel методом итераций Крамера и Гаусса
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах -1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: .
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х 3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
Квадратное уравнение в Excel
В этой статье вы узнаете как решить квадратное уравнение в Excel на конкретном примере. Подробно разберем решение несложно задачи с картинками.
Ход решения
Запустим программу Microsoft Office Excel. Я пользуюсь 2007 версией. Для начала объединим ячейки A1:A5 и запишем в них формулу квадратного уравнения в виде ax2+bx+c=0.Далее нам нужно возвести x в квадрат, для этого нужно сделать цифру 2 надстрочным интервалом. Выделим двойку и нажмем правой кнопкой мыши.
Получим формулу вида ax 2 +bx+c=0
В ячейке A2 введем текстовое значение a= , в ячейке A3 b= и в ячейке A4 с= соответственно. Эти значения будут вводиться с клавиатуры в следующих ячейках (B2,B3,B4).
Введем текст для значений, которые будут считаться. В ячейке C2 d=, C3 x1= C4 x2=. Подстрочный интервал для xсделаем аналогично надстрочному интервалу в x 2
Перейдем к вводу формул для решения
Дискриминант квадратного трехчлена равен b 2 -4ac
В ячейку D2 введем соответствующую формулу для возведения числа во вторую степень:
Квадратное уравнение имеет два корня, в случае если дискриминант больше нуля. В ячейку C3 введем формулу для x1
Для расчета x2 введем похожую формулу, но со знаком плюс
Соответственно при введенных значениях a,b,c сначала считается дискриминант, если его значения меньше нуля выводится сообщение «Корней нет», иначе получаем значения x1 и x2.
Защита листа в Excel
Нам нужно защитить лист, на котором мы производили расчеты. Без защиты нужно оставить ячейки, в которые можно вводить значения a,b,c, то есть ячейки B2 B3 B4. Для этого выделим данный диапазон и зайдем в формат ячеек, перейдем во вкладку Рецензирования, Защитить лист и уберем флажок с позиции Защищаемая ячейка. Нажмем кнопку OK, подтвердив внесенные изменения.
Этот диапазон ячеек будет не защищен при защите листа. Выполним защиту листа, для этого перейдем на вкладку Рецензирование пункт Защита листа. Пароль наберем 1234. Нажмем OK.
Теперь мы сможем изменять значения ячеек B2,B3,B4. При попытке изменения других ячеек мы получим сообщение следующего содержания: «Ячейка или диаграмма защищена от изменений. А так же совет по снятию защиты.
Нелинейные
уравнения – это уравнения вида f(x)=0,
где f(x)
– нелинейная функция. Решение уравнения
f(x)=0
сводится к поиску таких значений х*
(корней уравнения), которые превращают
уравнение в тождество. Различают
нелинейные алгебраические уравнения
и трансцендентные.
Например,
нелинейное алгебраическое уравнение
ax2
+
вx
+с =0
имеет два корня, которые могут быть
действительными или мнимыми. Например,
уравнение х2
+ 2=0 имеет два мнимых корня х1=
-2
и х2=
--2
.
В
дальнейшем будет идти речь о вычислении
только действительных корней.
Трансцендентным
называется
уравнение,
если в f(x)
входит хотя бы одна трансцендентная
функция. Например, sin(x)
–1=0;
Решение
нелинейных уравнений выполняют в два
этапа:
-
Этап
отделения
корней. -
Этап
уточнения
корней
, т.е. поиск коней с заданной точностью.
Этап
отделения корней
Для
этого построим график заданной функции
f(x)=0.
В столбце А располагаем изменение
аргумента, а в столбце В табулируемую
функцию. Строим график. На графике
выделяем границы корня и в этих границах
берем начальное приближение корня
(нарисовать график, выделить корни и
взять начальное приближение).
Этап
уточнение корня
Команда
Подбор
параметров
Порядок
уточнения:
1.
В ячейку A1
вводим
начальное приближение корня Х1.
2.
В ячейку В1
вводим
формулу с заданной функцией.
3.
Выполняем команды Сервис,
Подбор
параметра.
Появляется окно Подбор
параметра (рис.
7.7).
4.
В поле «Установить
в ячейке»
записать адрес первой формулы (можно
снять окно и щелкнуть ячейку В1,
затем восстановить окно).
5.
В поле «Значение»
установить 0.
6.
В поле «Изменяя
значение
ячейки«
установить адрес А1
(снять окно и щелкнуть А1).
7.
Щелкнуть ОК.
Появляется окно Результат
подбора параметра
(рис. 7.8), а в ячейке А1
будет уточненное значение корня.
Рис.
7.8
Рис.
7.7
7.5. Вычисления по итерационным формулам
Итерационной
называется формула типа yi+1
= f
(yi)
. Пример1.
Вычисление
задано итерационной формулой yi+1=(x/yi2
+2yi)/3
Начальное
приближении у0=1
и значение х= 27.
Составим
ЭТ для вычисления:
1.
В ячейку a2
запишем
значение х равное 27
(рис. 7.9).
2.
В ячейку b2
запишем
значение у0
равное 1.
3
Рис.
7.9
. В ячейку b3
запишем формулу =
($A$1/B1^2+2*B1)/3,
которую копируем вниз
Пример
2. Заданы
итерационные формулы
x
i
=2xi-1
и yi=
xi-1
+ 3yi-1
при
изменении
i=2,3,4,5.
При
i=2
х2
= 2х1
и y2=
x1
+ 3y1
Начальные
значения x1=1
; y1=1
(рис. 7.10) запишем в В2 и С2 соответственно.
В ячейки В3 и С3 запишем формулы для х2
и у2
. Выделяем В3:С3 и копируем вниз до С6.
Результат вычисления на рис. 7.11.
Рис.
7.10
Рис.
7.11
Пример
3.
Решение
задач следующего типа:
Даны
действительные числа у1, у2,…у5, которые
записаны в В2:В6
Составить
ЭТ для вычисления
и
определения min(z12,
z22,
…,z52)
при i=1,2,…,5
Рис.
7.12
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Министерство
общего образования
Российской федерации
Уральский государственный технический университет-УПИ
филиал
в г.Краснотурьинске
Кафедра
вычислительной техники
Курсовая работа
По
численным методам
Решение
линейных уравнений методом простой итерации
c помощью
программы Microsoft Excel
Руководитель Кузьмина
Н.В.
Студент Нигматзянов
Т.Р.
Группа М-177Т
2002
Задание.
Тема: «Нахождение с
заданной точностью корня уравнения F(x)=0 на промежутке
[a;b] методом простой
итерации».
Контрольный пример:
0,25-х+sinx=0
Условия задачи: для заданной функции F(x) на
интервале [0,5;2] найти корень уравнения F(x)=0
методом простой итерации.
Корень вычислить
дважды(с помощью автоматического и ручного расчета).
Предусмотреть построение графика функции на заданном
интервале.
Содержание.
Введение 4
1.Теоретическая часть 5
2.Описание хода работы 7
3.Входные и выходные
данные 8
Заключение 9
Приложение 10
Библиографический список 12
Введение.
В ходе данной работы мне необходимо ознакомиться с
различными методами решения уравнения и найти корень нелинейного уравнения
0,25-х+sin(x)=0 численным методом – методом простой итерации. Для
проверки правильности нахождения корня необходимо решить уравнение графически
,найти приближенное значение и сравнить его с полученным результатом.
1.Теоретичесакя часть.
Метод простой итерации.
Итерационный
процесс состоит в последовательном уточнении начального приближения х0 (корня
уравнения). Каждый такой шаг называется итерацией.
Для использования этого метода исходное нелинейное уравнение записывается
в виде: х=j(х), т.е. выделяется х; j(х) –
непрерывна и дифференцируема на интервале (а; в). Обычно это можно сделать несколькими
способами:
Например:
arcsin(2x+1)-x2=0 (f(x)=0)
Способ 1.
arcsin(2x+1)=x2
sin(arcsin(2x+1))=sin(x2)
2x+1=sin(x2)
x=0.5(sinx2-1)
(x=j(x))
Способ 2.
x=x+arcsin(2x+1)-x2
(x=j(x))
Способ 3.
x2=arcsin(2x+1)
x=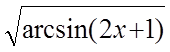
(x=j(x)),знак берется в зависимости от интервала [а;b].
Преобразование должно
быть таким, чтобы ½j(x)<1½
для всех принадлежащих интервалу [a;b].В
таком случае процесс итерации сходится.
Пусть известно начальное
приближение корня x=c0.Подставляя
это значение в правую часть уравнения x=j(x),получаем новое
приближение корня:c=j(c0).Далее, подставляя каждый раз новое значение
корня в x=j(x),получаем последовательность значений
c2=j(c1)
…
cn=j(cn-1) n=1,2,3,…
Процесс итераций следует
продолжать до тех пор,пока для двух последовательных приближений не будет
выполнено условие: ½cn-cn-1½<e
Решать уравнения численными
методами можно с помощью языков программирования, но программа Excel дает возможность справиться сданной задачей более простым
способом.
Программа Excel
реализует метод простой итерации двумя способами с помощью ручного расчета и с
автоматическим контролем точности.

 |

1.
 |
|||
j
 |
|||||||||||||
с0 с2
с4 с6 с8 корень
с9 с7 с5 с3
с1
х
Рис. График итерационного процесса
|
2.Описание хода работы.
1.
Запустил МЕ.
2.
Построил график функции y=x и y=0,25+sin(x) на
отрезке [0,5;2] с шагом 0,1 назвал лист «График».
3.
Выбрал команду Сервис®Параметры.
Открыл вкладку Вычисления.
Включил режим Вручную.
Отключил флажок Пересчет перед сохранением. Сделал значение поля Пре-дельное
число итераций равным 1,относительную погрешность 0,001.
4.
Ввел в ячейку А1 строку «Решение
уравнения x=0,25+sin(x) методом простой итерации».
5.
Ввел в ячейку А3 текст «Начальное
значение»,в ячейку А4 текст «Начальный флаг»,в ячейку В3 значение 0,5 ,в ячейку
В4 слово ИСТИНА.
6.
Присвоил ячейкам В3 и В4 имя
«нач_зн» и «нач».
В ячейке В6 будет выполняться проверка,равна ли истина значению ячейки
«нач».Если это так,х будет установлено равным начальному значению, в противоположном
случае равным ячейке В7,т.е. 0,25+синуса х.В ячейке В7 выч-исляется 0,25-синуса
ячейки В6,и тем организуется циклическая ссылка.
7.
В ячейку А6 ввел y=x,и в
ячейку А7 y=0,25+sin(x).В ячейку В6 формулу:
=ЕСЛИ(нач;нач_зн;В7).
В ячейку В7 формулу: y=0,25+sin(B6).
8.
В ячейку А9 ввел слово
Погрешность.
9.
В ячейку В9 ввел формулу: =В7-В6.
10.
С помощью команды Формат-Ячейки(вкладка
Число) преобразовал ячейку В9 в экспоненциальный формат с двумя
цифрами после запятой.
11.
Затем организовал вторую
циклическую ссылку-для подсчета количества ите-раций.В ячейку А11 ввел текст
«Количество итераций».
12.
В ячейку В11 ввел формулу:
=ЕСЛИ(нач;0;В12+1).
13.
В ячейку В12 ввел =В11.
14.
Для выполнения расчета установил
табличный курсор в ячейку В4 и нажал клавишу F9(Вычислить)
для запуска решения задачи.
15.
Изменил значение начального флага
на ЛОЖЬ,и снова нажал F9.При каждом нажатии F9 выполняется
одна итерация и вычисляется следующее приближен-ное значение х.
16.
Нажимал клавишу F9 до
тех пор, пока значение х не достигло необходимой точности.
При автоматическом расчете:
17.
Перешел на другой лист.
18.
Повторил пункты с 4 по 7,только в
ячейку В4 ввел значение ЛОЖЬ.
19.
Выбрал команду Сервис®Параметры(вкладка
Вычисления).Установил зна-чение поля Предельное число
итераций равным 100,относительную погреш-ность равной 0,0000001.Включил
ркжим Автоматически.
3.Входные и выходные данные.
Входные:
Начальный флаг ЛОЖЬ.
Начальное значение 0,5
Функция
y=0,25-x+sin(x)
Границы
интервала [0,5;2]
Точность
вычисления при ручном расчете 0,001
при автоматическом
Выходные:
1.
Ручной расчет:
число итераций 37
корень уравнения 1,17123
2.
Автоматический расчет:
число итераций 100
корень уравнения 1,17123
3.
Решение уравнения графическим
способом:
корень уравнения 1,17
Заключение.
В ходе данной курсовой работы я ознакомился с
различными методами решения уравнений:
·
Аналитическим методом
·
Графическим методом
·
Численным методом
Но так как
большинство численных методов решения уравнений являются итерационными, то я на
практике использовал этот метод.
Нашел с заданной точностью корень уравнения
0,25-x+sin(x)=0 на промежутке [0,5;2] методом простой итерации.
Приложение.
1.Ручной расчет.
2.Автоматический расчет.
3.Решение уравнения 0.25-x-sin(x)=0
графическим способом.
Библиографический список.
1.
Волков Е.А. «Числовые методы».
2.
Самарский А.А. «Введение в
числовые методы».
3.
Игалеткин И.И. «Числовые методы».
Содержание
- 1 Варианты решений
- 1.1 Способ 1: матричный метод
- 1.2 Способ 2: подбор параметров
- 1.3 Способ 3: метод Крамера
- 1.4 Способ 4: метод Гаусса
- 1.5 Помогла ли вам эта статья?
- 2 Решение уравнений методом подбора параметров Excel
- 3 Как решить систему уравнений матричным методом в Excel
- 4 Решение системы уравнений методом Крамера в Excel
- 5 Решение систем уравнений методом Гаусса в Excel
- 6 Примеры решения уравнений методом итераций в Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
- Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
- Теперь для нахождения корней уравнения, прежде всего, нам нужно отыскать матрицу, обратную существующей. К счастью, в Эксель имеется специальный оператор, который предназначен для решения данной задачи. Называется он МОБР. Он имеет довольно простой синтаксис:
=МОБР(массив)Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
- Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
- Запускается окно аргументов функции МОБР. Оно по числу аргументов имеет всего одно поле – «Массив». Тут нужно указать адрес нашей таблицы. Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK», но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter. Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter, а произвести набор сочетания клавиш Ctrl+Shift+Enter. Выполняем эту операцию.
- Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
- Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
=МУМНОЖ(Массив1;Массив2)Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
- В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
- Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
- После данного действия в предварительно выделенной ячейке отобразятся корни уравнения: X1, X2, X3 и X4. Они будут расположены последовательно. Таким образом, можно сказать, что мы решили данную систему. Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней. Если равенство будет соблюдено, то это означает, что представленная система уравнений решена верно.
Урок: Обратная матрица в Excel
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
3x^2+4x-132=0
- Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
=3*x^2+4*x-132Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
- Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
- Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
- После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
- Результат вычисления корня уравнения будет находиться в той ячейке, которую мы назначили в поле «Изменяя значения». В нашем случае, как видим, x будет равен 6.
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Урок: Подбор параметра в Excel
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
- Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
- Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
- Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
=МОПРЕД(массив)Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
- Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
- Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
- Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
- Аналогичным образом производим подсчет определителей для остальных трех таблиц.
- На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
- Теперь пора найти корни уравнения. Корень уравнения будет равен отношению определителя соответствующей преобразованной матрицы на определитель первичной таблицы. Таким образом, разделив поочередно все четыре определителя преобразованных матриц на число -148, которое является определителем первоначальной таблицы, мы получим четыре корня. Как видим, они равны значениям 5, 14, 8 и 15. Таким образом, они в точности совпадают с корнями, которые мы нашли, используя обратную матрицу в способе 1, что подтверждает правильность решения системы уравнений.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
14x1+2x2+8x3=110
7x1-3x2+5x3=32
5x1+x2-2x3=17
- Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
- Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
=B8:E8-$B$7:$E$7*(B8/$B$7)Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
- После этого копируем полученную строку и вставляем её в строчку ниже.
- Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
- Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
- В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
=B13:E13-$B$12:$E$12*(C13/$C$12)После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
- Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
=B17:E17/D17Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
- Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
=(B16:E16-B21:E21*D16)/C16Жмем привычное уже нам сочетание клавиш для применения формулы массива.
- Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
=(B15:E15-B20:E20*C15-B21:E21*D15)/B15Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
- Теперь смотрим на числа, которые получились в последнем столбце последнего блока строк, рассчитанного нами ранее. Именно эти числа (4, 7 и 5) будут являться корнями данной системы уравнений. Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Да Нет
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
Хn+1 = Xn– F (Xn) / M, n = 0, 1, 2, … .
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
Скачать решения уравнений в Excel
Корень на заданном промежутке один.
Задача решения уравнения встает не только перед студентами и школьниками. В Excel можно использовать различные способы выполнения этой задачи. О способе решения путем подбора параметра пойдет речь в этой статье.
Нахождение корней нелинейного уравнения с использованием средства
«Подбор параметра» сводится в двум этапам:
- определение приблизительных границ отрезков и количества корней графическим методом;
- подбор на каждом отрезке значения корня, удовлетворяющего заданной точности вычислений.
Примером может служить решение квадратного уравнения, которое в общем виде задается выражением
«Y(x) = ax2 + bx +
c» . Для того, чтобы построенная электронная таблица позволяла бы находить решения подобных уравнений с любыми коэффициентами, лучше вынести коэффициенты в отдельные ячейки, а в формулах для вычисления значений функции использовать ссылки на эти ячейки. Впрочем, это дело вкуса. Можно при составлении формулы использовать значения коэффициентов, а не ссылки на них.
Чтобы оценить примерные границы отрезков и количество корней, можно использовать табличное задание значений функции, т.е. задать несколько значений переменной и вычислить соответствующие значения функции. Опять же, для того, чтобы можно было моделировать расчеты для квадратных уравнений с различными коэффициентами, шаг табулирования лучше задать в отдельной ячейке. Начальное значение переменной можно будет изменять путем ввода в ячейку «
А6» . Для вычисления следующего значения в ячейку
«А7» введена формула «
=А6+$
B$4» , т.е. использована абсолютная ссылка на ячейку с шагом табулирования.
Далее с помощью
маркера заполнения формируется ряд формул для вычисления последующих значений переменной, в приведенном примере используется 20 значений.
Вводится формула для вычисления значения функции (для рассматриваемого примера в ячейку «
В6» ) и формируется ряд аналогичных формул для остальных ячеек. В формуле использованы абсолютные ссылки на ячейки с коэффициентами уравнения.
По построенной таблице строится
точечная диаграмма .
Если начальное значение Х и шаг выбраны неудачно, и на диаграмме нет пересечений с осью абсцисс, то можно ввести другие значения и добиться нужного результата.
Можно было бы найти решение уже на этом шаге, но для этого понадобилось бы гораздо больше ячеек и шаг, равный заданной точности вычислений (0,001). Чтобы не создавать громоздких таблиц, далее используется
«Подбор параметра» из группы
«Прогноз» на вкладке
«Данные» . Предварительно необходимо выделить место под начальные значения переменной (корней в примере два) и соответствующие значения функции. В качестве «
х1» выбирается первое из значений, дающих наиболее близкое к нулю значение функции (в примере 0,5). В
ячейку
L6 введена формула для вычисления функции. В окне подбора параметра необходимо указать для какой ячейки (
L6 ), какое значение (
) нужно получить, и в какой ячейке для этого изменять значения (
К6 ).
Для поиска второго корня необходимо ввести второе из значений, дающих наиболее близкое к нулю значение функции (в примере 9,5), и повторить подбор параметра для ячейки
L9 (в ячейку скопирована формула из ячейки
L6 ).
Предложенное оформление коэффициентов функции в отдельные ячейки позволяет без изменения формул решать другие подобные уравнения.
Подбор параметра имеется и в более ранних версиях программы.
|
Решить нелинейное уравнение методом итераций |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |























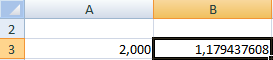










































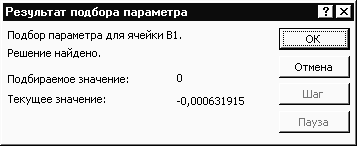
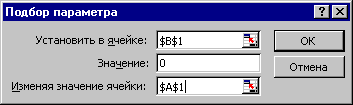
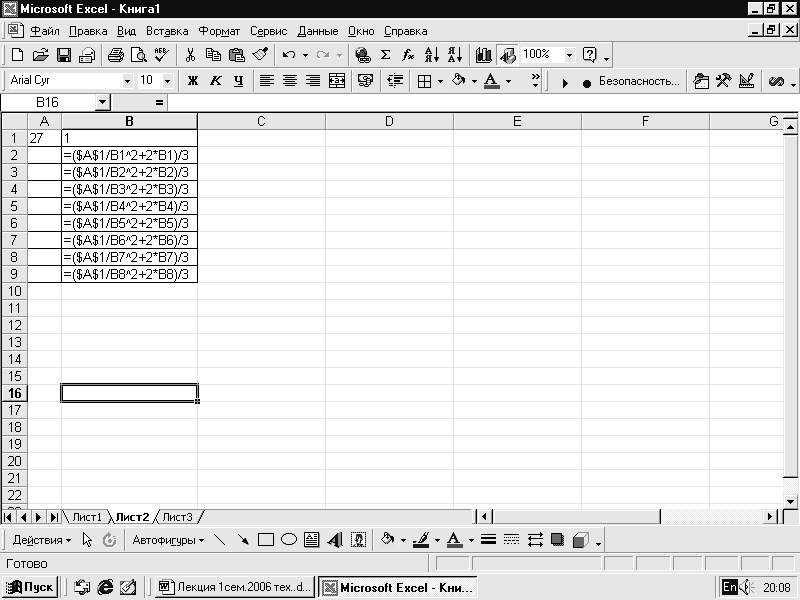
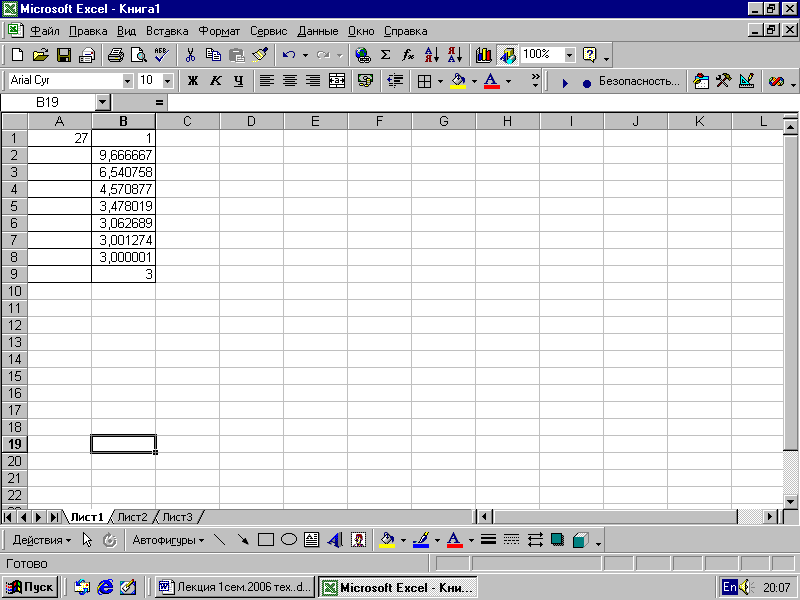
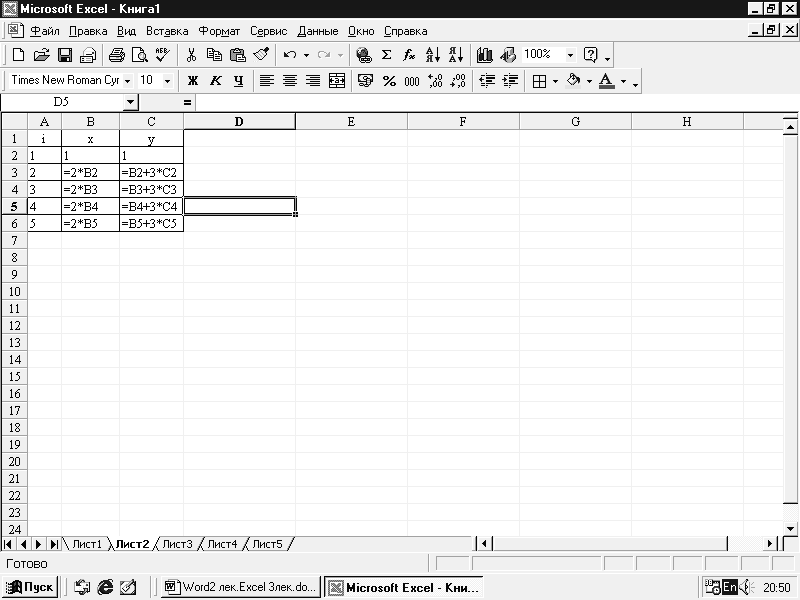
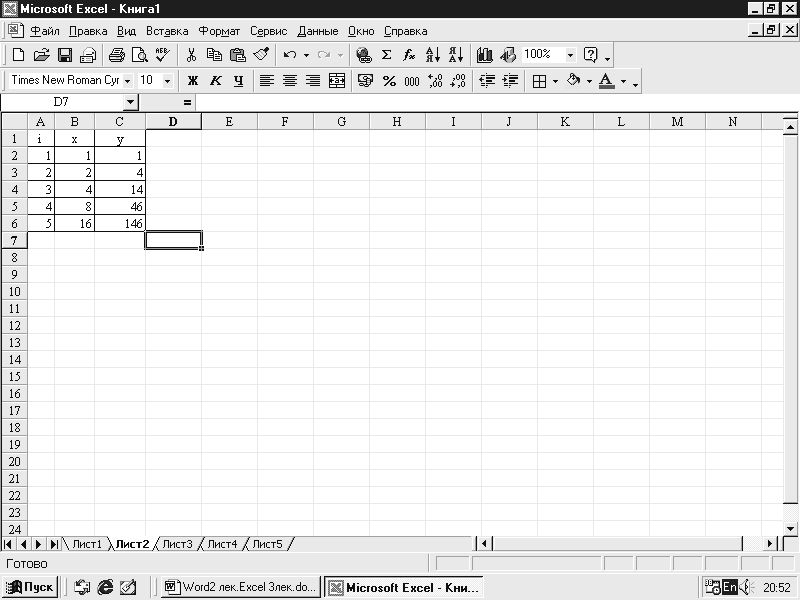
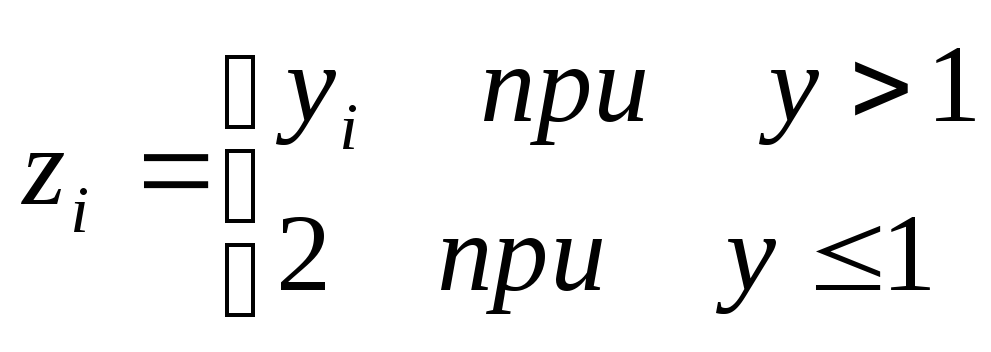
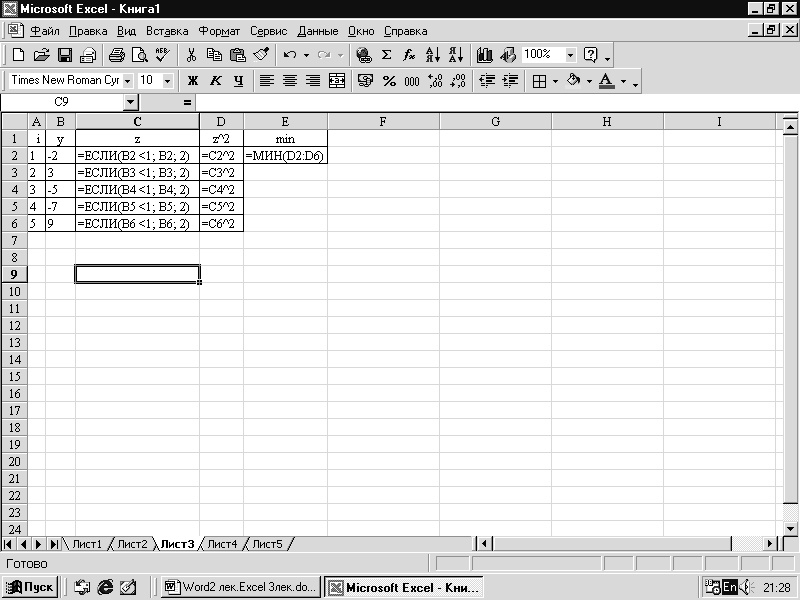
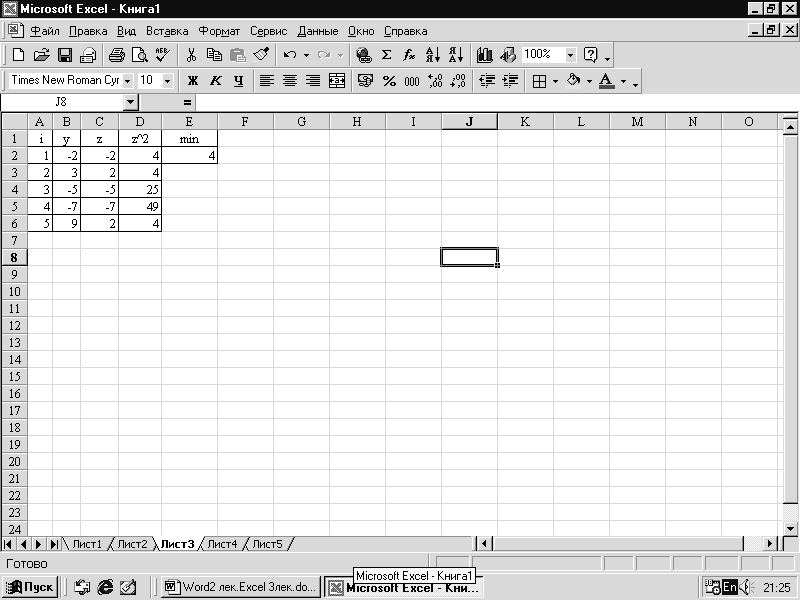


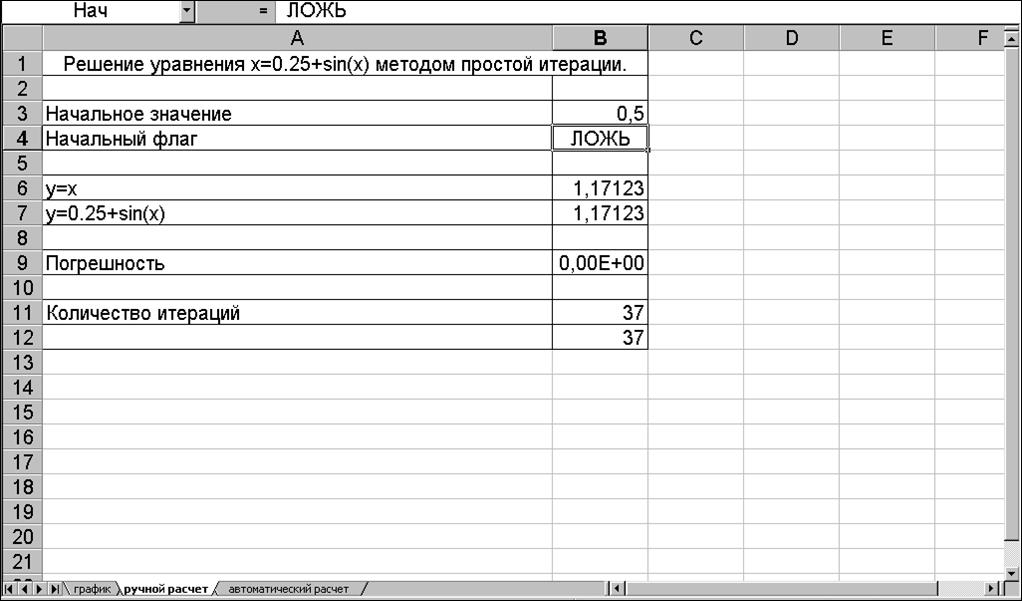
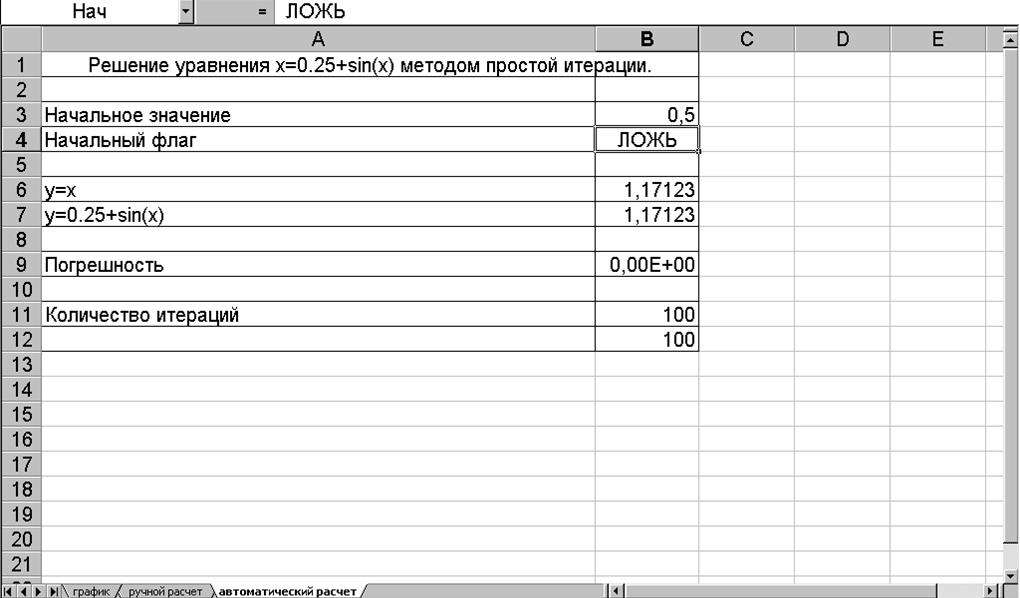
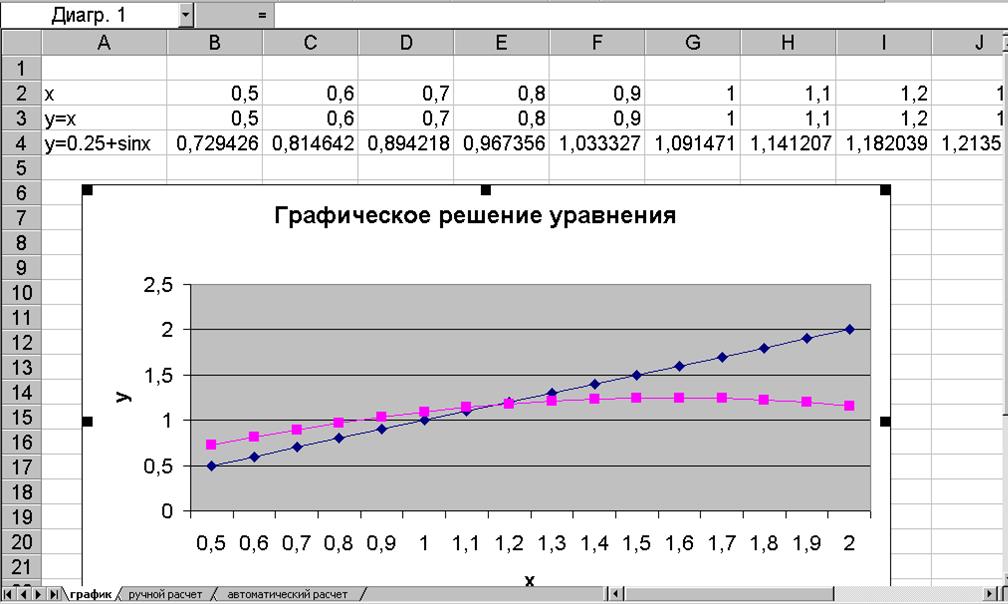






 Если не учитывать такую мелочь, что результат неверный. А если подставить так, как препод сказал (кстати, он про модуль забыл), то получится как раз то решение, которое у меня — 27 шагов
Если не учитывать такую мелочь, что результат неверный. А если подставить так, как препод сказал (кстати, он про модуль забыл), то получится как раз то решение, которое у меня — 27 шагов