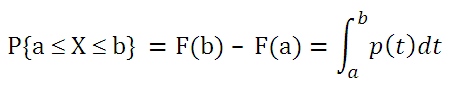Формула Бернулли в Excel
В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!
Понравилось? Добавьте в закладки
Схема независимых испытаний
В общем виде схема повторных независимых испытаний записывается в виде задачи:
Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.
Эта вероятность вычисляется по формуле Бернулли:
$$
P_n(k)=C_n^k cdot p^k cdot (1-p)^{n-k}=C_n^k cdot p^k cdot q^{n-k}. qquad(1)
$$
Здесь $C_n^k$ — число сочетаний из $n$ по $k$.
Еще: онлайн калькуляторы для формулы Бернулли.
Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:
- Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
- Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
- События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.
Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.
Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.
Формула Бернулли в Эксель
Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП(), выдающая определенную вероятность биномиального распределения.
Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0).
Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).
Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:
Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):
- Событие произойдет в точности $k$ раз из $n$:
=БИНОМ.РАСП(k;n;p;0)
$$P_n(k)=C_n^k cdot p^k cdot q^{n-k}$$ - Событие произойдет от $k_1$ до $k_2$ раз:
=БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
$$P_n(k_1le X le k_2)=sum_{i=k_1}^{k_2} C_n^i cdot p^i cdot q^{n-i}$$ - Событие произойдет не более $k_3$ раз:
=БИНОМ.РАСП(k_3;n;p;1)
$$P_n(0le X le k_3)=sum_{i=0}^{k_3} C_n^i cdot p^i cdot q^{n-i}$$ - Событие произойдет не менее $k_4$ раз:
=1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
$$P_n(k_4le X le n)=sum_{i=k_4}^{n} C_n^i cdot p^i cdot q^{n-i}$$ - Событие произойдет хотя бы один раз:
=1-БИНОМ.РАСП(0;n;p;0)
$$P_n( X ge 1)=1-P_n(0)=1-q^{n}$$ - Наивероятнейшее число наступлений события $m$:
=ОКРУГЛВВЕРХ(n*p-q;0)
$$np-q le m le np+p$$
Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.
Полезное: расчетный файл по формуле Бернулли
Нужна помощь в решении задач по теории вероятностей?
Примеры решений задач
Рассмотрим решение типовых задач.
Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.
Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:
$$
P_7(5)=C_{7}^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146.
$$
Для вероятности 6 или 7 попаданий суммируем:
$$
P_7(6)+P_7(7)=C_{7}^6 cdot 0,75^6 cdot 0,25^1+C_{7}^7 cdot 0,75^7 cdot 0,25^0= \
= 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495.
$$
А вот это решение в файле эксель:
Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?
Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_{10}(k)=C_{10}^k cdot 0,5^kcdot 0,5^{10-k}=C_{10}^k cdot 0,5^{10}$$
Приступим к вычислениям:
$$1. P_{10}(2)=C_{10}^2 cdot 0,5^{10} = frac{10!}{2!8!}cdot 0,5^{10} approx 0,044.$$
$$2. P_{10}(4)+P_{10}(5)=C_{10}^4 cdot 0,5^{10} + C_{10}^5 cdot 0,5^{10}=left( frac{10!}{4!6!} + frac{10!}{5!5!} right)cdot 0,5^{10} approx 0,451.$$
$$3. P_{10}(0)+P_{10}(1)+P_{10}(2)=C_{10}^0 cdot 0,5^{10} + C_{10}^1 cdot 0,5^{10}+ C_{10}^2 cdot 0,5^{10}=left( 1+10+ frac{10!}{2!8!} right)cdot 0,5^{10} approx 0,055.$$
$$4. P_{10}(7)+P_{10}(8)+P_{10}(9)+P_{10}(10)=\ = C_{10}^7 cdot 0,5^{10} + C_{10}^8 cdot 0,5^{10}+ C_{10}^9 cdot 0,5^{10}+ C_{10}^10 cdot 0,5^{10} =\=left(frac{10!}{3!7!}+ frac{10!}{2!8!} + 10 +1right)cdot 0,5^{10} approx 0,172.$$
$$5. P_{10}(ge 1)=1-P_{10}(0)=1-C_{10}^0 cdot 0,5^{10} = 1- 0,5^{10} approx 0,999.$$
Наивероятнейшее число мальчиков найдем из неравенства:
$$
10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, \
4,5 le m le 5,5,\
m=5.
$$
Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).
Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:
Видно, что ответы совпадают.
Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?
Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.
Решайте свои задачи и советуйте наш сайт друзьям. Удачи!
Полезная страница? Сохрани или расскажи друзьям
Полезные ссылки
Расчетный файл эксель для расчетов по формуле Бернулли
|
|
Решебник задач по вероятности
17 авг. 2022 г.
читать 2 мин
Вероятность описывает вероятность того, что некоторое событие произойдет.
Мы можем рассчитать вероятности в Excel, используя функцию PROB , которая использует следующий синтаксис:
ПРОБ(x_диапазон, вероятностный_диапазон, нижний_предел, [верхний_предел])
куда:
- x_range: диапазон числовых значений x.
- prob_range: диапазон вероятностей, связанных с каждым значением x.
- нижний_предел: нижний предел значения, для которого вы хотите получить вероятность.
- upper_limit: Верхний предел значения, для которого вы хотите получить вероятность. По желанию.
В этом руководстве представлено несколько примеров использования этой функции на практике.
Пример 1: Вероятность игры в кости
На следующем изображении показана вероятность выпадения кубика с определенным значением при данном броске:
Поскольку кости с одинаковой вероятностью выпадут на каждом значении, вероятность одинакова для каждого значения.
На следующем рисунке показано, как найти вероятность того, что кубик выпадет на число от 3 до 6:
Вероятность оказывается равной 0,5 .
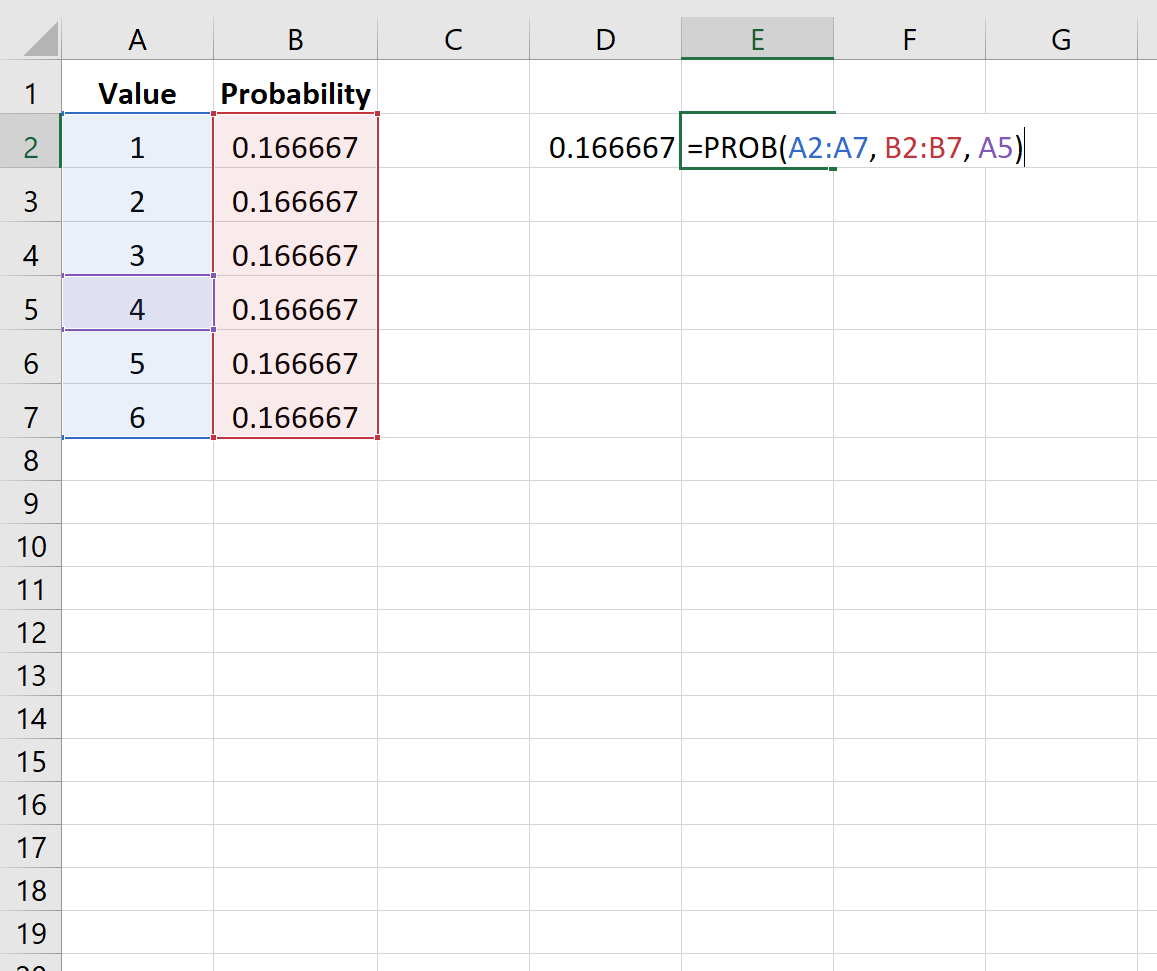
Обратите внимание, что аргумент верхнего предела является необязательным. Таким образом, мы могли бы использовать следующий синтаксис, чтобы найти вероятность того, что кости приземлятся только на 4:
Вероятность оказывается равной 0,166667 .
Пример 2: Вероятность продаж
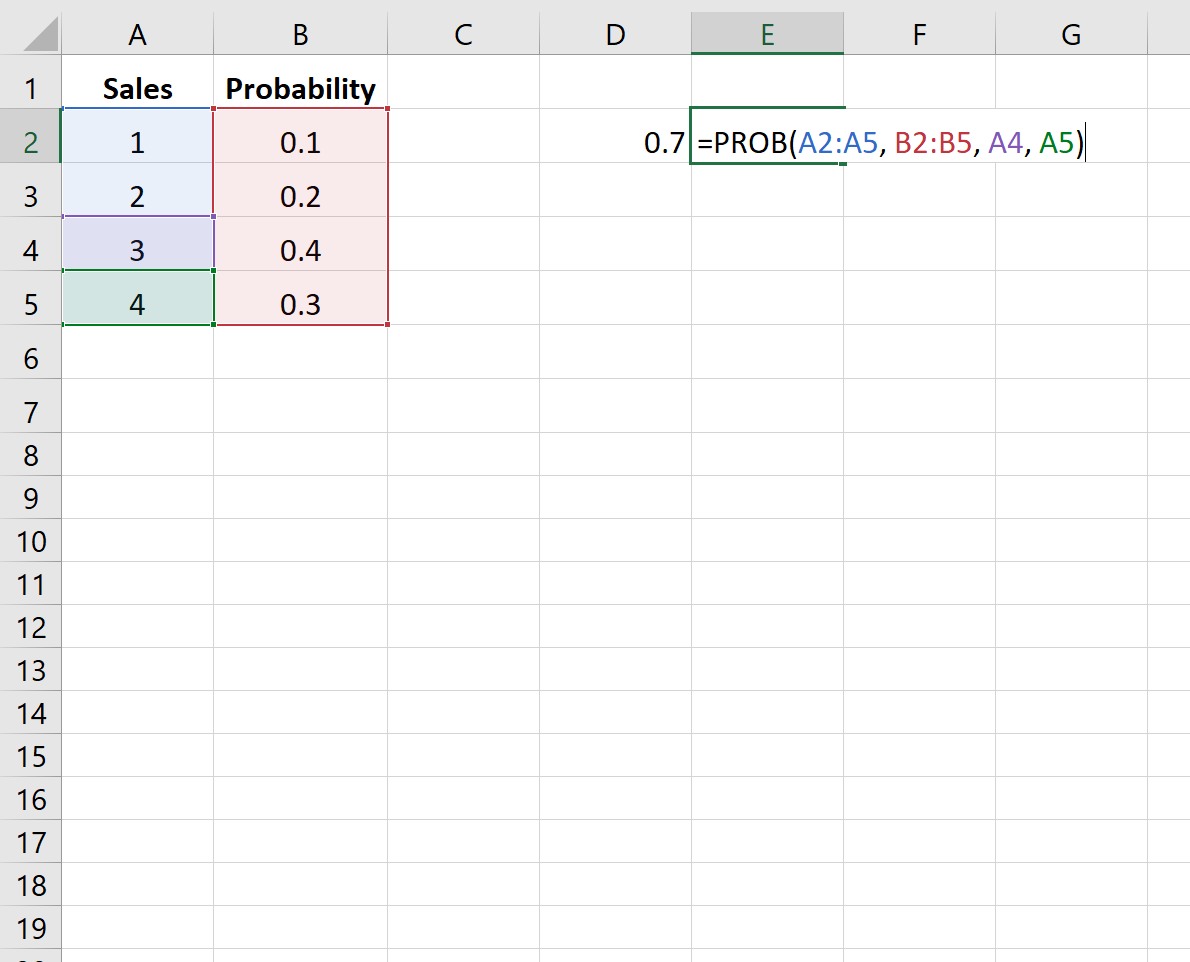
На следующем изображении показана вероятность того, что компания продаст определенное количество товаров в предстоящем квартале:
На следующем рисунке показано, как найти вероятность того, что компания совершит 3 или 4 продажи:
Вероятность оказывается равной 0,7 .
Дополнительные ресурсы
Как рассчитать относительную частоту в Excel
Как рассчитать кумулятивную частоту в Excel
Как создать частотное распределение в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!
Схема независимых испытаний
В общем виде схема повторных независимых испытаний записывается в виде задачи:
Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.
Эта вероятность вычисляется по формуле Бернулли:
$$ P_n(k)=C_n^k cdot p^k cdot (1-p)^=C_n^k cdot p^k cdot q^. qquad(1) $$
Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:
- Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
- Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
- События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.
Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.
Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.
Формула Бернулли в Эксель
Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП() , выдающая определенную вероятность биномиального распределения.
Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0) .
Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).
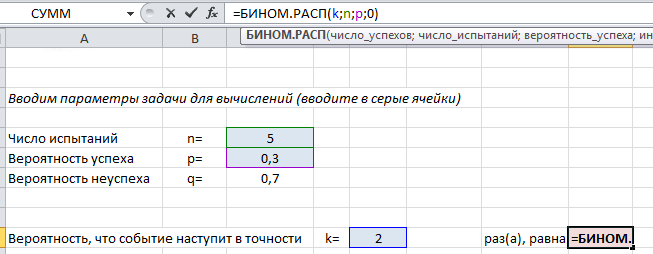
Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:
Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):
- Событие произойдет в точности $k$ раз из $n$:
=БИНОМ.РАСП(k;n;p;0)
$$P_n(k)=C_n^k cdot p^k cdot q^$$ - Событие произойдет от $k_1$ до $k_2$ раз:
=БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
$$P_n(k_1le X le k_2)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не более $k_3$ раз:
=БИНОМ.РАСП(k_3;n;p;1)
$$P_n(0le X le k_3)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не менее $k_4$ раз:
=1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
$$P_n(k_4le X le n)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет хотя бы один раз:
=1-БИНОМ.РАСП(0;n;p;0)
$$P_n( X ge 1)=1-P_n(0)=1-q^$$ - Наивероятнейшее число наступлений события $m$:
=ОКРУГЛВВЕРХ(n*p-q;0)
$$np-q le m le np+p$$
Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.
Примеры решений задач
Рассмотрим решение типовых задач.
Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.
Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:
$$ P_7(5)=C_<7>^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146. $$
Для вероятности 6 или 7 попаданий суммируем:
$$ P_7(6)+P_7(7)=C_<7>^6 cdot 0,75^6 cdot 0,25^1+C_<7>^7 cdot 0,75^7 cdot 0,25^0= = 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495. $$
А вот это решение в файле эксель:

Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?
Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_<10>(k)=C_<10>^k cdot 0,5^kcdot 0,5^<10-k>=C_<10>^k cdot 0,5^<10>$$ Приступим к вычислениям:
$$1. P_<10>(2)=C_<10>^2 cdot 0,5^ <10>= frac<10!><2!8!>cdot 0,5^ <10>approx 0,044.$$ $$2. P_<10>(4)+P_<10>(5)=C_<10>^4 cdot 0,5^ <10>+ C_<10>^5 cdot 0,5^<10>=left( frac<10!> <4!6!>+ frac<10!> <5!5!>
ight)cdot 0,5^ <10>approx 0,451.$$ $$3. P_<10>(0)+P_<10>(1)+P_<10>(2)=C_<10>^0 cdot 0,5^ <10>+ C_<10>^1 cdot 0,5^<10>+ C_<10>^2 cdot 0,5^<10>=left( 1+10+ frac<10!> <2!8!>
ight)cdot 0,5^ <10>approx 0,055.$$ $$4. P_<10>(7)+P_<10>(8)+P_<10>(9)+P_<10>(10)= = C_<10>^7 cdot 0,5^ <10>+ C_<10>^8 cdot 0,5^<10>+ C_<10>^9 cdot 0,5^<10>+ C_<10>^10 cdot 0,5^ <10>==left(frac<10!><3!7!>+ frac<10!> <2!8!>+ 10 +1
ight)cdot 0,5^ <10>approx 0,172.$$ $$5. P_<10>(ge 1)=1-P_<10>(0)=1-C_<10>^0 cdot 0,5^ <10>= 1- 0,5^ <10>approx 0,999.$$
Наивероятнейшее число мальчиков найдем из неравенства:
$$ 10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, 4,5 le m le 5,5, m=5. $$
Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).
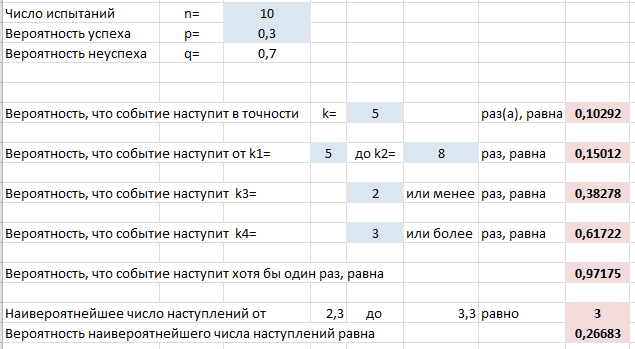
Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:

Видно, что ответы совпадают.
Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?
Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.

Решайте свои задачи и советуйте наш сайт друзьям. Удачи!
Даны определения Функции распределения случайной величины и Плотности вероятности непрерывной случайной величины. Эти понятия активно используются в статьях о статистике сайта ]]> www.excel2.ru ]]> . Рассмотрены примеры вычисления Функции распределения и Плотности вероятности с помощью функций MS EXCEL.
Введем базовые понятия статистики, без которых невозможно объяснить более сложные понятия.
Генеральная совокупность и случайная величина
Пусть у нас имеется генеральная совокупность (population) из N объектов, каждому из которых присуще определенное значение некоторой числовой характеристики Х.
Примером генеральной совокупности (ГС) может служить совокупность весов однотипных деталей, которые производятся станком.
Поскольку в математической статистике, любой вывод делается только на основании характеристики Х (абстрагируясь от самих объектов), то с этой точки зрения генеральная совокупность представляет собой N чисел, среди которых, в общем случае, могут быть и одинаковые.
В нашем примере, ГС — это просто числовой массив значений весов деталей. Х – вес одной из деталей.
Если из заданной ГС мы выбираем случайным образом один объект, имеющей характеристику Х, то величина Х является случайной величиной. По определению, любая случайная величина имеет функцию распределения, которая обычно обозначается F(x).
Функция распределения
Функцией распределения вероятностей случайной величины Х называют функцию F(x), значение которой в точке х равно вероятности события X файл примера ):
В справке MS EXCEL Функцию распределения называют Интегральной функцией распределения (Cumulative Distribution Function, CDF).
Приведем некоторые свойства Функции распределения:
- Функция распределения F(x) изменяется в интервале [0;1], т.к. ее значения равны вероятностям соответствующих событий (по определению вероятность может быть в пределах от 0 до 1);
- Функция распределения – неубывающая функция;
- Вероятность того, что случайная величина приняла значение из некоторого диапазона [x1;x2): P(x1 Примечание: В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности дискретных случайных величин. Перечень этих функций приведен в статье Распределения случайной величины в MS EXCEL.
Непрерывные распределения и плотность вероятности
В случае непрерывного распределения случайная величина может принимать любые значения из интервала, в котором она определена. Т.к. количество таких значений бесконечно велико, то мы не можем, как в случае дискретной величины, сопоставить каждому значению случайной величины ненулевую вероятность (т.е. вероятность попадания в любую точку (заданную до опыта) для непрерывной случайной величины равна нулю). Т.к. в противном случае сумма вероятностей всех возможных значений случайной величины будет равна бесконечности, а не 1.
Выходом из этой ситуации является введение так называемой функции плотности распределения p(x). Чтобы найти вероятность того, что непрерывная случайная величина Х примет значение, заключенное в интервале (а; b), необходимо найти приращение функции распределения на этом интервале:
Как видно из формулы выше плотность распределения р(х) представляет собой производную функции распределения F(x), т.е. р(х) = F’(x).
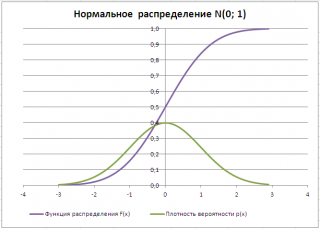
Типичный график функции плотности распределения для непрерывной случайно величины приведен на картинке ниже (зеленая кривая):
Примечание: В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности непрерывных случайных величин. Перечень этих функций приведен в статье Распределения случайной величины в MS EXCEL.
В литературе Функция плотности распределения непрерывной случайной величины может называться: Плотность вероятности, Плотность распределения, англ. Probability Density Function (PDF).
Чтобы все усложнить, термин Распределение (в литературе на английском языке — Probability Distribution Function или просто Distribution) в зависимости от контекста может относиться как Интегральной функции распределения, так и кее Плотности распределения.
Из определения функции плотности распределения следует, что p(х)>=0. Следовательно, плотность вероятности для непрерывной величины может быть, в отличие от Функции распределения, больше 1. Например, для непрерывной равномерной величины, распределенной на интервале [0; 0,5] плотность вероятности равна 1/(0,5-0)=2. А для экспоненциального распределения с параметром лямбда=5, значение плотности вероятности в точке х=0,05 равно 3,894. Но, при этом можно убедиться, что вероятность на любом интервале будет, как обычно, от 0 до 1.
Напомним, что плотность распределения является производной от функции распределения, т.е. «скоростью» ее изменения: p(x)=(F(x2)-F(x1))/Dx при Dx стремящемся к 0, где Dx=x2-x1. Т.е. тот факт, что плотность распределения >1 означает лишь, что функция распределения растет достаточно быстро (это очевидно на примере экспоненциального распределения).
Примечание: Площадь, целиком заключенная под всей кривой, изображающей плотность распределения, равна 1.
Примечание: Напомним, что функцию распределения F(x) называют в функциях MS EXCEL интегральной функцией распределения. Этот термин присутствует в параметрах функций, например в НОРМ.РАСП (x; среднее; стандартное_откл; интегральная). Если функция MS EXCEL должна вернуть Функцию распределения, то параметр интегральная, д.б. установлен ИСТИНА. Если требуется вычислить плотность вероятности, то параметр интегральная, д.б. ЛОЖЬ.
Примечание: Для дискретного распределения вероятность случайной величине принять некое значение также часто называется плотностью вероятности (англ. probability mass function (pmf)). В справке MS EXCEL плотность вероятности может называть даже «функция вероятностной меры» (см. функцию БИНОМ.РАСП() ).
Вычисление плотности вероятности с использованием функций MS EXCEL
Понятно, что чтобы вычислить плотность вероятности для определенного значения случайной величины, нужно знать ее распределение.
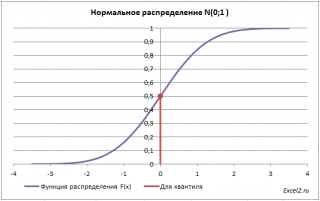
Найдем плотность вероятности для стандартного нормального распределения N(0;1) при x=2. Для этого необходимо записать формулу =НОРМ.СТ.РАСП(2;ЛОЖЬ) =0,054 или =НОРМ.РАСП(2;0;1;ЛОЖЬ) .
Напомним, что вероятность того, что непрерывная случайная величина примет конкретное значение x равна 0. Для непрерывной случайной величины Х можно вычислить только вероятность события, что Х примет значение, заключенное в интервале (а; b).
Вычисление вероятностей с использованием функций MS EXCEL
1) Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению (см. картинку выше), приняла положительное значение. Согласно свойству Функции распределения вероятность равна F(+∞)-F(0)=1-0,5=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу =НОРМ.СТ.РАСП(9,999E+307;ИСТИНА) -НОРМ.СТ.РАСП(0;ИСТИНА) =1-0,5.
Вместо +∞ в формулу введено значение 9,999E+307= 9,999*10^307, которое является максимальным числом, которое можно ввести в ячейку MS EXCEL (так сказать, наиболее близкое к +∞).
2) Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению, приняла отрицательное значение. Согласно определения Функции распределения, вероятность равна F(0)=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу =НОРМ.СТ.РАСП(0;ИСТИНА) =0,5.
3) Найдем вероятность того, что случайная величина, распределенная по стандартному нормальному распределению, примет значение, заключенное в интервале (0; 1). Вероятность равна F(1)-F(0), т.е. из вероятности выбрать Х из интервала (-∞;1) нужно вычесть вероятность выбрать Х из интервала (-∞;0). В MS EXCEL используйте формулу =НОРМ.СТ.РАСП(1;ИСТИНА) — НОРМ.СТ.РАСП(0;ИСТИНА) .
Все расчеты, приведенные выше, относятся к случайной величине, распределенной по стандартному нормальному закону N(0;1). Понятно, что значения вероятностей зависят от конкретного распределения. В статье Распределения случайной величины в MS EXCEL приведены распределения, для которых в MS EXCEL имеются соответствующие функции, позволяющие вычислить вероятности.
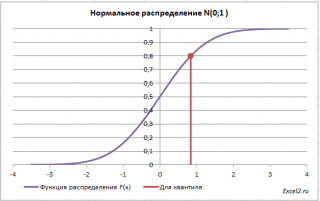
Обратная функция распределения (Inverse Distribution Function)
Вспомним задачу из предыдущего раздела: Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению, приняла отрицательное значение.
Вероятность этого события равна 0,5.
Теперь решим обратную задачу: определим х, для которого вероятность, того что случайная величина Х примет значение =НОРМ.СТ.ОБР(0,5) =0.
Однозначно вычислить значение случайной величины позволяет свойство монотонности функции распределения.
Обратите внимание, что для вычисления обратной функции мы использовали именно функцию распределения, а не плотность распределения. Поэтому, в аргументах функции НОРМ.СТ.ОБР() отсутствует параметр интегральная, который подразумевается. Подробнее про функцию НОРМ.СТ.ОБР() см. статью про нормальное распределение.
Обратная функция распределения вычисляет квантили распределения, которые используются, например, при построении доверительных интервалов. Т.е. в нашем случае число 0 является 0,5-квантилем нормального распределения. В файле примера можно вычислить и другой квантиль этого распределения. Например, 0,8-квантиль равен 0,84.
В англоязычной литературе обратная функция распределения часто называется как Percent Point Function (PPF).
Примечание: При вычислении квантилей в MS EXCEL используются функции: НОРМ.СТ.ОБР() , ЛОГНОРМ.ОБР() , ХИ2.ОБР(), ГАММА.ОБР() и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье Распределения случайной величины в MS EXCEL.
События, характеризующие данные, могут носить случайный характер и появляться с разной вероятностью.
Вероятность события p есть отношение числа благоприятных исходов m к числу всех возможных исходов n этого события: p=m/n. Например, вероятность появления туза в наугад выбранной карте из колоды в 52 карты равна 4/52=0.0769, так как m=4, а n=52.
Если известно соответствие между появлениями (величинами) x1, x2, …, xn случайного события (переменной) X и соответствующими вероятностями их реализации p1, p2, …, pn, то говорят, что известен закон распределения случайной величины F(x). Большинство встречающихся на практике распределений вероятностей реализовано в Excel.
Распределения вероятностей имеют числовые характеристики.
Функции Excel для вычисления числовых характеристик распределения вероятностей. Они входят в группу Статистические. При вычислении функций в качестве случайных величин используйте следующие значения:
Математическое ожидание случайной величины (среднее арифметическое), характеризующее центр распределения вероятностей, вычисляется функцией СРЗНАЧ. СРЗНАЧ(A1:A7) = 9.
Дисперсия, характеризует разброс случайной величины относительно центра распределения вероятностей и вычисляется функцией ДИСПР. ДИСПР(A1:A7) = 4.857.
Среднеквадратичное отклонение есть квадратный корень из дисперсии, характеризует разброс случайной величины в единицах случайной величины и вычисляется функцией СТАНДОТКЛОНП. СТАНДОТКЛОНП(A1:A7) = 2.203893.
Квантиль случайной величины с законом распределения F(x) есть значение случайной величины x при заданной вероятности p., т.е. есть решение уравнения F(x)=p. Медиана есть квантиль с вероятностью p=0.5.
Excel, вместо квантилей содержит функции вычисления х для определенных уровней р: квартили (кварта – четверть), децили (дециль – десятая часть), персентили (персент – процент). Различают нижний квартиль с вероятностью p=0.25 и верхний квартиль с вероятностью p=0.75. Децили это квантили с вероятностью 0.1, 0.2, …, 0.9.
Функцию КВАРТИЛЬ используют, чтобы разбить данные на группы. В качестве второго аргумента указывают уровень (четверть), для которого нужно вернуть решение: 0 – минимальное значение распределения, 1 – первый, нижний квартиль, 2 – медиана, 3 – третий, верхний квартиль, 4 – максимальное значение. Например, КВАРТИЛЬ(A1:A7;3) = 10, т.е. 75% всех значений меньше 10, КВАРТИЛЬ(A1:A7;2) = 9.
Функция ПЕРСЕНТИЛЬ вычисляет квантиль указанного уровня вероятности и используется для определения порога приемлемости значений. В качестве второго аргумента указывают уровень 0.1, 0.2, …, 0.9. ПЕРСЕНТИЛЬ(A1:A7;0,9) = 11.8, т.е. 90% всех значений меньше 11.8.
Excel содержит инструмент Ранг и персентиль, который на основе набора данных формирует выходную таблицу, содержащую порядковый и процентный ранги для каждого значения в наборе данных. См. справку по F1. Ниже приведен пример установки надстройки Пактет анализа
Распределения вероятностей, реализованные в Excel.
Каждый закон распределения описывает процессы разной вероятностной природы и характеризуется специфическими параметрами:
равномерное распределение – n случайных чисел выпадает с одной и той же вероятностью p=1/n; характеризуется нижней и верхней границей; примером является появление чисел 1, 2, …, 6 при бросании игральной кости (p=1/6);
биномиальное распределение моделирует взаимосвязь числа успешных испытаний m и вероятностей успеха каждого испытания p при общем количестве испытаний n — функции БИНОМРАСП и КРИТБИНОМ;
нормальное (гауссово) распределение описывает процессы, в которых на результат воздействует большое число независимых случайных факторов, среди которых нет сильно выделяющихся – функции НОРМРАСП, НОРМСТРАСП, НОРМОБР, НОРМСТОБР и НОРМАЛИЗАЦИЯ;
распределение Пуассона, предсказывает число случайных событий на определенном отрезке времени или на определенном пространстве, позволяет аппроксимировать биномиальное распределение – функция ПУАССОН;
экспоненциальное (показательное) распределение, моделирует временные задержки между событиями, описывает процессы в задачах массового обслуживания и в задачах с «временем жизни» — ЭКСПРАСП;
распределение хи-квадрат, связано с нормальным, возвращает одностороннюю вероятность распределения и используется для сравнения предполагаемых и наблюдаемых значений – функция ХИ2РАСП;
распределение Стьюдента, связано с нормальным, возвращает вероятность для t-распределения Стьюдента и используется для проверки гипотез при малом объеме выборки – функция СТЬЮДРАСП;
F-распределение (Фишера), связано с нормальным и может быть использовано в F-тесте, который сравнивает степени разброса двух множеств данных – fраспобр;
гамма-распределение используется для изучения случайных величин, имеющих асимметричное распределение, в теории очередей – функция ГАММАРАСП;
а также другие распределения – функции БЕТАРАСП, ВЕЙБУЛЛ, ОТРБИНОМРАСП, ГИПЕРГЕОМЕТ, ЛОГНОРМРАСП и др.
Биномиальное распределение характеризуется числом успешных испытаний m, вероятностью успеха каждого испытания p и общим количеством испытаний n. Классическим примером использования биномиального распределения является выборочный контроль качества больших партий товара, изделий в торговле, на производстве, когда сплошная проверка невозможна. Из партии выбирают n образцов и регистрируют число бракованных m. Бракованными могут быть 1, 2, … , n образцов, но вероятности реального числа бракованных будут различными. Если контрольная вероятность брака ниже допустимой вероятности, то можно гарантировать достаточное качество всей партии.
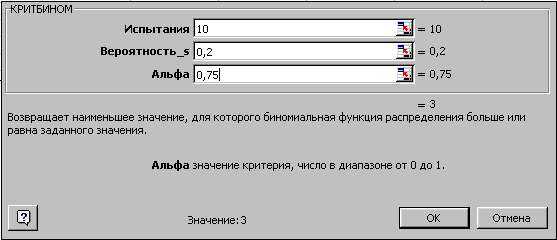
В Excel функция БИНОМРАСП вычисляет вероятность отдельного значения распределения по заданным m, n и р, а функция КРИТБИНОМ – случайное число по заданной вероятности. Обычно функция КРИТБИНОМ используется для определения наибольшего допустимого числа брака.
В качестве примера построим график плотности вероятности биномиального распределения для n=10 (1, 2, …, 10) и p=0.2. Введите исходные данные, как показано на рисунке:
Далее в ячейку В4 введите статистическую функцию БИНОМРАСП и заполните ее параметры как показано на рисунке:
Здесь параметр Число_s есть число успешных испытаний m, Испытания – число независимых испытаний n, Вероятность_s – вероятность успеха каждого испытания p. Параметр Интегральный равен 0, если требуется получить плотность распределения (вероятность для значения m), и равен 1, если требуется получить вероятность с накоплением (вероятность того, что число успешных испытаний не меньше значения аргумента Число_s).
Формулу из В4 размножьте в ячейки В5:В13. Ниже показан результат:
В колонке В вычислены вероятности успешных испытаний m=1, 2, …, 10. Теперь по диапазону В4:В13 постройте график или гистограмму биномиальной функции плотности распределения – результат на рисунке. Поэкспериментируйте, изменяя значение вероятности в ячейке В1: 0.3, 0.4, 0.8, проследите за изменениями формы графика.
Для иллюстрации функции КРИТБИНОМ используем предыдущий пример – необходимо найти число m, для которого вероятность интегрального распределения больше или равна 0.75. Вызовите функцию КРИТБИНОМ и заполните параметры. Вы должны получить значение 3. Это означает, что при вероятности интегрального распределения >= 0.75 будет не менее трех (m>=3) успешных испытаний.
Нормальное распределение характеризуется средним арифметическим (математическим ожиданием) m и стандартным (среднеквадратичным) отклонением r. Дисперсия равна r 2 . Краткое обозначение распределения N(m,r 2 ). График нормального распределения симметричен относительно центра распределения (точки m), чем меньше r, тем больше вероятность появления случайной величины. В пределы [m—r,m+r] нормально распределенная случайная величина попадает с вероятностью 0,683 в пределы [m-2r,m+2r] — с вероятностью 0,955 и т.д.
При m=0 и r=1 нормальное распределение называется стандартным или нормированным – N(0,1).
Нормальное распределение имеет очень широкий круг приложений. В качестве примера построим график плотности вероятностей нормального распределения при m=15 и r=1,5 в диапазоне [m-3r,m+3r] c шагом 0,5. Результат показан на рисунке.
Выполните следующие действия:
в ячейку А4 введите формулу =B1-3*B2, в ячейку А5 формулу =A4+B$3 и размножьте ее по ячейку А22;
в ячейку В4 введите функцию НОРМРАСП из группы Статистические – параметры заполните как на рисунке;
размножьте формулу из ячейки В4 по ячейку В22 и по диапазону В4:В22 постройте график; на 2-ом шаге мастера диаграмм в закладке Ряд введите подписи к оси х из диапазона А4:А22.
|
anton626666 Пользователь Сообщений: 4 |
нужно выбрать из диапазона чисел наиболее вероятное. Помогите, времени совсем нет. |
|
McCinly Пользователь Сообщений: 278 |
=МОДА(диапазон_ячеек) — Возвращает наиболее часто встречающееся или повторяющееся значение в массиве или интервале данных, наверное оно же и наиболее вероятное. |
|
anton626666 Пользователь Сообщений: 4 |
Моду пробовал. Она выдает действительно наиболее часто встречающееся значение, а мне надо наиболее вероятное рассчитанное. |
|
ждите телепатов или пример давайте |
|
|
anton626666 Пользователь Сообщений: 4 |
Нужно что то наподобие среднего значения, но по теории вероятности (мат. ожидание). Есть 20 чисел от 1 до 10. Надо найти (посчитать) наиболее вероятное. |
|
Libera Пользователь Сообщений: 112 |
{quote}{login=anton626666}{date=15.02.2010 06:40}{thema=}{post}Нужно что то наподобие среднего значения, но по теории вероятности (мат. ожидание). Есть 20 чисел от 1 до 10. Надо найти (посчитать) наиболее вероятное.{/post}{/quote} |
|
anton626666 Пользователь Сообщений: 4 |
А если из каждое число встречается только один раз? Как найти наиболее вероятное значение из диапазона? |
|
Юрий М Модератор Сообщений: 60585 Контакты см. в профиле |
{quote}{login=anton626666}{date=15.02.2010 07:17}{thema=}{post}А если из каждое число встречается только один раз? Как найти наиболее вероятное значение из диапазона?{/post}{/quote} |
|
{quote}{login=anton626666}{date=15.02.2010 07:17}{thema=}{post}А если из каждое число встречается только один раз? Как найти наиболее вероятное значение из диапазона?{/post}{/quote}среднее арифметическое. |
|
|
{quote}{login=anton626666}{date=15.02.2010 07:17}{thema=}{post}А если из каждое число встречается только один раз? Как найти наиболее вероятное значение из диапазона?{/post}{/quote} |
|
|
Igor67 Пользователь Сообщений: 3729 |
{quote}{login=anton626666}{date=15.02.2010 07:17}{thema=}{post}А если из каждое число встречается только один раз? Как найти наиболее вероятное значение из диапазона?{/post}{/quote} ИМХО 50/50 или выпадет или нет:) |
|
{quote}{login=anton626666}{date=15.02.2010 07:17}{thema=}{post}А если из каждое число встречается только один раз? Как найти наиболее вероятное значение из диапазона?{/post}{/quote} у вас было написано что диапазон из 20 чисел формирующися числами от 1 до 10. В такой ситуации невозможно чтобы ни одно число не повторялось |
|
|
vikttur Пользователь Сообщений: 47199 |
{quote}{login=anton626666}{date=15.02.2010 06:17}{thema=}{post}а мне надо наиболее вероятное рассчитанное.{/post}{/quote} |
|
Микки Пользователь Сообщений: 3280 |
#15 16.02.2010 11:55:56 {quote}{login=vikttur}{date=16.02.2010 11:47}{thema=Re: }{post}{quote}{login=anton626666}{date=15.02.2010 06:17}{thema=}{post}а мне надо наиболее вероятное рассчитанное.{/post}{/quote} |
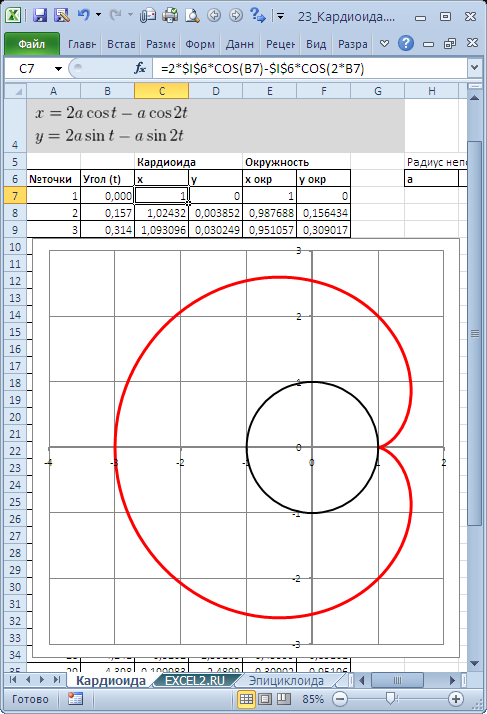
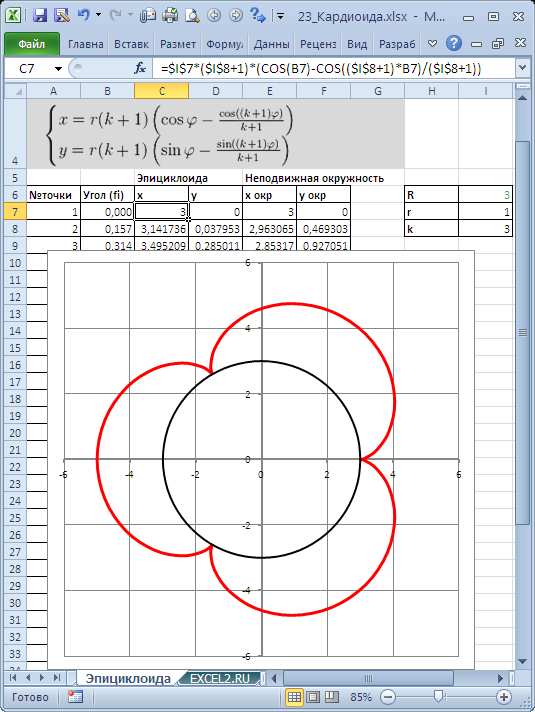
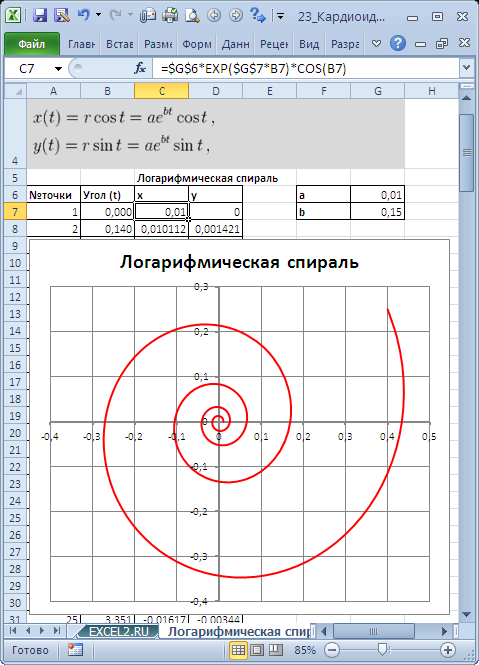
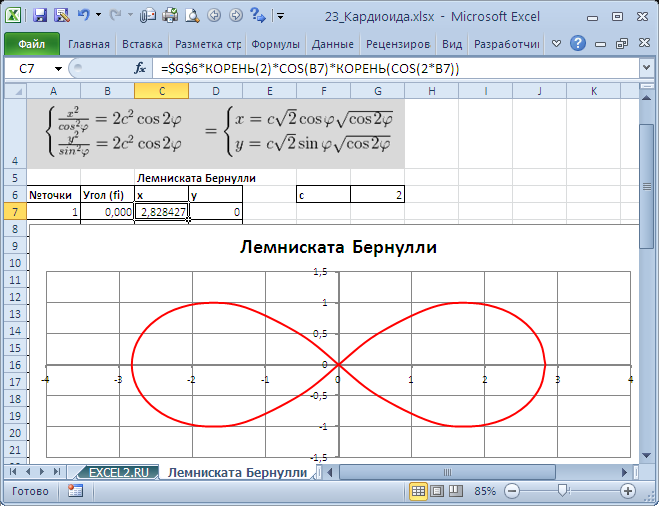
Плоские алгебраические кривые в EXCEL
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см. файл примера ):
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье Эллипс и окружность в MS EXCEL построены окружность и эллипс.
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Формула Бернулли в Excel
В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!
Схема независимых испытаний
В общем виде схема повторных независимых испытаний записывается в виде задачи:
Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.
Эта вероятность вычисляется по формуле Бернулли:
$$ P_n(k)=C_n^k cdot p^k cdot (1-p)^=C_n^k cdot p^k cdot q^. qquad(1) $$
Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:
- Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
- Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
- События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.
Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.
Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.
Формула Бернулли в Эксель
Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП() , выдающая определенную вероятность биномиального распределения.
Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0) .
Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).
Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:
Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):
- Событие произойдет в точности $k$ раз из $n$:
=БИНОМ.РАСП(k;n;p;0)
$$P_n(k)=C_n^k cdot p^k cdot q^$$ - Событие произойдет от $k_1$ до $k_2$ раз:
=БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
$$P_n(k_1le X le k_2)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не более $k_3$ раз:
=БИНОМ.РАСП(k_3;n;p;1)
$$P_n(0le X le k_3)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не менее $k_4$ раз:
=1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
$$P_n(k_4le X le n)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет хотя бы один раз:
=1-БИНОМ.РАСП(0;n;p;0)
$$P_n( X ge 1)=1-P_n(0)=1-q^$$ - Наивероятнейшее число наступлений события $m$:
=ОКРУГЛВВЕРХ(n*p-q;0)
$$np-q le m le np+p$$
Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.
Примеры решений задач
Рассмотрим решение типовых задач.
Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.
Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:
$$ P_7(5)=C_^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146. $$
Для вероятности 6 или 7 попаданий суммируем:
$$ P_7(6)+P_7(7)=C_^6 cdot 0,75^6 cdot 0,25^1+C_^7 cdot 0,75^7 cdot 0,25^0= \ = 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495. $$
А вот это решение в файле эксель:
Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?
Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_(k)=C_^k cdot 0,5^kcdot 0,5^=C_^k cdot 0,5^$$ Приступим к вычислениям:
$$1. P_(2)=C_^2 cdot 0,5^ = fraccdot 0,5^ approx 0,044.$$ $$2. P_(4)+P_(5)=C_^4 cdot 0,5^ + C_^5 cdot 0,5^=left( frac + frac right)cdot 0,5^ approx 0,451.$$ $$3. P_(0)+P_(1)+P_(2)=C_^0 cdot 0,5^ + C_^1 cdot 0,5^+ C_^2 cdot 0,5^=left( 1+10+ frac right)cdot 0,5^ approx 0,055.$$ $$4. P_(7)+P_(8)+P_(9)+P_(10)=\ = C_^7 cdot 0,5^ + C_^8 cdot 0,5^+ C_^9 cdot 0,5^+ C_^10 cdot 0,5^ =\=left(frac+ frac + 10 +1right)cdot 0,5^ approx 0,172.$$ $$5. P_(ge 1)=1-P_(0)=1-C_^0 cdot 0,5^ = 1- 0,5^ approx 0,999.$$
Наивероятнейшее число мальчиков найдем из неравенства:
$$ 10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, \ 4,5 le m le 5,5,\ m=5. $$
Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).
Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:
Видно, что ответы совпадают.
Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?
Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.
Изучение распределения Бернулли средствами Excel
Цель данной работы – изучить задачу теории вероятностей о повторении однородных независимых испытаний. Для небольшого числа испытаний n < 30 эта задача была разрешена Бернулли, при большем числе испытаний используются предельные формулы Пуассона и Лапласа. При использовании компьютера область применения исходной формулы Бернулли может быть расширена до n = 200, поэтому представляется возможность оценить точность предельных формул Пуассона – Лапласа. На практическом занятия осваиваются также приемы работы с электронной таблицей Excel – как организовать вычисления по формулам Бернулли, Пуассона, Лапласа; как строятся графики зависимостей и как эти графики форматируются к стандартному виду; как работать с большими таблицами и по заданному аргументу находить в таблице значение функции; и многое другое.
Изучение распределения Бернулли средствами Excel
Распределение Бернулли зависит от двух параметров n и p (q = 1 – p). На рабочем листе Exсel предлагается построить графики распределения при различных значениях параметра p (0 < p < 1) и при различных значениях другого параметра n (n = 10, 20, 30, 50). Эти графики позволят заметить характерные особенности распределения Бернулли. Кроме этого, полезно убедиться, что характеристики распределения правильно воспроизводятся известными формулами: M(m) = np, D(m) = npq. Далее полезно также убедиться в справедливости правила «3-х сигм»: M(m) – 3×sm< m < M(m) + 3×sm , где ; значения m, выходящие за пределы указанного интервала, маловероятны (их вероятность меньше 0,01).
Ниже приведен фрагмент рабочего листа таблицы Excel.
| A | B | C | D | E | F | G | H | I | J |
| Распределение Бернулли | |||||||||
| Pn(m)=n!/m!/(n-m)!*p^m*q^(n-m) | |||||||||
| Pn(m)=Pn(m-1)*(n-m+1)/m*p/q | Pn(0)=q^n | ||||||||
| n = | n = | n = | n = | n = | |||||
| p = | 0,1 | p = | 0,3 | p = | 0,5 | p = | 0,7 | p = | 0,9 |
| q = | 0,9 | q = | 0,7 | q = | 0,5 | q = | 0,3 | q = | 0,1 |
| M = | M = | M = | M = | M = | |||||
| D = | 0,9 | D = | 2,1 | D = | 2,5 | D = | 2,1 | D = | 0,9 |
| M-3Sm= | -1,84605 | M-3Sm= | -1,34741 | M-3Sm= | 0,256584 | M-3Sm= | 2,652587 | M-3Sm= | 6,15395 |
| M+3Sm= | 3,84605 | M+3Sm= | 7,347413 | M+3Sm= | 9,743416 | M+3Sm= | 11,34741 | M+3Sm= | 11,84605 |
| m | р=0,1 | m | р=0,3 | m | р=0,5 | m | р=0,7 | m | р=0,9 |
| 0,34868 | 0,02825 | 0,00098 | 5,9E-06 | 1E-10 | |||||
| 0,38742 | 0,12106 | 0,00977 | 0,00014 | 9E-09 | |||||
| 0,19371 | 0,23347 | 0,04395 | 0,00145 | 3,64E-07 | |||||
| 0,05740 | 0,26683 | 0,11719 | 0,00900 | 8,75E-06 | |||||
| 0,01116 | 0,20012 | 0,20508 | 0,03676 | 0,00014 | |||||
| 0,00149 | 0,10292 | 0,24609 | 0,10292 | 0,00149 | |||||
| 0,00014 | 0,03676 | 0,20508 | 0,20012 | 0,01116 | |||||
| 8,75E-06 | 0,00900 | 0,11719 | 0,26683 | 0,05740 | |||||
| 3,65E-07 | 0,00145 | 0,04395 | 0,23347 | 0,19371 | |||||
| 9E-09 | 0,00014 | 0,00977 | 0,12106 | 0,38742 | |||||
| 1E-10 | 5,9E-06 | 0,00098 | 0,02825 | 0,34868 |
Рассмотрим внимательно первый блок (столбцы A, B таблицы Excel).
В строках 5 и 6 задаем значения параметров n = 10, p = 0,1. В следующих строках вычисляем q = 1 – p, M = S m Pn(m), D = S m 2 Pn(m) – M^2, M-3Sm = M – 3*КОРЕНЬ(D), M+3Sm = M + 3*КОРЕНЬ(D). Последние 4 формулы можно набрать позже, когда будет заполнен диапазон B14:B24, содержащий значения Pn(m). Отметим полезный прием: в столбце А записываем текст и сдвигаем его вправо, а в столбце В – вычисляем числовое значение и сдвигаем его влево. Получается понятный комментарий к выполненным действиям. Лист Excel, помимо всего прочего, является отчетным документом, поэтому не стоит экономить на комментариях и заголовках. Из информации в строках 8 – 11 первого блока, видно, что, действительно, M = np = 10´0,1 = 1; D = npq = 10´0,1´0,9 = 0,9; и что все вероятные значения m не превзойдут 4.
Значения Pn(m) удобно вычислять по реккурентной формуле (эта формула приведена в строке 3 рабочего листа). Начальное значение Pn(0) = q n вычисляем в ячейке В14. При наборе реккурентной формулы в ячейке В15 следует зафиксировать (знаками $) неизменяемые значения n, p, q. Далее формула копируется ниже до ячейки В24.
Заполнив первый блок, копируем его несколько раз вправо и в новых блоках заменяем значение параметра p на p = 0,3; p = 0,5; p = 0,7; p = 0,9. Все автоматически пересчитывается. В блоках серым фоном выделены значения Pn(m), которые признаны значимыми по правилу «3-х сигм».
Теперь строим графики. Выделяем значения m вместе с заголовком в ячейке А13, далее при нажатой клавише Ctrl выделяем мышкой значения Pn(m) для p = 0,1; 0,3; 0,5; 0,7; 0,9. Выделять диапазоны надо вместе с заголовками в строке 13, тогда эти заголовки автоматически будут отображены в легенде (пояснениях к каждой линии на графике). Вызываем Мастер диаграмм, выбираем тип диаграммы – точечная, легенда – внизу, линии сетки – основные, заголовок: “Распределение Бернулли при разных p (n=10)”. В результате получаем следующий график, который почти не требует дополнительного форматирования:
Из этого графика видно, как меняется асимметрия распределения при увеличении параметра p: при p = 0,5 распределение симметричное, при p < 0,5 – распределение скошено влево (положительная асимметрия), а при p > 0,5 – скошено вправо (отрицательная асимметрия).
Как уже указывалось выше, заголовки из строки 13 автоматически переносятся в легенду диаграммы. Но тогда хотелось бы, чтобы они автоматически корректировались при изменении параметра p. Поэтому в качестве заголовка в ячейке В13 набрана формула =»р=»&ТЕКСТ(B9;»0,0″). Функция ТЕКСТ(Число;Формат) переводит в символьную форму значение p из ячейки В9; в тексте заголовка это число будет округлено до одного знака после запятой. Остальные заголовки в строке 13 корректируются автоматически при копировании.
Теперь переходим к изучению зависимости распределения Бернулли от второго параметра n. Скопируем все 5 готовых блоков вправо, начиная со столбца K, и заменим в новых блоках значения параметров: n = 10, 20, 30, 40, 50 и p = 0,1 (для всех новых блоков). Естественно, новые таблицы надо продлить вниз до строки 64 (они теперь будут иметь разную длину). Ненужную информацию можно скрыть с помощью условного форматирования. Так, таблица для n = 10 фактически обрывается на строке 24, поэтому можно сделать так, чтобы дальнейшие значения m и нулевые значения Pn(m) выводились серым цветом на белом фоне (тогда они почти не будут видны). Условный формат для колонки m задаем по условию:
Обратите внимание, что в ссылке на ячейку L8 зафиксирован только номер строки. Для колонки Pn(m) с заголовком n=10 условие будет более простое: значение равно 0 . При копировании отформатированного блока, копируются также все условные форматы.
Наконец, надо заменить заголовки в строке 13 на формулы =»n=»&ТЕКСТ(L8;»0″).
| K | L | M | N | O | P | Q | R | S | T |
| n = | n = | n = | n = | n = | |||||
| p = | 0,1 | p = | 0,1 | p = | 0,1 | p = | 0,1 | p = | 0,1 |
| q = | 0,9 | q = | 0,9 | q = | 0,9 | q = | 0,9 | q = | 0,9 |
| M = | M = | M = | M = | M = | |||||
| D = | 0,9 | D = | 1,8 | D = | 2,7 | D = | 3,6 | D = | 4,5 |
| M-3Sm= | -1,84605 | M-3Sm= | -2,02492 | M-3Sm= | -1,9295 | M-3Sm= | -1,6921 | M-3Sm= | -1,36396 |
| M+3Sm= | 3,84605 | M+3Sm= | 6,024922 | M+3Sm= | 7,929503 | M+3Sm= | 9,6921 | M+3Sm= | 11,36396 |
| m | n=10 | m | n=20 | m | n=30 | m | n=40 | m | n=50 |
| 0,348678 | 0,121577 | 0,042391 | 0,014781 | 0,005154 | |||||
| 0,387420 | 0,270170 | 0,141304 | 0,065693 | 0,028632 | |||||
| 0,193710 | 0,285180 | 0,227656 | 0,142334 | 0,077943 | |||||
| 0,057396 | 0,190120 | 0,236088 | 0,200323 | 0,138565 | |||||
| 0,01116 | 0,089779 | 0,177066 | 0,205887 | 0,180905 | |||||
| 0,001488 | 0,031921 | 0,102305 | 0,164710 | 0,184925 | |||||
| 0,000138 | 0,008867 | 0,047363 | 0,106756 | 0,154104 | |||||
| 8,75E-06 | 0,00197 | 0,018043 | 0,057614 | 0,107628 | |||||
| 3,65E-07 | 0,000356 | 0,005764 | 0,026407 | 0,064278 | |||||
| 9E-09 | 5,27E-05 | 0,001565 | 0,010432 | 0,033329 | |||||
| 1E-10 | 6,44E-06 | 0,000365 | 0,003593 | 0,015183 | |||||
| 6,51E-07 | 7,38E-05 | 0,001089 | 0,006135 | ||||||
| 5,42E-08 | 1,3E-05 | 0,000292 | 0,002215 | ||||||
| 3,71E-09 | 2E-06 | 7E-05 | 0,000719 | ||||||
| 2,06E-10 | 2,69E-07 | 1,5E-05 | 0,000211 | ||||||
| 9,15E-12 | 3,19E-08 | 2,89E-06 | 5,63E-05 | ||||||
| 3,18E-13 | 3,33E-09 | 5,01E-07 | 1,37E-05 | ||||||
| 8,31E-15 | 3,04E-10 | 7,86E-08 | 3,04E-06 | ||||||
| 1,54E-16 | 2,44E-11 | 1,12E-08 | 6,2E-07 | ||||||
| 1,8E-18 | 1,71E-12 | 1,44E-09 | 1,16E-07 | ||||||
| 1E-20 | 1,05E-13 | 1,68E-10 | 2E-08 |
Интересно, что хотя таблицы продолжаются до строки 64, фактически (согласно правилу «3-х сигм») их можно было оборвать на строке 25 (это отразится только на значениях M и D в строках 8, 9). Все готово для построения нового графика, из которого будет видно, как с увеличением n распределение Бернулли приближается к некой стандартной форме – к распределению Лапласа, или к, так называемому, нормальному закону распределения Гаусса.
Считается, что при n ³ 30 распределение уже практически нормальное. Этот вопрос еще будет обсуждаться ниже при изучении распределения Лапласа. Там же рассмотрим применение кумуляты.
Таблица формул Excel для теории вероятностей и статистики
Комбинаторика и вероятность
Ниже вы найдете основные формулы Excel, которые могут применяться при решении вероятностных задач и задач по комбинаторике.
Выдает случайное число в интервале от 0 до 1 (равномерно распределенное).
Выдает случайное число в заданном интервале.
Вычисляет отдельное значение биномиального распределения.
Определяет гипергеометрическое распределение.
Вычисляет значение нормальной функции распределения.
Выдает обратное нормальное распределение.
Выдает стандартное нормальное интегральное распределение.
Выдает обратное значение стандартного нормального распределения.
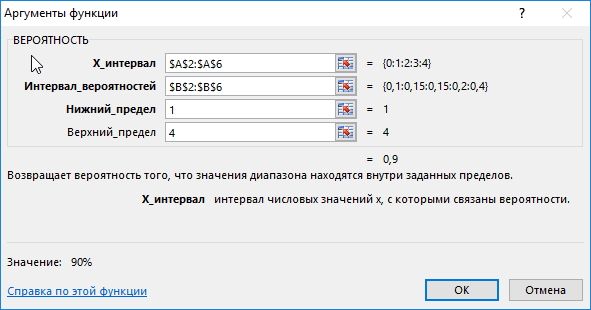
Определяет вероятность того, что значение из диапазона находится внутри заданных пределов.
Математическая статистика
При решении задач по математической статистике можно использовать те формулы, что перечислены выше, а также следующие (сгруппированы для удобства: обработка выборки, разные распределения, остальные формулы):
Обработка выборки: формулы Excel
| ЧИСЛКОМБ / COMBIN |
| ФАКТР / FACT |
| СЛЧИС / RAND |
| СЛУЧМЕЖДУ / RANDBETVEEN |
| БИНОМРАСП / BINOMDIST |
| ГИПЕРГЕОМЕТ / HYRGEOMDIST |
| НОРМРАСП / NORMDIST |
| НОРМОБР / NORMINV |
| НОРМСТРАСП / NORMSDIST |
| НОРМСТОБР / NORMSINV |
| ПЕРЕСТ / PERMUT |
| ВЕРОЯТНОСТЬ / PROB |
Вычисляет среднее абсолютных значений отклонений точек данных от среднего.
Вычисляет среднее арифметическое аргументов.
Вычисляет среднее геометрическое.
Вычисляет среднее гармоническое.
Определяет эксцесс множества данных.
Находит медиану заданных чисел.
Определяет значение моды множества данных.
Определяет квартиль множества данных.
Определяет асимметрию распределения.
Оценивает стандартное отклонение по выборке.
Оценивает дисперсию по выборке.
Законы распределений: формулы Excel
| СРОТКЛ / AVEDEV |
| СРЗНАЧ / AVERAGE |
| СРГЕОМ / GEOMEAN |
| СРГАРМ / HARMEAN |
| ЭКСЦЕСС / KURT |
| МЕДИАНА / MEDIAN |
| МОДА / MODE |
| КВАРТИЛЬ / QUARTILE |
| СКОС / SKEW |
| СТАНДОТКЛОН / STDEV |
| ДИСП / VAR |
Определяет интегральную функцию плотности бета-вероятности.
Определяет обратную функцию к интегральной функции плотности бета-вероятности.
Вычисляет одностороннюю вероятность распределения хи-квадрат.
Вычисляет обратное значение односторонней вероятности распределения хи-квадрат.
Находит экспоненциальное распределение.
Находит F-распределение вероятности.
Определяет обратное значение для F-распределения вероятности.
Находит преобразование Фишера.
Находит обратное преобразование Фишера.
Находит обратное гамма-распределение.
Выдает распределение Пуассона.
Выдает t-распределение Стьюдента.
Выдает обратное t-распределение Стьюдента.
Выдает распределение Вейбулла.
Другое (корреляция, регрессия и т.п.)
| БЕТАРАСП / BETADIST |
| БЕТАОБР / BETAINV |
| ХИ2РАСП / CHIDIST |
| ХИ2ОБР / CHIINV |
| ЭКСПРАСП / EXPONDIST |
| FРАСП / FDIST |
| FРАСПОБР / FINV |
| ФИШЕР / FISHER |
| ФИШЕРОБР / FISHERINV |
| ГАММАРАСП / GAMMADIST |
| ГАММАОБР / GAMMAINV |
| ПУАССОН / POISSON |
| СТЬЮДРАСП / TDIST |
| СТЬЮДРАСПОБР / TINV |
| ВЕЙБУЛЛ / WEIBULL |
Определяет доверительный интервал для среднего значения по генеральной совокупности.
Находит коэффициент корреляции между двумя множествами данных.
Подсчитывает количество чисел в списке аргументов.
Подсчитывает количество непустых ячеек, удовлетворяющих заданному условию внутри диапазона.
Определяет ковариацию, то есть среднее произведений отклонений для каждой пары точек.
Вычисляет значение линейного тренда.
Находит параметры линейного тренда.
Определяет коэффициент корреляции Пирсона.
Справочный файл по формулам Excel
Нужна шпаргалка по функциям Excel под рукой? Скачивайте файл: Математические и статистические формулы Excel
Полезные ссылки
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике:
Функция распределения и плотность вероятности в EXCEL
Даны определения Функции распределения случайной величины и Плотности вероятности непрерывной случайной величины. Эти понятия активно используются в статьях о статистике сайта www.excel2.ru . Рассмотрены примеры вычисления Функции распределения и Плотности вероятности с помощью функций MS EXCEL .
Введем базовые понятия статистики, без которых невозможно объяснить более сложные понятия.
Генеральная совокупность и случайная величина
Пусть у нас имеется генеральная совокупность (population) из N объектов, каждому из которых присуще определенное значение некоторой числовой характеристики Х.
Примером генеральной совокупности (ГС) может служить совокупность весов однотипных деталей, которые производятся станком.
Поскольку в математической статистике, любой вывод делается только на основании характеристики Х (абстрагируясь от самих объектов), то с этой точки зрения генеральная совокупность представляет собой N чисел, среди которых, в общем случае, могут быть и одинаковые.
В нашем примере, ГС — это просто числовой массив значений весов деталей. Х – вес одной из деталей.
Если из заданной ГС мы выбираем случайным образом один объект, имеющей характеристику Х, то величина Х является случайной величиной . По определению, любая случайная величина имеет функцию распределения , которая обычно обозначается F(x).
Функция распределения
Функцией распределения вероятностей случайной величины Х называют функцию F(x), значение которой в точке х равно вероятности события X файл примера ):
В справке MS EXCEL Функцию распределения называют Интегральной функцией распределения ( Cumulative Distribution Function , CDF ).
Приведем некоторые свойства Функции распределения:
- Функция распределения F(x) изменяется в интервале [0;1], т.к. ее значения равны вероятностям соответствующих событий (по определению вероятность может быть в пределах от 0 до 1);
- Функция распределения – неубывающая функция;
- Вероятность того, что случайная величина приняла значение из некоторого диапазона [x1;x2): P(x 1 Примечание : В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности дискретных случайных величин. Перечень этих функций приведен в статье Распределения случайной величины в MS EXCEL .
Непрерывные распределения и плотность вероятности
В случае непрерывного распределения случайная величина может принимать любые значения из интервала, в котором она определена. Т.к. количество таких значений бесконечно велико, то мы не можем, как в случае дискретной величины, сопоставить каждому значению случайной величины ненулевую вероятность (т.е. вероятность попадания в любую точку (заданную до опыта) для непрерывной случайной величины равна нулю). Т.к. в противном случае сумма вероятностей всех возможных значений случайной величины будет равна бесконечности, а не 1. Выходом из этой ситуации является введение так называемой функции плотности распределения p(x) . Чтобы найти вероятность того, что непрерывная случайная величина Х примет значение, заключенное в интервале (а; b), необходимо найти приращение функции распределения на этом интервале:
Как видно из формулы выше плотность распределения р(х) представляет собой производную функции распределения F(x), т.е. р(х) = F’(x).
Типичный график функции плотности распределения для непрерывной случайно величины приведен на картинке ниже (зеленая кривая):
Примечание : В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности непрерывных случайных величин. Перечень этих функций приведен в статье Распределения случайной величины в MS EXCEL .
В литературе Функция плотности распределения непрерывной случайной величины может называться: Плотность вероятности, Плотность распределения, англ. Probability Density Function (PDF) .
Чтобы все усложнить, термин Распределение (в литературе на английском языке — Probability Distribution Function или просто Distribution ) в зависимости от контекста может относиться как Интегральной функции распределения, так и кее Плотности распределения.
Из определения функции плотности распределения следует, что p(х)>=0. Следовательно, плотность вероятности для непрерывной величины может быть, в отличие от Функции распределения, больше 1. Например, для непрерывной равномерной величины , распределенной на интервале [0; 0,5] плотность вероятности равна 1/(0,5-0)=2. А для экспоненциального распределения с параметром лямбда =5, значение плотности вероятности в точке х=0,05 равно 3,894. Но, при этом можно убедиться, что вероятность на любом интервале будет, как обычно, от 0 до 1.
Напомним, что плотность распределения является производной от функции распределения , т.е. «скоростью» ее изменения: p(x)=(F(x2)-F(x1))/Dx при Dx стремящемся к 0, где Dx=x2-x1. Т.е. тот факт, что плотность распределения >1 означает лишь, что функция распределения растет достаточно быстро (это очевидно на примере экспоненциального распределения ).
Примечание : Площадь, целиком заключенная под всей кривой, изображающей плотность распределения , равна 1.
Примечание : Напомним, что функцию распределения F(x) называют в функциях MS EXCEL интегральной функцией распределения . Этот термин присутствует в параметрах функций, например в НОРМ.РАСП (x; среднее; стандартное_откл; интегральная ). Если функция MS EXCEL должна вернуть Функцию распределения, то параметр интегральная , д.б. установлен ИСТИНА. Если требуется вычислить плотность вероятности , то параметр интегральная , д.б. ЛОЖЬ.
Примечание : Для дискретного распределения вероятность случайной величине принять некое значение также часто называется плотностью вероятности (англ. probability mass function (pmf)). В справке MS EXCEL плотность вероятности может называть даже «функция вероятностной меры» (см. функцию БИНОМ.РАСП() ).
Вычисление плотности вероятности с использованием функций MS EXCEL
Понятно, что чтобы вычислить плотность вероятности для определенного значения случайной величины, нужно знать ее распределение.
Найдем плотность вероятности для стандартного нормального распределения N(0;1) при x=2. Для этого необходимо записать формулу =НОРМ.СТ.РАСП(2;ЛОЖЬ) =0,054 или =НОРМ.РАСП(2;0;1;ЛОЖЬ) .
Напомним, что вероятность того, что непрерывная случайная величина примет конкретное значение x равна 0. Для непрерывной случайной величины Х можно вычислить только вероятность события, что Х примет значение, заключенное в интервале (а; b).
Вычисление вероятностей с использованием функций MS EXCEL
1) Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению (см. картинку выше), приняла положительное значение. Согласно свойству Функции распределения вероятность равна F(+∞)-F(0)=1-0,5=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу =НОРМ.СТ.РАСП(9,999E+307;ИСТИНА) -НОРМ.СТ.РАСП(0;ИСТИНА) =1-0,5. Вместо +∞ в формулу введено значение 9,999E+307= 9,999*10^307, которое является максимальным числом, которое можно ввести в ячейку MS EXCEL (так сказать, наиболее близкое к +∞).
2) Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению , приняла отрицательное значение. Согласно определения Функции распределения, вероятность равна F(0)=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу =НОРМ.СТ.РАСП(0;ИСТИНА) =0,5.
3) Найдем вероятность того, что случайная величина, распределенная по стандартному нормальному распределению , примет значение, заключенное в интервале (0; 1). Вероятность равна F(1)-F(0), т.е. из вероятности выбрать Х из интервала (-∞;1) нужно вычесть вероятность выбрать Х из интервала (-∞;0). В MS EXCEL используйте формулу =НОРМ.СТ.РАСП(1;ИСТИНА) — НОРМ.СТ.РАСП(0;ИСТИНА) .
Все расчеты, приведенные выше, относятся к случайной величине, распределенной по стандартному нормальному закону N(0;1). Понятно, что значения вероятностей зависят от конкретного распределения. В статье Распределения случайной величины в MS EXCEL приведены распределения, для которых в MS EXCEL имеются соответствующие функции, позволяющие вычислить вероятности.
Обратная функция распределения (Inverse Distribution Function)
Вспомним задачу из предыдущего раздела: Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению, приняла отрицательное значение.
Вероятность этого события равна 0,5.
Теперь решим обратную задачу: определим х, для которого вероятность, того что случайная величина Х примет значение =НОРМ.СТ.ОБР(0,5) =0.
Однозначно вычислить значение случайной величины позволяет свойство монотонности функции распределения.
Обратите внимание, что для вычисления обратной функции мы использовали именно функцию распределения , а не плотность распределения . Поэтому, в аргументах функции НОРМ.СТ.ОБР() отсутствует параметр интегральная , который подразумевается. Подробнее про функцию НОРМ.СТ.ОБР() см. статью про нормальное распределение .
Обратная функция распределения вычисляет квантили распределения , которые используются, например, при построении доверительных интервалов . Т.е. в нашем случае число 0 является 0,5-квантилем нормального распределения . В файле примера можно вычислить и другой квантиль этого распределения. Например, 0,8-квантиль равен 0,84.
В англоязычной литературе обратная функция распределения часто называется как Percent Point Function (PPF).
Примечание : При вычислении квантилей в MS EXCEL используются функции: НОРМ.СТ.ОБР() , ЛОГНОРМ.ОБР() , ХИ2.ОБР(), ГАММА.ОБР() и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье Распределения случайной величины в MS EXCEL .
Функция ВЕРОЯТНОСТЬ для расчета вероятности событий в Excel
Очень часто при работе в Excel необходимо использовать вычисления вероятности появления некоторого события. Для этого используется статистическая функция ВЕРОЯТНОСТЬ.
Примеры использования функции вероятность для расчетов в Excel
Стоит отметить, что используются часто в Excel и другие статистические функции, к примеру:
Функция выполняет вычисление вероятности того, что значения с интервала находятся в заданных пределах. В случае, если верхний предел не будет задан, то будет возвращена вероятность того, что значения аргумента x_интервал будет равно значению аргумента под названием нижний_предел.
Вычисление процента вероятности события в Excel
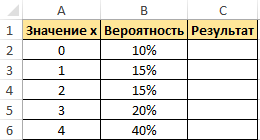
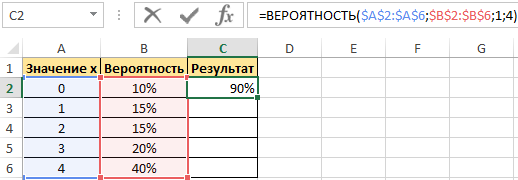
Пример 1. Дана таблица диапазона числовых значений, а также вероятностей, которые им соответствуют:
Необходимо при использовании данной статистической функции вычислить вероятность события, что значение с указанного интервала входит в интервал [1;4].
Для этого введем функцию со следующими аргументами:
- х_интервал – это начальные данные (0, …, 4);
- интервал вероятностей является множеством вероятностей для начальных данных (0,15; 0,1; 0,15; 0,2; 0,4);
- нижний предел равен значению 1;
- верхний предел равен 4.
В результате выполненных вычислений получим:
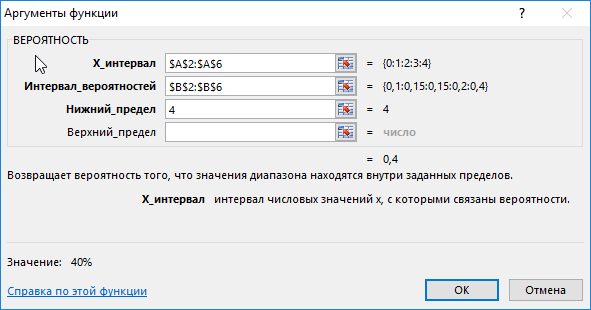
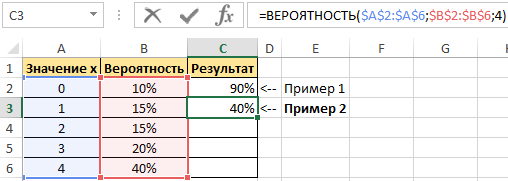
Пример 2. В условии предыдущего примера нужно вычислить вероятность события «значение х равно 4».
Введем в ячейку С3 введем функцию с такими аргументами:
- х_интервал – начальные параметры (0, …, 4);
- интервал вероятностей – совокупность вероятностей для параметров (0,1; 0,15; 0,2; 0,15; 0,4);
- нижний предел – 4;
В данном примере верхний предел не указан, поскольку необходимо конкретное значение вероятности, а именно для значения 4.
Функция ВЕРОЯТНОСТЬ при нескольких условиях интервалов
Пример 3. В условии примера 1 нужно вычислить вероятность того, что значения интервала [0; 4] будут находится находятся внутри интервалов [0;1] и [3;4].
Описание формул аналогичные предыдущим примерам.
В результате выполненных вычислений получим:
Таким образом составив формулу можно с помощью данной функции вычислить процент вероятности при нескольких условиях.
Решение задач на вычисление вероятности в Excel
Пример 4.В партии 20 изделий, из них 5 бракованных. Найти вероятность того, что в выборке из 4 изделий ровно одно бракованное.
Решение. В данной задаче, прежде всего, определим значения параметров: число_успехов_ в_ выборке = 1; размер_ выборки = 4; число_ успехов_ в_ совокупности = 5; размер_ совокупности = 20.
Искомую вероятность можно рассчитать с помощью функции =ГИПЕРГЕОМЕТ(1; 4; 5; 20), которая дает значение 0,4696.
Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно событияА.
Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность события А в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность ненаступления события А в каждом испытании также постоянна и равна q = 1 – р.
Вероятность того, что при n повторных независимых испытаниях событие А осуществится ровно k раз вычисляется по формуле Бернулли: .
Для нахождения наиболее вероятного числа успехов k по заданным n и р можно воспользоваться неравенствами np – q £ k£ np + p или правилом: если число np + p не целое, то k равно целой части этого числа.
В случае, если n велико, р мало, а , используют асимптотическую формулу Пуассона вычисления вероятности наступления события А ровно k раз при n повторных независимых испытаниях:
.
Пример 5. Вероятность того, что расход электроэнергии на протяжении одних суток не превысит установленной нормы, равна р = 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Решение. Вероятность нормального расхода электроэнергии на протяжении каждых из 6 суток постоянна и равна p = 0,75. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q = 1— р = 1 — 0,75 = 0,25. Искомая вероятность по формуле Бернулли равна = 0,297. Для вычисления в Excel используем формулу =БИНОМРАСП(4; 6; 0,75; 0), которая дает значение 0,297. При этом определены следующие значения параметров: число_ успехов = 4; число_ испытаний = 6; вероятность_ успеха = 0,75; интегральная = 0. Подробно с синтаксисом функции БИНОМРАСП можно ознакомиться с помощью справки.
Пример 6. Телефонная станция обслуживает 400 абонентов. Для каждого абонента вероятность того, что в течение часа он позвонит на станцию, равна 0,01. Найти вероятность, что в течение часа ровно 5 абонентов позвонят на станцию.
Решение.Так как р = 0,01 мало и n = 400 велико, то будем пользоваться приближенной формулой Пуассона при l = 400 × 0,01 = 4. Тогда Р400(5) » » 0,156293. Для вычисления в Excel используем формулу =ПУАССОН(5; 4; 0), которая дает значение 0,156293. При этом определены следующие значения параметров: количество_ событий = 5; среднее(λ) = 4; интегральная = 0. Подробно с синтаксисом функции ПУАССОН можно ознакомиться в справке.
В случае, когда число повторных испытаний большое и формула Бернулли неприменима, используют формулы Лапласа.
Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие А появится в n испытаниях ровно k раз, приближенно равна (тем точнее, чем больше n) значению функции

.
Имеются таблицы, в которых помещены значения функции .
Интегральная теорема Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие А появится в n испытаниях от k1 до k2 раз, приближенно равна определенному интегралу:

.
При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами для интеграла 
.
Пример 7. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.
Решение. По условию n = 400; k = 80; р = 0,2; q = 0,8. Воспользуемся асимптотической формулой Лапласа: 

. Для вычисления в Excel используем формулу =НОРМРАСП(80; 80; 8; 0), которая дает значение 0,04986. При этом определены следующие значения параметров: k = 80; среднее= np = 80; стандартное_откл =

= 8, интегральная = 0. Подробно с синтаксисом функции НОРМРАСП можно ознакомиться с помощью справки.
Пример 8. Вероятность того, что деталь не прошла проверку ОТК, равна 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
Решение.Воспользуемся интегральной формулой Лапласа: n = 400; k1= 70; k2=100; р = 0,2; q = 0,8; 
является нечетной, то P400(70; 100) = Ф(2,5)+ + Ф(1,25) = 0,4938 + 0,3944 = 0,8882.
Для вычисления в Excel используем формулу нормального распределения =НОРМРАСП(100; 80; 8; 1) — НОРМРАСП(70; 80; 8; 1), которая дает значение 0,8882. При этом параметр интегральная = 1, остальные значения параметров определяются аналогично примеру, рассмотренному выше.
Оценка статьи:
Загрузка…
Adblock
detector
| ДОВЕРИТ / CONFIDENCE |
| КОРРЕЛ / CORREL |
| СЧЁТ / COUNT |
| СЧЁТЕСЛИ / COUNTIF |
| КОВАР / COVAR |
| ПРЕДСКАЗ / FORECAST |
| ЛИНЕЙН / LINEST |
| ПИРСОН / PEARSON |
События,
характеризующие данные, могут носить
случайный характер и появляться с разной
вероятностью.
Вероятность
события p
есть отношение числа благоприятных
исходов m
к числу всех возможных исходов n
этого
события:
p=m/n.
Например, вероятность появления туза
в наугад выбранной карте из колоды в 52
карты равна 4/52=0.0769, так как m=4,
а n=52.
Если
известно соответствие между появлениями
(величинами) x1,
x2,
…, xn
случайного события (переменной)
X
и
соответствующими вероятностями их
реализации p1,
p2,
…, pn,
то говорят, что известен закон
распределения случайной величины
F(x).
Большинство встречающихся на практике
распределений вероятностей реализовано
в Excel.
Распределения
вероятностей имеют числовые характеристики.
Функции
Excel
для вычисления числовых характеристик
распределения вероятностей. Они входят
в группу Статистические.
При вычислении функций в качестве
случайных величин используйте следующие
значения:
Математическое
ожидание
случайной величины (среднее арифметическое),
характеризующее центр распределения
вероятностей, вычисляется функцией
СРЗНАЧ. СРЗНАЧ(A1:A7)
= 9.
Дисперсия,
характеризует разброс случайной величины
относительно центра распределения
вероятностей и вычисляется функцией
ДИСПР. ДИСПР(A1:A7)
= 4.857.
Среднеквадратичное
отклонение
есть квадратный корень из дисперсии,
характеризует разброс случайной величины
в единицах случайной величины и
вычисляется функцией СТАНДОТКЛОНП.
СТАНДОТКЛОНП(A1:A7) = 2.203893.
Квантиль
случайной величины с законом распределения
F(x)
есть значение случайной величины x
при заданной вероятности p.,
т.е. есть решение уравнения F(x)=p.
Медиана
есть квантиль с вероятностью p=0.5.
Excel,
вместо квантилей содержит функции
вычисления х
для определенных уровней р:
квартили
(кварта – четверть), децили
(дециль
– десятая часть),
персентили
(персент – процент). Различают нижний
квартиль с вероятностью p=0.25
и верхний квартиль с вероятностью
p=0.75.
Децили это квантили с вероятностью 0.1,
0.2, …, 0.9.
Функцию
КВАРТИЛЬ используют, чтобы разбить
данные на группы. В качестве второго
аргумента указывают уровень (четверть),
для которого нужно вернуть решение: 0 –
минимальное значение распределения, 1
– первый, нижний квартиль, 2 – медиана,
3 – третий, верхний квартиль, 4 –
максимальное значение. Например,
КВАРТИЛЬ(A1:A7;3)
= 10, т.е. 75% всех значений меньше 10,
КВАРТИЛЬ(A1:A7;2) = 9.
Функция
ПЕРСЕНТИЛЬ вычисляет квантиль указанного
уровня вероятности и используется для
определения порога приемлемости
значений. В качестве второго аргумента
указывают уровень 0.1, 0.2, …, 0.9.
ПЕРСЕНТИЛЬ(A1:A7;0,9) = 11.8, т.е. 90% всех значений
меньше 11.8.
Excel
содержит инструмент Ранг
и персентиль,
который на основе набора данных формирует
выходную таблицу, содержащую порядковый
и процентный ранги для каждого значения
в наборе данных. См. справку по F1.
Ниже приведен пример установки надстройки
Пактет
анализа
Распределения
вероятностей, реализованные в Excel.
Каждый
закон распределения описывает процессы
разной вероятностной природы и
характеризуется специфическими
параметрами:
-
равномерное
распределение
– n
случайных чисел выпадает с одной и той
же вероятностью p=1/n;
характеризуется нижней и верхней
границей; примером является появление
чисел 1, 2, …, 6 при бросании игральной
кости (p=1/6); -
биномиальное
распределение
моделирует взаимосвязь числа успешных
испытаний m
и вероятностей успеха каждого испытания
p
при общем количестве испытаний n
— функции БИНОМРАСП и КРИТБИНОМ; -
нормальное
(гауссово) распределение
описывает процессы, в которых на
результат воздействует большое число
независимых случайных факторов, среди
которых нет сильно выделяющихся –
функции НОРМРАСП, НОРМСТРАСП, НОРМОБР,
НОРМСТОБР и НОРМАЛИЗАЦИЯ; -
распределение
Пуассона, предсказывает
число случайных событий на определенном
отрезке времени или на определенном
пространстве, позволяет аппроксимировать
биномиальное распределение – функция
ПУАССОН; -
экспоненциальное
(показательное) распределение,
моделирует временные задержки между
событиями, описывает процессы в задачах
массового обслуживания и в задачах с
«временем жизни» — ЭКСПРАСП; -
распределение
хи-квадрат,
связано с нормальным, возвращает
одностороннюю вероятность распределения
и используется для сравнения предполагаемых
и наблюдаемых значений – функция
ХИ2РАСП; -
распределение
Стьюдента,
связано с нормальным, возвращает
вероятность для t-распределения Стьюдента
и используется для проверки гипотез
при малом объеме выборки – функция
СТЬЮДРАСП; -
F-распределение
(Фишера), связано с нормальным и может
быть использовано в F-тесте, который
сравнивает степени разброса двух
множеств данных – fраспобр; -
гамма-распределение
используется для изучения случайных
величин, имеющих асимметричное
распределение, в теории очередей –
функция ГАММАРАСП; -
а
также другие распределения – функции
БЕТАРАСП, ВЕЙБУЛЛ, ОТРБИНОМРАСП,
ГИПЕРГЕОМЕТ, ЛОГНОРМРАСП и др.
Биномиальное
распределение
характеризуется
числом успешных испытаний m,
вероятностью успеха каждого испытания
p
и общим количеством испытаний n.
Классическим примером использования
биномиального распределения является
выборочный контроль качества больших
партий товара, изделий в торговле, на
производстве, когда сплошная проверка
невозможна. Из партии выбирают n
образцов и регистрируют число бракованных
m.
Бракованными могут быть 1, 2, … , n
образцов, но вероятности реального
числа бракованных будут различными.
Если контрольная вероятность брака
ниже допустимой вероятности, то можно
гарантировать достаточное качество
всей партии.
В
Excel
функция БИНОМРАСП вычисляет вероятность
отдельного значения распределения по
заданным m,
n
и р,
а функция КРИТБИНОМ – случайное число
по заданной вероятности. Обычно функция
КРИТБИНОМ используется для определения
наибольшего допустимого числа брака.
В
качестве примера построим график
плотности вероятности биномиального
распределения для n=10
(1, 2, …, 10) и p=0.2.
Введите исходные данные, как показано
на рисунке:
Далее
в ячейку В4 введите статистическую
функцию БИНОМРАСП и заполните ее
параметры как показано на рисунке:
Здесь
параметр Число_s
есть число успешных испытаний m,
Испытания
– число независимых испытаний n,
Вероятность_s
–
вероятность успеха каждого испытания
p.
Параметр Интегральный
равен 0, если требуется получить плотность
распределения (вероятность для значения
m),
и равен 1, если требуется получить
вероятность с накоплением (вероятность
того, что число успешных испытаний не
меньше значения аргумента Число_s).
Формулу
из В4 размножьте в ячейки В5:В13. Ниже
показан результат:
В
колонке В вычислены вероятности успешных
испытаний m=1,
2, …, 10. Теперь по диапазону В4:В13 постройте
график или гистограмму биномиальной
функции плотности распределения –
результат на рисунке. Поэкспериментируйте,
изменяя значение вероятности в ячейке
В1: 0.3, 0.4, 0.8, проследите за изменениями
формы графика.
Для
иллюстрации функции КРИТБИНОМ используем
предыдущий пример – необходимо найти
число m,
для которого вероятность интегрального
распределения больше или равна 0.75.
Вызовите функцию КРИТБИНОМ и заполните
параметры. Вы должны получить значение
3. Это означает, что при вероятности
интегрального распределения >= 0.75
будет не менее трех (m>=3)
успешных испытаний.
Нормальное
распределение
характеризуется
средним арифметическим (математическим
ожиданием) m
и стандартным (среднеквадратичным)
отклонением r.
Дисперсия равна r2.
Краткое обозначение распределения
N(m,r2).
График нормального распределения
симметричен относительно центра
распределения (точки m),
чем меньше r,
тем больше вероятность появления
случайной величины. В пределы [m—r,m+r]
нормально распределенная случайная
величина попадает с вероятностью 0,683 в
пределы [m-2r,m+2r]
— с вероятностью 0,955 и т.д.
При
m=0
и r=1
нормальное распределение называется
стандартным
или нормированным – N(0,1).
Нормальное
распределение имеет очень широкий круг
приложений. В качестве примера построим
график плотности вероятностей нормального
распределения при m=15
и r=1,5
в диапазоне [m-3r,m+3r]
c
шагом 0,5. Результат показан на рисунке.
Выполните
следующие действия:
-
в
ячейку А4 введите формулу =B1-3*B2, в ячейку
А5 формулу =A4+B$3 и размножьте ее по ячейку
А22; -
в
ячейку В4 введите функцию НОРМРАСП из
группы Статистические
– параметры заполните как на рисунке; -
размножьте
формулу из ячейки В4 по ячейку В22 и по
диапазону В4:В22 постройте график; на
2-ом шаге мастера диаграмм в закладке
Ряд
введите подписи к оси х
из диапазона А4:А22.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Распределения вероятностей в MS EXCEL. Нормальное распределение, Биномиальное распределение, распределение Стьюдента, Вейбулла, Фишера и др. Оценка параметров распределения, вычисление математического ожидания и дисперсии. Функции MS EXCEL: НОРМ.РАСП(), СТЬЮДЕНТ.РАСП(), ХИ2.РАСП() и др. Рассмотрены ВСЕ распределения, имеющиеся в MS EXCEL 2010.
Взаимосвязь некоторых распределений в MS EXCEL
Рассмотрим взаимосвязь Биномиального распределения, распределения Пуассона, Нормального распределения и Гипергеометрического распределения. Определим условия, когда возможна аппроксимация одного распределения другим, приведем примеры и графики.
update Опубликовано: 06 ноября 2016
Функция распределения и плотность вероятности в MS EXCEL
Даны определения Функции распределения случайной величины и Плотности вероятности непрерывной случайной величины. Эти понятия активно используются в статьях о статистике сайта <noindex> www.excel2.ru </noindex> . Рассмотрены примеры вычисления Функции распределения и Плотности …
update Опубликовано: 13 октября 2016
Нормальное распределение. Непрерывные распределения в MS EXCEL
Рассмотрим Нормальное распределение. С помощью функции MS EXCEL НОРМ.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел, распределенных по нормальному закону, произведем оценку параметров распределения, среднего значения …
update Опубликовано: 23 октября 2016
Равномерное дискретное распределение в MS EXCEL
Рассмотрим Равномерное дискретное распределение, построим график функции распределения, вычислим среднее значение и дисперсию. Сгенерируем случайные значения (выборку) с помощью функции MS EXCEL СЛУЧМЕЖДУ() . На основании выборки оценим среднее и …
update Опубликовано: 27 октября 2016
Гипергеометрическое распределение. Дискретные распределения в MS EXCEL
Рассмотрим Гипергеометрическое распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL ГИПЕРГЕОМ.РАСП() построим графики функции распределения и плотности вероятности. Приведем пример аппроксимации гипергеометрического распределения биномиальным.
update Опубликовано: 07 ноября 2016
Биномиальное распределение. Дискретные распределения в MS EXCEL
Рассмотрим Биномиальное распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL БИНОМ.РАСП() построим графики функции распределения и плотности вероятности. Произведем оценку параметра распределения p, математического ожидания распределения …
update Опубликовано: 29 октября 2016
Распределения случайной величины в MS EXCEL
В статье приведен перечень распределений вероятности, имеющихся в MS EXCEL 2010 и в более ранних версиях. Даны ссылки на статьи с описанием соответствующих функций MS EXCEL.
update Опубликовано: 23 октября 2016
Распределение Пуассона. Дискретные распределения в MS EXCEL
Рассмотрим распределение Пуассона, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL ПУАССОН.РАСП() построим графики функции распределения и плотности вероятности. Произведем оценку параметра распределения, его математического ожидания и …
update Опубликовано: 06 ноября 2016
Равномерное непрерывное распределение в MS EXCEL
Рассмотрим равномерное непрерывное распределение. Вычислим математическое ожидание и дисперсию. Сгенерируем случайные значения с помощью функции MS EXCEL СЛЧИС() и надстройки Пакет Анализа, произведем оценку среднего значения и стандартного отклонения.
update Опубликовано: 08 ноября 2016
Логнормальное распределение. Непрерывные распределения в MS EXCEL
Рассмотрим Логнормальное распределение. С помощью функции MS EXCEL ЛОГНОРМ .РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел, распределенных по логнормальному закону, произведем оценку параметров распределения, среднего …
update Опубликовано: 08 ноября 2016
Экспоненциальное распределение. Непрерывные распределения в MS EXCEL
Рассмотрим Экспоненциальное распределение, вычислим его математическое ожидание, дисперсию, медиану. С помощью функции MS EXCEL ЭКСП.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметра …
update Опубликовано: 08 ноября 2016
Гамма распределение. Непрерывные распределения в MS EXCEL
Рассмотрим Гамма распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL ГАММА.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметров …
update Опубликовано: 09 ноября 2016
Распределение Вейбулла. Непрерывные распределения в MS EXCEL
Рассмотрим распределение Вейбулла, вычислим его математическое ожидание, дисперсию, медиану. С помощью функции MS EXCEL ВЕЙБУЛЛ.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметров …
update Опубликовано: 09 ноября 2016
Бета распределение. Непрерывные распределения в MS EXCEL
Рассмотрим Бета-распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL БЕТА.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметров распределения.
update Опубликовано: 10 ноября 2016
Случайная выборка из генеральной совокупности в MS EXCEL
Инструмент Пакета анализа MS EXCEL «Выборка» извлекает случайную выборку из входного диапазона, рассматривая его как генеральную совокупность. Также случайную выборку можно извлечь с помощью формул.
update Опубликовано: 14 ноября 2016
© Copyright 2013 — 2023 Excel2.ru. All Rights Reserved
В этой статье объясняется, как можно рассчитать вероятность в Excel с помощью функции ВЕРОЯТНОСТЬ с несколькими примерами.
Вероятность — это математическая мера, которая определяет вероятные шансы на то, что событие (или набор событий) произойдет в ситуации. Другими словами, это просто вероятность того, что что-то произойдет. Вероятность события измеряется путем сравнения количества благоприятных событий с общим количеством возможных исходов.
Например, когда мы подбрасываем монету, шанс получить «голову» составляет половину (50%), как и вероятность получить «хвост». Потому что общее количество возможных исходов равно 2 (голова или хвост). Предположим, в вашем местном сводке погоды говорится, что вероятность дождя составляет 80%, затем, вероятно, пойдет дождь.
Существует множество приложений вероятности в повседневной жизни, таких как спорт, прогноз погоды, опросы, карточные игры, прогнозирование пола ребенка в утробе матери, статика и многое другое.
Вычисление вероятности может показаться сложным процессом, но MS Excel предоставляет встроенную формулу для простого вычисления вероятности с помощью функции ВЕРОЯТНОСТЬ. Давайте посмотрим, как найти вероятность в Excel.
Рассчитайте вероятность с помощью функции ВЕРОЯТНОСТЬ
Обычно вероятность рассчитывается путем деления количества благоприятных событий на общее количество возможных исходов. В Excel вы можете использовать функцию ВЕРОЯТНОСТЬ для измерения вероятности события или диапазона событий.
Функция ВЕРОЯТНОСТЬ — это одна из статистических функций в Excel, которая вычисляет вероятность того, что значения из диапазона находятся в указанных пределах. Синтаксис функции ВЕРОЯТНОСТЬ следующий:
= PROB(x_range, prob_range, [lower_limit], [upper_limit])куда,
- x_range: это диапазон числовых значений, который показывает различные события. Значения x связаны с вероятностями.
- prob_range: это диапазон вероятностей для каждого соответствующего значения в массиве x_range, и значения в этом диапазоне должны составлять до 1 (если они указаны в процентах, должны складываться до 100%).
- lower_limit (необязательно): это нижнее предельное значение события, для которого вы хотите получить вероятность.
- upper_limit (необязательно) : это верхнее предельное значение события, для которого вы хотите получить вероятность. Если этот аргумент игнорируется, функция возвращает вероятность, связанную со значением lower_limit.
Пример вероятности 1
Давайте узнаем, как использовать функцию ВЕРОЯТНОСТЬ на примере.
Прежде чем приступить к расчету вероятности в Excel, следует подготовить данные для расчета. Вы должны ввести дату в таблицу вероятностей с двумя столбцами. Диапазон числовых значений следует ввести в один столбец, а соответствующие вероятности — в другой столбец, как показано ниже. Сумма всех вероятностей в столбце B должна быть равна 1 (или 100%).
После ввода числовых значений (продажи билетов) и их вероятностей их получения вы можете использовать функцию СУММ, чтобы проверить, составляет ли сумма всех вероятностей в сумме «1» или 100%. Если общее значение вероятностей не равно 100%, функция ВЕРОЯТНОСТЬ вернет # ЧИСЛО! ошибка.
Допустим, мы хотим определить вероятность того, что продажи билетов находятся в диапазоне от 40 до 90. Затем введите данные верхнего и нижнего пределов в таблицу, как показано ниже. Нижний предел установлен на 40, а верхний предел установлен на 90.
Чтобы рассчитать вероятность для данного диапазона, введите следующую формулу в ячейку B14:
=PROB(A3:A9,B3:B9,B12,B13)Где A3: A9 — это диапазон событий (продаж билетов) в числовых значениях, B3: B9 содержит вероятность получения соответствующего количества продаж из столбца A, B12 — это нижний предел, а B13 — верхний предел. В результате формула возвращает значение вероятности 0,39 в ячейке B14.
Затем щелкните значок «%» в группе «Число» на вкладке «Главная», как показано ниже. И вы получите «39%», что является вероятностью продажи билетов от 40 до 90.
Расчет вероятности без верхнего предела
Если верхний предел (последний) аргумент не указан, функция ВЕРОЯТНОСТЬ возвращает вероятность, равную значению lower_limit.
В приведенном ниже примере аргумент upper_limit (последний) опущен в формуле, формула возвращает «0,12» в ячейке B14. Результат равен «B5» в таблице.
Когда мы переведем его в процент, мы получим «12%».
Пример 2: Вероятности игры в кости
Давайте посмотрим, как рассчитать вероятность на более сложном примере. Предположим, у вас есть два кубика, и вы хотите найти вероятность выпадения суммы при броске двух кубиков.
В таблице ниже показана вероятность того, что каждый кубик выпадет на определенное значение при конкретном броске:
Когда вы бросаете два кубика, вы получаете сумму чисел от 2 до 12. Цифры в красном — это сумма двух чисел на кубиках. Значение в C3 равно сумме C2 и B3, C4 = C2 + B4 и так далее.
Вероятность выпадения 2 возможна только тогда, когда мы получаем 1 на обоих кубиках (1 + 1), поэтому шанс = 1. Теперь нам нужно рассчитать шансы на выпадение с помощью функции СЧЁТЕСЛИ.
Нам нужно создать другую таблицу с суммой бросков в одном столбце и их шансом получить это число в другом столбце. Нам нужно ввести приведенную ниже формулу шанса броска в ячейку C11:
=COUNTIF($C$3:$H$8,B11)Функция СЧЁТЕСЛИ подсчитывает количество шансов на общее количество бросков. Здесь указан диапазон $ C $ 3: $ H $ 8 и критерий B11. Диапазон делается абсолютной ссылкой, поэтому он не корректируется, когда мы копируем формулу.
Затем скопируйте формулу из C11 в другие ячейки, перетащив ее в ячейку C21.
Теперь нам нужно вычислить индивидуальные вероятности суммы чисел, выпавших на барабанах. Для этого нам нужно разделить значение каждого шанса на общее значение шансов, которое составляет 36 (6 x 6 = 36 возможных бросков). Используйте приведенную ниже формулу, чтобы найти индивидуальные вероятности:
=B11/36Затем скопируйте формулу в остальные ячейки.
Как видите, у 7 наибольшая вероятность выпадения.
Теперь предположим, что вы хотите найти вероятность получения бросков выше 9. Для этого вы можете использовать приведенную ниже функцию ВЕРОЯТНОСТЬ:
=PROB(B11:B21,D11:D21,10,12)Здесь B11: B21 — диапазон событий, D11: D21 — связанные вероятности, 10 — нижний предел, а 12 — верхний предел. Функция возвращает 0,17 в ячейке G14.
Как видите, вероятность выпадения двух кубиков при сумме бросков больше 9 составляет 0,17 или 17%.
Вы также можете рассчитать вероятность без функции ВЕРОЯТНОСТЬ, используя простой арифметический расчет.
Как правило, вы можете найти вероятность наступления события, используя эту формулу:
P(E) = n(E)/n(S)Где,
- n (E) = количество появлений события.
- n (S) = Общее количество возможных результатов.
Например, предположим, что у вас есть два мешка, заполненные шарами: «Мешок А» и «Мешок Б». В сумке A 5 зеленых, 3 белых, 8 красных и 4 желтых шара. В мешке B 3 зеленых шара, 2 белых шара, 6 красных и 4 желтых шара.
Какова вероятность того, что два человека одновременно выберут 1 зеленый шар из мешка A и 1 красный шар из мешка B? Вот как это вычислить:
Чтобы определить вероятность подобрать зеленый шар из мешка A, используйте эту формулу:
=B2/20Где B2 — количество красных шаров (5), деленное на общее количество шаров (20). Затем скопируйте формулу в другие ячейки. Теперь у вас есть индивидуальные вероятности подобрать каждый цветной шар из мешка A.
Используйте приведенную ниже формулу, чтобы найти индивидуальные вероятности попадания шаров в мешок B:
=F2/15Здесь вероятность конвертируется в проценты.
Вероятность собрать зеленый шар из мешка A и красный шар из мешка B вместе:
=(probability of picking a green ball from bag A) x (probability of picking a red ball from bag B)=C2*G3Как видите, вероятность вытащить зеленый шар из мешка A и красный шар из мешка B одновременно составляет 3,3%.
Вот и все.