Наименьшую существенную разницу excel - Word и Excel - помощь в работе с программами

Содержание

Вычисление разницы
- Способ 1: вычитание чисел
- Способ 2: денежный формат
- Способ 3: даты
- Способ 4: время
Вопросы и ответы

Вычисление разности является одним из самых популярных действий в математике. Но данное вычисление применяется не только в науке. Мы его постоянно выполняем, даже не задумываясь, и в повседневной жизни. Например, для того, чтобы посчитать сдачу от покупки в магазине также применяется расчет нахождения разницы между суммой, которую дал продавцу покупатель, и стоимостью товара. Давайте посмотрим, как высчитать разницу в Excel при использовании различных форматов данных.

Вычисление разницы

Учитывая, что Эксель работает с различными форматами данных, при вычитании одного значения из другого применяются различные варианты формул. Но в целом их все можно свести к единому типу:

X=A-B

А теперь давайте рассмотрим, как производится вычитание значений различных форматов: числового, денежного, даты и времени.

Способ 1: вычитание чисел

Сразу давайте рассмотрим наиболее часто применимый вариант подсчета разности, а именно вычитание числовых значений. Для этих целей в Экселе можно применить обычную математическую формулу со знаком «-».

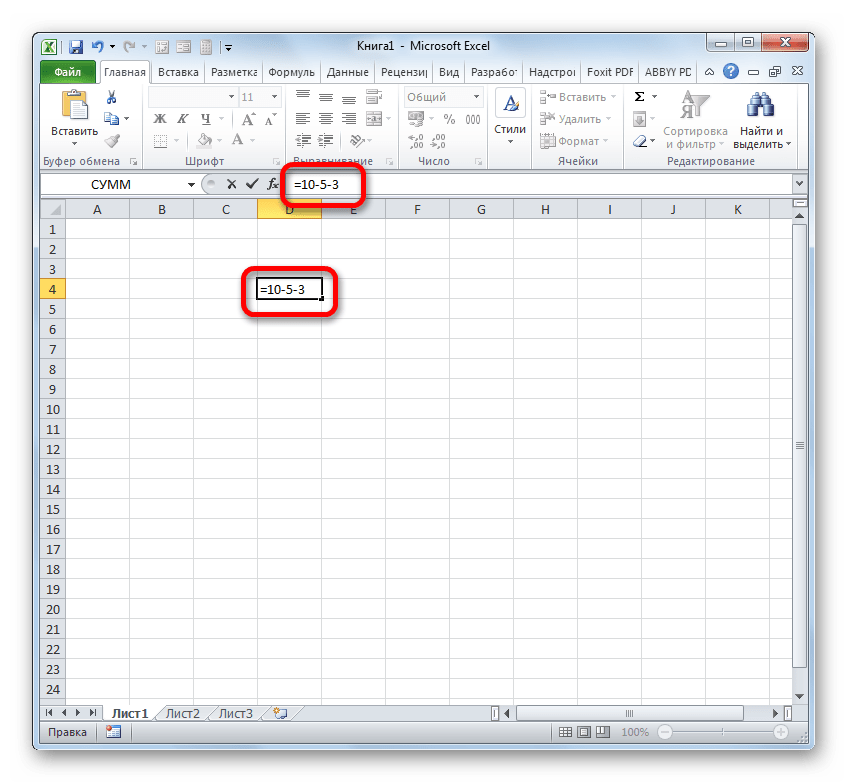
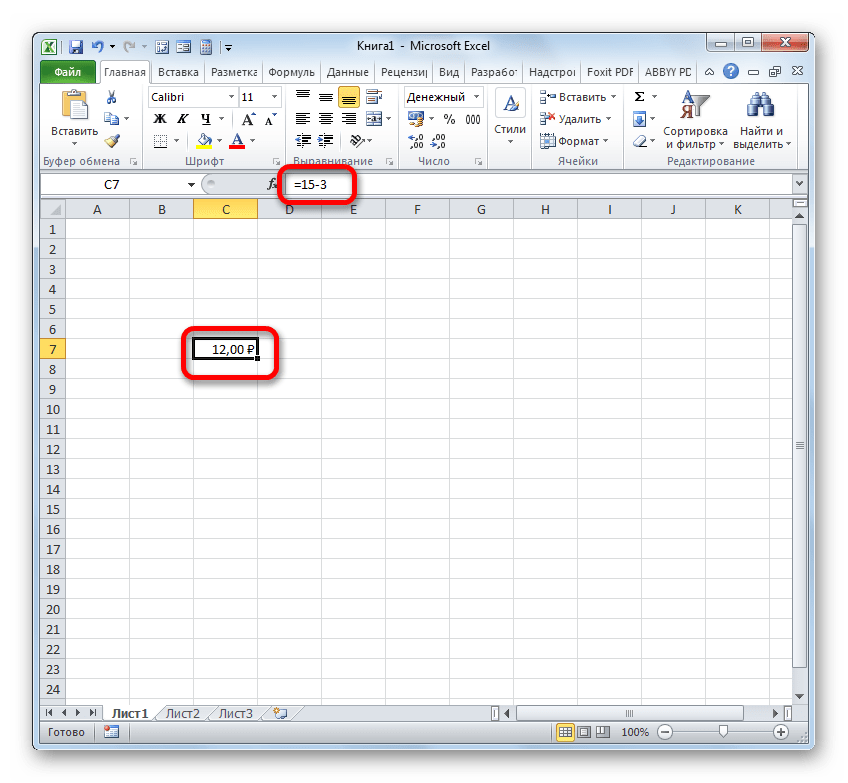
Если вам нужно произвести обычное вычитание чисел, воспользовавшись Excel, как калькулятором, то установите в ячейку символ «=». Затем сразу после этого символа следует записать уменьшаемое число с клавиатуры, поставить символ «-», а потом записать вычитаемое. Если вычитаемых несколько, то нужно опять поставить символ «-» и записать требуемое число. Процедуру чередования математического знака и чисел следует проводить до тех пор, пока не будут введены все вычитаемые. Например, чтобы из числа 10 вычесть 5 и 3, нужно в элемент листа Excel записать следующую формулу:
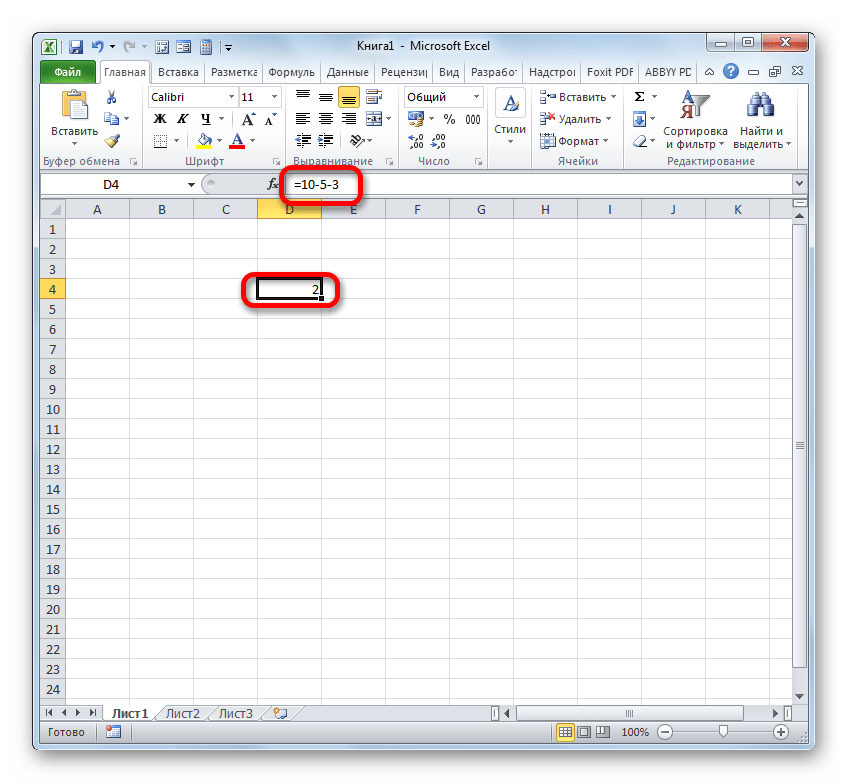
=10-5-3

После записи выражения, для выведения результата подсчета, следует кликнуть по клавише Enter.

Как видим, результат отобразился. Он равен числу 2.

Но значительно чаще процесс вычитания в Экселе применяется между числами, размещенными в ячейках. При этом алгоритм самого математического действия практически не меняется, только теперь вместо конкретных числовых выражений применяются ссылки на ячейки, где они расположены. Результат же выводится в отдельный элемент листа, где установлен символ «=».

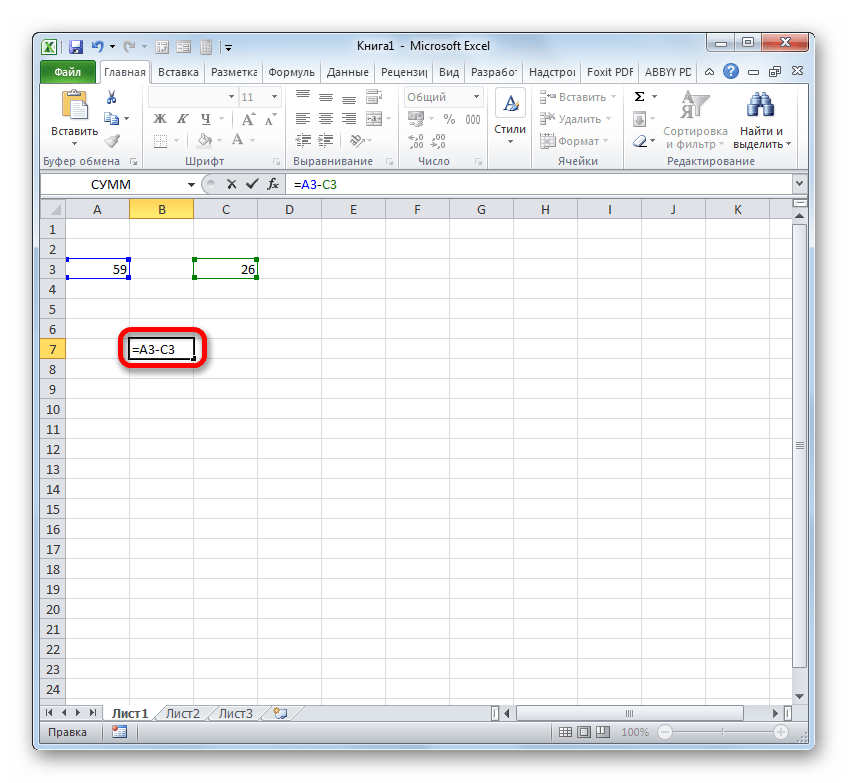
Посмотрим, как рассчитать разницу между числами 59 и 26, расположенными соответственно в элементах листа с координатами A3 и С3.

Выделяем пустой элемент книги, в который планируем выводить результат подсчета разности. Ставим в ней символ «=». После этого кликаем по ячейке A3. Ставим символ «-». Далее выполняем клик по элементу листа С3. В элементе листа для вывода результата должна появиться формула следующего вида:
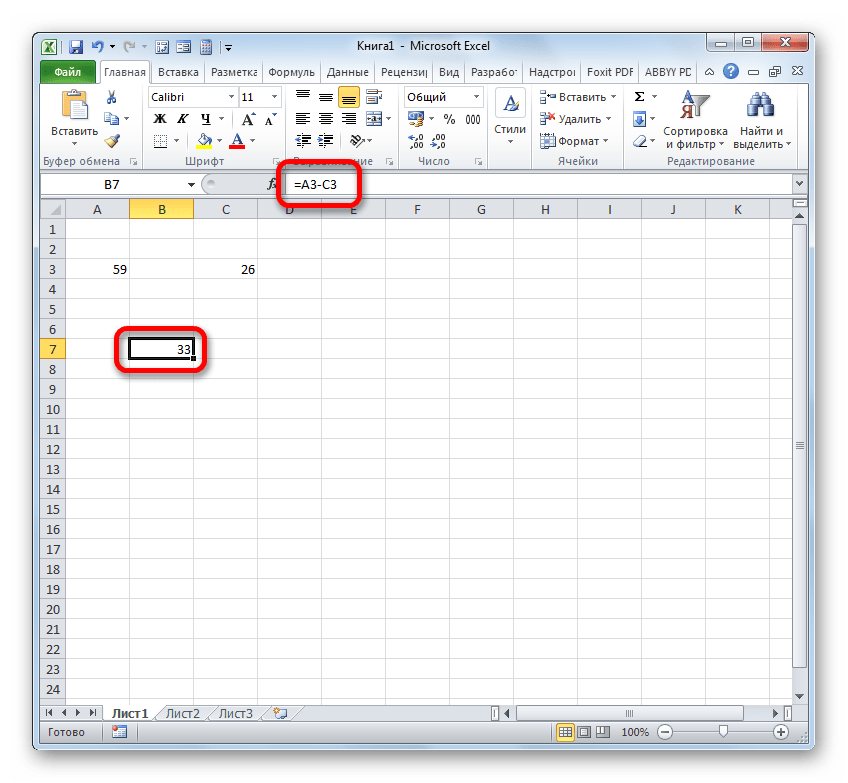
=A3-C3

Как и в предыдущем случае для вывода результата на экран щелкаем по клавише Enter.

Как видим, и в этом случае расчет был произведен успешно. Результат подсчета равен числу 33.

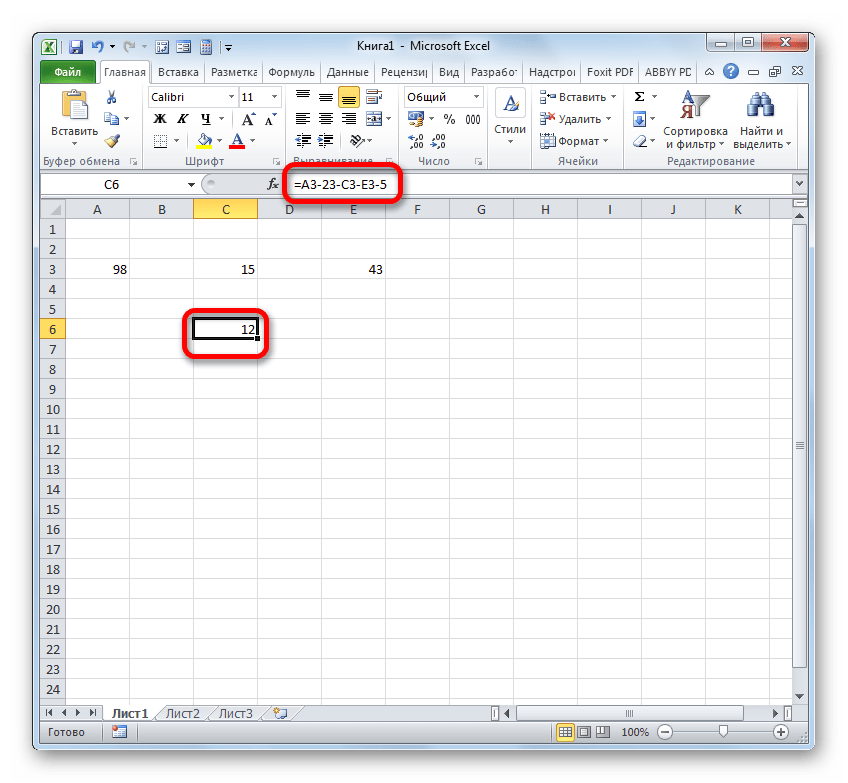
Но на самом деле в некоторых случаях требуется произвести вычитание, в котором будут принимать участие, как непосредственно числовые значения, так и ссылки на ячейки, где они расположены. Поэтому вполне вероятно встретить и выражение, например, следующего вида:

=A3-23-C3-E3-5

Урок: Как вычесть число из числа в Экселе

Способ 2: денежный формат

Вычисление величин в денежном формате практически ничем не отличается от числового. Применяются те же приёмы, так как, по большому счету, данный формат является одним из вариантов числового. Разница состоит лишь в том, что в конце величин, принимающих участие в расчетах, установлен денежный символ конкретной валюты.

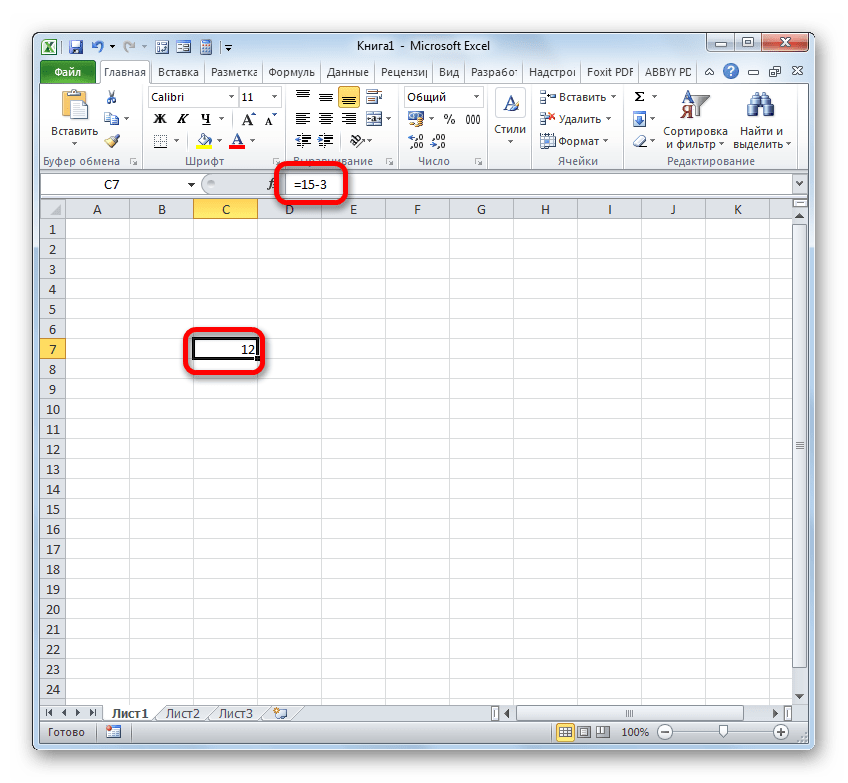
Собственно можно провести операцию, как обычное вычитание чисел, и только потом отформатировать итоговый результат под денежный формат. Итак, производим вычисление. Например, вычтем из 15 число 3.

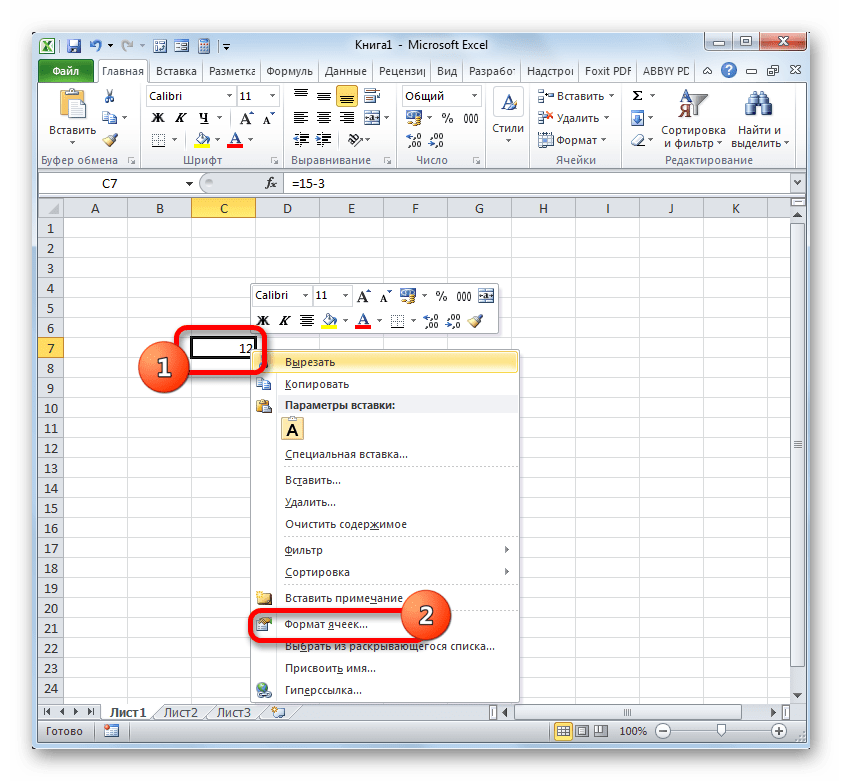
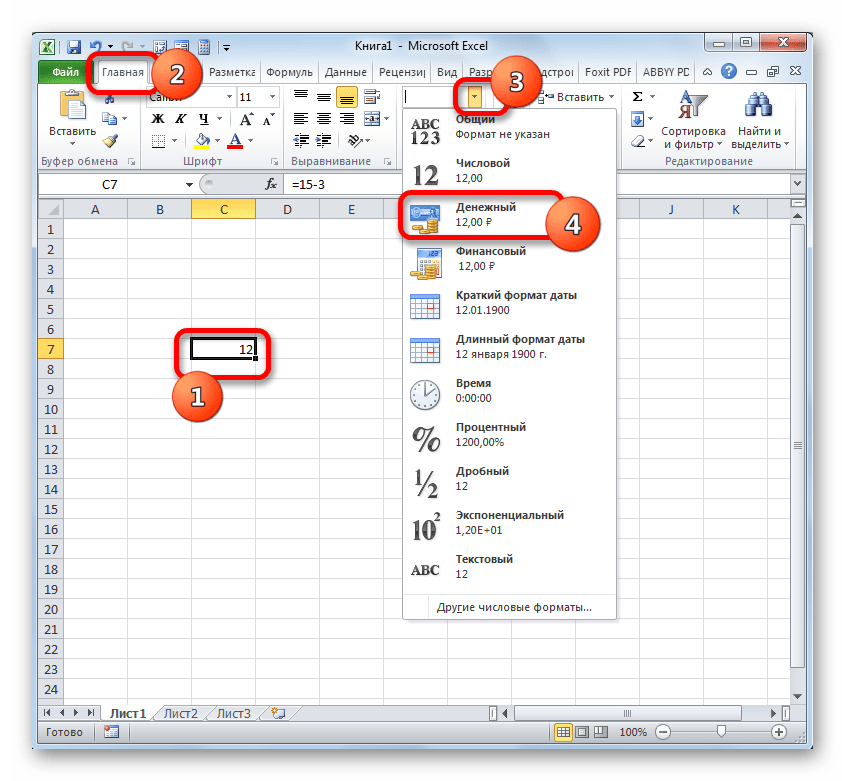
После этого кликаем по элементу листа, который содержит результат. В меню выбираем значение «Формат ячеек…». Вместо вызова контекстного меню можно применить после выделения нажатие клавиш Ctrl+1.

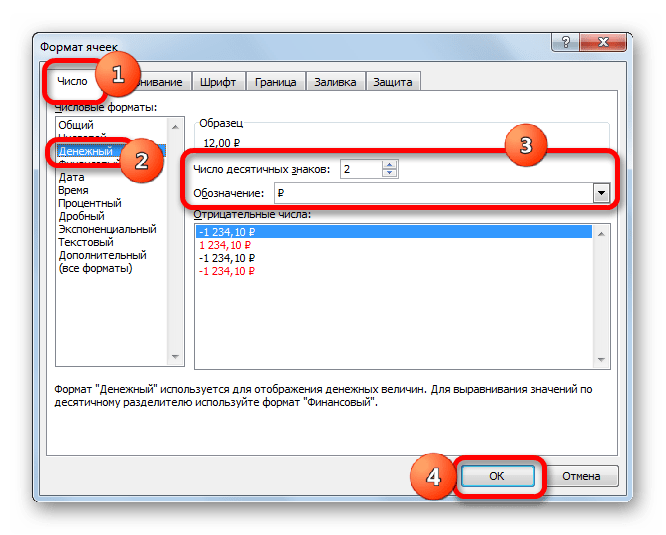
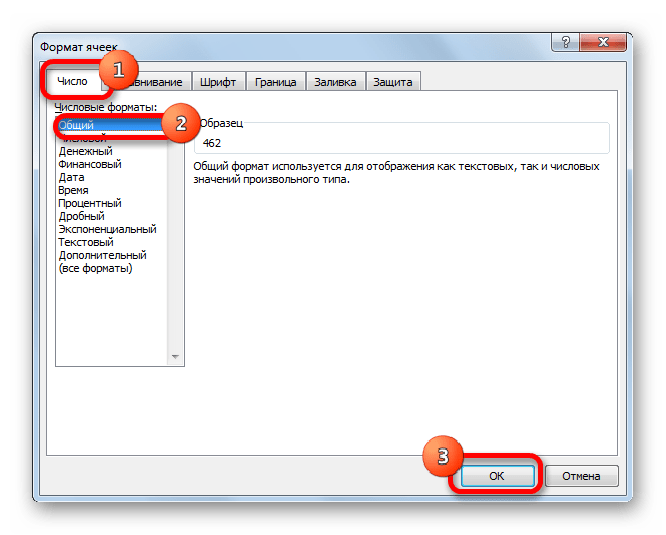
При любом из двух указанных вариантов производится запуск окна форматирования. Перемещаемся в раздел «Число». В группе «Числовые форматы» следует отметить вариант «Денежный». При этом в правой части интерфейса окна появятся специальные поля, в которых можно выбрать вид валюты и число десятичных знаков. Если у вас Windows в целом и Microsoft Office в частности локализованы под Россию, то по умолчанию должны стоять в графе «Обозначение» символ рубля, а в поле десятичных знаков число «2». В подавляющем большинстве случаев эти настройки изменять не нужно. Но, если вам все-таки нужно будет произвести расчет в долларах или без десятичных знаков, то требуется внести необходимые коррективы.
Вслед за тем, как все необходимые изменения сделаны, клацаем по «OK».

Как видим, результат вычитания в ячейке преобразился в денежный формат с установленным количеством десятичных знаков.

Существует ещё один вариант отформатировать полученный итог вычитания под денежный формат. Для этого нужно на ленте во вкладке «Главная» кликнуть по треугольнику, находящемуся справа от поля отображения действующего формата ячейки в группе инструментов «Число». Из открывшегося списка следует выбрать вариант «Денежный». Числовые значения будут преобразованы в денежные. Правда в этом случае отсутствует возможность выбора валюты и количества десятичных знаков. Будет применен вариант, который выставлен в системе по умолчанию, или настроен через окно форматирования, описанное нами выше.

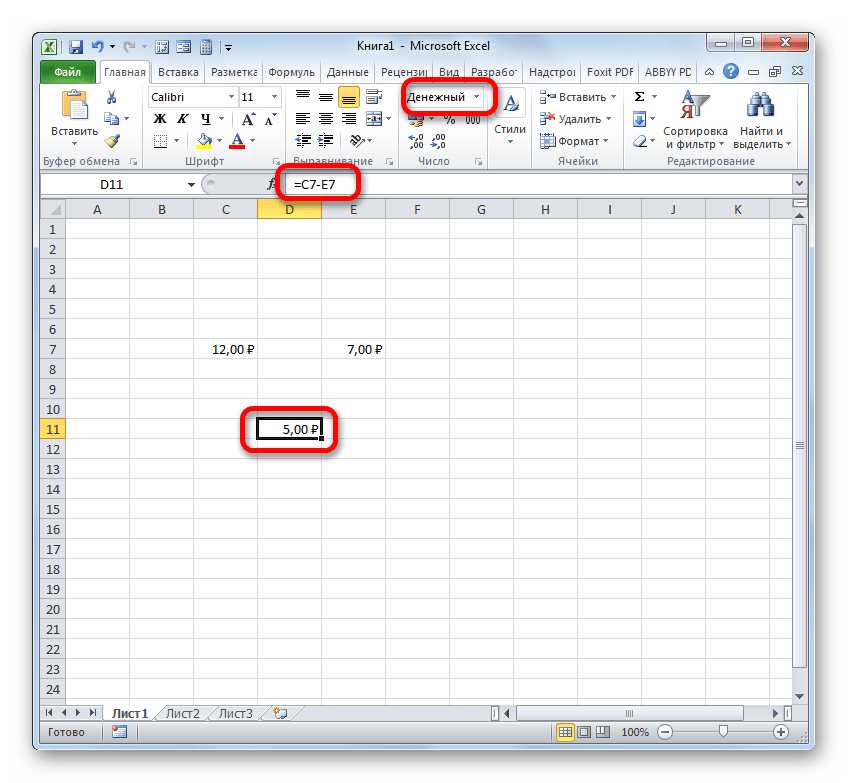
Если же вы высчитываете разность между значениями, находящимися в ячейках, которые уже отформатированы под денежный формат, то форматировать элемент листа для вывода результата даже не обязательно. Он будет автоматически отформатирован под соответствующий формат после того, как будет введена формула со ссылками на элементы, содержащие уменьшаемое и вычитаемые числа, а также произведен щелчок по клавише Enter.

Урок: Как изменить формат ячейки в Экселе

Способ 3: даты

А вот вычисление разности дат имеет существенные нюансы, отличные от предыдущих вариантов.

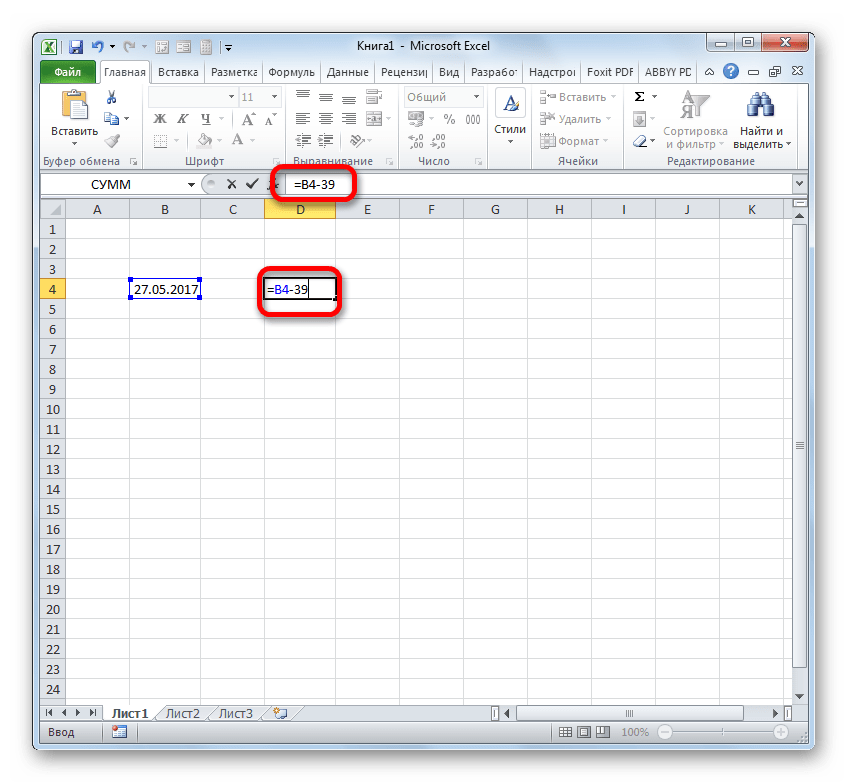
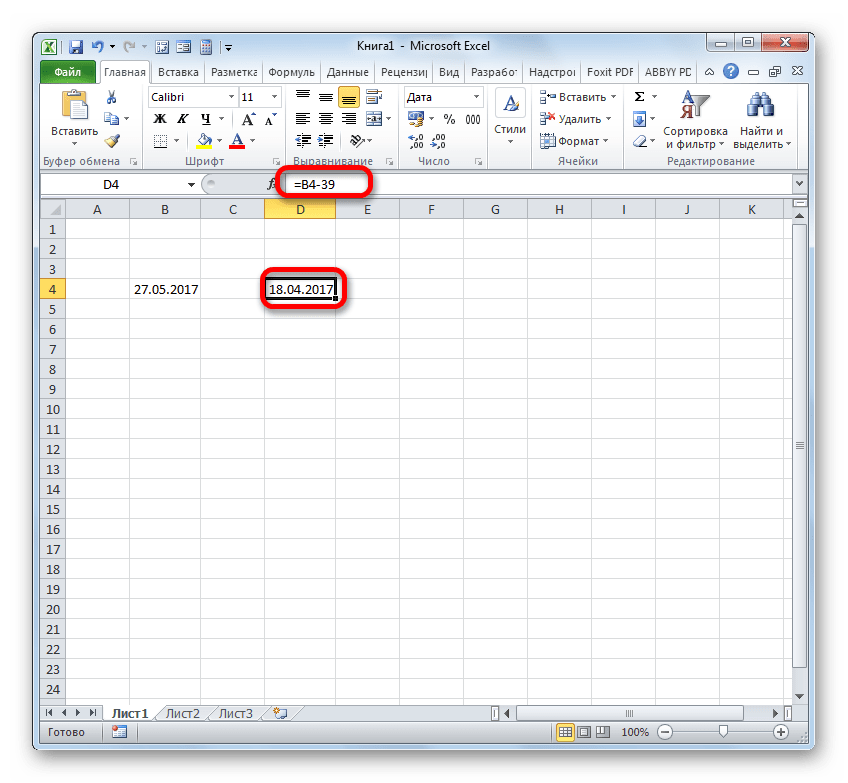
Если нам нужно вычесть определенное количество дней от даты, указанной в одном из элементов на листе, то прежде всего устанавливаем символ «=» в элемент, где будет отображен итоговый результат. После этого кликаем по элементу листа, где содержится дата. Его адрес отобразится в элементе вывода и в строке формул. Далее ставим символ «-» и вбиваем с клавиатуры численность дней, которую нужно отнять. Для того, чтобы совершить подсчет клацаем по Enter.

Результат выводится в обозначенную нами ячейку. При этом её формат автоматически преобразуется в формат даты. Таким образом, мы получаем полноценно отображаемую дату.

Существует и обратная ситуация, когда требуется из одной даты вычесть другую и определить разность между ними в днях.

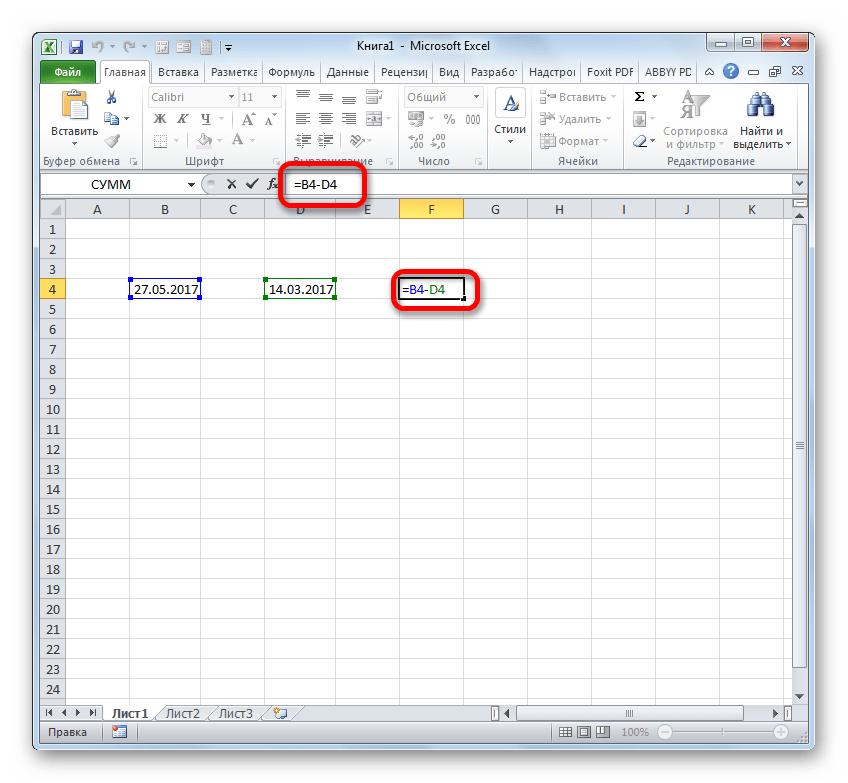
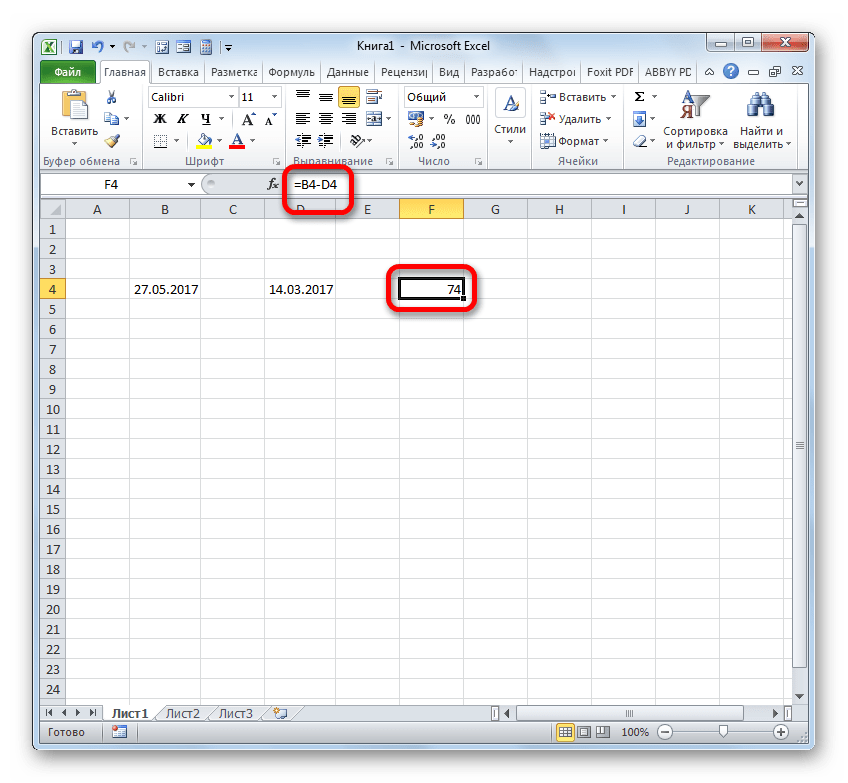
Устанавливаем символ «=» в ячейку, где будет отображен результат. После этого клацаем по элементу листа, где содержится более поздняя дата. После того, как её адрес отобразился в формуле, ставим символ «-». Клацаем по ячейке, содержащей раннюю дату. Затем клацаем по Enter.

Как видим, программа точно вычислила количество дней между указанными датами.

Также разность между датами можно вычислить при помощи функции РАЗНДАТ. Она хороша тем, что позволяет настроить с помощью дополнительного аргумента, в каких именно единицах измерения будет выводиться разница: месяцы, дни и т.д. Недостаток данного способа заключается в том, что работа с функциями все-таки сложнее, чем с обычными формулами. К тому же, оператор РАЗНДАТ отсутствует в списке Мастера функций, а поэтому его придется вводить вручную, применив следующий синтаксис:

=РАЗНДАТ(нач_дата;кон_дата;ед)

«Начальная дата» — аргумент, представляющий собой раннюю дату или ссылку на неё, расположенную в элементе на листе.

«Конечная дата» — это аргумент в виде более поздней даты или ссылки на неё.

Самый интересный аргумент «Единица». С его помощью можно выбрать вариант, как именно будет отображаться результат. Его можно регулировать при помощи следующих значений:

«d» — результат отображается в днях;
«m» — в полных месяцах;
«y» — в полных годах;
«YD» — разность в днях (без учета годов);
«MD» — разность в днях (без учета месяцев и годов);
«YM» — разница в месяцах.

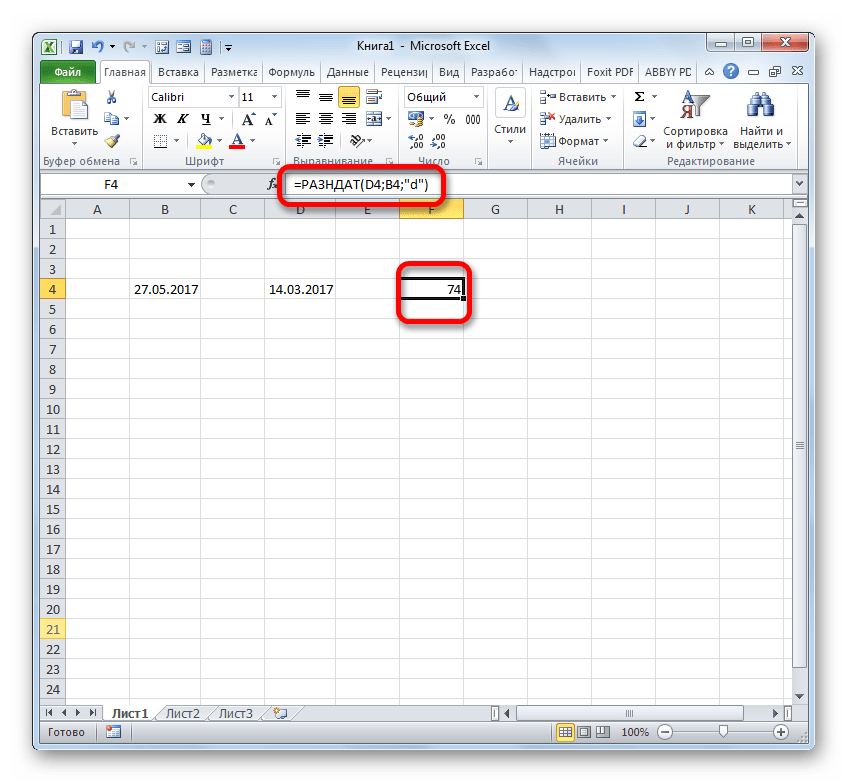
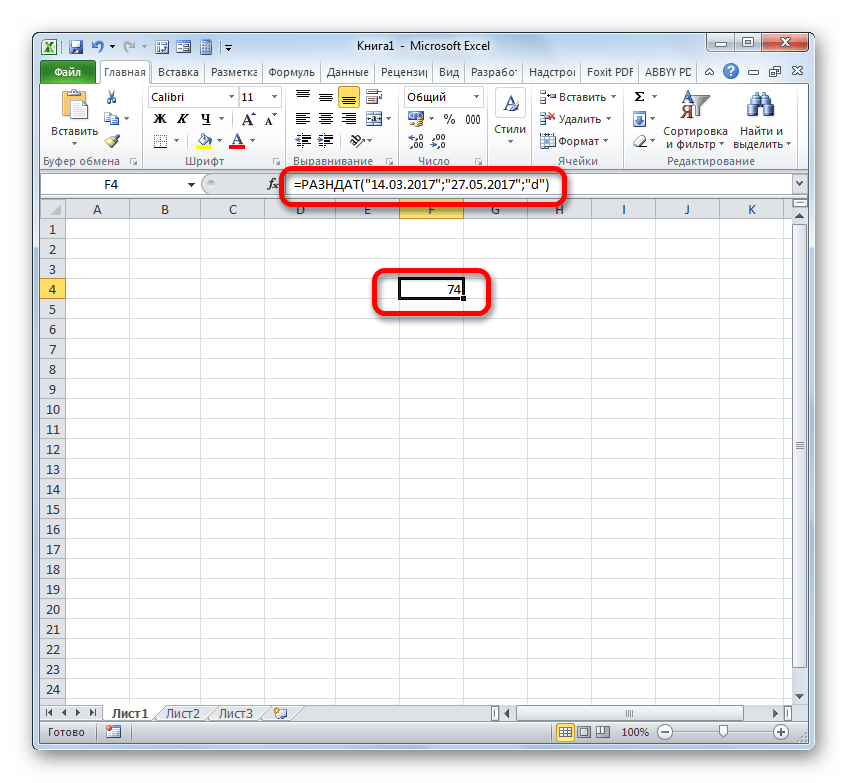
Итак, в нашем случае требуется вычислить разницу в днях между 27 мая и 14 марта 2017 года. Эти даты расположены в ячейках с координатами B4 и D4, соответственно. Устанавливаем курсор в любой пустой элемент листа, где хотим видеть итоги расчета, и записываем следующую формулу:

=РАЗНДАТ(D4;B4;"d")

Жмем на Enter и получаем итоговый результат подсчета разности 74. Действительно, между этими датами лежит 74 дня.

Если же требуется произвести вычитание этих же дат, но не вписывая их в ячейки листа, то в этом случае применяем следующую формулу:

=РАЗНДАТ("14.03.2017";"27.05.2017";"d")

Опять жмем кнопку Enter. Как видим, результат закономерно тот же, только полученный немного другим способом.

Урок: Количество дней между датами в Экселе

Способ 4: время

Теперь мы подошли к изучению алгоритма процедуры вычитания времени в Экселе. Основной принцип при этом остается тот же, что и при вычитании дат. Нужно из более позднего времени отнять раннее.

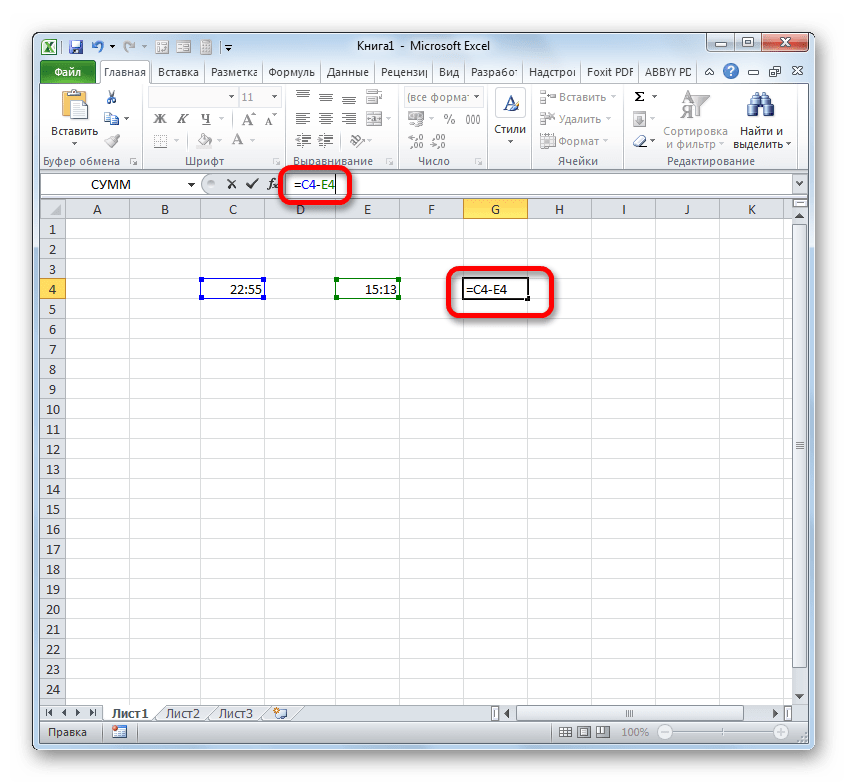
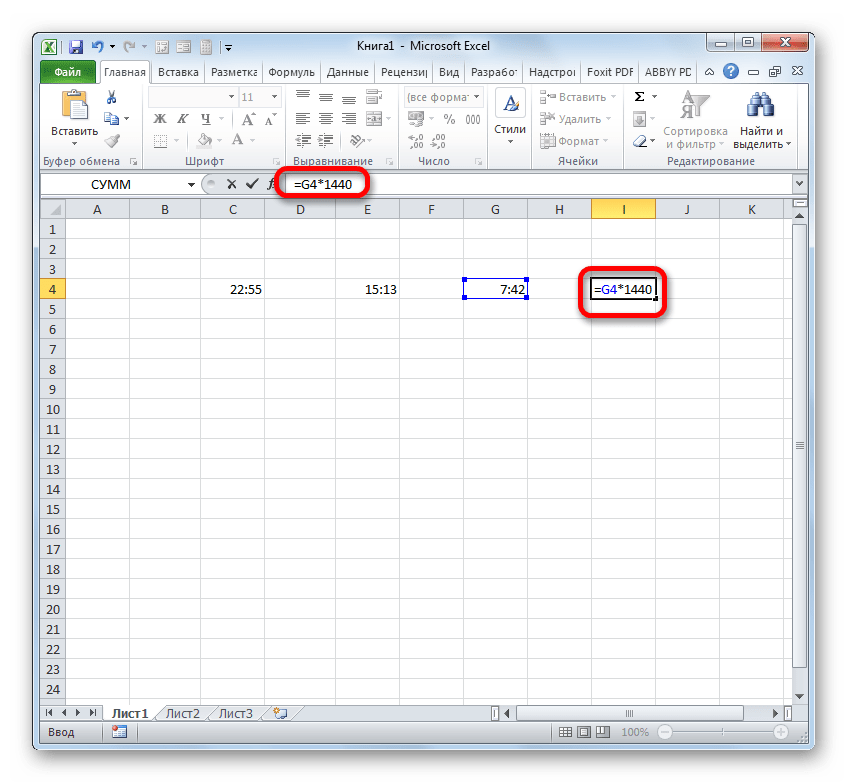
Итак, перед нами стоит задача узнать, сколько минут прошло с 15:13 по 22:55. Записываем эти значения времени в отдельные ячейки на листе. Что интересно, после ввода данных элементы листа будут автоматически отформатированы под содержимое, если они до этого не форматировались. В обратном случае их придется отформатировать под дату вручную. В ту ячейку, в которой будет выводиться итог вычитания, ставим символ «=». Затем клацаем по элементу, содержащему более позднее время (22:55). После того, как адрес отобразился в формуле, вводим символ «-». Теперь клацаем по элементу на листе, в котором расположилось более раннее время (15:13). В нашем случае получилась формула вида:
=C4-E4

Для проведения подсчета клацаем по Enter.

Но, как видим, результат отобразился немного не в том виде, в котором мы того желали. Нам нужна была разность только в минутах, а отобразилось 7 часов 42 минуты.
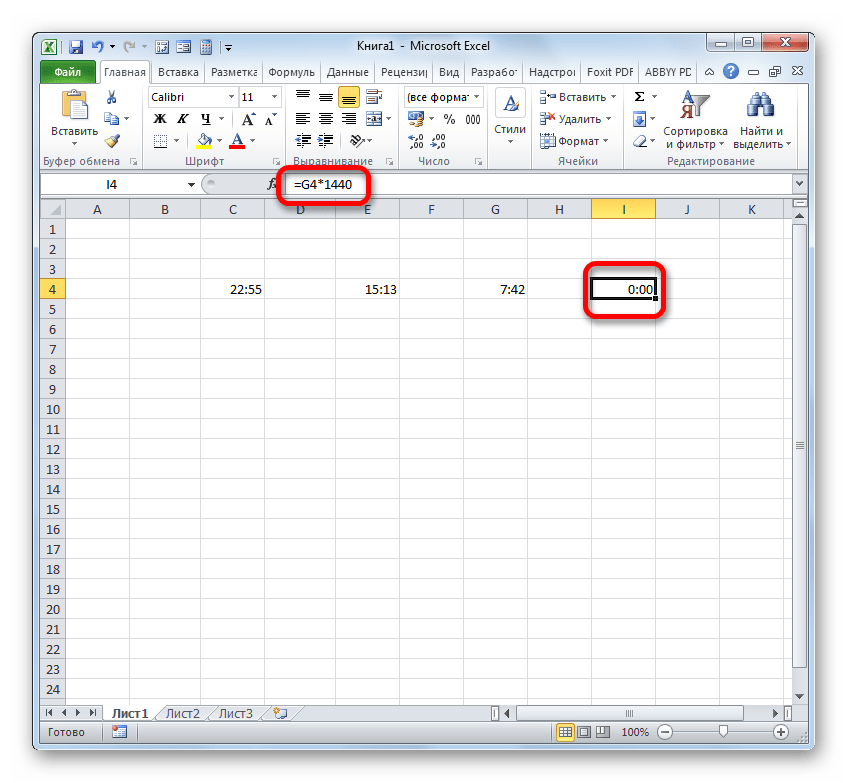
Для того, чтобы получить минуты, нам следует предыдущий результат умножить на коэффициент 1440. Этот коэффициент получается путем умножения количества минут в часе (60) и часов в сутках (24).

Итак, устанавливаем символ «=» в пустой ячейке на листе. После этого производим клик по тому элементу листа, где находится разность вычитания времени (7:42). После того, как координаты данной ячейки отобразились в формуле, жмем на символ «умножить» (*) на клавиатуре, а затем на ней же набираем число 1440. Для получения результата клацаем по Enter.

Но, как видим, опять результат отобразился некорректно (0:00). Это связано с тем, что при умножении элемент листа был автоматически переформатирован в формат времени. Для того, чтобы отобразилась разность в минутах нам требуется вернуть ему общий формат.

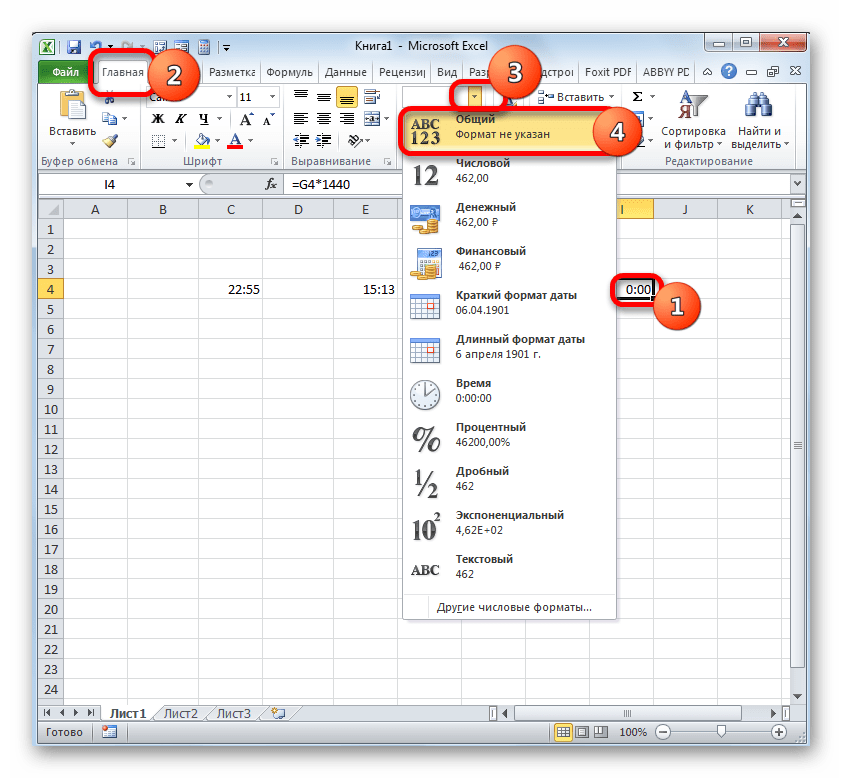
Итак, выделяем данную ячейку и во вкладке «Главная» клацаем по уже знакомому нам треугольнику справа от поля отображения форматов. В активировавшемся списке выбираем вариант «Общий».

Можно поступить и по-другому. Выделяем указанный элемент листа и производим нажатие клавиш Ctrl+1. Запускается окно форматирования, с которым мы уже имели дело ранее. Перемещаемся во вкладку «Число» и в списке числовых форматов выбираем вариант «Общий». Клацаем по «OK».

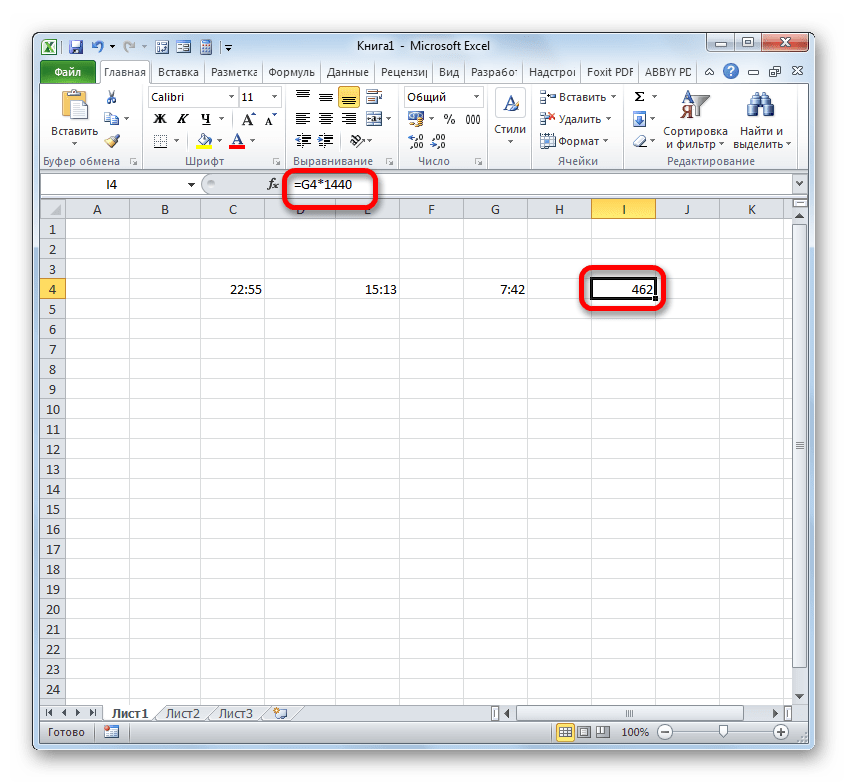
После использования любого из этих вариантов ячейка переформатируется в общий формат. В ней отобразится разность между указанным временем в минутах. Как видим, разница между 15:13 и 22:55 составляет 462 минуты.

Урок: Как перевести часы в минуты в Экселе

Как видим, нюансы подсчета разности в Excel зависят от того, с данными какого формата пользователь работает. Но, тем не менее, общий принцип подхода к данному математическому действию остается неизменным. Нужно из одного числа вычесть другое. Это удается достичь при помощи математических формул, которые применяются с учетом специального синтаксиса Excel, а также при помощи встроенных функций.

Источник

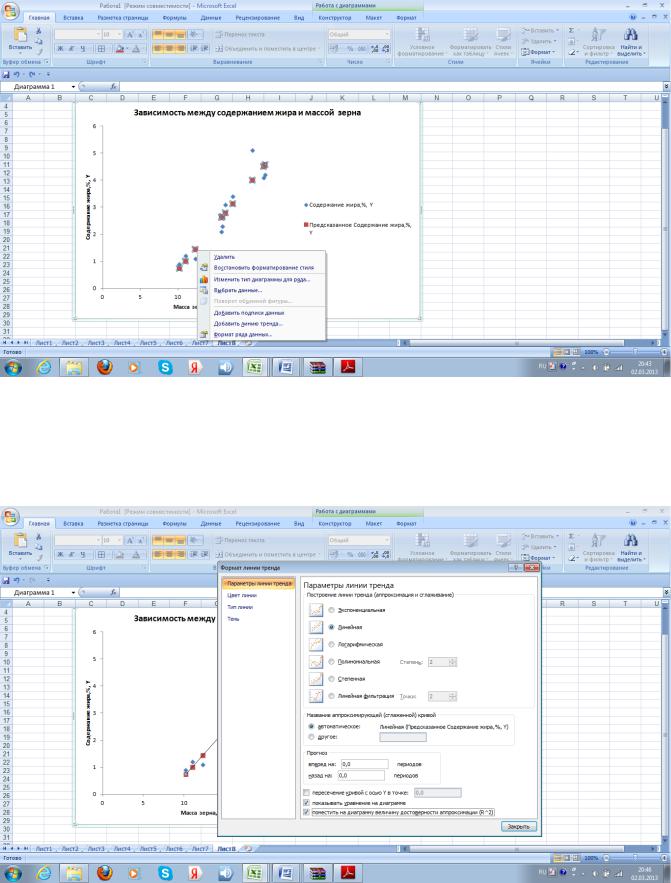
Для построения теоретической линии и уравнения регрессии подведем курсор мышки к данным графика (фактическим точкам жира), при нажатии на правую клавишу появляется контекстное меню, выберем Добавить линию тренда (рис. 7.7)

Рис. 7.7. Контекстное меню для работы с данными.

После выбора Добавить линию тренда появляется всплывающее окно с параметрами линии тренда. Так как мы предполагаем, что наша зависимость носит прямолинейный характер, для аппроксимации и сглаживания эмпирической линии выберем Линейная. Выберем

автоматическое сглаживание, галочкой укажем показать уравнение на диаграмме и поместить R^2 (рис.7.8).

Рис. 7.8. Формат линии тренда.

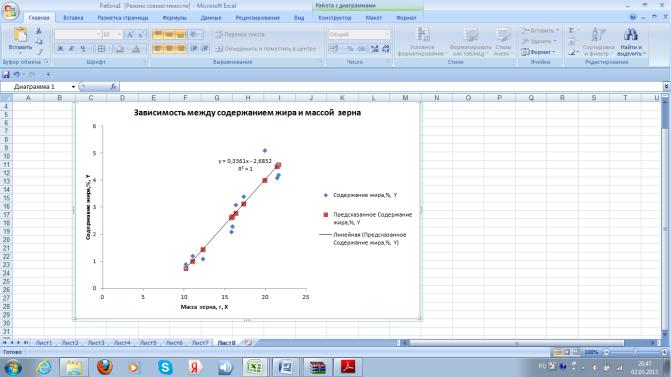
После выбора параметров линии тренда на листе 8 в автоматическом режиме получаем график зависимости между содержанием жира и массой зерна с наименованием осей У. Х и расшифровкой легенды графика (рис. 7,9). На графике голубыми кубиками отмечено фактическое содержание жира, красными ромбиками предсказанное или теоретическое содержание жира.

На графике показано уравнение регрессии: Y= 0,34X – 2.68. Как из таблицы на рис.7.5, так и из этого уравнения видно, что коэффициент регрессии составляет 0,34%. Данный коэффициент свидетельствует, что увеличении массы зерна на 1 г, содержание жира увеличивается на 0,34%.

Рис. 7.9. График зависимости между содержанием жира и массой зерна.

8. Дисперсионный анализ данных однофакторного вегетационного и полевого опытов с полной рандомизацией вариантов» Работа 10 .

Однофакторный дисперсионный анализ

Пример. Влияние азотных удобрений на урожайность овса, г/сосуд

	Варианты опыта		Повторность
	1	2	3	4

1.	Без удобрения (st)	15,8	15,5	16,1	15,0
2.	Аммиачная селитра	29,3	30,4	28,1	31,6
3.	Сульфат аммония	25,8	26,8	25,9	24,7
4.	Мочевина	25,7	24,0	23,8	25,7

1. В активный лист программы Excel введем исходные данные вышеприведенного примера, расположив таблицу в следующем виде (рис.8.1):

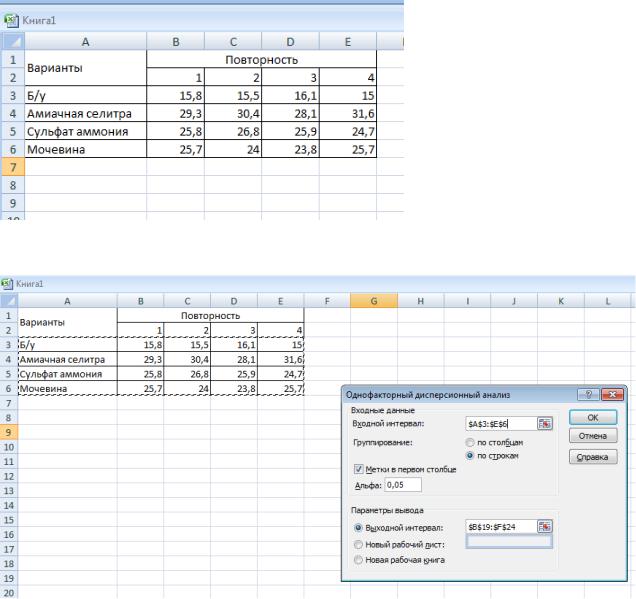
Рис. 8.1. Исходные данные

2. Из Пакета анализа выберем инструмент Однофакторный дисперсионный анализ

Рис. 8.2. Диалоговое окно Однофакторный дисперсионный анализ.

3.В появившемся окне укажем входной интервал А3:E6. Входной интервал должен включать только диапазон, состоящий из перечня вариантов и цифровых данных по этим вариантам

(рис.8.2).

4.Группирование по строкам (рис.8.2).

5.Укажем метки в первом столбце (рис.8.2). Это необходимо для того, чтобы в выходных таблицах автоматически печатались наименования вариантов.

6.Альфа – выбор уровня значимости 0,05 или 0,01

7.Выбираем выходной интервал для размещения результатов дисперсионного анализа: на данном листе или новом листе и нажимаем ОК (рис. 8.2.)

8.Получаем таблицу дисперсионного анализа «Однофакторный дисперсионный анализ» (рис.8. 3.)

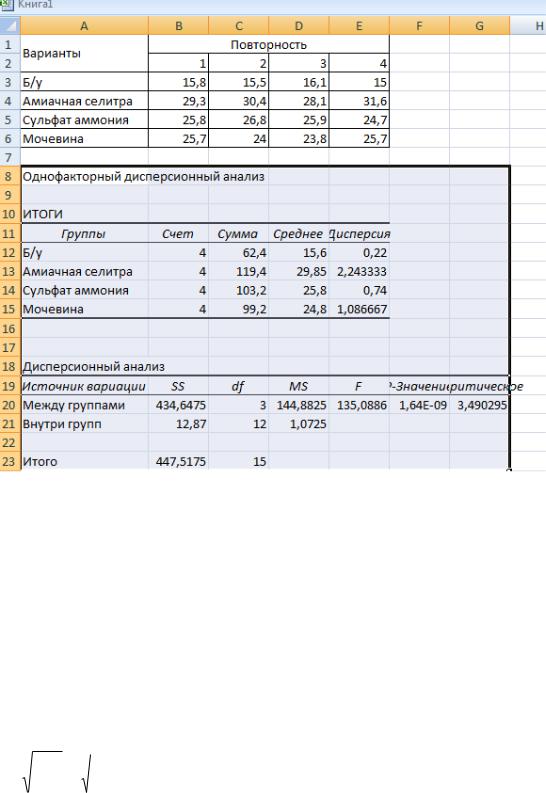
Рис. 8.3. Таблица дисперсионного анализа

9. В первой итоговой таблице Excel под Группами подразумевается «Варианты», Счет – это повторность каждого варианта (n =4).

10. Во второй таблице термины и формулы подразумевают: Между группами – «Варианты», Внутри групп – «Остаток», SS – сумма квадратов отклонений (СКО или Сy), df – степени свободы, MS – средний квадрат отклонений или дисперсия – S2 .

11. Fф = 135,08; F05 = 3,49 Так как Fф > F05, H0≠0, нулевая гипотеза отвергается – в опыте в целом есть существенные различия, поэтому необходимо рассчитать НСР.

В Пакете анализа программы Excel, а также в большинстве других статистических пакетов не предусмотрена оценка существенности средних по НСР – четвертый этап дисперсионного анализа, поэтому ошибку разности (Sd) можно рассчитать для нашего примера следующим образом:

2 1,0725

0,73

HCP

∙*S

= 2,18∙ 0,73 = 1,59 г/ сосуд

t05 = 2,18 при df (cce) = 12 степенях свободы для остатка

К сожалению, необходимо отметить, что в Пакете данных программы Excel невозможно провести дисперсионный анализ как однофакторного полевого опыта, заложенного методом организованных повторений (Работа 11), так и многофакторного полевого опыта с организованными повторениями и расщепленными делянками (Работа 12).

Инструменты в Пакете анализа «Двухфакторный дисперсионный анализ с повторениями и без повторений» предназначены для обработки данных двухфакторного вегетационного опыта (опыта с независимыми выборками).

9. Дисперсионный анализ данных двухфакторного вегетационного и полевого опытов с полной рандомизацией вариантов.

Двухфакторный дисперсионный анализ с повторениями.

Пример. В полевом опыте, проведенном методом полной рандомизации (независимые выборки) изучается два фактора: фактор А – полив в 2-х градациях (а0– без полива, а2 – полив), фактор В – дозы минеральных удобрений (в1 – NPK в2 – 2NPK в3 – 3NPK). Опыт проведен в 4- х кратной повторности (n=4).

Урожай зерна ячменя в двухфакторном опыте 2х3, ц/га

Орошение, А		Удобрения, В

NPK		2NPK	3NPK

	24,1		28,4	28,7
Без полива	25,8		29,7	30,4

23,0		30,1	32,0

	27,0		27,4	27,0

	30,7		46,7	59,4

Полив	34,4		45,4	50,7
34,0		47,1	64,5

	31,0		46,3	60,1

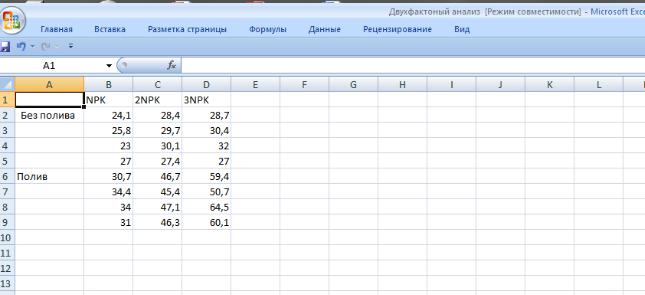
1. В активный лист программы Excel введем исходные данные вышеприведенного примера, расположив таблицу в следующем виде (рис.9.1):

Рис. 9. 1 Исходные данные

2. Из Пакета анализа выберем инструмент Двухфакторный дисперсионный анализ с

повторениями

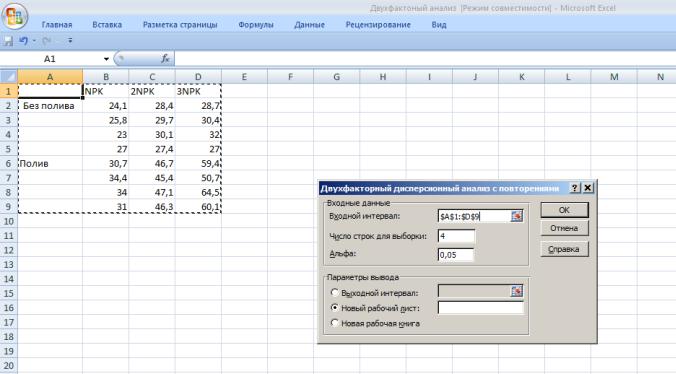
3.В появившемся окне укажем входной интервал А1:D9. Входной интервал должен включать только диапазон, состоящий из перечня вариантов и цифровых данных по этим вариантам (рис.9. 2).

4.В окне Число строк для выборки – укажем 4 (это повторность опыта) (рис.9.2).

5.Альфа – выбор уровня значимости 0,05 или 0,01

7.Выбираем выходной интервал для размещения результатов дисперсионного анализа: выбираем на новом листе и нажимаем ОК (рис. 9.2.)

8.Получаем таблицу дисперсионного анализа «Двухфакторный дисперсионный анализ с повторениями» (рис. 9.3.)

Рис.9. 3. Таблица дисперсионного анализа

9.В первой итоговой таблице Excel представлены суммы и средние значения по факторам А и В, которые удобнее представить в виде обобщенной таблицы средних по изучаемым вариантам. Счет – это повторность каждого варианта (n =4).

10.Во второй таблице термины и формулы подразумевают: Выборка – «Фактор А», Столбцы – «Фактор В», Взаимодействие – «Взаимодействие АВ», Внутри – «Остаток». SS – сумма

квадратов отклонений (СКО или Сy), df – степени свободы, MS – средний квадрат отклонений или дисперсия – S2 .

11.С помощью двухфакторного дисперсионного анализа по критерию Фишера оценивается

отдельно существенность изучаемых факторов и их взаимодействия. В нашем примере для фактора А Fф = 249,78; F05 = 4,41, для фактора В Fф = 60,66; F05 = 3,55, для взаимодействия АВ Fф = 29,85; F05 = 3,55. Так как Fф > F05, H0≠0, нулевая гипотеза отвергается – действие и взаимодействие полива и удобрений значимо на 5% ном уровне значимости. Для оценки существенности разности средних необходимо рассчитать НСР.

2S 2

2 7,8332

1,98

2,10 1,98 4,15

HCP

ц/га.

t05 = 2,10 при df (cce) = 18 степенях свободы для остатка

S A		2S 2				2 7,8332		1,14		HCPA	t	S A 2,10 1,14 2,39 ц/га.
	e

d	n	b					4 3			05	05	d


			2S 2
S B				2 7,8332	1,40		HCPB	t	S A 2,10 1,39 2,93 ц/га.
		e
d	n	a					4 2			05	05	d

Итоговая таблица

Фактор А –					Фактор В – удобрения	В среднем по
полив									NPK		2NPK		3NPK	фактору А
Без полива					25,0		28,9		29,5		27,8
Полив									32,5		46,4		58,7		45,9
В среднем по					28,8		37,6		44,1
фактору В

HCP 4,15 ; HCPA 2,39	; HCPB	2,93
05										05				05
С помощью HCP 4,15	оцениваются различия между частными средними (с
										05

поливом и без полива при разных дозах удобрений: 28,9 – 25, 0; 58,7 – 29,5; 46,4 –

32,5 и т.д.).

	HCPA	2,39 оценивает только главный эффект фактора А ( 45,9 – 27,8), а
	05
HCPB	2,93 различия главного эффекта фактора В ( 44,1 – 28,8; 37,6 – 28,8; 44,1 –
05
37,6).

Рекомендуемая литература

1.Microsoft Excel – Викиучебник. http://ru.wikibooks.org/wiki/Microsoft_Excel

2.Макарова Н.В., Трофимец В.Я. Статистика в Excel: Учеб. пособие.– М.: Финансы и статистика, 2002. – 368 с.: ил.

3.Мурашкин С.В., Николаева З.В. Методы учётов и статистическая обработка экспериментальных данных при использовании программы Microsoft Еxcel на примере исследований сосущих вредителей яблони. — Великие Луки: Редакционно-издательский отдел ФГОУ ВПО «Великолукская ГСХА», 2006, 120 с.

4.Обработка экспериментальных данных в MS Excel : методические указания к выполнению лабораторных работ для студентов дневной формы обучения / сост. Е. Г. Агапова, Е. А. Битехтина. – Хабаровск : Изд-во Тихоокеан. гос. унта, 2012. – 32 с.

Учебное издание

Усманов Раиф Рафикович

ВЫПОЛНЕНИЕ ЗАДАНИЙ ПО КУРСУ «ОСНОВЫ НАУЧНЫХ ИССЛЕДОВАНИЙ В АГРОНОМИИ»

В ПРОГРАММЕ «EXCEL»

Методические указания

Подписано в печать 2013 г. Формат Усл. печ. л. Тираж 120 экз. Зак.

Издательство РГАУ – МСХА имени К.А. Тимирязева 127550, Москва, Тимирязевская ул., 44

Тел.: 977-00-12, 977-26-90, 977-40-64

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

A T-test is a way of deciding if there are statistically significant differences between datasets, using a Student’s t-distribution. The T-Test in Excel is a two-sample T-test comparing the means of two samples. This article explains what statistical significance means and shows how to do a T-Test in Excel.

Instructions in this article apply to Excel 2019, 2016, 2013, 2010, 2007; Excel for Microsoft 365 and Excel Online.

Image Source, Getty Images

What is Statistical Significance?

Imagine you want to know which of two dice will give a better score. You roll the first die and get a 2; you roll the second die and get a 6. Does this tell you the second die usually gives higher scores? If you answered, “Of course not,” then you already have some understanding of statistical significance. You understand the difference was due to the random change in the score, each time a die is rolled. Because the sample was very small (only one roll) it didn’t show anything significant.

Now imagine you roll each die 6 times:

The first die rolls 3, 6, 6, 4, 3, 3; Mean = 4.17
The second die rolls 5, 6, 2, 5, 2, 4; Mean = 4.00

Does this now prove the first die gives higher scores than the second? Probably not. A small sample with a relatively small difference between the means makes it likely the difference is still due to random variations. As we increase the number of dice rolls it becomes difficult to give a common sense answer to the question — is the difference between the scores the result of random variation or is one actually more likely to give higher scores than the other?

Significance is the probability that an observed difference between samples is due to random variations. Significance is often called the alpha level or simply ‘α.’ The confidence level, or simply ‘c,’ is the probability that the difference between the samples is not due to random variation; in other words, that there’s a difference between the underlying populations. Therefore: c = 1 – α

We can set ‘α’ at whatever level we want, to feel confident we’ve proven significance. Very often α=5% is used (95% confidence), but if we want to be really sure that any differences are not caused by random variation, we might apply a higher confidence level, using α=1% or even α=0.1%.

Various statistical tests are used to calculate significance in different situations. T-tests are used to determine whether the means of two populations are different and F-tests are used to determine whether the variances are different.

Why Test for Statistical Significance?

When comparing different things, we need to use significance testing to determine if one is better than the other. This applies to many fields, for example:

In business, people need to compare different products and marketing methods.
In sports, people need to compare different equipment, techniques, and competitors.
In engineering, people need to compare different designs and parameter settings.

If you want to test whether something performs better than something else, in any field, you need to test for statistical significance.

What is a Student’s T-Distribution?

A Student’s t-distribution is similar to a normal (or Gaussian) distribution. These are both bell-shaped distributions with most results close to the mean, but some rare events are quite far from the mean in both directions, referred to as the tails of the distribution.

The exact shape of the Student’s t-distribution depends on the sample size. For samples of more than 30 it’s very similar to the normal distribution. As the sample size is reduced, the tails get larger, representing the increased uncertainty that comes from making inferences based on a small sample.

How to Do a T-Test in Excel

Before you can apply a T-Test to determine whether there’s a statistically significant difference between the means of two samples, you must first perform an F-Test. This is because different calculations are performed for the T-Test depending on whether there’s a significant difference between the variances.

You will need the Analysis Toolpak add-in enabled to perform this analysis.

Checking and Loading the Analysis Toolpak Add-In

To check and activate the Analysis Toolpak follow these steps:

Select the FILE tab >select Options.
In the Options dialogue box, select Add-Ins from the tabs on the left-hand side.
At the bottom of the window, select the Manage drop-down menu, then select Excel Add-ins. Select Go.
Ensure the check-box next to Analysis Toolpak is checked, then select OK.
The Analysis Toolpak is now active and you are ready to apply F-Tests and T-Tests.

Performing an F-Test and a T-Test in Excel

Enter two datasets into a spreadsheet. In this case, we’re considering the sales of two products during a week. The mean daily sales value for each product is also calculated, together with its standard deviation.
Select the Data tab > Data Analysis
Select F-Test Two-Sample for Variances from the list, then select OK.

The F-Test is highly sensitive to non-normality. It may therefore be safer to use a Welch test, but this is more difficult in Excel.
Select the Variable 1 Range and Variable 2 Range; set the Alpha (0.05 gives 95% confidence); select a cell for the top left corner of the output, considering that this will fill 3 columns and 10 rows. Select OK.

For the for Variable 1 Range, the sample with the largest standard deviation (or variance) must be selected.
View the F-Test results to determine whether there is a significant difference between the variances. The results give three important values:
- F: The ratio between the variances.
- P(F<=f) one-tail: The probability that variable 1 doesn’t actually have a larger variance than variable 2. If this is larger than alpha, which is generally 0.05, then there’s no significant difference between the variances.
- F Critical one-tail: The value of F that would be required to give P(F<=f)=α. If this value is greater than F, this also indicates there’s no significant difference between the variances.
P(F<=f) can also be calculated using the FDIST function with F and the degrees of freedom for each sample as its inputs. Degrees of freedom is simply the number of observations in a sample minus one.
Now that you know whether there is a difference between the variances you can select the appropriate T-Test. Select the Data tab > Data Analysis, then select either t-Test: Two-Sample Assuming Equal Variances or t-Test: Two-Sample Assuming Unequal Variances.
Regardless of which option you chose in the previous step, you will be presented with the same dialogue box to enter the details of the analysis. To start, select the ranges containing the samples for Variable 1 Range and Variable 2 Range.
Assuming you want to test for no difference between the means, set the Hypothesized Mean Difference to zero.
Set the significance level Alpha (0.05 gives 95% confidence), and select a cell for the top left corner of the output, considering that this will fill 3 columns and 14 rows. Select OK.
Review the results to decide if there’s a significant difference between the means.

Just as with the F-Test, if the p-value, in this case P(T<=t), is greater than alpha, then there’s no significant difference. However, in this case there are two p-values given, one for a one-tail test and the other for a two-tail test. In this case, use the two-tail value since either variable having a greater mean would be a significant difference.

Thanks for letting us know!

Get the Latest Tech News Delivered Every Day

Источник

Содержание

Использование описательной статистики
Подключение «Пакета анализа»
Размах вариации
Вычисление коэффициента вариации
Шаг 1: расчет стандартного отклонения
Шаг 2: расчет среднего арифметического
Шаг 3: нахождение коэффициента вариации
Простая формула для расчета объема выборки
Пример расчета объема выборки
Задачи о генеральной доле
По части судить о целом
Как рассчитать объем выборки
Как определить статистические выбросы и сделать выборку для их удаления в Excel
Способ 1: применение расширенного автофильтра
Способ 2: применение формулы массива
СРЗНАЧ()
СРЗНАЧЕСЛИ()
МАКС()
МИН()

Использование описательной статистики

Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.

В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:

Медиана;
Мода;
Дисперсия;
Среднее;
Стандартное отклонение;
Стандартная ошибка;
Асимметричность и др.

Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.

Подключение «Пакета анализа»

Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.

Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».

В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».

Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».

После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.

Размах вариации

Размах вариации – разница между максимальным и минимальным значением:

Ниже приведена графическая интерпретация размаха вариации.

Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.

С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.

Вычисление коэффициента вариации

Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.

В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.

Шаг 1: расчет стандартного отклонения

Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.

Синтаксис данных функций выглядит соответствующим образом:

= СТАНДОТКЛОН(Число1;Число2;…)
= СТАНДОТКЛОН.Г(Число1;Число2;…)
= СТАНДОТКЛОН.В(Число1;Число2;…)

Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.

Выполняется активация Мастера функций, который запускается в виде отдельного окна с перечнем аргументов. Переходим в категорию «Статистические» или «Полный алфавитный перечень». Выбираем наименование «СТАНДОТКЛОН.Г» или «СТАНДОТКЛОН.В», в зависимости от того, по генеральной совокупности или по выборке следует произвести расчет. Жмем на кнопку «OK».

Открывается окно аргументов данной функции. Оно может иметь от 1 до 255 полей, в которых могут содержаться, как конкретные числа, так и ссылки на ячейки или диапазоны. Ставим курсор в поле «Число1». Мышью выделяем на листе тот диапазон значений, который нужно обработать. Если таких областей несколько и они не смежные между собой, то координаты следующей указываем в поле «Число2» и т.д. Когда все нужные данные введены, жмем на кнопку «OK»

В предварительно выделенной ячейке отображается итог расчета выбранного вида стандартного отклонения.

Шаг 2: расчет среднего арифметического

Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция – СРЗНАЧ. Вычислим её значение на конкретном примере.

«Вставить функцию»

В статистической категории Мастера функций ищем наименование «СРЗНАЧ». После его выделения жмем на кнопку «OK».

Запускается окно аргументов СРЗНАЧ. Аргументы полностью идентичны тем, что и у операторов группы СТАНДОТКЛОН. То есть, в их качестве могут выступать как отдельные числовые величины, так и ссылки. Устанавливаем курсор в поле «Число1». Так же, как и в предыдущем случае, выделяем на листе нужную нам совокупность ячеек. После того, как их координаты были занесены в поле окна аргументов, жмем на кнопку «OK».

Результат вычисления среднего арифметического выводится в ту ячейку, которая была выделена перед открытием Мастера функций.

Шаг 3: нахождение коэффициента вариации

Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.

«Главная»

«Число»

«Процентный»

Снова возвращаемся к ячейке для вывода результата. Активируем её двойным щелчком левой кнопки мыши. Ставим в ней знак «=». Выделяем элемент, в котором расположен итог вычисления стандартного отклонения. Кликаем по кнопке «разделить» (/) на клавиатуре. Далее выделяем ячейку, в которой располагается среднее арифметическое заданного числового ряда. Для того, чтобы произвести расчет и вывести значение, щёлкаем по кнопке Enter на клавиатуре.

Как видим, результат расчета выведен на экран.

Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.

Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:

Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.

После этого, чтобы рассчитать значение и показать результат на экране монитора, щелкаем по кнопке Enter.

Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.

Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.

Разделы: Математика

Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.

Сегодня мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
Для начала вспомним:

– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)

– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)

– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).

– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).

– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).

Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.

Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):

23 25 24 25 30 24 30 26 28 26
32 33 31 31 25 33 25 29 30 28
23 30 29 24 33 30 30 28 26 25
26 29 27 29 26 28 27 26 29 28
29 30 27 30 28 32 28 26 30 26
31 27 30 27 33 28 26 30 31 29
27 30 30 29 27 26 28 31 29 28
33 27 30 33 26 31 34 28 32 22
29 30 27 29 34 29 32 29 29 30
29 29 36 29 29 34 23 28 24 28

рассчитать числовые характеристики:

моду
медиану
размах ряда
построить полигон частот
построить столбчатую и круговую диаграммы
раскрыть смысловую сторону каждой характеристики

1. Занести данные в EXCEL, каждое число в отдельную ячейку.

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем – статистические, в списке: МОДА

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_о = 29 (чел) – Фирм у которых в штате 29 человек больше всего.

Используя тот же путь вычисляем медиану.

Вставка – Функция – Статистические – Медиана.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_е = 29 (чел) – среднее значение сотрудников в фирме.

Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.

Вставка – Функция – Статистические – МАКС.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наибольшее значение = 36.

Вставка – Функция – Статистические – МИН.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наименьшее значение = 22.

36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.

Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения x_i случайной величины меняются от 22 до 36 включительно шагом 1.

x_i	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
n_i

Чтобы сосчитать частоту каждого значения воспользуемся

Вставка – Функция – Статистические – СЧЕТЕСЛИ.

В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22

Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.

x_i	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
n_i	1	3	4	5	11	9	13	18	16	6	4	6	3	0	1

Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические – СУММА). Должно получиться 100 (количество всех фирм).

Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)

Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.

Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).

Диаграмма – Стандартные – Круговая.

Диаграмма – Стандартные – Гистограмма.

4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.

Простая формула для расчета объема выборки

где: n – объем выборки;

z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности. Этот показатель характеризует возможность, вероятность попадания ответов в специальный – доверительный интервал. На практике уровень доверительности часто принимают за 95% или 99%. Тогда значения z будут соответственно 1,96 и 2,58;

p – вариация для выборки, в долях. По сути, p – это вероятность того, что респонденты выберут той или иной вариант ответа. Допустим, если мы считаем, что четверть опрашиваемых выберут ответ «Да», то p будет равно 25%, то есть p = 0,25;

q = (1 – p);

e – допустимая ошибка, в долях.

Пример расчета объема выборки

Компания планирует провести социологическое исследование с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».

Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95%, тогда нормированное отклонение z = 1,96. Вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они – «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. Допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.

Подставляем эти данные в формулу и считаем:

Получаем объем выборки n = 96 человек.

Задачи о генеральной доле

На вопрос «Накрывает ли доверительный интервал заданное значение p₀?» — можно ответить, проверив статистическую гипотезу H₀:p=p₀. При этом предполагается, что опыты проводятся по схеме испытаний Бернулли (независимы, вероятность p появления события А постоянна). По выборке объема n определяют относительную частоту p^* появления события A: где m — количество появлений события А в серии из n испытаний. Для проверки гипотезы H₀ используется статистика, имеющая при достаточно большом объеме выборки стандартное нормальное распределение (табл. 1).
Таблица 1 – Гипотезы о генеральной доле

Гипотеза	H₀:p=p₀	H₀:p₁=p₂
Предположения	Схема испытаний Бернулли	Схема испытаний Бернулли
Оценки по выборке
Статистика K
Распределение статистики K	Стандартное нормальное N(0,1)	Стандартное нормальное N(0,1)

Пример №1. С помощью случайного повторного отбора руководство фирмы провело выборочный опрос 900 своих служащих. Среди опрошенных оказалось 270 женщин. Постройте доверительный интервал, с вероятностью 0.95 накрывающий истинную долю женщин во всем коллективе фирмы.
Решение. По условию выборочная доля женщин составляет (относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
(относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле

Значение u_кр находим по таблице функции Лапласа из соотношения 2Ф(u_кр)=γ, т.е. Функция Лапласа (приложение 1) принимает значение 0.475 при u_кр=1.96. Следовательно, предельная ошибка Функция Лапласа (приложение 1) принимает значение 0.475 при u_кр=1.96. Следовательно, предельная ошибка и искомый доверительный интервал
(p – ε, p + ε) = (0.3 – 0.18; 0.3 + 0.18) = (0.12; 0.48)
Итак, с вероятностью 0.95 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0.12 до 0.48.

Пример №2. Владелец автостоянки считает день «удачным», если автостоянка заполнена более, чем на 80 %. В течение года было проведено 40 проверок автостоянки, из которых 24 оказались «удачными». С вероятностью 0.98 найдите доверительный интервал для оценки истинной доли «удачных» дней в течение года.
Решение. Выборочная доля «удачных» дней составляет
По таблице функции Лапласа найдем значение u_кр при заданной
доверительной вероятности
По таблице функции Лапласа найдем значение u_кр при заданной
доверительной вероятности
Ф(2.23) = 0.49, u_кр = 2.33.
Считая отбор бесповторным (т.е. две проверки в один день не проводилось), найдем предельную ошибку:
где n=40, N = 365 (дней). Отсюда
где n=40, N = 365 (дней). Отсюда
и доверительный интервал для генеральной доли: (p – ε, p + ε) = (0.6 – 0.17; 0.6 + 0.17) = (0.43; 0.77)
С вероятностью 0.98 можно ожидать, что доля «удачных» дней в течение года находится в интервале от 0.43 до 0.77.

Пример №3. Проверив 2500 изделий в партии, обнаружили, что 400 изделий высшего сорта, а n–m – нет. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю высшего сорта с точностью до 0.01?
Решение ищем по формуле определения численности выборки для повторного отбора.

Ф(t) = γ/2 = 0.95/2 = 0.475 и этому значению по таблице Лапласа соответствует t=1.96
Выборочная доля w = 0.16; ошибка выборки ε = 0.01

Пример №4. Партия изделий принимается, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 0.97. Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости α=0,02 принять партию?
Решение. Сформулируем основную и альтернативную гипотезы.
H₀:p=p₀=0,97 — неизвестная генеральная доля p равна заданному значению p₀=0,97. Применительно к условию — вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, равна 0.97; т.е. партию изделий можно принять.
H₁:p<0,97 – вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, меньше 0.97; т.е. партию изделий нельзя принять. При такой альтернативной гипотезе критическая область будет левосторонней.
Наблюдаемое значение статистики K (таблица) вычислим при заданных значениях p₀=0,97, n=200, m=193

Критическое значение находим по таблице функции Лапласа из равенства

По условию α=0,02 отсюда Ф(Ккр)=0,48 и Ккр=2,05. Критическая область левосторонняя, т.е. является интервалом (-∞;-K_kp)= (-∞;-2,05). Наблюдаемое значение К_набл=-0,415 не принадлежит критической области, следовательно, на данном уровне значимости нет оснований отклонять основную гипотезу. Партию изделий принять можно.

Пример №5. Два завода изготавливают однотипные детали. Для оценки их качества сделаны выборки из продукции этих заводов и получены следующие результаты. Среди 200 отобранных изделий первого завода оказалось 20 бракованных, среди 300 изделий второго завода — 15 бракованных.
На уровне значимости 0.025 выяснить, имеется ли существенное различие в качестве изготавливаемых этими заводами деталей.
Решение. Это задача о сравнении генеральных долей двух совокупностей. Сформулируем основную и альтернативную гипотезы.
H₀:p₁=p₂ — генеральные доли равны. Применительно к условию — вероятность появления бракованного изделия в продукции первого завода равна вероятности появления бракованного изделия в продукции второго завода (качество продукции одинаково).
H₀:p₁≠p₂ — заводы изготавливают детали разного качества.
Для вычисления наблюдаемого значения статистики K (таблица) рассчитаем оценки по выборке.

Наблюдаемое значение равно

Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
По условию α=0,025 отсюда Ф(Ккр)=0,4875 и Ккр=2,24. При двусторонней альтернативе область допустимых значений имеет вид (-2,24;2,24). Наблюдаемое значение K_набл=2,15 попадает в этот интервал, т.е. на данном уровне значимости нет оснований отвергать основную гипотезу. Заводы изготавливают изделия одинакового качества.

По части судить о целом

О возможности судить о целом по части миру рассказал российский математик П.Л. Чебышев. «Закон больших чисел» простым языком можно сформулировать так: количественные закономерности массовых явлений проявляются только при

достаточном числе наблюдений

. Чем больше выборка, тем лучше случайные отклонения компенсируют друг друга и проявляется общая тенденция.
А.М. Ляпунов чуть позже сформулировал центральную предельную теорему. Она стала фундаментом для создания формул, которые позволяют рассчитать вероятность ошибки (при оценке среднего по выборке) и размер выборки, необходимый для достижения заданной точности.
Строгие формулировки:

С увеличением числа случайных величин их среднее арифметическое стремится к среднему арифметическому математических ожиданий и перестает быть случайным. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
Таким образом з.б.ч. гарантирует устойчивость для средних значений некоторых случайных событий при достаточно длинной серии экспериментов.

Распределение случайной величины, которая получена в результате сложения большого числа независимых случайных величин (ни одно из которых не доминирует, не вносит в сумму определяющего вклада и имеет дисперсию значительно меньшею по сравнению с дисперсией суммы) имеет распределение, близкое к нормальному.
Из ц.п.т. следует, что ошибки выборки также подчиняется нормальному распределению.

Еще раз: чтобы корректно оценивать популяцию по выборке, нам нужна не обычная выборка, а репрезентативная выборка достаточного размера. Начнем с определения этого самого размера.

Как рассчитать объем выборки

Достаточный размер выборки зависит от следующих составляющих:

изменчивость признака (чем разнообразней показания, тем больше наблюдений нужно, чтобы это уловить);
размер эффекта (чем меньшие эффекты мы стремимся зафиксировать, тем больше наблюдений необходимо);
уровень доверия (уровень вероятности при который мы готовы отвергнуть нулевую гипотезу)

ЗАПОМНИТЕ
Объем выборки зависит от изменчивости признака и планируемой строгости эксперимента

Формулы для расчета объема выборки:

Формулы расчета объема выборки

Ошибка выборки значительно возрастает, когда наблюдений меньше ста. Для исследований в которых используется 30-100 объектов применяется особая статистическая методология: критерии, основанные на распределении Стьюдента или бутстрэп-анализ. И наконец, статистика совсем слаба, когда наблюдений меньше 30.

График зависимости ошибки выборки от ее объема при оценке доли признака в г.с.

Чем больше неопределенность, тем больше ошибка. Максимальная неопределенность при оценке доли — 50% (например, 50% респондентов считают концепцию хорошей, а другие 50% плохой). Если 90% опрошенных концепция понравится — это, наоборот, пример согласованности. В таких случаях оценить долю признака по выборке проще.

Для экспонирования и выделения цветом значений статистических выбросов от медианы можно использовать несколько простых формул и условное форматирование.

Первым шагом в поиске значений выбросов статистики является определение статистического центра диапазона данных. С этой целью необходимо сначала определить границы первого и третьего квартала. Определение границ квартала – значит разделение данных на 4 равные группы, которые содержат по 25% данных каждая. Группа, содержащая 25% наибольших значений, называется первым квартилем.

Границы квартилей в Excel можно легко определить с помощью простой функции КВАРТИЛЬ. Данная функция имеет 2 аргумента: диапазон данных и номер для получения желаемого квартиля.

В примере показанному на рисунке ниже значения в ячейках E1 и E2 содержат показатели первого и третьего квартиля данных в диапазоне ячеек B2:B19:

Вычитая от значения первого квартиля третьего, можно определить набор 50% статистических данных, который называется межквартильным диапазоном. В ячейке E3 определен размер межквартильного диапазона.

В этом месте возникает вопрос, как сильно данное значение может отличаться от среднего значения 50% данных и оставаться все еще в пределах нормы? Статистические аналитики соглашаются с тем, что для определения нижней и верхней границы диапазона данных можно смело использовать коэффициент расширения 1,5 умножив на значение межквартильного диапазона. То есть:

Нижняя граница диапазона данных равна: значение первого квартиля – межкваритльный диапазон * 1,5.
Верхняя граница диапазона данных равна: значение третьего квартиля + расширенных диапазон * 1,5.

Как показано на рисунке ячейки E5 и E6 содержат вычисленные значения верхней и нижней границы диапазона данных. Каждое значение, которое больше верхней границы нормы или меньше нижней границы нормы считается значением статистического выброса.

Чтобы выделить цветом для улучшения визуального анализа данных можно создать простое правило для условного форматирования.

Способ 1: применение расширенного автофильтра

Наиболее простым способом произвести отбор является применение расширенного автофильтра. Рассмотрим, как это сделать на конкретном примере.

Выделяем область на листе, среди данных которой нужно произвести выборку. Во вкладке «Главная» щелкаем по кнопке «Сортировка и фильтр». Она размещается в блоке настроек «Редактирование». В открывшемся после этого списка выполняем щелчок по кнопке «Фильтр».

Есть возможность поступить и по-другому. Для этого после выделения области на листе перемещаемся во вкладку «Данные». Щелкаем по кнопке «Фильтр», которая размещена на ленте в группе «Сортировка и фильтр».

После этого действия в шапке таблицы появляются пиктограммы для запуска фильтрования в виде перевернутых острием вниз небольших треугольников на правом краю ячеек. Кликаем по данному значку в заглавии того столбца, по которому желаем произвести выборку. В запустившемся меню переходим по пункту «Текстовые фильтры». Далее выбираем позицию «Настраиваемый фильтр…».

Активируется окно пользовательской фильтрации. В нем можно задать ограничение, по которому будет производиться отбор. В выпадающем списке для столбца содержащего ячейки числового формата, который мы используем для примера, можно выбрать одно из пяти видов условий:
- равно;
- не равно;
- больше;
- больше или равно;
- меньше.
Давайте в качестве примера зададим условие так, чтобы отобрать только значения, по которым сумма выручки превышает 10000 рублей. Устанавливаем переключатель в позицию «Больше». В правое поле вписываем значение «10000». Чтобы произвести выполнение действия, щелкаем по кнопке «OK».

Как видим, после фильтрации остались только строчки, в которых сумма выручки превышает 10000 рублей.

Но в этом же столбце мы можем добавить и второе условие. Для этого опять возвращаемся в окно пользовательской фильтрации. Как видим, в его нижней части есть ещё один переключатель условия и соответствующее ему поле для ввода. Давайте установим теперь верхнюю границу отбора в 15000 рублей. Для этого выставляем переключатель в позицию «Меньше», а в поле справа вписываем значение «15000».
Кроме того, существует ещё переключатель условий. У него два положения «И» и «ИЛИ». По умолчанию он установлен в первом положении. Это означает, что в выборке останутся только строчки, которые удовлетворяют обоим ограничениям. Если он будет выставлен в положение «ИЛИ», то тогда останутся значения, которые подходят под любое из двух условий. В нашем случае нужно выставить переключатель в положение «И», то есть, оставить данную настройку по умолчанию. После того, как все значения введены, щелкаем по кнопке «OK».

Теперь в таблице остались только строчки, в которых сумма выручки не меньше 10000 рублей, но не превышает 15000 рублей.

Аналогично можно настраивать фильтры и в других столбцах. При этом имеется возможность сохранять также фильтрацию и по предыдущим условиям, которые были заданы в колонках. Итак, посмотрим, как производится отбор с помощью фильтра для ячеек в формате даты. Кликаем по значку фильтрации в соответствующем столбце. Последовательно кликаем по пунктам списка «Фильтр по дате» и «Настраиваемый фильтр».

Снова запускается окно пользовательского автофильтра. Выполним отбор результатов в таблице с 4 по 6 мая 2016 года включительно. В переключателе выбора условий, как видим, ещё больше вариантов, чем для числового формата. Выбираем позицию «После или равно». В поле справа устанавливаем значение «04.05.2016». В нижнем блоке устанавливаем переключатель в позицию «До или равно». В правом поле вписываем значение «06.05.2016». Переключатель совместимости условий оставляем в положении по умолчанию – «И». Для того, чтобы применить фильтрацию в действии, жмем на кнопку «OK».

Как видим, наш список ещё больше сократился. Теперь в нем оставлены только строчки, в которых сумма выручки варьируется от 10000 до 15000 рублей за период с 04.05 по 06.05.2016 включительно.

Мы можем сбросить фильтрацию в одном из столбцов. Сделаем это для значений выручки. Кликаем по значку автофильтра в соответствующем столбце. В выпадающем списке щелкаем по пункту «Удалить фильтр».

Как видим, после этих действий, выборка по сумме выручки будет отключена, а останется только отбор по датам (с 04.05.2016 по 06.05.2016).

В данной таблице имеется ещё одна колонка – «Наименование». В ней содержатся данные в текстовом формате. Посмотрим, как сформировать выборку с помощью фильтрации по этим значениям.
Кликаем по значку фильтра в наименовании столбца. Последовательно переходим по наименованиям списка «Текстовые фильтры» и «Настраиваемый фильтр…».

Опять открывается окно пользовательского автофильтра. Давайте сделаем выборку по наименованиям «Картофель» и «Мясо». В первом блоке переключатель условий устанавливаем в позицию «Равно». В поле справа от него вписываем слово «Картофель». Переключатель нижнего блока так же ставим в позицию «Равно». В поле напротив него делаем запись – «Мясо». И вот далее мы выполняем то, чего ранее не делали: устанавливаем переключатель совместимости условий в позицию «ИЛИ». Теперь строчка, содержащая любое из указанных условий, будет выводиться на экран. Щелкаем по кнопке «OK».

Как видим, в новой выборке существуют ограничения по дате (с 04.05.2016 по 06.05.2016) и по наименованию (картофель и мясо). По сумме выручки ограничений нет.

Полностью удалить фильтр можно теми же способами, которые использовались для его установки. Причем неважно, какой именно способ применялся. Для сброса фильтрации, находясь во вкладке «Данные» щелкаем по кнопке «Фильтр», которая размещена в группе «Сортировка и фильтр».

Второй вариант предполагает переход во вкладку «Главная». Там выполняем щелчок на ленте по кнопке «Сортировка и фильтр» в блоке «Редактирование». В активировавшемся списке нажимаем на кнопку «Фильтр».

При использовании любого из двух вышеуказанных методов фильтрация будет удалена, а результаты выборки – очищены. То есть, в таблице будет показан весь массив данных, которыми она располагает.

Способ 2: применение формулы массива

Сделать отбор можно также применив сложную формулу массива. В отличие от предыдущего варианта, данный метод предусматривает вывод результата в отдельную таблицу.

На том же листе создаем пустую таблицу с такими же наименованиями столбцов в шапке, что и у исходника.

Выделяем все пустые ячейки первой колонки новой таблицы. Устанавливаем курсор в строку формул. Как раз сюда будет заноситься формула, производящая выборку по указанным критериям. Отберем строчки, сумма выручки в которых превышает 15000 рублей. В нашем конкретном примере, вводимая формула будет выглядеть следующим образом:
=ИНДЕКС(A2:A29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))

Естественно, в каждом конкретном случае адрес ячеек и диапазонов будет свой. На данном примере можно сопоставить формулу с координатами на иллюстрации и приспособить её для своих нужд.

Так как это формула массива, то для того, чтобы применить её в действии, нужно нажимать не кнопку Enter, а сочетание клавиш Ctrl+Shift+Enter. Делаем это.

Выделив второй столбец с датами и установив курсор в строку формул, вводим следующее выражение:
=ИНДЕКС(B2:B29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))

Жмем сочетание клавиш Ctrl+Shift+Enter.

Аналогичным образом в столбец с выручкой вписываем формулу следующего содержания:
=ИНДЕКС(C2:C29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))

Опять набираем сочетание клавиш Ctrl+Shift+Enter.

Во всех трех случаях меняется только первое значение координат, а в остальном формулы полностью идентичны.

Как видим, таблица заполнена данными, но внешний вид её не совсем привлекателен, к тому же, значения даты заполнены в ней некорректно. Нужно исправить эти недостатки. Некорректность даты связана с тем, что формат ячеек соответствующего столбца общий, а нам нужно установить формат даты. Выделяем весь столбец, включая ячейки с ошибками, и кликаем по выделению правой кнопкой мыши. В появившемся списке переходим по пункту «Формат ячейки…».

В открывшемся окне форматирования открываем вкладку «Число». В блоке «Числовые форматы» выделяем значение «Дата». В правой части окна можно выбрать желаемый тип отображения даты. После того, как настройки выставлены, жмем на кнопку «OK».

Теперь дата отображается корректно. Но, как видим, вся нижняя часть таблицы заполнена ячейками, которые содержат ошибочное значение «#ЧИСЛО!». По сути, это те ячейки, данных из выборки для которых не хватило. Более привлекательно было бы, если бы они отображались вообще пустыми. Для этих целей воспользуемся условным форматированием. Выделяем все ячейки таблицы, кроме шапки. Находясь во вкладке «Главная» кликаем по кнопке «Условное форматирование», которая находится в блоке инструментов «Стили». В появившемся списке выбираем пункт «Создать правило…».

В открывшемся окне выбираем тип правила «Форматировать только ячейки, которые содержат». В первом поле под надписью «Форматировать только ячейки, для которых выполняется следующее условие» выбираем позицию «Ошибки». Далее жмем по кнопке «Формат…».

В запустившемся окне форматирования переходим во вкладку «Шрифт» и в соответствующем поле выбираем белый цвет. После этих действий щелкаем по кнопке «OK».

На кнопку с точно таким же названием жмем после возвращения в окно создания условий.

Теперь у нас имеется готовая выборка по указанному ограничению в отдельной надлежащим образом оформленной таблице.

СРЗНАЧ()

Статистическая функция СРЗНАЧ возвращает среднее арифметическое своих аргументов.

Данная функция может принимать до 255 аргументов и находить среднее сразу в нескольких несмежных диапазонах и ячейках:

Если в рассчитываемом диапазоне встречаются пустые или содержащие текст ячейки, то они игнорируются. В примере ниже среднее ищется по четырем ячейкам, т.е. (4+15+11+22)/4 = 13

Если необходимо вычислить среднее, учитывая все ячейки диапазона, то можно воспользоваться статистической функцией СРЗНАЧА. В следующем примере среднее ищется уже по 6 ячейкам, т.е. (4+15+11+22)/6 = 8,6(6).

Статистическая функция СРЗНАЧ может использовать в качестве своих аргументов математические операторы и различные функции Excel:

СРЗНАЧЕСЛИ()

Если необходимо вернуть среднее арифметическое значений, которые удовлетворяют определенному условию, то можно воспользоваться статистической функцией СРЗНАЧЕСЛИ. Следующая формула вычисляет среднее чисел, которые больше нуля:

В данном примере для подсчета среднего и проверки условия используется один и тот же диапазон, что не всегда удобно. На этот случай у функции СРЗНАЧЕСЛИ существует третий необязательный аргумент, по которому можно вычислять среднее. Т.е. по первому аргументу проверяем условие, по третьему – находим среднее.

Допустим, в таблице ниже собрана статистика по стоимости лекарств в городе. В одной аптеке лекарство стоит дороже, в другой дешевле. Чтобы посчитать стоимость анальгина в среднем по городу, воспользуемся следующей формулой:

Если требуется соблюсти несколько условий, то всегда можно применить статистическую функцию СРЗНАЧЕСЛИМН, которая позволяет считать среднее арифметическое ячеек, удовлетворяющих двум и более критериям.

МАКС()

Статистическая функция МАКС возвращает наибольшее значение в диапазоне ячеек:

МИН()

Статистическая функция МИН возвращает наименьшее значение в диапазоне ячеек:

Источники

https://lumpics.ru/descriptive-statistics-in-excel/
https://statanaliz.info/statistica/opisanie-dannyx/variatsiya-razmakh-srednee-linejnoe-otklonenie/
https://www.hd01.ru/info/kak-poschitat-razmah-v-excel/
http://galyautdinov.ru/post/formula-vyborki-prostaya
https://math.semestr.ru/group/interval-estimation-share.php
https://tidydata.ru/sample-size
https://exceltable.com/formuly/raschet-statisticheskih-vybrosov
https://lumpics.ru/how-to-make-a-sample-in-excel/
https://office-guru.ru/excel/statisticheskie-funkcii-excel-kotorye-neobhodimo-znat-96.html

Источник

Как в эксель посчитать разницу между двумя числами

Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.

Предположим, вы хотите узнать, сколько складских запасов невыгодно (вычитайте прибыльные позиции из общего запаса). Или, возможно, вам нужно узнать, сколько сотрудников приближаются к возрасту выхода на пенсию (вычесть из общего числа сотрудников количество сотрудников в возрасте до 55 лет).

Что необходимо сделать

Существует несколько способов вычитания чисел, в том числе:

Вычитание чисел в ячейке

Для простого вычитания используйте арифметические операторы — (минус).

Например, если ввести в ячейку формулу =10-5, в результате в ячейке отобразится 5.

Вычитание чисел в диапазоне

При добавлении отрицательного числа все равно, что вычитать одно число из другого. С помощью функции СУММ можно складывать отрицательные числа в диапазоне.

Примечание: В Excel не существует функции ВЫЧЕСТЬ. Используйте функцию СУММ, преобразуя все числа, которые необходимо вычесть, в их отрицательные значения. Например, функция СУММ(100,-32,15,-6) возвращает результат 77.

Пример

Чтобы вычесть числа различными способами, выполните указанные здесь действия.

Выберите все строки в приведенной ниже таблице, а затем нажмите клавиши CTRL+C.

Вычитает 9000 из 15000 (что равно 6000).

Добавляет все число в списке, включая отрицательные (чистый результат — 16 000).

Выделите на листе ячейку A1 и нажмите клавиши CTRL+V.

Чтобы переключиться между просмотром результатов и просмотром формул, нажмите клавиши CTRL+’ (ударение) на клавиатуре. Можно также нажать кнопку Показать формулы (на вкладке Формулы).

Использование функции СУММ

Функция СУММ суммирует все числа, которые вы указали в качестве аргументов. Каждый аргумент может быть диапазон, ссылка на ячейку, массив, константа или формулалибо результатом выполнения другой функции. Например, СУММ(A1:A5) суммирует все числа в диапазоне ячеек A1–A5. Другим примером является сумм(A1, A3, A5), которая суммирует числа, содержащиеся в ячейках A1, A3 и A5 (аргументы — A1, A3 и A5).

Как в экселе посчитать разницу в процентах между двумя числами?

Посчитать разницу в процентах между двумя числами, довольно часто встречающаяся задача в повседневной жизни. Рассмотрим подробный пошаговый алгоритм, как решить подобную задачу.

Перед нами представлена таблица, в которой есть два столбца: «число №1» и «Число №2». Задача посчитать разниму между двумя этими числами с помощью программы эксель.

Добавляем в таблицу четвертый столбец и называем его «Разница в процентах».

Рассчитаем разницу в процентах между числами, для этого ячейки «D3» пишем формулу: =(B3-C3)/B3, где «B3» — это первое число, а «C3» — это второе число. Копируем данную формулу на другие ячейки, получаем первый результат.

Теперь нужно настроить отображение в процентах, для этого выделяем диапазон ячеек с «D3» по «D8», наводим курсор на выделенную область и жмем правую кнопку мыши. Появившемся в новом меню, выбираем: «Формат ячейки».

Откроется панель настроек «Формат ячеек», в которой активируем закладку «Число» и в качестве формата чисел выбираем процентный.

После нажатия кнопки «Ок», информация обновиться и мы сделали расчет разницы в процентах между двумя числами в программе эксель.

Вычисление разницы в Microsoft Excel

Вычисление разницы

Способ 1: вычитание чисел

«=»

«-»

С3

Способ 2: денежный формат

Способ 3: даты

А вот вычисление разности дат имеет существенные нюансы, отличные от предыдущих вариантов.

Если нам нужно вычесть определенное количество дней от даты, указанной в одном из элементов на листе, то прежде всего устанавливаем символ «=» в элемент, где будет отображен итоговый результат. После этого кликаем по элементу листа, где содержится дата. Его адрес отобразится в элементе вывода и в строке формул. Далее ставим символ «-» и вбиваем с клавиатуры численность дней, которую нужно отнять. Для того, чтобы совершить подсчет клацаем по Enter.

«=»

«-»

Enter

«Конечная дата» — это аргумент в виде более поздней даты или ссылки на неё.

«d» — результат отображается в днях;
«m» — в полных месяцах;
«y» — в полных годах;
«YD» — разность в днях (без учета годов);
«MD» — разность в днях (без учета месяцев и годов);
«YM» — разница в месяцах.

Опять жмем кнопку Enter. Как видим, результат закономерно тот же, только полученный немного другим способом.

Способ 4: время

«=»

22:55)

«-»

15:13

Мы рады, что смогли помочь Вам в решении проблемы.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

Источник

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28