Нахождение собственных чисел матрицы в excel

Как найти собственные числа и собственные векторы матрицы в excel

Собственные числа матрицы. Примеры решений

Пример 1. Найти собственные числа и собственные векторы матрицы

Решение находим с помощью калькулятора. Составим характеристическое уравнение:

Отсюда собственные числа данной матрицы: λ₁=-1, λ₂=7
Найдем собственные векторы, соответствующие этим собственным значениям
Подставим собственное число λ₁=-1 в систему однородных уравнений (A-λE)X=0 и найдем ее нетривиальное решение.

Ранг матрицы r=1, ФСР содержит (n—r)=1 решение. Пусть x₂=1, тогда x₁=-1. Получаем собственный вектор

Рассмотрим собственное значение λ₂=7

Положим x₂=1, тогда x₁=1. Получаем собственный вектор

Пример 2. Найти собственные числа и собственные векторы матрицы

Решение. Составим характеристическое уравнение:

Собственные числа данной матрицы: λ_1,2=3, λ₃=6
Найдем собственные векторы, соответствующие λ=3.

Ранг матрицы r=1, ФСР содержит (n—r)=3-1=2 решения. Зададим два набора значений свободных переменных и составим два собственных вектора

Найдем собственные векторы, соответствующие λ=6.

Ранг матрицы r=2 , ФСР содержит (n—r)=3-1=1 решение. Зададим значение свободной переменной и составим собственный вектор

Перейти к онлайн решению своей задачи

Как найти собственные числа и собственные векторы матрицы в excel

Argument ‘Topic id’ is null or empty

© Николай Павлов, Planetaexcel, 2006-2021
info@planetaexcel.ru

Использование любых материалов сайта
допускается строго с указанием прямой ссылки на источник, упоминанием
названия сайта, имени автора и неизменности исходного текста
и иллюстраций.

ИП Павлов Николай Владимирович
ИНН 633015842586
ОГРН 310633031600071

Источник

Векторы и матрицы в эксель

Матрицы в Excel: операции (умножение, деление, сложение, вычитание, транспонирование, нахождение обратной матрицы, определителя)

Программа Microsoft Office Excel позволяет выполнять операции с матрицами с помощью встроенных функций и формул. Рассмотрим основные операции над матрицами:

• умножение и деление матрицы на число;
• сложение, вычитание и умножение матриц;
• транспонирование матрицы;
• нахождение обратной матрицы;
• вычисление определителя.

Введем условные обозначения. Матрица А размерностью i x j — это прямоугольная таблица чисел, состоящая из i строк и j столбцов, а_ij — элемент матрицы.

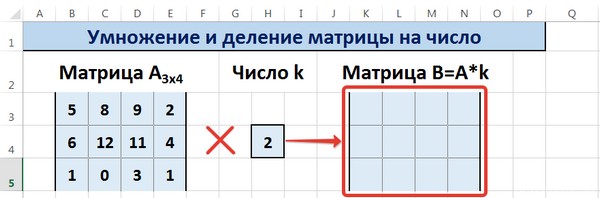
Умножение и деление матрицы на число в Excel

Способ 1

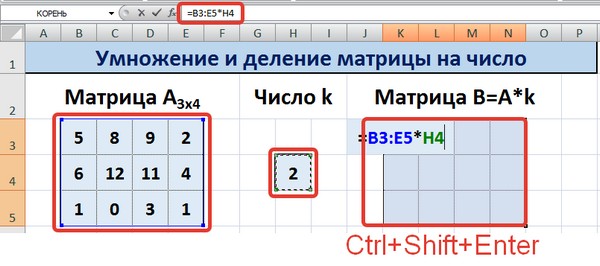
Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.

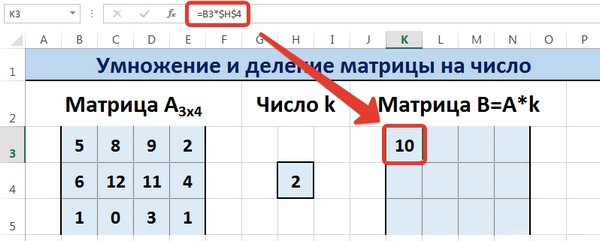
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а₁₁ матрицы А.

Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.

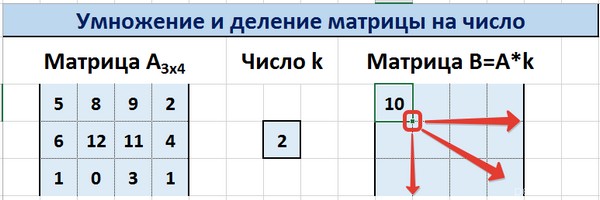
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.

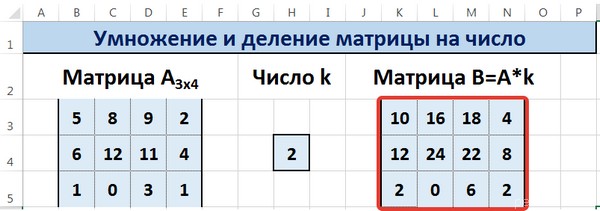
Таким образом, мы умножили матрицу А в Excel и получим матрицу В.

Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.

Способ 2

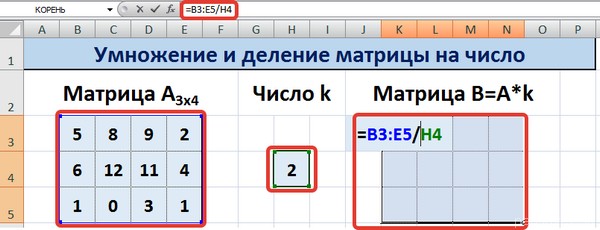
Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.

Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.

Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/».

Сложение и вычитание матриц в Excel

Способ 1

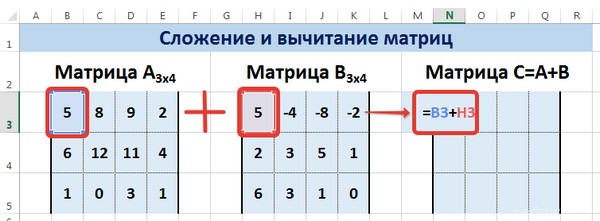
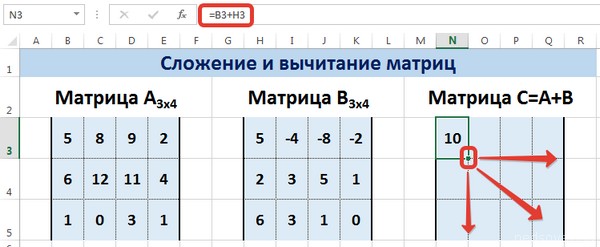
Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. с_ij = а_ij + b_ij.

Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+H3, где B3 и H3 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.

С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.

Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — H3 и скопируем её на весь диапазон матрицы С.

Способ 2

Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.

Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.

Умножение матриц в Excel

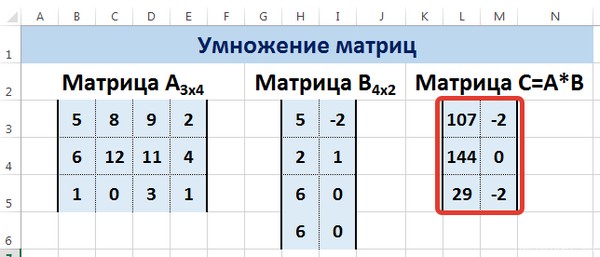
Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.

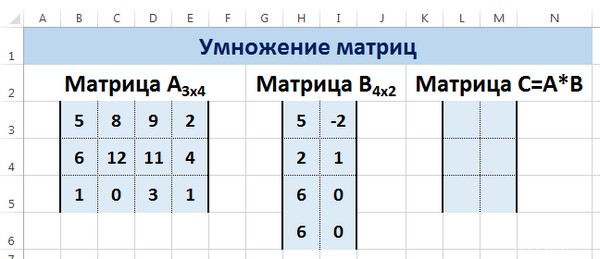
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.

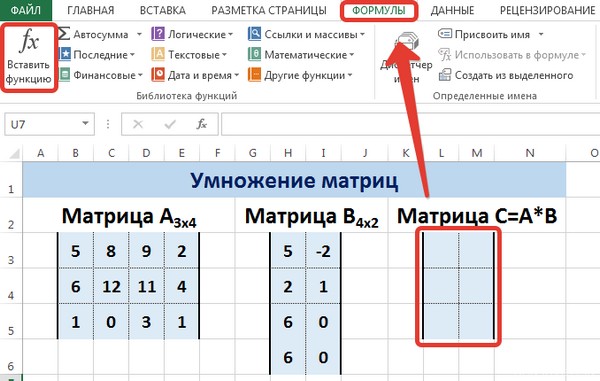
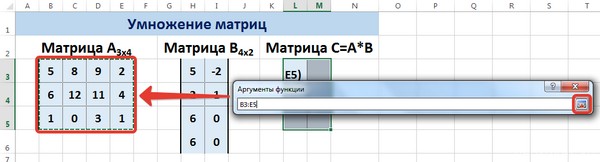
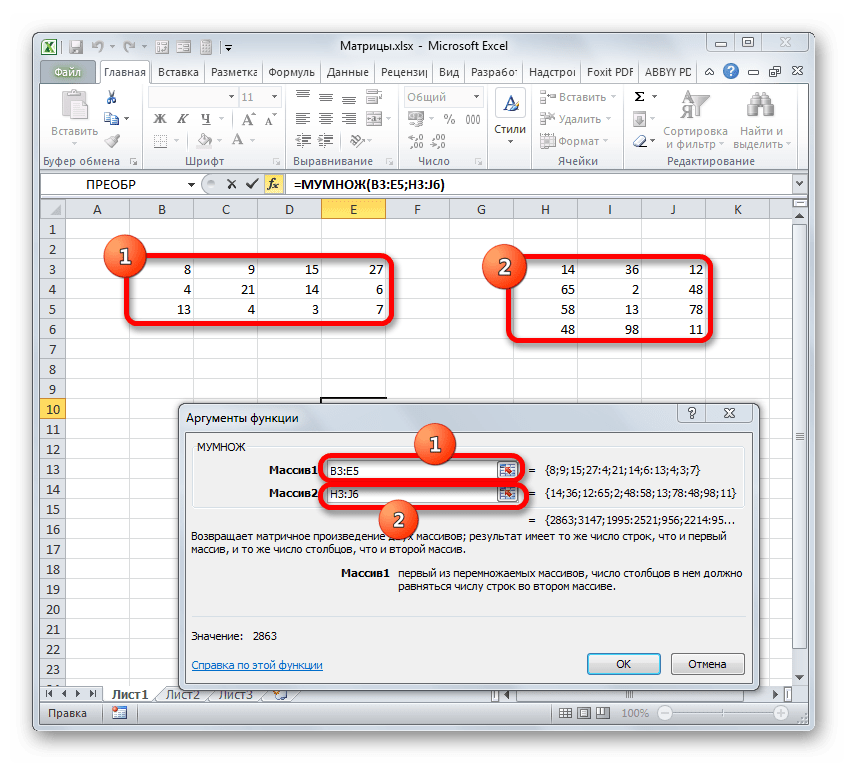
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.

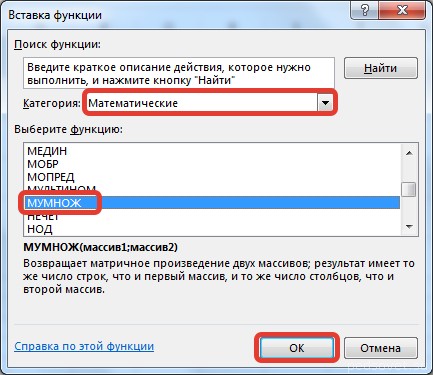
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.

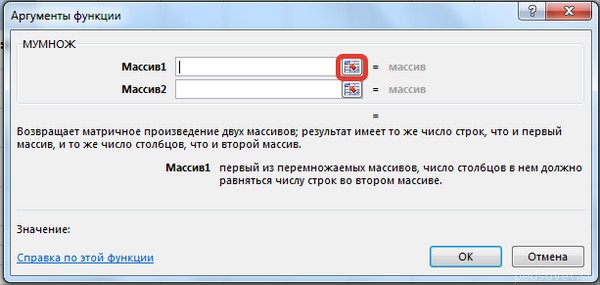
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.

Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.

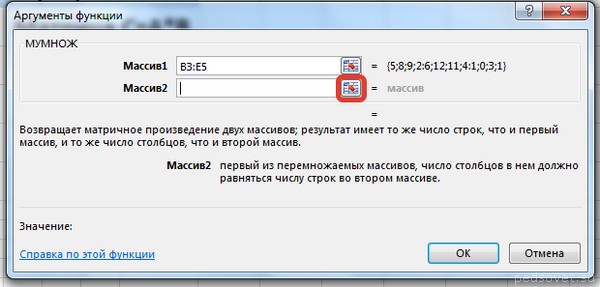
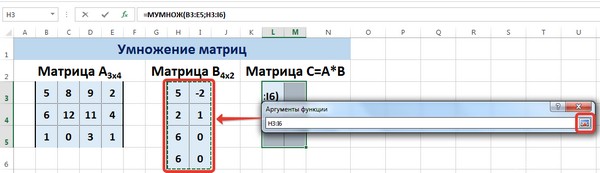
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.

Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.

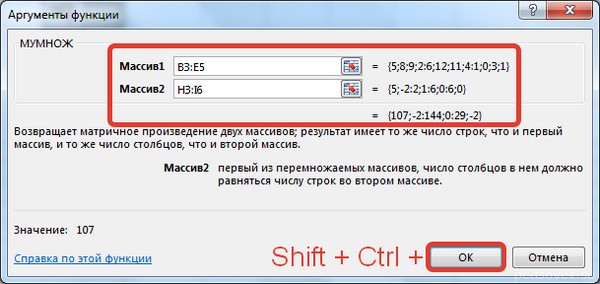
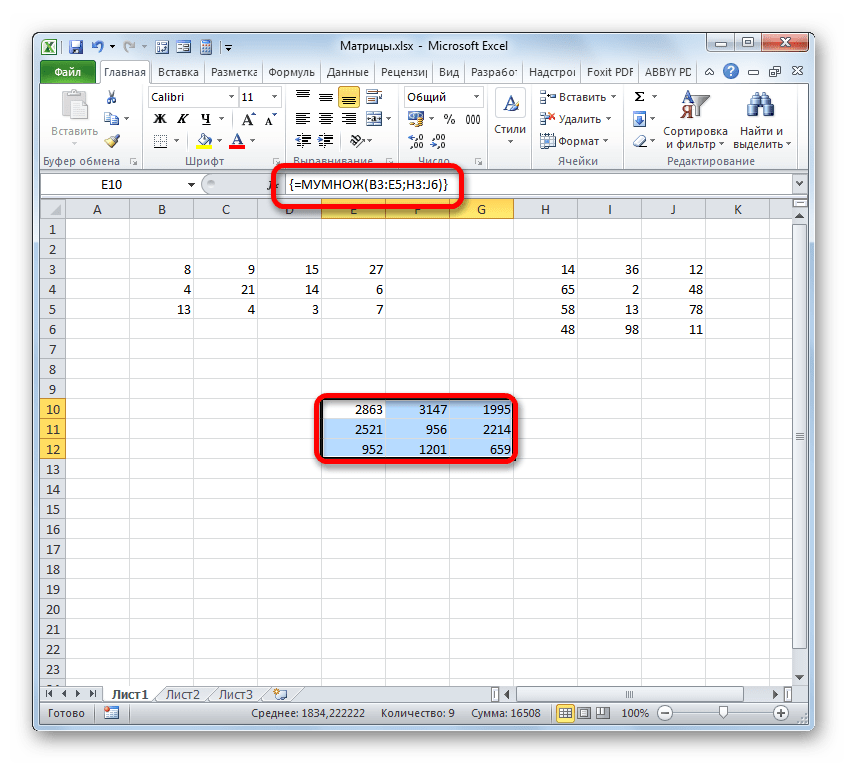
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.

Мы получим результат умножения матриц А и В.

Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.

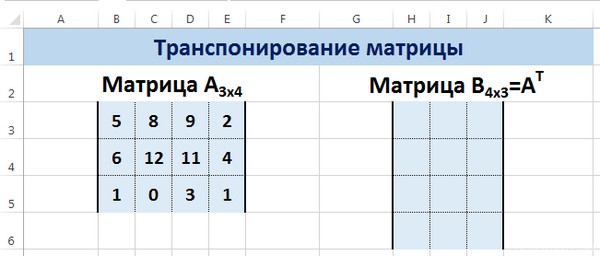
Транспонирование матрицы в Excel

Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу А Т .

Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу А Т , причем размерность этой матрицы будет 4х3.

Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.

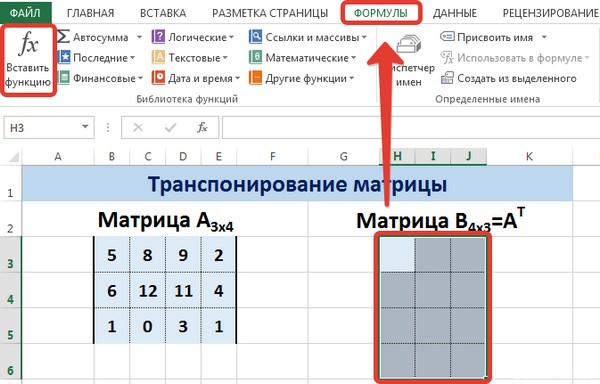
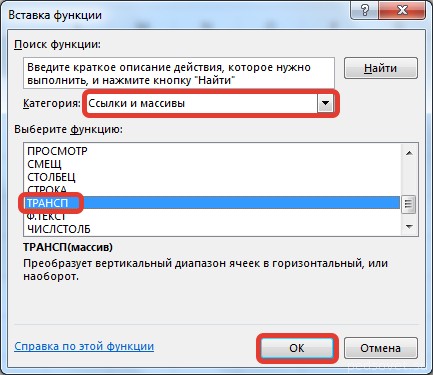
На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.

В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А Т .

Нажмите для увеличения

Мы получили транспонированную матрицу.

Нахождение обратной матрицы в Excel

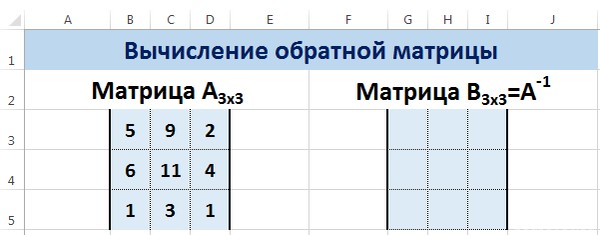
Матрица А -1 называется обратной для матрицы А, если АžА -1 =А -1 žА=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).

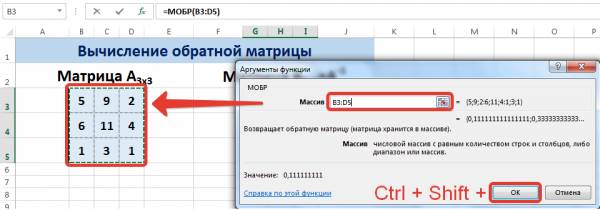
Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().

Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.

В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.

В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А -1 .

Нажмите для увеличения

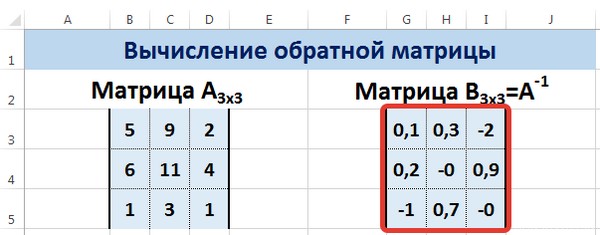
Мы получили обратную матрицу.

Нахождение определителя матрицы в Excel

Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.

Как найти определить матрицы в Excel

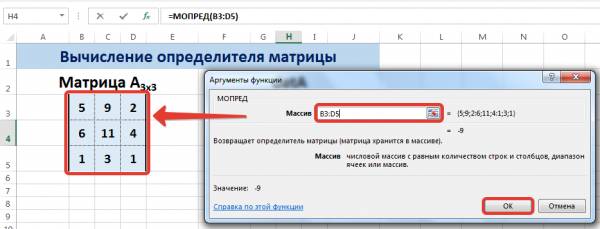
Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().

Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.

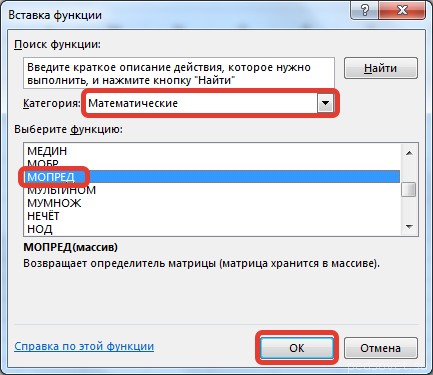
В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.

В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.

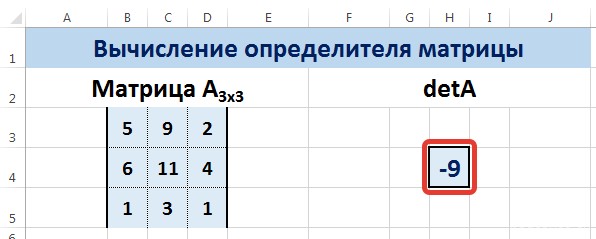
Нажмите для увеличения

Мы вычислили определитель матрицы А.

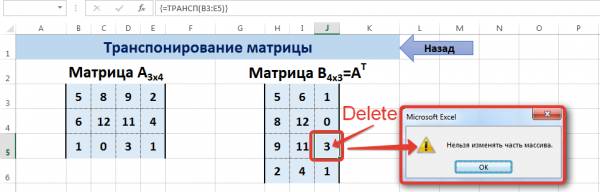
В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.

Нажмите для увеличения

Мы можем удалить только все элементы этой матрицы.

Видеоурок

Кратко об авторе:

Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Векторы и матрицы в Excel

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Векторы и матрицы в Excel

C овокупность n чисел , заданных в определенном по­рядке, называется n -мерным вектором. Числа a _i – компонент s или координат s вектора, n —размерностью вектора.

Два n -мерных вектора и называются равными, если все их соответствующие компоненты равны: .

Суммой двух n -мерных векторов и называется n -мерный вектор

.

Операция сложения векторов обладает свойствами коммутативности и ассоциативности .

Вектор , все компоненты которого равны нулю, называется нуль-вектором. Нуль-вектор ведет себя при сложения векторов аналогично числу нуль в арифметике.

Вектор называется противоположным вектору . Очевидно,

Операция вычитания векторов определяется как сложение с противоположным вектором .

Под произведением вектора на число  понимают вектор .

Умножение вектора на число обладает свойством ассоциативности и свойством дистрибутивности относительно векторного и числового сомножителей .

Модуль (норма, длина) вектора .

Пример вычисления модуля вектора (2, 5, 3, -4) приведен на рисунке 1.

Р
исунок 1 – Вычисление длины вектора

Здесь применены функция = КОРЕНЬ ( число ), где аргументом функции может быть либо конкретное число, либо адрес ячейки, в которой оно записано, и функция = СУММКВ ( число1 ; число2 ;…), где аргументами функции являются адреса ячеек (адрес массива) с координатами вектора.

В общем случае скалярное произведение двух векторов , где — угол между векторами. Скалярным произведение двух n -мерных векторов и может быть определено как сумма произведений одноименных координат данных векторов:

.

Операция скалярного умножения векторов обладает следующими свойствами:

.

В Excel скалярное произведение векторов вычисляется с помощью функции = СУММПРОИЗВ ( массив1 ; массив2;… ), где массив1 ; массив2;…- от 2 до 30 массивов, чьи компонент нужно перемножить, а затем сложить полученные произведения. Все массивы должны иметь одну и то же размерность (пример на рисунке 2).

Векторным произведением вектора на вектор называется вектор , длина которого численно равна площади параллелограмма построенного на векторах и , перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от к вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора (рисунок 3).

Треугольник, стороны которого есть стороны параллелограмма и его диагонали имеет площадь, равную половине величины векторного произв
едения двух векторов.

Р
исунок 2 – Определение скалярного произведения двух векторов

Значение векторного произведения определяется следующим образом:

На рисунке 4 приведен пример вычисления векторного произведения векторов, площади параллелограмма, треугольника. Проверка правильности вычисления векторного произведения заключается в проверке соответствия нулю величины скалярных произведений векторов и

Р
исунок 4 – Вычисление векторного произведения векторов

Перейдем к рассмотрению основных операций матричного исчисления.

Числа, расположенные в виде прямоугольной таблицы, состоящей из m строк и n столбцов, образуют матрицу размера m х n :

Две матрицы A и B одного и того же размера m × n являются равными, если равны все их соответствующие элементы:

Матрица, состоящая из одного столбца (т. е. если n = 1) или из од- ной строки (т. е. если m = 1), называется вектором — столбцом или, соответственно, вектором — строкой.

Матрица называется нулевой, если все ее элементы равны нулю. Нулевая матрица обозначается

При n = m матрица называется квадратной, а число ее строк (столбцов) – порядком матрицы. Элементы квадратной матрицы образуют ее главную диагональ.

Квадратная матрица называется треугольной, если все ее элементы, расположенные по одну сторону от главной диагонали, равны нулю:

Квадратная матрица называется единичной, если все элементы ее главной диагонали равны единице, а остальные — нулю:

Если в матрице А заменить строки столбцами, сохранив их порядок, то получится новая матрица

называемая транспонированной по отношению к матрице А.

Если А=А Т , то такая матрица называется симметричной.

В Excel для транспонирования матриц используется функция =ТРАНСП(массив) – рисунок 5.

Р
исунок 5 – Вызов функции ТРАНСП

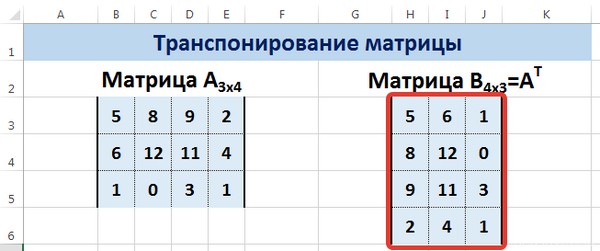
Пример. Имеем исходную матрицу

.

Из определения ясно, что транспонированной будет матрица А Т :

.

Решение задачи в Excel представлено на рисунке 6

Рисунок 6 – Транспонирование матрицы

Порядок решения следующий:

— определить место для транспонированной матриц (в рассматриваемом примере это G2:I4);

— в ячейку размещения первого элемента транспонированной матрицы ввести формулу =ТРАНС(С2:E5);

— выделить массив ячеек, в которых будут размещаться все элементы транспонированной матрицы;

— нажать Shit + Ctrl + Enter .

Суммой матриц А и В одинакового размера является матрица С , элементы которой равны сумме соответствующих элементов суммируемых матриц:

Произведение матрицы на число  — то матрица, элементы которой получаются умножением всех элементов исходной матрицы на данное число:

Умножение матрицы на матрицу определяется только при условии, что число столбцов первого сомножителя А равно числу строк второго сомножителя В . Под произведением матрицы размером m x k на матрицу размером k x n понимают матрицу размером m x n , элемент которой равен скалярному произведению i -й строки матрицы на j -й столбец матрицы :

В Excel для вычисления произведения матриц используется функция

= МУМНОЖ ( массив1 ; массив2 ), где массивы – совокупности элементов перемножаемых матриц (рисунок 7).

Р
исунок 7 – Умножение матриц

Формула для расчета произведения матриц должна быть введена как формула массива!

Пусть даны матрицы

Вычислим их произведение в Excel (рисунок 8).

— шаг1 – определение области размещения результата (на рисунке 8 выделена пункитом);

— шаг 2 – ввод в начальную ячейку результирующего массива формулы умножения матриц;

—
шаг 3 – выделить результирующий массив и нажать F2;

—
шаг 3 – нажать Shift+Ctrl+Enter.

Рисунок 8 – Вычисление произведения матриц

Действие умножения матрицы на матрицу обладает свойствами:

Отметим, что в общем случае

Если условие равенства произведения матриц при изменении их последовательности выполняется, то матрицы называются перестановочными между собой.

При умножении квадратной матрицы саму на себя получаем квадратную матрицу второй степени, при n -кратном умножении получим квадратную матрицу n -го порядка ( n -й степени).

Определитель (или детерминант) матрицы – одно из основных понятий линейной алгебры. Это многочлен, комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов. Определитель характеризует содержание матрицы. В частности, если в матрице есть линейно-зависимые строки или столбцы, – определитель равен нулю.

Для матрицы первого порядка значение определителя равно единственному элементу этой матрицы.

Для матрицы 2х2 определитель вычисляется как

Для матриц более высоких порядков n x n определитель можно вычислить, применив следующую рекурсивную формулу:

, где – дополнительный минор к элементу .

Возможно разложение как по строкам, так и по столбцам.

В
Excel определитель вычисляется с помощью функции = МОПРЕД ( массив ), где массив есть совокупность элементов матрицы (рисунок 9).

Рисунок 9 – Расчет определителя матрицы

Квадратная матрица называется неособенной ( невырожденной ), если ее определитель не равен нулю. В противном случае она называется особенной ( вырожденной ) или сингулярной .

Детерминант треугольной матрицы равен произведению ее диагональных элементов

Обратной матрицей к матрице называют такую матрицу, для которой
А А -1 = E

Обратную матрицу можно найти по следующей формуле:

, где – определитель матрицы, – транспонированная матрица.

Н
а рисунке 10 приведен пример определения обратной матрицы с помощью функции Excel = МОБР ( массив ).

Рисунок 10 – Расчет обратной матрицы

Заметим, что функция применяется к массиву как в ранее приведенных примерах.

Проверим выполнение условия А А -1 = E (рисунок 11)

Р
исунок 11- Произведение матрицы на обратную матрицу

Собственным числом квадратной матрицы

называется такое число , которое обращает определитель матрицы в 0: .

Или, по-другому, собственными числами матрицы А являются корни уравнения и только они.

Матрица называется характеристической матрицей матрицы А , многочлен называется характеристическим многочленом матрицы А , уравнение называется характеристическим уравнением матрицы А.

Для вычисления собственных чисел существуют классические приемы, сводящиеся к решению полиномиальных уравнений. Собственные числа определяют системы компьютерной математики. Найдем все собственные числа произвольной квадратной матрицы с помощью Excel на примере квадратной матрицы размерностью 3х3:

Необходимо найти такие значения  , при котором

Оформим лист Excel следующим образом (рисунок 12):

Рисунок 12 – Вычисление собственного числа матрицы

В ячейку B2 введено =2-F2; в ячейку С3 — =-6-F2; в ячейку D4 — =1-F2.

Из рисунка 12 видно, что при  =0 определитель также равен 0, т.е.  =0 есть первое собственное число матрицы.

Д

ля определения других собственных числе воспользуемся поиском (Меню Сервис-Поск решения …) – рисунок 13, установив целевую ячейку $E$2, в которой вычисляется значение определителя матрицы. Требуемое значение определителя – 0. Поиск осуществляется путем подбора значения  , отображаемом в ячейке $F$2.

Рисунок 13 – Вычисление собственного числа матрицы

О щелчку на кнопке Выполнить, появляется окно Результат поиска решения (рисунок 14).

Рисунок 14 – Результат поиска решения

Выбираем Сохранить найденное решение и Тип отчета – Результаты . Щелкаем на Ок. Получаем ожидаемый результат  =0.

П
овторим выполненные действия, введя в окне Поиск решения ограничение $F$2>=1 (рисунок 15):

Рисунок 15 – Ввод ограничения

В результате поиска получаем второе значение собственного числа:  =3.

Повторим поиск при ограничении.

Если установить в ограничениях  >=4, то поиск не находит решения. Ищем отрицательное собственное число и устанавливаем в ограничениях 

П
ри добавлении в систему ограничений Е1>=-10 (рисунок 16) поиск нашел третье собственное число, равное -6 (рисунок 17)

Р
исунок 16 – Поиск собственного числа при двухстороннем ограничении

Рисунок 17 — Результат поиска третьего собственного числа

Собственным вектором соответствующим собственному числу λ называют такой вектор , который удовлетворяет матричному равенству:

Найдем собственный вектор матрицы

Данная матрица имеет собственные числа: λ1 = 0 λ2 = 3 λ3 = -6.

1. Заносим содержимое ячеек матрицы в ячейки таблицы (B2:D4).

2. В ячейку (B6) вводим λ для которого необходимо найти собственный вектор. Пусть λ = 3.

3. В ячейки (F2:F4) поместим любые числа: F2 = 1; F3 = 1; F4 = 1.

4. В ячейки (G2:G4) заносим произведение матрицы (ячейки В2:В4) на вектор (ячейки F2:F4).

5. В ячейки (H2:H4) заносим умножение столбца на собственное число λ находящийся в ячейки (B6).

6. В ячейки (I2:I4) заносим разность столбцов (F2:F4) и (H2:H4).

7. В главном меню открываем Сервис — Поиск решения . Вводим следующие данные: Целевая ячейка $I$2, Равной значению (0); Изменяя ячейки $F$2:$F$4; Ограничения $I$3=0; $I$4=0.

Нажать кнопку « Выполнить ».

В
ячейках (F2:F4) появятся числа, эти это и есть собственный вектор для данного собственного числа (рисунок 18).

Рисунок 18 – Определение собственного вектора матрицы

Последовательно выполнить операции п.п. 2, 3, 7 при остальных значениях собственных чисел матрицы.

Задания для самостоятельной работы

Повторить решение всех примеров, приведенных в Лекции №5.

Сформировать случайным образом два вектора, состоящих из 5 элементов. Элементы векторов должны быть в диапазоне -5…+15

Определить длину векторов.

Вычислить сумму и разность векторов.

Определить скалярное произведение этих векторов.

Определить угол между векторами.

Определить векторное произведение двух векторов.

Проверить правильность вычисления векторного произведения путем определения скалярного произведения каждого из исходных векторов с результатом вычисления векторного произведения.

Сформировать случайным образом матрицу размером 4х4 и матрицу 4х3. Элементы матрицы должны быть в диапазоне -10…+20.

Получить транспонированные матрицы исходных матриц.

Проверить правильность решения путем умножения исходной матрицы на транспонированную.

Определить произведение исходных матриц.

Найти матрицу 3-го порядка для исходной квадратной матрицы.

Определить детерминант исходной квадратной матрицы.

Перемножение одной матрицы на другую в Microsoft Excel

Одной из частых операций, которую выполняют при работе с матрицами, является перемножение одной из них на другую. Программа Excel является мощным табличным процессором, который предназначен, в том числе и для работы над матрицами. Поэтому у него имеются инструменты, которые позволяют перемножить их между собой. Давайте узнаем, как это можно выполнить различными способами.

Процедура перемножения матриц

Сразу нужно сказать, что перемножить между собой можно далеко не все матрицы, а только те, которые соответствуют определенному условию: число столбцов одной матрицы должно быть равным числу строк другой и наоборот. Кроме того, исключается наличие в составе матриц пустых элементов. В этом случае тоже выполнить требуемую операцию не получится.

Способов перемножить матрицы в Экселе все-таки не так уж и много — всего два. И оба они связаны с применением встроенных функций Excel. Разберем в деталях каждый из данных вариантов.

Способ 1: функция МУМНОЖ

Наиболее простым и популярным вариантом среди пользователей является применение функции МУМНОЖ. Оператор МУМНОЖ относится к математической группе функций. Как раз его непосредственной задачей и является нахождение произведения двух матричных массивов. Синтаксис МУМНОЖ имеет такой вид:

Таким образом этот оператор имеет два аргумента, которые представляют собой ссылки на диапазоны двух перемножаемых матриц.

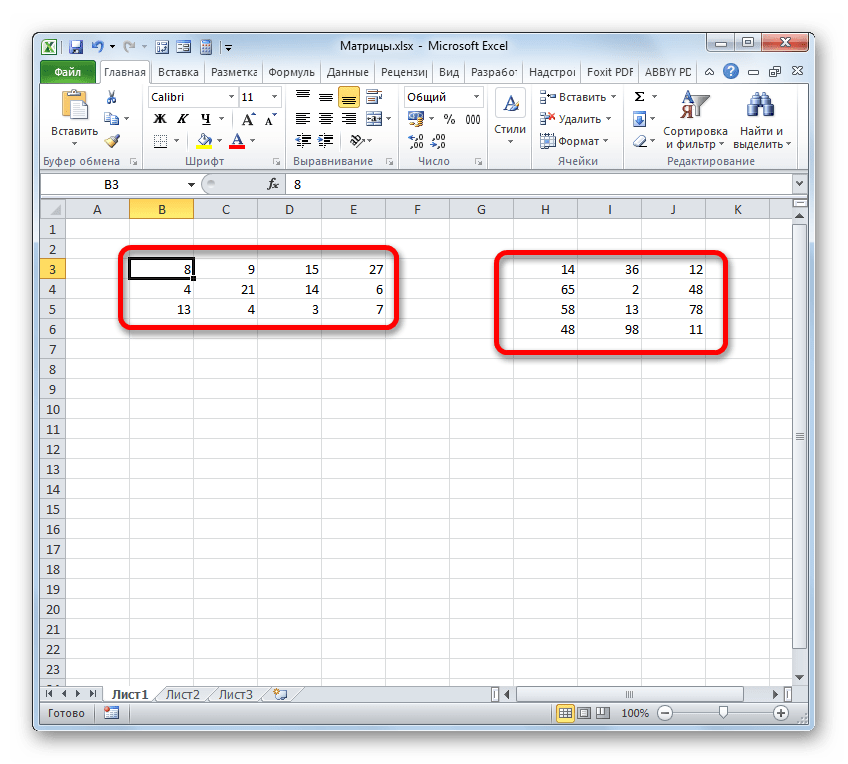
Теперь давайте посмотрим, как используется функция МУМНОЖ на конкретном примере. Имеется две матрицы, число строк одной из которых, соответствует количеству столбцов в другой и наоборот. Нам нужно перемножить два этих элемента.

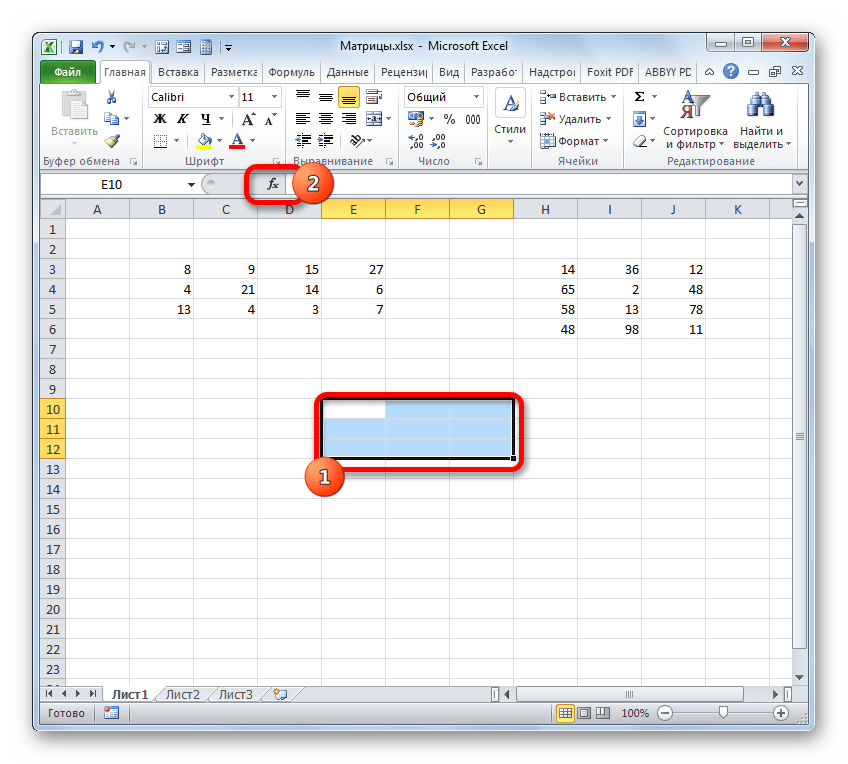
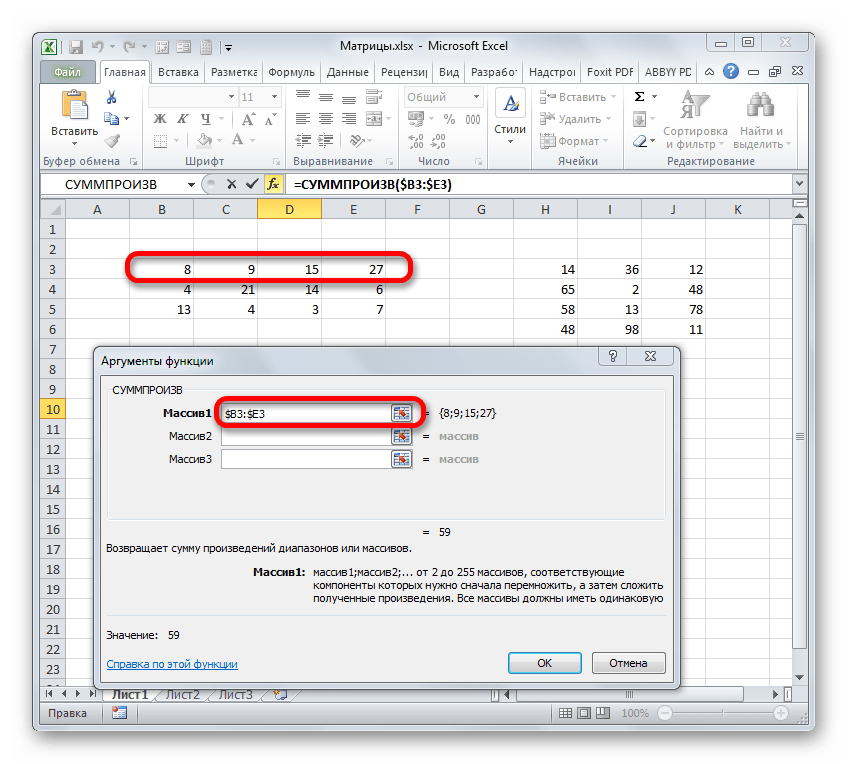
Выделяем диапазон, где будет отображаться результат умножения, начиная с его верхней левой ячейки. Размер данного диапазона должен соответствовать числу строк у первой матрицы и числу столбцов у второй. Клацаем по пиктограмме «Вставить функцию».

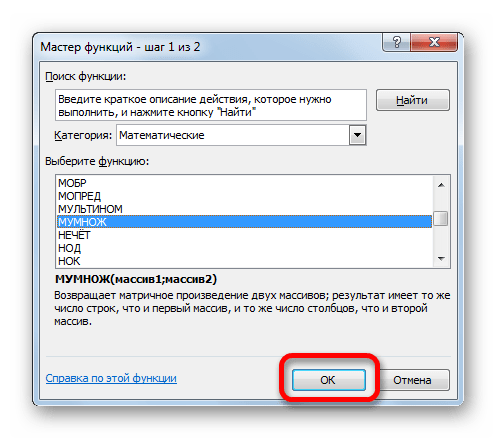
Активируется Мастер функций. Перемещаемся в блок «Математические», кликаем по наименованию «МУМНОЖ» и клацаем по кнопке «OK» в нижней части окна.

После того, как оба аргумента внесены, не спешим жать на кнопку «OK», так как мы имеем дело с функцией массива, а это значит, что для получения корректного результата обычный вариант завершения работы с оператором не подойдет. Данный оператор предназначен не для того, чтобы выводить результат в одну ячейку, так как выводит его в целый диапазон на листе. Итак, вместо нажатия кнопки «OK» жмем комбинацию кнопок Ctrl+Shift+Enter.

Как видим, после этого предварительно выделенный диапазон был заполнен данными. Это и есть результат умножения матричных массивов. Если взглянуть на строку формул, после выделения любого из элементов данного диапазона, то мы увидим, что сама формула обернута в фигурные скобки. Это и есть признак функции массива, который добавляется после нажатия сочетания клавиш Ctrl+Shift+Enter перед выводом результат на лист.

Способ 2: использование составной формулы

Кроме того, существует ещё один способ умножения двух матриц. Он более сложный, чем предыдущий, но тоже заслуживает упоминания, как альтернативный вариант. Данный способ предполагает использование составной формулы массива, которая будет состоять из функции СУММПРОИЗВ и вложенного в неё в качестве аргумента оператора ТРАНСП.

На этот раз выделяем на листе только левый верхний элемент массива пустых ячеек, который рассчитываем использовать для вывода результата. Щелкаем по значку «Вставить функцию».

Мастер функций запускается. Перемещаемся в блок операторов «Математические», но на этот раз выбираем наименование СУММПРОИЗВ. Клацаем по кнопке «OK».

Происходит открытие окна аргументов вышеуказанной функции. Данный оператор предназначен для перемножения различных массивов между собой. Его синтаксис следующий:

В качестве аргументов из группы «Массив» используется ссылка на конкретный диапазон, который нужно перемножить. Всего может быть использовано от двух до 255 таких аргументов. Но в нашем случае, так как мы имеем дело с двумя матрицами, нам понадобится как раз два аргумента.

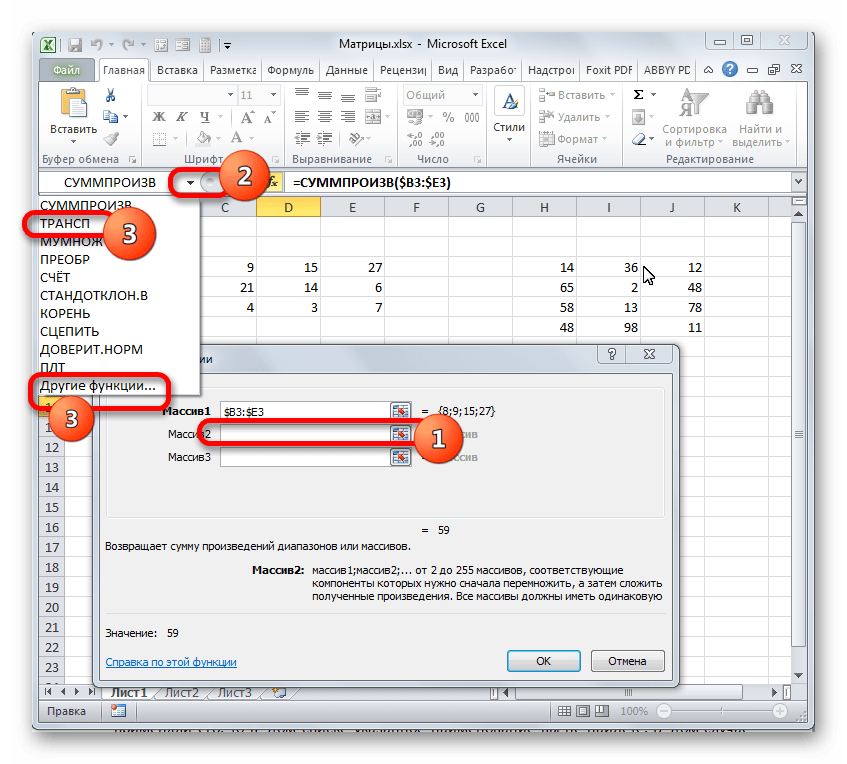
Ставим курсор в поле «Массив1». Тут нам нужно будет ввести адрес первой строки первой матрицы. Для этого, зажав левую кнопку мыши, нужно просто выделить её на листе курсором. Тут же координаты данного диапазона будут отображены в соответствующем поле окна аргументов. После этого следует зафиксировать координаты полученной ссылки по столбцам, то есть, эти координаты нужно сделать абсолютными. Для этого перед буквами в выражении, которое вписано в поле, устанавливаем знак доллара ($). Перед координатами, отображенными в цифрах (строки), это делать не следует. Также, можно вместо этого выделить всё выражение в поле и трижды нажать на функциональную клавишу F4. В данном случае абсолютными тоже станут лишь координаты столбцов.

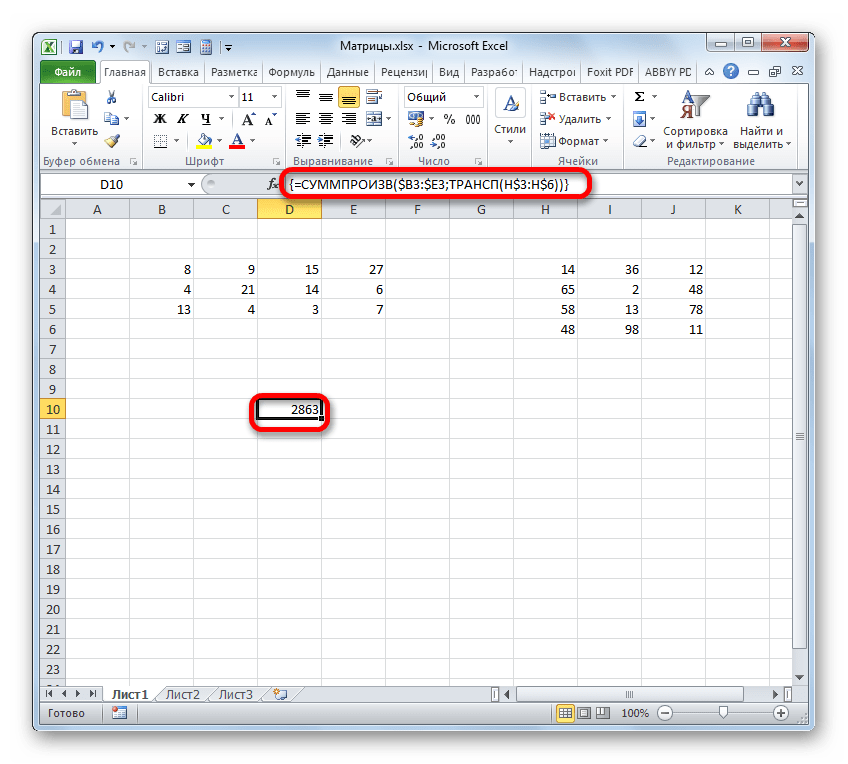
После этого устанавливаем курсор в поле «Массив2». С этим аргументом будет посложнее, так как по правилам умножения матриц, вторую матрицу нужно «перевернуть». Для этого используем вложенную функцию ТРАНСП.

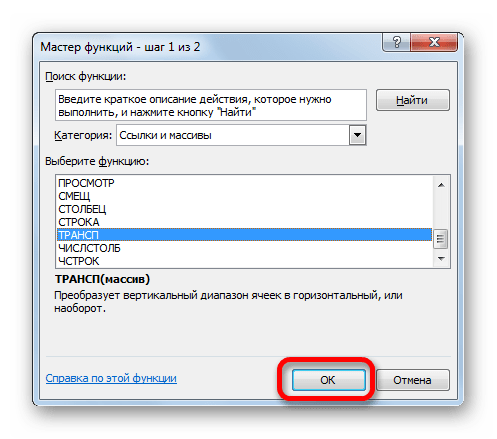
Чтобы перейти к ней, клацаем по значку в виде треугольника, направленного острым углом вниз, который размещен слева от строки формул. Открывается список недавно используемых формул. Если вы в нем найдете наименование «ТРАНСП», то щелкайте по нему. Если же вы давно использовали данный оператор или вообще никогда не применяли его, то в этом списке указанное наименование вы не отыщите. В этом случае требуется нажать по пункту «Другие функции…».

Открывается уже хорошо знакомое нам окно Мастера функций. На этот раз перемещаемся в категорию «Ссылки и массивы» и выбираем наименование «ТРАНСП». Щелкаем по кнопке «OK».

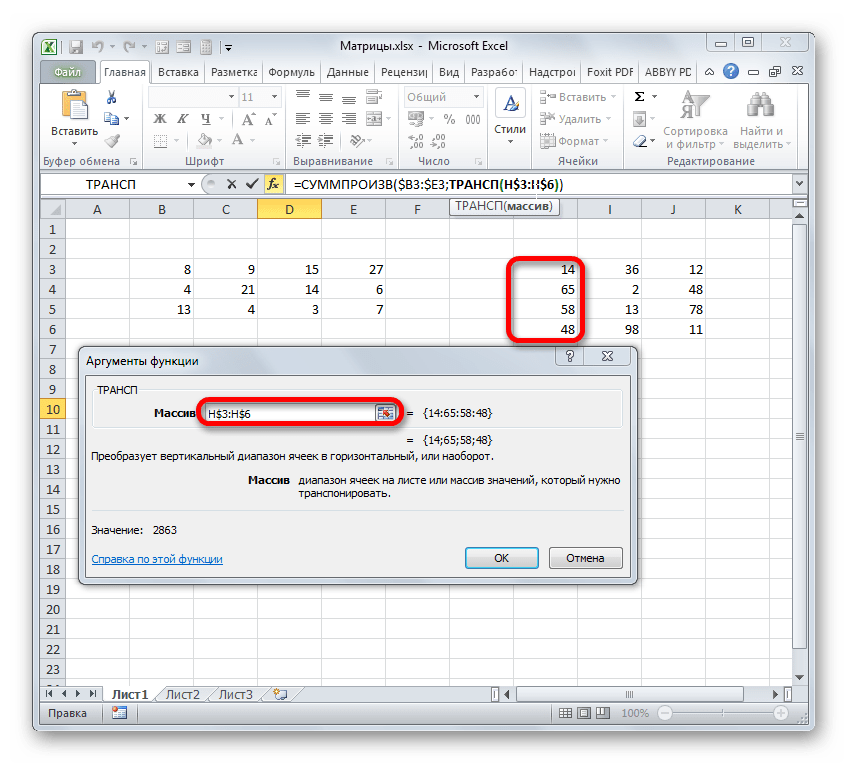
Производится запуск окна аргументов функции ТРАНСП. Данный оператор предназначен для транспонирования таблиц. То есть, попросту говоря, он меняет местами столбцы и строки. Это нам и нужно сделать для второго аргумента оператора СУММПРОИЗВ. Синтаксис функции ТРАНСП предельно простой:

То есть, единственным аргументом данного оператора является ссылка на тот массив, который следует «перевернуть». Вернее, в нашем случае даже не на весь массив, а только на его первый столбец.

Итак, устанавливаем курсор в поле «Массив» и выделяем первый столбец второй матрицы на листе с зажатой левой кнопкой мыши. Адрес отобразится в поле. Как и в предыдущем случае, тут тоже нужно сделать определенные координаты абсолютными, но на этот раз не координаты столбцов, а адреса строк. Поэтому ставим знак доллара перед цифрами в ссылке, которая отображается в поле. Можно также выделить всё выражение и дважды кликнуть по клавише F4. После того, как нужные элементы стали иметь абсолютные свойства, не жмем на кнопку «OK», а так же, как и в предыдущем способе, применяем нажатие комбинации клавиш Ctrl+Shift+Enter.

Но на этот раз у нас заполнился не массив, а только одна ячейка, которую мы ранее выделили при вызове Мастера функций.

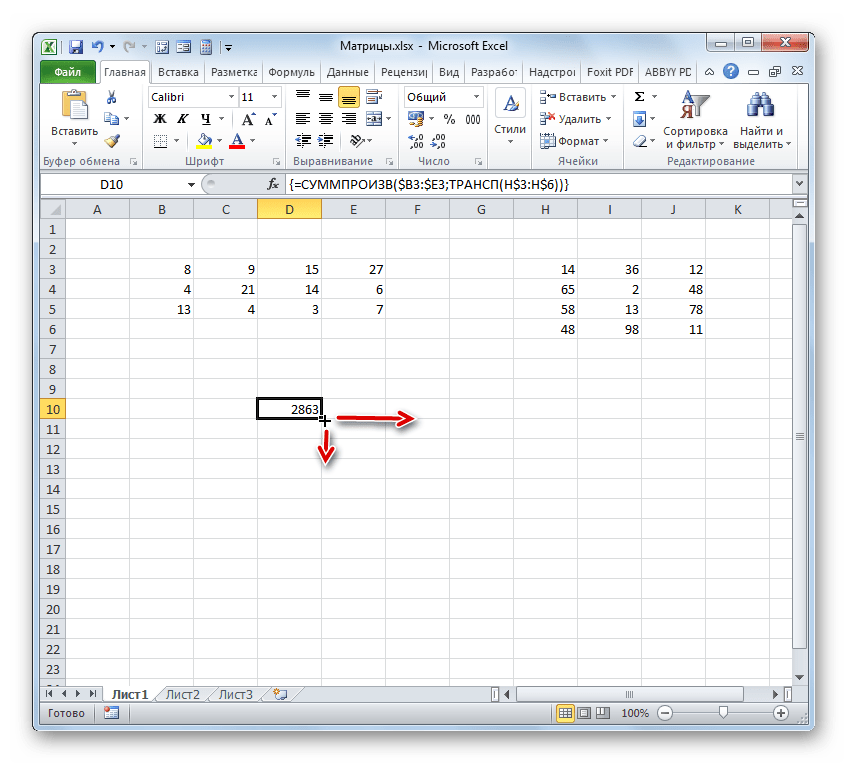
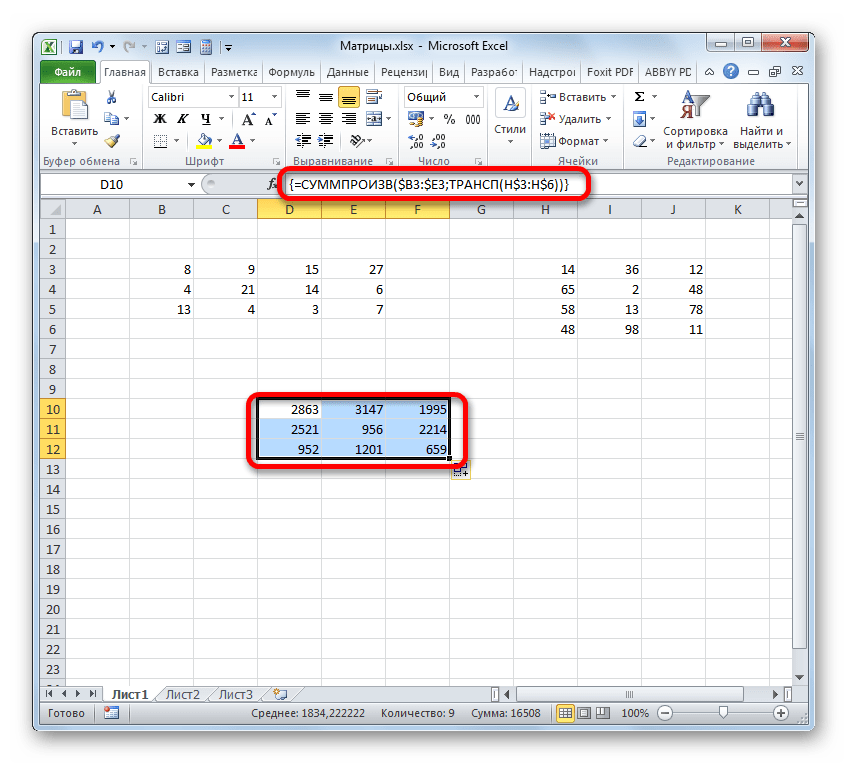
Нам нужно заполнить данными такой же по размеру массив, как и в первом способе. Для этого следует скопировать формулу, полученную в ячейке, на равнозначный диапазон, который будет равен количеству строк первой матрицы и количеству столбцов второй. В конкретно нашем случае получается три строки и три столбца.

Для копирования прибегнем к использованию маркера заполнения. Наводим курсор на нижний правый угол ячейки, в которой расположена формула. Курсор преобразуется в черный крестик. Это и есть маркер заполнения. Зажимаем левую кнопку мыши и протягиваем курсор по всему вышеуказанному диапазону. Сама начальная ячейка с формулой должна стать левым верхним элементом данного массива.

Как видим, выделенный диапазон заполнен данными. Если их сравнить с тем результатом, который мы получили благодаря применению оператора МУМНОЖ, то увидим, что значения полностью идентичны. Это означает, что умножение двух матриц выполнено верно.

Как видим, несмотря на то, что был получен равнозначный результат, использовать функцию для умножения матриц МУМНОЖ значительно проще, чем применять для этих же целей составную формулу из операторов СУММПРОИЗВ и ТРАНСП. Но все-таки данный альтернативный вариант тоже нельзя оставить без внимания при изучении всех возможностей перемножения матриц в Microsoft Excel.

Помимо этой статьи, на сайте еще 12604 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Источник