Нахождение обратных матриц в excel

Содержание

  • Выполнение расчетов
    • Расчет определителя
    • Расчет обратной матрицы
  • Вопросы и ответы

Обратная матрица в Microsoft Excel

Приложение Excel выполняет целый ряд вычислений, связанных с матричными данными. Программа обрабатывает их, как диапазон ячеек, применяя к ним формулы массива. Одно из таких действий – это нахождение обратной матрицы. Давайте выясним, что представляет собой алгоритм данной процедуры.

Выполнение расчетов

Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.

Расчет определителя

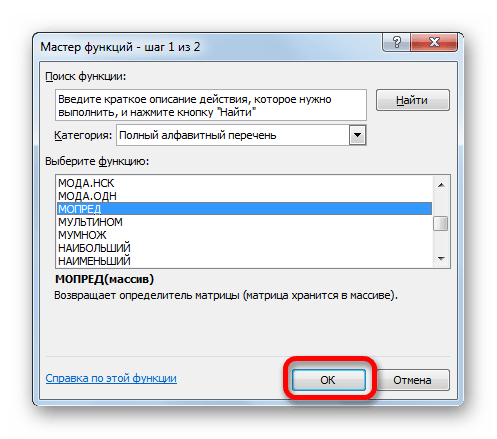
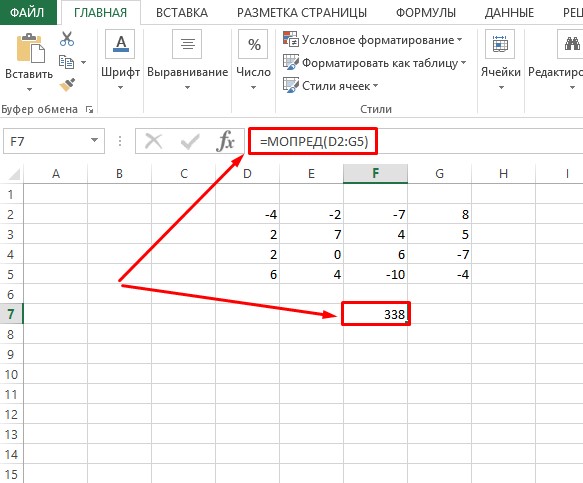
Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.

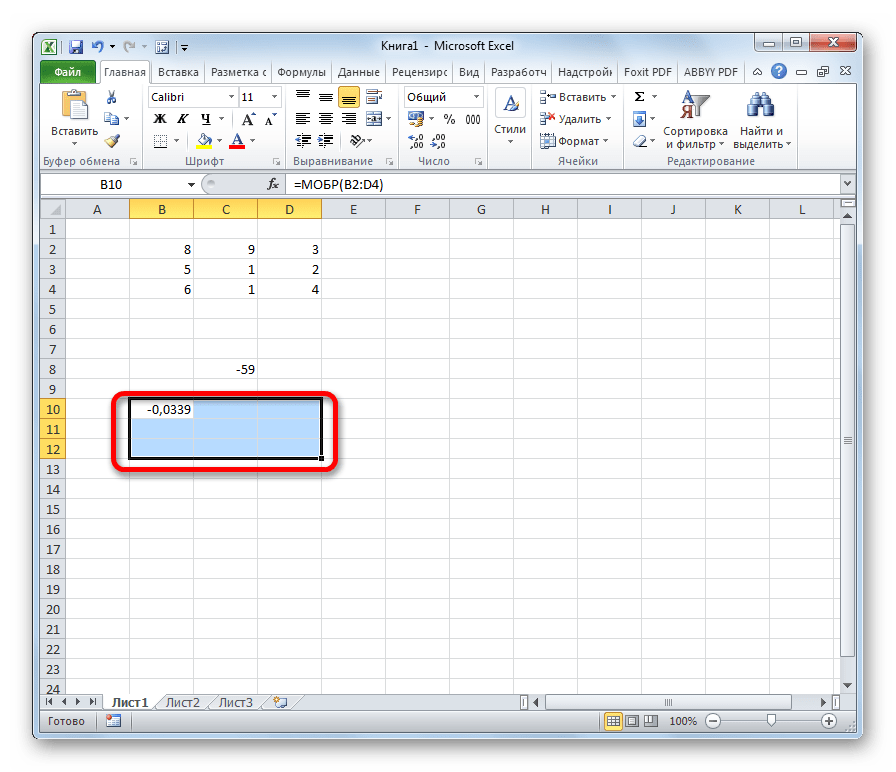
  1. Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.

    2. Переход в мастер функций в Microsoft Excel

  2. Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».

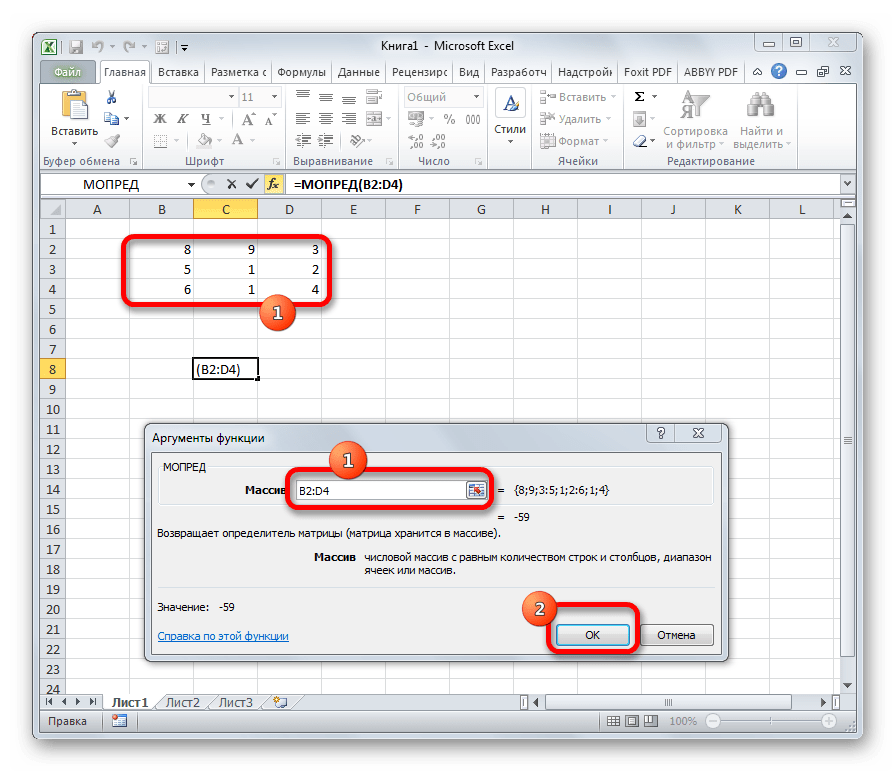
    3. Переход в аргументы функции МОПРЕД в Microsoft Excel

  3. Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».

    4. Аргументы функции МОПРЕД в Microsoft Excel

  4. Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.

Определитель матрицы в Microsoft Excel

Расчет обратной матрицы

Теперь можно преступить к непосредственному расчету обратной матрицы.

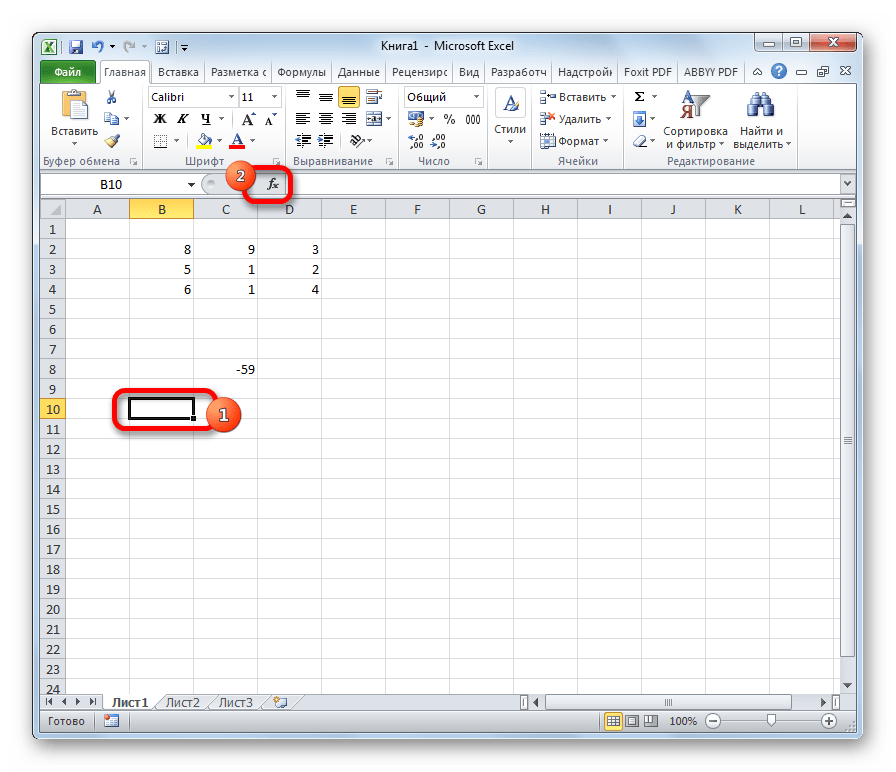
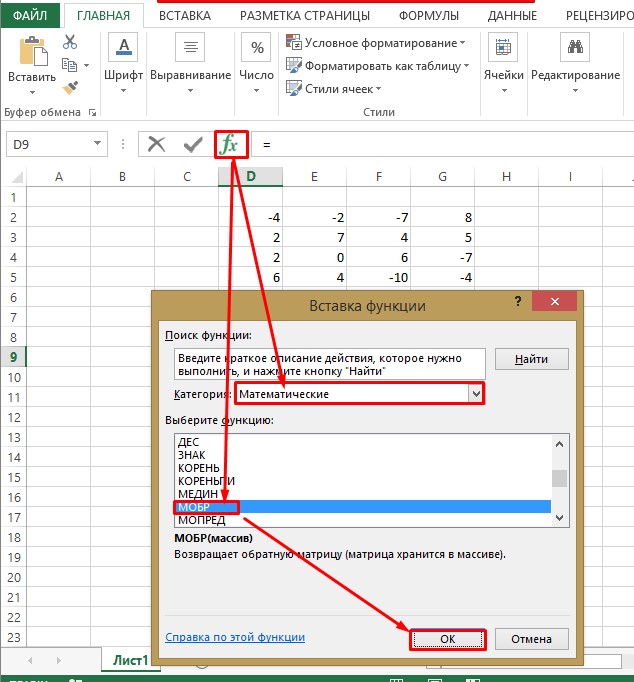
  1. Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.

    2. Кнопка вставить функцию в Microsoft Excel

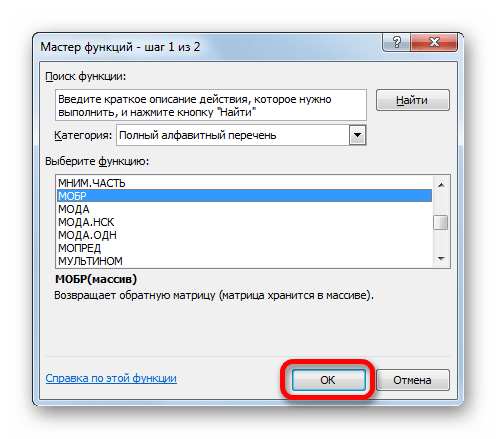
  2. В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».

    3. Переход в аргументы функции МОБР в Microsoft Excel

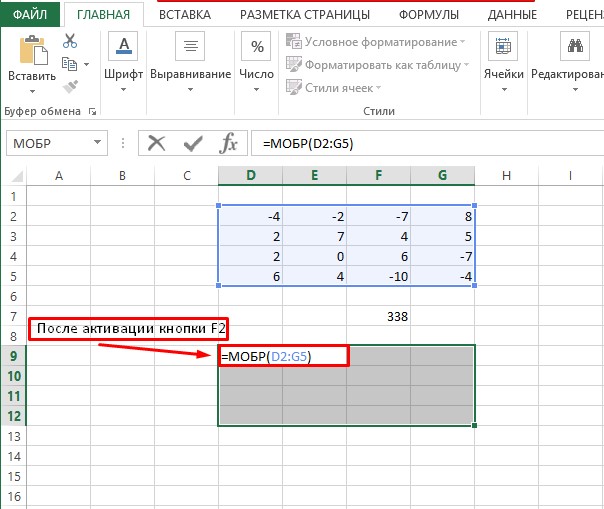
  3. В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».

    4. Аргументы функции МОБР в Microsoft Excel

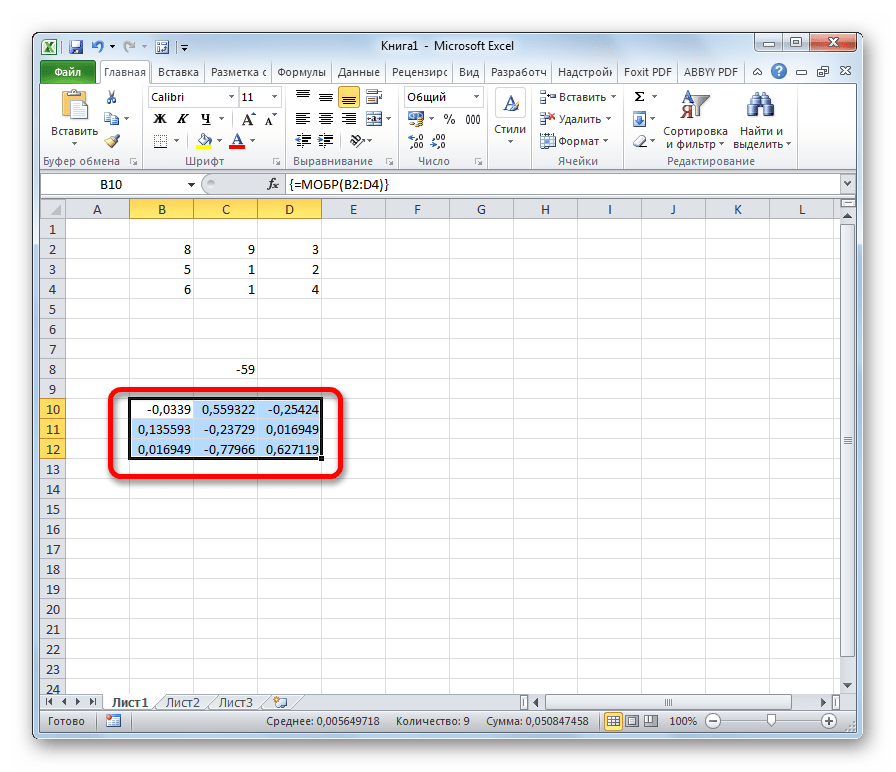
  4. Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.

    5. Выделение диапазона в Microsoft Excel

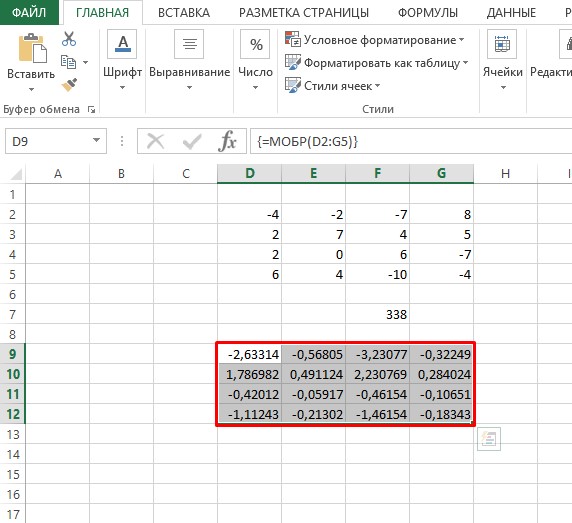
  5. Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.

Обратная матрица вычислена в Microsoft Excel

На этом расчет можно считать завершенным.

Lumpics.ru

Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.

Еще статьи по данной теме:

Помогла ли Вам статья?

Источник

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

Функция МОБР возвращает обратную матрицу для матрицы, храняной в массиве.

Примечание: Если у вас установлена текущая версия Microsoft 365, можно просто ввести формулу в верхней левой ячейке диапазона вывода и нажать клавишу ВВОД, чтобы подтвердить использование формулы динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.

Синтаксис

МОБР(массив)

Аргументы функции МОБР описаны ниже.

  • Массива    Обязательный. Числовой массив с равным количеством строк и столбцов.

Замечания

  • Массив может быть задан как диапазон ячеек, например A1:C3 как массив констант, например {1;2;3: 4;5;6: 7;8;9} или как имя диапазона или массива.

  • Если какие-либо ячейки в массиве пустые или содержат текст, функции МОБР возвращают #VALUE! ошибку «#ВЫЧИС!».

  • МоБР также возвращает #VALUE! если массив не имеет равного числа строк и столбцов.

  • Обратные матрицы, такие как определители, обычно используются для решения систем математических уравнений с несколькими переменными. Произведением матрицы и обратной является матрица удостоверений — квадратный массив, в котором диагональные значения равны 1, а все остальные — 0.

  • В качестве примера вычисления обратной матрицы, рассмотрим массив из двух строк и двух столбцов A1:B2, который содержит буквы a, b, c и d, представляющие любые четыре числа. В таблице приведена обратная матрица для массива A1:B2.

Столбец A

Столбец B

Строка 1

d/(a*d-b*c)

b/(b*c-a*d)

Строка 2

c/(b*c-a*d)

a/(a*d-b*c)

  • Функция МОБР производит вычисления с точностью до 16 значащих цифр, что может привести к незначительным ошибкам округления.

  • Некоторые квадратные матрицы невозможно инвертировать и возвращают #NUM! в функции МОБР. Определител непревратимой матрицы 0.

Примеры

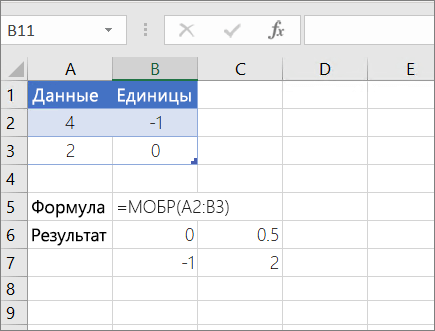
Пример 1. МОБР

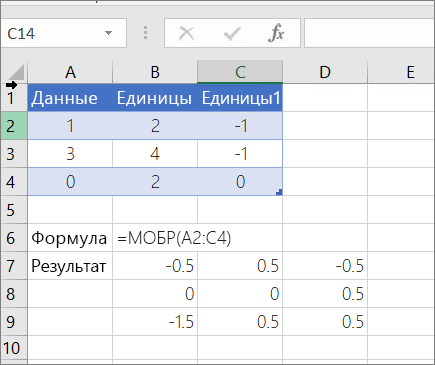
Пример 2. МОБР

Чтобы указанные выше формулы вычислялись правильно, нужно вводить их в виде формул массивов. После ввода формулы нажмите ввод, если у вас есть текущая Microsoft 365 подписка. в противном случае нажмите CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, возвращается единственный результат.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Нужна дополнительная помощь?

Источник

Excel обладает мощным инструментарием, позволяющим выполнять множество математических, статистических, логических и прочих задач. В программе также можно выполнить такое действие, как нахождение обратной матрицы. Ниже мы на практическом примере рассмотрим, как именно это сделать.

Примечание: Найти обратную матрицу можно только при условии, что исходная является квадратной (количество столбцов и строк одинаковое). К тому же, ее определитель не должен равняться цифре 0.

Этап 1. Вычисляем определитель

В программе данное действие выполняется с помощью функции МОПРЕД.

  1. Переходим в свободную ячейку, в которой планируем производить расчеты, после чего кликаем по кнопке “Вставить функцию” (fx) слева от строки формул.Вставка функции в ячейку таблицы Эксель
  2. В открывшемся окне вставки функций выбираем категорию “Математические”, в которой кликаем по оператору “МОПРЕД”, затем – по кнопке OK.Выбор функции МОПРЕД в Эксель
  3. В следующем окне нужно заполнить единственный аргумент функции – “Массив”, в значении которого указываем координаты нашей матрицы. Сделать это можно вручную, прописав адреса ячеек, используя клавиши клавиатуры. Либо можно сначала кликнуть внутри области ввода информации, затем зажав левую кнопку мыши выделить диапазон ячеек непосредственно в самой таблице. Когда все готово, нажимаем кнопку OK.Заполнение аргумента функции МОПРЕД в Excel
  4. В выбранной ячейке отобразился результат, а именно, определитель матрицы. С учетом наших данных получилось число 157894, что значит, что у нашей матрицы обратная матрица существует, так как определитель не равен нулю.Результат расчетов по функции МОПРЕД в Эксель

Этап 2. Находим обратную матрицу

Итак, после того, как мы вычислили, что определитель матрицы не равен нулю, можно приступить к нахождению обратной.

  1. Встаем в ячейку, которая станет самым верхним левым элементом новой обратной матрицы. Заходим в окно Вставки функции, нажав на соответствующую кнопку.Вставка функции в ячейку таблицы Excel
  2. В категории “Математические” выбираем функцию “МОБР”, после чего щелкаем по кнопке OK.Выбор функции МОБР в Эксель
  3. Аналогично заполнению значения аргумента “Массив” для функции МОПРЕД, рассмотренной в первом разделе, указываем координаты первичной матрицы, после чего нажимаем OK.Заполнение аргумента функции МОБР в Excel
  4. Получаем требуемый результат в выбранной ячейке.Результат расчетов по функции МОБР в Эксель
  5. Чтобы скопировать функцию в другие ячейки, выделяем область, которая совпадает по количеству столбцов и строк с начальной матрицей. Затем нажимаем клавишу F2 на клавиатуре, после чего жмем комбинацию Ctrl+Shift+Enter.Нахождение обратной матрицы в Эксель
  6. Все готово. В результате выполненных действий нам удалось найти обратную матрицу.Вычисление обратной матрицы в Excel

Заключение

Нахождение обратной матрицы – не такая распространенная математическая задача, как, например, сложение, вычитание, умножение, деление, расчеты с процентами и т.д. Но, если все же возникнет такая потребность, вовсе необязательно делать это вручную на листке бумаги, ведь Эксель позволяет быстро и безошибочно справиться с этой задачей.

Источник

На чтение 4 мин Опубликовано 28.12.2020

Обратная матрица – это сложное математическое понятие, для нахождения которой необходимо выполнить множество непростых действий на бумаге. Однако программа Excel решает данную задачу в более короткие сроки и без особых усилий со стороны исполнителя. Давайте разберемся, каким образом можно найти обратную матрицу в несколько этапов на одном из примеров.

Замечание эксперта! Обязательным условием для нахождения обратной матрицы, является соответствие исходных данных квадратной матрице, а определителя нулю.

Содержание

  1. Находим значение определителя
  2. Определяем значение обратной матрицы
  3. Сферы использования расчетов с обратной матрицей
  4. Заключение

Находим значение определителя

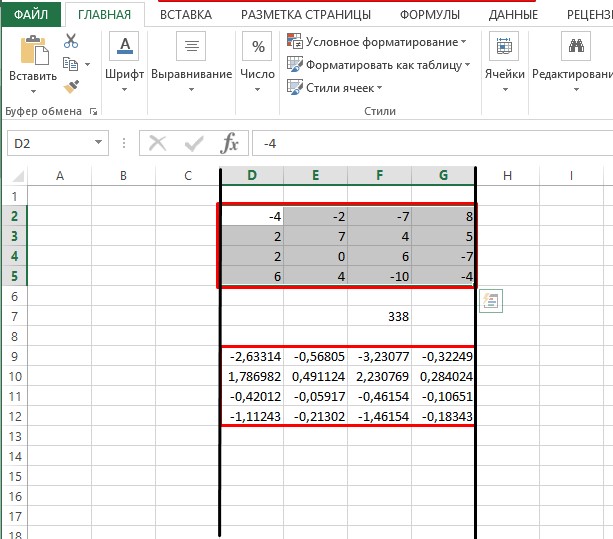
Чтобы выполнить это действие, необходимо воспользоваться функцией МОПРЕД. Как именно это делается, рассмотрим на примере:

  1. Записываем квадратную матрицу в любом свободном месте.
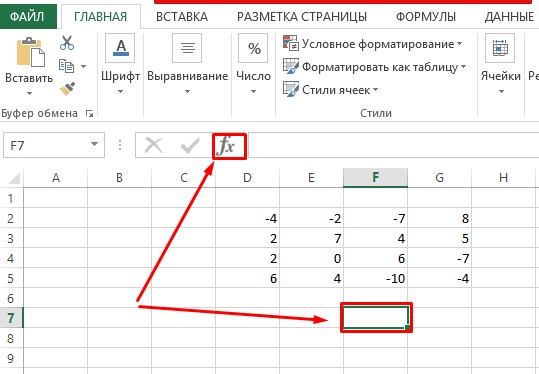
  2. Выбираем свободную ячейку, после чего находим напротив строки формул кнопку «fx» («Вставить функцию») и кликаем по ней ЛКМ.

obratnaya-matrica-v-excel-kak-najti-obratnuyu-matricu-v-ehksel-v-2-ehtapa

1
  1. Должно открыться окно, где в строке «Категория:» останавливаемся на «Математические», а ниже выбираем функцию МОПРЕД. Соглашаемся с выполненными действиями кликнув по кнопке «ОК».
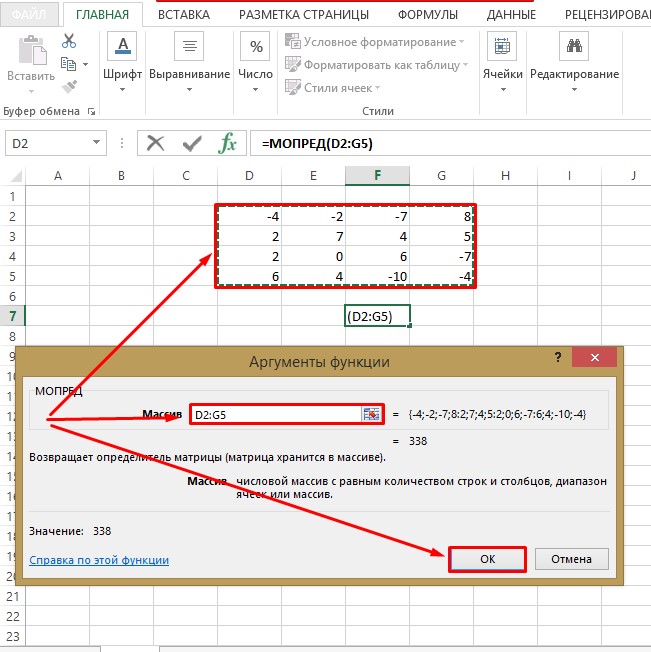
  2. Далее в открывшемся окне заполняем координаты массива.

Совет! Заполнить адресацию можно одним из двух способов: вручную или кликнув кнопкой мыши в месте ввода информации о массиве и, определив выделением зоны место расположения квадратной матрицы, получить адрес массива автоматически.

  1. После проверки введенных ручным или автоматическим образом данных жмите «ОК».

obratnaya-matrica-v-excel-kak-najti-obratnuyu-matricu-v-ehksel-v-2-ehtapa

2
  1. После всех проведенных манипуляций свободная ячейка должна отобразить определитель матрицы, значение которого понадобится для нахождения обратной матрицы. Как видно по скриншоту, после вычислений получилось число 338, а, следовательно, потому как определитель не равен 0, то обратная матрица существует.

obratnaya-matrica-v-excel-kak-najti-obratnuyu-matricu-v-ehksel-v-2-ehtapa

3

Определяем значение обратной матрицы

Как только вычисление определителя закончено, можно переходить к определению обратной матрицы:

  1. Выбираем место расположения верхнего элемента обратной матрицы, открываем окно «Вставка функции».
  2. Выбираем категорию «Математические».
  3. В расположившихся снизу функциях пролистываем список и останавливаем выбор на МОБР. Кликаем по кнопке «ОК».

obratnaya-matrica-v-excel-kak-najti-obratnuyu-matricu-v-ehksel-v-2-ehtapa

4
  1. Аналогично ранее выполняемым действиям при нахождении значений определителя вписываем координаты массива с квадратной матрицей.
  2. Убеждаемся в правильности выполненных действий и жмем «ОК».
  3. В выбранной верхней левой ячейке будущей обратной матрицы появится результат.
  4. Для копирования формулы для нахождения значений в других ячейках используем свободное выделение. Для этого, зажав ЛКМ, растягиваем на всю область будущей обратной матрицы.

obratnaya-matrica-v-excel-kak-najti-obratnuyu-matricu-v-ehksel-v-2-ehtapa

5
  1. Жмем на клавиатуре кнопку F2 и переходим к набору комбинации «Ctrl+Shift+Enter». Готово!

obratnaya-matrica-v-excel-kak-najti-obratnuyu-matricu-v-ehksel-v-2-ehtapa

6

Рекомендация эксперта! Для удобства выполнения действий по нахождению обратной матрицы в таблице Excel расположение массива с квадратной матрицей и выбранная область для ячеек с обратной матрицей должны располагаться на одном уровне по отношению к столбцам. Таким образом будет проще определить границы адресации второго массива. Пример указан на иллюстрации ниже.

obratnaya-matrica-v-excel-kak-najti-obratnuyu-matricu-v-ehksel-v-2-ehtapa

7

Сферы использования расчетов с обратной матрицей

Экономика – это область, которая требует проведения постоянных и очень сложных расчетов. Для облегчения используется матричная система расчетов. Нахождение обратной матрицы – это быстрый способ обработки большого объема информации за максимально короткие сроки, конечный результат которого будет представлен в наиболее удобном для восприятия виде.

Другая область применения – это 3D моделирование изображений. Всевозможные программы имеют встроенные инструменты для проведения подобного рода расчетов, что в значительной степени облегчает работу конструкторам при производстве расчетов. Наиболее популярной программой среди 3D моделистов считается Компас-3D.

Существуют и другие сферы деятельности, где можно применить систему расчетов обратной матрицы, но все же основной программой для проведения матричных расчетов можно считать Excel.

Заключение

Нахождение обратной матрицы нельзя назвать такой же распространенной математической задачей, как вычитание, сложение или деление, но если появилась необходимость в ее решении, то все действия могут произведены в табличном процессоре Excel. Если человеческий фактор склонен допускать ошибки, то компьютерная программа выдаст 100% точный результат.

Оцените качество статьи. Нам важно ваше мнение:

Источник


Для вычисления обратной матрицы в MS EXCEL существует специальная функция

МОБР()

или англ.

MINVERSE

.

Понятие обратной матрицы определено только для квадратных матриц, определитель которых отличен от нуля.


СОВЕТ

: О нахождении определителя матрицы читайте статью

Вычисление определителя матрицы в MS EXCEL

Матрица А

-1

называется обратной для исходной матрицы А порядка n, если

справедливы равенства

А

-1

*А=Е и А*А

-1

=Е, где Е единичная матрица порядка n.

Для вычисления обратной матрицы в MS EXCEL существует специальная функция

МОБР()

.

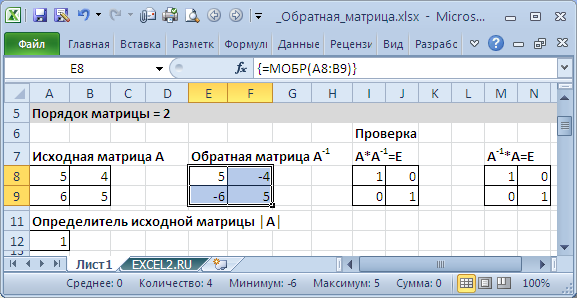
Если элементы исходной матрицы 2 х 2 расположены в диапазоне

А8:В9

, то для получения

транспонированной матрицы

нужно (см.

файл примера

):

  • выделить диапазон 2 х 2, который не пересекается с исходным диапазоном

    А8:В9

    ,

    например,

    Е8:F9
  • в

    Cтроке формул

    ввести формулу

    =

    МОБР

    (A8:B9)

    и нажать комбинацию клавиш

    CTRL+SHIFT+ENTER

    , т.е. нужно ввести ее как

    формулу массива

    (формулу можно ввести прямо в ячейку, предварительно нажав клавишу

    F2

    )

Если матрица большей размерности, то перед вводом формулы нужно выделить соответственно больший диапазон ячеек.

Массив может быть задан не только как интервал ячеек, например

A8:B9

, но и как

массив констант

, например

=МОБР({5;4: 3;2})

. Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией. Массив в этом случае указывается по строкам: например, сначала первая строка 5;4, затем через двоеточие записывается следующая строка 3;2. Элементы отделяются точкой с запятой.

Ссылка на массив также может быть указана как ссылка на

именованный диапазон

.

Некоторые квадратные матрицы не могут быть обращены: в таких случаях функция

МОБР()

возвращает значение ошибки #ЧИСЛО!. Матрицы не могут быть обращены, у которых определитель равен 0.

Если функция

МОБР()

вернула значение ошибки #ЗНАЧ!, то либо число строк в массиве не равно числу столбцов, либо какая-либо из ячеек в массиве пуста или содержит текст. Т.е. функция

МОБР()

пустую ячейку воспринимает не как содержащую 0 (как например, это делает

СУММ()

), а как ошибочное значение.

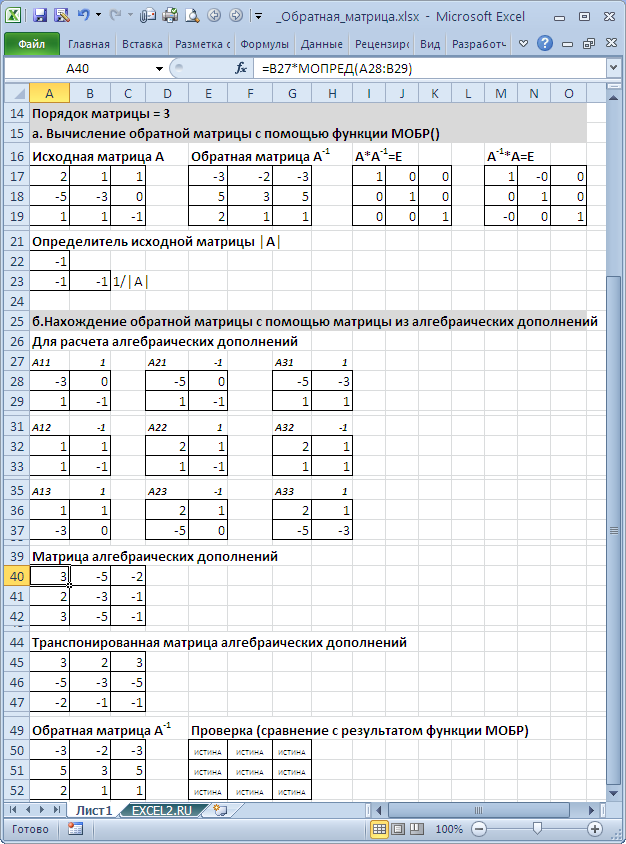
Вычисление обратной матрицы с помощью матрицы из алгебраических дополнений


СОВЕТ

: Этот раздел стоит читать только продвинутым пользователям MS EXCEL. Кроме того материал представляет только академический интерес, т.к. есть функция

МОБР()

.

В

файле примера

приведен расчет обратной матрицы 3-го порядка через матрицу алгебраических дополнений.

Порядок действий при вычислении обратной матрицы:

  • Вычисляем определитель

    матрицы

    А

    (далее — Det(A)) и убеждаемся, что он отличен от нуля (в противном случае матрица

    А

    необратима)

  • Строим матрицу из алгебраических дополнений элементов исходной матрицы
  • Транспонируем матрицу

    из алгебраических дополнений

  • Умножаем каждый элемент транспонированной матрицы

    из алгебраических дополнений на 1/Det(A) и получаем обратную матрицу

В качестве проверки можно

перемножить исходную и обратную матрицы

. В результате должна получиться единичная матрица.

Источник

Понравилась статья? Поделить с друзьями:
  • Научно исследовательская работа word
  • Научная работа по excel
  • Научиться считать в excel
  • Научиться строить графики функций в excel
  • Научиться составлять формулы excel