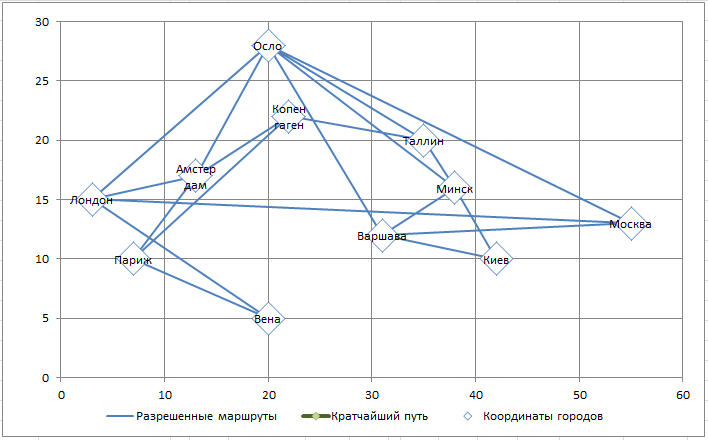
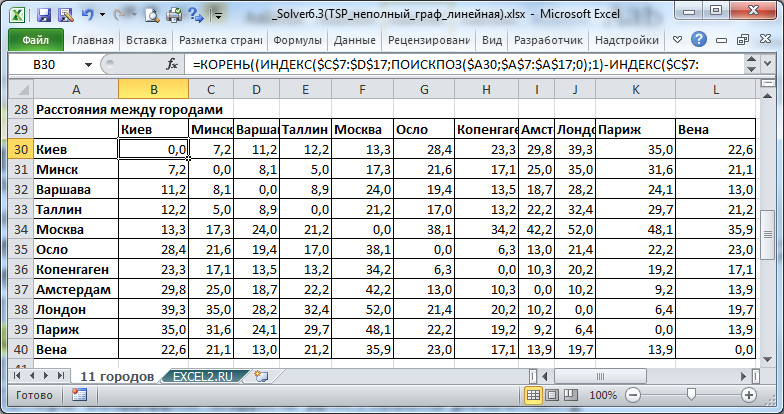
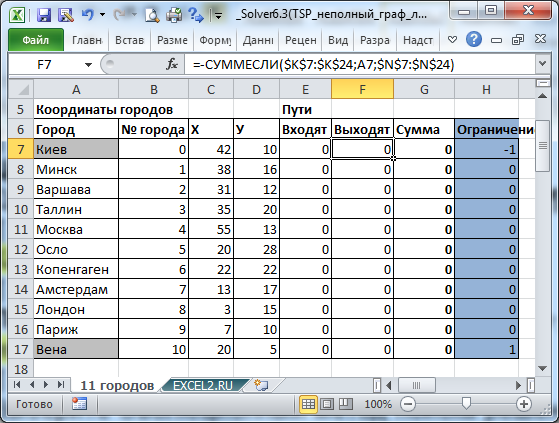
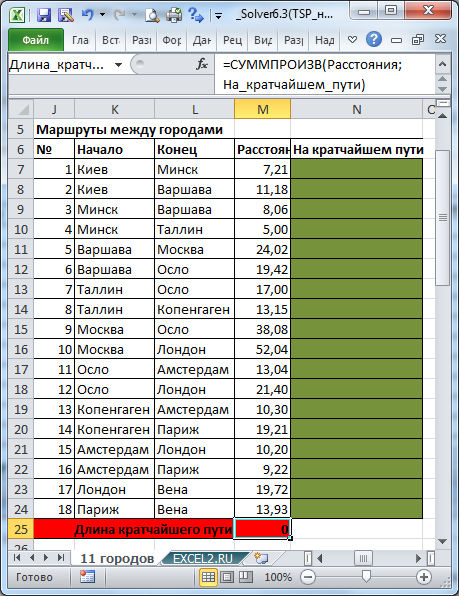
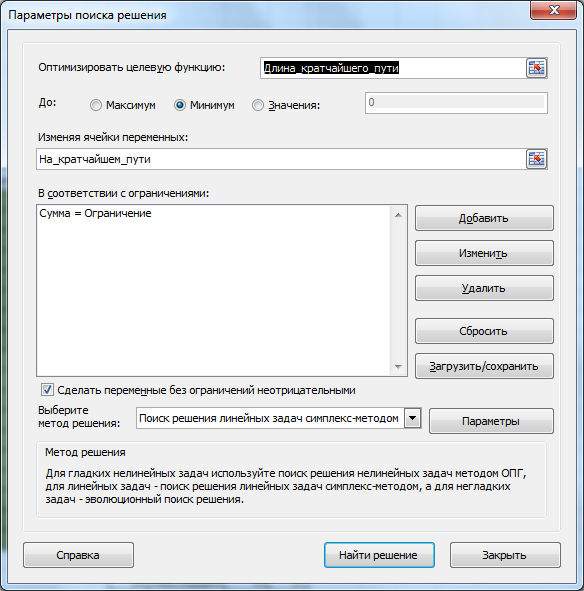
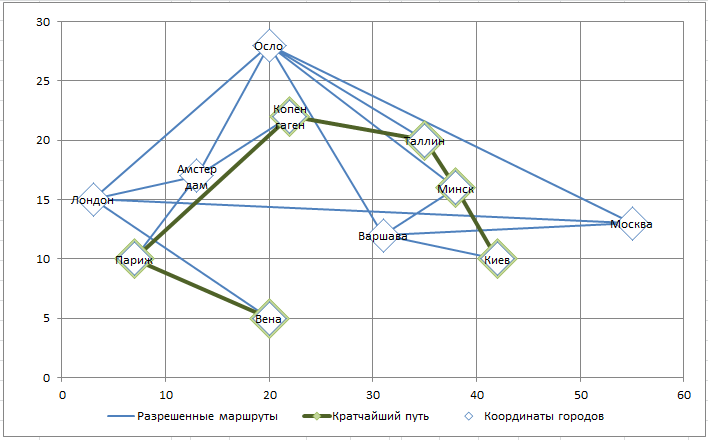
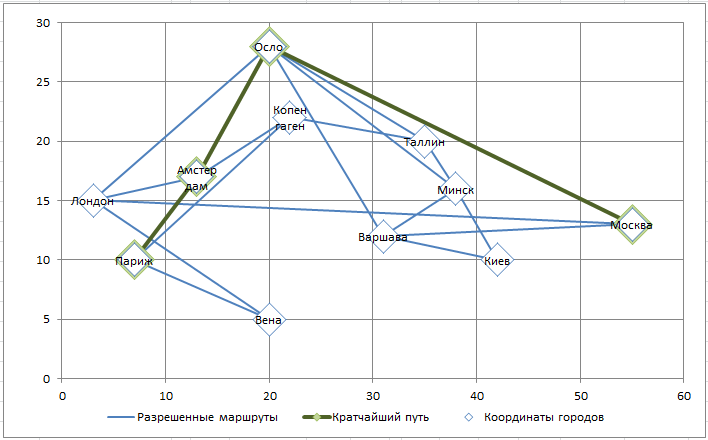
Необходимо найти кратчайший путь между 2-мя заданными городами. Построим линейную модель и с помощью надстройки Поиск решения решим задачу.
В статье
Поиск решения MS EXCEL (6.3). Задача коммивояжера (полный граф, линейная модель)
рассматривались модели, в которых коммивояжёру требуется посетить все имеющиеся города. В этой задаче посещение всех городов не требуется.
Задача
Имеется 11 городов, координаты которых известны. Маршруты проложены только между некоторыми городами (неполный граф). Найти кратчайший путь между 2-мя заданными городами. Построить Линейную модель.
Создание модели
Так как даны координаты городов, то сначала найдем расстояния между ними (см.
файл примера
).
Расстояния рассчитаем с помощью формулы: =
КОРЕНЬ((ИНДЕКС($C$7:$D$17;ПОИСКПОЗ($A30;$A$7:$A$17;0);1)-ИНДЕКС($C$7:$D$17;ПОИСКПОЗ(B$29;$A$7:$A$17;0);1))^2 +(ИНДЕКС($C$7:$D$17;ПОИСКПОЗ($A30;$A$7:$A$17;0);2)-ИНДЕКС($C$7:$D$17;ПОИСКПОЗ(B$29;$A$7:$A$17;0);2))^2)
Теперь создадим линейную модель для решения задачи с помощью
Поиска решения
.
Совет
: Вводная статья про
Поиск решения
в MS EXCEL 2010
находится здесь
.
Обратите внимание, что не все города соединены сообщением (столбцы J:M), например нет прямого маршрута между Москвой и Парижем. Также для модели принципиально направление маршрута: Москва — Лондон, это не тоже самое, что Лондон-Москва (при необходимости список маршрутов можно расширить).
Переменные (выделено зеленым)
. В качестве переменных модели следует взять номера маршрутов между городами: если маршрут включен в кратчайший путь, то переменная =1, если нет, то =0.
Ограничения (выделено синим)
. Необходимо, чтобы из каждого города, в котором побывал путешественник, был входящий и выходящий маршрут. Так как входящий маршрут обозначается 1, а исходящий -1, то их сумма, равная 0, будет означать, что в город вошли и вышли (включен в кратчайший путь). Исключение составляют город – начальная точка путешествия (сумма =-1) и город – конечная точка (сумма =1). Изменяя ограничение в синем столбце, можно задавать начальные и конечные пункты путешествия.
Целевая функция (выделено красным)
.
Длина маршрута должна быть минимальной.
Примечание
: для удобства настройки
Поиска решения
используются
именованные диапазоны
.
Выберите Линейный метод поиска решения, т.к. созданная модель является линейной.
Найденное
Решение
Поиск решения
гарантировано найдет самый короткий маршрут, т.к. модель линейная.
Изменив начальный и конечный пункт путешествия, и перезапустив
Поиск решения
, получим другой маршрут.
Будьте внимательны, не все пары конечных и начальных пунктов допустимы. Например, задав путешествие из Москвы в Копенгаген,
Поиск решения
не найдет маршрут, т.к. для этого потребуется «двигаться назад», а в маршрутах между городами обратные пути не прописаны (маршруты, конечно, можно добавить в столбцы J:M, но не забудьте изменить и другие формулы).
Рассмотрим методику решения в Excel
задачи о нахождении кратчайшего пути.
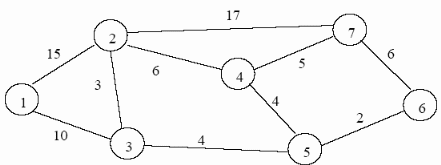
Задача 3. Задача выбора кратчайшего
пути задана сетью, изображенной на рис.
3.1. Найдите кратчайший путь от узла с
номером 1 до узла с номеров 8, если c12=1
км, c13=4 км,
c14=6 км, c23=3
км, c26=5 км,
c27=1 км, c34=3
км, c35=5 км,
c45=1 км, c48=4
км, c54=1 км,
c56=1 км, c58=2
км, c65=1 км,
c67=3 км, c68=4
км, c72=1 км,
c76=3 км, c78=7
км.
На рис. 3.2 представлены Таблица
кратчайших расстояний и План
перевозок товара по кратчайшему
пути, сформированные на рабочем листе
Excel. Здесь в Таблице кратчайших
расстояний мы видим, что если между
отдельными складами отсутствует
возможность перевозки товара, то в
соответствующие ячейки таблицы
(выделенные темным фоном) заносится
любое большое число (большее на порядок
или два порядка, в данном случае 100).
Не сложно заметить, что данная задача
решается аналогично решению транспортной
задачи с промежуточными пунктами. В
целевую ячейку, в данном случае C24,
необходимо занести формулу:
=СУММПРОИЗВ(C4:I10;C16:I22).
Рис. 3.2. Таблицы задачи поиска кратчайшего
пути (до поиска решения)
Рис. 3.3. Окно поиска решения с
накладываемыми ограничениями
Используя меню СервисПоиск
решения открываем
диалоговое окно Поиск решения
(см. рис. 3.3), в котором устанавливаем
целевую ячейку равной минимальному
значению, определяем диапазон изменяемых
ячеек и ограничения и запускаем процедуру
вычисления, щелкнув по кнопке Выполнить.
Рис. 3.4. Таблицы задачи поиска кратчайшего
пути (после поиска решения)
Результат решения данной задачи
представлен на рис. 3.4.
После того, как Excel найдет
решение, можно определить кратчайший
путь следующим образом. В первой строке
Плана перевозок товара по кратчайшему
пути нетрудно видеть, что из первого
пункта автомобиль следует в пункт 2, так
как в столбце под потребителем 2 стоит
единица в ячейке, что означает заезд в
этот пункт. Далее смотрим на строку 2
(поставщик 2), так как следующее отправление
автомобиля происходит из этого пункта.
В этой строке единица стоит в столбце
7, значит автомобиль движется из пункта
2 в пункт 7. После этого смотрим строку
с поставщиком 7, и так далее пока не
появится конченый пункт 8.
Таким образом, мы видим, что кратчайший
путь перевозки товара следующий:
127658.
Расстояние перевозки при этом составит
8 км. Аналогично данную задачу можно
решить и на максимум, т.е. найти самый
длинный путь доставки товара.
Задания к лабораторной работе № 3 «Задача о нахождении кратчайшего пути»
Решите задачу 3, используя данные о
расстояниях между узлами транспортной
сети, представленные в табл. 3.1.
Таблица 3.1
Варианты заданий для самостоятельного решения
|
c(ij) |
Расстояние между смежными узлами по вариантам |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
c(12) |
1 |
20 |
18 |
6 |
17 |
1 |
3 |
6 |
14 |
12 |
|
c(13) |
5 |
6 |
9 |
9 |
14 |
19 |
17 |
6 |
1 |
14 |
|
c(14) |
16 |
8 |
12 |
7 |
9 |
15 |
10 |
18 |
6 |
10 |
|
c(23) |
2 |
12 |
4 |
9 |
1 |
15 |
13 |
1 |
10 |
19 |
|
c(26) |
1 |
9 |
17 |
20 |
9 |
18 |
11 |
11 |
8 |
2 |
|
c(27) |
16 |
3 |
16 |
17 |
11 |
12 |
3 |
10 |
18 |
14 |
|
c(34) |
15 |
3 |
20 |
10 |
7 |
18 |
20 |
7 |
9 |
16 |
|
c(35) |
17 |
2 |
11 |
20 |
8 |
12 |
20 |
2 |
13 |
11 |
|
c(45) |
17 |
12 |
9 |
11 |
11 |
2 |
12 |
6 |
11 |
3 |
|
c(48) |
17 |
3 |
4 |
4 |
6 |
12 |
10 |
18 |
10 |
4 |
|
c(54) |
17 |
1 |
8 |
3 |
19 |
4 |
7 |
15 |
2 |
18 |
|
c(56) |
10 |
8 |
10 |
6 |
5 |
9 |
20 |
7 |
20 |
12 |
|
c(58) |
5 |
11 |
3 |
19 |
4 |
8 |
16 |
2 |
2 |
20 |
|
c(65) |
1 |
19 |
7 |
6 |
19 |
10 |
16 |
6 |
8 |
11 |
|
c(67) |
6 |
16 |
2 |
10 |
8 |
20 |
20 |
6 |
1 |
15 |
|
c(68) |
14 |
17 |
11 |
2 |
11 |
5 |
13 |
17 |
14 |
16 |
|
c(72) |
10 |
11 |
15 |
4 |
3 |
20 |
7 |
4 |
4 |
19 |
|
c(76) |
7 |
1 |
7 |
9 |
12 |
20 |
14 |
14 |
5 |
17 |
|
c(78) |
1 |
18 |
13 |
9 |
4 |
7 |
1 |
9 |
14 |
13 |
Вариант подбирается по последней цифре
шифра.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подборка по базе: Простые задачи.docx, Нютон котес Решение интегрального уравнения.docx, Практичечкая задача семинар 4.docx, Бурлуцкая Е.С. ПСО — задачи (гос. группа).docx, Практические задачи.docx, Учебник по EXCEL.doc, Конспект урока_ _Решение задач на тему_ энергия_.doc, Кейс Задача 1 Гарибян Юлия.docx, Логические задачи 3-4 кл..doc, Урок по теме «Системы счисления в задачах.pptx
Решение задач в Excel
Нахождение кратчайшего пути
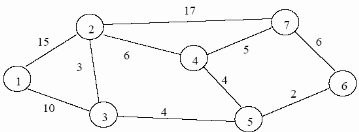
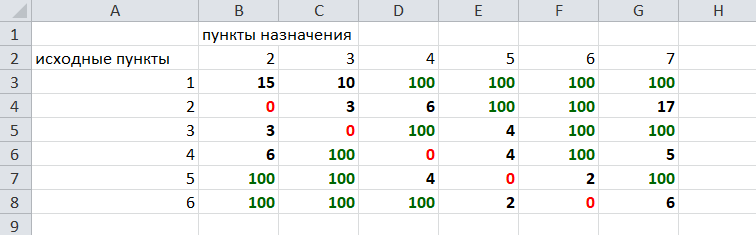
Определим кратчайший путь между вершинами 1 и 7 на представленном графе.
Составим таблицу. Номера вершин от 2 до 7 расположим по горизонтали. Это пункты назначения, то есть вершины, в которые мы придем. Вершины от 1 до 6 расположим по вертикали – это исходные пункты. Пункты назначения начинаем нумеровать со второго, так как вершина 1 – это исходный пункт и в него прийти нельзя. Исходные пункты нумеруем от 1 до 6, так как пункт 7 – конечный и выход из него невозможен.
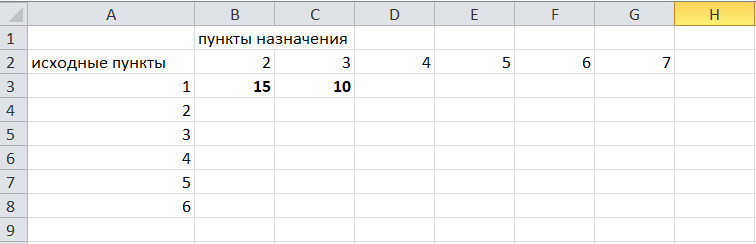
Внутри таблицы запишем расстояния. Так расстояние из вершины 1 в вершину 2 равно 15, значит на пересечении строки «исходный пункт1» и столбца «пункт назначения 2» ставим число 15.
Расстояние из вершины 1 в вершину 3 равно 10, значит на пересечении строки «исходный пункт1» и столбца «пункт назначения 3» ставим число 10.
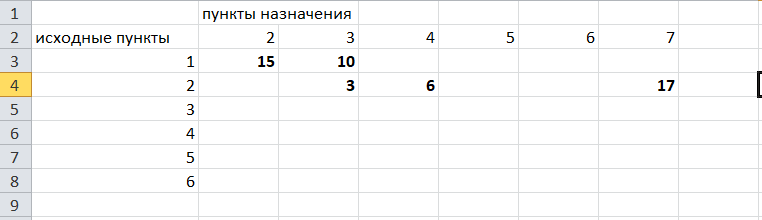
По графу видим, что из вершины 2 можно попасть в вершину 3 (это расстояние равно 3)или в вершину 4 (расстояние равно 6), или в вершину 7 (расстояние равно 17). На пересечении строки «исходный пункт 2» и столбца «пункт назначения 3» ставим число 4. На пересечении строки «исходный пункт 2» и столбца «пункт назначения 4» ставим число 6. На пересечении строки «исходный пункт 2» и столбца «пункт назначения 7» ставим число 17.
Аналогично заполним в таблицу расстояния из вершины 3 в вершины 2 и 5, которые соответственно равны 3 и 4.
По графу мы видим, что из вершины 4 можно попасть в вершины 2,5,7, расстояние до которых соответственно равны 6,4,5. Занесем эти числа в таблицу:
По графу мы также видим, что из вершины 5 можно попасть в вершины 3,4, 6, расстояние до которых соответственно 4,4,2.
А из вершины 6 можно попасть в вершины 5 и 7, расстояния до которых 2 и 6. Занесем эти расстояния в нашу таблицу:
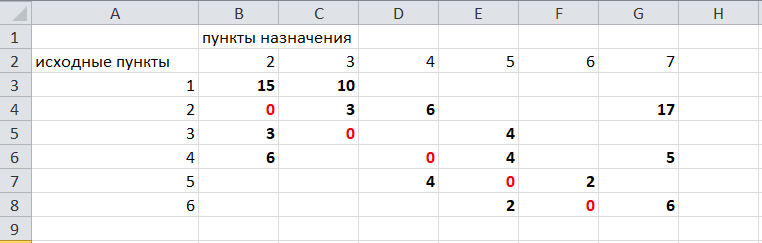
Путь из вершины 2 в вершину 2, из 3 в 3 и т.д. будет равен 0. Занесем эти величины в таблицу:
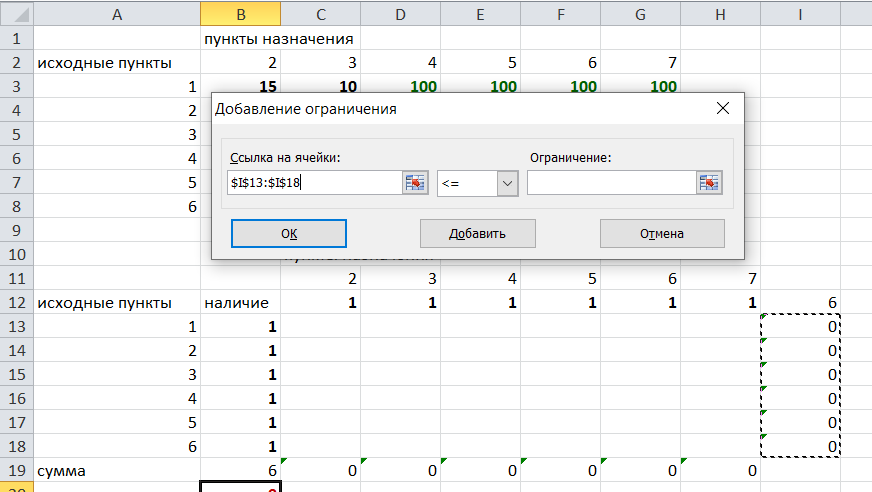
Пустые клеточки в нашей таблице говорят о том, что пути в некоторые вершины нет. Например, рассмотрим строку «исходный пункт 1». Из пункта 1 нет пути в пункты назначения 4,5,6,7. Но оставить соответствующие клетки пустыми мы не можем. Поэтому, чтобы программа поиска решения в Excel начала правильно работать, мы в эти ячейки запишем числа, намного большие самого большого из уже записанных. Тогда, так как мы будем искать кратчайший путь, программа эти значения будет отбрасывать. Например, так как самое большое число в таблице 15, а 100 > 15, мы в пустые ячейки таблицы запишем 100 (Можете записать 500 или 1000, любое число, которое вам нравится). Получим таблицу:
(Цвет записи чисел менять необязательно!)
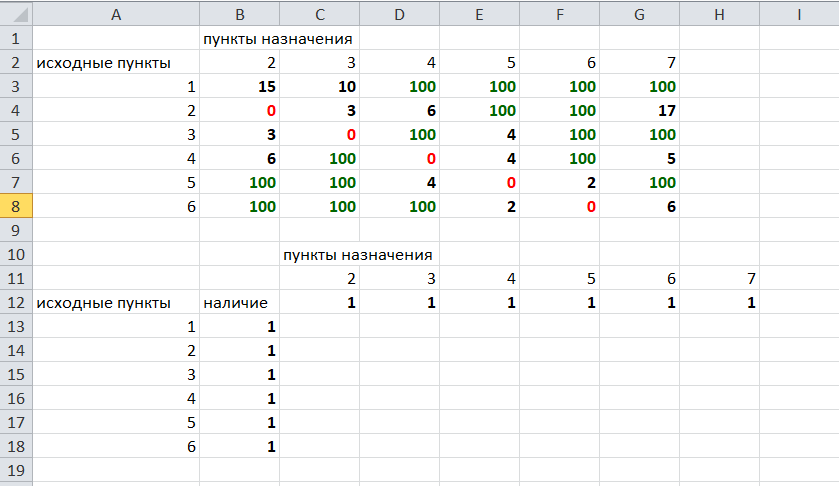
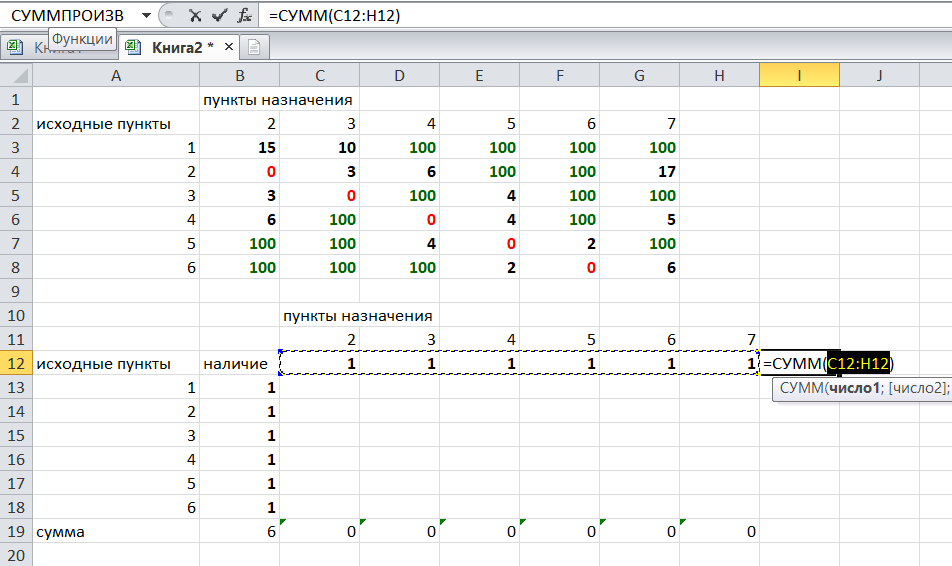
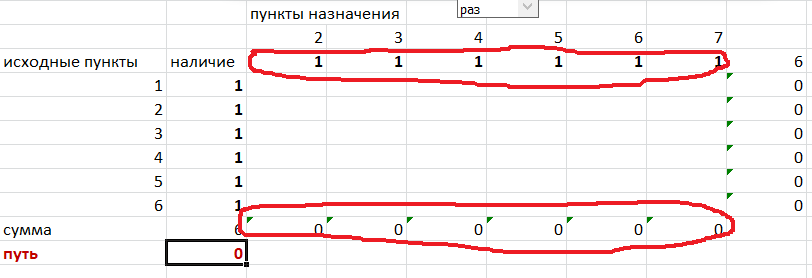
Теперь составим вторую таблицу «План перемещения по кратчайшему пути». Начало работы по составлению таблицы полностью совпадает с составлением первой таблицы, но внутреннюю часть таблицы заполнять не будем. Записываем пункты назначения по горизонтали и исходные пункты по вертикали, но вставим дополнительную строку и дополнительный столбец «наличие», которые заполним единицами.
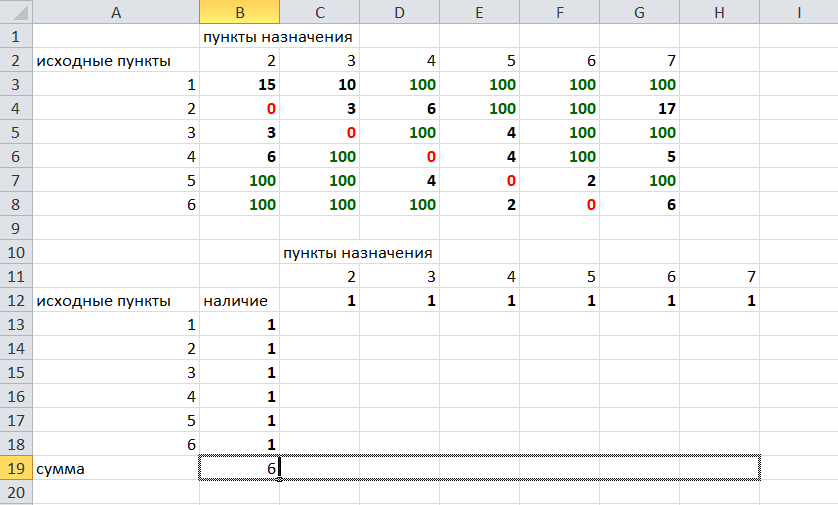
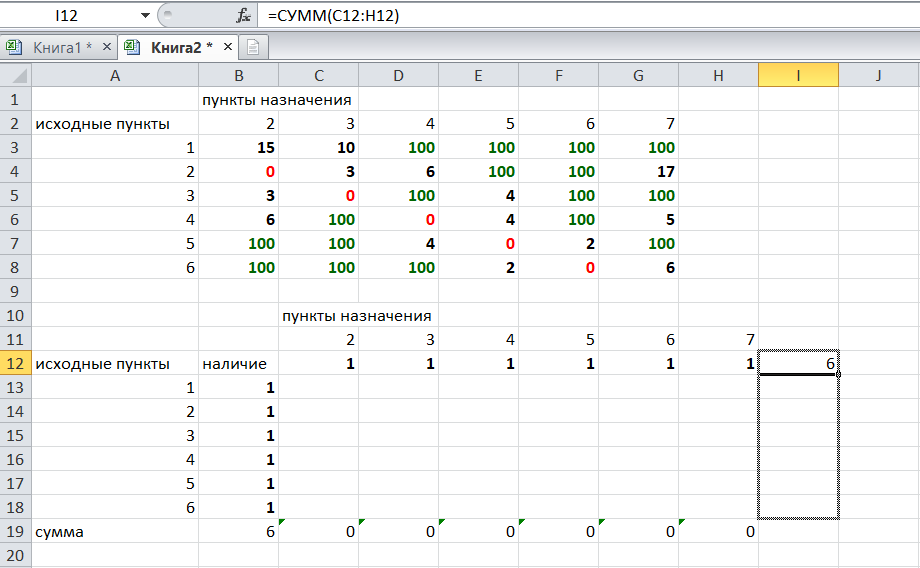
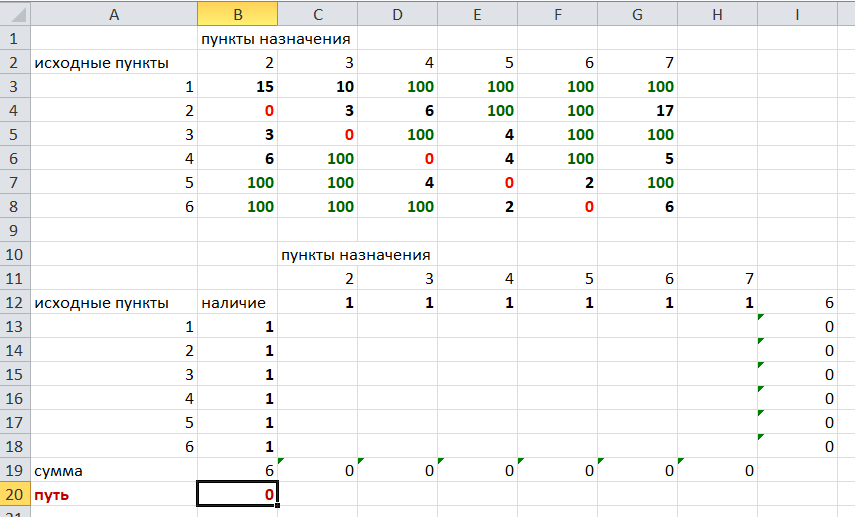
В строке внизу таблицы найдем суммы по столбцам:
Получим в ячейке В20 число 6. Найдем суммы столбцов для пунктов назначения 2,3,..7, протянув ячейку В20:
Получим:
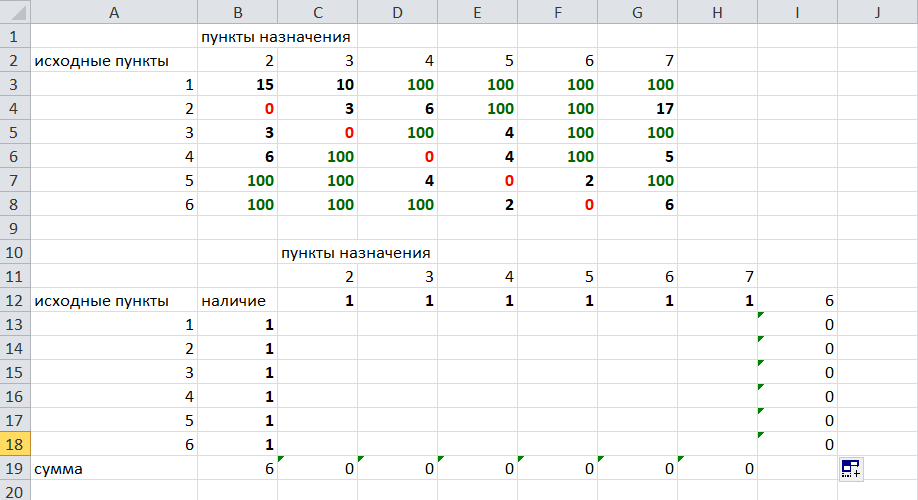
Теперь найдем суммы по строкам с исходными пунктами:
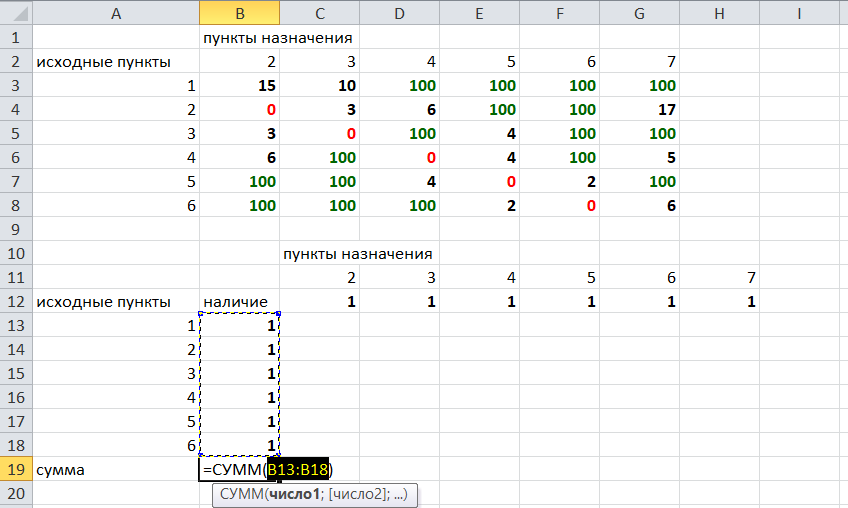
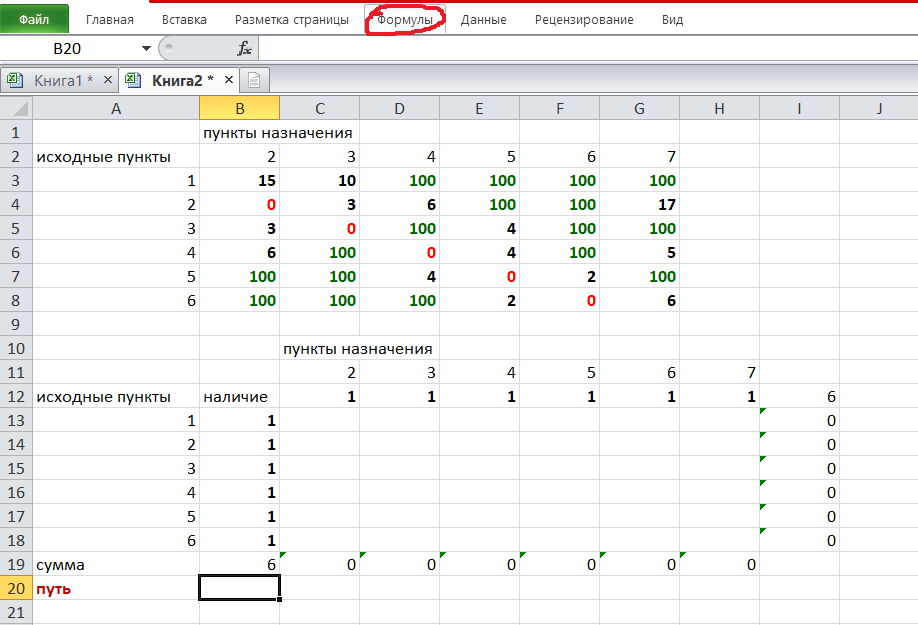
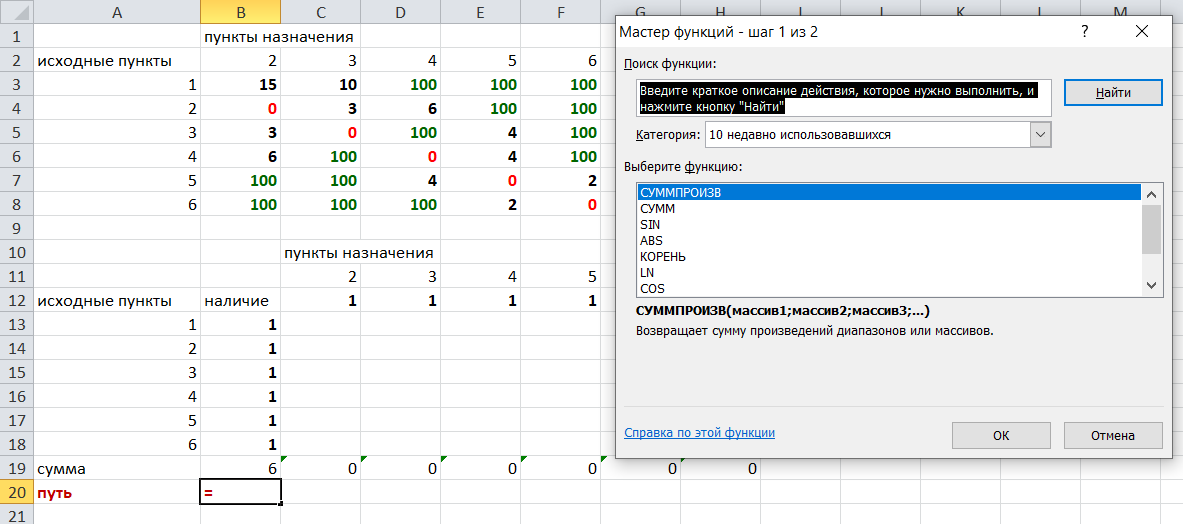
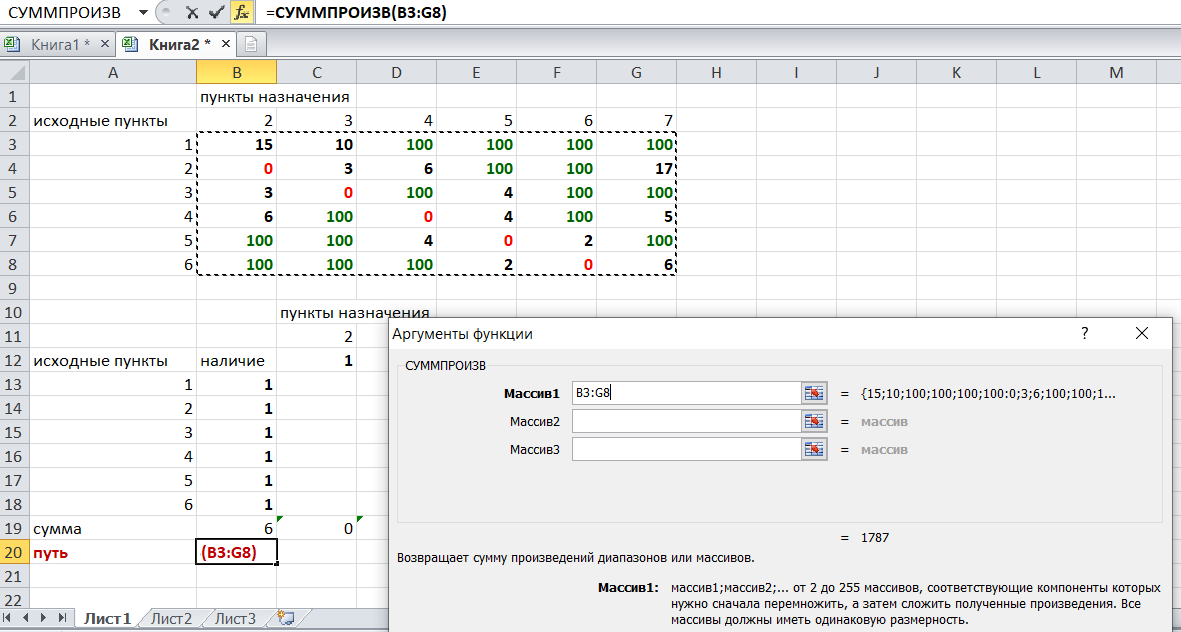
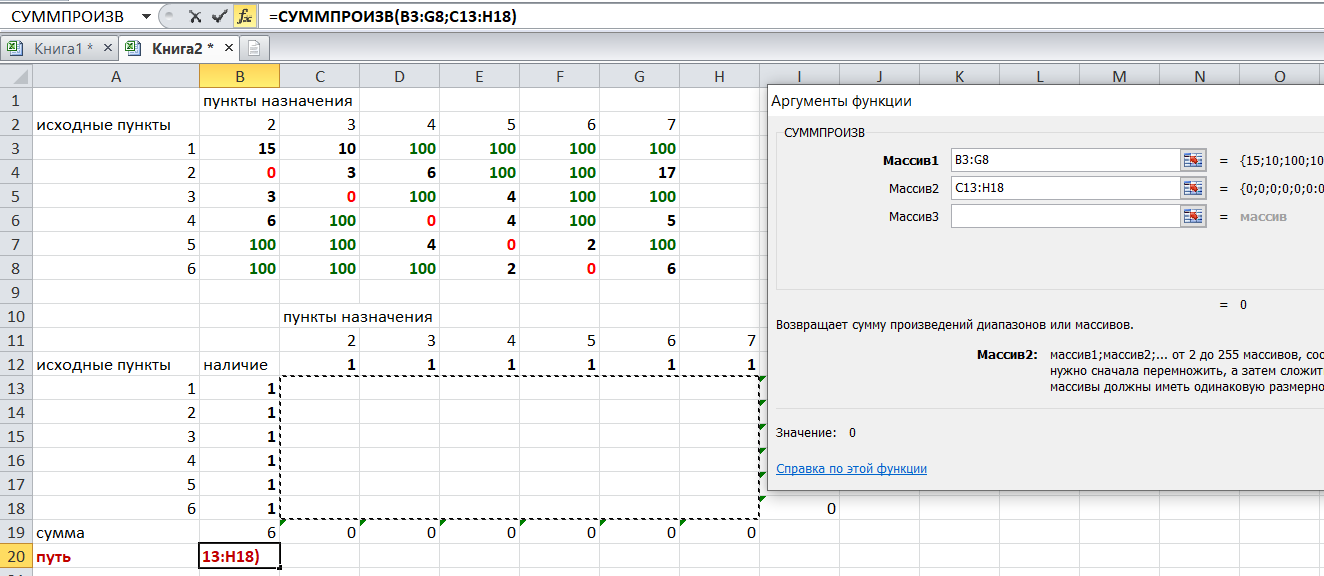
Теперь зададим формулой весь пройденный путь, это сумма произведений ячеек второй и первой таблиц. Для этого выделяем ячейку соответствующую пройденному пути, заходим на вкладку формулы, выбираем вставить функцию, находим СУММПРОИЗВ:
В качестве массива 1 выделяем все ячейки внутри первой таблицы:
В качестве массива 2 выбираем ячейки внутри второй таблицы:
Массив 3 не заполняем. Нажимаем ОК.
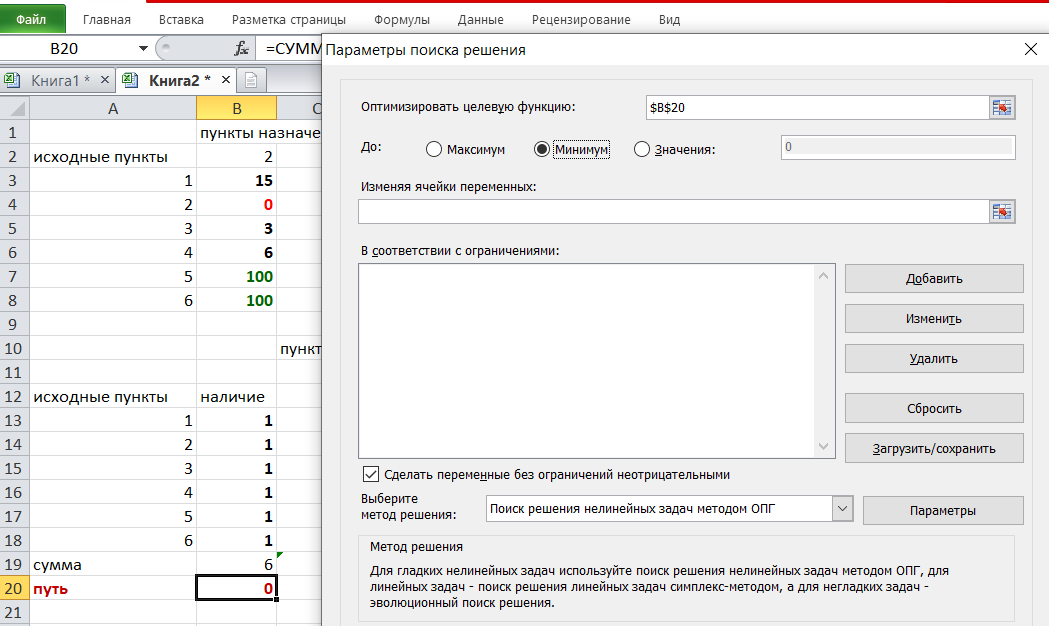
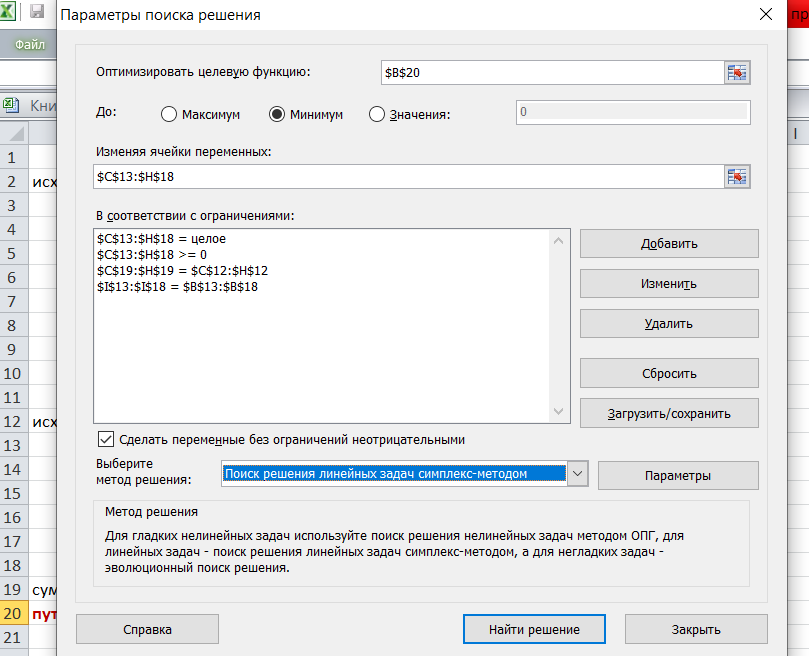
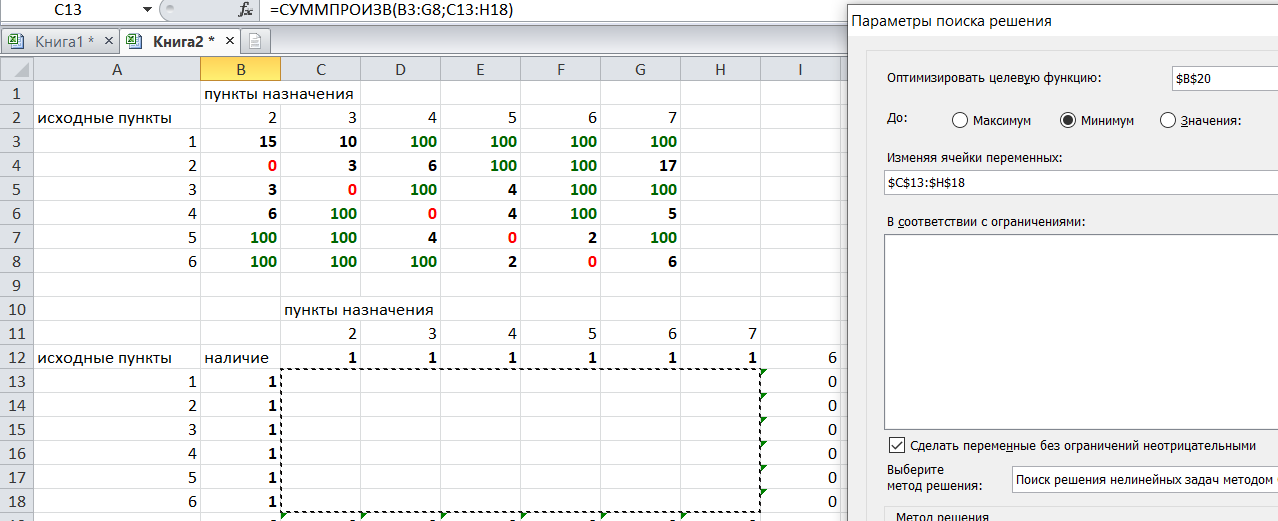
Выделяем ячейку соответствующую пройденному пути, там у нас пока записано число 0. На вкладке «данные» находим «поиск решения». Нам надо, чтобы пройденный путь был самым коротким, поэтому выбираем «оптимизировать целевую функцию» на «минимум».
Изменять будем ячейки, стоящие внутри второй таблицы.
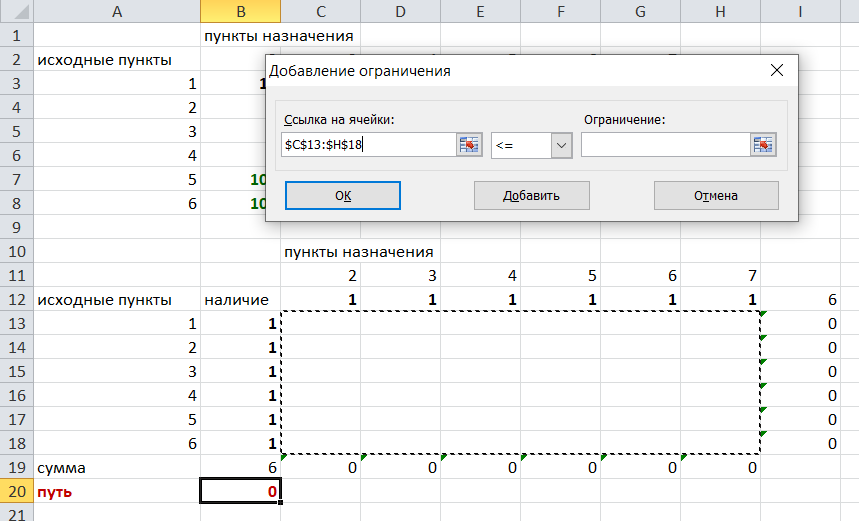
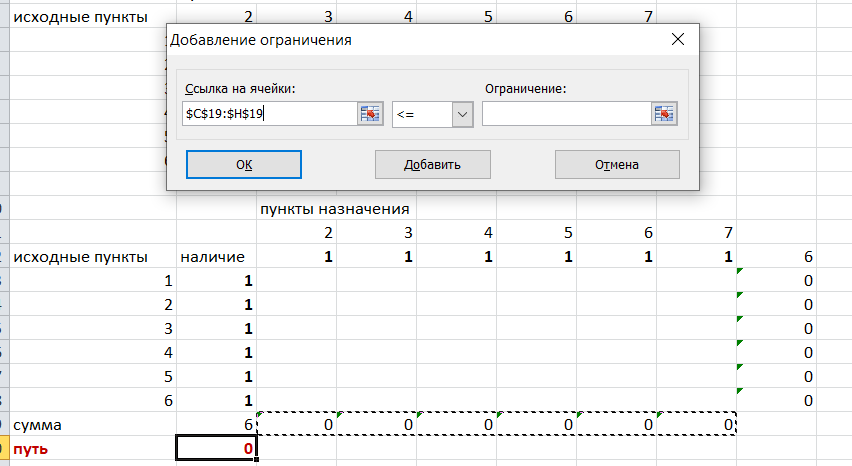
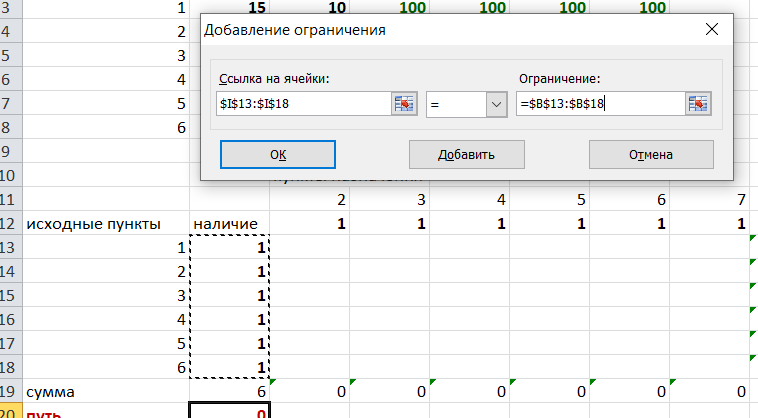
Теперь необходимо добавить ограничения. Числа стоящие внутри второй таблицы должны быть положительными.
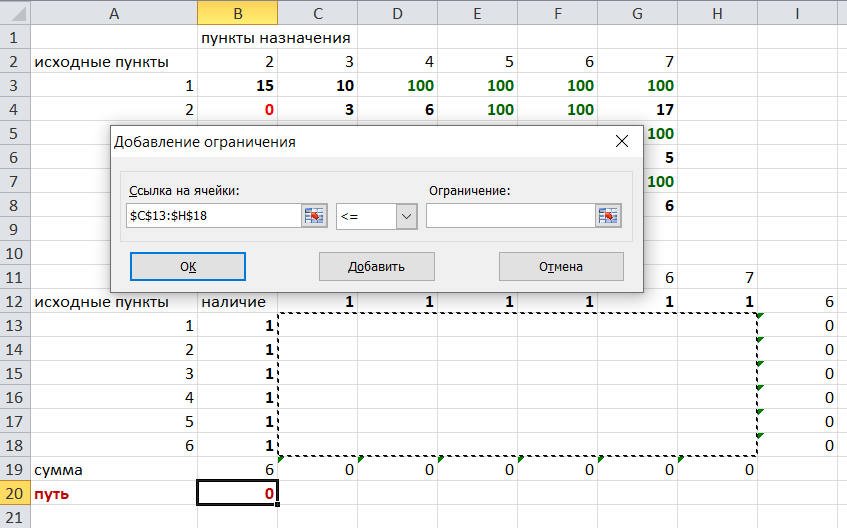
Числа внутри второй таблицы должны быть неотрицательными, добавим это ограничение:
Выделяем ячейки
Добавляем условие неотрицательности:
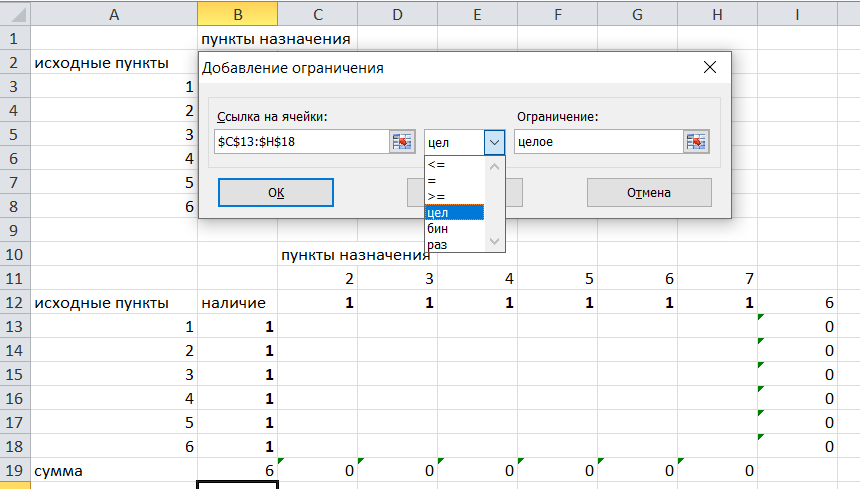
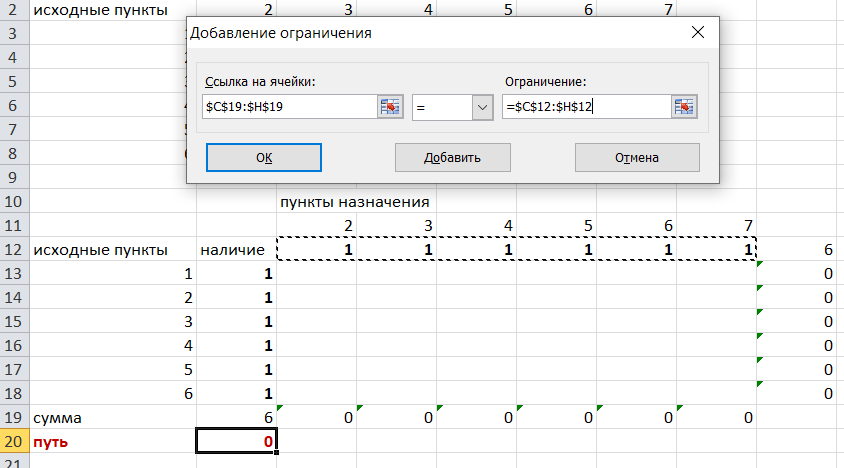
Суммы по столбцам внутри второй таблице должны быть равны 1. Это условие будет означать, что выйдя из какой-то вершины, мы можем попасть только в одну вершину, а не в 2 или 3 вершины сразу. То есть должны быть равны значения в выделенных ячейках:
Добавим это ограничение:
В качестве ограничения выбираем ячейки с 1:
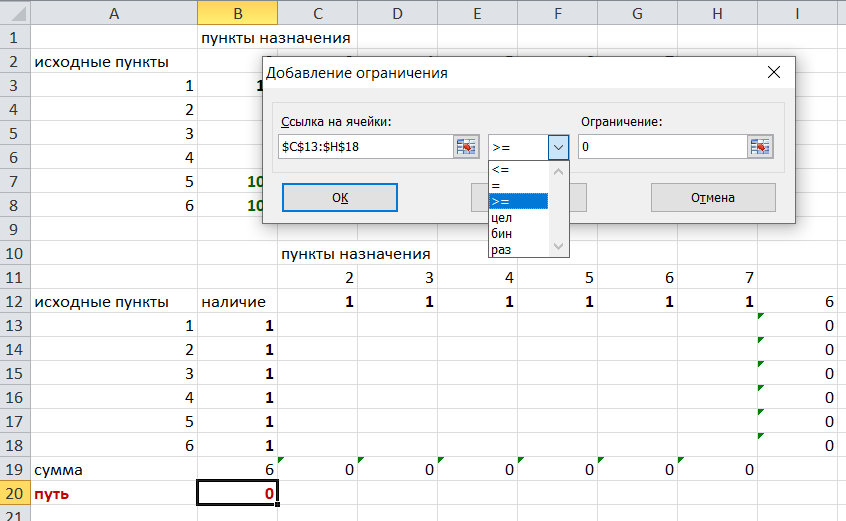
И добавим последнее ограничение. Суммы по строкам должны быть равны 1. То есть движение может идти только из одной вершины в одну. Нам надо добавить равенство значений в выделенных ячейках:
Добавим это ограничение:
Нажимаем ОК. Выбираем Поиск решения линейных задач симплекс-методом. Находим решение.
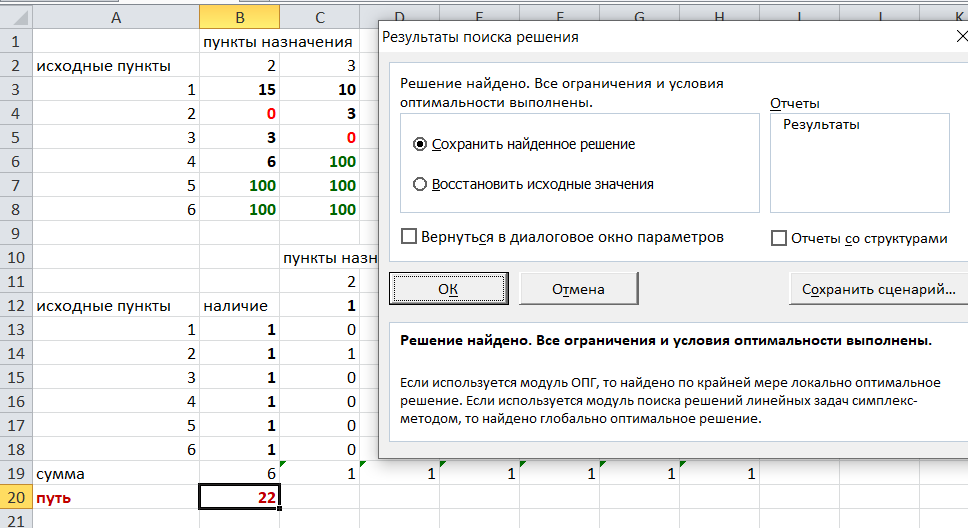
Нажимаем ОК.
Получившееся решение:
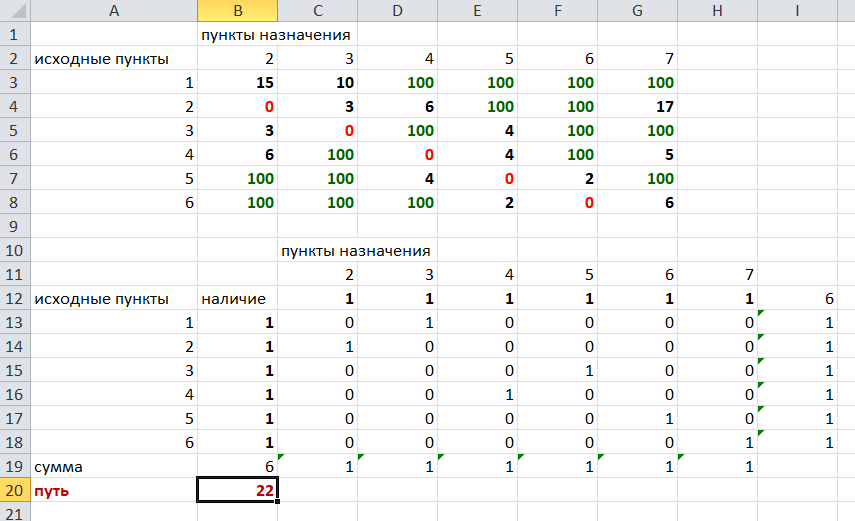
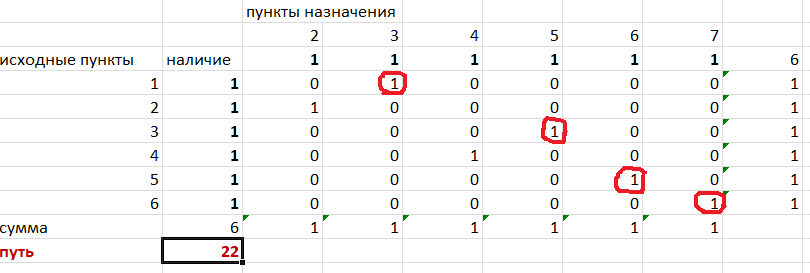
Их второй таблицы мы видим, что кратчайший путь из вершины 1 в вершину 7 составит 22. Давайте посмотрим, по каким вершинам он пройдет.
Из первой строки мы находим, что 1 стоит только в столбце «пункт назначения3». Все остальные ячейки 0. Это значит, что из первой вершины движение по кратчайшему пути идет только в вершину 3. Поэтому далее мы должны сразу перейти в строку «исходные пункты3». В этой строке 1 стоит в «пункте назначения 5». Значит из вершины 3 переходим в вершину 5. По оставшимся строкам видим, что движение идет в вершину 6 и 7. Таким образом кратчайший путь 1-3-5-6-7 и составляет он 22 (условные единицы, если исходные расстояния были даны в км, значит 22 км).
Ответ: путь 1-3-5-6-7 – кратчайший. Его длина 22.
Решите предложенную задачу по описанному алгоритму в Excel. Полученное решение высылайте на эл. почту.
Поиск кратчайшего маршрута
- Подробности
- Создано 27 Март 2011
| Содержание |
|---|
| Описание задачи |
| Решение задачи |
| Настройка параметров Excel |
| Алгоритм |
| Формула |
| Решение |
| Форматирование |
| Заключение |
При решении сложных алгоритмических задач с использование электронных таблиц иногда приходится сталкиваться с ошибками из-за возникновения циклических ссылок в расчетах. В подавляющем большинстве случаев эта ошибка связана с неверным построением формул. Но нередко цикл заложен в алгоритме решения задачи. Немногие знают, что Excel позволяет производить итерационные вычисления без использования макросов.
В примере к статье с помощью итерационных вычислений показано решение задачи по поиску кратчайшего маршрута в лабиринте. Задача, на первый взгляд, не совсем экономическая, но на практике может быть применена при оптимизации логистических и технологических процессов. В качестве другого популярного примера итерационных вычислений можно привести задачу распределения косвенных затрат при расчете полной себестоимости продукции. Здесь циклические вычисления возникают при распределении затрат вспомогательных служб: например, котельная использует электроэнергию, производимую в энергоцехе, который, в свою очередь, отапливается той же самой котельной. Совсем не обязательно решать подобную задачу распределения затрат через итерации, но знать потенциальные возможности Excel будет в любом случае нелишним.
Описание задачи
Итак, имеется карта лабиринта с предопределенными координатами входа и выхода. Карта представлена в виде прямоугольной таблицы, где каждая ячейка может быть либо стеной, либо проходом. По периметру имеется ограждение в виде стен, внутри стены могут располагаться произвольным образом. Единичный ход представляет собой шаг в одном из четырех направлений от текущей ячейки: вверх, вниз, вправо или влево. Требуется проложить кратчайший маршрут от входа к выходу.
 |
Решение задачи
Настройка параметров Excel
В примере использованы формулы, работающие только с включенным режимом итерационных вычислений. Это режим устанавливается в параметрах Excel, в Excel 2000-2003 через меню СервисПараметрыВычисления. В Excel 2007-2010 через диалог настройки общих параметров (раздел Формулы):
Кроме установки числа итераций (зависит от размера лабиринта), желательно установить ручной режим вычислений. В противном случае будет серьезно замедлен расчет при любом изменении исходных данных.
Также в примере установлен R1C1 режим отображения формул, что облегчает понимание алгоритмов при равнозначных по смыслу вертикальных и горизонтальных ссылках.
Алгоритм
Задача по поиску кратчайшего маршрута в лабиринте широко известна в математике и прикладном программировании. Общий смысл алгоритма можно изложить следующим образом:
1. Изначально все доступные для прохода ячейки очищаются. В дальнейшем в каждую ячейку проставляются номера шагов.
2. В ячейку «входа» устанавливается значение «1».
3. Цикл пока ячейка, обозначающая «выход», не заполнена номером. Выход из цикла также осуществляется, если за полный проход не было сделано никаких исправлений – в этом случае решения задачи нет.
3.1 Цикл по всем ячейкам
3.1.1 В каждую ячейку устанавливается минимальный номер из соседних и текущей ячейки плюс единица. При этом пустые соседние ячейки в сравнение не попадают.
4. При успешном результате оптимальным маршрутом является любая последовательность с последовательным увеличением номера на единицу от «входа» к «выходу».
Также популярным решением этой задачи является рекуррентный вызов процедуры перемещения из одной ячейки в другую до достижения выхода.
Формула
Любая ячейка внутри лабиринта на листе «Маршрут» содержит следующую формулу:
=IF(Карта!RC<>0;-1; IF(INT(RC[-1])=INT(MIN(IF(RC[-1]>=0;RC[-1];999);IF(R[-1]C>=0;R[-1]C;999);IF(RC[1]>=0;RC[1];999);IF(R[1]C>0;R[1]C;999)));INT(RC[-1])+1,1; IF(INT(R[-1]C)=INT(MIN(IF(RC[-1]>=0;RC[-1];999);IF(R[-1]C>=0;R[-1]C;999);IF(RC[1]>=0;RC[1];999);IF(R[1]C>0;R[1]C;999)));INT(R[-1]C)+1,2; IF(INT(RC[1])=INT(MIN(IF(RC[-1]>=0;RC[-1];999);IF(R[-1]C>=0;R[-1]C;999);IF(RC[1]>=0;RC[1];999);IF(R[1]C>0;R[1]C;999)));INT(RC[1])+1,3; IF(INT(R[1]C)=INT(MIN(IF(RC[-1]>=0;RC[-1];999);IF(R[-1]C>=0;R[-1]C;999);IF(RC[1]>=0;RC[1];999);IF(R[1]C>0;R[1]C;999)));INT(R[1]C)+1,4; 0)))))
Формула очень сложная (в Excel 2000-2003 достигается максимум по уровням вложенных скобок внутри одной формулы) и требует дополнительных пояснений. Общий смысл на самом деле соответствует описанному ранее циклическому алгоритму. Т.е. определяется минимум из соседних ячеек. При этом «стены» (отрицательные значения) не обрабатываются за счет замены их значений на большое число (999).
Дополнительно к описанному алгоритму вводится дробная часть числа, обозначающая направление движения от предыдущей ячейки. Все сравнения производятся над целыми числами (функция INT). Дробная часть введено только для облегчения показа маршрута через условное форматирование ячейки. Также только для целей условного форматирования в строках 18-117 находится служебная таблица с расчетами координат следующей ячейки оптимального маршрута. В примере заготовлено максимально 100 шагов для анализа. Расчет для показа маршрута можно было организовать каким-либо другим способом.
Обратите внимание, на преимущество R1C1 адресации – сразу видно, что формула абсолютна одинаковая во всех ячейках. Без использования итерационных вычислений будет выдана ошибка — циклическая ссылка в формулах . Действительно, все соседние ячейки лабиринта ссылаются друг на друга.
Решение
После изменений в расположении стен и проходов на листе «Карта» требуется перейти на лист «Лабиринт» и запустить ручной пересчет Excel. Это проще всего сделать через нажатие клавиши F9. Карта отобразит начальный лабиринт и маршрут оптимального перемещения. Стены выделены серым цветом, маршрут — желтым.
 |
В заголовке окна выводится количество шагов, либо сообщение о невозможности прокладки маршрута между входом и выходом. Проверьте разные варианты расположения стен в лабиринте.
Форматирование
Ячейки внутри лабиринта содержат формулы, и соответственно вычисленные значения. В примере эти значения скрыты – видим только цвет фона. Числа скрыты, во-первых, для простоты восприятия («для красоты»), во-вторых, чтобы продемонстрировать возможности специального формата Excel. Вызовите диалог формата ячейки (проще всего это делается через сочетание клавиш Ctrl+1):
 |
Пользовательский формат «;;;» обозначает, что для положительных, отрицательных, нулевых и текстовых значений необходимо показывать пустую ячейку.
Для раскраски ячеек использованы условные форматы двух типов:
 |
1. «Стены» вычисляются через формулу как значение «-1».
2. Ячейка попадает в оптимальный маршрут, если ее координата вычислена в служебной таблице. Здесь функция CELL(«address»; RC) выводит адрес текущей ячейки в формате R1C1. Служебная таблица собирает координаты маршрута от «выхода» к «входу», используя целую и дробную часть каждой ячейки лабиринта.
Заключение
Расширение масштаба лабиринта требует копирования формул и добавления строк в служебную таблицу для показа маршрута. Обратите только внимание, что ячейка «входа» не содержит формулу – там значение первого шага (1,1). Также, вероятно потребуется увеличить параметр «Предельное число итераций». Будьте осторожны с увеличением размеров лабиринта — скорость расчетов будет замедляться в геометрической прогрессии.
Описанная в примере задача гораздо проще и элегантнее решается с помощью программы на VBA. Можно использовать как простые циклы, так и рекурсивные вызовы процедур. Вероятно, для тех, кто не очень «дружит» с программированием, приведенный пример решения задачи с помощью формул будет также непонятен. В любом случае, надеемся, что статья будет являться для вас дополнительным стимулом по изучению возможностей формул Excel и VBA.
Пользовательский формат числа
Смотри также
» Перекрестный расчет себестоимости
При разработке экономических моделей одной из самых интересных задач является решение проблемы перекрестных связей между формулами….
» Объединение строк
У продвинутых пользователей Excel очень популярен вопрос о возможности объединения диапазона ячеек, содержащих текст, в одну строку при…
» Распределение начислений по платежам
При ведении финансового учета в электронных таблицах обычно ограничиваются, так называемым «котловым» методом расчета задолженности…
» Календарный план выпуска изделий
Одной из самых сложных задач экономического менеджмента является составление календарного плана выпуска продукции в условиях…
» Судоку
Пример решения головоломки «Судоку 9х9» без программирования. К экономике отношения не имеет, зато отлично показывает возможности Excel в…

Всероссийский заочный финансово-экономический институт Кафедра экономико-математический методов и моделей
-
Тема:
-
Поиск минимального пути
-
в графе в среде Excel
-
Работу выполнила: студентка 3-го курса
-
спец. Финансы и кредит
-
Алипова И.С.
-
Руководитель: к.т.н., доц. Уродовских
-
Виктор Николаевич
1. Содержательная постановка задачи
-
Граф — совокупность двух конечных множеств: множества точек, которые называются вершинами, и множества пар вершин, которые называются ребрами.
-
Граф ориентированный, если рассматривае-мые пары вершин упорядочены, то есть на каждом ребре задается направление; в противном случае – граф неориентированный.
-
Последовательность неповторяющихся ребер, ведущая от некоторой вершины к другой, образует путь.
-
Граф называется связным, если для любых двух его вершин существует путь, их соединяющий; в противном случае граф называется несвязным.

Для определенного географического района можно построить граф, вершины которого интерпретируются как точка пересечения дорог или населенные пункты. Тогда каждое ребро графа будет соответствовать наличию автомобильной дороги между двумя соседними населенными пунктами или перекрестками. В качестве веса ребра следует принять длину соответствующего участка дороги в км.
-
Для определенного географического района можно построить граф, вершины которого интерпретируются как точка пересечения дорог или населенные пункты. Тогда каждое ребро графа будет соответствовать наличию автомобильной дороги между двумя соседними населенными пунктами или перекрестками. В качестве веса ребра следует принять длину соответствующего участка дороги в км.
-
Задача нахождения минимального пути в графе между двумя фиксирующими парами вершин формулируется как задача поиска кратчайшего маршрута.
-
Из всех возможных маршрутов перемещения, связывающих исходный пункт с конечным, необходимо найти такой маршрут, суммарная длина участков дорог которого минимальна.

2. Решение задачи о min пути в ориентированном графе с помощью MS Excel. 2.1. Определение конкретных значений парамет-ров исходной задачи
-
Данная задача относится к классу задач оптимизации в графах. Особенность ее решения в том, что предварительно следует определить m переменных, где m – число дуг исходного графа, а также сформировать и ввести в ячейки рабочего листа n ограничений, где n – число вершин исходного графа.
-
С этой целью рассмотрим задачу на примере нахождения минимального пути в транспортной сети города Липецка от дома до института.

Возьмем карту города Липецка(масштаб – в 1 см 250 м) и выберем маршруты транспорта, которые нам подходят (в данном случае от остановки ул. Меркулова до ул. Плеханова).
-
Возьмем карту города Липецка(масштаб – в 1 см 250 м) и выберем маршруты транспорта, которые нам подходят (в данном случае от остановки ул. Меркулова до ул. Плеханова).
-
Возможные маршруты движения можно задать в виде схемы, формально представляющей собой ориентирован-ный связный граф, состоящий из 13 вершин и 19 дуг (рис. 1). При этом 1 и 13 вершины – начальный и конечный пункты, а промежуточные вершины – перекрестки дорог.

Длина автодороги между двумя вершинами, выраженная в см, равна значению весовой функции для каждой дуги, которое указано рядом с изображением этой дуги в графе.
-
Длина автодороги между двумя вершинами, выраженная в см, равна значению весовой функции для каждой дуги, которое указано рядом с изображением этой дуги в графе.
-
Требуется найти маршрут, соединяющий начальный пункт 1 с конечным пунктом 13, так чтобы общая длина пути была минимальной.
-
Переменными математической модели данной задачи о минимальном пути в ориентированном графе являются 19 переменных: x1 3, х1 2, х1 4, х2 3, х2 5, х3 6, х3 7, х4 9, х5 4, х5 6, х6 8, х7 8, х8 9, х8 10, х9 13, х10 12, х10 11, х11 12, х12 13. Каждая из этих переменных хi j принимает значение 1, если дуга (i, j) входит в минимальный путь, и 0 – в противном случае.
-
Целевой функцией в данной задаче является суммарная длина пути связывающего пункты 1 и 13.


х1 3 + х1 2 + х1 4 = 1; (1)
-
х1 3 + х1 2 + х1 4 = 1; (1)
-
х12 13 + х9 13 = 1; (2)
-
х1 2 – х2 3 – х2 5 = 0; (3)
-
х1 3 + х2 3 – х3 7 – х3 6 = 0; (4)
-
х2 5 – х5 6 – х 5 4 = 0; (5)
-
х5 6 + х3 6 – х 6 8 = 0; (6)
-
х3 7 – х 7 8 = 0; (7)
-
х7 8 + х6 8 – х8 9 – х8 10 = 0; (8)
-
х8 10 – х10 11– х10 12 = 0; (9)
-
х11 12 + х10 12 – х12 13 =0; (10)
-
х5 4 + х1 4 – х4 9 = 0; (11)
-
х4 9 + х8 9 – х9 13 = 0; (12)
-
х10 11 – х11 12 = 0; (13)
-
х1 3, х1 2, х1 4, х2 3, х2 5, х3 6, х3 7, х4 9, х5 6, х6 8, х7 8, х8 9, х8 10, х 9 13, х10 12, х10 11, х11 12, х12 13 Є { 0, 1}.(14)

2.2. Решение исходной задачи
-
Введем исходные данные для решения задачи
-
1) внесем необходимые надписи в ячейки A1:F1 на листе Excel (см. рис.).

2) В ячейки A2:A20 введем индексы начальных вершин (i), а в ячейки B2:B20 – индексы конечных вершин (j) всех имеющихся дуг исходного графа.
-
2) В ячейки A2:A20 введем индексы начальных вершин (i), а в ячейки B2:B20 – индексы конечных вершин (j) всех имеющихся дуг исходного графа.
-
3) В ячейки C2:C20 введем значения коэффициентов целевой функции (Таблица 1).
-
4) В ячейку F2 введем формулу, которая представляет собой целевую функцию: = СУММПРОИЗВ(C2:C20; D2:D20) .
-
5) В ячейку E2 введем формулу, которая представляет собой левую часть первого ограничения (1): =СУММ(D2:D4).
-
6) В ячейку E14 введем формулу для левой части второго ограничения (2): = СУММ(D20:D16).
-
7) В ячейку E3 введем значение левой части третьего ограничения (3) : = D3 – СУММ(D5:D6). И так вводим формулы для остальных ограничений (4) – (13) (Таблица 1).

^

2. Поиск решения
-
Для дальнейшего решения задачи следует вызвать мастер поиска решения (Сервис / Поиск решения).
-
Установим целевую ячейку $F$2, равной минимальному значению.
-
В поле с именем Изменяя ячейки введем абсолютный адрес ячеек $D$2:$D$20.
-
Зададим первое ограничение, равное 1, используя в качестве исходной ячейки $E$2. Добавим второе ограничение ($E$14), равное 1.
-
Далее добавляем группу ограничений для промежуточных вершин, выбрав диапазон ячеек $E$3:$E$20, равные 0.
-
Зададим последнее ограничение (14) на булевы значения переменных, выбрав диапазон ячеек $D$2:$D20,в качестве знака ограничения выберем «двоичн» и ограничение оставим «двоичное».

6) В окне дополнительных параметров поиска решения выберем отметки Линейная модель и Неотрицательные значения.
-
6) В окне дополнительных параметров поиска решения выберем отметки Линейная модель и Неотрицательные значения.
-
После выполнения расчетов программой MS Exсel будет получено количественное решение, которое имеет следующий вид (Таблица 2).

^

Результатом решения задачи о минимальном пути в графе является найденные оптимальные значения переменных: х1 2=1, х2 5=1, х5 4=1, х4 9=1, х9 13=1, остальные переменные равны 0. Найденному оптимальному решению соответствует значение целевой функции: fopt = 29,8см.
-
Результатом решения задачи о минимальном пути в графе является найденные оптимальные значения переменных: х1 2=1, х2 5=1, х5 4=1, х4 9=1, х9 13=1, остальные переменные равны 0. Найденному оптимальному решению соответствует значение целевой функции: fopt = 29,8см.
-
Вывод
-
Анализ найденного решения показывает, что минимальный путь в исходном ориентированном графе, соединяющий вершину 1 с вершиной 13, содержит дуги: (1,2), (2,5), (5,4), (4,9), (9,13).
-
Таким образом, оптимальный маршрут перемещения из исходного пункта в конечный включает в себя последовательное перемещение между соседними пунктами (перекрестками дорог): из 1 в 2, из 2 в 5, из 5 в 4, из 4 в 9, из 9 в 13 (Рис. 2). При этом общая длина пути будет равна 29,8*250=7450м или 7,45км.

Рис.2. Минимальный путь между вершинами 1 и 13 в исходном графе
-
Рис.2. Минимальный путь между вершинами 1 и 13 в исходном графе