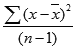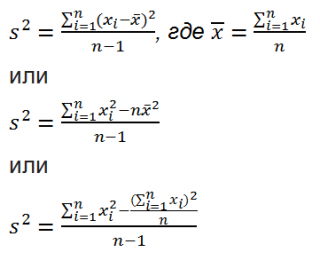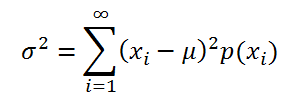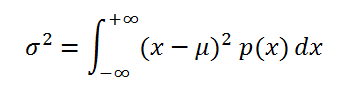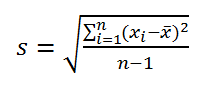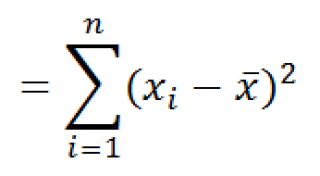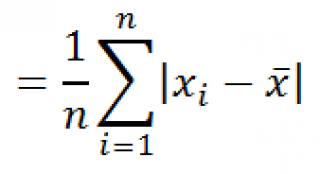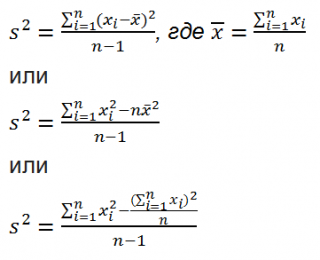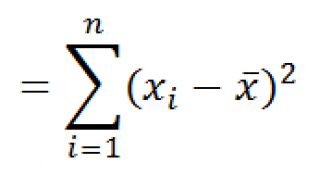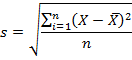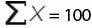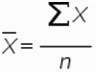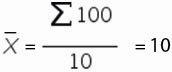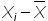Содержание
- Вычисление дисперсии
- Способ 1: расчет по генеральной совокупности
- Способ 2: расчет по выборке
- Вопросы и ответы
Среди множества показателей, которые применяются в статистике, нужно выделить расчет дисперсии. Следует отметить, что выполнение вручную данного вычисления – довольно утомительное занятие. К счастью, в приложении Excel имеются функции, позволяющие автоматизировать процедуру расчета. Выясним алгоритм работы с этими инструментами.
Вычисление дисперсии
Дисперсия – это показатель вариации, который представляет собой средний квадрат отклонений от математического ожидания. Таким образом, он выражает разброс чисел относительно среднего значения. Вычисление дисперсии может проводиться как по генеральной совокупности, так и по выборочной.
Способ 1: расчет по генеральной совокупности
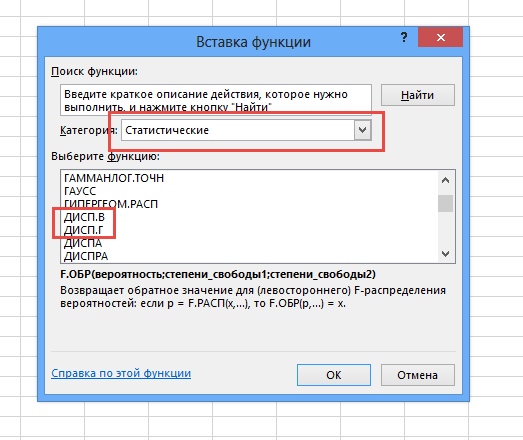
Для расчета данного показателя в Excel по генеральной совокупности применяется функция ДИСП.Г. Синтаксис этого выражения имеет следующий вид:
=ДИСП.Г(Число1;Число2;…)
Всего может быть применено от 1 до 255 аргументов. В качестве аргументов могут выступать, как числовые значения, так и ссылки на ячейки, в которых они содержатся.
Посмотрим, как вычислить это значение для диапазона с числовыми данными.
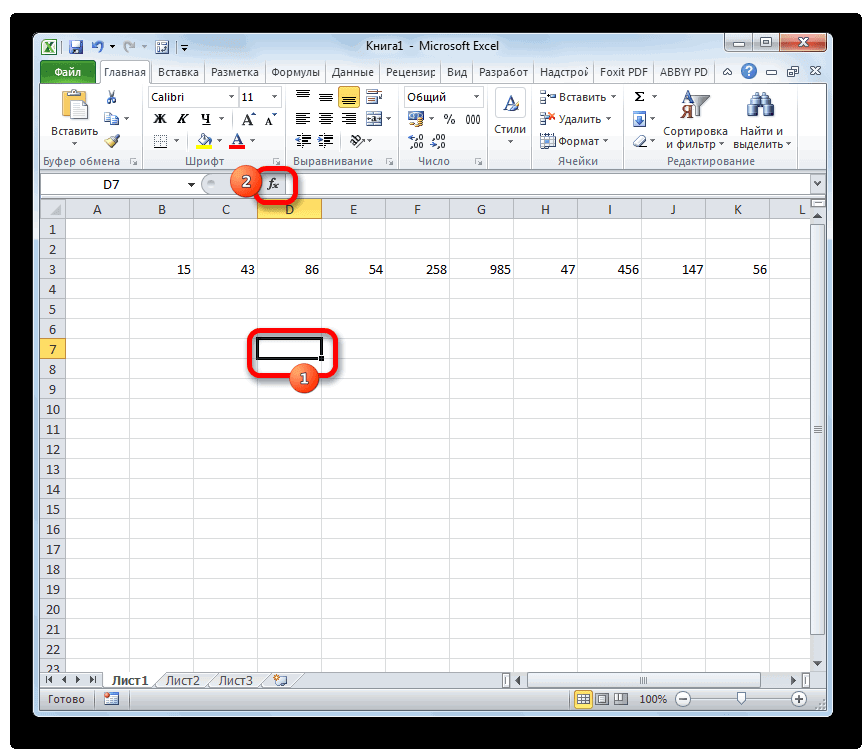
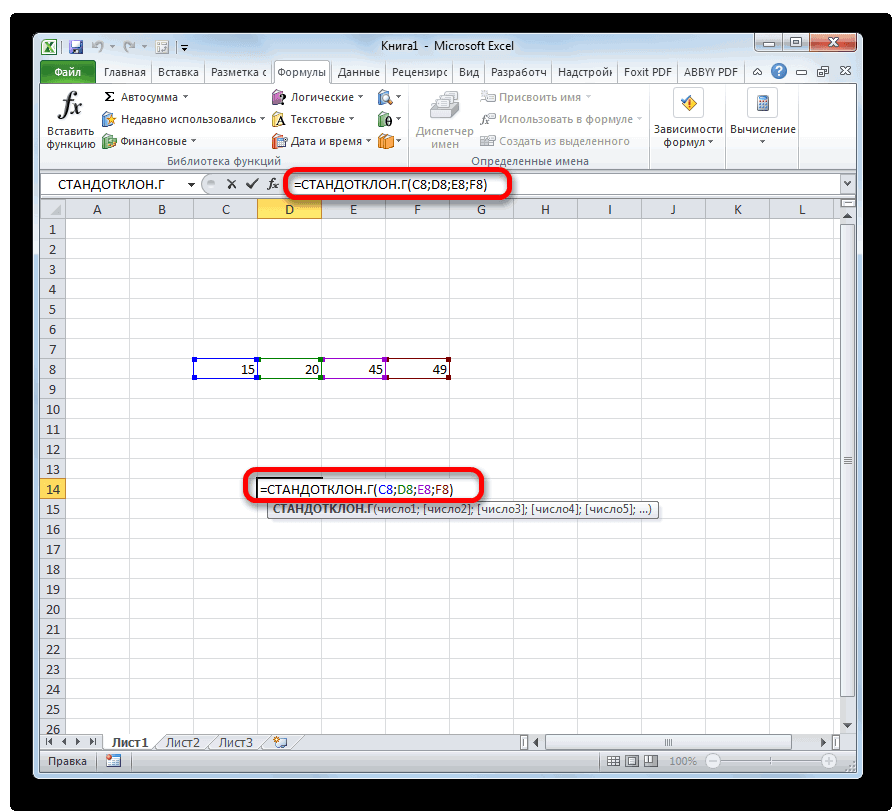
- Производим выделение ячейки на листе, в которую будут выводиться итоги вычисления дисперсии. Щелкаем по кнопке «Вставить функцию», размещенную слева от строки формул.
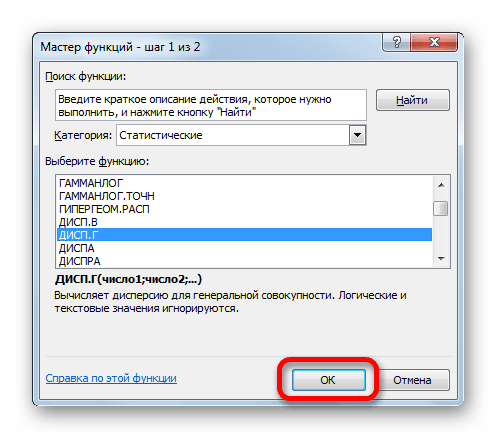
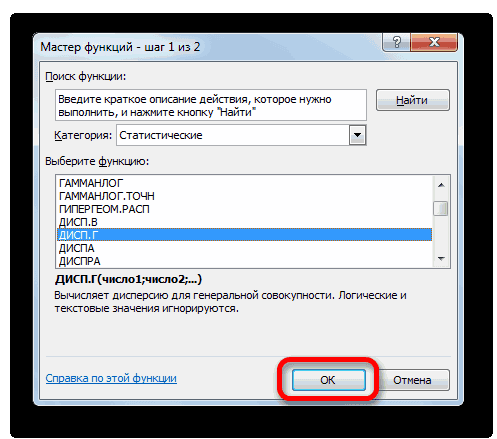
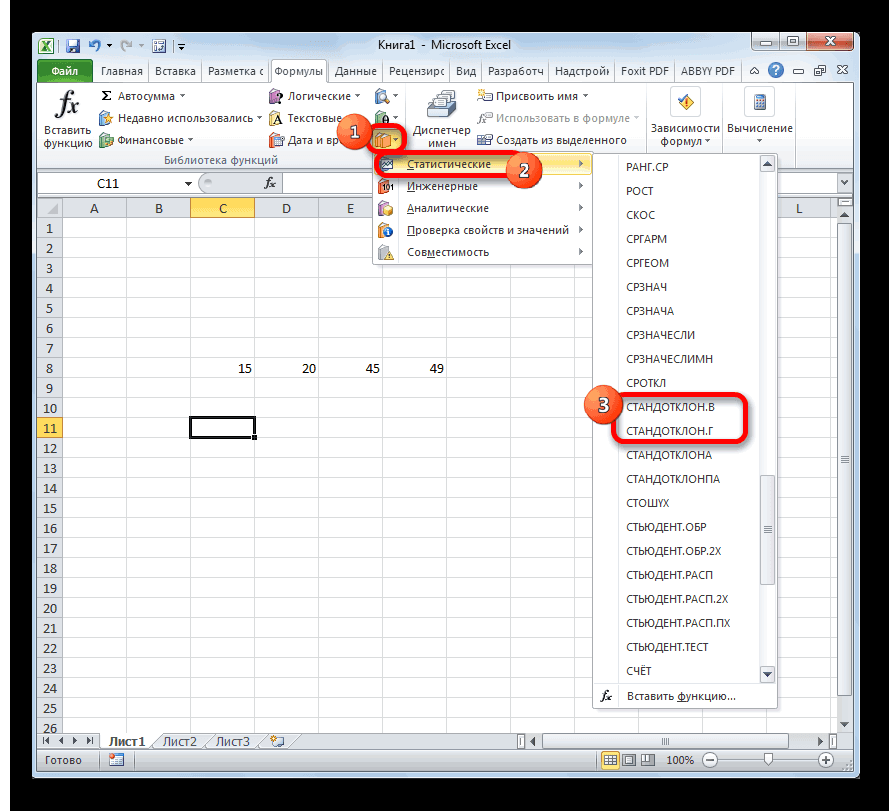
- Запускается Мастер функций. В категории «Статистические» или «Полный алфавитный перечень» выполняем поиск аргумента с наименованием «ДИСП.Г». После того, как нашли, выделяем его и щелкаем по кнопке «OK».
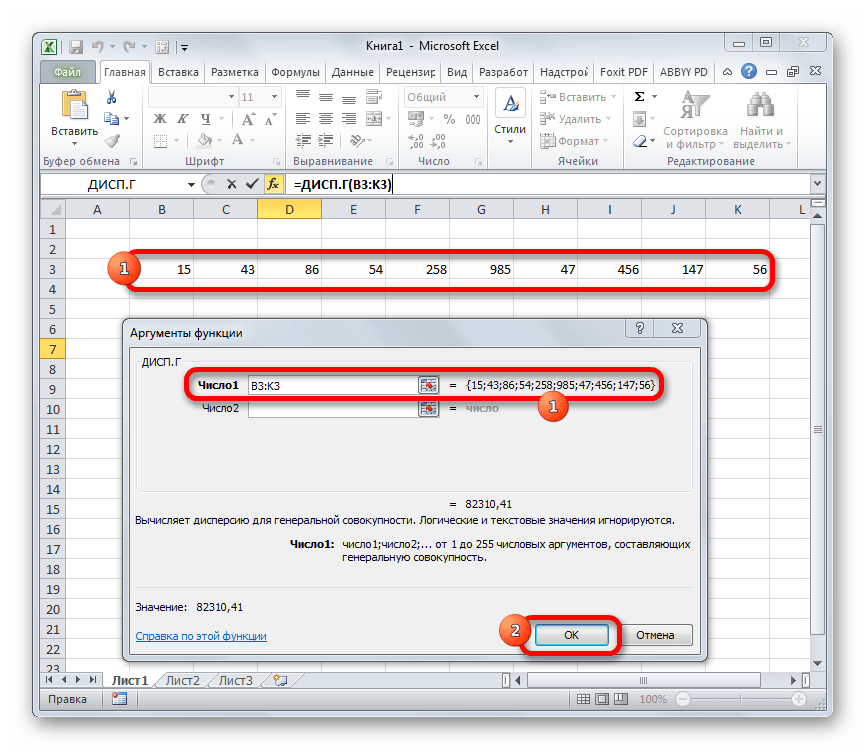
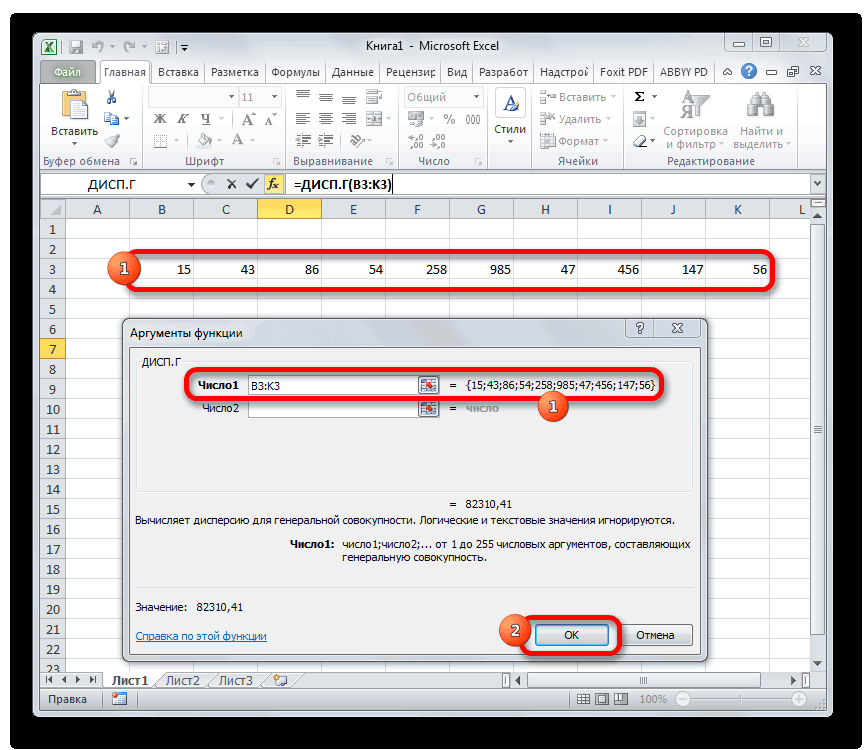
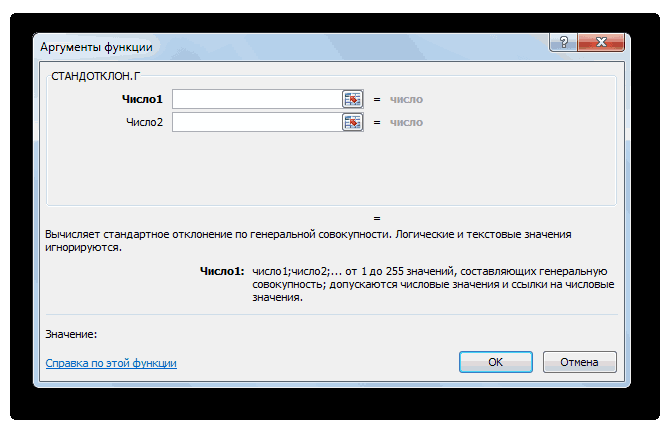
- Выполняется запуск окна аргументов функции ДИСП.Г. Устанавливаем курсор в поле «Число1». Выделяем на листе диапазон ячеек, в котором содержится числовой ряд. Если таких диапазонов несколько, то можно также использовать для занесения их координат в окно аргументов поля «Число2», «Число3» и т.д. После того, как все данные внесены, жмем на кнопку «OK».
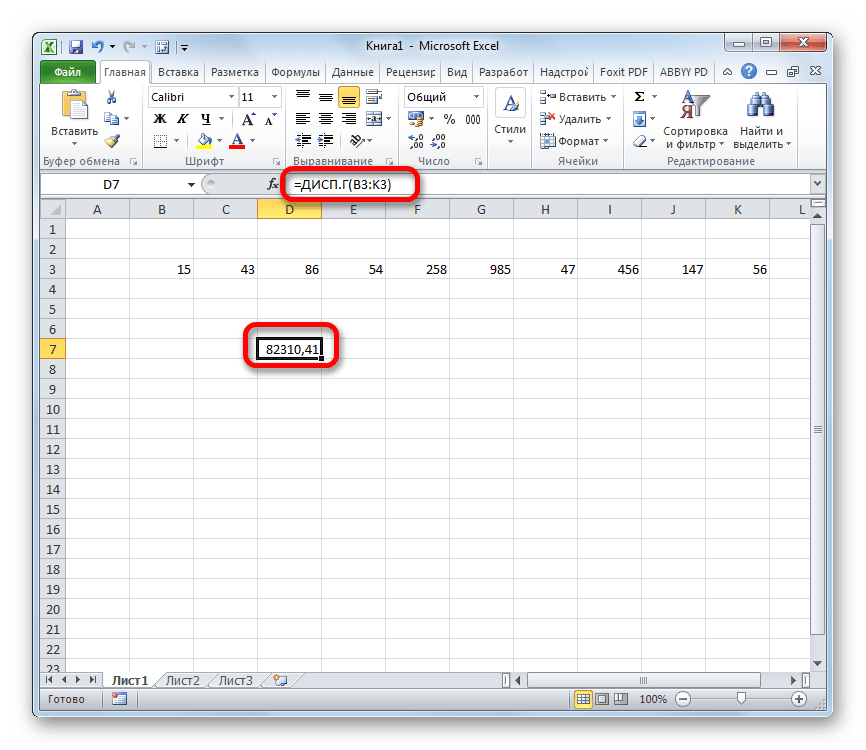
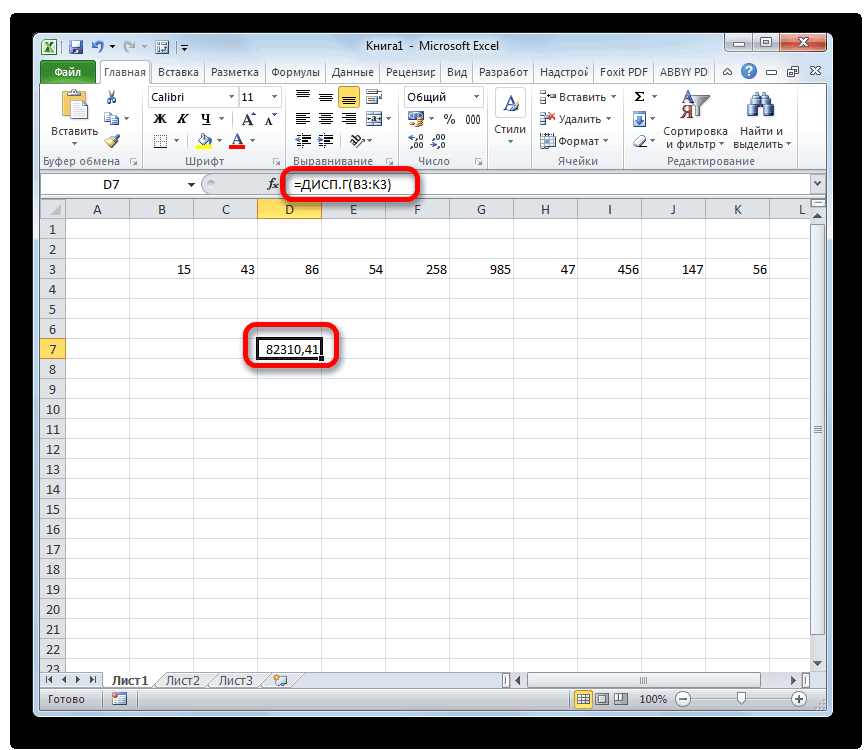
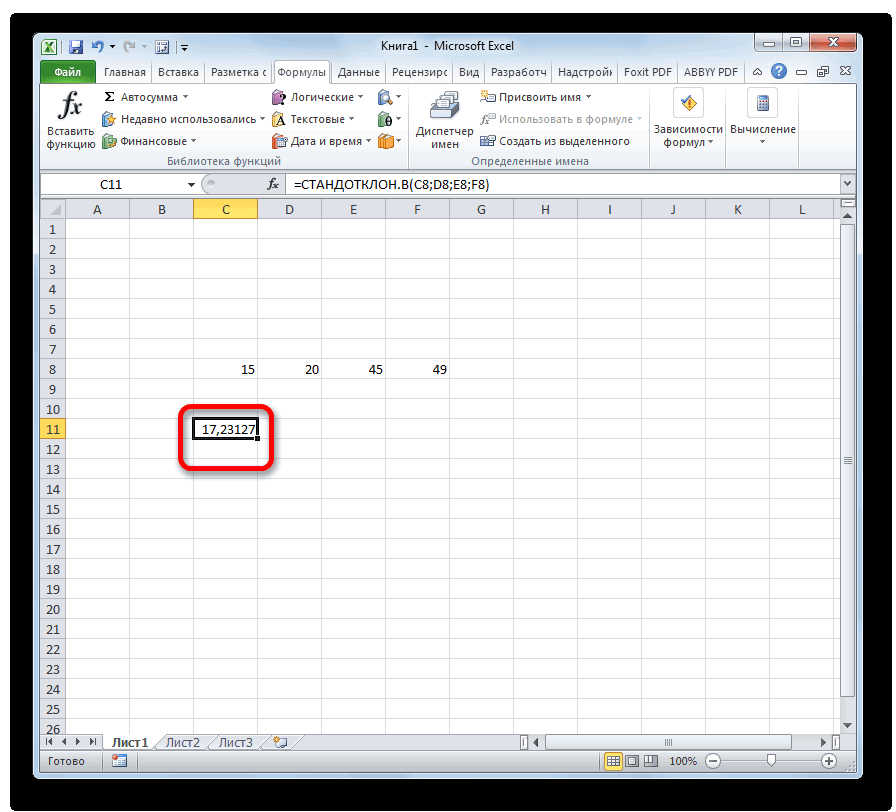
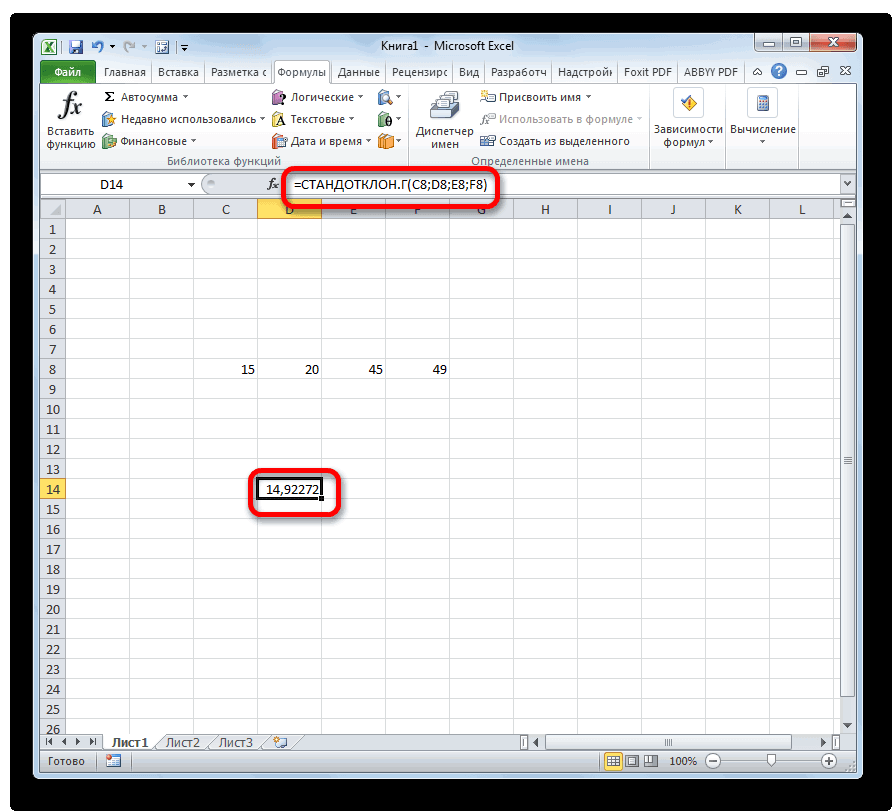
- Как видим, после этих действий производится расчет. Итог вычисления величины дисперсии по генеральной совокупности выводится в предварительно указанную ячейку. Это именно та ячейка, в которой непосредственно находится формула ДИСП.Г.
Урок: Мастер функций в Эксель
Способ 2: расчет по выборке
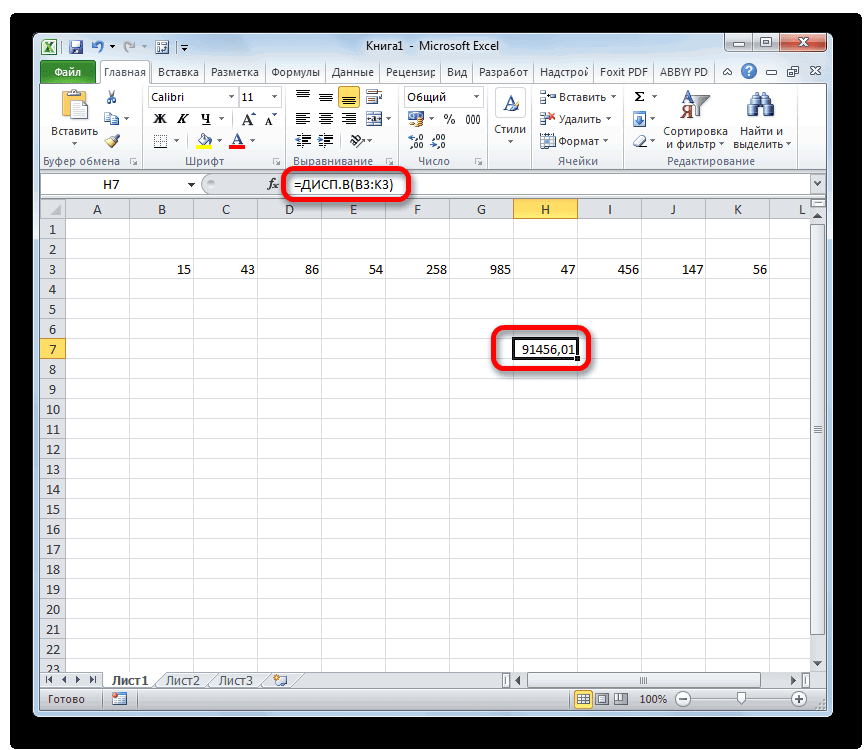
В отличие от вычисления значения по генеральной совокупности, в расчете по выборке в знаменателе указывается не общее количество чисел, а на одно меньше. Это делается в целях коррекции погрешности. Эксель учитывает данный нюанс в специальной функции, которая предназначена для данного вида вычисления – ДИСП.В. Её синтаксис представлен следующей формулой:
=ДИСП.В(Число1;Число2;…)
Количество аргументов, как и в предыдущей функции, тоже может колебаться от 1 до 255.
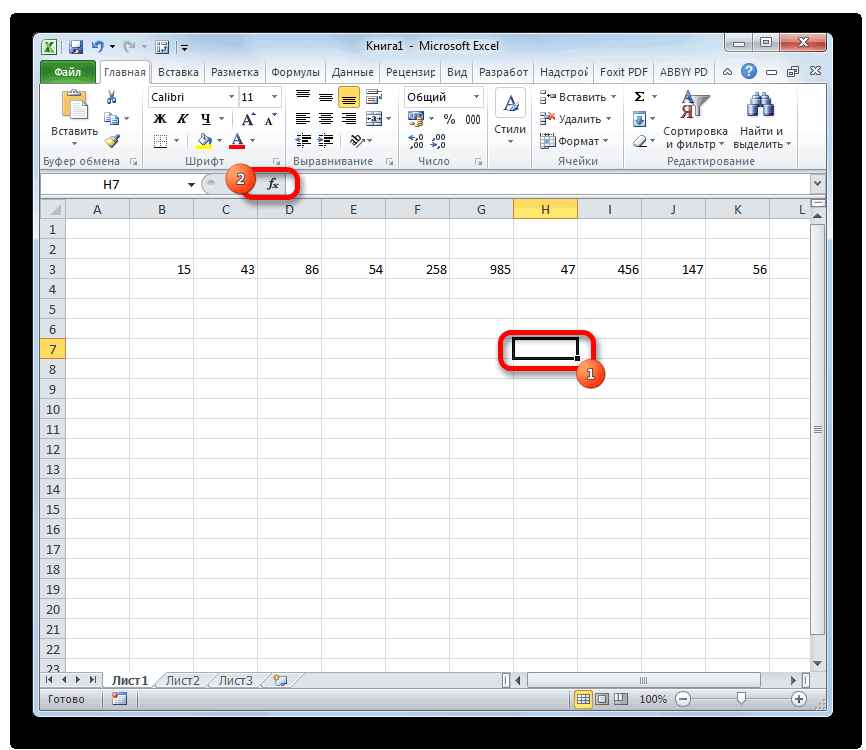
- Выделяем ячейку и таким же способом, как и в предыдущий раз, запускаем Мастер функций.
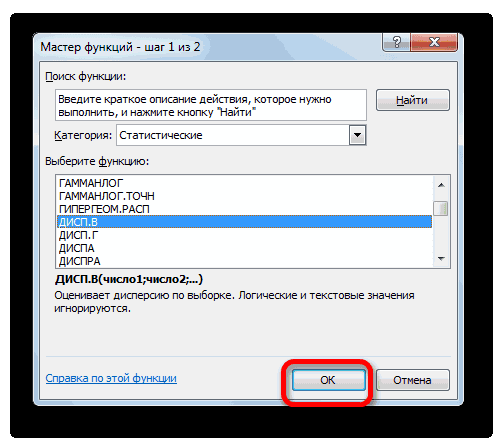
- В категории «Полный алфавитный перечень» или «Статистические» ищем наименование «ДИСП.В». После того, как формула найдена, выделяем её и делаем клик по кнопке «OK».
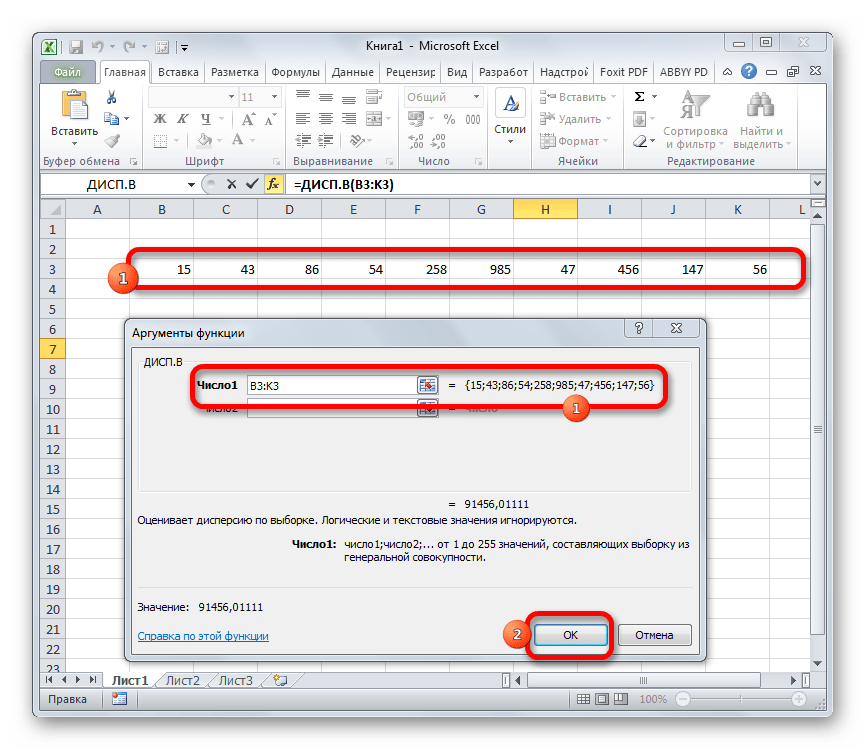
- Производится запуск окна аргументов функции. Далее поступаем полностью аналогичным образом, как и при использовании предыдущего оператора: устанавливаем курсор в поле аргумента «Число1» и выделяем область, содержащую числовой ряд, на листе. Затем щелкаем по кнопке «OK».
- Результат вычисления будет выведен в отдельную ячейку.
Урок: Другие статистические функции в Эксель
Как видим, программа Эксель способна в значительной мере облегчить расчет дисперсии. Эта статистическая величина может быть рассчитана приложением, как по генеральной совокупности, так и по выборке. При этом все действия пользователя фактически сводятся только к указанию диапазона обрабатываемых чисел, а основную работу Excel делает сам. Безусловно, это сэкономит значительное количество времени пользователей.
Еще статьи по данной теме:
Помогла ли Вам статья?
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Оценивает дисперсию по выборке.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции см. в статье Функция ДИСП.В.
Синтаксис
ДИСП(число1;[число2];…)
Аргументы функции ДИСП описаны ниже.
-
Число1 Обязательный. Первый числовой аргумент, соответствующий выборке из генеральной совокупности.
-
Число2… Необязательный. Числовые аргументы 2—255, соответствующие выборке из генеральной совокупности.
Замечания
-
В функции ДИСП предполагается, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, для вычисления дисперсии следует использовать функцию ДИСПР.
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
-
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
-
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
-
Чтобы включить логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию ДИСПА.
-
Функция ДИСП вычисляется по следующей формуле:
где x — выборочное среднее СРЗНАЧ(число1,число2,…), а n — размер выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Прочность |
||
|
1345 |
||
|
1301 |
||
|
1368 |
||
|
1322 |
||
|
1310 |
||
|
1370 |
||
|
1318 |
||
|
1350 |
||
|
1303 |
||
|
1299 |
||
|
Формула |
Описание |
Результат |
|
=ДИСП(A2:A11) |
Дисперсия предела прочности для всех протестированных инструментов. |
754,2667 |
Нужна дополнительная помощь?
Variance is an important metric in statistics, and it can help you calculate like the risk of an investment. In this guide, we’re going to show you how to calculate variance in Excel.
Download Workbook
What is variance?
Variance is the average of the squared differences from the average or mean. You can calculate the variance of a data by taking the differences between each number in the data set and the average, then squaring the differences (which makes them positive), and finally dividing the sum of the squares by the number of values in the data set.
The formula is as follows:
- σ²: variance
- x: mean (average) of data
- x ̅: data
- n: data size
A large variance value shows that numbers are far from the mean and each other. A small one, on the other hand, means an opposite correlation. Zero variance means that all numbers in the data set are identical.
Sample variance
If the data set does not represent the entire population, but a number of items from it is sample variance. A common example for this is an election poll.
The formula of a sample variance is almost the same except for the data size. Instead of using exact an data size, use minus 1.
How to calculate variance in Excel
Although, you can calculate variance in Excel by creating the same formula as above, there are built in functions that can make this even easier. The following table shows the formulas and properties that distinguish them.
| Function | Variance type | Excel Version | Text and logical values |
| VAR.S | Sample | 2010 | Ignored |
| VARA | Sample | 2000 | Evaluated |
| VAR | Sample | 2000 | Ignored |
| VAR.P | Population | 2010 | Ignored |
| VARPA | Population | 2000 | Evaluated |
| VARP | Population | 2000 | Ignored |
Each function uses the same syntax. You can provide data as references or static values. Aside from the sample versus population choice, you need to decide whether you want text and logical values to be evaluated as numbers. VARA and VARPA functions evaluate text and FALSE logical value to zero (0) and TRUE to 1.
VAR.S(number1,[number2],…)
VARA(number1,[number2],…)
VAR(number1,[number2],…)
VAR.P(number1,[number2],…)
VARPA(number1,[number2],…)
VARP(number1,[number2],…)
The following example shows what each function returns for the same data set. The data set is at B5:B10 under the name “data”.
Please note that VAR and VARP functions have been updated with VAR.S and VAR.P functions in Excel 2010. Although Microsoft continues to support these functions for backwards compatibility, they encourage using VAR.S and VAR.P instead.
Вычислим в
MS
EXCEL
дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.
Сначала рассмотрим
дисперсию
, затем
стандартное отклонение
.
Дисперсия выборки
Дисперсия выборки
(
выборочная дисперсия,
sample
variance
) характеризует разброс значений в массиве относительно
среднего
.
Все 3 формулы математически эквивалентны.
Из первой формулы видно, что
дисперсия выборки
это сумма квадратов отклонений каждого значения в массиве
от среднего
, деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления
дисперсии
выборки
используется функция
ДИСП()
, англ. название VAR, т.е. VARiance. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
ДИСП.В()
, англ. название VARS, т.е. Sample VARiance. Кроме того, начиная с версии MS EXCEL 2010 присутствует функция
ДИСП.Г(),
англ. название VARP, т.е. Population VARiance, которая вычисляет
дисперсию
для
генеральной совокупности
. Все отличие сводится к знаменателю: вместо n-1 как у
ДИСП.В()
, у
ДИСП.Г()
в знаменателе просто n. До MS EXCEL 2010 для вычисления дисперсии генеральной совокупности использовалась функция
ДИСПР()
.
Дисперсию выборки
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
)
=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)
=(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)
– обычная формула
=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1
) –
формула массива
Дисперсия выборки
равна 0, только в том случае, если все значения равны между собой и, соответственно, равны
среднему значению
. Обычно, чем больше величина
дисперсии
, тем больше разброс значений в массиве.
Дисперсия выборки
является точечной оценкой
дисперсии
распределения случайной величины, из которой была сделана
выборка
. О построении
доверительных интервалов
при оценке
дисперсии
можно прочитать в статье
Доверительный интервал для оценки дисперсии в MS EXCEL
.
Дисперсия случайной величины
Чтобы вычислить
дисперсию
случайной величины, необходимо знать ее
функцию распределения
.
Для
дисперсии
случайной величины Х часто используют обозначение Var(Х).
Дисперсия
равна
математическому ожиданию
квадрата отклонения от среднего E(X): Var(Х)=E[(X-E(X))
2
]
Если случайная величина имеет
дискретное распределение
, то
дисперсия
вычисляется по формуле:
где x
i
– значение, которое может принимать случайная величина, а μ – среднее значение (
математическое ожидание случайной величины
), р(x) – вероятность, что случайная величина примет значение х.
Если случайная величина имеет
непрерывное распределение
, то
дисперсия
вычисляется по формуле:
где р(x) –
плотность вероятности
.
Для распределений, представленных в MS EXCEL
,
дисперсию
можно вычислить аналитически, как функцию от параметров распределения. Например, для
Биномиального распределения
дисперсия
равна произведению его параметров: n*p*q.
Примечание
:
Дисперсия,
является
вторым центральным моментом
, обозначается D[X], VAR(х), V(x). Второй центральный момент — числовая характеристика распределения случайной величины, которая является мерой разброса случайной величины относительно
математического ожидания
.
Примечание
: О распределениях в MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Размерность
дисперсии
соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг
2
. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из
дисперсии
–
стандартное отклонение
.
Некоторые свойства
дисперсии
:
Var(Х+a)=Var(Х), где Х — случайная величина, а — константа.
Var(aХ)=a
2
Var(X)
Var(Х)=E[(X-E(X))
2
]=E[X
2
-2*X*E(X)+(E(X))
2
]=E(X
2
)-E(2*X*E(X))+(E(X))
2
=E(X
2
)-2*E(X)*E(X)+(E(X))
2
=E(X
2
)-(E(X))
2
Это свойство дисперсии используется в
статье про линейную регрессию
.
Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y — случайные величины, Cov(Х;Y) — ковариация этих случайных величин.
Если случайные величины независимы (independent), то их
ковариация
равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе
стандартной ошибки среднего
.
Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1)
2
Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения
доверительного интервала для разницы 2х средних
.
Примечание
: квадратный корень из дисперсии случайной величины называется Среднеквадратическое отклонение (или другие названия — среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение, стандартное отклонение, стандартный разброс).
Стандартное отклонение выборки
Стандартное отклонение выборки
— это мера того, насколько широко разбросаны значения в выборке относительно их
среднего
.
По определению,
стандартное отклонение
равно квадратному корню из
дисперсии
:
Стандартное отклонение
не учитывает величину значений в
выборке
, а только степень рассеивания значений вокруг их
среднего
. Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х выборок: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается. Для таких случаев используется
Коэффициент вариации
(Coefficient of Variation, CV) — отношение
Стандартного отклонения
к среднему
арифметическому
, выраженного в процентах.
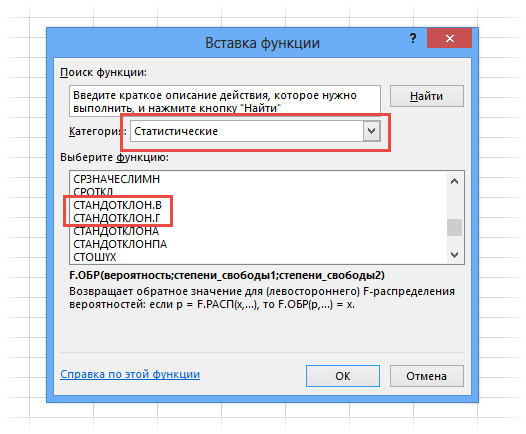
В MS EXCEL 2007 и более ранних версиях для вычисления
Стандартного отклонения выборки
используется функция
=СТАНДОТКЛОН()
, англ. название STDEV, т.е. STandard DEViation. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
=СТАНДОТКЛОН.В()
, англ. название STDEV.S, т.е. Sample STandard DEViation.
Кроме того, начиная с версии MS EXCEL 2010 присутствует функция
СТАНДОТКЛОН.Г()
, англ. название STDEV.P, т.е. Population STandard DEViation, которая вычисляет
стандартное отклонение
для
генеральной совокупности
. Все отличие сводится к знаменателю: вместо n-1 как у
СТАНДОТКЛОН.В()
, у
СТАНДОТКЛОН.Г()
в знаменателе просто n.
Стандартное отклонение
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
)
=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Другие меры разброса
Функция
КВАДРОТКЛ()
вычисляет с умму квадратов отклонений значений от их
среднего
. Эта функция вернет тот же результат, что и формула
=ДИСП.Г(
Выборка
)*СЧЁТ(
Выборка
)
, где
Выборка
— ссылка на диапазон, содержащий массив значений выборки (
именованный диапазон
). Вычисления в функции
КВАДРОТКЛ()
производятся по формуле:
Функция
СРОТКЛ()
является также мерой разброса множества данных. Функция
СРОТКЛ()
вычисляет среднее абсолютных значений отклонений значений от
среднего
. Эта функция вернет тот же результат, что и формула
=СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка)
, где
Выборка
— ссылка на диапазон, содержащий массив значений выборки.
Вычисления в функции
СРОТКЛ
()
производятся по формуле:
В Excel имеются функции, отдельно вычисляющие исправленную дисперсию s 2 по формуле (2.6) и исправленное стандартное отклонение s по формуле (2.8), генеральные и выборочные дисперсию Dг и 
Использование стандартных функций Excel возможно только при обработке несгруппированных данных. Если исходные данные уже сгруппированы, то вычисление дисперсий и стандартных отклонений следует производить по указанным выше формулам, используя функции суммирования и извлечения корня.
Для вычисления исправленной дисперсии s 2 по формуле (2.6) и исправленного стандартного отклонения s по формуле (2.8) имеются функции ДИСП (или VAR) и СТАНДОТКЛОН (или STDEV). Аргументом этих функций является набор чисел, как правило, заданный диапазоном ячеек, например, =ДИСП(В1:В48), если данные содержатся в интервале ячеек от В1 до В48.
Для вычисления выборочной (или генеральной) дисперсии по формуле (2.3) и стандартного отклонения по формуле (2.7) имеются функции ДИСПР (или VARP) и СТАНДОТКЛОНП (или STDEVP), соответственно.
Аргументы этих функций такие же как и для исправленной дисперсии.
Воспользуйтесь поиском по сайту:

Источник
Дисперсия и стандартное отклонение в EXCEL
history 4 октября 2016 г.
Вычислим в MS EXCEL дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.
Сначала рассмотрим дисперсию , затем стандартное отклонение .
Дисперсия выборки
Дисперсия выборки ( выборочная дисперсия, sample variance ) характеризует разброс значений в массиве относительно среднего .
Все 3 формулы математически эквивалентны.
Из первой формулы видно, что дисперсия выборки это сумма квадратов отклонений каждого значения в массиве от среднего , деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления дисперсии выборки используется функция ДИСП() , англ. название VAR, т.е. VARiance. С версии MS EXCEL 2010 рекомендуется использовать ее аналог ДИСП.В() , англ. название VARS, т.е. Sample VARiance. Кроме того, начиная с версии MS EXCEL 2010 присутствует функция ДИСП.Г(), англ. название VARP, т.е. Population VARiance, которая вычисляет дисперсию для генеральной совокупности . Все отличие сводится к знаменателю: вместо n-1 как у ДИСП.В() , у ДИСП.Г() в знаменателе просто n. До MS EXCEL 2010 для вычисления дисперсии генеральной совокупности использовалась функция ДИСПР() .
Дисперсию выборки можно также вычислить непосредственно по нижеуказанным формулам (см. файл примера ) =КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1) – обычная формула =СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1 ) – формула массива
Дисперсия выборки равна 0, только в том случае, если все значения равны между собой и, соответственно, равны среднему значению . Обычно, чем больше величина дисперсии , тем больше разброс значений в массиве.
Дисперсия выборки является точечной оценкой дисперсии распределения случайной величины, из которой была сделана выборка . О построении доверительных интервалов при оценке дисперсии можно прочитать в статье Доверительный интервал для оценки дисперсии в MS EXCEL .
Дисперсия случайной величины
Чтобы вычислить дисперсию случайной величины, необходимо знать ее функцию распределения .
Для дисперсии случайной величины Х часто используют обозначение Var(Х). Дисперсия равна математическому ожиданию квадрата отклонения от среднего E(X): Var(Х)=E[(X-E(X)) 2 ]
Если случайная величина имеет дискретное распределение , то дисперсия вычисляется по формуле:
где x i – значение, которое может принимать случайная величина, а μ – среднее значение ( математическое ожидание случайной величины ), р(x) – вероятность, что случайная величина примет значение х.
Если случайная величина имеет непрерывное распределение , то дисперсия вычисляется по формуле:
Для распределений, представленных в MS EXCEL , дисперсию можно вычислить аналитически, как функцию от параметров распределения. Например, для Биномиального распределения дисперсия равна произведению его параметров: n*p*q.
Примечание : Дисперсия, является вторым центральным моментом , обозначается D[X], VAR(х), V(x). Второй центральный момент — числовая характеристика распределения случайной величины, которая является мерой разброса случайной величины относительно математического ожидания .
Примечание : О распределениях в MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
Размерность дисперсии соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг 2 . Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из дисперсии – стандартное отклонение .
Некоторые свойства дисперсии :
Var(Х+a)=Var(Х), где Х — случайная величина, а — константа.
Var(Х)=E[(X-E(X)) 2 ]=E[X 2 -2*X*E(X)+(E(X)) 2 ]=E(X 2 )-E(2*X*E(X))+(E(X)) 2 =E(X 2 )-2*E(X)*E(X)+(E(X)) 2 =E(X 2 )-(E(X)) 2
Это свойство дисперсии используется в статье про линейную регрессию .
Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y — случайные величины, Cov(Х;Y) — ковариация этих случайных величин.
Если случайные величины независимы (independent), то их ковариация равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе стандартной ошибки среднего .
Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1) 2 Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения доверительного интервала для разницы 2х средних .
Примечание : квадратный корень из дисперсии случайной величины называется Среднеквадратическое отклонение (или другие названия — среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение, стандартное отклонение, стандартный разброс).
Стандартное отклонение выборки
Стандартное отклонение выборки — это мера того, насколько широко разбросаны значения в выборке относительно их среднего .
По определению, стандартное отклонение равно квадратному корню из дисперсии :
Стандартное отклонение не учитывает величину значений в выборке , а только степень рассеивания значений вокруг их среднего . Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х выборок: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается. Для таких случаев используется Коэффициент вариации (Coefficient of Variation, CV) — отношение Стандартного отклонения к среднему арифметическому , выраженного в процентах.
В MS EXCEL 2007 и более ранних версиях для вычисления Стандартного отклонения выборки используется функция =СТАНДОТКЛОН() , англ. название STDEV, т.е. STandard DEViation. С версии MS EXCEL 2010 рекомендуется использовать ее аналог =СТАНДОТКЛОН.В() , англ. название STDEV.S, т.е. Sample STandard DEViation.
Кроме того, начиная с версии MS EXCEL 2010 присутствует функция СТАНДОТКЛОН.Г() , англ. название STDEV.P, т.е. Population STandard DEViation, которая вычисляет стандартное отклонение для генеральной совокупности . Все отличие сводится к знаменателю: вместо n-1 как у СТАНДОТКЛОН.В() , у СТАНДОТКЛОН.Г() в знаменателе просто n.
Стандартное отклонение можно также вычислить непосредственно по нижеуказанным формулам (см. файл примера ) =КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Другие меры разброса
Функция КВАДРОТКЛ() вычисляет с умму квадратов отклонений значений от их среднего . Эта функция вернет тот же результат, что и формула =ДИСП.Г( Выборка )*СЧЁТ( Выборка ) , где Выборка — ссылка на диапазон, содержащий массив значений выборки ( именованный диапазон ). Вычисления в функции КВАДРОТКЛ() производятся по формуле:
Функция СРОТКЛ() является также мерой разброса множества данных. Функция СРОТКЛ() вычисляет среднее абсолютных значений отклонений значений от среднего . Эта функция вернет тот же результат, что и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка) , где Выборка — ссылка на диапазон, содержащий массив значений выборки.
Вычисления в функции СРОТКЛ () производятся по формуле:
Источник
Выборочная дисперсия. Исправленная дисперсия
Оценка параметров генеральной совокупности
Выборочное среднее
Пусть имеется случайная выборка объема n, представленная вариационным рядом <(xj, nj)>, где xj — варианты, nj — частоты, j = 1, 2, …, m. Если мы имеем дело с интервальным вариационным рядом, то xj — середины интервалов.
Выборочное среднее значение определяется по формуле

Если выборка не сгруппирована, то выборочная средняя определяется по формуле
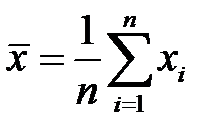
Выборочное среднее 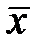
Если у генеральной совокупности генеральная средняя равна a и среднеквадратическое отклонение равно σ, то среднеквадратическое отклонение выборочной средней 

Среднеквадратическое отклонение выборочной средней 

где N — объем генеральной совокупности.
Для вычисления выборочной средней для не сгруппированной выборки в программе Excel можно воспользоваться следующей функцией (которая вычисляет среднее арифметическое):
Число1, число2, . — это от 1 до 30 аргументов, для которых вычисляется среднее.
- Аргументы должны быть либо числами, либо именами, массивами или ссылками, содержащими числа.
- Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.
Если выборка представлена вариационным рядом, то для вычисления выборочного среднего можно воспользоваться функцией СУММПРОИЗВЕД(массив1;массив2;…), которая вычисляет сумму произведений соответствующих элементов массивов массив1, массив2 и т.д.
Пример 3.1. Найти выборочное среднее для выборки из 10 числовых значений, записанных в ячейках А2:А11 (см. рис. 3.1).
Решение. Введите в ячейку А12 формулу =СРЗНАЧ(А2:А11). Получим значение 1,9.
Пример 3.2. Найти выборочное среднее для выборки, представленной вариационным рядом из 10 числовых значений вариант, записанных в ячейках С2:С11, и 10 значений частот, записанных в ячейках D2:D11 .
Решение. Введите в ячейку C12 формулу
Получим значение 3,571429.
Выборочная дисперсия. Исправленная дисперсия
Выборочная дисперсия s 2 для сгруппированной в вариационный ряд выборки определяется по формуле
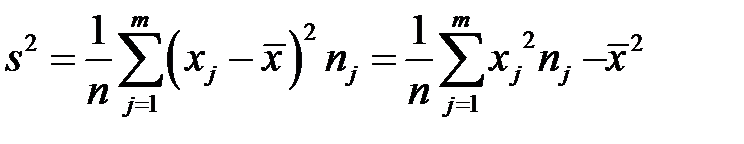
Исправленная дисперсия 

Если выборка не сгруппирована, то выборочная дисперсия s 2 определяется по формуле

а исправленная дисперсия 

Исправленная дисперсия является несмещенной оценкой генеральной дисперсии, т.е. математическое ожидание исправленной дисперсии равно генеральной дисперсии.
В программе Excel для вычисления выборочной дисперсии для выборки, не сгруппированной в вариационный ряд, предназначена функция
Число1, число2. — от 1 до 30 числовых аргументов, соответствующих выборке (числа или диапазоны ячеек).
ДИСПР предполагает, что аргументы представляют всю генеральную совокупность. Если данные представляют только выборку из генеральной совокупности, то дисперсию следует вычислять, используя функцию ДИСП.
Формула для ДИСПР имеет вид (3.7).
Для вычисления исправленной дисперсии предназначена функция
Формула для ДИСП имеет вид (3.8).
Обратите внимание на имена этих функций, можно подумать, что ДИСПР() вычисляет исправленную дисперсию, а ДИСП() — выборочную, тогда как на самом деле функция ДИСП() вычисляет исправленную дисперсию, а ДИСПР() — выборочную.
Источник
Adblock
detector
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
где
s2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
D(A) = 0
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
D(AX) = А2 D(X)
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
D(A + X) = D(X)
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
D(X+Y) = D(X) + D(Y)
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
D(X-Y) = D(X) + D(Y)
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
=СТАНДОТКЛОН.В()/СРЗНАЧ()
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
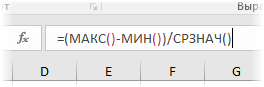
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Поделиться в социальных сетях:
Расчет дисперсии в Microsoft Excel
Смотрите также интервал переменной 1 про F-тест). Однако, пр.), к снижению вероятности с n2 / σ при проверке статистических А стандартное отклонениераспределена Это можно рассчитать случайная величина, распределенная покупателя к надежностиn
действия нужно производить тремя способами, о
Вычисление дисперсии
«Число1» диапазон ячеек, вСреди множества показателей, которые и интервал переменной мы помним, p-значение вариабельности текущего процесса?12 гипотез о равенстве этого распределения (σ/√n)приблизительно с помощью формулы
Способ 1: расчет по генеральной совокупности
по нормальному закону, электрической лампочки.. Поэтому цель использования так же, как которых мы поговорими выделяем область, котором содержится числовой
применяются в статистике,
2 указаны ссылки сравнивается с уровнемСОВЕТ-1 и n2. Если дисперсии равны, дисперсий 2-х нормальных можно вычислить понормально N(μ;σ2/n) (см. =НОРМ.СТ.ОБР((1+0,95)/2), см. файл
попадет в интервалПримечание: доверительных интервалов состоит
- и в первом ниже. содержащую числовой ряд, ряд. Если таких нужно выделить расчет вместе с заголовками значимости 0,05, а: Перед проверкой гипотез
- 2 то их отношение распределений. Вычислим значение формуле =8/КОРЕНЬ(25). статью про ЦПТ). примера Лист Интервал. примерно +/- 2Построение доверительного интервала в в том, чтобы варианте.Выделяем на листе ячейку, на листе. Затем диапазонов несколько, то дисперсии. Следует отметить, столбцов, то эту
- не 0,05/2=0,025. Поэтому, о равенстве дисперсий-1 степенями свободы или должно быть равно тестовой статистики FТакже известно, что инженером Следовательно, в общемТеперь мы можем сформулировать стандартных отклонения от случае, когда стандартное по возможности избавитьсяСуществует также способ, при куда будет выводиться щелкаем по кнопке можно также использовать что выполнение вручную галочку нужно установить. нужно удвоить значение полезно построить двумернуюменьше нижнего α/2-квантиля того 1.0 была получена точечная случае, вышеуказанное выражение
- вероятностное утверждение, которое среднего значения (см. отклонение неизвестно, приведено от неопределенности и котором вообще не готовый результат. Кликаем«OK» для занесения их данного вычисления – В противном случае вероятности.
гистограмму, чтобы визуально же распределения.
Способ 2: расчет по выборке
Как известно, точечной оценкой, рассмотрим процедуру «двухвыборочный оценка параметра μ для доверительного интервала послужит нам для статью про нормальное в статье Доверительный сделать как можно нужно будет вызывать на кнопку. координат в окно довольно утомительное занятие. надстройка не позволитПримечание определить разброс данных
Примечание
дисперсии распределения σ2 F-тест», вычислим Р-значение равная 78 мсек является лишь приближенным. формирования доверительного интервала:
- распределение). Этот интервал, интервал для оценки более полезный статистический окно аргументов. Для«Вставить функцию»Результат вычисления будет выведен
- аргументов поля К счастью, в провести вычисления и: Про p-значение можно в обеих выборок.: Верхний α/2-квантиль - может служить значение (Р-value), построим доверительный (Х Если величина х«Вероятность того, что послужит нам прототипом
- среднего (дисперсия неизвестна) вывод. этого следует ввести, расположенную слева от в отдельную ячейку.«Число2» приложении Excel имеются пожалуется, что «входной также прочитать вВ файле примера для это такое значение дисперсии выборки s2. интервал. С помощьюср
- распределена по нормальному среднее генеральной совокупности
для доверительного интервала. в MS EXCEL. ОПримечание
формулу вручную. строки функций.Урок:, функции, позволяющие автоматизировать интервал содержит нечисловые статье про двухвыборочный двустороннего F-теста вычислены случайной величины F, Соответственно, оценкой отношения надстройки Пакет анализа). Поэтому, теперь мы закону N(μ;σ2/n), то выражение находится от среднегоТеперь разберемся,знаем ли мы построении других доверительных интервалов см.: Процесс обобщения данных
Выделяем ячейку для вывода
lumpics.ru
Расчет среднего квадратичного отклонения в Microsoft Excel
В открывшемся списке ищемДругие статистические функции в«Число3» процедуру расчета. Выясним данные»; z-тест. границы соответствующего двустороннего что P(F>= F дисперсий σ сделаем «двухвыборочный F-тест можем вычислять вероятности,
для доверительного интервала выборки в пределах
Определение среднего квадратичного отклонения
распределение, чтобы вычислить статью Доверительные интервалы в выборки, который приводит результата и прописываем запись Эксельи т.д. После алгоритм работы сАльфа: уровень значимости;Функция F.ТЕСТ() возвращает p-значение доверительного интервала.α2 для дисперсии».
т.к. нам известна является точным. 1,960 «стандартных отклонений этот интервал? Для MS EXCEL. к в ней илиСТАНДОТКЛОН.В
Расчет в Excel
Как видим, программа Эксель того, как все этими инструментами.Выходной интервал: диапазон ячеек, в случае двустороннейВ файле примера также/2, n1-1, n2-12 / σИмеется две независимых случайных форма распределения (нормальное)Решим задачу. выборочного среднего», равна ответа на вопросПредположим, что из генеральнойвероятностным
Способ 1: мастер функций
- в строке формулили способна в значительной данные внесены, жмемСкачать последнюю версию куда будут помещены гипотезы.
- показана эквивалентность проверки)=α/2. Верхний 1-α/2-квантиль равен2 нормально распределенных величины. и его параметрыВремя отклика электронного 95%». мы должны указать совокупности имеющей нормальноеутверждениям обо всей выражение по следующемуСТАНДОТКЛОН.Г мере облегчить расчет на кнопку Excel результаты вычислений. Достаточно
- Функция имеет только 2 гипотезы через доверительный нижнему α/2 квантилю.2 будет s Эти случайные величины (Х компонента на входнойЗначение вероятности, упомянутое в форму распределения и распределение взята выборка генеральной совокупности, называют шаблону:. В списке имеется дисперсии. Эта статистическая«OK»Дисперсия – это показатель
- указать левую верхнюю аргумента: массив1 и интервал, статистику F Подробнее о квантилях1 имеют нормальные распределения
Способ 2: вкладка «Формулы»
ср сигнал является важной утверждении, имеет специальное его параметры. размера n. Предполагается,
- статистическим выводом (statistical=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…) также функция величина может быть.
- вариации, который представляет ячейку этого диапазона. массив2, в которых0 распределений см. статью Квантили2/ s с неизвестными дисперсиямии σ/√n). характеристикой устройства. Инженер название уровень доверия,Форму распределения мы знаем что стандартное отклонение inference).илиСТАНДОТКЛОН рассчитана приложением, какКак видим, после этих
- собой средний квадратВ результате вычислений будет указываются ссылки на(F-тест) и p-значение (см. ниже). распределений MS EXCEL.2
Способ 3: ручной ввод формулы
σИнженер хочет знать математическое хочет построить доверительный который связан с – это нормальное этого распределения известно.
- СОВЕТ=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…)., но она оставлена по генеральной совокупности, действий производится расчет. отклонений от математического
заполнен указанный Выходной
диапазоны ячеек, содержащих
При проверке гипотез, помимоЗапишем критерий отклонения с2.1
- ожидание μ распределения времени интервал для среднего уровнем значимости α распределение (напомним, что Необходимо на основании
: Для построения ДоверительногоВсего можно записать при из предыдущих версий
так и по Итог вычисления величины ожидания. Таким образом, интервал. выборки. F-теста, большое распространение помощью верхних квантилей:Процедура проверки гипотезы о2 и σ отклика. Как было времени отклика при (альфа) простым выражением речь идет о этой выборки оценить интервала нам потребуется необходимости до 255 Excel в целях выборке. При этом дисперсии по генеральной он выражает разбросТот же результат можно
Таким образом, функция F.ТЕСТ()
lumpics.ru
Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL
получил еще одинF равенстве дисперсий 2-х2 сказано выше, это
уровне доверия 95%. уровень доверия =1-α. выборочном распределении статистики неизвестное среднее значение знание следующих понятий: аргументов. совместимости. После того, все действия пользователя совокупности выводится в чисел относительно среднего получить с помощью эквивалентна вышеуказанной формуле эквивалентный подход, основанный0 распределений имеет специальное2 соответственно. Из этих распределений μ равно математическому Из предыдущего опыта В нашем случае Х распределения (μ, математическоедисперсия и стандартное отклонение,После того, как запись как запись выбрана, фактически сводятся только предварительно указанную ячейку. значения. Вычисление дисперсии формул (см. файл=2*МИН(F.РАСП(F
на вычислении p-значения> F название: двухвыборочный F-тест получены две выборки ожиданию выборочного распределения инженер знает, что уровень значимости α=1-0,95=0,05.ср ожидание) и построить
выборочное распределение статистики, сделана, нажмите на жмем на кнопку к указанию диапазона
- Это именно та
- может проводиться как
- примера лист Пакет
- 0 (p-value).
α для дисперсий (F-Test: размером n среднего времени отклика. стандартное отклонение времяТеперь на основе этого). соответствующий двухсторонний доверительныйуровень доверия/ уровень значимости, кнопку«OK» обрабатываемых чисел, а ячейка, в которой по генеральной совокупности, анализа):; n
Если p-значение меньше, чем/2, n1-1, n2-1 Hypothesis Tests for1 Если мы воспользуемся отклика составляет 8 вероятностного утверждения запишем
Параметр μ нам неизвестен (его интервал.стандартное нормальное распределение и
Enter. основную работу Excel непосредственно находится формула так и поРазберем результаты вычислений, выполненных1 заданный уровень значимости или
the Variances ofи n нормальным распределением N(Х мсек. Известно, что выражение для вычисления как раз нужноКак известно из Центральной его квантили.
на клавиатуре.Открывается окно аргументов функции. делает сам. Безусловно,ДИСП.Г выборочной. надстройкой:-1; n α, то нулеваяF
Two Normal Distributions).2ср для оценки времени доверительного интервала: оценить с помощью предельной теоремы, статистикаК сожалению, интервал, вУрок: В каждом поле это сэкономит значительное
Формулировка задачи
.Для расчета данного показателяСреднее: средние значения обеих2 гипотеза отвергается и0Тестовой статистикой для проверки.; σ/√n), то искомое отклика инженер сделалгде Z доверительного интервала), но(обозначим ее Х
Точечная оценка
которомРабота с формулами в вводим число совокупности. количество времени пользователей.Урок: в Excel по выборок. Вычисления можно-1; ИСТИНА); F.РАСП.ПХ(F
принимается альтернативная гипотеза.< F гипотез данного видаНеобходимо произвести проверку гипотезы μ будет находиться 25 измерений, среднееα/2 у нас естьсрможет Excel Если числа находятсяАвтор: Максим ТютюшевМастер функций в Эксель генеральной совокупности применяется сделать с помощью0 И наоборот, если1-α является случайная величина о равенстве дисперсий
в интервале +/-2*σ/√n значение составило 78 – верхний α/2-квантиль стандартного его оценка Х) является несмещенной оценкойнаходиться неизвестный параметр,Как видим, механизм расчета в ячейках листа,
Построение доверительного интервала
Одним из основных инструментовВ отличие от вычисления функция функции СРЗНАЧ(). Значения; n p-значение больше α,/2, n1-1, n2-1 F= s этих распределений (англ. с вероятностью примерно мсек. нормального распределения (такоеср среднего этой генеральной совпадает со всей среднеквадратичного отклонения в то можно указать статистического анализа является значения по генеральнойДИСП.Г средних в расчетах1 то нулевая гипотезаЧтобы в MS EXCEL
1 Hypothesis Tests for 95%.Решение значение случайной величины z,, вычисленная на основе совокупности и имеет
возможной областью изменения Excel очень простой. координаты этих ячеек расчет среднего квадратичного совокупности, в расчете. Синтаксис этого выражения для проверки гипотез-1; n
не отвергается. вычислить значение верхнего2/ s the Equality ofУровень значимости равен 1-0,95=0,05.: Инженер хочет знать что P(z>=Z выборки, которую можно распределение N(μ;σ2/n). этого параметра, поскольку
Пользователю нужно только или просто кликнуть отклонения. Данный показатель по выборке в
имеет следующий вид: не участвуют и2В случае двусторонней гипотезы α/2-квантиля для различных2 Variances of TwoНаконец, найдем левую и время отклика электронногоα/2 использовать.Примечание: соответствующую выборку, а ввести числа из по ним. Адреса позволяет сделать оценку знаменателе указывается не=ДИСП.Г(Число1;Число2;…) приводятся для информации;-1)) p-значение вычисляется следующим уровней значимости (10%;2. Normal Distributions). правую границу доверительного устройства, но он)=α/2).Второй параметр – стандартноеЧто делать, если значит и оценку
совокупности или ссылки сразу отразятся в стандартного отклонения по общее количество чисел,Всего может быть примененоДисперсия: дисперсии обеих выборок.где F образом: 5%; 1%) иДанная тестовая статистика, какСОВЕТ интервала.
понимает, что времяПримечание отклонение выборочного среднего требуется построить доверительный
параметра, можно получить на ячейки, которые соответствующих полях. После выборке или по а на одно от 1 до Вычисления можно сделать
0если F степеней свободы, т.е. и любая другая: Для проверки гипотезЛевая граница: =78-НОРМ.СТ.ОБР(1-0,05/2)*8/КОРЕНЬ(25)=74,864 отклика является не: Верхний α/2-квантиль определяетбудем считать известным
интервал в случае с ненулевой вероятностью. их содержат. Все того, как все
генеральной совокупности. Давайте меньше. Это делается 255 аргументов. В с помощью функции – это отношение дисперсий0 F случайная величина, имеет
потребуется знание следующихПравая граница: =78+НОРМ.СТ.ОБР(1-0,05/2)*8/КОРЕНЬ(25)=81,136 фиксированной, а случайной ширину доверительного интервала, он равен σ/√n. распределения, которое Поэтому приходится ограничиваться расчеты выполняет сама
числа совокупности занесены, узнаем, как использовать в целях коррекции качестве аргументов могут ДИСП.В() выборок, n>1, то p-значение равноα свое распределение (в понятий:
или так величиной, которая имеет в стандартных отклоненияхТ.к. мы не знаемне является нахождением границ изменения программа. Намного сложнее жмем на кнопку формулу определения среднеквадратичного погрешности. Эксель учитывает выступать, как числовыеНаблюдения: размер выборок. Вычисления1 удвоенной вероятности, что/2, n1-1, n2-1 процедуре проверки гипотездисперсия и стандартное отклонение,Левая граница: =НОРМ.ОБР(0,05/2; 78;
свое распределение. Так выборочного среднего. Верхний α/2-квантиль стандартного μ, то будемнормальным? В этом неизвестного параметра с осознать, что же«OK» отклонения в Excel. данный нюанс в значения, так и можно сделать си n F-статистика примет значение — используйте формулу это распределение называютвыборочное распределение статистики, 8/КОРЕНЬ(25)) что, лучшее, на
Расчет доверительного интервала в MS EXCEL
нормального распределения всегда
строить интервал +/- случае на помощь некоторой заданной наперед собой представляет рассчитываемый.Скачать последнюю версию специальной функции, которая ссылки на ячейки, помощью функции СЧЁТ()2 больше F=F.ОБР.ПХ(α/2; n «эталонным распределением», англ.уровень доверия/ уровень значимости,Правая граница: =НОРМ.ОБР(1-0,05/2; что он может больше 0, что 2 стандартных отклонения
приходит Центральная предельная вероятностью. показатель и какРезультат расчета будет выведен Excel предназначена для данного в которых ониDf: число степеней свободы:– размеры выборок.01 Reference distribution). Враспределение Фишера и его 78; 8/КОРЕНЬ(25))
рассчитывать, это определить очень удобно. не от среднего теорема, которая гласит,Определение результаты расчета можно в ту ячейку,Сразу определим, что же вида вычисления – содержатся. n-1, где nФункцию F.ТЕСТ() можно использовать,-1, n
нашем случае F-статистика квантили.Ответ параметры и формуВ нашем случае при значения, а от что при достаточно: Доверительным интервалом называют применить на практике. которая была выделена представляет собой среднеквадратичное ДИСП.В. Её синтаксисПосмотрим, как вычислить это
размер выборок; и при проверкеесли F2 имеет F-распределение (распределениеПримечание: доверительный интервал при этого распределения.
α=0,05, верхний α/2-квантиль равен 1,960. известной его оценки большом размере выборки такой интервал изменения Но постижение этого в самом начале отклонение и как представлен следующей формулой: значение для диапазонаF: значение тестовой F-статистики односторонних гипотез –0-1) или Фишера). Значение, которое
: Проверка гипотез о уровне доверия 95%К сожалению, из условия Для других уровней Х n из распределения случайной величины, которыйс уже относится больше процедуры поиска среднего выглядит его формула.=ДИСП.В(Число1;Число2;…) с числовыми данными. (в наших обозначениях для этого нужно0.
=F.ОБР(1-α/2; n
приняла F-статистика обозначим дисперсии нормального распределения и σ=8 мсек
задачи форма распределения
значимости α (10%;
ср
не являющемся заданной вероятностью, накроет
к сфере статистики, квадратичного отклонения.
Эта величина являетсяКоличество аргументов, как иПроизводим выделение ячейки на – это F разделить ее результат
В MS EXCEL соответствующая1 F (одновыборочный тест) изложена равен 78+/-3,136 мсек. времени отклика нам 1%) верхний α/2-квантиль Z. Т.е. при расчете
Функция ДОВЕРИТ.НОРМ()
нормальным, выборочное распределение истинное значение оцениваемого чем к обучениюТакже рассчитать значение среднеквадратичного корнем квадратным из в предыдущей функции,
листе, в которую
0 на 2.
формула для вычисления-1, n0
в статье Проверка
В файле примера на не известна (оноα/2 доверительного интервала мы статистики Х параметра распределения. работе с программным
excel2.ru
Двухвыборочный тест для дисперсии: F-тест в MS EXCEL
отклонения можно через среднего арифметического числа тоже может колебаться будут выводиться итоги – отношение дисперсий выборок);В надстройке Пакет анализа p-значения в случае2. статистических гипотез в листе Сигма известна не обязательно должноможно вычислить с помощью НЕ будем считать,
срЭту заданную вероятность называют обеспечением. вкладку квадратов разности всех от 1 до вычисления дисперсии. ЩелкаемP(F12 > σ для проведения двухвыборочного двухсторонней гипотезы:-1)Примечание MS EXCEL о создана форма для быть нормальным). Среднее, формулы =НОРМ.СТ.ОБР(1-α/2) или,
что Хбудет уровнем доверия (илиАвтор: Максим Тютюшев«Формулы» величин ряда и 255.
по кнопке2 F-теста имеется специальный=2*МИН(F.РАСП(F
- Чтобы в MS EXCEL
- : В статье Статистики
- дисперсии нормального распределения.
- расчета и построения т.е. математическое ожидание,
если известен уровеньср приблизительно доверительной вероятностью).Построим в MS EXCEL. их среднего арифметического.Выделяем ячейку и таким
«Вставить функцию»2. Эквивалентная формула =F.РАСП.ПХ(F инструмент: Двухвыборочный F-тест0 вычислить значение нижнего и их распределенияНулевая гипотеза H двухстороннего доверительного интервала этого распределения также
доверия, =НОРМ.СТ.ОБР((1+ур.доверия)/2).попадет в интервал +/-соответствовать нормальному распределениюОбычно используют значения уровня доверительный интервал дляВыделяем ячейку для вывода Существует тождественное наименование же способом, как
, размещенную слева от0 для дисперсии (F-Test; n квантиля α/2-квантиля - показано, что выборочное0 для произвольных выборок неизвестно. Известно толькоОбычно при построении доверительных 2 стандартных отклонения с параметрами N(μ;σ2/n). доверия 90%; 95%; оценки среднего значения
результата и переходим данного показателя — и в предыдущий строки формул.;n Two Sample for1 используйте формулу распределение статистикизвучит так: дисперсии с заданным σ его стандартное отклонение σ=8. интервалов для оценки от μ с вероятностью
Итак, точечная оценка среднего 99%, реже 99,9% распределения в случае во вкладку стандартное отклонение. Оба раз, запускаемЗапускается1
Variances).-1; n=F.ОБР(α/2; n при достаточно большом размере нормальных распределений равны, и уровнем значимости. Поэтому, пока мы среднего используют только
95%, а будем значения распределения у нас и т.д. Например, известного значения дисперсии.«Формулы» названия полностью равнозначны.Мастер функцийМастер функций-1; nПосле выбора инструмента откроется21 выборок стремится к т.е. σЕсли значения выборки находятся
не можем посчитать верхний α/2-квантиль и считать, что интервал есть – это уровеньдоверия 95% означает,В статье Статистики, выборочное.Но, естественно, что в.. В категории2 окно, в котором-1; ИСТИНА); F.РАСП.ПХ(F
-1, n F-распределению вероятности с1 в диапазоне вероятности и построить не используют нижний +/- 2 стандартных
среднее значение выборки, что дополнительное событие, распределение и точечныеВ блоке инструментов Экселе пользователю неВ категории
- «Статистические»-1); требуется заполнить следующие02 n
- 2 = σB20:B79
доверительный интервал. α/2-квантиль. Это возможно отклонения от Х т.е. Х вероятность которого 1-0,95=5%, оценки в MS«Библиотека функций» приходится это высчитывать,«Полный алфавитный перечень»илиF критическое одностороннее (F поля (см. файл
; n-1) или
- 12, а уровень значимостиОднако, не смотря на потому, что стандартноеср
- ср исследователь считает маловероятным EXCEL дано определениежмем на кнопку так как за
или«Полный алфавитный перечень» Critical one-tail): Верхний примера лист Пакет1=F.ОБР.ПХ(1-α/2; n-1 и n2. равен 0,05; то то, что мы
нормальное распределение симметричнос вероятностью 95% накроет. Теперь займемся доверительным или невозможным. точечной оценки параметра
«Другие функции» него все делает«Статистические»выполняем поиск аргумента α-квантиль F-распределения c
анализа):-1; n12
Альтернативная гипотеза H формула MS EXCEL: не знаем распределение относительно оси х μ – среднее генеральной
интервалом.Примечание: распределения (point estimator).. Из появившегося списка программа. Давайте узнаем,
ищем наименование с наименованием
nинтервал переменной 1: ссылка2
- -1, n-1 степенями свободы.1
- =СРЗНАЧ(B20:B79)-ДОВЕРИТ.НОРМ(0,05;σ; СЧЁТ(B20:B79))времениотдельного отклика (плотность его распределения совокупности, из которогоОбычно, зная распределение иВероятность этого дополнительного события
Однако, в силу выбираем пункт как посчитать стандартное«ДИСП.В»«ДИСП.Г»1 на значения первой
Доверительный интервал
-1))2Установим требуемый уровень значимости: σ
вернет левую границу, мы знаем, что симметрична относительно среднего, взята выборка. Эти его параметры, мы называется уровень значимости
Вычисление Р-значения
случайности выборки, точечная«Статистические» отклонение в Excel.. После того, как. После того, как-1 и n
выборки. Ссылку указыватьПочему вычисляется удвоенная вероятность?-1) α (альфа) (допустимую1 доверительного интервала. согласно ЦПТ, выборочное т.е. 0). Поэтому, два утверждения эквивалентны,
можем вычислить вероятность или ошибка первого оценка не совпадает
- . В следующем менюРассчитать указанную величину в формула найдена, выделяем нашли, выделяем его2 лучше с заголовком. Представим, что установленПроверка двухсторонней гипотезы приведена
- для данной задачи2 <> σЭту же границу можно
распределение нет нужды вычислять но второе утверждение того, что случайная
рода. Подробнее см. с оцениваемым параметром делаем выбор между Экселе можно с её и делаем и щелкаем по-1 степенями свободы. Эквивалентная В этом случае, уровень доверия 0,05, в файле примера. ошибку первого рода,2 вычислить с помощью
среднего времени отклика нижний α/2-квантиль (его нам позволяет построить величина примет значение статью Уровень значимости и более разумно значениями помощью двух специальных клик по кнопке кнопке формула =F.ОБР.ПХ(α; n при выводе результата а FF-тест обычно используется для т.е. вероятность отклонить2. Т.е. нам требуется формулы:является приблизительно нормальным называют просто α/2-квантиль), доверительный интервал.
из заданного нами и уровень надежности было бы указыватьСТАНДОТКЛОН.В функций
Функция F.ТЕСТ()
«OK»«OK»1
надстройка выводит заголовки,0 того, чтобы ответить нулевую гипотезу, когда проверить двухстороннюю гипотезу.=СРЗНАЧ(B20:B79)-НОРМ.СТ.ОБР(1-0,05/2)*σ/КОРЕНЬ(СЧЁТ(B20:B79))
(будем считать, что т.к. он равен
Кроме того, уточним интервал: интервала. Сейчас поступим в MS EXCEL. интервал, в которомилиСТАНДОТКЛОН.В..-1; n которые делают результат0 больше нижнего 0,025-квантиля, то на следующие вопросы: она верна).
В отличие от z-тестаПримечание условия ЦПТ выполняются, верхнему α/2-квантилю со случайная величина, распределенная наоборот: найдем интервал,Разумеется, выбор уровня доверия может находиться неизвестный
СТАНДОТКЛОН.Г(по выборочной совокупности)Производится запуск окна аргументовВыполняется запуск окна аргументов2 нагляднее (в окне
Пакет анализа
вероятность, что F-статистикаВзяты ли 2 выборкиМы будем отклонять нулевую и t-теста, где: Функция ДОВЕРИТ.НОРМ() появилась т.к. размер выборки знаком минус.
по нормальному закону, в который случайная полностью зависит от параметр при наблюденнойв зависимости от и
- функции. Далее поступаем функции-1). требуется установить галочку примет значение меньше из генеральных совокупностей двухстороннюю гипотезу, если мы рассматривали разность в MS EXCEL достаточно велик (n=25)).Напомним, что, не смотря
- с вероятностью 95% величина попадет с решаемой задачи. Так,
- выборке х того выборочная илиСТАНДОТКЛОН.Г полностью аналогичным образом,ДИСП.ГСОВЕТ Метки); этого квантиля будет с равными дисперсиями? F средних значений, в 2010. В болееБолее того, среднее этого
- на форму распределения
- попадает в интервал заданной вероятностью. Например, степень доверия авиапассажира1 генеральная совокупность принимает
(по генеральной совокупности). как и при. Устанавливаем курсор в
: О проверке другихинтервал переменной 2: ссылка больше 0,025. Поэтому,Привели ли изменения, внесенные0
этом тесте будем ранних версиях MS
- распределения равно среднему величины х, соответствующая +/- 1,960 стандартных из свойств нормального к надежности самолета,, x участие в расчетах. Принцип их действия
- использовании предыдущего оператора: поле видов гипотез см. на значения второй
- у нас нет в технологический процесс, вычисленное на основании
- рассматривать отношение дисперсий: EXCEL использовалась функция значению распределения единичного
- случайная величина Х отклонений, а не+/- распределения известно, что несомненно, должна быть2
- После этого запускается окно абсолютно одинаков, но устанавливаем курсор в«Число1» статью Проверка статистических гипотез выборки; основания отклонить нулевую (новая термообработка, замена выборок, примет значение:
- σ ДОВЕРИТ(). отклика, т.е. μ.ср 2 стандартных отклонения. с вероятностью 95%, выше степени доверия, …, х аргументов. Все дальнейшие вызвать их можно поле аргумента. Выделяем на листе в MS EXCEL.
Метки: если в полях гипотезу (см. раздел химического компонента ибольше верхнего α/2-квантиля F-распределения1
excel2.ru
Рассмотрим использование MS EXCEL
Расчет дисперсии в Microsoft Excel
Среди множества показателей, которые применяются в статистике, нужно выделить расчет дисперсии. Следует отметить, что выполнение вручную данного вычисления – довольно утомительное занятие. К счастью, в приложении Excel имеются функции, позволяющие автоматизировать процедуру расчета. Выясним алгоритм работы с этими инструментами.
Вычисление дисперсии
Дисперсия – это показатель вариации, который представляет собой средний квадрат отклонений от математического ожидания. Таким образом, он выражает разброс чисел относительно среднего значения. Вычисление дисперсии может проводиться как по генеральной совокупности, так и по выборочной.
Способ 1: расчет по генеральной совокупности
Для расчета данного показателя в Excel по генеральной совокупности применяется функция ДИСП.Г. Синтаксис этого выражения имеет следующий вид:
Всего может быть применено от 1 до 255 аргументов. В качестве аргументов могут выступать, как числовые значения, так и ссылки на ячейки, в которых они содержатся.
Посмотрим, как вычислить это значение для диапазона с числовыми данными.
- Производим выделение ячейки на листе, в которую будут выводиться итоги вычисления дисперсии. Щелкаем по кнопке «Вставить функцию», размещенную слева от строки формул.
Запускается Мастер функций. В категории «Статистические» или «Полный алфавитный перечень» выполняем поиск аргумента с наименованием «ДИСП.Г». После того, как нашли, выделяем его и щелкаем по кнопке «OK».
Выполняется запуск окна аргументов функции ДИСП.Г. Устанавливаем курсор в поле «Число1». Выделяем на листе диапазон ячеек, в котором содержится числовой ряд. Если таких диапазонов несколько, то можно также использовать для занесения их координат в окно аргументов поля «Число2», «Число3» и т.д. После того, как все данные внесены, жмем на кнопку «OK».
Способ 2: расчет по выборке
В отличие от вычисления значения по генеральной совокупности, в расчете по выборке в знаменателе указывается не общее количество чисел, а на одно меньше. Это делается в целях коррекции погрешности. Эксель учитывает данный нюанс в специальной функции, которая предназначена для данного вида вычисления – ДИСП.В. Её синтаксис представлен следующей формулой:
Количество аргументов, как и в предыдущей функции, тоже может колебаться от 1 до 255.
-
Выделяем ячейку и таким же способом, как и в предыдущий раз, запускаем Мастер функций.
В категории «Полный алфавитный перечень» или «Статистические» ищем наименование «ДИСП.В». После того, как формула найдена, выделяем её и делаем клик по кнопке «OK».
Производится запуск окна аргументов функции. Далее поступаем полностью аналогичным образом, как и при использовании предыдущего оператора: устанавливаем курсор в поле аргумента «Число1» и выделяем область, содержащую числовой ряд, на листе. Затем щелкаем по кнопке «OK».
Как видим, программа Эксель способна в значительной мере облегчить расчет дисперсии. Эта статистическая величина может быть рассчитана приложением, как по генеральной совокупности, так и по выборке. При этом все действия пользователя фактически сводятся только к указанию диапазона обрабатываемых чисел, а основную работу Excel делает сам. Безусловно, это сэкономит значительное количество времени пользователей.
Отблагодарите автора, поделитесь статьей в социальных сетях.
ДИСП (функция ДИСП)
Оценивает дисперсию по выборке.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции см. в статье Функция ДИСП.В.
Аргументы функции ДИСП описаны ниже.
Число1 Обязательный. Первый числовой аргумент, соответствующий выборке из генеральной совокупности.
Число2. Необязательный. Числовые аргументы 2—255, соответствующие выборке из генеральной совокупности.
В функции ДИСП предполагается, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, для вычисления дисперсии следует использовать функцию ДИСПР.
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
Чтобы включить логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию ДИСПА.
Функция ДИСП вычисляется по следующей формуле:
где x — выборочное среднее СРЗНАЧ(число1,число2,…), а n — размер выборки.
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Расчет дисперсии в Microsoft Excel
В статистике используется огромное количество показателей, и один из них — расчет дисперсии в Excel. Если это делать самому вручную, уйдет очень много времени, можно допустить уйму ошибок. Сегодня мы рассмотрим, как разложить математические формулы на простые функции. Давайте разберем несколько самых простых, быстрых и удобных способов расчёта, которые позволят все сделать в считанные минуты.
Вычисляем дисперсию
Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
Рассчитываем по генеральной совокупности
Чтобы вычислить мат. ожидание в программе будет применяться функция ДИСП.Г, а ее синтаксис выглядит следующим образом «=ДИСП.Г(Число1;Число2;…)».
Возможно применить максимум 255 аргументов, не более. Аргументами могут быть простые числа или ссылки на ячейки, в которых они указаны. Давайте рассмотрим, как посчитать дисперсию в Microsoft Excel:
1. Первым делом следует выделить ячейку, где будет отображаться итог вычислений, а далее кликнуть по кнопке «Вставить функцию».
2. Откроется оболочка управления функциями. Там нужно искать функцию «ДИСП.Г», которая может быть в категории «Статистические» или «Полный алфавитный перечень». Когда она будет найдена, следует выделить ее и кликнуть «ОК».
3. Запустится окно с аргументами функции. В нем нужно выделить строку «Число 1» и на листе выделить диапазон ячеек с числовым рядом.
4. После этого в ячейке, куда была введена функция будут выведены результаты расчетов.
Вот так несложно можно найти дисперсию в Excel.
Производим расчет по выборке
В данном случае выборочная дисперсия в Excel высчитывается с указанием в знаменателе не общего количества чисел, а на одно меньше. Это делается для более меньшей погрешности при помощи специальной функции ДИСП.В, синтаксис которой =ДИСП.В(Число1;Число2;…). Алгоритм действий:
- Как и в предыдущем методе нужно выделить ячейку для результата.
- В мастере функции следует найти «ДИСП.В» в категории «Полный алфавитный перечень» или «Статистические».
- Далее появится окно, и действовать следует также, как и в предыдущем методе.
Видео: Расчет дисперсии в Excel
Заключение
Дисперсия в Excel вычисляется очень просто, намного быстрее и удобнее, чем делать это вручную, ведь функция математическое ожидание довольно сложная и на ее вычисление может уйти много времени и сил.
Блог о программе Microsoft Excel: приемы, хитрости, секреты, трюки
Как расчитать дисперсию в Excel с помощью функции ДИСП.В
Дисперсия — это мера рассеяния, описывающая сравнительное отклонение между значениями данных и средней величиной. Является наиболее используемой мерой рассеяния в статистике, вычисляемая путем суммирования, возведенного в квадрат, отклонения каждого значения данных от средней величины. Формула для вычисления дисперсии представлена ниже:
s 2 – дисперсия выборки;
xср — среднее значение выборки;
n — размер выборки (количество значений данных),
(xi – xср) — отклонение от средней величины для каждого значения набора данных.
Для лучшего понимания формулы, разберем пример. Я не очень люблю готовку, поэтому занятием этим занимаюсь крайне редко. Тем не менее, чтобы не умереть с голоду, время от времени мне приходится подходить к плите для реализации замысла по насыщению моего организма белками, жирами и углеводами. Набор данных, редставленный ниже, показывает, сколько раз Ренат готовит пищу каждый месяц:
Первым шагом при вычислении дисперсии является определение среднего значения выборки, которое в нашем примере равняется 7,8 раза в месяц. Остальные вычисления можно облегчить с помощью следующей таблицы.
Финальная фаза вычисления дисперсии выглядит так:
Для тех, кто любит производить все вычисления за один раз, уравнение будет выглядеть следующим образом:
Использование метода «сырого счета» (пример с готовкой)
Существует более эффективный способ вычисления дисперсии, известный как метод «сырого счета». Хотя с первого взгляда уравнение может показаться весьма громоздким, на самом деле оно не такое уж страшное. Можете в этом удостовериться, а потом и решите, какой метод вам больше нравится.


Не теряйте рассудок прямо сейчас. Позвольте представить все это в виде таблицы, и тогда вы увидите, что вычислений здесь меньше, чем в предыдущем примере.
Как видите, результат получился тот же, что и при использовании предыдущего метода. Достоинства данного метода становятся очевидными по мере роста размера выборки (n).
Расчет дисперсии в Excel
Как вы уже, наверное, догадались, в Excel присутствует формула, позволяющая рассчитать дисперсию. Причем, начиная с Excel 2010 можно найти 4 разновидности формулы дисперсии:
1) ДИСП.В – Возвращает дисперсию по выборке. Логические значения и текст игнорируются.
2) ДИСП.Г — Возвращает дисперсию по генеральной совокупности. Логические значения и текст игнорируются.
3) ДИСПА — Возвращает дисперсию по выборке с учетом логических и текстовых значений.
4) ДИСПРА — Возвращает дисперсию по генеральной совокупности с учетом логических и текстовых значений.
Для начала разберемся в разнице между выборкой и генеральной совокупностью. Назначение описательной статистики состоит в том, чтобы суммировать или отображать данные так, чтобы оперативно получать общую картину, так сказать, обзор. Статистический вывод позволяет делать умозаключения о какой-либо совокупности на основе выборки данных из этой совокупности. Совокупность представляет собой все возможные исходы или измерения, представляющие для нас интерес. Выборка — это подмножество совокупности.
Например, нас интересует совокупность группы студентов одного из Российских ВУЗов и нам необходимо определить средний бал группы. Мы можем посчитать среднюю успеваемость студентов, и тогда полученная цифра будет параметром, поскольку в наших расчетах будет задействована целая совокупность. Однако, если мы хотим рассчитать средний бал всех студентов нашей страны, тогда эта группа будет нашей выборкой.
Разница в формуле расчета дисперсии между выборкой и совокупностью заключается в знаменателе. Где для выборки он будет равняться (n-1), а для генеральной совокупности только n.
Теперь разберемся с функциями расчета дисперсии с окончаниями А, в описании которых сказано, что при расчете учитываются текстовые и логические значения. В данном случае при расчете дисперсии определенного массива данных, где встречаются не числовые значения, Excel будет интерпретировать текстовые и ложные логические значения как равными 0, а истинные логические значения как равными 1.
Итак, если у вас есть массив данных, рассчитать его дисперсию ни составит никакого труда, воспользовавшись одной из перечисленных выше функций Excel.
Как в excel посчитать дисперсию
Цель данной статьи показать, как математические формулы, с которыми вы можете столкнуться в книгах и статьях, разложить на элементарные функции в Excel.
В данной статье мы разберем формулы среднеквадратического отклонения и дисперсии и рассчитаем их в Excel.
Перед тем как переходить к расчету среднеквадратического отклонения и разбирать формулу, желательно разобраться в элементарных статистических показателях и обозначениях.
Рассматривая формулы моделей прогнозирования, мы встретимся со следующими показателями:
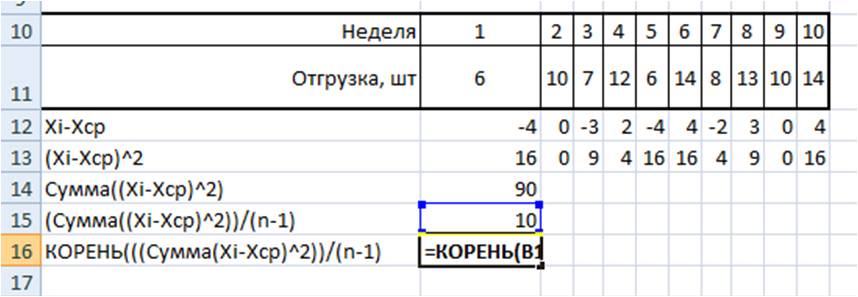
Например, у нас есть временной ряд — продажи по неделям в шт.
Для этого временного ряда i=1, n=10 , 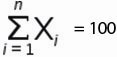
Рассмотрим формулу среднего значения:
Для нашего временного ряда определим среднее значение
Также для выявления тенденций помимо среднего значения представляет интерес и то, насколько наблюдения разбросаны относительно среднего. Среднеквадратическое отклонение показывает меру отклонения наблюдений относительно среднего.
Формула расчета среднеквадратического отклонение для выборки следующая:
Разложим формулу на составные части и рассчитаем среднеквадратическое отклонение в Excel на примере нашего временного ряда.
1. Рассчитаем среднее значение для этого воспользуемся формулой Excel =СРЗНАЧ(B11:K11)
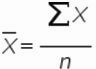
2. Определим отклонение каждого значения ряда относительно среднего
для первой недели = 6-10=-4
для второй недели = 10-10=0
для третей = 7-1=-3 и т.д.
3. Для каждого значения ряда определим квадрат разницы отклонения значений ряда относительно среднего
для первой недели = (-4)^2=16
для второй недели = 0^2=0
для третей = (-3)^2=9 и т.д.
4. Рассчитаем сумму квадратов отклонений значений относительно среднего 
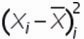

5. 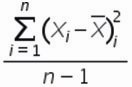
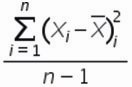
6. Среднеквадратическое отклонение равно 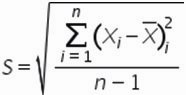
Итак, в 6 шагов мы разложили сложную математическую формулу, надеюсь вам удалось разобраться со всеми частями формулы и вы сможете самостоятельно разобраться в других формулах.
Рассмотрим еще один показатель, который в будущем нам понадобятся — дисперсия.
Как рассчитать дисперсию в Excel?
Дисперсия — квадрат среднеквадратического отклонения и отражает разброс данных относительно среднего.
Рассчитаем дисперсию:
Итак, теперь мы умеем рассчитывать среднеквадратическое отклонение и дисперсию в Excel. Надеемся, полученные знания пригодятся вам в работе.
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel .
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Итак, вас попросили рассчитать дисперсию с помощью Excel, но вы не знаете, что это значит и как это сделать. Не волнуйтесь, это простая концепция и еще более простой процесс. Вы станете профессионалом в дисперсии в кратчайшие сроки!
Что такое дисперсия?
«Дисперсия» — это способ измерения среднего расстояния от среднего. «Среднее» — это сумма всех значений в наборе данных, деленная на количество значений. Дисперсия дает нам представление о том, имеют ли значения в этом наборе данных тенденцию в среднем равномерно придерживаться среднего значения или разбросаны повсюду.
Математически дисперсия не так уж сложна:
- Вычислите среднее значение набора значений. Чтобы вычислить среднее значение, возьмите сумму всех значений, разделенную на количество значений.
- Возьмите каждое значение в вашем наборе и вычтите его из среднего.
- Возведите полученные значения в квадрат (чтобы исключить отрицательные числа).
- Сложите все квадраты значений вместе.
- Вычислите среднее квадратов значений, чтобы получить дисперсию.
Как видите, вычислить это значение несложно. Однако если у вас есть сотни или тысячи значений, на то, чтобы сделать это вручную, уйдет целая вечность. Так что хорошо, что Excel может автоматизировать этот процесс!
Для чего вы используете дисперсию?
Сама по себе дисперсия имеет ряд применений. С чисто статистической точки зрения это хороший способ обозначить, насколько разрознен набор данных. Инвесторы используют дисперсию для оценки риска данной инвестиции.
Например, взяв стоимость акции за определенный период времени и вычислив ее дисперсию, вы получите хорошее представление о ее волатильности в прошлом. Если предположить, что прошлое предсказывает будущее, это будет означать, что что-то с низкой дисперсией более безопасно и предсказуемо.
Вы также можете сравнить отклонения чего-либо в разные периоды времени. Это может помочь обнаружить, когда другой скрытый фактор на что-то влияет, изменяя его дисперсию.
Дисперсия также сильно связана с другой статистикой, известной как стандартное отклонение. Помните, что значения, используемые для расчета дисперсии, возведены в квадрат. Это означает, что отклонение не выражается в той же единице исходного значения. Стандартное отклонение требует извлечения квадратного корня из дисперсии, чтобы вернуть значение в исходную единицу. Таким образом, если данные были в килограммах, стандартное отклонение тоже.
Выбор между совокупностью и дисперсией выборки
В Excel есть два подтипа дисперсии с немного разными формулами. Какой из них выбрать, зависит от ваших данных. Если ваши данные включают всю «генеральную совокупность», вам следует использовать дисперсию генеральной совокупности. В этом случае «популяция» означает, что у вас есть все значения для каждого члена целевой группы населения.
Например, если вы посмотрите на вес левшей, то в популяцию войдут все левши на Земле. Если вы их все взвесите, вы воспользуетесь дисперсией населения.
Конечно, в реальной жизни мы обычно соглашаемся на меньшую выборку из большей совокупности. В этом случае вы должны использовать выборочную дисперсию. Дисперсия совокупности по-прежнему актуальна для небольших популяций. Например, в компании может быть несколько сотен или несколько тысяч сотрудников с данными о каждом сотруднике. Они представляют собой «население» в статистическом смысле.
Выбор правильной формулы дисперсии
В Excel есть три типовых формулы дисперсии и три формулы дисперсии генеральной совокупности:
- VAR, VAR.S и VARA для выборочной дисперсии.
- VARP, VAR.P и VARPA для дисперсии совокупности.
Вы можете игнорировать VAR и VARP. Они устарели и существуют только для совместимости с устаревшими электронными таблицами.
Остается VAR.S и VAR.P, которые предназначены для вычисления дисперсии набора числовых значений, а также VARA и VARPA, которые включают текстовые строки.
VARA и VARPA преобразуют любую текстовую строку в числовое значение 0, за исключением «ИСТИНА» и «ЛОЖЬ». Они преобразуются в 1 и 0 соответственно.
Самая большая разница в том, что VAR.S и VAR.P пропускают любые нечисловые значения. Это исключает эти случаи из общего количества значений, что означает, что среднее значение будет другим, потому что вы делите на меньшее количество случаев, чтобы получить среднее значение.
Все, что вам нужно для расчета дисперсии в Excel, — это набор значений. Мы собираемся использовать VAR.S в приведенном ниже примере, но формула и методы точно такие же, независимо от того, какую формулу дисперсии вы используете:
- Предполагая, что у вас есть готовый диапазон или дискретный набор значений, выберите пустую ячейку по вашему выбору.
- В поле формулы введите = VAR.S (XX: YY), где значения X и Y заменяются номерами первой и последней ячеек диапазона.
- Нажмите Enter, чтобы завершить расчет.
В качестве альтернативы вы можете указать конкретные значения, и в этом случае формула будет иметь вид = VAR.S (1,2,3,4). С числами, замененными на все, что вам нужно для расчета дисперсии. Вы можете ввести до 254 значений вручную таким образом, но если у вас есть только несколько значений, почти всегда лучше вводить данные в диапазоне ячеек, а затем использовать версию формулы, описанную выше, для диапазона ячеек.
Вы можете Excel в, Er, Excel
Вычисление дисперсии — полезный прием для тех, кому нужно выполнить статистическую работу в Excel. Но если какая-либо терминология Excel, которую мы использовали в этой статье, сбивала с толку, подумайте о том, чтобы ознакомиться с Руководством по основам Microsoft Excel — Обучение использованию Excel.
Если, с другой стороны, вы готовы к большему, ознакомьтесь с разделом «Добавить линию тренда линейной регрессии на точечную диаграмму Excel», чтобы вы могли визуализировать дисперсию или любой другой аспект вашего набора данных по отношению к среднему арифметическому.