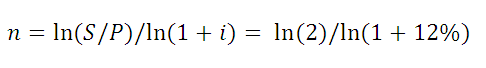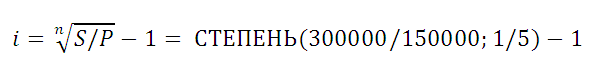Начисление процентов для вкладов в excel

Фиксируйте свои лучшие моменты с помощью наших премиум-шаблонов фотоальбомов.

СКАЧАТЬ ШАБЛОНЫ СЕЙЧАС.

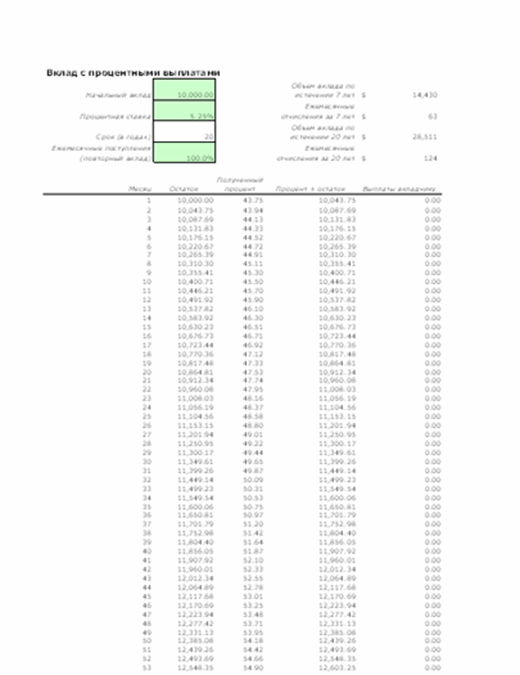
Таблица расчета процентных выплат по вкладу

Таблица расчета процентных выплат по вкладу

Excel

Скачать

Поделиться

Другие похожие шаблоны

Счет за услуги по присмотру за домашними животными

Excel

Отчет о прибылях и убытках за 1 год

Excel

Выписка по счету

Excel

Ипотечный калькулятор

Excel

Найдите вдохновение для вашего следующего проекта с тысячами идей на выбор

Адресные книги

Анимация и трехмерное оформление

Бизнес

Бизнес-планы

Бланки и общие шаблоны

Буклеты

Бюджеты

В дорогу

Весна

Визитные карточки

Временные шкалы

Все праздники

Выпускной

День рождения

Диаграммы

Для учебы

Документы и отчетность

Домашнее обучение

Еда и питание

Журналы

Запасы

Записки

Здоровье и фитнес

Зима

Игры и развлечения

Инфографика

Информационные бюллетени

Календари

Карты

Квитанции

Коммерческие предложения

Конверты

Лето

Листовки

Меню

Наклейки

Написание текстов

Образование

Обучение

Объявления

Опросы

Осень

Открытки

Письма

Плакаты

Планирование и учет

Платежные ведомости

Повестки

Подготовка

Поздравления

Презентации

Прибыль и убытки

Приглашения

Программы

Протоколы

Публикация

Расписания

Ребенок

Резюме и сопроводительные письма

Рождество

Свадьба

Семейные развлечения

Сертификаты

Снова в школу

Социальные сети

Списки

Схемы

Счета

Темы

Титульные страницы факсов

Украшения

Управление финансами

Фотоальбомы

Функция ЭФФЕКТ в Excel предназначена для расчета фактической годовой процентной ставки (иное название – эффективная ставка), на основе известных данных, таких как номинальная годовая ставка, число периодов начисления сложных процентов, и возвращает соответствующее числовое значение.

Примеры использования функции ЭФФЕКТ в Excel

Пример 1. Предприниматель получил ссуду в банковской организации на 1 год с эффективной процентной ставкой 23,5%. Определить значение номинальной ставки, если по условию договора выплаты по кредиту необходимо проводить ежемесячно.

Исходная таблица данных:

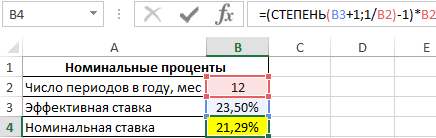
Связь между значениями эффективной и номинальной ставок описывается следующей формулой:

=(СТЕПЕНЬ(B3+1;1/B2)-1)*B2

Полученный результат:

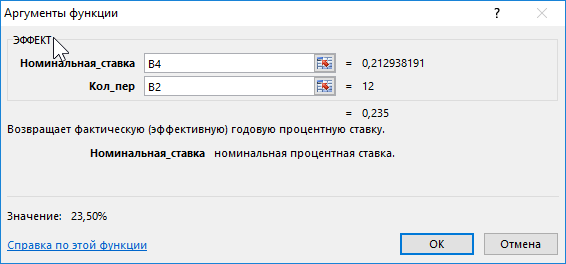
Проверим полученный результат, проведя пересчет эффективной ставки с помощью функции:

Описание аргументов:

• B4 – полученное выше числовое значение номинальной ставки;
• B2 – число периодов погашения.

Результат:

Полученное значение 0,235 соответствует 23,5% (значению эффективной ставки по условию). Расчет номинальной ставки также можно производить с помощью функции НОМИНАЛ.



Формула расчета процентов по вкладу в Excel

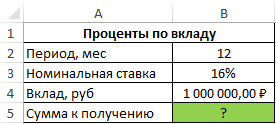
Пример 2. Вкладчику предложили сделать депозит в банк под 16% годовых (номинальная ставка), при этом расчете производится с использованием сложных процентов (эффективная ставка). По условиям договора вкладчик сможет снять только полученные проценты. Определить сумму к получению, если размер депозита – 1 млн. рублей, капитализация – ежемесячная.

Исходные данные:

Формула для расчета:

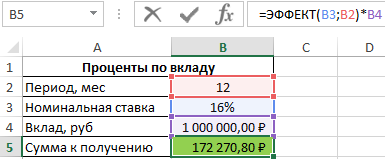
=ЭФФЕКТ(B3;B2)*B4

Описание аргументов:

• B2 – число периодов капитализации;
• B3 – номинальная ставка;
• B4 – сумма вклада.

Результат расчетов:

Для сравнения, доход от вклада при использовании простых процентов составил бы 1000000*0,16=160000 рублей, поэтому для вкладчика выгодно использовать предложенный вариант со сложными процентами.

Как посчитать проценты на депозит в Excel для выбора вклада

Пример 3. Два банка предлагают сделать депозитный вклад на одинаковую сумму (250000 рублей) на 1 год при следующих условиях:

1. Номинальная ставка – 24%, простые проценты, 12 периодов капитализации.
2. Номинальная ставка 22%, сложные проценты, начисляемые по итогам каждого периода, 4 периода капитализации.

Определить выгодный вариант, отобразить схему выплат.

Исходные данные:

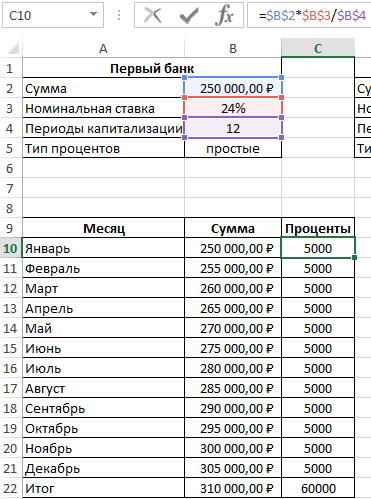
В первом случае таблица выплат выглядит так:

Проценты – постоянная величина, рассчитываемая по формуле:

=$B$2*$B$3/$B$4

Описание аргументов (для создания абсолютной ссылки используйте клавишу F4):

• $B$2 – начальная сумма вклада;
• $B$3 – годовая ставка;
• $B$4 – число периодов капитализации вклада.

Сумма накопленных средств за каждый период рассчитывается как как сумма средств на счету за прошедший период и процентов, начисленных за текущий период. В итоге первый банк начислит 60000 рублей процентов, и вкладчик сможет забрать 310000 рублей.

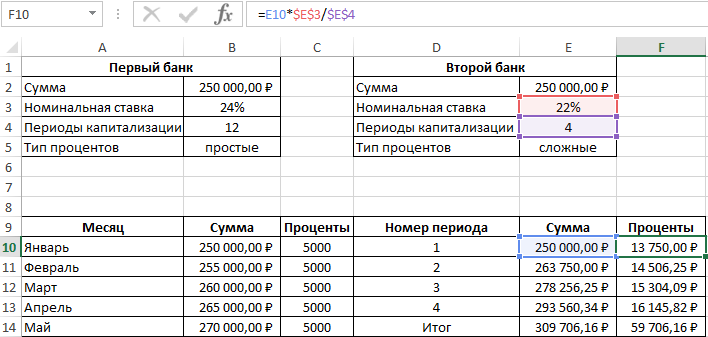
Таблица начисления процентов по условиям второго банка:

В данном случае проценты не являются фиксированной величиной и зависят от итоговой суммы накоплений за предыдущий период (поэтому ссылка на ячейку L2 – абсолютная):

=L3*$E$3/$E$4

При расчете суммы за каждый период к текущему значению необходимо прибавить проценты за предыдущий период.

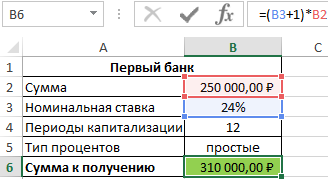
Для быстрого расчета итоговой суммы используем формулы:

1. Первый банк:



2. Второй банк:

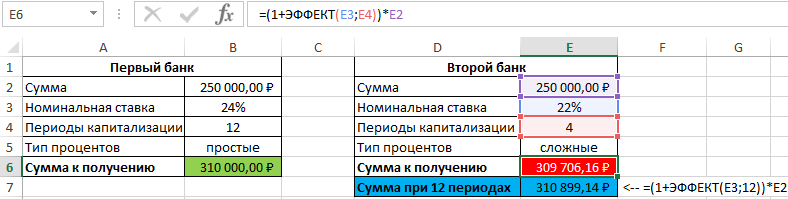
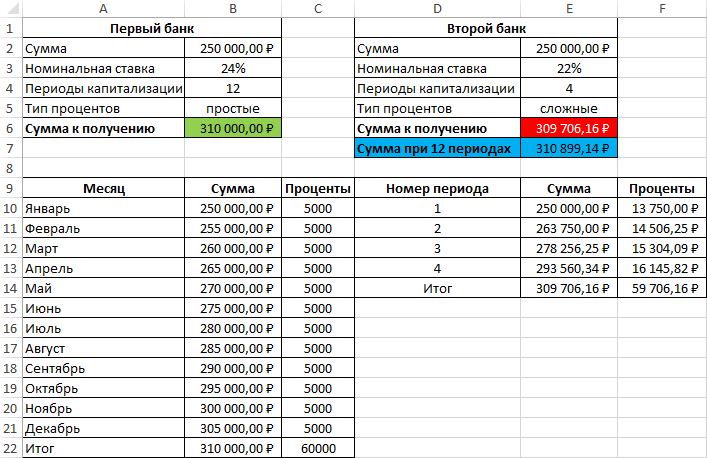
Результаты расчетов:

Несмотря на то, что второй банк предлагает расчет с использованием сложных процентов, предложение первого банка оказалось выгоднее. Если бы число периодов капитализации совпадало (12), во втором банке вкладчик получил бы 310899,1 рублей, то есть больше денег, несмотря на более низкую номинальную процентную ставку.

Особенности использования функции ЭФФЕКТ в Excel

Функция имеет следующий синтаксис:

=ЭФФЕКТ(номинальная_ставка;кол_пер)

Описание аргументов:

• номинальная_ставка – обязательный аргумент, характеризующий числовое (десятичная дробь) или процентное значение номинальной годовой ставки;
• кол_пер – обязательный аргумент, характеризующий числовое значения числа периодов за год, на протяжении которых начисляются сложные проценты.

Примечания 1:

1. Аргумент кол_пер может принимать дробные числа, значения которых будут усечены до целого числа (в отличие от операции округления, при усечении отбрасывается дробная часть).
2. Каждый из двух аргументов функции ЭФФЕКТ должен быть представлен числовым (или процентным для аргумента номинальная_ставка) значением либо текстовой строкой, которая может быть преобразована в число. При вводе не преобразуемых к числовым значениям текстовых строк и имен, а также данных логического типа функция ЭФФЕКТ будет возвращать код ошибки #ЗНАЧ!.
3. Аргумент номинальная_ставка принимает значения из диапазона положительных чисел, а кол_пер – из диапазона от 1 до +∞. Если данные условия не выполняются, например, функции =ЭФФЕКТ(0;12) или =ЭФФЕКТ(12%;0) вернут код ошибки #ЧИСЛО!.
4. Функция ЭФФЕКТ использует для расчетов формулу, которая может быть записана в Excel в виде: =СТЕПЕНЬ(1+(A1/A2);A2)-1, где:

• A1 – номинальная годовая ставка;
• A2 – число периодов, в которые происходит начисление сложных процентов.

Примечания 2:

• Для понимания термина «сложные проценты» рассмотрим пример. Владелец капитала предоставляет денежные средства в долг и планирует получить прибыль, величина которой зависит от следующих факторов: сумма средств, которая предоставляется в долг; длительность периода кредитования (использования предоставленных средств); начисляемые проценты за использование.
• Проценты могут начисляться различными способами: базовая сумма остается неизменной (простые проценты) и база изменяется при наступлении каждого последующего периода выплат (сложные). При использовании сложных процентов сумма задолженности (прибыли) увеличивается быстрее при одинаковых сумме и периоде кредитования, в сравнении с применением простых процентов (особенно, если периодов начисления процентов (капитализации) достаточно много.
• Для получения результата в формате процентов необходимо установить соответствующий формат данных в ячейке, в которой будет введена функция ЭФФЕКТ.

В предыдущем посте я обещала облегчить вашу учетную участь и рассказать вам о том, как обычный Excel может помочь с выбором депозита. Причем, выгодного вам, а не только банку. Обещала – выполняю. Следуя моей инструкции, вы легко сможете определить, какие условия по банковским вкладам принесут вам наибольший доход.

За расчет потенциальной доходности в Microsoft Excel отвечает специальная функция БС (Будущая Стоимость (Future Value (FV) – о ней мы говорили здесь). Для того, чтобы ее вызвать, нажмите на символ f _{x ,} слева от строки ввода значений и адресов ячеек.

В открывшемся Мастере функций в строке поиска функций введите БС и нажмите Ввод. Кликните мышью на подсвеченной синим цветом строке БС, как показано ниже.

Составляющим формулы расчета будущей стоимости FV = PV(1+r)ⁿ в Excel соответствуют следующие функции:

Общее название	Функция в Excel	Краткое описание
FV (Future Value)	БС (Будущая Стоимость)	Будущая сумма вклада
PV (Present Value)	ПС (Текущая Стоимость)	Текущая стоимость вклада
n	КПЕР (Количество Периодов)	Число периодов начисления процентов по вкладу
r	СТАВКА	Процентная ставка по вкладу

Заполняем (вручную или указав адреса соответствующих ячеек) поля данными из нашего примера. Напомню, что мы решили открыть депозит, разместив на нем 10 000 рублей сроком 5 лет и под 10% годовых.

Ставку по вкладу указываем в виде десятичной дроби, т.е. 10% превратятся в 0,1. В Кпер ставим количество лет – у нас вклад на 5 лет, значит 5. Поле Плт оставляем пустым. В поле ПС начальную сумму вклада указываем со знаком “минус”, т.к. мы эти деньги отдаем, а не получаем.

Поле Тип заполняем с учетом того, как производится выплата процентов по нашему вкладу:

• если в конце срока (на языке финансистов такой поток платежей называется постнумерандо), то ставим “0” или оставляем поле пустым;
• если в начале срока (на языке финансистов такой поток платежей называется пренумерандо), то ставим “1”.

В случае если проценты по вкладу начисляются ежемесячно или ежеквартально, то в поле Ставка годовую процентную ставку следует разделить на 12 или 4 соответственно в виде десятичной дроби. Вместе с этим нужно внести изменения в Кпер, пересчитав количество выплат: при ежемесячном начислении в течение 5 лет ставим 60 (12 мес. х 5 лет); при квартальном – 20 (4 кв. х 5 лет).

А теперь: внимание – вопрос. Как изменится доходность нашего вклада в случае начисления банком сложных процентов в конце каждого месяца, а не года, как мы считали до этого, на протяжении 5 лет? Давайте посмотрим. Напомню, до этого у нас получалась сумма в размере 16 105 руб. Заполняем поля и нажимаем “ОК”.

Получаем 16 453 рубля. Как видите, разница 343 рубля. А главное: чем больше сумма вашего вклада и время его размещения, тем ощутимей будет прибавка. Такова магия сложных процентов. Отсюда – вывод. Проценты по вашему вкладу должны:

• капитализироваться;
• капитализироваться ежемесячно.

Чем чаще начисляются проценты и добавляются к сумме вашего вклада, тем лучше работают ваши деньги. Кстати, хотите узнать, как скоро ваш вклад удвоится? Нет ничего проще. Воспользуйтесь правилом 72.

• Разделите число 72 на предлагаемую банком процентную ставку, и вы получите то число лет, которое нужно для увеличения ваших вложений в 2 раза.

А сейчас (барабанная дробь) испытайте чувство гордости за себя. Потому что теперь вы можете рассчитать это в Excel. Для этого вызовите функцию Кпер, заполните данные из нашего примера (10% годовых, 5 лет, выплата процентов в конце года) и добавьте в поле БС ожидаемую сумму вклада в размере 20 000 руб. (10 000 руб. х 2). Вуаля!

А еще есть правило волшебной двадцатки. Суть его в том, что для обеспечения завтра того уровня дохода, к которому вы привыкли сегодня, вам нужна сумма в 20 раз превышающая ваш годовой доход. Посчитайте и впечатлитесь полученной цифрой.

Но, как гласит народная мудрость, о деньгах и здоровье вспоминают тогда, когда они заканчиваются. И часто бывает так, что изменить что-либо уже поздно. Стоит ли рисковать? Когда все, что вам нужно сделать – это подумать о завтра сегодня.

• Если у вас есть вопросы, пишите их в комментариях ниже, я вам отвечу. Также вы всегда можете обратиться ко мне за консультацией, пройти мои курсы и вебинары.

Обучение торговле на бирже

Рассмотрим Сложный процент (Compound Interest) – начисление процентов как на основную сумму долга, так и на начисленные ранее проценты.

Немного теории

Владелец капитала, предоставляя его на определенное время в долг, рассчитывает на получение дохода от этой сделки. Размер ожидаемого дохода зависит от трех факторов: от величины капитала, предоставляемого в кредит, от срока, на который предоставлен кредит, и от величины ссудного процента или иначе процентной ставки.

Существуют различные методы начисления процентов. Основное их различие сводится к определению исходной суммы (базы), на которую начисляются проценты. Эта сумма может оставаться постоянной в течение всего периода или меняться. В зависимости от этого различают метод начисления по

простым

и сложным процентам.

При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования

простых процентов

изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент».

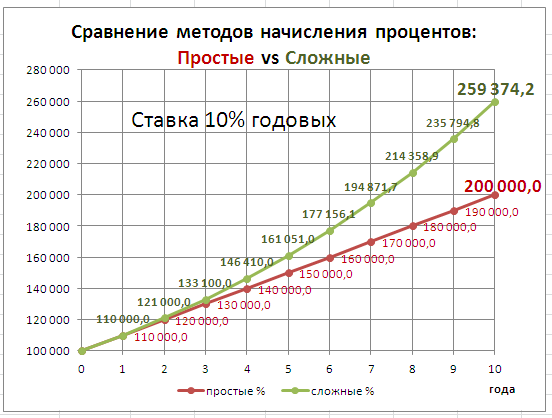
В

файле примера

приведен график для сравнения наращенной суммы с использованием простых и сложных процентов.

В этой статье рассмотрим начисление по сложным процентам в случае постоянной ставки. О переменной ставке в случае сложных процентов

читайте здесь

.

Начисление процентов 1 раз в год

Пусть первоначальная сумма вклада равна Р, тогда через один год сумма вклада с присоединенными процентами составит =Р*(1+i), через 2 года =P*(1+i)*(1+i)=P*(1+i)^2, через n лет – P*(1+i)^n. Таким образом, получим формулу наращения для сложных процентов: S = Р*(1+i)^n где S — наращенная сумма, i — годовая ставка, n — срок ссуды в годах, (1+ i)^n — множитель наращения.

Начисление процентов несколько раз в год

В рассмотренном выше случае капитализация производится 1 раз в год. При капитализации m раз в год формула наращения для сложных процентов выглядит так: S = Р*(1+i/m)^(n*m) i/m – это ставка за период. На практике обычно используют дискретные проценты (проценты, начисляемые за одинаковые интервалы времени: год (m=1), полугодие (m=2), квартал (m=4), месяц (m=12)).

В MS EXCEL вычислить наращенную сумму к концу срока вклада по сложным процентам можно разными способами.

Рассмотрим задачу

: Пусть первоначальная сумма вклада равна 20т.р., годовая ставка = 15%, срок вклада 12 мес. Капитализация производится ежемесячно в конце периода.

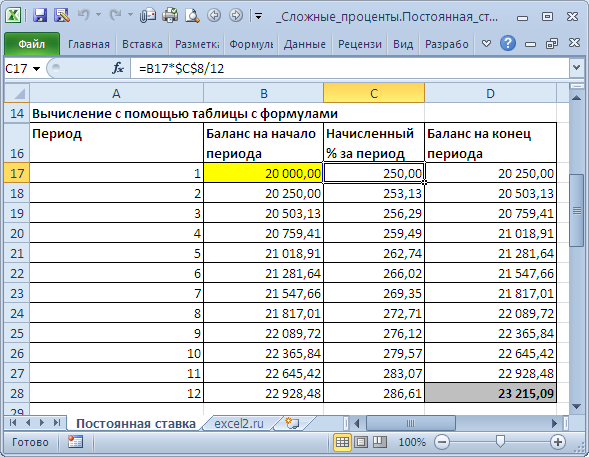
Способ 1. Вычисление с помощью таблицы с формулами

Это самый трудоемкий способ, но зато самый наглядный. Он заключается в том, чтобы последовательно вычислить величину вклада на конец каждого периода. В

файле примера

это реализовано на листе

Постоянная ставка

.

За первый период будут начислены проценты в сумме

=20000*(15%/12)

, т.к. капитализация производится ежемесячно, а в году, как известно, 12 мес. При начислении процентов за второй период, в качестве базы, на которую начисляются %, необходимо брать не начальную сумму вклада, а сумму вклада в конце первого периода (или начале второго). И так далее все 12 периодов.

Способ 2. Вычисление с помощью формулы Наращенных процентов

Подставим в формулу наращенной суммы S = Р*(1+i )^n значения из задачи. S = 20000*(1+15%/12)^12 Необходимо помнить, что в качестве процентной ставки нужно указывать ставку за период (период капитализации). Другой вариант записи формулы – через функцию

СТЕПЕНЬ()

=20000*СТЕПЕНЬ(1+15%/12; 12)

Способ 3. Вычисление с помощью функции БС().

Функция

БС()

позволяет определить

будущую стоимость

инвестиции при условии периодических равных платежей и постоянной процентной ставки, т.е. она предназначена прежде всего для расчетов в случае

аннуитетных платежей

. Однако, опустив 3-й параметр (ПЛТ=0), можно ее использовать и для расчета сложных процентов.

=-БС(15%/12;12;;20000)

Или так

=-БС(15%/12;12;0;20000;0)

Примечание .

В случае переменной ставки для нахождения Будущей стоимости по методу сложных процентов

используется функция

БЗРАСПИС()

.

Определяем сумму начисленных процентов

Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. на 5 лет с ежегодным начислением сложных процентов по ставке 12 % годовых. Определить сумму начисленных процентов.

Сумма начисленных процентов I равна разности между величиной  наращенной суммы S и начальной суммой Р. Используя формулу для определения наращенной суммы S = Р*(1+i )^n, получим: I = S – P= Р*(1+i)^n – Р=P*((1+i)^n –1)=150000*((1+12%)^5-1) Результат: 114 351,25р. Для сравнения: начисление по простой ставке даст результат 90 000р. (см.

файл примера

).

Определяем Срок долга

Рассмотрим задачу: Клиент банка положил на депозит некую сумму с ежегодным начислением сложных процентов по ставке 12 % годовых. Через какой срок сумма вклада удвоится? Логарифмируя обе части уравнения S = Р*(1+i)^n, решим его относительно неизвестного параметра n.

В

файле примера

приведено решение, ответ 6,12 лет.

Вычисляем ставку сложных процентов

Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. с ежегодным начислением сложных процентов. При какой годовой ставке сумма вклада удвоится через 5 лет?

В

файле примера

приведено решение, ответ 14,87%.

Примечание

. Об эффективной ставке процентов

читайте в этой статье

.

Учет (дисконтирование) по сложным процентам

Дисконтирование основывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Рассмотрим 2 вида учета: математический и банковский.

Математический учет

. В этом случае решается задача обратная наращению по сложным процентам, т.е. вычисления производятся по формуле Р=S/(1+i )^n Величину Р, полученную дисконтированием S, называют современной, или текущей стоимостью, или приведенной величиной S. Суммы Р и S эквивалентны в том смысле, что платеж в сумме S через n лет равноценен сумме Р, выплачиваемой в настоящий момент. Здесь разность D = S — P называется дисконтом.

Пример

. Через 7 лет страхователю будет выплачена сумма 2000000 руб. Определить современную стоимость суммы при условии, что применяется ставка сложных процентов в 15% годовых. Другими словами, известно: n = 7 лет, S = 2 000 000 руб., i = 15% .

Решение. P = 2000000/(1+15% )^7 Значение текущей стоимости будет меньше, т.к. открыв

сегодня

вклад на сумму Р с ежегодной капитализацией по ставке 15% мы получим через 7 лет сумму 2 млн. руб.

Тот же результат можно получить с помощью формулы

=ПС(15%;7;;-2000000;1)

Функция

ПС()

возвращает приведенную (к текущему моменту) стоимость инвестиции и

рассмотрена здесь

.

Банковский учет

. В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле: Р = S*(1- dсл )^n где dcл — сложная годовая учетная ставка.

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.

Сравнив формулу наращения для сложных процентов S = Р*(1+i )^n и формулу дисконтирования по сложной учетной ставке Р = S*(1- dсл )^n придем к выводу, что заменив знак у ставки на противоположный, мы можем для расчета дисконтированной величины использовать все три способа вычисления наращения по сложным процентам, рассмотренные в разделе статьи

Начисление процентов несколько раз в год

.

Расчет сложных процентов в случае регулярного пополнения вклада

В

файле примера

(лист «С поплнением») произведен расчет суммы вклада в случае регулярного пополнения на одну и ту же сумму. Для этого использована функция

БС()

.

Если сумма вклада пополняется нерегулярно и/или различными платежами, то для расчета необходимо использовать таблицу, которая также приведена в файле примера. Естественно, в случае регулярных и равновеликих платежей итоговые суммы вычисленные с помощью таблицы и функции БС() — совпадают.

Как при помощи Excel провести вычисление будущей стоимости платежей и суммы банковского вклада

Будущая стоимость является оборотной стороной временных изменений денег. Будущая стоимость говорит о том, сколько будет стоить известная сумма денег (или известная серия выплат) через некоторый промежуток времени. Синтаксис функции БС следующий: БС(ставка;кпер;плт;пс;тип) .

Будущая стоимость платежей

В этом примере мы предположим, что открыли накопительный счет для своего ребенка, чтобы к окончанию школы насобирать ему сумму, необходимую для платного обучения в университете. Начиная со следующего месяца, вы будете ежемесячно откладывать 50 долларов на этот счет под 3% годовых. Следующая формула показывает, что к совершеннолетию у вашего сына на счету будет 14297,02 долларов (рис. 1): =БС(,03/12;18*12;-50;0;0) .

Рис. 1. Вычисление будущей суммы платежей

Годовую процентную ставку 3% мы преобразуем в месячную; 18 лет также преобразуем в месяцы. Приведенная стоимость отсутствует, так как вы только что открыли счет. Аргумент Тип равен нулю, так как вносить суммы вы начинаете со следующего месяца.

Будущая стоимость суммы вклада

В следующем примере вычисляется будущая стоимость суммы денег, которая не будет пополняться, и с нее не будут сниматься деньги. Предположим, что вы открыли пенсионный счет, внесли на него 20 тысяч долларов и планируете через 15 лет выйти на пенсию (рис. 2): =БС(,08;15;0;-20000;0) .

Рис. 2. Вычисление будущей стоимости вклада

В данном примере предполагается, что пенсионный вклад гарантирует получение 8% годовых. Значение -20000 представляет двадцать тысяч долларов, уходящих от вас в банк. В результате мы получаем 63443,38 долларов — эту сумму вы получите через 15 лет при выходе на пенсию.

Округление в финансовых формулах

При использовании финансовых формул проблема округления значений ощущается особенно остро. Excel предлагает несколько функций для выполнения этой задачи: ОКРУГЛ, ОКРУГЛВНИЗ И ОКРУГЛВВЕРХ. Чтобы предотвратить накопительные ошибки, округляйте только конечный получаемый результат. Другими словами, избегайте округления промежуточных данных. Обычно результаты финансовых расчетов отображаются в виде чисел с двумя десятичными разрядами или вообще без таковых. В промежуточных расчетах это предполагает получение результатов с точностью до цента или доллара.

В отдельных случаях вычисления базируются на приблизительных данных или данных, полученных в результате эмпирического анализа или подбора параметров. Поэтому уже давно обычной практикой стало применение округленных значений (чтобы не утруждать себя вводом длинных значений). Предположим, что вы арендуете торговое помещение площадью 1537 квадратных метров по цене 43,55 долларов за квадратный метр. Простое умножение приводит к получению суммы $66936,35.

Однако вы знаете, что арендная плата может изменяться (скажем, в диапазоне от 42 до 45 долларов). В результате конечная сумма аренды будет колебаться в небольших пределах. Чтобы избежать излишней неточности, конечную сумму можно округлить до ближайших ста или даже тысячи долларов. Одна из потенциальных опасностей, привнесенная современными технологиями, — это быть обманутым видимой точностью на самом деле приблизительных оценок.

Будущая стоимость платежей и суммы вклада

Также можно вычислить будущую стоимость и уже существующего вклада, на который периодически будут добавляться (или сниматься) деньги. В предлагаемом примере мы собираемся вносить ежемесячные платежи в сумме 900 долларов по закладной на сумму 150 тысяч долларов. Процентная ставка составляет 5,75% годовых. Следующая формула вычисляет, сколько мы останемся должны через пять лет: =БС(,0575/12;5*12;-900;150000;0) .

Платежи вносятся ежемесячно, поэтому все остальные аргументы мы соотносим с месяцами — количество лет умножается, а процентная ставка делится на 12. Текущий баланс показан как приход денег, хотя на самом деле они не поступают в настоящий момент — это движение было, когда мы изначально покупали дом. Так как область определения задачи распространяется на пять будущих лет, начиная с текущего момента, совершенно не имеет значения, когда на самом деле был выполнен начальный платеж.

Лучше представить себе данную задачу следующим образом. Некто одолжил вам 150 тысяч долларов, чтобы выкупить закладную на дом, хотя на самом деле этого не произошло. Вычисленное значение — 137435,10 — это сумма выходного потока по истечении пяти лет.

Источник

Функция ЭФФЕКТ для расчета годовой процентной ставки в Excel

Функция ЭФФЕКТ в Excel предназначена для расчета фактической годовой процентной ставки (иное название – эффективная ставка), на основе известных данных, таких как номинальная годовая ставка, число периодов начисления сложных процентов, и возвращает соответствующее числовое значение.

Примеры использования функции ЭФФЕКТ в Excel

Пример 1. Предприниматель получил ссуду в банковской организации на 1 год с эффективной процентной ставкой 23,5%. Определить значение номинальной ставки, если по условию договора выплаты по кредиту необходимо проводить ежемесячно.

Исходная таблица данных:

Связь между значениями эффективной и номинальной ставок описывается следующей формулой:

Проверим полученный результат, проведя пересчет эффективной ставки с помощью функции:

• B4 – полученное выше числовое значение номинальной ставки;
• B2 – число периодов погашения.

Полученное значение 0,235 соответствует 23,5% (значению эффективной ставки по условию). Расчет номинальной ставки также можно производить с помощью функции НОМИНАЛ.

Формула расчета процентов по вкладу в Excel

Пример 2. Вкладчику предложили сделать депозит в банк под 16% годовых (номинальная ставка), при этом расчете производится с использованием сложных процентов (эффективная ставка). По условиям договора вкладчик сможет снять только полученные проценты. Определить сумму к получению, если размер депозита – 1 млн. рублей, капитализация – ежемесячная.

Формула для расчета:

• B2 – число периодов капитализации;
• B3 – номинальная ставка;
• B4 – сумма вклада.

Для сравнения, доход от вклада при использовании простых процентов составил бы 1000000*0,16=160000 рублей, поэтому для вкладчика выгодно использовать предложенный вариант со сложными процентами.

Как посчитать проценты на депозит в Excel для выбора вклада

Пример 3. Два банка предлагают сделать депозитный вклад на одинаковую сумму (250000 рублей) на 1 год при следующих условиях:

1. Номинальная ставка – 24%, простые проценты, 12 периодов капитализации.
2. Номинальная ставка 22%, сложные проценты, начисляемые по итогам каждого периода, 4 периода капитализации.

Определить выгодный вариант, отобразить схему выплат.

В первом случае таблица выплат выглядит так:

Проценты – постоянная величина, рассчитываемая по формуле:

Описание аргументов (для создания абсолютной ссылки используйте клавишу F4):

• $B$2 – начальная сумма вклада;
• $B$3 – годовая ставка;
• $B$4 – число периодов капитализации вклада.

Сумма накопленных средств за каждый период рассчитывается как как сумма средств на счету за прошедший период и процентов, начисленных за текущий период. В итоге первый банк начислит 60000 рублей процентов, и вкладчик сможет забрать 310000 рублей.

Таблица начисления процентов по условиям второго банка:

В данном случае проценты не являются фиксированной величиной и зависят от итоговой суммы накоплений за предыдущий период (поэтому ссылка на ячейку L2 – абсолютная):

При расчете суммы за каждый период к текущему значению необходимо прибавить проценты за предыдущий период.

Для быстрого расчета итоговой суммы используем формулы:

1. Первый банк:
2. Второй банк:

Несмотря на то, что второй банк предлагает расчет с использованием сложных процентов, предложение первого банка оказалось выгоднее. Если бы число периодов капитализации совпадало (12), во втором банке вкладчик получил бы 310899,1 рублей, то есть больше денег, несмотря на более низкую номинальную процентную ставку.

Особенности использования функции ЭФФЕКТ в Excel

Функция имеет следующий синтаксис:

• номинальная_ставка – обязательный аргумент, характеризующий числовое (десятичная дробь) или процентное значение номинальной годовой ставки;
• кол_пер – обязательный аргумент, характеризующий числовое значения числа периодов за год, на протяжении которых начисляются сложные проценты.

1. Аргумент кол_пер может принимать дробные числа, значения которых будут усечены до целого числа (в отличие от операции округления, при усечении отбрасывается дробная часть).
2. Каждый из двух аргументов функции ЭФФЕКТ должен быть представлен числовым (или процентным для аргумента номинальная_ставка) значением либо текстовой строкой, которая может быть преобразована в число. При вводе не преобразуемых к числовым значениям текстовых строк и имен, а также данных логического типа функция ЭФФЕКТ будет возвращать код ошибки #ЗНАЧ!.
3. Аргумент номинальная_ставка принимает значения из диапазона положительных чисел, а кол_пер – из диапазона от 1 до +∞. Если данные условия не выполняются, например, функции =ЭФФЕКТ(0;12) или =ЭФФЕКТ(12%;0) вернут код ошибки #ЧИСЛО!.
4. Функция ЭФФЕКТ использует для расчетов формулу, которая может быть записана в Excel в виде: =СТЕПЕНЬ(1+(A1/A2);A2)-1, где:

• A1 – номинальная годовая ставка;
• A2 – число периодов, в которые происходит начисление сложных процентов.

• Для понимания термина «сложные проценты» рассмотрим пример. Владелец капитала предоставляет денежные средства в долг и планирует получить прибыль, величина которой зависит от следующих факторов: сумма средств, которая предоставляется в долг; длительность периода кредитования (использования предоставленных средств); начисляемые проценты за использование.
• Проценты могут начисляться различными способами: базовая сумма остается неизменной (простые проценты) и база изменяется при наступлении каждого последующего периода выплат (сложные). При использовании сложных процентов сумма задолженности (прибыли) увеличивается быстрее при одинаковых сумме и периоде кредитования, в сравнении с применением простых процентов (особенно, если периодов начисления процентов (капитализации) достаточно много.
• Для получения результата в формате процентов необходимо установить соответствующий формат данных в ячейке, в которой будет введена функция ЭФФЕКТ.

Источник

Депозитный калькулятор вкладов в Excel. Расчет доходности вкладов

Почему важно иметь под рукой калькулятор вкладов

Если вы думаете сделать вклад, то важно понять, какой доход вы получите к концу срока. Кроме того, важно понимать какая сумма процентов будет выплачиваться каждый месяц. Эти проценты можно тратить и деньги будут работать на вас.

Еще одной важной причиной держать калькулятор вкладов всегда под рукой является необходимость проверки вашего банка. Банк не всегда верно считает и выплачивает проценты по вкладу. Чтоб проверить банк, нужно иметь независимый инструмент для расчета дохода по депозиту.

? Скачать калькулятор вкладов в Excel

Ссылка на калькулятор представлена ниже.
Данный калькулятор подходит для расчета вкладов ВТБ, Сбербанка, банка Тинькофф, Райффайзенбанка и других банков РФ.
Скачать калькулятор в Excel можно по ссылке Калькулятор вкладов Excel.

Профессиональные калькуляторы вкладов

Мы рекомендуем скачать себе на телефон профессиональные мобильные калькуляторы вкладов.
Ниже представлены 2 калькулятора вкладов, которые можно установить на свой телефон. После их установки не нужен Excel. Да и расчёт получается точнее, т.к. есть учёт курсов валют и ключевой ставки ЦБ.

Бесплатный калькулятор вкладов для Windows 10

• Точный расчет вклада любого банка РФ
• Учет пополнений и снятий
• Возможность посчитать несколько вкладов
• Абсолютно бесплатен
• Понятная и подробная статистика
• Возможность учесть фиксированную и плавающую ставку, неснижаемый остаток, макс. дату пополнения

Банковский калькулятор вкладов для Андроид

• Подходит для расчета вкладов любого банка: Тинькофф, Сбербанка, ВТБ, МКБ
• Учитывает при расчете налоги и ставку рефинансирования
• Есть возможность задать пополнения и снятия
• Удобный график выплат и возможность посмотреть ваш доход на сегодня
• Возможность учитывать несколько вкладов и знать сколько денег всего

Основные возможности, которые предоставляет калькулятор вкладов в Excel

1. Расчет вклада с помесячной и годовой капитализацией
2. Расчет валютных и рублевых вкладов.
3. Расчет суммы вклада в конце срока
4. Расчет процентов по вкладу.
5. Учет налогов, если ставка по вкладу превышает ставку, установленную ЦБ.
6. Достоинства данного калькулятора — что его можно использовать офлайн, т.е. без выхода в интернет.

Калькулятор вкладов онлайн — расчет вкладов со множеством параметров.

Калькулятор вкладов поможет вам правильно выбрать вклад. Просто нужно посчитать и сравнить несколько вкладов. Доходность какого будет лучше, тот и выбрать.
Если у вас один рублевый вклад, а один валютный, то придется провести конверсию по курсу ЦБ.

Также доступна онлайн версия депозитного калькулятора — калькулятор вкладов онлайн

Онлайн версия калькулятора является достаточно точной и позволяет посчитать различные вклады при различных условиях. К примеру вклады могут иметь плавающую ставку в зависимости от сроков — чем больше срок, тем выше ставка.

Калькулятор позволяте получить результаты расчета в Excel файле. Это полноценный Excel 2003. Можно распечатать ваши расчеты для похода в банк.
Все это можно рассчитать с помощью онлайн версии кредитного калькулятора, просто задаете номер дня и новую ставку.

Далее нажимаем рассчитать и получаем график платежей по вкладу и сумму к получению. Аналогично, если сумма вклада зависит от суммы — устанавливаем переключатель «Плавающая в зависимости от размера» для процентной ставки. Отдельный интерес составляет учет налогов — все вклады, ставка по которым превышает ставку рефинансирования ЦБ + 5 процентов. Для них происходит начисление налога по вкладу в размере 35 процентов от налогооблогаемой части.

Читайте также: Налоги на вклад: как они начисляются? Пример расчета
Следует отменить, что с налогов по ставке 35 процентов нельзя получить налоговый вычет на ипотеку, т.е. хотя это налоги на ваши доходы, которые являются официальными. Банк сам отчисляет налог и автоматически уменьшает доход по вкладу на сумму налогов.

Однако нужно внимательно проверять банк — рассчитывать вклад с помощю указанного выше депозитного калькулятора. Оставляйте свои пожелания к калькулятору вкладов. Все ваши пожелания будут учитываться в доработках .

Популярные вопросы по вкладам

На новую сумму вклада начисляются проценты. Значит в следующем месяце вы получите больше.

Источник