В статистике есть целый набор показателей, которые характеризуют центральную тенденцию. Выбор того или иного индикатора в основном зависит от характера данных, целей расчетов и его свойств.
Что подразумевается под характером данных? Прежде всего, мы говорим о количественных данных, которые выражены в числах. Но набор числовых данных может иметь разное распределение. Под распределением понимаются частоты отдельных значений. К примеру, в классе из 23 человек 2 школьника написали контрольную работу на двойку, 5 – на тройку, 10 – на четверку и 6 – на пятерку. Это и есть распределение оценок. Распределение очень наглядно можно представить с помощью специальной диаграммы – гистограммы. Для данного примера получится следующая гистограмма.
Во многих случаях количество уникальных значений намного больше, а распределение похоже на нормальное. Ниже приведена примерная иллюстрация нормального распределения случайных чисел.
Итак, центральная тенденция. Если частоты анализируемых значений распределены по нормальному закону, то есть симметрично вокруг некоторого центра, то центральная тенденция определяется вполне однозначно – это есть тот самый центр, и математически он соответствует средней арифметической.
Как нетрудно заметить, в этом же центре находится и максимальная частота значений. То есть при нормальном распределении центральная тенденция есть не только средняя арифметическая, но и максимальная частота, которая в статистике называется модой или модальным значением.
На диаграмме оба значения центральной тенденции совпадают и равны 10.
Но такое распределение встречается далеко не всегда, а при малом числе данных – совсем редко. Чаще бывает так, что частоты распределяются асимметрично. Тогда мода и среднее арифметическое не будут совпадать.
На рисунке выше среднее арифметическое по-прежнему составляет 10, а вот мода уже равна 9. Что в таком случае считать значением центральной тенденции? Ответ зависит от поставленных целей анализа. Если интересует уровень, сумма отклонений от которого равна нулю со всеми вытекающим отсюда свойствами и последствиями, то это средняя арифметическая. Если нужно максимально частое значение, то это мода.
Итак, зачем нужна мода? Приведу пару примеров. Экономист планово-экономического отдела обувной фабрики интересуется, какой размер обуви пользуется наибольшим спросом. Средний размер обуви, скорее всего, здесь не подойдет, тем более, что число может получится дробным. А вот мода – как раз нужный показатель.
Расчет моды
Теперь посмотрим, как рассчитать моду. Мода – это то значение в анализируемой совокупности данных, которое встречается чаще других, поэтому нужно посмотреть на частоты значений и отыскать максимальное из них. Например, в наборе данных 3, 4, 6, 7, 3, 5, 3, 4 модой будет значение 3 – повторяется чаще остальных. Это в дискретном ряду, и здесь все просто. Если данных много, то моду легче всего найти с помощью соответствующей гистограммы. Бывает так, что совокупность данных имеет бимодальное распределение.
Без диаграммы очень трудно понять, что в данных не один, а два центра. К примеру, на президентских выборах предпочтения сельских и городских жителей могут отличаться. Поэтому распределение доли отданных голосов за конкретного кандидата может быть «двугорбым». Первый «горб» – выбор городского населения, второй – сельского.
Немного сложнее с интервальными данными, когда вместо конкретных значений имеются интервалы. В этом случае говорят о модальном интервале (при анализе доходов населения, например), то есть интервале, частота которого максимальна относительно других интервалов. Однако и здесь можно отыскать конкретное модальное значение, хотя оно будет условным и примерным, так как нет точных исходных данных. Представим, что есть следующая таблица с распределением цен.
Для наглядности изобразим соответствующую диаграмму.
Требуется найти модальное значение цены.
Вначале нужно определить модальный интервал, который соответствует интервалу с наибольшей частотой. Найти его так же легко, как и моду в дискретном ряду. В нашем примере это третий интервал с ценой от 301 до 400 руб. На графике – самый высокий столбец. Теперь нужно определить конкретное значение цены, которое соответствует максимальному количеству. Точно и по факту сделать это невозможно, так как нет индивидуальных значений частот для каждой цены. Поэтому делается допущение о том, что интервалы выше и ниже модального в зависимости от своей частоты имеют разные вес и как бы перетягивают моду в свою сторону. Если частота интервала следующего за модальным больше, чем частота интервала перед модальным, то мода будет правее середины модального интервала и наоборот. Давайте еще раз посмотрим на рисунок, чтобы понять формулу, которую я напишу чуть ниже.
На рисунке отчетливо видно, что соотношение высоты столбцов, расположенных слева и справа от модального определяет близость моды к левому или правому краю модального интервала. Задача по расчету модального значения состоит в том, чтобы найти точку пересечения линий, соединяющих модальный столбец с соседними (как показано на рисунке пунктирными линиями) и нахождении соответствующего значения признака (в нашем примере цены). Зная основы геометрии (7-й класс), по данному рисунку нетрудно вывести формулу расчета моды в интервальном ряду.
Формула моды имеет следующий вид.
Где Мо – мода,
x0 – значение начала модального интервала,
h – размер модального интервала,
fМо – частота модального интервала,
fМо-1 – частота интервала, находящего перед модальным,
fМо1 – частота интервала, находящего после модального.
Второе слагаемое формулы моды соответствует длине красной линии на рисунке выше.
Рассчитаем моду для нашего примера.
Таким образом, мода интервального ряда представляет собой сумму, состоящую из значения начального уровня модального интервала и отрезка, который определяется соотношением частот ближайших интервалов от модального.
Расчет моды в Excel
В настоящее время большинство вычислений делается в MS Excel, где для расчета моды также предусмотрена специальная функция. В Excel 2013 я таких нашел ажно 3 штуки.
МОДА – пережиток старых изданий Excel. Функция оставлена для совмещения со старыми версиями.
МОДА.ОДН – рассчитывает моду по заданным значениям. Здесь все просто. Вставили функцию, указали диапазон данных и «Ок».
МОДА.НСК – позволяет рассчитать сразу несколько модальных значений (одинаковых максимальных частот) для одного ряда данных, если они есть. Функцию нужно вводить как формулу массива, перед этим выделив количество ячеек равное количеству требуемых модальных значений. Иногда действительно модальных значений может быть несколько. Однако для этих целей предварительно лучше посмотреть на диаграмму распределения.
Моду для интервальных данных одной функцией в Excel рассчитать нельзя. То есть такая функция в готовом виде не предусмотрена. Придется прописывать вручную.
Следующая статья посвящена медиане.
До встречи на statanaliz.info.
Поделиться в социальных сетях:
- Гистограмма в Excel
Диаграмма гистограммы (Содержание)
- Гистограмма в Excel
- Почему гистограмма важна в Excel?
- Типы / формы гистограммы
- Где находится гистограмма?
- Как создать гистограмму в Excel?
Гистограмма в Excel
Если мы хотим увидеть, как часто каждое значение встречается в наборе данных. Гистограмма — это наиболее часто используемый график, показывающий распределение частот.
Что такое гистограмма в Excel?
Гистограмма — это графическое представление распределения числовых данных. Проще говоря, гистограмма — это столбчатая диаграмма, которая показывает частоту данных в определенном диапазоне. Он обеспечивает визуализацию числовых данных, используя количество точек данных, попадающих в указанный диапазон значений (также называемых «ячейками»).
Диаграмма гистограммы в Excel классифицируется или состоит из 5 частей:
- Заголовок: заголовок описывает информацию о гистограмме.
- Ось X: Ось X — это сгруппированные интервалы, которые показывают шкалу значений, в которых находятся измерения.
- Ось Y: Ось Y — это шкала, показывающая, сколько раз значения, полученные в заданных интервалах, соответствуют оси X.
- Бары: этот параметр имеет высоту и ширину. Высота столбца показывает, сколько раз значения были получены в течение интервала. Ширина полос показывает интервал или расстояние или область, которая покрыта.
- Легенда: предоставляет дополнительную информацию об измерениях.
Почему гистограмма важна в Excel?
Есть много преимуществ использования гистограммы в Excel.
- Гистограмма диаграммы показывает визуальное представление распределения данных.
- Гистограмма диаграммы отображает большой объем данных и вхождение значений данных.
- Легко определить медиану и распределение данных.
Типы / формы гистограммы
В зависимости от распределения данных гистограмма может быть следующего типа:
- Нормальное распределение
- Бимодальное Распределение
- Правильно перекошенное распределение
- Распределение влево
- Случайное распределение
Теперь мы объясним одну за другой формы гистограммы в Excel.
Нормальное распределение:
Это также известно как распределение в форме колокола. При нормальном распределении, точки с такой же вероятностью встречаются на одной стороне от среднего, как и на другой стороне. Это похоже на изображение ниже:
Бимодальное Распределение:
Это также называется распределением с двумя пиками. В этом расст. Есть два пика. При таком распределении в одном наборе данных объединяются результаты двух процессов с разными распределениями. Данные разделяются и анализируются как нормальное распределение. Это похоже на изображение ниже:
Правильно перекошенное распределение:
Это также называется положительно перекошенным распределением. В этом распределении, большое количество значений данных встречается на левой стороне и меньшее количество значений данных на правой стороне. Это распределение происходит, когда данные имеют границу диапазона в левой части гистограммы. Например, граница 0. Это расст. выглядит как на картинке ниже:
Распределение по левому краю:
Это также называется отрицательно перекошенным распределением. В этом распределении большое количество значений данных встречается справа, а меньшее количество значений данных — слева. Это распределение происходит, когда данные имеют границу диапазона в правой части гистограммы. Например, граница, такая как 100. Это расст. выглядит как на картинке ниже:
Случайное распределение:
Это также называется мультимодальным распределением. В этом случае несколько процессов с нормальным распределением объединяются. Это имеет несколько пиков, поэтому данные должны быть разделены и проанализированы отдельно. Это расст выглядит как на картинке ниже:
Где гистограмма находится в Excel?
Параметр диаграммы гистограммы находится в наборе инструментов анализа. Пакет инструментов анализа представляет собой надстройку для анализа данных Microsoft Excel. Эта надстройка не загружается автоматически в Excel. Прежде чем использовать это, мы должны загрузить его в первую очередь.
Действия по загрузке надстройки Analysis ToolPak:
- Нажмите на вкладку Файл. Нажмите кнопку «Параметры».
- Откроется диалоговое окно «Параметры Excel». Нажмите на кнопку Надстройки на левой боковой панели.
- Откроется диалоговое окно надстроек ниже.
- Выберите параметр «Надстройки Excel» в поле «Управление» и нажмите кнопку « Перейти» .
- Откроется диалоговое окно «Надстройки».
- Выберите поле «Пакет инструментов анализа» и нажмите кнопку « ОК» .
- Пакет инструментов для анализа теперь загружен в Excel и будет доступен на вкладке ДАННЫЕ с названием «Анализ данных».
Примечание. Если возникает ошибка, так как пакет Analysis ToolPak в настоящее время не установлен на вашем компьютере, нажмите кнопку «Да», чтобы установить его.
Как создать гистограмму в Excel?
Перед созданием диаграммы гистограммы в Excel мы должны создать ячейки в отдельном столбце.
Контейнеры — это числа, представляющие интервалы, в которые мы хотим сгруппировать набор данных. Эти интервалы должны быть последовательными, не перекрывающимися и иметь одинаковый размер.
Существует два способа создания гистограммы в Excel:
- Если вы работаете в Excel 2016, есть опция встроенной гистограммы.
- Если вы работаете с Excel 2013, 2010 или более ранней версией, вы можете создать гистограмму, используя Data Analysis ToolPak.
Создание диаграммы гистограммы в Excel 2016:
- В Excel 2016, в разделе диаграммы, опция диаграммы гистограммы добавляется как встроенная диаграмма.
- Выберите весь набор данных.
- Нажмите вкладку INSERT.
- В разделе «Графики» нажмите «Вставить статическую диаграмму».
- В разделе ГИСТОГРАММА щелкните значок диаграммы ГИСТОГРАММА.
- Гистограмма будет отображаться на основе вашего набора данных.
- Вы можете выполнить форматирование, щелкнув правой кнопкой мыши диаграмму на вертикальной оси и выбрав опцию Форматировать ось.
Создание диаграммы гистограммы в Excel 2013, 2010 или более ранней версии:
Загрузите пакет анализа данных, как показано в приведенных выше шагах. Вы также можете активировать этот ToolPak в версии Excel 2016.
Примеры гистограммы в Excel
Гистограмма в Excel очень проста и удобна в использовании. Давайте разберемся с работой гистограммы в Excel с некоторыми примерами.
Вы можете скачать этот шаблон гистограммы Excel здесь — Шаблон гистограммы Excel
Пример № 1
Давайте создадим набор баллов (из 100) 30 студентов, как показано ниже:
Для создания гистограммы нам нужно создать интервалы, с которыми мы хотим найти частоту. Эти интервалы называются мусорными ведрами.
Ниже приведены интервалы или интервалы оценки для вышеуказанного набора данных.
Для создания диаграммы гистограммы в Excel выполните следующие действия:
- Нажмите на вкладку ДАННЫЕ.
- Теперь перейдите на вкладку «Анализ» с крайней правой стороны. Нажмите на вариант анализа данных.
- Откроется диалоговое окно «Анализ данных». Выберите опцию «Гистограмма» и нажмите «ОК».
- Откроется диалоговое окно гистограммы.
- В диалоговом окне «Гистограмма» мы введем следующие данные:
Выберите диапазон ввода (в соответствии с нашим примером — с колонкой баллов B)
Выберите диапазон корзины (столбец интервалов D)
- Если вы хотите включить заголовки столбцов в диаграмму, нажмите «Метки». В противном случае оставьте флажок снятым.
- Нажмите на Выходной диапазон. Если вы хотите получить гистограмму на том же листе, укажите адрес ячейки или нажмите «Новый лист».
- Выберите параметр вывода диаграммы и нажмите ОК.
- Это создаст таблицу распределения частот и диаграмму гистограммы в указанном адресе ячейки.
Ниже приведены пункты, которые необходимо учитывать при создании бина или интервалов:
- Первый бин включает в себя все значения ниже. Для бункера 30 частота 5 включает в себя все оценки ниже 30.
- Последняя ячейка равна 90. Если значения выше, чем у последней ячейки, Excel автоматически создает другую ячейку — Больше. Этот бин включает в себя любые значения данных, которые выше, чем последний бин. В нашем примере есть 3 значения, которые выше, чем последний бин 90.
- Эта диаграмма называется статической гистограммой. Значит, если вы хотите внести какие-либо изменения в исходные данные, вам придется заново создать гистограмму.
- Вы можете сделать форматирование этой диаграммы, как и другие диаграммы.
Пример № 2
Давайте возьмем другой пример с 15 точками данных, которые являются зарплатой компании.
Теперь мы создадим ячейки для указанного набора данных.
Для создания диаграммы гистограммы в Excel мы будем следовать тем же шагам, что и ранее, предпринятые в примере 1.
- Нажмите на вкладку ДАННЫЕ. Выберите параметр «Анализ данных» в разделе «Анализ».
- Откроется диалоговое окно «Анализ данных». Выберите опцию гистограммы и нажмите ОК.
- Откроется диалоговое окно гистограммы.
- Выберите диапазон ввода с точками данных зарплаты.
- Выберите диапазон бинов с колонкой бинов.
- Нажмите «Выходной диапазон», поскольку мы хотим вставить диаграмму на тот же лист, и выберем адрес ячейки, в которую мы хотим вставить диаграмму.
- Выберите опцию Chart Output и нажмите OK.
- Таблица ниже будет выглядеть так:
Объяснение:
- Первый бин $ 25000 будет включать все точки данных, которые меньше, чем это значение.
- Последняя ячейка More будет включать все точки данных, которые превышают $ 65 000. Его создает автоматически в Excel.
Pros
- Гистограмма очень полезна при работе с большим количеством данных.
- Диаграмма гистограммы показывает данные в графической форме, которую легко сравнить с цифрами и понять.
Cons
- Гистограмму диаграммы очень сложно извлечь из поля ввода гистограммы. Значит сложно указать точное число.
- При работе с гистограммой возникает проблема с несколькими категориями.
Что нужно помнить о гистограмме в Excel
- Диаграмма гистограммы используется для непрерывных данных, где ячейка определяет диапазон данных.
- Контейнеры обычно определяются как последовательные и непересекающиеся интервалы.
- Контейнеры должны быть смежными и иметь одинаковый размер (но не обязательно).
- Если вы работаете с Excel 2013, 2010 или более ранней версией, вам необходимо активировать пакет надстроек Excel для анализа данных.
Рекомендуемые статьи
Это было руководство к гистограмме в Excel. Здесь мы обсуждаем его типы и как создать гистограмму в Excel вместе с примерами Excel и загружаемым шаблоном Excel. Вы также можете посмотреть на эти полезные графики в Excel —
- Шаги для сводной диаграммы в Excel 2016
- Создать инновационную круговую диаграмму в MS Excel
- Бесплатные функции Excel — диаграммы и графики
- VBA Чарты | Определение | Примеры
Мультимодальное распределение — это вероятностное распределение с двумя или более модами.
Если вы создадите гистограмму для визуализации мультимодального распределения, вы заметите, что она имеет более одного пика:
Если распределение имеет ровно два пика, то оно считается бимодальным распределением , которое является особым типом мультимодального распределения.
Это отличается от одномодального распределения, которое имеет только один пик:
Хотя одномодальные распределения, такие как нормальное распределение , чаще всего используются для объяснения тем в статистике, мультимодальные распределения на самом деле довольно часто встречаются на практике, поэтому полезно знать, как их распознавать и анализировать.
Примеры мультимодальных распределений
Вот несколько примеров мультимодальных распределений.
Пример 1: Распределение баллов за экзамен
Предположим, профессор дает экзамен своему классу. Кто-то из студентов учился, а кто-то нет. Когда профессор создает гистограмму экзаменационных баллов, она следует мультимодальному распределению с одним пиком вокруг низких баллов для студентов, которые не учились, и другим пиком вокруг высоких баллов для студентов, которые учились:
Пример 2: Высота разных видов растений
Предположим, ученый идет по полю и измеряет высоту различных растений. Сама того не осознавая, она измеряет рост трех разных видов: один довольно высокий, другой среднего роста и третий довольно низкий.
Когда она создает гистограмму для визуализации распределения высоты, она обнаруживает, что она мультимодальна — каждый пик представляет наиболее распространенную высоту трех разных видов.
Пример 3: Распределение клиентов
Владелец ресторана отслеживает, сколько клиентов посещает каждый час. Когда он создает гистограмму для визуализации распределения клиентов, он обнаруживает, что распределение является мультимодальным — есть пик в обеденное время и еще один пик во время ужина.
Что вызывает мультимодальные распределения?
Обычно существует одна из двух основных причин мультимодальных распределений:
1. Несколько групп объединены в одну кучу.
Мультимодальные распределения могут возникать, когда вы собираете данные для нескольких групп, не осознавая этого.
Например, если ученый по незнанию измеряет высоту трех разных видов растений, расположенных на одном поле, распределение всех растений будет мультимодальным при размещении на одной и той же гистограмме.
2. Существует лежащий в основе феномен.
Мультимодальные распределения также могут возникать из-за некоторых лежащих в их основе явлений.
Например, количество клиентов, посещающих ресторан каждый час, следует мультимодальному распределению, поскольку люди, как правило, едят вне дома в два разных времени: обед и ужин. Это основное человеческое поведение вызывает мультимодальное распределение.
Как анализировать мультимодальные распределения
Мы часто описываем распределения, используя среднее значение или медиану , так как это дает нам представление о том, где находится «центр» распределения.
К сожалению, для бимодального распределения бесполезно знать среднее значение и медиану. Например, средний балл за экзамен для студентов в приведенном выше примере равен 81:
Однако очень немногие студенты на самом деле набрали близко к 81 баллу. В данном случае среднее значение вводит в заблуждение. Большинство студентов на самом деле набрали около 74 или около 88 баллов.
Лучший способ анализа и интерпретации бимодальных распределений — просто разбить данные на две отдельные группы, а затем проанализировать расположение центра и разброс для каждой группы отдельно.
Например, мы можем разбить результаты экзамена на «низкие баллы» и «высокие баллы», а затем найти среднее значение и стандартное отклонение для каждой группы.
При расчете сводной статистики для данного распределения, например, среднего значения, медианы или стандартного отклонения, обязательно визуализируйте распределение, чтобы определить, является ли оно одномодальным или мультимодальным.
Если распределение является мультимодальным, его описание с использованием одного среднего значения, медианы или стандартного отклонения может ввести в заблуждение.
«Бимодальный» перенаправляется сюда. Для музыкальной концепции см. Бимодальность .
Рисунок 1. Простое бимодальное распределение, в данном случае смесь двух нормальных распределений с одинаковой дисперсией, но разными средними значениями. На рисунке показана функция плотности вероятности (pdf), которая представляет собой равновзвешенное среднее значение колоколообразных pdf двух нормальных распределений. Если бы веса не были равны, результирующее распределение все равно могло бы быть бимодальным, но с пиками разной высоты.
Рисунок 2. Бимодальное распределение.
Рисунок 3. Двумерное мультимодальное распределение.
В статистике , А бимодальное распределение является распределением вероятностей с двумя различными режимами , которые также могут быть отнесены как бимодальное распределение. Они проявляются в виде отдельных пиков (локальных максимумов) в функции плотности вероятности , как показано на рисунках 1 и 2. Категориальные, непрерывные и дискретные данные могут формировать бимодальные распределения.
В более общем смысле, мультимодальное распределение — это распределение вероятностей с двумя или более модами, как показано на рисунке 3.
Терминология
Когда два режима не равны, больший режим называется основным режимом, а другой — второстепенным. Наименее частое значение между режимами известно как антимод . Разница между основной и второстепенной модами называется амплитудой . Во временных рядах основная мода называется акрофазой, а антимодика — батифазой .
Классификация Галтунга
Галтунг ввел систему классификации (AJUS) для распределений:
- A: одномодальное распределение — пик посередине
- J: одномодальный — пик на обоих концах
- U: бимодальный — пики на обоих концах
- S: бимодальный или мультимодальный — несколько пиков
С тех пор эта классификация была немного изменена:
- J: (изменено) — пик справа
- L: одномодальный — пик слева
- F: без пика (плоский)
В соответствии с этой классификацией бимодальные распределения классифицируются как тип S или U.
Примеры
Бимодальные распределения встречаются как в математике, так и в естественных науках.
Распределения вероятностей
Важные бимодальные распределения включают распределение арксинусов и бета-распределение . Другие включают U-квадратичное распределение .
Отношение двух нормальных распределений также распределяется бимодально. Позволять
где a и b постоянны, а x и y распределены как нормальные переменные со средним значением 0 и стандартным отклонением 1. R имеет известную плотность, которая может быть выражена как конфлюэнтная гипергеометрическая функция .
Распределение обратной части в т распределенной случайной величины является бимодальным , когда число степеней свободы больше , чем один. Аналогично, величина, обратная нормально распределенной переменной, также распределяется бимодально.
Т статистики генерируется из набора данных взяты из распределения Коши является бимодальным.
Встречи в природе
Примеры переменных с бимодальным распределением включают время между извержениями определенных гейзеров , цвет галактик , размер рабочих- ткачей , возраст заболеваемости лимфомой Ходжкина , скорость инактивации препарата изониазид у взрослых в США, абсолютную величину из новых звезд , и циркадных паттернов активности этих сумеречных животных, которые активны как в утренних и вечерних сумерках. В науке о рыболовстве мультимодальные распределения длин отражают разные годовые классы и, таким образом, могут использоваться для оценок возрастного распределения и роста популяции рыб. Осадки обычно распределяются бимодальным образом. При отборе проб из горных галерей, пересекающих вмещающую породу и минерализованные жилы, распределение геохимических переменных будет бимодальным. Бимодальное распределение также наблюдается при анализе трафика, когда пик трафика приходится на час пик с утра, а затем снова в час пик после полудня. Это явление также наблюдается в ежедневном распределении воды, поскольку потребность в воде в виде душа, приготовления пищи и использования туалета обычно достигает пика в утренние и вечерние периоды.
Эконометрика
В эконометрических моделях параметры могут быть распределены бимодально.
Происхождение
Математический
Бимодальное распределение чаще всего возникает как смесь двух разных одномодальных распределений (т. Е. Распределений, имеющих только одну моду). Другими словами, бимодально распределенная случайная величина X определяется как с вероятностью или с вероятностью, где Y и Z являются унимодальными случайными величинами и являются коэффициентом смеси.
Смеси с двумя отдельными компонентами не обязательно должны быть бимодальными, а двухкомпонентные смеси с одномодальными плотностями компонентов могут иметь более двух режимов. Непосредственной связи между количеством компонентов в смеси и количеством мод результирующей плотности нет.
Особые распределения
Бимодальные распределения, несмотря на то, что они часто встречаются в наборах данных, изучаются очень редко. Это может быть связано с трудностями при оценке их параметров частотными или байесовскими методами. Среди тех, что были изучены:
- Бимодальное экспоненциальное распределение.
- Альфа-косонормальное распределение.
- Бимодальное кососимметричное нормальное распределение.
- Смесь распределений Конвея-Максвелла-Пуассона была адаптирована к бимодальным данным подсчета.
Бимодальность также естественно возникает в распределении катастроф на пороге .
Биология
В биологии известно пять факторов, способствующих бимодальному распределению размеров популяций:
- начальное распределение индивидуальных размеров
- распределение темпов роста среди особей
- размер и зависимость скорости роста каждой особи от времени
- коэффициенты смертности, которые могут по-разному влиять на каждый размерный класс
- метилирование ДНК в геноме человека и мыши.
Бимодальное распределение размеров рабочих- ткачей-муравьев возникает из-за существования двух различных классов рабочих, а именно основных рабочих и второстепенных рабочих.
Распределение фитнеса эффектов мутаций как для целых геномов и отдельных генов , также часто оказываются бимодальным с большинством мутаций быть либо нейтральными , либо летальными с относительно небольшого числа , имеющего промежуточного эффекта.
Общие свойства
Смесь двух одномодальных распределений с разными средними значениями не обязательно является бимодальным. Комбинированное распределение роста мужчин и женщин иногда используется в качестве примера бимодального распределения, но на самом деле разница в средних ростах мужчин и женщин слишком мала по сравнению со стандартными отклонениями для получения бимодальности.
Бимодальные распределения обладают тем особенным свойством, что, в отличие от унимодальных распределений, среднее значение может быть более надежной оценкой выборки, чем медиана. Это явно тот случай, когда распределение имеет U-образную форму, как распределение арксинуса. Это может быть неверно, если у распределения есть один или несколько длинных хвостов.
Моменты смесей
Позволять
где g i — распределение вероятностей, а p — параметр смешивания.
Моменты f ( x ) равны
куда
и S я и К я являюсь перекосом и эксцесса из I — го распределения.
Смесь двух нормальных распределений
Нередко встречаются ситуации, когда исследователь полагает, что данные получены из смеси двух нормальных распределений. В связи с этим данная смесь достаточно подробно изучена.
Смесь двух нормальных распределений имеет пять параметров для оценки: два средних, две дисперсии и параметр смешивания. Смесь двух нормальных распределений с равными стандартными отклонениями является бимодальной только в том случае, если их средние значения различаются как минимум на двойное стандартное отклонение. Оценка параметров упрощается, если дисперсии можно считать равными ( гомоскедастический случай).
Если средние двух нормальных распределений равны, то комбинированное распределение является унимодальным. Условия унимодальности комбинированного распределения были выведены Эйзенбергером. Необходимые и достаточные условия для того, чтобы смесь нормальных распределений была бимодальной, были идентифицированы Рэем и Линдси.
Смесь двух примерно равных массовых нормальных распределений имеет отрицательный эксцесс, поскольку две моды по обе стороны от центра масс эффективно уменьшают хвосты распределения.
Смесь двух нормальных распределений с сильно неравной массой имеет положительный эксцесс, поскольку меньшее распределение удлиняет хвост более доминирующего нормального распределения.
Смеси других распределений требуют оценки дополнительных параметров.
Тесты на унимодальность
- Смесь унимодальна тогда и только тогда, когда
или
где p — параметр перемешивания, а
и где μ 1 и μ 2 — средние значения двух нормальных распределений, а σ 1 и σ 2 — их стандартные отклонения.
- Следующий тест для случая p = 1/2 был описан Шиллингом и др . Позволять
Коэффициент разделения ( S ) равен
Если дисперсии равны, то S = 1. Плотность смеси унимодальна тогда и только тогда, когда
- Достаточным условием унимодальности является
- Если два нормальных распределения имеют равные стандартные отклонения, достаточным условием унимодальности является
Сводные статистические данные
Бимодальные распределения являются часто используемым примером того, как сводные статистические данные, такие как среднее значение , медиана и стандартное отклонение, могут вводить в заблуждение при использовании в произвольном распределении. Например, в распределении на рисунке 1 среднее значение и медиана будут около нуля, даже если ноль не является типичным значением. Стандартное отклонение также больше, чем отклонение каждого нормального распределения.
Хотя было предложено несколько, в настоящее время не существует общепризнанной сводной статистики (или набора статистических данных) для количественной оценки параметров общего бимодального распределения. Для смеси двух нормальных распределений обычно используются средние и стандартные отклонения вместе с параметром смешивания (весом для комбинации) — всего пять параметров.
D Эшмана
Статистический показатель, который может быть полезен, — это D Эшмана:
где μ 1 , μ 2 — средние значения, а σ 1 σ 2 — стандартные отклонения.
Для смеси двух нормальных распределений требуется D > 2 для четкого разделения распределений.
A ван дер Эйка
Этот показатель представляет собой средневзвешенное значение степени соответствия частотного распределения. А в диапазоне от -1 (совершенной бимодальности ) до +1 (совершенной унимодальности ). Он определяется как
где U — унимодальность распределения, S — количество категорий, имеющих ненулевые частоты, а K — общее количество категорий.
Значение U равно 1, если распределение имеет любую из трех следующих характеристик:
- все ответы находятся в одной категории
- ответы равномерно распределяются по всем категориям
- ответы равномерно распределяются между двумя или более смежными категориями, при этом остальные категории не имеют ответов
В других дистрибутивах данные должны быть разделены на «слои». Внутри слоя ответы либо равны, либо равны нулю. Категории не обязательно должны быть смежными. Вычисляется значение A для каждого слоя ( A i ) и определяется средневзвешенное значение для распределения. Веса ( w i ) для каждого слоя — это количество ответов в этом слое. В символах
Равномерное распределение имеет = 0: когда все ответы попадают в одну категорию А = +1.
Одна теоретическая проблема с этим индексом заключается в том, что он предполагает, что интервалы расположены на одинаковом расстоянии. Это может ограничить его применимость.
Бимодальное разделение
Этот индекс предполагает, что распределение представляет собой смесь двух нормальных распределений со средними ( μ 1 и μ 2 ) и стандартными отклонениями ( σ 1 и σ 2 ):
Коэффициент бимодальности
Коэффициент бимодальности Сарла b равен
где γ — асимметрия, а κ — эксцесс . Эксцесс здесь определяется как стандартизованный четвертый момент вокруг среднего. Значение b находится между 0 и 1. Логика этого коэффициента состоит в том, что бимодальное распределение со светлыми хвостами будет иметь очень низкий эксцесс, асимметричный характер или и то, и другое — все это увеличивает этот коэффициент.
Формула для конечной выборки:
где n — количество элементов в образце, g — асимметрия образца, а k — избыточный эксцесс образца .
Значение b для равномерного распределения составляет 5/9. Это также его значение для экспоненциального распределения . Значения больше 5/9 могут указывать на бимодальное или мультимодальное распределение, хотя соответствующие значения также могут быть результатом сильно искаженных одномодальных распределений. Максимальное значение (1.0) достигается только распределением Бернулли с двумя различными значениями или суммой двух различных дельта-функций Дирака (двухдельта-распределение).
Распределение этой статистики неизвестно. Это связано со статистикой, предложенной ранее Пирсоном — разницей между эксцессом и квадратом асимметрии ( см. Ниже ).
Амплитуда бимодальности
Это определяется как
где A 1 — амплитуда меньшего пика, а A an — амплитуда антимоды.
A B всегда <1. Большие значения указывают на более отчетливые пики.
Бимодальное соотношение
Это соотношение левого и правого пиков. Математически
где A l и A r — амплитуды левого и правого пиков соответственно.
Параметр бимодальности
Этот параметр ( B ) принадлежит Уилкоку.
где A l и A r — амплитуды левого и правого пиков соответственно, а P i — логарифм по основанию 2 доли распределения в i- м интервале. Максимальное значение ΣP равно 1, но значение B может быть больше этого.
Для использования этого индекса берется журнал значений. Затем данные делятся на интервал шириной Φ, значение которого равно log 2. Ширина пиков принимается равной четырехкратной 1 / 4Φ, центрированной по их максимальным значениям.
Индексы бимодальности
- Индекс Ванга
Индекс бимодальности, предложенный Ван и др., Предполагает, что распределение является суммой двух нормальных распределений с равными дисперсиями, но разными средними значениями. Это определяется следующим образом:
где μ 1 , μ 2 — средние, а σ — стандартное отклонение.
где p — параметр перемешивания.
- Индекс Старрока
Другой индекс бимодальности был предложен Стурроком.
Этот индекс ( B ) определяется как
Когда m = 2 и γ равномерно распределен, B распределен экспоненциально.
Эта статистика представляет собой разновидность периодограммы . Он страдает от обычных проблем оценки и спектральной утечки, присущих этой форме статистики.
- индекс де Микеле и Аккатино
Другой индекс бимодальности был предложен де Микеле и Аккатино. Их индекс ( B ) равен
где μ — среднее арифметическое образца, а
где m i — количество точек данных в i- м интервале, x i — центр i- го интервала, а L — количество интервалов.
Авторы предложили значение отсечения 0,1 для B, чтобы различать бимодальное ( B > 0,1) и одномодальное ( B <0,1) распределение. Для этого значения не было предложено никакого статистического обоснования.
- Индекс Сэмбрука Смита
Еще один индекс ( B ) был предложен Sambrook Smith et al.

где p 1 и p 2 — пропорции, содержащиеся в первичной (с большей амплитудой) и вторичной (с меньшей амплитудой) моде, а φ 1 и φ 2 — размеры φ первичной и вторичной моды. Размер φ определяется как минус один, умноженный на логарифм размера данных, взятых в базу 2. Это преобразование обычно используется при изучении отложений.
Авторы рекомендовали значение отсечения 1,5, при этом B больше 1,5 для бимодального распределения и меньше 1,5 для унимодального распределения. Никакого статистического обоснования этого значения не было.
- Индекс Чаудхури и Агравала
Другой параметр бимодальности был предложен Чаудхури и Агравалом. Этот параметр требует знания дисперсии двух субпопуляций, составляющих бимодальное распределение. Он определяется как

где n i — количество точек данных в i- й субпопуляции, σ i 2 — дисперсия i- й субпопуляции, m — общий размер выборки, а σ 2 — дисперсия выборки.
Это средневзвешенное значение дисперсии. Авторы предполагают, что этот параметр можно использовать в качестве цели оптимизации для разделения выборки на две субпопуляции. Никакого статистического обоснования этому предположению дано не было.
Статистические тесты
Доступен ряд тестов, чтобы определить, распределяется ли набор данных бимодальным (или мультимодальным) способом.
Графические методы
При изучении отложений размер частиц часто бывает двухрежимным. Эмпирически было обнаружено, что полезно построить график зависимости частоты от логарифма (размера) частиц. Обычно это дает четкое разделение частиц на бимодальное распределение. В геологических приложениях логарифм обычно берется с основанием 2. Преобразованные логарифмические значения называются единицами фи (Φ). Эта система известна как шкала Крамбейна (или фи).
Альтернативный метод заключается в построении логарифма размера частиц в зависимости от совокупной частоты. Этот график обычно состоит из двух достаточно прямых линий с соединительной линией, соответствующей антимоде.
- Статистика
Приблизительные значения для нескольких статистических данных можно получить из графических графиков.
где Среднее — это среднее значение, StdDev — стандартное отклонение, Skew — асимметрия, Kurt — эксцесс, а φ x — значение переменной φ в x- м проценте распределения.
Унимодальное и бимодальное распределение
Пирсон в 1894 г. был первым, кто разработал процедуру проверки того, можно ли разложить распределение на два нормальных распределения. Этот метод требовал решения полинома девятого порядка . В следующей статье Пирсон сообщил, что для любой асимметрии распределения 2 + 1 <эксцесс. Позже Пирсон показал, что
где b 2 — эксцесс, а b 1 — квадрат асимметрии. Равенство справедливо только для двухточечного распределения Бернулли или суммы двух различных дельта-функций Дирака . Это самые крайние возможные случаи бимодальности. В обоих случаях эксцесс равен 1. Поскольку они оба симметричны, их асимметрия равна 0, а разница равна 1.
Бейкер предложил преобразование для преобразования бимодального распределения в одномодальное.
Было предложено несколько тестов на унимодальность по сравнению с бимодальностью: Холдейн предложил один, основанный на вторых центральных различиях. Позднее Ларкин представил тест, основанный на F-тесте; Бенетт создал его на основе G-теста Фишера . Токеши предложил четвертый тест. Тест, основанный на отношении правдоподобия, был предложен Хольцманном и Фоллмером.
Предложен метод, основанный на оценках и тестах Вальда. Этот метод позволяет различать одномодальные и бимодальные распределения, если известны лежащие в основе распределения.
Антимодовые тесты
Статистические тесты для антирежима известны.
- Метод Оцу
Метод Оцу обычно используется в компьютерной графике для определения оптимального разделения двух распределений.
Общие тесты
Для того, чтобы проверить , если распределение является иным , чем унимодальны, несколько дополнительных испытания были разработаны: на тесте пропускной способности , то испытание погружения , тем тестовый избыток масс , МАРЫ тесты, то тестовое существование режима , то тестовое огибающей , то тест — диапазон , а седло тест .
Реализация теста погружного доступна для языка программирования R . Значения p для значений статистики падения находятся в диапазоне от 0 до 1. Значения P менее 0,05 указывают на значительную мультимодальность, а значения p более 0,05, но менее 0,10 предполагают мультимодальность с маргинальной значимостью.
Тест Сильвермана
Сильверман представил метод начальной загрузки для количества режимов. Тест использует фиксированную полосу пропускания, что снижает мощность теста и его интерпретируемость. Недостаточно сглаженные плотности могут иметь чрезмерное количество режимов, количество которых во время начальной загрузки нестабильно.
Тест Баджье-Аггарвала
Баджье и Аггарвал предложили тест, основанный на эксцессе распределения.
Особые случаи
Дополнительные тесты доступны для ряда особых случаев:
- Смесь двух нормальных распределений
Исследование плотности смеси данных двух нормальных распределений показало, что разделение на два нормальных распределения было затруднительным, если средние значения не были разделены на 4–6 стандартных отклонений.
В астрономии алгоритм Kernel Mean Matching используется для определения принадлежности набора данных к одному нормальному распределению или к смеси двух нормальных распределений.
- Бета-нормальное распределение
Это распределение является бимодальным для определенных значений параметров is. Был описан тест на эти значения.
Кривые оценки параметров и аппроксимации
Предполагая, что распределение известно как бимодальное или было показано, что оно является бимодальным одним или несколькими из приведенных выше тестов, часто бывает желательно подобрать кривую к данным. Это может быть сложно.
Байесовские методы могут быть полезны в сложных случаях.
Программное обеспечение
- Два нормальных распределения
Пакет для R доступен для тестирования на бимодальность. Этот пакет предполагает, что данные распределены как сумма двух нормальных распределений. Если это предположение неверно, результаты могут быть ненадежными. Он также включает функции для подбора суммы двух нормальных распределений к данным.
Если предположить, что распределение представляет собой смесь двух нормальных распределений, то для определения параметров можно использовать алгоритм максимизации ожидания. Для этого доступно несколько программ, включая Cluster и пакет R nor1mix.
- Другие дистрибутивы
Пакет mixtools, доступный для R, может тестировать и оценивать параметры ряда различных дистрибутивов. Доступен пакет для смеси двух правосторонних гамма-распределений.
Доступно несколько других пакетов для R, подходящих для смешанных моделей; к ним относятся flexmix, mcclust, agrmt и mixdist.
Язык статистического программирования SAS также может соответствовать множеству смешанных распределений с помощью процедуры PROC FREQ.
Смотрите также
- Чрезмерная дисперсия
использованная литература
Введение в описательную статистику
Перевод
Ссылка на автора
Описательный статистический анализ помогает вам понять ваши данные и является очень важной частью машинного обучения. Это связано с тем, что машинное обучение сводится к прогнозированию. С другой стороны, статистика сводится к тому, чтобы делать выводы из данных, что является необходимым начальным шагом. В этом посте вы узнаете о наиболее важных описательных статистических концепциях. Они помогут вам лучше понять, что ваши данные пытаются вам сказать, что приведет к общей лучшей модели машинного обучения и понимания.
Оглавление:
- Введение
- Нормальное распределение
- Центральная тенденция (средняя, мода, медиана)
- Меры изменчивости (диапазон, межквартильный диапазон)
- Дисперсия и стандартное отклонение
- модальность
- перекос
- эксцесс
- Резюме
Введение
Выполнение описательного статистического анализа вашего набора данных абсолютно необходимо. Многие люди пропускают эту часть и поэтому теряют много ценной информации о своих данных, что часто приводит к неправильным выводам. Потратьте время и тщательно запустите описательную статистику и убедитесь, что данные соответствуют требованиям для дальнейшего анализа.
Но, прежде всего, мы должны рассмотреть статистику:
Статистика — это раздел математики, который занимается сбором, интерпретацией, организацией и интерпретацией данных.
В статистике есть две основные категории:
1. Описательная статистика:В «Описательной статистике» вы описываете, представляете, обобщаете и систематизируете свои данные (совокупность) с помощью численных расчетов, графиков или таблиц.
2. Логическая статистика:Логическая статистика создается более сложными математическими вычислениями и позволяет нам выявлять тенденции и делать предположения и прогнозы о населении на основе изучения выборки, взятой из нее.
Нормальное распределение
Нормальное распределение является одним из наиболее важных понятий в статистике, поскольку почти все статистические тесты требуют нормально распределенных данных. Это в основном описывает, как выглядят большие выборки данных при их построении. Его иногда называют «кривой колокола» или «кривой Гаусса».
Инференциальная статистика и расчет вероятностей требуют нормального распределения. По сути, это означает, что если ваши данные обычно не распространяются, вам нужно быть очень осторожным, какие статистические тесты вы применяете к ним, поскольку они могут привести к неправильным выводам.
Нормальное распределение дается, если ваши данные симметричны, имеют форму колокола, центрированы и унимодальны.
В идеальном нормальном распределении каждая сторона является точным зеркалом другой. Это должно выглядеть как распределение на картинке ниже:
Вы можете видеть на картинке, что распределение имеет форму колокола, что просто означает, что оно не сильно пиковое. Унимодал означает, что есть только один пик.
Главная тенденция
В статистике мы имеем дело со средним, модой и медианой. Их также называют «центральной тенденцией». Это всего лишь три вида «средних» и, безусловно, самые популярные.
Среднее значение просто среднееи считается наиболее надежным показателем центральной тенденции делать предположения о населении из одной выборки. Центральная тенденция определяет склонность значений ваших данных группироваться вокруг их среднего значения, режима или медианы. Среднее значение рассчитывается как сумма всех значений, деленная на количество значений.
Режим — это значение или категория, которые чаще всего встречаются в данных.Поэтому в наборе данных нет режима, если число не повторяется или если ни одна категория не совпадает. Возможно, в наборе данных имеется более одного режима, но об этом я расскажу в разделе «Модальность» ниже.
Режим также является единственным показателем центральной тенденции, который можно использовать для категориальных переменных, поскольку вы не можете вычислить, например, среднее значение для переменной «пол». Вы просто сообщаете категориальные переменные в виде чисел и процентов.
Медиана — это «среднее» значение или средняя точка в ваших данныхи также называется «50-й процентиль». Обратите внимание, что на медиану гораздо меньше влияют выбросы и перекос данных, чем на среднее. Я объясню это на примере: представьте, что у вас есть набор призов на жилье, который колеблется в основном от 100 000 до 300 000 долларов, но содержит несколько домов стоимостью более 3 миллионов долларов. Эти дорогие дома будут сильно влиять, а значит, так как это сумма всех значений, деленная на количество значений. Медиана не будет сильно затронута этими выбросами, поскольку это только «среднее» значение всех точек данных. Поэтому медиана — это гораздо более подходящая статистика, чтобы сообщать о ваших данных.
При нормальном распределении все эти показатели попадают в одну среднюю точку. Это означает, что среднее, мода и медиана все равны
Меры изменчивости
Наиболее популярными показателями изменчивости являются диапазон, межквартильный диапазон (IQR), дисперсия и стандартное отклонение. Они используются для измерения количества разброса или изменчивости в ваших данных.
Диапазон описывает разницу между самой большой и самой маленькой точками в ваших данных.
Межквартильный диапазон (IQR) является мерой статистического разброса между верхним (75-м) и нижним (25-м) квартилями.
В то время как диапазон измеряет, где находятся начало и конец вашей точки данных, межквартильный диапазон является мерой того, где лежит большинство значений.
Разницу между стандартным отклонением и дисперсией часто трудно понять новичкам, но я подробно объясню это ниже.
Дисперсия и стандартное отклонение
Стандартное отклонение и дисперсия также измеряют, как диапазон и IQR, насколько разбросаны наши данные (например, дисперсия). Поэтому они оба получены из среднего значения.
Дисперсия вычисляется путем нахождения разницы между каждой точкой данных и среднего значения, возводя их в квадрат, суммируя и затем беря среднее из этих чисел.
Квадраты используются во время расчета, потому что они взвешивают выбросы в большей степени, чем точки, близкие к среднему. Это препятствует тому, чтобы различия выше среднего нейтрализовали различия ниже среднего.
Проблема с дисперсией состоит в том, что из-за возведения в квадрат она не находится в той же единице измерения, что и исходные данные.
Допустим, вы имеете дело с набором данных, который содержит значения в сантиметрах. Ваша разница будет в сантиметрах в квадрате и, следовательно, не лучшее измерение.
Вот почему стандартное отклонение используется чаще, потому что оно находится в исходной единице. Это просто квадратный корень дисперсии, и поэтому он возвращается к исходной единице измерения.
Давайте рассмотрим пример, который иллюстрирует разницу между дисперсией и стандартным отклонением:
Представьте себе набор данных, который содержит значения в сантиметрах от 1 до 15, что дает среднее значение 8. Возведение в квадрат разницы между каждой точкой данных и средним значением и усреднение квадратов дает дисперсию 18,67 (квадратные сантиметры), тогда как стандартное отклонение составляет 4,3 сантиметра.
Когда у вас низкое стандартное отклонение, ваши точки данных, как правило, близки к среднему. Высокое стандартное отклонение означает, что ваши данные распределены в широком диапазоне.
Стандартное отклонение лучше всего использовать, когда данные являются одномодальными. При нормальном распределении примерно 34% точек данных лежат между средним и одним стандартным отклонением выше или ниже среднего. Поскольку нормальное распределение является симметричным, 68% точек данных находятся между одним стандартным отклонением выше и одним стандартным отклонением ниже среднего. Приблизительно 95% находятся между двумя стандартными отклонениями ниже среднего и двумя стандартными отклонениями выше среднего. И примерно 99,7% находятся между тремя стандартными отклонениями выше и тремя стандартными отклонениями ниже среднего.
Картинка ниже прекрасно это иллюстрирует.
С помощью так называемой «Z-Score» вы можете проверить, сколько стандартных отклонений ниже (или выше) среднего значения, лежит конкретная точка данных. С пандами вы можете просто использовать Функция std (), Чтобы лучше понять концепцию нормального распределения, теперь мы обсудим понятия модальности, симметрии и пика.
модальность
Модальность распределения определяется количеством пиков, которые оно содержит.В большинстве дистрибутивов есть только один пик, но возможно, что вы встретите дистрибутивы с двумя или более пиками.
На рисунке ниже показаны наглядные примеры трех типов модальности:
Унимодальный означает, что у распределения есть только один пик, что означает, что у него есть только один часто встречающийся счет, сгруппированный сверху. Бимодальное распределение имеет два часто встречающихся значения (два пика), а мультимодальное имеет два или несколько часто встречающихся значений.
перекос
Асимметрия — это измерение симметрии распределения.
Поэтому он описывает, насколько распределение отличается от нормального распределения, либо слева, либо справа. Значение асимметрии может быть положительным, отрицательным или нулевым. Обратите внимание, что идеальное нормальное распределение будет иметь нулевую асимметрию, потому что среднее значение равно медиане.
Ниже вы можете увидеть иллюстрацию различных типов асимметрии:
Мы говорим о перекосе позитива, если данные сложены влево, который оставляет хвост, указывающий направо.
Отрицательный перекос происходит, если данные накапливаются вправо, который оставляет хвост, указывающий налево. Обратите внимание, что положительные перекосы встречаются чаще, чем отрицательные.
Хорошим измерением асимметрии распределения является коэффициент асимметрии Пирсона, который обеспечивает быструю оценку симметрии распределений. Чтобы вычислить асимметрию в пандах, вы можете просто использовать Функция «skew ()»
эксцесс
Куртоз измеряет, является ли ваш набор данных «тяжелым» или «легким» по сравнению с обычным распределением. Наборы данных с высоким эксцессом имеют тяжелые хвосты и больше выбросов, а наборы данных с низким эксцессом имеют тенденцию иметь легкие хвосты и меньше выбросов. Обратите внимание, что гистограмма — это эффективный способ показать как асимметрию, так и эксцесс в наборе данных, потому что вы можете легко определить, если что-то не так с вашими данными. График вероятности также является отличным инструментом, потому что нормальное распределение будет следовать по прямой линии.
Вы можете увидеть оба набора данных с положительным перекосом на изображении ниже:
Хороший способ математически измерить эксцесс распределения — это эксцентричное измерение эксцесса.
Теперь мы обсудим три наиболее распространенных типа куртоза.
Нормальное распределение называетсяmesokurticи имеет эксцесс или около нуля.platykurticРаспределение имеет отрицательный эксцесс и хвосты очень тонкие по сравнению с нормальным распределением.Leptokurticраспределения имеют эксцесс, превышающий 3, а жирные хвосты означают, что распределение дает более экстремальные значения и что оно имеет относительно небольшое стандартное отклонение.
Если вы уже поняли, что распределение искажено, вам не нужно рассчитывать его эксцесс, поскольку распределение уже не является нормальным. В пандах вы можете просмотреть эксцесс, просто позвонив Функция «kurtosis ()»,
Резюме
Этот пост дал вам хорошее введение в описательную статистику. Вы узнали, как выглядит нормальное распределение и почему оно важно. Кроме того, вы получили знания о трех различных типах средних (среднее, модальное и медианное), также называемых центральной тенденцией. После этого вы узнали о диапазоне, межквартильном диапазоне, дисперсии и стандартном отклонении. Затем мы обсудили три типа модальности, и вы можете описать, насколько распределение отличается от нормального распределения с точки зрения асимметрии. Наконец, вы узнали о распределениях лептокуртов, мезокуртов и платикуртов.
Этот пост изначально был опубликован в моем блоге (https://machinelearning-blog.com).
$begingroup$
This histogram is part of a task about descriptive statistics. I thought it would be easy, and it is, but i am not sure about this one. First I described this histogram as slightly positively skewed. The skewness coefficient supported this. But then those three peaks caught my eyes and i was confused, because i’ve learned that it wouldn’t make any sense to talk about skewness (or kurtosis) if the distribution is a bimodal or multimodal one. So, my question is one of several. Mainly: Is this a multimodal distribution? Can you say this for sure? Or is this a matter of interpretation? Along these lines the secondary questions are: If it is a multimodal distribution and especially if it is a matter of interpretation, would it be reasonable to describe the skewness, the kurtosis and the seemingly multimodal aspect? Because: from the histogram and the coefficients it seems i could say something about all three aspects. Or is it truely a strict rule, that you can’t really talk about skewness/kurtosis, if it is bimodal or multimodal? In this case, i would be back to my initial question: Is this a multimodal distribution and can you be sure?
asked Jun 2, 2015 at 22:43
$endgroup$
3
$begingroup$
You can fit various types of distributions, multimodal and unimodal, and assess model fit using statistics like BIC. I would guess, given your histogram, that the different distributions will have similar fit, so it will be difficult to claim that the distribution is in fact multimodal. If you had more pronounced dual (or more) peaks, then I would guess that the data would better support bimodality (or multimodality) based on measures of model fit. But it’s hard to say without actually fitting those distributions and looking at the model fit statistics.
I want to comment on kurtosis though. I have seen people say that low kurtosis indicates bimodality, while large kurtosis indicates unimodality. This is patently false. Take a bimodal distribution with very small kurtosis. Now mix it with a much wider distribution, with small mixing probability. The resulting distribution will have exactly the same bimodality, but huge kurtosis. Kurtosis measures nothing about the peak (flatness, sharpness, or modality). It measures the outlier (potential rare, extreme observation) characteristic of a distribution only. See https://en.wikipedia.org/wiki/Talk:Kurtosis#Why_kurtosis_should_not_be_interpreted_as_.22peakedness.22 for a clear explanation.
answered Oct 6, 2017 at 13:39
BigBendRegionBigBendRegion
5,1531 gold badge15 silver badges23 bronze badges
$endgroup$
«Bimodal» redirects here. For the musical concept, see Bimodality.
Figure 1. A simple bimodal distribution, in this case a mixture of two normal distributions with the same variance but different means. The figure shows the probability density function (p.d.f.), which is an equally-weighted average of the bell-shaped p.d.f.s of the two normal distributions. If the weights were not equal, the resulting distribution could still be bimodal but with peaks of different heights.
Figure 2. A bimodal distribution.
Figure 3. A bivariate, multimodal distribution
Figure 4. A non-example: a unimodal distribution, that would become multimodal if conditioned on either x or y.
In statistics, a multimodal distribution is a probability distribution with more than one mode. These appear as distinct peaks (local maxima) in the probability density function, as shown in Figures 1 and 2. Categorical, continuous, and discrete data can all form multimodal distributions. Among univariate analyses, multimodal distributions are commonly bimodal.[citation needed]
Terminology[edit]
When the two modes are unequal the larger mode is known as the major mode and the other as the minor mode. The least frequent value between the modes is known as the antimode. The difference between the major and minor modes is known as the amplitude. In time series the major mode is called the acrophase and the antimode the batiphase.[citation needed]
Galtung’s classification[edit]
Galtung introduced a classification system (AJUS) for distributions:[1]
- A: unimodal distribution – peak in the middle
- J: unimodal – peak at either end
- U: bimodal – peaks at both ends
- S: bimodal or multimodal – multiple peaks
This classification has since been modified slightly:
- J: (modified) – peak on right
- L: unimodal – peak on left
- F: no peak (flat)
Under this classification bimodal distributions are classified as type S or U.
Examples[edit]
Bimodal distributions occur both in mathematics and in the natural sciences.
Probability distributions[edit]
Important bimodal distributions include the arcsine distribution and the beta distribution (iff both parameters a and b are less than 1). Others include the U-quadratic distribution.
The ratio of two normal distributions is also bimodally distributed. Let
where a and b are constant and x and y are distributed as normal variables with a mean of 0 and a standard deviation of 1. R has a known density that can be expressed as a confluent hypergeometric function.[2]
The distribution of the reciprocal of a t distributed random variable is bimodal when the degrees of freedom are more than one. Similarly the reciprocal of a normally distributed variable is also bimodally distributed.
A t statistic generated from data set drawn from a Cauchy distribution is bimodal.[3]
Occurrences in nature[edit]
Examples of variables with bimodal distributions include the time between eruptions of certain geysers, the color of galaxies, the size of worker weaver ants, the age of incidence of Hodgkin’s lymphoma, the speed of inactivation of the drug isoniazid in US adults, the absolute magnitude of novae, and the circadian activity patterns of those crepuscular animals that are active both in morning and evening twilight. In fishery science multimodal length distributions reflect the different year classes and can thus be used for age distribution- and growth estimates of the fish population.[4] Sediments are usually distributed in a bimodal fashion. When sampling mining galleries crossing either the host rock and the mineralized veins, the distribution of geochemical variables would be bimodal. Bimodal distributions are also seen in traffic analysis, where traffic peaks in during the AM rush hour and then again in the PM rush hour. This phenomenon is also seen in daily water distribution, as water demand, in the form of showers, cooking, and toilet use, generally peak in the morning and evening periods.
Econometrics[edit]
In econometric models, the parameters may be bimodally distributed.[5]
Origins[edit]
Mathematical[edit]
A bimodal distribution commonly arises as a mixture of two different unimodal distributions (i.e. distributions having only one mode). In other words, the bimodally distributed random variable X is defined as 




Mixtures with two distinct components need not be bimodal and two component mixtures of unimodal component densities can have more than two modes. There is no immediate connection between the number of components in a mixture and the number of modes of the resulting density.
Particular distributions[edit]
Bimodal distributions, despite their frequent occurrence in data sets, have only rarely been studied[citation needed]. This may be because of the difficulties in estimating their parameters either with frequentist or Bayesian methods. Among those that have been studied are
- Bimodal exponential distribution.[6]
- Alpha-skew-normal distribution.[7]
- Bimodal skew-symmetric normal distribution.[8]
- A mixture of Conway-Maxwell-Poisson distributions has been fitted to bimodal count data.[9]
Bimodality also naturally arises in the cusp catastrophe distribution.
Biology[edit]
In biology five factors are known to contribute to bimodal distributions of population sizes[citation needed]:
- the initial distribution of individual sizes
- the distribution of growth rates among the individuals
- the size and time dependence of the growth rate of each individual
- mortality rates that may affect each size class differently
- the DNA methylation in human and mouse genome.
The bimodal distribution of sizes of weaver ant workers arises due to existence of two distinct classes of workers, namely major workers and minor workers.[10]
The distribution of fitness effects of mutations for both whole genomes[11][12] and individual genes[13] is also frequently found to be bimodal with most mutations being either neutral or lethal with relatively few having intermediate effect.
General properties[edit]
A mixture of two unimodal distributions with differing means is not necessarily bimodal. The combined distribution of heights of men and women is sometimes used as an example of a bimodal distribution, but in fact the difference in mean heights of men and women is too small relative to their standard deviations to produce bimodality when the two distribution curves are combined.[14]
Bimodal distributions have the peculiar property that – unlike the unimodal distributions – the mean may be a more robust sample estimator than the median.[15] This is clearly the case when the distribution is U shaped like the arcsine distribution. It may not be true when the distribution has one or more long tails.
Moments of mixtures[edit]
Let
where gi is a probability distribution and p is the mixing parameter.
The moments of f(x) are[16]
where
and Si and Ki are the skewness and kurtosis of the ith distribution.
Mixture of two normal distributions[edit]
It is not uncommon to encounter situations where an investigator believes that the data comes from a mixture of two normal distributions. Because of this, this mixture has been studied in some detail.[17]
A mixture of two normal distributions has five parameters to estimate: the two means, the two variances and the mixing parameter. A mixture of two normal distributions with equal standard deviations is bimodal only if their means differ by at least twice the common standard deviation.[14] Estimates of the parameters is simplified if the variances can be assumed to be equal (the homoscedastic case).
If the means of the two normal distributions are equal, then the combined distribution is unimodal. Conditions for unimodality of the combined distribution were derived by Eisenberger.[18] Necessary and sufficient conditions for a mixture of normal distributions to be bimodal have been identified by Ray and Lindsay.[19]
A mixture of two approximately equal mass normal distributions has a negative kurtosis since the two modes on either side of the center of mass effectively reduces the tails of the distribution.
A mixture of two normal distributions with highly unequal mass has a positive kurtosis since the smaller distribution lengthens the tail of the more dominant normal distribution.
Mixtures of other distributions require additional parameters to be estimated.
Tests for unimodality[edit]
- When the components of the mixture have equal variances the mixture is unimodal if and only if[20]
or
where p is the mixing parameter and
and where μ1 and μ2 are the means of the two normal distributions and σ is their standard deviation.
- The following test for the case p = 1/2 was described by Schilling et al.[14] Let
The separation factor (S) is
If the variances are equal then S = 1. The mixture density is unimodal if and only if
- A sufficient condition for unimodality is[21]
- If the two normal distributions have equal standard deviations
a sufficient condition for unimodality is[21]
Summary statistics[edit]
Bimodal distributions are a commonly used example of how summary statistics such as the mean, median, and standard deviation can be deceptive when used on an arbitrary distribution. For example, in the distribution in Figure 1, the mean and median would be about zero, even though zero is not a typical value. The standard deviation is also larger than deviation of each normal distribution.
Although several have been suggested, there is no presently generally agreed summary statistic (or set of statistics) to quantify the parameters of a general bimodal distribution. For a mixture of two normal distributions the means and standard deviations along with the mixing parameter (the weight for the combination) are usually used – a total of five parameters.
Ashman’s D[edit]
A statistic that may be useful is Ashman’s D:[22]
where μ1, μ2 are the means and σ1, σ2 are the standard deviations.
For a mixture of two normal distributions D > 2 is required for a clean separation of the distributions.
van der Eijk’s A[edit]
This measure is a weighted average of the degree of agreement the frequency distribution.[23] A ranges from -1 (perfect bimodality) to +1 (perfect unimodality). It is defined as
where U is the unimodality of the distribution, S the number of categories that have nonzero frequencies and K the total number of categories.
The value of U is 1 if the distribution has any of the three following characteristics:
- all responses are in a single category
- the responses are evenly distributed among all the categories
- the responses are evenly distributed among two or more contiguous categories, with the other categories with zero responses
With distributions other than these the data must be divided into ‘layers’. Within a layer the responses are either equal or zero. The categories do not have to be contiguous. A value for A for each layer (Ai) is calculated and a weighted average for the distribution is determined. The weights (wi) for each layer are the number of responses in that layer. In symbols
A uniform distribution has A = 0: when all the responses fall into one category A = +1.
One theoretical problem with this index is that it assumes that the intervals are equally spaced. This may limit its applicability.
Bimodal separation[edit]
This index assumes that the distribution is a mixture of two normal distributions with means (μ1 and μ2) and standard deviations (σ1 and σ2):[24]
Bimodality coefficient[edit]
Sarle’s bimodality coefficient b is[25]
where γ is the skewness and κ is the kurtosis. The kurtosis is here defined to be the standardised fourth moment around the mean. The value of b lies between 0 and 1.[26] The logic behind this coefficient is that a bimodal distribution with light tails will have very low kurtosis, an asymmetric character, or both – all of which increase this coefficient.
The formula for a finite sample is[27]
where n is the number of items in the sample, g is the sample skewness and k is the sample excess kurtosis.
The value of b for the uniform distribution is 5/9. This is also its value for the exponential distribution. Values greater than 5/9 may indicate a bimodal or multimodal distribution, though corresponding values can also result for heavily skewed unimodal distributions.[28] The maximum value (1.0) is reached only by a Bernoulli distribution with only two distinct values or the sum of two different Dirac delta functions (a bi-delta distribution).
The distribution of this statistic is unknown. It is related to a statistic proposed earlier by Pearson – the difference between the kurtosis and the square of the skewness (vide infra).
Bimodality amplitude[edit]
This is defined as[24]
where A1 is the amplitude of the smaller peak and Aan is the amplitude of the antimode.
AB is always < 1. Larger values indicate more distinct peaks.
Bimodal ratio[edit]
This is the ratio of the left and right peaks.[24] Mathematically
where Al and Ar are the amplitudes of the left and right peaks respectively.
Bimodality parameter[edit]
This parameter (B) is due to Wilcock.[29]
where Al and Ar are the amplitudes of the left and right peaks respectively and Pi is the logarithm taken to the base 2 of the proportion of the distribution in the ith interval. The maximal value of the ΣP is 1 but the value of B may be greater than this.
To use this index, the log of the values are taken. The data is then divided into interval of width Φ whose value is log 2. The width of the peaks are taken to be four times 1/4Φ centered on their maximum values.
Bimodality indices[edit]
- Wang’s index
The bimodality index proposed by Wang et al assumes that the distribution is a sum of two normal distributions with equal variances but differing means.[30] It is defined as follows:
where μ1, μ2 are the means and σ is the common standard deviation.
where p is the mixing parameter.
- Sturrock’s index
A different bimodality index has been proposed by Sturrock.[31]
This index (B) is defined as
When m = 2 and γ is uniformly distributed, B is exponentially distributed.[32]
This statistic is a form of periodogram. It suffers from the usual problems of estimation and spectral leakage common to this form of statistic.
- de Michele and Accatino’s index
Another bimodality index has been proposed by de Michele and Accatino.[33] Their index (B) is
where μ is the arithmetic mean of the sample and
where mi is number of data points in the ith bin, xi is the center of the ith bin and L is the number of bins.
The authors suggested a cut off value of 0.1 for B to distinguish between a bimodal (B > 0.1)and unimodal (B < 0.1) distribution. No statistical justification was offered for this value.
- Sambrook Smith’s index
A further index (B) has been proposed by Sambrook Smith et al[34]

where p1 and p2 are the proportion contained in the primary (that with the greater amplitude) and secondary (that with the lesser amplitude) mode and φ1 and φ2 are the φ-sizes of the primary and secondary mode. The φ-size is defined as minus one times the log of the data size taken to the base 2. This transformation is commonly used in the study of sediments.
The authors recommended a cut off value of 1.5 with B being greater than 1.5 for a bimodal distribution and less than 1.5 for a unimodal distribution. No statistical justification for this value was given.
- Otsu’s method
Otsu’s method for finding a threshold for separation between two modes relies on minimizing the quantity
where ni is the number of data points in the ith subpopulation, σi2 is the variance of the ith subpopulation, m is the total size of the sample and σ2 is the sample variance. Some researchers (particularly in the field of digital image processing) have applied this quantity more broadly as an index for detecting bimodality, with a small value indicating a more bimodal distribution.[35]
Statistical tests[edit]
A number of tests are available to determine if a data set is distributed in a bimodal (or multimodal) fashion.
Graphical methods[edit]
In the study of sediments, particle size is frequently bimodal. Empirically, it has been found useful to plot the frequency against the log( size ) of the particles.[36][37] This usually gives a clear separation of the particles into a bimodal distribution. In geological applications the logarithm is normally taken to the base 2. The log transformed values are referred to as phi (Φ) units. This system is known as the Krumbein (or phi) scale.
An alternative method is to plot the log of the particle size against the cumulative frequency. This graph will usually consist two reasonably straight lines with a connecting line corresponding to the antimode.
- Statistics
Approximate values for several statistics can be derived from the graphic plots.[36]
where Mean is the mean, StdDev is the standard deviation, Skew is the skewness, Kurt is the kurtosis and φx is the value of the variate φ at the xth percentage of the distribution.
Unimodal vs. bimodal distribution[edit]
Pearson in 1894 was the first to devise a procedure to test whether a distribution could be resolved into two normal distributions.[38] This method required the solution of a ninth order polynomial. In a subsequent paper Pearson reported that for any distribution skewness2 + 1 < kurtosis.[26] Later Pearson showed that[39]
where b2 is the kurtosis and b1 is the square of the skewness. Equality holds only for the two point Bernoulli distribution or the sum of two different Dirac delta functions. These are the most extreme cases of bimodality possible. The kurtosis in both these cases is 1. Since they are both symmetrical their skewness is 0 and the difference is 1.
Baker proposed a transformation to convert a bimodal to a unimodal distribution.[40]
Several tests of unimodality versus bimodality have been proposed: Haldane suggested one based on second central differences.[41] Larkin later introduced a test based on the F test;[42] Benett created one based on Fisher’s G test.[43] Tokeshi has proposed a fourth test.[44][45] A test based on a likelihood ratio has been proposed by Holzmann and Vollmer.[20]
A method based on the score and Wald tests has been proposed.[46] This method can distinguish between unimodal and bimodal distributions when the underlying distributions are known.
Antimode tests[edit]
Statistical tests for the antimode are known.[47]
- Otsu’s method
Otsu’s method is commonly employed in computer graphics to determine the optimal separation between two distributions.
General tests[edit]
To test if a distribution is other than unimodal, several additional tests have been devised: the bandwidth test,[48] the dip test,[49] the excess mass test,[50] the MAP test,[51] the mode existence test,[52] the runt test,[53][54] the span test,[55] and the saddle test.
An implementation of the dip test is available for the R programming language.[56] The p-values for the dip statistic values range between 0 and 1. P-values less than 0.05 indicate significant multimodality and p-values greater than 0.05 but less than 0.10 suggest multimodality with marginal significance.[57]
Silverman’s test[edit]
Silverman introduced a bootstrap method for the number of modes.[48] The test uses a fixed bandwidth which reduces the power of the test and its interpretability. Under smoothed densities may have an excessive number of modes whose count during bootstrapping is unstable.
Bajgier-Aggarwal test[edit]
Bajgier and Aggarwal have proposed a test based on the kurtosis of the distribution.[58]
Special cases[edit]
Additional tests are available for a number of special cases:
- Mixture of two normal distributions
A study of a mixture density of two normal distributions data found that separation into the two normal distributions was difficult unless the means were separated by 4–6 standard deviations.[59]
In astronomy the Kernel Mean Matching algorithm is used to decide if a data set belongs to a single normal distribution or to a mixture of two normal distributions.
- Beta-normal distribution
This distribution is bimodal for certain values of is parameters. A test for these values has been described.[60]
Parameter estimation and fitting curves[edit]
Assuming that the distribution is known to be bimodal or has been shown to be bimodal by one or more of the tests above, it is frequently desirable to fit a curve to the data. This may be difficult.
Bayesian methods may be useful in difficult cases.
Software[edit]
- Two normal distributions
A package for R is available for testing for bimodality.[61] This package assumes that the data are distributed as a sum of two normal distributions. If this assumption is not correct the results may not be reliable. It also includes functions for fitting a sum of two normal distributions to the data.
Assuming that the distribution is a mixture of two normal distributions then the expectation-maximization algorithm may be used to determine the parameters. Several programmes are available for this including Cluster,[62] and the R package nor1mix.[63]
- Other distributions
The mixtools package available for R can test for and estimate the parameters of a number of different distributions.[64] A package for a mixture of two right-tailed gamma distributions is available.[65]
Several other packages for R are available to fit mixture models; these include flexmix,[66] mcclust,[67] agrmt,[68] and mixdist.[69]
The statistical programming language SAS can also fit a variety of mixed distributions with the PROC FREQ procedure.
Number of joggers in a park by time of the day (X in hours) in a bimodal probability distribution
Example software application[edit]
The CumFreqA [70] program for the fitting of composite probability distributions to a data set (X) can divide the set into two parts with a different distribution. The figure shows an example of a double generalized mirrored Gumbel distribution as in distribution fitting with cumulative distribution function (CDF) equations:
X < 8.10 : CDF = 1 - exp[-exp{-(0.092X^0.01+935)}]
X > 8.10 : CDF = 1 - exp[-exp{-(-0.0039X^2.79+1.05)}]
See also[edit]
- Overdispersion
References[edit]
- ^ Galtung, J. (1969). Theory and methods of social research. Oslo: Universitetsforlaget. ISBN 0-04-300017-7.
- ^ Fieller E (1932). «The distribution of the index in a normal bivariate population». Biometrika. 24 (3–4): 428–440. doi:10.1093/biomet/24.3-4.428.
- ^ Fiorio, CV; HajivassILiou, VA; Phillips, PCB (2010). «Bimodal t-ratios: the impact of thick tails on inference». The Econometrics Journal. 13 (2): 271–289. doi:10.1111/j.1368-423X.2010.00315.x. S2CID 363740.
- ^ Introduction to tropical fish stock assessment
- ^ Phillips, P. C. B. (2006). «A remark on bimodality and weak instrumentation in structural equation estimation» (PDF). Econometric Theory. 22 (5): 947–960. doi:10.1017/S0266466606060439. S2CID 16775883.
- ^ Hassan, MY; Hijazi, RH (2010). «A bimodal exponential power distribution». Pakistan Journal of Statistics. 26 (2): 379–396.
- ^ Elal-Olivero, D (2010). «Alpha-skew-normal distribution». Proyecciones Journal of Mathematics. 29 (3): 224–240. doi:10.4067/s0716-09172010000300006.
- ^ Hassan, M. Y.; El-Bassiouni, M. Y. (2016). «Bimodal skew-symmetric normal distribution». Communications in Statistics — Theory and Methods. 45 (5): 1527–1541. doi:10.1080/03610926.2014.882950. S2CID 124087015.
- ^ Bosea, S.; Shmuelib, G.; Sura, P.; Dubey, P. (2013). «Fitting Com-Poisson mixtures to bimodal count data» (PDF). Proceedings of the 2013 International Conference on Information, Operations Management and Statistics (ICIOMS2013), Kuala Lumpur, Malaysia. pp. 1–8.
- ^ Weber, NA (1946). «Dimorphism in the African Oecophylla worker and an anomaly (Hym.: Formicidae)» (PDF). Annals of the Entomological Society of America. 39: 7–10. doi:10.1093/aesa/39.1.7.
- ^ Sanjuán, R (Jun 27, 2010). «Mutational fitness effects in RNA and single-stranded DNA viruses: common patterns revealed by site-directed mutagenesis studies». Philosophical Transactions of the Royal Society of London B: Biological Sciences. 365 (1548): 1975–82. doi:10.1098/rstb.2010.0063. PMC 2880115. PMID 20478892.
- ^ Eyre-Walker, A; Keightley, PD (Aug 2007). «The distribution of fitness effects of new mutations». Nature Reviews Genetics. 8 (8): 610–8. doi:10.1038/nrg2146. PMID 17637733. S2CID 10868777.
- ^ Hietpas, RT; Jensen, JD; Bolon, DN (May 10, 2011). «Experimental illumination of a fitness landscape». Proceedings of the National Academy of Sciences of the United States of America. 108 (19): 7896–901. Bibcode:2011PNAS..108.7896H. doi:10.1073/pnas.1016024108. PMC 3093508. PMID 21464309.
- ^ a b c Schilling, Mark F.; Watkins, Ann E.; Watkins, William (2002). «Is Human Height Bimodal?». The American Statistician. 56 (3): 223–229. doi:10.1198/00031300265. S2CID 53495657.
- ^ Mosteller, F.; Tukey, J. W. (1977). Data Analysis and Regression: A Second Course in Statistics. Reading, Mass: Addison-Wesley. ISBN 0-201-04854-X.
- ^ Kim, T.-H.; White, H. (2003). «On more robust estimation of skewness and kurtosis: Simulation and application to the S & P 500 index» (PDF).
- ^ Robertson, CA; Fryer, JG (1969). «Some descriptive properties of normal mixtures». Skandinavisk Aktuarietidskrift. 69 (3–4): 137–146. doi:10.1080/03461238.1969.10404590.
- ^ Eisenberger, I (1964). «Genesis of bimodal distributions». Technometrics. 6 (4): 357–363. doi:10.1080/00401706.1964.10490199.
- ^ Ray, S; Lindsay, BG (2005). «The topography of multivariate normal mixtures». Annals of Statistics. 33 (5): 2042–2065. arXiv:math/0602238. doi:10.1214/009053605000000417. S2CID 36234163.
- ^ a b Holzmann, Hajo; Vollmer, Sebastian (2008). «A likelihood ratio test for bimodality in two-component mixtures with application to regional income distribution in the EU». AStA Advances in Statistical Analysis. 2 (1): 57–69. doi:10.1007/s10182-008-0057-2. S2CID 14470055.
- ^ a b Behboodian, J (1970). «On the modes of a mixture of two normal distributions». Technometrics. 12 (1): 131–139. doi:10.2307/1267357. JSTOR 1267357.
- ^ Ashman KM; Bird CM; Zepf SE (1994). «Detecting bimodality in astronomical datasets». The Astronomical Journal. 108: 2348–2361. arXiv:astro-ph/9408030. Bibcode:1994AJ….108.2348A. doi:10.1086/117248. S2CID 13464256.
- ^ Van der Eijk, C (2001). «Measuring agreement in ordered rating scales». Quality & Quantity. 35 (3): 325–341. doi:10.1023/a:1010374114305. S2CID 189822180.
- ^ a b c Zhang, C; Mapes, BE; Soden, BJ (2003). «Bimodality in tropical water vapour». Quarterly Journal of the Royal Meteorological Society. 129 (594): 2847–2866. Bibcode:2003QJRMS.129.2847Z. doi:10.1256/qj.02.166. S2CID 17153773.
- ^ Ellison, AM (1987). «Effect of seed dimorphism on the density-dependent dynamics of experimental populations of Atriplex triangularis (Chenopodiaceae)». American Journal of Botany. 74 (8): 1280–1288. doi:10.2307/2444163. JSTOR 2444163.
- ^ a b Pearson, K (1916). «Mathematical contributions to the theory of evolution, XIX: Second supplement to a memoir on skew variation». Philosophical Transactions of the Royal Society A. 216 (538–548): 429–457. Bibcode:1916RSPTA.216..429P. doi:10.1098/rsta.1916.0009. JSTOR 91092.
- ^ SAS Institute Inc. (2012). SAS/STAT 12.1 user’s guide. Cary, NC: Author.
- ^ Pfister, R; Schwarz, KA; Janczyk, M.; Dale, R; Freeman, JB (2013). «Good things peak in pairs: A note on the bimodality coefficient». Frontiers in Psychology. 4: 700. doi:10.3389/fpsyg.2013.00700. PMC 3791391. PMID 24109465.
- ^ Wilcock, PR (1993). «The critical shear stress of natural sediments». Journal of Hydraulic Engineering. 119 (4): 491–505. doi:10.1061/(asce)0733-9429(1993)119:4(491).
- ^ Wang, J; Wen, S; Symmans, WF; Pusztai, L; Coombes, KR (2009). «The bimodality index: a criterion for discovering and ranking bimodal signatures from cancer gene expression profiling data». Cancer Informatics. 7: 199–216. doi:10.4137/CIN.S2846. PMC 2730180. PMID 19718451.
- ^ Sturrock, P (2008). «Analysis of bimodality in histograms formed from GALLEX and GNO solar neutrino data». Solar Physics. 249 (1): 1–10. arXiv:0711.0216. Bibcode:2008SoPh..249….1S. doi:10.1007/s11207-008-9170-3. S2CID 118389173.
- ^ Scargle, JD (1982). «Studies in astronomical time series analysis. II – Statistical aspects of spectral analysis of unevenly spaced data». The Astrophysical Journal. 263 (1): 835–853. Bibcode:1982ApJ…263..835S. doi:10.1086/160554.
- ^ De Michele, C; Accatino, F (2014). «Tree cover bimodality in savannas and forests emerging from the switching between two fire dynamics». PLOS ONE. 9 (3): e91195. Bibcode:2014PLoSO…991195D. doi:10.1371/journal.pone.0091195. PMC 3963849. PMID 24663432.
- ^ Sambrook Smith, GH; Nicholas, AP; Ferguson, RI (1997). «Measuring and defining bimodal sediments: Problems and implications». Water Resources Research. 33 (5): 1179–1185. Bibcode:1997WRR….33.1179S. doi:10.1029/97wr00365.
- ^ Chaudhuri, D; Agrawal, A (2010). «Split-and-merge procedure for image segmentation using bimodality detection approach». Defence Science Journal. 60 (3): 290–301. doi:10.14429/dsj.60.356.
- ^ a b Folk, RL; Ward, WC (1957). «Brazos River bar: a study in the significance of grain size parameters». Journal of Sedimentary Research. 27 (1): 3–26. Bibcode:1957JSedR..27….3F. doi:10.1306/74d70646-2b21-11d7-8648000102c1865d.
- ^ Dyer, KR (1970). «Grain-size parameters for sandy gravels». Journal of Sedimentary Research. 40 (2): 616–620. doi:10.1306/74D71FE6-2B21-11D7-8648000102C1865D.
- ^ Pearson, K (1894). «Contributions to the mathematical theory of evolution: On the dissection of asymmetrical frequency-curves». Philosophical Transactions of the Royal Society A. 185: 71–90. Bibcode:1894RSPTA.185…71P. doi:10.1098/rsta.1894.0003.
- ^ Pearson, K (1929). «Editorial note». Biometrika. 21: 370–375.
- ^ Baker, GA (1930). «Transformations of bimodal distributions». Annals of Mathematical Statistics. 1 (4): 334–344. doi:10.1214/aoms/1177733063.
- ^ Haldane, JBS (1951). «Simple tests for bimodality and bitangentiality». Annals of Eugenics. 16 (1): 359–364. doi:10.1111/j.1469-1809.1951.tb02488.x. PMID 14953132.
- ^ Larkin, RP (1979). «An algorithm for assessing bimodality vs. unimodality in a univariate distribution». Behavior Research Methods & Instrumentation. 11 (4): 467–468. doi:10.3758/BF03205709.
- ^ Bennett, SC (1992). «Sexual dimorphism of Pteranodon and other pterosaurs, with comments on cranial crests». Journal of Vertebrate Paleontology. 12 (4): 422–434. doi:10.1080/02724634.1992.10011472.
- ^ Tokeshi, M (1992). «Dynamics and distribution in animal communities; theory and analysis». Researches on Population Ecology. 34 (2): 249–273. doi:10.1007/bf02514796. S2CID 22912914.
- ^ Barreto, S; Borges, PAV; Guo, Q (2003). «A typing error in Tokeshi’s test of bimodality». Global Ecology and Biogeography. 12 (2): 173–174. doi:10.1046/j.1466-822x.2003.00018.x. hdl:10400.3/1408.
- ^ Carolan, AM; Rayner, JCW (2001). «One sample tests for the location of modes of nonnormal data». Journal of Applied Mathematics and Decision Sciences. 5 (1): 1–19. CiteSeerX 10.1.1.504.4999. doi:10.1155/s1173912601000013.
- ^ Hartigan, J. A. (2000). «Testing for Antimodes». In Gaul W; Opitz O; Schader M (eds.). Data Analysis. Studies in Classification, Data Analysis, and Knowledge Organization. Springer. pp. 169–181. ISBN 3-540-67731-3.
- ^ a b Silverman, B. W. (1981). «Using kernel density estimates to investigate multimodality». Journal of the Royal Statistical Society, Series B. 43 (1): 97–99. Bibcode:1981JRSSB..43…97S. doi:10.1111/j.2517-6161.1981.tb01155.x. JSTOR 2985156.
- ^ Hartigan, JA; Hartigan, PM (1985). «The dip test of unimodality». Annals of Statistics. 13 (1): 70–84. doi:10.1214/aos/1176346577.
- ^ Mueller, DW; Sawitzki, G (1991). «Excess mass estimates and tests for multimodality». Journal of the American Statistical Association. 86 (415): 738–746. doi:10.1080/01621459.1991.10475103. JSTOR 2290406.
- ^ Rozál, GPM Hartigan JA (1994). «The MAP test for multimodality». Journal of Classification. 11 (1): 5–36. doi:10.1007/BF01201021. S2CID 118500771.
- ^ Minnotte, MC (1997). «Nonparametric testing of the existence of modes». Annals of Statistics. 25 (4): 1646–1660. doi:10.1214/aos/1031594735.
- ^ Hartigan, JA; Mohanty, S (1992). «The RUNT test for multimodality». Journal of Classification. 9: 63–70. doi:10.1007/bf02618468. S2CID 121960832.
- ^ Andrushkiw RI; Klyushin DD; Petunin YI (2008). «A new test for unimodality». Theory of Stochastic Processes. 14 (1): 1–6.
- ^ Hartigan, J. A. (1988). «The Span Test of Multimodality». In Bock, H. H. (ed.). Classification and Related Methods of Data Analysis. Amsterdam: North-Holland. pp. 229–236. ISBN 0-444-70404-3.
- ^ Ringach, Martin Maechler (originally from Fortran and S.-plus by Dario; NYU.edu) (5 December 2016). «diptest: Hartigan’s Dip Test Statistic for Unimodality — Corrected» – via R-Packages.
- ^ Freeman; Dale (2012). «Assessing bimodality to detect the presence of a dual cognitive process» (PDF). Behavior Research Methods. 45 (1): 83–97. doi:10.3758/s13428-012-0225-x. PMID 22806703. S2CID 14500508.
- ^ Bajgier SM; Aggarwal LK (1991). «Powers of goodness-of-fit tests in detecting balanced mixed normal distributions». Educational and Psychological Measurement. 51 (2): 253–269. doi:10.1177/0013164491512001. S2CID 121113601.
- ^ Jackson, PR; Tucker, GT; Woods, HF (1989). «Testing for bimodality in frequency distributions of data suggesting polymorphisms of drug metabolism—hypothesis testing». British Journal of Clinical Pharmacology. 28 (6): 655–662. doi:10.1111/j.1365-2125.1989.tb03558.x. PMC 1380036. PMID 2611088.
- ^ Inc., Advanced Solutions International. «Sections & Interest Groups» (PDF). www.amstat.org.
- ^ «Archived copy» (PDF). Archived from the original (PDF) on 2013-11-03. Retrieved 2013-11-01.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ «Cluster home page». engineering.purdue.edu.
- ^ Mächler, Martin (25 August 2016). «nor1mix: Normal (1-d) Mixture Models (S3 Classes and Methods)» – via R-Packages.
- ^ Young, Derek; Benaglia, Tatiana; Chauveau, Didier; Hunter, David; Elmore, Ryan; Hettmansperger, Thomas; Thomas, Hoben; Xuan, Fengjuan (10 March 2017). «mixtools: Tools for Analyzing Finite Mixture Models» – via R-Packages.
- ^ «discrimARTs» (PDF). cran.r-project.org. Retrieved 22 March 2018.
- ^ Gruen, Bettina; Leisch, Friedrich; Sarkar, Deepayan; Mortier, Frederic; Picard, Nicolas (28 April 2017). «flexmix: Flexible Mixture Modeling» – via R-Packages.
- ^ Fraley, Chris; Raftery, Adrian E.; Scrucca, Luca; Murphy, Thomas Brendan; Fop, Michael (21 May 2017). «mclust: Gaussian Mixture Modelling for Model-Based Clustering, Classification, and Density Estimation» – via R-Packages.
- ^ Ruedin, Didier (2 April 2016). «agrmt». cran.r-project.org.
- ^ Macdonald, Peter; Du, with contributions from Juan (29 October 2012). «mixdist: Finite Mixture Distribution Models» – via R-Packages.
- ^ CumFreq, free program for fitting of probability distributions to a data set. On line: [1]
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Поделиться ссылкой:
Так как я часто имею дело с большим количеством данных, у меня время от времени возникает необходимость генерировать массивы значений для проверки моделей в Excel. К примеру, если я хочу увидеть распределение веса продукта с определенным стандартным отклонением, потребуются некоторые усилия, чтобы привести результат работы формулы СЛУЧМЕЖДУ() в нормальный вид. Дело в том, что формула СЛУЧМЕЖДУ() выдает числа с единым распределением, т.е. любое число с одинаковой долей вероятности может оказаться как у нижней, так и у верхней границы запрашиваемого диапазона. Такое положение дел не соответствует действительности, так как вероятность возникновения продукта уменьшается по мере отклонения от целевого значения. Т.е. если я произвожу продукт весом 100 грамм, вероятность, что я произведу 97-ми или 103-граммовый продукт меньше, чем 100 грамм. Вес большей части произведенной продукции будет сосредоточен рядом с целевым значением. Такое распределение называется нормальным. Если построить график, где по оси Y отложить вес продукта, а по оси X – количество произведенного продукта, график будет иметь колоколообразный вид, где наивысшая точка будет соответствовать целевому значению.
Таким образом, чтобы привести массив, выданный формулой СЛУЧМЕЖДУ(), в нормальный вид, мне приходилось ручками исправлять пограничные значения на близкие к целевым. Такое положение дел меня, естественно, не устраивало, поэтому, покопавшись в интернете, открыл интересный способ создания массива данных с нормальным распределением. В сегодняшней статье описан способ генерации массива и построения графика с нормальным распределением.
Характеристики нормального распределения
Непрерывная случайная переменная, которая подчиняется нормальному распределению вероятностей, обладает некоторыми особыми свойствами. Предположим, что вся производимая продукция подчиняется нормальному распределению со средним значением 100 грамм и стандартным отклонением 3 грамма. Распределение вероятностей для такой случайной переменной представлено на рисунке.
Из этого рисунка мы можем сделать следующие наблюдения относительно нормального распределения — оно имеет форму колокола и симметрично относительно среднего значения.
Стандартное отклонение имеет немаловажную роль в форме изгиба. Если посмотреть на предыдущий рисунок, то можно заметить, что практически все измерения веса продукта попадают в интервал от 95 до 105 граммов. Давайте рассмотрим следующий рисунок, на котором представлено нормальное распределение с той же средней – 100 грамм, но со стандартным отклонением всего 1,5 грамма
Здесь вы видите, что измерения значительно плотней прилегают к среднему значению. Почти все производимые продукты попадают в интервал от 97 до 102 грамм.
Небольшое значение стандартного отклонения выражается в более «тощей и высокой кривой, плотно прижимающейся к среднему значению. Чем больше стандартное, тем «толще», ниже и растянутее получается кривая.
Создание массива с нормальным распределением
Итак, чтобы сгенерировать массив данных с нормальным распределением, нам понадобится функция НОРМ.ОБР() – это обратная функция от НОРМ.РАСП(), которая возвращает нормально распределенную переменную для заданной вероятности для определенного среднего значения и стандартного отклонения. Синтаксис формулы выглядит следующим образом:
=НОРМ.ОБР(вероятность; среднее_значение; стандартное_отклонение)
Другими словами, я прошу Excel посчитать, какая переменная будет находится в вероятностном промежутке от 0 до 1. И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных.
Давайте попробуем разобрать на примере. Выстроим график распределения вероятностей от 0 до 1 с шагом 0,01 для среднего значения равным 100 и стандартным отклонением 1,5.
Как видим из графика точки максимально сконцентрированы у переменной 100 и вероятности 0,5.
Этот фокус мы используем для генерирования случайного массива данных с нормальным распределением. Формула будет выглядеть следующим образом:
=НОРМ.ОБР(СЛЧИС(); среднее_значение; стандартное_отклонение)
Создадим массив данных для нашего примера со средним значением 100 грамм и стандартным отклонением 1,5 грамма и протянем нашу формулу вниз.
Теперь, когда массив данных готов, мы можем выстроить график с нормальным распределением.
Построение графика нормального распределения
Прежде всего необходимо разбить наш массив на периоды. Для этого определяем минимальное и максимальное значение, размер каждого периода или шаг, с которым будет увеличиваться период.
Далее строим таблицу с категориями. Нижняя граница (B11) равняется округленному вниз ближайшему кратному числу. Остальные категории увеличиваются на значение шага. Формула в ячейке B12 и последующих будет выглядеть:
=ЕСЛИ(A12;B11+$B$6; «»)
В столбце X будет производится подсчет количества переменных в заданном промежутке. Для этого воспользуемся формулой ЧАСТОТА(), которая имеет два аргумента: массив данных и массив интервалов. Выглядеть формула будет следующим образом =ЧАСТОТА(Data!A1:A175;B11:B20). Также стоит отметить, что в таком варианте данная функция будет работать как формула массива, поэтому по окончании ввода необходимо нажать сочетание клавиш Ctrl+Shift+Enter.
Таким образом у нас получилась таблица с данными, с помощью которой мы сможем построить диаграмму с нормальным распределением. Воспользуемся диаграммой вида Гистограмма с группировкой, где по оси значений будет отложено количество переменных в данном промежутке, а по оси категорий – периоды.
Осталось отформатировать диаграмму и наш график с нормальным распределением готов.
Итак, мы познакомились с вами с нормальным распределением, узнали, что Excel позволяет генерировать массив данных с помощью формулы НОРМ.ОБР() для определенного среднего значения и стандартного отклонения и научились приводить данный массив в графический вид.
Для лучшего понимания, вы можете скачать файл с примером построения нормального распределения.
Построим диаграмму распределения в Excel. А также рассмотрим подробнее функции круговых диаграмм, их создание.
График нормального распределения имеет форму колокола и симметричен относительно среднего значения. Получить такое графическое изображение можно только при огромном количестве измерений. В Excel для конечного числа измерений принято строить гистограмму.
Внешне столбчатая диаграмма похожа на график нормального распределения. Построим столбчатую диаграмму распределения осадков в Excel и рассмотрим 2 способа ее построения.
Имеются следующие данные о количестве выпавших осадков:
Первый способ. Открываем меню инструмента «Анализ данных» на вкладке «Данные» (если у Вас не подключен данный аналитический инструмент, тогда читайте как его подключить в настройках Excel):
Выбираем «Гистограмма»:
Задаем входной интервал (столбец с числовыми значениями). Поле «Интервалы карманов» оставляем пустым: Excel сгенерирует автоматически. Ставим птичку около записи «Вывод графика»:
После нажатия ОК получаем такой график с таблицей:
В интервалах не очень много значений, поэтому столбики гистограммы получились низкими.
Теперь необходимо сделать так, чтобы по вертикальной оси отображались относительные частоты.
Найдем сумму всех абсолютных частот (с помощью функции СУММ). Сделаем дополнительный столбец «Относительная частота». В первую ячейку введем формулу:
Способ второй. Вернемся к таблице с исходными данными. Вычислим интервалы карманов. Сначала найдем максимальное значение в диапазоне температур и минимальное.
Чтобы найти интервал карманов, нужно разность максимального и минимального значений массива разделить на количество интервалов. Получим «ширину кармана».
Представим интервалы карманов в виде столбца значений. Сначала ширину кармана прибавляем к минимальному значению массива данных. В следующей ячейке – к полученной сумме. И так далее, пока не дойдем до максимального значения.
Для определения частоты делаем столбец рядом с интервалами карманов. Вводим функцию массива:
Вычислим относительные частоты (как в предыдущем способе).
Построим столбчатую диаграмму распределения осадков в Excel с помощью стандартного инструмента «Диаграммы».
Частота распределения заданных значений:
Круговые диаграммы для иллюстрации распределения
С помощью круговой диаграммы можно иллюстрировать данные, которые находятся в одном столбце или одной строке. Сегмент круга – это доля каждого элемента массива в сумме всех элементов.
С помощью любой круговой диаграммы можно показать распределение в том случае, если
- имеется только один ряд данных;
- все значения положительные;
- практически все значения выше нуля;
- не более семи категорий;
- каждая категория соответствует сегменту круга.
На основании имеющихся данных о количестве осадков построим круговую диаграмму.
Доля «каждого месяца» в общем количестве осадков за год:
Круговая диаграмма распределения осадков по сезонам года лучше смотрится, если данных меньше. Найдем среднее количество осадков в каждом сезоне, используя функцию СРЗНАЧ. На основании полученных данных построим диаграмму:
Получили количество выпавших осадков в процентном выражении по сезонам.
В двух словах: Добавляем полосу прокрутки к гистограмме или к графику распределения частот, чтобы сделать её динамической или интерактивной.
Уровень сложности: продвинутый.
На следующем рисунке показано, как выглядит готовая динамическая гистограмма:
Что такое гистограмма или график распределения частот?
Гистограмма распределения разбивает по группам значения из набора данных и показывает количество (частоту) чисел в каждой группе. Такую гистограмму также называют графиком распределения частот, поскольку она показывает, с какой частотой представлены значения.
В нашем примере мы делим людей, которые вызвались принять участие в мероприятии, по возрастным группам. Первым делом, создадим возрастные группы, далее подсчитаем, сколько людей попадает в каждую из групп, и затем покажем все это на гистограмме.
На какие вопросы отвечает гистограмма распределения?
Гистограмма – это один из моих самых любимых типов диаграмм, поскольку она дает огромное количество информации о данных.
В данном случае мы хотим знать, как много участников окажется в возрастных группах 20-ти, 30-ти, 40-ка лет и так далее. Гистограмма наглядно покажет это, поэтому определить закономерности и отклонения будет довольно легко.
«Неужели наше мероприятие не интересно гражданам в возрасте от 20 до 29 лет?»
Возможно, мы захотим немного изменить детализацию картины и разбить население на две возрастные группы. Это покажет нам, что в мероприятии примут участие большей частью молодые люди:
Динамическая гистограмма
После построения гистограммы распределения частот иногда возникает необходимость изменить размер групп, чтобы ответить на различные возникающие вопросы. В динамической гистограмме это возможно сделать благодаря полосе прокрутки (слайдеру) под диаграммой. Пользователь может увеличивать или уменьшать размер групп, нажимая стрелки на полосе прокрутки.
Такой подход делает гистограмму интерактивной и позволяет пользователю масштабировать ее, выбирая, сколько групп должно быть показано. Это отличное дополнение к любому дашборду!
Как это работает?
Краткий ответ: Формулы, динамические именованные диапазоны, элемент управления «Полоса прокрутки» в сочетании с гистограммой.
Формулы
Чтобы всё работало, первым делом нужно при помощи формул вычислить размер группы и количество элементов в каждой группе.
Чтобы вычислить размер группы, разделим общее количество (80-10) на количество групп. Количество групп устанавливается настройками полосы прокрутки. Чуть позже разъясним это подробнее.
Далее при помощи функции ЧАСТОТА (FREQUENCY) я рассчитываю количество элементов в каждой группе в заданном столбце. В данном случае мы возвращаем частоту из столбца Age таблицы с именем tblData.
=ЧАСТОТА(tblData;C13:C22)=FREQUENCY(tblData,C13:C22)
Функция ЧАСТОТА (FREQUENCY) вводится, как формула массива, нажатием Ctrl+Shift+Enter.
Динамический именованный диапазон
В качестве источника данных для диаграммы используется именованный диапазон, чтобы извлекать данные только из выбранных в текущий момент групп.
Когда пользователь перемещает ползунок полосы прокрутки, число строк в динамическом диапазоне изменяется так, чтобы отобразить на графике только нужные данные. В нашем примере задано два динамических именованных диапазона: один для данных — rngGroups (столбец Frequency) и второй для подписей горизонтальной оси — rngCount (столбец Bin Name).
Элемент управления «Полоса прокрутки»
Элемент управления Полоса прокрутки (Scroll Bar) может быть вставлен с вкладки Разработчик (Developer).
На рисунке ниже видно, как я настроил параметры элемента управления и привязал его к ячейке C7. Так, изменяя состояние полосы прокрутки, пользователь управляет формулами.
Гистограмма
График – это самая простая часть задачи. Создаём простую гистограмму и в качестве источника данных устанавливаем динамические именованные диапазоны.
Есть вопросы?
Что ж, это был лишь краткий обзор того, как работает динамическая гистограмма.
Да, это не самая простая диаграмма, но, полагаю, пользователям понравится с ней работать. Определённо, такой интерактивной диаграммой можно украсить любой отчёт.
Более простой вариант гистограммы можно создать, используя сводные таблицы.
Пишите в комментариях любые вопросы и предложения. Спасибо!
Урок подготовлен для Вас командой сайта office-guru.ru
Источник: /> Перевел: Антон Андронов
Правила перепечаткиЕще больше уроков по Microsoft Excel
Оцените качество статьи. Нам важно ваше мнение:

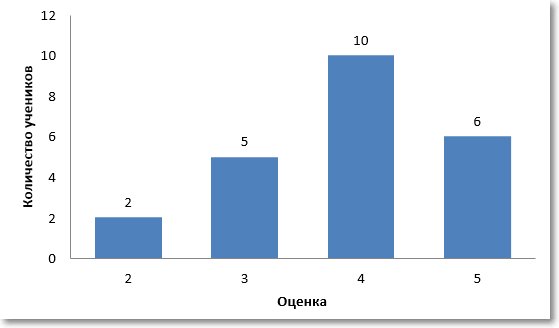
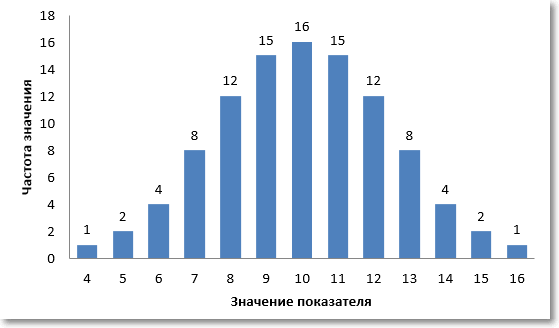
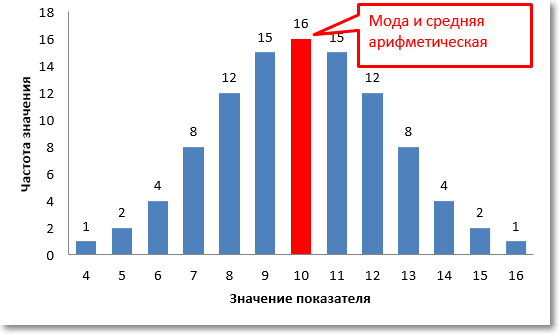
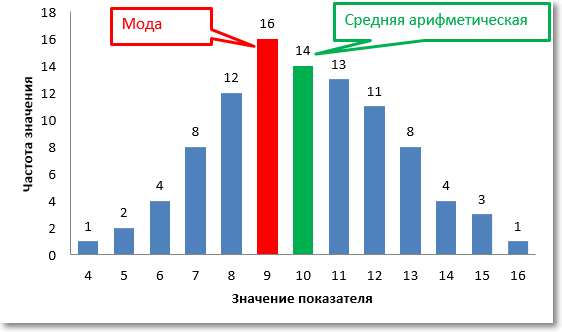
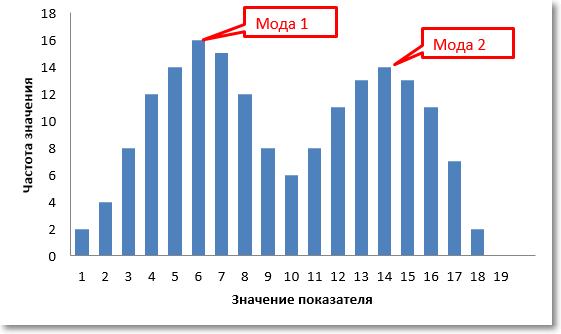
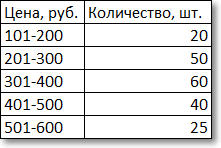
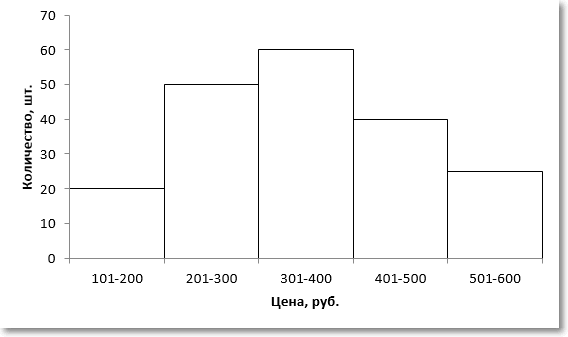
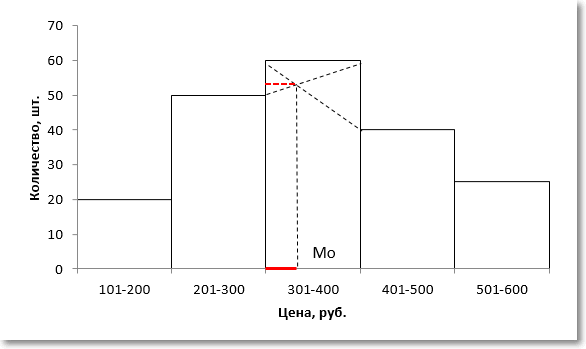
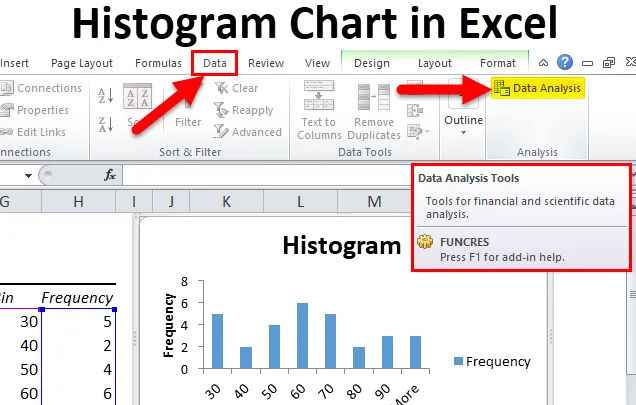





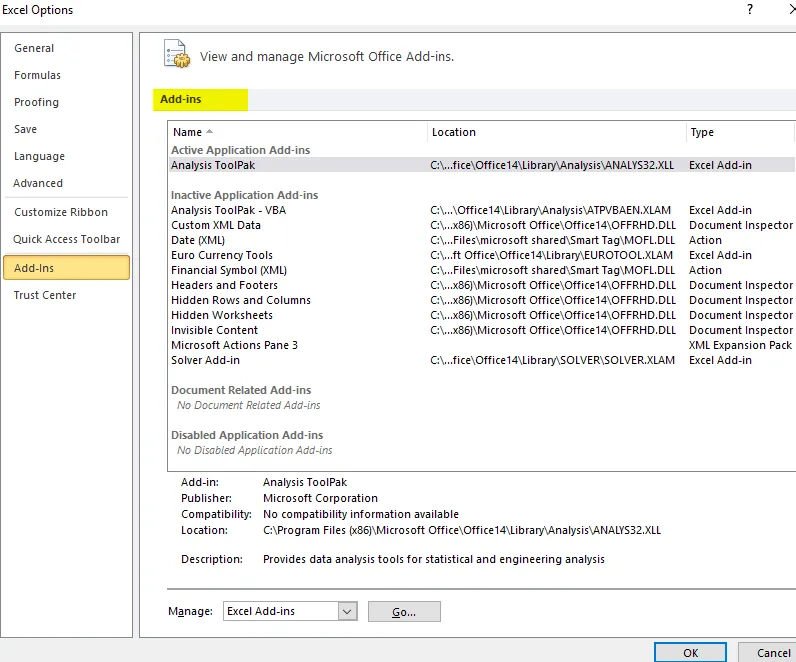
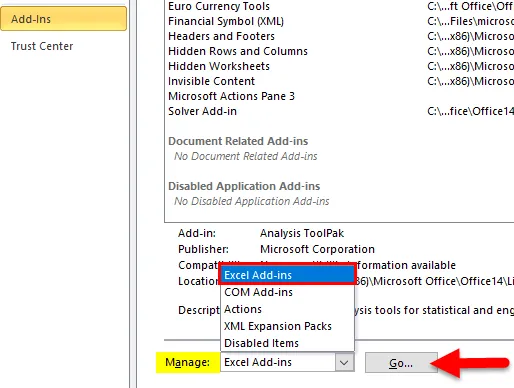
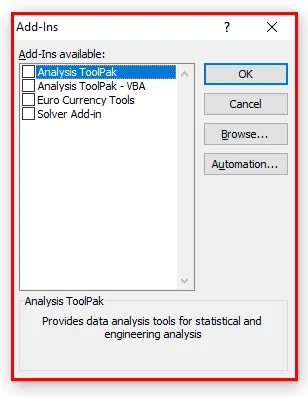
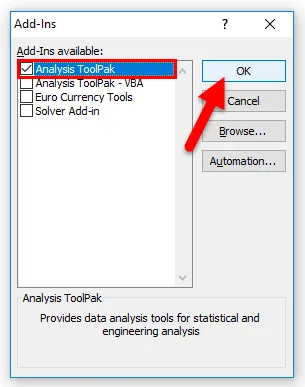
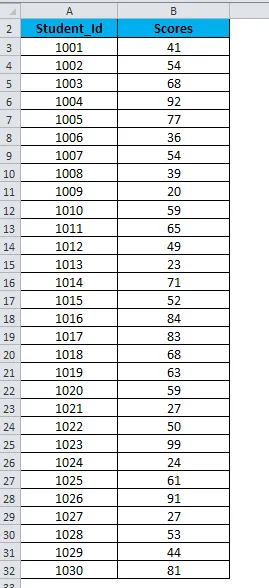
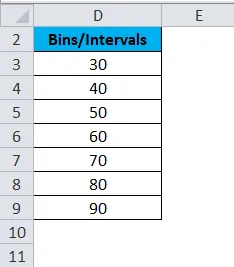
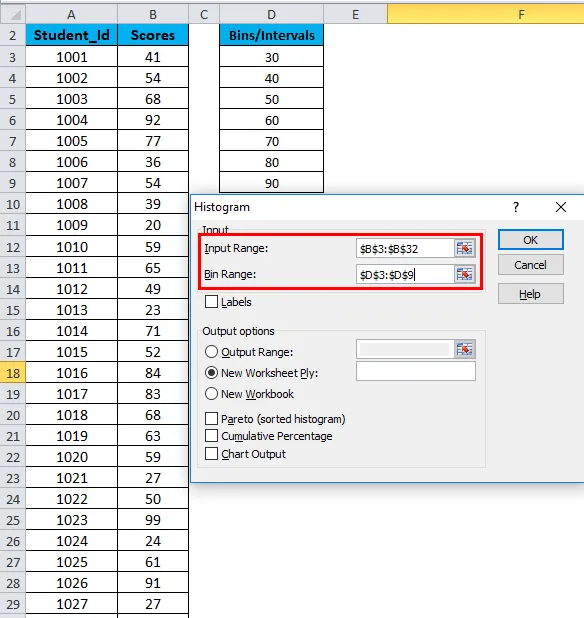
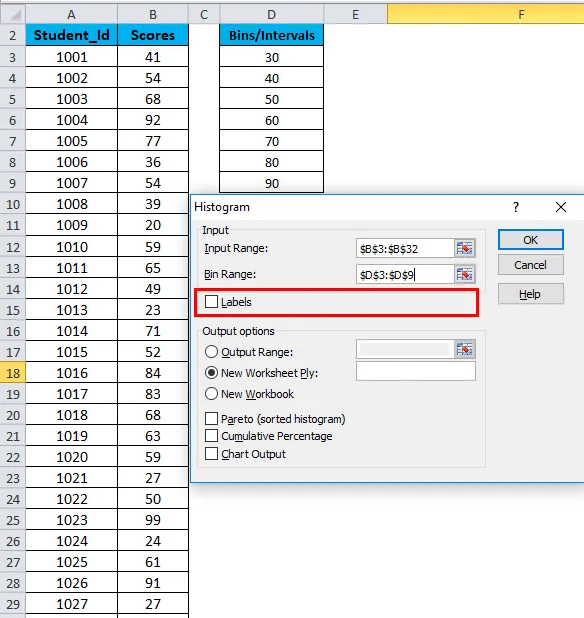
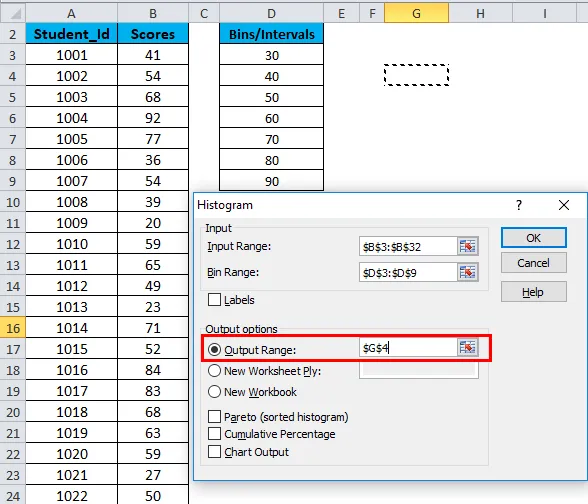
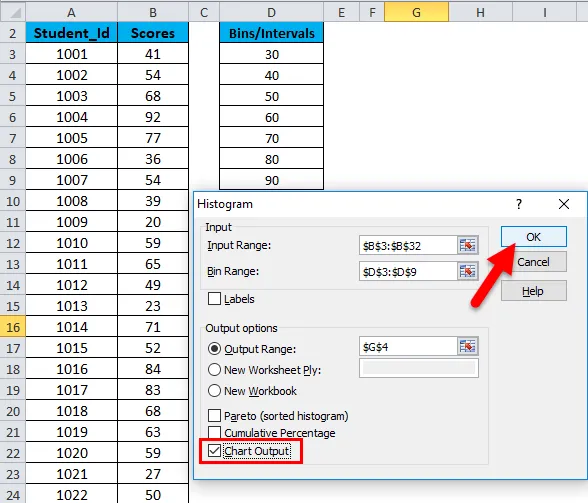
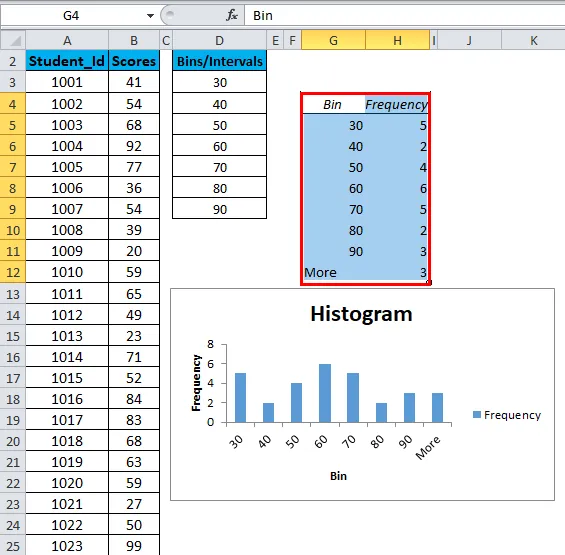
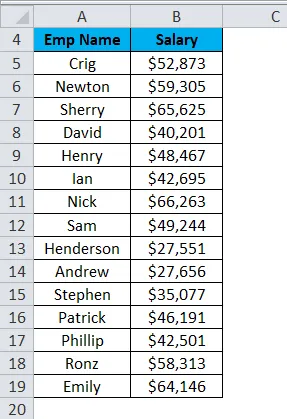
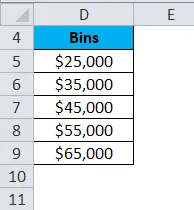
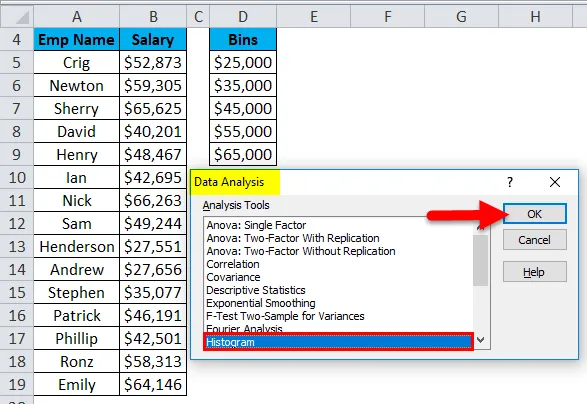
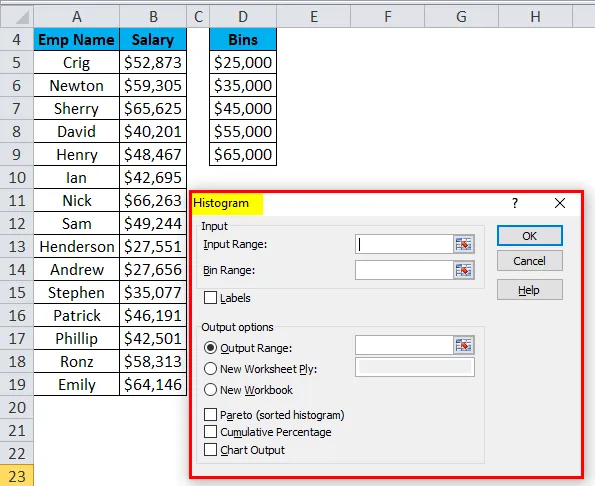
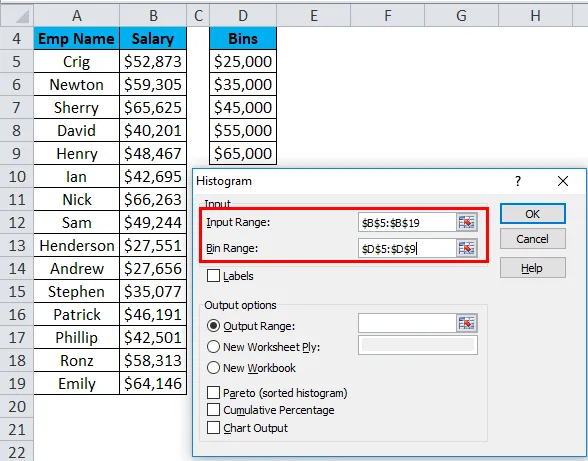
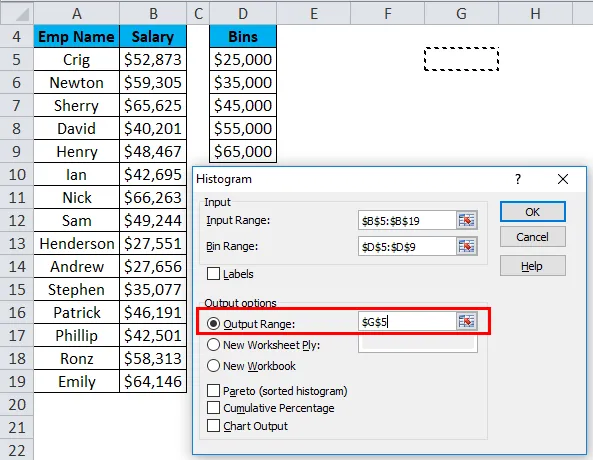
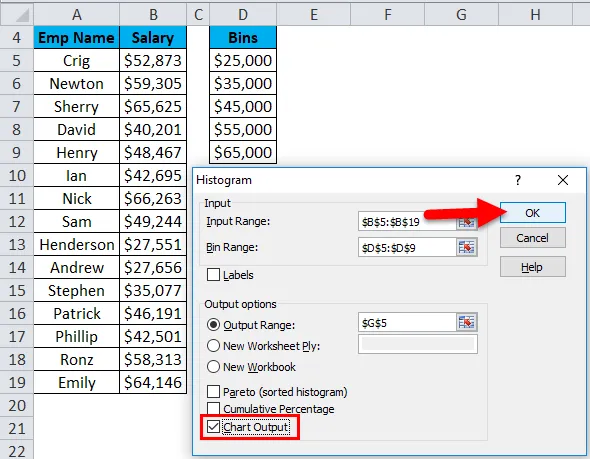
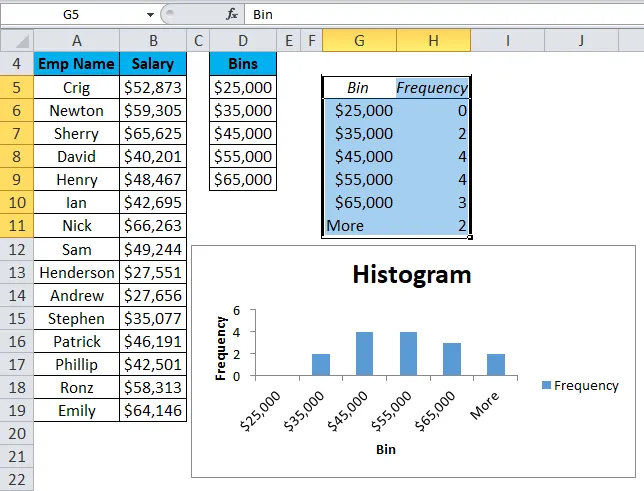
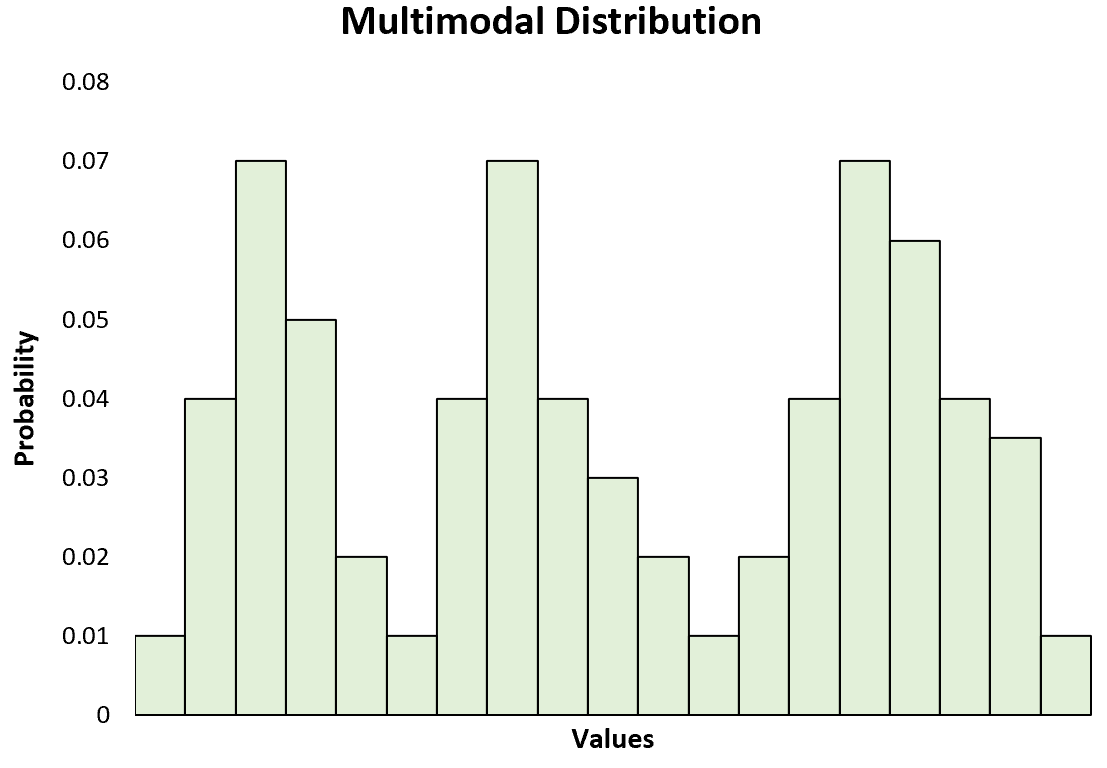
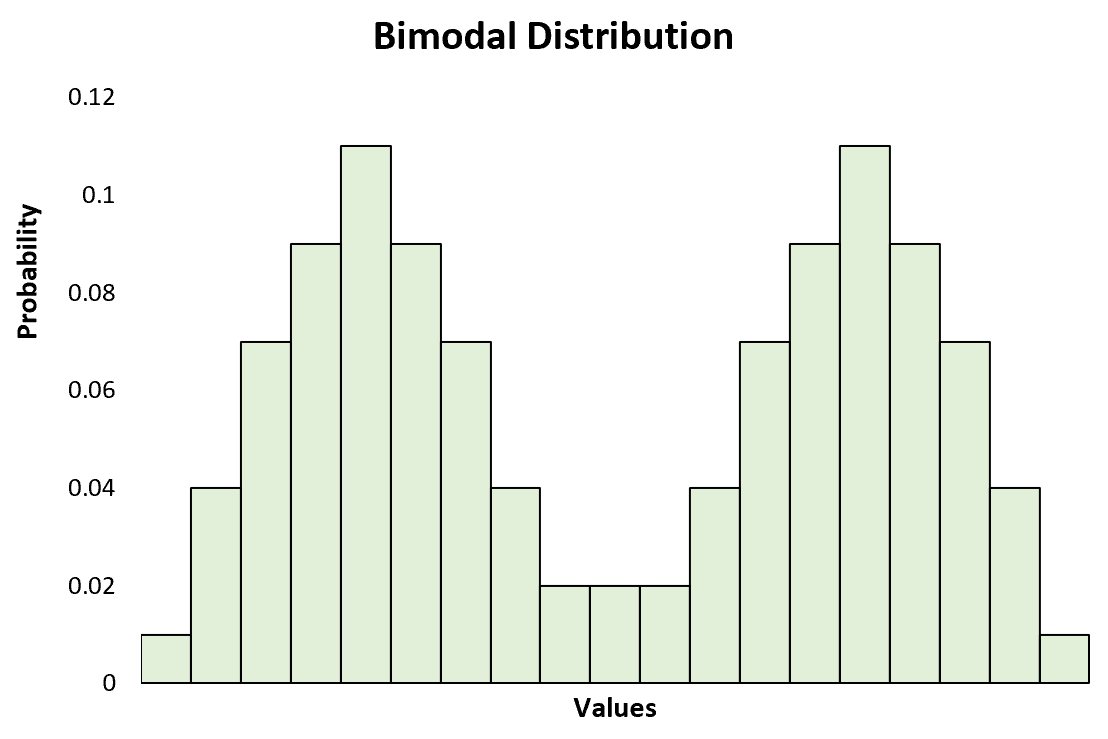
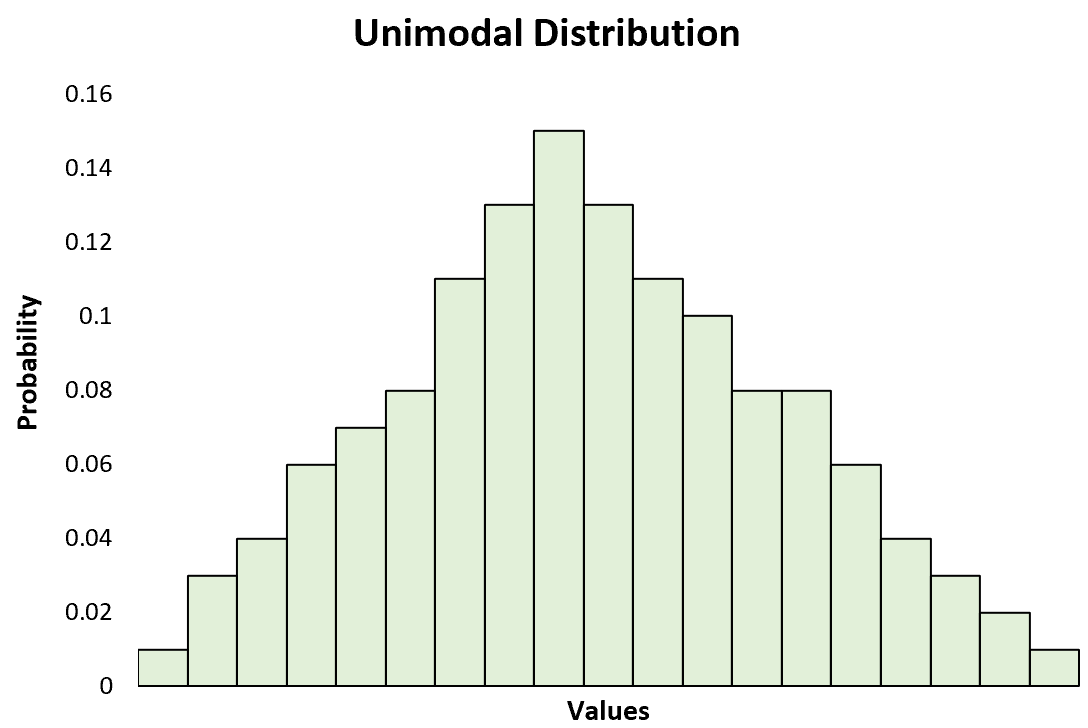
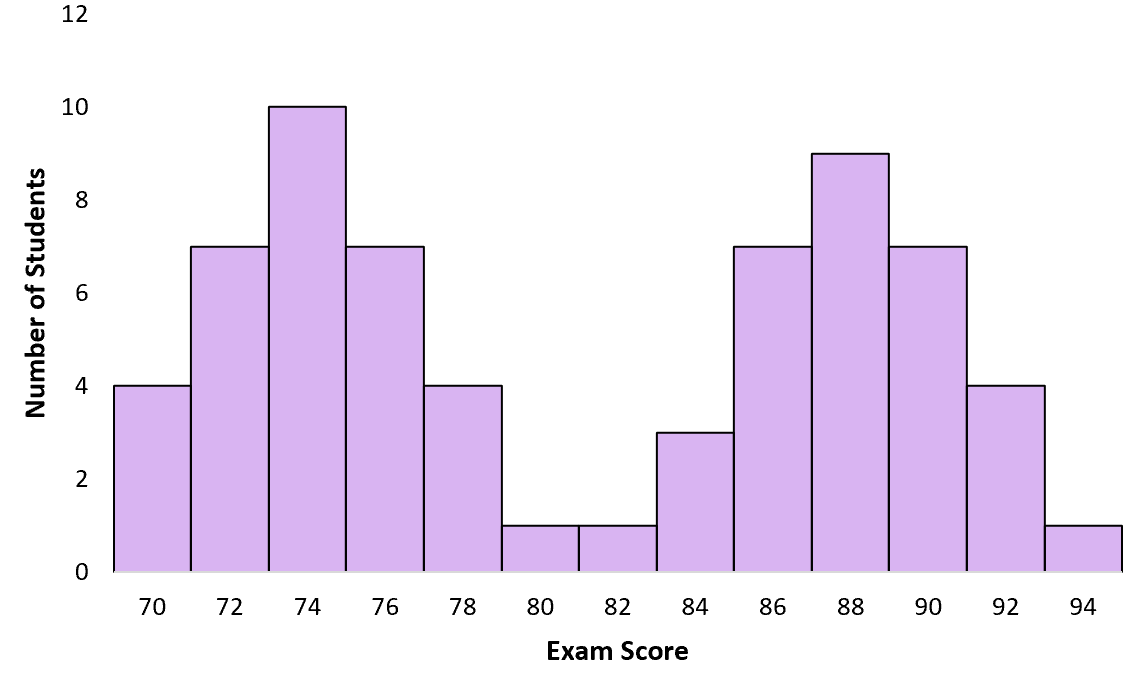
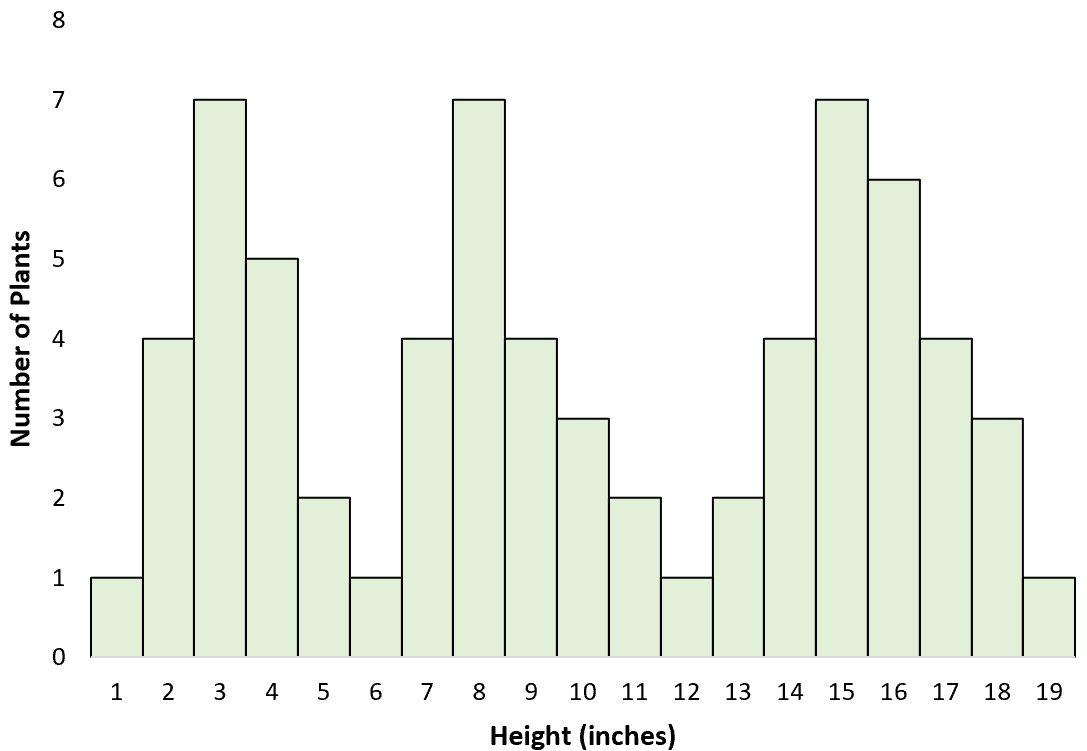
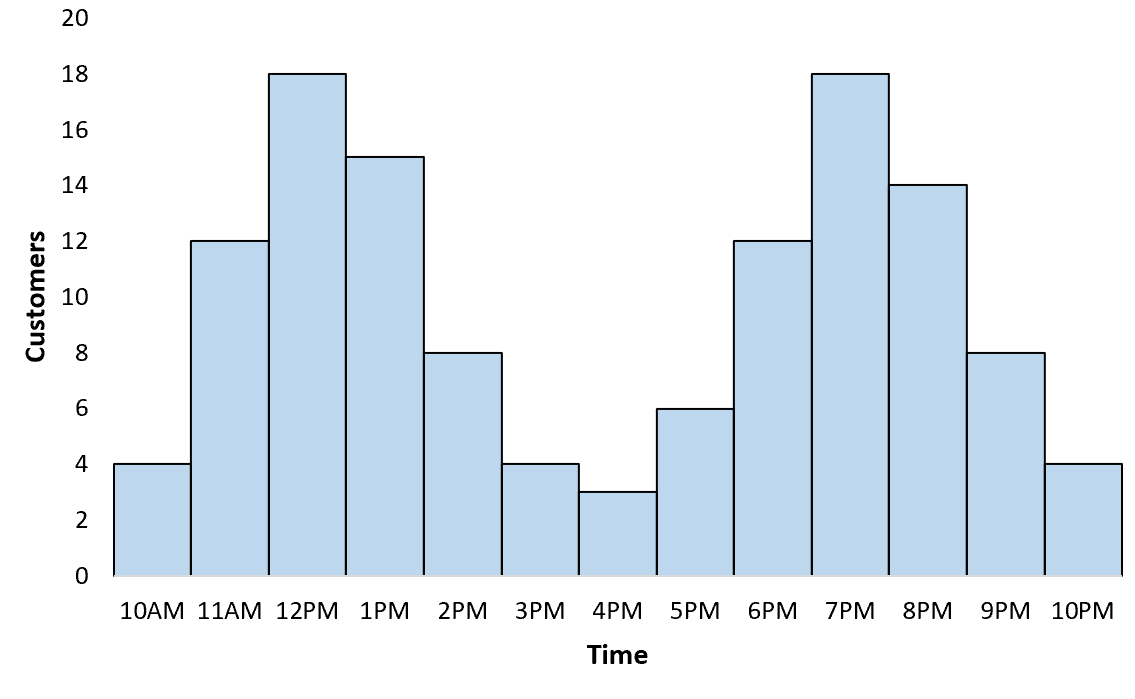
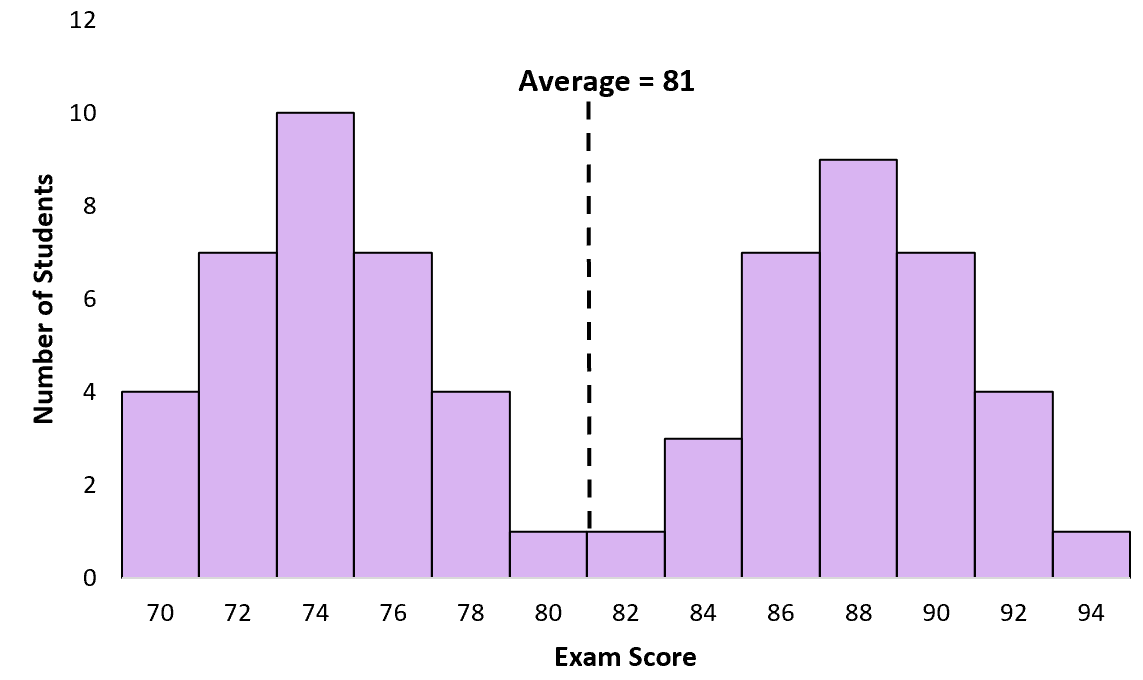






![nu _ {2} = p [ sigma _ {1} ^ {2} + delta _ {1} ^ {2}] + (1-p) [ sigma _ {2} ^ {2} + дельта _ {2} ^ {2}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd347d2f8b3d56aabc3d31c665a87d7194243ca7)
![nu _ {3} = p [S_ {1} sigma _ {1} ^ {3} +3 delta _ {1} sigma _ {1} ^ {2} + delta _ {1} ^ { 3}] + (1-p) [S_ {2} sigma _ {2} ^ {3} +3 delta _ {2} sigma _ {2} ^ {2} + delta _ {2} ^ {3}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4fd23eab0e3bd3597aa37e75a91d0e19fb3516a)
![nu _ {4} = p [K_ {1} sigma _ {1} ^ {4} + 4S_ {1} delta _ {1} sigma _ {1} ^ {3} +6 delta _ { 1} ^ {2} sigma _ {1} ^ {2} + delta _ {1} ^ {4}] + (1-p) [K_ {2} sigma _ {2} ^ {4} + 4S_ {2} delta _ {2} sigma _ {2} ^ {3} +6 delta _ {2} ^ {2} sigma _ {2} ^ {2} + delta _ {2} ^ {4}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/493aa3991ef31a6b20174271fdefb9840b42644a)























![B = { frac {1} {N}} left [ left ( sum _ {1} ^ {N} cos (2 pi m gamma) right) ^ {2} + left ( сумма _ {1} ^ {N} sin (2 pi m gamma) right) ^ {2} right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a3687e495c370c4379c0d9a288e5a3442608e00)




















