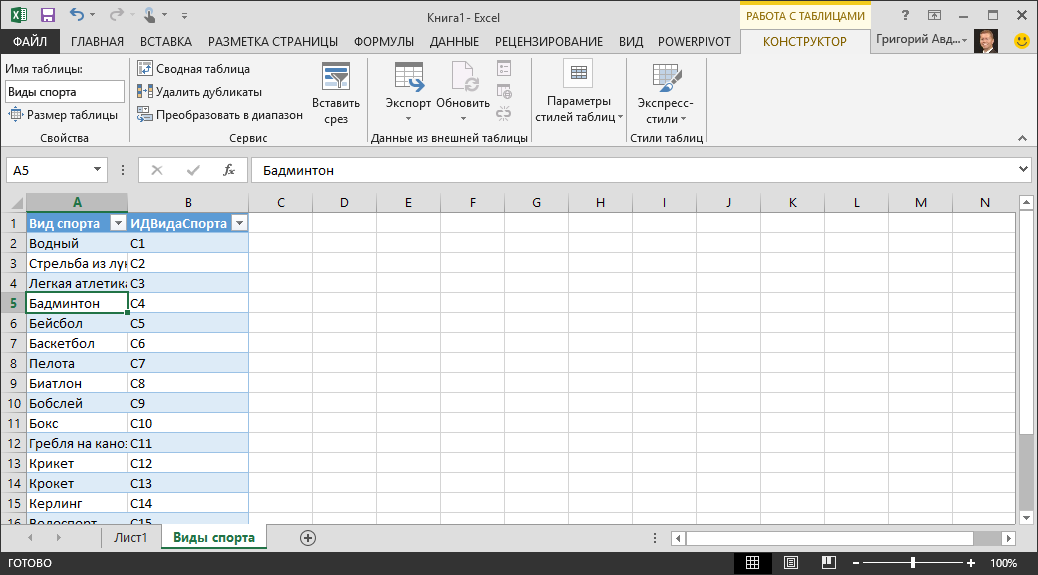
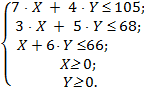Сборник заданий по разделу:
ОМПЬЮТЕРНОЕ
МОДЕЛИРОВАНИЕ В MS EXCEL

Иванов Иван
Для всех специальностей СПО
Разработала:
преподаватель
Белева Людмила Федоровна
Сыктывкар,2016 год
Пояснительная записка:
Учебно-методическое пособие предназначено для студентов всех специальностей и может быть использовано, в управлении образовательным процессом как одно из дидактических средств обучения.
Изучение содержания данного учебно-методического пособия обеспечит возможность студенту научиться строить и исследовать модели с помощью ЭВМ, применять и использовать электронные таблицы для решения данной категории задач.
МАТЕМАТИЧЕСКИЙ АППАРАТ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ
ВЕРОЯТНОСТЬ СЛУЧАЙНОГО СОБЫТИЯ
Событие, которое может произойти, а может и не произойти, называют случайным событием. Например, поражение мишени или промах при выстреле – случайные события. Выигрыш команды во встрече с соперником, проигрыш или ничейный результат – это тоже примеры случайных событий.
Вообще, пусть определенное испытание проводится многократно в одних и тех же условиях и при этом каждый раз фиксируется, произошло или нет интересующее нас событие А. Число m называют частотой события А, а отношение m/n – относительной частотой, где n – общее число испытаний.
Задача 1.
Определить относительную частоту выпадения орла.
Для этого: введите формулы в расчетные ячейки.
|
Формула |
Комментарий |
Результаты |
|
|
А1 |
=ЦЕЛОЕ (СЛЧИС()+0,5) |
Выпадение орла или решки |
0 или 1 |
|
A2 |
Копируем формулу |
||
|
А3 |
до |
||
|
A4 |
|||
|
A5 |
500 |
||
|
A6 |
|||
|
…. |
строки |
||
|
А500 |
включительно |
||
|
А501 |
=СЧЕТЕСЛИ(А1:А500;1) |
Число выпадений орла |
234 |
|
А502 |
=СЧЕТ(А1:А500) |
Число бросков |
500 |
|
А503 |
= А501/ А502*100 |
Относительная частота |
0,49 |
Вообще, результаты наблюдений и опытов показывают, что при большом числе испытаний, проводимых в одних и тех же условиях, относительная частота принимает достаточно устойчивое значение.
Такое определение называют статистическим определением вероятности.
Задача 2. Бросание кубика
Найдите статистическую вероятность для каждого значения выпадения очков 1,2,3,4,5,6.
Для этого: введите формулы в расчетные ячейки.
|
A |
B |
C |
D |
|
|
1 |
=ЦЕЛОЕ(СЛЧИС()*6+1 |
1 |
{=ЧАСТОТА(A1:A500;B1:B6)} |
=С1/500*100 |
|
2 |
Копируем формулу |
2 |
||
|
3 |
до |
3 |
||
|
4 |
500 |
4 |
||
|
5 |
строки |
5 |
||
|
6 |
включительно |
6 |
||
|
…. |
||||
|
500 |
Дополнение: рассмотрим событие В, которое означает выпадение числа очков, кратного 3. Это событие происходит при двух исходах испытания: когда выпало 3 очка и когда выпало 6 очков. Эти исходы называют благоприятными исходами для события В. При бросании кубика из 6 равновозможных исходов испытания благоприятными для события В являются лишь два исхода. Отношение числа благоприятных исходов к числу всех равновозможных исходов равно 2/6. Это отношение называют вероятностью события В и пишут Р(В)=2/6=1/3.
Вероятностью события называют отношение числа благоприятных для него исходов испытания к числу всех равновозможных исходов.
В рассмотренном примере посмотрим назначения ячеек D3 и D6, их сумма 32,6 колеблется около 33%. Таким образом, классическое и статистическое определение вероятности совпадают с определенной степенью точности.
Задача 3.
Проверить, что вероятность выпадения оба раза решки равна 0,25.
Решение.
Для этого: введите формулы в расчетные ячейки.
|
A |
B |
C |
D |
E |
F |
|
|
1 |
=ЦЕЛОЕ(СЛЧИС()+0,5) |
=ЦЕЛОЕ(СЛЧИС()+0,5) |
=A1+B1 |
0 |
{=ЧАСТОТА (C1:C50;D1:B3)} |
=E1/50*100 |
|
2 |
Копируем формулу |
1 |
||||
|
3 |
до |
2 |
||||
|
4 |
50 |
|||||
|
5 |
строки |
|||||
|
6 |
включительно |
|||||
|
… |
||||||
Задача 4.
Из 25 экзаменационных билетов по геометрии ученик успел приготовить 11 первых 8 последних билетов. Какова вероятность того, что на экзамене ему достанется билет, который он не подготовил?
Решение.
Общее число равновозможных исходов при выборе билетов на экзамене 25. Пусть М – событие, заключающееся в том, что ученику достанется на экзамене билет, к которому он не подготовился. Число благоприятных для М исходов (но не для ученика) равно 25-(11+8). Значит Р (М) =6/26=0,24. Проверим это. Для этого: введите формулы в расчетные ячейки.
|
A |
B |
C |
D |
||||||
|
1 |
=ЦЕЛОЕ (СЛЧИС()*25+1) |
=ЕСЛИ(A911;1;0) |
=ЕСЛИ(A1 |
=B1+C1 |
|||||
|
2 |
Копируем формулу |
Копируем формулу |
Копируем формулу |
Копируем формулу |
|||||
|
3 |
до |
||||||||
|
4 |
49 |
||||||||
|
5 |
строки |
||||||||
|
… |
включительно |
||||||||
|
49 |
Число неудачных билетов |
=СЧЁТЕСЛИ(D1:D49;2) |
|||||||
|
50 |
Число всех билетов |
=СЧЁТ(D1:D49) |
|||||||
|
52 |
Относительная вероятность в % |
=D50/D51*100 |
Задача 5.
Антон и Игорь бросают белый и черный игральные кубики и подсчитывают сумму выпавших очков. Они договорились, что если при очередной попытке в сумме выпадает 8 очков, то выигрывает Антон, а если в сумме выпадает 7 оков, то выигрывает Игорь. Является ли такая игра справедливой?
Решение.
При бросании кубиков на белом кубике может выпасть 1,2,3,4,5 или 6 очков.
Каждому числу очков, выпавших на белом кубике, соответствует шесть вариантов числа очков, выпавших на черном кубике. Все равновозможные исходы этого испытания приведены в таблице:
|
(1,1) |
(2,1) |
(3,1) |
(4,1) |
(5,1) |
(6,1) |
|
(1,2) |
(2,2) |
(3,2) |
(4,2) |
(5,2) |
(6,2) |
|
(1,3) |
(2,3) |
(3,3) |
(4,3) |
(5,3) |
(6,3) |
|
(1,4) |
(2,4) |
(3,4) |
(4,4) |
(5,4) |
(6,4) |
|
(1,5) |
(2,5) |
(3,5) |
(4,5) |
(5,5) |
(6,5) |
|
(1,6) |
(2,6) |
(3,6) |
(4,6) |
(5,6) |
(6,6) |
В каждой паре на первом месте записано число очков, выпавших на белом кубике, на втором – число очков на черном кубике. Общее число равновозможных исходов равно 36. Пусть событие А означает, что при бросании кубиков в сумме выпало 8 очков, а событие В означает, что в сумме выпало 7 очков. Для события А благоприятными являются следующие 5 исходов:(2;6), (3,5), (4;4), (5,3), (6;2). Для события В благоприятными являются следующие 6 исходов:(1;6), (2,5), (3,4), (4;3), (5,2), (6;1). Отсюда: Р (А)=5/36 Р(В)=6/36.Поэтому делаем вывод шансов выиграть у Игоря больше, чем у Антона. Значит, такая игра не является справедливой.
Проверим это. Для этого: введите формулы в расчетные ячейки.
|
A |
B |
C |
D |
E |
F |
|
|
1 |
=ЦЕЛОЕ(СЛЧИС()*6+1) |
=ЦЕЛОЕ(СЛЧИС()*6+1) |
=A1+B1 |
1 |
{=ЧАСТОТА(C1:C100;D1:D12)} |
=Е1/100*100 |
|
2 |
Копируем формулу |
Копируем формулу |
2 |
|||
|
3 |
до |
до |
3 |
|||
|
4 |
100 |
100 |
4 |
|||
|
5 |
строки |
строки |
5 |
|||
|
… |
6 |
|||||
|
… |
||||||
|
12 |
||||||
|
100 |
Задача 6.
На карточках написаны натуральные числа от 1 до 10 включительно, после чего карточки перевернули и перемешали. Затем наугад открыли одну карточку. Какова вероятность того, что на ней будет написано простое число или число, большее 7?
Решение.
Пусть событие А означает, что на каточке написано простое число, а событие В означает число, большее 7. Для события А благоприятными являются 4 исхода 10 равновозможных(появление одного из чисел 2,3,5,7), то есть вероятность события А равна 0,4.
Для события В благоприятными являются 3 исхода из 10 равновозможных(появление чисел 8,9,10), то есть вероятность события В равна 0,3.
Нас интересует событие С, когда на карточке написано простое число или число, большее 7. Событие С наступает тогда, когда наступает одно из событий А или В. Очевидно, что эти события являются несовместимыми. Значит, вероятность события С равна сумме вероятностей событий А и В, то есть: Р(С)= Р(А) + Р(В)=0,4+0,3=0,7.
Проверим это. Для этого: введите формулы в расчетные ячейки.
|
A |
B |
C |
D |
E |
F |
G |
H |
|
|
1 |
2 |
3 |
5 |
7 |
7 |
|||
|
2 |
1 |
=ЦЕЛОЕ(СЛЧИС()*10+1) |
=ЕСЛИ(B2=C$1;1;0) |
=ЕСЛИ(B2=D$1;1;0) |
=ЕСЛИ(B2=Е$1;1;0 |
=ЕСЛИ(B2= F$1;1;0) |
=ЕСЛИ(B27;1;0) |
=СУММ(C2:G2) |
|
3 |
2 |
Копируем формулу |
||||||
|
4 |
до |
|||||||
|
5 |
97 |
|||||||
|
… |
||||||||
|
98 |
=СЧЁТЕСЛИ (H2:H97;»0″) |
|||||||
|
99 |
=Н98/97 |
Задача 7.
В результате многократных наблюдений установили, что вероятность попадания в мишень одного стрелка равна 0,9, а другого – 0,8. Каждый из стрелков сделал по одному выстрелу по мишени. Какова вероятность того, что мишень будет поражена?
Решение.
Рассмотрим такие события: А – первый стрелок попал в мишень; В – второй стрелок попал в мишень; С – мишень поражена. События А и В независимые. Однако воспользоваться в этом случае умножением вероятностей нельзя, так как событие С наступает не только, тогда, когда оба стрелка попали в мишень, но и тогда, когда в мишень попал хотя бы один из них.
Поступим иначе. Рассмотрим события Ā, B, С, противоположные соответственно событиям А, В, С. События Ā, B являются независимыми, так как промах при выстреле по мишени первого стрелка ( событие Ā) не зависит от промаха второго стрелка( событие B). Событие С означает совместное появление событий Ā,B. Поэтому Р(С)= Р(Ā) • Р(B).
Из свойств вероятностей противоположных событий вытекает, что Р(Ā)=1-0,9=0,1;
Р(B)=1-0,8=0,2; Отсюда получаем Р(С)= Р(Ā) •Р(B)=0,1•0,2=0,02. Так как события С и С противоположные, то теперь несложно найти вероятность события С: Р(С)= 1-Р(С)=1-0,02=0,98. Значит, вероятность того, что мишень будет поражена, равна 0,98.
Проверим это на компьютере. Для этого: введите формулы в расчетные ячейки.
|
A |
B |
C |
D |
E |
F |
|
|
1 |
1 |
=СЛЧИС() |
=СЛЧИС() |
=ЕСЛИ(B10,1;1;0) |
=ЕСЛИ(C10,2;1;0) |
=C1+D1 |
|
2 |
2 |
заполнить |
заполнить |
заполнить |
заполнить |
заполнить |
|
3 |
3 |
|||||
|
4 |
4 |
|||||
|
5 |
5 |
|||||
|
6 |
6 |
|||||
|
7 |
7 |
|||||
|
… |
||||||
|
97 |
||||||
|
98 |
98 |
=СЧЁТЕСЛИ(F1:F97;»0″) |
||||
|
99 |
99 |
=F98/A97 |
Задания для самостоятельного выполнения:
-
На карточках написали цифры 1,2,3, после чего карточки перевернули и перемешали. Затем последовательно открыли карточки и положили в ряд. Какова вероятность того, что получится трехзначное число, большее 300?
-
Для экзамена подготовили билеты с номерами от 1 до 25. Какова вероятность того,
что взятый наугад учеником билет имеет:
а) однозначный номер;
б) двухзначный номер?
-
Многократные испытания показали, что для некоторого стрелка вероятность выбить при стрельбе 10 очков равна 0,1, а вероятность выбить 9 очков равна 0,3. Чему равна для этого стрелка вероятность выбить не менее 9 очков?
МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ
Случай является неотъемлемой частью нашей жизни. Если случай помог нам в чем-то, мы говорим — повезло, если оказался не в нашу пользу, мы сокрушаемся — что за судьба! Многие ученые посвятили свой талант изучению закономерностей случайных событий. Знание законов случайностей может быть полезным в разных сферах: от определения вероятности некоторого события, например выигрыша в лотерею, до использования статистических закономерностей в научных опытах. Ниже будут смоделированы ситуации, которые в теории вероятности получили название «случайных блужданий».
ЗАДАЧА. Бросание монеты
I ЭТАП. ПОСТАНОВКА ЗАДАЧИ
Описание задачи
У вас есть 10 монет. Вы хотите увеличить свой капитал в два раза, испытав заодно и свою судьбу. Суть игры проста. Играя с маклером, вы делаете ставку и бросаете монету. Если выпадет «орел», маклер выдает вам сумму вашей ставки, в противном случае — вы ему отдаете эту сумму. Ставка может быть любой: от 1 до 10 монет. Удвоение начального капитала или банкротство приводит к незамедлительному прекращению этого сеанса игры и расчету. Игра может продолжиться по вашему усмотрению.
Цель моделирования
Моделируя возможные игровые ситуации, в частности, варьируя ставки в данной игре, выяснить, какая тактика чаще приводит к результату (положительному или отрицательному).
Предупредить потенциальных игроков о степени риска и невозможности обогащения за счет азартных игр.
Формализация задачи
|
Уточняющий вопрос Что моделируется? Каков характер процесса? Чем определяется выигрыш/проигрыш? Какие объекты участвуют? Чем характеризуется игрок? Чем характеризуется монета? Какую роль выполняет маклер? |
Ответ Процесс игры Случайный Монетой: орел/решка Игрок, маклер и монета Начальным капиталом Кнач Ставкой СТ Текущей наличностью Ктек |
II ЭТАП. РАЗРАБОТКА МОДЕЛИ
Информационная модель
Здесь моделируется игра. Игра — это процесс, в котором участвуют три объекта: игрок, маклер и случай, который в данной игре представлен монетой. Маклер определяет проигрыш или выигрыш игрока, выплачивает выигрыш.
Математическая модель процесса складывается из следующих рассуждений.
Имитировать результат падения монеты можно с помощью функции СЛЧИС(). Эта функция выдает случайные числа х в диапазоне 0 ≤ х ˂ 1. Поскольку вероятность выпадения той или иной стороны «половина на половину», то, если СЛЧИС() ˂ 0,5, то результат «орел» (1), в противном случае — «решка» (0).
Формула падения монеты при броске имеет следующий вид:
Бросок = ЕСЛИ(СЛЧИС() ˂ 0,5; 1; 0).
|
Объект |
Параметры |
Действия |
|
|
Название |
Значение |
||
|
Игрок |
Начальным капиталом Кнач Ставкой СТ Текущей наличностью Ктек |
Исходные данные Исходные данные Расчетные данные |
Выбор ставки Вычисление наличности Продолжение игры |
|
Маклер |
Бросок Выигрыш Проигрыш |
Расчетные данные Расчетные данные Расчетные данные |
Выплата проигранного Прекращение игры по банкротству |
|
Монета |
Вероятность угадывания результата Положение «орел/решка» |
Константа Расчетные данные |
Подбрасывание монет Определение результата падения |
Формула изменения наличности игрока:
Наличность = ЕСЛИ (Бросок=1; Наличность+Ставка; Наличность-Ставка)
Формула определения выигрыша:
Выигрыш = ЕСЛИ(Наличность ˂ 2*Нач.Капитал;»-«; «банк») здесь выдается сообщение «банк» при увеличении наличности вдвое или больше, что является условием прекращения игры.
Функция определения проигрыша:
Проигрыш = ЕСЛИ (Наличность ˃ 0; «банкрот») здесь выдается сообщение «банкрот» по окончании наличности, что также является условием прекращения игры.
Компьютерная модель
Для моделирования выберем среду электронной таблицы. В этой среде информационная и математическая модель объединяются в таблицу, которая содержит три области: исходные данные; расчетные данные (результаты); статистика по экспериментам.
В ячейку А7 вводится формулу:=ЕСЛИ(СЛЧИС()
В ячейку В7 вводится формулу:=ЕСЛИ(A7=1;$B$4+$D$4;$B$4-$D$4)
В ячейку C7 вводится формулу:=ЕСЛИ(B7B$4;”-“;”банк”)
В ячейку D7 вводится формулу:=ЕСЛИ(B70;”-“;”банкрот”)
В ячейку B8 вводится формулу:=ЕСЛИ(A8=1;B7+$D$4;B7-$D$4)
Ввести в таблицу исходные данные.
|
A |
B |
C |
D |
|
|
1 |
БРОСАНИЕ МОНЕТЫ |
|||
|
2 |
||||
|
3 |
Исходные данные |
|||
|
4 |
Начальный капитал |
10 |
ставка |
1 |
|
5 |
Результаты |
|||
|
6 |
Бросок |
Наличность |
Выиграш |
Проигрыш |
|
7 |
Формула 1 |
Формула 2 |
Формула 3 |
Формула 4 |
|
8 |
||||
|
… |
Статистика по экспериментам |
|||
|
… |
Ставка |
№ сеанса |
Количество бросков до результата |
Результат |
|
… |
III ЭТАП. КОМПЬЮТЕРНЫЙ ЭКСПЕРИМЕНТ
План эксперимента
Тестирование
Проверить правильность ввода формул.
Эксперимент 1
Исследовать выпадение «орла» и «решки» в течение сеанса игры.
Эксперимент 2
Собрать статистические данные о выигрыше и проигрыше в течение нескольких сеансов игры с различными значениями ставок и исследовать их.
Проведение исследования
Тестирование
Введите в таблицу контрольные исходные данные и расчетные формулы в первую строку. Результаты сравнить с приведенными в таблице.
IV ЭТАП. АНАЛИЗ РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ
На основе области «Статистика» сделать выводы по поводу ставки в одну монету; других ставок. Выбрать и обосновать собственную тактику игры (ставку).
Задания для самостоятельного выполнения:
Задача 1. Игра в рулетку
Казино процветает из-за того, что у владельца всегда есть некоторое преимущество перед игроком. Например, в одном из вариантов рулетки колесо имеет 38 лунок: 36 пронумерованы и разбиты на черный и красный цвет, а две оставшиеся имеют № 0 и 00 и выкрашены зеленым. Игрок, ставя на красное или черное, имеет на выигрыш 18 шансов из 38, а на то, что он проиграет, — 20 шансов из 38. Пусть у вас имеется некоторый начальный капитал, который вы хотите удвоить. Постройте компьютерную модель ситуации.
Задача 2. Игра в кости
Два игрока бросают по две игровые кости. Сумма очков, выпавших на двух игровых костях, накапливается. Игра прекращается, когда один из игроков достигает суммы 101.
Игра повторяется до трех побед.
Задача 3. Лотерея «Спортлото»
Смоделируйте серию игр в 5 из 36. Изберите следующую тактику игры:
-
зачеркивать в билетах одну и ту же комбинацию из «счастливых билетов»
-
бросать кубик и из количества точек на верхней грани составлять набор чисел.
Задача 4. Очередь
За два часа обеденного перерыва 40 человек встали в очередь за билетами.
Кассирша обслуживает одного клиента в среднем одну минуту. Каждый клиент «мучает» вопросами кассиршу до пяти минут(случайным образом). Построить модель ситуации и исследовать ее. Ответьте на вопросы:
-
Хватит ли на обслуживание всех клиентов 2 часов?
-
Если не хватит, то, сколько будет обслужено?
-
Как влияет время расспросов на время обслуживания очереди?
ИГРАЛЬНАЯ КОСТЬ. ИМИТАЦИЯ БРОСАНИЯ ИГРАЛЬНОЙ КОСТИ (VBA)
Microsoft Excel имеет встроенный язык программирования — Visual Basic for Аpplications (VBA). Этот язык позволяет создавать приложения, выполняемые в среде Microsoft Office. Редактор Visual Basic for Application позволяет существенно расширить возможности Excel.
С помощью VBA можно легко и быстро создавать различные приложения, даже не являясь специалистом в области программирования. Редактор Visual Basic for Application имеет графическую инструментальную среду, позволяющую создавать экранные формы и управляющие элементы. С его помощью можно создавать свои собственные функции для Excel, вызываемые мастером функций, разрабатывать макросы, создавать собственные меню и многое другое.
ЗАДАЧА. Снова бросаем игральный кубик
Разработайте программу, которая будет имитировать многократное бросание одной игральной кости, а также определять и показывать количество выпадений на кубике того или иного числа. Программа должна делать ставки, позволять начинать бросание кости, останавливать его в любой момент и переустанавливать результаты подсчета.
Игральную кость можно рассматривать как генератор случайных чисел в целочисленном интервале [1..N] с одинаковой вероятностью выпадения всех чисел интервала.
Создание интерфейса
П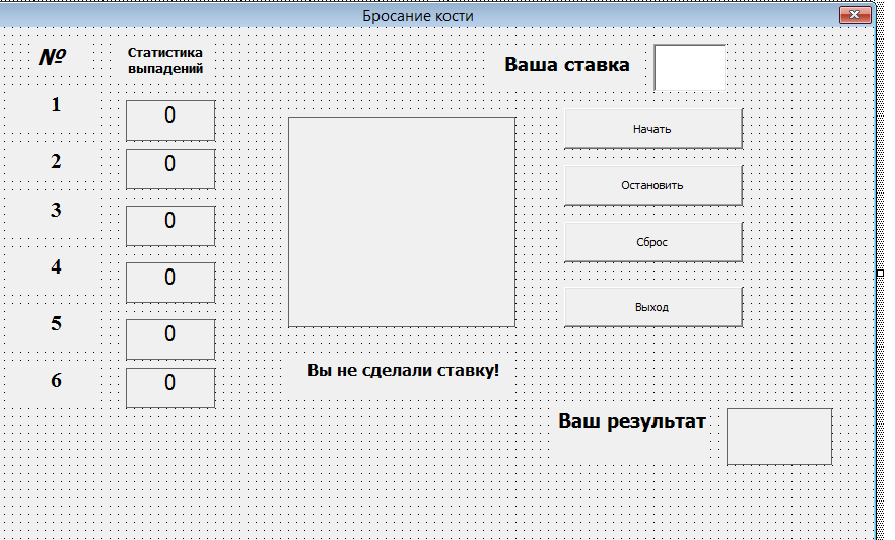
Запустите VBA, начните новый проект и разместите на форме элемент управления Image, 18 надписей и четыре кнопки.
Н
Рисунок 1.
азначение каждого элемента управления: (см. рисунок 1)
-
элемент управления Image — для графического представления игральной кости (одной ее грани);
-
надписи — для показа количества выпадений того или иного числа и для подписей к ним;
-
кнопки:
Выход — для завершения программы по щелчку на ней;
Начать — чтобы начать бросание по щелчку на кнопке;
Остановить — чтобы остановить бросание по щелчку на ней;
Сброс — чтобы обнулить счет по щелчку на кнопке.
В этой программе присутствует повторяющийся процесс (бросание кости и вывод результата) через регулярные интервалы времени функция — timer.
Код:
Private Sub atimer()
Dim Kost, a, d, stavka As Integer
stavka = CDbl(TextBox2.Text)
PauseTime = 1
Start = timer
Do While timer
DoEvents
Randomize
kost = Int(Rnd * 6) + 1
Select Case kost
Case 1
Image1.Picture = LoadPicture(«C:UsersDesktopkosti1.bmp»)
Label1.Caption = Label1.Caption + 1
Case 2
Image1.Picture = LoadPicture(«C:UsersDesktopkosti2.bmp»)
Label2.Caption = Label2.Caption + 1
Case 3
Image1.Picture = LoadPicture(«C:UsersDesktopkosti3.bmp»)
L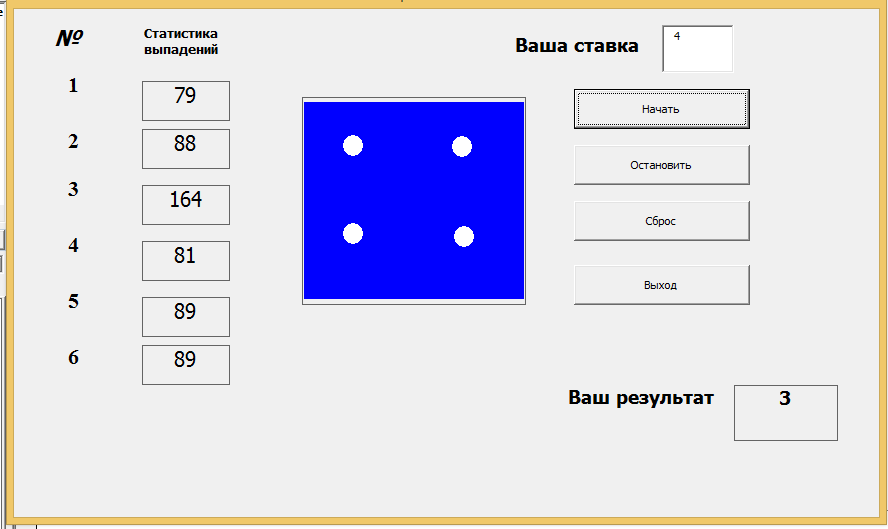
Label3.Caption = Label3.Caption + 1
Case 4
Image1.Picture = LoadPicture(«C:UsersDesktopkosti4.bmp»)
Label4.Caption = Label4.Caption + 1
Case 5
Image1.Picture = LoadPicture(«C:UsersDesktopkosti5.bmp»)
Label5.Caption = Label2.Caption + 1
C
Рисунок 2.
ase 6
Image1.Picture = LoadPicture(«C:UsersDesktopkosti6.bmp»)
Label6.Caption = Label6.Caption + 1
End Select
Loop
If stavka = kost Then
Label15.Caption = Label15.Caption + 3
Else
Label15.Caption = Label15.Caption — 2
End If
End Sub
Private Sub CommandButton1_Click()
stavka = CDbl(TextBox2.Text)
Label18.Visible = False
If stavka 0 Then
atimer
Else
Label18.Visible = True
Label18.Caption = «Вы не сделали ставку !!!»
End If
End Sub
Private Sub CommandButton2_Click()
PauseTime = 0
End Sub
Private Sub CommandButton3_Click()
Label1.Caption = «0»
Label2.Caption = «0»
Label3.Caption = «0»
Label4.Caption = «0»
Label5.Caption = «0»
Label6.Caption = «0»
Label15.Caption = «0»
TextBox2.Text = » «
End Sub
Private Sub CommandButton4_Click()
UserForm1.Hide
End Sub
Заключение:
Тема работы со случайными числами является очень актуальной, так как случайные числанаходят своё применение в приложениях различных типов и имеет большое практическое значение. Не одна задача современного программирования (в криптографии) не обходится без решения вопроса генерирования случайных данных.
Задания для самостоятельного выполнения:
Задача 1. Эксперимент состоит в подсчете числа бросаний двух костей до выпадения двух шестерок. Требуется найти среднее число бросаний, необходимых для получения двух шестерок. (Проводится N экспериментов).
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ В ЭКОНОМИКЕ
Задача 1. Пусть известно, что в штате больницы состоит 6 санитарок, 8 медсестер, 10 врачей, 3 заведующих отделениями, главный врач, заведующий аптекой, заведующий хозяйством и заведующий больницей. Общий месячный фонд зарплаты составляет 10 000 у. е. Необходимо определить, какими должны быть оклады сотрудников больницы.
Построим модель решения этой задачи. За основу возьмем оклад санитарки, а остальные оклады будем вычислять, исходя из него: во сколько-то раз или на сколько-то больше. Говоря математическим языком, каждый оклад является линейной функцией от оклада санитарки: , где С – оклад санитарки; Аi и Bi – коэффициенты, которые для каждой должности определяются следующим образом:
– медсестра получает в 1,5 раза больше санитарки (;
);
– врач – в 3 раза больше санитарки (;
);
– заведующий отделением – на 30 у. е. больше, чем врач (;
);
– заведующий аптекой – в 2 раза больше санитарки (;
);
– заведующий хозяйством – на 40 у.е. больше медсестры (;
);
– главный врач – в 4 раза больше санитарки (;
);
– заведующий больницей – на 20 у.е. больше главного врача (;
).
Зная количество человек на каждой должности, нашу модель можно записать как уравнение:
где N1 – число санитарок, N2 – число медсестер и т. д.
В этом уравнении нам известны А1…А8, В1…В8 и N1…N8, а С неизвестно.
Анализ уравнения показывает, что задача составления расписания свелась к решению линейного уравнения относительно С. Решим его.
– Заполните таблицу в соответствии с образцом:
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
Должность |
Коэф. А |
Коэф. В |
Зарплата сотрудника |
Кол-во сотрудников |
Суммарная зарплата |
Зарплата санитарки |
|
2 |
Санитарка |
1 |
0 |
=B2*$G$2+C2 |
6 |
=D2*E2 |
150 |
|
3 |
Медсестра |
1,5 |
0 |
8 |
|||
|
4 |
Врач |
3 |
0 |
10 |
|||
|
5 |
Зав.отделением |
3 |
30 |
3 |
|||
|
6 |
Зав. аптекой |
2 |
0 |
1 |
|||
|
7 |
Завхоз |
1,5 |
40 |
1 |
|||
|
8 |
Главврач |
4 |
0 |
1 |
|||
|
9 |
Зав. больницей |
4 |
20 |
1 |
|||
|
10 |
Итого |
=СУММ(F2:F9) |
В ячейке F10 вычислите суммарный фонд заработной платы больницы. Рабочий лист электронной таблицы будет выглядеть, как показано ниже:
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
Должность |
Коэф. А |
Коэф. В |
Зарплата сотрудника |
Кол-во сотрудников |
Суммарная зарплата |
Зарплата санитарки |
|
2 |
Санитарка |
1 |
0 |
150 |
6 |
900 |
150 |
|
3 |
Медсестра |
1,5 |
0 |
225 |
8 |
1800 |
|
|
4 |
Врач |
3 |
0 |
450 |
10 |
4500 |
|
|
5 |
Зав.отделением |
3 |
30 |
480 |
3 |
1440 |
|
|
6 |
Зав. аптекой |
2 |
0 |
300 |
1 |
300 |
|
|
7 |
Завхоз |
1,5 |
40 |
265 |
1 |
265 |
|
|
8 |
Главврач |
4 |
0 |
600 |
1 |
600 |
|
|
9 |
Зав. больницей |
4 |
20 |
620 |
1 |
620 |
|
|
10 |
10425 |
Как видите, взяв оклад санитарки за 150, мы превысили месячный фонд зарплаты.
Определите оклад санитарки так, чтобы расчетный фонд был равен заданному.
Для этого:
– активизируйте команду Подбор параметра;
– в поле «Установить в ячейке» появившегося окна введите ссылку на ячейку F10, содержащую формулу;
– в поле «Значение» наберите искомый результат 10000.
– В поле «Изменяя значение ячейки» введите ссылку на изменяемую ячейку G2 и щелкните кнопкой ОК. Таблица будет выглядеть следующим образом:
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
Должность |
Коэф. А |
Коэф. В |
Зарплата сотрудника |
Кол-во сотрудников |
Суммарная зарплата |
Зарплата санитарки |
|
2 |
Санитарка |
1 |
0 |
143,80 |
6 |
862,77 |
143,79 |
|
3 |
Медсестра |
1,5 |
0 |
215,69 |
8 |
1 725,55 |
|
|
4 |
Врач |
3 |
0 |
431,39 |
10 |
4 313,87 |
|
|
5 |
Зав. отделением |
3 |
30 |
461,39 |
3 |
1 384,16 |
|
|
6 |
Зав. аптекой |
2 |
0 |
287,59 |
1 |
287,59 |
|
|
7 |
Завхоз |
1,5 |
40 |
255,69 |
1 |
255,69 |
|
|
|
Главврач |
4 |
0 |
575,18 |
1 |
575,18 |
|
|
|
Зав. больницей |
4 |
20 |
595,18 |
1 |
595,18 |
|
|
|
Итого |
10 000,00 |
Задача об использовании сырья
Что такое линейное программирование
Многие экономические процессы описываются математическими моделями, в которых требуется найти такие значения переменных параметров, при которых достигается максимальное или минимальное значение линейной функции от этих переменных, при различных ограничениях, задаваемых линейными управлениями или неравенствами. Искомые переменные, называются контролируемыми факторами, функция – целевой функцией. Задачи такого типа называются задачами линейного программирования.
Модели линейного программирования в экономике и управлении используются как инструмент оптимизации при планировании производства, составление планов перевозов и т.д.
Постановка задачи
Предприятие выпускает курс n видов продукции, которые обозначим: P1, P2,…, Pn. Для этого используется m вида сырья: S1, S2, … , Sm, запасы которого равны соответственно b1, b2, … , bm. Известно, что расход i-го вида сырья для производства единицы j-го вида продукции Pj равен aij. От реализации единицы j-го вида продукции Pj предприятие получает доход, равный Cj. Требуется составить такой план производства каждого вида продукции, чтобы при имеющихся запасах сырья обеспечить предприятию максимальный суммарный доход.
Математическая модель
Построение математической модели осуществляется в три этапа:
-
Определение переменных, для которых будет составляться математическая модель.
-
Формирование целевой функции.
-
Формирование системы ограничений.
Составим план производства для ателье, занимающегося пошивом туристического снаряжения – палаток. Для пошива используется три вида материалов (сырья): водоотталкивающая ткань, утеплитель, москитная сетка. Представим данные с двумя видами продукции (палатки двух моделей) и тремя видами материалов (водоотталкивающая ткань, утеплитель, москитная сетка) в виде таблицы.
|
Материалы(Si) |
Запасы материалов (bi), м |
Расход материалов на продукцию Pj, м |
|
|
Палатка (модель 1) |
Палатка (модель 2) |
||
|
Водооттал. ткань |
105 |
7 |
4 |
|
Утеплитель |
68 |
3 |
5 |
|
Москитная сетка |
66 |
1 |
6 |
|
Удельный доход от реализации (Сj) |
5 |
6 |
Ячейки, выделенные фоном, содержат значения расхода каждого вида сырья (материалов) на производство единицы каждого вида продукции. Это и есть матрица aij. Такой расход сырья называется удельным. Обозначим план пошива палаток модели 1 через X (шт.), а план пошива палат моделей палаток модели 2 через Y (шт.). При таком плане расход материалов, например водоотталкивающей ткани, составит 7 X + 4 Y метров. Поскольку расход материала не может превышать имеющиеся запасы, получаем ограничения по расходу водоотталкивающей ткани 7 X + 4 Y 105. Аналогические рассуждения приводят к ограничениям и по другим видам материалов. Кроме того, значения X и Y не могут быть отрицательными. Сформулированные условия запишем в виде системы неравенств, которым должны удовлетворять неизвестные X и Y:
Доход от реализации одной палатки модели 1 равен 5 единицам стоимости (например, 5 тыс. руб.), а доход от реализации палатки модели 2 — 6 единицам стоимости тогда суммарный доход предприятия от реализации всей произведенной продукции определится формулой: Z =5 X + 6 Y. Следовательно, Z есть функция от X и Y. Z(X, Y) является целевой функцией, поскольку целью производства является получение максимального дохода.
Таким образом, математическая формулировка задачи звучит так: требуется найти такое решение системы линейных неравенств (1)-(5),при котором целевая функция Z(X, Y) принимает максимальное значение.
Решение с помощью электронных таблиц
П
Таблица 1.
одготовим данные, как это показано в таб.1. В ячейках В2 и В3 будет получено решение, т.е. найдены объемы производства каждого вида продукции, при которых суммарных доход, вычисляемый в ячейках В17, принимает максимальное значение. Диапазон ячеек В13:В15 содержит формулы, с помощью которых задаются левые части неравенств (1)-(2), ограничивающих расход сырья. Диапазон ячеек D13:D15 содержит запасы материалов.
|
A |
B |
C |
D |
|
|
1 |
Объем производства |
|||
|
2 |
Палатки (модель 1) |
|||
|
3 |
Палатки (модель 2) |
|||
|
4 |
||||
|
5 |
||||
|
6 |
Материалы |
Запасы материалов |
Палатки (модель 1) |
Палатки (модель 2) |
|
7 |
Водооттал. ткань |
105 |
7 |
4 |
|
8 |
Утеплитель |
68 |
3 |
5 |
|
9 |
Москитная сетка |
66 |
1 |
6 |
|
10 |
Удельный доход от реализации |
5 |
6 |
|
|
11 |
||||
|
12 |
Ограничения |
|||
|
13 |
=C7*$B$2+D7*$B$3 |
|
105 |
|
|
14 |
=C8*$B$2+D8*$B$3 |
|
68 |
|
|
15 |
=C9*$B$2+D9*$B$3 |
|
66 |
|
|
16 |
||||
|
17 |
Суммарный доход |
=C10*B2+D10*B3 |
Установим курсор в ячейку В17, в которой должно быть вычислено значение целевой функции, и выполним команду Поиск решения. В открывшемся окне необходимо произвести установки, показанные на рис. 1.
Д
Рисунок 1.
ля этого выполняются следующие действия:
В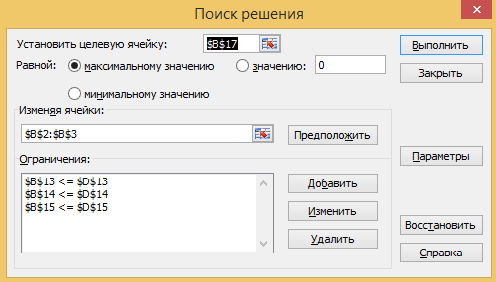
-
Для поля Равной выбирается параметр максимальному значению.
-
В поле Изменяя ячейки вводится диапазон ячеек с неизвестными В2:В3.
-
Щелчком на кнопке Добавить вызывается окно Добавить ограничение.
-
Для ввода первого ограничения в поле Ссылка на ячейку указывается адрес ячейки В13, а в поле Ограничение – адрес ячейки D13. Между ними выбирается знак отношения и нажимается кнопка Добавить. Аналогично добавляются два оставшихся ограничения.
-
Щелчком на кнопке параметры вызывается окно Параметры поиска решения (рис. 2), в котором необходимо отметить, что ищутся неотрицательные значения X и Y и используется линейная модель. Это означает то, что целевая функция линейно зависит от переменных X и Y.
Неотрицательные решения системы линейных неравенств, при которых целевая функция (суммарный доход) принимает максимальное значение, табличный процессор Microsoft Excel находит приближенно, используя итерационный метод поиска, который называется методом Ньютона. Поэтому в качестве параметров указывается предельное число итераций и относительная погрешность. С такого рода параметрами мы встречались при решении задачи теплопроводности методов итераций.
Рисунок 2.
П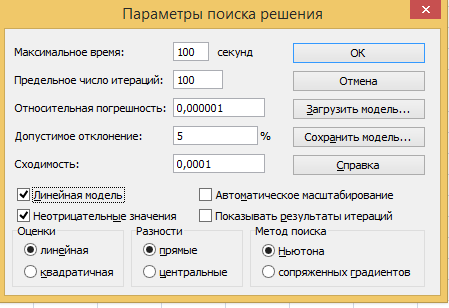
В результате в ячейках В2 и В3 будет получено решение – объем производства палаток первой и второй моделей (таб.2), а в ячейке В17 – максимальный доход, полученный от реализации такого объема продукции. Как исследовало ожидать, полученные значения совпадают с результатами графического метода решения задачи: X = 11, Y = 7, Z = 97.
Таблица 2. Результаты решение задачи
|
A |
B |
C |
D |
|
|
1 |
Объем производства |
|||
|
2 |
Палатки (модель 1) |
11 |
||
|
3 |
Палатки (модель 2) |
7 |
||
|
4 |
||||
|
5 |
||||
|
6 |
Материалы |
Запасы материалов |
Палатки (модель 1) |
Палатки (модель 2) |
|
7 |
Водооттал. ткань |
105 |
7 |
4 |
|
8 |
Утеплитель |
68 |
3 |
5 |
|
9 |
Москитная сетка |
66 |
1 |
6 |
|
10 |
Удельный доход от реализации |
5 |
6 |
|
|
11 |
||||
|
12 |
Ограничения |
|||
|
13 |
105 |
|
105 |
|
|
14 |
68 |
|
68 |
|
|
15 |
53 |
|
66 |
|
|
16 |
||||
|
17 |
Суммарный доход |
97 |
Задания для самостоятельного выполнения:
Задача 1.
Предположим, что мы решили производить несколько видов конфет. Назовем их условно «А», «В», «С». Известно, что реализация 10 килограммов конфет «А» дает прибыль 9 у. е., «В» – 10 у. е., «С» – 16 у. е.
Конфеты можно производить в любых количествах, но запасы сырья ограничены. Необходимо определить, каких конфет и сколько десятков килограммов необходимо произвести, чтобы общая прибыль от реализации была максимальной.
Нормы расхода сырья на производство 10 кг конфет каждого вида приведены ниже.
|
Сырье |
Нормы расхода сырья |
Запас сырья |
||
|
А |
В |
С |
||
|
Какао |
18 |
15 |
12 |
360 |
|
Сахар |
6 |
4 |
8 |
192 |
|
Наполнитель |
5 |
3 |
3 |
180 |
|
Прибыль |
9 |
10 |
16 |
Задача 2.
Ваше предприятие выпускает изделия 1, изделия 2, изделия 3, используя общий склад комплектующих. Каждое изделие состоит из деталей, имеющихся на складе. В связи с ограниченностью запаса необходимо найти оптимальное соотношение объемов выпуска изделий. Прибыль, получаемая от каждого изделия, равна соответственно 47,32; 31,55; 22,08. Число деталей, идущих на каждое изделие, указано в таблице.
|
Наличие на складе |
Изделие 1 |
Изделие 2 |
Изделие 3 |
|
|
Деталь 1 |
450 |
1 |
1 |
0 |
|
Деталь 2 |
250 |
1 |
0 |
0 |
|
Деталь 3 |
800 |
2 |
2 |
1 |
|
Деталь 4 |
450 |
1 |
1 |
0 |
|
Деталь 5 |
600 |
2 |
1 |
1 |
Задача 3.
В ресторане готовятся фирменные блюда трех видов (блюдо А, блюдо В и блюдо С) с использованием при приготовлении ингредиентов трех видов (ингредиент 1, ингредиент 2 и ингредиент 3). Расход ингредиентов в граммах на блюдо задается следующей таблицей:
|
Вид ингредиента |
Блюдо А |
Блюдо В |
Блюдо C |
|
Ингредиент 1 |
20 |
50 |
10 |
|
Ингредиент 2 |
20 |
0 |
40 |
|
Ингредиент 3 |
20 |
10 |
10 |
Стоимость приготовления блюд одинакова (100 руб.).
Ежедневно в ресторан поступает 5 кг ингредиента 1 и по 4 кг ингредиентов видов 2 и 3. Каково оптимальное соотношение дневного производства блюд различного вида, если производственные мощности ресторана позволяют использовать весь запас поступивших продуктов?
Задача 4.
Пошивочная мастерская планирует выпуск двух видов костюмов: мужских и женских. На женский костюм требуется 1 м шерсти, 2 м лавсана и 1 человеко-день трудозатрат. На мужской костюм — 3,5 м шерсти, 0,5 м лавсана и 1 человеко-день трудозатрат. Всего имеется 350 м шерсти и 240 м лавсана, 150 человеко-дней трудозатрат. Предусматривается выпуск не менее 110 костюмов, причем, необходимо обеспечить прибыль не менее 1400 руб. Определите оптимальное количество костюмов каждого вида, если прибыль от реализации женского костюма составляет 10 руб., а мужского — 20 руб.
ПОСТРОЕНИЕ И ИССЛЕДОВАНИЕ ОПТИМИЗАЦИОННОЙ МОДЕЛИ НА VBA
Задача 1.
В ходе производственного процесса из листов материала получают заготовки деталей двух типов А и В тремя различными способами, при этом количество получаемых заготовок при каждом методе различается.
| Тип заготовки | Способы раскроя | ||
| 1-й |
2-й |
3-й |
|
|
А |
10 |
3 |
8 |
|
В |
3 |
6 |
4 |
Необходимо выбрать оптимальное сочетание способов раскроя, для того чтобы получить 500 заготовок типа А и 300 заготовок типа В.
Формальная модель:
Параметрами, значения которых требуется определить, являются количества листов материала, которые будут раскроены различными способами:
X1— количество листов, раскроенное способом 1;
X2— количество листов, раскроенное способом 2;
X3— количество листов, раскроенное способом 3.
Ограничения:
Определяются значениями требуемых количеств заготовок типа А и В:
10X1+3X2+8X3=500 и 3X1+6X2+4X3=300
Кроме того, количества листов не могут быть отрицательными: X10, X20, X30 и дробными X1, X2, X3 – целые.
Создание интерфейса:
Запустите V BA, начните новый проект и разместите на форме 8 надписей; одну кнопку.
P
Рисунок 1.
rivate Sub CommandButton1_Click()
D
F = 300
For x1 = 0 To 100
For x2 = 0 To 100
For x3 = 0 To 100
If (10 * x1 + 3 * x2 + 8 * x3 = 500) And (3 * x1 + 6 * x2 + 4 * x3 = 300) Then
If x1 + x2 + x3
F = x1 + x2 + x3
Label1.Caption = x1
Label2.Caption = x2
Label3.Caption = x3
Label4.Caption = F
End If
End If
Next x3
Next x2
Next x1
End Sub
Задания для самостоятельного выполнения:
Задача 1.
Фабрика производит два вида красок: первый – для наружных, а второй – для внутренних работ. Для производства красок используется два ингредиента: А и В. Максимально возможные суточные запасы этих ингредиентов составляют 6 и 8 т соответственно. Известные расходы А и В на 1 т красок:
|
Ингредиенты |
Расход ингредиентов, т.ингр./т.краски |
Запас, т.ингр./сут |
|
|
Краска 1-го вида |
Краска 2-го вида |
||
|
А |
1 |
2 |
6 |
|
В |
2 |
1 |
8 |
Изучение рынка сбыта показало, что суточный спрос на краску 2-го вида никогда не превышает спроса на краску 1-го вида более, чем на 1 т. Кроме того, спрос на краску 2-го вида не превышает 2 т /сут. Оптовые цены 1 т красок равны: 3 т. руб. для краски 1-го вида и 2 т. руб. для краски 2-го вида. Найти какое количество краски каждого вида необходимо производить, чтобы доход от реализации продукции был максимальным.
Задача 2.
Фабрика производит два вида красок: первый – для наружных, а второй – для внутренних работ. Для производства красок используется два ингредиента: А и В. Максимально возможные суточные запасы этих ингредиентов составляют 6 и 8 т соответственно. Известные расходы А и В на 1 т красок:
|
Ингредиенты |
Расход ингредиентов, т.ингр./т.краски |
Запас, т.ингр./сут |
|
|
Краска 1-го вида |
Краска 2-го вида |
||
|
А |
1 |
2 |
6 |
|
В |
2 |
1 |
8 |
Изучение рынка сбыта показало, что суточный спрос на краску 2-го вида никогда не превышает спроса на краску 1-го вида более чем на 1 т. Кроме того, спрос на краску 2-го вида не превышает 2 т /сут. Оптовые цены 1 т красок равны: 3 т. руб. для краски 1-го вида и 2 т. руб. для краски 2-го вида. Найти какое количество краски каждого вида необходимо производить, чтобы доход от реализации продукции был максимальным.
Транспортная задача
Рассмотрим еще одну типовую задачу линейного программирования.
Постановка задачи
Транспортной задачей называют составления плана перевозок от поставщиков к потребителям с помощью некоторых транспортных средств. Составленный план должен обеспечивать выполнение таких условий, как:
-
Полное удовлетворение спроса потребителей;
-
Вывоз всей продукции от поставщика;
-
Минимизация транспортных затрат.
Математическая модель
Рассмотрим простейший вариант транспортной задачи. В т пунктах отправления (складах) А1, А2, …, Ат находится однородный груз в количестве а1, а2, …, ат единиц соответственно. Потребность в этом грузе в п пунктах назначения (магазинах) В1, В2, …, Вп составляет b1, b2, …, bn соответственно. Будем считать, что сумма запасов на складах равна суммарным потребностям в магазинах, т.е. =
. Такая модель называется замкнутой.
Обозначим через Сij удельные затраты, т.е. затраты на перевозку единицы груза из i—го пункта в j-й пункт назначения, а через Xij – неизвестный объем груза, который надор перевезти из j— го пункта отправления в j-й пункт назначения.
Перевозку груза надо организовать таким образом, чтобы суммарные затраты на перевозки были минимальными. Суммарные затраты на перевозки Z определяются следующим образом: необходимо просуммировать все объемы перевозок груза, умноженные на соответствующие удельные затраты, т.е. Z=. Суммарные затраты являются целевой функцией.
Искомыми величинами являются объемы Xij перевозок груза, отправляемые каждым поставщиком каждому потребителю при выполнении указанных условий.
Рассмотрим транспортную задачу на примере четырех складов и четырех магазинов.
Задача. Известно, что на складах имеется запас муки в количестве 45, 100, 20, 75 мешков. А магазины имеют потребность в этом товаре в количестве 30, 80, 95, 35 мешков.
|
Магазин № 1 |
Магазин №2 |
Магазин №3 |
Магазин №4 |
||
|
b1 = 30 |
b2 = 80 |
b3 = 95 |
b4 = 35 |
||
|
Склад № 1 |
a1 = 45 |
6 |
3 |
7 |
10 |
|
Склад № 2 |
a2 = 100 |
10 |
4 |
12 |
10 |
|
Склад № 3 |
a3 = 20 |
5 |
9 |
8 |
11 |
|
Склад № 4 |
a4 = 75 |
4 |
2 |
4 |
8 |
Ячейки, выделенные фоном, содержат удельные стоимости перевозок Cij. Например, стоимость перевозки единицы груза (мешка) со склада № 3 в магазин № 4 составляет 11 денежных единиц. Проверим замкнутость модели. Для этого просуммируем все запасы муки на складах: 45 + 100 + 20 + 75 = 240. Найдем суммарные потребности магазинов в муке: 30 + 80 + 95 + 35 = 240. Таким образом, модель является замкнутой, т. е. потребность магазинов в муке равна запасу на складах.
Весь груз со складов должен быть вывезен. Этот факт для i-го склада можно отразить следующим образом: Xi1 + Xi2 + Xi3 + Xi4 = ai. Весь груз в магазины должен быть ввезен. Для j-го магазина будет справедливо следующее: X1j + X2j + X3j + X4j = bj.
Таким образом, удовлетворению спроса магазинов отвечает выполнение системы уравнений:
Вывоз всего груза со складов достигается при выполнении системы уравнений:
Получается общая система из 8 уравнений с 16 неизвестными, которая имеет, вообще говоря, бесконечное множество решений. Среди этих решений интерес представляют неотрицательные решения, при которых суммарные затраты по всем маршрутам будут минимальны, т. е. целевая функция может быть представлена следующим образом:
Z = C11 X11 + … + C14X14 + C21 · X 21 + … + С24 · X24 + C31 · X31 +…+ C34 · X34 +C41 · X41 +…+ C44 · X44.
Решение с помощью электронных таблиц
Р
Таблица 1.
ассмотрим решение задачи на примере табличного процессора Microsoft Excel.
Представим данные в виде, показанном в таблице 1.
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
Матрица перевозок |
||||||
|
2 |
Магазин 1 |
Магазин 2 |
Магазин 3 |
Магазин 4 |
|||
|
3 |
Склад № 1 |
=сумм |
|||||
|
4 |
Склад № 2 |
=сумм |
|||||
|
5 |
Склад № 3 |
=сумм |
|||||
|
6 |
Склад № 4 |
=сумм |
|||||
|
7 |
=сумм |
=сумм |
=сумм |
=сумм |
|||
|
8 |
|||||||
|
9 |
|||||||
|
10 |
|||||||
|
11 |
bj |
30 |
80 |
95 |
35 |
||
|
12 |
ai |
Магазин 1 |
Магазин 2 |
Магазин 3 |
Магазин 4 |
||
|
13 |
45 |
Склад № 1 |
6 |
3 |
7 |
10 |
|
|
14 |
100 |
Склад № 2 |
10 |
4 |
12 |
10 |
|
|
15 |
20 |
Склад № 3 |
5 |
9 |
8 |
11 |
|
|
16 |
75 |
Склад № 4 |
4 |
2 |
4 |
8 |
|
|
17 |
|||||||
|
18 |
|||||||
|
19 |
Сумм. затраты: |
=СУММПРОИЗВЕД(С3:F16;C13:F16) |
Исходными данными являются удельные затраты на перевозки (диапазон ячеек C13:F16), запасы муки на складах (диапазон ячеек A13:A16), потребности магазинов в муке ( диапазон ячеек С11:F11).
Диапазон ячеек C3:F6 предназначен для получения искомого решения-объемов перевозок груза. Суммируя объемы перевозок в каждой строке, задаем левые части уравнений-ограничений, обеспечивающий вывоз всего груза с каждого склада. Суммированием объемов перевозок по столбцам задаются левые части уравнений-огранечений, удовлетворяющих спрос каждого магазина в муке. Формула =СУММПРОИЗВ (С3:F6; C13:F16), вычисляющая целевую функцию(суммарные затраты) Z, размещена в ячейке С19. Встроенная функция СУММПРОИЗВ суммирует произведения, полученные построчным перемножением содерживого ячеек из диапозонов С3:F6; C13:F16.
Например, СУММПРОИЗВ (А1:В2;А3:B4) =A1*A3+B1*B3+A2*A4+B2*B4.
Рисунок 1.
Установите курсор в ячейку С19, в которой должно быть выполнено значение целевой функции.
Выполним команду Поиск решения.
В открышевшемся окне необходимо провести установки, показанные на рис.1.
В
Таблица 2.
результате будет найдено решение, представленное в таблице 2.
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
Матрица перевозок |
||||||
|
2 |
Магазин 1 |
Магазин 2 |
Магазин 3 |
Магазин 4 |
|||
|
3 |
Склад № 1 |
0 |
10 |
35 |
0 |
45 |
|
|
4 |
Склад № 2 |
30 |
70 |
0 |
0 |
100 |
|
|
5 |
Склад № 3 |
0 |
0 |
20 |
0 |
20 |
|
|
6 |
Склад № 4 |
0 |
0 |
40 |
35 |
75 |
|
|
7 |
30 |
80 |
95 |
35 |
|||
|
8 |
|||||||
|
9 |
|||||||
|
10 |
|||||||
|
11 |
bj |
30 |
80 |
95 |
35 |
||
|
12 |
ai |
Магазин 1 |
Магазин 2 |
Магазин 3 |
Магазин 4 |
||
|
13 |
45 |
Склад № 1 |
6 |
3 |
7 |
10 |
|
|
14 |
100 |
Склад № 2 |
10 |
4 |
12 |
10 |
|
|
15 |
20 |
Склад № 3 |
5 |
9 |
8 |
11 |
|
|
16 |
75 |
Склад № 4 |
4 |
2 |
4 |
8 |
|
|
17 |
|||||||
|
18 |
|||||||
|
19 |
Сумм.затраты: |
1455 |
Искомые объемы перевозок представлены в ячейках C3:F6. Со склада №1 мука будет отправлена в магазины №2 и 3 в объемах 10 и 35 мешков соответсвенно, со склада №2 – в магазины №1 и 2 в объемах 30 и 70 мешков, со склада №3 — в магазин №3 в объеме 20 мешков, со склада №4 в магазины №3 и 4 в объемах 40 и 35 мешков. Минимальные затраты на перевозки составляют 1455 денежных единиц.
Задания для самостоятельного выполнения:
Задача 1. Найти оптимальный объем перевозок товаров с 3 заводов на 5 региональных складов. То есть минимизировать затраты на перевозку грузов от заводов-производителей на торговые склады.
Производительность каждого завода и затраты на перевозку от завода на каждый склад приведены в таблице:
|
Заводы |
Поставки |
Затраты |
||||
|
склад 1 |
склад 2 |
склад 3 |
склад 4 |
склад 5 |
||
|
Завод 1 |
310 |
10 |
8 |
6 |
5 |
4 |
|
Завод 2 |
260 |
6 |
5 |
4 |
3 |
6 |
|
Завод 3 |
280 |
3 |
4 |
5 |
5 |
9 |
Технология работы:
– Заполните таблицу в соответствии с образцом:
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
Заводы |
Всего |
склад 1 |
склад 2 |
склад 3 |
склад 4 |
склад 5 |
|
2 |
Завод 1 |
=СУММ (С2:G2) |
1 |
1 |
1 |
1 |
1 |
|
3 |
Завод 2 |
Заполнить вниз |
1 |
1 |
1 |
1 |
1 |
|
4 |
Завод 3 |
1 |
1 |
1 |
1 |
1 |
|
|
5 |
Допустим, что от каждого завода на каждый склад перевозится ед.продукции |
||||||
|
6 |
Итого |
=СУММ (С2;С4) |
|||||
|
7 |
|||||||
|
8 |
Потреб. складов |
180 |
80 |
200 |
160 |
220 |
|
|
9 |
Заводы |
Поставки |
Затраты |
||||
|
10 |
Завод 1 |
310 |
10 |
8 |
6 |
5 |
4 |
|
11 |
Завод 2 |
260 |
6 |
5 |
4 |
3 |
6 |
|
12 |
Завод 3 |
280 |
3 |
4 |
5 |
5 |
9 |
|
13 |
|||||||
|
14 |
Перевозка |
=СУММ (С14:G14) |
=С2*С10+С3*С11+С4*С12 |
Количество перевезенных грузов не может превышать производственных возможностей заводов. Количество доставляемых грузов не должно быть меньше потребностей складов. То есть производство должно быть не меньше потребностей. Число перевозок не может быть отрицательным.
Задача 2.
Авиакомпания по заказу армии должна перевезти на некотором участке 700 человек. В распоряжении компании имеется два типа самолетов, которые можно использовать для перевозки. Самолет первого типа перевозит 30 пассажиров и имеет экипаж 3 человека, второго типа – 65 и 5 соответственно.
Эксплуатация 1 самолета первого типа обойдется 5000$, а второго 9000$. Сколько надо использовать самолетов каждого типа, если для формирования экипажей имеется не более 60 человек.
МОДЕЛИРОВАНИЕ ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Задача. Для снабжения населенных пунктов, расположенных в труднодоступной местности, требуется разместить железнодорожную станцию и аэродром таким образом, чтобы суммарное расстояние (и, соответственно, стоимость) воздушных перевозок от станции и от аэродрома к населенным пунктам было оптимальным.
Координаты населенных пунктов приведены в табл. 1.
Таблица 1
|
Номера населенных пунктов |
Координаты населенных пунктов |
|
|
Х |
У |
|
|
1 |
2,0 |
8,0 |
|
2 |
10,0 |
9,0 |
|
3 |
1,0 |
2,0 |
|
4 |
4,0 |
9,0 |
|
5 |
9,0 |
5,0 |
Решение.
Из условия задачи следует, что надо найти оптимальное, с точки зрения экономии затрат на воздушные перевозки, местоположение двух объектов: аэродрома и железнодорожной станции. Такое возможно, если суммарная протяженность воздушных трасс между всеми объектами будет минимальной. Как известно, кратчайшее расстояние между двумя точками определяется отрезком, соединяющим эти точки.
Для решения задачи введем обозначения (табл. 2).
Таблица 2
|
Объект |
Координата Х |
Координата У |
|
Населенный пункт №1 |
Х1 |
У1 |
|
Населенный пункт №2 |
Х2 |
У2 |
|
Населенный пункт №3 |
Х3 |
У3 |
|
Населенный пункт №4 |
Х4 |
У4 |
|
Населенный пункт №5 |
Х5 |
У5 |
|
Аэродром |
ХА |
УА |
|
Железнодорожная станция |
ХС |
УС |
Минимальное расстояние от железнодорожной станции до i-го населенного пункта (i = 1, …, 5) через аэропорт можно определить следующим образом:
Решение с помощью электронных таблиц
В соответствующие ячейки Табл. 3 введите расчетные формулы.
Таблица 3
|
№ |
Адрес ячейки |
Содержимое ячейки (формула) |
|
1 |
Е5 |
=КОРЕНЬ(($B$12-B5)^2+($C$12-C5)^2) |
|
2 |
E6—E9 |
Скопировать формулу из Е5 в E6—E9 |
|
3 |
В16 |
=КОРЕНЬ((B14-B12)^2+(C14-C12)^2)+СУММ(Е5:Е9) |
Компьютерная модель
|
A |
B |
C |
D |
E |
|
|
1 |
Моделирование расположения аэродрома и железнодорожной станции |
||||
|
2 |
Расположение населенных пунктов |
||||
|
3 |
Объект, населенный пункт |
Координата |
Расстояние между Аэродромом и населенными пунктами |
||
|
x |
y |
||||
|
4 |
|||||
|
5 |
Населенный пункт №1 |
2,0 |
8,0 |
||
|
6 |
Населенный пункт №2 |
10,0 |
9,0 |
||
|
7 |
Населенный пункт №3 |
1,0 |
2,0 |
||
|
8 |
Населенный пункт №4 |
4,0 |
9,0 |
||
|
9 |
Населенный пункт №5 |
9,0 |
5,0 |
||
|
10 |
|||||
|
11 |
Оптимальные координаты объектов (аэродрома и железнодорожных станций) |
||||
|
12 |
Аэродром |
||||
|
13 |
Железнодорожная станция |
||||
|
14 |
|||||
|
15 |
|||||
|
16 |
Оптимальное суммарное расстояние от аэродрома до станции и всех населенных пунктов |
Эксперимент № 1
-
Применяя надстройку Excel «Поиск решения» ( Поиск решения), назначьте в качестве целевой ячейки В16 и установите переключатель Равной: равным минимальному значению.
-
Укажите в качестве изменяемых ячеек ячейки $B$12:$C$12; $B$14:$C$14 (координаты аэродрома и станции). Ограничения не вводите.
Щелкните по кнопке Выполнить. Фрагмент рабочего листа
|
A |
B |
C |
D |
E |
|
|
1 |
Моделирование расположения аэродрома и железнодорожной станции |
||||
|
2 |
Расположение населенных пунктов |
||||
|
3 |
Объект, населенный пункт |
Координата |
Расстояние между Аэродромом и населенными пунктами |
||
|
x |
y |
||||
|
4 |
|||||
|
5 |
Населенный пункт №1 |
2,0 |
8,0 |
2,5 |
|
|
6 |
Населенный пункт №2 |
10,0 |
9,0 |
5,7 |
|
|
7 |
Населенный пункт №3 |
1,0 |
2,0 |
6,6 |
|
|
8 |
Населенный пункт №4 |
4,0 |
9,0 |
1,5 |
|
|
9 |
Населенный пункт №5 |
9,0 |
5,0 |
5,2 |
|
|
10 |
|||||
|
11 |
Оптимальные координаты объектов (аэродрома и железнодорожных станций) |
||||
|
12 |
Аэродром |
4,5 |
7,6 |
||
|
13 |
|||||
|
14 |
Железнодорожная станция |
4,5 |
7,6 |
||
|
15 |
|||||
|
16 |
Оптимальное суммарное расстояние от аэродрома до станции и всех населенных пунктов |
21,5 |
-
Постройте диаграмму, выберите тип Точечная.
-
Проанализируйте результат.
На основе полученных данных моделирования можно сделать следующий вывод: моделирование, проводимое в условиях, когда ограничения не заданы, приводит к совпадению координат расположения железнодорожной станции и аэродрома. Это вытекает и из простого анализа расчетной формулы. Минимальное расстояние будет, когда координаты объектов совпадут. В реальных условиях такие объекты располагаются на безопасном расстоянии друг от друга, кроме того, есть и некоторые технические критерии обеспечения нормальных условий функционирования объектов.
Эксперимент № 2
Усложним задачу. Введем ограничения. Предположим, что в указанном районе есть озеро и проходит железная дорога. Координаты ограничивающие местоположение аэродрома и станции, приведены в табл. 4
Таблица 4
|
Объект |
Координата Х |
Координата У |
|
Озеро |
≥ 0 и ≤4 |
≥ 3 и ≤ 6 |
|
Железная дорога |
≥ 6 |
=1 |
Рисунок 1.
-
Установите курсор в ячейку В16.
-
Введите условия ограничения на расположение аэродрома и станции. В частности, примите во внимание, что аэродром не должен находиться внутри области, чьи координаты указаны в табл. 4, а железнодорожная станция, наоборот, должна находиться на железной дороге.
-
Произведите поиск решения.
Фрагмент рабочего листа (после ввода ограничений)
|
A |
B |
C |
D |
E |
|
|
1 |
Моделирование расположения аэродрома и железнодорожной станции |
||||
|
2 |
Расположение населенных пунктов |
||||
|
3 |
Объект, населенный пункт |
Координата |
Расстояние между Аэродромом и населенными пунктами |
||
|
x |
y |
||||
|
4 |
|||||
|
5 |
Населенный пункт №1 |
2,0 |
8,0 |
3,8 |
|
|
6 |
Населенный пункт №2 |
10,0 |
9,0 |
5,8 |
|
|
7 |
Населенный пункт №3 |
1,0 |
2,0 |
5,9 |
|
|
8 |
Населенный пункт №4 |
4,0 |
9,0 |
3,2 |
|
|
9 |
Населенный пункт №5 |
9,0 |
5,0 |
3,9 |
|
|
10 |
|||||
|
11 |
Оптимальные координаты объектов (аэродрома и железнодорожных станций) |
||||
|
12 |
Аэродром |
5,2 |
6,1 |
||
|
13 |
|||||
|
14 |
Железнодорожная станция |
6,0 |
1,0 |
||
|
15 |
|||||
|
16 |
Оптимальное суммарное расстояние от аэродрома до станции и всех населенных пунктов |
27,5 |
ЗАДАЧИ ТЕОРИИ РАСПИСАНИЙ
Постановка задач теории расписаний
В задачах теории расписаний рассматриваются комплексы работ, связанных общим объектом или общим исполнителем, направленные на достижение определенной цели. Модели теории расписаний позволяют найти наиболее дешевый или наиболее быстрый порядок выполнения работ.
К задачам выбора самого дешевого порядка выполнения работ относится известная задача о шлюзе. Шлюз может пропускать в порядке очереди только по одному судну. Если создается очередь, то необходимо определить такой порядок прохождения судов через шлюз, при котором будет минимален ущерб от простоя. В такой формулировке задача появилась еще в XIX веке.
При выборе наиболее быстрого по времени варианта работ минимизируется отрезок времени от начала работ до их окончания (достижения цели). Простейшей задачей такого типа является задача и двух станках. На двух станках надо обработать N деталей. Каждая из деталей обрабатывается сначала на одном станке, а затем – на втором. Время обработки каждой детали на каждом станке известно. Задача состоит в том, что необходимо определить такой порядок обработки деталей, при котором время выполнения всей работы будет минимальным. Порядок обработки, минимизируется время T, называется оптимальным.
Задача о шлюзе
Математическая модель
Через шлюз последовательно должны пройти N судов. Известно время (в часах) шлюзования каждого судна – ti и ущерб от 1 часа простоя судна — Ui денежных единиц. Здесь индекс обозначает порядковый номер судна в очереди. Например, t1 – это время шлюзования 1-го судна, t2 – время шлюзования 2-го судна, u2 – стоимость 1 часа простоя в ожидании своей очереди 2-го судна и т.д. Время простоя в очереди, например, 4-го судна, если оно ждет, пока через шлюз пройдут первые три, равно: t1 + t2 + t3 , а материальный ущерб от простоя 4-го судна равен: u4(t1 + t2 + t3).
Показатель экономической эффективности работы шлюза связан с суммарным ущербом от простоя судов в ожидании своей очереди на шлюзовании. Например, если к шлюзу подошли одновременно 4 судна и они пропускаются через шлюз в порядке их номеров, то суммарный ущерб от простоя (S) вычисляется так: S = u2 • t1 + u3(t1 + t2) + u4(t1 + t2 + t3).
В общем случае, если в очереди находятся N судов, то суммарный ущерб от простоя выражается формулой: S = .
Задача состоит в том, чтобы определить такой порядок пропускания судов через шлюз, при котором величина S будет минимальна.
Математический анализ этой задачи приводит к следующему ответу: минимум величины S достигается в том случае, если суда пропускаются в порядке убывания величины . Этот принцип можно пояснить на следующем примере. Пусть к шлюзу подошли одновременно два судна, время шлюзования которых одинаково (t1 = t2 ), но стоимость простоя разная. Тогда в первую очередь надо пропустить то судно, у которого простой стоит дороже. Если же у двух судов в очереди одинаковая стоимость простоя ( u1 = u2 ), то вперед надо пропустить то судно, у которого меньше время шлюзования.
Критерию убывания величины равносилен критерий возрастания величины
. При вычислениях можно использовать как тот, так и другой критерий.
Решение в электронных таблицах
Рассмотрим пример для пяти судов, выстроившихся в очередь к шлюзу в порядке из прибытия. Данные приведены в таблице 1.
|
№ судна |
1 |
2 |
3 |
4 |
5 |
|
Время шлюзования |
45 |
36 |
28 |
24 |
72 |
|
Ущерб от простоя |
5 |
12 |
7 |
4 |
3 |
Вычислим общий ущерб от простоя по формуле:
S= u2 • t1 + u3 •(t1 + t2) + u4 •(t1 + t2 + t3) + u5 •(t1 + t2 + t3 + t4).
Если шлюзование судов проводить в таком порядке, то ущерб от простоя не будет минимальным. В нашем случае сумма ущерба составляет 1942 денежные единицы:
S=12•45+7•(45+36)+4•(45+36+28)+3•(45+36+28+24) =1942.
Найдем оптимальный порядок (расписание) шлюзования судов, обеспечивающий минимальный ущерб от простоя.
Чтобы найти ущерб от простоя, в ячейках С6:F6 вычислим суммы вида : , а в ячейку B7 поместим формулу = СУММПРОИЗВ(C3:F3;C6:F6).
В соответствии с этой формулой вычисляется сумма произведений: C3*C6+D3*D6+E3*E6+F3*F6 Таблица 2.
|
A |
B |
C |
D |
E |
F |
|
|
1 |
№ судна |
1 |
2 |
3 |
4 |
5 |
|
2 |
Время простоя |
45 |
36 |
28 |
24 |
72 |
|
3 |
Ущерб от простоя |
5 |
12 |
7 |
4 |
3 |
|
4 |
||||||
|
5 |
||||||
|
6 |
=B2 |
=C6+C2 |
=D6+D2 |
=E6+E2 |
||
|
7 |
=СУММПРОИЗВ(C3:F3;C6:F6) |
В 4-ю строку таблицы впишем формулы, по которым для каждого судна сосчитается величина k= . Затем отсортируем столбцы диапазона ячеек B1:F4 в порядке возрастания значений k в 4-й строке. Указание на то, что производится сортировка столбцов, задается с помощью диалогового окна Параметры сортировки: столбцы диапозона; cортировать по – строка 4, по возрастанию.
После проведения сортировки в диапазоне ячеек B1:F1 будет содержаться порядок прохождения судов через шлюз со следующими номерами: № 2, 3, 4, 1, 5. При такой очередности общий ущерб от простоя будет минимальным и составит 1347 денежных единиц, в то время как при шлюзовании судов в порядке их прибытия общий ущерб составлял 1942 денежных единицы. Таблица 3.
|
A |
B |
C |
D |
E |
F |
|
|
1 |
№ судна |
2 |
3 |
4 |
1 |
5 |
|
2 |
Время простоя |
36 |
28 |
24 |
45 |
72 |
|
3 |
Ущерб от простоя |
12 |
7 |
4 |
5 |
3 |
|
4 |
k |
3 |
4 |
6 |
9 |
24 |
|
5 |
||||||
|
6 |
36 |
64 |
88 |
133 |
||
|
7 |
Общий ущерб |
1347 |
ИССЛЕДОВАНИЕ МЕТОДОВ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЁННЫХ ИНТЕГРАЛОВ
Задача 1. Вычислить по формуле прямоугольников с шагом
. Заметим, что этот интеграл легко может быть вычислен аналитически:
Чтобы найти приближённое значение интеграла , нужно:
-
разделить отрезок [a, b] на n равных частей точками х0= а, х1, х2,…, х n -1, х n = b;
-
в
ычислить значения подынтегральной функции в точках деления, т.е. нати у 0 = f (x0), у 1 =f (x1), у 2 = f (x2), у n -1 = f (xn-1), у n = f (xn) ;
-
воспользоваться одной из приближённых формул.
Метод прямоугольников:
Простейшим приближённым методом является метод прямоугольников.
Геометрически идея способа вычисления определённого интеграла по формуле прямоугольников состоит в том, что площадь криволинейной трапеции АВСD заменяется суммой площадей прямоугольников, одна сторона которых равна, а другая —
Для нахождения определённого интеграла методом прямоугольников необходимо ввести значения подынтегральной функции f(x) в рабочую таблицу Excel в диапазоне х [0;3 ] с заданным шагом
х = 0,1.
|
A |
B |
|
|
1 |
Аргумент |
Функция |
|
2 |
0 |
=A2^2 |
|
3 |
0,1 |
|
|
4 |
0,2 |
|
|
5 |
||
|
6 |
||
|
7 |
||
|
8 |
||
|
9 |
||
|
… |
||
|
32 |
||
|
33 |
= 0,1* Сумм (В3:В32) |
В ячейке В33 появляется приближённое значение искомого интеграла (9,455) .
Сравнивая полученное приближённое значение с истинным значением интеграла (9), можно видеть, что ошибка приближения метода прямоугольников в данном случае равна= 0,455
Метод трапеций:
Криволинейная трапеция заменяется на сумму нескольких трапеций и приближённое значение определённого интеграла находится как сумма площадей трапеций.
Для нахождения определенного интеграла методом трапеций, как и в случае использования метода прмоугольников, значения подынтегральной функции f(x) должны быть введены рабочую таблицу Excel в диапазоне х [0;3] с заданным шагом
х = 0,1.
|
A |
B |
|
|
1 |
Аргумент |
Функция |
|
2 |
0 |
=A2^2 |
|
3 |
0,1 |
|
|
4 |
0,2 |
|
|
5 |
||
|
6 |
||
|
7 |
||
|
8 |
||
|
9 |
||
|
… |
||
|
32 |
||
|
33 |
=0,1*((B2+B32)/2+СУММ(B2:B31)) |
В ячейке В34 появляется приближённое значение искомого интеграла (9,005) .
Сравнивая полученное приближённое значение с истинным значением интеграла (9), можно видеть, что ошибка приближения метода трапеций в данном случае равна= 0,005
Метод трапеций обычно даёт более точное значение интеграла, чем метод прямоугольников
Задача 2. Вычислить по формуле прямоугольников с шагом
.
Решение с помощью VBA
С
Рисунок 1.
оздание интерфейса:
Код программы:
Private Sub CommandButton3_Click()
End
End Sub
Рисунок 1.
Private Sub UserForm_Initialize()
With Me.ComboBox1
.AddItem «Метод_Трапеции»
.AddItem «Метод_Прямоугольников»
End With
End Sub
Private Sub CommandButton2_Click()
Dim n As Single, a As Single, x As Single
Dim b As Single, s As Single, s1 As Single
Dim s2 As Single, z As Single, i As String
i = ComboBox1.Value
a = TextBox1.Text
b = TextBox2.Text
n = TextBox3.Text
Select Case i
Case Is = «Метод_Трапеции»
h = (b — a) / n: s = 0
x = a + h
Do While x
s = s + fun(x)
x = x + h
Loop
s = (h / 2) * (fun(a) + 2 * s + fun(b))
T
Рисунок 2.
extBox4.Text = s
Case Is = «Метод_Прямоугольников»
h = (b — a) / n: s1 = 0
x = a + h
Do While x
s1 = s1 + fun(x)
x = x + h
Loop
s1 = h * s1
TextBox5.Text = s1
End Select
End Sub
Function fun(x As Single) As Single
fun = x ^ 2
End Function
Задания для самостоятельного выполнения:
Задача 1. Методом прямоугольников и методом трапеций найти следующие интегралы:
-
при
x=0,1;
-
при
x=0,1.
Задание 2. Построить график и вычислить площадь криволинейной трапеции, ограниченной линиями y=x2sin x, y=0, x=a, x=b (ai = a+(b-a) СЛЧИС()).
Литература:
-
Информатика и ИКТ. Профильный уровень: учебник для 11 класса. / И.Г. Семакин, Е.К. Хеннер, Л.В.Шестакова.— М.: БИНОМ, Лаборатория знаний, 2012. — 330 с.
-
Информатика. Сборник элективных курсов. А.А.Чернов. Волгоград: Учитель, 2007г
-
http://иванов-м.рф/informatika_11/informatika_materialy_zanytii_11_20.html
-
Куклина И. Д. Применение электронных таблиц при изучении приближенных методов вычисления интеграла // Информатика и образование. — М. — 2010. — № 9. — С. 94 —96.
-
Попова О. Н. Моделирование задачи оптимального управления// Информатика и образование. — М. — 2002. — № 10. — С. 78 —82.
-
Гельман В.Я. Решение математических задач средствами Excel: Практикум. – СПб.: Питер, 2003. – 240 с.
-
Тимофеева Н.М. Как решать задачи? / “В мир информатики” № 67 (“Информатика” № 2/2006).
2
Грамотный расчет плановых показателей по движению денежных потоков, выручки и прибыли — один из ключевых факторов в управлении организацией. На сегодняшний день разработано немало инструментов, призванных облегчить решение поставленной задачи. Однако многие из них требуют длительного освоения и высокого уровня базовых навыков, да и стоимость подобных решений не всегда соизмерима с функционалом, которые они обеспечивают. Впрочем, есть и альтернативный вариант, позволяющий провести анализ данных в нужном формате, и получить на выходе желаемый результат. Финансовая модель бизнеса в Excel, построенная с соблюдением принципов, гарантирует получение качественной прогнозной отчетности, необходимой для эффективного контроля за организационными процессами.

Общее представление
При разработке шаблонов для экономического планирования учитываются основные показатели деятельности предприятия, к числу которых относятся:
- доходы и расходы;
- прибыль;
- денежные потоки;
- активы и обязательства.
Несмотря на внешнюю схожесть с бюджетной системой, специфика использования такого инструмента, как финансовое моделирование в эксель, предусматривает большее количество упрощений и вариативных параметров. Подобный подход обуславливается целевыми задачами, решение которых является целью прогнозирования. Отчетная таблица призвана обеспечить возможность быстрой оценки потенциальных результатов операционной деятельности и стабильности состояния организации при изменении внешних и внутренних факторов.
Построение финмодели в Excel от Microsoft или в Google docs предусматривает внесение части информации вручную, тогда как зависимые данные определяются с помощью базовых формул. Благодаря этому любая корректировка позволяет моментально пересчитать итоговые значения, оценить риски и проанализировать перспективы получения прибыли.
За счет проделанной работы формируются три типа отчетности:
- балансовые показатели предприятия;
- аналитика результатов (ОФР);
- отчет по движению денежных средств (ОДДС).
Грамотное применение полученных результатов упрощает управленческий процесс — так же, как и использование программных решений от компании «Клеверенс», исключающих вероятность технических ошибок при учете активов организации.

Финансовое моделирование проекта в Excel: что нужно знать
Для тех, кто планирует самостоятельно разобраться в особенностях и нюансах создания рабочей модели, лучшим вариантом станет последовательный переход от простых вещей к более сложным. Планомерный подход позволит избежать неточностей, связанных с использованием формул и подстановкой значений. Пошаговый план выглядит следующим образом:
- Создайте предварительный вариант с минимальным количеством данных, и задайте локальные критерии расчета для зависимых переменных. В качестве примера можно привести выручку относительно цены продукции и объемов реализации, фонд оплаты труда при сдельной работе, социальные отчисления ФОТ и т.д.
- Обобщите параметры в рамках общей системы, и проведите предварительную проверку функциональности готовой структуры. Ключевой критерий — схождение баланса, отклонения в котором свидетельствуют о допущенных ошибках. Небольшое количество формул позволяет без особых усилий выявить проблемные зоны, требующие корректировки.
- Детализируйте финансовый расчет бизнес-плана в Excel, дополнив его новыми базовыми показателями. Раскройте специфику формирования себестоимости продукции, уточните периоды взаиморасчетов с поставщиками исходя из имеющихся коммерческих условий, привяжите к производственным объемам корреляцию, учитывающую величину переходящего товарного остатка. При добавлении параметров также следует проверять работоспособность системы, чтобы исключить «перекос» формульных значений.
Поэтапная реализация проекта управления отчетностью позволяет не только отследить взаимозависимость ключевых факторов, но и лучше понять структуру доходов и расходов, исходя из которой можно выбрать грамотный курс развития организации.

Готовые решения для всех направлений
Сократите издержки в работе склада до 70% : ускорьте складские операции, устраните ошибки человеческого фактора и забудьте про потерю и пересортицу товаров.
Узнать больше
У вас всегда будут актуальные ценники на товарах и витринах, товар перестанет теряться при перемещении между магазинами, а в вашей системе учета — только точные остатки по товарам.
Узнать больше
С маркировкой вы на 100% исключите приемку контрафактного товара на свой склад, а также сможете отслеживать полную цепочку поставок товара от производителя.
Узнать больше
Скорость, точность приёмки и отгрузки товаров на складе — краеугольный камень в E-commerce бизнесе. Начни использовать современные, более эффективные мобильные инструменты.
Узнать больше
Повысьте точность учета имущества организации, уровень контроля сохранности и перемещения каждой единицы. Мобильный учет снизит вероятность краж и естественных потерь.
Узнать больше
Повысьте эффективность деятельности производственного предприятия за счет внедрения мобильной автоматизации для учёта товарно-материальных ценностей.
Узнать больше
Первое в России готовое решение для учёта товара по RFID-меткам на каждом из этапов цепочки поставок.
Узнать больше
Исключи ошибки сопоставления и считывания акцизных марок алкогольной продукции при помощи мобильных инструментов учёта.
Узнать больше
Получение сертифицированного статуса партнёра «Клеверенс» позволит вашей компании выйти на новый уровень решения задач на предприятиях ваших клиентов..
Узнать больше
Используй современные мобильные инструменты для проведения инвентаризации товара. Повысь скорость и точность бизнес-процесса.
Узнать больше
Показать все решения по автоматизации
Как построить финансовую модель компании в Excel: инструкция пошагово
В качестве наглядного примера рассмотрим вариант для предприятия, специализирующегося на розничной торговле. Подобный выбор не случаен, поскольку производственные процессы априори отличаются более сложной структурой, предполагающей материальные затраты, амортизацию, незавершенные к окончанию периода циклы, а также разнородные формы складских запасов. Кроме того, коммерческая деятельность, связанная с продажами, допускает исключение дебиторской задолженности — в тех ситуациях, когда клиентам не предоставляются опции с рассрочкой или отсрочкой платежей.
Подсчет доходов
Ключевым фактором на первом этапе выступает объем реализации. Самый простой вариант — внесение в фин модель, формируемую в Эксель, показателя выручки в денежном выражении, который позже может быть детализирован как производная от перемножения цены и количества для каждой позиции в номенклатуре. Подобный параметр также позволяет грамотно рассчитать расходы на закупку продукции.
Одной из главных сложностей на этой стадии выступает построение плана продаж. В ситуациях, когда отчетная таблица составляется для обычного тестирования, можно взять любые значения «с потолка», однако, если вы сразу рассчитываете на результат, способный принести практическую пользу — стоит заняться планированием более детально.
К числу важных факторов, требующих учета при прогнозировании, следует отнести величину налога на добавленную стоимость, по умолчанию включенного в цену реализации. Несмотря на то что налоговые отчисления формально поступают в структуре выручки, их нельзя отнести к доходной статье, поэтому выделение НДС позволит рассчитать чистую прибыль с каждой позиции.

Кроме того, нелишним станет добавление аналитики по номенклатуре, отражающей такие характеристики операционной деятельности, как:
- доля возврата продукции;
- типы клиентов (физические или юридические лица);
- реквизиты торговой точки или региона продаж.
Важно понимать, что на предварительном этапе чрезмерно подробная детализация может привести к лишней путанице, тогда как основной задачей проекта выступает составление базового плана по доходности.
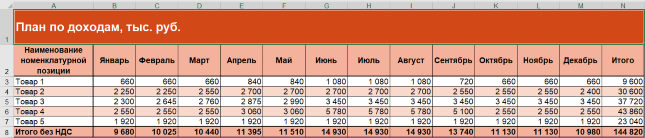
Пример планирования расходов
Расходные статьи изначально также рассматриваются в общей перспективе. Для обобщенной структуры достаточно выделить несколько элементов, таких как:
- Материальные затраты. В рамках упрощенной версии будем считать, что в эту категорию входит только приобретение товаров без НДС, количество которых полностью совпадает с объемом реализации. Исходя из этого, критериями получаемой величины станут стоимость закупки и количество продаж.
- Зарплатный фонд. Опять же, для базового варианта достаточно указать общую сумму, без дробления на отдельные элементы.
- Социальные отчисления. В этом случае используются зависимые переменные, рассчитываемые с помощью формулы. Как правило, стандартным показателем считается 30% от величины ФОТ, плюс дополнительные страховые взносы, размер которых определяется классом риска профессиональной деятельности, определенным для предприятия. В качестве примера возьмем минимально возможный размер, составляющий 0,2%.
- Амортизация. Даже с учетом того, что наше условное предприятие занимается исключительно розничной торговлей, на его балансе все равно могут быть основные средства и нематериальные активы, относящиеся к собственности. Стандартная практика — расчет среднемесячной суммы, базирующийся на теоретических или практических критериях.
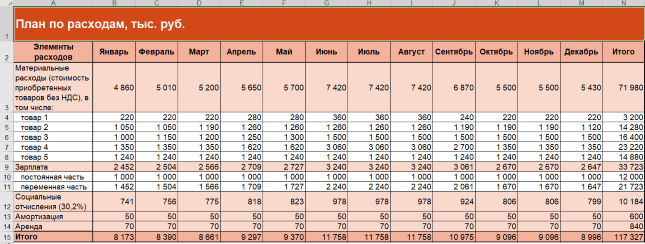
- Иные расходы. Фактически начальная стадия детализации, предполагающая отражение постоянных трат компании, легко поддающихся планированию. В рассматриваемую категорию можно включить затраты на аренду торговых площадей, размещение рекламы, представительские и командировочные компенсации, и т.п.
Указанного списка вполне достаточно для реализации проектной модели, после проверки которой можно перейти сначала к дроблению базовых значений, а затем и к обобщению полученных данных.
Составление планового отчета о финансовых результатах
Отправной точкой формирования отчетности выступает подсчет прибылей и убытков за отдельно взятый период. Аналогичное правило применяется и к построению бюджетной аналитики, поскольку для заполнения балансового раздела необходимы результирующие показатели. В случае с тестовой версией достаточно взять плановые значения основной операционной деятельности, где разность между доходами и расходами определяет итог на конкретном временном этапе.
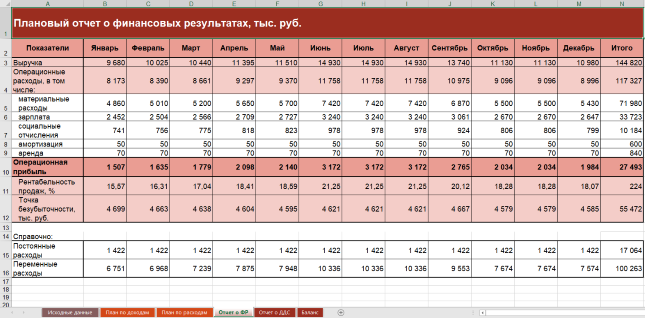
Это позволяет перейти к построению ОФР, для которого характерна взаимосвязь с балансом и ОДДС:
|
Финансовые результаты |
Балансовая строка |
ДДС |
|
Прибыль или убыток от операционной деятельности |
Нераспределенная величина добавляется к данным за предшествующий период |
— |
|
Выручка |
— |
Входящие поступления от взаиморасчетов с клиентами. Суммовой параметр корректируется с учетом переведенных авансов и текущей задолженности по следующей формуле: Поступления = Выручка + Авансовые платежи — Задолженность по отгрузкам |
|
Расходы |
— |
Выплаты, учитывающие предоплату и долговые обязательства перед кредиторами. Для расчета применяется формульное значение: Платежи = Денежные затраты + Авансы выданные — Кредиторская задолженность |
Для большей информативности следует дополнить отчет еще двумя строками:
- Рентабельность реализации — расчетный критерий, равный соотношению между операционной прибылью и выручкой.
- Порог безубыточности, выраженный в деньгах — предусматривает предварительное разделение постоянных и переменных расходных статей.
Формирование отчетности ОДДС

На этой стадии основной задачей выступает обобщение денежных поступлений и оттоков, расчет чистой разницы между ними, и суммирование полученного значения с оставшимися средствами на начало периода, позволяющее вычислить планируемый остаток. Результирующая сумма связывает аналитический базис с балансом. В рамках рассматриваемого примера возьмем за основу несколько допущений:
- Предприятие специализируется только на профильной деятельности, не осуществляя сторонних закупок и финансовых операций, и не меняя состав учредителей. Единственным видом операций остается текущая категория.
- Оплата поставляемой продукции делится на две стадии: 60% авансовым платежом, перечисляемым в месяце, предшествующем отгрузке товара, и 40% — расчет по факту приемки на склад.
- Для выплат в рамках ФОТ также предусмотрены два перевода: половину составляет аванс, выдаваемый в период начисления, вторые 50% оплачиваются в следующем календарном отрезке так же, как и страховые взносы.
В качестве прочих расходов можно взять арендную плату — взаиморасчеты с собственником торгового помещения проводятся ежемесячно, сразу после выставления счета.
Результатом подстановки указанных значений становится модель ОДДС, отражающая специфику движения денежных потоков в рамках деятельности организации.
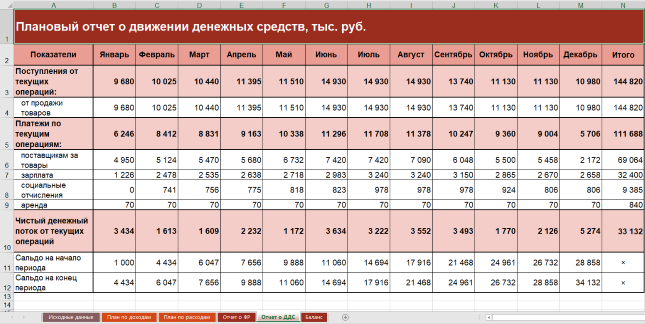
Сведение планового баланса
Обобщим технику составления в сводной таблице:
|
Показатель на начало периода |
Формула |
Пояснения |
|
Основные средства |
Баланс на начало предыдущего месяца — Амортизация за месяц (ОФР) |
— |
|
Запасы |
— |
Неизменны и равняются нулю из-за допущения, согласно которому весь объем реализуется за период |
|
Дебиторская задолженность |
Баланс на первое число предыдущего месяца + Платежи контрагентам за поставку (ОДДС) — Материальные расходы (ОФР) |
В рассматриваемом примере отсутствует дебиторская задолженность |
|
Денежные средства |
Остаток на момент начала периода (баланс) + Чистый поток (ОДДС) |
— |
|
Уставный капитал |
— |
1000 рублей (ввиду условия об отсутствии новых учредителей) |
|
Нераспределенная прибыль |
Начальный показатель (баланс) + Поступление за месяц (ОФР) |
— |
|
Кредиторская задолженность |
Значение отправной точки + Начисления ФОТ, социальным выплатам и аренде (ОФР) — Соответствующие платежи (ОДДС) |
Общие требования
Примеры построения проекта финансовой модели предприятия в программе Excel, в том числе рассмотренный в данной статье, позволяют вывести ряд основных критериев, которые нужно учитывать при планировании. Итоговый результат моделирования должен соответствовать следующим стандартам.

Простота
Очевидно, что чем сложнее структура деятельности организации — тем более детализированными должны быть аналитические инструменты, используемые для анализа эффективности. Однако практика показывает, что грамотный подход к упрощению позволяет избежать ошибок в процессе построения, и способствует более быстрому освоению функциональных механизмов на начальных этапах.
Удобство использования
Последовательная организация блоков гарантирует формирование комплексного представления об экономической составляющей, а также о нюансах составления и ведения отчетности на различных временных интервалах.
Наглядность
Распространенный недостаток — разнесение предпосылок и выводов, затрудняющее определение взаимосвязи между корректируемыми данными и показателями, на которые они влияют. Грамотная визуализация — важный аспект, исключающий сложности адаптации.
Как подготовить финансовую модель
В процессе моделирования можно учитывать различные факторы, включая не только персональные управленческие потребности, но и банковские требования, актуальные в ситуациях, когда необходимо представить подробный инвестиционный проект. Отсутствие практических навыков и наличие достаточного свободного времени — повод для самостоятельного освоения такого эффективного аналитического инструмента, как Эксель. Однако в ситуациях, когда отчет требуется быстро, и должен соответствовать строгим критериям — лучше обратиться за помощью к специалистам.
Заключение
Приведенный пример рассматривает алгоритм создания базовой отчетности, оставляющей широкий диапазон возможностей для дальнейшей оптимизации. Структурирование категорий, группировка данных, учет большего количества внешних факторов — все это позволяет получить более точные результаты, которые станут основой для принятия верных решений, направленных на развитие бизнеса. Финансовое моделирование в Excel помогает понять, как планируемые мероприятия отразятся на прибыли и убытках предприятия, и какие аспекты имеют наибольшее влияние с точки зрения увеличения показателей экономической стабильности и ликвидности — как в текущем периоде, так и в долгосрочной перспективе.
Количество показов: 25426
Хотите просчитать плановые значения выручки, прибыли и денежных потоков? На помощь придет финансовое моделирование в Excel. В статье рассказываем о базовых принципах построения модели и делимся готовым решением. На выходе вы получите прогнозную отчетность. Усильте с ее помощью контроль над процессами в организации.
Финансовая модель бизнеса: что это
Финансовая модель предприятия – это плановые показатели его деятельности по:
- доходам;
- расходам;
- прибыли;
- денежным потокам;
- активам;
- обязательствам.
Этим она похожа на систему бюджетов. Отличается от них бóльшими упрощениями и вариативными параметрами. Последнее объясняется целью создания: быстрая оценка изменений финансовых результатов и имущественного положения под влиянием разных факторов. Например, в результате смены условий расчетов с контрагентами, покупки нового оборудования, повышения зарплаты персоналу и т.п.
Обычно финансовая модель строится в Excel или Google-таблицах. Часть исходных данных вносится вручную (план по объему продаж, месячный фонд оплаты труда, нормы потребления материалов на единицу изделия и т.д.). Зависимые от них показатели задаются с помощью формул. Они обеспечивают моментальный пересчет итоговых значений выручки, операционной прибыли, дебиторки, денежных притоков и т.д.
Итоговый результат финансового моделирования – три формы отчетности:
- баланс;
- отчет о финансовых результатах (ОФР);
- отчет о движении денежных средств (ОДДС).
Скачайте финансовую модель в Excel, о создании которой рассказываем в статье. Файл – Простая финансовая модель для торговли в Excel (Fail-Fin-model-v-Excel)
Финансовое моделирование проекта: что надо знать
Если вы решили самостоятельно построить финансовую модель в Excel, то идите от простого к сложному и от общих моментов к деталям. Так проще не запутаться в большом количестве формул и ссылок.
Вот пошаговый план реализации.

Рисунок 1. Построение финансовой модели: рекомендуемые этапы
Опробуем данный подход на практике. Рассмотрим пример для организации, которая занимается розничной торговлей. Такой выбор не случайный. Любое производство сложнее торговли, так как в нем предполагаются:
- материальные затраты;
- амортизация оборудования;
- возможно, незавершенный производственный процесс на конец месяца, поэтому необходимость разделения затрат и расходов;
- разнородные складские запасы в виде материалов и продукции.
Кроме того, продажи в розницу исключают вариант формирования дебиторской задолженности покупателей, если исходить из того, что отсрочки и рассрочки не предоставляются.
Финансовая модель (ФМ) в Excel: считаем доходы
Отправная точка на данном этапе – объем продаж. Можно пойти простым путем и внести только денежное значение выручки. Позже детализировать его как произведение цены и количества в разрезе номенклатурных позиций.
Мы сразу поступим вторым способом. Это даст количественный параметр, который необходим для корректного подсчета расходов на приобретение товаров.
Основная сложность этапа: откуда взять данные по плану продаж? Все зависит от вашей цели:
- если она пока в том, чтобы построить и «обкатать» работоспособность ФМ, то берите любые данные. Например, за прошлый год или произвольные;
- если вам одновременно нужны и модель, и качественные результаты расчета по ней, то займитесь планированием отдельно.
Мы ратуем за то, чтобы на данном этапе не уходить в детали. Но разумно уже сейчас подумать: чем будете усложнять и этим приближаться к реальности?
Вот два совета.
Первый. Покажите отдельно НДС, который «сидит» в цене реализации. Он приходит в поступлениях от покупателей, но это не доход вашей организации. Добавив его в таблицу, вы посчитаете выручку-нетто или чистый доход. Заодно определите будущие платежи в бюджет по данному налогу*.
____________________
Примечание: в бюджет платится разница между НДС, который начислен к уплате, и тем, который предъявляется к возмещению по собственным закупкам.
____________________
Второй. Введите аналитику по продажам. Самое простое – это номенклатурные позиции. Дополнительно к ним:
- процент возврата товаров;
- категория клиента (физическое лицо или организация);
- номер магазина или наименование региона, если есть несколько точек продаж.
Помним: пока излишняя детализация лишь запутает. Поэтому получаем в Excel простой план по доходам.
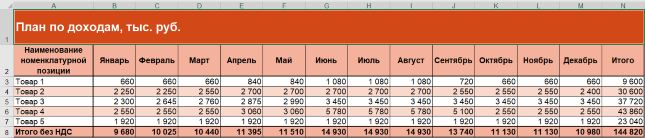
Рисунок 2. Упрощенный план по доходам в Excel
Построение финансовых моделей: пример планирования расходов
Определимся с расходами также пока в первом приближении. Обобщим полный перечень трат компании в разрезе элементов. Это будут:
- материальные траты. В упрощенном варианте предположим, что к ним относятся только траты на покупку товара без НДС и что организация продает в течение месяца столько, сколько закупает. Значит, величину определим как произведение цены приобретения и объема продаж;
- зарплата работников. Ограничимся единой суммой фонда оплаты труда за месяц без разбивки по составляющим;
- социальные отчисления. Для них составим формульную зависимость. Обычно это 30% плюс процент взносов «на травматизм» в Фонд социального страхования от начисленной оплаты труда. Данный процент зависит от класса профессионального риска по организации. Мы взяли минимальное значение 0,2%;
- амортизация. Вводим строку в ФМ, если в собственности предприятия есть основные средства и нематериальные активы. Указываем единую сумму для каждого месяца на основе средних фактических или предполагаемых значений;
- прочие расходы. Это отчасти уход в детализацию. Однако если в компании есть постоянные легко планируемые траты, то зафиксируйте их. К ним относятся: арендные платежи, траты на рекламу, на командировки и т.п.
Для упрощенной ФМ такого списка достаточно. А это четыре совета на будущее о том, чем усложнить.
Первый. Введите дополнительные позиции в материальные расходы. Например, такие:
- отопление, водоснабжение, электроэнергия;
- упаковка;
- ГСМ на автотранспорт, если он есть на балансе;
- канцелярские принадлежности и т.п.
Второй. Отдельной строкой покажите входной НДС. Когда ставка – одна (20%), то его сумма – это произведение 20% на совокупные материальные траты без НДС. Когда примешивается еще 10%, тогда:
- либо упрощайте и считайте налог по максимальной ставке;
- либо усложняйте, применяя средневзвешенное значение ставки исходя из доли в закупках с НДС по 20% и 10% в прошлые периоды.
Третий. Разделите оплату труда на составляющие:
- выделите в зарплате продавцов оклад (постоянную часть) и премию, зависящую от объема продаж (переменную компоненту);
- покажите отдельной строкой зарплату других работников, которая не завязана на количественные показатели и является постоянной.
Четвертый. Учтите изменения амортизации, если в планах организации значатся покупка или продажа основных средств и нематериальных активов.
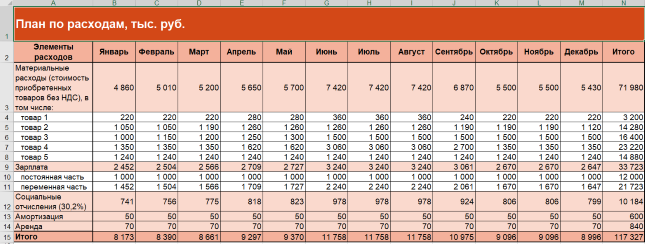
Рисунок 3. Финансовая модель бизнеса в Excel: план по расходам
То, что мы посчитали, является основой для:
- вычисления прибыли/убытка в ОФР;
- корректировки накопленного финансового результата в балансе;
- построения притоков и оттоков в ОДДС.
Перейдем ко второму этапу – обобщению данных в системе финансовых отчетов. Рассмотрим, как это делается.
Составляем плановый отчет о финансовых результатах
Формирование фактической отчетности начинается с подсчета прибыли/убытка за период. Такое же правило действует для моделей и бюджетов. Ведь чтобы заполнить раздел баланса про собственный капитал, нужна величина финансового результата.
Мы подсчитали плановые доходы и расходы по операционной деятельности. Этого достаточно, чтобы составить упрощенный отчет. Вот его возможный вариант.
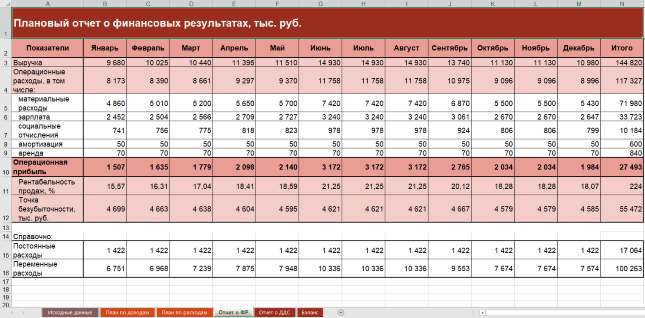
Рисунок 4. Упрощенный ОФР в Excel-модели
В нем разница между доходами и расходами показывает прибыль или убыток. Мы рассматриваем только основную деятельность без прочей. Поэтому выходим на операционный финансовый результат.
ОФР тесно связан с балансом и ОДДС. Смотрите в таблице, куда и какую информацию он передает.
Таблица 1. Взаимосвязь плановых ОФР, баланса и ОДДС
| Строка ОФР | Связанная строка баланса | Связанная строка ОДДС |
| Операционная прибыль (убыток) | Нераспределенная прибыль (убыток) – добавляется к значениям предыдущего периода | – |
| Выручка (операционные доходы) | – |
Поступления от покупателей и заказчиков – сумма выручки корректируется на авансы полученные и дебиторскую задолженность по формуле: Поступления = Выручка + Авансы полученные – Дебиторская задолженность* |
| Операционные расходы | – |
Платежи по текущей деятельности – сумма денежных** расходов корректируется на авансы выданные и кредиторскую задолженность по формуле: Платежи = Денежные расходы + Авансы выданные – Кредиторская задолженность |
|
Примечание: * в примере ФМ формируется по организации розничной торговли. Поэтому полагаем: авансов и дебиторки от покупателей нет. Значит, поступления равняются выручке; ** денежные расходы – те, которые приводят к оттоку денег (зарплата, налоги, материальные). Для сравнения: к неденежным относится амортизация |
Чтобы плановый ОФР оказался более информативным, дополним строками:
- рентабельность продаж. Это расчетный показатель, который равняется отношению прибыли (в данном случае – операционной) к выручке;
- точка безубыточности в денежном выражении. Для ее расчета предварительно разделили расходы на постоянные и переменные. Об особенностях классификации затрат по такому принципу читайте в статье «Расчет себестоимости».
Формируем плановый отчет о движении денежных средств
Здесь задача:
- обобщить денежные притоки и оттоки;
- рассчитать чистый денежный поток как разницу между ними;
- прибавить его значение к остатку денег на начало периода и вычислить остаток денег на конец. Через эту сумму ОДДС связан с балансом.
Для создаваемой ФМ исходим из допущений:
- организация занимается только основной деятельностью. При этом не покупает оборудование и ценные бумаги, не берет и не дает взаймы, не принимает новых учредителей. Значит, формируется один вид денежных операций – текущий. О двух других – инвестиционных и финансовых – читайте в статье «Анализ движения денежных средств компании»;
- товары оплачиваются поставщику двумя платежами: 60% – аванс в месяце, который предшествует поставке, 40% – окончательный расчет сразу после принятия на склад;
- зарплата выплачивается двумя переводами: 50% – аванс в месяце начисления, 50% – перевод остатка в периоде, который следует за отработанным;
- страховые взносы перечисляются в месяце, идущем за их начислением;
- прочая составляющая расходов по обычным видам деятельности представлена арендой. Платежи по ней производятся в месяце начисления арендной платы.
Получаем вариант ОДДС.
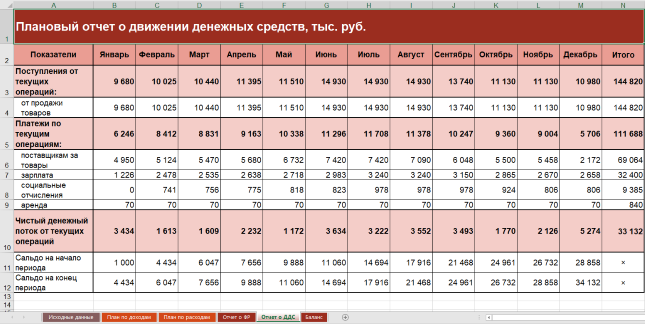
Рисунок 5. Упрощенный отчет о движении денежных средств в ФМ
Сводим плановый баланс
Предположим, что у организации:
- нет входящих остатков по запасам, дебиторской и кредиторской задолженности;
- имущество включает одно основное средство и деньги;
- в пассиве – только уставный капитал и нераспределенная прибыль.
Схема заполнения балансовых строк окажется следующей.
Таблица 2. Техника сведения упрощенного баланса
| Показатель на начало месяца | Расчетная формула | Пояснения |
| Основные средства | Основные средства на начало предыдущего месяца (баланс) – Амортизация за месяц (ОФР) | – |
| Запасы | – | Неизменны и равняются нулю из-за допущения: закупаемые товары полностью распродаются в течение месяца |
| Дебиторская задолженность | Дебиторская задолженность на начало предыдущего месяца (баланс) + Платежи поставщикам за товары (ОДДС) – Материальные расходы (ОФР) | В примере нет дебиторки покупателей, так как организация торгует в розницу |
| Денежные средства | Денежные средства на начало предыдущего месяца (баланс) + Чистый денежный поток за месяц (ОДДС) | – |
| Уставный капитал | – | Неизменен и равняется 1000 тыс. руб. из-за допущения: новых учредителей в течение года не было |
| Нераспределенная прибыль | Нераспределенная прибыль на начало предыдущего месяца (баланс) + Прибыль за месяц (ОФР) | – |
| Кредиторская задолженность | Кредиторская задолженность на начало предыдущего месяца + Начисления по зарплате, социальным отчислениям и аренде (ОФР) – Платежи по зарплате, социальным отчислениям и аренде (ОДДС) | – |
Формат баланса будет таким.
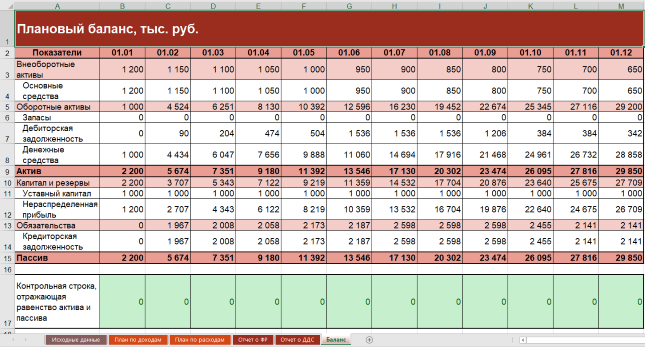
Рисунок 6. Упрощенный баланс в финансовой модели в Excel
Детализация финансовой модели в Excel
О возможных вариантах усложнения исходных данных рассказывали выше. Здесь остановимся на детализации строк плановой отчетности. Вот несколько советов:
- используйте разные группировки расходов в ОФР. Мы обобщили их по элементам. Такой подход называется «по характеру расходов». Но он – не единственный. Можно одновременно с ним или вместо него использовать функциональную классификацию с выделением себестоимости продаж, а также расходов на сбыт и управление. Подробнее про такие варианты читайте в статье «БДР: бюджет доходов и расходов»;
- добавьте другие виды прибыли в ОФР. Например, валовую. Она покажет разницу между продажной и закупочной ценами товаров. Если в организации есть прочие операции, то в отчете не обойтись без чистой прибыли. Читайте о видах финансового результата в материале «Анализ финансовых результатов деятельности компании»;
- включите в ОФР строки для прочих доходов и расходов. Растущая организация не сможет обходиться без них. Например, взятие кредита приведет к появлению процентных платежей по нему. Они – это прочий расход;
- расширьте ОДДС за счет инвестиционных и финансовых операций, если собираетесь приобретать оборудование и брать взаймы. Не смешивайте такие денежные потоки с текущими;
- детализируйте сложносоставные строки в балансе. Например, из запасов выделите товары, материалы, готовую продукцию и незавершенное производство (последние два пункта – неактуальны для торговли). Из состава дебиторки: авансы выданные поставщикам и долги покупателей. По аналогии поступите с кредиторкой и покажите в отдельных статьях: авансы полученные, задолженность перед поставщиками, перед персоналом по оплате труда, по налогам и страховым взносам, перед учредителями по дивидендам.
Не забудьте скачать Excel-файл с полученной финансовой моделью из начала статьи.
Финансовое моделирование в Excel помогает понять:
- как планируемые руководством мероприятия отразятся на величине имущества, капитала, обязательств, доходов, расходов и прибыли;
- какие факторы больше других влияют на прибыль, ликвидность и финансовую устойчивость организации.
Важна роль ФМ и в план-фактном анализе. В течение отчетного периода сравнивайте ожидания из нее с тем, как получилось в реальности. Это хороший способ контролировать ситуацию: понимать суть нарождающихся тенденций и того, к чему они приведут бизнес.
Аннотация. Это первый учебник из серии, который поможет ознакомиться с программой Excel и ее возможностями объединения и анализа данных, а также научиться легко использовать их. С помощью этой серии учебников вы научитесь создавать с нуля и совершенствовать рабочие книги Excel, строить модели данных и создавать удивительные интерактивные отчеты с использованием надстройки Power View. В этих учебниках приводится описание возможностей средств бизнес-аналитики Майкрософт в Excel, сводных таблиц, Power Pivot и Power View.
Примечание: В этой статье описаны модели данных Excel 2013. Тем не менее те же функции моделирования данных и Power Pivot, Excel 2013, также относятся к Excel 2016.
Вы узнаете, как импортировать и просматривать данные в Excel, строить и совершенствовать модели данных с использованием Power Pivot, а также создавать с помощью надстройки Power View интерактивные отчеты с возможностью публикации, защиты и предоставления общего доступа.
Учебники этой серии
-
Импорт данных в Excel 2013 и создание модели данных
-
Расширение связей модели данных с Excel, Power Pivot и DAX
-
Создание отчетов Power View на основе карт
-
Объединение интернет-данных и настройка параметров отчета Power View по умолчанию
-
Справка по Power Pivot
-
Создание впечатляющих отчетов Power View, часть 2
В этом учебнике вы начнете работу с пустой книги Excel.
Разделы учебника
-
Импорт данных из базы данных
-
Импорт данных из электронной таблицы
-
Импорт данных с помощью копирования и вставки
-
Создание связи между импортированными данными
-
Контрольная точка и тест
В конце учебника есть тест, с помощью которого можно проверить свои знания.
В этом учебном ряду используются данные об олимпийских медалях, странах, принимающих олимпийских играх, а также различных олимпийских соревнованиях. Мы рекомендуем вам перейти к каждому учебнику по порядку. Кроме того, в учебниках Excel 2013 с Power Pivot включена. Дополнительные сведения о Excel 2013 можно найти здесь. Чтобы получить инструкции по Power Pivot, щелкните здесь.
Импорт данных из базы данных
Начнем работу с учебником с пустой книги. В этом разделе вы узнаете, как подключиться к внешнему источнику данных и импортировать их в Excel для дальнейшего анализа.
Сначала загрузим данные из Интернета. Эти данные об олимпийских медалях являются базой данных Microsoft Access.
-
Чтобы скачать файлы, которые мы используем в этом ряду учебников, перейдите по следующим ссылкам: Скачайте каждый из четырех файлов в папку, которую легко найти, например «Загрузки» или «Мои документы», или в новую папку:
> OlympicMedals.accdb Access
>OlympicSports.xlsx Excel книги
> Population.xlsx Excel книги
>DiscImage_table.xlsx Excel книги -
Откройте пустую книгу в Excel 2013.
-
Выберите пункт ДАННЫЕ > Получение внешних данных > Из Access. Лента динамически изменяется по ширине книги, поэтому команды на ленте могут выглядеть не так, как в представленных ниже окнах. В первом окне показана лента при развернутой книге, а во втором ширина книги изменена таким образом, что она занимает лишь часть окна.
-
Выберите файл ОлимпийскиеМедали.accdb и нажмите кнопку Открыть. Появится окно «Выбор таблицы», в котором отобразятся таблицы, найденные в базе данных. Таблицы в базе данных похожи на листы или таблицы в Excel. Установите флажок Разрешить выбор нескольких таблиц. Затем нажмите кнопку ОК.
-
Появится окно «Импорт данных».
Примечание: Обратите внимание на то, что в нижней части окна вы можете добавить эти данные в модель данных ,показанную на следующем экране. Модель данных создается автоматически при одновременном импорте или работе с двумя или более таблицами. Модель данных интегрирует таблицы, позволяя провести большой анализ с помощью с помощью Power Pivot, таблиц и Power View. При импорте таблиц из базы данных существующие связи между ними используются для создания модели данных в Excel. Модель данных в Excel, но ее можно просматривать и изменять непосредственно с помощью Power Pivot надстройки. Модель данных подробно рассмотрена далее в этом учебнике.
Выберите параметр Отчет таблицы, который импортирует таблицы в Excel и подготавливает таблицу для анализа импортируемых таблиц, и нажмите кнопку ОК.
-
После завершения импорта данных будет создана сводная таблица на основе импортированных таблиц.
Теперь, когда данные импортированы в Excel и автоматически создана модель данных, можно приступить к их просмотру.
Просмотр данных в сводной таблице
Просматривать импортированные данные удобнее всего с помощью сводной таблицы. В сводной таблице можно перетаскивать поля (похожие на столбцы в Excel) из таблиц (например, таблиц, импортированных из базы данных Access) в разные области, настраивая представление данных. Сводная таблица содержит четыре области: ФИЛЬТРЫ, СТОЛБЦЫ, СТРОКИ и ЗНАЧЕНИЯ.
Возможно, придется поэкспериментировать, чтобы определить, в какие области следует перетащить поле. Можно перетаскивать из таблиц любое количество полей, пока представление данных в сводной таблице не примет нужный вид. Не бойтесь перетаскивать поля в любые области сводной таблицы — это не повлияет на базовые данные.
Рассмотрим в сводной таблице данные об олимпийских медалях, начиная с призеров Олимпийских игр, упорядоченных по дисциплинам, типам медалей и странам или регионам.
-
В разделе Поля сводной таблицы разверните таблицу Medals, щелкнув расположенную рядом с ней стрелку. В развернутой таблице Medals найдите поле NOC_CountryRegion и перетащите его в область СТОЛБЦЫ. Аббревиатура NOC обозначает Национальный олимпийский комитет — организационную единицу уровня страны или региона.
-
Затем перетащите виды спорта из таблицы Disciplines в область СТРОКИ.
-
Давайте отфильтруем дисциплины, чтобы отображались только пять видов спорта: стрельба из лука (Archery), прыжки в воду (Diving), фехтование (Fencing), фигурное катание (Figure Skating) и конькобежный спорт (Speed Skating). Это можно сделать в области Поля сводной таблицы или в фильтре Метки строк в самой сводной таблице.
-
Щелкните в любом месте этой Excel, чтобы выбрать ее. В списке полей таблицы, в котором расширена таблица Disciplines, наведите курсор на поле Discipline и справа от поля появится стрелка в списке. Щелкните стрелку вниз, щелкните (Выделить все),чтобы удалить все выбранные фигуры, а затем прокрутите список вниз и выберите Archery, Diving, Fencing, Figure Skating и Speed Skating. Нажмите кнопку ОК.
-
Либо щелкните в разделе сводной таблицы Метки строк стрелку раскрывающегося списка рядом с полем Метки строк, нажмите кнопку (Выбрать все), чтобы снять отметку со всех выбранных параметров, а затем прокрутите вниз и выберите пункты Archery, Diving, Fencing, Figure Skating и Speed Skating. Нажмите кнопку ОК.
-
-
В разделе Поля сводной таблицы перетащите поле Medal из таблицы Medals в область ЗНАЧЕНИЯ. Поскольку значения должны быть числовыми, Excel автоматически изменит поле Medal на Count of Medal.
-
В таблице Medals снова выберите поле Medal и перетащите его в область ФИЛЬТРЫ.
-
Давайте отфильтруем сводную таблицу таким образом, чтобы отображались только страны или регионы, завоевавшие более 90 медалей. Вот как это сделать.
-
В сводной таблице щелкните стрелку раскрывающегося списка рядом с полем Метки столбцов.
-
Выберите Фильтры по значению, а затем — Больше…
-
Введите 90 в последнем поле (справа). Нажмите кнопку ОК.
-
Сводная таблица будет иметь следующий вид:
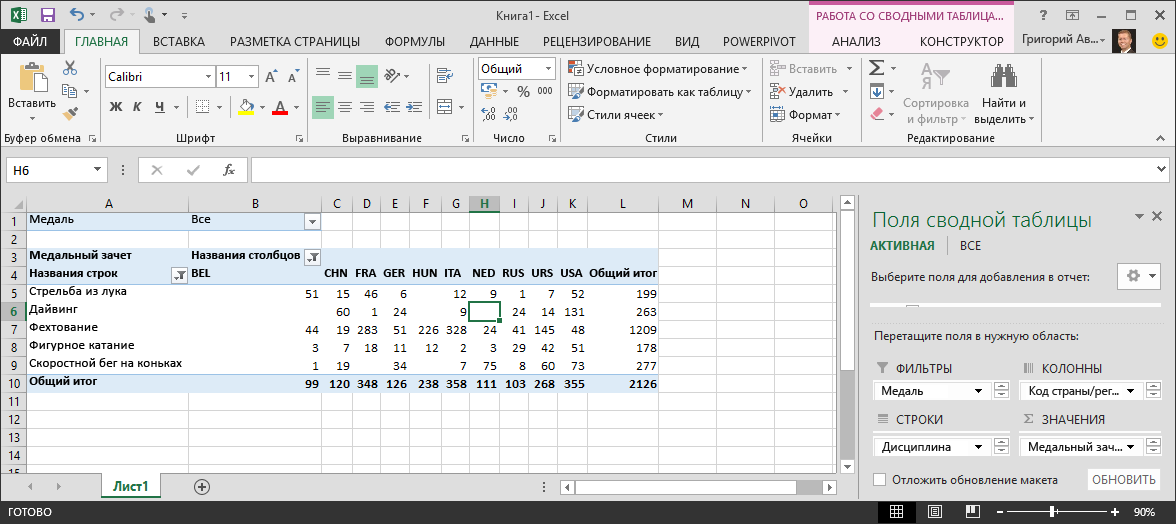
Не затрачивая особых усилий, вы создали сводную таблицу, которая содержит поля из трех разных таблиц. Эта задача оказалась настолько простой благодаря заранее созданным связям между таблицами. Поскольку связи между таблицами существовали в исходной базе данных и вы импортировали все таблицы сразу, приложение Excel смогло воссоздать эти связи в модели данных.
Но что делать, если данные происходят из разных источников или импортируются не одновременно? Обычно можно создать связи с новыми данными на основе совпадающих столбцов. На следующем этапе вы импортируете дополнительные таблицы и узнаете об этапах создания новых связей.
Импорт данных из таблицы
Теперь давайте импортируем данные из другого источника, на этот раз из существующей книги, а затем укажите связи между существующими и новыми данными. Связи по возможности анализировать наборы данных в Excel и создавать интересные и иммерсивные визуализации на личных данных, которые вы импортируете.
Начнем с создания пустого листа, а затем импортируем данные из книги Excel.
-
Вставьте новый лист Excel и назовите его Sports.
-
Перейдите к папке, в которой содержатся загруженные файлы образцов данных, и откройте файл OlympicSports.xlsx.
-
Выберите и скопируйте данные на листе Sheet1. При выборе ячейки с данными, например, ячейки А1, можно нажать клавиши Ctrl + A, чтобы выбрать все смежные данные. Закройте книгу OlympicSports.xlsx.
-
На листе Sports поместите курсор в ячейку А1 и вставьте данные.
-
Нажмите клавиши Ctrl + T, чтобы отформатировать выделенные данные в виде таблицы. Кроме того, можно отформатировать данные в виде таблицы через ленту, выбрав команду ГЛАВНАЯ > Форматировать как таблицу. Поскольку у данных есть заголовки, установите флажок Таблица с заголовками в окне Создание таблицы, как показано ниже.
Форматирование данных в виде таблицы имеет множество преимуществ. Таблице можно присвоить имя, чтобы ее было легче идентифицировать. Также можно установить связи между таблицами, позволяющие просматривать и анализировать данные в сводных таблицах, Power Pivot и Power View. -
Присвойте таблице имя. В средстве > КОНСТРУКТОР > свойства, найдите поле Имя таблицы и введите Sports. Книга будет выглядеть так же, как на следующем экране.
-
Сохраните книгу.
Импорт данных с помощью копирования и вставки
Теперь, когда данные из книги Excel импортированы, давайте сделаем то же самое с данными из таблицы на веб-странице или из любого другого источника, дающего возможность копирования и вставки в Excel. На следующих этапах мы добавим из таблицы города, принимающие Олимпийские игры.
-
Вставьте новый лист Excel и назовите его Hosts.
-
Выделите и скопируйте приведенную ниже таблицу вместе с заголовками.
|
City |
NOC_CountryRegion |
Alpha-2 Code |
Edition |
Season |
|
Melbourne / Stockholm |
AUS |
AS |
1956 |
Summer |
|
Sydney |
AUS |
AS |
2000 |
Summer |
|
Innsbruck |
AUT |
AT |
1964 |
Winter |
|
Innsbruck |
AUT |
AT |
1976 |
Winter |
|
Antwerp |
BEL |
BE |
1920 |
Summer |
|
Antwerp |
BEL |
BE |
1920 |
Winter |
|
Montreal |
CAN |
CA |
1976 |
Summer |
|
Lake Placid |
CAN |
CA |
1980 |
Winter |
|
Calgary |
CAN |
CA |
1988 |
Winter |
|
St. Moritz |
SUI |
SZ |
1928 |
Winter |
|
St. Moritz |
SUI |
SZ |
1948 |
Winter |
|
Beijing |
CHN |
CH |
2008 |
Summer |
|
Berlin |
GER |
GM |
1936 |
Summer |
|
Garmisch-Partenkirchen |
GER |
GM |
1936 |
Winter |
|
Barcelona |
ESP |
SP |
1992 |
Summer |
|
Helsinki |
FIN |
FI |
1952 |
Summer |
|
Paris |
FRA |
FR |
1900 |
Summer |
|
Paris |
FRA |
FR |
1924 |
Summer |
|
Chamonix |
FRA |
FR |
1924 |
Winter |
|
Grenoble |
FRA |
FR |
1968 |
Winter |
|
Albertville |
FRA |
FR |
1992 |
Winter |
|
London |
GBR |
UK |
1908 |
Summer |
|
London |
GBR |
UK |
1908 |
Winter |
|
London |
GBR |
UK |
1948 |
Summer |
|
Munich |
GER |
DE |
1972 |
Summer |
|
Athens |
GRC |
GR |
2004 |
Summer |
|
Cortina d’Ampezzo |
ITA |
IT |
1956 |
Winter |
|
Rome |
ITA |
IT |
1960 |
Summer |
|
Turin |
ITA |
IT |
2006 |
Winter |
|
Tokyo |
JPN |
JA |
1964 |
Summer |
|
Sapporo |
JPN |
JA |
1972 |
Winter |
|
Nagano |
JPN |
JA |
1998 |
Winter |
|
Seoul |
KOR |
KS |
1988 |
Summer |
|
Mexico |
MEX |
MX |
1968 |
Summer |
|
Amsterdam |
NED |
NL |
1928 |
Summer |
|
Oslo |
NOR |
NO |
1952 |
Winter |
|
Lillehammer |
NOR |
NO |
1994 |
Winter |
|
Stockholm |
SWE |
SW |
1912 |
Summer |
|
St Louis |
USA |
US |
1904 |
Summer |
|
Los Angeles |
USA |
US |
1932 |
Summer |
|
Lake Placid |
USA |
US |
1932 |
Winter |
|
Squaw Valley |
USA |
US |
1960 |
Winter |
|
Moscow |
URS |
RU |
1980 |
Summer |
|
Los Angeles |
USA |
US |
1984 |
Summer |
|
Atlanta |
USA |
US |
1996 |
Summer |
|
Salt Lake City |
USA |
US |
2002 |
Winter |
|
Sarajevo |
YUG |
YU |
1984 |
Winter |
-
В Excel поместите курсор в ячейку А1 на листе Hosts и вставьте данные.
-
Отформатируйте данные в виде таблицы. Как описано выше, для форматирования данных в виде таблицы нажмите клавиши Ctrl + T или выберите пункт меню ГЛАВНАЯ > Форматировать как таблицу. Поскольку у данных есть заголовки, установите флажок Таблица с заголовками в окне Создание таблицы.
-
Присвойте таблице имя. На вкладках РАБОТА С ТАБЛИЦАМИ > КОНСТРУКТОР > Свойства найдите поле Имя таблицы и введите слово Hosts.
-
Выберите столбец Edition и на вкладке ГЛАВНАЯ задайте для него числовой формат с 0 десятичных знаков.
-
Сохраните книгу. Книга будет иметь следующий вид:
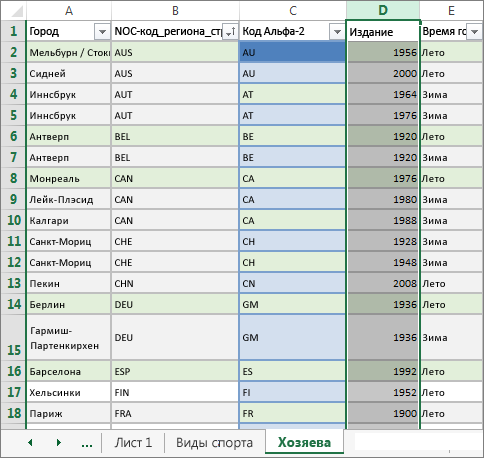
Теперь, когда у нас есть книги Excel с таблицами, можно создать отношения между ними. Создание связей между таблицами позволяет объединить данные двух таблиц.
Создание связи между импортированными данными
Мы уже можем начать использовать поля в сводной таблице из импортированных таблиц. Если не удается определить, как объединить поля в сводную таблицу, нужно создать связь с существующей моделью данных. На следующих этапах вы узнаете, как создать связь между данными, импортированными из разных источников.
-
На листе Лист1в верхней части поля таблицы щелкните Все, чтобы просмотреть полный список доступных таблиц, как показано на следующем экране.
-
Прокрутите список, чтобы увидеть новые таблицы, которые вы только что добавили.
-
Разверните пункт Sports и выберите пункт Sport, чтобы добавить в сводную таблицу. Обратите внимание, что Excel выдаст запрос на создание связи, как показано ниже.
Это уведомление появляется по той причине, что вы использовали поля таблицы, которая не является частью базовой модели данных. Один из способов добавить таблицу в модель данных заключается в создании связи с таблицей, которая уже есть в модели данных. Для создания связи в одной из таблиц должен содержаться столбец уникальных, не повторяющихся значений. В образце данных в таблице Disciplines, импортированной из базы данных, содержится поле с кодами видов спорта SportID. Эти же коды присутствуют в виде поля в импортированных нами данных Excel. Попробуем создать связь.
-
Нажмите кнопку СОЗДАТЬ… в выделенной области Поля сводной таблицы, чтобы открыть диалоговое окно Создание связи, как показано на приведенном ниже снимке экрана.
-
В области Таблица выберите пункт Disciplines из раскрывающегося списка.
-
В области Столбец (чужой) выберите пункт SportID.
-
В области Связанная таблица выберите пункт Sports.
-
В области Связанный столбец (первичный ключ) выберите пункт SportID.
-
Нажмите кнопку ОК.
Сводная таблица изменится с учетом новой связи. Но пока она имеет не совсем правильный вид из-за порядка полей в области СТРОКИ. Дисциплина — это подкатегория вида спорта, но поскольку мы расположили дисциплины выше видов спорта в области СТРОКИ, она не организована должным образом. Этот нежелательный порядок показан на приведенном ниже снимке экрана.
-
В области СТРОКИ переместит sport выше дисциплины. Это гораздо лучше, и в ней отображаются нужные данные, как показано на следующем экране.
При этом Excel создает модель данных, которую можно использовать глобально во всей книге в любой сводной таблице и диаграмме, а также в Power Pivot и отчете Power View. Основой модели данных являются связи между таблицами, определяющие пути навигации и вычисления данных.
В следующем учебнике Расширение связей модели данных с помощью Excel 2013,Power Pivot и DAX, вы можете использовать полученные сведения и расширить модель данных с помощью мощной и наглядной надстройки Excel под названием Power Pivot. Вы также узнаете, как вычислять столбцы в таблице и использовать его, чтобы в модель данных можно было добавить несвязанные таблицы.
Контрольная точка и тест
Повторение изученного материала
Теперь у вас есть книга Excel, которая содержит сводную таблицу с доступом к данным в нескольких таблицах (некоторые из них были импортированы отдельно). Вы освоили операции импорта из базы данных, из другой книги Excel, а также посредством копирования и вставки данных в Excel.
Чтобы данные работали вместе, потребовалось создать связь между таблицами, которую Excel использует для согласования строк. Вы также узнали, что наличие в таблице столбцов, согласующих данные в другой таблице, необходимо для создания связей и поиска связанных строк.
Вы готовы перейти к следующему учебнику этого цикла. Вот ссылка:
Расширение связей модели данных с использованием Excel 2013, Power Pivot и DAX
ТЕСТ
Хотите проверить, насколько хорошо вы усвоили пройденный материал? Приступим. Этот тест посвящен функциям, возможностям и требованиям, о которых вы узнали в этом учебнике. Внизу страницы вы найдете ответы на вопросы. Удачи!
Вопрос 1. Почему так важно преобразовывать импортируемые данные в таблицы?
A. Их не нужно преобразовывать в таблицы, потому что все импортированные данные преобразуются в таблицы автоматически.
Б. При преобразовании импортируемых данных в таблицы они исключаются из модели данных. Они доступны в сводных Power Pivot и Power View только в том случае, если они исключены из модели данных.
C. Если преобразовать импортированные данные в таблицы, их можно включить в модель данных, и они будут доступны в сводных таблицах, Power Pivot и Power View.
D. Импортированные данные нельзя преобразовать в таблицы.
Вопрос 2. Какие из указанных ниже источников данных можно импортировать в Excel и включить в модель данных?
A. Базы данных Access и многие другие базы данных.
B. Существующие файлы Excel.
C. Все, что можно скопировать и вставить в Excel, а также отформатировать как таблицу, включая таблицы данных на веб-сайтах, документы и любые иные данные, которые можно вставить в Excel.
D. Все вышеперечисленное.
Вопрос 3. Что произойдет в сводной таблице, если изменить порядок полей в четырех областях полей сводной таблицы?
A. Ничего. После размещения полей в области полей сводной таблицы их порядок изменить нельзя.
B. Формат сводной таблицы изменится в соответствии с макетом, но это не повлияет на базовые данные.
C. Формат сводной таблицы изменится в соответствии с макетом, но при этом базовые данные будут изменены без возможности восстановления.
D. Базовые данные изменятся, что приведет к созданию новых наборов данных.
Вопрос 4. Что необходимо для создания связи между таблицами?
A. Ни в одной из таблиц не может быть столбца, содержащего уникальные, не повторяющиеся значения.
B. Таблица не должна быть частью книги Excel.
C. Столбцы не должны быть преобразованы в таблицы.
D. Ни один из вышеперечисленных ответов не является правильным.
Ответы на вопросы теста
-
Правильный ответ: C
-
Правильный ответ: D
-
Правильный ответ: B
-
Правильный ответ: D
Примечания: Ниже перечислены источники данных и изображений в этом цикле учебников.
-
Набор данных об Олимпийских играх © Guardian News & Media Ltd.
-
Изображения флагов из справочника CIA Factbook (cia.gov).
-
Данные о населении из документов Всемирного банка (worldbank.org).
-
Авторы эмблем олимпийских видов спорта Thadius856 и Parutakupiu.
Обобщающий урок в 11 классе по теме «Информационные технологии накопления, обработки и хранения данных». Разработан по программе Макаровой Н.В. К уроку прилагается конспект, мультимедийная презентация актуализации знаний в форме игры «Своя игра», презентация для проведения урока, практические работы (готовые для распечатки) и домашнее задание. Так же прилагается электронная ведомость в Excel для наглядного отображения итогов урока.