Моделирование в excel курсовая - Word и Excel - помощь в работе с программами

Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа № 15 имени Пяти Героев Советского Союза

Иследовательская работа

Тема:

«Создание и исследование моделей

в электронной таблице Excel»

Секция информатики

Выполнила: Сотникова Полина Андреевна,

ученица 10 «А» класса

Руководитель: Титаренко Алексей Анатольевич,

учитель информатики

г. Хабаровск

2016

Содержание

Актуальность темы…………………………………………………………………………………………………………………3

Введение………………………………………………………………………………………………………………………………..4

Создание информационных моделей…………………………………………………………………………………..5

Формулы в Excel…………………………………………………………………………………………………………………….7

Этапы разработки и исследования моделей………………………………………………………………………..10

Исследование физических моделей в электронных таблицах…………………………………………..11

Исследование биологической модели развития популяций………………………………………………14

Оптимизационное моделирование в экономике…………………………………………………………………17

Заключение…………………………………………………………………………………………………………………………….20

Список использованной литературы…………………………………………………………………………………….21

Актуальность темы

Часто для исследования предметов, процессов и явлений человек создает модели окружающего мира.

Наглядные модели часто используются в процессе обучения. На уроке географии мы изучаем нашу планету используя её модели – карты и глобусы, при изучении химии мы используем модели молекул и кристаллических решеток, изучаем строение человека по анатомическим муляжам скелета и органов на биологии.

Модели играют чрезвычайно важную роль в проектировании и создании различных технических устройств, машин и механизмов, зданий, электрических цепей и т.д. Без предварительного создания чертежей невозможно изготовить даже простую деталь, не говоря уже о сложном механизме. Кроме чертежей,в проектировании часто изготавливают макеты. Разработка электрической схемы обязательно предшествует созданию электрических цепей.

Развитие науки невозможно без создания теоретических моделей (теорий, законов, гипотез), отражающих строение, свойства и поведение реальных объектов. Соответствие теоретических моделей действительности проверяется с помощью опытов и экспериментов.

Все художественное творчество фактически является процессом создания моделей. Например, такой литературный жанр, как басня, переносит реальные отношения между людьми на отношения между животными и фактически создает модели человеческих отношений.

Введение

Моделирование – это метод познания, состоящий в создании и исследовании моделей – неких новых объектов, которые отражают существенные особенности изучаемого объекта, явления или процесса.Модель – это некий новый объект, который отражает существенные особенности изучаемого объекта,явления или процесса. Модели позволяют представить в наглядной форме объекты и процессы, недоступные для непосредственного восприятия (очень большие или очень маленькие объекты, очень быстрые или очень медленные процессы).

Компьютерные модели стали обычным инструментом математического моделирования и применяются в физике, астрофизике, механике, химии, биологии, экономике, социологии, метеорологии, других науках и прикладных задачах в различных областях радиоэлектроники, машиностроения, автомобилестроения и прочих. Компьютерные модели используются для получения новых знаний о моделируемом объекте или для приближенной оценки поведения систем, слишком сложных для аналитического исследования. Компьютерное моделирование является одним из эффективных методов изучения сложных систем. Компьютерные модели проще и удобнее исследовать в силу их возможности проводить вычислительные эксперименты, в тех случаях когда реальные эксперименты затруднены из-за финансовых или физических препятствий или могут дать непредсказуемый результат. Логичность и формализованность компьютерных моделей позволяет определить основные факторы, определяющие свойства изучаемого объекта-оригинала (или целого класса объектов). В частности, моделирование в электронных таблицах может быть использовано для описания ряда объектов, обладающих одинаковыми наборами свойств. С помощью таблиц могут быть построены как статические, так и динамические информационные модели в различных предметных областях, а простота использования программ создания таблиц помогает составлять модели людям без знания сложных языков программирования.

Создание информационных моделей:

Информационные модели отражают различные типы систем объектов, в которых реализуются различные структуры взаимодействия и взаимосвязи между элементами системы. Для отражения систем с различными структурами используются различные типы информационных моделей: табличные, иерархические и сетевые. В программе Excelдоступно создание табличного типа моделей.

Табличные информационные модели:

Одним из наиболее часто используемых типов информационных моделей является прямоугольная таблица, состоящая из столбцов и строк. Такой тип моделей применяется для описания ряда объектов, обладающих одинаковыми наборами свойств.

В табличной информационной модели обычно перечень объектов размещен в ячейках первого столбца таблицы, а значения их свойств – в других столбцах.

С помощью электронной таблицы Excelпостроим таблицу стоимости продуктов. В первом столбце таблицы будет содержаться перечень продуктов, а во втором – интересующее нас свойство (цена).

С помощью специальных инструментов, встроенных в программу Excelможно визуализировать таблицу, представив ее в виде графика или круговой диаграммы. Для этого нужно выделить таблицу, зайти во вкладку «Вставка» и выбрать нужный формат визуализации.

Визуализация круговой диаграммой

Визуализация столбчатой диаграммой

Формулы в Excel

В таблицах Excelможно не только вводить и визуализировать данные, но и производить простые и сложные расчеты над данными.Все это реализуется при помощи формул в ячейках. Формула выполняет вычисления или другие действия с данными в листе.

Порядок ввода формулы

Для начала определим, в какой ячейке должен стоять результат расчета. Затем выделим эту ячейку (нажмем на нее левой кнопкой мышки и ячейка станет активной).

Вводить формулу надо со знака равенства. Это надо для того, чтобы Excel понял, что в ячейку вводится именно формула, а не данные.

Выделим произвольную ячейку, например D1. В строке формул введем =2+3 и нажмем Enter. В ячейке появится результат (5). А в строке формул сверху останется сама формула.

При обработке формулы с большим количеством вычислений, наблюдается определенный приоритет.

В первую очередь выполняются выражения внутри скобок.
Умножение и деление имеют более высокий приоритет чем сложение и вычитание.
Операторы с одинаковым приоритетом выполняются слева направо.

Так, в примере выше, сначала выполняется действие в скобках (5-4=1), потом первое умножение (100*1=100), затем второе умножение (38*2=76), сложение (100+26=126), и в конце вычитание (126-76=50).

Также, можно выполнять действия над числами, содержащимися в ячейках. Для этого, вместо цифр, в формулах нужно использовать ссылки на ячейки – букву латинского алфавита, обозначающую столбец и цифру, обозначающую строку.

Так, в ячейку D3 была введена формула D1+D2. В результате сложились числа,стоящие в ячейках D1(4) и D2(6) и полученный результат – 10 был записан в ячейку D3.

Для складывания нескольких ячеек используется функция СУММ. Для суммирования трех чисел формула запишется следующим образом

Но можно облегчить себе работу и вместо перечисления каждой ячейки записать диапазон, с помощью двоеточия

Истинное значение функции СУММ раскрывается, когда необходимо сложить большое количество ячеек в Excel. В примере ниже требуется просуммировать 12 значений. Функция СУММ позволяет сделать это несколькими щелчками мышью, если же использовать оператор сложения, то провозиться придется долго.

В таблицах Excelможно не только проводить простейшие вычисления над числами, но и возводить в степень, извлекать корень, производить сравнение чисел и многое другое.

Этапы разработки и исследования моделей

Использование компьютера для исследования информационных моделей различных объектов и систем позволяет изучить их изменения в зависимости от значения тех или иных параметров. Процесс разработки моделей и их исследования на компьютере можно разделить на несколько основных этапов.

На первом этапе исследования объекта или процесса обычно строится описательная информационная модель. Такая модель выделяет существенные с точки зрения целей проводимого исследования параметры объекта, а несущественными параметрами пренебрегает.

На втором этапе создается формализованная модель, то есть описательная информационная модель записывается с помощью какого-либо формального языка. В такой модели с помощью формул, уравнений, неравенств и пр. фиксируются формальные соотношения между начальными и конечными значениями свойств объектов, а также накладываются ограничения на допустимые значения этих свойств.

Однако далеко не всегда удается найти формулы, явно выражающие искомые величины через исходные данные. В таких случаях используются приближенные математические методы, позволяющие получать результаты с заданной точностью.

На третьем этапе необходимо формализованную информационную модель преобразовать в компьютерную модель, то есть выразить ее на понятном для компьютера языке. Существуют два принципиально различных пути построения компьютерной модели:

1) построение алгоритма решения задачи и его кодирование на одном из языков программирования;

2) построение компьютерной модели с использованием одного из приложений (электронных таблиц, СУБД и пр.).

В процессе создания компьютерной модели полезно разработать удобный графический интерфейс, который позволит визуализировать формальную модель, а также реализовать интерактивный диалог человека с компьютером на этапе исследования модели.

Четвертый этап исследования информационной модели состоит в проведении компьютерного эксперимента. Если компьютерная модель существует в виде программы на одном из языков программирования, ее нужно запустить на выполнение и получить результаты.

Если компьютерная модель исследуется в приложении, например в электронных таблицах, можно провести сортировку или поиск данных, построить диаграмму или график и так далее.

Пятый этап состоит в анализе полученных результатов и корректировке исследуемой модели. В случае различия результатов, полученных при исследовании информационной модели, с измеряемыми параметрами реальных объектов можно сделать вывод, что на предыдущих этапах построения модели были допущены ошибки или неточности. Например, при построении описательной качественной модели могут быть неправильно отобраны существенные свойства объектов, в процессе формализации могут быть допущены ошибки в формулах и так далее. В этих случаях необходимо провести корректировку модели, причем уточнение модели может проводиться многократно, пока анализ результатов не покажет их соответствие изучаемому объекту.

Исследование физических моделей в электронных таблицах:

Рассмотрим процесс построения и исследования модели на конкретном примере движения тела, брошенного под углом к горизонту.

Задача: В процессе тренировке теннисистов используются автоматы по бросания мячика в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в мишень определенного размера, находящуюся на известном расстоянии.

Качественная описательная модель: Сначала построим качественную описательную модель процесса движения тела с использованием физических объектов, понятия и законов, то есть в данном случае идеализированную модель движения объекта. Из условия задачи можно сформулировать следующие основные предположения:

Мячик мал по сравнению с Землей, поэтому его можно считать материальной точкой;
Изменение высоты мячика мало, поэтому ускорение свободного падения можно считать постоянной величиной g= 9,8 мс и движение по оси ОУ можно считать равноускоренным;
Скорость бросания тела мала, поэтому сопротивлением воздуха можно пренебречь и движение по оси ОХ можно считать равномерным

Формальная модель: Для формализации модели используем известные из курса физики формулы равномерного и равноускоренного движения. При заданных начальной скорости v0 и угле бросания aзначения координат дальности полета х и высоты у от времени можно записать следующими формулами:

X=v0*cos*t;

Y=v0*sinα*t – g*t²/2

Пусть мишень высотой h будет размещаться на расстоянии sот автомата. Из первой формулы выражаем время, которое понадобится мячику, чтобы преодолеть расстояние s:

t = s/(v0*cos2α)

Представляем это значение для tв формулу для у. Получаем l – высоту мячика над землей на расстоянии s:

l = s*tgα – g*s²/(2*v0²*cosα²)

Формализуем теперь условие попадания мячика в мишень. Попадание произойдет, если значение высоты lмячика в мишень. Попадание произойдет, если значение высоты lмячика будет удовлетворять условию в форме неравенства:

0≤l ≤ h

Если l<0, то это означает «недолет», а если l>h, то это означает «перелет».

Создание модели:

Для ввода начальной скорости будем использовать ячейку В1, а для ввода угла – ячейку В2
Введем в ячейки А5:А18 значения времени с интервалом в 0,2 с.
В ячейки В5 и С5 введем формулы:

=$B$1*cos(Радианы($B$2))*А5

=$B$1*sin(РАДИАНЫ($B$2))*A5-4,9*A5*A5

Скопируем формулы в ячейки В6:В18 и С6:С18 соответственно.

Визуализируем модель, построив график зависимости координаты у от координаты х (траекторию движения тела).

Построить диаграмму типа График, в которой используется в качестве категории диапазон ячеек В5:В18, а в качестве значений – диапазон ячеек С5:С18.

Исследование модели: Исследуем модель и определим с заданной точностью 0,1 диапазон изменений угла, который обеспечивает попадание в мишень, находящуюся на расстоянии 30 м и имеющую высоту 1 м, при заданной начальной скорости 18 м/с. Воспользуемся для этого методом Подбор параметра.

Установить для ячеек точность один знак после запятой

Ввести в ячейки B21, B22 и В23 значения расстояния до мишени S = 30 м, начальной скорости Vо = 18 м/с и угла α= 35⁰, а в ячейку В25 – формулу для вычисления высоты мячика над поверхностью для заданных условий:

=B21*TAN(РАДИАНЫ(B23))-(9,81*B21^2)/(2*B22^2*COS(РАДИАНЫ(B23))^2)

Для заданных начальных условий определим углы, которые обеспечивают попадание в мишень на высотах 0 и 1 м.

Выделить ячейку В25 и ввести команду [Сервис-Подбор параметра…]. На появившейся диалоговой панели ввести в поле Значение: наименьшую высоту попадания в мишень ( то есть 0). В поле Изменяя значение ячейки: ввести адрес ячейки, содержащей значение угла (в данном случае $B$23).

В ячейке В23 появится значение 32,6. Повторить процедуру подбора параметра для максимальной высоты попадания в мишень – в ячейке В23 получим значение 36,1.

Таким образом, исследование компьютерной модели в электронных таблицах показало, что существует диапазон значений для угла бросания от 32,6 до 36,1⁰, который обеспечивает попадание в мишень высотой 1 м, находящуюся на расстоянии 30 м, мячиком брошенным со скоростью 18 м/с.

Исследование биологической модели развития популяций

В биологии при исследовании развития биосистем строятся динамические модели изменения численности популяций различных живых существ (бактерий, рыб, животных и пр.) с учетом различных факторов. Взаимовлияние популяций рассматривается в моделях типа «хищник-жертва».

Формальная модель. Изучение динамики численности популяций естественно начать с простейшей модели неограниченного роста, в которой численность популяции ежегодно увеличивается на определенный процент. Математическую модель можно записать с помощью рекуррентной формулы, связывающей численность популяции следующего года с численностью популяции текущего года, с использованием коэффициента роста а:

X(n+1) = a * x(n)

Например, если ежегодный прирост численности популяции составляет 5%, то а = 1,05. В модели ограниченного роста учитывается эффект перенаселенности, связанный с нехваткой питания, болезнями и так далее, который замедляет рост популяции с увеличением ее численности. Введем коэффициент перенаселенности b, значение которого обычно существенно меньше а (b<<а). Тогда коэффициент ежегодного увеличения численности равен (а — b*х(n)) и формула принимает вид:

X(n+1) = (a – b * x(n)) * x(n)

В модели ограниченного роста с отловом учитывается, что на численность популяций промысловых животных и рыб оказывает влияние величина ежегодного отлова. Если величина ежегодного отлова равна с, то формула принимает вид:

X(n+1) = (a – b * x(n)) * x(n) — c

Популяции обычно существуют не изолированно, а во взаимодействии с другими популяциями. Наиболее важным типом такого взаимодействия является взаимодействие между жертвами и хищниками (например, караси-щуки, зайцы-волки и так далее). В модели «хищник-жертва» количество жертв х(n) и количество хищников у(n) связаны между собой. Количество встреч жертв с хищниками можно считать пропорциональным произведению количеств жертв и хищников, а коэффициент f характеризует возможность гибели жертвы при встрече с хищниками. В этом случае численность популяции жертв ежегодно уменьшается на величину f * х(n)* у(n) и формула для расчета численности жертв принимает вид:

X(n+1) = (a – b * x(n)) * x(n) – c – f* x(n) * y(n)

Численность популяции хищников в отсутствие жертв (в связи с отсутствием пищи) уменьшается, что можно описать рекуррентной формулой

Y(n+1) = d* y(n)

где значение коэффициента d < 1 характеризует скорость уменьшения численности популяции хищников. Увеличение популяции хищников можно считать пропорциональной произведению собственно количеств жертв и хищников, а коэффициент е характеризует величину роста численности хищников за счет жертв. Тогда для численности хищников можно использовать

формулу:

y(n+1) = d*y(n) + e*x(n)*y(n)

Компьютерная модель. Построим в электронных таблицах компьютерную модель, позволяющую исследовать численность популяций с использованием различных моделей: неограниченного роста, ограниченного роста, ограниченного роста с отловом и «хищник—жертва».

В ячейки В1 и В6 внести начальные значения численности популяций жертв и хищников.

В ячейки В2:В5 внести значения коэффициентов a, b, cи f, влияющих на изменение численности жертв.

В ячейки В7 и В8 внести значения коэффициентов dи е, влияющих на изменение численности хищников

В столбце Dбудем вычислять численность популяции в соответствии с моделью неограниченного роста, в столбце Е – ограниченного роста, в столбце F–ограниченного роста с отловом, в столбцах Gи H–«хищник-жертва».

В ячейки D1, E1, F1 и G1 внести значения начальной численности популяций жертв, в ячейку Н1 – хищников.

В ячейку D2 внести рекуррентную формулу неограниченного роста =$B$2*D1

В ячейку Е2 внести рекуррентную формулу неограниченного роста =($B$2-$B$3*E1)*E1

В ячейку F2 внести рекуррентную формулу ограниченного роста с отловом =($B$2-$B$3*F1)*F1-$B$4

В ячейку G2 внести рекуррентную формулу изменения количества жертв =($B$2-$B$3*G1)*G1-$B$4-$B$5*G1*H1

В ячейку Н2 внести рекуррентную формулу изменения количества хищников =$B$7*H1+$B$8*G1*H1

Скопировать внесенные формулы в ячейки столбцов командой [Правка-Заполнить-Вниз].

В ячейках столбцов ознакомиться с динамикой изменения численности популяций.

Выделить столбцы данных и построить диаграмму типа График. Появятся графики изменения численности популяций в соответствии с моделями неограниченного роста, ограниченного роста, ограниченного роста с отловом, моделью хищник-жертва.

Исследование модели: Изменяя значения начальных численностей популяций, а также коэффициенты, можно получать различные варианты изменения численности популяций в зависимости от времени.

Оптимизационное моделирование в экономике

В сфере управления сложными системами (например, в экономике) применяется оптимизационное моделирование, в процессе которого осуществляется поиск наиболее оптимального пути развития системы.

Критерием оптимальности могут быть различные параметры; например, в экономике можно стремиться к максимальному количеству выпускаемой продукции, а можно к ее низкой себестоимости. Оптимальное развитие соответствует экстремальному (максимальному или минимальному) значению выбранного целевого параметра.

Развитие сложных систем зависит от множества факторов (параметров), следовательно, значение целевого параметра зависит от множества параметров. Выражением такой зависимости является целевая функция

К = F(X1,X2,…,Xn),

где К — значение целевого параметра; X1,X2,…,Xn — параметры, влияющие на развитие системы.

Цель исследования состоит в нахождении экстремума этой функции и определении значений параметров, при которых этот экстремум достигается. Если целевая функция нелинейна, то она имеет экстремумы, которые находятся определенными методами.

Однако часто целевая функция линейна и, соответственно, экстремумов не имеет. Задача поиска оптимального режима при линейной зависимости приобретает смысл только при наличии определенных ограничений на параметры. Если ограничения на параметры (система неравенств) также имеют линейный характер, то такие задачи являются задачами линейного программирования. (Термин «линейное программирование» в имитационном моделировании понимается как поиск экстремумов линейной функции, на которую наложены ограничения.) Рассмотрим в качестве примера экономического моделирования поиск вариантов оптимального раскроя листов материала на заготовки определенного размера.

Содержательная постановка проблемы. В ходе производственного процесса из листов материала получают заготовки деталей двух типов А и Б тремя различными способами, при этом количество получаемых заготовок при каждом методе различается.

Тип Заготовки	1 способ раскроя	2 способ раскроя	3 способ раскроя
А	10	3	8
Б	3	6	4

Необходимо выбрать оптимальное сочетание способов раскроя, для того чтобы получить 500 заготовок первого типа и 300 заготовок второго типа при расходовании наименьшего количества листов материала.

Формальная модель. Параметрами, значения которых требуется определить, являются количества листов материала, которые будут раскроены различными способами:

Х1 — количество листов, раскроенное способом 1;

Х2 — количество листов, раскроенное способом 2;

Х3 — количество листов, раскроенное способом 3.

Тогда целевая функция, значением которой является количество листов материала, примет вид:

F = Х1+ Х2 + Х3.

Ограничения определяются значениями требуемых количеств заготовок типа А и Б, тогда с учетом количеств заготовок, получаемых различными способами, должны выполняться два равенства: 10Х1+ ЗХ2 + 8Х3 = 500;

ЗХ1 + 6Х2 + 4Х3 = 300.

Кроме того, количества листов не могут быть отрицательными, поэтому должны выполняться неравенства:

X1>= 0; Х2>= 0; Х3 >= 0.

Таким образом, необходимо найти удовлетворяющие ограничениям значения параметров, при которых целевая функция принимает минимальное значение. Компьютерная модель. Будем искать решение задачи путем создания и исследования компьютерной модели в электронных таблицах Excel.

Оптимизационное моделирование

Ячейки В2, С2 и D2 выделить для значений параметров Х1, Х2 и Х3.

В ячейку В4 ввести формулу для вычисления целевой функции:

=В2+С2+D2

В ячейку В7 ввести формулу вычисления количества заготовок типа А:

=10*B2+3*C2+8*D2.

В ячейку В8 ввести формулу вычислений количества заготовок типа Б:

=3*B2+6*C2+4*D2

Исследование модели: Для поиска оптимального набора значений параметров, который соотвествует минимальному значению целевой функции, воспользоваться надстройкой электронных таблиц Поиск решения.

На вкладке Данные нажмите кнопку Поиск решения.
На появившейся диалоговой панели Поиск решения установить:

Адрес целевой ячейки
Вариант оптимизации значения целевой ячейки (максимизация, минимизация или подбор значения)
Адреса ячеек, значения которых изменяются в процессе поиска решения ( в которых хранятся значения параметров)

Ограничения (типа «=» для ячеек, хранящих количество деталей, и типа «≥» для параметров).

Щелкнуть по кнопке Выполнить. В ячейке целевой функции появится значение 69,4, а в ячейках параметров значения 0,11,58.

Таким образом, для изготовления 500 деталей А и 300 деталей Б требуется 71 лист материала, при этом 12 листов нужно раскроить по второму, а 59 по третьему способу.

Заключение

Моделирование глубоко проникает в теоретическое мышление. Более того, развитие любой науки в целом можно трактовать — в весьма общем, но вполне разумном смысле, — как «теоретическое моделирование». Важная познавательная функция моделирования состоит в том, чтобы служить импульсом, источником новых теорий. Нередко бывает так, что теория первоначально возникает в виде модели, дающей приближённое, упрощённое объяснение явления, и выступает как первичная рабочая гипотеза, которая может перерасти в «предтеорию» — предшественницу развитой теории. При этом в процессе моделирования возникают новые идеи и формы эксперимента, происходит открытие ранее неизвестных фактов. Такое «переплетение» теоретического и экспериментального моделирования особенно характерно для развития физических теорий.

Моделирование — не только одно из средств отображения явлений и процессов реального мира, но и — несмотря на описанную выше его относительность — объективный практический критерий проверки истинности наших знаний, осуществляемой непосредственно или с помощьюустановления их отношения с другой теорией, выступающей в качестве модели, адекватность которой считается практически обоснованной. Применяясь в органическом единстве с другими методами познания, моделирование выступает как процесс углубления познания, его движения от относительно бедных информацией моделей к моделям более содержательным, полнее раскрывающим сущность исследуемых явлений действительности.

В своем проекте я показала, как использовать электронные таблицы Excelдля моделирования и анализа созданных моделей.

Список использованной литературы

Н. Угринович «Информатика и информационные технологии»
Н. Угринович «Информатика и ИКТ»
http://on-line-teaching.com/excel/lsn003.html
http://www.excel-office.ru/formulivexcel/formulivexcel

Источник

Подборка по базе: Практическая работа № 2.docx, Практическая работа № 11.docx, Практическая работа 6.docx, Контрольная работа ТИПЫ ТЕОРИЙ И МОДЕЛИ СОЦИАЛЬНОЙ РАБОТЫ.docx, контрольная работа 6 кл декабрь.docx, Лабораторная работа клубень луковица.docx, Контрольная работа по разделу Человек в экономических отношениях, Практическая работа _Решение генетических задач на законы Г.Менд, Исследовательская работа_Капитонв Игорь.pptx, Практическая работа №2 (2).docx

Проведение имитационных экспериментов в среде MS Excel можно осуществить двумя способами — с помощью встроенных функций и путем использования инструмента «Генератор случайных чисел» дополнения «Анализ данных» (Analysis ToolPack). В курсовой работе будет использован первый способ проведения имитационных экспериментов — с помощью встроенных функций MS Excel.

Следует отметить, что применение встроенных функций целесообразно лишь в том случае, когда вероятности реализации всех значений случайной величины считаются одинаковыми. Тогда для имитации значений требуемой переменной можно воспользоваться математическими функциями СЛЧИС или СЛУЧМЕЖДУ. Форматы функций приведены в табл. 3.
Таблица 3.

Математические функции для генерации случайных чисел

Наименование функции	Формат функции
Оригинальная версия	Локализованная версия
RAND	СЛЧИС	СЛЧИС () — не имеет аргументов
RANDBETWEEN	СЛУЧМЕЖДУ	СЛУЧМЕЖДУ (нижн_граница; верхн_граница)

Функция «СЛЧИС»

Функция СЛЧИС () возвращает равномерно распределенное случайное число E, большее, либо равное 0 и меньшее 1, т. е.: 0 ≤ E < 1. Вместе с тем, путем несложных преобразований, с ее помощью можно получить любое случайное вещественное число. Например, чтобы получить случайное число между a и b, достаточно задать в любой ячейке ЭТ следующую формулу:
=СЛЧИС () * (b-a) +a

Эта функция не имеет аргументов. Если в ЭТ установлен режим автоматических вычислений, принятый по умолчанию, то возвращаемый функцией результат будет изменяться всякий раз, когда происходит ввод или корректировка данных. В режиме ручных вычислений пересчет всей ЭТ осуществляется только после нажатия клавиши [F9].

Настройка режима управления вычислениями производится установкой соответствующего флажка в подпункте «Вычисления» пункта «Параметры» темы «Сервис» главного меню.

В целом применение данной функции при решении задач финансового анализа ограничено рядом специфических приложений. Однако ее удобно использовать в некоторых случаях для генерации значений вероятности событий, а также вещественных чисел.

Функция «СЛУЧМЕЖДУ»

Как следует из названия этой функции, она позволяет получить случайное число из заданного интервала. При этом тип возвращаемого числа (т. е. вещественное или целое) зависит от типа заданных аргументов.

В качестве примера, сгенерируем случайное значение для переменной Q (объем выпуска продукта). Согласно табл. 1., эта переменная принимает значения из диапазона 150 — 300.

Введем в любую ячейку ЭТ формулу:
=СЛУЧМЕЖДУ (150; 300) (Результат: 210).
Если задать аналогичные формулы для переменных P и V, а также формулу для вычисления NPV и скопировать их требуемое число раз, можно получить генеральную совокупность, содержащую различные значения исходных показателей и полученных результатов. После чего, используя статистические функции, нетрудно рассчитать соответствующие параметры распределения и провести вероятностный анализ. Продемонстрируем изложенный подход на решении примера 1. Перед тем, как приступить к разработке шаблона, целесообразно установить в ЭТ режим ручных вычислений.

Приступаем к разработке шаблона. С целью упрощения и повышения наглядности анализа выделим для его проведения в рабочей книге MS Excel два листа.

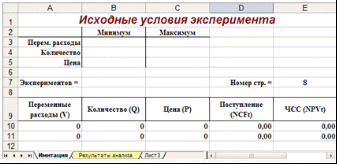
Первый лист — «Имитация», предназначен для построения генеральной совокупности (рис. 1.). Определенные в данном листе формулы и собственные имена ячеек приведены в табл. 4. и 5.

Рис. 1. Лист «Имитация»
Таблица 4.

Формулы листа «Имитация»

Ячейка	Формула
Е7	=B7+10-2
A10	=СЛУЧМЕЖДУ ($B$3; $C$3)
A11	=СЛУЧМЕЖДУ ($B$3; $C$3)
B10	=СЛУЧМЕЖДУ ($B$4; $C$4)
B11	=СЛУЧМЕЖДУ ($B$4; $C$4)
C10	=СЛУЧМЕЖДУ ($B$5; $C$5)
C11	=СЛУЧМЕЖДУ ($B$5; $C$5)
D10	= (B10* (C10-A10) -Пост_расх-Аморт) * (1-Налог) +Аморт
D11	= (B11* (C11-A11) -Пост_расх-Аморт) * (1-Налог) +Аморт
E10	=ПС (Норма; Срок; -D10) -Нач_инвест
E11	=ПС (Норма; Срок; -D11) -Нач_инвест

Таблица 5.

Имена ячеек листа «Имитация»

Адрес ячейки	Имя	Комментарии
Блок A10: A11	Перем_расх	Переменные расходы
Блок B10: B11	Количество	Объем выпуска
Блок C10: C11	Цена	Цена изделия
Блок D10: D11	Поступления	Поступления от проекта NCFt
Блок E10: E11	ЧСС	Чистая современная стоимость NPV

Первая часть листа (блок ячеек А1. Е7) предназначена для ввода диапазонов изменений ключевых переменных, значения которых будут генерироваться в процессе проведения эксперимента. В ячейке В7 задается общее число имитаций (экспериментов). Формула, заданная в ячейке Е7, вычисляет номер последней строки выходного блока, в который будут помещены полученные значения. Смысл этой формулы будет раскрыт позже.

Вторая часть листа (блок ячеек А9. Е11) предназначена для проведения имитации. Формулы в ячейках А10. С11 генерируют значения для соответствующих переменных с учетом заданных в ячейках В3. С5 диапазонов их изменений. Обратим внимание на то, что при указании нижней и верхней границы изменений используется абсолютная адресация ячеек.

Формулы в ячейках D10. E11 вычисляют величину потока платежей и его чистую современную стоимость соответственно. При этом значения постоянных переменных берутся из следующего листа шаблона — «Результаты анализа».

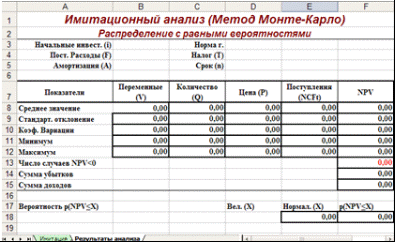
Лист «Результаты анализа» кроме значений постоянных переменных содержит также функции, вычисляющие параметры распределения изменяемых (Q, V, P) и результатных (NCF, NPV) переменных и вероятности различных событий. Определенные для данного листа формулы и собственные имена ячеек приведены в табл. 6. и 7. Общий вид листа показан на рис. 2.
Таблица 6.

Формулы листа «Результаты анализа»

Ячейка	Формула
B8	=СРЗНАЧ (Перем_расх)
B9	=СТАНДОТКЛОНП (Перем_расх)
B10	=B9/B8
B11	=МИН (Перем_расх)
B12	=МАКС (Перем_расх)
C8	=СРЗНАЧ (Количество)
C9	=СТАНДОТКЛОНП (Количество)
C10	=C9/C8
C11	=МИН (Количество)
C12	=МАКС (Количество)
D8	=СРЗНАЧ (Цена)
D9	=СТАНДОТКЛОНП (Цена)
D10	=D9/D8
D11	=МИН (Цена)
D12	=МАКС (Цена)
E8	=СРЗНАЧ (Поступления)
E9	=СТАНДОТКЛОНП (Поступления)
E10	=E9/E8
E11	=МИН (Поступления)
E12	=МАКС (Поступления)
F8	=СРЗНАЧ (ЧСС)
F9	=СТАНДОТКЛОНП (ЧСС)
F10	=F9/F8
F11	=МИН (ЧСС)
F12	=МАКС (ЧСС)
F13	=СЧЁТЕСЛИ (ЧСС; «<0»)
F14	=СУММЕСЛИ (ЧСС; «<0»)
F15	=СУММЕСЛИ (ЧСС; «>0»)
Е18	=НОРМАЛИЗАЦИЯ (D18; $F$8; $F$9)
F18	=НОРМСТРАСП (E18)

Таблица 7.

Имена ячеек листа «Результаты анализа»

Адрес ячейки	Имя	Комментарии
B2	Нач_инвест	Начальные инвестиции
B3	Пост_расх	Постоянные расходы
B4	Аморт	Амортизация
D2	Норма	Норма дисконта
D3	Налог	Ставка налога на прибыль
D4	Срок	Срок реализации прока

Рис. 2. Лист «Результаты анализа»
Поскольку формулы листа содержат ряд новых функций, приведем необходимые пояснения.

Функции МИН () и МАКС () вычисляют минимальное и максимальное значение для массива данных из блока ячеек, указанного в качестве их аргумента. Имена и диапазоны этих блоков приведены в табл. 7.

Функция СЧЕТЕСЛИ () осуществляет подсчет количества ячеек в указанном блоке, значения которых удовлетворяют заданному условию. Функция имеет следующий формат:
=СЧЕТЕСЛИ (блок; «условие»).
В данном случае, заданная в ячейке F13, эта функция осуществляет подсчет количества отрицательных значений NPV, содержащихся в блоке ячеек ЧСС (см. табл. 7).

Механизм действия функции СУММЕСЛИ () аналогичен функции СЧЕТЕСЛИ (). Отличие заключается лишь в том, что эта функция суммирует значения ячеек в указанном блоке, если они удовлетворяют заданному условию. Функция имеет следующий формат:
=СУММЕСЛИ (блок; «условие»).
В данном случае, заданные в ячейках F14, F15, функции осуществляет подсчет суммы отрицательных (ячейка F14) и положительных (ячейка F14) значений NPV, содержащихся в блоке ЧСС. Смысл этих расчетов будет объяснен позже.

Две последние формулы (ячейки Е18 и F18) предназначены для проведения вероятностного анализа распределения NPV и требуют небольшого теоретического отступления.

В рассматриваемом примере мы исходим из предположения о независимости и равномерном распределении ключевых переменных Q, V, P. Однако какое распределение при этом будет иметь результатная величина — показатель NPV, заранее определить нельзя.

Одно из возможных решений этой проблемы — попытаться аппроксимировать неизвестное распределение каким-либо известным. При этом в качестве приближения удобнее всего использовать нормальное распределение. Это связано с тем, что в соответствии с центральной предельной теоремой теории вероятностей при выполнении определенных условий сумма большого числа случайных величин имеет распределение, приблизительно соответствующее нормальному.

В прикладном анализе для целей аппроксимации широко применяется частный случай нормального распределения — т. н. стандартное нормальное распределение. Математическое ожидание стандартно распределенной случайной величины Е равно 0: M (E) = 0. График этого распределения симметричен относительно оси ординат и оно характеризуется всего одним параметром — стандартным отклонением s, равным 1.

Приведение случайной переменной E к стандартно распределенной величине Z осуществляется с помощью т.н. нормализации — вычитания средней и последующего деления на стандартное отклонение:
(2)
Как следует из (2), величина Z выражается в количестве стандартных отклонений. Для вычисления вероятностей по значению нормализованной величины Z используются специальные статистические таблицы.

В MS Excel подобные вычисления осуществляются с помощью статистических функций НОРМАЛИЗАЦИЯ () и НОРМСТРАСП ().

Источник

Министерство сельского
хозяйства РФ

ФГОУ ВПО Тюменская
государственная сельскохозяйственная
академия

Институт экономики и
финансов

Кафедра экономико-математических
методов и

вычислительной техники

КУРСОВОЙ ПРОЕКТ

Оптимизация состава и
использования

машинно-тракторного парка

Выполнил:

студент гр.
341

Зарубина М.В.

Проверил:

доцент, к.с.-х.н.

Селюкова Г.П.

Тюмень-2012

Содержание

ВВЕДЕНИЕ

1. ИСТОРИЯ ПРИМЕНЕНИЯ МАТЕМАТИЧЕСКИХ
МЕТОДОВ
В ЭКОНОМИКЕ

2. ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

2.1. Постановка задачи линейного
программирования .

2.2. Математическая запись модели.

2.3. Развернутая экономико-математическая
модель.

2.4. Алгоритм решения транспортной
задачи.

3. РЕШЕНИЕ ЗАДАЧИ И
АНАЛИЗ ОПТИМАЛЬНОГО ПЛАНА

3.1. Постановка задачи.

3.2. Развернутая экономико-математическая
модель

3.3. Алгоритм решения задачи
с помощью сервисной функции
Excel

3.4. Анализ оптимального
решения

3.5. Анализ устойчивости
оптимального решения

ЗАКЛЮЧЕНИЕ

СПИСОК ЛИТЕРАТУРЫ

ПРИЛОЖЕНИЯ

Введение

Моделирование, как метод
научного познания, стало применяться
еще в глубокой древности и
постепенно захватило все новые
области научных познаний: техническое
конструирование, строительство и
архитектуру, астрономию, физику, химию,
биологию и, наконец, общественные науки.
Большие успехи и признание практически
во всех отраслях современной науки принес
методу моделирования XX век. Однако методология
моделирования долгое время развивалась
независимо отдельными науками. Отсутствовала
единая система понятий, единая терминология.
Лишь постепенно стала осознаваться важная
роль моделирования как универсального
метода научного познания.

Успехи в области экономической
науки, в разработке и внедрении
более совершенных методов организации
и управления, не возможны без применения
математического моделирования, являющегося
важным средством проверки достоверности
выдвигаемых гипотез в различных
областях деятельности. Метод математического
моделирования позволяет отразить
самые существенные стороны экономической
действительности, показать взаимосвязь
этих сторон через соотношение характеризующих
их величин. Математическое моделирование
дает неограниченные возможности для
выражения связей и отношений
между множеством экономических
явлений, относящихся к самым
различным сферам общественного
производства, оно позволяет вскрывать
новые отношения и зависимости
в экономике.

Данный курс охватывает достаточно
обширный круг математических методов
и моделей, в том числе и
моделей оптимизации, которые нашли
широкое применение в экономической
науке. Например, в модели поведения
потребителя предполагается. Что
он ищет максимум полезности. Модели фирмы
основаны на предпосылке максимума
прибыли для предпринимателя. Модели
рынка – на предпосылке оптимальных
стратегий участников обмена. Модели
общего равновесия – на предпосылке
цен оптимального плана. Модели воспроизводства
– на предпосылке оптимального роста.
Большой интерес в современных условиях
представляют собой социально-экономические
модели, позволяющие проследить динамику
и дать прогноз основным социально-экономическим
показателям, модели рыночной экономики,
эколого-экономические модели. Преимущество
знания основ математического моделирования
заключается в том, что при правильности
заложенных предпосылок количественных
характеристик, полученные на основе модели
выводы являются практически бесспорными.
Жизнь требует, чтобы экономисты имели
научно обоснованные количественные представления
об экономических категориях и законах
общественного производства. Математическое
выражение экономических категорий и
закономерностей не только повышает степень
обоснованности экономической теории,
но и увеличивает практическую ценность
ее выводов и заключений.

1. ИСТОРИЯ ПРИМЕНЕНИЯ
МАТЕМАТИЧЕСКИХ МЕТОДОВ
В ЭКОНОМИКЕ.

Применение математических
методов, в том числе и методов математического
моделирования, в экономике в целом имеет
длительную историю. В качестве примера
приведем характеристику математического
метода исследования основателем классической
школы буржуазной политической экономии
В. Петти (1623 — 1687). В предисловии к «Политической
арифметике» В. Петти указывал, что его
способ исследования «не обычный, ибо
вместо того, чтобы употреблять слова
только в сравнительной и превосходной
степени и прибегать к умозрительным аргументам,
я вступил на путь выражения своих мнений
на языке чисел, весов и мер, что я уже давно
стремился пойти по этому пути, чтобы показать
пример политической арифметики».

Революционный демократ, крупнейший
экономист домарксовского периода
Н. Г. Чернышевский (1828 — 1889) в замечаниях
на трактат Д, С. Миля «Основания политической
экономии» писал: «Мы видели уже много
примеров тому, какими приемами пользуется
политическая экономия для решения своих
задач. Эти приемы математические. Иначе
и быть не может, потому что предмет науки
— количества, подлежащие счету и мере,
понимаемые только через вычисление и
измерение».

Понятие об экономике как
науке возникло в период расцвета
греческой рабовладельческой демократии,
когда были сделаны первые попытки
не просто заметить, а теоретически
осмыслить факты экономической
жизни.
Слово «экономия», от которого произошли
такие понятия, как «экономика», «экономическая
наука» и т. д., в переводе с греческого
имеет смысл науки о ведении домашнего
хозяйства. По своему основному содержанию
она должна была заниматься вопросами
рационального хозяйствования. Однако
поскольку богатое греческое рабовладельческое
хозяйство являлось сложной производственной
системой, на которой отражались все процессы,
происходившие в обществе, то эта наука
неизбежно затрагивала и более общие проблемы:
из каких хозяйственных единиц должно
состоять разумно построенное государство;
в каком отношении эти единицы должны
обменивать производимые ими товары; какую
роль играют торговля и деньги? Проблемы
экономической науки в таком виде сформулировал
великий греческий философ Аристотель,
которого принято считать ее основателем.
Аристотель первым пытался рассмотреть
экономические закономерности, господствующие
в обществе, выдвинул идею о различии между
потребительной и меновой стоимостями
товаров, высказал мысль о превращении
денег в капитал и т. д.

Таким образом, еще в Древней
Греции в экономической науке
возникли два направления исследований:
во-первых, это анализ методов рационального
управления народным хозяйством и, во-вторых,
изучение основных экономических закономерностей.
В дальнейшем первое направление
превратилось в науку о рациональном
управлении деятельностью производительных
единиц любого уровня — от производственного
участка до экономики в целом.
Второе направление дало начало экономической
теории — науке, изучающей основные
экономические закономерности сменяющих
друг друга общественно-экономических
формаций. Оба направления экономической
науки развивались и развиваются
в тесной связи между собой, их
общность особенно заметна в исследованиях,
направленных на изучение экономики
страны как целого.
В системе экономических наук главенствующее
положение занимает экономическая теория:
она служит теоретической и методологической
основой всего комплекса экономических
наук. Применение математических методов
в экономике началось именно в теоретико-экономических
исследованиях.

Обычно в качестве исторически
первой модели общественного производства
называют экономическую таблицу
Ф. Кене (1694 — 1774). В 1758 г. он опубликовал
первый вариант своей «Экономической
таблицы», второй вариант — «Арифметическая
формула» — был опубликован в 1766 году.
К. Маркс высоко оценил таблицу Ф. Кенэ.
«Это попытка, — писал Маркс, — сделанная
во второй трети XIII столетия, в период
детства политической экономии, была в
высшей степени гениальной идеей, бесспорно
самой гениальной из всех, какие только
выдвинула до сего времени политическая
экономия».

Представители буржуазной политической
экономии уже с середины XIX века в
своих теоретических исследованиях
начинают использовать все более
и более сложный математический
аппарат. В последнее тридцатилетие
XIX века складывается самостоятельное
математическое направление в буржуазной
политической экономии.

Математическая школа
возникла в рамках так называемого
неоклассического направления в
политической экономии, главным содержанием
которого является теория предельной
полезности (маржинализм). В ходе развитие
неоклассического направления проблемы
социально-экономической динамики
незаметно исчезают из анализа, постепенно
осуществляется переход к общим
проблемам функционирования экономических
систем, рыночных и ценовых механизмов,
реализации принципа экономичности
и рациональности в условиях совершенной
конкуренции, условий частного и
общего равновесия.

Родоначальником математической
школы считается французский
ученый О. Курно (1801 — 1877). В 1838 г. вышла его
книга «Исследование математических
принципов теории богатства» (О. Курно
был известным математиком, философом,
историком и экономистом).

Видными представителями
математической школы являются Г. Госсен
(1810 — 1859) в Германии, В. Джевонс (1835 — 1882)
в Англии, Л. Вальрас (1834 — 1910) в Швейцарии,
Г. Кассель (1866 — 1944) в Швеции, Ф. Эджворд
(1845 — 1926) в Англии, В. Парето (1848 — 1923) в Италии,
В. Дмитриев )1868 — 1913) в России.

Представители математического
направления в буржуазной политической
экономии достигли известных успехов
в области математического моделирования,
в раскрытии ряда объективных закономерностей
производства, обмена, распределения и
потребления. В этой связи необходимо
отметить важность работ русского экономиста
В. К. Дмитриева. Его основная работа «Экономические
очерки. Опыт органического синтеза трудовой
ценности и теории предельной полезности»
была опубликована в 1904 году. В своих работах
В, К. Дмитриев предвосхитил ряд выводов,
которые позднее были получены В. Леонтьевым
на основе анализа моделей «затраты
— выпуск». В частности, эти выводы важны
для подсчета коэффициентов полных материальных
и трудовых затрат. Кроме того, стремясь
примирить трудовую теорию стоимости
с теорией предельной полезности, что,
естественно, сделать невозможно, он тем
не менее поставил проблему соотношения
категорий стоимости и полезности.

Родоначальники математической
школы рассматривали математические
методы, математическое моделирование
связей между элементами экономической
системы как методы исследования,
а не как методы изложения, иллюстраций
экономических положений и законов,
полученных других путем. Изложение
же выводов, полученных математически,
может быть дано и на обычном языке,
или в математической форме, но без
доказательства. Так, Л. Вальрас писал:
«Весьма немногие из нас в состоянии
прочесть «Математические начала натуральной
философии» Ньютона или «Небесную
механику» Лапласа, и тем не менее мы
все принимаем на веру сделанное сведущими
людьми описание мира астрономических
явлений согласно закону всеобщего тяготения.
Почему точно таким же образом не принять
описание мира экономических явлений,
сделанного согласно закону свободной
конкуренции».

Представители математической
школы с помощью математических
методов стремились разрешить не
отдельные частные проблемы экономической
теории, а охватить весь экономический
процесс в целом, дать общую картину взаимозависимости
всех экономических явлений. Так, по мнению
Парето, процесс научного прогресса проходит
через три стадии:
1.
мы ограничиваемся констатированием существованиям
взаимодействия между отдельными элементами
экономической системы, не входя в дальнейшее
их изучение;

2. мы знаем
отдельные связи, существующие между отдельными
элементами;

3. мы имеем
возможность вычислить величину всех
этих элементов и дать совершенно точное
выражение условий равновесия. Идеал всякой
науки — достижение третьей стадии.

Математический метод
рассматривается как основной, важнейший
метод, который только один в состоянии
дать экономической теории научную
законченность.

Основным научным результатом
неоклассического направления является
разработка моделей частного и общего
равновесия и, условий использования
ресурсов, их оптимального распределения
по различным направлениям, условий
равновесия обмена и потребления. Сюда
относятся разработка моделей поведения
потребителя, построение функций спроса,
зависимостей спроса от цен и дохода,
построение производственной функции,
моделей поведения фирмы, моделей
общего экономического равновесия, прежде
всего модели Л. Вальраса и ее модификаций.

2. ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

2.1. Постановка
задачи линейного программирования.

Оптимизировать производство
продукции четырех видов. Для
ее изготовления используются ресурсы
(табл.1): трудовые, сырье и финансы.
Необходимо, чтобы производство продукции
обеспечивало максимальную прибыль.

1.Прибыль, нормы
расхода ресурсов и их наличия.

Показатели	Виды продукции	Наличие ресурсов
№1	№2	№3	№4
Прибыль	60	70	120	130
Трудовые ресурсы	1	1	1	1	16
Сырье	6	5	4	3	110
Финансы	4	6	10	13	100

2.2. Математическая
запись модели.

Условные обозначения:

Х_j – переменные, количество
выпускаемой продукции j-го вида;

j – номер переменной;

b_i – объем ограничений,
количество i-го ресурса;

i – номер ограничения;

а_ij
– технико-экономические коэффициенты,
норма расхода i – го ресурса для выпуска
единицы продукции j – го вида;

с_j – коэффициенты целевой
функции, прибыль от производства единицы
продукции j-того вида.

Математическая модель

F =

x_j ≥ 0

j = i =

2.3. Развернутая
экономико-математическая модель.

Система переменных:

х₁ – количество продукции
№1

х₂ – количество продукции
№2

х₃ – количество продукции
№3

х₄ – количество продукции
№4

Система ограничений:

по использованию трудовых ресурсов:

х₁ + х₂ + х₃ + х₄ ≤
16

по использованию сырья:

6х₁ + 5х₂ + 4х₃ + 3х₄
≤ 110

по использованию финансов:

4х₁ + 6х₂ + 10х₃ + 13х₄
≤ 100

Целевая функция – максимум прибыли:

F = 60х₁ + 70х₂ + 120х₃ + 130х₄
max

Числовая модель

F = 60х₁ + 70х₂ + 120х₃
+ 130х₄ max

х₁ + х₂ + х₃
+ х₄ ≤ 16

6х₁ + 5х₂ +
4х₃ + 3х₄ ≤ 110

4х₁ + 6х₂ +
10х₃ + 13х₄ ≤ 100

х_j ≥ 0, j
=

2.4. Алгоритм решения транспортной
задачи.

1. Постановка задачи.

Составить оптимальный план
перевозок минеральных удобрений
со складов на поля севооборота, чтобы
транспортные затраты были минимальными.
Имеется три склада с удобрениями, где
хранится 600 т. минеральных удобрений:
1 – 200 т., 2 – 150 т., 3 – 250 т. Потребность четырех
полей севооборота в минеральных удобрениях
475 т.: 1 поле – 100 т., 2 – 150 т., 3 – 150 т., 4 –
75 т. Транспортные затраты на перевозку
1 тонны удобрений с каждого склада на
каждое поле приведены в таблице 2.

2. Транспортные
издержки, ден. ед. за тонну.

Склады удобрений	Поля севооборота
первое	второе	третье	четвертое
№1	4	2	3	1
№2	3	6	2	5
№3	6	3	4	2

Запасы удобрений больше,
чем потребность в них на 125
тонн, модель открытая. Для решения
задачи в Excel не требуется приводить
модель к закрытому типу.

2. Решение транспортной
задачи в Excel.

Заполнение
таблицы исходных данных в Excel

Заполняется первая часть таблицы, в которой все показатели будут вычисляться в процессе решения задачи (рис.1)

поля севооборотов являются потребителями;

склады – поставщики удобрений;
в ячейках С5:F7 будут высвечиваться результаты перевозок – это изменяемые ячейки;
в ячейки В5:В7 вводится формула сумма значений ячеек всей строки: в В5 =СУММ(С5:F5); в В6 =СУММ(С6:F6); в В7 =СУММ(С7:F7)
в ячейки С8:F8 вводится формула – сумма значений ячеек всего столбца: в С8 =СУММ(С5:С7); в D8 =СУММ(D5:D7); в Е8 =СУММ(Е5:Е7); в F8 =СУММ(F5:F7).

Рис.1. Исходные данные
в Excel.

Заполняется вторая часть таблицы (рис.1.)

в строке 9 (ячейки С9:F9) вводится потребность в удобрениях каждого поля севооборота;

в столбце В (ячейки В10:В12) вводится наличие удобрений на каждом складе;
в ячейки С10:F12 – вводятся технико-экономические коэффициенты – транспортные расходы на перевозку удобрений соответствующего склада на соответствующее поле севооборота.

Заполняется последняя строка таблицы (рис.1)

в ячейки С13:F13 – вводится функция
– сумма произведения массива значений
на массив технико-экономических коэффициентов
соответствующего столбца;

в С13 =СУММПРОИЗВ(С5:С7;С10:С12)
в D13 =СУММПРОИЗВ(D5:D7;D10:D12)
в E13 =СУММПРОИЗВ(E5:E7;E10:E12)
в F13 =СУММПРОИЗВ(F5:F7;F10:F12)

в ячейку
В13 вводится Целевая функция =СУММ(С13:F13)

Заполнение
окна «Поиск решения»

курсор устанавливается в Целевую ячейку (В13)
В меню выбрать Сервис, Поиск решения
Заполнить окно «Поиск решения» (рис.2):

если в поле «Установить целевую ячейку» высвечивается адрес, который не является адресом Целевой ячейки, то необходимо отодвинуть окно и щелкнуть мышью по целевой ячейке – в поле появится адрес целевой ячейки В13.

установить переключатель в положение Равной минимальному значению.
в поле «Изменяя ячейки» мышью ввести интервал ячеек строки значения из таблицы «Переменные» $С$5:$F$7.
заполнить поле Ограничения
щелкнуть мышью в поле ограничения
щелкнуть мышью на кнопке Добавить
заполнить окно Добавление ограничения:

Первым всегда вводится Граничное условие – все переменные должны быть больше или равны нулю (рис.3)

щелкнуть мышью в поле Ссылка на ячейку
выделить мышью интервал ячеек $С$5:$F$7
изменить знак, выбрав из списка >=
щелкнуть мышью в поле Ограничения
ввести с клавиатуры ноль
нажать кнопку Добавить

в новом окне Добавление ограничения ввести следующее ограничение – вывоз удобрений со складов не должен превышать из начилия на складах. (рис.4)

щелкнуть мышью в поле Ссылка на ячейку
выделить мышью интервал ячеек $B$5:$B$7
оставить знак без изменения <=
щелкнуть мышью в поле Ограничения
выделить мышью интервал ячеек $B$10:$B$12
нажать кнопку Добавить

Рис.2. Заполнение
окна Поиск решения

Рис.3. Ввод условия
не отрицательности переменных

Рис.4. Ввод второго
ограничения

В новом окне Добавление ограничение ввести следующее ограничение – потребность полей севооборотов в удобрениях должна быть удовлетворена полностью или с избытком (рис.5)

щелкнуть мышью в поле Ссылка на ячейку

выделить мышью интервал ячеек $C$8:$F$8
изменить знак на противоположный >=
щелкнуть мышью в поле Ограничения
выделить мышью интервал ячеек $C$9:$F$9
нажать кнопку ОК.

заполняется окно Параметры

в окне Поиск решения нажать кнопку параметры
в окне параметры установить флажку в положения Линейная модель и показывать результаты итераций
нажать кнопку ОК

Рис.5. Ввод третьего
ограничения

Получение оптимального
решения и отчета по устойчивости

в окне Поиск решения нажать кнопку выполнить
на экране появиться окно Результаты поиска решения, в котором следует выбрать тип отчета Устойчивость и нажать кнопку ОК
на экране останется таблица-модель с оптимальным планом перевозок (рис.6), а перед листом модели будет создан лист Отчет по устойчивости (рис.7)
для решения задачи потребовалось 11 итераций

Рис.6. Модель с
оптимальным решением

3. Анализ
оптимального решения

По оптимальному плану
необходимо ( рис.6)

С первого склада перевести сто т. удобрений на одно поле, 25 тонн- на второе поле и 75 т. на четвертое поле
Со второго склада – 150 т., т.е. все перевезти на 3 поле;
С третьего склада-125 т., т.е. все перевезти на второе поле.

При этом на третьем складе
останется 125т. удобрений. Потребность
всех полей севооборота в удобрениях будет
удовлетворена.

При таком плане перевозок
затраты на перевозку удобрений
со складов на поля севооборотов будут
минимальными и составят 1200 ден.ед.

Рис.7. Отчет по
устойчивости «Ячейки переменных»

Рис.8. Отчет по
устойчивости «Ограничения»

4.Анализ
устойчивости оптимального решения

По таблице Изменяемые
ячейки ( рис.7)

Нормированная
стоимость показывает, что если:

со второго склада перевести 1т. удобрений на 2 или 4 поле севооборота, то затраты увеличатся на 5 ден. ед.;
с третьего перевезти 1т. удобрений на 1 поле севооборота, то затраты увеличатся на 1 ден.ед.

Допустимое
увеличение и уменьшение коэффициентов
целевой функции показывают, что оптимальный
план не изменится, если затраты на перевозку
будут находиться в пределах:

с первого склада — на первое поле — от 0 до 4; на 2 поле – от 2 до 3; на 3 поле – 3; на 4 поле – 1 ден.ед.;
со 2 склада – на 1 поле – от 0 и выше; на 2 поле – от 1 и выше; на 3 поле — от 0 до 2; на 4 поле – от 0 и выше ден.ед.;
с 3 склада – на 1 поле – от 5 и выше; на 2 поле – от 2 до 3; на 3 поле – от 4 и выше; на 4 поле – от 2 и выше ден.ед

По таблице Ограничения
(рис.8)

Теневая
цена показывает, что:

если количество удобрений увеличить на 1т.:
на 1 складе, то затраты снизятся на 1 ден.ед.
на 2 складе, то затраты снизятся на 2 ден.ед.
на 3 складе, то затраты не изменятся
если потребность в удобрениях увеличить на 1т.:
на 1 поле, то затраты увеличатся на 5 ден.ед.
на 2 поле, то затраты увеличатся на 3 ден.ед.
на 3 поле, то затраты увеличатся на 4 ден.ед
на 4 поле, то затраты увеличатся на 2 ден.ед

Допустимые
увеличение и уменьшение объемов ограничений показывают, что план перевозок
останется оптимальным, если:

на складах количество удобрений будет находиться в пределах:
на 1 складе – от 175 до 325 т.
на 2 складе – от 125 до 150 т.
на 3 складе – от 125 т. и выше.
Потребность полей севооборота будет в пределах:
1 поля – от 0 до 125 т.
2 поля – от 25 до 275 т.
3 поля – от 150 до 175 т.
4 поля – от 0 до 100 т.

Источник