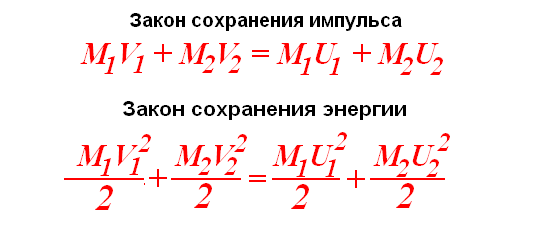Моделирование технологического процесса в excel

Это вторая статья посвященная моделированию работы производственных линий. В первой – «Моделирование в Excel сбалансированной производственной линии» – речь шла о производственной линии с участками одинаковой мощности. Идея провести такое моделирование возникла у меня после прочтения книги Джефа Кокса, Ди Джейкоба и Сьюзан Бергланд «Новая цель. Как объединить бережливое производство, шесть сигм и теорию ограничений». В книге приводилось описание игры, моделирующей работу сбалансированной производственной линии и производственной линии с участком–ограничением.

В предыдущей статье я описал модель работы сбалансированной производственной линии. Приведу основные выводы:

1. Пропускная способность сбалансированной производственной линии не зависит от ее длины (от числа участков).
2. Пропускная способность сбалансированной производственной линии падает при росте вариабельности на отдельных участках.
3. Для достижения теоретической величины пропускной способности производственной линии требуется существенное увеличение запасов перед каждым участком.

В настоящей статье представлен анализ модели производственной линии с участком–ограничением.

Скачать статью в формате Word, примеры в формате Excel

Правила игры, моделирующие сбалансированную производственную линию.Играющие (четверо или более человек) садятся за стол, имитируя производственную линию, состоящую из последовательных участков. Можно сесть и по кругу, но важно обозначить первого и последнего в цепочке. Цель игры – продвинуть как можно больше фишек по производственной цепочке до склада готовой продукции. Каждому игроку перед началом игры выдается некоторое количество фишек, например, четыре – аналог запасов, расположенных у рабочего места. Кроме того, значительный запас фишек располагается перед первым игроком – склад материалов. Первый игрок кидает кубик с шестью гранями от 1 до 6, и передает второму игроку столько фишек, сколько выпало. Передать можно только те фишки, что лежат перед игроком. Так, если выпала шестерка, а перед игроком находится четыре фишки, то он передает следующему игроку четыре. Игроки кидают кубик последовательно. Последний игрок кидает кубик, и «выпускает» продукцию, то есть перемещает фишки от себя за пределы играющих – на склад готовой продукции. Начиная со второго круга игры, каждый раз, когда наступает черед первого игрока кидать кубик, он берет четыре фишки со склада материалов и кладет их перед собой, далее кидает кубик. Игра состоит, например, из 20 кругов.

Изменим правила игры для моделирования производственной линии с участком–ограничением. Ограничение – участок, производительность которого ниже, чем у других участков. Позволим каждому игроку кидать два кубика, а игроку, который изображает ограничение, – один кубик. Чтобы участок–ограничение не простаивал, вне зависимости от производительности предыдущих участков, создадим перед ним достаточный стартовый запас фишек, например, десять. Чтобы не создавать в системе излишков незавершенного производства (фишек), на старте игры выдадим 4 фишки только первому игроку (остальные игроки будут довольствоваться тем, что поступит к ним с предыдущего участка непосредственно перед ходом). Кроме того, «привяжем» передачу материалов в производство (фишек первому игроку) к выпуску участка–ограничения. На языке теории ограничений (ТОС) это называется – канат (иногда встречается термин веревка). То есть, если ограничение передало следующему участку 2 фишки, то в следующем круге первый участник получит только две фишки со склада материалов.

Математическое ожидание (среднее) одного броска на участке–ограничении составляет 3,5 очка. Все остальные участки обладают существенно большей производительностью. Их среднее одного броска составляет 7 очков. Можно ожидать, что за 20 кругов на склад готовой продукции переместится в среднем 3,5 х 20 = 70 фишек. Ранее мы увидели, что для сбалансированной линии среднее не достигается из-за бросков вхолостую: не всегда перед игроком лежит достаточное для передачи число фишек. Посмотрим, что покажет моделирование сейчас.

Для изучения поведения производственной цепочки я создал Excel-модель на основе генератора случайных чисел и таблицы данных. Для краткости число фишек, поступивших на склад готовой продукции, я назвал выпуском (вслед за авторами книги «Новая цель»). Поскольку функция СЛУЧМЕЖДУ (генератор случайных чисел) пересчитывается всякий раз, когда в Excel вводятся новые данные, можно просто нажимать F9 и графики будут изменяться, показывая колебания параметров вокруг довольно стабильных средних значений.

Вот, какие закономерности мне удалось выявить.

1. Выпуск уменьшается от первого участка вплоть до участка–ограничения (рис. 1), затем достигает значения близкого к среднему ожидаемому – 70 – на участке–ограничении. В дальнейшем выпуск продолжает плавно снижаться в зависимости от длины производственной цепочки (числа участников). Такое поведение на первый взгляд выглядит странным, учитывая, что для сбалансированной линии выпуск не зависел от длины линии (рис. 2), а колебался вокруг среднего.

Рис. 1. Выпуск в зависимости от длины производственной цепочки с участком-ограничением

Рис. 2. Выпуск в зависимости от длины производственной цепочки для сбалансированной линии

Объяснение такому поведению линии с участком-ограничением довольно простое. За счет того что производительность участков, не являющихся ограничением, в среднем существенно выше, чем запасы перед ними, конца цепочки достигают почти все фишки, попавшие в систему… Но иногда перед участком будет больше фишек, чем выпадет очков на двух кубиках (например, три фишки, а выпали два очка). В этом случае не все фишки пройдут сквозь систему. Ситуация не фатальна, так как на следующем круге с большой вероятностью выпадет достаточно очков, чтобы «подчистить» должок. Но… на последнем круге игры времени на «подчистку» не остается. Это и приводит к наблюдаемой на рисунке 1 закономерности.

2. Факт снижения выпуска при увеличении длины производственной цепочки мне показался интересным, так как он не соответствует тем описаниям, которые встречались мне в литературе по теории ограничений. Там ситуация выглядит так, что после прохождения участка–ограничения, продукция незавершенного производства быстро (без задержек) доставляется к последнему звену цепочки.

Я рассчитал условную вероятность потерь в каждом звене после участка–ограничения в течение одного, двух и трех кругов игры. Потери возникают, если очков на двух кубиках выпало меньше, чем поступило фишек с предыдущего участка. Барабан [1] процесса – участок–ограничение. Именно он задает объем выпуска, который должен быть доставлен до конца цепочки. К сожалению, производственная линия с участком–ограничением не справляется с доставкой к концу линии всей продукции, вышедшей с участка–ограничения. Вычисление потерь приведено на листе «потери» Excel-файла. Получилась расчетная (теоретическая) величина потерь в предложенной модели на уровне 0,22 [2] фишки на один участок. И действительно, реальные потери ведут себя в соответствии с теоретическим предсказанием (рис. 3; красная линия соответствует среднему  значению, пунктирная линия – среднему + два сигма).

Рис. 3. Потери на отдельных участках после прохождения участка-ограничения

3. Если участок-ограничение держать на «голодном пайке» (рис. 4), то есть уменьшить стартовые запасы перед ним (напомню, что по правилам игры мы выдали 10 фишек), то выпуск системы существенно сокращается. Особенно это уменьшение заметно, если вначале игры перед участком-ограничением разместить от нуля до трех–четырех фишек. Если запас составляет 5–6 фишек (приблизительно равен производительности участка), то на участке–ограничении существенных потерь не происходит. При запасе в 10 и более фишек (приблизительно в два раза превышающем производительность участка) вероятность потерь приближается к нулю [3].

Рис. 4. Потери на участке-ограничении в зависимости от стартовых запасов перед этим участком

4. При уменьшении вариабельности игрального «кубика» выпуск растет (рис. 5; уменьшение вариабельности соответствует движению справа налево по оси абсцисс). Причем, растет более стремительно, чем для сбалансированной линии (рис. 6).

Рис. 5. Выпуск в зависимости от величины вариабельности процесса для линии с участком-ограничением

Рис. 6. Выпуск в зависимости от вариабельности процесса для сбалансированной линии

Что значит в модели уменьшить вариабельность? Сокращение вариабельности соответствует, например, замене обычного кубика на монету с двумя сторонами: 3 и 4. Размах значений будет равен единице (4 минус 3). Для кубика с шестью гранями размах = 5 (6 минус 1). При бросании монетки выпуск соответствует теоретической величине – 70 фишек (рис. 7). Потерь на участках после ограничения практически не возникает. Если вместо кубика взять тетраэдр с гранями 2, 3, 4 и 5, то выпуск составит 68–69 фишек; для обычного шестигранного кубика – 66–67; для восьмигранника с гранями от 0 до 7 выпуск будет всего около 57 фишек.

Рис. 7. Зависимость выпуска от длины и типа производственной линии и величины вариабельности процессов

Нельзя не отметить еще одну особенность линии с участком–ограничением, хорошо наблюдаемую на рисунке 7. Ограничение позволяет сделать процесс более предсказуемым. Посмотрите, насколько линии на графиках слева более гладкие. Вот, что на эту тему говорится в «Новой цели»: В случае системного ограничения у вас есть одно бутылочное горлышко – основное ограничение, и вы знаете, в чем оно состоит. При наличии сбалансированной линии, даже с учетом процесса, задающего ритм, у вас возникает ограничение мощностей и практически  не остается резервов, поэтому при росте вариабельности процесса может возникнуть множество узких мест. Более того, они будут постоянно возникать, то здесь, то там. Принято считать, что ограничение [узкое место] – недостаток. ТОС считает, что бутылочное горлышко – одна из ключевых особенностей бутылки. Оно было сознательно спроектировано таким образом. Его цель – регулирование потока.

Вид графиков это подтверждает!

4. Но самое замечательное в производственной линии с участком-ограничением – это объем запасов незавершенного производства. Напомню, что для сбалансированной линии средние запасы к концу игры составляли 113,5 фишек. Для линии с участком–ограничением объем запасов находится на уровне 15 ± 5 (рис. 8). Почти на порядок меньше!

Рис. 8. Запасы в системе по окончанию игры

Надо также понимать, что с ростом запасов перед участком–ограничением растет и объем запасов, накапливающийся в системе в целом (рис. 9). Более того, в рамках сформулированных правил игры стартовые запасы перед участком–ограничением являются единственным фактором, определяющим объем запасов в системе по окончании игры.

Рис. 9. Зависимость объема запасов в системе на конец игры от стартовых запасов перед участком-ограничением

С другой стороны (см. рис. 4), при росте стартовых запасов перед ограничением до 10–12 фишек удается избежать потерь на участке–ограничении. Так что, начиная с некоторого значения (порядка 10–12 фишек), увеличение запасов в системе не приводит к росту пропускной способности всей системы (рис. 10).

Рис. 10. Выпуск в зависимости от размера запасов в системе на момент окончания игры

5. Нельзя не отметить некоторого лукавства, содержащегося в модели… 🙂 Предложенная линия с участком–ограничением «потребляет» почти вдвое больше ресурсов, чем сбалансированная линия: каждый ход мы кидаем два кубика вместо одного. Наметил себе задачу – попытаться усовершенствовать модель, чтобы суммарные ресурсы в двух линиях (сбалансированной и с участком–ограничением) были бы приблизительно одинаковыми. Тогда сравнение будет более корректным. Тем не менее, полученные в настоящем анализе выводы, в любом случае представляют интерес.

Основные выводы моделирования поведения производственной линии с участком–ограничением:

1. Пропускная способность производственной линии с участком–ограничением зависит от длины линии, точнее, от числа участков, расположенных после участка–ограничения и не зависит от числа участков, расположенных до ограничения.
2. Пропускная способность линии с участком–ограничением падает при росте вариабельности на отдельных участках, но это падение не такое большое, как у сбалансированной линии.
3. Линия с участком–ограничением более устойчива к вариабельности процессов на отдельных участках, чем сбалансированная линия!
4. Чтобы уменьшить потери на участке–ограничении перед участком  следует иметь запасы (буфер) на уровне производительности участка. Двойной запас по сравнению с производительностью практически исключает потери.
5. Система с участком–ограничением не накапливает запасы незавершенного производства с течением времени.

---

[1] Еще один термин теории ограничений. Барабан – участок, задающий ритм процесса; по аналогии с барабанщиком, определяющим ритм шагов марширующих.

[2] Я провел расчет для трех кругов игры. Понятно, что с увеличением числа кругов будет расти размер потерь, но этот рост будет быстро затухать. На мой взгляд, теоретический размер потерь будет порядка 0,22.

[3] Приближается… но не равняется нулю. Долго нажимая F9, я иногда получал потери порядка 0,1 фишки даже при стартовом запасе в 14 фишек.

history 14 июня 2022 г.

Группы статей
• Приложения

Краткое описание модели

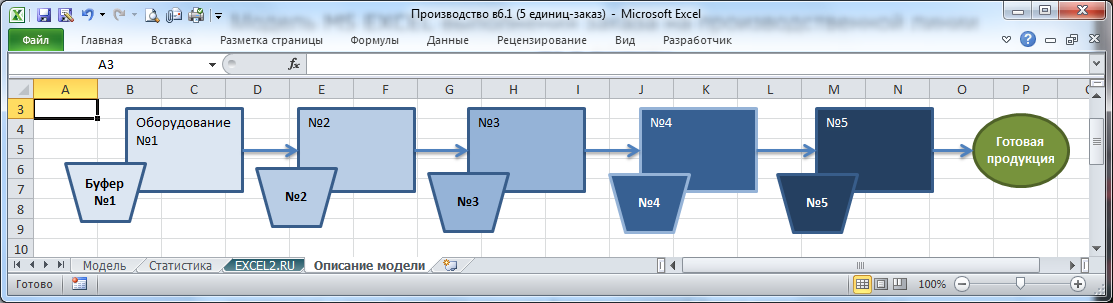
Построим в MS EXCEL модель производственной линии, состоящей из 5 единиц оборудования. Каждая единица обрабатывает детали и передает дальше по цепочке пока не будет изготовлена готовая продукция.

Оборудование может простаивать из-за поломки (задается вероятность

выхода из строя оборудования

и случайная

величина длительности простоя

), также существует ненулевая вероятность получить

брак

при производстве деталей (совсем как в жизни).

Задается

производительность оборудования

(шт деталей/ час), как правило одна из единиц меньше по производительности, чем остальные. Эта единица называется

Узким местом

(bottleneck).

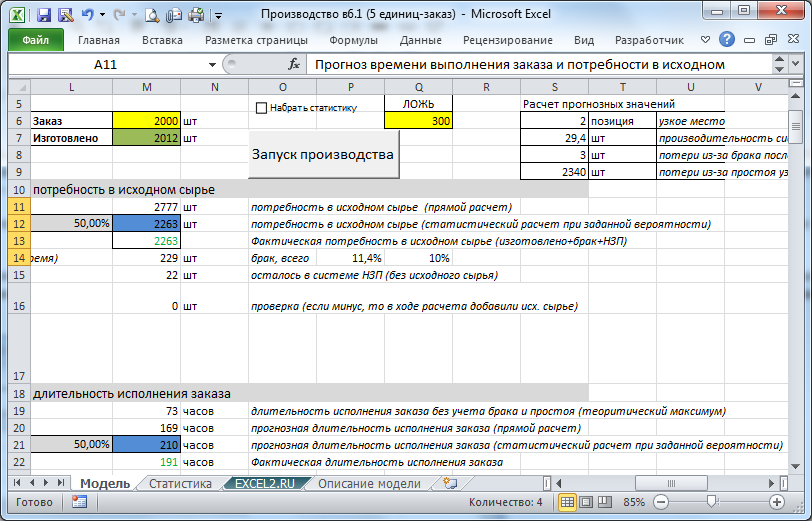
Поступивший заказ на изготовление N штук готовой продукции анализируется: вычисляется прогнозное время выполнения заказа и оценивается потребность в исходном сырье.

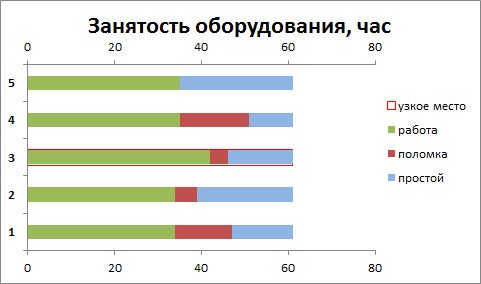
После нажатия кнопки «Запуск производства» сырье запускается в производство (выполняется программа на языке программирования VBA), на каждом временном шаге определяется работоспособность оборудования (не случилась ли поломка в соответствии с заданной вероятностью), а также вычисляется количество годных и бракованных изделий. Годные изделия, т.е. НЗП (незавершенное производство) передаются на следующий передел. Между оборудованием введены буферы для хранения НЗП. После завершения заказа выводится детальная информация о работе каждого оборудования и всей линии в целом (время простоя, полезная работа, количество брака и годных деталей, фактически потребленное сырье и время изготовления заказа). Строятся диаграммы.

Производительность линии определяется оборудованием с наименьшей производительностью (с учетом % брака) —

Узким местом

. Задача модели обеспечить Узкое место достаточным НЗП, чтобы оно не простаивало. Так как другие единицы оборудования имеют избыточную производительность, то в случае их бесперебойной работы буферы после них будут переполняться — в реальном производстве это будет приводить к увеличению инвестиций в оборотные средства. Поэтому модель позволяет ввести критический уровень буфера, после которого он перестает пополняться (предшествующая единица оборудования временно приостанавливает работу). Кроме того, модель минимизирует остаточный НЗП в системе (тот который остается после завершения выполнения заказа). Это достигается предварительным расчетом потребности в исходном сырье (статистический расчет при заданной вероятности брака и простоя).

Данная упрощенная модель работает только с единичным заказом, работа программы завершается сразу после того как этот заказ выполнен.

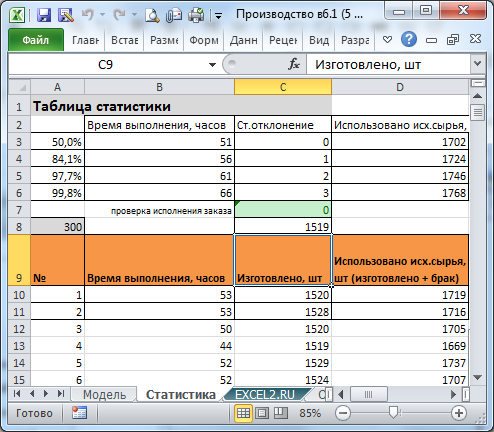
Набор статистики и оценка величин

У модели 2 основных задачи — оценить время исполнения заказа и спрогнозировать потребность в сырье для его выполнения. Поскольку обе этих величины являются случайными величинами (так как заданы ненулевые вероятности простоя и брака), то вычислить их точно невозможно. Можно лишь дать оценку среднего значения этих случайных величин. Для этого нужно оценить среднее и дисперсию неизвестного распределения этой случайной величины (см.

эту статью о точечных оценках

).

Оценить среднее время исполнения заказа и среднее значение потребности в сырье можно, в принципе, обычными формулами зная % брака и вероятность простоя (это также реализовано в модели). Но, гораздо точнее набрать статистику и оценить эти величины статистическими методами. Кроме того, у нас появится возможность построить интервальную оценку (например, «Заказ будет выполнен в течение 120 часов с 95% вероятностью»).

Для набора статистики модель прогоняет несколько десятков раз производство данного заказа и вычисляет среднее время выполнение заказа (количество прогонов задается в желтой ячейке Q6), а также время за которое заказ будет выполнен, скажем, с 95% вероятности. Аналогичные вычисления производятся и для оценки потребности в сырье.

Эти дополнительные вычисления с лихвой окупаются: после завершения «реального» производства с оцененным количеством исходного сырья, в НЗП остается (в среднем) материал примерно равный производительности системы за 1 шаг времени (как правило, в буфере перед последней единицы оборудования). Также мы знаем точность нашего предсказания времени изготовления заказа и можем, например, не только дать точечную оценку этой величины, но и построить

доверительный интервал

.

После изменения любого параметра системы (вероятность брака и простоя, длительность простоя, величина заказа, производительность оборудования) необходимо заново запускать набор статистики.

Как работать с программой

Программу можно скачать, нажав кнопку

Файл примера

внизу или вверху статьи.

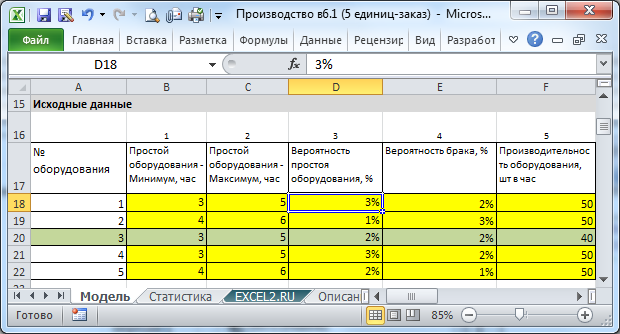
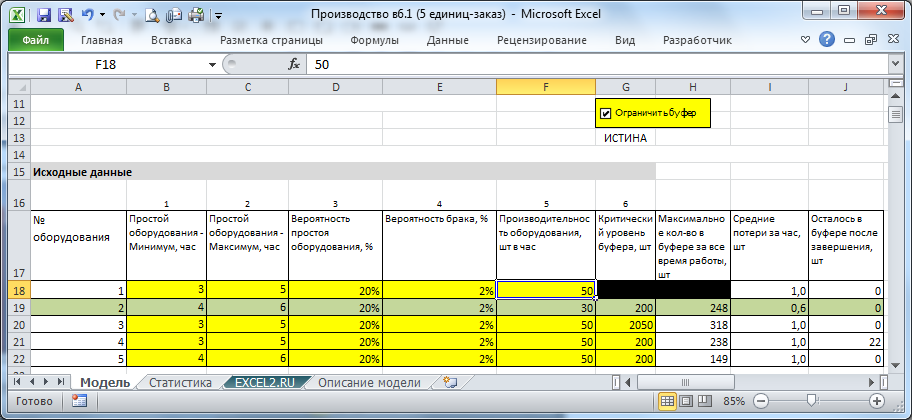
Шаг1: заполнить таблицу B18:G22 с исходными данными

Ячейки, которые требуют заполнения — выделены желтым. Основные данные, это конечно «Производительность оборудования, шт в час». При разработке модели предполагалось, что производительность оборудования отличается на 20-30%, максимум на 50%. Иначе, какой смысл объединять в производственную линию столь разное оборудование? При этом одна из единиц имеет минимальную производительность (узкое место) и определяет производительность всей системы. Можно, конечно задать всем машинам одинаковую производительность, или задать разницу по производительности в 200-300%  или определить 2 узких места — программа будет работать, но алгоритм затачивался именно на 1 узкое место.

Как было сказано выше, в модели полагается, что оборудование может простаивать, например из-за поломки, остановки на ремонт или отсутствия персонала (но не из-за отсутствия материала для обработки). В это время полезной работы не совершается. Вероятность такого простоя задается в % (на каждом временном шаге есть небольшая, например 2-3 %, вероятность того что машина работать не будет). Длительность простоя задается в часах (задается диапазон, например от 3 и до 5 часов). Конечно, в модели можно задавать любые разумные значения, но устанавливать вероятность более 20% вряд ли имеет смысл — что это за оборудование, если оно постоянно простаивает?

Даже если поломка не случилась, производственника ждет еще одна напасть — брак. Вероятность этого события также может быть любой разумной от 0 до 20%. Можно и больше задать, модель выдержит, но возникнет вопрос «Есть ли у Вас технология?».

Для того, чтобы наиболее производительные машины не производили горы незавершенной продукции, которые Узкое место не сможет перерабатывать в том же темпе, в программе можно задать «Критический уровень буфера, шт» выше которого предшествующая машина останавливает свое производство (на Узкое место это естественно не распространяется). Как только уровень НЗП понизится ниже этого уровня — машина вновь заработает. Данную опцию можно отключать с помощью флажка.

Также необходимо указать размер заказа — количество продукции, которое нужно изготовить. Обычно размер заказа выбирается таким образом, чтобы он был выполнен за 100-800 циклов (часов).

Шаг2. Набор статистики

Для того, чтобы оценить

время выполнения заказа

и

потребность в исходном сырье

потребуется набрать статистику, т.е. «прогнать» модель несколько десятков раз с заданными параметрами (вероятности брака и простоя, а также величины заказа). Поскольку в модели присутствуют случайные величины, каждый раз будут получаться слегка различные значения

времени выполнения заказа

и

количества исходного сырья.

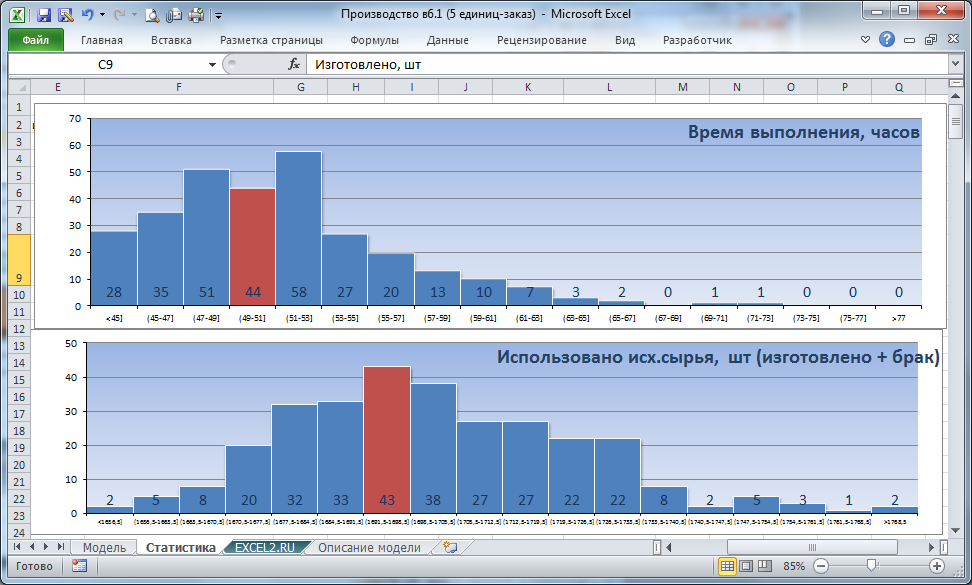
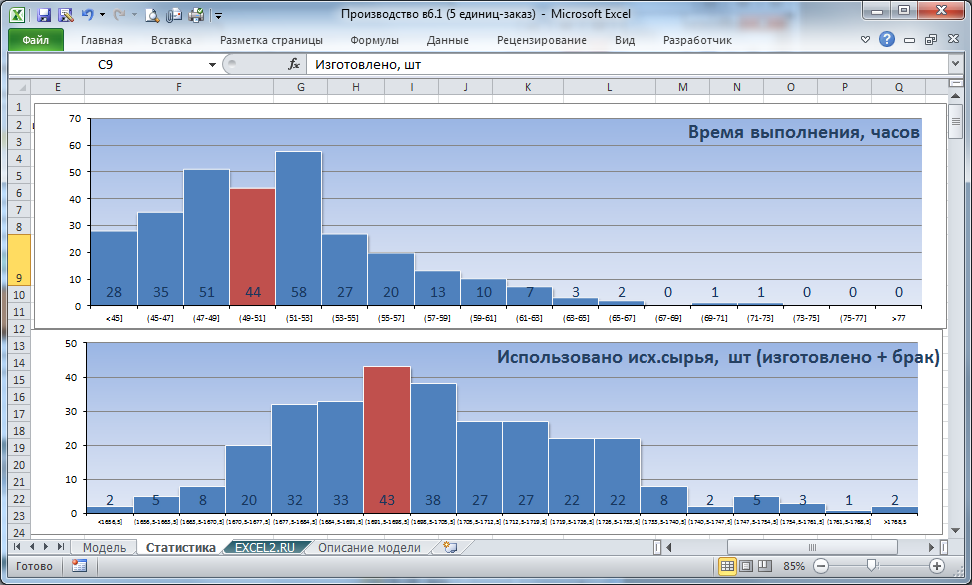
Для набора статистики нужно установить флажок «Набрать статистику» (связанная с ней ячейка Q5 отобразит значение ИСТИНА) и нажать кнопку Запуск производства. Через 5-7 секунд расчеты будут завершены и на листе Статистика будут построены гистограммы — это оценка плотности распределения случайных величин

время выполнения заказа

и

количество исходного сырья.

Теперь у нас есть не только средние значения этих величин, но и

стандартное отклонение

, позволяющего оценить степень разбросов около

среднего

.

Шаг3. Расчет и отображение результатов

После завершения набора статистики переходим к моделированию. Для моделирования производственного процесса нужно снять флажок «Набрать статистику» (связанная с ней ячейка Q5 отобразит значение ЛОЖЬ) и нажать кнопку Запуск производства.

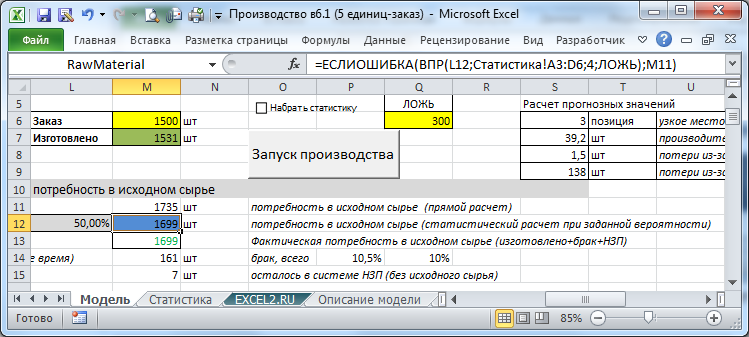
Как видно из картинки выше, прогнозные величины

время выполнения заказа

и

количество исходного сырья

(в синих ячейках) совпадают или близки к фактическим (зеленые ячейки и ячейки с числами, выделенные зеленым цветом шрифта). Так заказ выполнен с небольшим превышением в 5 шт, прогнозная потребность в исходном сырье совпала точно, а время исполнения отклонилось на 20 часов от среднего (258 против 278 прогнозных часов). Почему потребность в исходном сырье совпала, а время выполнения на 7% меньше? Дело в том, что стандартное отклонение величины

количество исходного сырья

составляет 24,6 шт (см. лист Статистика), что составляет 0,7% от среднего, а стандартное отклонение величины

время выполнения заказа

составляет 9% от среднего. Т.е. разброс второй величины значительно больше, что снижает точность прогнозирования. Почему разброс величины

время выполнения заказа

на порядок больше? Дело в том, что на разброс величины

количество исходного сырья

влияет только % брака, а на разброс величины

время выполнения заказа

влияет еще и вероятность простоя, а также случайная длительность простоя.

Подобные рассуждения о результатах модели позволяют определить факторы уже реальной производственной системы, на которые нужно воздействовать, чтобы повысить точность оценки предсказания/ исполнения заказа, сократить срок исполнения заказа или снизить НЗП. В нашем случае, для повышения точности прогнозирования заказа (и сокращения времени исполнения), очевидно, нужно снижать вероятность простоя. Для построения целевого ориентира программа позволяет смоделировать идеальную производственную систему, в которой нет простоев и/или брака.

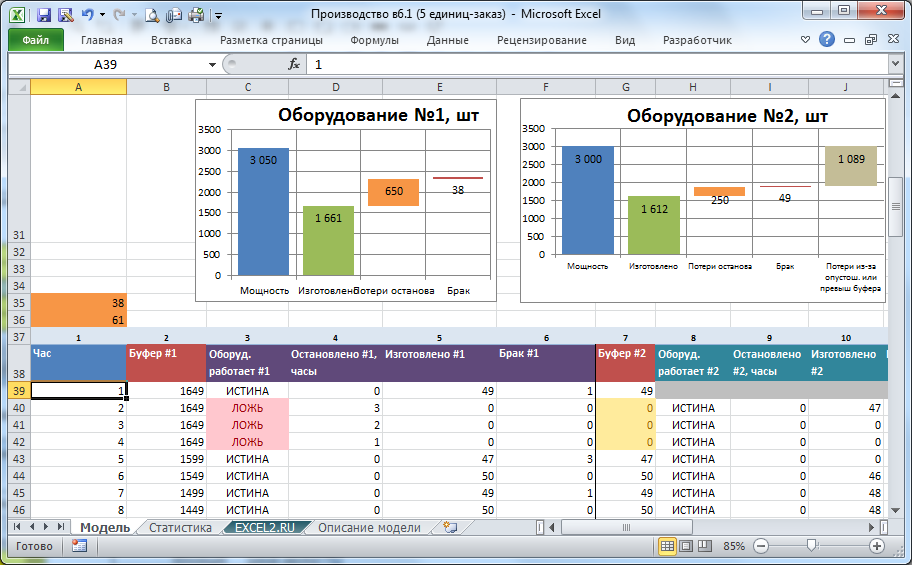
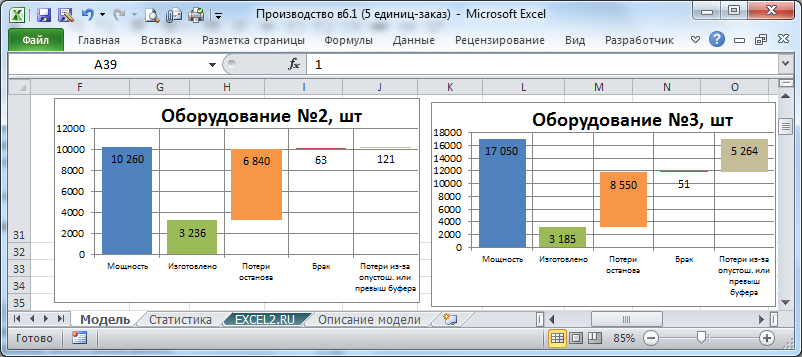
После завершения расчета на листе Модель для каждой единицы отображаются диаграммы, позволяющие оценить чем занималась конкретная единица в течение всего времени производства.

На диаграмме выше видно как различается работа «узкого места» (№2) и оборудования с более высокой производительностью (№3). Если узкое место не работало только из-за вынужденного останова, то оборудование №3 простаивало из-за опустошения предшествующего буфера или из-за превышения объемов наработанного НЗП в последующем буфере.

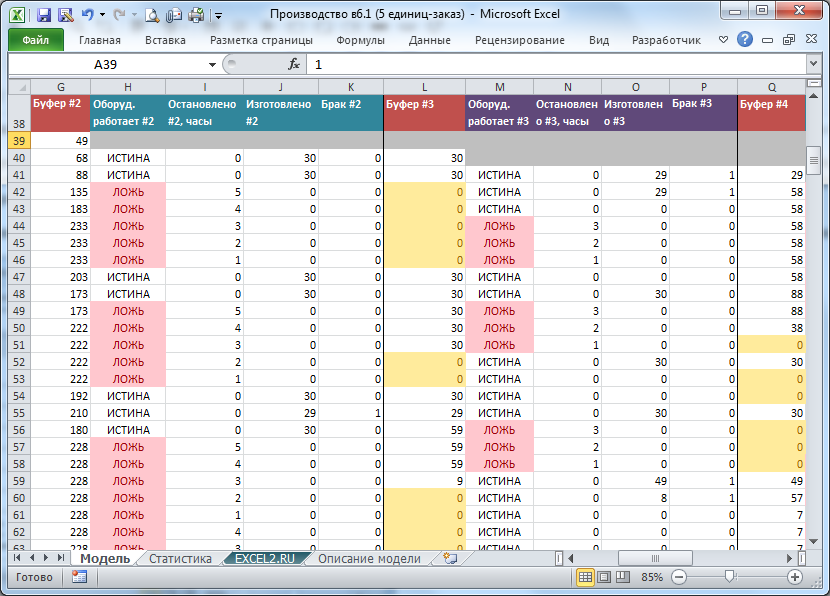
Также на листе доступна детальная расшифровка работы по каждому часу.

Реализация модели в MS EXCEL

Модель полностью построена на решениях MS EXCEL подробно описанных на сайте excel2.ru:

• 
  построение диаграмм

  ,
  

• 
  работа с функциями

  ,
  

• 
  условное форматирование

  ,
  

• 
  выпадающие списки

  ,
  

• 
  именованные диапазоны

  ,
  

• 
  элементы управления формы
  
• 
  гистограмма распределения

  .
  

Так же рекомендуется иметь представление об

Описательной статистике

и

Функции распределения

.

Что дальше?

Данная программа имеет демонстрационные цели. Дальнейшее совершенствование возможно в следующих направлениях:

• вместо 1 заказа можно обрабатывать несколько, с указанием желаемого времени изготовления;
• реализовать систему «вытягивания» (в производство запускает ровно столько изделий, сколько востребовано заказами);
• сделать несколько различных продуктов, использовать разные типы полуфабрикатов;
• ввести операцию сборки изделия из разных полуфабрикатов и настраиваемую длину производственных цепочек;
• учесть рабочее время оборудования и наличие персонала;
• ввести в модель стоимостные параметры (цена ресурсов, стоимость 1ч работы оборудования;
• предложить варианты оптимизации производственной системы (максимизация пропускной способности системы, максимизация прибыли за период и т.д.)

Примечание

: если требуется использовать данную модель для расчета производственной линии состоящей из двух, трех или четырех единиц оборудования, то нужно сделать производительность лишних единиц в разы больше, чем остальных.

Введение

В системах, связанных с экономикой, руководящим работникам необходимо постоянно принимать решения следующих категорий:

1. Стратегические решения.
2. Тактические решения.
3. Оперативные решения.

Если принимаемые решения обладают низким интеллектуальным уровнем, то простота представления реальных ситуаций обычно ведёт к неточностям при выработке прогнозов, а, кроме того, к убыткам и добавочным финансовым потерям. Чтобы избежать возникновения подобных ситуаций и обеспечить устойчивое экономическое положение, существуют разнообразные системы поддержки выработки решений, усовершенствование которых превращается в наиболее актуальную проблему при наличии жёсткой конкуренции.

Существенным условием для таких программ считается возможность имитации вырабатываемых решений, апробации вероятных коррекций в экономической системе, появляющихся в результате влияния разных факторов, то есть нахождение ответа на вопрос типа, «что случится, если…». Это позволит существенно сократить риски от осуществления решений и сэкономить ресурсы, чтобы достичь поставленной цели.

Такие возможности предоставляют имитационные модели, которые обладают следующим набором качеств:

1. Возможность регулировать уровень сложности модели.
2. Присутствие случайных факторов.
3. Возможность описать процесс, развивающийся по времени.
4. Обязательное использование электронной вычислительной машины.

Имитационные модели предназначаются для того, чтобы оценить варианты намечаемых коррекций, обладать игровой формой для обучения работников, визуально отобразить работу исследуемого объекта во времени и так далее. Реализовать модели можно при помощи универсальных языков программирования, к примеру,Pascal, Basic, пакетов прикладных программ, таких как,Excel, MathCAD, и так далее. Выбор конкретного метода моделирования определяется сложностью задачи, наличием необходимых ресурсов и так далее.

«Моделирование в Excel» 👇

Однако имитационное моделирование применяется экономистами и другими специалистами только в малом проценте случаев, в которых можно было бы при помощи моделей поиметь важную для выработки решений информацию.Причина этого явления кроется в отсутствии инструкций по проведению имитационного моделирования при помощи общеизвестного и доступного инструментария, а именно, пакетов прикладного программного обеспечения, такого как Excel и MathCAD, которые могут обеспечить простую платформу для моделирования.Поэтому примеры формирования имитационных моделей при помощи, например, приложения Excel, помогают их широкому распространению в кругу работников, не владеющих языками моделирования и методиками, имеющимися в средах моделирования.

Электронные таблицы Excel как инструмент формирования имитационных моделей

Имитационное моделирование при помощи табличного процессора является отдельным направлением, имеющем свои особенности. Применение таких систем позволяет лучше понять происходящие процессы, в сравнении с использованием специализированных программ, обладающих высокой стоимостью и требующих много времени для их освоения, а также не позволяющих увидеть применяемые механизмы. Например, специалисты полагают, что имитация при помощи таблиц Excel позволяет лучше представить работу систем массового обслуживания, чем даже теория очередей, а также помогает в развитии интуиции, предоставляет даже не знающим программирования пользователям опыт формирования разных моделей. Специалисты предлагают следующие этапы обучения моделированию в Excel:

1. Базовые понятия.
2. Введение в теорию вероятности и статистику.
3. Процесс имитационного моделирования в ручном режиме.
4. Имитационное моделирование при помощи электронных таблиц.
5. Генерирование случайных чисел.
6. Осуществление анализа исходных данных.
7. Осуществление анализа итогов моделирования.

При формировании моделей в Excelприменяются следующие главные подходы к осуществлению имитации:

1. Подход, который ориентирован на события.
2. Подход, имеющий ориентацию на процессы.
3. Подход, направленный на сканирование активностей.

Первый подход служит для описания изменений в системе, которые происходят при совершении любого случайного события, например, получение заявки, завершение обслуживания. При его формировании при помощи электронных таблиц обычно применяется одна строчка для каждого события.

Если используется подход, ориентированный на процесс, то выполняется моделирование очерёдности событий для каждой заявки, и чтобы его реализовать, применяется одна строчка для каждого требования (используется при моделировании систем массового обслуживания).

Сканирование активностей состоит в описании действий, возникающих в системе за фиксированный временной интервал (день, неделя, месяц, год), и при его осуществлении, как правило, применяется одна строчка для каждого отрезка времени. К примеру, это может быть моделирование системы управления запасами.

Использование программного пакета MSExcelобладает следующими преимуществами:

1. В составе пакета Excelесть значительное число встроенных функций из области математики, статистики и других областей, включая возможность генерации случайных значений.
2. Excelдаёт возможность сохранять информацию и иметь к ней доступ.
3. Программный пакетExcelпозволяет строить графики и диаграммы.
4. Программный пакет Excel обладает встроенным языкомVBA (VisualBasicforApplication).
5. Программный пакет Excelшироко распространён среди специалистов, то есть имеется на компьютере практически у всех.
6. Наличие возможности экспорта информационных данных в иные программные приложения.

Помимо этих достоинств, возможен просмотр любой формулы, занесённой в ячейку таблицы, что увеличивает уровень доверия к итогам моделирования.

Федеральное агентство по образованию

Федеральное государственное образовательное учреждение

среднего профессионального образования

КУЗНЕЦКИЙ МЕТАЛЛУРГИЧЕСКИЙ ТЕХНИКУМ

«Компьютерное моделирование в Excel,

как способ исследования физических процессов»

Учебно-исследовательская работа

Преподаватель информатики

Василевская С.Н.

г. Новокузнецк, 2013

СОДЕРЖАНИЕ

Введение 3

Компьютерное моделирование, как способ исследования физических процессов 4

Демонстрация программы 6

Заключение 9

Литература 10

Введение

Издавна человек применяет модели. Это полезно при изучении сложных процессов или систем, конструировании новых устройств или сооружений. Обычно модель более доступна для исследования, чем реальный объект (а есть такие объекты, экспериментировать с которыми невозможно или недопустимо).

Модель — это некоторый материальный или идеальный (мысленно представляемый) объект, замещающий объект-оригинал, сохраняя его характеристики, важные для данной задачи.

Процесс построения модели называют моделированием.

Все способы моделирования можно разделить на две большие группы. В одном случае моделью является предмет, воспроизводящий те или иные геометрические, физические и т.п. характеристики оригинала. Это — материальное (физическое) моделирование. Исследование таких моделей — реальные эксперименты с ними.

По иному происходит работа с информационными (идеальными) моделями, являющимися описаниями объектов-оригиналов с помощью схем, графиков, формул, чертежей и т.п. Одним из важнейших видов информационного моделирования является математическое — когда описания формулируются на языке математики. Соответственно, и исследование таких моделей ведется с использованием математических методов. Именно математическим моделированием мы пользуемся при решении количественных задач на занятиях физики и химии.

Математические модели, используемые при решении современных практических задач, настолько сложны, что исследовать их вручную практически невозможно. Приходится прибегать к помощи компьютера.

Оптимизационные модели описывают некоторую систему совокупностью соотношений, причем ряд параметров в этих соотношениях — во власти человека. Назначение таких моделей — найти такое сочетание значений этих параметров, при котором будет получен наилучший результат из возможных. Наиболее широко они используются в экономических расчетах.

Компьютерное моделирование,

как способ исследования физических процессов

Всякая модель создается для вполне определенной цели, и это в значительной степени определяет ее выбор.

Поэтому, первое, что необходимо сделать — поставить задачу, т.е. определить вопросы, ответы на которые мы хотим получить, и необходимые для этого исходные данные.

Во-вторых, нужно выбрать среди законов, которым подчиняется моделируемая система, существенные для поиска ответов на поставленные вопросы. Возможно, придется выдвигать и какие-то предположения. Найденные закономерности следует представить в форме математических соотношений.

В своей работе я ставил цель исследовать возможности программы Excel при компьютерном моделировании на простом примере построения модели движения двух шариков в замкнутом пространстве.

Конечно, при изучении физики компьютерное моделирование ни в коем случае не должно подменять собой физическую лабораторию и вытеснять реальный эксперимент. И это правильно. Но, тем не менее, в преподавании физики компьютерное моделирование может прочно занять вполне определенную нишу. Речь идет не только о численном моделировании экспериментов, которые по тем или иным причинам не могут быть выполнены в учебной лаборатории. Даже моделирование физических явлений, в принципе доступных непосредственному наблюдению, имеет определенную ценность. Компьютерное моделирование дает студентам один из важнейших инструментов, облегчающих проникновение в тайны науки.
С точки зрения преподавателя, очевидное, лежащее на поверхности достоинство компьютерного моделирования заключается в возможности создавать впечатляющие и запоминающиеся зрительные образы. Такие наглядные образы способствуют пониманию изучаемого явления и запоминанию важных деталей в гораздо большей степени, нежели соответствующие математические уравнения. Моделирование позволяет придать наглядность абстрактным законам и концепциям, привлечь внимание студентов к тонким деталям изучаемого явления, ускользающим при непосредственном наблюдении. Графическое отображение результатов моделирования на экране компьютера одновременно с анимацией изучаемого явления или процесса позволяет учащимся легко воспринимать большие объемы содержательной информации.

Интерактивный характер моделирующих компьютерных программ также представляет собой важный аргумент в пользу применения моделирования. При пассивном поглощении информации студенты быстро теряют интерес к предмету. Обучение становится намного эффективнее при необходимости управлять работой программы, часто взаимодействовать с ней и реагировать на ее запросы. Хорошая интерактивная компьютерная программа не должна вести учащегося по строго предопределенному пути, пусть даже и тщательно выверенному автором, а, напротив, должна предоставлять выбор из множества разнообразных возможностей.

Без опоры на численные методы практически невозможно понять свойства предложенной математической модели явления и сделать какие-либо заключения об ее соответствии реальной действительности, а тем самым и о нашем понимании изучаемого явления. Правильность наших представлений о реальном изучаемом явлении можно проверить с помощью вычислительного эксперимента на компьютере.

Поэтому для современного этапа развития физической науки характерно становление (в дополнение к экспериментальной и теоретической физике) третьей ее ветви – вычислительной физики, в основе которой лежит компьютерное моделирование физических явлений. Компьютерный эксперимент, выполняемый не с реальной физической системой, а с ее математической моделью, не только во многом обогащает и облегчает изучение фундаментальных принципов и традиционных разделов курса физики, но и дает ключ к изучению многих трудных для усвоения вопросов, недоступных традиционным методам. В частности, с помощью компьютерных моделей можно изучать нелинейные явления, где аналитические методы зачастую оказываются бессильными.

В компьютерных моделях объекты наделяются определяющими их свойствами, которые задают их реакции на различные виды манипуляций.

Типичная форма компьютерной модели – это электронная таблица, в которой пользователь может изучить влияние, вызываемое изменением величины, содержащейся в одной из ячеек таблицы, на величины, находящиеся в других ячейках таблицы и связанные с первой величиной формулами. Модель, построенная в виде электронной таблицы, позволяет представить математический или финансовый процесс почти любого типа – от расчета сужающего устройства в автоматике до расчета экономической эффективности системы автоматического регулирования.

Разумеется, перечисленные выше преимущества моделирования можно реализовать при использовании высококачественных программных продуктов, таких как 3DMax, MatLab, AutoCad, MatCad и другие, для работы в которых требуются профессиональные навыки программиста. К сожалению, сложившуюся на сей день ситуацию с предложением учебных компьютерных программ трудно назвать благополучной.

Поэтому цель моей работы – самостоятельная реализация моделей с помощью электронных таблиц Excel.

Основные этапы деятельности при построении компьютерной модели физического процесса:

— постановка задачи,

— выбор цели моделирования,

— анализ моделируемого объекта,

— выделение существенных для решения заданной задачи свойств,

— выбор оптимального представления модели,

— анализ соответствия полученной модели заданной задаче,

— демонстрация действия модели,

— защита модели.

Демонстрация программы

Программу Excel студенты изучают на занятиях по дисциплинам «Информатика» и «Информационные технологии в профессиональной деятельности».

Для имитации движений в электронных таблицах предусмотрена возможность использовать язык программирования Basic, который также изучается студентами всех специальностей.

Демонстрируется компьютерная модель абсолютно упругого удара.

Программа Excel позволяет осуществлять часть расчетов, легко конструировать интерфейс программы средствами рабочего листа (см рис. 1). Для изображения шаров может быть использована диаграмма пузырькового типа.

Рис. 1 Вид программы

Сама модель рассчитывается по формулам школьной физики:

Из приведенных законов выводим формулы расчета координат шариков

В ячейках электронной таблицы задаем необходимые параметры: массу 1 и 2 шара и их скорости. Целесообразнее выбрать в диапазоне от 1 до 10 кг., а скорости – в диапазоне от -10 до +10 м/с.

Пишем текст программы на событие щелчка мыши по кнопке «Старт!».

Текст программы на языке Basic.

Private Sub CommandButton1_Click()

xxn1 = Cells(2, 5)

xxn2 = Cells(2, 6)

dx1 = Cells(2, 2) / 100

dx2 = Cells(2, 4) / 100

x1 = xxn1

x2 = xxn2

m1 = Cells(2, 1)

m2 = Cells(2, 3)

For i = 1 To 2000

If x1

Beep

dx1 = Abs(dx1)

End If

If x2 = 9.5 Then

Beep

dx2 = -1 * Abs(dx2)

End If

If x1 = x2 — 1 Then

Beep

a = dx1

dx1 = (dx1 * (m1 — m2) + 2 * dx2 * m2) / (m1 + m2)

dx2 = a + dx1 — dx2

End If

x1 = x1 + dx1

x2 = x2 + dx2

Cells(5, 2) = x1

Cells(5, 4) = x2

For j = 1 To 500000

Next j

DoEvents

Next i

End Sub

Проверить работу программы можно следующим образом: при равенстве масс тел и одинаковых по абсолютному значению, но противоположно направленных скоростях получается симметричная картинка.

При желании можно вывести в ячейки листа значения изменяющихся скоростей, координат, пройденные пути и т.п. Это позволит наблюдать за изменениями значений при анализе явления соударения.

Заключение

Компьютерные модели могут использоваться для исследования процессов без построения системы, в которой они реально происходят. Такие модели позволяют ускорить процессы, протекающие слишком медленно или замедлить их (чтобы легче было наблюдать, например, движение пули или ракеты).

Компьютерные модели могут предназначаться для моделирования различных технических систем, например трубопровода, оснащенного из запорно-регулирующей арматурой, электрических цепей и т.д.

В своей работе я постарался исследовать возможности доступных компьютерных программ, таких как Excel и Basic, знакомых каждому студенту, для моделирования различных физических процессов и расчета реальных устройств. Эти возможности, бесспорно пригодятся любому студенту в учебе и дальнейшей практической деятельности.

Литература

1. Безручко В.Т.. Практикум по курсу «Информатика». Работа в Windows 2000, Word, Excel: Учеб. пособие. — 2-е изд., доп. и перераб. — М.: Финансы и статистика, 2003.-544 с.: ил.

2. Васильков Ю. В.. Компьютерные технологии вычислений в математическом моделировании М., «Финансы и статистика» 1999

3. Ефимова О., В. Морозов, Н. Угринович. Курс компьютерной технологии с основами информатики. Учебное пособие для старших классов. М., ABF, ООО «Фирма «Издательство АСТ», 1999. — 432 с., ил.

4. Кормен Т., Лейзерсон Ч., Ривест Р Алгоритмы: построение и анализ. М., «МЦНМО», 1999.

5. Соха Дж., Рахмел Д., Холл Д. Изучи сам Visual Basic 5/ Пер. с англ. А.Н. Филимонов; Худ. обл. М.В. Драко. – Мн.: ООО «Попурри», 1998. – 320с.: ил.

6. Чекмарев А. Средства визуального проектирования. BHV-СПб, 1998.

7. Экштайн В. «Компьютерное моделирование взаимодействия частиц с поверхностью твердого тела.» М. 1995 г.

8. Информатика. Еженедельная газета Издательского дома «Первое сентября». №13, 1-7 апреля 2002