Моделирование свободного падения тела в excel

Вычислительный эксперимент со свободным падением тела таблица excel

Что такое модель объекта или процесса и зачем её создавать? Какие бывают модели? Что такое информационная модель? Основные этапы моделирования Алгоритмическая модель Моделирование в языках программирования Моделирование в среде MS Excel

MS Excel – разновидность электронной таблицы. Это программа обработки числовых данных, хранящая и обрабатывающая данные в прямоугольных таблицах.

Таким образом, с помощью этой программы можно решать задачи исследовательского характера, требующие большого количества вычислений.

Рассмотрим задачу и сследовани я физических моделей . П остро им информационн ую модел ь движения тела, брошенного под углом к горизонту

1 этап. Содержательная постановка задачи «Бросание мячика в площадку». В процессе тренировок теннисистов используются автоматы по бросанию мячика в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в площадку определенной длины, находящуюся на известном расстоянии.

Проведём формализацию задачи. Формулируем основные предположения:

· мячик мал по сравнению с Землей, поэтому его можно считать материальной точкой;

· изменение высоты мячика мало, поэтому ускорение свободного падения можно считать постоянной величиной g = 9,8 м/с 2 и движение по оси 0 Y можно считать равноускоренным;

· скорость бросания тела мала, поэтому сопротивлением воздуха можно пренебречь и движение по оси О X можно считать равномерным.

Вывод: можно использовать формулы для равноускоренного движения, известные из курса физики.

При заданных начальной скорости v ₀ и угле бросания α значения координат дальности полета x и высоты y от времени можно описать следующими формулами:

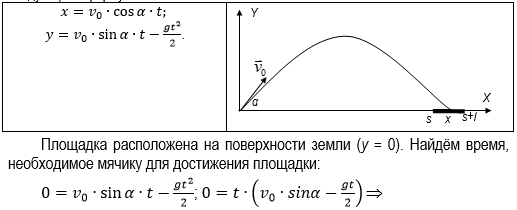
Площадка расположена на расстоянии s и имеет длину l . Попадание произойдет, если значение координаты х мячика будет удовлетворять условию: s ≤ х ≤ s + l . Если х s , то это означает «недолет», а если х > s + l , то это означает «перелет».

2 этап. Построение компьютерной модели движения тела в среде MS Excel .

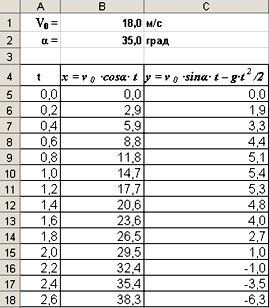
В ячейки B 5 и C 5 введем формулы для вычисления х и у : =$B$1*COS( РАДИАНЫ ($B$2))*A5 =$B$1*SIN( РАДИАНЫ ($B$2))*A5-4,9*A5*A5 1 Для ввода начальной скорости будем использовать ячейку B 1, а для ввода угла – ячейку B 2. Введём значения, как показано на рисунке. 2 3 Введем в ячейки A 5: A 18 значения времени с интервалом в 0,2 с. 4 Скопируем формулы в ячейки В6:В18 и С6:С18 соответственно. После этого должно получиться так, как показано на рисунке: 5 Построи м диаграмму типа График, в которой используется в качестве категории диапазон ячеек B 5: B 18, а в качестве значений — диапазон ячеек С5:С18.

3 этап. Исследование модели. Исследуем модель и определим с заданной точностью 0,1 градуса значения диапазона углов бросания, которые обеспечивают попадание мячика в мишень (например, при скорости бросания v ₀ = 18 м/с в площадку длиной l = 1 м , находящуюся на расстоянии S = 30 м ).

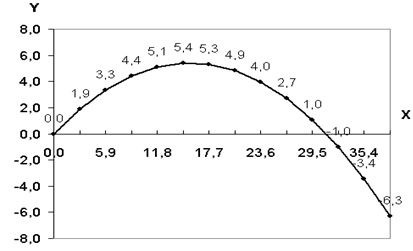Установить для ячеек точность один знак после запятой.

· в ячейку B 21 значение начальной скорости;

· в ячейку B 22 – значение угла бросания;

· в ячейку B 23 – значение расстояния до мишени;

· в ячейку B 25 формулу для вычисления координаты x мячика на поверхности для заданных начальных условий: =B21^2*SIN(РАДИАНЫ(2*B22))/9,81. Получится так, как показано на рисунке:

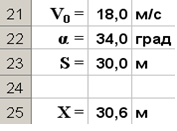
Для определения диапазона углов используем метод Подбор параметра. Этот метод позволяет задать значение функции и найти значение аргумента функции, который обеспечивает требуемое значение функции.

Функцией в нашем случае будет являться зависимость координаты тела x от параметра, т.е. угла бросания α. Для определения диапазона углов, необходимо определить два угла, которые обеспечивают попадания в ближний и дальний края площадки. Для заданных начальных условий (скорости бросания и расстояния до мишени) проведем поиск углов, которые дают попадание в площадку на расстояниях S = 30 м и S + l = 31 м.

Ищем значение угла бросания, которое обеспечит попадание мячика в ближний край площадки, т.е. какой угол α обеспечивает значение функции x = 30 метров .

Выделить ячейку В25, содержащую значение высоты мячика, и ввести команду [Сервис-Подбор параметра…].

В появившемся диалоговом окне ввести в поле Значение: расстояние до ближнего края площадки (т.е. 30).

В поле Изменяя значение ячейки: ввести адрес ячейки В$22, содержащей значение угла бросания.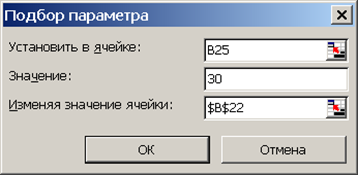

В ячейке В22 появится значение 32,6, т.е. значение минимального угла бросания мячика, которое обеспечивает попадание в площадку при заданных начальных условиях.

Далее, найдем угол бросания, который обеспечит попадание мячика в дальний край площадки, т.е. какой угол α обеспечивает значение функции x = 30 м + 1 м = 31 м .

Выделить ячейку В25, содержащую значение координаты х мячика, и ввести команду [Сервис-Подбор параметра…].

В появившемся диалоговом окне ввести в поле Значение: расстояние до дальнего края площадки (т.е. 30).

В поле Изменяя значение ячейки: ввести адрес ячейки В$22, содержащей значение угла бросания.

В ячейке В22 появится значение 34,9, т.е. значение максимального угла бросания мячика, которое обеспечивает попадание в площадку при заданных начальных условиях.

Итак, существует диапазон значений угла бросания мячика от 32,6 ° до 34,9 ° , в котором обеспечивается попадание в площадку длиной 1 м, находящуюся на расстоянии 30 м, мячиком, брошенным со скоростью 18 м/с.

Можно п овторит ь исследование модели при другом начальном значении угла (например, 55°).

Источник

Практическая работа №38. Компьютерное моделирование свободного падения в электронных таблицах. Образец выполнения практической работы представлен в файле Книга 1.

Практическая работа №38

Компьютерное моделирование свободного падения в электронных таблицах

Дата проведения занятия – 18.06.2020г.

Дисциплина:Информатика и ИКТ

Группа:2 «Парикмахер»

Тип занятия:Практическая работа

Цели занятия:

— научить студентов моделировать физические процессы на компьютере;

— развитие логического мышления, познавательного интереса студентов;

— развитие самостоятельности при изучении нового материала и выполнении заданий;

— способствовать воспитанию дисциплины и исполнительности, ответственному отношению к образовательному процессу.

Задание:

Сопоставить процессы падения твердого шара радиуса r с одной и той же высоты в разных средах:

• в пустоте (без сопротивления)

Образец выполнения практической работы представлен в файле Книга 1.

Ход работы:

1. Откройте ЭТ Excel. Заполните таблицу исходными данными:

1) В строки 1-6 внесите параметры модели (константы)

2) В строки 8-13 внесите вычисляемые параметры моделив соответствии с формулами

• k1 = 6π ∙ μ ∙ r k2 = с2 ∙ δ ∙ ρ = 0,4 ∙π∙ r ∙r ∙ ρс m = ∙π∙ r ∙ r ∙ r ∙ ρжел,

• где π =3,14 r= I4 ρc = d2 μ воздуха = d4 ρ воздуха =d3 μ воды = d6 ρ воды =d5

3) задайте шаг по времени 0,1 сек в ячейку d15

— Используя функцию автозаполнения , начиная со строки 18, заполните столбцы А и В

4) Для заполнения основной таблицы используйте следующие формулы:

D19=F19=H19 = $I$2 C19=E19=G19 = $I$3

C20 =С19- $I$5*$D$15 D20 =D19-$I$5*$D$15^2/2 +C19*$D$15

Е20 =E19+($G$10*E19+$G$11*E19^2-$G$9*$I$5)*$D$15/$G$9

F20 =F19+E19*$D$15

G20 =G19+($G$12*G19+$G$13*G19^2-$G$9*$I$5)*$D$15/$G$9

H20 =H19+G19*$D$15

5) используя автозаполнение, доведите столбцы D F H до первого отрицательного значения.

Источник

Практическое занятие. Проведение исследования на основе использования готовой компьютерной модели. Теоретические сведения

Практическое занятие

Проведение исследования на основе использования готовой компьютерной модели

Цель работы: реализация на компьютере математической модели движения тела при свободном падении в плотной среде с использованием электронных таблиц и программирования

Оборудование: персональный компьютер, учебные элементы.

Теоретические сведения

Моделирование – это метод познания, состоящий в создании и исследовании моделей.

Модель (фр.сл. мodele, ит. сл. modelo, лат. сл. modelus) – мера, образец. Модель — некий новый объект, который отражает некоторые существенные свойства изучаемого явления или процесса

Один и тот же объект может иметь множество моделей, а разные объекты могут описываться одной моделью.

Всё разнообразие моделей можно разделить на два больших класса: натуральные модели и информационные модели.

Типы информационных моделей: Табличные – объекты и их свойства представлены в виде списка, а их значения размещаются в ячейках прямоугольной формы. Перечень однотипных объектов размещен в первом столбце (или строке), а значения их свойств размещаются в следующих столбцах (или строках) Иерархические – объекты распределены по уровням. Каждый элемент высокого уровня состоит из элементов нижнего уровня, а элемент нижнего уровня может входить в состав только одного элемента более высокого уровня Сетевые – применяют для отражения систем, в которых связи между элементами имеют сложную структуру Предметом изучения информатики являются методы и технологии информационного моделирования с помощью компьютера – компьютерное моделирование. Компьютерной модельюназывают модель, построенную для исполнителя, ориентированного на вычислительное устройство. Это не особый вид модели, а способ изучения известных моделей с помощью компьютера. Компьютерная математическая модель –это программа, реализующая расчёты состояния моделируемой системы по её математической модели. Математическое моделирование –это связь между объектами в виде математических соотношений. При этом информационные объекты представляются в виде математических объектов. Пример. Модель равноускоренного движения: St = So + VoT + aT^2/2 Если исходить из общих задач моделирования, то наиболее естественна такая классификация: 4. дескриптивные (описательные) модели; 5. оптимизационные модели; 6. многокритериальные модели; 7. игровые модели. Дескриптивные (описательные) модели.Например, моделирование движения кометы, вторгшейся в Солнечную систему, производится с целью предсказания траектории ее полета, расстояния, на котором она пройдет от Земли, и т.д. В этом случае цели моделирования носят описательный характер, поскольку нет никаких возможностей повлиять на движение кометы, что-то в нем изменить. Оптимизационные моделииспользуются для описания процессов, на которые можно воздействовать, пытаясь добиться достижения заданной цели. В этом случае в модель входит один или несколько параметров, доступных влиянию. Например, меняя тепловой режим в зернохранилище, можно задаться целью подобрать такой режим, чтобы достичь максимальной сохранности зерна, т.е. оптимизировать процесс хранения. Многокритериальные модели.Нередко приходится оптимизировать процесс по нескольким параметрам одновременно, причем цели могут быть весьма противоречивыми. Например, зная цены на продукты и потребность человека в пище, нужно организовать питание больших групп людей (в армии, детском летнем лагере и др.) физиологически правильно и, одновременно с этим, как можно дешевле. Ясно, что эти цели совсем не совпадают, т.е. при моделировании будет использоваться несколько критериев, между которыми нужно искать баланс. Игровые моделимогут иметь отношение не только к компьютерным играм, но и к весьма серьезным вещам. Например, полководец перед сражением при наличии неполной информации о противостоящей армии должен разработать план: в каком порядке вводить в бой те или иные части и т.д., учитывая и возможную реакцию противника. Есть специальный раздел современной математики — теория игр, — изучающий методы принятия решений в условиях неполной информации. Компьютерная реализация моделей может быть осуществлена: 8. с помощью табличного процессора (MS Excel); 9. путем создания программ на традиционных языках программирования (Паскаль, Бейсик и др.), а также на их современных версиях; 10. с помощью специальных пакетов прикладных программ для решения математических задач (3D MAX и т.п.). Основные этапы разработки и исследования моделей на компьютере 11. Построение описательной информационной модели 12. Формализация модели (формальный язык) 13. Преобразование в компьютерную модель: 14. запись алгоритма на языке программирования 15. использование одного из приложений (электронных таблиц, СУБД) 16. Проведение компьютерного эксперимента (запуск программы, сортировка или поиск данных, построение графиков и диаграмм) 17. Анализ полученных результатов и корректировка исследуемой модели. Контрольные вопросы 18. Что означает понятие модель в научном познании? 19. Какие типы моделей вам известны? 20. Дать определение информационной модели. 21. Что такое компьютерное моделирование? 22. Назовите основные этапы математического моделирования. 23. Назовите основные этапы решения задачи на ЭВМ. _______________________________ Пример решения задачи с помощью программы MS Excel Задача:Из трех продуктов 1,2,3 составляют смесь. В состав смеси должно входить не менее 6 единиц химического вещества А, 8 единиц – вещества В и не менее 12 единиц вещества С. 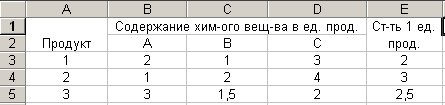Структура химических веществ приведена в следующей таблице: Таблица 1 Составьте наиболее дешевую смесь. Решение: 24. Добавим 2 столбца количество и сумма. В столбец Количество поставим свое значение. Сумму найдем, умножив количество на стоимость 1 единицы продукта. Таблица 2 25. Для нахождения поиска решения введем ограничения Таблица 3 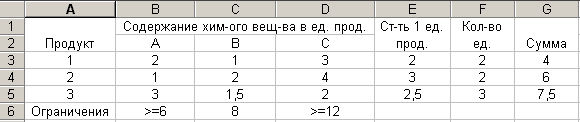26. Введем строку Смесь и найдем состав Таблица 4 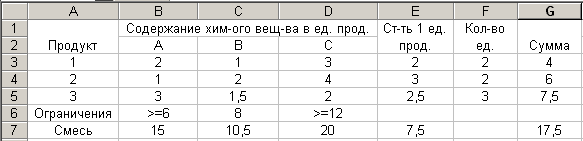27. С помощью поиска решения найдем наиболее дешевую смесь Таблица 5 28. Таблица с формулами 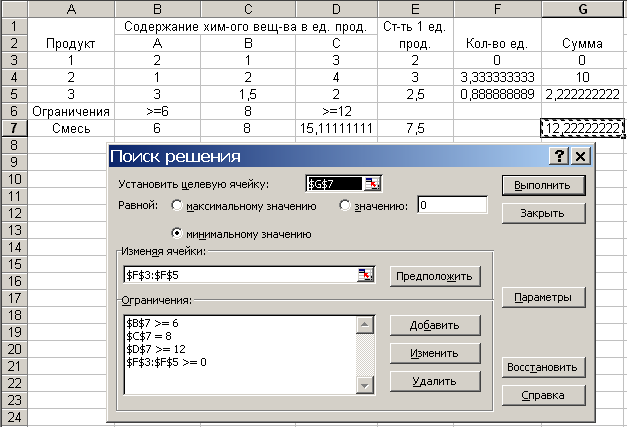29. Результаты поиска решения Составление математической модели для алгоритма оптимизации. 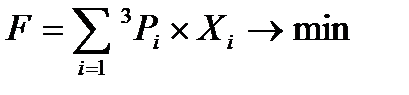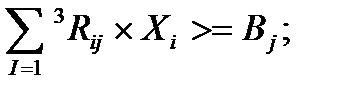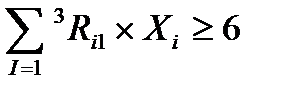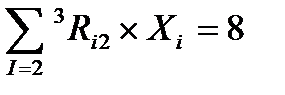Введем обозначения I – номер строки, продукт J – номер столбца, химического вещества R_ij – норма расхода одного продукта в смеси X_j – содержание j-го химического вещества в продукте P_i – стоимость 1 продукции B_j – ограничения Целевая функция Общая формула для ограничений 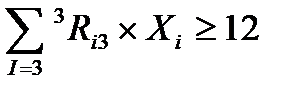Практическая часть Задание 30. Выполнить вычислительный эксперимент со свободным падением тела (таблица стр. 34-35, 11 класс, часть 2) 31. Рассчитать время падения шара в воде с точностью до 0,01 секунды (готовая программа на Паскале стр. 36, 11 класс, часть 2)

Содержание отчета

1. Название работы.

3. Задание и его решение.

4. Вывод по работе.

Литература

1. И.Г. Семакин, Т.Ю. Шеина, Л.В. Шестакова. Информатика, углубленный уровень,10 класс ч. 1, БИНОМ, 2014 год

Источник