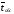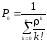СОДЕРЖАНИЕ
ВВЕДЕНИЕ 3
1.Постановка
задач массового обслуживания 5
1.1.
Общие сведения о СМО 5
1.2.
Моделирование СМО в табличном процессоре
Excel 11
1.3.
Постановка задачи 13
2.
Выполнение расчётов 14
2.1.
Разработка расчётного инструментария 14
2.2.
Расчёт контрольного примера 15
3.
Состав проводимых численных экспериментов 20
3.1.
Результаты расчётов 20
3.2.
Изменение параметров 24
3.3.
Выводы по проделанной работе 25
ЗАКЛЮЧЕНИЕ 27
СПИСОК
ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 28
ВВЕДЕНИЕ
Возникновение
теории массового обслуживания относится
к началу XX в. и связано с необходимостью
решения задач строительства и развития
телефонных сетей. Большой вклад в
развитие и становления теории массового
обслуживания внесли зарубежные ученые
Ф.В. Иоханнсен, А. К. Эрланг, а также
отечественный математик А.Я. Хинчин,
систематизировавший достигнутые к тому
времени основные положения теории
массового обслуживания в монографии
«Работы по теории массового обслуживания»
(1963) [2]. В зарубежной практике указанное
направление исследований известно под
названием «Теории очередей».
Теорию
массового обслуживания следует
рассматривать как раздел прикладной
математики, изучающий процессы, связанные
с удовлетворением массового спроса на
выполнение какого-либо вида услуг с
учетом случайного характера спроса и
обслуживания.
Задача
теории массового обслуживания –
установить зависимость результирующих
показателей работы системы массового
обслуживания (вероятности того, что
заявка будет обслужена; математического
ожидания числа обслуженных заявок и
т.д.) от входных показателей (количества
каналов в системе, параметров входящего
потока заявок и т.д.). Результирующими
показателями или интересующими нас
характерисуноктиками СМО являются –
показатели эффективности СМО, которые
описывают способна ли данная система
справляться с потоком заявок.
Задачи
теории массового обслуживания носят
оптимизационный характер и в конечном
итоге включают экономический аспект
по определению такого варианта системы,
при котором будет обеспечен минимум
суммарных затрат от ожидания обслуживания,
потерь времени и ресурсов на обслуживание
и простоев каналов обслуживания.
В
качестве примеров СМО в финансово-экономической
сфере можно привести системы, представляющие
собой банки различных типов (коммерческие,
инвестиционные, ипотечные, инновационные,
сберегательные), страховые организации
(государственные, акционерные общества,
компании, фирмы, ассоциации, кооперативы),
налоговые инспекции, аудиторские службы,
различные системы связи (в том числе
телефонные станции), погрузочно-разгрузочные
комплексы (порты, товарные станции),
автозаправочные станции, различные
предприятия и организации сферы
обслуживания (магазины, парикмахерские,
больницы).
-
Постановка задач массового обслуживания
-
Общие сведения о смо
Каждая
система массового обслуживания (СМО)
может быть представлена в виде
определенного числа обслуживающих
единиц, которые называются каналами
обслуживания. В качестве канала могут
рассматриваться различного вида приборы
и приспособления, вычислительная машина,
коллектив людей или отдельный исполнитель,
выполняющий определенный вид работ. По
числу каналов СМО делится на одноканальные
и многоканальные системы.
Функционирование
любой СМО заключается в обслуживании
поступающего в нее потока заявок или
требований. Заявки обычно поступают
нерегулярно, образуя случайный поток
заявок (требований). На обслуживание
заявки также необходимо определенное
время. Случайный характер потока заявок
и времени обслуживания приводит к
неравномерной загрузке СМО. В какие-то
периоды времени скапливается большое
количество заявок (они либо становятся
в очередь, либо покидают СМО, не получив
обслуживания), в другие периоды СМО
может работать с недогрузкой или
простаивать [9].
Систематизируем
основные термины и понятия, используемые
в теории массового обслуживания.
Системой
массового обслуживания называется
любая система, предназначенная для
обслуживания каких-либо заявок
(требований), поступающих в нее в случайные
моменты времени [7].
Под обслуживанием понимается
удовлетворение потребности в чем-то.
По своей природе обслуживание может
иметь самый различный характер.
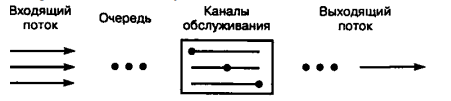
Основными
элементами СМО являются входной поток
заявок, очередь (может отсутствовать),
каналы обслуживания и выходящий поток.
Обобщенная структурная схема СМО
показана на рисунке 1:
Рисунок
1 — Обобщенная структурная схема СМО
В
зависимости от формирования СМО, ее
различают на:
-
Системы
с отказами, в которых при занятости,
заявка не встает в очередь и при это
она покидает систему обслуживания. -
Системы
с неограниченными ожиданиями, в которых
заявка встает в очередь, если в момент
поступления все каналы были заняты.
Существуют
и системы смешанного типа с ожиданием
ограниченной длиной очереди, это когда
заявка получает отказ, если приходит в
момент, когда все места в очереди заняты.
Заявка, попавшая в очередь, обязательно
обслуживается [1].
По
числу каналов обслуживания СМО делятся
на одноканальные и многоканальные.
В
зависимости от расположения источника
требований системы могут быть разомкнутыми,
(источник заявок находится вне системы)
и замкнутыми (источник находится в самой
системе) [5].
Характеристики
СМО
Заявки
характеризуются:
-
интенсивность
потока заявок (число заявок в единицу
времени); -
вероятность
отказа в обслуживании (доля не обслуженных
заявок). Очередь характеризуется: -
m
– длина очереди; -
–
средняя
длина очереди; -
– среднее
время ожидания в очереди; -
– вероятность
попадания в очередь (доля заявок,
попавших в очередь). Каналы обслуживания
характеризуются; -
n
– число каналов обслуживания; -
–
среднее
время обслуживания одной заявки; -
–
интенсивность
обслуживания (число обслуженных заявок
в единицу времени);
; -
среднее
число занятых каналов;
; -
– среднее
число свободных каналов;
-
коэффициент
загрузки канала; -
–
вероятность
обслуживания (доля обслуженных заявок); -
интенсивность
нагрузки; ρ
; -
– среднее
время простоя каналов; -
–
среднее
время пребывания заявки в СМО; -
–
среднее
число заявок в СМО.
Параметры
структуры СМО
Каждая
система массового обслуживания
обладает определенной структурой,
характеризующейся совокупностью
параметров [3]. Основным компонентом
структуры СМО являются каналы обслуживания.
В зависимости от числа каналов различают
одноканальные и многоканальные СМО.
Дисциплина
очереди
Дисциплина
очереди определяет
принцип, в соответствии с которым
поступающие на вход обслуживающей
системы требования подключаются из
очереди к процедуре обслуживания [8].
Наиболее
распространенный принцип ее построения
основан на правиле
«первым
пришел – первым обсуживаешься» (часто
обозначается аббревиатурой FIFO
– от английского First-In-First-Out).
Второе правило (например, при обработке
документов) – «последним пришел –
первым обслуживаешься» (обозначается
аббревиатурой LIFO – от англ. Last-In-First-Out)
[10].
Могут использоваться случайный отбор
заявок, учет определенных приоритетов,
вводиться ограничение на время пребывания
заявки в очереди.
Входящий
поток
Входящий
поток наиболее распространен в практике
это простейший поток заявок, обладающий
свойствами стационарности, ординарности
и отсутствия последствия.
-
Свойством
стационарности, которое выражает
неизменность вероятностного режима
потока по времени. Это значит, что число
требований, поступающих в систему в
равные промежутки времени, в среднем
должно быть постоянным. Например, число
вагонов, поступающих под погрузку в
среднем в сутки должно быть одинаковым
для различных периодов времени [6]. -
Отсутствие
последствия, которое обслуживает
взаимную независимость поступления
того или иного числа требований на
обслуживание в непересекающиеся
промежутки времени. Это значит, что
число требований, поступающих в данный
отрезок времени, не зависит от числа
требований, обслуженных в предыдущем
промежутке времени. -
Свойством
ординарности, которое выражает
практическую невозможность одновременного
поступления двух или более требований
(вероятность такого события неизмеримо
мала по отношению к рассматриваемому
промежутку времени, когда последний
устремляют к нулю).
Входящий
поток требований представляет собой
совокупность требований, которые
поступают в систему и нуждаются в
обслуживании. Входящий поток требований
изучается с целью установления
закономерностей этого потока и дальнейшего
улучшения качества обслуживания [4].
В
большинстве случаев входящий поток
неуправляем и зависит от ряда случайных
факторов. Число требований, поступающих
в единицу времени, случайная величина.
Случайной величиной является также
интервал времени между соседними
поступающими требованиями. Однако
среднее количество требований, поступивших
в единицу времени, и средний интервал
времени между соседними поступающими
требованиями предполагаются заданными.
Среднее
число требований, поступающих в систему
обслуживания за единицу времени,
называется интенсивностью поступления
требований.
На
практике условия простейшего потока
не всегда строго выполняются. Часто
имеет место не стационарность процесса
(в различные часы дня и различные дни
месяца поток требований может меняться,
он может быть интенсивнее утром или в
последние дни месяца) [7]. Существует
также наличие последствия, когда
количество требований на отпуск товаров
в конце месяца зависит от их удовлетворения
в начале месяца.
Простейшей
одноканальной моделью с вероятностным
входным потоком и процедурой обслуживания
является модель, характеризуемая
показательным распределением как
длительностей интервалов между
поступлениями требований, так и
длительностей обслуживания. При этом
плотность распределения длительностей
интервалов между поступлениями требований
имеет вид:

где
— интенсивность поступления заявок в
систему.
Под
интенсивностью потока понимают:
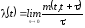
где
m(t, t+)
— среднее число событий в интервале (t,
t+).
Плотность
распределения длительностей обслуживания:

где
— интенсивность обслуживания.
Выходящий
поток
Совокупность
обслуженных и потерянных заявок образует
выходящий поток СМО.
В
зависимости от структуры выходящего
потока различают СМО без потерь и СМО
с потерями. Для СМО без потерь характерно
отсутствие ограничений на число мест
в очереди и на время пребывания заявки
в системе. По этой причине выходящий
поток будет состоять лишь из обслуженных
заявок.
В
свою очередь, поток потерянных заявок
может состоять из потока заявок,
получивших отказ, и потока не «терпеливых»
заявок, покинувших систему, так как их
время пребывания превысило допустимую
величину.
Выходящий
поток в общем случае распадается на
поток обслуженных и поток потерянных
заявок.
Выходящий
поток заявок связан с потоком обслуживания
в канале, где длительность обслуживания
tобс
является случайной величиной и подчиняется
закону распределения с плотностью:
где
μ – интенсивность потока обслуживания,
т.е. среднее число заявок, обслуживаемых
в единицу времени:
(чел./мин,
р./ дн., кг/ч, докум./дн.),
где
— среднее время обслуживания.
Важной
характеристикой СМО, объединяющей λ и
μ, является интенсивность нагрузки:

СМО
с отказами
Заявка,
поступившая в систему с отказами, при
этом все каналы заняты, получает отказ
и покидает систему необслуженной.
Показателем качества обслуживания
выступает вероятность получения отказа.
Предполагается, что все каналы доступны
в равной степени всем заявкам, входящий
поток является простейшим, длительность
(время) обслуживания одной заявки
распределена по показательному закону
[2].
По
ниже написанным формулам можно рассчитать
СМО с отказами:
-
Вероятность
простоя каналов обслуживания, когда
нет заявок (k
= 0):
-
Вероятность
отказа в обслуживании, когда поступившая
на обслуживание заявка найдет все
каналы занятыми (k
= n):

-
Вероятность
обслуживания:

-
Среднее
число занятых обслуживанием каналов:

-
Доля
каналов, занятых обслуживанием:

-
Абсолютная
пропускная способность СМО:

1.2.
Моделирование с помощью табличного
процессора Excel
Имитация
с помощью табличных процессоров
(spreadsheet simulation) представляет собой
отдельное направление со своими
особенностями. Его сторонники утверждают,
что использование данных систем улучшает
понимание происходящих процессов
гораздо лучше, чем применение
специализированного программного
обеспечения, имеющего высокую стоимость
и требующего время для изучения, а также
скрывающего используемые механизмы
(хотя такие среды довольно широко
используются, особенно GPSS, поскольку
предоставляют больше возможностей и
позволяют моделировать сложные системы)
[1].
Так,
Grossman в своей публикации «Spreadsheet Modeling
and Simulation Improves Understanding of Queues» утверждал,
что имитация с помощью таблиц Excel гораздо
лучше дает представление о системах
массового обслуживания, чем теория
очередей, и также развивает интуицию,
дает даже незнакомым с программированием
специалистам опыт реализации различных
моделей [1]. Однако эти подходы (реализация
с помощью Excel и сред моделирования) не
являются взаимоисключающими, а скорее
дополняют друг друга.
В
том случае, если обслуживание заявок
может происходить в нескольких узлах,
то говорят, что данная система является
многоканальной. Рассмотрим двухканальную
СМО. Предположим, что вновь поступившая
заявка поступает в тот канал, который
раньше других освободился (а при
одновременном освобождении заявка
поступит в первый узел), тогда процесс
моделирования можно представить
следующим образом (рисунок 2) (исходные
данные: tz =8 мин., to =7 мин.; t0 =9 ч.).
Рисунок
2 — Двухканальная СМО
Для
каждого канала выполняется расчет
времени начала и окончания обслуживания.
Решение о том, в каком канале будет
происходить обслуживание, принимается
на основе данных о времени освобождения
каждого из них. Время начала обслуживания
заявки равно максимальному значению
из следующих величин: время освобождения
найденного канала и время прибытия
заявки
Е8=ЕСЛИ(МАКС(F$7:F7)<=МАКС(H$7:H7);МАКС(F$7:F7;C8);»»)
F8=ЕСЛИ(ЕТЕКСТ(E8);»»;E8+D8)
G8=ЕСЛИ(МАКС(F$7:F7)>МАКС(H$7:H7);МАКС(H$7:H7;C8);»»)
H8=ЕСЛИ(ЕТЕКСТ(G8);»»;G8+D8).
Время
ожидания обслуживания определяется по
формуле I8=ЕСЛИ(ЕТЕКСТ(E8);G8-C8;E8-C8) (рисунок
3).
Рисунок
3 — Моделирование СМО в Excel
Соседние файлы в папке Курсовая 4 курс СМО
- #
- #
Подборка по базе: 3Отчетность экономических субъектов и ее анализ.docx, Лабунец Л.В.Цифровое моделирование оптических отражательных хара, Введение в компьютерное моделирование.pdf, Расчет основных технико- экономических показателей на примере те, Отчетность экономических субъектов и ее анализ_.docx, Анализ операций банка на рынке драгоценных металлов в современны, состав экономических районов.docx, Контрольная работа по разделу Человек в экономических отношениях, ПЗ_3.3. Моделирование свободного падения тел с учетом сопротивле, Игровое моделирование в аналитической деятельности1(1).docx
) и т.д., обеспечивающие следующие дополнительные возможности Excel: генерация случайных чисел, автоматизация запуска экспериментов, анализ и представление выходной информации и т.д. Генерация случайных чисел может быть также выполнена с помощью надстройки Excel, называемой «Пакет анализа данных».
Наконец
, отметим, что в связи с продолжением развития данного программного обеспечения, возможно, будущие версии будут предоставлять больше возможностей и обеспечивать более эффективную имитацию.
2. Имитационное моделирование систем массового
обслуживания
В
разных областях техники, в организации производства, в экономике и медицине
, в социальной сфере, в военном деле и во многих других сферах человеческой деятельности постоянно возникает необходимость решения вероятностных задач, связанных с работой систем массового обслуживания
(СМО). Многообразие приложений теории массового обслуживания определяет постоянно растущий интерес к ней, а сложность возникающих задач не позволяет получить исчерпывающие решения на базе аналитических методов. В таких ситуациях часто прибегают к имитационному моделированию. Для имитации подобных систем предназначен язык моделирования GPSS, а также создаются сложные программные системы
(ObjectSim, Pigrim
[10]), позволяющие реализовать модели систем массового обслуживания с помощью развитой CASE- оболочки путем выбора и связи различных строительных блоков. Среди работ, описывающих моделирование СМО с помощью электронных таблиц можно привести следующие — [3-7]. Авторы рассматривают моделирование систем с неограниченным
, ограниченным по времени и/или длине очереди ожиданием, которые располагают от 1 до 12 обслуживающими устройствами [7]. При этом различают два основных подхода к моделированию СМО: ориентированный на события и ориентированный на процессы. Событийный подход имеет преимущества в отношении гибкости и эффективности вычислений, однако менее подходит для обучения, поскольку скрывает «жизненный цикл» заявок и является менее понятным на интуитивном уровне. Кроме того, для его реализации требуется управляющая событиями подпрограмма, что приводит к необходимости использования внутреннего языка VBA [11]. Рассмотренные ниже модели будут реализованы с использованием процессно-ориентированного подхода.
Рассмотрим структуру СМО. Каждая СМО состоит из определенного числа обслуживающих единиц, которые называются каналами обслуживания. На вход
СМО
поступает поток требований (заявок). Таким образом, различают следующие элементы
СМО:
1. входной поток заявок;
2. очередь;
3. узел обслуживания;
4. выходной поток.
На рис. 2.1 указаны эти элементы для следующей СМО: бензоколонка занимается заправкой автомобилей.
Рис
. 2.1 – Пример системы массового обслуживания
Входной поток заявок может быть случайным или детерминированным. В первом случае время между поступлением двух заявок является случайной величиной
, а во втором – величиной детерминированной (поступление происходит в соответствие с определенным графиком). Интенсивность потока
λ
– частота появления событий, поступающих в СМО в единицу времени. В СМО может поступать несколько входных потоков, имеющих различные характеристики
(интервал поступления, приоритет и т.д.).
Очередь
– место, где поступившие заявки ждут начала обслуживания. В том случае
, если элемент очередь в системе отсутствует, то данная система без ожидания
. Это означает, что в том случае, если в момент поступления заявки все каналы обслуживания заняты, то эта заявка покидает систему необслуженной.
Очередь может иметь ограниченную или неограниченную длину. Кроме того, время ожидания в очереди может быть ограничено (говорят, что рассматриваются нетерпеливые заявки). Следующая характеристика очереди – дисциплина очереди
. Она связана с правилом, в соответствии с которым обслуживаются клиенты
. Различают следующие дисциплины: первый пришел – первый ушел, первый пришел – последний ушел, а также существуют дисциплины с приоритетами
Рассмотрим теперь характеристики средств обслуживания. Системы обслуживания характеризуются по числу каналов обслуживания (например, если на рис. 2.1 машины могут быть обслужены несколькими устройствами, то система
будет многоканальной), числу фаз обслуживания. Время обслуживание может быть случайной величиной или детерминированным.
Также существую системы, в которых обслуженные требования после некоторой задержки опять поступают на вход. Такие системы называются замкнутыми
В
качестве показателей эффективности СМО рассматриваются: среднее время
, которое клиент проводит в очереди, средняя длина очереди, среднее время
, которое клиент проводит в
системе обслуживания
(
TotalTimeSystem
TimeSystem
N
=
, где
TotalTimeSystem
— общее время пребывания в системе для всех заявок, а
N
-число заявок), среднее число клиентов в системе обслуживания
, вероятность того, что система окажется свободной и т.д.
2.1 Одноканальная система массового обслуживания
Рассмотрим простую систему массового обслуживания: число каналов равно единице
, время ожидания неограниченно, время между заявками и время обслуживания заявок являются случайными величинами с показательным законом распределения (среднее значение времени обслуживания равно
to
, среднее время между заявками —
tz
) (рис.2.2).
Рис
. 2.2 – Одноканальная система массового обслуживания
Рассмотрим процесс поступления десяти заявок, если
tz
=0,5 ч.,
to
=1 ч.
В
[6]использован следующий способ моделирования такой системы
(рис.2.3). Величины времени обслуживания и между заявками рассчитываются согласно способу моделирования случайной величины с показательным законом распределения
D9=-$F$4*LN(СЛЧИС())
E9=-$F$3*LN(СЛЧИС()).
В
последнем столбце рассчитывается величина
Wn
Xn Yn
+
−
F7=C7+D7-E7.
Если ее значение является отрицательным, то это означает, что следующая заявка поступит после того, как будет обслужена текущая и потому время ее ожидания будет равно нулю, а в противном случае, время ожидания составит
Wn
Xn Yn
+
−
С
9=0
С
10=ЕСЛИ(F9>0;F9;0).
Изменим исходные данные (
tz
=1 ч.,
to
=0,5 ч.). Из рис. 2.4 можно увидеть, что в
этом случае уменьшится время ожидания обслуживания.
Рис
.2.3 – Результаты моделирования одноканальной СМО при
tz
=0,5 ч.,
to
=1 ч.
Рис
. 2.4 – Результаты моделирования одноканальной СМО при
tz
=1 ч.,
to
=0,5 ч.
Теперь выполним моделирование, учитывая начальное время
tn
. Пусть
tz
=8 мин
.,
to
=7 мин.;
tn
=9 ч. Рассмотрим процесс поступления семи заявок (рис.2.5).
Определение времени между заявками и времени обслуживания (мин.) остается без изменения.
Для того чтобы перевести эти значения в используемый формат времени необходимо осуществить следующие операции
F8=E8/1440
D8=D7+C8/1440.
Т
.е. время поступления очередной заявки равно сумме времени прибытия предыдущей и случайной величины, распределенной по показательному закону.
Время начала обслуживания первой поступившей заявки равно времени ее поступлению
G8=D8.
Начиная со второй заявки, эта величина будет определяться как максимальное значение из момента окончания обслуживания предыдущей заявки и
времени поступления текущей
G9=ЕСЛИ(D9>=H8;D9;H8).
Время окончания обслуживания рассчитывается по формуле
H8=G8+F8.
Период ожидания равен разности времени начала обслуживания и времени поступления
I8=G8-D8.
Также встречаются системы, в которых новая заявка может поступить только после того, как была обслужена предыдущая. В качестве примера, можно назвать систему
, которая периодически может выходить из строя и требовать ремонта (ее отказы в данном случае рассматриваются как заявки): время между ее отказами и время обслуживания распределено по показательному закону. Очевидно, что не может произойти выход из строя системы прежде, чем будет выполнен ремонт предыдущего отказа. Такие заявки будем называть не перекрывающимися.
Для того чтобы выполнить моделирование данной СМО необходимо изменить только расчет времени прибытия заявки, которое будет равно сумме момента окончания обслуживания предыдущей заявки и случайной величины, распределенной по показательному закону
D9=H8+C9/1440.
Результаты моделирования представлены на рис.2.6 (
tz
=5 мин.,
to
=6 мин.).
Можно заметить, что в Диаграмме заявок теперь отсутствуют периоды ожидания обслуживания
Рис
. 2.5 – Моделирование одноканальной СМО с учетом начального времени
Рис
. 2.6 – Моделирование одноканальной СМО с не перекрывающимися заявками
Задачи
1. Выполните имитацию работы банка, осуществляющего прием вкладов.
Размер депозита является случайной величиной с нормальным законом распределения
(среднее значение
—
MD
; среднее квадратическое отклонение
—
SD
). Время между приходом двух вкладчиков – случайная величина с показательным законом распределения (среднее значение —
tz
), а
время обслуживания равномерно распределено на интервале [
a
;
b
].
Пусть исходные значения равны величинам:
MD
=30000 руб.;
SD
=10000 руб
.;
tz
=1 час;
a
=20 мин.;
b
=30 мин.;
tn
=9 ч., число заявок равно 5.
Определите время прихода последнего клиента, среднее время пребывания клиента в системе. Какой общий размер вкладов будет осуществлен а) после прихода пяти клиентов; б) к моменту времени 12:00 ч
.?
Рис
.2.7 – Система массового обслуживания «Банк»
2. Проведите 10 экспериментов и рассчитайте величины:
• среднее время ожидания;
• среднее число обслуженных заявок за период с 9:00 до 15:00 ч.
3. Предположите, что
tn
=0 и выполните имитацию описанным на рис. 2.3 способом
4. Пусть банковская автоматизированная система может выходить из строя, что приводит к необходимости вызова специалистов, устраняющих неполадку
. Выполните имитацию периодов нормальной работы системы и ее ремонта, если данные величины являются случайными с показательным законом распределения, а
tz
=30 дней,
to
=3 ч. Рассмотрите процесс поступления
5 заявок (отказов).
2.2 Двухканальная система массового обслуживания
В
том случае, если обслуживание заявок может происходить в нескольких узлах
, то говорят, что данная система является многоканальной. Рассмотрим двухканальную
СМО (рис.2.8). Предположим, что вновь поступившая заявка поступает в тот канал, который раньше других освободился (а при одновременном освобождении заявка поступит в первый узел), тогда процесс моделирования можно представить следующим образом (рис. 2.9) (исходные данные:
tz
=8 мин.,
to
=7 мин.;
0
t
=9 ч.).
Рис
. 2.8 – Двухканальная система массового обслуживания
Рассмотрим основные отличия от предыдущей модели. Для каждого канала выполняется расчет времени начала и окончания обслуживания. Решение о том, в
каком канале будет происходить обслуживание, принимается на основе данных о
времени освобождения каждого из них. Время начала обслуживания заявки
равно максимальному значению из следующих величин: время освобождения найденного канала и время прибытия заявки
Е
8=ЕСЛИ(МАКС(F$7:F7)<=МАКС(H$7:H7);МАКС(F$7:F7;C8);»»)
F8=ЕСЛИ(ЕТЕКСТ(E8);»»;E8+D8)
G8=ЕСЛИ(МАКС(F$7:F7)>МАКС(H$7:H7);МАКС(H$7:H7;C8);»»)
H8=ЕСЛИ(ЕТЕКСТ(G8);»»;G8+D8).
Время ожидания обслуживания определяется по формуле
I8=ЕСЛИ(ЕТЕКСТ(E8);G8-C8;E8-C8).
Рис
. 2.9 — Моделирование двухканальной системы массового обслуживания
Задачи
1. Магазин, располагающий двумя кассами
, занимается продажей продовольственных товаров (рис. 2.10). Время между приходом двух покупателей
– случайная величина с
показательным законом распределения
(среднее значение —
tz
), а время обслуживания равномерно распределено на интервале [
a
;
b
]. Сумма покупки является случайной величиной с нормальным законом распределения (среднее значение —
MD
; среднее квадратическое отклонение —
SD
). Пусть исходные значения равны величинам
:
MD
=400 руб.;
SD
=100 руб.;
tz
=10 мин.;
a
=3 мин.;
b
=7 мин.;
tn
=9 ч. Выполните моделирование поступления семи заявок (покупателей).
Определите время прихода седьмого клиента. Какой размер выручки
получит магазин а) после того, как было обслужено семь покупателей; б) к моменту времени 10:00 ч.?
2. Предположите, что рассматриваемый поток клиентов – это потенциальные покупатели
, которые с вероятностью
P
могут совершить покупку (
P
=0,6).
3. Пусть время обслуживания – дискретная случайная величина со следующим законом распределения
Значение
, мин
1 2
3 4
Вероятность
0,2 0,2 0,4 0,2
Выполните имитацию, учитывая данное условие.
4. Проведите 10 экспериментов и рассчитайте величины:
• среднее время ожидания;
• средний размер выручки.
Рис
.2.10 – Система массового обслуживания «Магазин»
2.3 Система массового обслуживания с ограниченным по
времени
ожиданием
Ожидание наступления обслуживания может быть ограничено двумя условиями
: длиной очереди и временем. Во втором случае заявка покидает
систему необслуженной, если время ее ожидание превысило некоторое значение
TOMax
, в противном случае – поступает в канал обслуживания (рис. 2.11).
Если время ожидания заявок равно нулю, то система называется СМО без ожидания
(рис. 2.12). В качестве примера можно привести поступление телефонных звонков в справочную службу: если оператор занят разговором с другим клиентом, то поступившие в этом период звонки получают отказ в обслуживании
Рис
. 2.11– Система массового обслуживания с ограниченным по времени ожиданием
Рис
. 2.12 – Система массового обслуживания без ожидания
Считая
, что время между заявками и обслуживания является случайной величиной с показательным законом распределения, выполним имитацию данной системы со следующими исходными данными:
tz
=8 мин.,
to
=7 мин.;
0
t
=9 ч.;
TOMax
= 1 мин. Результаты представлены на рис. 2.13. В столбце «Поступление на
обслуживание
» принимается решение о том, будет ли начато обслуживание заявки
. Для этого рассчитывается промежуток времени между поступлением заявки и освобождением канала и сравнивается с максимальным временем ожидания заявки
Е
9=ЕСЛИ((МАКС(G$8:G8)-C9)>$D$4;»Нет»;»Да»).
В
случае поступления заявки на обслуживание определяется время его начала и окончания
F9=ЕСЛИ(E9= «Да»;МАКС(C9;G$8:G8); «»)
G9=ЕСЛИ(ЕТЕКСТ(F9);»»;F9+D9).
В
последнем столбце «Ожидание» рассчитывается время ожидания (для всех заявок, независимо от, того были ли они обслужены)
H9=ЕСЛИ(ЕТЕКСТ(G9);МАКС(G$8:G8;C9)-C9;F9-C9).
Так
, из рис.2.13 видно, что в данной реализации период ожидания шестой заявки превысил максимально допустимое значение, и поэтому обслуживания не произошло
Рис
. 2.13 – Моделирование системы массового обслуживания с ограниченным по времени ожиданием
Задачи
1. Менеджер фирмы принимает заказы от клиентов на выполнение различных работ
(рис.2.14). Заказы поступают посредством телефонной связи. Время между двумя звонками является случайной величиной с показательным
законом распределения (среднее значение —
tz
), время обслуживания
(принятия заказа) – случайная величина с нормальным законом распределения
(среднее значение —
to
, среднее квадратическое отклонение
—
sto
). В том случае, если звонок поступил в то время, когда менеджер занят приемом другого заказа, то он получает отказ в обслуживании.
Стоимость заказа клиента равномерно распределена на интервале [
a
;
b
].
Выполните моделирование данной системы при следующих исходных данных
:
tz
=15 мин.;
to
=15 мин.;
sto
=2 мин.;
a
=5000 руб.;
b
=15000 руб.;
tn
=9 ч
. Рассмотрите поступление шести звонков и определите следующие величины
: число отказов в обслуживании; общая сумма заказов; время поступления последнего звонка.
Рис
.2.14 – Система обслуживания «Прием заказов»
2. Проведите 10 экспериментов и рассчитайте величины:
• среднее число отказов в обслуживании;
• среднюю сумму заказов;
• среднее время завершения моделирования (время окончания обслуживания последней заявки).
3. Выполните моделирование, считая, что вероятность совершения заказа клиентом равна
P
(
P
=0,7).
4. Предположите, что фирма наняла еще одного менеджера и вновь поступивший звонок направляется к свободному в данный момент работнику
5. Пусть новое оборудование фирмы позволяет поступившим звонкам ожидать освобождения менеджера в течение времени
TOMax
. Выполните моделирование при
TOMax
=2 мин. (число каналов обслуживания равно единице
), рассчитайте среднее число отказов (за 10 реализаций) и сравните данное значение с полученным во втором задании.
6. Рассмотрите ситуацию, когда максимальное время ожидания каждой заявки определяется также поведением клиентов и его значение – случайная величина с дискретным законом распределения:
Значение
0 1
2
Вероятность
0,25 0,5 0,25
Татарникова Виктория Викторовна1, Гусева Елена Николаевна2
1Магнитогорский государственный технический университет им. Г.И.Носова, студент группы ФЭУПОб-12 института экономики и управления
2Магнитогорский государственный технический университет им. Г.И.Носова, кандидат педагогических наук, доцент кафедры бизнес-информатики и информационных технологий
Аннотация
В статье рассматривается применение компьютерного моделирования в решении задач систем массового обслуживания в Microsoft Excel на примере задачи о сортировочной станции. Акцентируется внимание на удобстве расчетов, рассмотрении различных вариантов решения поставленной задачи и анализируется эффективность работы СМО.
Tatarnikova Victoria Victorovna1, Guseva Elena Nikolaevna2
1Nosov Magnitogorsk State Technical University, student group FEUPOb-12 Institute of Economics and Management
2Nosov Magnitogorsk State Technical University, Associate Professor, Department of Business Informatics and Information Technologies
Abstract
The article deals with the use of computer modeling in solving the problems of queuing systems in Microsoft Excel as an example the problem of the yard. The attention is focused on the convenience of calculation, considering various options for solving the problem and analyze the effectiveness of the CFR.
Библиографическая ссылка на статью:
Татарникова В.В., Гусева Е.Н. Использование компьютерного моделирования в решении задач о системах массового обслуживания // Современные научные исследования и инновации. 2016. № 6 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2016/06/69373 (дата обращения: 07.04.2023).
Одно из важных направлений прикладной математики связано с исследованием систем мaссового обслуживания (СМО). СМО – это системы, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания. Примерами СМО являются магазины, телефонные станции, кассы, ремонтные мастерские, автозаправочные станции, ЭВМ, обрабатывающая запросы от удаленных терминалов [1,7, 9].
При изучении СМО используются методы имитационного моделирования и статистических испытаний (или метод Монте-Карло). При этом создается компьютерная модель, имитирующая поведение системы, с помощью ее производят большое количество реализаций анализируемого процесса и сохраняют получающиеся значения выходных величин. Получающиеся результаты приобретают статистическую устойчивость и после соответствующей математической обработки могут рассматриваться как характеристики изучаемой системы [3,8,12,13]. Имитационные модели используются при изучении социологических, экономических процессов функционирования сложных технических систем (например, ядерного реактора), а также в процессе обучения.
Каждая из систем массового обслуживания состоит из каналов (или приборов) обслуживания, на которые в случайные моменты времени поступает поток заявок или требований. После приема заявки канал оказывается занят на некоторое время обслуживания , после чего он освобождается и ожидает следующей заявки. На входе СМО может накапливаться несколько заявок, они либо становятся в очередь, либо покидают СМО необслуженными [3,5].
Последовательность событий, происходящих друг за другом в случайные моменты времени, называется потоком событий. Если поток событий задается только моментами времени наступления этих событий, то он называется однородным. Поток неоднородных событий характеризуется:
- совокупностью вызывающих моментов времени ,;
- набором признаков событий, к которым относятся принадлежность заявки к тому или иному источнику, приоритет заявки, возможность обслуживания тем или иным каналом и т.д.
Интенсивность потока рассчитывается как отношение числа событий ко времени наблюдения: . В случае, когда вероятность появления заданного числа событий в течение интервала ∆τ зависит исключительно от продолжительности интервала ∆τ и не зависит от времени τ, прошедшего с начала запуска системы, поток событий называется стационарным [10,13].
Любая СМО состоит из приборов обслуживания , каждый из которых имеет накопитель заявок и канала обслуживания заявок . В накопители заявок может одновременно находится заявок, где –емкость i-ого накопителя. В накопитель поступает поток заявок , а в канал – поток обслуживаний . При изучение сложных систем массового обслуживания рассматривают специальные Q-схемы, образующие многоканальные и многофазные сети массового обслуживания. Связи между элементами таких СМО изображают в виде стрелок, которые показывают направления движения заявок. В некоторых случаях говорят о замкнутых СМО, имеющих обратную связь, по которой выходной поток обслуженных заявок снова поступает на вход того или иного прибора обслуживания. В общем случае процесс функционирования СМО любой сложности можно однозначно задать с помощью Q-схемы, учитывающей:
- множество входящих потоков W;
- множество потоков обслуживания U;
- правила R сопряжения элементов СМО;
- множество собственных параметров H;
- оператор алгоритмов обслуживания заявок A;
- вектором состояния Z, элементов которого характеризуют состояния всех приборов обслуживания и их накопителей.
Для изучения функционирования СМО методом статистических испытаний (методом Монте-Карло) стоится имитационная модель процесса и с помощью генератора случайных чисел производится «розыгрыш» случайных событий (входных сигналов и внешних воздействий) в соответствии с заданными законами распределения. Компьютер моделирует более 1000 реализаций исследуемого процесса, выходные сигналы и подвергаются статистической обработке.
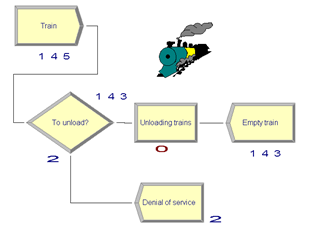
Рассмотрим пример решения задачи о грузовой сортировочной станции в Arena и сравним с получившимися данными в Microsoft Excel.
На грузовой станции имеется два выгрузочных фронта. Интенсивность подхода составов под выгрузку составляет 0,4 состава в сутки. Среднее время разгрузки одного состава – 2 суток. Приходящий поезд отправляется на другую станцию, если в очереди на разгрузку стоят более трёх составов.
Оценить эффективность работы выгрузочных фронтов грузовой станции: вероятность, что выгрузочные фронты свободны, вероятность, что состав останется без разгрузки, относительную пропускную способность, абсолютную пропускную способность, среднее число поездов, ожидающих разгрузки, среднее число заявок в системе, среднее время пребывания заявки в очереди, среднее время пребывания заявки в системе. Как изменятся данные показатели, если интенсивность подхода составов увеличится до 0,5?
Решение таких задач, не смотря на разработанный математический аппарат, не очень удобно производить вручную. Для наиболее быстрого и эффективного решения, можно использовать различные программные средства: табличный процессор Microsoft Excel и среду имитационного моделирования Arena Rockwell Software. Табличный процессор при решении таких задач может помочь в вычислении приблизительных характеристик исследуемой СМО. Эти значения дают общее представление об эффективности работы системы и конечно не могут учесть массу случайных факторов, влияющих на ее работу. Кроме того, для многих подобных задач не менее важно представить логику работы системы, очереди, увидеть и понять какое количество поступивших составов получают отказ в обслуживании [5,6,8]. Эти вещи позволяет реализовать Arena (рис.1). Для решения задачи был выбран период моделирования равный 12 месяцам, что позволило получить представление о длительном периоде работы системы и наиболее приближенных к реальности показателях системы.
Рисунок 1. Логика задачи в Arena
По условию задачи n = 2, m = 3, т. е. грузовая станция представляет собой многоканальную систему с ограниченной очередью. Интенсивность потока обслуживаний равна μ =1/2 = 0,5. Интенсивность нагрузки канала (трафик) равна ρ = 0,4 ∙ 2 = 0,8. Теперь рассчитаем характеристики для интенсивности подхода составов, равной 0,4: вероятность того, что выгрузочный фронт свободен; вероятность того, что состав будет отправлен на другую станцию; относительную пропускную способность; абсолютную пропускную способность; среднее число составов, ожидающих разгрузки; среднее время ожидания разгрузки; среднее число занятых фронтов (среднее число заявок под обслуживанием); среднее число составов, находящихся у разгрузочного фронта; среднее время пребывания состава у разгрузочного фронта.
Произведем вычисления для интенсивности подхода составов, равной 0,4. Решение проиллюстрировано в таблице 1. Аналогично произведем вычисления для характеристик системы массового обслуживания с интенсивностью прихода составов равной 0,5.
Таблица 1 – Расчет характеристик для грузовой станции в Microsoft Excel
|
Характеристики многоканальной СМО с отказами |
||||
| Число каналов обслуживания | n |
2 |
2 |
|
| Максимальное число составов в очереди | m |
3 |
3 |
|
| Интенсивность прихода составов | λ |
0,4 |
0,5 |
|
| Время разгрузки 1 состава | tоб |
2 |
2 |
|
| Интенсивность разгрузки составов | μ |
0,5 |
0,5 |
|
| Приведенная интенсивность | ρ |
0,8 |
1 |
|
| Вероятность, того что канал свободен | P0 |
0,47 |
0,39 |
|
| Вероятность отказа в разгрузке | Pотк |
0,010 |
0,02 |
|
| Относительная пропускная способность | Q |
0,99 |
0,98 |
|
| Абсолютная пропускная способность | A |
0,40 |
0,49 |
|
| Длина очереди | Nоч |
0,14 |
0,29 |
|
| Среднее время в очереди | Tоч |
0,06 |
0,15 |
|
| Среднее число занятых каналов | k |
0,79 |
0,98 |
|
| Среднее время нахождения состава в системе | Nсист |
0,93 |
1,27 |
|
| Среднее число составов в системе | Tсист |
2,33 |
2,54 |
Сравнивая получившиеся результаты, можно сказать, что вероятность того, что состав будет отправлен на другую станцию при интенсивности подхода составов равной 0,5 больше, чем при интенсивности, равной 0,4.
Исходя из данных, приведённых данных в таблице 1 и получившихся результатах имитационного моделирования (в отчетах среднее время ожидания разгрузки — 9,5ч, а вероятность отказа 1,3%) можно сделать вывод о том, что среднее время пребывания состава в ожидании разгрузки на другой станции невелико, что говорит о нормальной работе разгрузочного узла. При увеличении интенсивности похода составов выгрузочный узел продолжает работать эффективно.
Используя данные программы, можно с легкостью обрабатывать большой массив данных, производить расчеты, наблюдать за многоканальной системой обслуживания в динамике, анализируя все ее слабые и сильные стороны. Помимо этого анимация процессов в программе Arena и обширные статистические данные, собранные в отчетах, помогут опытному пользователю быстро разобраться с причинами возникающих проблем в системе.
Библиографический список
- Акопов А.С. Имитационное моделирование: учебник и практикум. – Москва: Юрайт, 2015.–390 с.
- Баженов Р.И., Лопатин Д.К. Об имитационном моделировании экономических процессов средствами специализированной программной среды // Молодой ученый. 2014. № 4. С. 88-92.
- Гусева Е. Н. Математика и информатика: [электронный ресурс] учеб. пособие/ Е. Н. Гусева, И.Ю. Ефимова, И.Н. Мовчан, Л.А. Савельева. – 3-е изд., стереотип. –М.: Флинта, 2015– 400 с. –Режим доступа: lf5.com/Knigi/Nauka-Obrazovanie/Matematika/Matematika-i-informatika-148-103807
- Гусева Е.Н. Математические основы информатики/ Е.Н. Гусева, И.И. Боброва, И.Ю. Ефимова, И.Н. Мовчан, С.А. Повитухин, Л.А. Савельева. – Магнитогорск: Изд-во Магнитогорск. гос. техн. ун-та им. Г.И. Носова, 2016.- 234 с.
- Гусева Е. Н. Теория вероятностей и математическая статистика: учеб. пособие – 5-е изд., доп. и перераб.: [электронный ресурс]/ Е. Н. Гусева. –М.: Флинта, 2011.– 220 с. – Режим доступа: http://www.knigafund.ru/books/116083/read
- Гусева Е.Н. Имитационное моделирование экономических процессов в среде «Arena»: учеб. пособие: [электронный ресурс]. М.: Флинта, 2011. – 132 с. – Режим доступа: http://www.knigafund.ru/books/114189
- Гусева Е.Н. Имитационное моделирование социально-экономических процессов. – Магнитогорск: изд-во Магнитогорск. гос. техн. ун-та им. Г.И. Носова, 2015. – 25с.
- Гусева Е.Н. Моделирование макроэкономических процессов: учеб. пособ.: [электронный ресурс]/ Е. Н. Гусева. – М.: Флинта, 2014.–214с.– Режим доступа: http://www.ozon.ru/context/detail/id/28975354/
- Гусева Е.Н. Основы имитационного моделирования экономических процессов: лаб. практикум / Е.Н. Гусева. – Магнитогорск: МаГУ, 2007. – 140с.
- Кийкова Е.В. Управление системой закупок товаров, работ и услуг для нужд бюджетного образовательного учреждения на основе имитационного моделирования // Современные проблемы науки и образования. –2013. № 1. С. 302.
- Кийкова Е.В., Лаврушина Е.Г. Значение изучения имитационного моделирования студентами вуза различных уровней подготовки // Современные проблемы науки и образования. –2014. № 3. С. 388.
- Лебединский Б.П., Желекова Е.Э. Имитационное моделирование систем массового обслуживания в программном продукте GPSS // Вестник Курганского государственного университета. Серия: Технические науки. – 2012. № 24. С. 66-69.
- Самаров К. Л. Элементы теории массового обслуживания Учебное пособие для студентов [Электронный ресурс]. – URL: http://www.resolventa.ru/data/metodstud/servtheory.pdf (дата обращения: 19.06.2016).
Количество просмотров публикации: Please wait
Все статьи автора «Татарникова Виктория Викторовна»
1. Пользовательская функция СХЕМАГР
Формулы финальных вероятностей P(S = Si) = pi, i = 0, 1, … , n, схемы гибели и размножения приведены в [1], сведения по VBA Excel изложены в [2, 3]. Программный код пользовательской функции СХЕМАГР, возвращающей финальные вероятности, приведен в листинге 1.1.
Листинг 1.1. Код функции СХЕМАГР и ее описания
Function СХЕМАГР(Загрузки As Variant) As Variant
n = UBound(Загрузки)
ReDim L(0 To n)
ReDim p(0 To n)
p(0) = 1:L(0) = 1
For i = 1 To n
L(i) = L(i — 1) * Загрузки(i):p(0) = p(0) + L(i)
Next
p(0) = 1 / p(0)
For i = 1 To n
p(i) = L(i) * p(0)
Next
СХЕМАГР = p
End Function
Sub InstallFunc1()
Application.MacroOptions Macro:=»СХЕМАГР», Description:=
«Возвращает финальные вероятности схемы гибели и » & _
«размножения по заданным загрузкам состояний, » & _
«начиная с состояния 0»
End Sub
Пример 1.1. В схеме гибели и размножения выполняются соотношения: λ0=1, λ1=2, λ2=3, μ1=0,5, μ2=1,5, μ3=2,5. Найти финальные вероятности.
Выделяется диапазон А1:D1, вызывается пользовательская функция СХЕМАГР и вводятся данные (рис. 1.1).
Рис. 1.1. Применение функции СХЕМАГР в примере 1.1
Команда Ctrl+Shift+Галочка (Ввод) возвращает в выделенном диапазоне значения финальных вероятностей (рис. 1.2).
Рис. 1.2. Финальные вероятности в примере 1.1
2. Пользовательская функция ЭРЛАНГ
Финальные вероятности n-канальной СМО с отказами находятся по формулам Эрланга [1, с. 351]. Характеристики эффективности системы:
Рпростой = р0, Ротк = рn, Q = 1 – рn, А= λ(1 – рn), k=ρ(1-pn),
k – среднее число занятых каналов. Код пользовательской функции ЭРЛАНГ, возвращающей финальные вероятности n-канальной СМО с отказами и значения параметров Q, А, k, приведен в листинге 2.1.
Листинг 2.1. Код функции ЭРЛАНГ и ее описания
Function ЭРЛАНГ(Инт_заяв, Инт_обсл, Каналов, _
P_F As String) As Variant
n = Каналов
ReDim L(0 To n)
ReDim p(0 To n)
Dim c(1 To 3)
p(0) = 1:L(0) = 1
For i = 1 To n
L(i) = L(i — 1) * Инт_заяв / Инт_обсл / i
p(0) = p(0) + L(i)
Next
p(0) = 1 / p(0)
For i = 1 To n
p(i) = L(i) * p(0)
Next
c(1) =1 — p(n):c(2) = Инт_заяв * c(1)
c(3) = Инт_заяв / Инт_обсл * c(1)
Select Case P_F
Case “P”
ЭРЛАНГ = p
Case “F”
ЭРЛАНГ = c
End Select
End Function
Sub InstallFunc2()
Application.MacroOptions Macro:=»ЭРЛАНГ», Description:=
«При Р возвращает финальные вероятности, при F – » & _
«значения Q, A и среднее число занятых каналов » & _
«СМО с отказами»
End Sub
Пример 2.1. В 2-канальной СМО с отказами λ=8, μ=6.
Найти: 1. Финальные вероятности; 2. Относительную пропускную способность; 3. Абсолютную пропускную способность; 4. Среднее число занятых каналов.
Выделяется диапазон А1:С1, вызывается пользовательская функция ЭРЛАНГ, вводятся числовые данные и “P” (рис. 2.1).
Рис. 2.1. 1-е применение функции ЭРГАНГ в примере 2.1
Команда Ctrl+Shift+Галочка (Ввод) возвращает в выделенном диапазоне значения финальных вероятностей (рис. 2.2).
Рис. 2.2. Финальные вероятности в примере 2.1
Выделяется диапазон А3:С3, вызывается пользовательская функция ЭРЛАНГ, вводятся числовые данные и “F” (рис. 2.3).
Рис. 2.3. 2-е применение функции ЭРГАНГ в примере 2.1
Команда Ctrl+Shift+Галочка (Ввод) возвращает в выделенном диапазоне значения пунктов 2-4 (рис. 2.4).
Рис. 2.4. Значения пунктов 2–4 примера 2.1
3. Пользовательская функция ОЧЕРЕДЬ
Код пользовательской функции ОЧЕРЕДЬ, возвращающей вероятность простоя n-канальной СМО с очередью, вероятность отказа, среднее число заявок в очереди, среднее число заявок в системе, среднее время ожидания заявки в очереди, среднее время пребывания заявки в системе, приведен в листинге 3.1.
Листинг 3.1. Код функции ОЧЕРЕДЬ и ее описания
Function ОЧЕРЕДЬ(Инт_заяв, Инт_обсл, _
Каналов, Условия_0_m) As Variant
Dim c(0 To 5) As Single
Dim w As Single, n As Integer, m As Integer, h As Integer
Dim x As Single, y As Single, S() As Single
w = Инт_заяв / Инт_обсл
n = Каналов:m = Условия_0_m:ReDim S(0 To n + 1)
h = Application.WorksheetFunction.Fact(n)
x = 1:S(0) = 1
For i = 1 To n + 1
If i < n + 1 Then
S(i) = S(i — 1) * w / i:x = x + S(i)
Else
S(i) = S(i — 1) * w / n / (1 — w / n)
y = x + S(i) * (1 — (w / n) ^ m):x = x + S(i)
End If
Next
x = 1 / x:y = 1 / y
If Условия_0_m = 0 Then
c(0) = x:c(1) = 0
c(2) = w ^ (n + 1) * x / h / n / (1 — w / n) ^ 2
c(3) = w ^ (n + 1) * x / h / n / (1 — w / n) ^ 2 + w
Else
c(0) = y
c(1) = w ^ (n + m) * y / h / n ^ m
c(2) = y * w ^ n * (w / n — (m + 1) * (w / n) ^ _
(m + 1) + m * (w / n) ^ (m + 2)) / h / (1 — w / n) ^ 2
c(3) = y * w ^ n * (w / n — (m + 1) * (w / n) ^ _
(m + 1) + m * (w / n) ^ (m + 2)) / h / + _
(1 — w / n) ^ 2 + w * (1 — c(1))
End If
c(4) = c(2) / Инт_заяв
c(5) = c(3) / Инт_заяв
ОЧЕРЕДЬ = c
End Function
Sub InstallFunc3()
Application.MacroOptions Macro:=»ОЧЕРЕДЬ», Description:=
«Возвращает вероятность простоя n-канальной СМО » & _
«с очередью, вероятность отказа, средние » & _
«значения заявок в очереди, заявок в системе, » & _
«время в очереди, время в системе»
End Sub
Параметр Условие_0_m принимает значение 0, если очередь неограниченная, иначе значение параметра равно числу мест в очереди.
Пример 3.1. В 1-канальной СМО с неограниченной очередью λ=2, μ=3. Найти: 1. Вероятность простоя; 2. Вероятность отказа; 3. Среднее число заявок в очереди; 4. Среднее число заявок в системе; 5. Среднее время ожидания заявки в очереди; 6. Среднее время пребывания заявки в системе.
Выделяется диапазон 1х6, например, диапазон А1:F1, вызывается функция ОЧЕРЕДЬ и вводятся данные (рис. 3.1).
Рис. 3.1. Применение функции ОЧЕРЕДЬ в примере 3.1
Команда Ctrl+Shift+Галочка (Ввод) возвращает в выделенном диапазоне значения требуемых параметров (рис. 3.2).
Рис. 3.2. Полученные результаты в примере 3.1
Пример 3.2. Решить задачу примера 3.1, если число каналов обслуживания равно 2, а число мест в очереди равно 3.
Выделяется диапазон А1:F1, вызывается функция ОЧЕРЕДЬ и вводятся данные (рис. 3.3).
Рис. 3.3. Применение функции ОЧЕРЕДЬ в примере 3.2
Возвращаемые результаты показаны на рисунке 3.4.
Рис. 3.4. Полученные результаты в примере 3.2

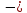 интенсивность
интенсивность
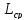 –
–

 –
– –
–
 среднее
среднее


 коэффициент
коэффициент –
– интенсивность
интенсивность

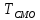 –
– –
–