Моделирование случайных процессов в excel - Word и Excel

ПРАКТИЧЕСКАЯ
РАБОТА №11

Моделирование
случайных процессов в Microsoft Excel

Упражнение 1. ВЕРОЯТНОСТНАЯ МОДЕЛЬ

Цель: Создание
вероятностной модели в электронных таблицах, знакомство с функцией для
генерации случайного числа.

Задание 1. Студенту для
поездки подходит 2 маршрута автобуса. У одного автобуса интервал 10 мин, у
другого — 15 мин. Определить среднее время ожидания и построить в одной системе
координат:

1) график времени ожидания за каждый день года,

2) график среднего времени ожидания для каждого дня
года.

Обоснование задачи. Так как
на остановку студент приходит по-разному, то время ожидания до прибытия
каждого из автобусов будет каждый раз меняться и будет являться случайной
величиной.

СЛУЧАЙНАЯ ВЕЛИЧИНА, СЛУЧАЙНАЯ ПЕРЕМЕННАЯ [random
value, random variable] — всякая наблюдаемая величина, изменяющаяся при
повторении условий, в которых она возникает.

ВЕРОЯТНОСТНАЯ МОДЕЛЬ – это модель, которая содержит
случайные элементы. Таким образом, при задании на входе модели некоторой совокупности
значений, на ее выходе могут получаться различающиеся между собой результаты в
зависимости от действия случайного фактора. Вероятностные модели базируются на
использовании больших серий испытаний со случайными параметрами, причем
точность полученных результатов зависит от количества проведенных опытов.

Для генерации случайной величины в Microsoft Excel
требуется в ячейку ввести формулу =СЛЧИС(). Эта функция возвращает
случайное число из диапазона [0;1).

Чтобы получить случайное вещественное число из
диапазона [0;а), можно использовать следующую формулу: =СЛЧИС()*a.

Если требуется получить случайное вещественное число
между a и b, можно использовать следующую формулу: =СЛЧИС()*(b-a)+a.

Порядок
выполнения.

1. Постройте
в Microsoft Excel таблицу
вида

2. Внесите в
таблицу исходные данные

a –
интервал ожидания 1 автобуса, а=10 минутам;

b –
интервал ожидания 2 автобуса, b=15 минутам;

d – количество
дней в исследуемом периоде (в году) d=365.

3. Заполните
расчетную таблицу формулами в соответствии с математической моделью, используя
абсолютную и относительную адресацию в формулах.

w₁ – время
ожидания 1 автобуса (случайное число на отрезке [0;а]);

w₂ – время
ожидания 2 автобуса ( случайное число на отрезке [0;b]);

x – время
ожидания за текущий день,

x = min (w₁, w₂)

t’_ср– среднее
время ожидания на текущий день, за n – кол-во дней, для которых
среднее подсчитано;

t_ср – среднее
время ожидания за год

t_ср= (x₁+x₂+…+x_n) / d

4.
Вычислите
время все параметры на исследуемый период (Скопируйте, если это нужно, формулы
вниз на все дни года, используя маркер заполнения)

5.
Построить
на одной диаграмме два графика по заданию (для x и t’ср)
на отдельном листе.

Задание 2. Используя
модель, построенную для решения задачи, определить

·
среднее
время ожидания, если ожидание 1 автобуса 10 мин, 2 автобуса — 60 мин

·
каково
среднее время ожидания, если интервалы автобусов совпадают?

Упражнение
2. БРОСАНИЕ МОНЕТЫ

Цель: моделируя
возможные игровые ситуации (варьируя ставки в данной игре) выяснить, какая
тактика чаще приводит к результату (положительному или отрицательному)

Задание 3. У вас есть 10
монет. Вы хотите увеличить свой капитал в два раза, испытав заодно и свою
судьбу. Суть игры проста, играя с маклером, вы делаете ставку и бросаете
монету. Если выпадет «орел», маклер выдает вам сумму вашей ставка, в противном
случае – вы ему отдаете сумму. Ставка может быть любой от 1 до 10 монет. Вы
можете назначить самую большую ставку в 10 монет, и тогда за один бросок
выяснится, «сорвали» ли вы банк или, наоборот, обанкротились. Опытные игроки
действуют более осторожно, начиная с маленькой ставки.

Удвоение начального капитала или банкротство приводит
к незамедлительному прекращению этого сеанса игры и расчету. Игра может
продолжиться по вашему усмотрению.

Имитировать результат падения монеты можно с помощью
функции СЛЧИС(). Поскольку вероятность выпадения той или иной стороны 50%,то,
если СЛЧИС()<0,5, то результат «орел» (1), в противном случает – «решка»
(0).

Формула
падения монеты при броске имеет следующий вид:

Бросок
= ЕСЛИ (СЛЧИС()<0,5; 1; 0)

Здесь
«1» на выходе функции означает, что игрок угадал, то есть выпал «орел», а «0» —
не угадал, то есть выпала «решка».

Формула
изменения наличности игрока:

Наличность=
ЕСЛИ(Бросок=1; Наличность+Ставка; Наличность-Ставка)

Формула
определения выигрыша:

Выигрыш=ЕСЛИ(Наличность<2*Начальный
капитал; «-»; «банк»)

Здесь
выдается сообщение «банк» при увеличении наличности вдвое или больше, что
является условием прекращением игры.

Функция
определения проигрыша:

Проигрыш=ЕСЛИ(Наличность>0;
«-»; «банкрот»)

Здесь
выдается сообщение «банкрот» по окончании наличности, что так же является
условием прекращения игры.

Порядок
выполнения работы

1. Создайте в
Microsoft Excel таблицу
вида:

2. Ввести
расчетные данные

3. Провести
следующие исследования

·
Исследовать
выпадения «орла» и «решки» в течение сеанса игры

·
Собрать
статистические данные о выигрыше и проигрыше в течение 10-20 сеансов игры с различными
значениями ставок и исследовать их.

4. Ответьте
на вопросы

·
Кто
чаще выигрывает: казино или игрок?

·
Сколько
в среднем надо сделать бросков до окончания игры?

Упражнение
3. ИГРА В КОСТИ

Цель: Создание игровой
модели, основанной на случайных событиях

Задание 4. Два игрока
бросают по две игральные кости. Сумма очков, выпавших на двух игровых костях,
накапливается. Игра прекращается, когда один из игроков достигает суммы 101.
Игра повторяется до трех побед.

Математическая модель складывается из следующих
рассуждений.

На игровой кости имеется 6 граней с количеством точек
от 1 до 6.

Модель, имитирующая бросание двух костей одним
игроком:

К1=ЦЕЛОЕ (1+6*СЛЧИС())

К2=ЦЕЛОЕ (1+6*СЛЧИС())

Случайные значения суммируются. Суммы бросков по
каждому игроку накапливаются в отдельных столбцах СУММА ПЕРВОГО и СУММА ВТОРОГО
и анализируются после каждого броска в столбце РЕЗУЛЬТАТ

ЕСЛИ (ИЛИ («Сумма первого»>101; «Сумма второго»>101);
«конец игры»; «-»)

Здесь, когда обе суммы меньше 101, в столбце
записывается «-»,а при превышении хотя бы одним игроком порога в столбце
записывается «конец игры». Кто победил, можно определить по соседним столбцам.

Игра прекращается при проявлении сообщения «конец
игры» в столбце РЕЗУЛЬТАТ

Создайте таблицу вида

Заполнить самостоятельно по предложенному материалу,
используя абсолютные и относительные ссылки.

Вопросы:

·
Как
части в нашей жизни происходят случайные процессы?

·
Все
ли случайные процессы можно смоделировать на компьютере?

·
Помогают
ли построенные модели для выбора в жизни?

Литература:

1. Дегтярева
И. Ю. Моделирование процессов. Вероятностные модели [текст] URL: http://www.metod-kopilka.ru/page-2-2-6-11.html

2. Информатика
и ИКТ. Задачник по моделированию. Базовый уровень /Под ред.
Н.В. Макаровой. – Питер. 2007. – 192 с.

Источник

Аннотация:

Тип урока: Комбинированный — урок формирования и закрепления умений и навыков практического использования MS Excel.

Цель урока: научиться моделировать случайные процессы в электронных таблицах

Оборудование урока:

приложение MS Windows – ЭТ MS Excel;
карточки – задания для практической работы.

Автор: Попова Маргарита Юрьевна
Место работы: МБОУ гимназия №1 г.Липецка
Добавил: Маргарита86

Уважаемые коллеги! Автор ждёт Ваши отзывы! Оставьте своё мнение о разработке!

Всего комментариев: 1

Порядок вывода комментариев:

Источник

Моделирование случайных чисел в Excel может быть выполнено двумя способами: с помощью встроенных функций и путем использовании инструмента «Генератор случайных чисел» дополнения «Анализ данных». Ниже будут рассмотрены способы моделирования случайных чисел и событий с использованием встроенных функций.

Моделирование простого события

Рассмотрим механизм моделирования простого события. Пусть имеется

событие	A, вероятность наступления которого равна PA .	Выберем с помощью
датчика	случайных чисел, равномерно распределенных	в интервале (0,1)

некоторое число z .	Известно,	что вероятность попадания в интервал (0, PA )
случайной величины	z равна величине PA . Поэтому если при розыгрыше число
z попало в этот интервал, то	следует считать, что событие	A	произошло.
Противоположное событие (не	A) произойдет с вероятностью	(1	– PA ) в том

случае, если z PA .

Процедура моделирования простого события в имитационной модели описывается алгоритмом, схема которого показана на рис. 1 [23]. Оператор 1 обращается к датчику случайных чисел, генерирующему случайную величину z .

Оператор 2 проверяет условие z PA . Если оно выполняется, считается, что произошло событие A. В противном случае считается, что произошло противопо-

ложное событие (не A).

ДСЧ(z)

Рис.1 – Моделирование простого события

В Excel данную операцию можно реализовать с помощью функции ЕСЛИ.

Пусть в ячейке А1 указана вероятность PA события, тогда моделирование его наступления будет выглядеть следующим образом

ЕСЛИ(СЛЧИС()<A1;”Событие А”;”Событие не А”).

Моделирование полной группы несовместных событий

Пусть имеется полная группа несовместных событий

вероятностями	P , P	,	…, Pk . При этом выполняется условие
1	2

Процедура моделирования

описывается алгоритмом, схема

кумулятивная вероятность

1.
группы	несовместных событий
показана	на рис. 2. Здесь	Li	—
… Pi .

ДСЧ(z)

Да

Нет

Z L2

Да

Нет

Да

Нет

Рис. 2 – Алгоритм моделирования полной группы несовместных событий

Оператор 1 обращается к датчику случайных чисел с равномерным распределением в интервале (0,1). Условный оператор 1 проверяет условие

попадания случайной величины z в интервал (0, L1 ). Если это условие

выполняется, то считается, что произошло событие A1 . Если условие в операторе

2 не выполняется, то алгоритм осуществляет проверку условий попадания

случайной величины в другие интервалы. Одно из событий A1, A2	,…, Ak	обя-
зательно произойдет.
Рассмотрим выполнение данных операций в Excel. Запишем в ячейки С2:С4
значения вероятностей	P , P	, P	событий	A , A	, A	(рис.3). В	ячейке	С5
	1	2	3		1	2	3

смоделируем случайную величину, распределенную равномерно на интервале (0,1). Тогда определение произошедшего события будет выглядеть следующим образом

С6=ЕСЛИ(C5<C2;»A1″;ЕСЛИ(C5<(C2+C3);»A2″;»A3″)).

Рис. 3 – Моделирование полной группы несовместных событий

Моделирование дискретной случайной величины

Дискретная случайная величина может быть задана табличной зависимостью:

…

Здесь p j – вероятность того, что дискретная случайная величина

X примет

значение x j . При этом p1 p2 … pn 1

. Разделим интервал (0,1) на

отрезков,

длины которых равны

заданным

вероятностям.

Если

случайное

число

z ,

вырабатываемое датчиком случайных чисел, равномерно распределенных в

интервале (0,1), попадет в интервал

pk , то случайная величина

примет

значение xk . Таким образом, при моделировании дискретных случайных величин фактически используется та же процедура, что и при моделировании полной группы несовместных событий.

Моделирование непрерывной случайной величины

Приведем способы моделирования непрерывных случайных чисел (на рис. 4 показаны формы распределения вероятностей) [23-24].

1. Показательное распределение

где

x	1	ln(z) ,

— случайная величина, распределенная по показательному закону;

— интенсивность потока (среднее значение	1	);

z— случайная величина, равномерно распределенная на интервале (0,1).

ВExcel данное вычисление выглядит следующим образом (пусть в ячейке А1 дано среднее значение, а в А2 — результат)

А2=-А1*LN(СЛЧИС()).

2.Равномерное распределение на интервале ( a,b )

xa z(b a) ,

xxcp x(z 0,5) ,

где x — случайная величина, распределенная по равномерному закону;

a и xср x

b — нижняя и верхняя границы интервала ( — среднее значение интервала ( a,b );

— величина интервала ( a,b );

a,b

) соответственно;

z— случайная величина, равномерно распределенная на интервале (0,1).

ВExcel это реализуется посредством формулы (пусть в ячейке А1 дана нижняя граница; в ячейке А2 – верхняя граница, а в А3 — результат)

А3=А1+СЛЧИС()*(А2-А1)

3. Нормальное распределение

Процедура розыгрыша нормально распределенной случайной величины

заключается в следующем.
Сложим 12 случайных величин	zi	с равномерным распределением в
интервале (0,1), т. е. составим сумму

v zi . i 1

Нормируем и центрируем случайную величину v , т. е. перейдем к величине

v 6.

От нормированной и центрированной величины		перейдем к случайной
величине	y ,	распределенной по нормальному	закону, с заданными
параметрами	M ( y) и ( y) по формуле
		y M ( y) ( y) ,

где M ( y) – известное математическое ожидание случайной величины y ;

( y) – известное среднее квадратическое отклонение случайной величины

Для реализации данного генератора в Excel нужно выполнить следующий расчет (в ячейке А1 дано среднее значение, А2 – среднее квадратическое отклонение, а в А3 — результат)

А3=А1+А2*((СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИ С()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС())-6)).

Рис. 4 – Графики законов распределения

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

При выполнении работы должны соблюдаться правила ТБ при работе за ПК и правила

поведения в компьютерном классе.

II. Постановка темы и целей урока. (2 мин) Слайд 1,2

III. Объяснение нового материала. (16 мин)

Предлагается учащимся решить следующую задачу «Бросание монеты» Слайд 3

I этап. Постановка задачи. Слайд 4

Бросание монеты

Решение задач на компьютере обычно разделяют на несколько этапов.

А. Описание задачи:

У вас есть 10 монет. Вы хотите увеличить свой капитал в два раза, испытав заодно и свою

судьбу. Суть игра проста. Играя с маклером, вы делаете ставку и бросаете монету. Если

выпадает «орел», маклер выдает вам сумму вашей ставки, в противном случае – вы ему

отдаете эту сумму. Ставка может быть любой: от 1 до 10. Вы можете назначить самую

большую ставку в 10 монет, и тогда за один бросок выясниться, «сорвали» ли вы банк

или, наоборот, обанкротились. Опытные игроки действуют более осторожно, начиная с

маленькой ставки.

B. Цель моделирования: Слайд 5

Выяснить, какая тактика чаще приводит к результату (положительному или

отрицательному).

C. Формализация задачи: Слайд 6

Каков характер процесса? Случайный

Чем характеризуется игрок? Начальным капиталом К

нач,

Ставкой СТ, Текущей

наличностью К

тек

Чем характеризуется монета? Положение (орел/решка)

II этап. Разработка модели. Слайд 8

A. Информационная модель: (Составление модели по условию задачи). Слайд 9

Источник

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Презентацию на тему «Моделирование случайных процессов в Excel»
можно скачать абсолютно бесплатно на нашем сайте. Предмет
проекта: Информатика. Красочные слайды и иллюстрации помогут вам
заинтересовать своих одноклассников или аудиторию.
Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад — нажмите на
соответствующий текст под плеером. Презентация
содержит 14 слайд(ов).

Слайды презентации

Слайд 1

Моделирование случайных процессов в среде табличного процессора

Муниципальное общеобразовательное учреждение гимназия №1 Учитель информатики: Попова М.Ю. Липецк 2013 9 класс

Слайд 2

Цель урока:

научиться моделировать случайные процессы в электронных таблицах

Слайд 3

Задача «Бросание монеты»

Слайд 4

I этап. Постановка задачи

Описание задачи: У вас есть 10 монет. Вы хотите увеличить свой капитал в два раза, испытав заодно и свою судьбу. Суть игра проста. Играя с маклером, вы делаете ставку и бросаете монету. Если выпадает «орел», маклер выдает вам сумму вашей ставки, в противном случае – вы ему отдаете эту сумму. Ставка может быть любой: от 1 до 10. Вы можете назначить самую большую ставку в 10 монет, и тогда за один бросок выясниться, «сорвали» ли вы банк или, наоборот, обанкротились. Опытные игроки действуют более осторожно, начиная с маленькой ставки.

Слайд 5

Цель моделирования: Выяснить, какая тактика чаще приводит к результату (положительному или отрицательному).

Слайд 6

Формализация задачи: Каков характер процесса? Чем характеризуется игрок?

Случайный

Начальным капиталом Кнач Ставкой СТ Текущей наличностью Ктек

Слайд 7

Формализация задачи: Чем характеризуется монета?

Положение (орел/решка)

Слайд 8

II этап. Разработка модели

Слайд 9

Информационная модель

Слайд 10

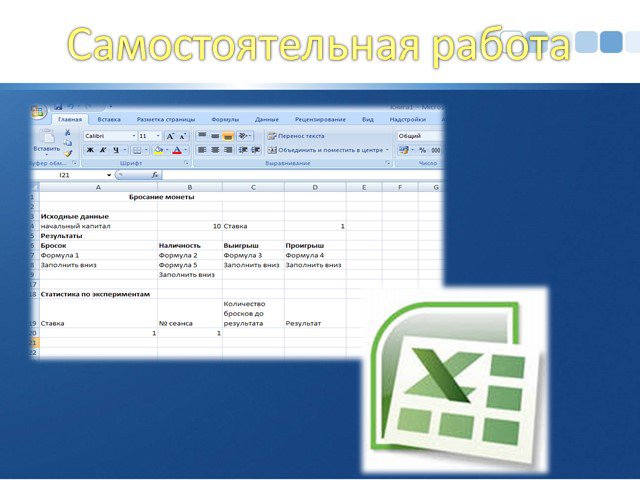
Самостоятельная работа

Слайд 11

Подведение итогов

Для чего нужна моделировать случайные процессы? Мои достижения на уроке: я научился… я понял, как… оформил результаты, используя… другой вариант

Слайд 12

Домашняя работа

Лотерея «Спортлото» Смоделируйте серию игр «5 из 36», организовав эксперименты и с одной, и с другой тактикой.

Слайд 13

Список использованных источников

Рисунок Excel: http://images.yandex.ru/yandsearch?text=excel&img_url=http%3A%2F%2Fcdn3.diggstatic.com%2Fstory%2F5_ways_to_fix_corrupted_excel_files%2Ft.png&pos=0&rpt=simage Рисунок бросание монеты: http://images.yandex.ru/yandsearch?text=%D0%B1%D1%80%D0%BE%D1%81%D0%B0%D0%BD%D0%B8%D0%B5%20%D0%BC%D0%BE%D0%BD%D0%B5%D1%82%D1%8B&img_url=http%3A%2F%2Fimg0.liveinternet.ru%2Fimages%2Fattach%2Fc%2F2%2F70%2F8%2F70008220_1296464644_image022.jpg&pos=1&uinfo=sw-1423-sh-787-fw-1198-fh-581-pd-1&rpt=simage

Слайд 14

Список похожих презентаций

Моделирование физических процессов

Задача. Построить математическую модель физического процесса — движения тела, брошенного под углом к горизонту. Выяснить зависимость расстояния и …

Построение диаграмм в Excel

Диаграммы являются средством наглядного представления данных и облегчают выполнение сравнений, выявление закономерностей и тенденций данных. Диаграммы …

Электронные таблицы Microsoft Excel

Понятие функции. Одним из компонентов формулы в MS Excel может являться функция. Функция — это подпрограмма, работающая по своему алгоритму. Для удобства …

Функции и формулы в MS EXCEL

Цель урока: -дать понятие функций и формулв Excel научить применять функции делать вычисления с помощью функций и формул. Понятие Функции В Excel. …

Создание баз данных в Excel

База данных. набор специфической информации. телефонная книга классный журнал поваренная книга. Структура базы данных. Поле – столбец, содержит данные …

Генератор случайных чисел

Бывают ситуации, когда требуется, чтобы результат работы программы был случайным в определенных пределах. Для реализации такой возможности во многих …

Встроенные функции в Microsoft Excel

Цель урока:. Изучение новых встроенных функций закрепление умения работать с табличным процессором MS Excel. С помощью, какой команды можно вставить …

Встроенные функции Excel

Для вычислений в таблице с помощью встроенных функций Excel 2007 рекомендуется использовать мастер функций. Диалоговое окно мастера функций доступно …

Возможности Microsoft Excel

Боброва Т.А., учитель информатики МОУ «БСОШ №2». Возможности MS Excel. Основные назначения табличного редактора Excel – это обработка числовых данных. …

Программа: Microsoft Excel

ПЛАН :. История Microsoft Excel Главная часть 1) Основное понятие о программе 2) Принцип работы 3) Основные функции IV. Заключение V. Использованные …

Ссылки и диаграммы в Excel

14. Ввод математических формул и вычисления по ним. (тип задания: с кратким ответом). Проверяемые элементы содержания: умение использовать формулы …

Конспекты

Моделирование социальных процессов

Класс: 9 Предмет: Информатика № урока __29__ Дата_________. . Тема урока:. Моделирование социальных процессов. Тип урока:. закрепление и развитие …

Связанные таблицы в MS Excel 2007

Государственное общеобразовательное учреждение ЦО №2. Московского района Санкт-Петербурга. Конспект урока по информатике в 11 классе. «Связанные …

Время и дата в VBA Excel

Время и дата в VBA Excel. Тема:. Время и дата в VBA ExcelЦели:. Образовательные:.

Cформировать представление о работе с датой. .

Cформировать …

Работа с MS Excel

Павлодарский педагогический колледж им. Б.Ахметова. Утверждаю. . . Заместитель директора по УР. _________. Е.А. Побережникова. «___» __________ …

Советы как сделать хороший доклад презентации или проекта

Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих
вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно
просто читать информацию со слайдов, ее аудитория может прочитать и сама.
Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста
позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая
информация, остальное лучше рассказать слушателям устно.
Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет
сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для
этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации,
а также правильно подобрать сочетание фона и текста.
Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете
первым, как закончите презентацию. Все приходит с опытом.
Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его
выступления.
Старайтесь говорить уверенно, плавно и связно.
Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете
меньше волноваться.

Источник