Моделирование решения математических задач в excel - Word и Excel

Цели урока:

Обучающие: Повторить и закрепить навыки
работы в MS Excel; научить применять современное
программное обеспечение в решении
математических задач, строить математические
модели в среде MS Excel.

Развивающие: Развивать: практические и
исследовательские навыки по составлению моделей
в электронных таблицах, научное мировоззрение
через связь информационных технологий с другими
школьными предметами, логическое и
алгоритмическое мышление, аналитические
способности, внимание, память.

Воспитательные: Воспитание общей и
информационной культуры, творческого подхода к
работе, желания экспериментировать,
самостоятельности в учебном труде.

Тип урока: Комплексного применения
знаний, обобщения и систематизации.

Программное и техническое обеспечение
урока:

компьютеры с ОС MS Windows XP;

пакет Microsoft Office;

мультимедийный проектор

Время проведения урока: один из
последних уроков в разделе «Информационное
моделирование».

План урока: (40 минут)

Орг. момент. (1 мин)
Проверка и актуализация знаний. / Тестирование
по теме (4 мин)./ Разминка (5 мин)
Теоретическая часть. (10 мин)
Практическая часть. (10 мин)
Самостоятельная работа. (8 мин)
Подведение итогов. Д/з (2 мин)

Ход урока:

1. Организационный момент.

Приветствие, проверка присутствующих.

С помощью проектора демонстрируется
на экране первый слайд презентации. Приложение 1

Сообщается тема урока: «Математическое
моделирование в среде электронных таблиц MS Excel
«.Озвучить цели и план урока.

2. Актуализация опорных знаний.

Пройденная нами тема «Электронные
таблицы»– одна из наиболее практически
значимых, востребованных, после текстового
редактора Word и его возможностей. Но электронные
таблицы не только позволяют автоматизировать
расчеты, но и являются эффективным средством
моделирования различных вариантов и ситуаций.
Меняя значения исходных данных, можно проследить
за изменением получаемых результатов и из
множества вариантов решения задачи выбрать
наиболее подходящий.

Перечислите, что вы научились делать,
изучая табличный процессор MS Excel?

– выполнять вычислительные операции
при помощи формул;

– составлять таблицы;

– строить графики и диаграммы.

Тестирование по теме «Электронные
таблицы».

Домашним заданием было повторить весь
изученный материал по теме «Электронные
таблицы». Чтобы проверить домашнее задание, я
предлагаю Вам ответить на вопросы электронного
теста. (Дети уже знакомы с работой системы
дистанционного обучения MyTestServer 1.1) Приложение 2

Перед началом работы учащиеся
прослушивают инструкцию по выполнению теста.

Тест состоит из 5 вопросов. Дается
только одна попытка, будьте внимательны, не
торопитесь. Время на тест 3 минуты.

После завершения тестирования каждому
ученику системой выставляется оценка, которую он
видит на экране своего монитора.

Сегодня на уроке мы будем использовать
электронные таблицы с их мощным вычислительным
потенциалом для решения математических задач –
построим математическую модель в среде MS Excel и
проведем небольшое исследование.

А для этого вспомним основные понятия
по теме “моделирование” (проводим устную разминку).

Вопросы разминки: Приложение 1

Моделирование – метод познания
окружающего мира, состоящий..

Модель – это объект, который
используется в качестве..

Различают ____________и ___________модели.

Натурные модели – это…

Информационные модели – это…

Основными видами информационных
моделей являются:_________ ,_________, __________.

А как вы думаете, математическая
модель к какому виду принадлежит?

Математическая модель – это модель,
построенная с использованием…

Приведите пример знаковой
информационной модели, рассматриваемой на
уроках математики.

Основным языком информационного
моделирования в науке является язык математики.

3. Теоретическая часть.

Какую бы жизненную задачу ни взялся
решать человек, первым делом он строит модель
заданного объекта. Очень часто задачи связаны с
потребностями человека.

Сегодня нам предстоит решить
следующую задачу:

Задача 1: Приложение
1

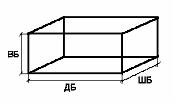
У маленького Васи есть небольшой
бассейн во дворе. Иногда Вася ходит к речке и
приносит воду в бассейн в небольшой цистерне
цилиндрической формы. Известны ширина ШБ, высота
ВБ, ДБ бассейна и объем цистерны Об Ц. Сколько раз
Васе нужно сходить к речке за водой, чтобы
наполнить бассейн наполовину?

Этот текст можно рассматривать как
словесную модель бассейна.

Постановка задачи: выяснение
условий

Какую форму может иметь бассейн?
(ответы детей).

А какой формы он в нашей задаче?– В
форме куба или параллелепипеда, потому, что даны
его параметры: ширина, высота, длина. А что еще нам
известно?

– объем цистерны.

Давайте попробуем решить задачу:
узнаем сколько раз (N) Васе нужно сходить к речке
за водой, чтобы наполнить бассейн наполовину.

Что для этого нужно знать?

– сколько цистерн воды помещается в
бассейн.

А как это узнать?

– определить объем бассейна (Об Б)

– сравнить половину объема бассейна и
объем цистерны (Об Б / Об Ц / 2).

4. Практическая часть.

Карточка – задание №1 Приложение 3

Задание для практической работы: Скопировать
в свою папку файл – шаблон Excel Приложение 4

Назвать лист номером задачи «Задача
1» (редактирование названия – двойной щелчок
мыши на «Лист 1»).

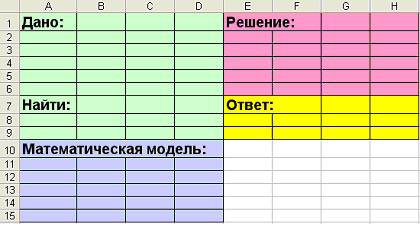
Оформить на листе решения разделы «Дано«,
«Найти«, «Математическая модель«,
«Решение«, «Ответ» (по образцу):

В ячейках А1и А7 напечатать
слова «Дано» и «Найти«.

Объединить ячейки А10, В10 и С10,
ввести текст: «Математическая модель«

Объединить ячейки Е1 и F1,
напечатать слово «Решение«.

В ячейку Е7 – «Ответ«.

Заполнить таблицу начальными
данными.

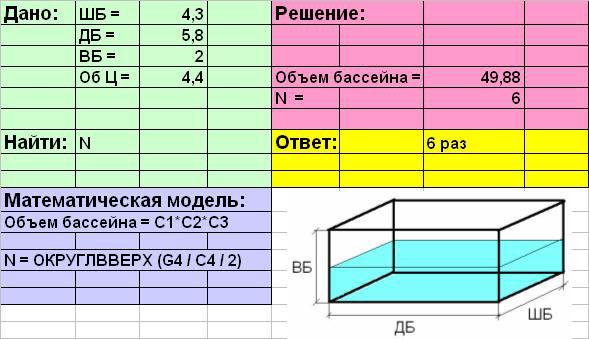
В ячейки В1:В4 ввести текст: ШБ=;
ДБ=; ВБ=; Об Ц=.

В ячейки С1:С4; ввести
соответствующие значения параметров: 4,3; 5,8; 2; 4,5.

Для наглядности, если есть
возможность, можно построить графическую модель
(рисунок задаче) в Painte и скопировать ее в
электронную таблицу или нарисовать бассейн
непосредственно в Excel.

Далее заполнить раздел таблицы
«Математическая модель».

Объединить ячейки А11, В11 и С11,
ввести формулы (тип данных – текст) в раздел
(пробел перед знаком «=»). «Объем бассейна
=С1*С2*С3«

Объединить ячейки А13, В13 и С13
и ввести текст «N = ОКРУГЛВВЕРХ(G4 / C4 / 2)«.
(для получения целого числа используем функцию
округления ОКРУГЛВВЕРХ)

В разделе «Решение»
создать сетку вычислений:

– Обозначить искомые и промежуточные
величины.

– Объединить ячейки Е4 и F4,
ввести текст: «Объем бассейна =«. В ячейку
Е5 – «N =«(тип данных – текст).

В ячейки G4 и G5; ввести
соответствующие формулы (тип данных – формулы):
=С1*С2*С3;

Используем функцию округления
дробного числа до целого:

Вставка-функция – математические –
ОКРУГЛВВЕРХ – число разрядов выбираем «0«.

=ОКРУГЛВВЕРХ(G4 / C4 / 2)

В разделе «Ответ» запишем
искомый результат в ячейку G7 (тип данных –
текст).

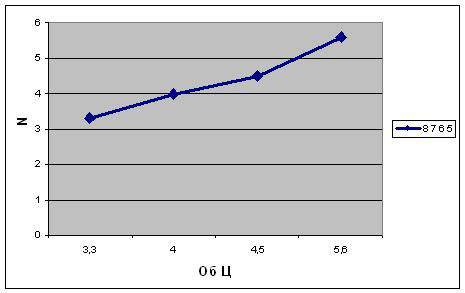
Проведем небольшое исследование:

Вопрос: Сколько раз Васе нужно будет
сходить к речке за водой, если он возьмет
цистерну емкостью 5,6 литров; 4 литра; 3,3
литра?

Меняем в ячейке С4 значение на 5,6
и электронные таблицы автоматически производят
пересчет.

Создадим таблицу значений Об Ц и
будем заносить в нее результаты вычислений N.

Введем в ячейку А20 и В2 текст
«Об Ц» и » N«. Заполним таблицу
данными.

Об Ц	N
3,3	8
4	7
4,5	6
5,6	5

Для графического представления
результатов выделить диапазон А21: В24,
построить график функции, отредактировать его.

Анализ полученных результатов.

5. Самостоятельная работа.

Задание для самостоятельной разработки:

Карточка – задание №2 Приложение
3

Задача 2. Пешеход начал движение из
начала координат со скоростью V=0,6 м/с.
Найдите, какой путь S прошел пешеход за одну
минуту t после начала движения, если он
двигался равномерно.

Постановка задачи: выяснение
условий

Скажите, что мы будем моделировать? –

– движение

Какие виды движения вы знаете? (ответы
детей)

Какое движение рассматривается в
нашей задаче?

– равномерное. Приложение 1

Давайте вспомним формулу расчета
скорости: V=s/t– отсюда s=V*t

Технология моделирования:

Назвать лист номером задачи «Задача 2»
(редактирование названия – двойной щелчок мыши
на «Лист 2»).
Выделить расчетную таблицу на листе «Задача1»
и скопировать ее на лист «Задача 2«.
Заполнить таблицу новыми начальными данными.
Ввести формулу (тип данных – текст) в раздел
«Математическая модель» (пробел перед
знаком «=»).
Ввести фоpмулу (тип данных – формулы) в
раздел «Решение«.
В разделе «Ответ» записать искомый
результат (тип данных – текст).

Создать таблицу значений t и занести в нее
результаты вычислений S. Заполнить таблицу
данными.
Для графического представления результатов
выделить область аргументов и функций, построить
график зависимости пути S от времени при t=40;60;90,
отредактировать график.

6. Итог урока.

Сегодня на уроке мы узнали, как можно
использовать электронные таблицы в решении
математических задач, научились строить
математические модели в. среде MS Excel

Домашним заданием будет: самим
придумать задачу, разработать ее математическую
модель.

У кого есть вопросы по пройденному материалу?

Спасибо за работу. Вы сегодня молодцы. Можете
быть свободны.

Источник

Решение математической задачи
с использованием компьютерного моделирования.

Этап
1. Постановка задачи.

Под задачей понимается некая проблема, которую надо решить. На
этапе постановки задачи необходимо:

1. описать
задачу,

2. определить
цели моделирования,

3. проанализировать
объект или процесс.

Описание задачи. Задача формулируется
на обычном языке, и описание должно быть понятным. Главное здесь — определить
объект моделирования и понять, что должен представлять собой результат.

Даны координаты двух противоположных вершин прямоугольника:
A(x1, y1), C(x2, y2). Стороны прямоугольника параллельны осям координат. Определить
в какой четверти координатной плоскости находится прямоугольник. Предложите
свои координаты, чтобы прямоугольник находился во 2 и 3 четвертях координатной
плоскости. Найдите периметр и площадь прямоугольника.

Цели
моделирования.

1. Познание
окружающего мира.

Зачем
человек создает модели? Чтобы ответить на этот вопрос, надо заглянуть в далекое
прошлое. Несколько миллионов лет назад, на заре человечества, первобытные люди
изучали окружающую природу, чтобы научиться противостоять природным стихиям,
пользоваться природными благами, просто выживать. Накопленные знания
передавались из поколения в поколение устно, позже письменно, наконец с помощью
предметных моделей. Так родилась, к примеру, модель земного шара — глобус, —
позволяющая получить наглядное представление о форме нашей планеты, ее вращении
вокруг собственной оси и расположении материков. Такие модели позволяют понять,
как устроен конкретный объект, узнать его основные свойства, установить законы
его развития и взаимодействия с окружающим миром моделей.

Создание объектов с заданными свойствами (задача
типа «Как сделать, чтобы…»).

Накопив
достаточно знаний, человек задал себе вопрос: «Нельзя ли создать объект с
заданными свойствами и возможностями, чтобы противодействовать стихиям или
ставить себе на службу природные явления?» Человек стал строить модели еще не
существующих объектов. Так родились идеи создания ветряных мельниц, различных
механизмов, даже обыкновенного зонтика. Многие из этих моделей стали в
настоящее время реальностью. Это объекты, созданные руками человека.

Определение последствий воздействия на объект и
принятие правильного решения (задача типа «Что будет,
если…»: что будет, если увеличить плату за проезд в транспорте, или что
произойдет, если закопать ядерные отходы в такой-то местности?)

Например,
для спасения Петербурга от постоянных наводнений, приносящих огромный ущерб,
решено было возвести дамбу. При ее проектировании было построено множество
моделей, в том числе и натурных, именно для того, чтобы предсказать последствия
вмешательства в природу.

Эффективность управления объектом (или
процессом).

Поскольку
критерии управления бывают весьма противоречивыми, то эффективным оно окажется
только при условии, если будут «и волки сыты, и овцы целы». Например, нужно
наладить питание в школьной столовой. С одной стороны, оно должно отвечать
возрастным требованиям (калорийное, содержащее витамины и минеральные соли), с
другой — нравиться большинству ребят и к тому же быть «по карману» родителям, а
с третьей — технология приготовления должна соответствовать возможностям
школьных столовых. Как совместить несовместимое? Построение модели поможет
найти приемлемое решение.

Определить координаты вершин B и D. Вычислить площадь и периметр
прямоугольника.

Выявить взаимосвязь между координатами вершин и расположением
прямоугольника на координатной плоскости.

Анализ
объекта.

На
этом этапе четко выделяют моделируемый объект, его основные свойства, его
элементы и связи между ними. Простой пример подчиненных связей объектов —
разбор предложения. Сначала выделяются главные члены (подлежащее, сказуемое),
затем второстепенные члены, относящиеся к главным, затем слова, относящиеся к
второстепенным, и т. д.

Что моделируется?

Система, состоящая из двух простых объектов: прямоугольника и
системы координат.

Что известно о прямоугольнике?

Прямоугольник задан двумя про-тивоположными вершинами А и С.
Координаты точки А – x₁, y₁; коорди-наты точки C – x₂, y₂

Чем характеризуется система координат?

Система координат — это две взаимно перпендикулярные
координатные прямые, пересекающиеся в точке, которая является началом отсчёта
для каждой из них.

Оси координат делят плоскость на 4 угла, которые называют координатными
четвертями. Четверть, образованная положительными полуосями (правый верхний
угол), считают первой

Этап
2. Разработка модели.

Информационная модель.

На этом этапе выясняются свойства,
состояния, действия и другие характеристики элементарных объектов в любой
форме: устно, в виде схем, таблиц. Формируется представление об элементарных
объектах, составляющих исходный объект, т. е. информационная модель. Модели
должны отражать наиболее существенные признаки, свойства, состояния и отношения
объектов предметного мира. Именно они дают полную информацию об объекте.

Например, в школе учащиеся знакомятся с
информационной моделью кровообращения. Предлагаемой в учебнике анатомии
информации достаточно для школьника, но мало для тех, кто проводит операции на
сосудах в больницах.

Информационные модели играют очень
важную роль в жизни человека.

Знания, получаемые вами в школе, имеют
вид информационной модели, цель которой — изучение предметов и явлений.

Уроки истории дают возможность построить
модель развития общества, а знание этой модели позволяет строить собственную
жизнь, либо повторяя ошибки предков, либо учитывая их.

На уроках географии вам сообщают
информацию о географических объектах: горах, реках, странах и др. Это тоже
информационные модели. Многое, о чем рассказывается на занятиях по географии,
вы никогда не увидите в реальности.

На уроках химии информация о свойствах
разных веществ и законах их взаимодействия подкрепляется опытами, которые есть
не что иное, как реальные модели химических процессов.

Информационная модель никогда не
характеризует объект полностью. Для одного и того же объекта можно построить
различные информационные модели.

Выбор наиболее существенной информации
при создании информационной модели и сложность этой модели обусловлены целью
моделирования.

Построение информационной модели
является отправным пунктом этапа разработки модели. Все входные параметры
объектов, выделенные при анализе, располагают в порядке убывания значимости и
проводят упрощение модели в соответствии с целью моделирования.

Знаковая модель.

Прежде
чем приступить к процессу моделирования, человек делает предварительные
наброски чертежей либо схем на бумаге, выводит расчетные формулы, т. е.
составляет информационную модель в той или иной знаковой форме, которая может
быть либо компьютерной, либо некомпьютерной.

Рисуем прямоугольник, отмечаем что дано, определяем, как найти
координаты двух других вершин.

Компьютерная модель

— это модель, реализованная средствами
программной среды.

Существует множество программных
комплексов, которые позволяют проводить исследование (моделирование)
информационных моделей. Каждая программная среда имеет свой инструментарий и
позволяет работать с определенными видами информационных объектов.

Человек уже знает, какова будет модель,
и использует компьютер для придания ей знаковой формы. Например, для построения
геометрических моделей, схем используются графические среды, для словесных или
табличных описаний — среда текстового редактора.

Основные функции компьютера при
моделировании систем:

·
исполнение роли вспомогательного средства для решения задач,
решаемых и обычными вычислительными средствами, алгоритмами, технологиями;

·
исполнение роли средства
постановки и решения новых задач, не решаемых традиционными средствами,
алгоритмами, технологиями;

·
исполнение роли средства конструирования компьютерных обучающих
и моделирующих сред типа: «обучаемый — компьютер — обучающий», «обучающий —
компьютер — обучаемый», «обучающий — компьютер — группа обучаемых», «группа
обучаемых — компьютер — обучающий», «компьютер — обучаемый — компьютер»;

·
исполнение роли средства моделирования для получения новых
знаний;

·
«обучение» новых моделей (самообучение моделей).

Выбираем для создания модели нашей задачи Microsoft Office Excel.
Строим таблицу для ввода заданных координат, для вычисления не заданных
координат, площади и периметра вводим формулы, строим по таблице график.

Этап
3. Компьютерный эксперимент.

Компьютерное моделирование — основа
представления знаний в ЭВМ. Компьютерное моделирование для рождения новой
информации использует любую информацию, которую можно актуализировать с помощью
ЭВМ. Прогресс моделирования связан с разработкой систем компьютерного
моделирования, а прогресс в информационной технологии — с актуализацией опыта
моделирования на компьютере, с созданием банков моделей, методов и программных
систем, позволяющих собирать новые модели из моделей банка.

Разновидность компьютерного
моделирования — вычислительный эксперимент, т. е. эксперимент, осуществляемый
экспериментатором над исследуемой системой или процессом с помощью орудия
эксперимента — компьютера, компьютерной среды, технологии.

Вычислительный эксперимент становится
новым инструментом, методом научного познания, новой технологией также из-за
возрастающей необходимости перехода от исследования линейных математических
моделей систем (для которых достаточно хорошо известны или разработаны методы
исследования, теория) к исследованию сложных и нелинейных математических
моделей систем (анализ которых гораздо сложнее). Грубо говоря, наши знания об
окружающем мире линейны, а процессы в окружающем мире нелинейны.

Вычислительный эксперимент позволяет
находить новые закономерности, проверять гипотезы, визуализировать ход событий
и т. д.

Чтобы дать жизнь новым конструкторским
разработкам, внедрить новые технические решения в производство или проверить
новые идеи, нужен эксперимент. В недалеком прошлом такой эксперимент можно было
провести либо в лабораторных условиях на специально создаваемых для него
установках, либо на натуре, т. е. на настоящем образце изделия, подвергая его
всяческим испытаниям.

С развитием вычислительной техники
появился новый уникальный метод исследования — компьютерный эксперимент.
Компьютерный эксперимент включает некоторую последовательность работы с
моделью, совокупность целенаправленных действий пользователя над компьютерной
моделью.

В нашей задаче меняем координаты вершин А и С, смотрим за
изменениями на графике и проверяем расчеты по формулам.

Эксперимент 1 Вводимые
координаты положительные

Эксперимент 2 Вводимые
координаты отрицательные

Эксперимент 3 Вводимые
координаты (x) отрицательные, (y)
положительные

Эксперимент 4 Вводимые
координаты (у) отрицательные, (х) положительные

Эксперимент 5 Вводимая
координата (у) вершины С отрицательна, все остальные положительные

Эксперимент 6 Вводимая
координата (у) вершины С положительна, все остальные отрицательные

Эксперимент 7 Вводимые
координаты одной заданной вершины положительные, другой вершины отрицательные

Этап
4. Анализ результатов моделирования.

Конечная цель моделирования — принятие решения,
которое должно быть выработано на основе всестороннего анализа полученных
результатов. Этот этап решающий — либо вы продолжаете исследование, либо
заканчиваете. Возможно, вам известен ожидаемый результат, тогда необходимо
сравнить полученный и ожидаемый результаты. В случае совпадения вы сможете
принять решение.

Основой для выработки решения служат
результаты тестирования и экспериментов. Если результаты не соответствуют целям
поставленной задачи, значит, допущены ошибки на предыдущих этапах. Это может
быть либо слишком упрощенное построение информационной модели, либо неудачный
выбор метода или среды моделирования, либо нарушение технологических приемов
при построении модели. Если такие ошибки выявлены, то
требуется корректировка модели, т. е. возврат к одному из предыдущих
этапов. Процесс повторяется до тех пор, пока результаты эксперимента
не будут отвечать целям моделирования. Главное, надо всегда помнить:
выявленная ошибка — тоже результат.
Как говорит народная мудрость, на ошибках учатся.

Теперь учащиеся смогут построить прямоугольник в любой четверти
координатной плоскости.

Источник

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

Количество изделий нам пока неизвестно. Это переменные.
В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.

Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

Заполнение аргументов:

Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
Тип – 0.
БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)^кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)¹⁶ = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.

Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

Делаем таблицу со значениями матрицы А.
Выделяем на этом же листе область для обратной матрицы.
Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
В поле аргумента «Массив» вписываем диапазон матрицы А.
Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Скачать примеры

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

Источник

Федеральное
агентство по образованию

ГОУ ВПО «Российский
государственный профессионально–педагогический

университет»

Уральское отделение
Российской академии образования

Академия
профессионального образования

Екатеринбург

2007

УДК

ББК

Городецкая
Н.В.
Математическое моделирование в MS
Excel:
Учеб. пособие. Екатеринбург: Изд-во ГОУ
ВПО «Рос. гос. проф.-пед. ун-т», 2007. 64 с.

Учебное пособие
содержит лабораторные работы,
ориентированные на знакомство с одной
из технологий – математическое
моделирование на основе среды Microsoft
Excel.

Лабораторные
работы включают необходимый теоретический
материал и непосредственные инструкции
по освоению математического моделирования
в среде Microsoft
Excel.

Пособие может быть
использовано для преподавания дисциплины
«Математическое моделирование» у
студентов специальности
050501 Профессиональное обучение
(информатика, вычислительная техника
и компьютерные технологии) (030500.06),
специализации «Компьютерные технологии».

Практикум подготовлен
при финансовой поддержке Российского
гуманитарного научного фонда в рамках
научно–исследовательского проекта
«Психолого–педагогические и
технологические условия применения
адаптивных методических систем в
дистанционных образовательных
технологиях» (№ 06−06−00475а).

Рецензенты: д-р
физ.-мат. наук, проф. В.Е. Третьяков
(ГОУ ВПО «Уральский государственный
университет»); д-р пед. наук, проф. Л.И.
Долинер (ГОУ ВПО «Российский
государственный профессионально-педагогический
университет»)

государственный
профессионально-

педагогический
университет», 2007

Преподавателю: как использовать это пособие

Данная
серия лабораторных работ предназначена
для знакомства обучаемых с технологией
использования математического
моделирования для решения задач. В
качестве конкретного инструментального
средства выбрана среда MicrosoftExcel.

Для
использования данного пособия в обучении
необходимо:

иметь
дискету, прилагаемую к пособию, для
установки рабочих файлов (без них работа
с пособием невозможна);
установить
на компьютере полную версию MicrosoftExcel(с возможностью
осуществлятьПоиск решения);
создать
(в случае отсутствия) в корневом каталоге
одного из дисков папку Учебнаяи
скопировать в папкуУчебнаяпапкуМАТ_МОД, содержащую учебные файлы
с прилагаемой дискеты.

Тому, кто хочет научиться

Если
Вы решили с помощью этого пособия
познакомиться с технологией использования
математического моделирования в среде
MicrosoftExcel,
рекомендуется:

расположиться
перед включенным компьютером с
установленной полной версией MicrosoftExcel;
выполнять
лабораторные работы как можно более
точно, поскольку тексты лабораторных
работ представляют собой в некотором
роде инструкции, соблюдение которых
обеспечит Вам успешную и комфортную
работу;
соблюдать
следует следующие правила:

текст,
который никак не выделен, следует только
читать;
определения,
отмеченные значком
,
необходимо запомнить;
обращать
внимание на текст, помеченный значком
;
практические
задания, отмеченные словом «Задание»,
следует обязательно и в полном объеме
выполнять на компьютере;
контрольные
задания следует также выполнять
самостоятельно; если Вы справитесь с
ними без помощи преподавателя, это
означает, что Вы усвоили материал;
на
контрольные вопросы нужно отвечать
устно – они подготовят Вас к компьютерным
тестовым вопросам;
для
повторения пройденного материала
следует использовать резюме;

делать
краткий конспект — это поможет Вам
ускорить усвоение материала;
отвечать
на все вопросы, приведенные в конце
каждой лабораторной работы;
приглашать
преподавателя тогда, когда это
предлагается сделать в тексте лабораторной
работы;
если
Вы занимаетесь без преподавателя,
выполняйте полностью все задания
лабораторных работ, отвечайте устно
на вопросы.

В книге
приняты следующие обозначения:

—
этот символ используется для выделения
определений;

—
так помечаются важные замечания;

—
резюме;

—
при встрече с таким символом следует
пригласить преподавателя (консультанта)
и показать ему результаты выполнения
заданий. Если Вы работаете самостоятельно,
просто пропустите текст, помеченный
этим символом;

ЛП– линейное программирование; ЦФ–
целевая функция;

РЗ– распределительная задача; ТЗ–
транспортная задача.

Соседние файлы в папке Исслед_опер

#
24.04.201517.92 Кб149lab_3(b).xls
#
24.04.201517.92 Кб88lab_3(а).xls
#
24.04.201527.14 Кб114lab_4(a).xls
#
24.04.201523.04 Кб91lab_4(b).xls
#
24.04.201519.97 Кб143lab_5.xls
#

Источник

Моделирование математических задач в среде MS Excel
Математическая модель – описание объекта или процесса математическими формулами,
связывающими их количественные параметры [1].
Многие объекты можно описать математическими формулами, связывающими их параметры. Эти
формулы составляют математическую модель оригинала. По формулам можно сделать расчеты с
различными значениями параметров и получить количественные характеристики модели. Расчеты в  свою
очередь, позволяют сделать выводы и обобщить их [2].
Электронная таблица является эффективным средством проведения численного моделированияя
ситуации или объекта, для математического описания которых используются ряд параметров. Табличный
процессор MS Excel позволяет провести быстрый расчет меняя исходные значения известных параметров
модели.
Рассмотрим следующий пример численного моделирования в среде MS Excel.
Задача. Чтобы из квадратного картонного листа со стороной а сделать коробку по углам вырезают
четыре квадрата и склеивают коробку по сторонам вырезов. Какова должна быть сторона вырезаемого
квадрата, чтобы коробка имела наибольшую вместимость [3]?
Рисунок – 1
Для решения задачи составим математическую модель в  MS Excel.
Моделирование в электронной таблице проведем в четыре этапа: постановка задачи, разработка
модели, компьютерный эксперимент и анализ результатов [2].
1. Постановка задачи [2].
Заданный объект: Квадратный лист (рис. 1).

Моделируемы объект: Коробка (ящик).
Цель моделирования: Найти сторону вырезаемых квадратов, которые обеспечивают
максимальную вместимость моделируемой коробки.
Как можно определить максимальный объем коробки? Меняя размер (х) вырезаемого квадрата
проследить как изменяется ее объем.
Как изменяется размер выреза (х)?  В интервале (0; a/2) с шагом Δх.
Какие параметры коробки меняются при изменении выреза? При изменении размера вырезаемого
квадрата (х) изменяются площадь дна (S) и объем коробки (V).
Какие ограничения существуют при вычислении? Вычисляемое значение сторон основания
коробки (квадрат)  (b) не должно быть отрицательным числом (b>0)
2. Разработка модели
Информационная модель:
Объект
Параметры
Квадратный лист
Вырезаемый квадрат
название
Сторона a
Сторона х
Шаг изменения Δх
значение
Исходные данные
Расчетные данные
Исходные данные
1 Коробка
Сторона  b
Площадь S
Объем V
Расчетные данные
Расчетные данные
Результат
Формулы для расчетов:
b=a2*x – сторона основания коробки
S=b2 – площадь основания коробки
V=S*x – объем коробки
Здесь a – сторона заданного квадратного листа, х – сторона вырезаемых квадратов.
Значение  х  меняется от 0 до a/2 с шагом Δх: x=x+ Δх
Компьютерное моделирование:
Исходные данные
Промежуточные вычисления (показаны формулы)
3. Компьютерный эксперимент.
Меняя значения a и Δх в ячейках B4 и  B5 проводим серию вычислении (например, при a=18; 24; 30, …
Δх=1; 0,5; 0,25, …)
При a=18, Δх=1:
Результаты вычислении
При a=18, Δх=0,5:
2 При a=24, Δх=0,5:
Результаты вычислении
При a=24, Δх=0,25:
4. Анализ результатов моделирования.
Эксперимент
Δх
Сторона
вырезаемого
квадрата  х
a=18
a=24
a=30
Δх=1
Δх=0,5
Δх=0,25
Δх=1
Δх=0,5
Δх=0,25
Δх=1
Δх=0,5
Δх=0,25
3
3
3
4
4
4
5
5
5
Наибольший
объем коробки
V
432
432
432
1024
1024
1024
2000
2000
2000
Выводы: Чтобы из квадратного картонного листа сделать коробку наибольшего объема из его
углов нужно вырезать квадраты, сторона которых будет равна 1/6 части заданного листа.
Покажем достоверность полученных результатов математическим способом решения
задачи, основываясь на тему нахождения  наибольшего значения функции.
Нахождение наибольшего и наименьшего значении функций используются при решении
практических задач [1].
При компьютерном моделировании была использована формула вычисления объема коробки
V=S∙x, т.е. V(х)=S∙x=(a2x)2∙x=(a24ax+4×2) ∙x= a2x4ax2+4×3, где  х ∈ (0; a/2).
Тепер найдем производную функции V(х):  V ‘(х)=a28ax+12×2
Решаем уравнение V ‘(х)=a28ax+12×2=0; найдем критические точки: x1=a/6; x2=a/2;
Выбираем точку, принадлежащую в (0; a/2):    a/6 ∈ (0; a/2).
На (0; a/2) при  х0; а при  х>a/6  выполняется V'(х)>0; значит функция  V(х) в
точке x=a/6 достигает наибольшего значения.
V(a/6)=(a2∙ a/6)2 ∙a/6  = 2∙ a3/27
3 Это доказывает истинность результатов компьютерного эксперимента:
При a=18   высота коробки  x=3; объем коробки  V(3)= 2∙ 183/27=432
При a=24 высота коробки  x=4; объем коробки    V(4)= 2∙ 243/27=1024
При a=30 высота коробки  x=5; объем коробки    V(5)= 2∙ 303/27=2000
Ответ: a/6
Задания для проектной деятельности
.
1. В прямоугольном треугольнике задана длина гипотенузы с. Найти длины катетов, при
которых треугольник имеет наибольшую площадь.
2. Среди прямоугольников, периметры которых равны а, найти прямоугольник, имеющий
наибольшую площадь [4].
3. Вписать прямоугольник наибольшей площади в остроугольный треугольник с основанием
а и высотой h [4].
4. Найти радиус цилиндра наибольшего объема, вписанного в сферу с радиусом R [4].
1. http://festival.1september.ru/articles/607393/
2. Информатика и ИКТ. Задачник по моделированию. 911 класс. Базовый уровень /Под.ред.
проф. Н.В. Макаровой. Питер, 2007. 192с.: ил.
Ссылка на литературу
3. Алгебра и начала анализа 10 класс. Общественно гуманитарное направление/Под ред.
Абылкасымова А., Шойынбеков К., Есенова М., Жумагулова З., 2010 год, «Мектеп», с
192.
4. Алгебра и начала анализа. 10 класс. Учебник для общеобразовательных организаций,
Издание 3. Под ред.Шыныбекова А.Н Алматы: Атамура, 2014 год, С. 336.
4

Источник

Решение задач оптимизации в Excel

Решение финансовых задач в Excel

Решение эконометрики в Excel

Решение логических задач в Excel

Решение математических задач в Excel

Оглавление

Преподавателю: как использовать это пособие

Тому, кто хочет научиться