Моделирование равномерного движения тела excel

МОУ «Сернурская средняя (полная) общеобразовательнаяшкола №2
имени Н.А. Заболоцкого

Элективный
курс по выбору для предпрофильной подготовки

«Моделирование
физических процессов

в
электронных  таблицах MS Excel»

Онучина Вера
Ивановна пос Сернур Республика Марий Эл ovi17@rambler.ru 88363398516

СОДЕРЖАНИЕ

Стр.

ВВЕДЕНИЕ                                                                                   3

ЭЛЕКТИВНЫЙ КУРС ДЛЯ ПРЕДПРОФИЛЬНОЙ ПОДГОТОВКИ «Моделирование физических
процессов в электронных таблицах»                                   5

1.2 Программа
курса                                                                      5

1.3. Содержание
занятий                                                                9

ЗАКЛЮЧЕНИЕ                                                                              26

СПИСОК ЛИТЕРАТУРЫ                                                              27

ПРИЛОЖЕНИЕ 1                                                                           28

ВВЕДЕНИЕ

ФИЗИКА — наука, в
которой математическое моделирование является важным методом исследования.
Сегодня кроме теоретической и экспериментальной физики можно выделить третий раздел
— вычислительную физику. Одним из наиболее перспективных направлений
использования информационных технологий в физическом образовании является
компьютерное моделирование физических процессов и явлений. Рост компьютеризации
школ дает возможность каждому учителю использовать на своих уроках
информационные технологии, что с одной стороны, активизирует внимание учащихся
и усиливает их интерес к уроку, а с другой – облегчает работу учащихся и
учителя. Компьютерные модели легко вписываются в традиционный урок, позволяя
учителю продемонстрировать на экране компьютера многие физические эффекты, а
также позволяют организовать новые нетрадиционные виды учебной деятельности.
При грамотном использовании компьютерных моделей физических явлений можно
достигнуть многого из того, что требуется для неформального усвоения курса
физики и для формирования физической картины мира.  Значительное число
компьютерных моделей, охватывающих почти весь школьный курс физики, содержится
в учебных электронных изданиях: “Физика в картинках”, “Открытая физика”, “Живая
физика”, «1 С Репетитор», «1 С Физика 7-11», «Физика 7-11 практикум», «Уроки
физики 7- 8 классы», «Кирилл и Мефодий 5-6» и другие.

Существуют
большие возможности моделирования физических задач в среде MS Excel.
Электронные таблицы, первоначально использовавшиеся для финансовых расчетов, все
шире применяются для сложных многошаговых технических расчетах. Так, применение
электронных таблиц на уроках физики может сократить время при проведении
однотипных расчетов, например при выполнении лабораторных работ, где требуется
рассчитывать одни и те же физические величины для нескольких опытов.
Использование электронных таблиц Excel обусловлено следующими причинами:
а) функциональные возможности программы Excel заведомо перекрывают все
потребности по автоматизации обработки данных  эксперимента, построению и
исследованию моделей; б) универсальная программа Excel обладает стандартным
интерфейсом; в) изучение Excel предусматривается программами общего образования
по информатике, следовательно, возможно эффективное использование Excel в
условиях осуществления межпредметных связей с информатикой и другими учебными
дисциплинами, например, с математикой; г) данная программа отличается
доступностью в изучении и простотой в управлении, что принципиально важно как
для ученика, так и для учителя; д) результаты деятельности на рабочем листе
Excel (тексты, таблицы, графики, формулы) «открыты» пользователю. Cреди всех известных программных
средств Excel обладает едва ли не самым богатым инструментарием для работы с
графиками. Программа позволяет с использованием приемов автозаполнения
представлять данные в табличной форме, оперативно их преобразовывать с использованием
огромной библиотеки функций, строить графики редактировать их практически по
всем элементам, увеличивать изображение какого-либо фрагмента графика, выбирать
функциональные масштабы по осям, экстраполировать графики и т.д

Электронные
таблицы наиболее эффективно могут использоваться при проведении:

—    
Демонстрационного
эксперимента;

—    
Лабораторных
работ;

—    
Физического
практикума;

—    
Решения
задач по различным темам курса физики;

—    
Контроля
знаний.

    В своей
работе как учитель физики и информатики  на протяжении ряда лет я использую
возможности компьютерного класса школы в преподавании физики. При прохождении
темы информатики «Табличные вычисления на компьютере» в части «Математическое
моделирование и решение задач с помощью электронных таблиц» я использую задачи
по кинематике и динамике, что способствует повторению, углублению и закреплению
материала этих тем по физике, а также демонстрация практического применения
электронных таблиц при изучении других предметов школьного курса ( в дальнейшем
при изучении  темы информатики «Программирование на Паскале» я повторяю эти
физические задачи, но демонстрация в электронных таблицах наглядней). Данный
курс «Моделирование физических процессов в электронных таблицах» является
обобщением опыта работы в этой области на протяжении ряда лет.

I.       ЭЛЕКТИВНЫЙ   КУРС ДЛЯ
ПРЕДПРОФИЛЬНОЙ ПОДГОТОВКИ «МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ПРОЦЕССОВ В ЭЛЕКТРОННЫХ
ТАБЛИЦАХ MS EXCEL». 9 класс.

1.1.         
Программа
курса

Пояснительная
записка.

В настоящее время
многие  ученики основной школы имеют дома компьютеры. Однако большинство из них
используют компьютер для всевозможных игр, просмотра видеороликов и музыки.
Меньшее время уделяется для учебных задач, которые сводятся в основном к набору
текстов, работе в графических редакторах.  Первоначально компьютеры
разрабатывались как ЭВМ,  и в современных компьютерах этот потенциал вычислений
только усиливается, что явно не используется хотя бы в домашних условиях.
Программная среда Ms Excel позволяет продемонстрировать возможности компьютера
в вычислительном эксперименте. Электронные таблицы, первоначально
использовавшиеся для финансовых расчетов, все шире применяются для сложных
многошаговых технических расчетов, что необходимо показать ученикам школы. Курс
«Моделирование физических процессов в программной среде Ms Excel» рассчитан на
использование  электронных таблиц для построения моделей физических процессов,
начиная с простейших — «Моделирование равномерного прямолинейного движения,
равноускоренного движения» —  до более сложных , как, например,  «Моделирование
движения тел с учетом многих сил действующих на тело». Кроме того,
предусматривается проведение лабораторных работ с оформлением результата с
использованием электронных таблиц.

Данный курс является межпредметным,
расширяющим  и углубляющим базовый курс физики и информатики. Он дает
возможность познакомить учащихся  с задачами  повышенного уровня сложности,
нестандартными задачами,  и, таким образом, способствовать осознанному выбору
профиля, связанного с физикой и информатикой.

Программа курса предполагает владение
учащимися  базовым уровнем знаний, умений и навыков  по информатике за курс 8
класса (электронные таблицы уже изучены ). Программа  курса  включает в себя
углубление  и расширение знаний и умений, связанных с развитием навыков
алгоритмического мышления при построении моделей в Ms Excel, использованию
самих электронных таблиц и построение моделей физических процессов  по физике.

Задачи, предлагаемые в данном курсе, 
решаются с использованием графического интерфейса электронных таблиц, что
позволяет повысить учебную мотивацию учащихся и проверить свои способности к
физике и информатике. Вместе с тем, содержание курса позволяет ученику любого
уровня активно включиться в учебно-познавательный процесс и максимально
проявить себя.

Цели курса :

— закрепить интерес учащихся к
изучению   физики и информатики,

— расширить знания о способах решения
задач,  построении графиков с использованием электронных таблиц,

— развивать умения самостоятельно
работать с различными источниками информации, решать творческие задачи,

— создать ориентационную и
мотивационную основу для осознанного выбора профиля обучения.

Задачи курса :

Предлагаемый курс должен обеспечить
реализацию следующих задач :

— углубить и расширить базовые знания
и умения учащихся,

— содействовать формированию у
школьников алгоритмического мышления,

— развивать умение анализировать,
сопоставлять, делать выводы.

Учебный план

№	Тема	Кол-во часов
Всего	Теория	Практика
1	Введение.	1	0,5	0,5
2	Место моделирования в деятельности человека; основные этапы моделирования, понятие компьютерного эксперимента.	3	2	1
3	Особенности построения моделей для электронной таблицы, построение физических моделей движения тел.	12	4	8
4	Итоговое занятие, защита проектов.	2	—	2
	Итого	18	6,5	11,5

Учебно-тематический
план

№	Тема	Кол-во часов
Всего	Теория	Практика
1	Введение.	1	0,5	0,5
2	Место моделирования в деятельности человека; основные этапы моделирования, понятие компьютерного эксперимента.	2	1	1
3.1	Моделирование. Особенности построения моделей для электронной таблицы, построение физических моделей движения тел.	1	1	—
3.2-3.4	Моделирование равномерного прямолинейного движения.	3	1	2
3.5-3.7	Моделирование  прямолинейного  равноускоренного движения.	3	1	2
3.8-3.10	Моделирование движения тела, брошенного под углом к горизонту.	3	1	2
3.11-3.13	Моделирование	3	1	2
4.1	Самостоятельная работа. Проект	1	—	1
4.2	Самостоятельная работа. Проект.	1	—	1
	Итого	18	6,5	11,5

1.2.         
Содержание занятий.

1 занятие.

Цель урока –
повторить основные элементы электронных таблиц и действия в электронных
таблицах.

 Учащиеся должны:

знать:

—     интерфейс приложения Ms Excel;

—     панели инструментов;

—     абсолютную и относительную
адресацию ячеек;

—     мастер функций;

—     мастер диаграмм;

уметь:

—     выделять столбцы, строки,
блоки, таблицы;

—     осуществлять ввод чисел,
текста, формул;

—     производить редактирование
данных;

—     производить действия над объектами;

—     производить расчеты с
использованием электронных таблиц;

—     строить по результатам
расчетов графики функций.

В конце урока
провести несложные расчеты задачи движения тела и построить график этого
движения.

2 занятие.

Цель урока:
ввести понятие моделирования, понятие компьютерного эксперимента.

На уроке вводится
понятие моделирование, место моделирования в деятельности человека, основные
этапы моделирования, понятие компьютерного эксперимента. Особенности построения
моделей для электронной таблицы, построение физических моделей движения тел.

Рассматриваются
примеры построения моделей,  использование компьютерного эксперимента для
демонстрации моделей (использование мультимедиа библиотеки школы). В конце
урока  в качестве домашнего задания рассмотреть пример построения модели из
папки «Другие задачи».

3 занятие.

Цель урока:
рассмотреть особенности построения моделей для электронной таблицы, построение
физических моделей движения тел.

На уроке
рассматривается построение физических моделей в электронных таблицах.
Указывается на порядок расположения записей, оформление листа и книги
электронной таблицы. Указывается на необходимость последовательно вносить
физические величины, в том порядке, в котором производятся вычисления. При
вводе данных необходимо учитывать относительную и абсолютную адресации, при
воде формул необходимо учитывать порядок выбора данных, чтобы не было
циклических ссылок. Сам вычислительный эксперимент в электронных таблицах
возможно применять разнообразными способами. В большинстве случаев достаточно
применение простых операций над данными, используя вставку функций из меню.

С помощью
электронных таблиц возможно решать задачи, которые не решаются в школьном курсе
физике 9 класса. Учащимся можно показать,  как используется метод приращений
для расчета движений тела под действием нескольких сил, какую роль играет
интервал приращений в оценке точности при выполнении расчетов. Как записываются
и рассчитываются приращения для времени, скорости, перемещения и других
величин. Как рассчитываются конечные величины с использованием приращений (эта
теоретическая часть изучается впоследствии в информатике в теме
«Программирование»). Сам метод приращений является сложным, поэтому он
последовательно применяется на занятиях 4 – 8. В своей итоговой работе ученики
могут  использовать этот метод.

4 занятие.

Цель занятия: Построение моделей
физических процессов в среде MS Excel.

Последовательность построения модели
физического процесса в среде MS Excel

В экспериментальной физике
графическое моделирование физического процесса используется для различных
целей.
Во-первых, графики строят для того, чтобы определить некоторые величины, —
обычно наклон или отрез, отсекаемый на оси ординат, прямой, изображающей
зависимость между двумя переменными.
Во-вторых, и это, пожалуй, самое главное, графиками пользуются для наглядности.

Графический метод дает возможность
наглядно проследить вид функциональной зависимости рассматриваемых величин и их
закономерное изменение

Графики позволяют также более
наглядно проводить сравнение экспериментальных данных с теоретической кривой.
В-третьих, графиками пользуются в экспериментальной работе, чтобы установить
эмпирическое соотношение между двумя величинами.
Пусть две физические величины связаны между собой функциональной зависимостью
вида у=f(х). При этом значения переменной х задаются непосредственно
экспериментатором (независимая переменная); а переменной у — рассчитывается по
известной функциональной зависимости для каждого заданного значения переменной х.
Моделирование функциональной зависимости состоит в получении набора точек (хi,
yi) (индекс i=0, 1, 2, 3, …) и построении соответствующего графика. В более
сложных случаях количество независимых переменных может быть больше.

Моделирование функциональной
зависимости можно проводить по аналитическим (точным) формулам или по
приближенным, полученным в результате решения некоторого исходного уравнения
численным (приближенным) методом. Количество смоделированных точек при работе с
аналитическими формулами колеблется от нескольких десятков до нескольких сотен;
при численном решении количество точек берется от нескольких сотен до
нескольких тысяч.

Все величины, входящие в
функциональную зависимость, разделяют на постоянные и переменные. Это
разделение необходимо для определения вида ссылки (абсолютная или
относительная, соответственно) при создании формулы.

Последовательность создания модели

1.                
Составить
математическую модель процесса или выписать все расчетные формулы.

2.                
На
рабочем листе заполнить таблицу исходных данных, которая должна включать в
себя:
1) начальные значения величин х и у, а также всех других, входящих в расчетные
формулы (например, начальная скорость, начальная координата и т.д.);
2) значения величин, входящих в функциональную зависимость (например, угол, под
которым произведен бросок);
3) границы изменения независимой переменной xo=хmin и хmax и/или шаг ее
изменения delta x = (xmax-xmin)/n, где n – подинтервалов, на которые
разбивается отрезок (x0=xmin; xmax) , т.е созданная таблица будет содержать n+1
точку);
4) значения табличных данных и констант (математических и физических).

3.                
Выполнить
(при необходимости) перевод величин из одной системы единиц в другую.

4.                
Составить
на основе расчетных формул рабочие формулы для вычисления всех переменных
величин с указанием вида ссылки на каждую из ячеек, содержащую необходимые
числовые данные. Ссылка на любые величины из таблицы исходных данных должна
быть абсолютной.

5.                
На том же
или отдельном листе (Расчеты) заполнить таблицу данных – содержит значения
переменных х и у (т.е. смоделированные точки). При этом начальные значения
переменных, как правило, копируются с установлением связи из таблицы исходных
данных. Каждое следующее значение независимой переменной отличается от
предыдущего на величину шага delta х. Значения переменной у рассчитываются по рабочим
формулам для каждого значения переменной х.

6.                
Построить
график зависимости у(х): тип диаграммы – Точечная, вид определяется источником
числовых данных (так, для экспериментальных данных, полученных с некоторой
погрешностью, используется только вид — Точечная; при вычислении же значений
переменных по формулам вид диаграммы, как правило, выбирается Точечная с
маркерами (или без них), соединенными сглаживающими отрезками).

7.                
Проверить
работу модели, изменяя исходные данные. Сделать вывод о границах ее
применимости и особенностях протекания данного процесса.

8.                
Добавить
на лицевом листе модели таблицу для расчета контрольной точки, где значение
переменной х берется из интервала (xmin; xmax), а значение переменной у
рассчитывается по известной функциональной зависимости для выбранного значения
переменной х.

9.                
Выполнить
предлагаемые в модели задания, решить задачи на данную тему.

5-7 занятия.

Цель: Моделирование равномерного
движения тела.

Рассмотрим моделирование такого
физического процесса, как движение тела с некоторой постоянной скоростью .
Поскольку ни одна из характеристик скорости (направление и величина) не
изменяется, движение будет происходить вдоль прямой линии, т.е. является
прямолинейным. Совместим с этой прямой ось ОХ. Каждую секунду координата x тела
будет получать одно и то же приращение, поэтому в любой момент времени может
быть найдена как x=Vx*t, где Vx — проекция вектора скорости на ось ОХ. Если в
начальный момент времени (t0 = 0) положение тела не совпадало с началом
отсчета, то уравнение будет иметь вид: x(t)=xo+Vx*t .

Проекция вектора скорости – величина
алгебраическая, т.е. она может быть и положительной, и отрицательной в
зависимости от того, какой угол alpha образует вектор скорости с направлением
оси ОХ. Если alpha=0 , Vx>0, т.е. в этом случае Vx=V, где V — модуль вектора
скорости, если alpha=180, V<0, и, следовательно, Vx=-V.

Графическое моделирование процесса
равномерного прямолинейного движения будет заключаться в построении графика
зависимости при различных значениях и направлениях скорости.

Переменные величины: время и координата тела; постоянные
– проекция скорости на ось ОХ (это означает, что ее числовое значение в
процессе движения не изменяется). Для построения графика x=f(t) необходимо
получить определенное число точек (t; x). Следовательно, необходимо задать шаг
изменения переменной t — delta t, рассчитываемый через временной интервал и
число точек или подинтервалов, на которые разбивается весь интервал: delta
t=(tmax-tmin)/n.

Выводы

1.                
Изменение
величины delta t не влияет на вид графика.
2. При увеличении проекции вектора скорости на ось OX, по оси «Коодината
x», происходит масштабирование графика функции.
3. При увеличении значения начальной координаты X0 можно увидеть, что график
функции будет распологаться выше оси OX на величину X0, и наоборот (при
уменьшении — ниже оси).
4. При изменении начальных данных в ячейках tmax и delta t вид графика почти не
изменяется (как указывалось выше), за исключением того, что график изображается
уже с масштабированием по обоим осям.
5. Зададим отрицательное значение проекции скорости. Вид графика изменился,
т.к. вид графика перемещения тела зависит от знака проекции вектора скорости
точки на данную координатную ось. Если в первом случае угол, который образует
вектор скорости с направлением оси OX был равен 0 град, то теперь этот угол
=180 град. По отношению к физике — он показывает обратное направление движения.

6. Знак «-» в значении координаты означает, что график будет смещен
вниз на величину |x|.

8-10 занятие.

Цель: Моделирование равноускоренного движения тела

Рассмотрим прямолинейное
равноускоренное движение ( a=const).
Поскольку движение происходит вдоль прямой, то для его описания достаточно
одной координаты. Пусть тело движется вдоль оси OY. Согласно определению,
ускорение рассчитывается по формуле

где в числителе стоит изменение скорости, а в
знаменателе — промежуток времени, за который это изменение произошло. Отсюда Поскольку движение
равноускоренное, каждую секунду скорость получает одно и то же приращение.
Перепишем это выражение в проекции на выбранное направление оси OY:

. Проекции скорости и ускорения могут быть как
положительными, так и отрицательными в зависимости от взаимного направления
векторов V, V0, a и
оси OY. При этом, если ay>0 (ay=a, где a — модуль вектора ускорения),
скорость получает положительное приращение, т.е. с течением времени она
увеличивается (ускоренное движение); если ay<0, скорость с течением времени уменьшается
(замедленное движение). Координата тела при этом будет изменяться по закону:

где y0 —
начальное положение тела, т.е. его координата в момент времени t0=0.

Дополнительные
задачи для домашнего задания.

11-13 занятия.

Цель:  Моделирование движения тела,
брошенного под углом к горизонту

Рассмотрим случай движения тела,
брошенного под углом к горизонту, происходящего только под действием силы
тяжести (трением
пренебрегаем).

В этом случае одной координаты для
описания движения недостаточно. Необходимо ввести систему координат XOY, при
этом ось OX направляют горизонтально, а ось OY – вертикально вверх или вниз. Теперь
положение тела задается двумя координатами (x, y), каждая из которых с течением
времени будет изменяться. Закон изменения координат можно установить из
следующих соображений.

Поскольку мы считаем, что никакие
силы, кроме силы тяжести на тело не действуют, движение вдоль оси OX будет
равномерным, и абсцисса тела меняется по закону x=Vx*t, где — проекция скорости на ось OХ.

Зададим систему координат YOX так,
что ось OY направлена вертикально вверх, с началом координат у поверхности
земли.

Сила тяжести, действующая на тело,
сообщает ему ускорение g, направленное, как и сама сила, вертикально вниз.
Поэтому проекция скорости на ось OY будет меняться по закону , гдеV0y, gy — проекция начальной
скорости и ускорения свободного падения на эту ось.

Ордината тела с течением времени
изменяется как .
Уравнение траектории, т.е. зависимость y(x), можно найти, исключив время из
последнего выражения. Выразим время через абсциссу: t=x/V0x и подставим в
уравнение ординаты: ,
где знаки проекций V0x, V0y зависят от направления осей координат.

В каждой точке траектории скорость
тела направлена по касательной к ней и может быть разложена на две составляющие
, где Vx=V0x.

Модуль скорости при этом .

В данной работе можно проследить за
взаимосвязями следующих величин: x и t, y и t, y и x, и, кроме того, установить,
как зависит дальность полета тела от угла, под которым его бросают, и от
величины его начальной скорости.

Для построения траектории движения
тела нужны формулы, позволяющие рассчи-тать координаты точки в различные
моменты времени:

а также дополнительные формулы для
вычисления проекций начальной скорости на оси координат OX и OY, перевода
градусной меры угла в радианы, интервала времени .

Проанализировать все рассмотренные
выше формулы и выделить исходные данные, переменные и постоянные величины.

Выводы

1. При изменении у0 происходит
смещение графика по оси ОУ. При у0>0 дальность полета увеличивается. При у0<0
дальность полета, соответственно, уменьшается .
2.При изменении V0 происходит изменение экстремума функции у(х) и масштабирование
графика по обоим осям. При увеличении V0 дальность полета увеличивается, при
уменьшении — соответственно уменьшается.
3. При увеличении tmax ордината одного или нескольких тел становится
отрицательной.
Наибольшая дальность полета наблюдается при значении угла 45 град!

Таким
образом, мы рассмотрели математическую модель равноускоренного движения, а
графическое моделирование будет заключаться в построении графиков зависимостей Vy=f(t) и y=f(t) при
различных значениях ay, V0y.

Анализ формул показывает, что
исходными данными в нашей модели будут:
1) координата тела уo в
момент времени, принимаемый за нулевой;
2) проекция начальной скорости на выбранную ось Voy;
3) проекция ускорения на выбранную ось ay;
4) временной интервал tmin — tmax,
в течение которого рассматривается движение.

Переменные
величины –
время, скорость и координата (они изменяются в процессе движения); постоянные – проекции ускорения и
начальной скорости на выбранную ось (в процессе движения остаются неизменными).

Дополнительные
задачи для домашнего задания.

14-16 занятия.

Цель:Моделирование колебательного
движения на примере математического маятника

Смещение тела, совершающего
механические гармонические колебания, с течением времени изменяется по закону
косинуса или синуса:
где A – амплитуда
движения, — фаза
колебаний, — начальная
фаза, — собственная
циклическая (круговая) частота колебаний.
Скорость – первая производная координаты по времени, и ускорение – вторая
производная координаты по времени, при этом также будут изменяться по
гармоническому закону:

Для преобразования выражений мы
воспользовались формулами приведения.

Отсюда видно, что скорость опережает
смещение по фазе на pi / 2, а ускорение — на pi, т.е. находится в противофазе
со смещением.

Примером одной из самых простых и
распространенных моделей колебательных систем является математический маятник –
идеализированная система, состоящая из материальной точки, массой m,
подвешенной на невесомой нерастяжимой нити длиной L и совершающей колебания в
вертикальной плоскости.
В случае малых углов отклонения, когда alpha<<1 рад., колебания маятника
можно считать гармоническими. Круговая частота гармонических колебаний
математического маятника в этом случае принимается равной
период колебаний –
Примечательно, что в случае свободных колебаний круговая частота и период
колебаний определяются свойствами самой системы и не зависят от начальных
условий (начального смещения или, что то же самое, начальной фазы).

Условие alpha<<1 рад. позволяет
свести формулы колебательного движения маятника к гармоническому виду
относительно горизонтальной оси координат ОХ.

Цель настоящей работы заключается в
том, чтобы построить графики зависимости x(t), v(t), a(t) и проследить за их
изменением при изменении параметров системы.

Перед началом работы с таблицей
необходимо разобрать ее строение и расположение данных в ячейках, а также
расчетные формулы, используемые для вычислений смещения, скорости и ускорения
колеблющегося тела.

Для создания ограничения ввода
исходных данных (alpha<5 град.) в ячейку таблицы B11 вставлено примечание: «(!)
Амплитуда угла меньше 5 град.». Вставка примечания в ячейку осуществляется по
команде MS Excel Вставка-Примечание…
При задании численного значения в ячейку C11 большего 5, в ячейке В10
появляется красная надпись «Ошибка ввода! Амплитуда угла отклонения меньше 5
град.» (1).

Для этого в ячейку В10 введена
формула:
=ЕСЛИ(ABS(C11)>5;»Ошибка ввода! Амплитуда угла отклонения меньше 5
град.»;»»)

Заполнение таблицы

1. Занести исходные числовые данные в
следующие ячейки:
1) амплитуду угла отклонения, град – в С11;
2) длину маятника, м – в С12;
3) конечный момент времени, с – в С17;
4) начальную фазу колебаний, град – в С19.
(!) Начальный момент времени (ячейка С16) удобно принять равным нулю

Пример числовых данных:
alpha max=2 град.; L=1 м; tmax=10 c; phi=30 град.

2. Для дальнейших действий необходимо
перевести углы, заданные в градусах, в радианы, так как тригонометрические
функции, используемые при расчетах координаты, скорости и ускорения, вычисляют
значение угла, заданного в радианах.  Ввести формулы, позволяющие рассчитать
период, частоту колебаний, амплитуду отклонения по координате, а также интервал
времени delta t.

Период колебаний.
, g=9,81 – ускорение
свободного падения
Ввести формулу в ячейку С13:
=2*ПИ()*КОРЕНЬ(C12/9,81)

Круговая частота : .
Ввести формулу в ячейку С14:
=2*ПИ()/C13

Амплитуда : .
Ввести формулу в ячейку С15:
=E11*C12

Вычисление шага .
Ввести формулу в ячейку С18:
=(С17-С16)/100
Здесь n=100 – количество интервалов , на которые разбивается выбранный
промежуток времени . Таким образом, таблица будет содержать n+1 = 101 точек.

5. Заполнить Таблицу данных «Время-Координата-Скорость-Ускорение».
1) Столбец G должен содержать значения времени, отличающиеся на величину delta
t. Заполнение столбца начнем с ячейки G8:
=С16
Тем самым содержимое ячейки С16 (начальный момент времени) копируется в ячейку G8
и одновременно устанавливается связь между ячейками: при изменении содержимого
ячейки С16 значение в ячейке G8 также автоматически изменится.
2) В ячейку G9 ввести:
=G8+$C$18
$C$18 – абсолютная ссылка на ячейку с константой .
3) Скопировать данную формулу в диапазон ячеек G10:G108 следующим образом:
— выделить ячейку G9;
— скопировать ее содержимое в буфер командой Правка-Копировать;
— выделить диапазон ячеек G10:G108;
— провести вставку формулы из буфера командой Правка-Вставить.
4) В столбцах H, I, J содержатся значения координаты, скорости и ускорения,
вычисляемые в соответствующие моменты времени из столбца G. Ввести в ячейки H8:J8
нужные формулы:

Координата .
Ввести формулу в ячейку H8:
=$C$15*SIN($C$14*G8+$E$19)
Скорость .
Ввести формулу в ячейку I8:
=$C$14*$C$15*COS($C$14*G8+$E$19)
Ускорение .
Ввести формулу в ячейку J8:
= – $C$14^2*$C$15*SIN($C$14*G8+$E$19)

5) Выделить блок ячеек H8:J8 и
скопировать формулы в диапазон H9:J108 (см. пп. 3)).

6. Изменить имя листа, содержащего
таблицу («Модель 3»), например, на «Колебания маятника». После окончания ввода
нажать клавишу {Enter} или щелкнуть мышкой в рабочем поле листа.
Таблица заполнена.

Построение графиков

По результатам расчетов необходимо
построить три графика: x(t), v(t) и a(t). Поскольку во всех случаях по оси Ox
откладывается одна и та же величина (время), все три зависимости можно
представить в одной системе координат. Такой способ построения применяется в
тех случаях, когда необходимо провести сравнение нескольких различных
(неоднородных) величин или исследовать поведение некоторой величины в
зависимости от начальных условиях или условий проведения эксперимента. Однако
он имеет и недостатки: он применим только тогда, когда сравниваемые величины
имеют один и тот же порядок.

1. Выделить диапазон ячеек G8:J108,
содержащих все необходимые данные. Программа Excel автоматически будет
рассматривать этот диапазон как три ряда данных, а именно:
1-ый ряд G8:H108 – зависимость координаты от времени;
2-ой ряд G8:G108; I8:I108 – зависимость скорости от времени;
3-ий ряд G8:G108; J8:J108 – зависимость ускорения от времени,
причем первая колонка (диапазон G8:G108) будет общей для всех остальных.
2. Выполнить команду Вставка-Диаграмма…
3. Провести пошаговое построение диаграммы:

Шаг 1. В диалоговом окне Тип диаграммы на
вкладке Стандартные указать тип диаграммы Точечная и вид – «Точечная диаграмма
со значениями, соединенными сглаживающими линиями» или «Точечная диаграмма со
значениями, соединенными сглаживающими линиями без маркеров». Нажать кнопку Далее.
Шаг 2. В окне Источник данных диаграммы на вкладке Диапазон данных проверить,
что диапазон данных выбран правильно и установлен флажок опции «Ряды в
столбцах».
Дать названия наборам точек: выбрать вкладку Ряд и в списке названий рядов
данных (поле Ряд) выделить имя первого набора – «Ряд 1», после чего в поле Имя:
ввести название – «Смещение». Аналогичным образом задать имена двух следующих
рядов данных – «Скорость» и «Ускорение». Как видно из рисунка, все маркеры
(точки) и сглаживающие линии графиков различны по цвету. Кроме того, маркеры
имеют различную форму. Для того, чтобы различать графики, на диаграмме
выводится так называемая легенда – сведения о способе вывода того или иного
графика (цвет линии, цвет и форма маркеров, название соответствующего им ряда
данных). Нажать кнопку Далее.
Шаг 3. Задать параметры диаграммы (окно Параметры диаграммы):
— на вкладке Заголовки ввести название диаграммы и наименование осей координат
с указанием единиц измерения величин, откладываемых по этим осям, следующим
образом:
— в поле Название диаграммы – «Графики колебательного процесса»;
— в поле Ось Х (категорий) – «Время t, с»;
— в поле Ось Y (значений) – «x (м); v (м/с); a (м/c2)»;
— на вкладке Линии сетки включить или отключить основные и промежуточные линии
сетки по каждой из осей;
— на вкладке Легенда установить флажок опции «Добавить легену» и указать ее
размещение на диаграмме. Нажать кнопку Далее;
Шаг 4. Выбрать расположение диаграммы на отдельном листе и ввести имя листа в соответствующем поле.
Нажать кнопку Готово.

Задание 1
1. Изменяя начальные данные (начальное смещение и фазу, длину маятника),
проследить за изменением вида графиков.
2. Разобрать вопрос о соотношении величин xmax и L.
3. Определить сдвиг фаз между колебаниями каждой пары величин. Это удобно
выполнить для случая, когда начальная фаза колебаний равна нулю.
4. Задать для диапазона G8:J108 соответствующий формат числовых данных
(числовой или экспоненциальный с определенным количеством десятичных знаков
после запятой).
5. Изменяя момент времени tmax (и, тем самым, — интервал delta t), определить
границы применимости данной модели.
6. Добавить в таблицу исходных данных контрольные точки для заданного момента
времени и вывести их на всех графиках.

Построение отдельных графиков

Провести построение каждого графика в
отдельности.

Построение графика зависимости x(t)

1. Выделить диапазон ячеек G8:H108,
содержащий данные для построения графика. Значения в столбце G (диапазон G8:G108)
будут откладываться по оси Oсь Х (время), значения в столбце H (диапазон H8:H108)
– по оси Oсь Y (координата).
2. Выбрать команду Вставка-Диаграмма…
3. Шаг 1. В диалоговом окне Тип диаграммы выбрать тип диаграммы Точечная и вид
– «Точечная диаграмма со значениями, соединенными сглаживающими линиями» или
«Точечная диаграмма со значениями, соединенными сглаживающими линиями без
маркеров». Нажать кнопку Далее.
Шаг 2. В окне Источник данных диаграммы на вкладке Диапазон данных проверить
правильность выбора диапазона и установить при необходимости флажок опции «Ряды
в столбцах». На вкладке Ряд задать название данного ряда данных, например, «Зависимость
x от t» или «Смещение». Нажать кнопку Далее.
Шаг 3. Задать параметры диаграммы (окно Параметры диаграммы):
— на вкладке Заголовки ввести название диаграммы и наименование осей координат
с указанием единиц измерения величин, откладываемых по этим осям, следующим
образом:
— в поле Название диаграммы – «График зависимости координаты от времени»;
— в поле Ось Х (категорий) – «Время t, с»;
— в поле Ось Y (значений) – «Координата x, м»;
— на вкладке Линии сетки включить или отключить основные и промежуточные линии
сетки по каждой из осей;
— на вкладке Легенда снять флажок опции «Добавить легенду» и нажать кнопку Далее;
Шаг 4. Выбрать расположение диаграммы на отдельном листе и ввести имя листа в
соответствующем поле. После этого нажать кнопку Готово.

Построение графиков v(t) и a(t)
провести аналогичным образом.

Замечание: Указывая диапазон данных, приходится
выделять одновременно два блока ячеек: G8:G108 и I8:I108 для графика скорости;
G8:G108 и J8:J108 для графика ускорения. В этом случае после выделения первого
блока (G8:G108) выделяют другой (I8:I108 или J8:J108), удерживая при этом
нажатой клавишу {Ctrl}.

Дополнительные
задачи для домашнего задания.

17-18 занятия

Цель:Выполнение итоговой работы: Моделирование 
свободного падения с учетом сопротивления среды.

ЗАКЛЮЧЕНИЕ

Предлагаемый в данном курсе
теоретический и задачный материал был апробирован с  учащимися  9 классов на
уроках информатики при изучении темы «Табличные вычисления на компьютере».  На
занятиях при использовании электронных
таблиц значительно возрастают возможности для сотрудничества между всеми
участниками учебного процесса. Диалог в виде проблемной беседы, обсуждения 
осуществляется на занятиях по решению задач и моделированию, в лабораторном
практикуме. Обсуждаются результаты выполненных с использованием компьютера и
предъявленных на электронном носителе домашних заданий. Это могут быть
результаты решения задач, представляемых в виде численных моделей, результаты
исследования «готовых» моделей, полученных от учителя, презентации. Обсуждению
подлежат цели, условия, порядок проведения измерений и обработки данных,
первичные, промежуточные и конечные результаты. Можно отметить возможность
выдвижения учениками гипотез и их быстрой проверки при вводе в компьютер новых
данных. Для организации взаимодействия, коммуникации во всех случаях
целесообразно использовать мультимедийный проектор.

Занятия помогли
ученикам  в дальнейшем при изучении курса информатики «Введение в
программирование»,  развили умения и навыки работы в электронных таблицах,
помогли расширить знания о различных физических процессах и их применении на
практике.

Предлагаемый курс
по выбору окажет помощь в повторении отдельных изученных ранее тем и улучшит
подготовку учащихся 9 класса к итоговой аттестации по физике и информатике, 
поможет определиться с дальнейшим профилем обучения.

Библиография

·                    
«Моделирование
физических процессов. Лабораторный практикум MS Excel». ОСО-2008,
Информатика и ИКТ http://oco.apkpro.ru/info/Model/mdl.htm

·                    
Физика.
Механика. 10 кл. Профильный уровень: учебн. для общеобразовательных учреждений
/ М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др.; под ред. Г.Я. Мякишева –
9-е изд., стереотип. – М.: Дрофа,2007.

·                    
Физика :
Учеб. для 10 кл. с углубл. изучением физики / О.Ф. Кабардин, В.А. Орлов, Э.Е.
Эвенчик и др.; Под ред. А.А. Пинского, О.Ф. Кабардина. – 8-е изд., перераб. и
доп. – М.: Просвещение, АО «Моск. учеб.», 2005.

Приложение 1 .

Дополнительные
задачи для домашнего задания.

2.                
Автомобиль
первую половину пути s₁ = s/2 прошёл со скоростью v₁ = 60 км/ч, оставшуюся часть пути (s₂ и s₃ ) – со скоростью v₂ = 20 км/ч, два последний участок пути s₃ – со скоростью v₃ = 35
км/ч. Найдите среднюю скорость v_ср автомобиля на всём пути.

Дополнительные
задания повышенного уровня:

а) варьируя
скорости на участках пути, найдите скорость движения        автомобиля на всём
пути;

б) выполните
задачу в электронной таблице и получите график зависимости средней скорости
автомобиля от скорости его движения на первой половине пути, если последней
задавать различные значения, сохраняя постоянными значения скоростей автомобиля
на втором и последнем участках пути.

2.  Между двумя
пунктами, расположенными вдоль реки на расстоянии s = 200
км один от другого, курсирует теплоход. Он проходит это расстояние по течению
за время t₁ = 6 ч, а против течения – за t₂ = 8 ч. Определите скорость течения
реки v₁ и скорость теплохода v₂ относительно стоячей воды.

Дополнительные
задания повышенного уровня:

а) варьируя
расстояние между двумя пунктами, найдите скорость течения реки и скорость
теплохода в стоячей воде;

 б) выполните
расчеты в электронных таблицах и получите  график зависимости скорости
теплохода в стоячей воде от расстояния между двумя пунктами, задавая последнему
различные значения. Заданное по условию время движения остаётся неизменным.

3. Автомобили
типа «Жигули» и «Волга» движутся прямолинейно и равномерно в одном направлении
со скоростями v₁ = 90
км/ч и v₂ = 108
км/ч. В начальный момент времени расстояние между ними равно 15
км. Через какое время «Волга» догонит идущие впереди неё «Жигули»?

Дополнительные
задания повышенного уровня:

а) варьируя
скорости автомобилей, определите, через какое время «Волга» догонит «Жигули»;

б) выполните расчеты
в электронных таблицах и получите графики зависимости координат автомобилей от
времени движения.

По графикам
определите время, через которое автомобиль «Волга» догонит автомобиль «Жигули».

4. Тело брошено
вертикально вверх со скоростью v₀ = 30 м/с. Начальная
координата х₀ = 0. Определите путь, пройденный телом за время,
равное 1,2,3,4,5 с. (Сопротивлением воздуха можно пренебречь.)

Дополнительные
задания повышенного уровня:

а) варьируя
время, найдите путь, пройденный телом;

б) выполните
расчеты в электронных таблицах и получите график зависимости пути, пройденного
телом, от времени движения, задавая последнему значения первых пяти секунд, но
сохраняя при этом постоянным значение начальной скорости.

5. Из аэростата,
находящегося на высоте h₀ = 540
м, выпал груз. Через какой промежуток времени t груз достигнет поверхности Земли, если аэростат поднимется
со скоростью v₀ = 6 м/с? (Сопротивлением воздуха
можно пренебречь.)

Дополнительные
задания повышенного уровня:

а) варьируя
высоту полёта аэростата, определите промежуток времени, через который груз
достигнет поверхности Земли;

б) выполните
расчеты в электронных таблицах и получите график зависимости промежутка
времени, через который груз достигнет поверхности Земли, от высоты полёта
аэростата, задавая последней различные значения при неизменной скорости
подъёма.

6. Тело брошено
под углом α к горизонту с начальной скоростью v₀ = 20 м/с. Начальные координаты: x₀ = 0
м, у₀ = 100 м. Определите время полёта t_п, дальность полёта, координаты х и у,
а также проекции скоростей v_x и v_у в моменты времени t, равные 0, 1, 2, …, 10 с,
максимальную высоту подъёма h_м. Поместите в таблицу
результаты для углов α, равных 0˚, 10˚, 20˚, …, 90˚. (Сопротивлением воздуха
можно пренебречь.)

Дополнительные
задания повышенного уровня:

а) выполните
расчеты в электронных таблицах и выведите  таблицу результатов;

б) выполните
расчеты в электронных таблицах и получите график зависимости координаты у от
координаты х тела для разных углов бросания.

7. Автомобиль
«Волга» движется по горизонтальному участку пути со скоростью Vo= 72
км/ч. Водитель, заметив препятствие, нажимает на тормоз. Определите тормозной
путь s автомобиля, если коэффициент
трения k=0,25.

Дополнительные
задания повышенного уровня:

а) варьируя
начальную скорость, найдите тормозной путь автомобиля;

б) выполните
расчеты в электронных таблицах и получите график зависимости тормозного пути
автомобиля от скорости, задавая последней различные значения, но сохраняя при
этом постоянным коэффициент трения.

8. Грузовой
автомобиль массой m=6 т движется на подъеме со
скоростью U=5 м/с. Угол наклона А=10⁰.
Определите коэффициент трения K, если
мощность двигателя N= 100 кВт.

Дополнительные
задания повышенного уровня:

а) варьируя
скорость автомобиля, определите коэффициент трения;

б) выполните
расчеты в электронных таблицах.

9. Шар массой m=0,4 кг привязан нитью к подвесу и
описывает окружность в горизонтальной плоскости. Какова длина l , если угол А, который она
составляет с вертикалью, равен 35⁰? Скорость шара U=6 м/с.

Дополнительные
задачи повышенного уровня:

а) варьируя угол,
который составляет нить с вертикалью, найдите длину нити

б) выполните
расчеты в электронных таблицах и получите графики движения к задаче.

10. Средняя
высота спутника h, который находится над
поверхностью Земли, равна 2000 км. Определите скорость U спутника и период обращения Т, если
радиус земли R=6400 км, масса Земли М=6*10²⁴
кг. Гравитационная постоянная G=6, 67*10^-11 Н*м²/кг²

Дополнительные
задания повышенного уровня:

а) варьируя
высоту спутника над поверхностью Земли, определите скорость и период обращения
спутника;

б) выполните
расчеты в электронных таблицах и получите на графики зависимостей скорости и
периода от высоты над поверхностью Земли, задавая высоте различные значения.

11. На движущемся
теплоходе вертикально вверх бросили мяч. Выполните расчеты в электронных
таблицах и получите  график траектории движения мяча: а) относительно берега;
б)относительно теплохода. По какой траектории будет двигаться мяч относительно
берега, если его бросают вертикально вниз в воду? Смоделируйте траекторию
движения мяча для этого случая.

12. Шар массой m1 свободно падает на тележку массой m2 , движущуюся со скоростью U1.С какой скоростью и в каком
направлении будет двигаться тележка? Выполните расчеты в электронных таблицах и
получите  графики динамической модели движения тел до и после их
взаимодействия.

Конкурс «Я иду на урок»

Моделирование прямолинейного движения тел

Цели урока

1. Образовательная: закрепить полученные знания, умения, навыки; научить школьников с помощью моделирования движения тел решать графическим способом физические задачи в табличном процессоре Excel и проводить компьютерный эксперимент.

2. Воспитательная: сформировать умение слушать выступающих, работать в мини-группах.

3. Развивающая: обеспечить развитие умений и навыков, связанных с публичными выступлениями (устная речь, ораторское искусство), с самостоятельным анализом информации, с использованием компьютерных технологий для эффективного решения поставленных задач.

Требования к знаниям и умениям:

Учащиеся должны знать: этапы решения задач моделирования на компьютере, физические формулы, описывающие равномерное и равнопеременное движения материальной точки.

Учащиеся должны уметь: • применять на практике алгоритмы моделирования движения тела • строить и исследовать компьютерные модели прямолинейного движения средствами табличного процессора Excel.

Оборудование: ПК учителя с мультимедиапроектором, презентация урока, ПК учеников для работы в табличном процессоре Excel.

Ход урока

I. Постановка целей и задач урока

Учитель. Из пункта А выехал грузовик с постоянной скоростью 72 км/ч. Одновременно с ним из пункта В, отстоящего от А на 1,5 км, начал двигаться мотоциклист. Считая движение мотоциклиста равноускоренным с a = 2 м/с², определите с помощью соответствующих графиков время, через которое мотоциклист догонит грузовик, и путь, пройденный каждым из них до встречи. Определите с точностью до 0,1 м/с² минимальное ускорение мотоциклиста, при котором это время не будет превышать 40 с.

Сегодня на уроке мы разрешим эту проблему, проведя моделирование прямолинейного движения тел в среде табличного процессора Excel: построим описательную модель, затем формализуем задачу, построим компьютерную модель и проведём эксперимент.

II. Проверка домашнего задания

Учитель. На дом вам было задано построить описательную модели сегодняшней задачи и формализовать её.

Мы с вами знаем, что в модели отражаются только существенные стороны моделируемого объекта или процесса. В проектируемой модели процесса движения какие несущественные свойства грузовика, мотоцикла, дороги и воздуха мы не учитываем?

Учащиеся. Для нас в этой задаче несущественными являются марка и цвет автомобиля, его грузоподъёмность, габариты мотоцикла и т.п. И мотоцикл, и грузовик мы моделируем материальными точками, поскольку их размер мал по сравнению с путём, который они проходят. В задаче мы не учитываем силу трения колёс и пренебрегаем сопротивлением воздуха. Считаем, что векторы скорости грузовика и ускорения мотоцикла не меняются по величине и направлению, т.е. движение происходит вдоль прямой.

Статья подготовлена при поддержке интернет-магазина «ZdesSvet». Если вы решили приобрести качественную и надежную люстру, которая будет служить и украшать ваш офис или дом долгие годы, то оптимальным решением станет обратиться в интернет-магазин «ZdesSvet». Перейдя по ссылке: «недорогие люстры потолочные в Москве», вы сможете, не отходя от экрана монитора, заказать потолочную люстру по выгодной цене. Более подробную информацию о ценах и акциях действующих на данный момент вы сможете найти на сайте www.Zdessvet.Ru.

Прежде чем перейти к этапу формализации задачи, сделаем чертёж. Поскольку движение прямолинейное, то траектория движения тел совпадает с осью X. Чертим ось X, принимаем, что в начальный момент времени (t = 0) грузовик находился в начале координат (х_г = 0). Тогда мотоцикл в начальный момент времени имел координату х_м = –1500. На чертеже покажем вектор скорости грузовика, пусть он по направлению совпадает с осью X. Поскольку мотоцикл догоняет грузовик, то направление вектора его ускорения тоже совпадает с направлением оси X. (Все построения выводятся на экран мультимедиапроектора.)

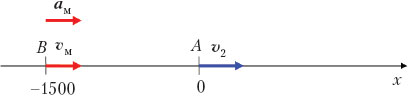
Проверяем уравнения движения грузовика и мотоцикла. (Слайд с верными формулами.)

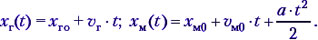
Формализация закончена. Сейчас мы с вами построим компьютерную табличную модель. (На экран мультипроектора выводится лист табличного процессора Excel с подготовленным шаблоном для построения табличной модели задачи. Такой же шаблон у учеников в папке «Общие документы» на их компьютерах.)

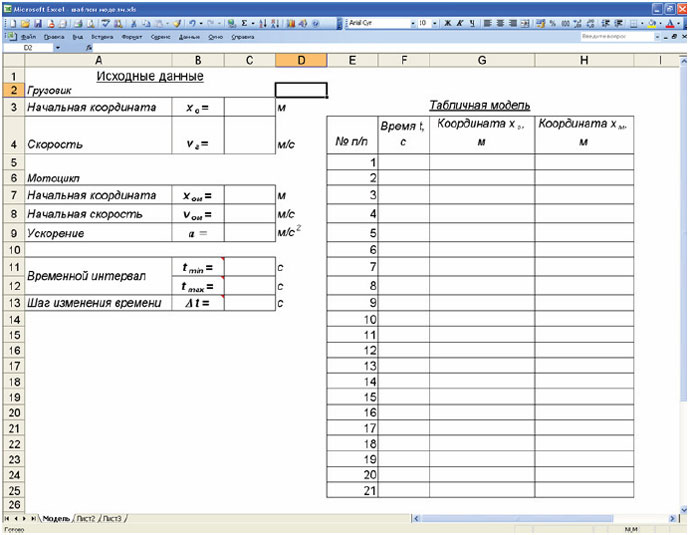
Шаблон для построения табличной модели задачи

III. Изложение нового материала

Учитель. Заполнение шаблона начинаем с ввода исходных данных в ячейки С3, С4, С10, С11, С12. Все данные вводим в СИ: С3 = 0; С4 = 20; С7 = –1500; С8 = 0; С9 = 2.

Начальный момент времени (ячейка С11) принимается равным нулю. Поскольку мы пока не знаем, сколько времени будут двигаться до встречи грузовик и мотоцикл, то примем максимальное время моделирования, например, 150 с.

По какой формуле мы рассчитываем шаг изменения времени?

Учащиеся. Находим разность максимального и минимального времени моделирования и делим её на количество подынтервалов.

Учитель. В ячейку С13 заносим шаг изменения времени, например, для 20 подынтервалов: С13 = (С12 – С11)/20.

Исходные данные заданы, переходим к заполнению табличной модели. В ячейку F5 заносим значение начального времени моделирования. В ячейку F6 – формулу для расчёта следующего момента времени: = F5 + С13.

Как получить значения последующих моментов времени?

Учащиеся. Надо скопировать формулу из ячейки F6 в ячейки, лежащие ниже.

Учитель. Прежде чем копировать эту формулу, что необходимо с ней сделать?

Учащиеся. В формуле надо с помощью абсолютной адресации указать, что при копировании её элемент С13 не должен подстраиваться по месту.

Учитель. Всё верно. Ячейка F6 должна содержать формулу = F5+С$13. Копируем её в ячейки F7:F25.

В ячейку G5 записываем формулу для расчёта координаты х_г: = C3 C4*F5.

Какие элементы введённой формулы мы должны зафиксировать с помощью абсолютной адресации?

Учащиеся. Необходимо зафиксировать начальную координату и скорость движения. Копируем формулу из ячейки G5 в ячейки G6:G25.

Учитель. В ячейку H5 вводим формулу для расчёта координаты х_м: =C$7+C$8*F5+C$9*F5*F5/2 и копируем её в ячейки H6:H25.

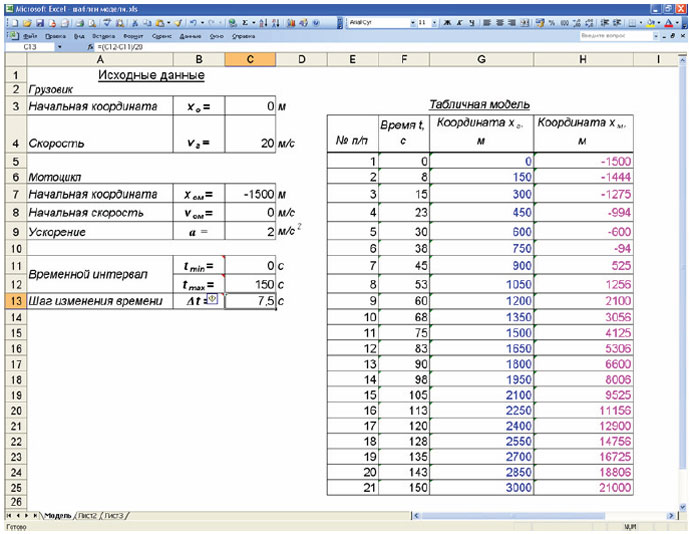
Готовая табличная модель задачи

Для наглядности по табличной модели построим точечную диаграмму и расположим её на отдельном листе с именем «График движения».

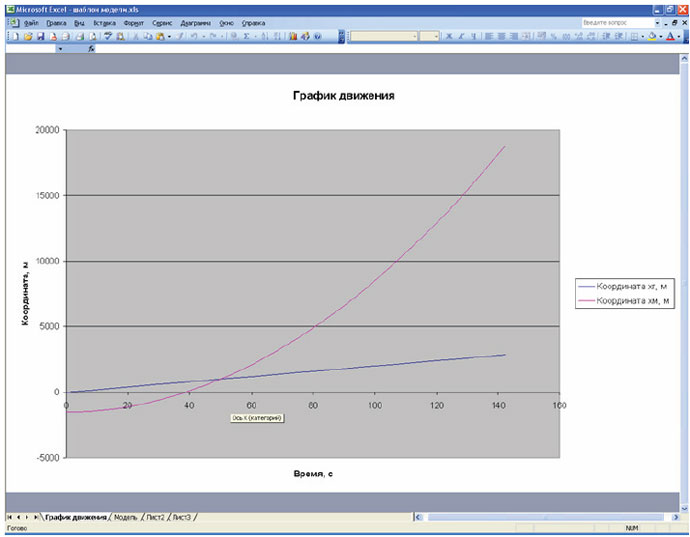
Точечная диаграмма графика движения

Из графика видно, что мотоцикл догонит грузовик за время меньше 60 с, поэтому в модели зададим максимальное время моделирования 60 с.

Для более точного определения величин по графику рекомендуется включить помимо основных промежуточные линии сетки в параметрах диаграммы.

Получаем ответ на первый вопрос задачи: мотоцикл догонит грузовик через 50 с. Грузовик до встречи пройдёт 1000 м, а мотоцикл – 2500 м.

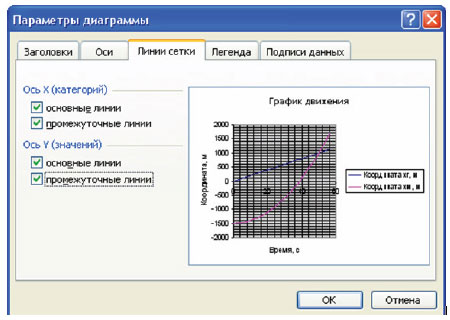
Одним из способов определения минимального ускорения мотоциклиста с точностью до 0,1 м/с², при котором время до встречи не будет превышать 40 с, является проведение компьютерного эксперимента. Будем изменять значение ускорения мотоцикла в ячейке С9 так, чтобы неопределённость наших знаний относительно требуемого значения ускорения каждый раз уменьшалась ровно в 2 раза. Исходное ускорение 2 м/с² даёт время встречи через 50 с, значит, искомое ускорение больше исходного. Введём, например, 4 м/с². При этом встреча произойдёт примерно через 33 с, значит, искомое ускорение принадлежит отрезку [2; 4]. Вводим в ячейку С9 значение ускорения из середины отрезка 3 м/с², получаем встречу примерно через 39 с, значит, искомое ускорение принадлежит отрезку [2; 3]. Вводим в ячейку С9 значение ускорения из середины отрезка 2,5, получаем встречу через ≈ 44 секунды, значит, искомое ускорение принадлежит отрезку [2,5; 3]. Вводим в ячейку С9 значение ускорения из середины отрезка 2,7, получаем встречу через ≈ 42 с, значит, искомое ускорение принадлежит отрезку [2,7; 3].

Нам остаётся провести эксперимент с двумя значениями ускорения. Для ускорения 2,9 м/с² получаем встречу через время чуть меньше 40 с, а для ускорения 2,8 м/с² получаем встречу через ≈ 41 с, значит, искомое ускорение составляет 2,9 м/с².

Вторым способом получения ответа на второй вопрос задачи является метод подбора параметра. В ячейку F18, например, где значение времени близко к заданному, принудительно вводим значение времени 40 с, в ячейку I18 введём формулу = G18-H18 (расстояние между грузовиком и мотоциклом). Выделяем ячейку I18, и из меню выбираем Сервис – Подбор параметра. В окне Подбор параметра в поле Значение вводим 0 (расстояние между грузовиком и мотоциклом). В поле Изменяемая ячейка вводим адрес ячейки С9, в которой будет производиться подбор ускорения.

III. Самостоятельная работа за компьютером

В папке «Общие документы» на каждом компьютере находится файл-книга Excel Шаблон модели.xls. Его необходимо скопировать в свою папку. В этой книге три листа: Задание, Модель, График движения, Ответы.

На листе Задание выберите задание по номеру компьютера и выполните его на листах Модель и График движения. Не забудьте заполнить лист Ответы.

IV. Подведение итогов работы и выставление
оценок

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

Федеральное
Государственное автономное образовательное
учреждение

высшего
профессионального образования

«СИБИРСКИЙ
ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ» (СФУ)

Институт
инженерной физики и радиоэлектроники

Кафедра
приборостроения и наноэлектроники

«Электронные
таблицы Microsoft Excel. Введение в математическое

моделирование»

РФ11-31Б
Д.Р.
Автахутдинов.

Студент,
____________ __________
______________

номер
группы подпись, дата
инициалы, фамилия

А.
Н. Шниперов

Преподаватель
__________
______________

подпись,
дата инициалы, фамилия

Красноярск
2012

1. Задания к лабораторной работе

1.1 Условные функции и автофильтры

1.
Построить таблицу «Список слушателей»,
приведенную в описании лабораторной
работы, добавить в неё ещё не менее 20
человек и выполнить для нее все
приведенные в описании примеры
вычислений с применением условных
функций. Добавить в эту таблицу еще три
столбца с оценками по дисциплинам
Информатика, Математика, Физика, перед
столбцом Баллы (оценки выставляются
по пятибалльной системе), подсчитать
значение среднего балла в столбце
Средний балл, который также необходимо
добавить. Заполнить столбец с информацией
о зачислении следующим образом:
зачисленными считаются все, набравшие
не менее 13 баллов либо набравшие 12
баллов, но имеющие по математике или
физике оценку 5. Ячейки столбца о
зачислении должны иметь значение
зачислен, остальные ячейки должны
остаться пустыми. Зачисленных слушателей
выделите полужирным шрифтом с помощью
условного форматирования. Набравших
не менее 11 баллов и не более 12 баллов
выделите в столбце Баллы заливкой
зеленого цвета.

2.
Выполнить сортировку:

• по
алфавиту,

• по
среднему баллу (по убыванию). Подсчитать
общее количество зачисленных, количество
зачисленных учащихся школы № 6, количество
набравших не менее 11 и не более 12 баллов
с помощью функции СЧЕТЕСЛИ и функции
суммирования для массивов.

3.
Выполнить фильтрацию данных:

• с
помощью команды Автофильтр, оставив
видимыми только тех,

кто
зачислены на курсы и учится в лицее №1;

• с
помощью команд Автофильтр и Расширенный
фильтр, выделить

всех
зачисленных, обучающихся в лицее № 1
или в школе № 6,

• с
помощью команды Расширенный фильтр,
выделив всех учащихся школы № 6, получивших
пятерку по математике и всех учащихся
лицея № 1, получивших пятерку по
информатике.

1.2. Моделирование прямолинейного равномерного и равноускоренного движения

На
отдельном листе решить графически
задачу: из пункта А
выехал

грузовик
с постоянной скоростью V₁
км/ч. Одновременно с ним из пункта В,
отстоящего от А
на расстоянии ∆S
км, начал двигаться мотоциклист. Дорога,
соединяющая пункты А
и
B,
является прямой. Считая движение
мотоциклиста равноускоренным с
ускорением а,
определить с помощью соответствующих
графиков время, через которое
мотоциклист догонит грузовик, и путь,
пройденный каждым из них до встречи.
На листе должны быть обозначены все
используемые данные, а также внесены
все, необходимые комментарии.

Рис
1. Данные для задания 2.

Соседние файлы в папке Лабораторная работа №2

• #

  13.06.201451.04 Кб86Лабораторная работа №2.xlsx

• #
• #