Моделирование при использовании excel

Введение

В системах, связанных с экономикой, руководящим работникам необходимо постоянно принимать решения следующих категорий:

1. Стратегические решения.
2. Тактические решения.
3. Оперативные решения.

Если принимаемые решения обладают низким интеллектуальным уровнем, то простота представления реальных ситуаций обычно ведёт к неточностям при выработке прогнозов, а, кроме того, к убыткам и добавочным финансовым потерям. Чтобы избежать возникновения подобных ситуаций и обеспечить устойчивое экономическое положение, существуют разнообразные системы поддержки выработки решений, усовершенствование которых превращается в наиболее актуальную проблему при наличии жёсткой конкуренции.

Существенным условием для таких программ считается возможность имитации вырабатываемых решений, апробации вероятных коррекций в экономической системе, появляющихся в результате влияния разных факторов, то есть нахождение ответа на вопрос типа, «что случится, если…». Это позволит существенно сократить риски от осуществления решений и сэкономить ресурсы, чтобы достичь поставленной цели.

Такие возможности предоставляют имитационные модели, которые обладают следующим набором качеств:

1. Возможность регулировать уровень сложности модели.
2. Присутствие случайных факторов.
3. Возможность описать процесс, развивающийся по времени.
4. Обязательное использование электронной вычислительной машины.

Имитационные модели предназначаются для того, чтобы оценить варианты намечаемых коррекций, обладать игровой формой для обучения работников, визуально отобразить работу исследуемого объекта во времени и так далее. Реализовать модели можно при помощи универсальных языков программирования, к примеру,Pascal, Basic, пакетов прикладных программ, таких как,Excel, MathCAD, и так далее. Выбор конкретного метода моделирования определяется сложностью задачи, наличием необходимых ресурсов и так далее.

«Моделирование в Excel» 👇

Однако имитационное моделирование применяется экономистами и другими специалистами только в малом проценте случаев, в которых можно было бы при помощи моделей поиметь важную для выработки решений информацию.Причина этого явления кроется в отсутствии инструкций по проведению имитационного моделирования при помощи общеизвестного и доступного инструментария, а именно, пакетов прикладного программного обеспечения, такого как Excel и MathCAD, которые могут обеспечить простую платформу для моделирования.Поэтому примеры формирования имитационных моделей при помощи, например, приложения Excel, помогают их широкому распространению в кругу работников, не владеющих языками моделирования и методиками, имеющимися в средах моделирования.

Электронные таблицы Excel как инструмент формирования имитационных моделей

Имитационное моделирование при помощи табличного процессора является отдельным направлением, имеющем свои особенности. Применение таких систем позволяет лучше понять происходящие процессы, в сравнении с использованием специализированных программ, обладающих высокой стоимостью и требующих много времени для их освоения, а также не позволяющих увидеть применяемые механизмы. Например, специалисты полагают, что имитация при помощи таблиц Excel позволяет лучше представить работу систем массового обслуживания, чем даже теория очередей, а также помогает в развитии интуиции, предоставляет даже не знающим программирования пользователям опыт формирования разных моделей. Специалисты предлагают следующие этапы обучения моделированию в Excel:

1. Базовые понятия.
2. Введение в теорию вероятности и статистику.
3. Процесс имитационного моделирования в ручном режиме.
4. Имитационное моделирование при помощи электронных таблиц.
5. Генерирование случайных чисел.
6. Осуществление анализа исходных данных.
7. Осуществление анализа итогов моделирования.

При формировании моделей в Excelприменяются следующие главные подходы к осуществлению имитации:

1. Подход, который ориентирован на события.
2. Подход, имеющий ориентацию на процессы.
3. Подход, направленный на сканирование активностей.

Первый подход служит для описания изменений в системе, которые происходят при совершении любого случайного события, например, получение заявки, завершение обслуживания. При его формировании при помощи электронных таблиц обычно применяется одна строчка для каждого события.

Если используется подход, ориентированный на процесс, то выполняется моделирование очерёдности событий для каждой заявки, и чтобы его реализовать, применяется одна строчка для каждого требования (используется при моделировании систем массового обслуживания).

Сканирование активностей состоит в описании действий, возникающих в системе за фиксированный временной интервал (день, неделя, месяц, год), и при его осуществлении, как правило, применяется одна строчка для каждого отрезка времени. К примеру, это может быть моделирование системы управления запасами.

Использование программного пакета MSExcelобладает следующими преимуществами:

1. В составе пакета Excelесть значительное число встроенных функций из области математики, статистики и других областей, включая возможность генерации случайных значений.
2. Excelдаёт возможность сохранять информацию и иметь к ней доступ.
3. Программный пакетExcelпозволяет строить графики и диаграммы.
4. Программный пакет Excel обладает встроенным языкомVBA (VisualBasicforApplication).
5. Программный пакет Excelшироко распространён среди специалистов, то есть имеется на компьютере практически у всех.
6. Наличие возможности экспорта информационных данных в иные программные приложения.

Помимо этих достоинств, возможен просмотр любой формулы, занесённой в ячейку таблицы, что увеличивает уровень доверия к итогам моделирования.

Цели мероприятия:

1. Дидактические:

• рассмотрение этапов информационного моделирования на примере решения
  конкретных задач;
• закрепление навыков работы в MS Excel;
• установление межпредметных связей: информатики и математики.

2. Развивающие:

• развитие познавательного интереса, воображения;
• развитие умений применять знания на практике.

3. Воспитательные:

• расширение научного кругозора;
• воспитание самостоятельности в работе.

Учебно-методическое обеспечение: презентация (Презентация),
ПО MS Excel, ПО MS PowerPoint, методические указания.

Оборудование: мультимедийная установка, персональные компьютеры.

Ход конференции

Преподаватель: Межпредметное значение информатики в значительной
степени проявляется именно через внедрение компьютерного моделирования в
различные научные и прикладные области: математику и физику, технику, биологию и
медицину, экономику, управление и многие другие. С помощью компьютерного
моделирования решаются многие научные и производственные задачи. Гибким
инструментом для компьютерного моделирования является MS Excel.

Возможности электронных таблиц Microsoft Excel весьма многогранны. Всем
известно, что Excel является мощным вычислительным инструментом, позволяющим
производить простые и сложные расчеты в различных областях человеческой
деятельности: математике, физике, инженерных науках, экономике, технологии. На
этом уроке мы рассмотрим использование электронных таблиц для решения
математических задач и уравнений.

Теоретическая часть

Преподаватель: Рассмотрим этапы информационного моделирования.

1. Модель задачи.

Пусть вам надо решить какую-либо задачу, и вы хотите воспользоваться для
этого помощью компьютера. С чего начать? Прежде всего, нужно разобраться, что
дано, что требуется получить, как связаны исходные данные и результаты.
Предположения, которые позволяют в море информации об изучаемом явлении или
объекте определить исходные данные, понять, что будет служить результатом и
какова связь между исходными данными и результатом, называют моделью задачи.
(Презентация. Слайд 2)

2. Понятие математической модели.

В моделировании есть два различных пути. Во-первых, это использование
натурных моделей. Но если модель должна отображать реальность в абстрактной
форме, то в таком случае всегда привлекаются средства математики, и мы имеем
дело с математической моделью.

Математическая модель выражает существенные признаки объекта или процесса
языком уравнений и других математических средств. (Презентация. Слайд 3)

Собственно говоря, в историческом аспекте сама математика обязана своим
существованием тому, что пыталась отражать, т.е. моделировать, на своем
специфическом языке закономерности окружающего мира.

Под математической моделью понимают систему математических соотношений –
формул, уравнений, неравенств и т.д., отражающих существенные свойства объекта
или процесса. (Презентация. Слайд 3)

Математическое моделирование в наше время гораздо более всеобъемлющее, нежели
моделирование натурное. Математический аппарат для моделирования объектов и
процессов реального мира ученые использовали очень давно, но огромный толчок
математическому моделированию дало появление ЭВМ, которые сегодня помогают в
этой деятельности. Использование математического моделирования – это самый общий
метод научных исследований.

Простой пример. Представьте, что нужно определить площадь поверхности
письменного стола. Как обычно поступают в таком случае? Измеряют длину и ширину
стола, а затем перемножают полученные числа. Это фактически означает, что
реальный объект – поверхность стола – заменяется абстрактной математической
моделью – прямоугольником. Площадь этого прямоугольника и считается искомой
величиной.

Как видно, из всех свойств стола мы выделили три: форму поверхности
(прямоугольник) и длины двух сторон. Для нас не важны ни цвет стола, ни
материал, из которого он сделан, ни то, как стол используется. (Если бы мы
решали другую задачу о столе, например, сколько стоит его изготовление, то
возможно, для нас важна была бы как раз эта информация.) (Презентация. Слайд 4)

Предположив, что поверхность стола – прямоугольник, мы легко указываем
исходные данные и находим результат. Они связаны соотношение S = a * b.
(Презентация. Слайд 5)

Сделанное предположение позволило «перевести» нашу задачу на язык чисел: и
исходные данные, и результат – числа, а соотношение между ними задается
математической формулой.

Анализировать математические модели проще и быстрее, чем экспериментально
определять поведение реального объекта. Кроме того, анализ математической модели
позволяет выделить наиболее существенные свойства данного объекта (процесса), на
которые надо обратить внимание при принятии решения.

3. Этапы решения задач на компьютере.

1 этап. Постановка задачи – точная формулировка условий и целей
решения, описание наиболее существенных свойств объекта. (Презентация. Слайд 6)

2 этап. Построение математической модели – описание наиболее
существенных свойств объекта с помощью математических формул. (Презентация.
Слайд 6)

3 этап. Создание компьютерной модели – выражение математической модели
на понятном для компьютера языке. Существуют два принципиально различных пути
построения компьютерной модели:

1. Построение алгоритма решения задачи и его кодирование на одном из языков
   программирования.
2. Построение компьютерной модели и использованием ПО компьютера
   (приложений Windows – электронных таблиц, СУБД и пр.). (Презентация. Слайд
   7)

4 этап. Проведение компьютерного эксперимента (исследование модели) –
если компьютерная модель существует в виде программы на одном из языков
программирования, то её нужно запустить на выполнение и получить результаты;
если компьютерная модель исследуется в приложении, например, в электронных
таблицах, можно провести сортировку или поиск данных, построить диаграмму или
график и т.д. (Презентация. Слайд

5 этап. Анализ полученных результатов и корректировка модели – в
случае различия результатов, полученных при исследовании модели, с измеряемыми
параметрами реальных объектов можно сделать вывод, что на предыдущих этапах
построения модели были допущены ошибки или неточности. В этом случае необходимо
провести корректировку модели, причём уточнение модели может проводиться
многократно, пока анализ результатов не покажет их соответствие изучаемому
объекту. (Презентация. Слайд 9)

Рассмотрим конкретные задачи математического моделирования. Для этого будем
использовать приложение Windows – электронные таблицы MS Excel. Для этих целей в
Excel имеется много возможностей: вычисление по формулам, построение диаграмм и
графиков, поиск решения, подбор параметра и т.д.

Практическая часть

Студент 1:

Задача 1. Необходимо покрасить краской стены кухни. Сколько
потребуется банок краски, если известно, что

• размеры кухни 405 × 310 × 285 см;
• 88% площади стен занимает кафельная плитка;
• 1 банка краски предназначена для покраски площади 5 м²?
  (Презентация. Слайд 10)

Решение.

Постановка задачи.

Дано:

a = 405 см – длина комнаты,
b = 310 см – ширина комнаты,
c = 285 см – высота комнаты,
1 – 0,88 = 0,12 – часть комнаты для покраски (без кафеля),
5 м² – площадь покраски при использовании 1 банки краски.

Найти: необходимое для покраски стен кухни количество банок краски.
(Презентация. Слайд 11)

Математическая модель.

S_{стен с кафелем} =2(a + b)c.
S_{стен для покраски} = 2(a + b)c * 0,12.

Чтобы определить, сколько потребуется банок краски, надо площадь для покраски
разделить на 5 м², т. е. S_{стен для покраски} /5 и результат
округлить до целых.

Моделирование в среде ЭТ.

Заносим данные задачи в электронную таблицу, вводим формулы.
Электронная таблица в режиме отображения формул. (Приложение
1. Презентация. Слайд 12)
Электронная таблица в режиме отображения значений. (Приложение
2. Презентация. Слайд 13)
С помощью MS Excel мы определили, что для покраски стен кухни необходима 1 банка
краски.

Студент 2:

Задача 2. Через иллюминатор корабля требуется вытащить сундук с
драгоценностями. Удастся ли это сделать?

Решение.

Постановка задачи.

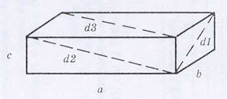
Иллюминатор корабля имеет форму круга. Будем считать, что сундук имеет форму
параллелепипеда. Чтобы вытащить сундук, необходимо, чтобы диаметр иллюминатора
был больше любой из трех диагоналей поверхности сундука. (Презентация. Слайд 14)

Математическая модель.

Пусть r – радиус иллюминатора,
a, b, c – размеры сундука,
d1, d2, d3 – диагонали боковых поверхностей сундука. (Презентация. Слайд 15)

Сундук можно вытаскивать через иллюминатор одной из трех боковых граней,
следовательно, достаточно, чтобы диагональ иллюминатора оказалась меньше одной
из трех диагоналей сундука, т.е. должно быть истинно хотя бы одно из условий:

ЕСЛИ((2*R>КОРЕНЬ(a^2+b^2));1;0)
ЕСЛИ((2*R>КОРЕНЬ(a^2+c^2));1;0)
ЕСЛИ((2*R>КОРЕНЬ(с^2+b^2));1;0)

(Презентация. Слайд 16)

Моделирование в среде ЭТ.

Заносим данные задачи в электронную таблицу, вводим формулы.
Электронная таблица в режиме отображения формул. (Приложение
3. Презентация. Слайд 17)
Электронная таблица в режиме отображения значений. (Приложение
4.Презентация. Слайд 18)

Компьютерный эксперимент.

В электронной таблице находим сумму трех условий. Если сумма равна 0, делаем
вывод «Сокровища недоступны», иначе «Сокровища доступны» (Слайд 19 Презентация).

Студент 3:

Задача 3. Решить уравнение х4-4х3-10х2+37х-14=0 (Слайд 20
Презентация).

Решение.

Необходимо построить график функции у = х⁴ – 4х³ – 10х²
+ 37х – 14. Точки пересечения графика с осью Х будут решениями данного
уравнения. Составляем в MS Excel таблицу значений функции. (Приложение
5. Презентация. Слайд 21)

Построим график функции (диаграмму). (Приложение 5.
Презентация. Слайд 22)

Мы видим, что график четырежды пересекает ось ОХ, значит уравнение х⁴
– 4х³ – 10х² + 37х –14 = 0 имеет четыре корня.

Из таблицы и графика можно определить промежутки, в которых находятся корни
этого уравнения:

х₁
[–3,5; –3], х₂
[0; 0,5], х₃
[2; 2,5], х₄
[4,5; 5].

(Презентация. Слайд 23)

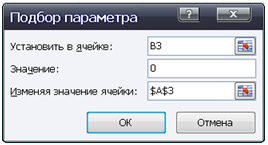
Затем с помощь анализа «что-если»/Подбор параметра можно
уточнить значения корней. Для этого следует активизировать ячейку со значением
функции у = 55,56, соответствующим значению аргумента х = -3,5, или ячейку со
значением у = -26, соответствующим х = -3, и выполнить команду Данные/группа
Работа с данными/Анализ «что-если»/Подбор параметра. Появится
одноименное диалоговое окно с тремя строками (Слайд 23 Презентация).

В первой строке указан адрес выбранного значения функции. Во второй нужно
установить курсор и занести подбираемое значение функции, указанное в правой
части данного уравнения (в нашем случае – число 0). А затем, установив курсор в
третьей строке, надо щелкнуть мышью на ячейке с соответствующим значением
аргумента, чтобы получить абсолютное значение этого адреса, затем щелкнуть ОК.

Аналогично проверяются корни из других промежутков.

Из результирующей таблицы выбираем корни уравнения. (Приложение
5. Презентация. Слайд 24)

Преподаватель: С особым вниманием следует применять этот способ для
решения уравнений, у которых графики функции не являются так называемыми
«гладкими» кривыми. Это касается, прежде всего, шага изменения аргумента при
построении графика соответствующей функции: он не должен быть слишком большим,
чтобы не пропустить значения некоторых корней.

Поясним это на примере решения уравнения.

Студент 4:

Задача 4. Решить уравнение log₂(x(1 – x)) – sin(π/x) + 2 =
0, область определения которого: x принадлежит промежутку (0;1). (Презентация.
Слайд 25)

Решение.

Если построить график соответствующей функции в области ее определения с
шагом h = 0,04, то получится один результат (Приложение 6.
Презентация. Слайд 27), но если построить тот же график с меньшим шагом h =
0,01, то мы получим иной результат. (Приложение 6.
Презентация. Слайд 27) Сравнение этих графиков показывает, что в первом случае
из-за слишком большого шага «потеряны» два первых корня. Всего же
рассматриваемое уравнение имеет шесть корней, которые уточняются с помощью
Подбора параметра. (Презентация. Слайд 28)

Вывод. (Презентация. Слайд 29)

1. С помощью электронных таблиц MS Excel можно решать математические задачи
   и уравнения.
2. При этом отрабатываются навыки работы в электронных таблицах, а именно:
   оформление таблицы, работа с формулами, построение диаграмм.

Литература:

1. О.К. Мясникова. Моделирование и формализация в курсе информатики. //
   Информатика и образование, №11-2003.
2. В.П. Кудинов. Решение уравнений с помощью MS Excel. // Информатика и
   образование, №3-2004.
3. Информатика и информационные технологии. Учебник для 10-11 классов /
   Н.Д. Угринович. – М.:Бином. Лаборатория знаний, 2003.

Тема: Моделирование в табличном процессоре MS Excel

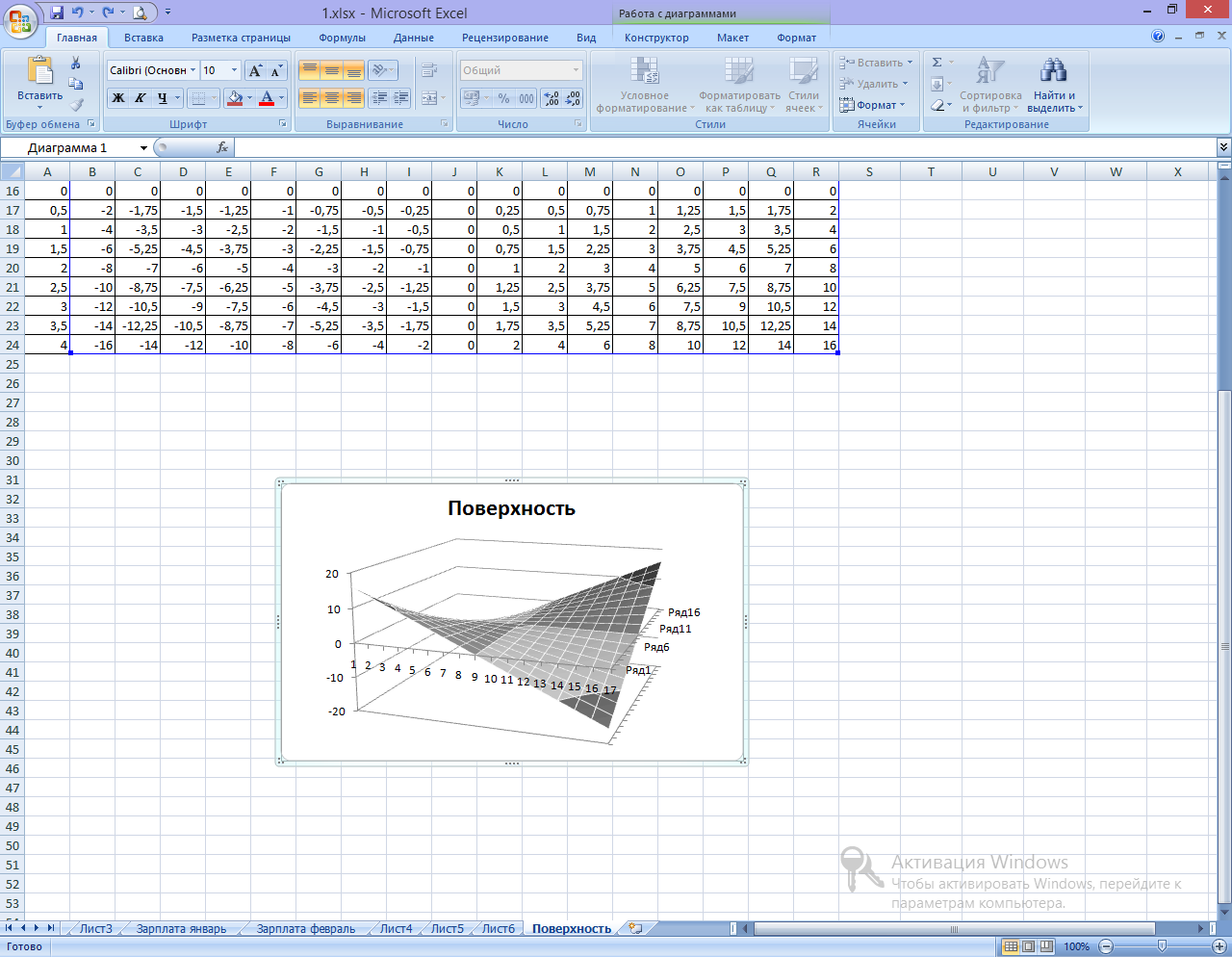
Цель занятия: применение табличного процессора MS Excel в моделировании. Построение поверхностей в трехмерной системе координат, форматирование и копирование созданных таблиц. Построение гистограмм.

ТСО: Компьютерный класс. Программное обеспечение (Windows XP), MS Office (Word, Excel).

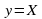
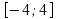
Задание 1. Построить график поверхности функции , заданной в промежутке с шагом 0,5.

Порядок работы

1. Запустить Excel.

2. Переименовать Лист7 → Поверхность.

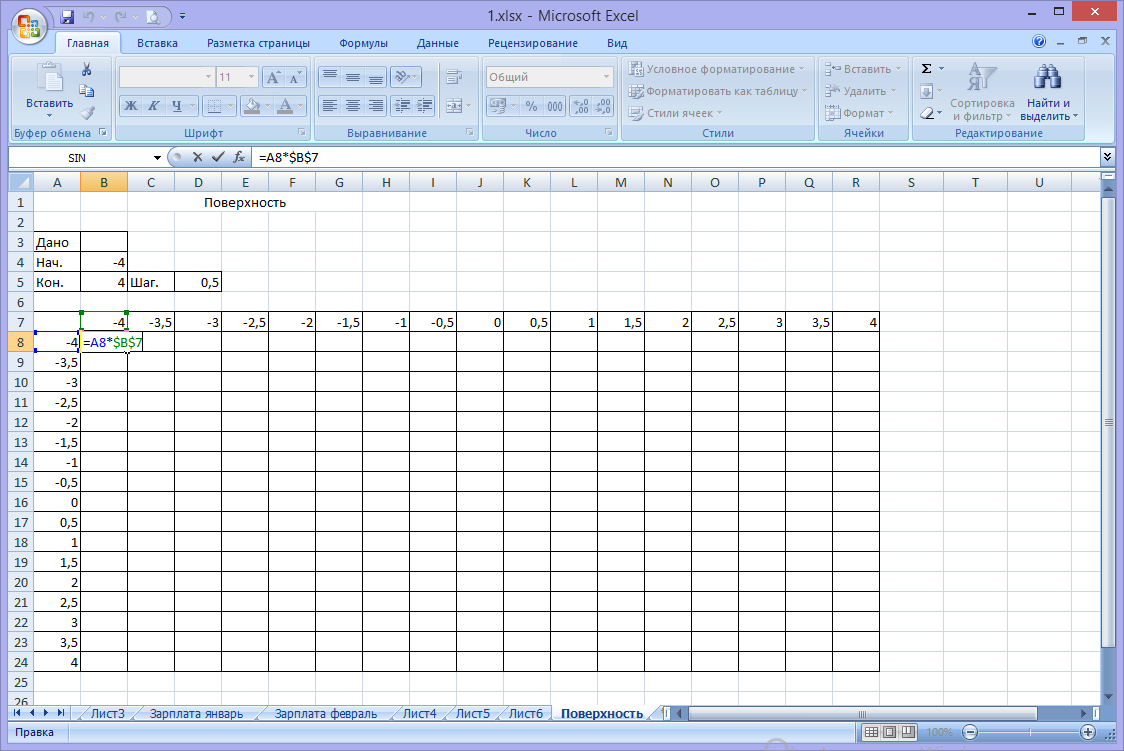
3. Ввести данные и заполнить столбец и строку, как указано на рисунке.

4. Составить расчетную формулу для заполнения столбца (диапазона) В8:В24 (это =A8*$B$7).

5. Заполнить столбец методом автокопирования.

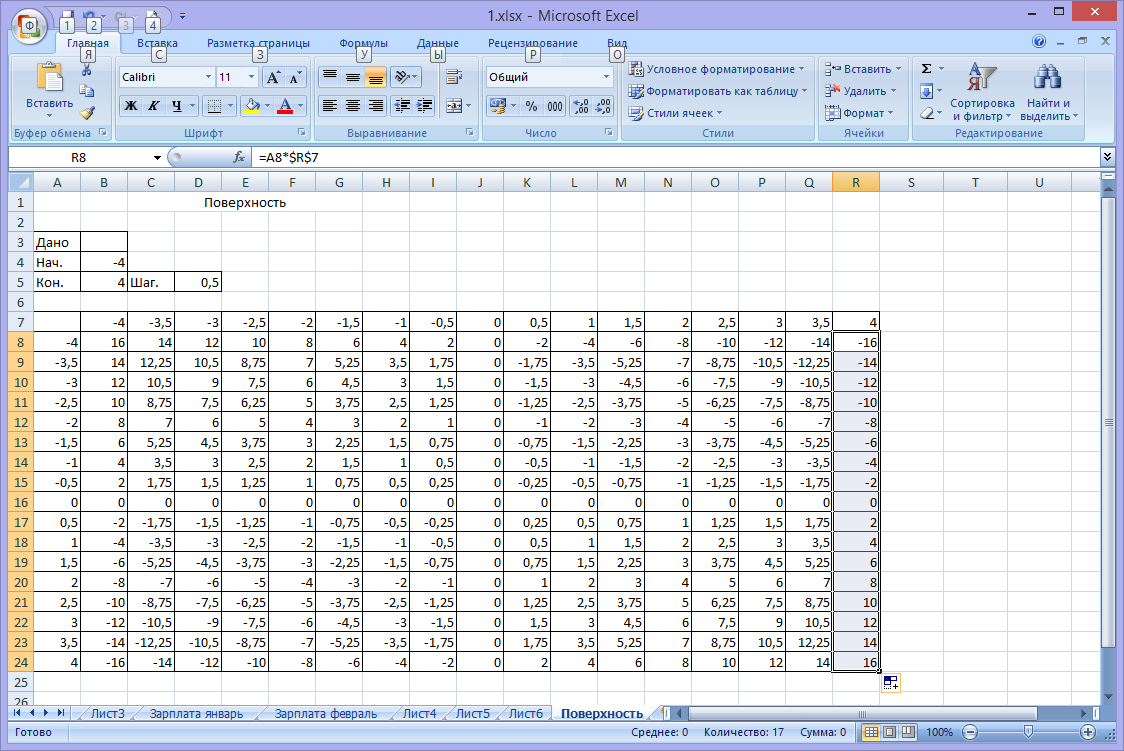
6. Скопировать исходную формулу и вставить в ячейку С8 и соответственно нужно изменить адрес ячейки $B$7 на $C$7 и получить расчетную формулу =A8*$C$7.

7. Повторить пункт 5.

8. Эти операции повторить до тех пор, пока не заполним таблицу.

9. Выделить диапазон В8:R24 и построить диаграмму «Поверхность».

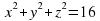
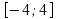
Задание 2. Построить поверхность в изометрической проекции, которая задается формулой в промежутке с шагом 0,5.

Формулы расчета значений таблицы в Excel:

=$A$2+B3 – для вычисления значений в интервале, столбец В.

=$A$2+C2– для вычисления значений в интервале, строка 2.

=КОРЕНЬ (16—В3^2-$С$2^2) – для вычисления значений в интервале, столбец С.

Ход выполнения задания

1. В ячейку A2 ввести значение шага 0,5 (абсолютный адрес).

2. В ячейку B3 ввести начальное значение заданного интервала, число – 4.

3. В ячейку B4 ввести первую форму = $A$2+B3, для расчета относительных адресов и нажать Enter.

4. Щелкнуть по ячейке В4. Подвести курсор к нижнему правому углу выделенной ячейки, как только курсор примет вид крестика «+», нажать левую клавишу мыши, и, не отпуская, протянуть маркер заполнения вниз, пока не увидите число 4 в ячейке В19.

5. В ячейку С2 ввести начальное значение из заданного интервала, число – 4.

6. В ячейку D2, ввести расчетную формулу =$A$2+C2, нажать Enter.

7. Щелкнуть по ячейке D2, и протянуть маркер заполнения курсором мыши по диапазону D2:S2, выделив все ячейки.

8. Установить курсор в ячейку С3, ввести формулу =КОРЕНЬ (16—В3^2–$С$2^2), и нажать Enter.

9. Щелкнуть повторно по ячейке С3.

10. Подвести курсор мыши к нижнему правому углу выделенной ячейки и, как только курсор примет вид крестика «+», нажать левую клавишу мыши и, не отпуская, протянуть маркер заполнения вниз, до ячейки С19.

11. Аналогичными действиями, нужно вводить формулы для ячеек D3, E3, … , S3, заменив адреса относительных ячеек на абсолютные адреса.

12. Щелкнуть повторно по ячейке D3.

13. Подвести курсор мыши к нижнему правому углу выделенной ячейки и, как только курсор примет вид крестика «+», нажать левую клавишу мыши, и, не отпуская, протянуть маркер заполнения вниз до ячейки D19.

14. В ячейку E3 ввести формулу =КОРЕНЬ (16—В3^2-$E$2^2), нажать Enter.

15. Щелкнуть повторно по ячейке E3.

16. Повторить пункт 10.

И соответственно ввести расчетные формулы в ячейках

F3 = КОРЕНЬ (16—В3^2—$F$2^2)

G3 = КОРЕНЬ (16—В3^2—$G$2^2)

…

…

S3 = КОРЕНЬ (16—В3^2—$S$2^2)

Для построения диаграммы, выделить в таблице область данных. Диаграмма строится стандартным образом. После получения диаграммы ее продемонстрировать.

Для более компактного размещения данных в Excel, нужно выполнить команду ФОРМАТ → Ячейки → Число → Числовой.

Задать число « Десятичных знаков» – 2.

И последняя операция – уменьшить размер столбцов.

Пример имитационной модели

NOTE:

To change the image on this slide, select the picture and delete it. Then click the Pictures icon in the placeholder to insert your own image.

§26

Информатика, 8 класс

Учитель информатики

Дворецкая Ю.Ю,

1

Основные темы параграфа

• Что такое имитационная модель
• Пример имитационного моделирования в электронной таблице

ОПРЕДЕЛЕНИЕ

ИМИТАЦИОННАЯ МОДЕЛЬ – это логико-математическое описание объекта, которое может быть использовано для экспериментирования на компьютере в целях проектирования, анализа и оценки функционирования объекта.

Имитационная модель имеет определенную минимальную опорную структуру, которую пользователь может дополнить и расширить с учетом специфики решаемых задач и базовых методов обработки.

ОПРЕДЕЛЕНИЕ

• ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ — это метод исследования, при котором изучаемая система заменяется моделью с достаточной точностью описывающей реальную систему и с ней проводятся эксперименты с целью получения информации об этой системе.

Отличие от математического моделирования

• имитационное моделирование исследует математические модели в виде алгоритмов , воспроизводящих функционирование исследуемой системы путем последовательного выполнения большого количества элементарных операций .
• в имитационных моделях для получения необходимой информации или результатов необходимо осуществлять их «прогон» в отличие от аналитических моделей, которые необходимо «решать».
• имитационные модели неспособны формировать свое собственное решение в том виде, в каком это имеет место в аналитических моделях, а могут лишь служить в качестве средства для анализа поведения системы в условиях, которые определяются экспериментатором.

Имитационные модели

В общем виде структуру имитационной модели в математической форме можно представляет следующим образом: ,

где E – результат действия системы;

x i – переменные и параметры, которыми мы можем управлять;

y i – переменные и параметры, которыми мы управлять не можем;

f – функциональная зависимость между x i и y i , которая определяет величину E .

Имитационные модели

Имитационная модель представляет собой комбинацию таких составляющих, как:

• компоненты;
• переменные;
• параметры;
• функциональные зависимости;
• ограничения;
• целевые функции.

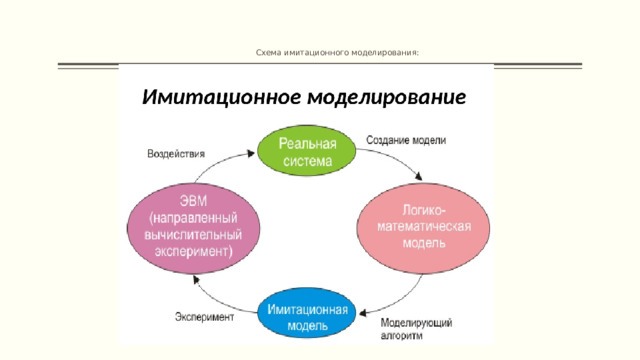
Схема имитационного моделирования:

НЕДОСТАТКИ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ:

• разработка имитационных моделей требует больших затрат, времени и сил;
• любая имитационная модель сложной системы менее объективна, чем аналитическая модель;
• результаты имитационного моделирования носят как правило частный характер, поэтому для предоставления обоснованных выводов необходимо провести серии модельных экспериментов.

Пример имитационного моделирования на компьютере

Имитационная модель воспроизводит поведение сложной системы, элементы которой могут вести себя случайным образом. Иначе говоря, поведение которых заранее предсказать нельзя.

Модель – эволюция популяций

• Пусть на определенном пространстве случайным образом расселяются живые организмы.
• В дальнейшем происходит процесс смены поколений: в каких-то местах расселения жизнь сохраняется, в каких-то исчезает.
• Эти процессы протекают в соответствии с законами эволюции (формальными правилами).

Цель моделирования — проследить изменения в расселении живых организмов со сменой поколений.

Имитационные модели

Законы эволюции:

• В следующем поколении в пустой ячейке жизнь может либо появиться, либо нет.
• В живой ячейке жизнь может либо сохраниться, либо исчезнуть
• На состояние данной ячейки влияют ее ближайшие соседи: два соседа слева и два соседа справа.
• Если ячейка была живая, и число живых соседей не превышает двух, то в следующем поколении в этой ячейке жизнь сохранится, иначе жизнь исчезнет (погибнет от перенаселения).
• Если в ячейке жизни не было, но среди ее соседей есть 1, 2 или 3 живые ячейки, то в следующем поколении в этой ячейке появится жизнь. В противном случае ячейка останется пустой.

Модельное описание процесса эволюции популяции

• Следует учитывать, что у ячеек, расположенных у края, число соседей меньше других.
• У ячейки номер 2 соседи: 1, 3 и 4.
• Но ячейка 1 всегда пустая.
• У ячейки номер 3 из четырех соседей живыми могут быть не больше трех (2,4,5).
• Аналогичная ситуация у крайних правых ячеек.

Кодирование

• Распределение живых организмов по ячейкам будем кодировать последовательностью из нулей и единиц.
• Ноль обозначает пустую ячейку , единица — живую .
• Например, расселение, отображенное на рис. 4.3, кодируется следующим образом:

00001001000100000000

Имитационные модели

Введем обозначения:

n — номер ячейки,

R (n) — значение двоичного числа, соответствующего этой ячейке в текущем поколении.

В рассматриваемом примере R (5) = R (8) =  R (12) = 1 .

Все остальные значения ячеек равны нулю.

Значения кода в n -й ячейке для следующего поколения будем обозначать S ( n ) .

Проанализировав правила эволюции, приходим к следующей формуле:

Если 1 R ( n — 2) + R ( n — 1) + R ( n ) + R ( n + 1) + R ( n + 2) 3, то S ( n ) = 1, иначе S ( n ) = 0.

Имитационные модели

Эта формула работает для значений n от 3 до 18 .

Всегда: S (1) = S (20) = 0 .

Для ячеек с номерами 2 и 19 в данной сумме нужно убрать по одному слагаемому. Но можно поступить иначе: для этого к отрезку добавим по одной фиктивной ячейке справа и слева.

Их номера будут, соответственно, 0 и 21. В этих ячейках, как и в ячейках 1 и 20, всегда будут храниться нули. Тогда написанную формулу можно применять для n от 2 до 19.

Итак, модель построена и формализована.

Имитационные модели

Для реализации применим табличный процессо р.

Моделью жизненного пространства будет строка электронной таблицы.

Первая строка — первое поколение,

вторая строка — второе поколение и т. д.

Тогда номера ячеек будут идентифицироваться именами столбцов таблицы.

Ячейка номер 0 — столбец А,

ячейка 1 — столбец В и т. д.,

ячейка 21 — столбец F.

=1; А1 + В1 + С1 + D1 + Е1 Далее, копируя эту формулу во все остальные ячейки второй строки с D2 по Т2, получаем картину распределения живых организмов во втором поколении. Чтобы получить третье поколение, достаточно скопировать вторую строку (блок С2:Т2) в третью строку (блок СЗ:ТЗ). Так можно продолжать сколько угодно. » width=»640″

• В первой строке выставляем единицы в ячейках, заселенных в первом поколении. Это будут ячейки F1, I1, М1 . Незаполненные ячейки по умолчанию приравниваются к нулю.
• Теперь в ячейки второй строки нужно записать формулы. Сделать это достаточно один раз. Например, в ячейку С2 занести следующую формулу:

ЕСЛИ(И(А1 + В1 + С1 + D1 + Е1 =1; А1 + В1 + С1 + D1 + Е1

• Далее, копируя эту формулу во все остальные ячейки второй строки с D2 по Т2, получаем картину распределения живых организмов во втором поколении.
• Чтобы получить третье поколение, достаточно скопировать вторую строку (блок С2:Т2) в третью строку (блок СЗ:ТЗ). Так можно продолжать сколько угодно.

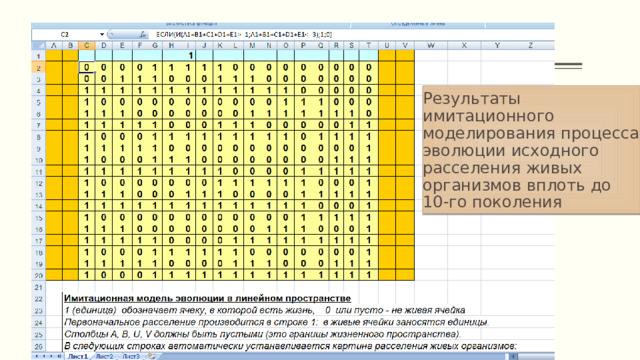
Результаты имитационного моделирования процесса эволюции исходного расселения живых организмов вплоть до 10-го поколения

Модель Дж. Конуэя «Жизнь»

В этой модели эволюция популяции живых организмов происходит в двумерном пространстве.

Рассматривается прямоугольная область, разделенная на квадратные ячейки. Тогда у каждой внутренней ячейки имеется 8 соседей. Судьба жизни в ячейке также зависит от состояния соседних клеток.

Но теперь правила эволюции такие:

• если клетка живая и в ее окружении более трех живых клеток, то она погибает от перенаселения;
• если же живых соседей меньше двух, то она погибает от одиночества.
• в пустой клетке в следующем поколении зарождается жизнь, если у нее есть ровно три живых соседа.

Домашнее задание

§26 конспект

Моделирование в электронных таблицах

Решим физическую задачу в Excel.  Построим компьютерную модель движения тела
в электронных таблицах. За основу возьмем формальную физическую модель
«Движение тела под углом к горизонту».

Найти через
какое время, и на каком расстоянии от места броска мячик упадет на землю. Если
начальная скорость мяча 20 м/с и угол броска 30, 45 и 60 градусов.

Надо построить математическую модель
задачи (формулу).Записать уравнение движения мат. точки относительно обеих
осей.

По этой модели построить электронную
таблицу для ввода и нахождения результатов.

 ;  

Ввести
начальные данные. Создать формулы:

Ячейка
F4
=$B$2*COS(РАДИАНЫ($B$3))*E4

Ячейка
G4
=$B$2*SIN(РАДИАНЫ($B$3))*E4-9,8*E4*E4/2

Ячейка
H4
=$B$2*SIN(РАДИАНЫ($B$4))*E4-9,8*E4*E4/2

Ячейка
I4
=$B$2*SIN(РАДИАНЫ($B$5))*E4-9,8*E4*E4/2

Скопировать формулы вниз по столбцам. Визуализировать
полученные данные с помощью графиков.

Для решения
общей оптимизационной задачи в Excel с использованием настройки Поиск решения следует
выполнить следующие действия:

1.                 
Ввести формулу для целевой
функции;

2.                 
Ввести формулы для ограничений
оптимизационной задачи;

3.                 
Выбрать в Excel пункт меню Сервис/Поиск
решения;

4.                 
В окне Поиск решения выбрать
целевую ячейку, изменяемые ячейки и добавить ограничения;

5.                 
Нажать кнопку Выполнить,
после чего будет получено решение оптимизационной
задачи.

Рассмотрим конкретную задачу условной
оптимизации (оптимизация с ограничениями). Решение
проблемы оптимизации перевозок на примере логистической задачи «Склады и
магазины города».

Постановка задачи:

Предположим, что компания, где вы
работаете, имеет два складских помещения, откуда товар поступает в пять ваших
магазинов, разбросанных по всему городу.

Каждый магазин в состоянии
реализовать определенное, известное нам количество товара. Каждый из складов
имеет ограниченную вместимость. Задача состоит в том, чтобы рационально выбрать
– с какого склада в какие магазины нужно доставлять товар, чтобы минимизировать
общие транспортные расходы.

Решение:

В математике подобные задачи
выбора оптимального маршрута по нескольким точкам относят к классу так называемых
«транспортных задач». Разработаны способы их решения. Excel предоставляет
пользователю один из них – с помощью настройки Поиск решения (Solver) в
меню Сервис (Tools).

Перед началом оптимизации
необходимо будет составить  таблицу на листе Excel –математическую модель,
описывающую ситуацию:

Подразумевается, что:

·        
серая таблица (B3:G5)
описывает стоимость доставки единицы от каждого склада до каждого магазина;

·        
лиловые ячейки (C14:G14)
описывают необходимое для каждого магазина количество товаров на реализацию;

·        
красные ячейки (J10:J11)
отображают емкость каждого склада – предельное количество товара, которое склад
может вместить;

·        
желтые (C12:G12) и синие
(H10:H11) ячейки – соответственно, суммы по строке и столбцу для зеленых ячеек;

·        
общая стоимость доставки (E17)
вычисляется как сумма произведений количества товаров на соответствующие им
стоимости доставки.

Таким
образом, наша задача сводится к подбору оптимальных значений зеленых ячеек.
Причем так, чтобы общая сумма по строке (синие ячейки) не превышала вместимости
склада (красные ячейки), и при этом каждый магазин получил необходимое ему
количество товаров на реализацию (сумма по каждому магазину в желтых ячейках
должна быть как можно ближе к требованиям – лиловым ячейкам).

Чтобы
выполнить такую оптимизацию, откроем меню Сервис (Tools) и выберем
команду Поиск решения (Solver). В Excel 2007 это будет кнопка Поиск
решения (Solver) на вкладке Данные (Data). Откроется вот такое окно:

В этом окне
нужно задать следующие настройки:

Целевая
ячейка – тут необходимо указать
конечную главную цель нашей оптимизации, т.е. розовую ячейку с общей стоимостью
доставки (E17). Целевую ячейку можно минимизировать (если это расходы, как в
нашем случае), максимизировать (если это, например, прибыль) или попытаться
привести к заданной константе.

Изменяемые
ячейки – здесь укажем зеленые ячейки
(C10:G11), варьируя значения которых, мы хотим добиться нашего результата –
минимальных затрат на доставку.

Ограничения
– список ограничений, которые надо учитывать при проведении оптимизации. В
нашем случае это ограничения на вместимость складов и потребности магазинов.
Для добавления ограничений в список нужно нажать кнопку Добавить и
ввести условие в появившееся окно:

Кроме очевидных ограничений,
связанных с физическими факторами (вместимость складов и средств перевозки,
ограничения бюджета и сроков и т.д.), иногда приходится добавлять ограничения
«специально для Excel». В нашем случае, например, нужно будет добавить вот
такое ограничение:

Оно
дополнительно уточнит, что объем перевозимого товара (зеленые ячейки) не может
быть отрицательным – для человека это очевидно, но для компьютера надо
прописать. После настройки всех необходимых параметров окно должно выглядеть
следующим образом:

Мы получим следующие результаты:

Следует
обратить внимание на то, как интересно распределились объемы поставок по
магазинам, не превысив при этом емкости складов и удовлетворив все запросы по
требуемому количеству товаров для каждого магазина.

Если найденное решение подходит, то
можно его сохранить, либо вернуться назад к исходным значениям и попробовать
еще раз с другими параметрами.

В практической деятельности человека
задачи, заключающиеся в поиске лучшего (оптимального) решения при наличии
различных критериев, встречаются часто. Решая такого рода задачи, учащиеся познают
суть математического моделирования
процессов и теории оптимизации.