Моделирование практические работы в excel с решением

Оптимизационное моделирование. Поиск решения

Большинство задач, решаемых с помощью электронной таблицы,
предполагают нахождение искомого результата по известным исходным данным. Но в
Excel есть инструменты, позволяющие решить и обратную задачу: подобрать
исходные данные для получения желаемого результата.

Одним из таких инструментов является Поиск решения,
который особенно удобен для решения так называемых «задач
оптимизации».

Начиная с версии Excel 2007 кнопка для запуска Поиска
решения появится на вкладке Данные. Для отображения этой кнопки
выполните следующую настройку: 

Параметры Excel – Надстройки – Надстройки Excel – Поиск
решения

Разберѐм порядок работы Поиска решения на
простом примере.

Пример 1. Распределение премии

Предположим, что Вы начальник производственного отдела и
Вам предстоит по-честному распределить премию в сумме 100 000 руб. между
сотрудниками отдела пропорционально их должностным окладам. Другими словами Вам
требуется подобрать коэффициент пропорциональности для вычисления размера
премии по окладу.

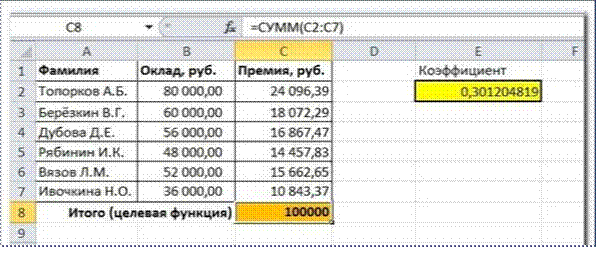
Первым делом создаѐм таблицу с исходными данными и
формулами, с помощью которых должен быть получен результат. В нашем случае
результат — это суммарная величина премии. Очень важно, чтобы целевая ячейка
(С8) посредством формул была связана с искомой изменяемой ячейкой (Е2). В
примере они связаны через промежуточные формулы, вычисляющие размер премии для
каждого сотрудника (С2:С7).

  Теперь запускаем Поиск решения и в открывшемся
диалоговом окне устанавливаем необходимые параметры. Внешний вид диалоговых
окон в разных версиях несколько различается:

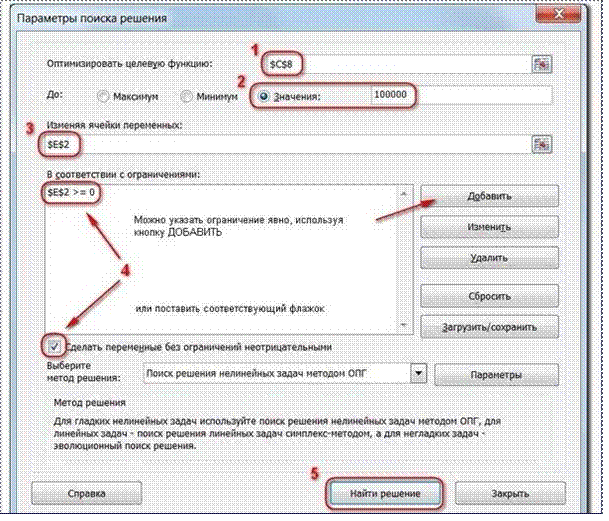
Целевая ячейка, в которой должен получиться желаемый
результат. Целевая ячейка может быть только одна

Варианты оптимизации:  максимальное возможное значение,
минимальное возможное значение или конкретное значение. Если требуется получить
конкретное значение, то его следует указать в поле ввода

Изменяемых ячеек может быть несколько: отдельные ячейки или
диапазоны. Собственно, именно в них Excel перебирает варианты с тем, чтобы
получить в целевой ячейке заданное значение Ограничения задаются с помощью
кнопки Добавить. Задание ограничений, пожалуй, не менее важный и сложный
этап, чем построение формул. Именно ограничения обеспечивают получение
правильного результата. Ограничения можно задавать как для отдельных ячеек, так
и для диапазонов. Помимовсем понятных знаков =, >=, <=, при задании
ограничений можно использовать варианты цел (целое), бин (бинарное
или двоичное, т.е. 0 или 1), раз (все разные — только начиная с версии
Excel 2010).

В данном примере ограничение только одно: коэффициент должен быть
положительным. Это ограничение можно задать по-разному: либо установить явно,
воспользовавшись кнопкойДобавить, либо поставить флажок Сделать
переменные без ограничений неотрицательными.

Для версий до Excel 2010 этот флажок можно найти в
диалоговом окне Параметры Поиска решения, которое открывается при
нажатии на кнопку Параметры

Кнопка, включающая итеративные вычисления с заданными
параметрами.

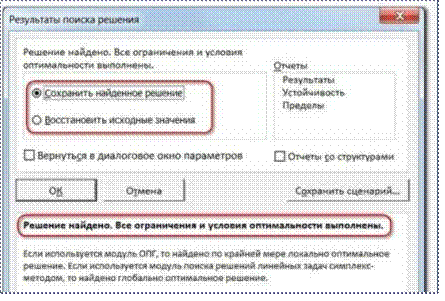
После нажатия кнопки Найти решение Вы уже можете
видеть в таблице полученный результат. При этом на экране появляется диалоговое
окно Результаты поиска решения.  

Если результат, который Вы видите в таблице Вас устраивает,
то в диалоговом окне Результаты поиска решения нажимаете ОК и
фиксируете результат в таблице. Если же результат Вас не устроил, то нажимаете Отмена
и возвращаетесь к предыдущему состоянию таблицы.

 Решение данной задачи выглядит так

Важно: при любых изменениях исходных данных для
получения нового результата Поиск решения придется запускать снова.

Разберѐм еще одну задачу оптимизации (получение
максимальной прибыли)

Пример 2. Мебельное производство (максимизация
прибыли)

Фирма производит две модели А и В сборных книжных полок.

Их производство ограничено наличием сырья
(высококачественных досок) и временем машинной обработки.

Для каждого изделия модели А требуется 3 м² досок, а
для изделия модели В — 4 м². Фирма может получить от своих поставщиков до
1700 м² досок в неделю.

Для каждого изделия модели А требуется 12 мин машинного
времени, а для изделия модели В — 30 мин. в неделю можно использовать 160 ч
машинного времени.

Сколько изделий каждой модели следует выпускать фирме в
неделю для достижения максимальной прибыли, если каждое изделие модели А
приносит 60 руб. прибыли, а каждое изделие модели В — 120 руб. прибыли?

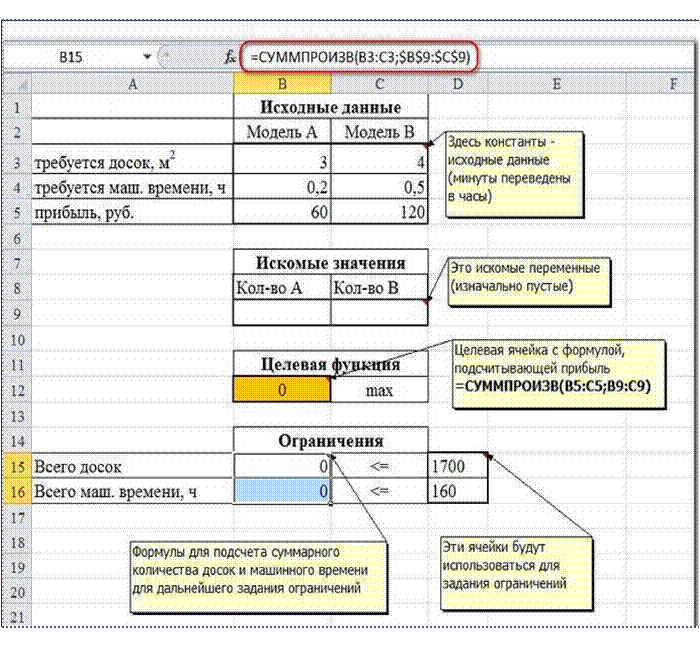
Сначала создаем таблицы с исходными данными и формулами.
Расположение ячеек на листе может быть абсолютно произвольным, таким как удобно
автору. Например, как на рисунке

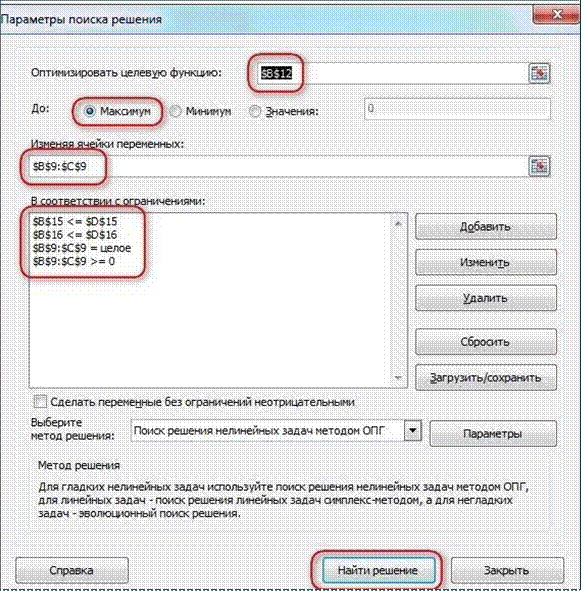
 Запускаем Поиск решения и в диалоговом окне
устанавливаем необходимые параметры

Целевая ячейка B12 содержит формулу для расчѐта
прибыли

Параметр оптимизации — максимум

Изменяемые ячейки B9:C9

Ограничения: найденные значения должны быть целыми,
неотрицательными; общее количество машинного времени не должно превышать 160 ч
(ссылка на ячейку D16); общее количество сырья не должно превышать 1700 м²
(ссылка на ячейку D15). Здесь вместо ссылок на ячейки D15 и D16 можно было
указать числа, но при использовании ссылок какие-либо изменения ограничений
можно производить прямо в таблице

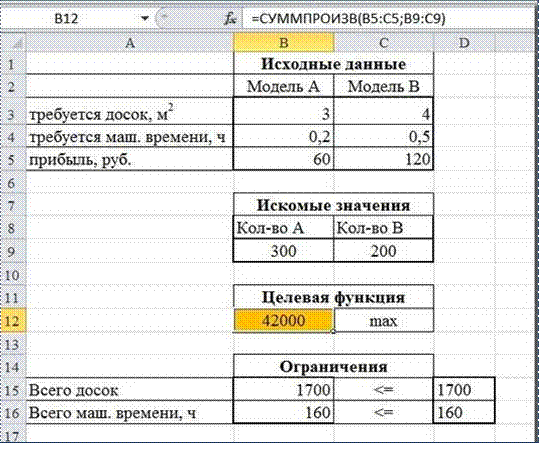
Нажимаем кнопку Найти решение (Выполнить) и после
подтверждения получаем результат

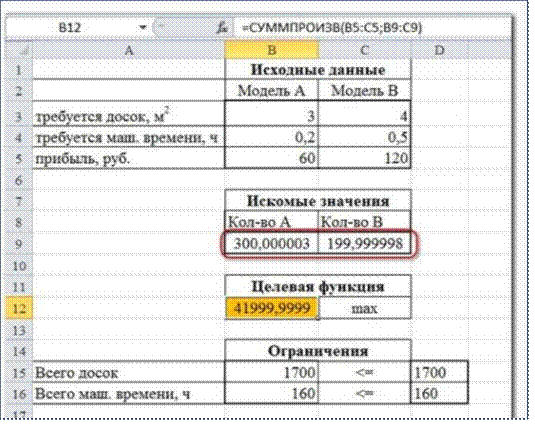
 Но даже если Вы правильно создали формулы и задали
ограничения, результат может оказаться неожиданным. Например, при решении
данной задачи Вы можете увидеть такой результат:

И это несмотря на то, что было задано ограничение целое.
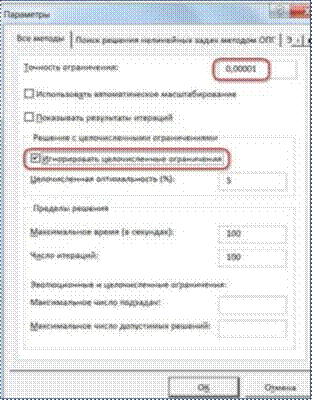
В таких случаях можно попробовать настроить параметры Поиска решения.
Для этого в окне Поиск решения нажимаем кнопкуПараметры и
попадаем в одноимѐнное диалоговое окно

Первый из выделенных параметров отвечает за точность
вычислений. Уменьшая его, можно добиться более точного результата, в нашем
случае — целых значений. Второй из выделенных параметров (доступен, начиная с
версии Excel 2010) даѐт ответ на вопрос: как вообще могли получиться
дробные результаты при ограничении целое? Оказывается Поиск решения
это ограничение просто проигнорировал в соответствии с установленным флажком.

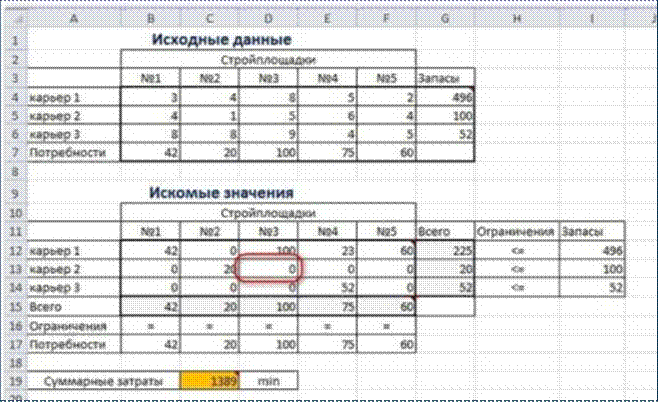
Пример 3. Транспортная задача (минимизация
затрат)

На заказ строительной компании песок перевозиться от трех
поставщиков (карьеров) пяти потребителям (строительным площадкам). Стоимость на
доставку включается в себестоимость объекта,  поэтому строительная компания
заинтересована обеспечить потребности своих стройплощадок в песке самым дешевым
способом.

Дано: запасы песка на карьерах; потребности в песке
стройплощадок; затраты на транспортировку между каждой парой
«поставщик-потребитель».

Нужно найти схему оптимальных перевозок для удовлетворения
нужд (откуда и куда), при которой общие затраты на транспортировку были бы
минимальными.

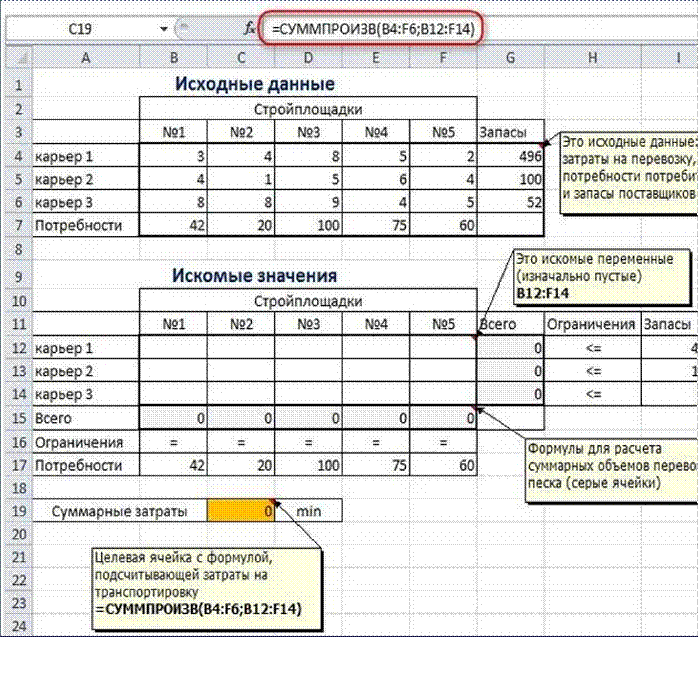
Пример расположения ячеек с исходными данными и
ограничениями, искомых ячеек и целевой ячейки показан на рисунке

В серых ячейках формулы суммы по строкам и столбцам, а в
целевой ячейке формула для подсчѐта общих затрат на транспортировку.

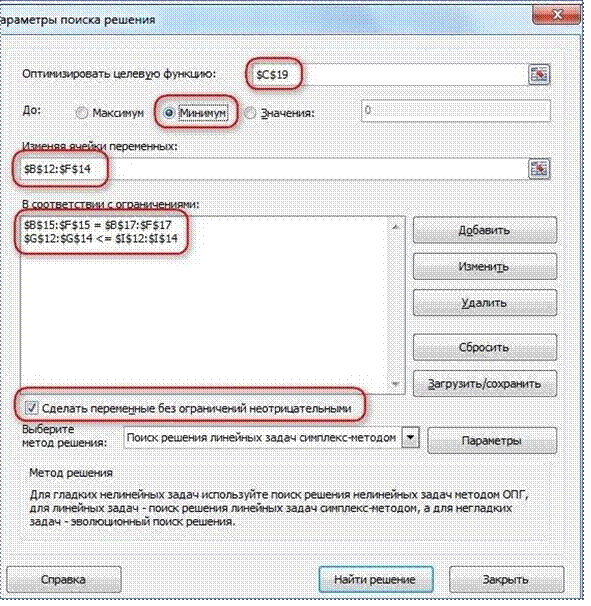
Запускаем Поиск решения и устанавливаем
необходимые параметры (см. рисунок)

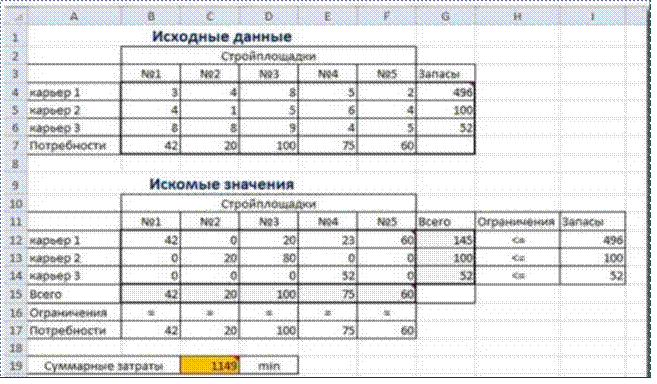
 Нажимаем Найти решение (Выполнить) и
получаем результат, изображенный ниже

 Иногда транспортные задачи усложняются с помощью
дополнительных ограничений. Например, по каким-то причинам невозможно возить
песок с карьера 2 на стройплощадку №3. Добавляем ещѐ одно ограничение $D$13=0.
И после запуска Поиска решения получаем другой результат

И последнее, на что следует обратить внимание, это выбор
метода решения. Если задача достаточно сложная, то для достижения результата
может потребоваться подобрать метод решения

Задача 4.(Старинная задача)

Крестьянин на базаре за 100 рублей купил 100 голов скота.
Бык стоит 10 рублей, корова 5 рублей, телѐнок 50 копеек. Сколько быков,
коров и телят купил крестьянин?

Практическая работа в EXCEL

«Моделирование знаковой модели: решение логического выражения»

Открыть EXCEL

Заполнить лист в соответствии с рисунком. Напишем основные логические операции.

Внимание! Русские слова пишутся заглавными русскими буквами (ЛОЖЬ, ИСТИНА); в адресах ячеек пишутся заглавные английские буквы (A2, B2)

Заполнить автоматически (навести курсор на правый нижний угол ячейки и появится черный крестик, провести им вниз) и получить значения логических функций

Пропустить две строки и ниже построить следующую таблицу

Чтобы решить логическое выражение, надо разбить на операции (соблюдать рейтинг логических операций!) и построить таблицу истинности логического выражения (А˅В)&НЕ(А˅В)

Сделать самостоятельно решить для следующих выражений:

А˅В˅ НЕ(А&В)

А˅В&С˅НЕ(А˅С)

Показать учителю и сохранить в своей папке под именем «Таблицы истинности»

Цели урока:

1. Обучающие: Повторить и закрепить навыки
   работы в MS Excel; научить применять современное
   программное обеспечение в решении
   математических задач, строить математические
   модели в среде MS Excel.




2. Развивающие: Развивать: практические и
   исследовательские навыки по составлению моделей
   в электронных таблицах, научное мировоззрение
   через связь информационных технологий с другими
   школьными предметами, логическое и
   алгоритмическое мышление, аналитические
   способности, внимание, память.




3. Воспитательные: Воспитание общей и
   информационной культуры, творческого подхода к
   работе, желания экспериментировать,
   самостоятельности в учебном труде.

Тип урока: Комплексного применения
знаний, обобщения и систематизации.

Программное и техническое обеспечение
урока:

• компьютеры с ОС MS Windows XP;

• пакет Microsoft Office;

• мультимедийный проектор

Время проведения урока: один из
последних уроков в разделе «Информационное
моделирование».

План урока: (40 минут)

1. Орг. момент. (1 мин)
2. Проверка и актуализация знаний. / Тестирование
   по теме (4 мин)./ Разминка (5 мин)
3. Теоретическая часть. (10 мин)
4. Практическая часть. (10 мин)
5. Самостоятельная работа. (8 мин)
6. Подведение итогов. Д/з (2 мин)

Ход урока:

1. Организационный момент.

Приветствие, проверка присутствующих.

С помощью проектора демонстрируется
на экране первый слайд презентации. Приложение 1

Сообщается тема урока: «Математическое
моделирование в среде электронных таблиц MS Excel
«.Озвучить цели и план урока.

2. Актуализация опорных знаний.

Пройденная нами тема «Электронные
таблицы»– одна из наиболее практически
значимых, востребованных, после текстового
редактора Word и его возможностей. Но электронные
таблицы не только позволяют автоматизировать
расчеты, но и являются эффективным средством
моделирования различных вариантов и ситуаций.
Меняя значения исходных данных, можно проследить
за изменением получаемых результатов и из
множества вариантов решения задачи выбрать
наиболее подходящий.

Перечислите, что вы научились делать,
изучая табличный процессор MS Excel?

– выполнять вычислительные операции
при помощи формул;

– составлять таблицы;

– строить графики и диаграммы.

Тестирование по теме «Электронные
таблицы».

Домашним заданием было повторить весь
изученный материал по теме «Электронные
таблицы». Чтобы проверить домашнее задание, я
предлагаю Вам ответить на вопросы электронного
теста. (Дети уже знакомы с работой системы
дистанционного обучения MyTestServer 1.1) Приложение 2

Перед началом работы учащиеся
прослушивают инструкцию по выполнению теста.

Тест состоит из 5 вопросов. Дается
только одна попытка, будьте внимательны, не
торопитесь. Время на тест 3 минуты.

После завершения тестирования каждому
ученику системой выставляется оценка, которую он
видит на экране своего монитора.

Сегодня на уроке мы будем использовать
электронные таблицы с их мощным вычислительным
потенциалом для решения математических задач –
построим математическую модель в среде MS Excel и
проведем небольшое исследование.

А для этого вспомним основные понятия
по теме “моделирование” (проводим устную разминку).

Вопросы разминки: Приложение 1

Моделирование – метод познания
окружающего мира, состоящий..

Модель – это объект, который
используется в качестве..

Различают ____________и ___________модели.

Натурные модели – это…

Информационные модели – это…

Основными видами информационных
моделей являются:_________ ,_________, __________.

А как вы думаете, математическая
модель к какому виду принадлежит?

Математическая модель – это модель,
построенная с использованием…

Приведите пример знаковой
информационной модели, рассматриваемой на
уроках математики.

Основным языком информационного
моделирования в науке является язык математики.

3. Теоретическая часть.

Какую бы жизненную задачу ни взялся
решать человек, первым делом он строит модель
заданного объекта. Очень часто задачи связаны с
потребностями человека.

Сегодня нам предстоит решить
следующую задачу:

Задача 1: Приложение
1

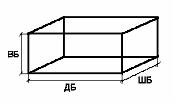
У маленького Васи есть небольшой
бассейн во дворе. Иногда Вася ходит к речке и
приносит воду в бассейн в небольшой цистерне
цилиндрической формы. Известны ширина ШБ, высота
ВБ, ДБ бассейна и объем цистерны Об Ц. Сколько раз
Васе нужно сходить к речке за водой, чтобы
наполнить бассейн наполовину?

Этот текст можно рассматривать как
словесную модель бассейна.

Постановка задачи: выяснение
условий

Какую форму может иметь бассейн?
(ответы детей).

А какой формы он в нашей задаче?– В
форме куба или параллелепипеда, потому, что даны
его параметры: ширина, высота, длина. А что еще нам
известно?

– объем цистерны.

Давайте попробуем решить задачу:
узнаем сколько раз (N) Васе нужно сходить к речке
за водой, чтобы наполнить бассейн наполовину.

Что для этого нужно знать?

– сколько цистерн воды помещается в
бассейн.

А как это узнать?

– определить объем бассейна (Об Б)

– сравнить половину объема бассейна и
объем цистерны (Об Б / Об Ц / 2).

4. Практическая часть.

Карточка – задание №1 Приложение 3

Задание для практической работы: Скопировать
в свою папку файл – шаблон Excel Приложение 4

Назвать лист номером задачи «Задача
1» (редактирование названия – двойной щелчок
мыши на «Лист 1»).

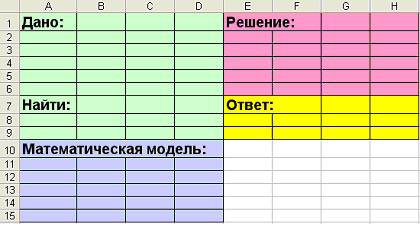
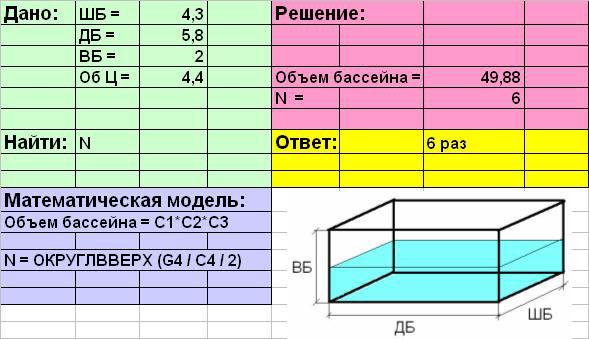
Оформить на листе решения разделы «Дано«,
«Найти«, «Математическая модель«,
«Решение«, «Ответ» (по образцу):

В ячейках А1и А7 напечатать
слова «Дано» и «Найти«.

Объединить ячейки А10, В10 и С10,
ввести текст: «Математическая модель«

Объединить ячейки Е1 и F1,
напечатать слово «Решение«.

В ячейку Е7 – «Ответ«.

 Заполнить таблицу начальными
данными.

В ячейки В1:В4 ввести текст: ШБ=;
ДБ=; ВБ=; Об Ц=.

В ячейки С1:С4; ввести
соответствующие значения параметров: 4,3; 5,8; 2; 4,5.

Для наглядности, если есть
возможность, можно построить графическую модель
(рисунок задаче) в Painte и скопировать ее в
электронную таблицу или нарисовать бассейн
непосредственно в Excel.

Далее заполнить раздел таблицы
«Математическая модель».

Объединить ячейки А11, В11 и С11,
ввести формулы (тип данных – текст) в раздел
(пробел перед знаком «=»). «Объем бассейна
=С1*С2*С3«

Объединить ячейки А13, В13 и С13
и ввести текст «N = ОКРУГЛВВЕРХ(G4 / C4 / 2)«.
(для получения целого числа используем функцию
округления ОКРУГЛВВЕРХ)

В разделе «Решение»
создать сетку вычислений:

– Обозначить искомые и промежуточные
величины.

– Объединить ячейки Е4 и F4,
ввести текст: «Объем бассейна =«. В ячейку
Е5 – «N =«(тип данных – текст).

В ячейки G4 и G5; ввести
соответствующие формулы (тип данных – формулы):
=С1*С2*С3;

Используем функцию округления
дробного числа до целого:

Вставка-функция – математические –
ОКРУГЛВВЕРХ – число разрядов выбираем «0«.

=ОКРУГЛВВЕРХ(G4 / C4 / 2)

В разделе «Ответ» запишем
искомый результат в ячейку G7 (тип данных –
текст).

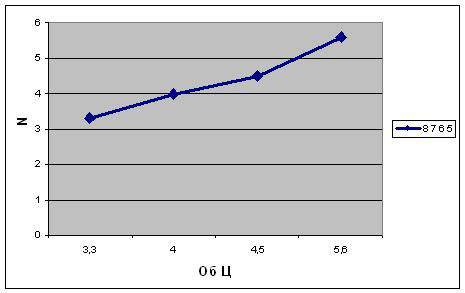
 Проведем небольшое исследование:

Вопрос: Сколько раз Васе нужно будет
сходить к речке за водой, если он возьмет
цистерну емкостью 5,6 литров; 4 литра; 3,3
литра?

Меняем в ячейке С4 значение на 5,6
и электронные таблицы автоматически производят
пересчет.

Создадим таблицу значений Об Ц и
будем заносить в нее результаты вычислений N.

Введем в ячейку А20 и В2 текст
«Об Ц» и » N«. Заполним таблицу
данными.

Для графического представления
результатов выделить диапазон А21: В24,
построить график функции, отредактировать его.

 Анализ полученных результатов.

5. Самостоятельная работа.

Задание для самостоятельной разработки:

Карточка – задание №2 Приложение
3

Задача 2. Пешеход начал движение из
начала координат со скоростью V=0,6 м/с.
Найдите, какой путь S прошел пешеход за одну
минуту t после начала движения, если он
двигался равномерно.

Постановка задачи: выяснение
условий

Скажите, что мы будем моделировать? –

– движение

Какие виды движения вы знаете? (ответы
детей)

Какое движение рассматривается в
нашей задаче?

– равномерное. Приложение 1

Давайте вспомним формулу расчета
скорости: V=s/t– отсюда s=V*t

Технология моделирования:

1. Назвать лист номером задачи «Задача 2»
   (редактирование названия – двойной щелчок мыши
   на «Лист 2»).
2. Выделить расчетную таблицу на листе «Задача1»
   и скопировать ее на лист «Задача 2«.
3. Заполнить таблицу новыми начальными данными.
4. Ввести формулу (тип данных – текст) в раздел
   «Математическая модель» (пробел перед
   знаком «=»).
5. Ввести фоpмулу (тип данных – формулы) в
   раздел «Решение«.
6. В разделе «Ответ» записать искомый
   результат (тип данных – текст).




7. Создать таблицу значений t и занести в нее
   результаты вычислений S. Заполнить таблицу
   данными.
8. Для графического представления результатов
   выделить область аргументов и функций, построить
   график зависимости пути S от времени при t=40;60;90,
   отредактировать график.

6. Итог урока.

Сегодня на уроке мы узнали, как можно
использовать электронные таблицы в решении
математических задач, научились строить
математические модели в. среде MS Excel

Домашним заданием будет: самим
придумать задачу, разработать ее математическую
модель.

У кого есть вопросы по пройденному материалу?

Спасибо за работу. Вы сегодня молодцы. Можете
быть свободны.

Практическая проверочная работа по теме «Моделирование в

Excel» для 11 класса

По материалам моих статей по теме «Моделирование»

https://урок.рф/library/izuchenie_temi_%C2%ABmodelirovanie%C2%

BB_v_11_klasse_chast_1_193503.html

и

https://урок.рф/library/izuchenie_temi_%C2%ABmodelirovanie%C2%

BB_v_11_klasse_chast_2_091345.html

составлена практическая проверочная работа в пяти вариантах

с ответами.

Вариант 1

1. Дана функция y=5sin

2

(x+l )-4cos(x-l)+6 . Построить таблицу

значений и график функции на интервале [-6.3; 6.7]. Ответить на

вопросы: а) значение функции в точке х=-2,3;

б) количество минимумов функции на данном интервале.

2. Работники предприятия имеют следующую заработную плату:

Иванов — 4567руб., Петров 7435руб., Сидоров — 8421руб., Попов — 6872руб.,

Васина —5994руб. Руководство предприятия выделило на поощрение

сотрудников 19000руб., пропорционально их заработной плате.

Определите:

а) коэффициент премии; б) премию Попова.

Вариант 2

1. Дана функция y=5cos

2

(x+1 )-4sin(x-1 )+6 . Построить таблицу

значений и график функции на интервале [—6.3; 6.7]. Ответить на

вопросы: а) Значение функции в точке х=2.7;

б) количество максимумов функции на данном интервале.

2. В живом уголке школы есть ёжик, белка, две морские свинки,

три хомячка и черепаха. В день ёж съедает 90 г корма по цене 123

руб./кг, белка 130 г по цене 260 руб./кг, морская свинка 160 г по цене 58

руб./кг, хомячок 80 г по цене 186 руб./кг, черепаха 35 г но цене 540

руб./кг. Руководство школы выделило 3000 руб. на содержание

животных. Определить: а) на сколько дней хватит закупленного корма;

б) сколько денег пойдет на содержание белки.

Вариант 3

1. Дана функция y=5cos(2x+1 )-4sin(x-1 )+6 . Построить таблицу