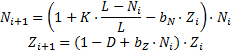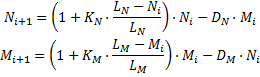Моделирование популяции животных в excel решение практическая работа

Единственный в мире Музей Смайликов Самая яркая достопримечательность Крыма

Скачать 94 Kb. Название Практическая Работа 10 Моделирование развития популяции Для выполнения работы откройте файлзаготовку Популяция xls Дата 24.10.2022 Размер 94 Kb. Формат файла Имя файла practice11-2bu_1.doc Тип Практическая работа #752052

---

Глава 2.      
Моделирование

Практические работы

Практическая работа № 6.       

Моделирование работы процессора

1.      
Напишите программу, которая моделирует работу процессора. Процессор
имеет 4 регистра, они обозначаются R0, R1, R2 и R3. Все команды состоят из трех
десятичных цифр: код операции, номер первого регистра и номер второго регистра
(или число от 0 до 9). Коды команд и примеры их использования приведены в
таблице:

Код операции	Описание	Пример	Псевдокод
1	запись константы	128	R2 := 8
2	копирование значения	203	R3 := R0
3	сложение	331	R1 := R1 + R3
4	вычитание	431	R1 := R1 – R3

Обратите внимание,
что результат записывается во второй регистр. Команды вводятся
последовательно как символьные строки. После ввода каждой строки программа
показывает значения всех регистров.

2.      
*Добавьте в систему команд умножение, деление и логические операции c
регистрами – «И», «ИЛИ», «исключающее ИЛИ».

3.      
*Добавьте в систему команд логическую операцию «НЕ». Подумайте, как
можно использовать второй регистр.

4.      
*Сделайте так, чтобы в команде с кодом 1 можно было использовать
шестнадцатеричные значения констант (0-9, A-F).

5.      
Добавьте обработку ошибок типа «неверная команда», «неверный номер
регистра», «деление на ноль».

6.      
*Добавьте команду «СТОП», которая прекращает работу программы. Введите
строковый массив, моделирующий память, и запишите в него программу –
последовательность команд. Ваша программа должна последовательно выполнять эти
команды, выбирая их из «памяти», пока не встретится команда «СТОП».

7.      
**Подумайте, как можно было бы организовать условный переход: перейти на
N байт вперед (или назад), если результат последней операции – ноль.

Практическая
работа № 7.       

Моделирование движения

1.      
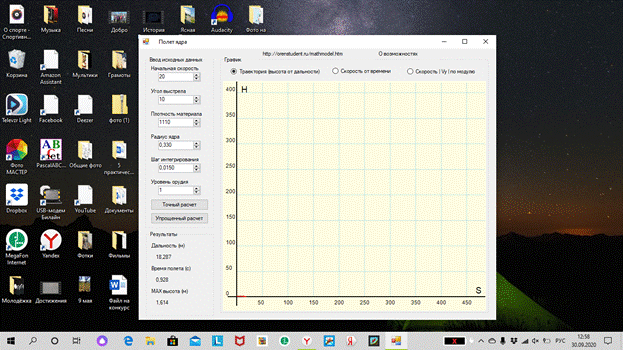
Парашютист массой 90 кг разгоняется в свободном падении до скорости
10 м/с и на высоте 50 м раскрывает парашют, площадь которого 55 м².
Коэффициент сопротивления парашюта равен 0,9. Выполните следующие задания:

·   
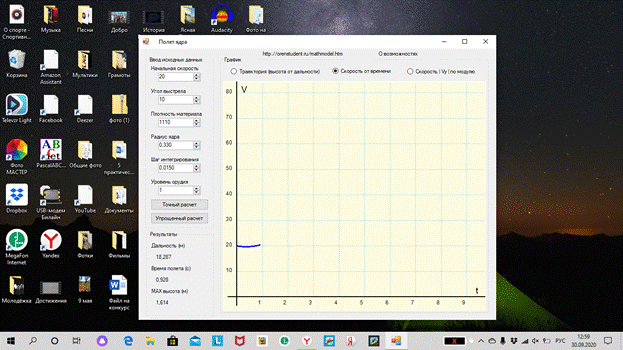
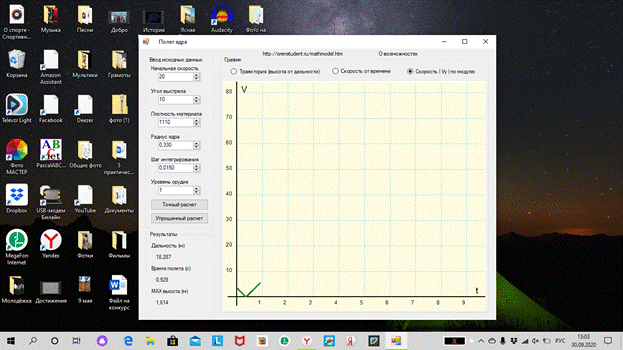
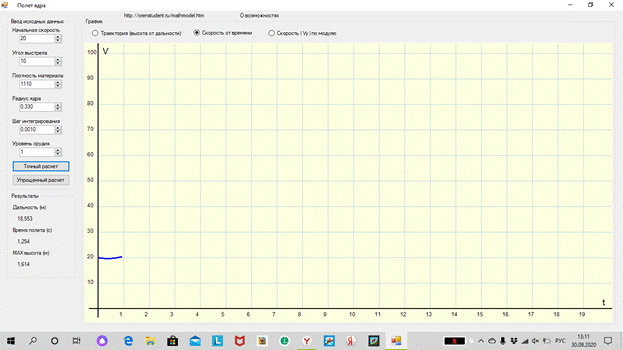
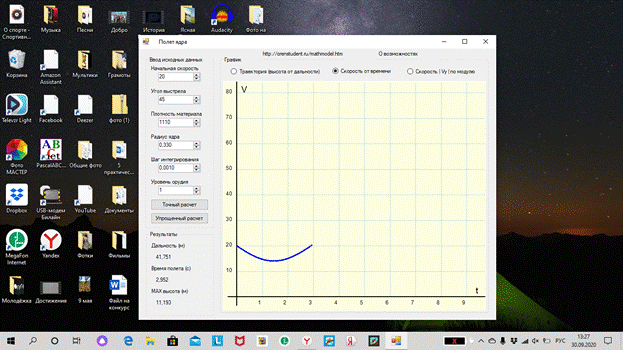
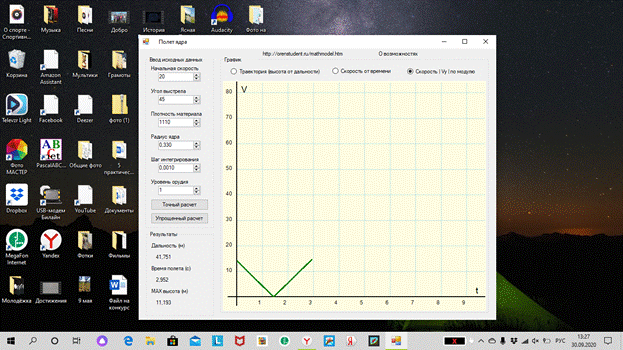
постройте графики изменения скорости и высоты полета в течение
первых 4 секунд;

·   
определите, с какой скоростью приземлится парашютист?

2.      
Напишите программу, которая моделирует полет мяча, брошенного
вертикально вверх, при

мм, г, м/с, с.

Остальные
необходимые данные есть в тексте § 9. Выполните следующие задания:

·    определите
время полета, максимальную высоту подъема мяча и скорость в момент приземления;

·   
вычислите время полета и максимальную высоту подъема мяча,
используя модель движения без сопротивления воздуха:

	без учёта сопротивления	с учётом сопротивления
Время полета, с	1,207	0,928
Максимальная высота, м	1,823	1,647
Дальность, м	18,485	18,289

·   
с помощью табличного процессора постройте траекторию движения
мяча, а также графики изменения скорости, ускорения и силы сопротивления;

·   
уменьшите шаг до 0,01 с и повторите моделирование; сделайте
выводы по поводу выбора шага в данной задаче.

Ответ:

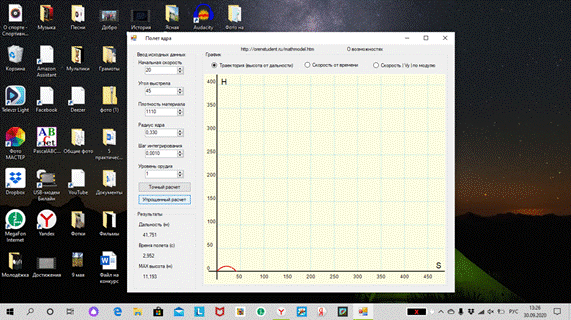
3.      
*Выполните моделирование движения мяча, брошенного под углом 45° к
горизонту:

·   
определите время полета, максимальную высоту и дальность полета
мяча, скорость в момент приземления;

	без учёта сопротивления	с учётом сопротивления
Время полета, с	2,952	2,720
Максимальная высота, м	11,193	10,950
Дальность полета, м	41,751	41,413

Практическая
работа № 8.       

Моделирование популяции животных

Для
выполнения работы откройте файл-заготовку Популяция.xls.

1.      
Постройте графики изменения численности популяции животных для моделей
ограниченного и неограниченного роста при ,  и
 в течение первых 15 периодов. 

2.      
Используя модель ограниченного роста из предыдущей задачи, выполните следующие
задания:

·   
определите количество животных в состоянии равновесия по
результатам моделирования; зависит ли оно от начальной численности?

Ответ:

От
начальной численности в данный момент ничего  не зависит, т.к это неизменяемая
величина, а численность животных зависит от периода времени.

·   
определите, на что влияет начальная численность животных;

Ответ:

Все будет зависеть от
кормовой базы, от наличия хищников, от паразитов, от болезней в популяции, от
разветвленных пищевых сетей.

·   
*определите максимально допустимый отлов теоретически, из модели
ограниченного роста с отловом; сравните это значение с результатами
моделирования

Ответ:

Практическая
работа № 9.       

Моделирование эпидемии

Для
выполнения работы откройте файл-заготовку Эпидемия.xls.

При эпидемии гриппа число больных
 изменяется по формуле

,

где – количество заболевших в -й день,
а – количество выздоровевших в тот же
день. Число заболевших рассчитывается согласно модели ограниченного роста:

,

где –
общая численность жителей, – коэффициент роста и – число переболевших (тех, кто уже
переболел и выздоровел, и поэтому больше не заболеет):

.

Считается, что в начале эпидемии
заболел 1 человек, все заболевшие выздоравливают через 7 дней и больше не
болеют.

Выполните моделирование развития эпидемии при  и  до
того момента, когда количество больных станет равно нулю. Постройте график
изменения количества больных.

Ответьте на следующие вопросы:

1.      
Когда закончится эпидемия?

Ответ:

Когда
количество выздоровевших в сутки начнёт превышать количество заболевших за
сутки.

2.      
Сколько человек переболеет, а сколько вообще не заболеет гриппом?

Ответ:

В
данный момент переболело 283 человека, т.е приблизительно 1/3 всего населения,
возможно, что всего переболеет 2/3 населения, а 1/3 населения вовсе не
заболеет, на это влияют такие факторы, как: отсутствие контакта с заболевшими,
крепкий иммунитет, профилактика и т.д

3.      
Каково максимальное число больных в один день?

Ответ:

65

4.    
Изменяя коэффициент , определите, при каких
значениях  модель явно перестает быть
адекватной.

Ответ:

При
отрицательных числах, при нуле и единице.

Практическая
работа № 10.  
Модель «хищник-жертва»

Для
выполнения работы откройте файл-заготовку ХищникЖертва.xls.

Выполните моделирование
биологической системы «щуки-караси»

где          – численность карасей

 – численность щук

при следующих
значениях параметров:

 –
коэффициент прироста карасей;        

 – предельная численность карасей;

 – начальная численность карасей;

 – начальная численность щук;

 –
коэффициент смертности щук без пищи;

 и  – коэффициенты модели.  

Постройте на
одном поле графики изменения численности карасей и щук в течение 10 периодов
моделирования.

Ответьте на следующие вопросы:

1.      
Что влияет на количество рыб в состоянии равновесия: начальная
численность хищников и жертв или значения коэффициентов модели?

Ответ:

Наибольшую
роль играет начальная численность животных.

2.      
На что влияет начальная численность хищников и жертв?

Ответ:

В
основном на численность вида в определенный период.

3.      
Подберите значения коэффициентов, при которых модель становится
неадекватна.

Ответ:

При
нуле и при отрицательных значениях.

 

Практическая
работа № 10а.

Модель «две популяции»

Для
выполнения работы откройте файл-заготовку ДвеПопуляции.xls.

Белки и бурундуки живут в одном
лесу и едят примерно одно и то же (конкурируют за пищу). Модель, описывающая
изменение численности двух популяций, имеет вид: 

Здесь  и
– численность белок и бурундуков;  и – их максимальные численности;  и – коэффициенты прироста;  и – коэффициенты взаимного влияния.

Выполните моделирование изменения
численности двух популяций в течение 10 периодов при , , , ,  и . Постройте графики изменения
численности обеих популяций на одном поле.

Ответьте на следующие вопросы:

1.      
Является ли эта модель системной? Почему?

Ответ:

Нет,
т.к система представляет собой определённые цели и задачи, а в нашей модели это
не прослеживается

2.      
Какова численность белок и бурундуков в состоянии равновесия?

Ответ:

Различна,
отличие составляет несколько десятков

3.      
Что влияет на состояние равновесия?

Ответ:

Среда
обитания животных, наличие корма, конкуренция — это самые основные черты,
влияющие на состояние равновесия.

4.      
На что влияет начальная численность животных?

Ответ:

  На количество животных в различные периоды времени.

Практическая
работа № 11.  
Саморегуляция

Для
выполнения работы откройте файл-заготовку Саморегуляция.xls.

Биологи выяснили, что для каждого
вида животных существует некоторая минимальная численность популяции, которая
необходима для выживания этой колонии. Это может быть одна пара животных
(например, для ондатр) или даже тысячи особей (для американских почтовых
голубей). Если количество животных становится меньше этого минимального
значения, популяция вымирает.  Для этого случая предложена следующая модель
изменения численности:

                                                                        ,                                                           (*)

Эта модель отличатся от модели
ограниченного роста только дополнительным множителем , где и
– некоторые числа (параметры),
смысл которых вам предстоит выяснить.

1.      
Выполните моделирование для 30 периодов при следующих значениях
параметров модели:

Сравните
результаты, которые дают модель классическая модель ограниченного роста и
модель (*). Сделайте выводы и опишите, в чём проявляется саморегуляция для этих
моделей.

Ответ:

2.    
Постепенно увеличивая коэффициент от 0 до 500, выясните с помощью
моделирования, как влияет этот коэффициент на саморегуляцию.

Ответ:

3.      
Через 10 периодов в результате изменения природных условия число
животных уменьшилось до 400 (то есть, ). Выполните моделирование при этих
условиях и опишите, как работает саморегуляция и чем отличается поведение двух
сравниваемых моделей.

Ответ:

4.    
Повторите моделирование п. 3 при  и сделайте аналогичные выводы:

Ответ:

5.      
Экспериментируя с моделями, найдите минимальную численность популяции , при которой она выживает в
соответствии с моделью (*). 

Ответ:

6.    
Сделайте выводы о смысле коэффициента  в
модели (*).

Ответ:

7.      
Сравните свойства саморегуляции для модели ограниченного роста  и модели
(*).

Ответ:

Практическая
работа № 12.  
Моделирование работы банка

Для моделирования
обслуживания клиентов в банке предложена следующая модель:

·   
за 1 минуту в банк входит случайное число клиентов, от 0 до  (распределение равномерное);

·   
на обслуживание клиентов требуется от  до  минут; время обслуживания определяется
для каждой рабочей минуты случайным образом (распределение равномерное);

·  
моделирование выполняется для интервала времени ,
равного 8-часам (рабочая смена). 

·   
число клиентов, находящихся в помещении банка, вычисляется по
формуле

где
 – количество клиентов, вошедших за
-ую минуту, а  – количество клиентов, обслуженных
за это время;

·  
если кассир обслуживает клиента за  минут,
то можно считать, что за 1 минуту он сделает часть работы, равную ; если предположить, что скорость
работы кассиров одинакова, то  касс за 1 минуту
обслужат  клиентов;

·  
если считать, что  клиентов равномерно
распределяются по  кассам, так что средняя длина
очереди равна , а среднее время ожидания в
течение этой минуты равно

·  
достаточным считается число касс, при которых среднее время
ожидания  превышает установленный предел не
более, чем 5% рабочего времени в течение дня.

Используя эту
вероятностную модель работы банка, напишите программу, с помощью которой
определите минимальное необходимое количество касс  при следующих исходных
данных:

, , , .

begin

Pmax:=4;

Tmin:=1;

Tmax:=9;

L:=480;

M:=15;

N:=0;

count:=0;

from ;  random ;import ;random; randint;

  for i : integer:=range(L) to

P=randint(0.Pmax)do;

T;Tmin ; random(); (Tmax  — Tmin);

R ; round(K / T);

N+= P-R;

if N < 0 then  N;0:

dT; N ; K ; T;

if dT > M then   count += 1;

end.

Практическая работа «Моделирование популяции животных»
Для выполнения работы откройте файл-заготовку Популяция.xls. (Файл прикреплен)
1. Постройте графики изменения численности популяции животных для моделей ограниченного и неограниченного роста при N0=140, K=0,3 и L=1000 в течение первых 15 периодов. Определите, когда модель неограниченного роста перестает быть адекватной (отклонение от модели ограниченного роста составляет более 10%).
2. Используя подбор параметра, определите, при каких коэффициентах K модель неограниченного роста остается адекватной в течение не менее 10 периодов.
3. Используя модель ограниченного роста из предыдущей задачи, выполните моделирование популяции с учетом отлова (R=100). Предполагается, что животных начали отлавливать через 10 лет после начала наблюдений.
— постройте график изменения численности животных;
— определите количество животных в состоянии равновесия по результатам моделирования; зависит ли оно от начальной численности?
— определите количество животных в состоянии равновесия теоретически, из модели ограниченного роста с отловом; сравните это значение с результатом моделирования;
— определите, на что влияет начальная численность животных;
— определите (по результатам моделирования) максимальный отлов R, при котором популяция не вымирает.
— *определите максимально допустимый отлов теоретически, из модели ограниченного роста с отловом; сравните это значение с результатами моделирования.

«Биологические модели развития популяций»

Из истории вопроса

В последнее время во всём мире возрос интерес к экологическим проблемам. Экология, как наука, использует самые разнообразные методы для решения этих проблем, в том числе и математический. Историю применения математики в экологии справедливо принято исчислять с выхода в свет книги Томаса Мальтуса «Опыт о законе народонаселения» в 1798 году. В ней впервые чётко сформулировано преставление о том, что численность населения (английское слово population породило современный русский термин «популяция»), которому предоставлена возможность неограниченно размножаться, растёт во времени в геометрической прогрессии.

Следующий шаг был связан с введением модели популяции, рост численности которой не беспределен и ограничен некоторым необходимым ей ресурсом. Такая модель достаточно хорошо описывала динамику многих природных популяций и была предложена П. Ф. Ферхюльстом   в 1838 году (в работе «Notice sur la lei qua la population suit dans son accroissement») и позднее получила название «логистической»:

Упомянутые выше работы были призваны описывать динамику отдельно взятой популяции, в первую очередь человеческого населения. Первые собственно математико-экологические работы, ставящие целью описание численности взаимодействующих между собой популяций, появились лишь в 20-х годах двадцатого столетия.

Самым важным результатом этих работ следует считать то, что в них было показано, как на основании биологически правдоподобных и допускающих экспериментальную проверку предположений о механизмах внутри- и межпопуляционных взаимодействий можно чисто математическими методами вывести  некоторые заключения о характере динамики системы. Наиболее известным заключение такого рода явился вывод о возможности колебаний численности в системе двух популяций, взаимодействующих по принципу хищник- жертва. Этот вывод стал очевидным после того, как независимо друг от друга австрийский биофизик Альфред Лотка  в своей работе «Элементы физической биологии» (1925) и итальянский математик Вито Вольтера, опубликовавший в 1926 году «Математическую теорию борьбы за существование», обосновали систему уравнений, описывающую взаимоотношения в системе хищник- жертва. В дальнейшем, Г. Ф. Гаузе была проведена экспериментальная проверка результатов, полученных А. Лотка и В. Вольтерра, которая и подтвердила правильность этих результатов.

Далее, к концу 30-х годов 20 века в развитии математической экологии наступила продолжительная пауза. Начало нового интенсивного этапа в данном направлении приходится на 60-е годы 20 века и связано с двумя обстоятельствами. Во- первых, катастрофические последствия воздействия человека на природу сделали задачу прогнозирования таких последствий весьма актуальной. Во- вторых, бурное развитие вычислительной техники и успехи её применения в решении различных задач породил естественные надежды на её применение и в экологической проблематике.

Описание  модели  «хищник-жертва»   (модель 1)

Одним из важных этапов решения задач экологии является разработка математических моделей экологических систем.

Рассмотрим биологическое сообщество, которое состоит из нескольких популяций биологических видов, живущих в общей среде, и построим модель двувидовой борьбы в популяциях. Напомним, что широко распространённым взаимодействием  между представителями различных видов является использование одними живыми организмами («хищниками») других организмов («жертв») в качестве пищи. При этом, «соперничество» жертвы с хищником выражается в изменении численности жертвы, которая в свою очередь сказывается на численности хищника.

Отметим, что  дальнейшее описание взаимоотношений между двумя видами биологических популяций (жертвами и хищниками) будет основано на следующих предположениях:

1. численности популяций жертв и хищников зависят только от времени и не зависят от пространственного распределения популяции на занимаемой территории;
2. естественная смертность жертв не учитываются;
3. скорость роста численности жертв уменьшается пропорционально численности хищников, а темп роста хищников увеличивается пропорционально численности жертв;
4. эффект «насыщения» у хищника не наступает, т. е. хищник всегда голоден.

Итак, содержательная постановка задачи заключается в следующем. Пусть на одной и той же территории проживают два различных вида биологических популяций с численностями  и Ci, где Ni— численность жертв и Ci— численность хищников  в момент времени i. Предположим, что единственным фактором, ограничивающим размножение жертв, является давление на них со стороны хищников, а размножение хищников ограничивается количеством добытой ими пищи (количеством жертв). Тогда, в отсутствие хищников численность жертв Ni растёт с коэффициентом прироста r, т.е. Ni+1=Ni +rNi, Ni—  количество жертв в момент времени i, r>0. Наличие хищника, разумеется, меняет вид этого уравнения, так как если численность хищника Ci , то, кроме естественного прироста, следует учесть убыль численности жертв в силу истребления жертв хищником. Эту убыль следует считать пропорциональной числу встреч между особями обоих видов, и она может быть выражена числом aNiCi , где a>0— коэффициент пропорциональности, характеризующий вымирание жертв вследствие их встречи с хищником, Ni— численность жертв в момент времени i и Ci— численность хищников в момент времени i.  Поэтому, считая, что численность жертв изменяется благодаря рождаемости (которая пропорциональна общей численности жертв с коэффициентом прироста равным r) и смертности, получим:

 Ni+1=Ni +rNi — aNiCi

Рассуждая аналогично, имеем: численность хищников Ci в отсутствие жертв убывает с некоторым естественным коэффициентом смертности q , т.е. Сi+1=Сi— qCi , где Ci— численность хищников в момент времени i, q>0. Численность хищников растёт тем быстрее, чем больше численность жертв. Это увеличение пропорционально числу встреч между особями обоих видов и выражается числом faNiCi, где f>0— коэффициент пропорциональности, характеризующий потребность в пище хищника, Ni— численность жертв в момент времени i и Ci— численность хищников в момент времени i.  Поэтому, считая, что численность хищников изменяется   благодаря встречам с жертвами и скорости вымирания (которая пропорциональна общей численности хищников с коэффициентом вымирания равным q), получим:

Сi+1=Сi  + faNiCi— qCi

Таким образом, взаимодействие хищника и жертвы можно описать с помощью  системы  уравнений:

 Ni+1=Ni +rNi — aNiCi

Сi+1=Сi  + faNiCi— qCi

Програмная реализация модели «хищник-жертва»

Данная модель была реализована на языке программирования Паскаль и в среде EXCEL. Ниже приведена программа на языке Паскаль.

program Model1;

var

T:integer;

N,C:array [0..100] of real;

i:integer;

r,a,q,f:real;

begin

writeln(‘введи количество дней’);

readln(T);

r:=0.2;

a:=0.005;

q:=0.1;

f:=0.1;

writeln(‘введи количество зайцев’);

readln(N[0]);

writeln(»введи количество волков’);

readln(C[0]);

for i:=0 to T do

begin

N[i+1]:=N[i]+r*N[i]-a*C[i]*N[i];

C[i+1]:=C[i]+f*a*C[i]*N[i]-q*C[i];

end;

writeln (‘ день     заяц       волк’);

for i:=0 to T do

writeln(i,’   ‘,N[i]:6:2,’    ‘,C[i]:6:2);

readln;

end.

Продемонстрируем часть  решения в среде Excel.

R=	0,2
A=	0,005
F=	0,1
Q=	0,05
дни	зайцы	волки
1	150	50
2	=B6+B1*B6-B2*C6*B6	=C6+B3*B2*C6*B6-B4*C6
3	=B7+B1*B7-B2*C7*B7	=C7+B3*B2*C7*B7-B4*C7
4	=B8+B1*B8-B2*C8*B8	=C8+B3*B2*C8*B8-B4*C8
5	=B9+B1*B9-B2*C9*B9	=C9+B3*B2*C9*B9-B4*C9
…	…	…

Результаты полученные в среде Excel и на языке Паскаль совпадают. Для большей наглядности продемонстрируем результаты полученные в Excel.

Анализ влияния параметров задачи на решение

Параметры задачи подобраны таким образом, чтобы смоделировать взаимоотношения между двумя видами биологических популяций.

Для программной реализации были использованы следующие данные

Время Т-100 дней

Коэффициент рождаемости R-0,2

Коэффициент пропорциональности, характеризующий вымирание жертв вследствие их встречи с хищником А-0,005

Коэффициент пропорциональности, характеризующий потребность в пище хищника F-0.1

Коэффициент смертности Q-0,05

Зависимость решения от величины отрезка времени

Исследуем зависимость решения от величины отрезка времени Т. Приведем результаты, полученные в Excel при следующих параметрах.

1. Т=30

1. Т=50

1. Т=100

На основе этих экспериментов можно проследить за колебаниями численностей жертв и хищников, а также сделать вывод о влиянии количества зайцев на количество волков.

Зависимость решения от начального количества хищников и жертв.

Сравним графики, полученные при численном решении задачи при Т=100

1. N[0]=70, C[0]=30.

1. N[0]=100, C[0]=30.

1. N[0]=150, C[0]=30.

1. N[0]=150, C[0]=50.

1. N[0]=150, C[0]=60.

Описание модели  «хищник-жертва» с учетом отлова (модель 2 )

Рассмотрим биологическое сообщество, которое состоит из нескольких популяций биологических видов, живущих в общей среде, и построим модель двувидовой борьбы в популяциях. Напомним, что широко распространённым взаимодействием  между представителями различных видов является использование одними живыми организмами («хищниками») других организмов («жертв») в качестве пищи. При этом, «соперничество» жертвы с хищником выражается в изменении численности жертвы, которая в свою очередь сказывается на численности хищника.

Отметим, что  дальнейшее описание взаимоотношений между двумя видами биологических популяций (жертвами и хищниками) будет основано на следующих предположениях:

1. численности популяций жертв и хищников зависят только от времени и не зависят от пространственного распределения популяции на занимаемой территории;
2. естественная смертность жертв не учитываются;
3. скорость роста численности жертв уменьшается пропорционально численности хищников, а темп роста хищников увеличивается пропорционально численности жертв;
4. эффект «насыщения» у хищника не наступает, т. е. хищник всегда голоден.

Итак, содержательная постановка задачи заключается в следующем. Пусть на одной и той же территории проживают два различных вида биологических популяций с численностями  и Ci, где Ni— численность жертв и Ci— численность хищников  в момент времени i. Предположим, что единственным фактором, ограничивающим размножение жертв, является давление на них со стороны хищников, а размножение хищников ограничивается количеством добытой ими пищи (количеством жертв). Тогда, в отсутствие хищников численность жертв Ni растёт с коэффициентом прироста r, т.е. Ni+1=Ni +rNi, Ni—  количество жертв в момент времени i, r>0. Наличие хищника, разумеется, меняет вид этого уравнения, так как если численность хищника Ci , то, кроме естественного прироста, следует учесть убыль численности жертв в силу истребления жертв хищником. Эту убыль следует считать пропорциональной числу встреч между особями обоих видов, и она может быть выражена числом aNiCi , где a>0— коэффициент пропорциональности, характеризующий вымирание жертв вследствие их встречи с хищником, Ni— численность жертв в момент времени i и Ci— численность хищников в момент времени i.  Поэтому, считая, что численность жертв изменяется благодаря рождаемости (которая пропорциональна общей численности жертв с коэффициентом прироста равным r) и смертности, получим:

 Ni+1=Ni +rNi — aNiCi

Рассуждая аналогично, имеем: численность хищников Ci в отсутствие жертв убывает с некоторым естественным коэффициентом смертности q , т.е. Сi+1=Сi— qCi , где Ci— численность хищников в момент времени i, q>0. Численность хищников растёт тем быстрее, чем больше численность жертв. Это увеличение пропорционально числу встреч между особями обоих видов и выражается числом faNiCi, где f>0— коэффициент пропорциональности, характеризующий потребность в пище хищника, Ni— численность жертв в момент времени i и Ci— численность хищников в момент времени i.  Поэтому, считая, что численность хищников изменяется   благодаря встречам с жертвами и скорости вымирания (которая пропорциональна общей численности хищников с коэффициентом вымирания равным q), получим:

Сi+1=Сi  + faNiCi— qCi

Введём в модели  управление за счёт отлова жертв и хищников. Пусть u1— доля отлова жертв в единицу времени, u2— доля отлова хищников в единицу времени. Предполагается, что отлов ограничен (финансовыми, техническими и др. средствами).

Тогда — численность  отлова жертв в момент времени i, — численность отлова хищников в момент времени i. Поэтому, учитывая, что отлов жертв и хищников ведёт к снижению численности обоих видов, уравнения перепишутся следующим образом:

Ni+1=Ni +rNi — aNiCi-u1Ni

Сi+1=Сi  + faNiCi— qCi-u2Ci

Программная реализация модели «хищник-жертва» с учетом отлова

Данная модель была реализована на языке программирования Паскаль и в среде EXCEL. Ниже приведена программа на языке Паскаль.

program Model2;

var

T:integer;

N,C:array [0..100] of real;

i:integer;

r,a,q,f,u1,u2:real;

begin

writeln(‘введи количество дней’);

readln(T);

r:=0.2;

a:=0.005;

q:=0.1;

f:=0.1;

writeln(‘введи процент отлова зайцев’);

readln(u1);

writeln(‘введи процент отлова волков’);

readln(u2);

writeln(‘введи количество зайцев’);

readln(N[0]);

writeln(‘введи количество волков’);

readln(C[0]);

for i:=0 to T do

begin

N[i+1]:=N[i]+r*N[i]-a*C[i]*N[i]-u1*N[i];

C[i+1]:=C[i]+f*a*C[i]*N[i]-q*C[i]-u2*C[i];

end;

writeln (‘ день     заяц       волк’);

for i:=0 to T do

writeln(i,’   ‘,N[i]:6:2,’    ‘,C[i]:6:2);

readln;

end.

Продемонстрируем часть  решения в среде Excel.

R=	0,2	U1=
A=	0,005	0,05
F=	0,1	U2=
Q=	0,05	0,05
дни	зайцы	волки
1	150	50
2	=B6+B1*B6-B2*C6*B6-C2*B6	=C6+B3*B2*C6*B6-B4*C6-C4*C6
3	=B7+B1*B7-B2*C7*B7-C2*B7	=C7+B3*B2*C7*B7-B4*C7-C4*C7
4	=B8+B1*B8-B2*C8*B8-C2*B8	=C8+B3*B2*C8*B8-B4*C8-C4*C8
5	=B9+B1*B9-B2*C9*B9-C2*B9	=C9+B3*B2*C9*B9-B4*C9-C4*C9
…	…	…

Результаты полученные в среде Excel и на языке Паскаль совпадают. Для большей наглядности продемонстрируем результаты полученные в Excel.

Анализ влияния параметров задачи на решение

Для программной реализации были использованы следующие данные

Время Т-100 дней

Коэффициент рождаемости R-0,2

Коэффициент пропорциональности, характеризующий вымирание жертв вследствие их встречи с хищником А-0,005

Коэффициент пропорциональности, характеризующий потребность в пище хищника F-0.1

Коэффициент смертности Q-0,05

Начальное количество зайцев N[0]=150

Начальное количество волков C[0]=50

Зависимость решения от величины отлова

Приведем результаты, полученные в Excel при следующих параметрах.

1. U1=0,05  ,   U2=0,05

1. U1=0,05  ,   U2=0,03

1. U1=0,05  ,   U2=0,07

Описание модели  «хищник-жертва» с учетом отлова (модель 3)

Содержательная постановки модели3 получена из модели 2 за счет изменения вида функций u1 и u2. Рассмотрим более подробно различие этих моделей.

В §5 были получены уравнения описывающие взаимодействия хищника и жертвы с учетом отлова.

В модели 2 мы предполагали, что функции u1 и u2 являются постоянными функциями.

В модели 3 отлов организуем  таким образом, чтобы поддержать численность жертв и хищников. Для этого представим функции u1 и u2 в виде следующих систем.

и

В этом случае уравнения полученные в §5 для модели 2 перепишутся следующим образом:

и

Программная реализация модели «хищник-жертва» с учетом отлова

Данная модель была реализована на языке программирования Паскаль и в среде EXCEL. Ниже приведена программа на языке Паскаль.

program Model3;

var

T:integer;

N,C:array [0..100] of real;

i:integer;

r,a,q,f:real;

begin

writeln(‘введи количество дней’);

readln(T);

r:=0.2;

a:=0.005;

q:=0.1;

f:=0.1;

writeln(‘введи количество зайцев’);

readln(N[0]);

writeln(‘введи количество волков’);

readln(C[0]);

for i:=0 to T do

begin

if N[i]>=200 then  N[i+1]:=N[i]+r*N[i]-a*C[i]*N[i]-0,05*N[i];

if N[i]<=100 then  N[i+1]:=N[i]+r*N[i]-a*C[i]*N[i];

if (N[i]<200) and (N[i]>100 ) then

               N[i+1]:=N[i]+r*N[i]-a*C[i]*N[i]-0,03*N[i];

If C[i]>=150 then

            C[i+1]:=C[i]+f*a*C[i]*N[i]-q*C[i]-0,05*C[i];

If C[i]<=50 then

            C[i+1]:=C[i]+f*a*C[i]*N[i]-q*C[i];

If (C[i]<150) and (C[i]>50) then

            C[i+1]:=C[i]+f*a*C[i]*N[i]-q*C[i]-0,03*C[i];

end;

writeln (‘ день     заяц       волк’);

for i:=0 to T do

writeln(i,’   ‘,N[i]:6:2,’    ‘,C[i]:6:2);

readln;

end.

Продемонстрируем часть  решения в среде Excel.

R=	0,2
A=	0,005
F=	0,1
Q=	0,05
дни	зайцы	волки
1	150	50
2	=B6+B1*B6-B2*B6*C6-ЕСЛИ(B6>200;0,05;0)*B6-ЕСЛИ(И(B6>=100;B6<=200);0,01;0)*B6	=C6+B3*B2*B6*C6-B4*C6-ЕСЛИ(И(C6>50;C6<150);0,03;0)*C6-ЕСЛИ(C6>=150;0,05;0)*C6
3	=B7+B1*B7-B2*B7*C7-ЕСЛИ(B7>200;0,05;0)*B7-ЕСЛИ(И(B7>=100;B7<=200);0,01;0)*B7	=C7+B3*B2*B7*C7-B4*C7-ЕСЛИ(И(C7>50;C7<150);0,03;0)*C7-ЕСЛИ(C7>=150;0,05;0)*C7
4	=B8+B1*B8-B2*B8*C8-ЕСЛИ(B8>200;0,05;0)*B8-ЕСЛИ(И(B8>=100;B8<=200);0,01;0)*B8	=C6+B3*B2*B8*C8-B4*C8-ЕСЛИ(И(C8>50;C8<150);0,03;0)*C8-ЕСЛИ(C8>=150;0,05;0)*C8
5	=B9+B1*B9-B2*B9*C9-ЕСЛИ(B9>200;0,05;0)*B9-ЕСЛИ(И(B9>=100;B9<=200);0,01;0)*B9	=C9+B3*B2*B9*C9-B4*C9-ЕСЛИ(И(C9>50;C9<150);0,03;0)*C9-ЕСЛИ(C9>=150;0,05;0)*C9
…	…	…

Результаты полученные в среде Excel и на языке Паскаль совпадают. Для большей наглядности продемонстрируем результаты полученные в Excel.

Анализ влияния параметров задачи на решение

Для программной реализации были использованы следующие данные

Коэффициент рождаемости R-0,2

Коэффициент пропорциональности, характеризующий вымирание жертв вследствие их встречи с хищником А-0,005

Коэффициент пропорциональности, характеризующий потребность в пище хищника F-0.1

Коэффициент смертности Q-0,05

Начальное количество зайцев N[0]=150

Начальное количество волков C[0]=50

Зависимость решения от величины отрезка времени

Исследуем зависимость решения от величины отрезка времени Т. Приведем результаты, полученные в Excel при следующих параметрах.

   и  

1. T=100

1. T=200

1. T=300

1. T=400

На основе этих экспериментов можно сделать вывод о том , что с течением времени количество зайцев и волков становится функцией близкой к постоянной.

Зависимость решения от величины отлова

Приведем результаты, полученные в Excel при следующих параметрах.

и

и

и

ЗАКЛЮЧЕНИЕ

В настоящее время задачи экологии имеют  первостепенное значение, так как стала актуальной проблема контроля над численностью популяций живых организмов в сложных экологических системах. Иногда требуется восстановить популяцию животных, находящихся на грани вымирания, а бывают случаи, когда нужно сократить число некоторых вредителей и удерживать их популяцию в заданном количестве. При этом необходимо учесть, как те или иные изменения численности одной популяции отражаются на количестве особей остальных видов данной экосистемы. Подобные задачи решаемы, если проанализирована математическая модель, соответствующая требуемой ситуации.

В данной экзаменационной работе построена, решена (теоретически и численно), а также исследована модель эффективного управления предприятием по отлову животных, взаимоотношения между которыми описаны с помощью системы «хищник- жертва», то есть цель экзаменационной работы достигнута.

Итак, все результаты, полученные численно, являются наглядными, а поэтому и необходимы математические модели, которые позволяют оценить возможные последствия воздействия человека на природу и организовать его деятельность так, чтобы не допустить «экологической катастрофы».

Слайд 1
Практическая работа
в MS Excel «Биологические модели развития популяций»
Учитель информатики

МБОУ гимназии № 45
Даниева З.Б.

---

Слайд 2
Тема
«Электронные таблицы и математическое моделирование»

---

Слайд 3
В биологии при исследовании развития биосистем строятся динамические модели изменения

численности популяций различных живых существ (бактерий, рыб, зверей и т.д.) с учётом различных факторов.

---

Слайд 4
Расчёт числа рыб в пруду с интервалом через год
Учёные установили,

что прирост числа какого-либо вида живых организмов за счёт рождаемости прямо пропорционален их количеству, а убыль за счёт смертности прямо пропорциональна квадрату их количества. Этот закон известен под названием закона Мальтуса.

---

Слайд 5
Задача.
В одном хозяйстве собираются разводить карпов. Прежде чем запускать

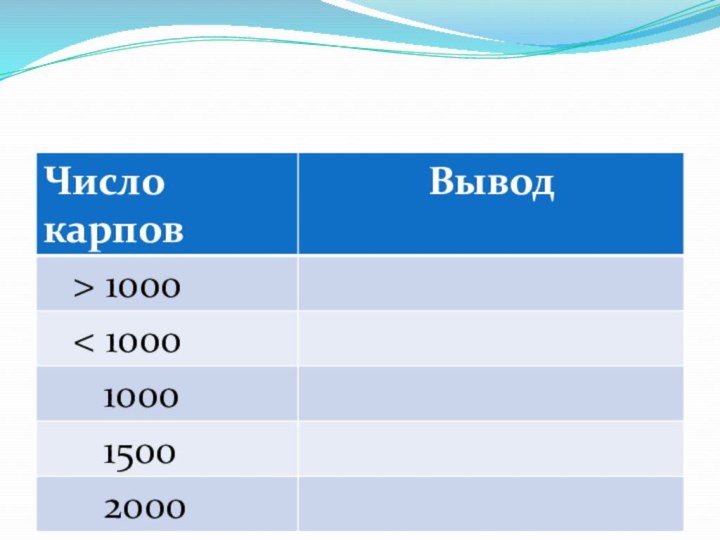
мальков в пруд, решили провести расчёты. Согласно закону Мальтуса изменение числа рыб за один год вычисляется по формуле
∆N=kN-qN2.

---

Слайд 6
Здесь N — число карпов в начале года, k– коэффициент

прироста, q – коэффициент смертности. Экспериментально установлено, что для данного вида рыб (карпы) и в данных условиях (состояние водоёма, наличие корма) k=1, q= 0,001.

---

Слайд 7
Если первоначально в пруд запущено N0 рыб, то из закона

следует, что количество карпов через год будет таким:
N1 = N0 + (kN0 – qN02).
Через два года
N2 = N1 + (kN1 – qN12)
и т.д. Можно написать общую формулу для вычисления количества рыб в i-том году после их запуска:
Ni=Ni-1 + (kNi-1 –qNi-12) для i= 1,2,3,…

---

Слайд 8
Заполним ЭТ для проведения по этой формуле расчета рыбного «поголовья»

в пруду в течение нескольких лет.

---

Слайд 9
Для получения результатов достаточно занести в ячейку F1 первоначальное число

рыб.
Из полученных результатов сделайте выводы.

---

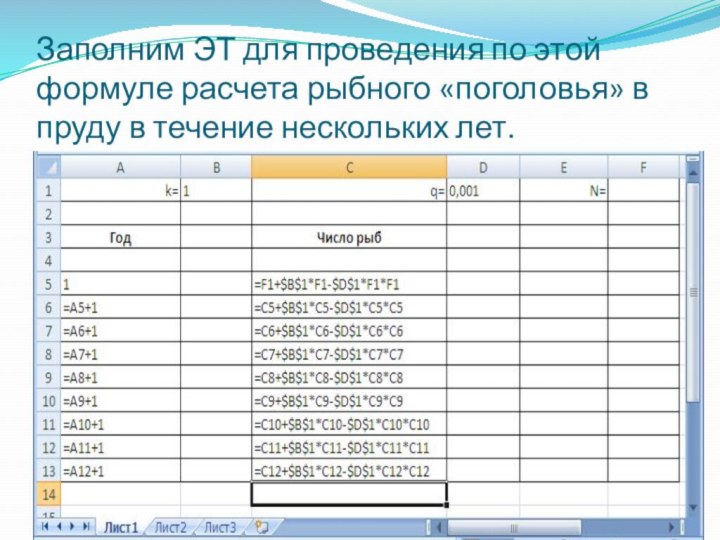
Слайд 10

---

Слайд 11
Выводы:
Невозможно иметь в пруду больше 1000 карпов.
Если начальное число рыб

меньше 1000, то оно постепенно будет расти до 1000 штук и далее не меняется.
Если сразу запустить 1000 рыб, то это количество останется неизменным и в последующие годы.
Если запустить сначала 1500 рыб, то через год их численность в два раза сократится, а затем все равно дойдёт до 1000.
Если запустить в пруд 2000 рыб, то через год все они вымрут.

---

Слайд 12
Литература
Информатика. 8 класс: учебник / И.Г. Семакин, Л.А. Залогова, С.В.

Русаков и др. М.: Лаборатория знаний, Изд – Бином, 2015

---