Моделирование гармонических колебаний в среде табличного процессора ms excel

Муниципальное автономное общеобразовательное учреждение

«Средняя общеобразовательная школа №1» г. Боровичи

Проект

«Моделирование гармонических колебаний в среде табличного процессора Microsoft Excel»

	Подготовила: Ученица 11 «А» класса Январева Мария Руководитель: Васильева Надежда Владимировна 2021г. г. Боровичи
Содержание Введение         1. Теоретическая часть         1.1 Гармонические колебания: понятие, основные параметры         1.2 Уравнение гармонического колебания         1.3 Табличный процессор MS Excel: понятие, основные инструменты         2. Практическая часть         2.1 Заполнение исходных параметров колебаний в таблице         2.2 Создание полосы прокрутки в MS Excel         2.3 Создание графика в MS Excel         Заключение         Список Литературы

Введение

В школьной программе по предмету «физика» изучаются гармонические колебания. Однако в действительности осуществить эксперименты, в которых можно наблюдать и изучать колебательный процесс и его характеристики сложно.  Microsoft Excel является отличным средством для моделирования различных динамических процессов. В этой работе с помощью функций MS Excel можно исследовать влияние параметров колебательного процесса на график колебаний.

Цель: смоделировать гармонические колебания с помощью табличного процессора Microsoft Excel.

Гипотеза: если изучить инструментарий табличного процессора Microsoft Excel, то с его помощью можно моделировать физические процессы.

Предмет: программа Microsoft Excel, как среда моделирования гармонических процессов.

Объект: График гармонических колебаний.

Задачи:

1) Изучить теоретический материал по теме Гармонические колебания.

2) Изучить теоретический материал о табличном процессоре Microsoft Excel.

3)Практически смоделировать Гармонические колебания в табличном процессоре Microsoft Excel.

1. Теоретическая часть

1.1 Гармонические колебания: понятие, основные параметры

Колебательное движение — это движение, точно или приблизительно повторяющееся через одинаковые промежутки времени, при котором тело многократно и в разных направлениях проходит положение  равновесия.

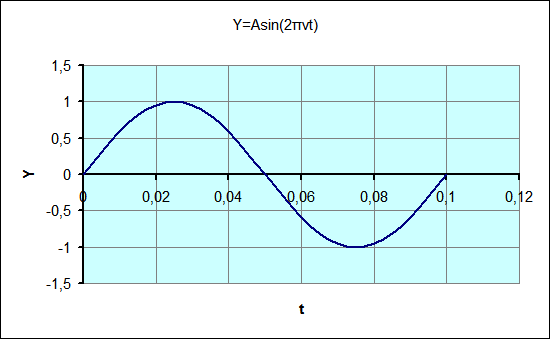
Гармонические колебания – колебания,  при которых физическая величина изменяется с течением времени по гармоническому закону.

Рис 1. График синусоиды

1.2 Уравнение гармонического колебания

x = a*sin*(ω*t+φ0)

• x – смещение тела
• a – амплитуда колебаний
• ω – циклическая частота колебаний
•  t – время
• φ0 – начальная фаза колебаний

Период колебаний (T) – это минимальный промежуток времени, через который происходит повторение движения тела.

Τ= t / n

Начальная фаза колебания (φ0) — это фаза колебаний в начальный момент времени.  

Циклическая (круговая) частота (ω) — это число колебаний тела за 2π с.

ω0 = 2π/T = 2πν

Амплитуда колебаний (a) — максимальное смещение от положения равновесия.

Это уравнение дает зависимость «x» от времени «t».

1.3 Табличный процессор MS Excel: понятие, основные инструменты

Microsoft Excel – это универсальная программа для работы с электронными таблицами, которая позволяет хранить, организовывать и анализировать информацию. В ней можно вести домашний бюджет, производить простые или сложные расчеты, организовывать дневники, составлять отчеты, строить графики, диаграммы и многое другое.

Основные инструменты MS Excel: рабочее поле, ячейка, диапазон ячеек, символьные и строковые величины, логические величины, формулы.

Рабочее поле – это экран дисплея, на котором электронная таблица предоставляется в виде прямоугольника, разделенного на строки и столбцы.

Ячейка – минимальный элемент электронной таблицы, над которым можно выполнять те или иные операции. Каждая ячейка имеет уникальное имя. Например: B2, C17, G150 и т.д.

Диапазон ячеек – его можно выделить из подряд идущих ячеек в строке, столбце или прямоугольнике. При задании диапазона указывают его начальную и конечную ячейки. Примеры диапазонов – A1:A100, B15:AZ12.

Для моделирования гармонических колебаний можно использовать:

 1)Формулы

      2)Полосы прокрутки

 3)График

2. Практическая часть

2.1 Заполнение исходных параметров колебаний в таблице

Ячейки электронной таблицы заполнены следующим образом: в ячейке B6 — значение амплитуды (a); B8 – значение круговой частоты (ω); B10 – значение фазы колебаний (α). Каждая из этих ячеек имеет формулу: B6 (=C6/10); B8 (=C8); B10 (=C10/100). (Заменим «φ0» на «α»).  

В столбце G вычисляются значения времени, возрастающие на 0,02, для этого в G4 введена формула (=G3+0,02).

В столбце H вычисляются значения X по формуле (=$B$6*SIN($B$8*G…+$B$10)) , где G меняется в зависимости от выбранной ячейки (заполняем с H3 вниз аналогичным способом). Для наглядности в ячейках G и H значения времени и координаты продолжены до 160 строчки.

В режиме отображения формул таблица выглядит следующим образом:

Рис.2. Режим отображения формул

В режиме отображения значений:

Рис.3. Режим отображения значений

2.2 Создание полосы прокрутки в MS Excel

С целью исследования влияния параметров гармонических колебаний на график колебательного процесса используем такую возможность как полосы прокрутки. Для каждой полосы прокрутки установлены максимальное и минимальное значение. Каждая полоса прокрутки привязана к соответствующей ячейке. Поправка положения ползунка на полосе прокрутки приводит к изменению значения в ячейке. Таким образом, изменяя значения амплитуды, круговой частоты и начальной фазы колебаний, можно наблюдать изменение графика.

1. Через меню Разработчик (Вставить/Элементы ActiveX) выбираем элемент «Полоса прокрутки».
2. Выбрав нужные ячейки, нужно вставить туда полосу прокрутки (меняем размер).
3. После вставки Полосы прокрутки она становится выделенной. Если нажать на любое другое место листа, то Полоса прокрутки перестанет быть выделенной.
4. Нажимаем на Полосу прокрутки правой кнопкой мыши и выбираем «Свойства».
5. В свойствах меняем значения «Max» и «Min» на те, которые необходимы (на 10 и 0, соответственно).
6. Чтобы привязать полосу прокрутки в строке «LinkedCell» выбираем ячейку, где будут находиться значения колебания.
7. Также можно изменить цвет полосы, для этого нужно найти строчки «BackColor» и «ForeColor». «BackColor» меняет фон полосы, а «ForeColor» цвет стрелок и ползунка.
8. Полоса прокрутки готова.

Полосы прокрутки находятся в ячейках D6E6, D8E8, D10E10 и привязаны к ячейкам C6, C8, C10. Полосы прокрутки меняют значения в этих ячейках от 0 до 10, так как установлено максимальное и минимальное значение.

2.3 Создание графика в MS Excel

1. Выделяем таблицу от G3 и H3 до G160 и H160, и переходим во вкладку «Вставка». Нажимаем на кнопку «График» и выбираем самый простой из них (находится на первом месте).
2. Программа произвела построения графика, но как видим, появилось две линии, нужно удалить одну из них (удалим линию «t»).
3. Легенда тоже не нужна, так как на графике всего одна линия. Поэтому нужно удалить легенду.
4. Теперь нужно значения в горизонтальной панели координат заменить на те, которые соответствуют столбцу «t» в таблице.
5. Нажимаем правой кнопки мыши на график. В меню перемещаемся по значению «Выбрать данные…».
6. В активировавшемся окне выбора источника нажать на правую кнопку «Изменить».
7. Запускается окошко «Подписи оси». В области «Диапазон подписей оси» указываем координаты массива с данными столбца «t». Ставим курсор в полость поля, а затем, произведя необходимый зажим левой кнопки мыши, выделяем все значения соответствующего столбца таблицы, исключая лишь его наименование. Как только координаты отобразятся в поле, клацаем по наименованию «OK».
8. В окне выбора источника данных нажимаем на «ОК».
9. Далее выбираем «Режим Конструктора» и нажимаем на график левой кнопкой мыши. Находим и нажимаем на «Макет», переходим во вкладку «Оси». В самом низу находится «Дополнительные параметры основной горизонтальной оси…». Меняем параметры горизонтальной оси. Аналогично делаем и с вертикальной осью.
10. После этого программа произведет редактирование ранее построенного графика согласно тем изменениям, которые были произведены в настройках.

Рис. 4. График колебательного процесса.

Заключение

Таким образом, данный график может применяться на уроках физики, что позволит ученикам явно проследить изменение графика колебаний при изменении различных параметров. А ученикам, увлекающимся информатикой, эта работа поможет для моделирования гармонических колебаний, поможет еще больше узнать о возможностях табличного процессора MS Excel.

Список литературы

1. Мякишев Г.Я. Учебник Физики 11 класса. Гармонические колебания. Просвещение, 2010. – 399с.

  2. Фаза колебаний. https://www.calc.ru/Faza-Kolebaniy.html

3. Гарнаев А.Ю. Самоучитель VBA. СПб: БХВ, Санкт Петербург, 1999.

4. Веденеева Е.А. Функции и формулы Excel 2007. Библиотека пользователя. – Санкт Петербург, 2008. –384с.

5. Полосы прокрутки. https://excel2.ru/articles/polosa-prokrutki-element-upravleniya-formy-v-ms-excel

6. График. https://exceltable.com/grafiki/grafiki-i-diagrammi-v-excel

1. Моделирование гармонических колебаний в среде табличного процессора MS Excel

Работа ученицы 10 класса
МОУ СОШ пос. Мизур
Цогоевой Ирины

2. Периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса, называются

ГАРМОНИЧЕСКИМИ
КОЛЕБАНИЯМИ
x
xm
0
xm
π/2
π
3π/2
T/4
T/2
3T/4
2π
T
φ
t

3. Уравнение гармонического колебания

x = xm cos(ω0 t + φ0)
x – смещение тела
t – время
xm – амплитуда колебаний
φ0- начальная фаза колебаний
ω – циклическая частота колебаний

4. Период колебаний

X
xm
t
T
Минимальный промежуток времени, через который
происходит повторение движения тела, называется
периодом колебаний T.
= t / n

5. Амплитуда колебания

X
xm
t
xm – амплитуда колебаний, т. е. максимальное
смещение от положения равновесия

6. Частота колебаний

X
1
Т
xm
T
Физическая величина, обратная периоду колебаний,
называется частотой колебаний. Частота колебаний
показывает, сколько колебаний совершается за 1 с.
Единица частоты – герц (Гц).

7. Циклическая частота колебаний

Циклическая или круговая частота — это число
колебаний тела за 2π с.
ω0 = 2π/T = 2π

8. Исследование влияния параметров гармонических колебаний на график колебательного процесса

9. Сложение колебаний

a1
a
a2
α
0
x1
a2
α1
x2
x
x1 = а1 cos (ω1t + α)
cos (ωt + α)
x2 = a2 cos (ω2t +α)
а² = а1² + а2² + 2 а1а2 cos (α2 – α1)
X
x=a

10. Сложение колебаний в MS Excel

11. Биения

12. Информатика, физика, математика – это не скучно!

Практическая работа Гармонические колебания.

«Построение графика функции в Excel»

1. Построить таблицу:

а) в первой строке необходимо задать аргумент функции от xn до xk с шагом h, используя автозаполнение (т.е. задаём интервал функции [-10;10] с шагом 0,5).

б) Во вторую строку вводим выражение (например: f(x)=sin x), точно также используя автозаполнение копируем его.

2. Выделить диапазон из двух строк.

3. Вкладка Вставка – панель Диаграммы – инструмент Точечная с гладкими кривыми.

Рисунок 1. Примерный график функции cos x в диапазоне [-10;10].

Построить диаграммы для функций:

1. f(x) = cos x;

2. f(x) = cos 2 x;

3. f(x) = 2 cos 2 x;

4. f(x) = sin x;

5. f(x) = sin 2 x;

6. f(x) = 2 sin 2 x.

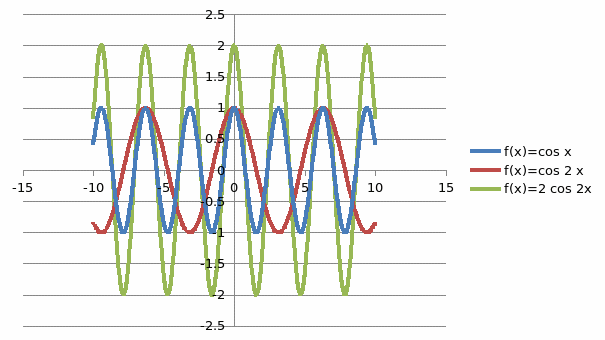
Сравнить полученные графики.

Рисунок 2. Сравнение функций cos x; cos 2 x; 2 cos 2 x;

Работа 2.2.
(К §1.4.4)

Самостоятельная работа: Численные эксперименты по обработке звука

График функции Y(x)
– наглядное (графическое) отображение
зависимости значения функции Y
от значения аргумента x.
График строится в пределах области
определения функции (области изменения
аргумента x) и области
значений Y. Если у функции
бесконечная область определения, то
для построения графика выбирается тот
ее отрезок, в пределах которого поведение
функции наиболее характерно. График
периодической функции, как минимум,
должен отражать один период изменения
значений функции.

Эксперимент 1: моделирование гармонических колебаний

Рассмотрим способ построения графика
периодической функции, описывающей
гармонические колебания. Гармоническими
колебаниями называются периодические
изменения со временем некоторой
физической величины, описываемые
функциями синуса или косинуса. В общем
виде они выглядят так:

Y=A·sin(2πνt
+ φ) или Y=A·cos(2πνt
+ φ)

Здесь A – амплитуда
колебаний; t – время
(аргумент функции); ν – частота колебаний,
измеряемая в герцах; φ – начальная фаза
колебаний.

Период функций sin и
cos равен 2π. Значение
функции (Y) изменяется
в интервале от –А до +А. График
функции синус называют синусоидой.

Звуковые колебания, описываемые
гармонической функцией, называются
гармоническими колебаниями. Чистые
музыкальные тона: до, ре, ми и др.
представляют собой гармонические
звуковые колебания разной частоты.
Гармонические звуковые колебания издает
камертон – эталонный источник музыкального
тона. Гармонические колебания совершает
математический маятник. В электрическом
колебательном контуре сила тока
периодически изменяется по гармоническому
закону.

Рассмотрим способ построения графика
гармонической функции в среде электронной
таблицы. Покажем, как это делается, на
примере табличного процессора MS
Excel.

Работа происходит в два этапа:

1 – табулирование функции;

2 – построение графика функции.

Полученная электронная таблица
представлена на рис.1.12.

Параметрами функции являются частота
колебаний ν и амплитуда А. Эти параметры
вводятся, соответственно, в ячейки С1 и
С2. Значение начальной фазы φ примем
равным нулю.

Табулирование – это построение
таблицы значений функции на некотором
интервале значений аргумента с постоянным
шагом. Шаг табулирования (∆t)
записан в ячейке G1.

Таблица помещена в ячейки А4:В25. В столбце
А расположены значения аргумента –
времени t, в столбце
В – значения функции
Y=A·sin(2πνt).
Изменение времени начинается
со значения t=0 (ячейка А5)
. В ячейке А6 записана формула: =A5+$G$1.
Далее эта формула копируется в следующие
ячейки столбца А. Таким образом
обеспечивается изменение времени с
постоянным шагом, хранящемся в ячейке
G1.

В ячейку В5 заносится формула:
=$C$2*SIN(2*ПИ()*$C$1*A5). По этой формуле вычисляется
значение функции от аргумента, находящегося
в ячейке А5. Стандартная функция ПИ()
возвращает значение числа Пифагора π.
Формула из ячейки В5 копируется вниз по
столбцу до ячейки В25.

На рис.1.12 показаны результаты табулирования
функции для значений ν=10 Гц, A=1.
Шаг табулирования принят равным 0,005.
При частоте 10 Гц период колебаний равен
1/10=0,1 с. При шаге табулирования 0,005 на
одном периоде укладывается 20 шагов. Это
вполне достаточное количество значений
для построения графика функции.

A B C D E F G H I J K L 1 Частота колебаний: 10 Гц Шаг табулирования 0,005 c 2 Амплитуда: 1 3 4 t (с) Y=A·sin(2πνt) 5 0 0 6 0,005 0,309016994 7 0,01 0,587785252 8 0,015 0,809016994 9 0,02 0,951056516 10 0,025 1 11 0,03 0,951056516 12 0,035 0,809016994 13 0,04 0,587785252 14 0,045 0,309016994 15 0,05 5,66604E-16 16 0,055 -0,309016994 17 0,06 -0,587785252 18 0,065 -0,809016994 19 0,07 -0,951056516 20 0,075 -1 21 0,08 -0,951056516 22 0,085 -0,809016994 23 0,09 -0,587785252 24 0,095 -0,309016994 25 0,1 6,43149E-16

Рис.1.12. Таблица и график гармонической
функции

Построение графика. Для графической
обработки данных в табличном процессоре
существует мастер построения диаграмм
и графиков. Его вызов происходит через
меню по командам: Вставка – Диаграммы.
Дальнейшие шаги алгоритма следующие:

1 –выбрать тип диаграммы: стандартные
– точечная, вид – сглаживающие
линии

2 – задать диапазон данных (значений
функции): в столбцах — В5:В25; закладка
РЯД, значения Х: А5:А25

3 – определить заголовок:
Y=A·sin(2πνt).
подписи под осями: t,
Y, линии сетки,
легенду (нет), подписи данных (нет).

4 – указать, на каком листе книги разметить
диаграмму.

ГОТОВО. График построен.

Толщину линий, цвет фона, вид координатной
сетки можно настроить отдельно, используя
контекстное меню (по правой кнопке
мыши), задавая нужные форматы объектов.

Человек слышит звуковые колебания, в
среднем, в диапазоне частот от 20Гц до
20кГц. Частота 10 Гц – это частота
инфразвука. Некоторые животные
воспринимают его на слух. Если же удвоить
частоту, то будет достигнута нижняя
частотная граница слышимости человека.
Но тогда на временном интервале 0,1
секунды поместится два периода колебаний.
Такой эксперимент легко выполнить на
построенной электронной таблице.
Измените значение частоты в ячейке С1
на 20, после чего будет пересчитана
таблица, а график примет вид, представленный
на рис.1.13.

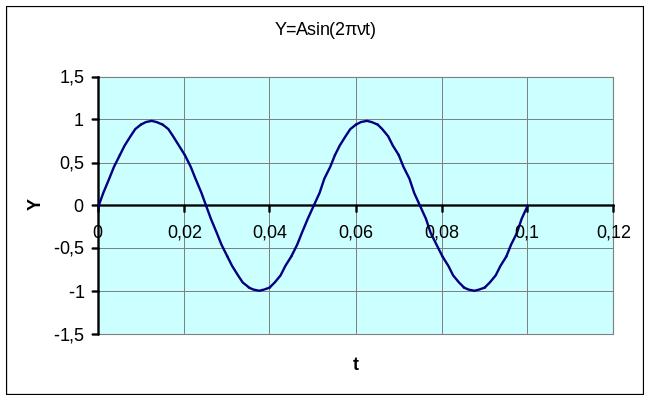
Рис.1.13. График звуковых колебаний для
ν=20 Гц

На интервале времени 0,1 секунды уложилось
2 периода функции. Следовательно, период
колебаний равен 0,05 секунды.

Задания

1 уровень

Проведите несколько экспериментов с
электронной таблицей для значений
частоты: 5 Гц, 15 Гц, 30 Гц, 40 Гц. В каждом
случае определите, сколько периодов
колебаний укладывается в интервал 0,1
секунды?

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание

Введение.

Глава 1.Исследование гармонических колебаний с помощью фигур Лиссажу

1.1 Гармонические колебания.

1.2 Фигуры Лиссажу.

Глава 2.Моделирование фигур Лиссажу в среде MS Excel

2.1 Анализ среды MS Excel

2.2 Построение фигур Лиссажу средствами MS Excel

2.3 Описание применения фигур Лиссажу для сравнения гармонических колебаний

Заключение

Список использованной литературы

Введение

Тема данной исследовательской работы: Моделирование фигур Лиссажу.

Настоящее исследование посвящено актуальной проблеме изучения фигур Лиссажу в курсах физики и математики.

Фигуры Лиссажу используют для сравнения гармонических колебаний, которые изучаются в курсе физики. Но в реальности провести опыты, в которых можно наблюдать и изучать колебательный процесс и его характеристики сложно. В ходе математического и компьютерного моделирования фигур Лиссажу можно исследовать соотношение между частотами и фазами гармонических колебаний.

Цель работы: показать возможности применения математических функций среды MS Excel для моделирования некоторых физических явлений.

Достижение поставленной цели предполагает решение следующих задач:

1.Проанализировать литературу по теме исследования.

2.Раскрыть понятие фигуры Лиссажу.

3.Рассмотреть способы построения графиков в среде MS Excel.

4.Разработать модель фигур Лиссажу в MS Excel для исследования гармонических колебаний.

Объектом исследования являются Фигуры Лиссажу. Предмет исследования: наглядное построение фигур Лиссажу. Методы исследования: для решения поставленных задач в работе используется теоретические и эмпирические методы.

Глава 1. Исследование гармонических колебаний с помощью фигур Лиссажу

1.1. Гармонические колебания

Гармонические колебания — колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону.

Гармоническое колебание, как математическая модель участвует в множестве физических процессов, которые можно использовать для передачи информации. Многие системы совершают движение по гармоническому закону вполне естественным образом. В пример можно привести обычное раскачивание на качелях, ритмичные движения ног продолжали незатухающие колебания механического маятника, которым и являются качели.

Способы представления гармонических колебаний:[1;82-84]

• Аналитическая форма (формула):

2. Графическое представление (построение): Этот способ наглядно может показать вид и свойства данного явления.

• Гармоническое колебание изменяется во времени периодически. Период каждого совершённого колебания равен .
• Амплитуда (наибольшее значение) равна . Скорость изменения колебания во времени определяется круговой частотой , которая численно равна скорости изменения аргумента косинуса и измеряется в рад/с. — начальная фаза колебательного процесса. При совершении единичного гармонического колебания фаза особой роли не играет, а когда совершается несколько подобных колебаний, то даёт понять о местонахождении колебаний на оси времени друг относительно друга. Если >0, то второе колебание сдвинуто влево, т.е. опережает первое, а если <0, то ситуация обратная.

3. Векторное представление (делает очень наглядным фазовые и амплитудные соотношения между ними):

Эта формула выводится, если известна начальная фаза и амплитуда, т.е. значения при

Возьмём за гипотенузу прямоугольного треугольника, тогда будет в качестве его катета. Можно сказать, что сейчас гармоническому колебанию дали геометрическое представление. Такое представление гармонического колебания называют векторной диаграммой.

1.2 Фигуры Лиссажу

Фигуры Лиссажу — траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Эти фигуры, впервые изученные французским учёным Жюлем Антуаном Лиссажу.

Устройство для построения фигур Лиссажу — осциллограф. Изобретение относится к радиоизмерительной технике и может быть использовано для исследования параметров электрических сигналов.

Известные способы регистрации фигур Лиссажу с помощью двух координатных регистрирующих устройств позволяют производить измерения в ограниченном диапазоне частот и при отсутствии помех. Целью изобретения является создание способа регистрации фигур Лиссажу в широком диапазоне частот и при наличии помех.

Эти фигуры используют для осциллографического метода сравнения частот.

Осциллографический метод сравнениячастот:[2;97-98]

В качестве устройства сравнения частот используется осциллограф с отключённой разверткой (Развертка— это линия, которую чертит луч на экране при отсутствии исследуемого сигнала в результате действия только одного развертывающего напряжения.), таким образом информацию получают с экрана осциллографа по изображению интерференционных фигур (фигур Лиссажу).

Измеряемый сигнал подают на вход КВО (канал вертикального отклонения), а сигнал образцового генератора известной частоты — на вход КГО (канал горизонтального отклонения). Плавным изменением частоты добиваются устойчивого изображения на экране осциллографа фигур Лиссажу. В этом методе отношение частот сравниваемых сигналов определяют путём подсчета числа пересечений фигуры Лиссажу с вертикальной осью и горизонтальной осью на экране осциллографа.

Из этой формулы можно вывести измеряемую частоту,

Закон гармонического осциллятора: [3;19]

Если закон дифференцировать по времени, то найдём закон изменения скорости при гармонических колебаниях:

Так же если повторить предыдущее действие, то найдём изменения ускорения при гармонических колебаниях:

После двух дифференцирований мы получим исходное выражение:

Перенеся слагаемые в одну сторону, то получим уравнение гармонического осциллографа:

Это уравнение встречается во всех разделах физики без исключения. Это уравнение описывает эволюцию малых отклонений динамических переменных от их устойчивых значений. Но для математика это обыкновенное уравнение 2-ого порядка с постоянными коэффициентами, в это уравнение входит функция со второй производной. Решением данного уравнения являются гармонические колебания.

Глава 2. Моделирование фигур Лиссажу в среде MS Excel

1.2. Анализ среды MS Excel

Microsoft Office Excel – это программа, предназначенная для работы с электронными таблицами, которая позволяет хранить, организовывать и анализировать информацию.

Excel – это универсальная программа, которая позволяет работать с различными форматами данных. В Excel можно вести домашний бюджет, производить как простые, так и очень сложные расчеты, хранить данные, организовывать различные дневники, составлять отчеты, строить графики, диаграммы и многое-многое другое.

Функции MS Excel:

1.Работа с числовыми данными. Например, составление самых различных бюджетов, начиная от домашнего, как самого простого, и, заканчивая бюджетом крупной организации.

2.Работа с текстом. Разнообразный набор инструментов для работы с текстовыми данными дает возможность представить даже самые сложные текстовые отчеты.

3.Создание графиков и диаграмм. Большое количество инструментов позволяет создавать самые различные варианты диаграмм, что дает возможность представить ваши данные наиболее ярко и выразительно.

4.Организация списков и баз данных. В Microsoft Office Excel изначально была заложена структура строк и столбцов, поэтому организовать работу со списками или создать базу данных является для Excel элементарной задачей..

2.2. Построение фигур Лиссажу средствами MS Excel

В рамках данного исследования продемонстрируем построение фигур Лиссажу в табличном процессоре MS Excel, для этого понадобятся формула:

Уравнение гармонического колебания физической величины X с циклической частотой W и амплитудой А можно записать в виде формулы:,

где F-начальная фаза. Вместо W может быть использовано 2Пи/T ,где Т-период колебаний.

Для построения фигур Лиссажу средствами MS Excel:

1.Необходимо подготовить следующую таблицу:

• Амплитуда колебаний — это наибольшее отклонение колеблющегося тела от положения равновесия.
• Циклическая частота – скалярная величина, мера частоты вращательного или колебательного движения.
• Начальная фаза – место, откуда начинается колебательный процесс в определённый момент времени (начало отсчёта).
• Время колебаний – это время колебания системы.
• Колебание Х – это колебание системы по оси OX.
• Колебание Y – это колебание системы по оси OY.

2.Столбец F начиная с ячейки F5 и далее заполнить значениями от 0,01 до 10 с шагом 0,01

(используя функцию автозаполнения)

3.В столбец G начиная с ячейки G5 и далее ввести формулу для колебания X:

4.В столбец H начиная с ячейки H5 и далее ввести формулу для колебания Y:

5.Должна получиться вот такая таблица с данными:

6.Теперь необходимо построить диаграмму по этим данным. Для этого нужно выделить два столбца со значениями колебаний X и Y. После этого нажимаем на пиктограмму мастера построения диаграмм.

7.Тип диаграммы выбираем «СТАНДАРТНЫЕ» — «ТОЧЕЧНАЯ» — «Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров» Нажимаем «Далее». Переходим на вкладку «РЯД» и называем «Ряд 1» — Колебание X ,а «Ряд 2» — Колебание Y. Нажимаем «Далее» теперь надо подписать название диаграммы «Фигуры Лиссажу». Нажимаем «Далее» и выбираем расположение диаграммы в текущем листе.

8.Должно получиться следующее:

2.3 Описание применения фигур Лиссажу для сравнения гармонических колебаний

Анализ литературы показал, что фигуры Лиссажу применяются: в радиотехнике для сравнения частот, в осциллографе. Если подать на входы «X» и «Y» осциллографа сигналы близких частот, то на экране можно увидеть фигуры Лиссажу. Этот метод широко используется для сравнения частот двух источников сигналов и для подстройки одного источника под частоту другого. Когда частоты близки, но не равны друг другу, фигура на экране вращается, причём период цикла вращения является величиной, обратной разности частот, например, при периоде оборота равен 2с. разница в частотах сигналов равна 0,5 Гц. При равенстве частот фигура застывает неподвижно, в любой фазе, однако на практике, за счёт кратковременных нестабильностей сигналов, фигура на экране осциллографа обычно чуть-чуть подрагивает. Использовать для сравнения можно не только одинаковые частоты, но и находящиеся в кратном отношении, например, если образцовый источник может выдавать частоту только 5 МГц, а настраиваемый источник — 2,5 МГц.

Заключение

Целью данной работы являлось рассказать и наглядно показать моделирование фигур Лиссажу.

В рамках исследования были решены следующие задачи:

1.Проанализированна литература по теме «Моделирование фигур Лиссажу»

2.Было раскрыты понятия: фигуры Лиссажу, гармоническое колебание, векторная диаграмма, развертка, Microsoft Office Excel, амплитуда колебаний, циклическая частота,

3.Рассмотрели способы построения графиков в среде MS Excel.

4.Разработали модель фигур Лиссажу в MS Excel для исследования гармонических колебаний.

В рамках исследования можно считать цель достигнутой.

Список использованной литературы

• Мусин, Ю. Р. Физика: колебания, оптика, квантовая физика : учебное пособие для среднего профессионального образования / Ю. Р. Мусин. — 2-е изд., испр. и доп. — Москва : Издательство Юрайт, 2020. — 329 с.
• Аминев, А. В. Основы радиоэлектроники: измерения в телекоммуникационных системах : учебное пособие для среднего профессионального образования / А. В. Аминев, А. В. Блохин ; под общей редакцией А. В. Блохина. — Москва : Издательство Юрайт, 2019. — 223 с. URL: https://urait.ru/bcode/442543 .(97-98 стр.)
• Штыков, В. В. Введение в радиоэлектронику : учебник и практикум для среднего профессионального образования / В. В. Штыков. — 2-е изд., испр. и доп. — Москва : Издательство Юрайт, 2019. — 228 с. URL: https://urait.ru/bcode/437093 .(82-84 стр.)URL: https://urait.ru/bcode/449189 .( 19 стр.)