Моделирование эпидемии в excel практическая работа 11 класс решение

Подборка по базе: Особенности работы с детьми.pptx, Титульный лист для практической работы.docx, Методические указания к выполнению контрольной работы (1).pdf, таблица индивидуальной работы.docx, Анализ работы УМР за январь.docx, Уголовный процесс Синергия Благодарю за заказ готовой работы! Бо, Практическая работа, организация работы в ЭИОС И ЭБС.docx, бланк Контрольной работы по Безопасности жизнедеятельности.doc, Карточки для индивидуальной работы на уроках математики в 3 клас, Выполнение контрольной работы по ГОУ для заочн.docx

1. Моделирование

Практические работы

1. Моделирование эпидемии

Для выполнения работы откройте файл-заготовку Эпидемия.xls.

При эпидемии гриппа число больных изменяется по формуле

,

где – количество заболевших в -й день, а – количество выздоровевших в тот же день. Число заболевших рассчитывается согласно модели ограниченного роста:

,

где – общая численность жителей, – коэффициент роста и – число переболевших (тех, кто уже переболел и выздоровел, и поэтому больше не заболеет):

.

Считается, что в начале эпидемии заболел 1 человек, все заболевшие выздоравливают через 7 дней и больше не болеют.

Выполните моделирование развития эпидемии при и до того момента, когда количество больных станет равно нулю. Постройте график изменения количества больных.

Ответьте на следующие вопросы:

1. Когда закончится эпидемия?

Ответ:

Эпидемия закончится на 40 день

1. Сколько человек переболеет, а сколько вообще не заболеет гриппом?

Ответ:

Переболело 980 человека, не заболело 20 человек из 1000

1. Каково максимальное число больных в один день?

Ответ:

Максимальное число больных в один день 648

1. Изменяя коэффициент , определите, при каких значениях модель явно перестает быть адекватной.

Ответ:

При К больше 1 модель перестаёт быть адекватной

1. *Сравните модель, использованную в этой работе, со следующей моделью:

, .

Анализируя результаты моделирования, докажите, что эта модель неадекватна. Какие допущения, на ваш взгляд, были сделаны неверно при разработке этой модели?

Ответ:

Модель не адекватна , так как Н не может принимать значения меньше 0. Число выздоровевших должно вычисляться каждый день для точности. Поэтому количество больных стало переходить в отрицательный вид.

Сравните поведение двух моделей при , и . Сделайте выводы.

Ответ:

Для выполнения работы откройте файл-заготовку Эпидемия.xls.
При эпидемии гриппа число больных изменяется по формуле
,
где – количество заболевших в -й день, а – количество выздоровевших в тот же день. Число заболевших рассчитывается согласно модели ограниченного роста:
,
где – общая численность жителей, – коэффициент роста и – число переболевших (тех, кто уже переболел и выздоровел, и поэтому больше не заболеет):
.
Считается, что в начале эпидемии заболел 1 человек, все заболевшие выздоравливают через 7 дней и больше не болеют.
Выполните моделирование развития эпидемии при и до того момента, когда количество больных станет равно нулю. Постройте график изменения количества боль-ных.
Ответьте на следующие вопросы:
1. Когда закончится эпидемия?
Ответ:

2. Сколько человек переболеет, а сколько вообще не заболеет гриппом?
Ответ:

3. Каково максимальное число больных в один день?
Ответ:

4. Изменяя коэффициент , определите, при каких значениях модель явно перестает быть адекватной.

 «Моделирование
эпидемии гриппа в Excel».

 Формулировка задачи: в городе, населённостью 1 млн. человек, начинается эпидемия
гриппа. Требуется отследить «развитие» эпидемии, для этого сформировать
таблицу, в которой отражены данные на каждый день эпидемии о: 

—    количестве заболевших на каждый
день,

—        
количестве
нетрудоспособных в связи с болезнью, если допустить, что заболевание длится 10
дней,

—        
количестве
обращений к врачу, если считать, что больной обращается дважды к врачу: в
начале заболевания и в конце,

—        
количестве
обращений к врачу, 

—        
количестве врачей
для обслуживания больных, если на одного врача допускается двадцать посещений
больных.

Построить графики, иллюстрирующие развитие эпидемии
гриппа: рост числа заболевших, количество нетрудоспособных в связи с болезнью,
число обращений к врачу, зависимость количества врачей, необходимых  для
обслуживания больных.

 Исходные данные:

—        
население города
1 млн. человек,

—        
допустим, в город
приехали 20 человек, которые являются переносчиками гриппа.

Объяснение хода выполнения работы.

Для вычисления количества заболевших в определенный день
эпидемии используется уравнение:

К=а×К₁×К₂ (1)

а =0,000002- коэффициент, характеризующий степень заразности
для гриппа,

К₁— не перенесшие заболевание (без иммунитета),

К₂— заболевшие вчера (они активно продуцируют
возбудитель)

III. Практическая часть. Выполнение расчетов. Построение

графиков.

Для решения поставленной задачи в Excel формируется следующая таблица:

Количество дней эпидемии целесообразно взять не более 36.

Для расчёта  количества «заболевших сегодня» в ячейку С3
вводится формула на основании уравнения (1):

=ОКРУГЛ(0,000002*B2*C2;0); в этой формуле используется
округление расчётных данных до целого значения. 

Для расчёта «не перенесших гриппа» необходимо вычесть из
количества не перенесших грипп в предыдущий день эпидемии количество заболевших
сегодня, для этого в ячейку В3 вводится формула =B2-C3 

Выделив ячейки В3 и С3, можно эти формулы скопировать эти
формулы на все дни эпидемии. При таком копировании координаты ячеек в формуле
будут относительными, т.е. меняться в зависимости от адреса ячеек, например, в
ячейке С4:    =ОКРУГЛ(0,000002*B3*C3;0)
,      а в ячейке В4: =B3-C4 
и т.д. После расчёта таблица выглядит так:

          Таким образом, в каждый последующий день
эпидемии расчёт числа заболевших производится относительно данных предыдущего
дня эпидемии.

По таблице видно, что пик заболеваемости приходится
на 16-ый день эпидемии, и уже к 28-му дню нет вновь заболевших гриппом.

Для расчёта на каждый день заболевших
всего необходимо сложить заболевших сегодня и заболевших всего в предыдущий
день, для этого в ячейку D3 вводится
формула =C3+D2 и затем
эта формула копируется в ячейки столбца D на все дни эпидемии. При этом координаты ячеек в формуле
будут относительными.

Для вычисления количества
нетрудоспособного населения на каждый день эпидемии в связи с болезнью надо
учитывать, что заболевание длится 10 дней, поэтому в первые десять дней
количество нетрудоспособных в каждый день эпидемии равно числу заболевших
сегодня плюс число получивших больничный лист вчера; формула вводится в ячейку E3:  =C3+E2 и затем копируется на первые десять
дней эпидемии. На 11-ый день эпидемии для расчёта количества нетрудоспособных
на каждый день эпидемии надо сложить число заболевших сегодня и число
получивших больничный лист вчера, и из полученной суммы вычесть число
заболевших в первый день эпидемии, т.к. они уже здоровы. В ячейке E12 вводится формула =C12+E11-C2 и затем копируется на остальные дни эпидемии.

Для расчёта числа обращений к врачу необходимо
учесть, что больной обращается дважды к врачу: в начале заболевания и в конце
заболевания- на десятый день болезни. Число обращений к врачу первые девять
дней эпидемии очевидно равно количеству заболевших сегодня, а на десятый день
эпидемии для расчёта числа обращений  к врачу к количеству заболевших сегодня
прибавляется число заболевших в первый день эпидемии. В ячейку F2 вводится формула =C2, и эта формула копируется на девять дней эпидемии, в ячейку F11  вводится формула =С11+С2 и затем эта
формула копируется на все остальные дни эпидемии. 

Последний расчёт- количество врачей для обслуживания больных
вычисляется в столбике G и равен числу
обращений к врачу делить на 20 (по условию задачи на одного врача допускается
20-ть посещений больных за один приём), для этого в ячейку G2 вводится формула  =ОКРУГЛ(F2/20;0).

После  всех расчётов таблица выглядит так:

IV. Анализ работы. Подведение итогов.

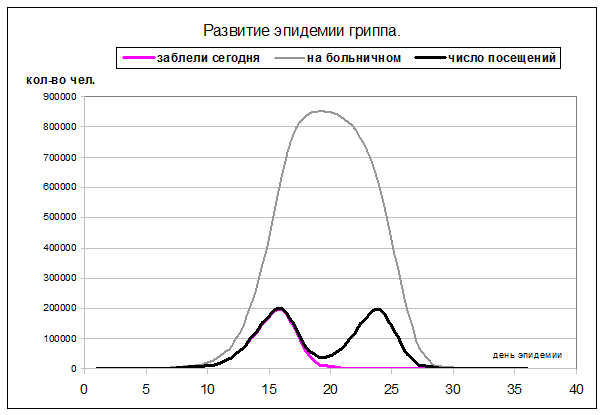
Для анализа расчётных данных удобно построить два графика, на
одном из которых представлены зависимости количества заболевших на каждый день
эпидемии, количества нетрудоспособных в связи с болезнью, т.е. находящихся «на
больничном», а также числа обращений к врачу в каждый день эпидемии.

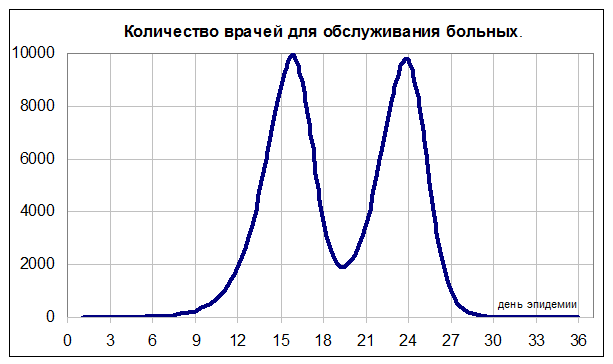
Анализ полученных данных можно предложить выполнить
студентами самостоятельно.

Примечание: для построения графиков желательно использовать тип графика
«точечный», выделив для первого графика данные в столбцах A,C,E,F; для второго графика данные в
столбцах A,G. При таком выборе типа графика 1-ый столбец рассматривается
как ось категорий.

График 1.

График 2.

Инфоурок

›

Информатика

›Другие методич. материалы›Дистанционный урок по информатике и ИКТ. Практическая работа «Разработка модели «Эпидемия гриппа»» 11 класс

Моделирование эпидемии

Для выполнения работы откройте файл-заготовку Эпидемия.xls.

При эпидемии гриппа число больных изменяется по формуле

,

где – количество заболевших в -й день, а – количество выздоровевших в тот же день. Число заболевших рассчитывается согласно модели ограниченного роста:

,

где – общая численность жителей, – коэффициент роста и – число переболевших (тех, кто уже переболел и выздоровел, и поэтому больше не заболеет):

.

Считается, что в начале эпидемии заболел 1 человек, все заболевшие выздоравливают через 7 дней и больше не болеют.

Выполните моделирование развития эпидемии при и до того момента, когда количество больных станет равно нулю. Постройте график изменения количества больных.

Ответьте на следующие вопросы:

1. Когда закончится эпидемия?

Ответ:

1. Сколько человек переболеет, а сколько вообще не заболеет гриппом?

Ответ:

1. Каково максимальное число больных в один день?

Ответ:

1. Изменяя коэффициент , определите, при каких значениях модель явно перестает быть адекватной.

Ответ:

1. *Сравните модель, использованную в этой работе, со следующей моделью:

, .

Анализируя результаты моделирования, докажите, что эта модель неадекватна. Какие допущения, на ваш взгляд, были сделаны неверно при разработке этой модели?

Ответ:

Сравните поведение двух моделей при , и . Сделайте выводы.

Ответ: