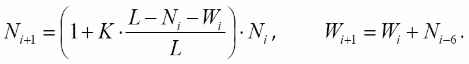«Моделирование
эпидемии гриппа в Excel».
Формулировка задачи: в городе, населённостью 1 млн. человек, начинается эпидемия
гриппа. Требуется отследить «развитие» эпидемии, для этого сформировать
таблицу, в которой отражены данные на каждый день эпидемии о:
— количестве заболевших на каждый
день,
—
количестве
нетрудоспособных в связи с болезнью, если допустить, что заболевание длится 10
дней,
—
количестве
обращений к врачу, если считать, что больной обращается дважды к врачу: в
начале заболевания и в конце,
—
количестве
обращений к врачу,
—
количестве врачей
для обслуживания больных, если на одного врача допускается двадцать посещений
больных.
Построить графики, иллюстрирующие развитие эпидемии
гриппа: рост числа заболевших, количество нетрудоспособных в связи с болезнью,
число обращений к врачу, зависимость количества врачей, необходимых для
обслуживания больных.
Исходные данные:
—
население города
1 млн. человек,
—
допустим, в город
приехали 20 человек, которые являются переносчиками гриппа.
Объяснение хода выполнения работы.
Для вычисления количества заболевших в определенный день
эпидемии используется уравнение:
К=а×К1×К2 (1)
а =0,000002- коэффициент, характеризующий степень заразности
для гриппа,
К1— не перенесшие заболевание (без иммунитета),
К2— заболевшие вчера (они активно продуцируют
возбудитель)
III. Практическая часть. Выполнение расчетов. Построение
графиков.
Для решения поставленной задачи в Excel формируется следующая таблица:
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
День |
Ещё |
Заболели |
Всего |
Кол-во (на |
число |
Количество |
|
2 |
1 |
1000000 |
20 |
||||
|
3 |
2 |
||||||
|
4 |
3 |
Количество дней эпидемии целесообразно взять не более 36.
Для расчёта количества «заболевших сегодня» в ячейку С3
вводится формула на основании уравнения (1):
=ОКРУГЛ(0,000002*B2*C2;0); в этой формуле используется
округление расчётных данных до целого значения.
Для расчёта «не перенесших гриппа» необходимо вычесть из
количества не перенесших грипп в предыдущий день эпидемии количество заболевших
сегодня, для этого в ячейку В3 вводится формула =B2-C3
Выделив ячейки В3 и С3, можно эти формулы скопировать эти
формулы на все дни эпидемии. При таком копировании координаты ячеек в формуле
будут относительными, т.е. меняться в зависимости от адреса ячеек, например, в
ячейке С4: =ОКРУГЛ(0,000002*B3*C3;0)
, а в ячейке В4: =B3-C4
и т.д. После расчёта таблица выглядит так:
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
день |
Ещё |
Заболели |
Всего |
Кол-во (на |
Число |
Количество |
|
2 |
1 |
1000000 |
20 |
||||
|
3 |
2 |
999960 |
40 |
||||
|
4 |
3 |
999880 |
80 |
||||
|
5 |
4 |
999720 |
160 |
||||
|
6 |
5 |
999400 |
320 |
||||
|
7 |
6 |
998760 |
640 |
||||
|
8 |
7 |
997482 |
1278 |
||||
|
9 |
8 |
994932 |
2550 |
||||
|
10 |
9 |
989858 |
5074 |
||||
|
11 |
10 |
979813 |
10045 |
||||
|
12 |
11 |
960129 |
19684 |
||||
|
13 |
12 |
922331 |
37798 |
||||
|
14 |
13 |
852606 |
69725 |
||||
|
15 |
14 |
733710 |
118896 |
||||
|
16 |
15 |
559240 |
174470 |
||||
|
17 |
16 |
364099 |
195141 |
||||
|
18 |
17 |
221998 |
142101 |
||||
|
19 |
18 |
158906 |
63092 |
||||
|
20 |
19 |
138855 |
20051 |
||||
|
21 |
20 |
133287 |
5568 |
||||
|
22 |
21 |
131803 |
1484 |
||||
|
23 |
22 |
131412 |
391 |
||||
|
24 |
23 |
131309 |
103 |
||||
|
25 |
24 |
131282 |
27 |
||||
|
26 |
25 |
131275 |
7 |
||||
|
27 |
26 |
131273 |
2 |
||||
|
28 |
27 |
131272 |
1 |
||||
|
29 |
28 |
131272 |
0 |
Таким образом, в каждый последующий день
эпидемии расчёт числа заболевших производится относительно данных предыдущего
дня эпидемии.
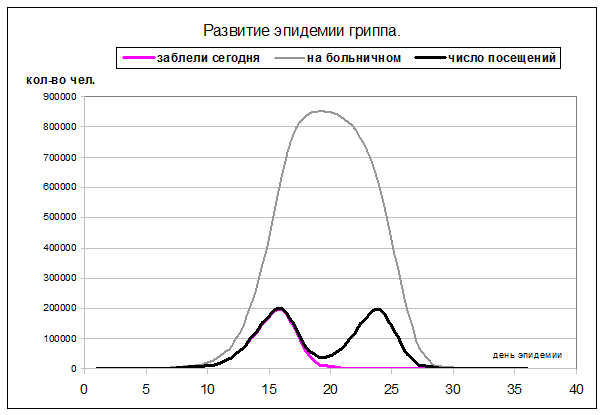
По таблице видно, что пик заболеваемости приходится
на 16-ый день эпидемии, и уже к 28-му дню нет вновь заболевших гриппом.
Для расчёта на каждый день заболевших
всего необходимо сложить заболевших сегодня и заболевших всего в предыдущий
день, для этого в ячейку D3 вводится
формула =C3+D2 и затем
эта формула копируется в ячейки столбца D на все дни эпидемии. При этом координаты ячеек в формуле
будут относительными.
Для вычисления количества
нетрудоспособного населения на каждый день эпидемии в связи с болезнью надо
учитывать, что заболевание длится 10 дней, поэтому в первые десять дней
количество нетрудоспособных в каждый день эпидемии равно числу заболевших
сегодня плюс число получивших больничный лист вчера; формула вводится в ячейку E3: =C3+E2 и затем копируется на первые десять
дней эпидемии. На 11-ый день эпидемии для расчёта количества нетрудоспособных
на каждый день эпидемии надо сложить число заболевших сегодня и число
получивших больничный лист вчера, и из полученной суммы вычесть число
заболевших в первый день эпидемии, т.к. они уже здоровы. В ячейке E12 вводится формула =C12+E11-C2 и затем копируется на остальные дни эпидемии.
Для расчёта числа обращений к врачу необходимо
учесть, что больной обращается дважды к врачу: в начале заболевания и в конце
заболевания- на десятый день болезни. Число обращений к врачу первые девять
дней эпидемии очевидно равно количеству заболевших сегодня, а на десятый день
эпидемии для расчёта числа обращений к врачу к количеству заболевших сегодня
прибавляется число заболевших в первый день эпидемии. В ячейку F2 вводится формула =C2, и эта формула копируется на девять дней эпидемии, в ячейку F11 вводится формула =С11+С2 и затем эта
формула копируется на все остальные дни эпидемии.
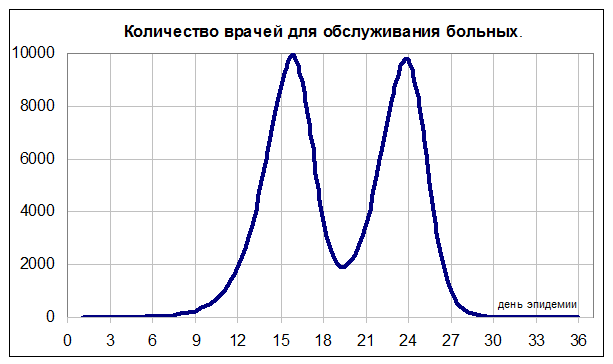
Последний расчёт- количество врачей для обслуживания больных
вычисляется в столбике G и равен числу
обращений к врачу делить на 20 (по условию задачи на одного врача допускается
20-ть посещений больных за один приём), для этого в ячейку G2 вводится формула =ОКРУГЛ(F2/20;0).
После всех расчётов таблица выглядит так:
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
день |
Ещё |
Заболели |
Всего |
Кол-во (на |
число |
Количество |
|
2 |
1 |
1000000 |
20 |
20 |
20 |
20 |
1 |
|
3 |
2 |
999960 |
40 |
60 |
60 |
40 |
2 |
|
4 |
3 |
999880 |
80 |
140 |
140 |
80 |
4 |
|
5 |
4 |
999720 |
160 |
300 |
300 |
160 |
8 |
|
6 |
5 |
999400 |
320 |
620 |
620 |
320 |
16 |
|
7 |
6 |
998760 |
640 |
1260 |
1260 |
640 |
32 |
|
8 |
7 |
997482 |
1278 |
2538 |
2538 |
1278 |
64 |
|
9 |
8 |
994932 |
2550 |
5088 |
5088 |
2550 |
128 |
|
10 |
9 |
989858 |
5074 |
10162 |
10162 |
5074 |
254 |
|
11 |
10 |
979813 |
10045 |
20207 |
20207 |
10065 |
503 |
|
12 |
11 |
960129 |
19684 |
39891 |
39871 |
19724 |
986 |
|
13 |
12 |
922331 |
37798 |
77689 |
77629 |
37878 |
1894 |
|
14 |
13 |
852606 |
69725 |
147414 |
147274 |
69885 |
3494 |
|
15 |
14 |
733710 |
118896 |
266310 |
266010 |
119216 |
5961 |
|
16 |
15 |
559240 |
174470 |
440780 |
440160 |
175110 |
8756 |
|
17 |
16 |
364099 |
195141 |
635921 |
634661 |
196419 |
9821 |
|
18 |
17 |
221998 |
142101 |
778022 |
775484 |
144651 |
7233 |
|
19 |
18 |
158906 |
63092 |
841114 |
836026 |
68166 |
3408 |
|
20 |
19 |
138855 |
20051 |
861165 |
851003 |
30096 |
1505 |
|
21 |
20 |
133287 |
5568 |
866733 |
846526 |
25252 |
1263 |
|
22 |
21 |
131803 |
1484 |
868217 |
828326 |
39282 |
1964 |
|
23 |
22 |
131412 |
391 |
868608 |
790919 |
70116 |
3506 |
|
24 |
23 |
131309 |
103 |
868711 |
721297 |
118999 |
5950 |
|
25 |
24 |
131282 |
27 |
868738 |
602428 |
174497 |
8725 |
|
26 |
25 |
131275 |
7 |
868745 |
427965 |
195148 |
9757 |
|
27 |
26 |
131273 |
2 |
868747 |
232826 |
142103 |
7105 |
|
28 |
27 |
131272 |
1 |
868748 |
90726 |
63093 |
3155 |
|
29 |
28 |
131272 |
0 |
868748 |
27634 |
20051 |
1003 |
|
30 |
29 |
131272 |
0 |
868748 |
7583 |
5568 |
278 |
|
31 |
30 |
131272 |
0 |
868748 |
2015 |
1484 |
74 |
|
32 |
31 |
131272 |
0 |
868748 |
531 |
391 |
20 |
|
33 |
32 |
131272 |
0 |
868748 |
140 |
103 |
5 |
|
34 |
33 |
131272 |
0 |
868748 |
37 |
27 |
1 |
|
35 |
34 |
131272 |
0 |
868748 |
10 |
7 |
0 |
|
36 |
35 |
131272 |
0 |
868748 |
3 |
2 |
0 |
|
37 |
36 |
131272 |
0 |
868748 |
1 |
1 |
0 |
IV. Анализ работы. Подведение итогов.
Для анализа расчётных данных удобно построить два графика, на
одном из которых представлены зависимости количества заболевших на каждый день
эпидемии, количества нетрудоспособных в связи с болезнью, т.е. находящихся «на
больничном», а также числа обращений к врачу в каждый день эпидемии.
Анализ полученных данных можно предложить выполнить
студентами самостоятельно.
Примечание: для построения графиков желательно использовать тип графика
«точечный», выделив для первого графика данные в столбцах A,C,E,F; для второго графика данные в
столбцах A,G. При таком выборе типа графика 1-ый столбец рассматривается
как ось категорий.
График 1.
График 2.
-
Скачать материал
-
28.10.2017
8869
-
RAR
71.9 кбайт -
531
скачивание -
Рейтинг:
4 из 5 -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Жмарёв Алексей Николаевич. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 6 лет и 5 месяцев
- Подписчики: 2
- Всего просмотров: 14440
-
Всего материалов:
11
Файлы
Рабочий лист подходит для учеников 7 класса, работающих по учебнику «Информатика. ФГОС», автор Л….
Обновлено: 15.04.2023
Для выполнения работы откройте файл-заготовку Эпидемия.xls.
При эпидемии гриппа число больных изменяется по формуле
,
где – количество заболевших в -й день, а – количество выздоровевших в тот же день. Число заболевших рассчитывается согласно модели ограниченного роста:
,
где – общая численность жителей, – коэффициент роста и – число переболевших (тех, кто уже переболел и выздоровел, и поэтому больше не заболеет):
.
Считается, что в начале эпидемии заболел 1 человек, все заболевшие выздоравливают через 7 дней и больше не болеют.
Выполните моделирование развития эпидемии при и до того момента, когда количество больных станет равно нулю. Постройте график изменения количества боль-ных.
Ответьте на следующие вопросы:
1. Когда закончится эпидемия?
Ответ:
2. Сколько человек переболеет, а сколько вообще не заболеет гриппом?
Ответ:
3. Каково максимальное число больных в один день?
Ответ:
4. Изменяя коэффициент , определите, при каких значениях модель явно перестает быть адекватной.
Моделирование распространения эпидемии
Питаюсь запустить пример модели распространения эпидемии из книги Кудрявцева. После трансляции в.
Моделирование распространения эпидемии
Вводим размеры поля Например: 4 4 Потом заполняем его с клавиатуры ( — здоровые клетки, -.
модель эпидемии
Здравствуйте. Делаю в AnyLogic модель эпидемии с помощью диаграммы состояний. Агент проходит 4.
Модель эпидемии.
Построить и исследовать модель эпидемии в городе с 300 тыс. жителей с фиксированным инкубационным.
Процесс развития эпидемии
Выявление основных особенностей. Процесс развития эпидемии представим в виде двух дифференциальных.
Обострения на фоне эпидемии
— вся статья в PDF. Пара клинических примеров из научной работы «Амбулаторные случаи психических.
Нет ли сейчас эпидемии приводящей к BSOD 0A?
Мне в последние дни позвонило несколько знакомых, у которых на компе выскакивает BSOD.
Кому нужны услуги программистов во время эпидемии?
Здравствуйте. Я не программист, я программировать начал недавно и программирую с форумами и.
Новый Facebook вирус приобрел масштабы эпидемии
Обнаруженный сегодня в крупнейшей соцсети фишинговый вирус продолжает бесконтрольное.
Какова вероятность того, что во время эпидемии не более 4 из десяти заболеют
В поликлинике работают 10 участковых врачей. Вероятность заболеть гриппом во время эпидемии для.
Из 200 сотрудников данного предприятия в разгар эпидемии заболеют ровно 60 челове
Добрый вечер. Имеется такая задача: В разгар эпидемии вероятность заболеть для каждого сотрудника.
Рабочие листы и материалы для учителей и воспитателей
Более 300 дидактических материалов для школьного и домашнего обучения
- Онлайн
формат - Диплом
гособразца - Помощь в трудоустройстве
Выберите документ из архива для просмотра:
Выбранный для просмотра документ Кейс № 20 Информатика 30.04.2020.docx
Кейс № 20 к уроку информатики в 11 проф. классе
Учитель Осипова С.А.
Дата проведения 30 апреля
Алгоритм работы на уроке
Откройте тетради. Оформите запись даты и темы урока.
30.04.2020
Постановка задачи: определите цель работы, выберите объект моделирования;
Разработка модели: информационная, математическая (в виде зависимостей – формул),
Построение компьютерной модели (моделируйте в excel );
Компьютерный эксперимент (заполните таблицу 2);
Запишите в дневник домашнее задание на след.урок:
Параграф 10 повторить.
Полученный файл Excel отправьте на электронную почту учителя (указывайте дату урока или номер кейса).
Выбранный для просмотра документ Модель_Эпидемия_гриппа.doc
рассмотрим ситуацию, когда в классе появляются ученики, заболевшие гриппом и разработаем модель развития эпидемии гриппа в классе.
Цель моделирования
Составить прогноз о том, сколько человек в классе будут больны в каждый день эпидемии, сколько дней продлится эпидемия.
Формализация задачи
Сделаем несколько упрощающих предположений:
1. В любой момент времени каждый ученик класса входит в одну из групп:
Носители инфекции ходят в школу и заражают других в течение одного дня. На следующий день они заболевают и перестают посещать занятия.
Заболевшие учащиеся болеют в течение 5 дней, после чего выходят на занятия.
Выздоровевшие учащиеся повторно не заболевают (у них вырабатывается иммунитет).
Скорость распространения инфекции задается коэффициентом k и зависит от многих факторов: возраст детей, наличие противогриппозных мероприятий, закаленность учащихся, степень общения в классе и т.п.
Будем прослеживать состояние класса день за днем. В каждый день состояние описывается следующим набором величин:
a – число здоровых учеников;
b – число носителей инфекции;
c – число больных учеников;
d – число выздоровевших учеников;
w – число присутствующих в классе;
n – всего учеников в классе.
Тогда справедливы следующие равенства:
n = a + b + c+ d;
Пусть в день t имеем состояние:
Каково будет состояние в классе на следующий день, через два дня, через три?
Ясно, что через 1 день b учеников перейдут из группы носителей в группу больных и число больных станет равно c+b . Если t , то выздоровевших учеников нет. Если t>=5 , то появятся выздоровевшие учащиеся и число больных станет меньше: c+b — (число учеников которые отболели уже 5 дней), они перейдут из числа больных в число выздоровевших.
Число учеников заразившихся гриппом в день t определяется по формуле : (так как количество учеников должно быть целым, то берем только целую часть от этого выражения).
Моделирование в электронной таблице (компьютерная модель
При сделанных нами предположениях ход эпидемии зависит от трех величин:
коэффициент k
количество учеников в классе n
число носителей инфекции в первый день эпидемии b
Эти три величины будем рассматривать в качестве управляющих параметров.
Заметим, что во 2-ой, 3-ий, 4-ый, 5-ый, 6-ой день выздоровевших учеников не будет, поэтому до 7-го дня характер эпидемии определяется теми же формулами, которые соответствуют 2-му дню.
Начиная с 7-го дня, учащиеся начинают выздоравливать, поэтому необходимо внести поправки в формулы в ячейках Е11 и F11.
Заполните столько строк расчетной таблицы, пока количество больных и носителей не станет равно 0.
Представьте в виде графика зависимость числа учеников в классе от дня эпидемии.
— количестве заболевших на каждый день,
— количестве нетрудоспособных в связи с болезнью, если допустить, что заболевание длится 10 дней,
— количестве обращений к врачу, если считать, что больной обращается дважды к врачу: в начале заболевания и в конце,
— количестве обращений к врачу,
— количестве врачей для обслуживания больных, если на одного врача допускается двадцать посещений больных.
Построить графики, иллюстрирующие развитие эпидемии гриппа: рост числа заболевших, количество нетрудоспособных в связи с болезнью, число обращений к врачу, зависимость количества врачей, необходимых для обслуживания больных.
— население города 1 млн. человек,
— допустим, в город приехали 20 человек, которые являются переносчиками гриппа.
Объяснение хода выполнения работы.
Для вычисления количества заболевших в определенный день эпидемии используется уравнение:
а =0,000002- коэффициент, характеризующий степень заразности для гриппа,
К1— не перенесшие заболевание (без иммунитета),
К2— заболевшие вчера (они активно продуцируют возбудитель)
III. Практическая часть. Выполнение расчетов. Построение
Для решения поставленной задачи в Excel формируется следующая таблица:
| A | B | C | D | E | F | G |
| День эпидемии | Ещё не перенесли грипп | Заболели сегодня | Всего заболели | Кол-во нетрудоспо-собных (на больничном) | число обращений к врачу | Количество врачей |
Количество дней эпидемии целесообразно взять не более 36.
=ОКРУГЛ(0,000002*B2*C2;0); в этой формуле используется округление расчётных данных до целого значения.
Выделив ячейки В3 и С3, можно эти формулы скопировать эти формулы на все дни эпидемии. При таком копировании координаты ячеек в формуле будут относительными, т.е. меняться в зависимости от адреса ячеек, например, в ячейке С4: =ОКРУГЛ(0,000002*B3*C3;0) , а в ячейке В4: =B3-C4 и т.д. После расчёта таблица выглядит так:
| A | B | C | D | E | F | G |
| день эпидемии | Ещё не перенесли грипп | Заболели сегодня | Всего заболели | Кол-во нетрудоспо-собных (на больничном) | Число обращений к врачу | Количество врачей |
Таким образом, в каждый последующий день эпидемии расчёт числа заболевших производится относительно данных предыдущего дня эпидемии.
Для расчёта на каждый день заболевших всего необходимо сложить заболевших сегодня и заболевших всего в предыдущий день, для этого в ячейку D3 вводится формула =C3+D2 и затем эта формула копируется в ячейки столбца D на все дни эпидемии. При этом координаты ячеек в формуле будут относительными.
Для вычисления количества нетрудоспособного населения на каждый день эпидемии в связи с болезнью надо учитывать, что заболевание длится 10 дней, поэтому в первые десять дней количество нетрудоспособных в каждый день эпидемии равно числу заболевших сегодня плюс число получивших больничный лист вчера; формула вводится в ячейку E3: =C3+E2 и затем копируется на первые десять дней эпидемии. На 11-ый день эпидемии для расчёта количества нетрудоспособных на каждый день эпидемии надо сложить число заболевших сегодня и число получивших больничный лист вчера, и из полученной суммы вычесть число заболевших в первый день эпидемии, т.к. они уже здоровы. В ячейке E12 вводится формула =C12+E11-C2 и затем копируется на остальные дни эпидемии.
Для расчёта числа обращений к врачу необходимо учесть, что больной обращается дважды к врачу: в начале заболевания и в конце заболевания- на десятый день болезни. Число обращений к врачу первые девять дней эпидемии очевидно равно количеству заболевших сегодня, а на десятый день эпидемии для расчёта числа обращений к врачу к количеству заболевших сегодня прибавляется число заболевших в первый день эпидемии. В ячейку F2 вводится формула =C2, и эта формула копируется на девять дней эпидемии, в ячейку F11 вводится формула =С11+С2 и затем эта формула копируется на все остальные дни эпидемии.
Последний расчёт- количество врачей для обслуживания больных вычисляется в столбике G и равен числу обращений к врачу делить на 20 (по условию задачи на одного врача допускается 20-ть посещений больных за один приём), для этого в ячейку G2 вводится формула =ОКРУГЛ(F2/20;0).
После всех расчётов таблица выглядит так:
| A | B | C | D | E | F | G |
| день эпидемии | Ещё не перенесли грипп | Заболели сегодня | Всего заболели | Кол-во нетрудоспо-собных (на больничном) | число посещений врача | Количество врачей |
IV. Анализ работы. Подведение итогов.
Выполните краткий анализ полученных данных.
Для выполнения работы откройте файл-заготовку Эпидемия.xls.
При эпидемии гриппа число больных изменяется по формуле
,
где – количество заболевших в -й день, а – количество выздоровевших в тот же день. Число заболевших рассчитывается согласно модели ограниченного роста:
,
где – общая численность жителей, – коэффициент роста и – число переболевших (тех, кто уже переболел и выздоровел, и поэтому больше не заболеет):
.
Считается, что в начале эпидемии заболел 1 человек, все заболевшие выздоравливают через 7 дней и больше не болеют.
Выполните моделирование развития эпидемии при и до того момента, когда количество больных станет равно нулю. Постройте график изменения количества боль-ных.
Ответьте на следующие вопросы:
1. Когда закончится эпидемия?
Ответ:
2. Сколько человек переболеет, а сколько вообще не заболеет гриппом?
Ответ:
3. Каково максимальное число больных в один день?
Ответ:
4. Изменяя коэффициент , определите, при каких значениях модель явно перестает быть адекватной.
Моделирование распространения эпидемии
Питаюсь запустить пример модели распространения эпидемии из книги Кудрявцева. После трансляции в.
Моделирование распространения эпидемии
Вводим размеры поля Например: 4 4 Потом заполняем его с клавиатуры ( — здоровые клетки, -.
модель эпидемии
Здравствуйте. Делаю в AnyLogic модель эпидемии с помощью диаграммы состояний. Агент проходит 4.
Модель эпидемии.
Построить и исследовать модель эпидемии в городе с 300 тыс. жителей с фиксированным инкубационным.
Процесс развития эпидемии
Выявление основных особенностей. Процесс развития эпидемии представим в виде двух дифференциальных.
Обострения на фоне эпидемии
— вся статья в PDF. Пара клинических примеров из научной работы «Амбулаторные случаи психических.
Нет ли сейчас эпидемии приводящей к BSOD 0A?
Мне в последние дни позвонило несколько знакомых, у которых на компе выскакивает BSOD.
Кому нужны услуги программистов во время эпидемии?
Здравствуйте. Я не программист, я программировать начал недавно и программирую с форумами и.
Новый Facebook вирус приобрел масштабы эпидемии
Обнаруженный сегодня в крупнейшей соцсети фишинговый вирус продолжает бесконтрольное.
Какова вероятность того, что во время эпидемии не более 4 из десяти заболеют
В поликлинике работают 10 участковых врачей. Вероятность заболеть гриппом во время эпидемии для.
Из 200 сотрудников данного предприятия в разгар эпидемии заболеют ровно 60 челове
Добрый вечер. Имеется такая задача: В разгар эпидемии вероятность заболеть для каждого сотрудника.
Для выполнения работы откройте файл-заготовку Эпидемия.xls.
При эпидемии гриппа число больных N изменяется по формуле
где – Zi количество заболевших в i-й день, а Vi – количество выздоровевших в тот же день. Число заболевших рассчитывается согласно модели ограниченного роста:
где L – общая численность жителей, K – коэффициент роста и Wi – число переболевших (тех, кто уже переболел и выздоровел, и поэтому больше не заболеет):
Считается, что в начале эпидемии заболел 1 человек, все заболевшие выздоравливают через 7 дней и больше не болеют.
Выполните моделирование развития эпидемии при L = 1000 и K = 0,5 до того момента, когда количество больных станет равно нулю. Постройте график изменения количества больных.
Ответьте на следующие вопросы:
1. Когда закончится эпидемия?
2. Сколько человек переболеет, а сколько вообще не заболеет гриппом?
3. Каково максимальное число больных в один день?
4. Изменяя коэффициент K, определите, при каких значениях K модель явно перестает быть адекватной.
5. *Сравните модель, использованную в этой работе, со следующей моделью:
Анализируя результаты моделирования, докажите, что эта модель неадекватна. Какие допущения, на ваш взгляд, были сделаны неверно при разработке этой модели?
Сравните поведение двух моделей при K = 0, K = 0,3 и K = 1. Сделайте выводы.
Читайте также:
- Сертификат прививок от столбняка
- Была ли чума в казахстане
- Эпидемия чумы в нагорном карабахе
- Эпидемия коронавируса в европе сейчас
- Вирус температура боль в пояснице
Моделирование эпидемии
Для выполнения работы откройте файл-заготовку Эпидемия.xls.
При эпидемии гриппа число больных изменяется по формуле
,
где – количество заболевших в -й день, а – количество выздоровевших в тот же день. Число заболевших рассчитывается согласно модели ограниченного роста:
,
где – общая численность жителей, – коэффициент роста и – число переболевших (тех, кто уже переболел и выздоровел, и поэтому больше не заболеет):
.
Считается, что в начале эпидемии заболел 1 человек, все заболевшие выздоравливают через 7 дней и больше не болеют.
Выполните моделирование развития эпидемии при и до того момента, когда количество больных станет равно нулю. Постройте график изменения количества больных.
Ответьте на следующие вопросы:
-
Когда закончится эпидемия?
Ответ:
-
Сколько человек переболеет, а сколько вообще не заболеет гриппом?
Ответ:
-
Каково максимальное число больных в один день?
Ответ:
-
Изменяя коэффициент , определите, при каких значениях модель явно перестает быть адекватной.
Ответ:
-
*Сравните модель, использованную в этой работе, со следующей моделью:
, .
Анализируя результаты моделирования, докажите, что эта модель неадекватна. Какие допущения, на ваш взгляд, были сделаны неверно при разработке этой модели?
Ответ:
Сравните поведение двух моделей при , и . Сделайте выводы.
Ответ:
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по теме Моделирование эпидемии гриппа
Содержание
-
1.
Презентация к уроку по теме Моделирование эпидемии гриппа -
2.
Модель Ферхюльста. Рост популяции, ограниченный ресурсамиПьер Ферхюльст1804 -
3.
– начальная численность– после 1 цикла деления– -
4.
В(1)- количество больных начальная, В(n) — количество -
5.
Модель эпидемии гриппаL – всего жителей Ni -
6.
В(1)- количество больных начальная =1, В(n) — -
7.
Математическая модель -
8.
ЦЕЛЬ: создать компьютерную модель эпидемии гриппа, (график)Реализация
Модель Ферхюльста. Рост популяции, ограниченный ресурсамиПьер Ферхюльст1804 — 1849Ограниченный рост. Зависимость величины скорости роста от численности (а) и численности от времени (б)N — численность популяции, t — время, K — максимальная скорость прироста, L –емкость популяции
Слайд 1Моделирование
ЭПИДЕМИИ ГРИППА
*
§23

Слайд 2Модель Ферхюльста.
Рост популяции, ограниченный ресурсами
Пьер Ферхюльст
1804 — 1849
Ограниченный рост. Зависимость
величины скорости роста от численности (а) и численности от времени (б)
N — численность популяции,
t — время,
K — максимальная скорость прироста,
L –емкость популяции

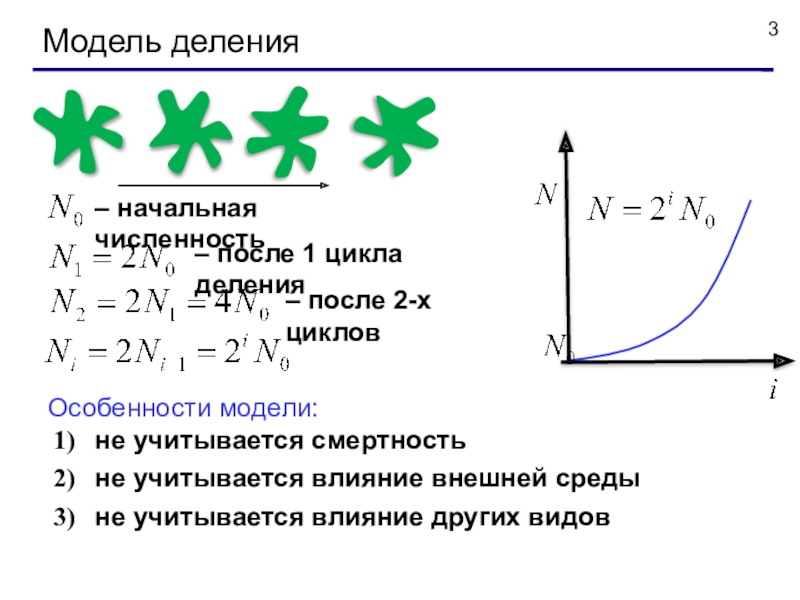
Слайд 3
– начальная численность
– после 1 цикла деления
– после 2-х циклов
Особенности модели:
не
учитывается смертность
не учитывается влияние внешней среды
не учитывается влияние других видов
Модель деления
Слайд 4В(1)- количество больных начальная,
В(n) — количество больных через n дней
k — коэффициент заражения = 0,5 ,
L=300 — всего людей,
Параметры модели
Модель ограниченного роста:

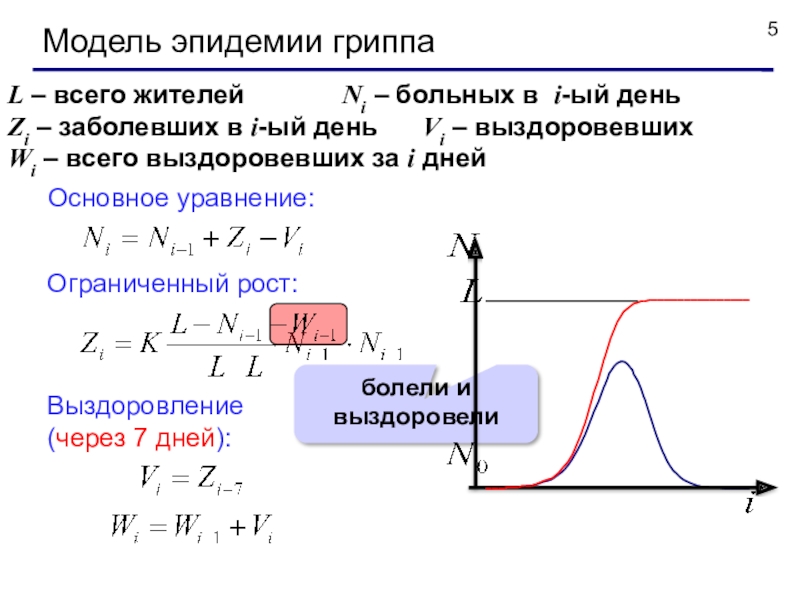
Слайд 5Модель эпидемии гриппа
L – всего жителей Ni – больных в i-ый
день
Zi – заболевших в i-ый день Vi – выздоровевших
Wi – всего выздоровевших за i дней
Основное уравнение:
Ограниченный рост:
Выздоровление
(через 7 дней):
Слайд 6В(1)- количество больных начальная =1,
В(n) — количество больных через n
дней
k — коэффициент заражения = 0,5 ,
L=300- всего людей,
V(n) –количество выздоровевших,
N(i)-число больных в i-й день
Z(i)- число заболевших в i-й день
W(i)-число выздоровевших за i дней
v(i)- выздоровевших в i-й день
Параметры модели

Слайд 8ЦЕЛЬ: создать компьютерную модель эпидемии гриппа, (график)
Реализация
Использовать табличный процессор Microsoft
Excel
Определить на каком шаге вычислений (год) когда эпидемия достигнет максимума.
Когда эпидемия закончится.
Практическая работа №14
(ст. 244, 116)