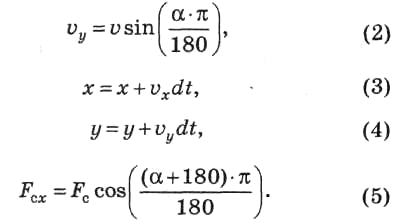Моделирование движения тела брошенного под углом к горизонту в excel

Решение задачи о движении тела, брошенного под углом к горизонту с помощью электронной таблицы.

При
изучении информатики ученики получили
первые навыки моделирования физических
процессов. На основе этих знаний можно
иначе подойти к изучению уже знакомых
явлений.

Предлагаем
изучить рассказ «Пуля и воздух» из
книги Я.И. Перельмана «Занимательная
физика».

Вот
выдержка из данного рассказа:

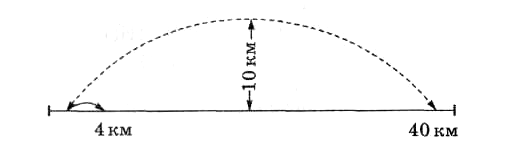
Покинув
ствол ружья под углом 45°, с начальной
скоростью 620 м/с, пуля описала бы дугу в
10км высотой; дальность полета составила
бы почти 40км. В действительности же пуля
при указанных условиях описывает
сравнительно небольшую дугу и дальность
ее полета составляет 4км. Изображенная
на том же чертеже дуга почти незаметна
рядом с первой; таков результат
противодействия воздуха!..

Полет
пули в пустоте и в воздухе.

Большая
дуга изображает путь, какой описала бы
пуля, если бы не существовало атмосферы.

Маленькая
дуга слева – действительный путь пули
в воздухе.

Задание

Создайте
компьютерную модель движения пули.
Используя данные из этого рассказа и
модель, определите коэффициент
сопротивления воздуха для пули, найдите,
при каком угле дальность полета будет
максимальной и чему она равна. Проверьте,
выполняется ли равенство дальности
полета для углов, сумма которых равна
90°.

Движение
пули в воздухе происходит под действием
двух сил: тяжести и сопротивления
воздуха. Сила сопротивления воздуха,
действующая на пулю, прямо пропорциональна
квадрату скорости (для больших скоростей)
и направлена в противоположную движению
сторону. Поэтому под действием силы
изменяется скорость, что приводит к
изменению силы. Поэтому с помощью
привычных методов решение данной задачи
весьма проблематично.

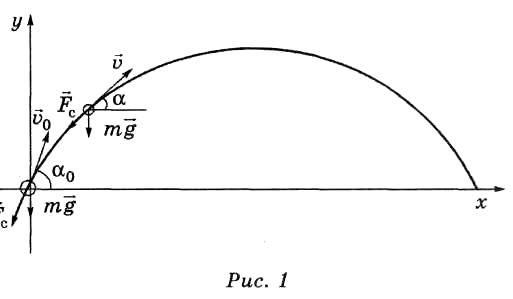
Математическая
модель движения пули

Время
движения пули разобьем на небольшие
интервалы и будем считать, что на
протяжении каждого из них скорость и
сила сопротивления остаются постоянными.
По истечении каждого интервала изменяются
скорость движения, сила сопротивления,
угол направления скорости и силы, т. е.
эти величины, изменяются скачкообразно.
На рисунке показаны два дискретных
положения пули.

Дискретный
процесс изменения физических величин
определяется рекуррентными формулами:

(Аргумент
функции α переводится из градусов в
радианы.)

(Учтено
то, что направление силы противоположно
скорости.)

Компьютерная
модель движения пули

Используем
табличную схему модели в электронных
таблицах.

В
ячейку В1 введем название «Движение
тела, брошенного под углом к горизонту,
с учетом сопротивления воздуха».

Исходными
данными для поставленной задачи являются
начальная скорость, угол выстрела, масса
пули, ускорение свободного падения,
коэффициент сопротивления воздуха и
шаг времени.

В
раздел «Исходные данные» внесем:

А4:
620

В4:
«м/с – начальная скорость»

А5:
45

В5:
«градусов – угол выстрела»

А6:
0,009

В6:
«кг – масса пули»

А7:
9,81

В7:
«м/с²
– ускорение свободного падения»

А8:
0

В8:
«Н*(с/м)²
–
коэффициент сопротивления воздуха»

А9:
0,52

В9:
«с – шаг времени»

В
раздел «Расчетная таблица» в строку
12 внесем по порядку буквы, обозначающие
физические величины: t,
α
,
v,
v_x,
v_y,
k,
F,
F_x,
F_y,
a_x,
a_v,
x,
y.

В
строку 13 вносим следующие формулы:

А13:
0

В13:
=А5

С13:
=А4

D13:
=С13*СОS(В13*ПИ()/180)

Е13:
=C13*SIN(B13*IIИ()/180)

F13:
=А8

G13:
=F13*C13^2

Н13:
=G13*COS((B13+180)*ПИ()/180)

I13:
=G13*SIN((B13+180)* ПИ
()/180)

J13:
=H13/$A$6

K13:
=I13/$A$6-$A$7

L13:
0

M13:
0

В
строку 14 вносим формулы:

А14:
=А13+$А$9

В14:
=АТАN
(Е14/D14)*180/ПИ()

С14:
=КОРЕНЬ(D13^2+Е14^2)

D14:
=D13+J13*$A$9

Е14:
=Е13+К13*$А$9

F14:
=F13

G14:
=F14*C14^2

Н14:
=G14*COS((B14+180)*
ПИ ()/180)

I14:
=G14*SIN((B14+180)* ПИ
()/180)

J14:
=H14/$A$6

K14:
=I14/$A$6-$A$7

L14:
=L13+D14*$A$9

M14:
=M13+E14*$A$9

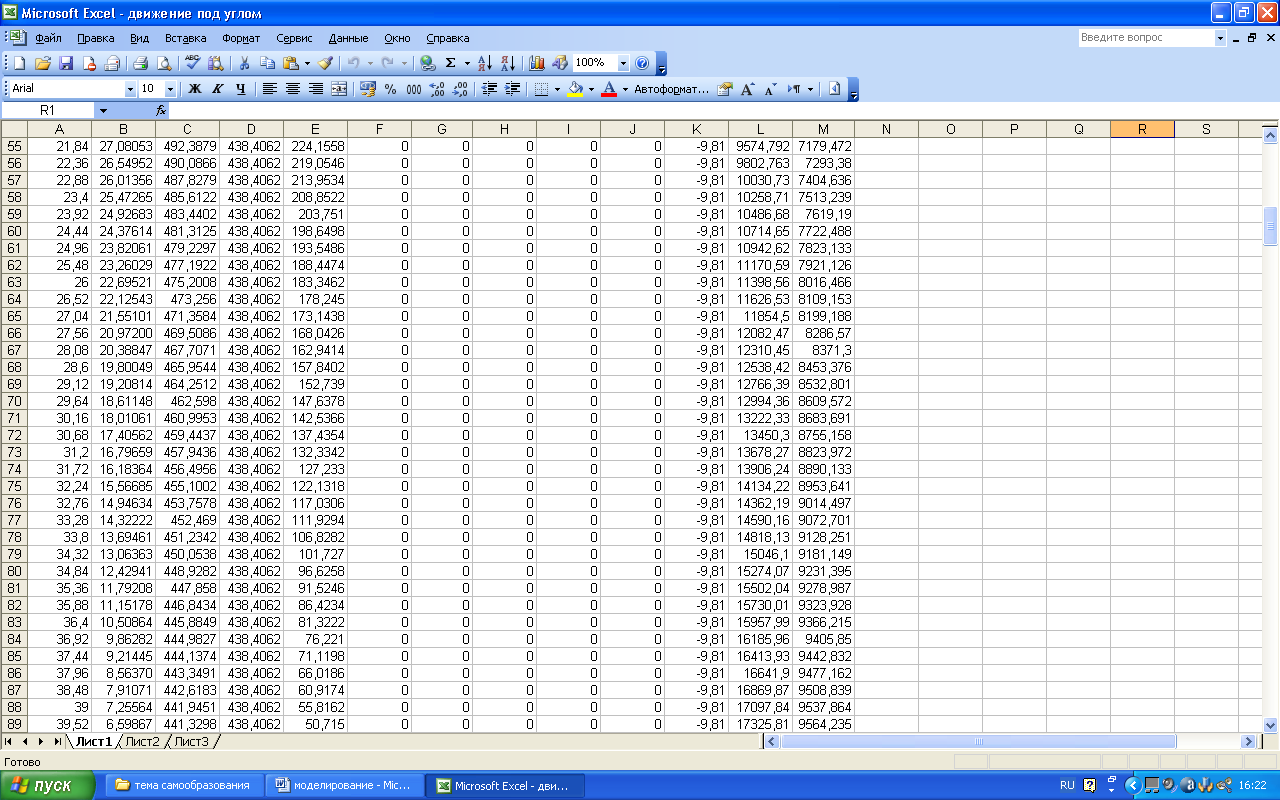
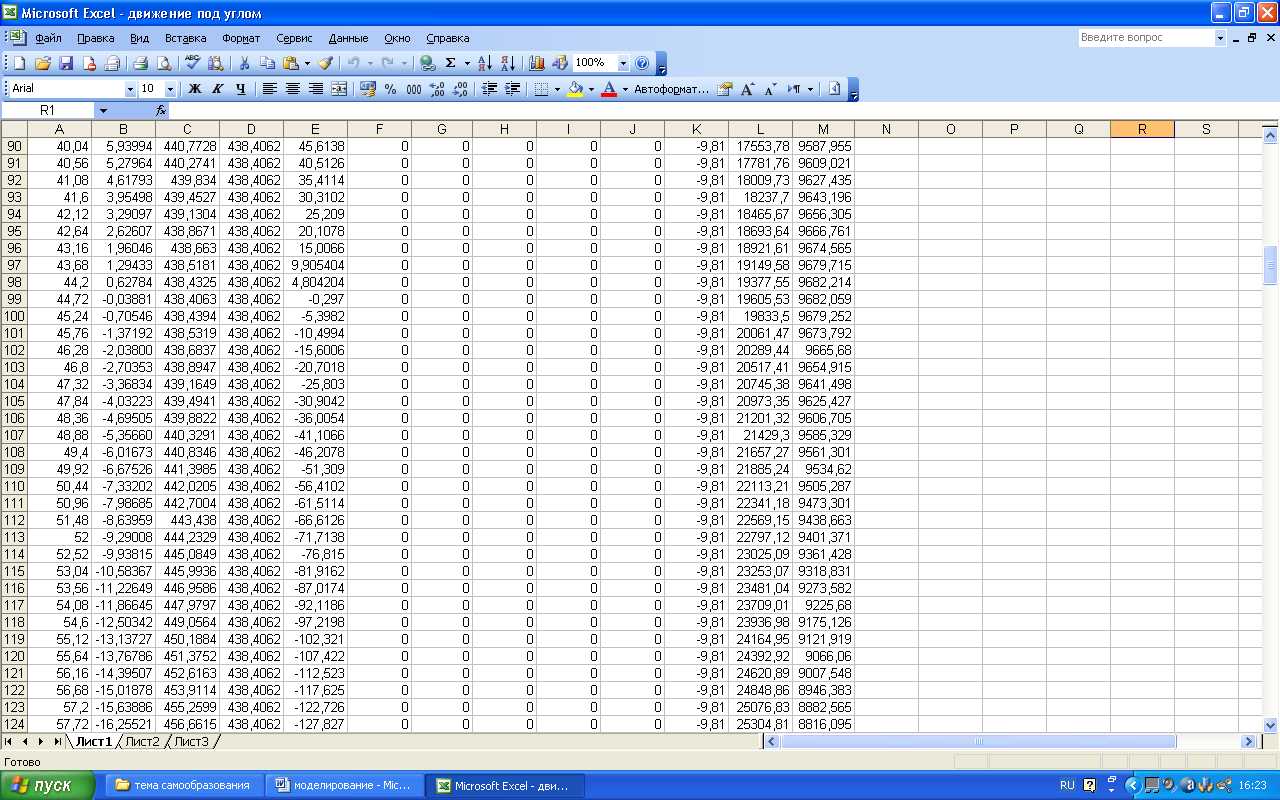
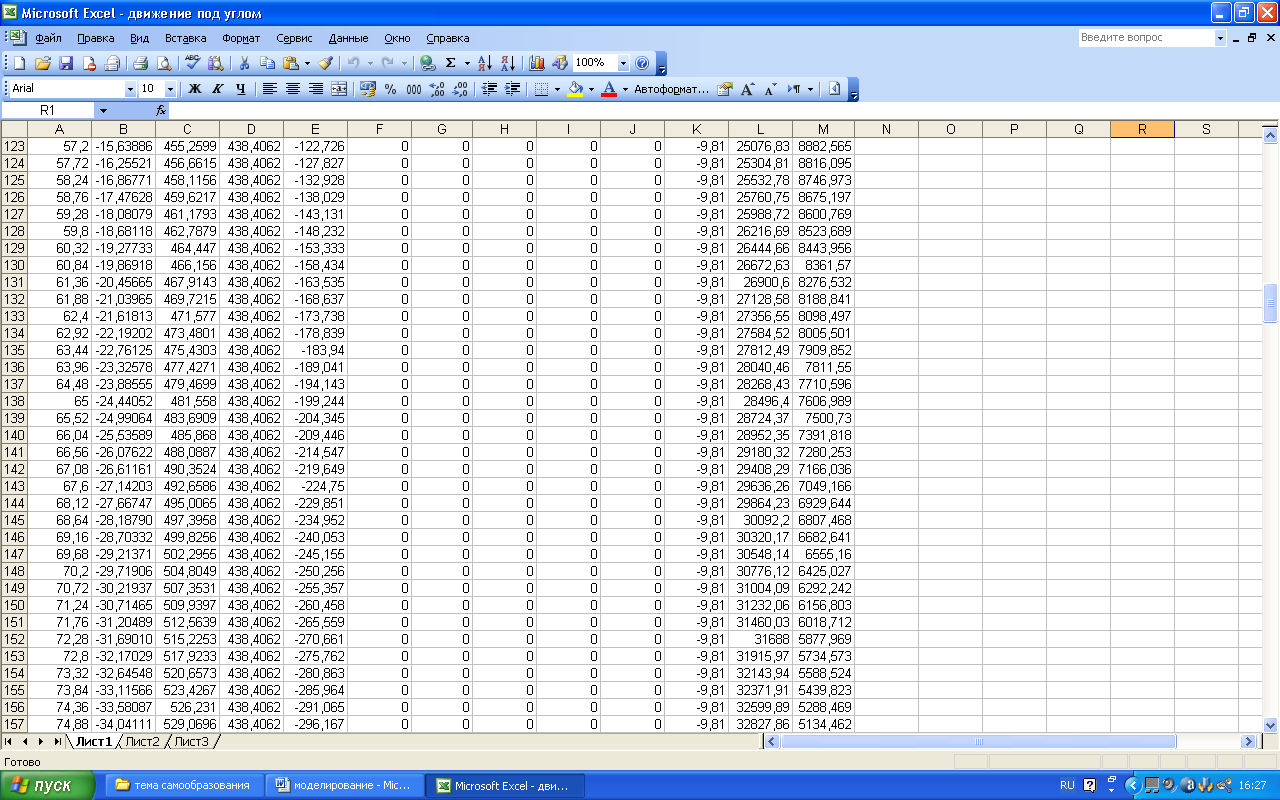
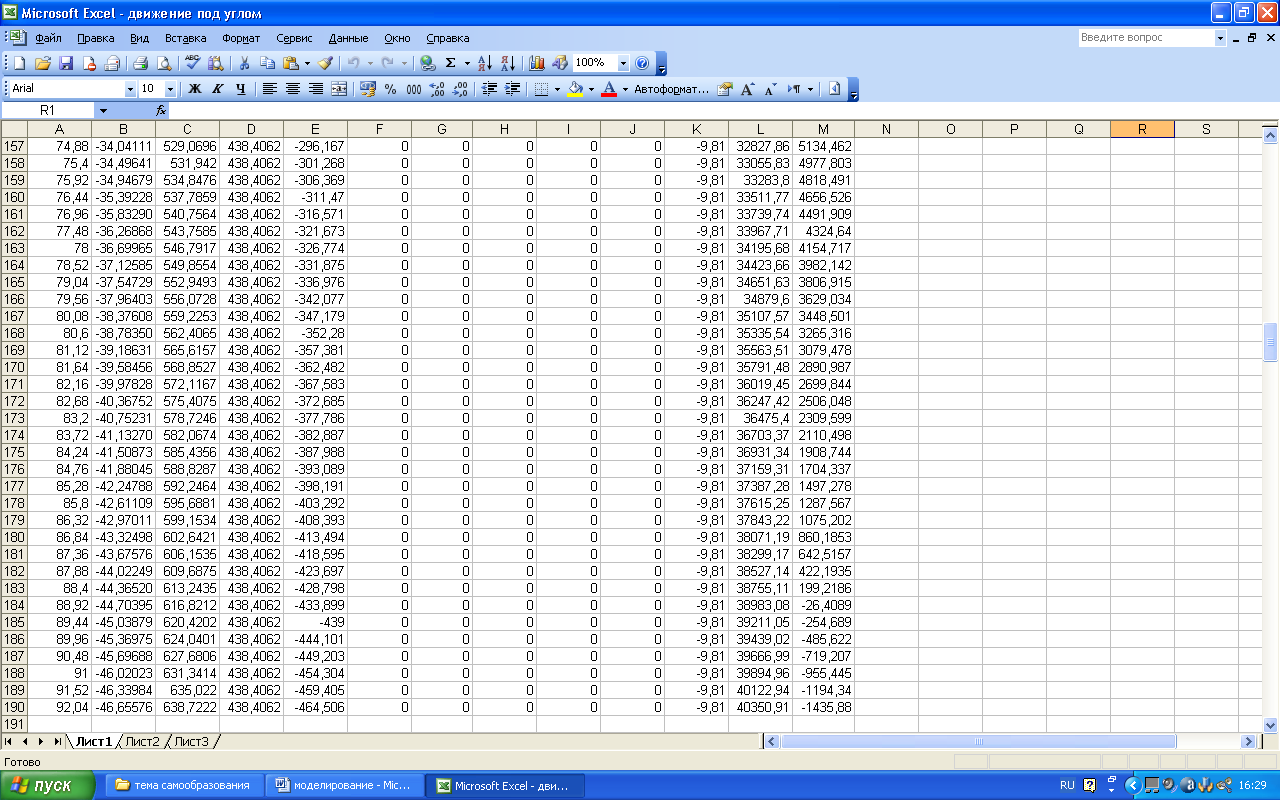
Остальные
строки расчетной таблицы (до 190-й строки)
заполняются вниз блоком А14:М14.

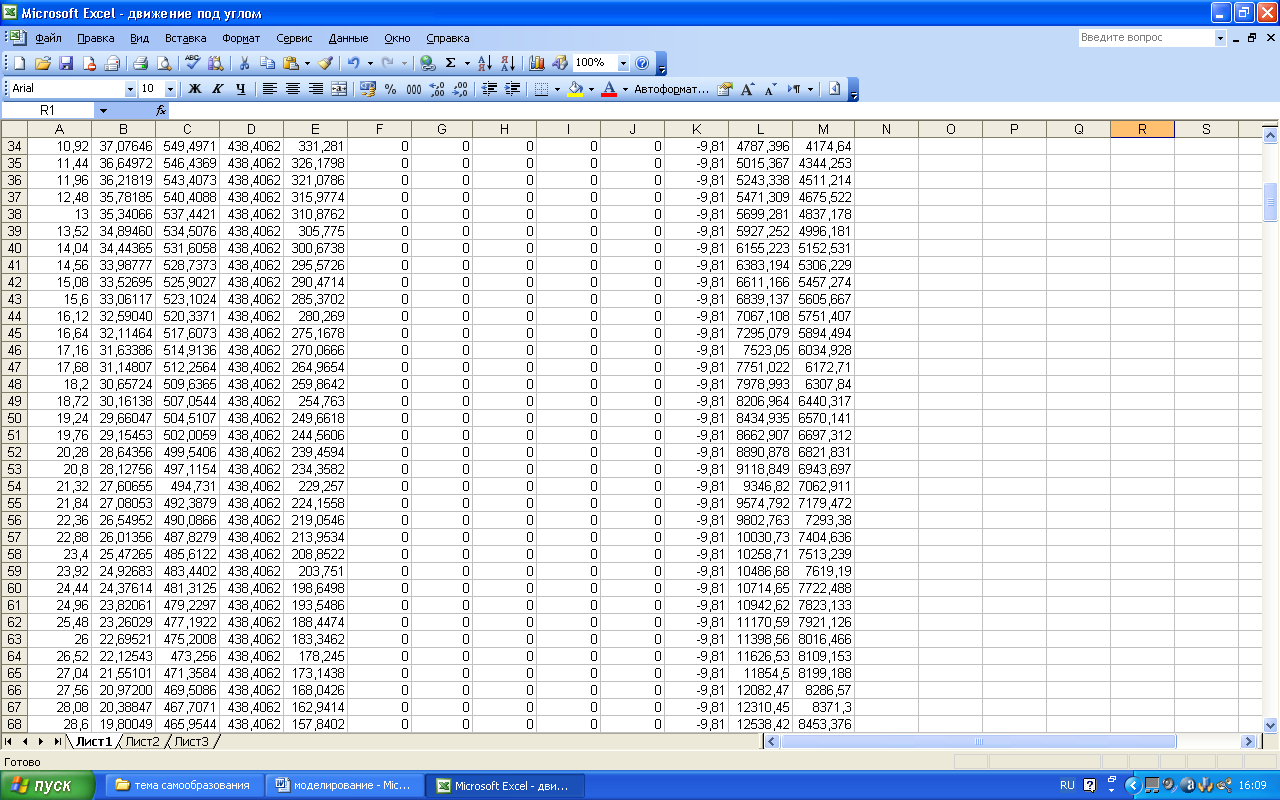
Бланк
электронной таблицы будет иметь вид:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Инфоурок

›

Информатика

›Другие методич. материалы›Лабораторная работа «Моделирование полёта тела, брошенного под углом к горизонту средствами EXCEL»

Моделирование задач (Полет тела, брошенного под углом к горизонту).

Здесь возможны модификации:

• Попадание в заданную площадку.

• Попадание в стенку с указанной высотой.

Задание 1: Формальная модель «Попадание в площадку тела, брошенного под углом к горизонту». Построить формальную модель решения задачи «Попадание в площадку тела, брошенного под углом к горизонту». В процессе тренировок теннисистов используются автоматы по бросанию мячика в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в площадку определенной длины, находящуюся на известном расстоянии.

Содержательная постановка задачи. В процессе тренировок теннисистов используются автоматы по бросанию мячика в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в площадку определенного размера, находящуюся на известном расстоянии.

Качественная описательная модель. Сначала построим качественную описательную модель процесса движения тела с использованием физических объектов, понятий и законов, т.е. в данном случае идеализированную модель движения объекта. Из условия задачи можно сформулировать следующие основные предположения:

мячик мал по сравнению с Землей, поэтому его можно считать материальной точкой;

изменение высоты мячика мало, поэтому ускорение свободного падения можно считать постоянной величиной g=9,8 м/с² и движение по оси Y можно считать равноускоренным;

скорость бросания тела мала, поэтому сопротивлением воздуха можно пренебречь и движение по оси X можно считать равномерным.

Формальная модель. Движение мячика по оси Х равномерное, а по оси Y равноускоренное, поэтому для формализации модели используем известные из курса физики формулы равномерного и равноускоренного движения. При заданных начальной скорости v₀ и угле бросания α значения координат дальности полета x и высоты y от времени можно описать следующими формулами:

x = v₀·cosα·t

y = v₀·sinα·t – g·t²/2

Площадка расположена на поверхности земли, поэтому из второй формулы можно выразить время, которое понадобится мячику, чтобы достичь площадки:

v₀·sinα·t – g·t²/2 = 0

t·(v₀·sinα – g·t/2) = 0

Значение времени t = 0 не имеет физического смысла, поэтому:

v₀·sinα – g·t/2 = 0

t = (2·v₀·sinα)/g

Подставим полученное выражение для времени в формулу для вычисления координаты х:

x = (v₀·cosα·2·v₀·sinα)/g = (v₀²·sin2α)/g

Формализуем теперь условие попадание мячика в площадку. Пусть площадка расположена на расстоянии s и имеет длину L. Тогда попадание произойдет, если значение координаты х мячика будет удовлетворять условию в форме неравенства:

s ≤ х ≤ s+L

Если хs, то это означает «недолет», а если хs+L, то это означает «перелет».

Заготовка программы для попадания в площадку:

program ploschadka;

uses graphABC, crt;

const xc=40; yc=240; s=300;

m=20; n=7; step=0.01; g=9.8;

var

x,y,t,a,v0,da:real;

xe,ye:integer; i:integer;

begin clrscr;

{возможен ввод начального угла в градусах:

write(‘a =’);readln(a); a:=a*pi/180;}

write(‘v0=’); readln(v0);

line(xc,10,xc,470);

line(10,yc,630,yc);

a:=pi/20; da:=pi/(6*n);

for i:=1 to n do

begin

a:=a+da;

t:=0;

repeat

x:=v0*cos(a)*t;

y:=v0*sin(a)*t-g*t*t/2;

xe:=round(xc+m*x);

ye:=round(yc-m*y);

setpixel(xe,ye,2);

t:=t+step;

until (ts/(v0*cos(a))) or (yeyc);

end;

end.

Задание:

1. Реализовать программу на компьютере. Оценить результат. C какой скоростью V0 и начальном угле a при заданном значении n будет зафиксировано наибольшее число попаданий в площадку? Результат записать в тетрадь для проверочных работ.

2. Разработать формальную модель при условии попадания мячика в стенку высотой h. Записать выкладки с пояснениями в тетрадь для проверочных работ.

3. Модифицировать программу таким образом, чтобы при попадании в стенку траектория полета мячика за стенкой не имела продолжения. Программу записать в тетрадь для проверочных работ.

4. Найти диапазон скоростей и углов для попадания в стенку.

5. C какой скоростью при заданном значении n будет зафиксировано наибольшее число попаданий в стенку? Результат записать в тетрадь для проверочных работ.

6. Приложение к программе:

Построение делений по оси y:

xt:=10; dx:=10

For i:=1 to 62 do

Begin

xt:=xt+dx;

line(xt,yc,xt,yc-5);

end;

Построение стенки высотой h на расстоянии s0:

line(s0,yc,s0,yc-h);

Соотношение для угла видимости ah (в радианах) верхней границы стенки высотой h на расстоянии s0:

ah:=arctan(2*h/s0); da:=ah/n;

Задание 2: Компьютерная модель «Попадание в площадку тела, брошенного под углом к горизонту»в электронных таблицах. На основе формальной модели «Попадание в площадку тела, брошенного под углом к горизонту» построить и исследовать компьютерную модель в электронных таблицах StarOffice Calc ( В ДАННОЙ РАБОТЕ СООТВЕТСТВУЮТ ВСЕ КОМАНДЫ В Microsoft Excel). Поэтому работаем в Microsoft Excel.

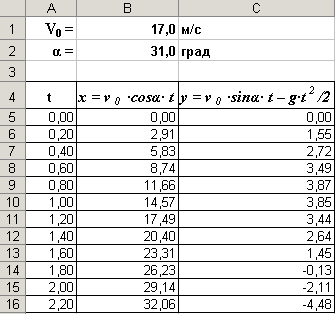
Выделим в таблице определенные ячейки для ввода значений начальной скорости v₀ и угла α и вычислим по формулам 3.1 значения координат тела x и y для определенных значений времени t с заданным интервалом.

Для преобразования значений углов из градусов в радианы используем функцию РАДИАНЫ().  

Проект «Движение тела, брошенного под углом к горизонту»

1	Запустить электронные таблицы Microsoft Excel. Для ввода начальной скорости будем использовать ячейку B1, а для ввода угла – ячейку B2.
2	Введем в ячейки A5:A16 значения времени с интервалом в 0,2 с.
3	В ячейки B5 и C5 введем формулы: =$B$1*COS(РАДИАНЫ($B$2))*A5 =$B$1*SIN(РАДИАНЫ($B$2))*A5-4,9*A5*A5
4	Скопируем формулы в ячейки В6:В16 и С6:С16 соответственно.

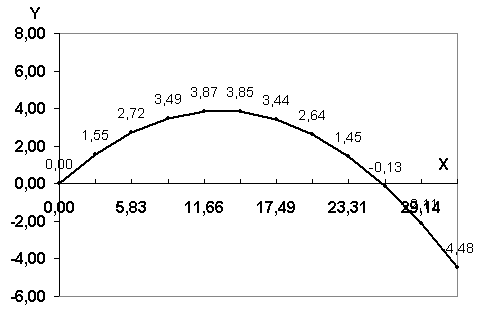
Визуализируем модель, построив график зависимости координаты y от координаты x (траекторию движения тела).

5

Построить диаграмму типа График, в которой используется в качестве категории диапазон ячеек B5:B16, а в качестве значений — диапазон ячеек С5:С16.

Исследуем модель и определим с заданной точностью 0,1 градуса значения диапазона изменений угла, которые обеспечивают попадание в площадку, находящуюся на расстоянии 25 м и длиной 2 м, при заданной начальной скорости 17 м/с. Воспользуемся для этого методом Подбор параметра.

6	Установить для ячеек точность один знак после запятой.
7	Ввести в ячейки B19 и B20 значения начальной скорости V0 = 17 м/c и угла α = 31 град, а в ячейку B22 формулу для вычисления координаты X мячика для заданных начальных условий: =B19^2*SIN(РАДИАНЫ(2*B20))/9,81
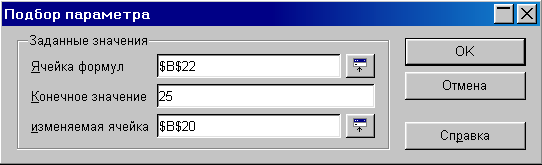
8	Выделить ячейку В22 и ввести команду [Сервис-Подбор параметра…]. На появившейся диалоговой панели ввести в поле Конечное значение координату ближнего края площадки – 25. В поле изменяемая ячейка ввести адрес ячейки, содержащей значение угла (в данном случае $В$20).
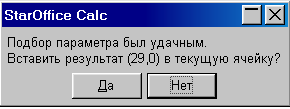
9	После щелчка по кнопке Да на появившейся панели StarOffice Calc в ячейку В20 будет записано значение 29,0.
10	Повторить процедуру подбора параметра для попадания в дальний край площадки, в ячейке В20 получим значение 33,2. Таким образом, существует диапазон значений угла бросания от 29,0 до 33,2 градусов, в котором обеспечивается попадание в площадку.
11	Повторить процедуру определения диапазона углов при начальном значении 55 град, получим значения предельных углов 56,8 и 61,0 градуса. С учетом точности вычислений данные для обоих диапазонов углов подтверждают результаты, полученные при исследовании компьютерной модели на языке ABCPascal

program stenka1;

uses graphABC,Crt;

const xc=40; {нач. коорд. по Х}

yc=240;{нач. коорд. по У}

h=50; {высота стенки}

s=300; {расстояние до стенки}

m=10; {множитель, через сколько пикселей ставится точка}

n=7; {число бросков}

step=0.005; {шаг по времени}

g=9.8; {ускорение св. падения}

var

x,y,t,a,v0,ah,da:real;

xe,ye:integer; i:integer;

begin

clrscr;

{write(‘угол в градусах a =’);readln(a); a:=a*pi/180;}

write(‘нач. скорость в м/с v0=’); readln(v0);

line(xc,10,xc,470);

line(10,yc,630,yc);

line(s,yc,s,yc-h);

ah:=arctan(3*h/s); {максимальный угол броска}

da:=ah/n; {промежуток в радианах между бросками}

a:=0; {нач. угол}

for i:=1 to n do

begin

a:=a+da;

t:=0;

repeat

x:=v0*cos(a)*t;

y:=v0*sin(a)*t-g*t*t/2;

xe:=round(xc+m*x);

ye:=round(yc-m*y);

setpixel(xe,ye,2);

t:=t+step;

until (ts/(v0*cos(a))) or (yeyc);

end;

end.

program stenka2;

uses graphABC,Crt;

const

xc=40; {нач. коорд. по Х}

yc=240;{нач. коорд. по У}

h=50; {высота стенки}

s=300; {расстояние до стенки}

m=10; {множитель, через сколько пикселей ставится точка}

n=7; {число бросков}

step=0.005; {шаг по времени}

g=9.8; {ускорение св. падения}

var

x,y,t,a,v0,ah,da:real;

xe,ye:integer; i:integer;

begin

clrscr;

{write(‘угол в градусах a =’);readln(a); a:=a*pi/180;}

write(‘нач. скорость в м/с v0=’); readln(v0);

line(xc,10,xc,470);

line(10,yc,630,yc);

line(s,yc,s,yc-h);

ah:=arctan(3*h/s); {максимальный угол броска}

da:=ah/n; {промежуток в радианах между бросками}

a:=0; {нач. угол}

for i:=1 to n do

begin

a:=a+da;

t:=0;

repeat

x:=v0*cos(a)*t;

y:=v0*sin(a)*t-g*t*t/2;

xe:=round(xc+m*x);

ye:=round(yc-m*y);

if (ye(yc-h)) and not(xes) then

setpixel(xe,ye,2);

if (ye

setpixel(xe,ye,2);

t:=t+step;

until (ts/(v0*cos(a))) or (yeyc);

end;

end.

3

Цели урока:

• выделить этапы моделирования.
• сформулировать основные задачи на каждом этапе
  моделирования.
• построить график функции.

Задачи урока:

Образовательные:

• научить обобщать материал и выделять главное
• научить применять полученные знания на
  практике

Воспитательная:

• формирование  самостоятельности и
  ответственности при изучении нового
  материала

Развивающая:

• развитие логического мышления

Методы обучения:

• лекция
• объяснительно — иллюстративный (презентация)
• фронтальный опрос

План урока:

1. Организационный момент
2. Объяснение новой темы
3. Практическая работа
4. Подведение итогов
5. Домашнее задание.

1. Организационный момент.

2. Изучение новой темы.

Ход урока

Поскольку мы занимаемся изучением информатики
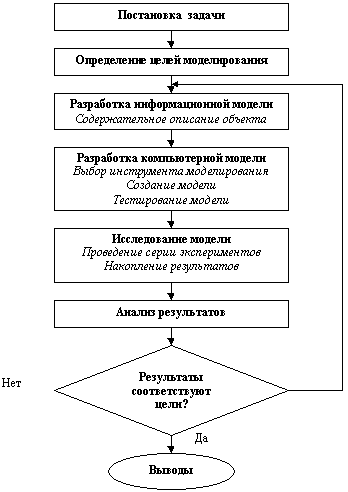
и компьютерных технологий, то и в моделировании
нас интересует ответ на вопрос: как создать
компьютерную модель? Представим этот вопрос
поэтапно в виде схемы.

Схема модели

Приложение 1

При решении конкретной задачи она может
уточняться и корректироваться в зависимости от
поставленной  задачи и цели моделирования.

Рассмотрим процесс построения и исследования
модели на конкретном примере движения тела,
брошенного под углом к горизонту.

I этап — Постановка задачи. В процессе
тренировок теннисистов используются автоматы по
бросанию мяча в определенное место площадки.

Цель: задать необходимую скорость и угол
бросания мяча для попадания в площадку
определенного размера, находящимся на известном
расстоянии. Исследовать движение мяча,
брошенного с начальной скоростью ?₀ под
углом ? к горизонту, когда сопротивлением
воздуха можно пренебречь.

II этап — Разработка информационной модели.
Построим описательную модель процесса движения
тела с использованием физических объектов,
понятий и законов, то есть идеализированную
модель движения объекта.

Из условия задачи сформулируем основные
предположения:

• мяч мал по сравнению с землей, поэтому его можно
  считать материальной точкой;
• изменение высоты мяча можно считать постоянной
  величиной g = 9,8 м/с² и движение по оси Y можно
  считать равноускоренным;
• скорость бросания тела мала, поэтому
  сопротивлением воздуха можно пренебречь и
  движение по оси Х можно считать равномерным.

 — Создание формализованной модели.
(Описание информационной модели записывается с
помощью какого-либо формального языка. В такой
модели с помощью формул, уравнений, неравенств и
так далее фиксируется формальные отношения
между начальными и конечными значениями свойств
объектов, а также накладываются ограничения на
допустимые значения этих свойств.)

Приложение 2

— Создание компьютерной модели. (Формальную
информационную модель преобразуем в
компьютерную, выразив ее на понятном для
компьютера языке. Для этого используем
программное обеспечение Microsoft Office ( электронные
таблицы EXCEL.)

Приложение 3

III этап — Компьютерный эксперимент.
(Компьютерная модель исследуется в приложении
электронные таблицы EXCEL, проводится сортировка
данных, строится график зависимости J ( t), Х(у).)

План эксперимента.

Тестирование

Провести тестовый расчет компьютерной модели
по данным, приведенным в таблице.

Приложение 4

Эксперимент

1. Исследовать движение мяча.
2. Исследовать изменение движения тела при
   изменении начальной скорости.
3. Исследовать изменение движения тела при
   изменении угла бросания.
4. Изменяя начальную скорость и угол бросания,
   исследовать характер движения тела и его
   положение по отношению к площадке.

Приложение 5

IV этап — Анализ результатов моделирования.
(Результаты и выводы, полученные в экспериментах,
оформите в виде отчета в текстовом документе. В
отчете приведите ответы на следующие вопросы:

1. Как движется тело, брошенное под углом к
   горизонту?
2. Как определить наивысшую точку подъема?
3. Как изменяется наибольшая высота подъема при
   увеличении начальной скорости и неизменном угле
   броска?
4. Как изменяется дальность полета при увеличении
   начальной скорости и неизменном угле броска?

Подведение итогов: выставление оценок за
проведенную исследовательскую работу.

Домашнее задание. Разработать и исследовать
физическую модель для решения задач по теме:
«Гармонические колебания».

Пример: Дан пружинный маятник, совершающий
гармонические незатухающие колебания
(сопротивление среды не учитывать). Жесткость
пружины k (Н/м) и масса груза m (кг). 

Исследовать зависимость периода колебания (Т),
от жесткости пружины (k), и построить график этой
зависимости. Предусмотреть возможность введения
любого значения массы груза (m). Жесткость k
меняется от 100 до 1000 Н/м, через каждые 100 Н/м.

Исследовать зависимость периода колебания (Т),
от массы груза (m), и построить график этой
зависимости. Предусмотреть возможность введения
любого значения жесткости пружины (k). Масса груза
m меняется от 1 до 10 кг, через каждые 1 кг.

Список  литературы

1. Горстко А. Б. Информатика для школьников и
   всех-всех-всех /
2. Горстко А. Б., Чердынцева М. И. — Ростов-на-Дону:
   Изд-во «Феникс», 1996.
3. Ракитина Е. А. Решение типовых задач по
   информационным технологиям / Ракитина Е. А.,
   Бешенков С. А., Галыгина И. В., Галыгина Л. В.
   //Информатика и образование . — 2004. — №4.
4. Информатика в школе. Решение типовых задач по
   информатике. Часть 2. : Москва «Образование и
   Информатика», Приложение к журналу
   «Информатика и образование». — №1. — 2004.
5. Кутугина Е.С Моделирование. Учебное пособие. —
   Томск, 2005. — 80с.