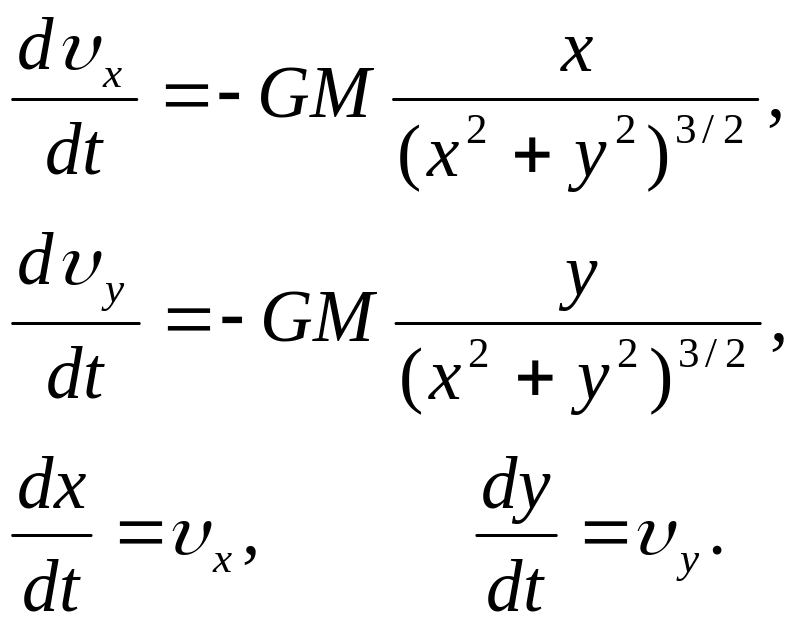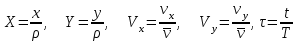Электронные
таблицы представляют собой класс
специальных программ для ведения
документации. Документ изображается
на экране в виде таблицы, у которой
именованы строки и столбцы. Каждая
клетка может содержать текст, числа или
формулу. С содержимым клеток можно
производить арифметические, алгебраические
и логические операции. Изменение
содержимого одной из клеток автоматически
ведет к изменению содержимого других
клеток, связанных с ним логически или
формулой. Таким образом, обработка
данных происходит автоматически,
результат получаем в виде готовых
таблиц. При необходимости результат
можно получить в виде графиков или же
диаграмм.
Использовать
систему Excel офисного
приложения Windows для
компьютерного моделирования имеет
смысл, если у исследователя нет на
компьютере какая-нибудь из систем
компьютерной математики. Применение
системы Excel оправдано и
с методической точки зрения, она позволяет
глубже понять пошаговую работу алгоритма
вычислений для разностных уравнений.
Если же пользователь научится согласно
алгоритму вычислять значения неизвестных
функций на первом шаге итерации, то он
будет понимать работу алгоритма решения.
Технология
решения (моделирования) физических
объектов с помощью пакета Excel
изложена также в работах [1, 2, 3].
1.1. Моделирование движения небесного тела под действием сил тяготения
Рассмотрим
технологию моделирования в системе
Excel
на примере движения материального тела
(планета) массой m
под действием притягивающего неподвижного
центра (Солнца). Например, любое
материальное тело движущееся под
действием силы притяжения небесного
тела (в частности, поля тяготения Солнца).
Задание на
моделирование.
Построить орбиту малой планеты по ее
координатам, рассчитанным с интервалом
в 5 суток, если в перигелии она находится
на расстоянии 0,5 а.е. от Солнца и имеет
скорость 0,026 а.е./сут. Считать, что планета
движется под действием притяжения
только со стороны Солнца. Влияние других
планет не учитывать.
Дифференциальные
уравнения движения могут
быть получены из закона Ньютона:
На (рис. 4.1) показана
материальное тело и действующие на нее
силы:
сила тяжести
направленная к центру О.
Найдя проекции на координатные оси всех
сил, действующих на материальную точку,
получаем следующую систему дифференциальных
уравнений:

(1.1)
с
общими для всех случаев начальными
условиями
,
предполагающими,
что материальное тело в начальный момент
времени лежит на оси
Ох в точке
х0,
не имеет соответствующей скорости вдоль
оси Ох
и имеет начальную скорость лишь вдоль
оси Оу, которая равна у0.
Решение.
Решение данной задачи средствами
программирования приведены в [2, 3].
Рассмотрим формулы,
позволяющие производить вычисления по
решению уравнений (1.1) методом Эйлера
Ti
=TI-1
+ DT;
RI=КОРЕНЬ(xI
* xI
+ YI
*YI).
AI,
X=
—GM*XI
/RI^3;
AI,
Y=
—GM*YI
/RI^3;
VI,
X=VI-1,
X
– AI-1,
X*DT;
VI,
Y=VI-1,
Y
– AI-1,
Y*DT;
Xi
=xi-1
+ vi-1,
x*
dt;
Yi
=Yi-1
+ vi-1,
Y*
dt;
Приведенные
формулы представляют собой готовую
схему алгоритма для вычислений.
Введем
свою систему единиц. Время измеряется
в сутках, расстояние в а.е. (астрономических
единицах), за единицу массы принята
масса Солнца. При таком выборе единиц
числовые значения исходных данных
таковы:
X
0=0,5;
Y
0=0;
V
0,x=0;
V
0,y=0,026;
—GM=-1/58^2;
DT=1.
Заполняем электронную
таблицу.
Первоначальный
вид электронной таблицы приведен на
рис. 4.1.
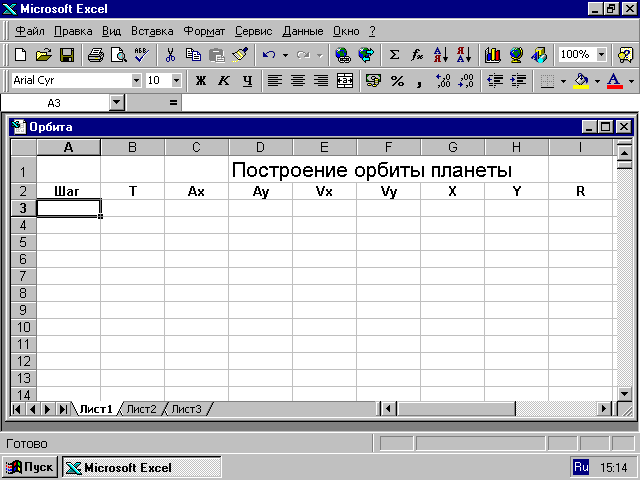
Рис. 4.2
Пояснения
к заполнению электронной таблицы
-
В
ячейку А3 внесено 1. -
В
ячейку А4 введена формула =А3+1. -
В
ячейку В3 внесено 0. -
В
ячейку В4 введена формула =В3+1. -
В
ячейку С3 введена формула =
(-1/(58^2))*G3/(I3^3,
которая скопирована в ячейку С1. -
В
ячейку D3
введена формула =(-1/(58^2))*H3/(I3^3),
которая скопирована в ячейку D1. -
В
ячейку Е3 внесено значение начальной
скорости по х
равная 0. -
В
ячейку Е4 введена формула =Е3+С3*1. -
В
ячейку F3
внесено значение начальной скорости
по y
равная 0,026. -
В
ячейку F4
введена формула =F3+D3*5
. -
В
ячейку G3
внесено начальная координата по х
равная 0,1. -
В
ячейку G4
введена формула =G3+E4*1. -
В
ячейку H3
внесено начальная координата по у
равная 0. -
В
ячейку H4
введена формула =H3+F4*1. -
В
ячейку I3
введена формула =КОРЕНЬ(G3^2+H3^2),
которая скопирована в ячейку I1. -
В
ячейку J3
введена формула =КОРЕНЬ(C3^2+D3^2),
которая скопирована в ячейку J1.
Таким образом, мы
заполнили две строки. В третьей строке
введены начальные значения, в строке
№4 формулы расчета. Выделяя строку №4
и растягивая мышью по вертикали, получаем
расчетные значения на каждый момент
времени.
Результаты
вычислений приведены в таблице 2.
Таблица 2
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
K |
|
|
1 |
||||||||||
|
2 |
Шаг |
T |
Ax |
Ay |
Vx |
Vy |
X |
Y |
R |
А |
|
3 |
1 |
0 |
-0,00119 |
0 |
0 |
0,026 |
0,5 |
0 |
0,5 |
0,001189 |
|
4 |
2 |
5 |
-0,0012 |
-0,00033 |
-0,00595 |
0,026 |
0,470273 |
0,13 |
0,487911 |
0,001249 |
|
5 |
3 |
10 |
-0,00109 |
-0,00067 |
-0,01196 |
0,024336 |
0,410458 |
0,251682 |
0,481476 |
0,001282 |
|
6 |
4 |
15 |
-0,00086 |
-0,00095 |
-0,01743 |
0,020985 |
0,323313 |
0,356607 |
0,481352 |
0,001283 |
|
7 |
5 |
20 |
-0,00055 |
-0,00112 |
-0,02174 |
0,016232 |
0,214624 |
0,437769 |
0,48755 |
0,001251 |
|
8 |
6 |
25 |
-0,00022 |
-0,00117 |
-0,02449 |
0,010618 |
0,092172 |
0,49086 |
0,499439 |
0,001192 |
|
9 |
7 |
30 |
7,75E-05 |
-0,00111 |
-0,02559 |
0,004762 |
-0,03578 |
0,514669 |
0,515911 |
0,001117 |
|
10 |
8 |
35 |
0,000313 |
-0,00099 |
-0,0252 |
-0,00081 |
-0,16179 |
0,510624 |
0,535643 |
0,001036 |
|
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
-17 |
15 |
70 |
0,000649 |
-1,2E-05 |
-0,00488 |
-0,01913 |
-0,67652 |
0,012422 |
0,676639 |
0,000649 |
|
18 |
16 |
75 |
0,00062 |
7,56E-05 |
-0,00163 |
-0,01919 |
-0,68467 |
-0,08351 |
0,689745 |
0,000625 |
|
19 |
17 |
80 |
0,000587 |
0,000154 |
0,001472 |
-0,01881 |
-0,67731 |
-0,17755 |
0,700196 |
0,000606 |
|
20 |
18 |
85 |
0,000549 |
0,000224 |
0,004404 |
-0,01804 |
-0,65529 |
-0,26774 |
0,707877 |
0,000593 |
Для построения
орбиты планеты выделяем ячейки G2:H20.
Из мастера диаграмм выбираем тип
диаграммы “Точечная”, далее “Точечная
диаграмма со значениями, соединенными
сглаживающими линиями без маркеров”.
В заголовке указываем название графика
“ Траектория орбиты”. Полученная
траектория орбиты приведена на рис.
4.3.
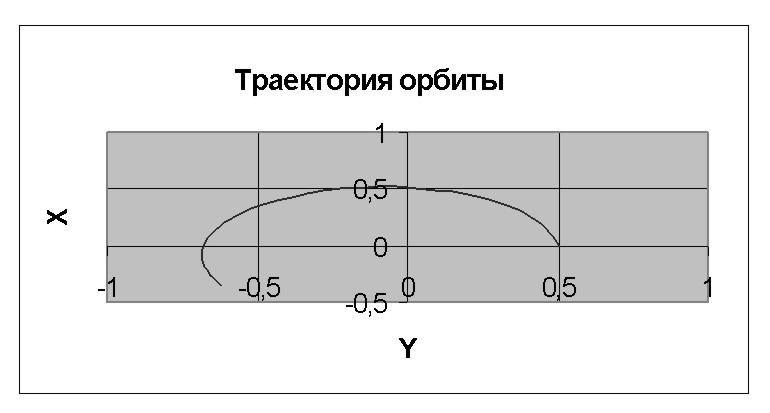
Рис.
4.3
Чтобы получить
график удаления планеты в различные
моменты итерации, выделяем ячейки
I2:I20.
Из мастера диаграмм выбираем тип
диаграммы “Лепестковая”,
далее “Лепестковая диаграмма является
аналогом графика в полярной системе
координат …”. В заголовке указываем
название диаграммы “ Удаление планеты
от Солнца“. Полученный график приведен
на рис. 4.4.
Для
построения графика зависимости ускорения
от времени выделяем ячейки С2:D20.
Из мастера диаграмм выбираем тип диаграмм
“График”,
далее “График отображает развитие
процесса во времени или по категориям”.
Выбираем “далее”,
выпадает меню “диапазон
данных”. В
меню “диапазон
данных”
выбираем “ряд”.
В “подписи
оси Х”
набираем =Лист1!$B$2:$B$20.
Указатель мыши подводим к “добавить”
и щелкаем левой кнопкой мыши, в “имя”
набираем – А, в “значения”
набираем =Лист1!$I$2:$I$20.
Указатель мыши подводим к “далее”
и щелкаем левой кнопкой мыши. В подписи
данных вводим название диаграммы “График
зависимости ускорения от времени”.
Указатель мыши подводим к “готово”,
щелкаем левой кнопкой мыши. График
готов. Рис. 4.5. Увеличение количества
шагов итерации дает более полное решение
задачи.
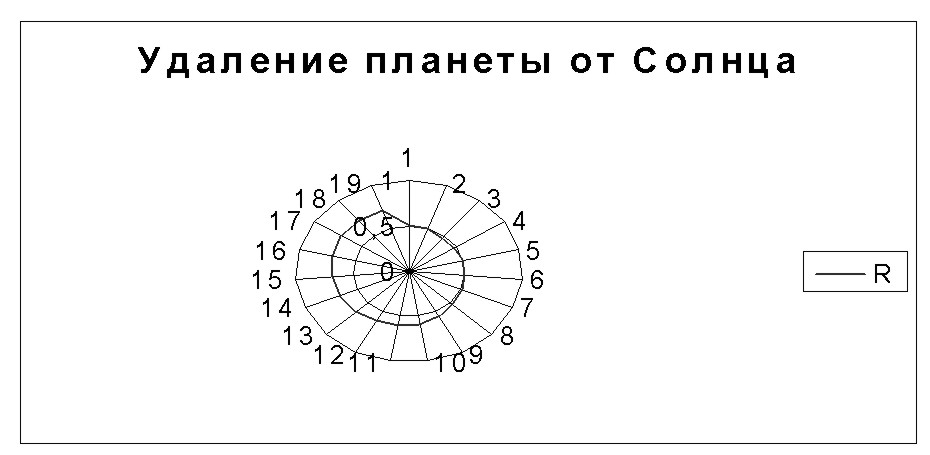
Рис.
4.4.
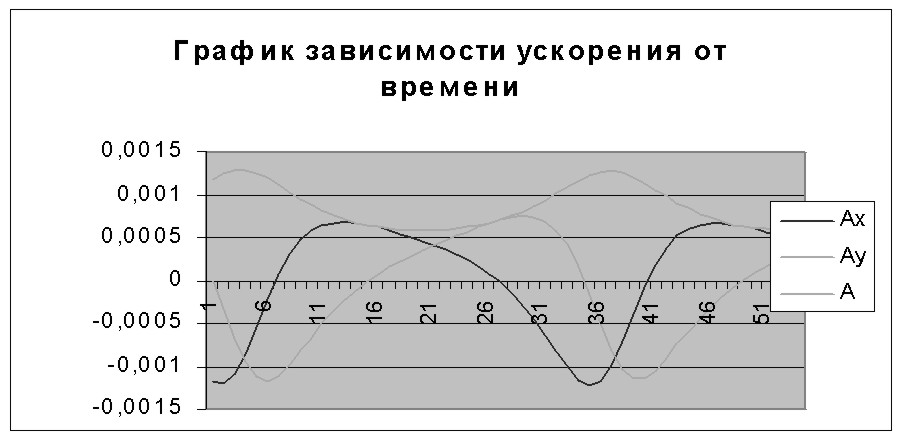
Рис.
4.5
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
© 2023 Prezi Inc.
Terms & Privacy Policy
Практическая работа
Тема: Моделирование и
формализация
(моделирование астрономических процессов)
(11 класс)
Подготовила:
учитель информатики и ИКТ
Тополева Н. И.
Астрономия
Задача
Сравнить скорость и расстояния пройденные космическими аппаратами «Вояджер-1», «Вояджер-2» и «Новые горизонты» . Составить табличную компьютерную модель и график.
Постановка задачи:
Цель моделирования — сравнить скорость и пройденное расстояние космическими аппаратами.
Объект моделирования — скорость космических аппаратов. Внутреннее строение в расчет не принимается. Будем рассматривать аппараты как элементы, обладающие некоторыми характеристиками:
Вид космического аппарата.
D1- дата старта космического корабля.
S – пройденный путь;
Т – время движения;
V — скорость движения, предполагая, что корабли движутся с постоянной скоростью.
Разработка модели:
Исходные данные:
V- скорость движения аппаратов.
T–время движения.
D1- дата старта космического корабля.
D2- расчетная дата.
СПРАВКА
Алгоритм построения модели:
Определить количество дней в пути (формула1).
Перевести данное значение в часы (формула2).
Вычислить скорость движения в км/час (формула).
Перевести данное значение в астр. ед./ч (формула).
Вычислить пройденный путь в астр. ед. (формула).
Формула1 Формула2
Установите
формат ячеек – «дата» диапазона (В3;С5)
В ячейку D3 запишите формулу: =C3-B3
Скопируйте (заполните) формулу вниз до ячейки D5
Умножим полученное значение на 24(сутки =24ч.).
Запишем формулу =D3*24 в ячейку Е3
Скопируйте (заполните) формулу вниз до ячейки E5
Расчет количества дней в пути.
Перевод полученного значения в часы.
Астрономия
Справка.
«Во́яджер» (англ. voyager — «путешественник») — название двух космических аппаратов, запущенных в 1977 году, а также проекта по исследованию дальних планет Солнечной системы с участием аппаратов данной серии.
Проект считается одним из самых успешных и результативных в истории межпланетных исследований. Оба «Вояджера» впервые передали качественные снимки Юпитера и Сатурна, а «Вояджер-2» впервые достиг Нептуна и Урана. «Вояджеры» стали третьим и четвёртым космическими аппаратами, покинувшими пределы Солнечной системы (первыми двумя были «Пионер-10» и «Пионер-11»).
12 декабря 2012 г. агентство по аэронавтике и космическим исследованиям (НАСА) сообщило, что автоматический аппарат «Вояджер-2» достиг границы Солнечной системы. Связь с «Вояджером-2» будет потеряна.
Читать текст полностью.
Подборка по базе: практическая работа№ 4.docx, 5 класс, практическая работа _Определение географических координ, Практическая работа философия 3.pdf, Физическая культура Практическая работа.docx, Контрольная работа (1).pdf, КОНТРОЛЬНАЯ РАБОТА баланс.docx, Курсовая Работа.docx, курсовая работа КОМПЛЕКСНЫЙ ЭКОНОМИЧЕСКИЙ АНАЛИЗ (2).docx, Практическая работа 1 (1).docx, Практическая работа по Теории организации.docx
Моделирование физических процессов в среде табличного процессора.
Краткие теоретические сведения
Второй закон Ньютона. В рассматриваемых ниже математических моделях физических процессов фундаментальную роль играет второй закон Ньютона. Он гласит, что ускорение, с которым движется тело, прямо пропорционально действующей на него силе (если их несколько — то равнодействующей этих сил) и обратно пропорционально его массе:
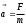
Свободное падение тела. Математическая модель свободного падения тела — уравнение второго закона Ньютона с учетом двух сил, действующих на тело — силы тяжести и силы сопротивления среды. Движение является одномерным; проецируя силу тяжести 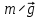
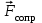
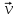
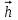
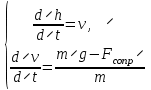
Сила сопротивления имеет две составляющие: 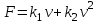
Коэффициенты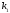
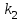
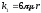
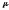

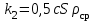
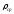
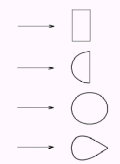 |
Диск Полусфера Шар |
c=1,11 c=0,55 c=0,4 |
Рис. 1. Значения коэффициента лобового сопротивления для некоторых тел, поперечное сечение которых имеет указанную на рисунке форму
Взлет ракеты. Исследуем ситуацию, когда масса тела не является величиной постоянной. Запишем второй закон Ньютона в более общей математической форме.
Построим простейшую модель вертикального взлета ракеты, приняв следующие гипотезы:
- масса ракеты уменьшается во время взлета по линейному закону:
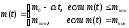
гдеm0 начальная масса ракеты, заправленной топливом; mкон остаточная масса после полного выгорания топлива; расход топлива;
- Сила тяги двигателя постоянна на всем участке взлета.
- плотность воздуха , входящая в коэффициент k2, убывает по мере подъема ракеты по закону = 0 . 10h, где h высота, 5,6 . 105 м1 .
Таким образом, модель будет описываться системой двух дифференциальных уравнений для функций v(t) и h(t):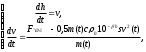
Движение тела, брошенного под углом к горизонту. Дифференциальные уравнения модели получаются из второго закона Ньютона проецированием скорости и перемещения на горизонтальную и вертикальную оси координат:
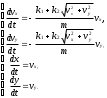

Здесь m масса тела; vx=vcos ,vy=vsin — величины проекций начальной скорости v на горизонтальную и вертикальную оси; угол начального наклона вектора скорости к горизонту; k1и k2 – коэффициенты, входящие в в формулу силы сопротивления.
Движение небесных тел. Рассмотрим модель движения космического тела (планеты, кометы, спутника) под действием силы всемирного тяготения в гравитационном поле, создаваемом телом с многократно большей массой.
Примем следующие предположения: «большое» тело находится в начале системы координат, другие тела на движение «малого» тела влияния не оказывают. Дифференциальные уравнения модели имеют вид
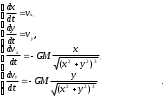
где M- масса «большого» тела; x, y — координаты «малого» тела, движение которого изучается; vx, vy – величины проекций скорости «малого» тела на горизонтальную и вертикальную оси, G = 6,67. 1011 м3/кг с2 гравитационная постоянная .
Обезразмеривание. В задаче о движении небесных тел особенно неудобно работать с размерными величинами, измеряемыми миллиардами километров, секунд и т.д. В качестве величин для обезразмеривания удобно принять характерное расстояние от Земли до Солнца ρ = 1,496∙1011 м, (так называемая астрономическая единица), период круговой орбиты 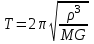
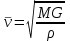
После обезразмеривания получаем
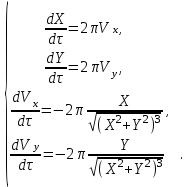
В безразмерных переменных уравнения вообще не содержат параметров. Единственное, что отличает разные режимы движения друг от друга – это начальные условия.
Движение заряженных частиц. Рассмотрим модель движения заряженной частицы в кулоновском поле другой заряженной частицы, положение которой фиксировано.
В системе координат, начало которой привязано к «большому» телу, дифференциальные уравнения модели имеют вид
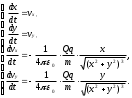
Они получаются из второго закона Ньютона и закона Кулона. 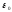
Метод Эйлера решения обыкновенных дифференциальных уравнений. Рассмотрим задачу Коши: Найти решение 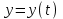
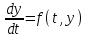
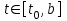
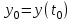
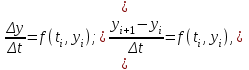
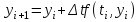
Здесь отрезок 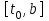
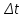
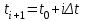
Вопрос о выборе конкретного значения 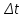
Пример выполнения задания
Задача. Парашютист спрыгивает с высоты h0 и раскрывает парашют на высоте h1. Определить, будет ли скорость приземления безопасной.
Цель моделирования. Определить конечную скорость движения тела и сравнить ее с безопасной (10 м/с).
Формализация. Будем считать, что форма человека близка к сферической, форма парашюта – полусферической. Тело характеризуется массой m, радиусом (r- человека и r1 – парашюта) и площадью поперечного сечения ( S и S1 соответственно). Среда характеризуется плотностью ρ и вязкостью μ. В ходе движения меняются время t, скорость v и высота h. Задача состоит в том, чтобы определить vкон в момент времени, когда h станет близкой к нулю.
Построение математической модели. Воспользуемся моделью (2):
Выбор метода исследования. Применим для решения системы дифференциальных уравнений метод Эйлера:

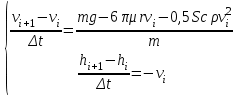
Построение компьютерной модели и ее проверка Выберем для моделирования среду табличного процессора Excel. Для проверки модели на адекватность рассмотрим движение без сопротивления среды (k1=0 и k2=0)
| Свободное падение тела | |||||||
| Параметры движения | Параметры тела | Параметры среды | Коэффициенты | ||||
| Время t0 | 0 | Масса m | 80 | Вязкость | 0,0182 | k1 | 0,000 |
| Скорость v0 | 0 | Радиус r | 0,3 | Плотность | 1,2 | k2 | 0,000 |
| Высота h0 | 1000 | Радиус r1 | 1,5 | ||||
| Высота h1 | 800 | Площадь S | 0,053 | ||||
| Шаг ∆t | 0,5 | Площадь S1 | 7,069 | ||||
| Коэффициент с | 0,40 | ||||||
| Коэффициент с1 | 0,55 |
Рис. 2 Исходные данные задачи о свободном падении (сопротивление среды не учитывается)
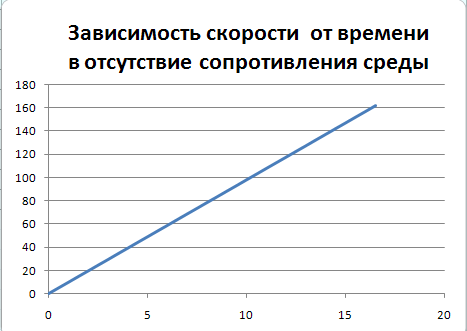
Изменение скорости и высоты со временем
| t | v | h | |
| 0 | 0 | 1000 | |
| 0,5 | 4,9 | 1000,0 | |
| 1 | 9,8 | 997,6 | |
| 1,5 | 14,7 | 992,7 | |
| 2 | 19,6 | 985,3 | |
| 2,5 | 24,5 | 975,5 | |
| 3 | 29,4 | 963,3 | |
| 3,5 | 34,3 | 948,6 | |
| 4 | 39,2 | 931,4 | |
| 4,5 | 44,1 | 911,8 | |
| 5 | 49,0 | 889,8 | |
| 5,5 | 53,9 | 865,3 | |
| 6 | 58,8 | 838,3 | |
| t | v | h | |
| 6,5 | 63,7 | 808,9 | |
| 7 | 68,6 | 777,1 | |
| 7,5 | 73,5 | 742,8 | |
| 8 | 78,4 | 706,0 | |
| 8,5 | 83,3 | 666,8 | |
| 9 | 88,2 | 625,2 | |
| 9,5 | 93,1 | 581,1 | |
| 10 | 98,0 | 534,5 | |
| 10,5 | 102,9 | 485,5 | |
| 11 | 107,8 | 434,1 | |
| 11,5 | 112,7 | 380,2 | |
| 12 | 117,6 | 323,8 | |
| 12,5 | 122,5 | 265,0 |
В отсутствие сопротивления среды скорость растет со временем по линейному закону, что соответствует аналитическому решению уравнений
Добавим силу сопротивления (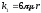
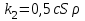
| Свободное падение тела с учетом сопротивления | |||||||
| Параметры движения | Коэффициенты‘>Параметры тела | Параметры среды | Коэффициенты
(без парашюта) |
||||
| Время t0 | 0 | Масса m | 80 | Вязкость | 0,0182 | k1 | 0,045 |
| Скорость v0 | 0 | Радиус r | 0,3 | Плотность | 1,2 | k2 | 0,013 |
| Высота h0 | 1000 | Радиус r1 | 1,5 | Коэффициенты
(с парашютом) |
|||
| Высота h1 | 800 | Площадь S | 0,053 | k1 | 0,515 | ||
| Шаг ∆t | 0,5 | Площадь S1 | 7,069 | k2 | 2,333 | ||
| Коэффициент с | 0,40 | ||||||
| Коэффициент с1 | 0,55 |
Изменение скорости и высоты со временем
| t | v | h |
| 0 | 0 | 1000 |
| 0,5 | 4,9 | 1000,0 |
| 1 | 9,8 | 997,6 |
| 1,5 | 14,7 | 992,7 |
| 2 | 19,6 | 985,3 |
| 2,5 | 24,4 | 975,5 |
| 3 | 29,3 | 963,3 |
| 3,5 | 34,1 | 948,7 |
| 4 | 38,9 | 931,6 |
| 4,5 | 43,7 | 912,2 |
| 5 | 48,4 | 890,3 |
| 5,5 | 53,1 | 866,1 |
| 6 | 57,8 | 839,6 |
| 6,5 | 62,4 | 810,7 |
| 7 | 10,3 | 779,5 |
| 7,5 | 13,7 | 774,3 |
| 8 | 15,8 | 767,5 |
| t | v | h |
| 8,5 | 17,0 | 759,6 |
| 9 | 17,6 | 751,1 |
| 9,5 | 17,9 | 742,3 |
| 10 | 18,1 | 733,3 |
| 10,5 | 18,2 | 724,3 |
| 11 | 18,2 | 715,2 |
| 11,5 | 18,2 | 706,1 |
| 12 | 18,2 | 697,0 |
| 12,5 | 18,2 | 687,9 |
| 13 | 18,2 | 678,8 |
| 13,5 | 18,2 | 669,7 |
| 14 | 18,2 | 660,6 |
| 14,5 | 18,2 | 651,5 |
| 15 | 18,2 | 642,3 |
| 15,5 | 18,2 | 633,2 |
| 16 | 18,2 | 624,1 |
| 16,5 | 18,2 | 615,0 |
В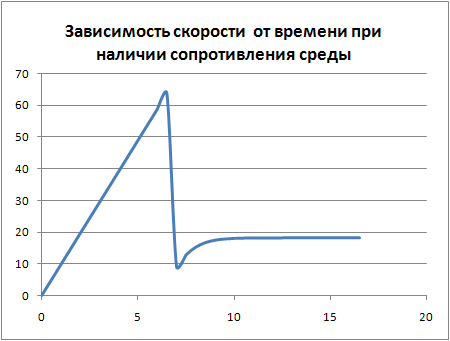
то скорость падения 18,2 м/с значительно превысит безопасную
Использование модели
Данная модель позволяет решать не только описательные, но и оптимизационные задачи, например:
- Найти оптимальную с точки зрения безопасности высоту раскрытия парашюта;
- Найти оптимальные размеры парашюта;
- Найти максимальную высоту, с которой можно спрыгнуть без парашюта и не пострадать и т.д.
Задание к лабораторной работе
- Определить цель моделирования
- Провести формализацию задачи: сделать предположения, определить состав параметров, характеризующих объект, сформулировать задачу математически.
- Построить математическую модель (определить состав набора входных и выходных параметров, их конкретные числовые значения, записать уравнения).
- Выбрать метод решения уравнений (в данном случае –один из численных методов). Записать решение уравнений в виде рекуррентных вычислительных схем.
- Определить значения параметров модели, начальные значения меняющихся в ходе движения величин, условия окончания вычислительных циклов.
- Построить компьютерную модель физического процесса в среде табличного процессора.
- Произвести проверку модели на адекватность.
- Выполнить конкретное задание из своего варианта работы.
- Качественно проанализировать результаты моделирования.
Варианты заданий
Вариант 1.
Парашютист прыгает с некоторой высоты и летит, не открывая парашюта; на какой высоте (или через какое время) ему следует открыть парашют, чтобы иметь к моменту приземления безопасную скорость (не большую 10 м/с)?
Вариант 2.
Промоделировать падения тела с заданными характеристиками (масса, форма) в различных вязких средах. Изучить влияние вязкости среды на характер движения. Скорость движения должна быть столь невелика, чтобы квадратичной составляющей силы сопротивления можно было пренебрегать.
Вариант 3.
Промоделировать падения тела с заданными характеристиками (масса, форма) в различных плотных средах. Изучить влияние плотности среды на характер движения. Скорость движения должна быть достаточно велика, чтобы линейной составляющей силы сопротивления можно было пренебрегать (на большей части пути).
Вариант 4.
Глубинная бомба, установленная на взрыв через заданное время, сбрасывается со стоящего неподвижно противолодочного корабля. Исследовать связь между глубиной, на которой произойдет взрыв, и формой корпуса (сферической, полусферической, каплевидной и т.д.).
Вариант 5.
Глубинная бомба, установленная на взрыв на заданной глубине, сбрасывается со стоящего неподвижно противолодочного корабля. Исследовать связь между временем достижения заданной глубины и формой корпуса (сферической, полусферической, каплевидной и т.д.).
Вариант 6.
Промоделировать полет ракеты.
Провести исследование соотношения входных параметров m0 и Fтяги, при которых ракета достигнет первой космической скорости 7,8 км/с?(и в соответствующий момент исчерпает горючее). Остальные входные параметры фиксировать произвольно. Порядки входных параметров: m0 ˜ 107 кг, mкон ˜ 105 кг, ˜ 105 кг/c, Fтяги ˜ 108 н.
Вариант 7.
Промоделировать полет тела, брошенного под углом к горизонту. Исследовать зависимость горизонтальной длины полета тела от одного из коэффициентов сопротивления среды, фиксировав все остальные параметры.
Вариант 8.
Найти траекторию полета кометы, залетевшей в Солнечную систему, у которой на расстоянии от Солнца 100 астрономических единиц (1 а.е. = 1,50.1011 м расстояние от Земли до Солнца) скорость v=10 км/с и направлена под углом = 30о к оси «комета-Солнце». Является ли эта траектория замкнутой? Если да, то сколько длится для нее период полета? Подобрать то значение угла , при котором траектория из незамкнутой превращается в замкнутую (скорость v фиксирована).
Вариант 9.
Проверить в компьютерном эксперименте выполнимость второго закона Кеплера, определяющего движение небесных тел по замкнутой траектории.
Вариант 10.
Проверить в компьютерном эксперименте выполнимость третьего закона Кеплера, определяющего движение небесных тел по замкнутой траектории.
Вариант 11.
Найти траекторию движения тела массой 1 г., несущего заряд величиной q=1.102 к, в поле заряда величиной Q = 5 .102 к. Начальное расстояние между зарядами 1 м, начальная скорость равна 1.101 м/с и направлена под углом 30о к оси, соединяющей заряды. Провести моделирование для случая зарядов одного знака.
Вариант 12.
Имеется неподвижная заряженная частица с зарядом Q и экран (см. рис.7.2). В точке А экрана находится мишень. При каких соотношениях величины начальной скорости v0 движущейся частицы (заряд q) и угла прицеливания она попадет в мишень? Расстояния обозначены на рисунке. Заряды частиц разных знаков.
Инфоурок
›
Информатика
›Другие методич. материалы›Лабораторная работа «Моделирование полёта тела, брошенного под углом к горизонту средствами EXCEL»
Скачать материал
Скачать материал




- Сейчас обучается 122 человека из 48 регионов


- Сейчас обучается 44 человека из 22 регионов


Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 211 241 материал в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 16.04.2018
- 725
- 11
- 16.04.2018
- 462
- 0
- 16.04.2018
- 833
- 2


Презентация по проблемам информатизации
- Учебник: «Информатика (базовый уровень)», Семакин И.Г., Хеннер Е.К., Шеина Т.Ю.
- Тема: Глава 2. Информационные источники и информационные технологии в проектной деятельности
- 16.04.2018
- 686
- 1



Вам будут интересны эти курсы:
-
Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
-
Курс повышения квалификации «Облачные технологии в образовании»
-
Курс повышения квалификации «Использование компьютерных технологий в процессе обучения в условиях реализации ФГОС»
-
Курс повышения квалификации «Введение в программирование на языке С (СИ)»
-
Курс профессиональной переподготовки «Управление в сфере информационных технологий в образовательной организации»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс повышения квалификации «Современные тенденции цифровизации образования»
-
Курс повышения квалификации «Специфика преподавания дисциплины «Информационные технологии» в условиях реализации ФГОС СПО по ТОП-50»
-
Курс повышения квалификации «Современные языки программирования интегрированной оболочки Microsoft Visual Studio C# NET., C++. NET, VB.NET. с использованием структурного и объектно-ориентированного методов разработки корпоративных систем»
-
Курс повышения квалификации «Применение интерактивных образовательных платформ на примере платформы Moodle»
-
Скачать материал
-
16.04.2018
3197
-
DOCX
58.5 кбайт -
81
скачивание -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Ким Светлана Владиславовна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 6 лет и 3 месяца
- Подписчики: 14
- Всего просмотров: 233992
-
Всего материалов:
134
Файлы
Рабочий лист подходит для учеников 7 класса, работающих по учебнику «Информатика. ФГОС», автор Л….