Моделирование броуновского движения в excel

Причём при s = T, где T – период последовательности, пара чисел zi и zi+s связана простой линейной зависимостью zi = zi+s.

Но при тестировании независимости БСВ zi мы как бы «забываем», что в действительности зависимость имеет место изначально, причём зависимость эта максимально жёсткая, полностью детерминированная. Понятно, что такое наше тестирование независимости может установить не независимость БСВ, а лишь некоторое ее подобие. Однако парадокс состоит в том, что в широких пределах применения датчиков это подобие оказывается весьма близким к тождеству: дискретная и детерминированная величина оказывается весьма близкой к нужной нам непрерывной и случайной величине. При компьютерном моделировании противоположности сходятся.

Как явная дискретность БСВ zi, так и явная их функциональная зависимость логически несовместимы с требованиями непрерывности и независимости, но на практике это имеет ограниченное значение – не большее, чем, например, значение неточности выполнения арифметических операций с плавающей точкой. В то же время сделанное здесь замечание о противоречивом характере требований к датчикам БСВ указывает на некоторые «подводные камни» статистического моделирования, на важность хорошего знания основ теории вероятностей и на необходимость применения только тех датчиков БСВ, которые разработаны и тщательно выверены компьютерными математиками-профессионалами.

3. Моделирование случайных факторов

Случайными факторами будем называть случайное событие, случайную величину, случайный процесс и вообще любые объекты, случайный выбор которых определяется соответствующими вероятностями. Под реализацией случайного фактора будем понимать сам акт случайного выбора одного такого объекта из заданного множества, наделённого вероятностной мерой.

Построение модели любого случайного фактора сводится к подходящему функциональному преобразованию базовых случайных величин zi. При моделировании случайных факторов будем исходить из того, что имеющийся в нашем распоряжении датчик БСВ идеален, т. е. величины zi на его выходе – равномерно распределённые (zi ~ R[0,1]) и независимые. Это позволит нам свободно конструировать модели разнообразных случайных факторов и устанавливать их свойства, опираясь только на положения теории вероятностей и не прибегая к громоздким процедурам статистического тестирования.

В то же время, в целях наглядности представления результатов, будем модели случайных факторов иллюстрировать примерами простой статистической обработки выборок, получаемых с помощью этих моделей.

3.1. Моделирование случайных событий и дискретных случайных величин

3.1.1. Моделирование случайных событий

Пусть задано некоторое множество элементарных исходов {A1, … , An} c их вероятностями p1, … , pn соответственно ( p1 +…+ pn =1).

Чтобы построить программную модель, «оживляющую» такую совокупность исходов, разобьём мысленно интервал значений БСВ (0 ≤ t ≤ 1) на n отрезков длиной

11

p1, p2, … , pn. Это всегда возможно, т. к.

p1 +…+ pn =1.

Например, можно определить

отрезки так:

α1

= (0,

p1),

α2

= (p1,

p1 + p2),

(9)

α3 = (p1 + p2, p1 + p2 + p3),

. . . . . . . . . . . .

αn = (p1 + p2 + … + pn-1, 1).

Алгоритм моделирования случайных исходов Aj состоит в том, чтобы, обратившись к датчику БСВ, определить, в какой из интервалов α1, α2, … , αn попало значение БСВ. Факт его попадания в конкретный интервал αj предопределяет переход алгоритма к процедуре имитации соответствующего, имеющего тот же номер, исхода Aj. Поскольку вероятность попадания БСВ в интервал αj равна его длине pj, то и

вероятность исхода Aj будет равна pj.

Пример 5 . На свободном листе Ms Excel в ячейку A1 введите формулу =СЛЧИС(). В соседнюю ячейку B1 введите =ЕСЛИ(A1<0,5;0;1). Эта формула выдаёт 0, если БСВ в ячейке A1 находится между 0 и 0,5, и выдаёт 1, если БСВ в ячейке A1 находится между 0,5 и 1. Таким образом, в ячейке B1 имитируется результат выбрасывания монеты. Нажмите несколько раз клавишу F9.

Скопируйте содержимое строки A1:B1 в диапазон A1:B20. Правым щелчком мыши выделите столбец A и выберите в открывшемся контекстном меню опцию Скрыть. Оставшийся видимым столбец B имитирует результат выбрасывания 20 монет. Положим, единица в столбце B означает выпадение герба. Промоделируйте несколько выбрасываний 20 монет нажатием ключа F9. Выделите диапазон B1:B20, чтобы на нижней серой индикаторной панели листа увидеть сумму этого диапазона, равную числу выпавших единиц (гербов). Повторяя нажатия F9, проверьте, часто ли происходит случайное событие, определяемое следующим высказыванием: «Число выпавших гербов меньше 7».

3.1.2. Моделирование дискретных случайных величин

Принцип моделирования дискретных с. в. не отличается от принципа моделирования случайных событий. Дискретная с. в. x задаётся конечным или счётным множеством возможных значений x1, x2, … и их вероятностями p1, p2, … . Она реализуется по тому же принципу, по которому моделируются случайные события. Интервал (0, 1) предварительно разбивается на отрезки, длины которых равны вероятностям p1, p2, … элементарных исходов Aj. При этом каждый конкретный исход Aj рассматривается здесь как выбор случайной величиной соответствующего значения x = xj.

В двух частных случаях этот общий алгоритм реализации дискретной с. в. целесообразно упростить.

Первый случай – это случай целочисленной с. в. x, принимающей значения 0, 1, … , n–1 с одинаковыми вероятностями, равными 1/n. Такую дискретную с. в. можно получить с помощью БСВ z одним оператором присваивания, реализующим формулу вычисления целой части:

12

Формулу (10) можно легко приспособить и к другим близким ситуациям. Например, для моделирования игральной кости с числом очков x от 1 до 6 можно результат её выбрасывания проимитировать по формуле

Второй случай, когда алгоритм реализации дискретной с. в. следует упрощать, это случай дискретной с. в. с бесконечным (счётным) множеством возможных значений. В такой ситуации часто можно построить компактную программу, лишь применяя рекурсивный вариант общего метода. Суть проблемы состоит в том, что перед программированием алгоритма разбить интервал (0, 1) на бесконечное число вероятностных отрезков с длинами p1, p2, … невозможно. Поэтому в программе сначала реализуется значение БСВ z, а затем выполняется построение и одновременно – проверка вероятностных отрезков интервала (0, 1), по одному (последовательно, одного за другим), до тех пор, пока не будет построен и проверен отрезок, в котором при его проверке обнаружится реализованное значение БСВ z. После этого случайной величине x присваивается соответствующее найденному отрезку значение xj. Благодаря такому последовательному построению и просмотру вероятностных отрезков, для реализации любого значения xj приходится строить лишь конечное их число. Конкретный пример использования этого метода для реализации пуассоновской с. в. приводится в [16].

Пример 6 . Пусть требуется реализовать дискретную с. в. x, принимающую значения 2; 5; 15; -30 и 3,14 с вероятностями 0,1; 0,15; 0,45; 0,2 и 0,1 соответственно. Если отрезки с длинами, равными перечисленным вероятностям, откладывать на числовой оси вправо от нуля, то их правыми границами будут точки 0,1; 0,25; 0,7; 0,9 и 1. Запишите на чистом листе Ms Excel в диапазоне B1:F2 табличку чисел:

0.1

0.25

0.7

0.9

1

2

5

15

-30

3.14

В ячейку A3 для получения БСВ введите формулу =СЛЧИС(). Теперь для реализации датчика нужной дискретной с. в. остаётся определить, между какими границами, указанными в верхней строке таблички, попадает значение БСВ, и выбрать соответствующее значение с. в. из нижней строки таблички.

Поскольку в Excel подобные условные операции организуются не самым очевидным образом, приведём подробную инструкцию, поясняющую, как это сделать.

В ячейку B3 введите формулу =ЕСЛИ(($A3<B$1)*($A3>A$1);1;0). Эта формула выдаёт 1, если значение ячейки A3 (это БСВ) находится в первом вероятностном отрезке, указанном ячейками A1 и B1, т. е. от 0 до 0,1 (ячейка A1 должна быть пустой). Скопируйте B3 вправо на диапазон B3:F3. В нём появляется строка из нулей и одной единицы, указывающей своим положением на то значение из таблички вверху, которое должно быть выбрано в качестве реализации с. в. x. Автоматический выбор этого значения организуйте в ячейке G3. Для этого запишите в неё формулу =СУММПРОИЗВ($B$2:$F$2;B3:F3). Нажимая ключ F9, убедитесь, что в G3 теперь появляются случайные значения нашей дискретной с. в.

Теперь скопируйте строку A3:G3 вниз на 10-20 строк, выделите и скройте столбцы A-F. Оставшийся видимым столбец G содержит только выборку значений заданной дискретной с. в. По ключу F9 эти значения обновляются.

13

3.1.3. Встроенные генераторы случайных величин

Многие пакеты и языки моделирования имеют встроенные генераторы различных дискретных и непрерывных с. в. Их использование имеет определённые достоинства и недостатки, с которыми целесообразно ознакомиться до принятия решения

отом, нужно ли разрабатывать собственный датчик.

ВMs Excel в меню Сервис/Анализ данных/Генерация случайных чисел пре-

доставляется возможность генерации выборок из следующего списка распределений: Равномерное, Нормальное, Бернулли, Биномиальное, Пуассона, Модельное и Дискретное. Рекомендуется поэкспериментировать с этими генераторами, т. к. они достаточно удобны в использовании. Их недостаток состоит лишь в том, что для обновления выборок требуется повторно проходить меню.

3.2. Моделирование непрерывных случайных величин

Для построения датчиков непрерывных с. в., имеющих заданное распределение вероятностей, разработано большое число алгоритмов [2, 6-15]. В современной учебной литературе по моделированию методы построения датчиков непрерывных с. в. наиболее полно разбираются в книге [8]. Основные методы реализации непрерывных с. в. разъясняются также в [16]. Вместе с тем, во многих языках и пакетах моделирования имеется большое число удобных для использования встроенных датчиков непрерывных с. в.

С учётом сказанного ниже приводятся лишь алгоритмы и формулы для реализации наиболее часто встречающихся непрерывных с. в. и некоторые примеры их реализации на Excel.

3.2.1. Моделирование равномерной случайной величины

С. в. x ~ R[A, B], равномерно распределённую на интервале A ≤ t ≤ B, можно реализовать путём линейного преобразования БСВ z:

x = (B–A)·z + A.

(12)

При этом из (12) получаем

M(x) = A + (B–A)/2,

(13)

D(x) = (B–A)2/12.

(14)

3.2.2. Моделирование экспоненциальной случайной величины

Экспоненциальная с. в. x имеет ф. р. в.

F(t) = 1 – e−λt ,

(15)

где t ≥ 0, параметр λ > 0 . Её м. о. и дисперсия

M(x) = 1/λ , D(x) = 1/λ2.

(16)

Экспоненциальную с. в. можно реализовать с помощью следующего преобразо-

вания БСВ z:

x = – (1/λ)·ln(z).

(17)

Пример 7 . На чистом листе Ms Excel в диапазоне A1:A1000 с помощью функции =СЛЧИС() создайте выборку из 1000 значений БСВ. Полагая λ = 1, в соответствии с (17) запишите в ячейке B1 формулу =-Ln(A1). Двойным щелчком по маркеру

14

заполнения скопируйте её в диапазон B1:B1000. В этом диапазоне получена выборка с. в. x с экспоненциальным распределением (15) при λ = 1.

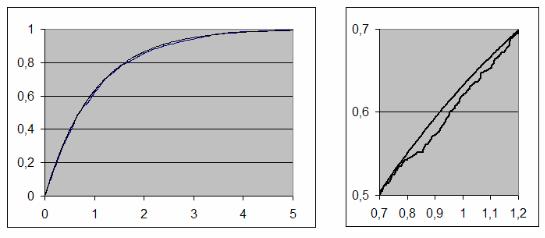
Проверьте вид распределения полученной с. в. путём построения её эмпирической ф. р. в. Для этого скопируйте диапазон B1:B1000 в буфер и вставьте в C1 посредством меню …Специальная вставка/значения, после чего отсортируйте диапазон C1:C1000 по возрастанию. В ячейки диапазона D1:D1000 запишите арифметическую прогрессию 0,001, 0,002, … , 1,000 и постройте диаграмму Точечная по диапазону C1:D1000, как в п. 2.4. Диаграмма будет выглядеть примерно как на рис. 3 («дрожащая» кривая линия, фрагмент которой справа увеличен).

Рис.3. Сравнение эмпирической и теоретической ф. р. в. экспоненциальной с. в.

Гладкую теоретическую кривую, приведенную на рис. 3, можно добавить к вашей диаграмме, если в ячейку E1 ввести формулу (15) для вычисления теоретического значения ф. р. в., в виде формулы =1-exp(-C1); затем её надо скопировать на весь диапазоне E1:E1000. Добавление этого диапазона данных к диаграмме производится через контекстное меню диаграммы Исходные данные…/Ряд/Добавить.

3.2.3. Моделирование эрланговской случайной величины

Эрланговская с.в. x порядка k ≥ 1 имеет ф. р. в.

k −1

i

F(t)

= 1−∑

(λt)

e−λt

,

и п. р. в.

i=0

i!

λ(λt)k −1

f (t) =

e−λt ,

(k −1)!

где параметр λ > 0 . Её м. о., дисперсия и начальные моменты r-го порядка таковы:

M(x) = k/λ ,

D(x) = k/λ2,

M(xr) = k(k+1) ··· (k+r–1)/λr.

(20)

Поскольку распределением Эрланга обладает сумма k независимых экспоненциальных с. в., имеющих одно и то же значение параметра λ, то, с учётом (17), сгенерировать эрланговскую с. в. x можно просто как сумму:

k

1

1

x = ∑i=1

−

ln zi

= −

ln(z1

… zk ) ,

(21)

λ

λ

где zi (i = 1, …, k) – независимые реализации БСВ.

15

3.2.4. Моделирование нормальной случайной величины

Утверждение, что некоторая с. в. x имеет нормальное распределение с м. о. M(x) = μ и дисперсией D(x) = σ2, записывают в виде x ~ N(μ, σ). П. р. в. этой с. в.

f (t )=

1

e−

(t −μ )2

2σ 2

.

(22)

2πσ

Её ф. р. в. F(t) не выражается в элементарных функциях в виде конечной формулы. Для реализации любой нормальной с. в. достаточно иметь датчик стандартной (т. е. нормированной и центрированной) нормальной с. в. x& ~ N(0,1) . Чтобы реализовать с. в. x с распределением (22) используют следующее линейное преобразование стандартной нормальной с. в. x& :

При этом стандартную нормальную с. в. часто реализуют приближённо, как сумму других с. в., основываясь на центральной предельной теореме теории вероятностей. Например, её можно реализовать в виде такой суммы двенадцати независимых значений БСВ:

i=1

Однако такой подход даёт плохое приближение для больших уклонений от среднего, превышающих 2σ.

Метод Бокса и Мюллера позволяет получить два независимых значения x&1 и x&2 стандартной нормальной с. в. из двух независимых значений z1 и z2 БСВ по формулам:

&

=

− 2 ln z1

sin(2π z2 ),

x1

(25)

&

=

− 2 ln z

cos(2π z

).

x

2

1

2

Этот метод точный, но считается трудоёмким [8]. Однако, как показывают эксперименты, это мнение устарело ввиду того, что современные персональные компьютеры оснащены арифметическими сопроцессорами. Точный метод (25) в действительности оказывается также и более быстрым, чем приближённый метод (24).

Приведём ещё формулу для чётных начальных моментов r-го порядка с. в. x& :

M (x&2k ) =(2k–1)!! = (2k–1)·(2k–3)· … ·1. (26)

Все её моменты нечётного порядка равны нулю. 3.2.5. Применение гистограмм и полигонов

В [22] приводятся алгоритмы реализации тех с. в., у которых п. р. в. имеют форму гистограммы (рис. 4 а) или полигона (рис. 4 б). Такие п. р. в. появляются обычно либо как результат обработки эмпирических данных, либо как результат аппроксимации теоретических распределений. Общая площадь, заключённая внутри гистограммы или полигона, равна единице (свойство п. р. в.).

16

Рис. 4. Гистограмма (а) и полигон (б)

Реализацию с. в. по заданной гистограмме можно осуществить путём случайного выбора номера интервала постоянства п. р. в. (вероятность каждого такого интервала гистограммы равна площади построенного на нём прямоугольника), и последующей реализации на этом интервале равномерной с. в.

Если п. р. в. f(t) задана в виде полигона, то можно перейти от неё к ф. р. в. F(t) и разыграть с. в. x методом обращения [16]. Поскольку F(t) является интегралом от п. р. в.:

F (t) = ∫t

f (s)ds ,

(27)

−∞

то здесь F(t) представляет собой кусочно-квадратичную зависимость, и её график агрегируется из отрезков разных параболических дуг. Тем не менее, из непрерывности f(t) следует, что график функции F(t) – гладкий, без изломов. Построенный методом обращения этой ф. р. в. генератор с. в. x должен содержать процедуру, которая по разыгранному значению БСВ z определяет на оси ординат графика F(t) тот интервал значений, на который проецируется одна из агрегированных дуг, и в который попало значение z. После этого x можно вычислить как значение обратной функции от z

по квадратному уравнению этого отрезка дуги.

Пример 8 . Предположим, график f(t) представляет собой две боковые стороны равнобедренного треугольника с основанием на отрезке (0, 2). Из равенства площади треугольника единице следует, что его высота равна 1. Из (27) по этой f(t) определяем:

t < 0,

/ 2,

0 ≤ t <1,

(29)

−t 2 / 2 −1,

1 ≤ t < 2,

2 ≤ t.

Применение к этой ф. р. в. обращения (28) приводит к следующей комбинированной формуле для генерации x:

2z ,

z <1/ 2,

(30)

x =

− 2 − 2z ,

1/ 2 ≤ z.

2

17

В связи с рассмотренным примером заметим, что описанную в нём «треугольную» п. р. в. имеет также сумма двух независимых БСВ. Следовательно, вместо (30) для генерации x можно использовать более простую формулу x = z1 + z2.

Это наблюдение позволяет предположить, что для генерации с. в., которые задаются кусочно-линейными п. р. в. – полигонами, – можно найти метод, более эффективный, чем метод обращения, если использовать суммирование равномерных или кусочно-равномерных случайных величин. По всей видимости, наряду с операцией суммирования в этом методе целесообразно было бы использовать операцию случайного выбора (т. н. смешивание) случайных величин.

Проверку этого предположения оставляем читателю.

3.3. Моделирование случайных процессов

Всякий случайный процесс – дискретный или непрерывный – моделируют последовательностью с. в., которые генерируются либо как статистически независимые, либо как взаимозависимые величины. При этом применяют разные способы реализации зависимости между с. в. Чаще всего, поскольку модель всегда имеет ка- кой-либо «физический смысл», способ реализации зависимости между с. в. определяется причинно-следственными связями, действующими в моделируемой системе. Во многих случаях идеализация и упрощение моделируемых причинноследственных отношений приводит к типичным математическим схемам описания случайных процессов. К числу таких типичных математических схем относятся Марковские процессы, Гауссовы процессы, Броуновское движение, случайное блуждание на прямой и др. [23, 24].

Свойства процессов, описываемых подобными схемами, хорошо изучены методами теории вероятностей. Но в тех случаях, когда в отношении этих процессов решаются задачи, отличающиеся от классических задач, или когда сами исследуемые процессы не вписываются в изученные математические схемы, используют статистическое моделирование. В качестве примера такого статистического моделирования рассмотрим моделирование Броуновского движения.

3.3.1. Броуновское движение на неограниченной плоскости

Процесс Броуновского движения на плоскости можно приближённо представить в виде последовательности случайных перемещений точечной частицы, выполняемых в дискретные моменты времени t = 0, 1, 2, … .

Будем полагать, что в момент t = 0 частица находится в начале системы координат. Перемещение частицы в любой из следующих моментов времени реализуется выбором случайного направления в пределах от 0 до 2π радиан и смещением частицы в этом направлении на шаг единичной длины.

Модель такого Броуновского движения легко можно реализовать средствами Ms Excel.

Пример 9 . Откройте чистый лист Excel, введите в ячейки A1, B1 и C1 три заголовка Угол, X, Y, и под ними (соответственно, в ячейках A2:C3) введите формулы:

Угол

X

Y

=2*ПИ()*СЛЧИС()

=COS(A2)

=SIN(A2)

=2*ПИ()*СЛЧИС()

=B2+COS(A3)

=C2+SIN(A3)

18

Нетрудно видеть, что непосредственно под заголовками полученной таблички вычисляется положение частицы в момент времени t = 0. В первой колонке реализуется случайное направление вектора перемещения частицы, во второй – абсцисса конца вектора (имеющего единичную длину), в третьей – его ордината. Последняя строка таблички – A3:C3 – формирует следующее положение частицы (в момент времени t = 1), определяемое расчётом смещения частицы относительно предыдущего положения (сформированного в ячейках B2 и C2). Эту строку A3:C3 можно копировать вниз. Скопируйте её до 1001-й строки листа. В результате в колонках B и C появляется последовательность из 1000 положений (координат) частицы, совершающей Броуновское движение на плоскости.

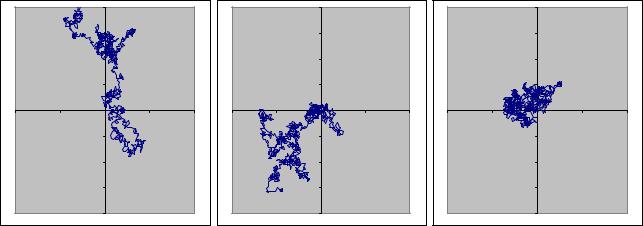
Выделите диапазон B2:C1001 и постройте по нему диаграмму типа Точечная вида Диаграмма со значениями, соединёнными отрезками без маркеров. Реализуйте несколько независимых Броуновских движений посредством нажатия клавиши F9. На рис. 5 показаны три реализации Броуновского процесса, полученные описанным способом.

40

30

20

10

0

-40

-20

0

20

40

-10

-20

-30

-40

40

30

20

10

0

-40

-20

0

20

40

-10

-20

-30

-40

40

30

20

10

0

-40

-20

0

20

40

-10

-20

-30

-40

Рис. 5. Реализации Броуновского движения на плоскости

Оцените на глаз расстояние, на которое частица удаляется от своего начального положения за 1000 шагов. Теоретически оно в среднем должно быть примерно равно квадратному корню из числа шагов (т. е. составлять около 32 единиц).

3.3.2. Броуновское движение в замкнутой области

При исследовании Броуновского движения, в котором нужно учитывать какиелибо ограничивающие факторы, аналитические методы математики оказываются малоэффективными. Статистическое моделирование позволяет учитывать подобные факторы без особого труда.

Пример 1 0 . На рис. 6 приведена траектория Броуновского движения в кольце, полученного путём небольшой модификации модели, рассмотренной в п. 3.2.1. Справа на рис. 6 показан увеличенный фрагмент этой же траектории частицы. Модель Броуновского движения в кольце отличается от модели Броуновского движения на неограниченной плоскости только тем, что посредством условного оператора =ЕСЛИ… выполняется проверка, не выходит ли новое случайное положение частицы за пределы кольца, и, если выходит, то расчётные координаты определяются как координаты «отражения» частицы от достигнутой границы кольца. Выполните са-

19

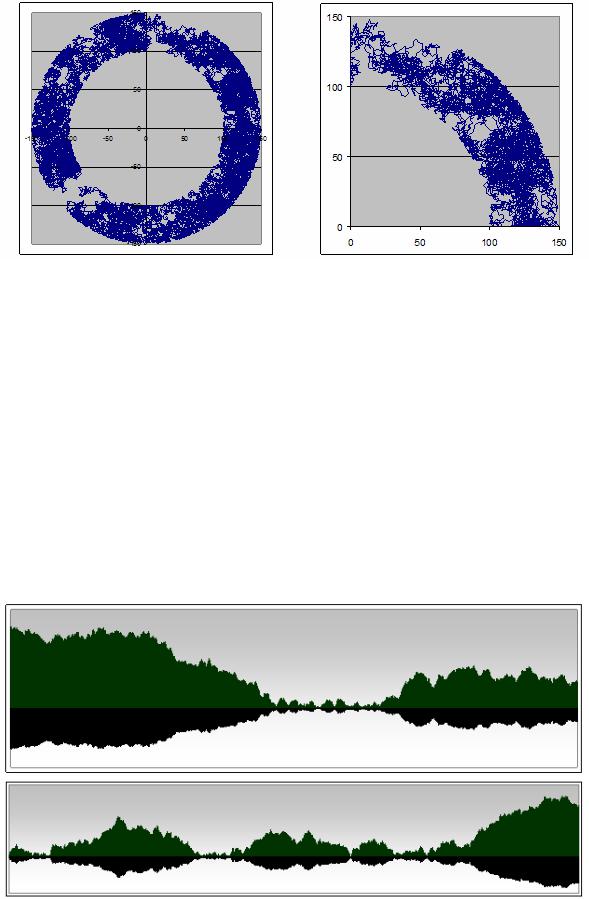
мостоятельно указанную несложную модификацию модели Броуновского движения на плоскости.

Рис. 6. Реализация Броуновского движения в кольце

При необходимости нетрудно ввести в модель и другие дополнительные факторы – мембраны и фильтры, влияющие на перемещение частицы, анизотропию направлений, удлиняющую смещение от центра по сравнению со смещением к центру (этим способом можно промоделировать вращающиеся цилиндры сепаратора) и т. д.

3.3.3. Фрактальные пейзажи

В математическом эссе [25] приводится обзор результатов относительно новой математической теории, основанной на теории множеств и теории размерностей, которая позволяет простыми средствами описывать и исследовать большое число пространственных (геометрических) закономерностей структурирования живой и неживой материи. В основе этой теории лежит понятие фрактала – множества точек, обладающего свойством наглядного или абстрактного (рис. 7) «самоподобия» (масштабной инвариантности) и характеризуемого наряду с обычной целой (Евклидовой) размерностью дробной размерностью Хаусдорфа-Безиковича.

Броуновское движение представляет собой одну из разновидностей фракталов.

Рис. 7. Случайные озёрно-лесные пейзажи (графики построены в Ms Excel)

20

Соседние файлы в предмете Теория вероятностей и математическая статистика

  • #

    15.06.2014375.81 Кб172.doc

  • #

    15.06.20142.34 Mб735_laba.xlsx

  • #

    15.06.20148.86 Кб506 laba.xlsx

  • #

    15.06.2014855.19 Кб507_laba.xlsx

  • #

    15.06.20141.23 Mб55laba_4.xlsx

  • #
  • #
  • #
  • #

    15.06.201441.28 Кб59Книга1.xlsx

  • #

    15.06.201433.28 Кб49лаб3.xls

  • #

    15.06.201427.36 Кб54лаба1 — копия.xlsx

Источник

Содержание

  • — Как сделать случайное блуждание в Excel?
  • — Броуновское движение — это то же самое, что винеровский процесс?
  • — Каков процесс броуновского движения?
  • — Как вы имитируете броуновское движение?
  • — Что такое броуновское движение простыми словами?
  • — Как броуновское движение используется в финансах?
  • — Следуют ли акции броуновскому движению?

Когда у вас открыт файл в Excel, перейдите в Файл -> Информация. Теперь на экране должны отображаться свойства в правом верхнем углу экрана. Щелкните текст заголовка и измените его на то, что хотите.

Случайная прогулка

  1. Заполните столбец A 8000 строками случайных чисел в интервале от -1 до 1. Используйте диалоговое окно Инструменты / Анализ данных / Генерация случайных чисел.
  2. В ячейку B1 введите значение 0 (начальное положение частицы).
  3. В ячейке B2 введите формулу = B1 + A1. …
  4. Постройте x-положение частицы (столбец B)

Броуновское движение — это то же самое, что винеровский процесс?

В большинстве ссылок Броуновское движение и винеровский процесс — одно и то же. … Вся коллекция называется винеровским процессом. Ясно, что винеровский процесс и любое броуновское движение, построенное на другом вероятностном пространстве, имеют одинаковое распределение, называемое мерой Винера.

Каков процесс броуновского движения?

Стандартный (одномерный) винеровский процесс (также называемый броуновским движением) — это случайный процесс {Wt} t≥0 +, индексированный неотрицательные действительные числа t со следующими свойствами: (1) W0 = 0. … В общем случае случайный процесс со стационарными независимыми приращениями называется процессом Леви; подробнее об этом позже.

Как вы имитируете броуновское движение?

Броуновское движение в одном измерении состоит из кумулятивного суммирования последовательности нормально распределенных случайных смещений, то есть броуновское движение можно смоделировать с помощью последовательное добавление членов случайного нормального распределения, а именно: X (0) ∽ N (0, σ2) X (1) ∽ X (0) + N (0, σ2) X (2) ∽ X (1) + N (0, σ2) …… .

Что такое броуновское движение простыми словами?

[brou′nē-ən] Случайное движение микроскопических частиц, взвешенных в жидкости или газе, вызванное столкновениями между этими частицами и молекулами жидкости или газа.. Это движение названо по имени шотландского ботаника Роберта Брауна (1773–1858). См. Также кинетическую теорию.

Как броуновское движение используется в финансах?

Броуновское движение — это простой непрерывный случайный процесс, который широко используется в физике и финансах для моделирование случайного поведения, которое развивается с течением времени. Примерами такого поведения являются случайные движения молекулы газа или колебания цены актива.

Следуют ли акции броуновскому движению?

Однако фондовые рынки предполагается, что валютные рынки, товарные рынки и рынки облигаций следуют броуновскому движению., где активы постоянно меняются в течение очень небольших интервалов времени, а положение, а именно изменение состояния активов, изменяется случайными величинами.

Интересные материалы:

Как быстрее всего отредактировать верхний или нижний колонтитул документа?
Как быстрее всего отшлифовать плинтусы?
Как быстрее всего получить алмазы у моих поющих монстров?
Как быстрее всего получить опыт в Fallout 4?
Как быстрее всего получить золото в Mobile Legends?
Как быстрее всего повысить уровень кораблей в World of Warships?
Как быстрее всего рассчитать валюту?
Как быстрее всего разрядить аккумулятор?
Как быстрее всего умножить двузначные числа?
Как быстро должна двигаться вода, чтобы не замерзнуть?

Источник

GBM2.png

A геометрическое броуновское движение (GBM) (также известное как экспоненциальное броуновское движение ) является непрерывным -время случайный процесс, в котором логарифм случайно изменяющейся величины следует броуновскому движению (также называемому винеровским процессом ) с дрифт. Это важный пример случайных процессов, удовлетворяющих стохастическому дифференциальному уравнению (SDE); в частности, он используется в математических финансах для моделирования цен акций в модели Блэка – Шоулза.

Содержание

  • 1 Техническое определение: SDE
  • 2 Решение SDE
  • 3 Свойства
  • 4 Моделирование примеров путей
  • 5 Многовариантная версия
  • 6 Использование в финансах
  • 7 Расширения
  • 8 См. Также
  • 9 Ссылки
  • 10 Внешние ссылки

Техническое определение : SDE

Говорят, что случайный процесс S t следует за GBM, если он удовлетворяет следующему стохастическому дифференциальному уравнению (SDE):

d S t знак равно μ S tdt + σ S td W t { displaystyle dS_ {t} = mu S_ {t} , dt + sigma S_ {t} , dW_ {t}}dS_ {t} = mu S_ {t} , dt + sigma S_ {t} , dW_ {t}

где W t { displaystyle W_ {t}}W_ {t} — это винеровский процесс или броуновское движение, а μ { displaystyle mu} му (‘процентный дрейф’) и σ { displaystyle sigma} sigma («волатильность в процентах») являются константами.

Первый используется для моделирования детерминированных тенденций, тогда как последний термин часто используется для моделирования набора непредсказуемых событий, происходящих во время этого движения.

Решение SDE

Для произвольного начального значения S 0 вышеуказанное SDE имеет аналитическое решение (в соответствии с интерпретацией Ито ):

S t = S 0 ехр ⁡ ((μ — σ 2 2) t + σ W t). { Displaystyle S_ {t} = S_ {0} exp left ( left ( mu — { frac { sigma ^ {2}} {2}} right) t + sigma W_ {t} right).}S_ {t} = S_ {0} exp left ( left ( mu - { frac { sigma ^ {2}} {2}} right) t + sigma W_ {t} right).

Для вывода требуется использование исчисления Ито. Применение формулы Ито приводит к

d (ln ⁡ S t) = (ln ⁡ S t) ′ d S t + 1 2 (ln ⁡ S t) ″ d S td S t = d S t S t — 1 2 1 S t 2 d S td S t { displaystyle d ( ln S_ {t}) = ( ln S_ {t}) ‘dS_ {t} + { frac {1} {2 }} ( ln S_ {t}) » , dS_ {t} , dS_ {t} = { frac {dS_ {t}} {S_ {t}}} — { frac {1} {2 }} , { frac {1} {S_ {t} ^ {2}}} , dS_ {t} , dS_ {t}}{displaystyle d(ln S_{t})=(ln S_{t})'dS_{t}+{frac {1}{2}}(ln S_{t})'',dS_{t},dS_{t}={frac {dS_{t}}{S_{t}}}-{frac {1}{2}},{frac {1}{S_{t}^{2}}},dS_{t},dS_{t}}

где d S td S t { displaystyle dS_ {t} , dS_ {t}}{ displaystyle dS_ {t} , dS_ {t}} — это квадратичная вариация SDE.

d S td S t знак равно σ 2 S t 2 d W T 2 + 2 σ S t 2 μ d W tdt + μ 2 S t 2 dt 2 { displaystyle dS_ {t} , dS_ {t} , = , sigma ^ {2} , S_ {t} ^ {2} , dW_ {t} ^ {2} +2 sigma S_ {t} ^ {2} mu , dW_ {t} , dt + mu ^ {2} S_ {t} ^ {2} , dt ^ {2}}{ displaystyle dS_ {t} , dS_ {t} , = , sigma ^ {2} , S_ {t} ^ {2} , dW_ {t} ^ {2} +2 сигма S_ {t} ^ {2} mu , dW_ {t} , dt + mu ^ {2} S_ { t} ^ {2} , dt ^ {2}}

Когда dt → 0 { displaystyle dt to 0}{ displaystyle dt to 0} , dt { displaystyle dt}{ displaystyle dt} сходится к 0 быстрее, чем d W t { displaystyle dW_ {t}}{ displaystyle dW_ {t}} , поскольку d W t 2 = O (dt) { displaystyle dW_ {t} ^ {2} = O (dt)}{ Displaystyle dW_ {t} ^ {2} = O (dt)} . Таким образом, указанная выше бесконечно малая может быть упрощена следующим образом:

d S td S t = σ 2 S t 2 dt { displaystyle dS_ {t} , dS_ {t} , = , sigma ^ {2} , S_ {t} ^ {2} , dt}{ displaystyle dS_ {t} , dS_ {t} , = , sigma ^ {2} , S_ {t} ^ {2} , dt}

Подставляя значение d S t { displaystyle dS_ {t}}{ displaystyle dS_ {t}} в приведенное выше уравнение и упрощая, получаем

ln ⁡ S t S 0 = (μ — σ 2 2) t + σ W t. { displaystyle ln { frac {S_ {t}} {S_ {0}}} = left ( mu — { frac { sigma ^ {2}} {2}} , right) t + sigma W_ {t} ,.} ln { frac {S_ {t}} {S_ {0}}} = left ( mu - { frac { sigma ^ {2}} {2}} , right) t + sigma W_ {t} ,.

Взяв экспоненту и умножив обе части на S 0 { displaystyle S_ {0}}S_ {0} , мы получим решение, заявленное выше.

Свойства

Приведенное выше решение S t { displaystyle S_ {t}}S_ {t} (для любого значения t) является нормальным логарифмическим распределенная случайная величина с ожидаемым значением и дисперсией, задаваемой

E ⁡ (S t) = S 0 e μ t, { displaystyle operatorname {E} (S_ {t}) = S_ {0} e ^ { mu t},}{ displaystyle operatorname {E} (S_ {t}) = S_ {0} e ^ { mu t},}
Var ⁡ (S t) = S 0 2 e 2 μ t (e σ 2 t — 1). { displaystyle operatorname {Var} (S_ {t}) = S_ {0} ^ {2} e ^ {2 mu t} left (e ^ { sigma ^ {2} t} -1 right).}{ displaystyle operatorname {Var} (S_ {t}) = S_ {0} ^ {2} e ^ {2 mu t} left (e ^ { sigma ^ {2} t} -1 справа).}

Их можно вывести, используя тот факт, что Z t = exp ⁡ (σ W t — 1 2 σ 2 t) { displaystyle Z_ {t} = exp left ( sigma W_ {t } — { frac {1} {2}} sigma ^ {2} t right)}{ displaystyle Z_ {t} = exp левый ( sigma W_ {t} - { frac {1} {2}} sigma ^ {2} t right)} — это мартингейл, и что

E ⁡ [exp ⁡ ( 2 σ W t — σ 2 t) ∣ F s] = e σ 2 (t — s) exp ⁡ (2 σ W s — σ 2 s), ∀ 0 ≤ s < t. {displaystyle operatorname {E} left[exp left(2sigma W_{t}-sigma ^{2}tright)mid {mathcal {F}}_{s}right]=e^{sigma ^{2}(t-s)}exp left(2sigma W_{s}-sigma ^{2}sright),quad forall 0leq s{ displaystyle operatorname {E} left [ exp left (2 sigma W_ {t} - sigma ^ {2} t right) mid { mathcal { F}} _ {s} right] = e ^ { sigma ^ {2} (ts)} exp left (2 sigma W_ {s} - sigma ^ {2} s right), quad forall 0 leq s <t.}

Функция плотности вероятности из S t { displaystyle S_ {t}}S_ {t} равно:

f S t (s; μ, σ, t) = 1 2 π 1 s σ t exp ⁡ ( — (ln ⁡ s — ln ⁡ S 0 — (μ — 1 2 σ 2) t) 2 2 σ 2 t). { displaystyle f_ {S_ {t}} (s; mu, sigma, t) = { frac {1} { sqrt {2 pi}}} , { frac {1} {s sigma { sqrt {t}}}} , exp left (- { frac { left ( ln s- ln S_ {0} — left ( mu — { frac {1} {2}) } sigma ^ {2} right) t right) ^ {2}} {2 sigma ^ {2} t}} right).}f_ {S_ {t}} (s; mu, sigma, t) = { frac {1} { sqrt {2 pi}} } , { frac {1} {s sigma { sqrt {t}}}} , exp left (- { frac { left ( ln s- ln S_ {0} - left ( mu - { frac {1} {2}} sigma ^ {2} right) t right) ^ {2}} {2 sigma ^ {2} t}} right).
Вывод функции плотности вероятности GBM

Чтобы получить Функция плотности вероятности для GBM, мы должны использовать уравнение Фоккера-Планка для оценки временной эволюции PDF:

∂ p ∂ t + ∂ ∂ S [μ (t, S) p (t, S)] знак равно 1 2 ∂ 2 ∂ S 2 [σ 2 (t, S) p (t, S)], p (0, S) = δ (S) { displaystyle { partial p over { partial t}} + { partial over { partial S}} [ mu (t, S) p (t, S)] = {1 over {2}} { partial ^ {2} over { partial S ^ {2}}} [ sigma ^ {2} (t, S) p (t, S)], quad p (0, S) = delta (S)}{ displaystyle { partial p over { partial t}} + { partial over { partial S}} [ mu (t, S) p (t, S)] = {1 over {2 }} { partial ^ {2} over { partial S ^ {2}}} [ sigma ^ {2} (t, S) p (t, S)], quad p (0, S) = дельта (S)}

где δ (S) { displaystyle delta (S)}{ displaystyle delta (S)} — это дельта-функция Дирака. Чтобы упростить вычисления, мы можем ввести логарифмическое преобразование x = log ⁡ (S / S 0) { displaystyle x = log (S / S_ {0})}{ displaystyle x = log (S / S_ {0})} , приводящее к форма GBM:

dx = (μ — 1 2 σ 2) dt + σ d W { displaystyle dx = left ( mu — {1 over {2}} sigma ^ {2} right) dt + sigma dW}{ displaystyle dx = left ( mu - {1 over {2}} sigma ^ {2} right) dt + sigma dW}

Тогда эквивалентное уравнение Фоккера-Планка для эволюции PDF принимает вид:

∂ p ∂ t + (μ — 1 2 σ 2) ∂ p ∂ x = 1 2 σ 2 ∂ 2 п ∂ Икс 2, п (0, Икс) знак равно δ (Икс) { Displaystyle { partial p over { partial t}} + left ( mu — {1 over {2}} sigma ^ { 2} right) { partial p over { partial x}} = {1 over {2}} sigma ^ {2} { partial ^ {2} p over { partial x ^ {2} }}, quad p (0, x) = delta (x)}{ displaystyle { partial p over { partial t}} + left ( mu - {1 over {2}} sigma ^ {2} right) { partial p over { partial x}} = {1 over {2}} sigma ^ {2} { partial ^ {2} p over { partial x ^ {2}}}, quad p (0, x) = delta (x)}

Определите V = μ — σ 2/2 { displaystyle V = mu — sigma ^ {2} / 2}{ displaystyle V = mu - sigma ^ {2} / 2} и D = σ 2/2 { displaystyle D = sigma ^ {2} / 2}{ displaystyle D = sigma ^ {2} / 2} . Путем введения новых переменных ξ = x — V t { displaystyle xi = x-Vt}{ displaystyle xi = x-Vt} и τ = D t { displaystyle tau = Dt}{ displaystyle tau = Dt} , производные в уравнении Фоккера-Планка могут быть преобразованы как:

∂ tp = D ∂ τ p — V ∂ ξ p ∂ xp = ∂ ξ p ∂ x 2 p = ∂ ξ 2 p { displaystyle { begin {align} partial _ {t} p = D partial _ { tau} pV partial _ { xi} p \ partial _ {x} p = partial _ { xi} p \ partial _ {x} ^ {2} p = partial _ { xi} ^ {2} p end {align}}}{ displaystyle { begin {align} partial _ {t} p = D partial _ { tau} pV partial _ { xi} p \ partial _ { x} p = partial _ { xi} p \ partial _ {x} ^ {2} p = partial _ { xi} ^ {2} p end {align}}}

Приводя к новой форме уравнения Фоккера-Планка:

∂ п ∂ τ знак равно ∂ 2 п ∂ ξ 2, п (0, ξ) = δ (ξ) { displaystyle { partial p over { partial tau}} = { partial ^ {2} p over { partial xi ^ {2}}}, quad p (0, xi) = delta ( xi)}{ displaystyle { partial p over { partial tau}} = { partial ^ {2} p over { partial xi ^ {2}}}, quad p (0, xi) = delta ( xi)}

Однако это каноническая форма уравнения теплопроводности. решение которого задается тепловым ядром :

p (τ, ξ) = 1 4 π τ exp ⁡ (- ξ 2 4 τ) { displaystyle p ( tau, xi) = {1 over { sqrt {4 pi tau}}} exp left (- { xi ^ {2} over {4 tau}} right)}{ displaystyle p ( tau, xi) = {1 over { sqrt {4 pi tau}}} exp left (- { xi ^ {2} over {4 tau}} right)}

Вставка исходных переменных приводит к PDF для GBM:

p (t, S) = 1 S 2 π σ 2 t exp ⁡ {- [log ⁡ (S / S 0) — (μ — 1 2 σ 2) t] 2 2 σ 2 t} { displaystyle p (t, S) = {1 over {S { sqrt {2 pi sigma ^ {2} t}}}} exp left {- { left [ log (S / S_ {0}) — left ( mu — {1 over {2}} sigma ^ {2} right) t right] ^ {2} over {2 sigma ^ {2} t}} right }}{ displaystyle p (t, S) = {1 over {S { sqrt {2 pi sigma ^ {2} t}}}} exp left {- { left [ log (S / S_ {0}) - left ( mu - {1 over {2}} sigma ^ {2} right) t right] ^ {2} over {2 sigma ^ {2} t}} right }}

При выводе дополнительных свойств GBM можно использовать SDE, решением которой является GBM, или можно использовать явное решение, данное выше. Например, рассмотрим журнал случайного процесса (S t). Это интересный процесс, потому что в модели Блэка – Шоулза он связан с логарифмической доходностью цены акций. Используя лемму Ито с f (S) = log (S), получаем

d log ⁡ (S) = f ′ (S) d S + 1 2 f ″ (S) S 2 σ 2 dt = 1 S (σ S d W t + μ S dt) — 1 2 σ 2 dt = σ d W t + (μ — σ 2/2) dt. { displaystyle { begin {alignat} {2} d log (S) = f ‘(S) , dS + { frac {1} {2}} f’ ‘(S) S ^ {2} sigma ^ {2} , dt \ [6pt] = { frac {1} {S}} left ( sigma S , dW_ {t} + mu S , dt right) — { frac {1} {2}} sigma ^ {2} , dt \ [6pt] = sigma , dW_ {t} + ( mu — sigma ^ {2} / 2) , dt. end {alignat}}}{displaystyle {begin{alignedat}{2}dlog(S)=f'(S),dS+{frac {1}{2}}f''(S)S^{2}sigma ^{2},dt\[6pt]={frac {1}{S}}left(sigma S,dW_{t}+mu S,dtright)-{frac {1}{2}}sigma ^{2},dt\[6pt]=sigma ,dW_{t}+(mu -sigma ^{2}/2),dt.end{alignedat}}}

Отсюда следует, что E ⁡ log ⁡ (S t) = log ⁡ (S 0) + (μ — σ 2/2) t { displaystyle operatorname {E} log (S_ {t}) = log (S_ {0}) + ( mu — sigma ^ {2} / 2) t}{ displaystyle operatorname {E} log (S_ {t}) = журнал (S_ {0}) + ( mu - sigma ^ {2} / 2) t} .

Этот результат также можно получить, применив логарифм к явному решению GBM:

журнал ⁡ (S t) = журнал ⁡ (S 0 exp ⁡ ((μ — σ 2 2) t + σ W t)) = журнал (S 0) + (μ — σ 2 2) t + σ W t. { Displaystyle { begin {alignat} {2} log (S_ {t}) = log left (S_ {0} exp left ( left ( mu — { frac { sigma ^ { 2}} {2}} right) t + sigma W_ {t} right) right) \ [6pt] = log (S_ {0}) + left ( mu — { frac { sigma ^ {2}} {2}} right) t + sigma W_ {t}. end {alignat}}}{ displaystyle { begin {alignat} {2} log (S_ {t}) = log left (S_ {0} exp left ( left ( mu - { frac { sigma ^ {2}} {2}} right) t + sigma W_ {t} right) right) \ [6pt] = log (S_ {0}) + left ( mu - { frac { sigma ^ {2}} {2}} right) t + sigm a W_ {t}. end {alignat}}}

Принятие математического ожидания дает тот же результат, что и выше: E ⁡ log ⁡ (S t) знак равно журнал ⁡ (S 0) + (μ — σ 2/2) t { displaystyle operatorname {E} log (S_ {t}) = log (S_ {0}) + ( mu — sigma ^ {2} / 2) t}{ displaystyle operatorname {E} log (S_ {t}) = журнал (S_ {0}) + ( mu - sigma ^ {2} / 2) t} .

Моделирование примеров путей

# Код Python для графика import numpy as np import matplotlib.pyplot as plt mu = 1 n = 50 dt = 0.1 x0 = 100 np.random.seed (1) sigma = np.arange (0.8, 2, 0.2) x = np.exp ((mu - sigma ** 2/2) * dt + sigma * np.random.normal (0, np.sqrt ( dt), size = (len (sigma), n)). T) x = np.vstack ([np.ones (len (sigma)), x]) x = x0 * x.cumprod (axis = 0) plt.plot (x) plt.legend (np.round (sigma, 2)) plt.xlabel ("$ t $") plt.ylabel ("$ x $") plt.title ("Реализации геометрического броуновского движения с различными отклонения  n $  mu = 1 $ ") plt.show ()

Mult ivariate version

GBM может быть расширен для случая, когда существует несколько коррелированных ценовых путей.

Каждый ценовой путь следует соответствующему процессу

d S ti = μ i S tidt + σ i S tid W ti, { displaystyle dS_ {t} ^ {i} = mu _ {i} S_ {t} ^ {i} , dt + sigma _ {i} S_ {t} ^ {i} , dW_ {t} ^ {i},}{ displaystyle dS_ {t} ^ {i} = mu _ {i} S_ {t} ^ {i} , dt + sigma _ {i} S_ {t} ^ {i} , dW_ {t} ^ {i},}

где винеровские процессы коррелированы так, что E ⁡ (d W tid W tj) = ρ i, jdt { displaystyle operatorname {E} (dW_ {t} ^ {i} , dW_ {t} ^ {j}) = rho _ {i, j} , dt}{ displaystyle operatorname {E} (dW_ {t} ^ {i} , dW_ {t} ^ {j}) = rho _ {i, j} , dt} где ρ i, i = 1 { displaystyle rho _ {i, i} = 1} rho _ {i, i} = 1 .

Для многомерного случая это означает, что

Cov ⁡ (S ti, S tj) = S 0 i S 0 je (μ i + μ j) t (e ρ i, j σ i σ jt — 1). { displaystyle operatorname {Cov} (S_ {t} ^ {i}, S_ {t} ^ {j}) = S_ {0} ^ {i} S_ {0} ^ {j} e ^ {( mu _ {i} + mu _ {j}) t} left (e ^ { rho _ {i, j} sigma _ {i} sigma _ {j} t} -1 right).}{ displaystyle operatorname {Cov} (S_ {t} ^ {i}, S_ {t} ^ {j}) = S_ {0} ^ {i} S_ {0} ^ {j} e ^ {( mu _ {i} + mu _ {j}) t} left (e ^ { rho _ {i, j} sigma _ {i} sigma _ {j} t} -1 right).}

Использование в финансах

Геометрическое броуновское движение используется для моделирования цен на акции в модели Блэка – Шоулза и является наиболее широко используемой моделью поведения курса акций.

Некоторые аргументы в пользу использования GBM для моделирования цен акций:

  • Ожидаемая доходность GBM не зависит от ценности процесса (цены акций), что согласуется с тем, что мы ожидаем в действительности.
  • Процесс GBM предполагает только положительные результаты. значений, как и реальные цены на акции.
  • Процесс GBM показывает ту же «грубость» на своем пути, что и реальные цены на акции.
  • Расчеты с процессами GBM относительно просты.

Однако GBM не является полностью реалистичной моделью, в частности, она не соответствует действительности в следующих пунктах:

  • В реальных ценах акций волатильность со временем изменяется (возможно, стохастически ), но в GBM волатильность считается постоянной.
  • В реальной жизни цены на акции часто показывают скачки, вызванные непредсказуемыми событиями или новостями, но в GBM этот путь является непрерывным (без разрывов).

Расширения

В попытке сделать GBM более реалистичным в качестве модели для цен на акции можно отказаться от предположения, что волатильность (σ { displaystyle sigma} sigma ) является постоянной. Если мы предположим, что волатильность является детерминированной функцией цены акции и времени, это называется моделью локальной волатильности. Если вместо этого мы предположим, что волатильность имеет свою собственную случайность — часто описываемую другим уравнением, управляемым другим броуновским движением, — модель называется моделью стохастической волатильности.

См. Также

Ссылки

Внешние ссылки

Источник

GBM2.png

А геометрическое броуновское движение (GBM) (также известен как экспоненциальное броуновское движение) является непрерывным случайный процесс в которой логарифм случайно изменяющейся величины следует за Броуновское движение (также называемый Винеровский процесс ) с дрейф.[1] Это важный пример случайных процессов, удовлетворяющих стохастическое дифференциальное уравнение (SDE); в частности, он используется в математические финансы моделировать цены на акции в Модель Блэка – Шоулза.

Техническое определение: SDE

Стохастический процесс Sт считается, что он следует за GBM, если он удовлетворяет следующим условиям стохастическое дифференциальное уравнение (SDE):

dS_ {t} = mu S_ {t} , dt + sigma S_ {t} , dW_ {t}

куда W_ {t} это Винеровский процесс или броуновское движение, и му (‘процентный дрейф’) и сигма («процентная волатильность») являются константами.

Первый используется для моделирования детерминированных тенденций, а второй термин часто используется для моделирования набора непредсказуемых событий, происходящих во время этого движения.

Решение SDE

Для произвольного начального значения S0 указанное выше СДУ имеет аналитическое решение (при Интерпретация Ито ):

S_ {t} = S_ {0} exp left ( left ( mu - { frac { sigma ^ {2}} {2}} right) t + sigma W_ {t} right).

Для вывода требуется использование Исчисление Ито. Применение Формула Ито приводит к

{ Displaystyle d ( ln S_ {t}) = ( ln S_ {t}) 'dS_ {t} + { frac {1} {2}} ( ln S_ {t})' ', dS_ {t} , dS_ {t} = { frac {dS_ {t}} {S_ {t}}} - { frac {1} {2}} , { frac {1} {S_ {t} ^ {2}}} , dS_ {t} , dS_ {t}}

куда { Displaystyle dS_ {t} , dS_ {t}} это квадратичная вариация ДЗО.

{ displaystyle dS_ {t} , dS_ {t} , = , sigma ^ {2} , S_ {t} ^ {2} , dW_ {t} ^ {2} +2 sigma S_ { t} ^ {2} mu , dW_ {t} , dt + mu ^ {2} S_ {t} ^ {2} , dt ^ {2}}

Когда { displaystyle dt to 0}, { displaystyle dt} сходится к 0 быстрее, чем { displaystyle dW_ {t}}, поскольку { displaystyle dW_ {t} ^ {2} = O (dt)}. Таким образом, указанное выше бесконечно малое можно упростить с помощью

{ Displaystyle dS_ {t} , dS_ {t} , = , sigma ^ {2} , S_ {t} ^ {2} , dt}

Подключаем значение { displaystyle dS_ {t}} в приведенном выше уравнении и упрощая, получаем

ln { frac {S_ {t}} {S_ {0}}} = left ( mu - { frac { sigma ^ {2}} {2}} , right) t + sigma W_ { t} ,.

Взяв экспоненту и умножив обе части на S_ {0} дает решение, заявленное выше.

Характеристики

Вышеупомянутое решение S_ {t} (для любого значения t) является лог-нормально распределенный случайная переменная с ожидаемое значение и отклонение данный[2]

{ displaystyle operatorname {E} (S_ {t}) = S_ {0} e ^ { mu t},}
{ displaystyle operatorname {Var} (S_ {t}) = S_ {0} ^ {2} e ^ {2 mu t} left (e ^ { sigma ^ {2} t} -1 right) .}

Их можно вывести, используя тот факт, что { displaystyle Z_ {t} = exp left ( sigma W_ {t} - { frac {1} {2}} sigma ^ {2} t right)} это мартингейл, и это

{ displaystyle operatorname {E} left [ exp left (2 sigma W_ {t} - sigma ^ {2} t right) mid { mathcal {F}} _ {s} right] = e ^ { sigma ^ {2} (ts)} exp left (2 sigma W_ {s} - sigma ^ {2} s right), quad forall 0 leq s <t.}

В функция плотности вероятности из S_ {t} является:

f_ {S_ {t}} (s; mu, sigma, t) = { frac {1} { sqrt {2 pi}}} , { frac {1} {s sigma { sqrt {t}}}} , exp left (- { frac { left ( ln s- ln S_ {0} - left ( mu - { frac {1} {2}} sigma ^ {2} right) t right) ^ {2}} {2 sigma ^ {2} t}} right).

Вывод функции плотности вероятности GBM

Чтобы получить функцию плотности вероятности для GBM, мы должны использовать Уравнение Фоккера-Планка для оценки временной эволюции PDF:

{ displaystyle { partial p over { partial t}} + { partial over { partial S}} [ mu (t, S) p (t, S)] = {1 over {2} } { partial ^ {2} over { partial S ^ {2}}} [ sigma ^ {2} (t, S) p (t, S)], quad p (0, S) = дельта (S)}

куда { displaystyle delta (S)} это Дельта-функция Дирака. Чтобы упростить вычисления, мы можем ввести логарифмическое преобразование { Displaystyle х = журнал (S / S_ {0})}, что приводит к форме GBM:

{ displaystyle dx = left ( mu - {1 over {2}} sigma ^ {2} right) dt + sigma dW}

Тогда эквивалентное уравнение Фоккера-Планка для эволюции PDF принимает вид:

{ displaystyle { partial p over { partial t}} + left ( mu - {1 over {2}} sigma ^ {2} right) { partial p over { partial x} } = {1 over {2}} sigma ^ {2} { partial ^ {2} p over { partial x ^ {2}}}, quad p (0, x) = delta (x )}

Определять { Displaystyle V = му - sigma ^ {2} / 2} и { Displaystyle D = sigma ^ {2} / 2}. Вводя новые переменные { Displaystyle xi = х-VT} и { displaystyle tau = Dt}, производные в уравнении Фоккера-Планка могут быть преобразованы как:

{ Displaystyle { begin {align} partial _ {t} p & = D partial _ { tau} pV partial _ { xi} p partial _ {x} p & = partial _ { xi } p partial _ {x} ^ {2} p & = partial _ { xi} ^ {2} p end {выровнено}}}

Приводя к новой форме уравнения Фоккера-Планка:

{ displaystyle { partial p over { partial tau}} = { partial ^ {2} p over { partial xi ^ {2}}}, quad p (0, xi) = дельта ( xi)}

Однако это каноническая форма уравнение теплопроводности. который имеет решение, данное тепловое ядро:

{ Displaystyle п ( тау, хи) = {1 над { sqrt {4 пи тау}}} ехр влево (- { хи ^ {2} над {4 тау}} верно)}

Добавление исходных переменных приводит к PDF для GBM:

{ displaystyle p (t, S) = {1 over {S { sqrt {2 pi sigma ^ {2} t}}}} exp left {- { left [ log (S / S_ {0}) - left ( mu - {1 over {2}} sigma ^ {2} right) t right] ^ {2} over {2 sigma ^ {2} t}} верно}}

При выводе дополнительных свойств GBM можно использовать SDE, решением которой является GBM, или можно использовать явное решение, данное выше. Например, рассмотрим журнал случайных процессов (Sт). Это интересный процесс, потому что в модели Блэка – Шоулза он связан с возврат журнала от стоимости акций. С помощью Лемма Ито с ж(S) = журнал (S) дает

{ displaystyle { begin {alignat} {2} d log (S) & = f '(S) , dS + { frac {1} {2}} f' '(S) S ^ {2} sigma ^ {2} , dt [6pt] & = { frac {1} {S}} left ( sigma S , dW_ {t} + mu S , dt right) - { frac {1} {2}} sigma ^ {2} , dt [6pt] & = sigma , dW_ {t} + ( mu - sigma ^ {2} / 2) , dt. end {alignat}}}

Следует, что { Displaystyle OperatorName {E} log (S_ {t}) = log (S_ {0}) + ( mu - sigma ^ {2} / 2) t}.

Этот результат также может быть получен путем применения логарифма к явному решению GBM:

{ Displaystyle { begin {alignat} {2} log (S_ {t}) & = log left (S_ {0} exp left ( left ( mu - { frac { sigma ^ { 2}} {2}} right) t + sigma W_ {t} right) right) [6pt] & = log (S_ {0}) + left ( mu - { frac { сигма ^ {2}} {2}} right) t + sigma W_ {t}. end {alignat}}}

Принятие ожидания дает тот же результат, что и выше: { Displaystyle OperatorName {E} log (S_ {t}) = log (S_ {0}) + ( mu - sigma ^ {2} / 2) t}.

Моделирование траекторий образца

# Python код для сюжетаимпорт тупой так как нпимпорт matplotlib.pyplot так как pltму = 1п = 50dt = 0.1x0 = 100нп.случайный.семя(1)сигма = нп.оранжевая(0.8, 2, 0.2)Икс = нп.exp(    (му - сигма ** 2 / 2) * dt    + сигма * нп.случайный.нормальный(0, нп.sqrt(dt), размер=(len(сигма), п)).Т)Икс = нп.vstack([нп.те(len(сигма)), Икс])Икс = x0 * Икс.шлепок(ось=0)plt.участок(Икс)plt.легенда(нп.круглый(сигма, 2))plt.xlabel("$ t $")plt.ярлык("$ x $")plt.заглавие(    "Реализации геометрического броуновского движения с различными дисперсиями. п $  mu = 1 $ ")plt.шоу()

Многовариантная версия

GBM можно расширить до случая, когда существует несколько коррелированных ценовых путей.

Каждый ценовой путь следует основному процессу

{ displaystyle dS_ {t} ^ {i} = mu _ {i} S_ {t} ^ {i} , dt + sigma _ {i} S_ {t} ^ {i} , dW_ {t} ^ {я},}

где винеровские процессы коррелированы так, что { Displaystyle OperatorName {E} (dW_ {t} ^ {i} , dW_ {t} ^ {j}) = rho _ {i, j} , dt} куда rho _ {я, я} = 1.

Для многомерного случая это означает, что

{ displaystyle operatorname {Cov} (S_ {t} ^ {i}, S_ {t} ^ {j}) = S_ {0} ^ {i} S_ {0} ^ {j} e ^ {( mu _ {i} + mu _ {j}) t} left (e ^ { rho _ {i, j} sigma _ {i} sigma _ {j} t} -1 right).}

Использование в финансах

Геометрическое броуновское движение используется для моделирования цен акций в модели Блэка – Шоулза и является наиболее широко используемой моделью поведения курса акций.[3]

Вот некоторые из аргументов в пользу использования GBM для моделирования цен на акции:

  • Ожидаемая доходность GBM не зависит от стоимости процесса (цены акций), что согласуется с тем, что мы ожидаем в реальности.[3]
  • Процесс GBM принимает только положительные значения, как и реальные цены на акции.
  • Процесс GBM демонстрирует ту же «грубость» на своем пути, что и реальные цены на акции.
  • Расчеты с процессами GBM относительно просты.

Однако GBM не является полностью реалистичной моделью, в частности, она не соответствует действительности по следующим пунктам:

  • В реальных ценах на акции волатильность со временем меняется (возможно, стохастически ), но в GBM волатильность считается постоянной.
  • В реальной жизни цены на акции часто демонстрируют скачки, вызванные непредсказуемыми событиями или новостями, но в GBM этот путь является непрерывным (без разрывов).

Расширения

В попытке сделать GBM более реалистичным в качестве модели цен на акции можно отказаться от предположения, что волатильность (сигма) постоянна. Если предположить, что волатильность детерминированный функция цены акции и времени, это называется местная волатильность модель. Если вместо этого мы предположим, что волатильность имеет собственную случайность — часто описываемую другим уравнением, управляемым другим броуновским движением, — модель называется стохастическая волатильность модель.

Смотрите также

  • Броуновская поверхность

Рекомендации

  1. ^ Росс, Шелдон М. (2014). «Вариации на тему броуновского движения». Введение в вероятностные модели (11-е изд.). Амстердам: Эльзевир. С. 612–14. ISBN  978-0-12-407948-9.
  2. ^ Эксендал, Бернт К. (2002), Стохастические дифференциальные уравнения: введение с приложениями, Springer, стр. 326, ISBN  3-540-63720-6
  3. ^ а б Халл, Джон (2009). «12,3». Опционы, фьючерсы и другие производные инструменты (7-е изд.).

внешняя ссылка

  • Геометрические модели броуновского движения для движения акций, за исключением редких случаев.
  • Моделирование геометрического броуновского движения на R и C #
  • Моделирование геометрического броуновского движения в Excel для моделирования цен на акции
  • «Интерактивное веб-приложение: случайные процессы, используемые в количественных финансах».
  • Сайт неньютоновского исчисления
Источник

Irina Done

I wand to create brownian motion model and fractional brownian motion model to predict and evaluate the stock price. Moreover, the reliability of a model i would like to check with the The average relative percentage error (ARPE) index. However, as a brand new in math lab i do not know how transfer math formulas into programming language, also during the calculation i should input data from excel.

My aim is to create graphs like that:

with formulas like these:

I will apriciate any help. Thanks!


Answers (0)

See Also

Community Treasure Hunt

Find the treasures in MATLAB Central and discover how the community can help you!

Start Hunting!

An Error Occurred

Unable to complete the action because of changes made to the page. Reload the page to see its updated state.

Источник

Понравилась статья? Поделить с друзьями:
  • Множество таблицы в excel
  • Моделирование биоритмов человека в excel скачать
  • Множество парето в excel
  • Моделирование биоритмов человека в excel практическая работа готовая
  • Множество значений функции excel