Содержание
- Процедура прогнозирования
- Способ 1: линия тренда
- Способ 2: оператор ПРЕДСКАЗ
- Способ 3: оператор ТЕНДЕНЦИЯ
- Способ 4: оператор РОСТ
- Способ 5: оператор ЛИНЕЙН
- Способ 6: оператор ЛГРФПРИБЛ
- Вопросы и ответы
Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.
Процедура прогнозирования
Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.
Способ 1: линия тренда
Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.
Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.
- Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.
- Теперь нам нужно построить линию тренда. Делаем щелчок правой кнопкой мыши по любой из точек диаграммы. В активировавшемся контекстном меню останавливаем выбор на пункте «Добавить линию тренда».
- Открывается окно форматирования линии тренда. В нем можно выбрать один из шести видов аппроксимации:
- Линейная;
- Логарифмическая;
- Экспоненциальная;
- Степенная;
- Полиномиальная;
- Линейная фильтрация.
Давайте для начала выберем линейную аппроксимацию.
В блоке настроек «Прогноз» в поле «Вперед на» устанавливаем число «3,0», так как нам нужно составить прогноз на три года вперед. Кроме того, можно установить галочки около настроек «Показывать уравнение на диаграмме» и «Поместить на диаграмме величину достоверности аппроксимации (R^2)». Последний показатель отображает качество линии тренда. После того, как настройки произведены, жмем на кнопку «Закрыть».
- Линия тренда построена и по ней мы можем определить примерную величину прибыли через три года. Как видим, к тому времени она должна перевалить за 4500 тыс. рублей. Коэффициент R2, как уже было сказано выше, отображает качество линии тренда. В нашем случае величина R2 составляет 0,89. Чем выше коэффициент, тем выше достоверность линии. Максимальная величина его может быть равной 1. Принято считать, что при коэффициенте свыше 0,85 линия тренда является достоверной.
- Если же вас не устраивает уровень достоверности, то можно вернуться в окно формата линии тренда и выбрать любой другой тип аппроксимации. Можно перепробовать все доступные варианты, чтобы найти наиболее точный.
Нужно заметить, что эффективным прогноз с помощью экстраполяции через линию тренда может быть, если период прогнозирования не превышает 30% от анализируемой базы периодов. То есть, при анализе периода в 12 лет мы не можем составить эффективный прогноз более чем на 3-4 года. Но даже в этом случае он будет относительно достоверным, если за это время не будет никаких форс-мажоров или наоборот чрезвычайно благоприятных обстоятельств, которых не было в предыдущих периодах.
Урок: Как построить линию тренда в Excel
Способ 2: оператор ПРЕДСКАЗ
Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:
=ПРЕДСКАЗ(X;известные_значения_y;известные значения_x)
«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.
«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.
«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.
Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.
При вычислении данным способом используется метод линейной регрессии.
Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.
- Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».
- Открывается Мастер функций. В категории «Статистические» выделяем наименование «ПРЕДСКАЗ», а затем щелкаем по кнопке «OK».
- Запускается окно аргументов. В поле «X» указываем величину аргумента, к которому нужно отыскать значение функции. В нашем случаем это 2018 год. Поэтому вносим запись «2018». Но лучше указать этот показатель в ячейке на листе, а в поле «X» просто дать ссылку на него. Это позволит в будущем автоматизировать вычисления и при надобности легко изменять год.
В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.
Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.
После того, как вся информация внесена, жмем на кнопку «OK».
- Оператор производит расчет на основании введенных данных и выводит результат на экран. На 2018 год планируется прибыль в районе 4564,7 тыс. рублей. На основе полученной таблицы мы можем построить график при помощи инструментов создания диаграммы, о которых шла речь выше.
- Если поменять год в ячейке, которая использовалась для ввода аргумента, то соответственно изменится результат, а также автоматически обновится график. Например, по прогнозам в 2019 году сумма прибыли составит 4637,8 тыс. рублей.
Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.
Урок: Экстраполяция в Excel
Способ 3: оператор ТЕНДЕНЦИЯ
Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:
=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.
Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.
Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.
- Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».
- Открывается окно аргументов оператора ТЕНДЕНЦИЯ. В поле «Известные значения y» уже описанным выше способом заносим координаты колонки «Прибыль предприятия». В поле «Известные значения x» вводим адрес столбца «Год». В поле «Новые значения x» заносим ссылку на ячейку, где находится номер года, на который нужно указать прогноз. В нашем случае это 2019 год. Поле «Константа» оставляем пустым. Щелкаем по кнопке «OK».
- Оператор обрабатывает данные и выводит результат на экран. Как видим, сумма прогнозируемой прибыли на 2019 год, рассчитанная методом линейной зависимости, составит, как и при предыдущем методе расчета, 4637,8 тыс. рублей.
Способ 4: оператор РОСТ
Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:
=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.
- Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».
- Происходит активация окна аргументов указанной выше функции. Вводим в поля этого окна данные полностью аналогично тому, как мы их вводили в окне аргументов оператора ТЕНДЕНЦИЯ. После того, как информация внесена, жмем на кнопку «OK».
- Результат обработки данных выводится на монитор в указанной ранее ячейке. Как видим, на этот раз результат составляет 4682,1 тыс. рублей. Отличия от результатов обработки данных оператором ТЕНДЕНЦИЯ незначительны, но они имеются. Это связано с тем, что данные инструменты применяют разные методы расчета: метод линейной зависимости и метод экспоненциальной зависимости.
Способ 5: оператор ЛИНЕЙН
Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:
=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.
- Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».
- В поле «Известные значения y», открывшегося окна аргументов, вводим координаты столбца «Прибыль предприятия». В поле «Известные значения x» вносим адрес колонки «Год». Остальные поля оставляем пустыми. Затем жмем на кнопку «OK».
- Программа рассчитывает и выводит в выбранную ячейку значение линейного тренда.
- Теперь нам предстоит выяснить величину прогнозируемой прибыли на 2019 год. Устанавливаем знак «=» в любую пустую ячейку на листе. Кликаем по ячейке, в которой содержится фактическая величина прибыли за последний изучаемый год (2016 г.). Ставим знак «+». Далее кликаем по ячейке, в которой содержится рассчитанный ранее линейный тренд. Ставим знак «*». Так как между последним годом изучаемого периода (2016 г.) и годом на который нужно сделать прогноз (2019 г.) лежит срок в три года, то устанавливаем в ячейке число «3». Чтобы произвести расчет кликаем по кнопке Enter.
Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.
Способ 6: оператор ЛГРФПРИБЛ
Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:
= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.
- В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».
- Запускается окно аргументов. В нем вносим данные точно так, как это делали, применяя функцию ЛИНЕЙН. Щелкаем по кнопке «OK».
- Результат экспоненциального тренда подсчитан и выведен в обозначенную ячейку.
- Ставим знак «=» в пустую ячейку. Открываем скобки и выделяем ячейку, которая содержит значение выручки за последний фактический период. Ставим знак «*» и выделяем ячейку, содержащую экспоненциальный тренд. Ставим знак минус и снова кликаем по элементу, в котором находится величина выручки за последний период. Закрываем скобку и вбиваем символы «*3+» без кавычек. Снова кликаем по той же ячейке, которую выделяли в последний раз. Для проведения расчета жмем на кнопку Enter.
Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.
Урок: Другие статистические функции в Excel
Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.
-
Формируемые
навыки и умения:—
освоение методики анализа статистических
данных;—
освоение методики прогнозирования
значений экономических показателей
с помощью функций и пакета анализа
MS
Excel;—
изучение и освоение методики проведения
корреляционного и регрессионного
анализа.
Теоретическая
поддержка
Наиболее
широкое распространение при построении
прогнозов развития в практике коммерческой
деятельности получили экономико-статистические
модели,
которые описывают зависимость исследуемого
экономического показателя от одного
или нескольких факторов, оказывающих
на него существенное влияние.
MS
Excel
предлагает широкий диапазон средств
для изучения экономической информации.
Множество встроенных статистических
функций (СРЗНАЧ, МЕДИАНА, МОДА и др.)
используют для проведения несложного
анализа данных.
Если
возможностей встроенных функций
недостаточно, то обращаются к
инструменту Описательная
статистика,
имеющийся в пакете «Статистический
анализ» MS
Excel.
Выходной диапазон инструмента Описательная
статистика
содержит следующие статистические
характеристики для каждой переменной
из входного диапазона: среднее, стандартная
ошибка, медиана, мода, стандартное
отклонение, дисперсия и др.
Корреляционный
анализ –
это раздел математической статистики,
посвященный изучению взаимосвязей
между случайными величинами. Основной
целью корреляционного анализа
является установление характера
влияния факторной переменной на
исследуемый показатель и определение
тесноты их связи с тем, чтобы с достаточной
степенью надежности строить модель
развития исследуемого показателя.
С
технической точки зрения проведение
корреляционного анализа сводится к
расчету коэффициентов парной корреляции,
значения которых помогут судить о
характере и тесноте связи между
исследуемым показателем и каждой
отобранной факторной переменной.
Коэффициент
парной корреляции
используется в качестве меры,
характеризующей степень линейной связи
двух переменных. Значение коэффициента
корреляции лежит в интервале от -1 (в
случае строгой линейной отрицательной
связи) до +1 (в случае строгой линейной
положительной связи). Соответственно,
положительное значение коэффициента
корреляции свидетельствует о прямой
связи между исследуемым и факторным
показателем, а отрицательное — об
обратной. Чем ближе значение коэффициента
корреляции к 1, тем теснее связь.
Качественно оценить тесноту связи
позволяет специальная шкала значений
коэффициентов корреляции, разработанная
профессором Колумбийского университета
США Чеддоком (таблица 3.1).
Таблица 3.1 — Шкала
значений коэффициентов корреляции
|
Размер |
0,1-0,3 |
0,3-0,5 |
0,5-0,7 |
0,7-0,9 |
0,9-0,99 |
|
Теснота связи |
слабая |
умеренная |
заметная |
высокая |
весьма высокая |
Для
количественной оценки взаимосвязи двух
наборов данных можно обратиться к
статистической функции КОРРЕЛ, вызывая
ее в диалоговом окне Мастера
функций.
Однако
чаще всего в экономических расчетах
приходится иметь дело сразу с несколькими
(более двух) наборами данных, взаимосвязи
которых требуется изучить. В этом случае
рассчитывают коэффициент
множественной корреляции, который
принимает значения от 0 до 1, но несет
в себе более универсальный смысл:
чем ближе его значение к 1, тем в большей
степени учтены факторы, влияющие на
зависимую переменную, тем более точной
выглядит построенная на основе отобранных
факторов модель.
В
таких случаях обращаются к инструменту
Корреляция,
содержащемуся в пакете «Статистический
анализ» Excel.
Для этого используют команду Анализ
данных из
меню Сервис.
В открывшемся окне Инструменты
анализа
вызывают инструмент Корреляция.
Регрессионный
анализ имеет
своей целью вывод, определение
(идентификацию) уравнения регрессии,
включая статистическую оценку его
параметров.
В
основе любой регрессионной модели
лежит уравнение (или система уравнений)
регрессии, которое показывает, каким
будет в среднем изменение зависимой
переменной у,
если независимые переменные х
примут конкретные значения. Это
обстоятельство позволяет применять
модель регрессии не только для анализа,
но и для прогнозирования.
Методика
построения и виды моделей тренда. Если
имеется некоторая совокупность данных,
характеризующих динамику исследуемого
показателя, то всегда можно попытаться
найти на графике наилучшую линию,
которая будет «ближайшей» к точкам
наблюдений в рамках всей их совокупности.
Чтобы составить прогноз развития
исследуемого показателя, используя
линии тренда Excel,
сначала необходимо с помощью Мастера
диаграмм
построить диаграмму его динамики на
основе базовых данных. Когда диаграмма
построена, открывается контекстное
меню, в котором содержится команда
«Добавить
линию тренда».
После ее выбора Excel
выведет окно диалога Линии
тренда,
содержащее две основные вкладки: Тип
и Параметры.
Прогнозирование
с применением функции экспоненциального
сглаживания. Для
составления прогнозов методом
экспоненциального сглаживания в Excel
предусмотрен инструмент Экспоненциальное
сглаживание.
Активизировать инструмент
Экспоненциальное
сглаживание
можно из меню Сервис
после загрузки надстройки Пакет
анализа
посредством команды Анализ
данных.
Инструмент Экспоненциальное
сглаживание
целесообразно применять для составления
прогнозов только на период, непосредственно
следующий за интервалом базовых
наблюдений.
Вычисление
скользящего среднего средствами Excel.
Инструмент
Скользящее
среднее
можно вызвать в диалоговом окне команды
Анализ данных
из меню Сервис.
Как правило, прогноз с применением
скользящего среднего составляется
на период, непосредственно следующий
за интервалом наблюдения.
Составление
линейных прогнозов средствами Excel
Функция рабочего
листа ЛИНЕЙН помогает определить
характер линейной связи между результатами
наблюдений и временем их фиксации и
дать ей математическое описание,
наилучшим образом аппроксимирующее
исходные данные.
Функция
ТЕНДЕНЦИЯ рассчитывает прогнозные
значения исследуемого показателя в
соответствии с линейным трендом.
Функция
ПРЕДСКАЗ аналогична функции ТЕНДЕНЦИЯ
за исключением того, что она определяет
лишь одну точку на линии тренда и не
может рассчитать массив, который
формирует эту линию. Поэтому ее удобно
использовать для оперативного вычисления
единичных прогнозов.
Использование
возможностей Excel
при построении нелинейных прогнозов
Функция
ЛГРФПРИБЛ работает подобно функции
ЛИНЕЙН. Различия между ними состоят
лишь в том, что ЛИНЕЙН определяет
параметры прямой линии, наилучшим
образом аппроксимирующей исходные
данные, а функция ЛГРФПРИБЛ —
экспоненциальной кривой.
В
то время как функция ЛГРФПРИБЛ рассчитывает
параметры уравнения экспоненциальной
кривой роста, которая аппроксимирует
наилучшим образом множество базовых
данных, функция РОСТ определяет точки,
лежащие на этой кривой.
Вызвать
функции ЛИНЕЙН, ТЕНДЕНЦИЯ, ПРЕДСКАЗ,
ЛГРФПРИБЛ и РОСТ можно в диалоговом
окне Мастера
функций
(категория «Статистические»), расположенном
на панели инструментов Стандартная.
Задание
1. Использование инструмента Описательная
статистика
В
рамках оценки конкурентоспособности
гастронома исследовать центральную
тенденцию и изменчивость уровня
рентабельности двадцати продовольственных
магазинов (гастрономов) области на
основе следующих собранных по ним
за отчетный период данных (таблица 3.2).
Таблица
3.2 — Данные об уровне рентабельности по
магазинам (гастрономам) области за
отчетный период
|
А |
В |
С |
D |
Е |
F |
G |
Н |
|
|
1 |
№ п/п |
Уровень |
||||||
|
2 |
1 |
0,94 |
||||||
|
3 |
2 |
1,22 |
||||||
|
4 |
3 |
0,8 |
||||||
|
5 |
4 |
1,67 |
||||||
|
6 |
5 |
1,56 |
||||||
|
7 |
6 |
0,94 |
||||||
|
8 |
7 |
1,23 |
||||||
|
9 |
8 |
0,87 |
||||||
|
10 |
9 |
1,22 |
||||||
|
11 |
10 |
1,43 |
||||||
|
12 |
11 |
0,16 |
||||||
|
13 |
12 |
0,44 |
||||||
|
14 |
13 |
0,8 |
||||||
|
15 |
14 |
1,03 |
||||||
|
16 |
15 |
0,55 |
||||||
|
17 |
16 |
1,22 |
||||||
|
18 |
17 |
1,17 |
||||||
|
19 |
18 |
0,02 |
||||||
|
20 |
19 |
0,28 |
||||||
|
21 |
20 |
1,22 |
Выполнение:
Порядок
обработки ряда данных с помощью
инструмента Описательная статистика
установлен в диалоговом окне Описательная
статистика,
которое можно вызвать из меню Сервис
через команду Анализ
данных.
Открывшееся окно диалога предлагает
пользователю определиться с набором
следующих параметров (рисунок 3.1):
1)
Входной
диапазон
(интервал) — предполагает ввод ссылки
на ячейки рабочего листа, которые
содержат анализируемые данные. Тогда
входной диапазон объединяет ячейки
В1:В21;
2)
Группирование
— требует установления переключателя
в положение «По столбцам» или «По
строкам» в зависимости от расположения
данных во входном диапазоне. Поскольку
данные об уровне рентабельности
расположены в таблице 3.2 в виде столбца,
то переключатель следует установить
в положение «По столбцам»;
3)
Метки в первой
строке/Метки в первом столбце
— позволяет определить название каждого
столбца (или строки) выходной таблицы.
Переключатель устанавливается в
положение «Метки в первой строке», если
первая строка во входном диапазоне
содержит названия столбцов. Когда в
первом столбце входного диапазона
находятся названия строк, переключатель
устанавливается в положение «Метки в
первом столбце». Если входной диапазон
не содержит меток, то необходимые
заголовки в выходном диапазоне создаются
на основе программы автоматически.
Учитывая, что в таблице 3.2 первая строка
содержит названия столбцов, переключатель
следует установить в положение «Метки
в первой строке»;
4)
Уровень
надежности
— используется, если в выходную
таблицу необходимо включить строку для
уровня надежности. Тогда в соответствующее
поле диалогового окна вводится требуемое
значение. В экономических расчетах, как
правило, значения уровня надежности
задают в размере 95 или 99 %. Например,
значение 95 % вычисляет уровень надежности
среднего со значимостью 0,05;
5)
К-й наибольший
— применяется, если в выходную таблицу
необходимо включить строку для k-го
наибольшего значения входного диапазона
данных. В соответствующем окне вводится
число k.
Если k
равно 1, эта строка будет содержать
максимум из набора данных. Например,
при оценке конкурентоспособности нашего
гастронома (пусть в таблице 3.2 он имеет
порядковый номер 7) для нас важно
проследить, попал ли уровень его
рентабельности в первую тройку наиболее
высокорентабельных предприятий, а
также, каков диапазон изменения уровня
рентабельности у трех самых
высокорентабельных магазинов. Тогда
для k-го
наибольшего в диалоговом окне надо
ввести цифру 3 (т.е. k
= 3). Это значит, что в выходной таблице,
кроме максимального значения уровня
рентабельности, будет отражен третий
за ним по убывающей размер уровня
рентабельности из всей исследуемой
совокупности данных;
6)
К-й наименьший
— применяется, если в выходную таблицу
необходимо включить строку для k-го
наименьшего значения входного диапазона
данных. В соответствующем окне вводится
число k.
Если k
равно 1, эта строка будет содержать
минимум из набора данных. Например, для
нас важно убедиться, что уровень
рентабельности исследуемого гастронома
не относится к пяти самым низким
показателям. Тогда в диалоговом окне
для k-го
наименьшего вводится цифра 5. Это значит,
что в выходной таблице, кроме минимального
значения уровня рентабельности, будет
отражен пятый за ним по возрастающей
размер уровня рентабельности;
7)
Выходной
диапазон —
предполагает введение ссылки на левую
верхнюю ячейку выходного диапазона.
Инструмент Описательная статистика
выводит два столбца сведений для
каждого набора данных. Левый столбец
содержит наименования рассчитанных
статистических величин, а правый —
их значения. В нашем случае выходная
таблица статистических характеристик
должна быть расположена, например, на
том же рабочем листе, что и входная, на
одном с ней уровне, но правее. Тогда
можно задать следующий выходной
диапазон — D1;

Новый лист
— применяют, чтобы открыть новый лист
в книге и вставить результаты анализа,
начиная с ячейки А1. При необходимости
в поле диалогового окна, расположенном
напротив соответствующего положения
переключателя, вводится имя нового
листа;
9)
Новая книга
— используется, когда необходимо
открыть новую книгу и вставить
результаты анализа в ячейку А1 на первом
листе этой книги;
10)
Итоговая
статистика
— требует установления флажка, который
означает, что в выходном диапазоне
необходимо получить полный список
статистических характеристик:
Среднее, Стандартная ошибка (среднего),
Медиана, Мода, Стандартное отклонение,
Дисперсия выборки, Эксцесс,
Асимметричность, Интервал, Минимум,
Максимум, Сумма, Счет, Наибольшее (k-e),
Наименьшее (k-e),
Уровень надежности.
Рисунок
3.1 — Окно диалога Описательная
статистика
Проведение
всех вышеобозначенных действий с данными
таблицы 3.2 позволяет получить следующую
итоговую таблицу обобщенных статистических
характеристик уровня рентабельности
исследуемых торговых предприятий
(таблица 3.3).
Таблица
3.3 — Статистическая оценка данных об
уровне рентабельности по магазинам
(гастрономам) области за отчетный год
|
А |
В |
С |
D |
Е |
|
|
1 |
№ п/п |
Уровень |
Результат |
||
|
2 |
1 |
0,94 |
|||
|
3 |
2 |
1,22 |
Среднее |
0,9385 |
|
|
4 |
3 |
0,8 |
Стандартная |
0,10199 |
|
|
5 |
4 |
1,67 |
Медиана |
0,985 |
|
|
6 |
5 |
1,56 |
Мода |
1,22 |
|
|
7 |
6 |
0,94 |
Стандартное |
0,45611 |
Продолжение
таблицы 3.3
|
А |
В |
С |
D |
Е |
|
|
1 |
№ п/п |
Уровень |
Результат |
||
|
8 |
7 |
1,23 |
Дисперсия выборки |
0,20803 |
|
|
9 |
8 |
0,87 |
Эксцесс |
-0,3986 |
|
|
10 |
9 |
1,22 |
Асимметричность |
-0,5196 |
|
|
11 |
10 |
1,43 |
Интервал |
1,65 |
|
|
12 |
11 |
0,16 |
Минимум |
0,02 |
|
|
13 |
12 |
0,44 |
Максимум |
1,67 |
|
|
14 |
13 |
0,8 |
Сумма |
18,77 |
|
|
15 |
14 |
1,03 |
Счет |
20 |
|
|
16 |
15 |
0,55 |
Наибольший(5) |
1,22 |
|
|
17 |
16 |
1,22 |
Наименьший(3) |
0,28 |
|
|
18 |
17 |
1,17 |
Уровень |
0,21347 |
|
|
19 |
18 |
0,02 |
|||
|
20 |
19 |
0,28 |
|||
|
21 |
20 |
1,22 |
Вывод:
Приведенные в таблице 3.3 данные позволяют
оперативно проследить, что уровень
рентабельности по двадцати исследуемым
предприятиям за анализируемый период
сложился в среднем 0,94+0,46
% и колебался в пределах 0,02-1,67 %.
С известной долей
условности можно предположить, что
приблизительно 68 % магазинов имели
уровень рентабельности между 0,48%
(0,94 — 0,46) и 1,4% (0,94 + 0,46).
Стандартное
отклонение (± 0,456) свидетельствует о
достаточно сильном разбросе размеров
уровня рентабельности предприятий
относительно его среднего значения,
т.е. отобранные магазины далеко не в
равной степени могут рассматриваться
в качестве конкурентов нашего предприятия.
Исследуемый
гастроном № 7, имея уровень рентабельности
1,23 %, не относится к тройке самых
высокорентабельных предприятий
(1,43-1,67 %), но, судя по медиане, принадлежит
к той половине предприятий, которая
обладает большей рентабельностью. Чаще
всего в выборке присутствует уровень
рентабельности 1,22 % (что тоже ниже
показателя нашего гастронома), а
отрицательное значение коэффициента
асимметрии свидетельствует о более
высокой плотности распределения
значений уровня рентабельности, больших
величины 1,22 % (левосторонней асимметрии).
Следовательно, по показателю рентабельности
у гастронома № 7 гораздо меньше реальных
конкурентов, чем общее количество
членов выборки. При этом рассчитанные
коэффициенты асимметрии и эксцесса
указывают на неоднородность исследуемого
массива данных и необходимость пересмотра
его состава. В этой связи для проведения
углубленного анализа реальных
конкурентов магазина № 7 по избранному
признаку целесообразно пересмотреть
и урезать выборку.
Задание
2. Проведение корреляционного анализа
Провести
корреляционный анализ товарооборота
на основе информации, подготовленной
с помощью электронных таблиц Excel
(таблица 3.4).
Для
проведения корреляционного анализа
объема товарооборота (исследуемый
показатель) могут быть отобраны следующие
факторы:
— товарооборачиваемость
в днях;
— удельный вес
торговой площади в общей площади
предприятия;
—
удельный вес торгово-оперативных
работников в их общей численности;
—
удельный вес товаров с высоким (в рамках
установленного действующим
законодательством предельного уровня)
уровнем торговых надбавок.
Таблица
3.4 — Исходные данные для проведения
корреляционного анализа
|
А |
В |
С |
D |
Е |
F |
|
|
1 |
||||||
|
2 |
Порядковый |
Объем |
Оборачиваемость дни |
Удельный |
Удельный |
Удельный |
|
3 |
1 |
28415 |
43,5 |
44,0 |
67,7 |
22,5 |
|
4 |
2 |
28231 |
43,0 |
44,0 |
67,7 |
18,0 |
|
5 |
3 |
29783 |
43,0 |
44,0 |
70,2 |
24,9 |
|
6 |
4 |
30969 |
43,5 |
47,8 |
70,0 |
24,4 |
|
7 |
5 |
30494 |
43,0 |
47,8 |
68,0 |
20,6 |
|
8 |
6 |
29757 |
42,5 |
47,8 |
68,0 |
19,0 |
|
9 |
7 |
30850 |
43,0 |
49,0 |
70,2 |
22,2 |
|
10 |
8 |
31325 |
41,5 |
49,0 |
70,0 |
21,6 |
|
11 |
9 |
31359 |
42,0 |
50,3 |
70,0 |
19,8 |
|
12 |
10 |
31610 |
41,5 |
50,3 |
70,0 |
19,7 |
|
13 |
11 |
32366 |
40,5 |
50,3 |
70,0 |
23,1 |
|
14 |
12 |
33313 |
40,0 |
50,3 |
70,0 |
23,9 |
|
15 |
13 |
33508 |
40,0 |
50,3 |
68,0 |
21,2 |
|
16 |
14 |
33374 |
39,0 |
50,3 |
68,0 |
20,4 |
|
17 |
15 |
34811 |
39,5 |
50,3 |
70,0 |
24,2 |
|
18 |
16 |
36046 |
39,0 |
49,0 |
70,0 |
26,5 |
Выполнение:
Для
количественной оценки взаимосвязи
объема данных обращаются к инструменту
Корреляция,
содержащемуся в пакете «Статистический
анализ» Excel.
Для этого используют команду Анализ
данных из
меню Сервис.
В открывшемся окне Инструменты
анализа
вызывают инструмент Корреляция,
диалоговое окно которого предлагает
пользователю определить следующие
параметры (рисунок 3.2):
1)
Входной
диапазон (интервал)
— предполагает ввод ссылки на ячейки
рабочего листа, которые содержат
анализируемые данные. Для данных
таблицы 3.4 входной диапазон имеет
вид — B2:F18;
2)
Группирование
— требует установления переключателя
в положение «По столбцам» или «По
строкам» в зависимости от расположения
данных во входном диапазоне. Поскольку
анализируемые наборы данных расположены
в таблице 3.4 в виде столбцов, то
переключатель следует установить в
положение «По столбцам»;
3)
Метки в первой
строке/Метки в первом столбце
— позволяет определить название каждого
столбца (или строки) выходной таблицы.
Переключатель устанавливается в
положение «Метки в первой строке», если
первая строка во входном диапазоне
содержит названия столбцов. Когда в
первом столбце входного диапазона
находятся названия строк, переключатель
устанавливается в положение «Метки в
первом столбце». Если входной диапазон
не содержит меток, то необходимые
заголовки в выходном диапазоне создаются
на основе программы автоматически.
Учитывая, что в таблице 3.4 первая строка
содержит названия столбцов, переключатель
следует установить в положение «Метки
в первой строке»;
4)
Выходной
диапазон —
предполагает введение ссылки на левую
верхнюю ячейку выходного диапазона.
Например, если необходимо, чтобы выходная
таблица располагалась на том же рабочем
листе, что и входная, и непосредственно
под ней, то можно задать выходной диапазон
ячейкой А21;
5)
Новый лист
— применяют, чтобы открыть новый лист
в книге и вставить результаты анализа,
начиная с ячейки А1. При необходимости
в поле диалогового окна, расположенном
напротив соответствующего положения
переключателя, вводится имя нового
листа;
6)
Новая книга
— используется, когда необходимо
открыть новую книгу и вставить
результаты анализа в ячейку А1 на первом
листе этой книги.
Рисунок
3.2 — Окно диалога Корреляция
Проведение
всех обозначенных действий с данными
таблицы 3.4 позволяет получить матрицу
значений парных коэффициентов
корреляции, рассчитанных для всех
возможных пар переменных без учета
влияния других факторов (таблица 3.5).
Поскольку коэффициент корреляции двух
наборов данных не зависит от
последовательности их обработки, то
выходная область занимает только
половину предназначенного для нее
места. Ячейки выходного диапазона,
имеющие совпадающие координаты строк
и столбцов, содержат значение 1, так как
каждая строка или столбец во входном
диапазоне полностью коррелирует с самим
собой.
Таблица
3.5 — Матрица парных коэффициентов
корреляции
|
А |
В |
С |
D |
E |
F |
|
|
21 |
Объем товарооборота, |
Оборачиваемость |
Удельный вес |
Удельный вес |
Удельный вес |
|
|
22 |
Объем товарооборота, |
1 |
||||
|
23 |
Оборачиваемость |
-0,90538094 |
1 |
|||
|
24 |
Удельный вес |
0,75014268 |
-0,690531 |
1 |
||
|
25 |
Удельный вес |
0,38663194 |
-0,153964 |
0,3726409 |
1 |
|
|
26 |
Удельный вес |
0,50878765 |
-0,276455 |
0,0374572 |
0,580400123 |
1 |
Вывод:
На основе приведенной матрицы можно
содержательно оценить связь значений
объема товарооборота с каждым из
отобранных факторов и выбрать наиболее
значимые из них для включения в модель.
Так, полученные коэффициенты корреляции,
характеризующие тесноту связи объема
товарооборота с отобранными факторами
(см. столбец В21:В26 таблицы 3.5), составляют
соответственно: -0,905 для фактора
«оборачиваемость товаров»; 0,750 для
фактора «удельный вес торговой площади
в общей»; 0,509 для фактора «удельный вес
товаров с высокими торговыми надбавками»;
0,387 для фактора «удельный вес
торгово-оперативного персонала в общей
численности работников». Согласно шкале
Чеддока (таблица 3.1), для данного торгового
предприятия показатель объема
товарооборота имеет весьма высокую
тесноту связи с фактором «оборачиваемость
товаров» и высокую — с фактором
«удельный вес торговой площади в
общей». Значение коэффициента корреляции,
рассчитанное для товарооборота и фактора
«удельный вес торгово-оперативного
персонала», свидетельствует о слабо
выраженной линейной связи между
этими показателями.
Знак
«-» перед коэффициентом корреляции в
ячейке В23 означает, что между объемом
товарооборота и размером товарооборачиваемости
в днях имеет место обратная связь, т.е.
при росте количества дней одного оборота
товарного запаса предприятия в днях
(иными словами — замедлении
товарооборачиваемости) объем его
реализации при прочих равных условиях
будет падать. С остальными факторами
объем товарооборота находится в
прямой зависимости.
Задание
3. Прогнозирование развития показателей
с помощью линии тренда Excel
Составить
прогноз товарооборота торгового
предприятия на 17-й месяц (см. данные
таблицы 3.6) с помощью команды Добавить
линию тренда.
Таблица 3.6 — Сведения
о динамике товарооборота торгового
предприятия
|
А |
В |
С |
D |
E |
F |
|
|
1 |
||||||
|
2 |
Порядковый номер |
Объем |
||||
|
3 |
1 |
28415 |
||||
|
4 |
2 |
28231 |
||||
|
5 |
3 |
29783 |
||||
|
6 |
4 |
30969 |
||||
|
7 |
5 |
30494 |
||||
|
8 |
6 |
29757 |
||||
|
9 |
7 |
30850 |
||||
|
10 |
8 |
31325 |
||||
|
11 |
9 |
31359 |
||||
|
12 |
10 |
31610 |
||||
|
13 |
11 |
32366 |
||||
|
14 |
12 |
33313 |
||||
|
15 |
13 |
33508 |
||||
|
16 |
14 |
33374 |
||||
|
17 |
15 |
34811 |
||||
|
18 |
16 |
36046 |
||||
|
19 |
Итого |
Выполнение:
Чтобы
составить прогноз развития исследуемого
показателя, используя линии тренда
Excel,
сначала необходимо с помощью Мастера
диаграмм
построить диаграмму (График)
его динамики на основе базовых данных
(ячейки В3:В19 таблицы 3.6).
Когда
диаграмма построена, необходимо щелкнуть
правой клавишей мыши на любой точке
графика, чтобы открылось контекстное
меню, в котором содержится команда
Добавить
линию тренда.
После ее выбора Excel
выведет окно диалога Линии
тренда,
содержащее две основные вкладки: Тип
и Параметры.
Вкладка
Тип
помогает пользователю выбрать тип линии
тренда, которая будет аппроксимировать
исходные данные. В диалоговом окне
предлагается пять типов линий тренда.
Для их построения Excel
использует модели следующего вида:
—
линейную (у
= mх
+ b);
—
полиномиальную (у
= b
+ m1x
+ m2x2
+…+ m6х6);
—
логарифмическую (у
= m
· ln
x
+ b);
—
экспоненциальную (у
= m
· еb·x);
—
степенную (у
= m
· хb).
После
задания типа линии тренда выделяют
вкладку Параметры.
Откроется ее окно диалога, в котором
пользователь определяет следующие
важные моменты:
1)
количество прогнозируемых периодов и
направление прогноза: вперед или назад;
2)
когда выбрана линейная, полиномиальная
или экспоненциальная кривая роста,
то в поле Пересечение
кривой с осью у в точке 0
задается ее у-пересечение:
если данное поле обозначить флажком,
то Excel
будет искать лучшее уравнение кривой,
которая на координатной плоскости
обязательно должна пройти через
начало координат;
3)
через установку флажка в соответствующих
полях окна диалога пользователь
решает, отражать ли на выходной диаграмме
уравнение, на основе которого была
построена линия тренда, и размер
квадрата коэффициента корреляции r2,
характеризующий качество аппроксимации.
C
помощью команды Добавить
линию тренда
составим сразу пять различных вариантов
прогноза товарооборота торгового
предприятия на 17-й месяц и при этом
по r2
оценить общее качество моделей, на
основе которых они были получены.
Используя
возможности Excel
по созданию в ячейках рабочего листа
формул, с помощью приведенных на графиках
уравнений кривых роста рассчитаем
значения прогноза товарооборота на
17-й месяц (таблица 3.7).
Таблица
3.7 — Прогноз товарооборота на 17-й месяц
|
Тип |
Формула |
Прогноз |
|
Линейная |
=437,43*17+27920 |
35356,3 |
|
Логарифмическая |
=2429,4*ln(17)+26981 |
33864,0 |
|
Полиномиальная |
=3,9737*17^3-88,245*17^2+925,09*17+27432 |
1 37178,5 |
|
Степенная |
=27215*17^0,0774 |
33887,9 |
|
Экспоненциальная |
=28081*е^(0,0138*17) |
35490,0 |
|
Рисунок |
Рисунок |
|
Рисунок |
Рисунок |
|
Рисунок |
Рисунок |
Вывод:
Приведенные на рисунках 3.3–3.8 графики
динамики товарооборота свидетельствуют,
что наибольшая степень приближения
линии тренда к базовым данным достигнута
в случае полиномиальной кривой роста
3-й степени (см. рисунок 3.6, r2
= 0,9519), наименьшая — в случае логарифмической
кривой (см. рисунок 3.5, r2
= 0,7779).
Задание
4. Прогнозирование с применением функции
экспоненциального сглаживания
Составить
прогноз товарооборота торгового
предприятия на основе данных таблицы
3.6 с помощью инструмента Экспоненциальное
сглаживание.
Выполнение:
Активизировать
инструмент Экспоненциальное
сглаживание
можно из меню Сервис
после загрузки надстройки Пакет
анализа
посредством команды Анализ
данных.
Открывшееся окно диалога Экспоненциальное
сглаживание
предлагает пользователю определиться
со следующими параметрами (рисунок
3.9):
1)
Входной
диапазон —
требует ссылки на ячейки, содержащие
данные об исследуемом показателе. Этот
диапазон должен состоять из одного
столбца или одной строки и содержать
данные как минимум в четырех ячейках.
В нашем примере параметр Входной
диапазон
включает ячейки В2:В19 (таблица 3.8);
2)
Фактор
затухания
— это корректировочный фактор,
минимизирующий нестабильность
совокупности данных. Он может иметь
значения в пределах от 0 до 1. По умолчанию
пользователя Excel
самостоятельно принимает значение
фактора затухания равным 0,3. В нашем
примере для параметра Фактор
затухания
введем значение 0,1;
3)
Метки
— требует установки флажка, если первая
строка или первый столбец входного
диапазона содержит заголовки (название
столбца или строки). В нашем примере
установим флажок для параметра Метки;
4)
Выходной
диапазон —
предполагает ссылку на верхнюю ячейку
выходного диапазона. В нашем примере
установим верхнюю ячейку Выходного
диапазона – С3;
5)
Вывод графика
— требует установки флажка, если
пользователю, кроме значения прогноза,
необходимо получить встроенную
диаграмму динамики фактических и
расчетных значений;
6)
Стандартные
погрешности
— требует установки флажка, если
пользователю для проведения оценки
качества прогнозов необходимо
включить в выходной диапазон столбец
со стандартными погрешностями e(t).
Рисунок 3.9 — Окно
диалога «Экспоненциальное сглаживание»
В
результате работы инструмента
Экспоненциальное
сглаживание
получаем следующие сглаженные показатели
товарооборота (см. столбец С таблицы
3.8), в том числе прогноз на 17-й месяц —
35 908 ден. ед.
Таблица
3.8 — Расчет прогноза товарооборота с
помощью инструмента Экспоненциальное
сглаживание
|
А |
В |
С |
|||||||
|
1 |
|||||||||
|
2 |
Порядковый |
Объем |
Экспоненциальное |
||||||
|
3 |
1 |
28415 |
#Н/Д |
|
|||||
|
4 |
2 |
28231 |
28415 |
||||||
|
5 |
3 |
29783 |
28249,4 |
||||||
|
6 |
4 |
30969 |
29629,6 |
||||||
|
7 |
5 |
30494 |
30835,1 |
||||||
|
8 |
6 |
29757 |
30528,1 |
||||||
|
9 |
7 |
30850 |
29834,1 |
||||||
|
10 |
8 |
31325 |
30748,4 |
||||||
|
11 |
9 |
31359 |
31267,3 |
||||||
|
12 |
10 |
31610 |
31349,8 |
||||||
|
13 |
11 |
32366 |
31584,0 |
||||||
|
14 |
12 |
33313 |
32287,8 |
||||||
|
15 |
13 |
33508 |
33210,5 |
||||||
|
16 |
14 |
33374 |
33478,2 |
||||||
|
17 |
15 |
34811 |
33384,4 |
||||||
|
18 |
16 |
36046 |
34668,3 |
||||||
|
19 |
17 |
35908,2 |
Задание
5. Прогнозирование с применением метода
скользящего среднего
5.1
При исследовании спроса на реализуемый
товар-новинку в фирменном магазине
в течение 20 дней было зафиксировано
определенное количество поступивших
на него жалоб со стороны покупателей
(таблица 3.9, ячейки В2:В21). Выяснить,
существует ли какая-либо тенденция
поступления жалоб с помощью инструмента
Скользящее
среднее.
Выполнение:
Инструмент
Скользящее
среднее
можно вызвать в диалоговом окне команды
Анализ данных
из меню Сервис.
Открывшееся окно диалога предлагает
пользователю задать следующие
основные параметры (рисунок 3.10):
1)
Входной
диапазон (интервал) — это
диапазон ячеек В2:В21 (см. таблицу 3.9);
2)
Интервал
усреднения
примем равным 3, т.е. будем определять
трехдневное скользящее среднее;
3)
Выходной
диапазон (интервал)
задаем именем ячейки С2. При этом
следует иметь в виду, что первые несколько
ячеек выходного диапазона будут всегда
содержать значение #Н/Д. Количество
таких ячеек равно значению выбранного
интервала усреднения минус один. Эта
ситуация связана с недостаточным
количеством базовых данных для вычисления
среднего значения первых результатов
наблюдений;
4)
Вывод графика
— требует установки флажка, который
означает, что пользователю, кроме
выходного массива (в нашем примере
— в столбце С), необходимо получить
график, который наглядно демонстрирует
линию тренда скользящего среднего.
Если флажок установлен, то Excel
самостоятельно создает график,
включающий две линии: одна из них строится
на основе базовых данных, другая — по
числовым значениям скользящего среднего.
Рисунок
3.10 — Окно диалога Скользящее
среднее
Таблица
3.9 — Оценка тенденции поведения показателей
исследуемого динамического ряда методом
скользящего среднего
|
А |
В |
С |
||
|
1 |
День |
Количество |
|
|
|
2 |
1 |
10 |
#Н/Д |
|
|
3 |
2 |
11 |
#Н/Д |
|
|
4 |
3 |
10 |
10,333 |
|
|
5 |
4 |
12 |
11 |
|
|
6 |
5 |
13 |
11,667 |
|
|
7 |
6 |
13 |
12,667 |
|
|
8 |
7 |
13 |
13 |
|
|
9 |
8 |
10 |
12 |
|
|
10 |
9 |
16 |
13 |
|
|
11 |
10 |
9 |
11,667 |
|
|
12 |
11 |
15 |
13,333 |
|
|
13 |
12 |
10 |
11,333 |
|
|
14 |
13 |
15 |
13,333 |
|
|
15 |
14 |
17 |
14 |
|
|
16 |
15 |
12 |
14,667 |
|
|
17 |
16 |
15 |
14,667 |
|
|
18 |
17 |
14 |
13,667 |
|
|
19 |
18 |
18 |
15,667 |
|
|
20 |
19 |
19 |
17 |
|
|
21 |
20 |
15 |
17,333 |
Вывод:
Приведенные в столбце С таблицы 3.9
выходные значения свидетельствуют (и
это наглядно подтверждает рисунок), что
показатель скользящего среднего имеет
тенденцию к увеличению. В данном
случае выявленная тенденция вызывает
опасения относительно дальнейшей судьбы
товара и требует принятия адекватных
мер со стороны его производителя.
5.2
Составить прогноз объема товарооборота
по торговому предприятию на основе
данных таблицы 3.6, используя расчет
скользящего среднего.
Выполнение:
—
на отдельном рабочем листе Excel
составим разработочную таблицу следующего
вида (таблица 3.10);
Таблица
3.10 — Методика составления прогноза
товарооборота на основе скользящего
среднего средствами Excel
(разработочная таблица)
|
А |
В |
С |
D |
Е |
|
|
1 |
|||||
|
2 |
Порядковый |
Объем |
Цепные |
Показатели |
Среднее |
|
3 |
1 |
28415 |
|||
|
4 |
2 |
28231 |
|||
|
5 |
3 |
29783 |
|||
|
6 |
4 |
30969 |
|||
|
7 |
5 |
30494 |
|||
|
8 |
6 |
29757 |
|||
|
9 |
7 |
30850 |
|||
|
10 |
8 |
31325 |
|||
|
11 |
9 |
31359 |
|||
|
12 |
10 |
31610 |
|||
|
13 |
11 |
32366 |
|||
|
14 |
12 |
33313 |
|||
|
15 |
13 |
33508 |
|||
|
16 |
14 |
33374 |
|||
|
17 |
15 |
34811 |
|||
|
18 |
16 |
36046 |
—
учитывая, что объем товарооборота
представляет собой абсолютный стоимостный
показатель, для расчета скользящего
среднего создадим в разработочной
таблице колонку относительных величин,
характеризующих динамику товарооборота
предприятия — цепных темпов прироста
(вводим в ячейку С4 формулу =В4/В3*100-100 и
копируем ее в ячейки С5:С18) (столбец С
таблицы 3.10);
—
выравнивание динамического ряда,
состоящего из 15 цепных темпов прироста
товарооборота, проведем, используя
интервал усреднения, равный, например,
5. Для расчета показателей выровненного
ряда (столбец D
таблицы 3.10) воспользуемся другим способом
создания скользящего среднего в Excel,
т.е. прямым введением формулы в
соответствующую ячейку рабочего
листа. Так, чтобы получить пятимесячное
скользящее среднее цепных темпов
прироста, в ячейку D8
таблицы 10 вводится формула =СРЗНАЧ(С4:С8).
Затем эта формула с помощью средства
Автозаполнение
копируется и вставляется в ячейки
D9:D18;
—
для составления прогноза товарооборота
на 17-й месяц в таблице 3.10 необходимо
занести еще три формулы: расчета среднего
изменения темпов его прироста: =(D18-D8)/10
(ячейка Е18), расчета прогнозируемого
цепного темпа прироста на 17-й месяц:
=D18+2*E18
(ячейка С20), расчета прогнозируемого
объема товарооборота: B18*(C20+100)/100
(ячейка В20). Результатом всех проведенных
операций становится итоговая таблица
3.11, содержащая все промежуточные
элементы и значения единой цепи
составления прогноза товарооборота.
Таблица
3.11 — Прогноз товарооборота на основе
скользящего среднего средствами Excel
(итоговая таблица)
|
А |
В |
С |
D |
Е |
|
|
1 |
|||||
|
2 |
Порядковый |
Объем |
Цепные |
Показатели |
Среднее |
|
3 |
1 |
28415 |
|||
|
4 |
2 |
28231 |
-0,648 |
#Н/Д |
|
|
5 |
3 |
29783 |
5,498 |
#Н/Д |
|
|
6 |
4 |
30969 |
3,982 |
#Н/Д |
|
|
7 |
5 |
30494 |
-1,534 |
#Н/Д |
|
|
8 |
6 |
29757 |
-2,417 |
0,976 |
|
|
9 |
7 |
30850 |
3,673 |
1,840 |
|
|
10 |
8 |
31325 |
1,540 |
1,049 |
|
|
11 |
9 |
31359 |
0,109 |
0,274 |
|
|
12 |
10 |
31610 |
0,800 |
0,741 |
|
|
13 |
11 |
32366 |
2,392 |
1,703 |
|
|
14 |
12 |
33313 |
2,926 |
1,553 |
|
|
15 |
13 |
33508 |
0,585 |
1,362 |
|
|
16 |
14 |
33374 |
-0,400 |
1,261 |
|
|
17 |
15 |
34811 |
4,306 |
1,962 |
|
|
18 |
16 |
36046 |
3,548 |
2,193 |
0,122 |
|
19 |
Прогноз |
||||
|
20 |
17 |
36924 |
2,436 |
Задание
6. Использование функции ЛИНЕЙН для
создания модели тренда
Составить
прогноз товарооборота торгового
предприятия по данным таблицы 3.6 с
помощью функции ЛИНЕЙН.
Выполнение:
Функция
рабочего листа ЛИНЕЙН помогает определить
характер линейной связи между результатами
наблюдений и временем их фиксации и
дать ей математическое описание,
наилучшим образом аппроксимирующее
исходные данные. Для построения трендовой
модели она использует уравнение вида
у = mх
+ b,
где у
— исследуемый показатель; х
= t
— временной
тренд; b,
m
— параметры уравнения, характеризующие
соответственно у-пересечение
и наклон линии тренда.
Вызвать
функцию ЛИНЕЙН можно в диалоговом окне
Мастера
функций
(категория «Статистические»),
расположенном на панели инструментов
Стандартная.
Используя
метод наименьших квадратов, функция
ЛИНЕЙН создает массив значений, который
описывает искомую модель тренда.
Учитывая, что создается массив значений,
функция должна задаваться пользователем
в виде формулы массива. Поэтому перед
началом работы с ЛИНЕЙН необходимо
на рабочем листе выделить диапазон
ячеек, достаточный для размещения
создаваемого ею массива значений. Так,
для прогнозирования товарооборота по
данным таблицы 3.6 обозначим ячейками
E10:F14
диапазон для формирования выходного
массива (таблица 3.12). После того, как
выделен выходной диапазон и пользователь
определился с аргументами функции
посредством диалогового окна ЛИНЕЙН,
следует нажать на клавиатуре кнопки
Ctrl+Shift+Enter.
Таблица 3.12 — Расчет
и оценка линейной модели тренда с помощью
функции ЛИНЕЙН
|
A |
B |
C |
D |
E |
F |
|
|
1 |
||||||
|
2 |
Порядковый |
Объем |
||||
|
3 |
1 |
28415 |
||||
|
4 |
2 |
28231 |
||||
|
5 |
3 |
29783 |
||||
|
6 |
4 |
30969 |
||||
|
7 |
5 |
30494 |
||||
|
8 |
6 |
29757 |
||||
|
9 |
7 |
30850 |
||||
|
10 |
8 |
31325 |
Линейная |
437,425 |
27920,1 |
|
|
11 |
9 |
31359 |
Статистика |
34,958505 |
338,033 |
|
|
12 |
10 |
31610 |
0,917921 |
644,603 |
||
|
13 |
11 |
32366 |
156,56746 |
14 |
||
|
14 |
12 |
33313 |
65055814 |
5817182 |
||
|
15 |
13 |
33508 |
||||
|
16 |
14 |
33374 |
||||
|
17 |
15 |
34811 |
||||
|
18 |
16 |
36046 |
Функция
ЛИНЕЙН имеет четыре аргумента (рисунок
3.11):
1)
Известные
значения у
— это множество уже известных значений
исследуемого показателя, на основе
которых будет производиться оценка
параметров уравнения тренда. Так, при
составлении прогноза товарооборота
торгового предприятия по данным
таблицы 3.6 известные значения у
представлены в виде столбца и находятся
в ячейках В3:В18;
2)
Известные
значения х
— при построении трендовой модели
представляют собой временной ряд,
соответствующий по размерам первому
аргументу. В нашем примере он находится
в ячейках А3:А18 таблицы 3.6 и отражает
порядковые номера месяца;
3)
Конст
— логическое значение, которое указывает
на необходимость расчета параметра b
(свободного члена) при построении модели
тренда. Если Конст
имеет значение ИСТИНА, то параметр b
вычисляется. Если Конст
имеет значение ЛОЖЬ, то параметр b
принимается равным нулю;
4)
Статистика
— логическое значение, которое указывает
на необходимость отражения на рабочем
листе дополнительной статистической
информации, позволяющей судить о качестве
построенной модели. Если этот аргумент
имеет значение ЛОЖЬ или ссылка на
него отсутствует, то функция ЛИНЕЙН не
рассчитывает статистические характеристики.
Если Статистика
задана значением ИСТИНА, то массив,
создаваемый функцией, содержит значения
следующих статистических величин
(таблица 3.13).
Таблица
3.13 — Значения статистических величин
функции ЛИНЕЙН
|
Стандартная |
Стандартная |
|
Квадрат |
Стандартная |
|
F-критерий |
Степень |
|
Сумма |
Остаточная |
Рисунок 3.11 — Окно
диалога функции ЛИНЕЙН
Вывод:
Число в ячейке Е10 представляет собой
наклон линии тренда (m
= 437,425), а
число в ячейке F10
— это у-пересечение
прямой линии (b
= 27920,1). Можно
составить линейную модель, описывающую
динамику товарооборота торгового
предприятия, которая принимает следующий
вид:
Y
= 27920,1 + 437,425x,
где
х = t
— порядковый номер месяца.
В
нашем примере коэффициент корреляции
(см. таблицу 3.12, ячейка Е12) r2
= 0,9179, что
указывает на высокое качество линейной
модели.
В
нашем примере Fкрит
находится по таблице F-распределения
на пересечении столбца 1 (так как в модели
только одна переменная х
— временной тренд) и строки 14 (см. ячейку
F13
таблицы 3.12). В приложении А находим для
распределения Фишера с (1;14) степенями
свободы, что при 5%-м уровне значимости
(доверительная вероятность 95 %) табличное
значение Fкp
= 4,6. Поскольку
F
= 156,567 > 4,6
(см. ячейку Е13 таблицы 3.12), то полученная
модель тренда полезна для использования
в прогнозировании.
Рассчитаем
значения t-статистики
для оценки параметров m
и b
построенной нами модели на основе данных
таблицы 3.12:
Табличное
значение tкрит
для уровня значимости 0,05 (доверительная
вероятность 0,95) с df
= 14 степенями свободы равно 2,145 (см.
приложение Б). Поскольку |tm|
> 2,145, |tf|
> 2,145, статистическая значимость
параметров построенной модели признается
весьма высокой.
Задание
7. Использование функции ТЕНДЕНЦИЯ для
построения прогнозов
Составить
прогноз товарооборота торгового
предприятия по данным таблицы 3.6 с
помощью функции ТЕНДЕНЦИЯ.
Выполнение:
Функция
ТЕНДЕНЦИЯ рассчитывает прогнозные
значения исследуемого показателя в
соответствии с линейным трендом. Она с
помощью метода наименьших квадратов
аппроксимирует прямой линией массивы
известных значений у
и известных
значений х,
а также определяет точки, лежащие на
этой линии, и прогнозирует значения
у
для вновь заданных значений х.
Но при этом ТЕНДЕНЦИЯ не приводит
математического описания и
статистических характеристик самой
модели тренда.
Вызвать
функцию ТЕНДЕНЦИЯ можно из окна диалога
Мастера
функций,
расположенного на панели Стандартная,
в категориях – Статистические.
ТЕНДЕНЦИЯ имеет четыре аргумента
(рисунок 3.12):
1)
Известные
значения у;
2)
Известные
значения х;
3)
Новые значения
х;
4)
Конст.
Первый,
второй и четвертый аргументы формируются
аналогично тому, как это происходит при
работе с функцией ЛИНЕЙН (соответственно
первым, вторым и третьим ее аргументом).
Третий
аргумент — это определяемые самим
пользователем значения х
(в модели тренда — времени t),
для которых ТЕНДЕНЦИЯ рассчитывает по
найденной модели соответствующие
значения у.
Так, при прогнозировании товарооборота
торгового предприятия с помощью функции
ТЕНДЕНЦИЯ на рабочем листе выделим
диапазон ячеек С3:С21, где ячейки С3:С18 —
для отражения значений каждой точки
базового интервала времени на линии
тренда (таблица 3.14), а ячейки С19:С21 — для
перспективной оценки товарооборота на
три ближайших месяца. Аргумент Новые
значения х
в этом случае будет задан ячейками
А3:А21, и формируется следующая формула
массива: =ТЕНДЕНЦИЯ(В3:В18;А3:А18;А3:А21).
По
окончании работы с окном диалога
ТЕНДЕНЦИЯ необходимо нажать на клавиатуре
кнопки Ctrl
+ Shift
+ Enter.
В выходном диапазоне (см. столбец С
таблицы 3.14) функция ТЕНДЕНЦИЯ
моментально отразит все рассчитанные
на основе линейной модели тренда значения
у,
соответствующие заданному аргументу
Новые значения
х (т.е. ячейкам
А3:А21). Из них значения, находящиеся в
ячейках С3:С18, будут относиться к базовому
временному интервалу, а в ячейках С19:С21
— содержать прогноз товарооборота на
17-й, 18-й и 19-й месяцы.
Рисунок 3.12 — Окно
диалога функции ТЕНДЕНЦИЯ
Таблица
3.14 — Расчет прогноза товарооборота с
помощью функции ТЕНДЕНЦИЯ
|
А |
В |
С |
|
|
1 |
|||
|
2 |
Порядковый |
Объем |
Тенденция |
|
3 |
1 |
28415 |
28358 |
|
4 |
2 |
28231 |
28795 |
|
5 |
3 |
29783 |
29232 |
|
6 |
4 |
30969 |
29670 |
|
7 |
5 |
30494 |
30107 |
|
8 |
6 |
29757 |
30545 |
|
9 |
7 |
30850 |
30982 |
|
10 |
8 |
31325 |
31419 |
|
11 |
9 |
31359 |
31857 |
|
12 |
10 |
31610 |
32294 |
|
13 |
11 |
32366 |
32732 |
|
14 |
12 |
33313 |
33169 |
|
15 |
13 |
33508 |
33607 |
|
16 |
14 |
33374 |
34044 |
|
17 |
15 |
34811 |
34481 |
|
18 |
16 |
36046 |
34919 |
|
19 |
17 |
35356 |
|
|
20 |
18 |
35794 |
|
|
21 |
19 |
36231 |
Задание
8. Использование функции ПРЕДСКАЗ для
построения прогнозов
Составить
прогноз товарооборота торгового
предприятия по данным таблицы 3.6 с
помощью функции ПРЕДСКАЗ.
Выполнение:
Функция
ПРЕДСКАЗ определяет лишь одну точку на
линии тренда и не может рассчитать
массив, который формирует эту линию.
Поэтому ее удобно использовать для
оперативного вычисления единичных
прогнозов. Функцию ПРЕДСКАЗ можно
вызвать в диалоговом окне Мастера
функций, в
категориях – Статистические,
она имеет только три аргумента (рисунок
3.13):
1)
X
— это точка данных (числовое значение),
для которой необходимо рассчитать
прогноз исследуемого показателя.
Так,
при прогнозировании товарооборота на
17-й,
18-й и 19-й месяцы
(таблица 3.15) в качестве аргумента X
определим ячейки А19:А21;
2)
Известные
значения у
(прогнозируемого показателя). В нашем
примере их можно задать в виде диапазона
ячеек В3:В18 (см. таблицу 3.15);
3)
Известные
значения х
(времени t).
Этот аргумент должен совпадать по
размерам с массивом Известные
значения у.
Этот аргумент в нашем примере охватывает
ячейки А3:А18.
Соответственно
обозначенным в окне диалога ПРЕДСКАЗ
аргументам формируется формула следующего
вида: =ПРЕДСКАЗ(А19:А21;В3:В18;А3:А18).
По
окончании работы с окном диалога ПРЕДСКАЗ
необходимо нажать на клавиатуре кнопки
Ctrl
+ Shift
+ Enter.
Рисунок 3.13 — Окно
диалога функции ПРЕДСКАЗ
Таблица
3.15 — Расчет прогноза товарооборота с
помощью функции ПРЕДСКАЗ
-
А
В
С
1
2
Порядковый
номер месяцаОбъем
товарооборота, ден. ед.3
1
28415
4
2
28231
5
3
29783
6
4
30969
7
5
30494
8
6
29757
Продолжение таблицы
3.15
-
А
В
С
Порядковый
номер месяцаОбъем
товарооборота, ден. ед.9
7
30850
10
8
31325
11
9
31359
12
10
31610
13
11
32366
14
12
33313
15
13
33508
16
14
33374
17
15
34811
18
16
36046
19
17
35356
ПРЕДСКАЗ
20
18
35794
21
19
36231
Задание
9. Анализ нелинейных процессов с помощью
функции ЛГРФПРИБЛ
Рассчитать
параметры модели тренда и дать ей
качественную оценку с помощью функции
ЛГРФПРИБЛ для базовых данных о динамике
товарооборота предприятия, приведенных
в таблице 3.6.
Выполнение:
Функция
ЛГРФПРИБЛ определяет параметры
экспоненциальной кривой, наилучшим
образом аппроксимирующей исходные
данные. Эта функция относится к категории
«Статистические»
и может быть вызвана с помощью окна
диалога Мастера
функций.
Функция
ЛГРФПРИБЛ имеет те же четыре аргумента,
что и функция ЛИНЕЙН и формирует
аналогичный массив результатов (рисунок
3.14). Поэтому она вводится как формула
для работы с массивами, т.е. требует:
во-первых, выделения диапазона ячеек,
в которых будет формироваться массив
результатов; во-вторых, после работы с
окном диалога ЛГРФПРИБЛ — нажатия
клавиш Ctrl
+ Shift
+ Enter.
Однако
следует учитывать, что дополнительная
статистика, которую отражает функция
ЛГРФПРИБЛ, основана на линейной модели
вида
In
у = х
ln
т + ln
b.
Поэтому
при оценке значений стандартных ошибок
параметров модели (СОт
и COb)
их необходимо сравнивать не с самими
значениями параметров, а с их натуральными
логарифмами — ln
m
и ln
b.
Последние можно рассчитать с помощью
функции LN
(категория «Математические»),
вызывая ее в окне диалога Мастера
функций.
С
этой целью на рабочем листе Excel
выделим диапазон ячеек D11:E15
для формирования выходного массива
(таблица 3.16). Работая с окном диалога
ЛГРФПРИБЛ, формируем следующую формулу
массива: =ЛГРФПРИБЛ(В3:В18;А3:А18;ИСТИНА;
ИСТИНА). Затем нажимаем клавиши Ctrl
+ Shift
+ Enter.
Рисунок 3.14 — Окно
диалога функции ЛГРФПРИБЛ
Таблица
3.16 — Расчет и оценка модели тренда с
помощью функции ЛГРФПРИБЛ
|
A |
B |
C |
D |
E |
|
|
1 |
|||||
|
2 |
Порядковый номер |
Объем |
|||
|
3 |
1 |
28415 |
|||
|
4 |
2 |
28231 |
|||
|
5 |
3 |
29783 |
|||
|
6 |
4 |
30969 |
|||
|
7 |
5 |
30494 |
|||
|
8 |
6 |
29757 |
|||
|
9 |
7 |
30850 |
|||
|
10 |
8 |
31325 |
|||
|
11 |
9 |
31359 |
Экспоненциальная оценка |
1,014 |
28080,897 |
|
12 |
10 |
31610 |
Статистика |
0,001 |
0,010 |
|
13 |
11 |
32366 |
0,922 |
0,020 |
|
|
14 |
12 |
33313 |
165,579 |
14 |
|
|
15 |
13 |
33508 |
0,065 |
0,005 |
|
|
16 |
14 |
33374 |
|||
|
17 |
15 |
34811 |
|||
|
28 |
16 |
36046 |
Вывод:
Приведенный в таблице 3.16 массив
результатов работы функции позволяет
построить следующую модель тренда, в
основе которой лежит уравнение
экспоненциальной кривой роста:
у
= 28080,897 · 1,01х,
где
х = t
— порядковый номер месяца.
Оценка
статистических характеристик приведенной
модели показывает, что качество ее
подгонки к фактическим значениям у
выше, чем модели, построенной с помощью
функции ЛИНЕЙН. Коэффициент r2
в данном случае имеет значение 0,922
(ячейка D13),
что несколько больше соответствующего
показателя в случае линейной модели,
равного 0,9179. В этой связи (и учитывая
однофакторный характер модели) можно
ожидать улучшение оценок F—
и t-статистики.
Следовательно, качество построенной
модели позволяет использовать ее
при составлении прогнозов развития
товарооборота на ближайшую перспективу.
Задание
10. Составление нелинейных прогнозов с
помощью функции РОСТ
Учитывая
оценку статистических характеристик
функции ЛГРФПРИБЛ, рассчитать прогноз
товарооборота по торговому предприятию
с помощью функции РОСТ. При этом необходимо
получить теоретические значения
товарооборота (оцененные на основе
найденной модели у
= 28080,897·1,01х)
для базового диапазона времени (т.е.
16 прошедших месяцев), а также спрогнозировать
динамику товарооборота на ближайшие 3
месяца.
Выполнение:
Функция
РОСТ определяет точки, лежащие на
экспоненциальной кривой роста. Она
работает точно так же, как ее линейный
аналог ТЕНДЕНЦИЯ, и имеет те же четыре
аргумента (рисунок 3.15).
Подобно
функции ТЕНДЕНЦИЯ, РОСТ вводится как
формула массива и требует выделения
достаточного числа ячеек для формирования
выходного диапазона результатов.
Для
формирования выходного массива
результатов выделим на рабочем листе
Excel,
соответственно, ячейки С3:С21 (таблица
3.17). Затем вызовем функцию РОСТ из окна
диалога Мастера
функций. При
работе с диалоговым окном РОСТ формула
массива принимает вид:
=РОСТ(В3:В18;А3:А18;А3:А21). Последнее действие
— нажать клавиши Ctrl
+ Shift
+ + Enter.
Рисунок 3.15 — Окно
диалога функции РОСТ
Таблица
3.17 — Расчет прогноза товарооборота с
помощью функции РОСТ
-
А
В
С
1
2
Порядковый
номер месяцаОбъем
товарооборота, ден. ед.РОСТ
3
1
28415
28470,4
4
2
28231
28865,2
5
3
29783
29265,6
6
4
30969
29671,5
7
5
30494
30083,0
8
6
29757
30500,3
9
7
30850
30923,3
10
8
31325
31352,2
11
9
31359
31787,0
12
10
31610
32227,9
13
11
32366
32674,9
14
12
33313
33128,1
15
13
33508
33587,5
16
14
33374
34053,4
17
15
34811
34525,7
18
16
36046
35004,5
19
17
35490,0
20
18
35982,3
21
19
36481,3
Задание
11. Прогнозирование с использованием
парной регрессии
Проанализировать
тесноту связи между товарооборотом
торгового предприятия и оборачиваемостью
товаров и найти уравнение парной
регрессии, которое наилучшим образом
опишет изучаемую зависимость. Исходные
данные представлены в таблице 3.18.
Таблица
3.18 — Исходные данные для поиска уравнения
связи переменных
-
А
В
С
1
2
Порядковый
номер месяцаОбъем
товарооборота, ден. ед.Оборачиваемость
товаров, дни3
1
28415
43,5
4
2
28231
43,0
5
3
29783
43,0
6
4
30969
43,5
7
5
30494
43,0
8
6
29757
42,5
9
7
30850
43,0
10
8
31325
41,5
11
9
31359
42,0
12
10
31610
41,5
13
11
32366
40,5
Продолжение таблицы
3.18
-
А
В
С
Порядковый
номер месяцаОбъем
товарооборота, ден. ед.Оборачиваемость
товаров, дни14
12
33313
40,0
15
13
33508
40,0
16
14
33374
39,0
17
15
34811
39,5
18
16
36046
39,0
19
Выполнение:
Чтобы
найти уравнение парной регрессии,
которое наилучшим образом опишет
изучаемую зависимость, обратимся к
графическому методу. С помощью Мастера
диаграмм построим
точечную диаграмму зависимости
товарооборота от оборачиваемости
товаров (см. рисунок 3.16).
Рисунок
3.16 — График зависимости товарооборота
от
товарооборачиваемости
товаров
После
того как диаграмма построена, необходимо
обратиться к команде Excel
«Добавить
линию тренда»
из контекстного меню панели Диаграмма.
Учитывая возможности Excel,
оценим качество аппроксимации базовых
данных каждым из пяти предлагаемых
окном диалога Линии
тренда типом
линий: для линейного уравнения
R2
= 0,8197; для уравнения логарифмической
кривой R2
= 0,8216; для уравнений полинома 4-й степени
R2
= 0,8287; для
уравнения степенной кривой R2
= 0,8155; для уравнения экспоненциальной
кривой R2
= 0,8142.
Полученные
результаты свидетельствуют, что наиболее
адекватно (судя по величине R2)
отражают зависимость товарооборота
от изменения товарооборачиваемости
кривые, построенные на основе уравнений
полиномов 4-й степени. На рисунке 3.17
приведена кривая роста, которую описывает
уравнение полинома 4-й степени. Рассчитанный
Excel
коэффициент R2
(0,8287) указывает на достаточно высокое
качество приближения базовых данных.
Рисунок
3.17 — Аппроксимация базовых данных
полиномиальной кривой роста
Проведем
оценку статистической значимости
параметров уравнения полинома 4-й
степени, построенного на основе
соответствующего массива базовых данных
(таблица 3.19, ячейки A2:F18)
с помощью функции ЛИНЕЙН. Для формирования
выходного массива значений параметров
уравнения и статистических характеристик
обозначим диапазон ячеек В20:F24.
Таблица
3.19 — Оценка статистической значимости
модели регрессии с помощью функции
ЛИНЕЙН (уравнение полинома 4-й степени)
|
А |
В |
С |
D |
E |
F |
|
|
1 |
||||||
|
2 |
Порядковый номер |
Объем товарооборота, |
Оборачиваемость |
х^2 |
х^3 |
х^4 |
|
3 |
1 |
28415 |
43,5 |
1892,3 |
82312,9 |
3580610,1 |
|
4 |
2 |
28231 |
43 |
1849,0 |
79507,0 |
3418801,0 |
|
5 |
3 |
29783 |
43 |
1849,0 |
79507,0 |
3418801,0 |
|
6 |
4 |
30969 |
43,5 |
1892,3 |
82312,9 |
3580610,1 |
|
7 |
5 |
30494 |
43 |
1849,0 |
79507,0 |
3418801,0 |
|
8 |
6 |
29757 |
42,5 |
1806,3 |
76765,6 |
3262539,1 |
|
9 |
7 |
30850 |
43 |
1849,0 |
79507,0 |
3418801,0 |
|
10 |
8 |
31325 |
41,5 |
1722,3 |
71473,4 |
2966145,1 |
|
11 |
9 |
31359 |
42 |
1764,0 |
74088,0 |
3111696,0 |
|
12 |
10 |
31610 |
41,5 |
1722,3 |
71473,4 |
2966145,1 |
|
13 |
11 |
32366 |
40,5 |
1640,3 |
66430,1 |
2690420,1 |
|
14 |
12 |
33313 |
40 |
1600,0 |
64000,0 |
2560000,0 |
|
15 |
13 |
33508 |
40 |
1600,0 |
64000,0 |
2560000,0 |
|
16 |
14 |
33374 |
39 |
1521,0 |
59319,0 |
2313441,0 |
|
17 |
15 |
34811 |
39,5 |
1560,3 |
61629,9 |
2434380,1 |
|
18 |
16 |
36046 |
39 |
1521,0 |
59319,0 |
2313441,0 |
|
19 |
17 (прогноз) |
36667 |
37,5 |
|||
|
20 |
2,269166117 |
-330,0698403 |
17765,93 |
-419248 |
3693351,7 |
|
|
21 |
Статистика |
100,6502388 |
16606,9862 |
1027052 |
28216610 |
290563825 |
|
22 |
0,828678371 |
1050,630858 |
#Н/Д |
#Н/Д |
#Н/Д |
|
|
23 |
13,30168019 |
11 |
#Н/Д |
#Н/Д |
#Н/Д |
|
|
24 |
58730919,23 |
12142077,21 |
#Н/Д |
#Н/Д |
#Н/Д |
При
определении в диалоговом окне ЛИНЕЙН
аргументов функции формируется
следующая формула массива:
=ЛИНЕЙН(В3:В18;С3:F18;ИСТИНА;ИСТИНА).
В
первой строке массива результатов,
отображенного функцией ЛИНЕЙН после
нажатия клавиш Ctrl
+ Shift
+ + Enter
(ячейки В20:F24
таблицы 3.19), находим уточненные в ходе
математических расчетов значения
параметров уравнения.
Вывод:
Модель связи товарооборота (у)
и оборачиваемости товаров (х),
построенная на основе уравнения полинома
4-й степени, имеет вид:
у
= 3693352 — 419248х + 17765,93х2
— 330,07х3
+ 2,269х4.
Заметьте,
что рассчитанный в массиве Статистика
коэффициент R2,
равный 0,8287 (ячейка В22), соответствует
значению R2,
приведенному на рисунке 3.17.
В
нашем примере (см. таблицу 3.19) значения
всех рассчитанных параметров уравнения
(ячейки В20:F20)
меньше по модулю значений их стандартных
ошибок (ячейки В21:F21).
Следовательно, надежность оценок
параметров регрессии не может быть
признана удовлетворительной и составленную
модель не следует применять для
прогнозирования исследуемого
показателя.
Используя
линии тренда Excel,
найдем уравнение другой кривой, для
которой значение R2
будет наибольшим. Таким образом,
наилучшее качество аппроксимации
исходных данных достигается в случае
уравнения логарифмической кривой
(рисунок 3.18).
Рисунок
3.18 — Аппроксимация базовых данных
логарифмической кривой роста
Статистическую
надежность сделанной оценки можно
проверить с помощью F-критерия,
расчетное значение которого в случае
парной регрессии определяют на основе
следующей формулы
.
Итак,
для уравнения парной регрессии с
коэффициентом R2,
равным 0,8216, F
=
64,5.
По
таблице F-распределения
(см. приложение А) находим, что при 5%-м
уровне значимости для распределения
Фишера с (1;14) степенями свободы Fкрит
= 4,60. Поскольку 64,5 > 4,60, можно сделать
вывод об адекватности и достаточной
точности модели. Следовательно, при
условии сохранения существовавшей
ранее взаимосвязи переменных на период
упреждения модель вида у
= -49619ln(х)
+ 216503 может
быть использована для прогнозирования.
Чтобы
составить прогноз объема товарооборота
на 17-й месяц, осталось определить значение
переменной х
(т.е. оборачиваемости товаров) для данного
месяца. Это значение может быть
получено (в зависимости от характера
показателя) на основе экстраполяционных
методов, методов экспертных оценок или
непосредственно задано составителем
прогноза. Так, будем полагать, что
рассматриваемое торговое предприятие
на 17-й месяц планирует проведение
определенных рекламных мероприятий
и выставки-продажи, что по оценкам
специалистов позволит ускорить
оборачиваемость товаров в среднем
на 1,5 дня. В этом случае товарооборачиваемость
по предприятию в прогнозируемом месяце
составит 37,5 дня.
Прогноз
объема товарооборота можно получить,
создав соответствующую модели формулу
в любой (предварительно выделенной)
ячейке рабочего листа. Выделим, к
примеру, ячейку В19 (см. таблицу 3.19) и
внесем в нее следующую формулу:
=-49619*ln(37,5)+216503.
После нажатия клавиши Enter
в ячейке В19 отразится прогноз объема
товарооборота на 17-й месяц, равный 36 667
ден. ед.
Задание
12. Расчет и оценка уравнения множественной
регрессии средствами Excel
Построить
модель множественной линейной
регрессии, которая позволит оценить
объем товарооборота на ближайшую
перспективу при заданных параметрах
независимых переменных: «оборачиваемость
товаров» и «удельный вес товаров с
высокими торговыми надбавками».
Исходные данные представлены в таблице
3.20.
Таблица
3.20 — Исходные данные
|
А |
В |
С |
D |
|
|
1 |
||||
|
2 |
Порядковый |
Объем товарооборота, |
Оборачиваемость |
Удельный вес |
|
3 |
1 |
28415 |
43,5 |
22,5 |
|
4 |
2 |
28231 |
43,0 |
18,0 |
|
5 |
3 |
29783 |
43,0 |
24,9 |
|
6 |
4 |
30969 |
43,5 |
24,4 |
|
7 |
5 |
30494 |
43,0 |
20,6 |
|
8 |
6 |
29757 |
42,5 |
19,0 |
|
9 |
7 |
30850 |
43,0 |
22,2 |
|
10 |
8 |
31325 |
41,5 |
21,6 |
|
11 |
9 |
31359 |
42,0 |
19,8 |
|
12 |
10 |
31610 |
41,5 |
19,7 |
|
13 |
11 |
32366 |
40,5 |
23,1 |
|
14 |
12 |
33313 |
40,0 |
23,9 |
|
15 |
13 |
33508 |
40,0 |
21,2 |
|
16 |
14 |
33374 |
39,0 |
20,4 |
|
17 |
15 |
34811 |
39,5 |
24,2 |
|
18 |
16 |
36046 |
39,0 |
26,5 |
Выполнение:
При
построении модели множественной
регрессии целесообразнее обратиться
к инструменту Excel
Регрессия,
который предлагает исчерпывающую
статистическую информацию о ее параметрах
и качестве. Порядок работы с инструментом
Регрессия
определяется соответствующим окном
диалога. Его можно вызвать через команду
Анализ данных
из контекстного меню панели Сервис.
Диалоговое окно Регрессия
предлагает пользователю определиться
с набором следующих параметров (рисунок
3.19):
1)
Входной
интервал У
— предлагает ввод ссылки на ячейки
рабочего листа, которые содержат диапазон
базовых данных зависимой переменной у
(исследуемого показателя). В нашем
примере Входной
интервал Y
– В2:В18;
2)
Входной
интервал X
— предполагает ввод ссылки на ячейки
рабочего листа, которые содержат диапазон
базовых данных независимых переменных
х1,
х2,
…, xk.
В нашем примере Входной
интервал Х
– С2:D18;
3)
Метки
— требует установления флажка, если
первая строка входного интервала
содержит заголовки (названия столбцов).
Если заголовки отсутствуют, то флажок
устанавливать не нужно — Excel
автоматически создаст соответствующие
названия для данных выходного диапазона.
В нашем примере – устанавливаем флажок;
4)
Уровень
надежности
— позволяет пользователю определить
необходимый уровень надежности оценки
выходного диапазона значений. По
умолчанию Excel
применяет уровень 95 %. Если его нужно
изменить, то для данного параметра
следует установить флажок и в специально
открывшееся поле ввести нужный
уровень надежности. В нашем — примере
флажок не устанавливаем;
5)
Константа-ноль
— требует установления флажка, если
для уравнения регрессии не нужно
рассчитывать параметр b
(свободный член). В этом случае Excel
принимает b,
равным нулю. В нашем примере – флажок
не устанавливаем;
6)
Выходной
диапазон —
предполагает ввод ссылки на верхнюю
левую ячейку выходного диапазона.
Выходной массив значений будет занимать
не менее семи столбцов и содержать три
основных раздела: 1. Регрессионная
статистика; 2. Дисперсионный анализ;
3. Параметры (коэффициенты) регрессии и
характеристики их статистической
значимости;
7)
Новый лист
— применяют, если результаты анализа
следует разместить на новом листе книги,
начиная с ячейки А1;

Новая книга
— используется, если результаты анализа
необходимо разместить на первом листе
специально открытой для этого новой
книги;
9)
Остатки
— требует установления флажка, если в
целях проведения углубленного
статистического анализа качества
модели в выходной диапазон, кроме трех
основных разделов, необходимо включить
значения отклонений фактических
данных исследуемого показателя от
соответствующих им точек регрессионной
прямой (У
фактическое — У
расчетное);
10)
Стандартизированные
остатки —
применяют с той же целью для включения
в выходной диапазон значений стандартных
остатков;
11)
График
остатков —
используется, если для статистического
анализа необходимо построить диаграммы
остатков для каждой независимой
переменной х;
12)
График подбора
— предполагает формирование на рабочем
листе диаграмм, позволяющих отследить
характер связи и степень разброса
наблюдаемых и предсказанных значений
исследуемого показателя у
с каждой независимой переменной х;
13)
График
нормальной вероятности
— требует установления флажка, если
пользователю необходимо получить
график нормального распределения
вероятности для исследуемого
показателя.
Рисунок
3.19 — Окно диалога Регрессия
Так,
в первом разделе выходного массива
«Регрессионная
статистика»
(см. ячейки А4:В8 таблицы 3.21) приведены
основные статистические характеристики
общего качества уравнения: коэффициент
множественной корреляции R,
коэффициент детерминации R2,
стандартная ошибка оценки. Значение
R2,
равное 0,892, свидетельствует о том, что
на основе полученного уравнения регрессии
можно объяснить 89,2 % вариации объема
товарооборота.
Статистические
характеристики второго раздела выходного
массива «Дисперсионный
анализ»
(ячейки A10:F14)
позволяют оценить меру разброса
(дисперсию) зависимой переменной у
и остаточной вариации (дисперсии)
отклонений вокруг линии регрессии.
Так, значение SSр
(ячейка С12) характеризует часть
дисперсии, объясненную регрессией, а
SSо
(ячейка С13) — часть дисперсии, не
объясненной регрессией из-за наличия
ошибок ε. При проведении регрессионного
анализа особый интерес представляет
изменение этих значений по мере
введения каждого регрессора. Качество
модели улучшится, если после введения
в нее нового фактора значение
объясненной части дисперсии возрастет,
а не объясненной — снизится.
В
ячейках D12:D13
отражены соответственно дисперсия
исходного ряда (МSp
= SSp
/ df,
где df
= k
— см. ячейку В12) и несмещенная дисперсия
остаточной компоненты (MS0
= SS0
/ df,
где df
= п — k
— 1 — см.
ячейку В13).
В
ячейке F12
второго раздела выходного массива
приведен уровень значимости для
оцененного F.
Значения
F-статистики
(53,72) выглядит вполне допустимым,
поскольку уровень значимости для нее
(5,2107)
остается гораздо ниже 5%-го предела,
принятого для табличных F-статистик.
Следовательно, есть основания ожидать,
что F-наблюдаемое
будет больше Fкрит.
Оценив
на основе первого и второго разделов
выходного массива общее качество модели
связи и убедившись в ее значимости,
можем перейти к третьему разделу (см.
ячейки A16:G19
таблицы 3.21), который содержит детальную
информацию о параметрах уравнения
регрессии. Приведенные в ячейках
В17:В19 значения параметров (коэффициентов)
уравнения позволяют придать формальный
вид модели, построенной с помощью
регрессионного анализа:
у
= 71650,26 – 1098,94х1
+
255,838х2,
где
х1
— оборачиваемость товаров, дни; х2
— удельный вес товаров с высокими
торговыми надбавками, %.
Оценить
значимость каждого параметра позволяют
значения t-статистики
(см. ячейки D17:D19).
Можно использовать приведенный в
выходном массиве уровень значимости
(см. ячейки Е17:Е19): если он не превышает
0,05 (т.е. 5%-го уровня), то рассчитанные
характеристики t-статистики
будут больше табличного значения.
Следовательно, статистическая
значимость рассчитанных параметров
уравнения весьма высока.
И,
наконец, наряду с точечными значениями
коэффициентов регрессии третий
раздел выходного массива позволяет
получить их интервальные оценки с
доверительной вероятностью 95 % (см.
ячейки F17:G19
таблицы 3.21):
58598,85
<
b
<
84701,68; -1370,81 <
m1
<
-827,08; 68,597 <
m2
<
443,079.
На
основании изложенного можно с 95%-й
уверенностью утверждать, что параметры
уравнения содержат информацию, значимую
для расчета исследуемого показателя.
Таблица
3.21 — Регрессионный анализ
|
А |
В |
С |
D |
E |
F |
G |
|
|
1 |
ВЫВОД |
||||||
|
2 |
|||||||
|
3 |
Регрессионная статистика |
||||||
|
4 |
Множественный |
0,94449 |
|||||
|
5 |
R-квадрат |
0,892061 |
|||||
|
6 |
Нормированный |
0,875455 |
|||||
|
7 |
Стандартная |
767,1098 |
|||||
|
8 |
Наблюдения |
16 |
|||||
|
9 |
|||||||
|
10 |
Дисперсионный |
||||||
|
11 |
df |
SS |
MS |
F |
Значимость |
||
|
12 |
Регрессия |
2 |
63223048,8 |
31611524,42 |
53,7193 |
5,2E-07 |
|
|
13 |
Остаток |
13 |
7649947,59 |
588457,5077 |
|||
|
14 |
Итого |
15 |
70872996,4 |
||||
|
15 |
|||||||
|
16 |
Коэффициенты |
Стандартная |
t-статистика |
P-Значение |
Нижние |
Верхние |
|
|
17 |
Y-пересечение |
71650,26 |
6041,29087 |
11,86009163 |
2,41E-08 |
58598,85 |
84701,68 |
|
18 |
Оборачиваемость |
-1098,94 |
125,841366 |
-8,732770177 |
8,46E-07 |
-1370,81 |
-827,08 |
|
19 |
Удельный |
255,8378 |
86,6708225 |
2,951832613 |
0,011232 |
68,59687 |
443,0787 |
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Любому бизнесу интересно заглянуть в будущее и правильно ответить на вопрос: «А сколько денег мы заработаем за следующий период?» Ответить на такого рода вопросы позволяют различные методики прогнозирования. В данной статье мы с вами рассмотрим несколько таких методик и произведем все необходимые расчеты в Excel. Еще больше про анализ данных в Excel мы рассказываем на нашем открытом курсе «Аналитика в Excel».
Постановка задачи
Исходные данные
Для начала, давайте определимся, какие у нас есть исходные данные и что нам нужно получить на выходе. Фактически, все что у нас есть, это некоторые исторические данные. Если мы говорим о прогнозировании продаж, то историческими данными будут продажи за предыдущие периоды.
Примечание. Собранные в разные моменты времени значения одной и той же величины образуют временной ряд. Каждое значение такого временного ряда называется измерением. Например: данные о продажах за последние 5 лет по месяцам — временной ряд; продажи за январь прошлого года — измерение.
Составляющие прогноза
Следующий шаг: давайте определимся, что нам нужно учесть при построении прогноза. Когда мы исследуем наши данные, нам необходимо учесть следующие факторы:
- Изменение нашей пронозируемой величины (например, продаж) подчиняется некоторому закону. Другими словами, в временном ряде можно проследить некую тенденцию. В математике такая тенденция называется трендом.
- Изменение значений в временном ряде может зависить от промежутка времени. Другими словами, при построении модели необходимо будет учесть коэффициент сезонности. Например, продажи арбузов в январе и августе не могут быть одинаковыми, т.к. это сезонный продукт и летом продажи значительно выше.
- Изменение значений в временном ряде периодически повторяется, т.е. наблюдается некоторая цикличность.
Эти три пункта в совокупность образуют регулярную составляющую временного ряда.
Примечание. Не обязательно все три элемента регулярной составляющей должны присутствовать в временном ряде.
Однако, помимо регулярной составляющей, в временном ряде присутствует еще некоторое случайное отклонение. Интуитивно это понятно – продажи могут зависеть от многих факторов, некоторые из которых могут быть случайными.
Вывод. Чтобы комплексно описать временной ряд, необходимо учесть 2 главных компонента: регулярную составляющую (тренд + сезонность + цикличность) и случайную составляющую.
Виды моделей
Следующий вопрос, на который нужно ответить при построении прогноза: “А какие модели временного ряда бывают?”
Обычно выделяют два основных вида:
- Аддитивная модель: Уровень временного ряда = Тренд + Сезонность + Случайные отклонения
- Мультипликативная модель: Уровень временного ряда = Тренд X Сезонность X Случайные отклонения
Иногда также выделают смешанную модель в отдельную группу:
- Смешанная модель: Уровень временного ряда = Тренд X Сезонность + Случайные отклонения
С моделями мы определились, но теперь возникает еще один вопрос: «А когда какую модель лучше использовать?»
Классический вариант такой:
— Аддитивная модель используется, если амплитуда колебаний более-менее постоянная;
— Мультипликативная – если амплитуда колебаний зависит от значения сезонной компоненты.
Пример:

Решение задачи с помощью Excel
Итак, необходимые теоретические знания мы с вами получили, пришло время применить их на практике. Мы будем с вами использовать классическую аддитивную модель для построения прогноза. Однако, мы построим с вами два прогноза:
- с использованием линейного тренда
- с использованием полиномиального тренда
Во всех руководствах, как правило, разбирается только линейный тренд, поэтому полиномиальная модель будет крайне полезна для вас и вашей работы!
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Модель с линейным трендом
Пусть у нас есть исходная информация по продажам за 2 года:

Учитывая, что мы используем линейный тренд, то нам необходимо найти коэффициенты уравнения
y = ax + b
где:
- y – значения продаж
- x – номер периода
- a – коэффициент наклона прямой тренда
- b – свободный член тренда
Рассчитать коэффициенты данного уравнения можно с помощью формулы массива и функции ЛИНЕЙН. Нам необходимо будет сделать следующую последовательность действий:
- Выделяем две ячейки рядом
- Ставим курсор в поле формул и вводим формулу =ЛИНЕЙН(C4:C27;B4:B27)
- Нажимаем Ctrl+Shift+Enter, чтобы активировать формулу массива
На выходе мы получили 2 числа: первое — коэффициент a, второе – свободный член b.

Теперь нам нужно рассчитать для каждого периода значение линейного тренда. Сделать это крайне просто — достаточно в полученное уравнение подставить известные номера периодов. Например, в нашем случае, мы прописываем формулу =B4*$F$4+$G$4 в ячейке I4 и протягиваем ее вниз по всем периодам.

Нам осталось рассчитать коэффициент сезонности для каждого периода. Учитывая, что у нас есть исторические данные за два года, разумно будет учесть это при расчете. Можем сделать следующим образом: в ячейке J4 прописываем формулу =(C4+C16)/СРЗНАЧ($C$4:$C$27)/2 и протягиваем вниз на 12 месяцев (т.е. до J15).

Что нам это дало? Мы посчитали, сколько суммарно продавалось каждый январь/каждый февраль и так далее, а потом разделили это на среднее значение продаж за все два периода.
То есть мы выяснили, как продажи двух январей отклонялись от средних продаж за два года, как продажи двух февралей отклонялись и так далее. Это и дает нам коэффициент сезонности. В конце формулы делим на 2, т.к. в расчете фигурировало 2 периода.
Примечание. Рассчитали только 12 коэффициентов, т.к. один коэффициент учитывает продажи сразу за 2 аналогичных периода.
Итак, теперь мы на финишной прямой. Нам осталось рассчитать тренд для будущих периодов и учесть коэффициент сезонности для них. Давайте амбициозно построим прогноз на год вперед.
Сначала создаем столбец, в котором прописываем номера будущих периодов. В нашем случае нумерация начинается с 25 периода.
Далее, для расчета значения тренда просто прописываем уже известную нам формулу =L4*$F$4+$G$4 и протягиваем вниз на все 12 прогнозируемых периодов.
И последний штрих — умножаем полученное значение на коэффициент сезонности. Вуаля, это и есть итоговый ответ в данной модели!
Модель с полиномиальным трендом
Конструкция, которую мы только что с вами построили, достаточно проста. Но у нее есть один большой минус — далеко не всегда она дает достоверные результаты.
Посмотрите сами, какая модель более точно аппроксимирует наши точки — линейный тренд (прямая зеленая линия) или полиномиальный тренд (красная кривая)? Ответ очевиден. Поэтому сейчас мы с вами и разберем, как построить полиномиальную модель в Excel.
Пусть все исходные данные у нас будут такими же. Для простоты модели будем учитывать только тренд, без сезонной составляющей.
Для начала давайте определимся, чем полиномиальный тренд отличается от обычного линейного. Правильно — формой уравнения. У линейного тренда мы разбирали обычный график прямой:

У полиномиального тренда же уравнение выглядит иначе:

где конечная степень определяется степенью полинома.
Т.е. для полинома 4 степени необходимо найти коэффициенты уравнения:

Согласитесь, выглядит немного страшно. Однако, ничего страшного нет, и мы с легкостью можем решить эту задачку с помощью уже известных нам методов.
- Ставим в ячейку F4 курсор и вводим формулу =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4});1;1). Функция ЛИНЕЙН позволяет произвести расчет коэффициентов, а с помощью функции ИНДЕКС мы вытаскиваем нужный нам коэффициент. В данном случае за выбор коэффициента отвечает самый последний аргумент. У нас стоит 1 — это коэффициент при самой высокой степени (т.е. при 4 степени, коэффициент). Кстати, узнать о самых полезных математических формулах Excel можно в нашем бесплатном гайде «Математические функции Excel».
- Аналогично прописываем формулу =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4});1;2) в ячейке ниже.
- Делаем такие же действия, пока не найдем все коэффициенты.
Кстати говоря, мы можем легко сами себя проверить. Давайте построим график наших продаж и добавим к нему полиномиальный тренд.
- Выделяем столбец с продажами
- Выбираем «Вставка» → «График» → «Точечный» → «Точечная диаграмма»
- Нажимаем на любую точку графика правой кнопкой мыши и выбираем «Добавить линию тренда»
- В открывшемся справа меню выбираем «Полиномиальная модель», меняем степень на 4 и ставим галочку на «Показывать уравнение на диаграмме»
Теперь вы наглядно можете видеть, как рассчитанный тренд аппроксимирует исходные данные и как выглядит само уравнение. Можно сравнить уравнение на графике с вашими коэффициентами. Сходится? Значит сделали все верно!
Помимо всего прочего, вы можете сразу оценить точность аппроксимации (не полностью, но хотя бы первично). Это делается с помощью коэффициента R^2. Тут у вас снова есть два пути:
- Вы можете вывести коэффициент на график, поставив галочку «Поместить на диаграмму величину достоверности аппроксимации»
- Вы можете рассчитать коэффициент R^2 самостоятельно по формуле =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4};;1);3;1)
Заключение
Мы с вами подробно разобрали вопрос прогнозирования — изучили необходимые термины и виды моделей, построили аддитивную модель в Excel с использованием линейного и полиномиального тренда, а также научились отображать результаты своих вычислений на графиках. Все это позволит вам эффективно внедрять полученные знания на работе, усложнять существующие модели и уточнять прогнозы. Чем большим количеством методов и инструментов вы будете владеть, тем выше будет ваш профессиональный уровень и статус на рынке труда.
Если вас интересуют еще какие-то модели прогнозирования — напишите нам об этом, и мы постараемся осветить эти темы в дальнейших своих статьях! Или запишитесь на курс «Excel Academy» от SF Education, где мы рассказываем про возможности Excel, необходимые для анализа.
Автор: Алексанян Андрон, эксперт SF Education
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Блог SF Education
Data Science
5 примеров экономии времени в Excel
Что для работодателя главное в сотруднике? Добросовестность, ответственность, профессионализм и, конечно же, умение пользоваться отведенным временем! Предлагаем познакомиться с очень нужными, на наш взгляд,…
Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Еще…Меньше
Если у вас есть статистические данные с зависимостью от времени, вы можете создать прогноз на их основе. При этом в Excel создается новый лист с таблицей, содержащей статистические и предсказанные значения, и диаграммой, на которой они отражены. С помощью прогноза вы можете предсказывать такие показатели, как будущий объем продаж, потребность в складских запасах или потребительские тенденции.
Сведения о том, как вычисляется прогноз и какие параметры можно изменить, приведены ниже в этой статье.
Создание прогноза
-
На листе введите два ряда данных, которые соответствуют друг другу:
-
ряд значений даты или времени для временной шкалы;
-
ряд соответствующих значений показателя.
Эти значения будут предсказаны для дат в будущем.
Примечание: Для временной шкалы требуются одинаковые интервалы между точками данных. Например, это могут быть месячные интервалы со значениями на первое число каждого месяца, годичные или числовые интервалы. Если на временной шкале не хватает до 30 % точек данных или есть несколько чисел с одной и той же меткой времени, это нормально. Прогноз все равно будет точным. Но для повышения точности прогноза желательно перед его созданием обобщить данные.
-
-
Выделите оба ряда данных.
Совет: Если выделить ячейку в одном из рядов, Excel автоматически выделит остальные данные.
-
На вкладке Данные в группе Прогноз нажмите кнопку Лист прогноза.
-
В окне Создание прогноза выберите график или гограмму для визуального представления прогноза.
-
В поле Завершение прогноза выберите дату окончания, а затем нажмите кнопку Создать.
В Excel будет создан новый лист с таблицей, содержащей статистические и предсказанные значения, и диаграммой, на которой они отражены.
Этот лист будет находиться слева от листа, на котором вы ввели ряды данных (то есть перед ним).
Настройка прогноза
Если вы хотите изменить дополнительные параметры прогноза, нажмите кнопку Параметры.
Сведения о каждом из вариантов можно найти в таблице ниже.
|
Параметры прогноза |
Описание |
|
Начало прогноза |
Выберите дату, с которой должен начинаться прогноз. При выборе даты начала, которая наступает раньше, чем заканчиваются статистические данные, для построения прогноза используются только данные, предшествующие ей (это называется «ретроспективным прогнозированием»). Советы:
|
|
Доверительный интервал |
Установите или снимите флажок Доверительный интервал, чтобы показать или скрыть его. Доверительный интервал — это диапазон вокруг каждого предсказанного значения, в который в соответствии с прогнозом (при нормальном распределении) предположительно должны попасть 95 % точек, относящихся к будущему. Доверительный интервал помогает определить точность прогноза. Чем он меньше, тем выше достоверность прогноза для данной точки. Доверительный интервал по умолчанию определяется для 95 % точек, но это значение можно изменить с помощью стрелок вверх или вниз. |
|
Сезонность |
Сезонность — это число для длины (количества точек) сезонного шаблона и автоматически обнаруживается. Например, в ежегодном цикле продаж, каждый из которых представляет месяц, сезонность составляет 12. Автоматическое обнаружение можно переопрепредидить, выбрав установить вручную и выбрав число. Примечание: Если вы хотите задать сезонность вручную, не используйте значения, которые меньше двух циклов статистических данных. При таких значениях этого параметра приложению Excel не удастся определить сезонные компоненты. Если же сезонные колебания недостаточно велики и алгоритму не удается их выявить, прогноз примет вид линейного тренда. |
|
Диапазон временной шкалы |
Здесь можно изменить диапазон, используемый для временной шкалы. Этот диапазон должен соответствовать параметру Диапазон значений. |
|
Диапазон значений |
Здесь можно изменить диапазон, используемый для рядов значений. Этот диапазон должен совпадать со значением параметра Диапазон временной шкалы. |
|
Заполнить отсутствующие точки с помощью |
Для обработки отсутствующих точек в Excel используется интерполяция, то есть отсутствующие точки будут заполнены в качестве взвешенного среднего значения соседних точек, если отсутствует менее 30 % точек. Чтобы нули в списке не были пропущены, выберите в списке пункт Нули. |
|
Использование агрегатных дубликатов |
Если данные содержат несколько значений с одной меткой времени, Excel находит их среднее. Чтобы использовать другой метод вычисления, например Медиана илиКоличество,выберите нужный способ вычисления из списка. |
|
Включить статистические данные прогноза |
Установите этот флажок, если хотите поместить на новом листе дополнительную статистическую информацию о прогнозе. При этом добавляется таблица статистики, созданная с помощью прогноза. Ets. Функция СТАТ и показатели, такие как коэффициенты сглаживания («Альфа», «Бета», «Гамма») и метрики ошибок (MASE, SMAPE, MAE, RMSE). |
Формулы, используемые при прогнозировании
При использовании формулы для создания прогноза возвращаются таблица со статистическими и предсказанными данными и диаграмма. Прогноз предсказывает будущие значения на основе имеющихся данных, зависящих от времени, и алгоритма экспоненциального сглаживания (ETS) версии AAA.
Таблицы могут содержать следующие столбцы, три из которых являются вычисляемыми:
-
столбец статистических значений времени (ваш ряд данных, содержащий значения времени);
-
столбец статистических значений (ряд данных, содержащий соответствующие значения);
-
столбец прогнозируемых значений (вычисленных с помощью функции ПРЕДСКАЗ.ЕTS);
-
два столбца, представляющие доверительный интервал (вычисленные с помощью функции ПРЕДСКАЗ.ЕTS.ДОВИНТЕРВАЛ). Эти столбцы отображаются только при проверке доверительный интервал в разделе Параметры.
Скачивание образца книги
Щелкните эту ссылку, чтобы скачать книгу с Excel FORECAST. Примеры функции ETS
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Статьи по теме
Функции прогнозирования
Нужна дополнительная помощь?
Тема урока: Модели статистического прогнозирования. Регрессионная модель Практическая работа №11 (1 часть) «Получение регрессионных моделей».
Цель урока:
Освоить способы построения по экспериментальным данным регрессионной модели и тренда средствами MO Excel.
Используемые программные средства: табличный процессор MO Excel.
Видеоматериалы:
-
Теоретический материал https://www.youtube.com/watch?v=DJr8a2kwWjc
-
Рассмотрение практической работы https://www.youtube.com/watch?v=Pj-hP8lqtGk
Ход урока.
1. Организационная часть.
Подготовьтесь к уроку. Откройте тетради и учебник на странице на § 18. Откройте файл с дистанционным материалом.
Запишите тему урока. Модели статистического прогнозирования. Регрессионная модель.
2. Постановка цели урока. Актуализация знаний
Статистика — наука о сборе, измерении и анализе массовых количественных данных.
Анализ данных — область информатики, занимающаяся построением и исследованием наиболее общих математических методов и вычислительных алгоритмов извлечения знаний из экспериментальных (в широком смысле) данных.
Вопросы ученикам: 1) Как Вы думаете, какое программное обеспечение имеет средства анализа данных? (табличный процессор Excel)
2) Какие именно возможности табличного процессора можно отнести к средствам анализа данных? ЗАПОМНИТЬ
К средствам анализа относятся:
• Обработка списка с помощью различных формул и функций;
• Построение диаграмм и использование карт Ms Excel;
• Проверка данных рабочих листов и рабочих книг на наличие ошибок;
• Структуризация рабочих листов;
• Автоматическое подведение итогов (включая мастер частичных сумм);
• Консолидация данных;
• Сводные таблицы;
• Специальные средства анализа выборочных записей и данных — подбор параметра, поиск решения, сценарии и др.
3) В каких областях могут найти практическое применение средства анализа табличного процессора Excel?
Цель нашего урока: научиться строить регрессионные модели средствами Excel.
В состав Microsoft Excel входит набор средств анализа данных (так называемый пакет анализа), предназначенный для решения сложных статистических и инженерных задач. Для проведения анализа данных с помощью этих инструментов следует указать входные данные и выбрать параметры; анализ будет проведен с помощью подходящей статистической или инженерной макрофункции, а результат будет помещен в выходной диапазон. Другие средства позволяют представить результаты анализа в графическом виде.
Статистические данные приводятся в виде длинных и сложных статистических таблиц, поэтому бывает весьма трудно обнаружить в них имеющиеся неточности и ошибки.
Графическое же представление статистических данных помогает легко и быстро выявить ничем не оправданные пики и впадины, явно не соответствующие изображаемым статистическим данным, аномалии и отклонения.
- Теоретическая часть.
Ознакомитесь с видеоматериалом урока Видео:
https://www.youtube.com/watch?v=DJr8a2kwWjc
MO Excel – это не просто электронная таблица с данными и формулами для вычислений. Это универсальная система обработки данных, которая может использоваться для анализа и представления данных в наглядной форме.
Мы уже с вами говорили о том, что решение задач планирования и управления постоянно требует учета зависимостей одних факторов от других. Таких примеров мы приводили очень много.
Один из таких примеров: определение зависимости время падения тела на землю от первоначальной высоты. Зависимость эта очевидна. Для её проверки можно провести эксперимент, сбрасывая предметы с разных этажей многоэтажного здания, данные занесены в таблицу. Таким образом, мы легко создадим табличную модель, на основе её построим график. Кроме этого нам не составит особого труда и составление функциональной зависимости, так как падение тел происходит согласно всем нам известному физическому закону. Тем самым у нас будет и математическая модель по которой мы легко рассчитаем время падения тел даже с очень большой высоты.
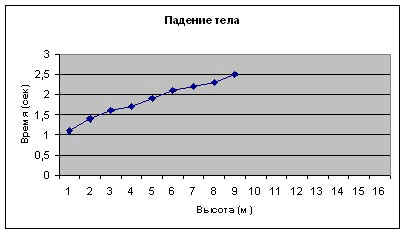
|
Н (м) |
t (сек) |
|
6 9 12 15 18 21 24 27 30 |
1,1 1,4 1,6 1,7 1,9 2,1 2,2 2,3 2,5 |
,
|
С, мг/куб.м |
Р, бол./тыс. |
|
2 |
19 |
|
2,5 |
20 |
|
2,9 |
32 |
|
3,2 |
34 |
|
3,6 |
51 |
|
3,9 |
55 |
|
4,2 |
90 |
|
4,6 |
108 |
|
5 |
171 |
Но не все зависимости так просты.
Н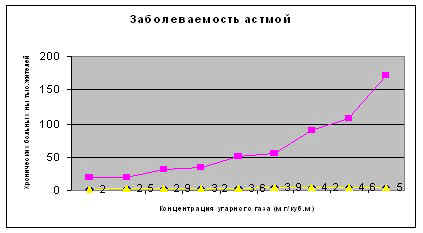
Любому человеку понятно, что такая зависимость существует. Очевидно, что чем хуже воздух, тем больше больных астмой. Но это качественное заключение. Его недостаточно для того, чтобы управлять этим процессом, нам потребуются более конкретные знания. Нужно установить, какие именно примеси сильнее всего влияют на здоровье людей, как связаны концентрация этих примесей в воздухе с числом заболеваний. Такую зависимость можно установить только путем сбора многочисленных данных, их анализа и обобщения.
В таких ситуациях на помощь приходит статистика: наука о сборе, изменении и анализе массовых количественных данных.
Специалисты по медицинской статистике проводят сбор данных. Они собирают сведения из разных городов о средней концентрации угарного газа в атмосфере и о заболеваемости астмой (число хронических больных на тысячу жителей). Полученные данные можно свести в таблицу, а также представить в виде точечной диаграммы.
При этом необходимо помнить, что статистические данные всегда являются приближенными, усредненными. Поэтому они носят оценочный характер. Однако, они верно отражают характер зависимости величин. И еще одно важное замечание: для достоверности результатов, полученных путем анализа статистических данных, этих данных должно быть много.
Из полученных данных можно сделать вывод, что при концентрации угарного газа до 3 мг/куб.м его влияние на заболеваемость астмой несильное. С дальнейшим ростом концентрации наступает резкий рост заболеваемости.
Построить табличную модель и графическую по экспериментальным данным
Но нужно ещё и получить формулу, отражающую эту зависимость. На языке математики это называется функцией зависимости Р от С: Р(С). Вид такой функции неизвестен, её следует искать методом подбора по экспериментальным данным. Понятно, что график искомой функции должен проходить близко к точкам диаграммы экспериментальных данных. Строить функцию так, чтобы ёе график точно проходил через все данные точки (рисунок 2), не имеет смысла. Во-первых, математический вид такой функции может оказаться слишком сложным. Во-вторых, уже говорилось о том, что экспериментальные значения являются приближенными.
Отсюда следуют основные требования к искомой функции:
-
она должна быть достаточно простой для использования её в дальнейших вычислениях;
-
г
рафик этой функции должен проходить вблизи экспериментальных точек так, чтобы отклонения этих точек от графика были минимальны и равномерны
Полученную функцию, график которой приведен на рисунке, принято называть в статистике регрессионной моделью. Регрессионная модель – это функция, описывающая зависимость между количественными характеристиками сложных систем.
Получение регрессионной модели происходит в два этапа:
-
подбор вида функции;
-
вычисление параметров функции.
Чаще всего выбор производится среди следующих функций:
y=ax+b – линейная функция;
y=ax2+bx+c – квадратичная функция;
y=aln(x)+b – логарифмическая функция;
y=aebx — экспоненциальная функция;
y=axb — степенная функция.
Если Вы выбрали (сознательно или наугад) одну из предлагаемых функций, то следующим шагом нужно подобрать параметры (a,b,c и пр.) так, чтобы функция располагалась как можно ближе к экспериментальным точкам. Для этого подходит метод наименьших квадратов (МНК). Суть его заключается в следующем: искомая функция должна быть построена так, чтобы сумма квадратов отклонений у – координат всех экспериментальных точек от у – координат графика функции была бы минимальной.
В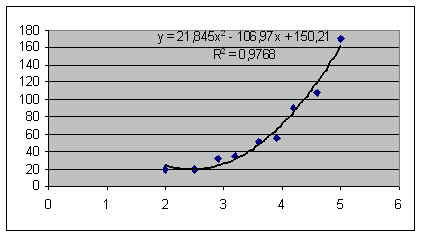
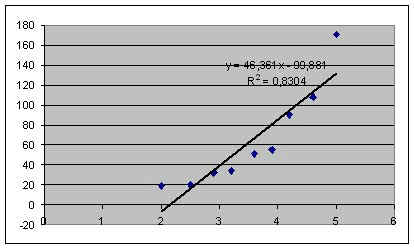
Данные рисунки получены с помощью MO Excel. График регрессионной модели называется трендом (trend – направление, тенденция).
Г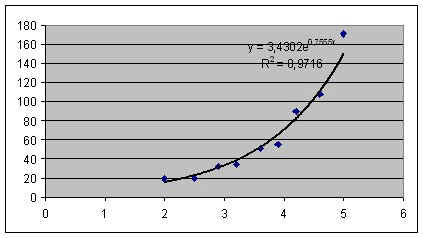
На графиках присутствует ещё одна величина, полученная в результате построения трендов. Она обозначена как R2. В статистике эта величина называется коэффициентом детерминированности. Именно она определяет, насколько удачной получится регрессионная модель. Коэффициент детерминированности всегда заключен в диапазоне от 0 до 1. Если он равен 1, то функция точно проходит через табличные значения, если 0, то выбранный вид регрессионной модели неудачен. Чем R2 ближе к 1, тем удачнее регрессионная модель.
Метод наименьших квадратов используется для вычисления параметров регрессионной модели. Этот метод содержится в математическом арсенале электронных таблиц.
Письменное задание. Составить конспект по §18
4. Практическая часть. Перед выполнением практической работы посмотрите видео
https://www.youtube.com/watch?v=Pj-hP8lqtGk
Выполнение практической работы в MO Excel.
Задание
По предложенной инструкции выполнить практическую работу, оформить отчет. Этапы работы:
1. Ввести табличные данные зависимости заболеваемости бронхиальной астмой от концентрации угарного газа в атмосфере (см. рисунок).
2. Представить зависимость в виде точечной диаграммы (см. рисунок).
Меню Вставка / Диаграмма / Точечная диаграмма
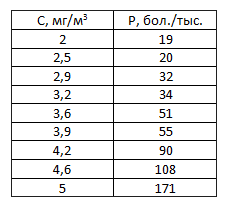
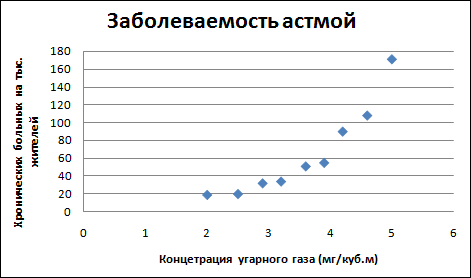
3.Скопировать и вставить ещё 4 диаграммы (Всего 5)
Выделили диаграмму / Скопировали / нажали на другую ячейку / Вставили.
4. К каждой диаграмме построить линии тренда
Нажать на диаграмму / меню Макет / Линия тренда / Дополнительные параметры линии тренда), задавая поочерёдно функции. 1диаграмма – экспоненциальная функция, 2 –линейная, 3 – логарифмическая, 4 – полиномиальная, 5 – степенная.
Не забудьте поставить галочки «Показать уравнение на диаграмме» и «Поместить на диаграмму величину достоверности аппроксимации R^2».

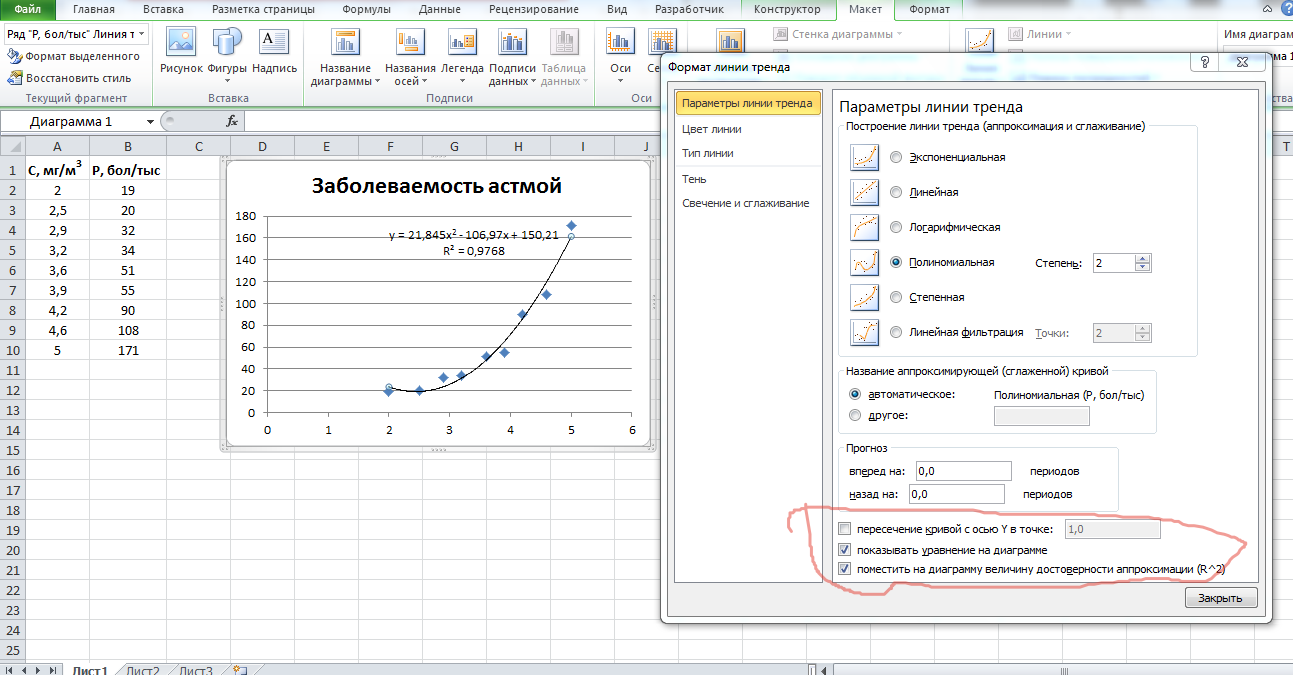
5. Результат работы:
-
файл в Excel
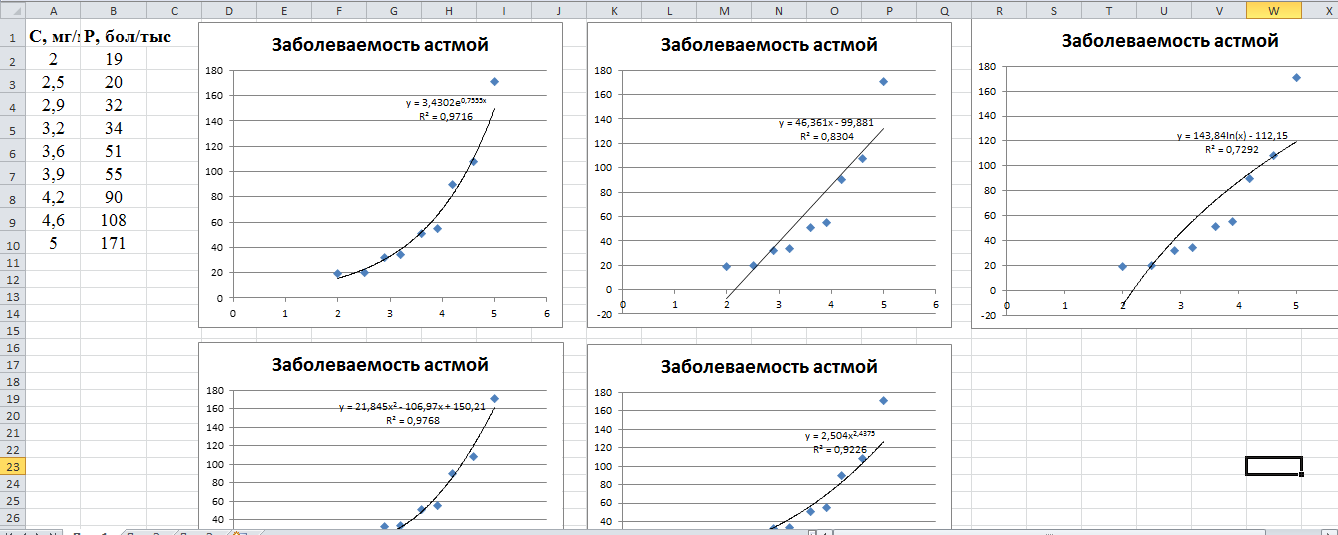
-
Сделать отчёт в тетради, прислать фото в ВК
Форма отчёта
Практическая работа
Отчет по практической работе
«Построение регрессионных моделей с помощью табличный процессор MO Excel»
|
Тип тренда |
Уравнение тренда |
R2 |
|
Линейный |
||
|
Квадратичный |
||
|
Логарифмический |
||
|
Степенной |
||
|
Экспоненциальный |
||
|
Полином третей степени |
Вывод: для графика, полученного по экспериментальным точкам больше всего подходит регрессионная модель, построенная с помощью ________________ функции._______________________________
Ёе формула имеет вид y=_______________________________
R2 = _________________
По полученной формуле рассчитайте y, при x = 15.
________________________________________________________________________________________________________
Вывод по работе: ____________________________________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________
Прислать в ВК: фото конспекта и отчёта, файл с практической работой в Excel.
Прислать до 03.02.22 включительно.
5. Домашнее задание:
Изучить § 18 и составленный конспект


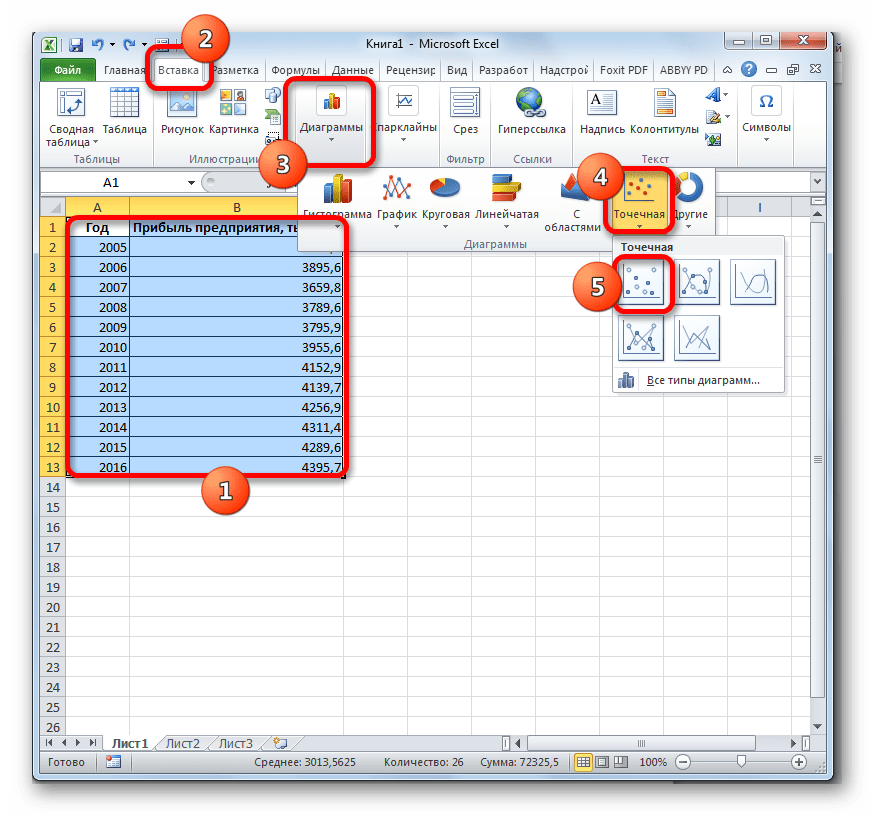
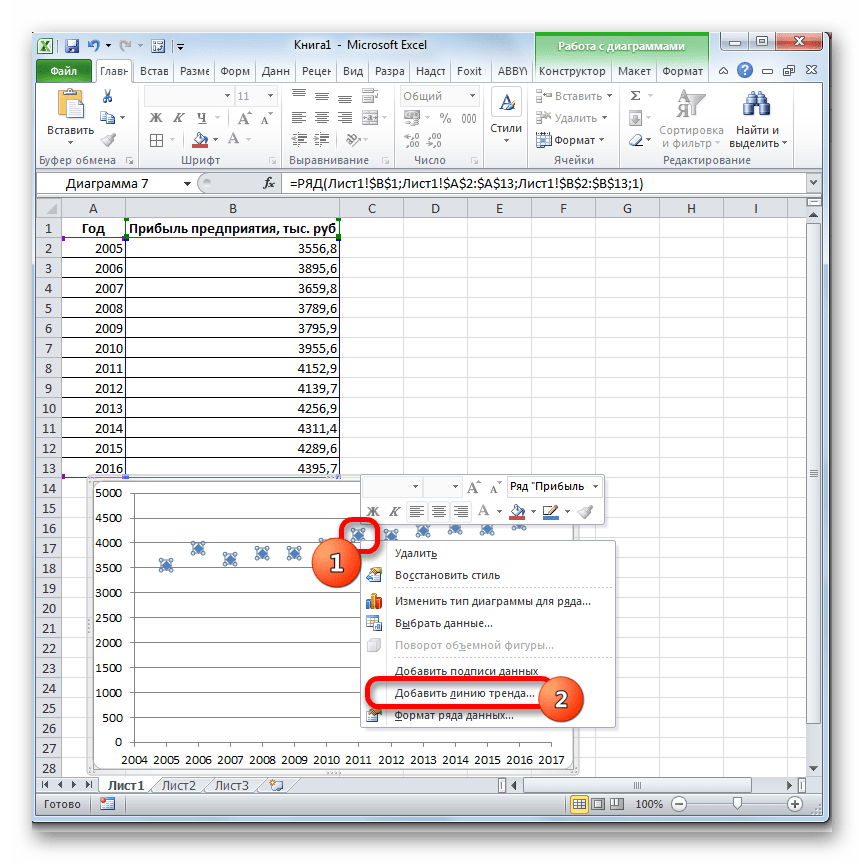
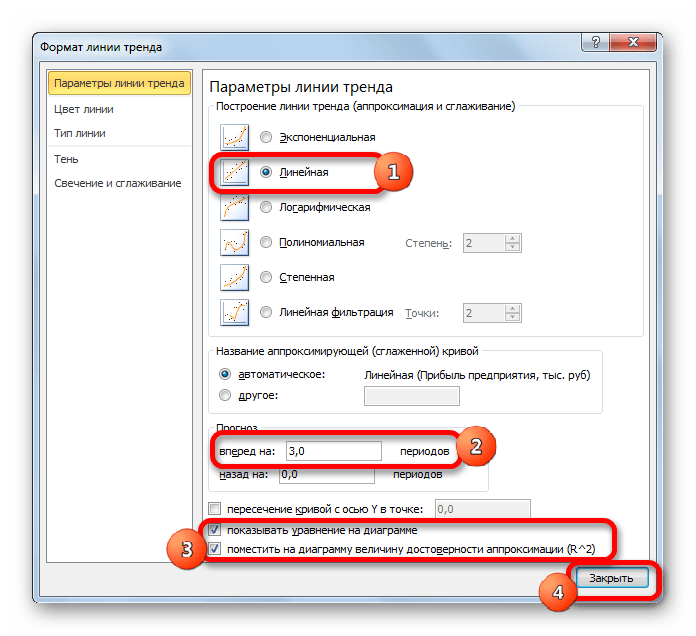
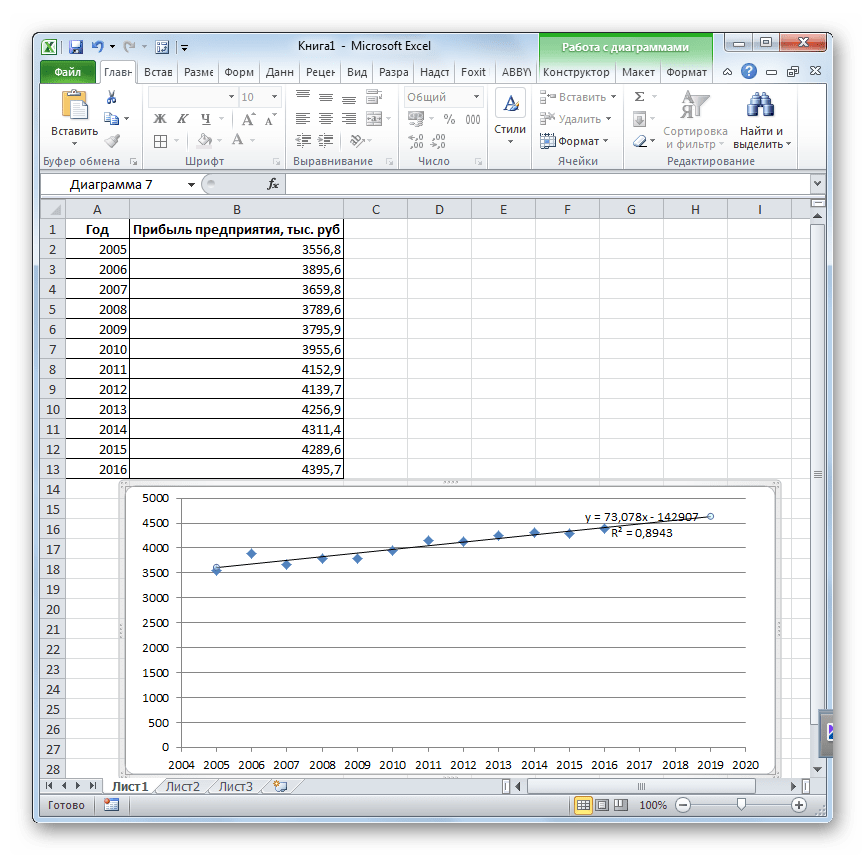
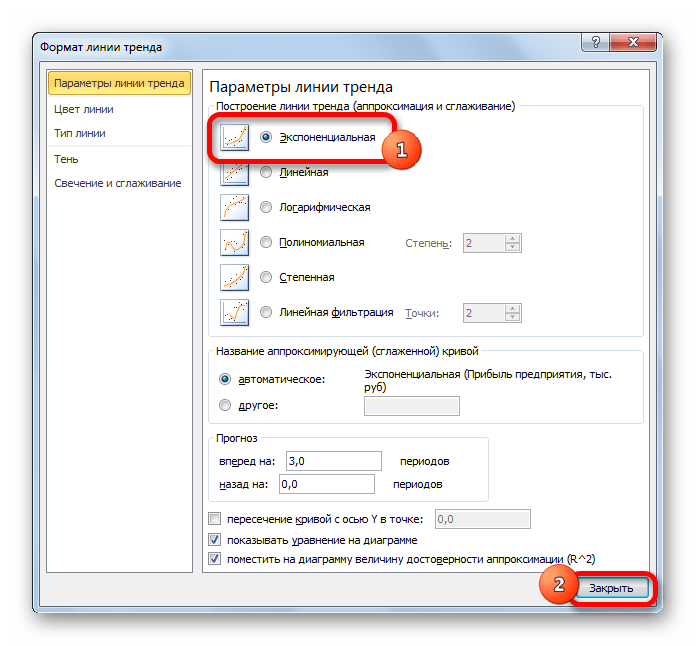

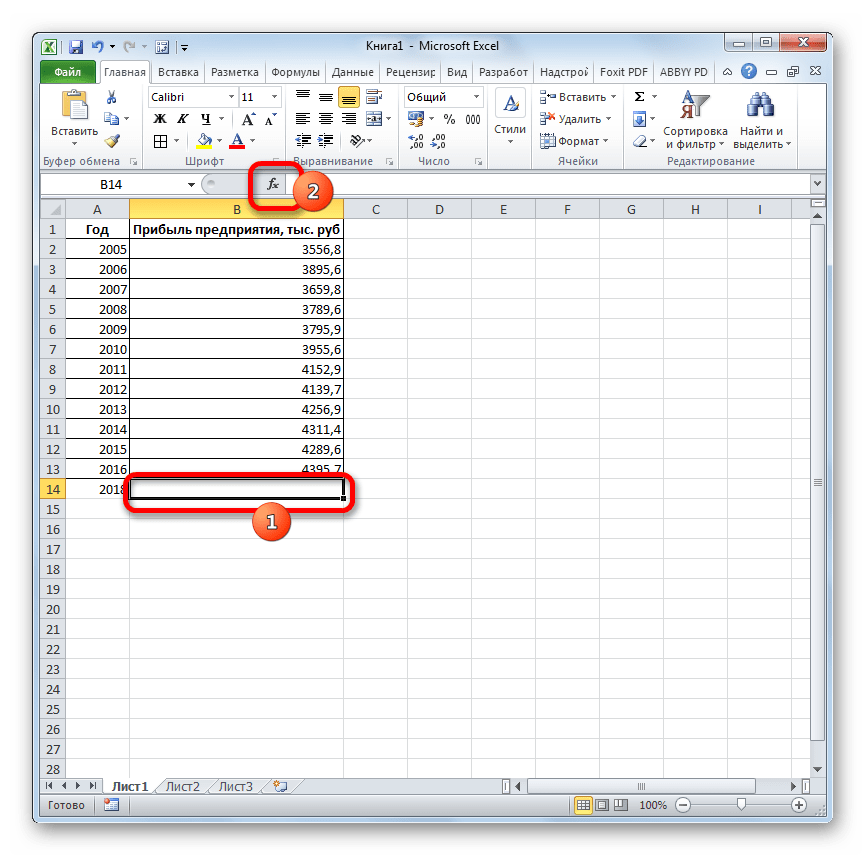
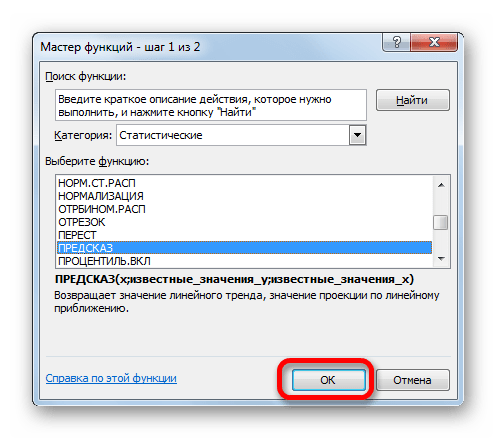
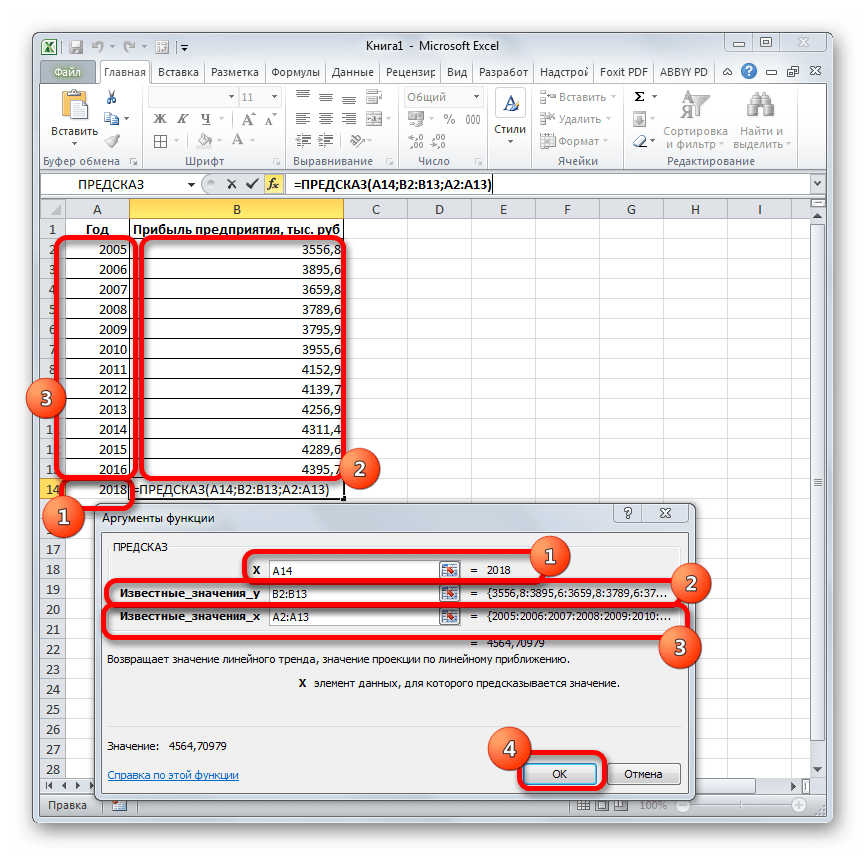
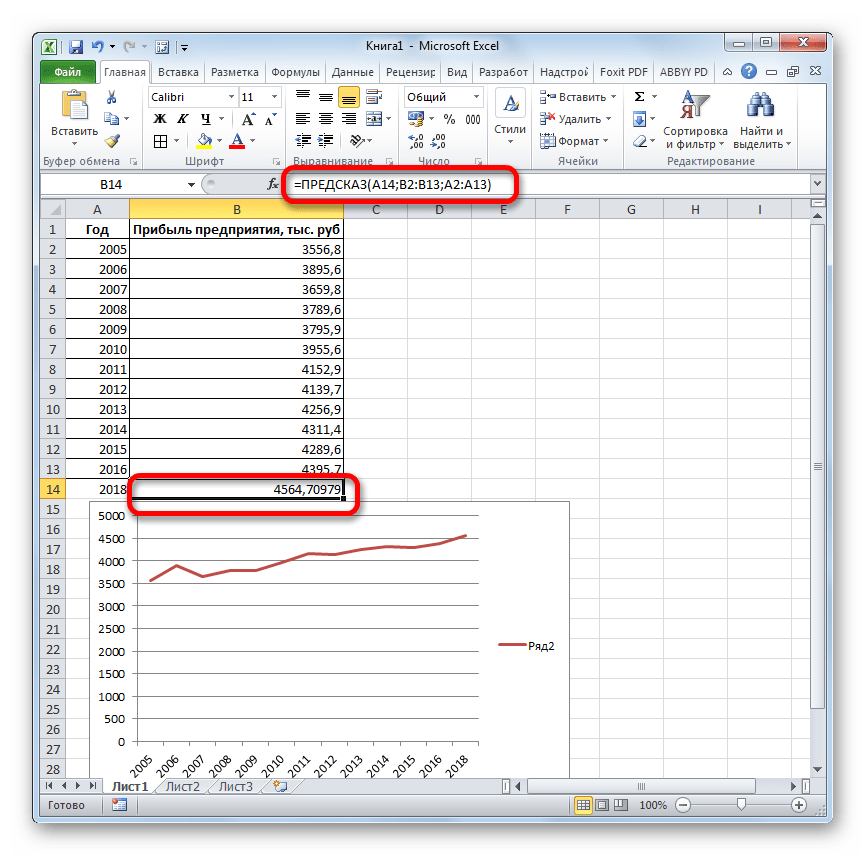
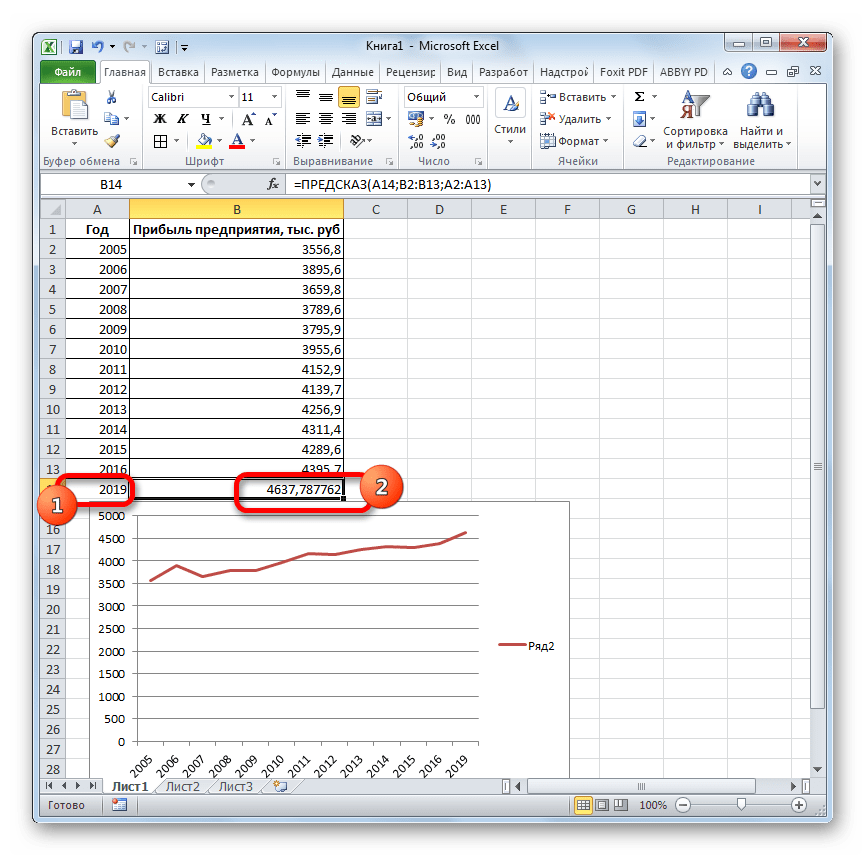
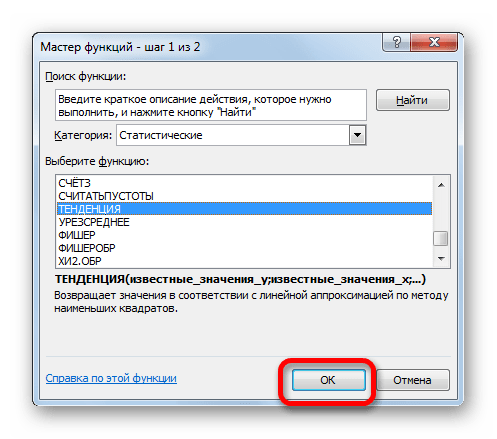
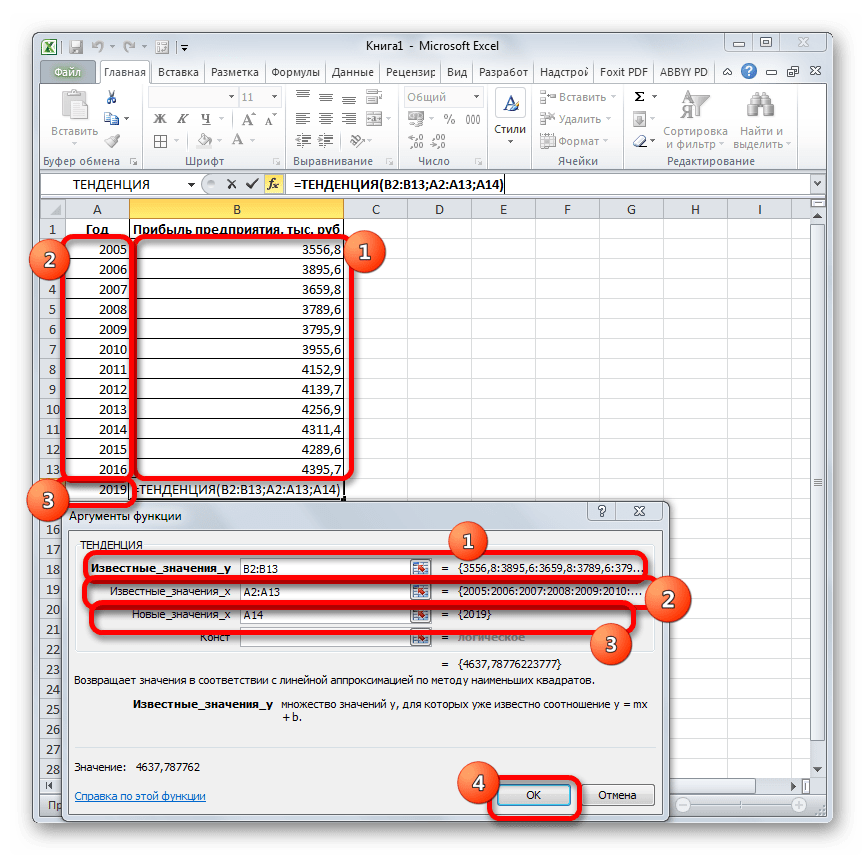
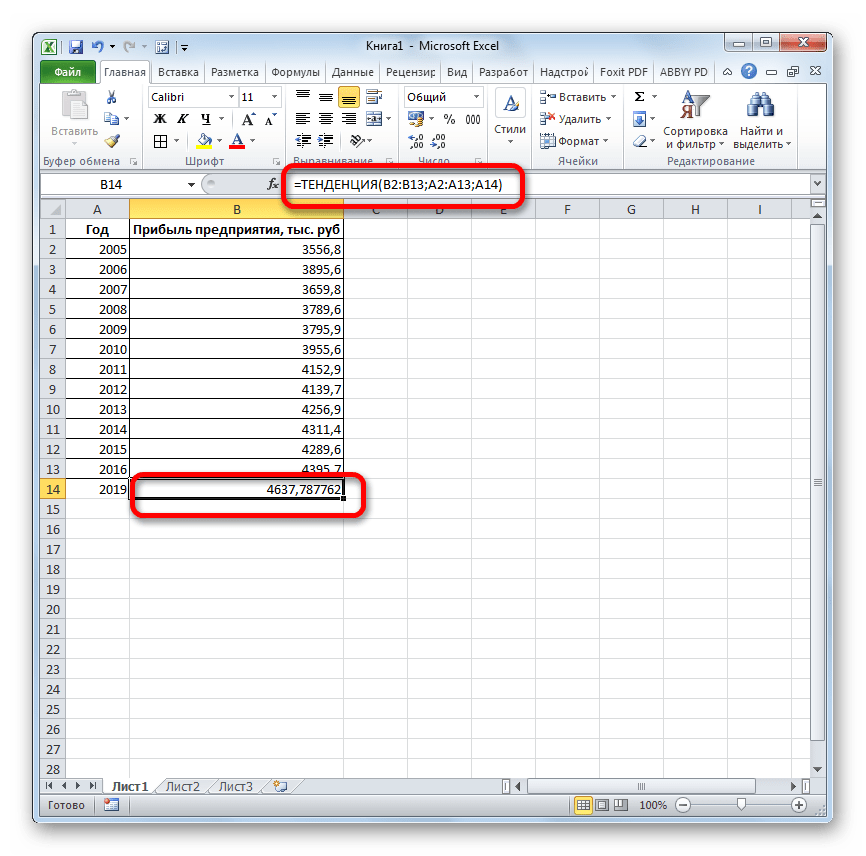
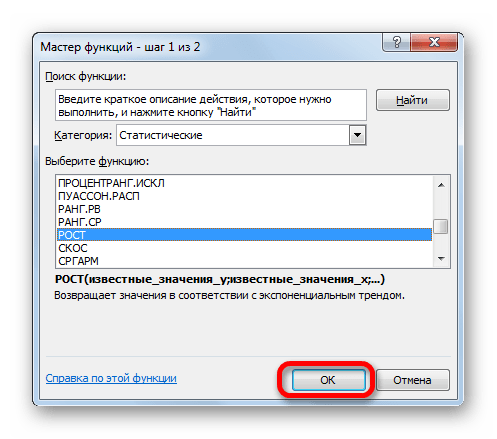
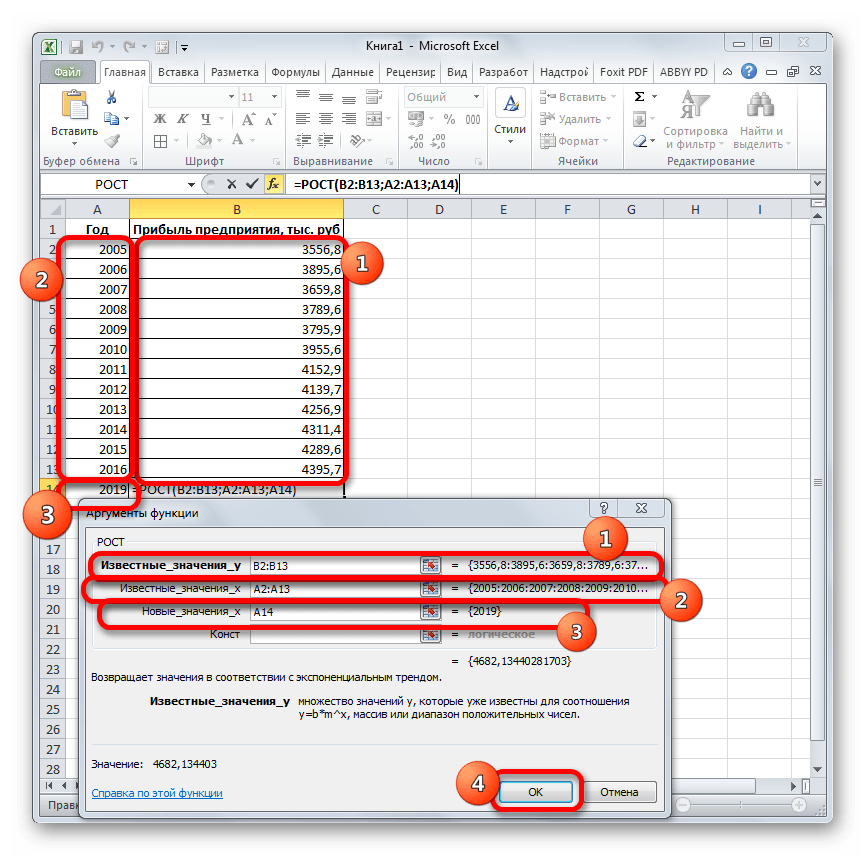
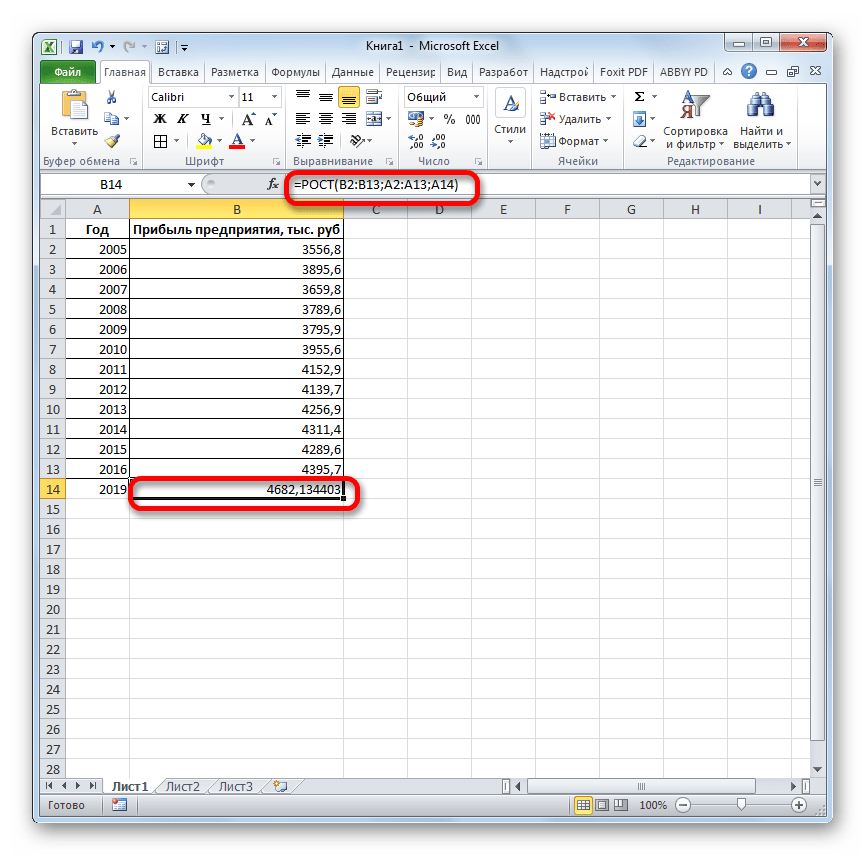
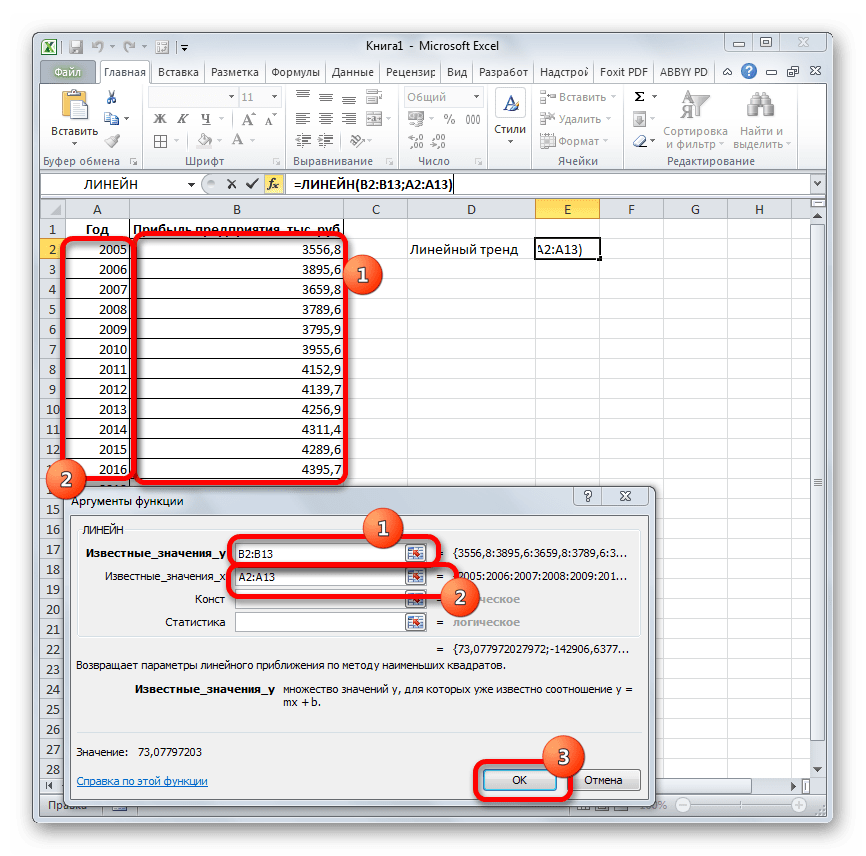
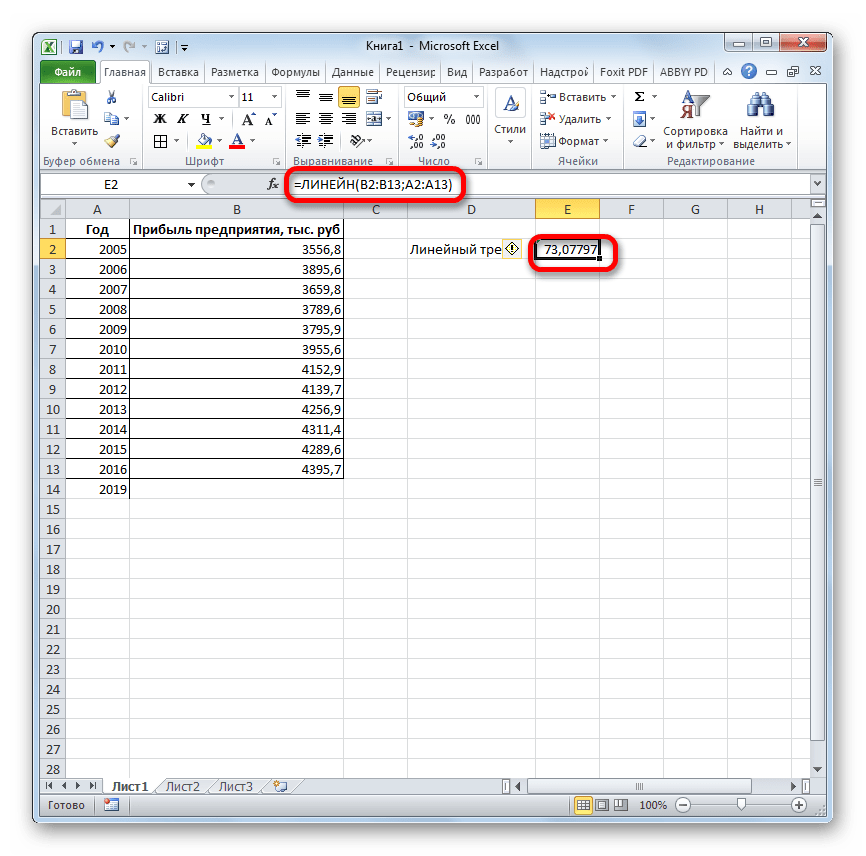
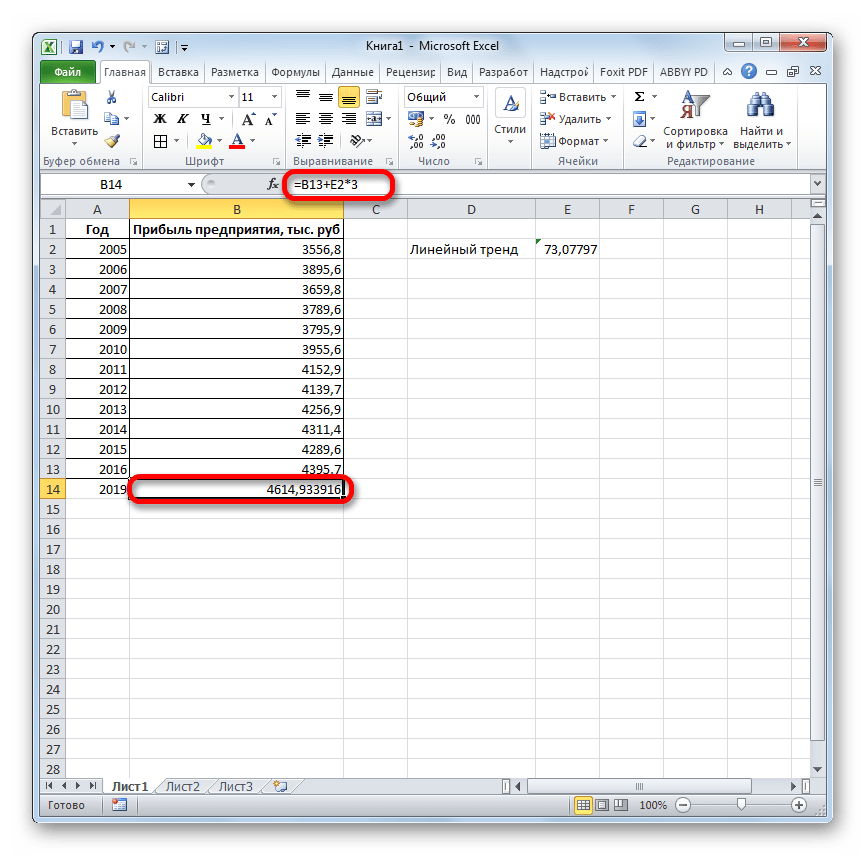
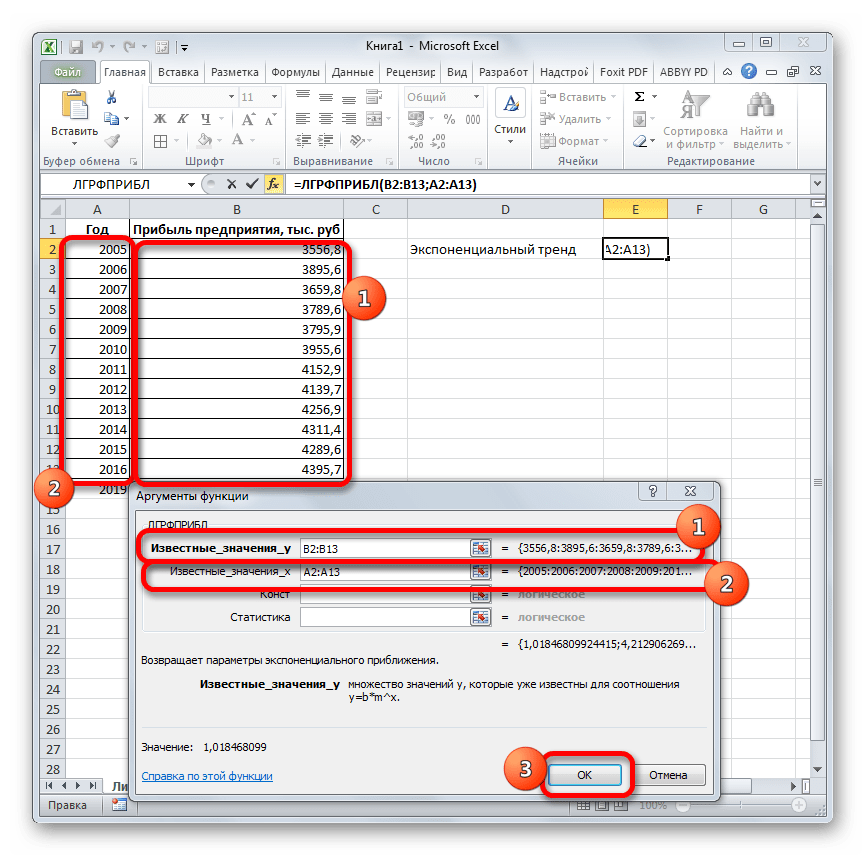
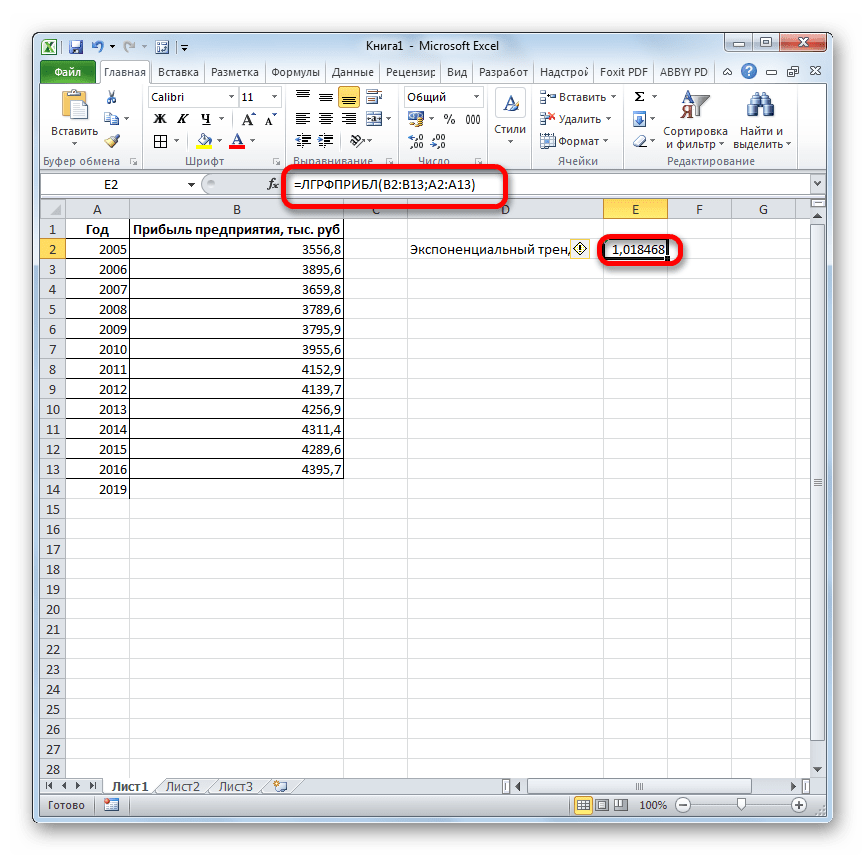













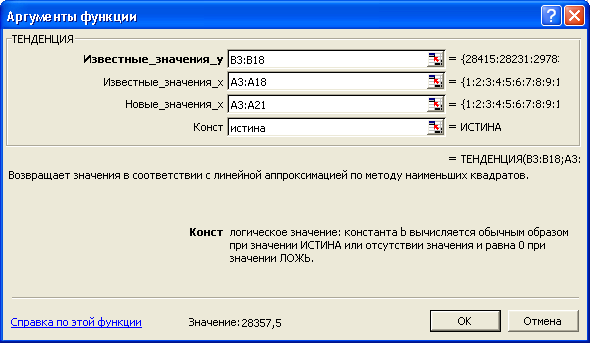


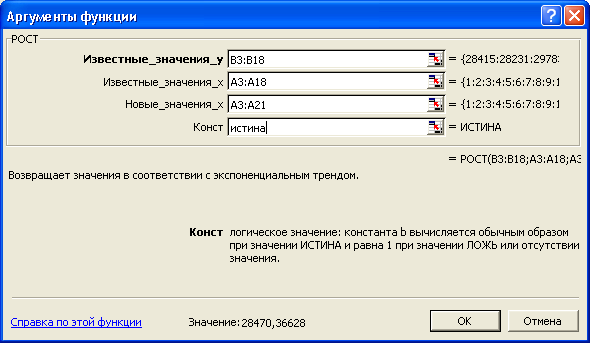
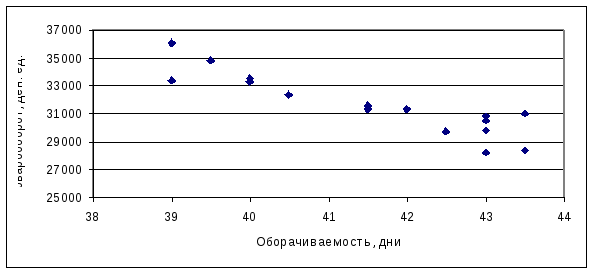



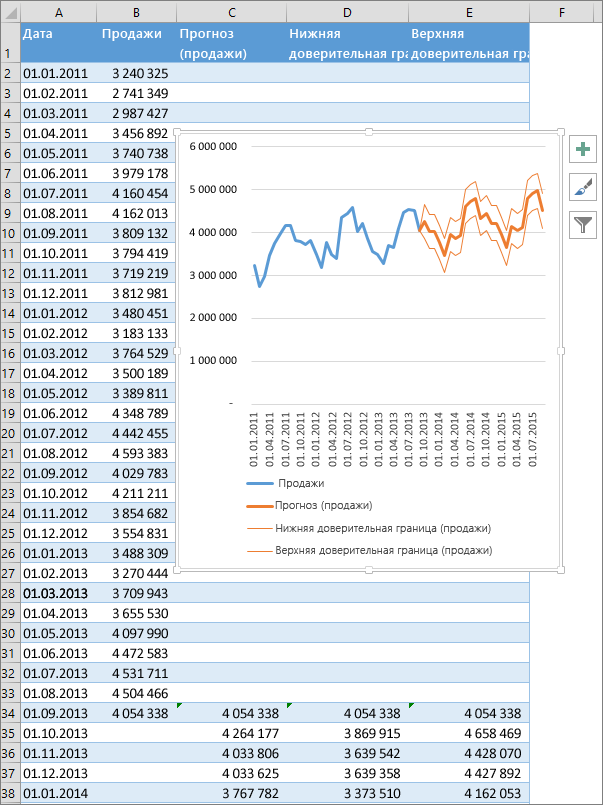

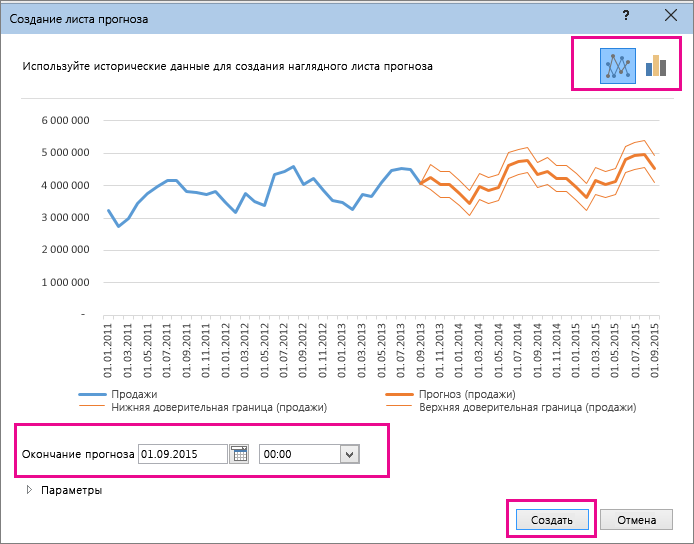
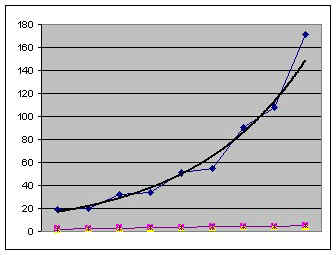 рафик этой функции должен проходить вблизи экспериментальных точек так, чтобы отклонения этих точек от графика были минимальны и равномерны
рафик этой функции должен проходить вблизи экспериментальных точек так, чтобы отклонения этих точек от графика были минимальны и равномерны