Мы занимаемся поиском, а не итерациями
В основном геймдизайн — это процесс поиска. Занимаясь дизайном, мы исследуем множество возможных конфигураций дизайна для решения конкретной дизайнерской задачи. Например, это может быть способ соединения комнат в подземелье, набор функций и навыков, которыми владеют различные игровые агенты, «магические числа», определяющие эффективность юнитов в боевой системе, или само сочетание возможностей, которые будут присутствовать в нашей игре.
Так же, как управляемый ИИ персонаж использует систему поиска пути для перемещения по игровому миру, дизайнеру необходимо перемещаться по очень высокоуровневому пространству возможных конфигураций, беря некую исходную конфигурацию и итеративно изменяя её. Мы внимательно рассматриваем отдельный аспект дизайна — боевую систему, одну из частей игрового мира, дерево технологий в стратегии — и пытаемся найти способ улучшить его, изменив эту конфигурацию.
Дизайнеры любят использовать для описания этого процесса термин «итерация», но больше здесь подошло бы слово «поиск». Правда в том, что когда мы создаём «итерации» дизайна, мы экспериментируем с разрабатываемой игрой. Мы делаем обоснованные предположения о небольших наборах модификаций, превращающих текущую конфигурацию дизайна в новую, которая, как нам кажется, будет лучше соответствовать критериям дизайна.
Такие «итерации» совсем непохожи на линейные изменения, которые обычно происходят в «итерациях» компьютерного кода; гораздо больше они напоминают поиск в лабиринте со множеством резких поворотов и вынужденных возвратов назад. Часто они приближают нас к цели, но часто оказывается непонятно, улучшилась ли от них игра. Иногда обнаруживается, что изменения дизайна, которые, по нашему мнению, должны были улучшить игру, имеют непредвиденные изъяны и нам нужно откатить них или попробовать заново.
Гейм-дизайн — это невероятно сложная дисциплина. Дизайн похож на тёмную комнату со множеством острых предметов; чрезвычайно сложно безопасно передвигаться по нему, отойдя от протоптанных дорог. Почти всегда по пути нас ожидают болезненные травмы, особенно если двигаться слишком быстро. И у нас довольно мало инструментов для освещения этой тёмной комнаты, а также мало чётко заданных и подробных техник выполнения такого процесса дизайнерского поиска.
Из-за существования этой тёмной комнаты мы и выполняем «итерации» — нам неизвестно, какими будут последствия решений, пока мы их не проверим. Другими словами, мы находимся в поиске (Уилл Райт в своём докладе на GDC 2004 назвал это «поиском в пространстве решений»).
Поэтому очень часто дизайн становится узким местом производительности, основным источником недостатков и крупнейшим фактором риска при разработке игр. Бесчисленное количество команд разработчиков оказывалось связанными по рукам и ногам непродуманными дизайнерскими решениями, пробуксовкой в творческом процессе, изменением функционала, неправильным восприятием целевого рынка и другими проблемами дизайна, приводившими к проблемам качества продукта.
С учётом всех опасностей, связанных с экспериментами в дизайне, неудивительно, что многие издатели и крупные разработчики так стремятся избегать риска, предпочитая строго придерживаться сложившихся и хорошо исследованных жанров, лицензий и жанровых допущений. Именно поэтому они не идут на хорошо известные им риски инноваций в дизайне, которые могут принести неизвестные результаты. Исследование тёмной комнаты слишком рискованно.
Нам хотелось бы найти способы изменить такое отношение. Вместо того, чтобы просто избегать инноваций, лучше найти способы улучшить наши дизайнерские навыки, расширить возможности и создать мощные инструменты, которые бы позволили сделать инновации в дизайне безопаснее и эффективнее.
Эта серия статей
Эта статья станет первой в цикле постов о моделировании решений — набора инструментов для декомпозиции решений в формальные модели, по которым затем можно будет выполнять поиск для нахождения наиболее желательного результата.
Моделирование и оптимизация решений часто используются в менеджменте, финансах, планировании проектов и многих других областях для усовершенствования процесса принятия решений и решения различных проблем принятия решений и оптимизаций. Это реализуется поиском среди возможных альтернатив, который быстрее, чем выбор, выполняемый людьми вручную.
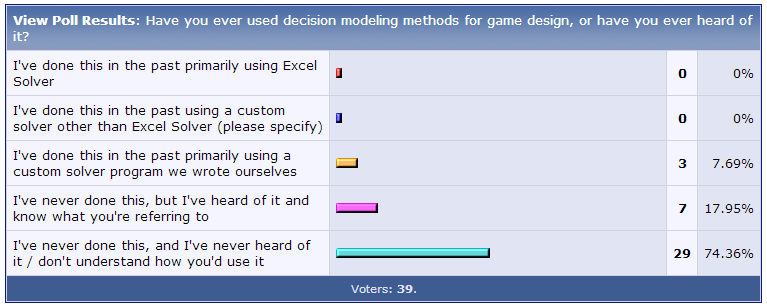
Несмотря на все свои потенциальные преимущества, моделирование и оптимизация решений, похоже, достаточно неизведанная тема для дизайнеров в игровой индустрии. Опрос профессиональных дизайнеров на популярном форуме разработчиков показал, что всего 25% респондентов хотя бы слышали о моделировании решений (decision modeling), и только 8% использовали его на практике. Похожий опрос, проводившийся среди дизайнеров через Facebook, показал примерно такие же результаты при схожем количестве респондентов.
При правильном использовании моделирование решений может значительно улучшить множество аспектов процесса дизайна:
- Оно может помочь в оптимизации конфигурации конкретных систем дизайна или оптимальных значений параметров игры.
- Оно способно пролить свет на решения как на сочетание функций, которые нужно включить в игру.
- Оно помогает моделировать решения, которые может принимать игрок, в частности, идентифицировать доминирующие стратегии или способы, которыми игрок способен «обыграть систему».
В этой серии статей я расскажу о примерах из всех трёх категорий использования.
Определение
Что же такое «моделирование решений»?
Если говорить просто, то:
Моделирование решений — это процесс симулирования решения с последующей автоматизацией поиска его вычисления.
Мы начинаем с задания некоего решения, потом пытаемся подобрать все факторы, из которых это решение состоит, а затем встроить их в модель, которая точно описывает решение, и указать множество входящих переменных и одну выходную переменную. Затем мы выполняем поиск оптимальных решений для множества переменных решения (или входящих переменных), создающих наилучший выходной результат из всех возможных.
Если всё будет сделано правильно, то мы сможем выполнить поиск по гораздо большему количеству возможных решений, чем это было бы сделано вручную или в воображении. Хоть мы и не можем применить эту систему ко всему, для некоторых задач мы можем получить более качественные результаты, вычислить их быстрее, а в некоторых случаях мы даже можем решить задачи, которые нельзя решить никаким другим способом.
Во время этого процесса мы также указываем множество из одного или нескольких условий, которые используются в качестве границ, подтверждающих правильность нашей модели. Такие условия могут ограничивать диапазон значений или тип входящих перменных, а также любые другие аспекты нашей модели.
Зачем строить модели?
Если вы играли в Sid Meier’s Civilization, то наверняка когда-нибудь задавались вопросом: «Постой-ка, как правильнее всего начинать развитие города? Надо ли сначала построить монумент, а затем склад? Или склад нужен первым? А может сначала храм, а потом уже склад? Какое решение лучше принять? Можно ли вообще ответить на этот вопрос?»
Также можно вспомнить механику боя в стратегии реального времени. Балансировка параметров множества юнитов в RTS — задача, печально известная своей сложностью. Что, если бы у нас была система, позволяющая ускорить решение задачи балансировки, отвечая на вопросы о балансировке боя игры без плейтестинга каждого решения? Что, если бы мы могли задавать системе вопросы? Например: «сколько мечников нужно, чтобы победить двух пикейщиков и трёх лучников?» Или: «какая наиболее дешёвая комбинация лучников и катапульт может победить вражескую сторожевую башню?»
На самом деле, такую систему можно создать!
Если у нас получится смоделировать эти задачи дизайна правильным образом, то мы сможем использовать инструменты автоматической оптимизации для поиска по всем возможным ответам для нахождения того, который лучше всего отвечает нашим критериям, без необходимости играть в игру тысячи раз.
Вот пример похожей задачи — пример, который мы решим в будущей статье серии.
Допустим, у нас есть игра под названием SuperTank. В SuperTank мы управляем огромным фантастическим танком, сражающимся на поле боя с другими супертанками. Перед каждым боем мы можем выбрать для своего танка определённую комбинацию вооружения.
У нас есть 100 кредитов, которые можно потратить на снаряжение. Супертанк игрока может нести на себе 50 тонн оружия, а также имеет 3 «критических» слота под специальное высокомощное вооружение.
В игре есть пять следующих типов оружия, и игрок может использовать любое количество каждого типа, или полностью отказаться от него:
Допустим, нам нужно, чтобы супертанк обладал максимально возможным значением урона (будем считать, что указан наносимый в секунду урон, вне зависимости от скорости стрельбы оружия). Также допустим, что всё оружие имеет одинаковую дальность, траекторию снарядов, точность и частоту стрельбы, то есть они идентичны во всём, кроме показанных в таблице значений.
Теперь быстро ответьте, сколько пулемётов, ракет, лазеров и т.д. нужно разместить на супертанке? Какая комбинация из одного или более видов оружия даст нам наибольший урон, не превышая при этом ограничений веса, цены и критических слотов?
Попробуйте решить задачу вручную или с помощью калькулятора.
Можно ли это сделать?
Если попробуете, то быстро убедитесь, что это на удивление сложная задача.
Возможно, существует способ её решения с помощью сложных математических уравнений, но мы дизайнеры, и математика не наш конёк.
Задумайтесь также, как изменится ответ при других параметрах. Изменится ли ответ, если вместо 50 тонн супертанк сможет вместить 60? Или если вместо 100 кредитов у нас будет 110 или 90? Как изменится оптимальное снаряжение? А если у нас будет 2 или 4 критических слота?
А теперь представьте, что у нас есть система, которая мгновенно вычисляет схему размещения оружия с набольшим уроном для любого множества параметров (Вес, Цена, Критические слоты). Достаточно ввести параметры оружия из таблицы, затем ввести параметры супертанка (50 тонн, 100 кредитов, 3 критических слота) — и БУМ! — мы получили наилучшее снаряжение.
Разве не было бы это замечательно?
Мы могли бы использовать эту систему для мгновенного получения ответа на всевозможные полезные вопросы:
- Как будет меняться оптимальная схема при изменении параметров супертанка?
- Как изменится оптимальное снаряжение при изменении параметров оружия?
- Какой максимальный урон может наносить супертанк при любых заданных параметрах (Вес, Цена, Критические слоты)?
- Являются ли все четыре параметра оружия (Урон, Вес, Цена, Критические слоты) соответствующим и сбалансированным для каждого вида оружия?
- Есть ли у нас слишком мощные пушки, которые используются слишком часто? Если какой-то из видов оружия настолько полезен, что всегда правильно использовать его, то оно всегда будет оптимальным решением, поэтому значимого выбора здесь не будет. В таком случае нам стоит или убрать оружие из игры, или изменить его баланс так, чтобы в определённых условиях оно не было полезным.
- Есть ли у нас редко или никогда не используемые виды оружия? Аналогично предыдущему пункту — если какой-то вид оружия так бесполезен, что правильным решением является никогда его не использовать, то тут тоже нет значимого выбора. В таком случае стоит или удалить оружие из игры, или изменить его баланс, чтобы в определённых условиях было разумно его использовать.
Всё это очень важные вопросы дизайна, ответы на которые должен хотеть знать любой дизайнер. Знание этих ответов будет невероятно полезно при балансировке игры SuperTank.
Всего в нескольких абзацах мы описали задачу, которую нам очень сложно решать вручную, но которая тривиально решается с помощью инструментов, встроенных в Microsoft Excel.
В будущей статье мы построим настоящую модель решений для этого примера, которая ответит на все перечисленные вопросы.
Вы увидите, что модель, которую можно создать за считанные минуты, позволит вам решить эту сложную задачу. Всего лишь за небольшое время мы создадим мощный инструмент, позволяющий нам быстро и надёжно исследовать пространство дизайна.
Дорожная карта
В этой серии статей мы проиллюстрируем ещё несколько сложных примеров, и создадим справочные электронные таблицы, чтобы вы смогли выполнить все эти примеры самостоятельно, из инструментов имея только установленный Excel. Среди этих примеров будут следующие:
- Простой пример боя для стратегической игры
- Модель для оптимизации координат нескольких телепортов-«червоточин» относительно друг друга и населённых секторов в космической массовой многопользовательской игре (MMO)
- Модель, определяющую уровень налогов для упрощённой модели города, чтобы уравновесить довольство жителей и поступление налогов в 4X-стратегии наподобие Sid Meier’s Civilization
- Модель выбора заклинаний и навыков для классов персонажей в массивной многопользовательской игре
- Модель оптимизации для определения оптимального порядка строительства планетарной колонии в 4X-стратегии наподобие классической Master of Orion
- Пример команды, пытающейся подобрать правильную комбинацию «фич» для игры, и модель решений, помогающую им выбрать соответствующие компромиссы
В целом, данная серия будет составлена из простых примеров нахождения оптимальных стратегий игрока в конкретных подсистемах игры, а затем перейдёт к моделям решений, позволяющим оптимизировать параметры игровых систем и оптимизиризующих комбинации наборов «фич».
В каждом из этих случаев мы опишем задачу, покажем как смоделировать её в Excel и решить её с помощью встроенного инструмента Solver (в русской версии — «Поиск решений») из Excel. В каждом случае вы увидите, что мы можем сделать это проще, быстрее и надёжнее, чем без применения Solver или аналогичного инструмента. Также для каждого примера я добавлю электронные таблицы, чтобы вы могли скачать их и проверить самостоятельно, воссоздать результаты и поэкспериментировать с собственными моделями.
Кроме того, не забывайте, что внутреннее представление — будь то электронная таблица, программа на языке высокого уровня, или что-то ещё — неважно. Важно не то, в чём мы работаем — в Excel и Solver, Java/C++/C#, или в чём-то ещё, а то, что мы моделируем задачу и стремимся её решить.
Зачем использовать модели решений?
Некоторые читатели сейчас могут быть настроены скептично. Кажется, что построение моделей решений требует много трудозатрат. Зачем нужны все эти усилия, если мы можем провести пользовательское тестирование в виде тестирования фокус-групп и бета-тестирования?
Для начала я скажу, что
моделирование решений применимо не к каждой задаче
. Некоторые задачи слишком сложны или их слишком трудно смоделировать с помощью таких техник, кроме того, в дизайне есть множество аспектов (например, эстетические соображения, ценность игры как развлечения и «ощущения» от игры), которые сложно или даже невозможно смоделировать численно. И моделирование решений совершенно точно не избавляет от необходимости группового тестирования, бета-тестирования или ежедневной игры в собственный проект в процессе его разработки.
Но даже с учётом всего этого, к концу серии статей вам станет ясно, что методы моделирования и оптимизации решений дают нам уникальный и мощный набор инструментов. Они могут полностью или частично решить множество задач, которые нельзя решить любым другим способом, а также снабдить вас ответами и информацией о всевозможных вопросах дизайна, которые сложно получить другим образом.
Как в случае с любым другими инструментом, его пользователь сам должен принимать решение о его применимости.
Существует множество случаев, когда модели решений могут быть неприемлемы или слишком громоздки. Но как вы увидите в серии статей, они ещё и на удивление полезны, и чем больше мы будем принимать правильных решений по дизайну и избавляться от багов на ранних этапах, ещё до стадии тестирования, тем больше вероятность того, что системы дизайна окажутся прочными, увлекательными и безошибочными.
Подумайте об инструментах, доступных типичному программисту. Работа программистов очень сложна, но она упрощается множеством инструментов, помогающих находить баги ещё до этапа тестирования. У них есть компиляторы, которые постоянно напоминают о сделанных опечатках; у них есть защитные практики программирования, выявляющие дефекты ПО; они проводят ревью кода, которые помогают распознать в чужом коде изъяны или указать на порочные практики программирования; кроме того, у них есть множество инструментов профилирования и статического анализа, позволяющие избавиться от всевозможных багов производительности и других дефектов.
Но у дизайнеров таких инструментов нет. Можно сказать, что наша работа так же сложна, но у нас нет компилятора, который бы сказал нам, что мы «совершили синтаксическую ошибку». У нас нет ни профайлера, ни инструментов отладки, ни инструментов статического анализа. Мы не может проводить ревью кода, потому что у нас нет никакого «кода». Мы пишем спецификации и дизайн-документы, и на этом всё; мы можем обмениваться диз-доками и спецификациями функций внутри команды и надеяться, что коллеги дадут нам хорошую обратную связь, но чаще всего нам нужно поместить систему в игру, чтобы понять, работает она или нет.
Это делает дизайн невероятно рискованным, долгим и затратным занятием.
Как и в случае с программированием, людям свойственно ошибаться и это неотъемлемая часть процесса, поэтому нам нужно как можно больше высококачественных инструментов, чтобы защитить себя и свои проекты.
Мы ещё очень далеко от обладания полноценными дизайнерскими инструментами, помогающими дизайнерам в исследовании пространства дизайна. Нам ещё нужно пройти путь, который сделали компиляторы, отладчики, профайлеры и инструменты статического анализа в программировании. Но мы уже видим рассвет нескольких специфических солверов и инструментов дизайна игр, в том числе тестировщика играбельности версии Cut the Rope под названием Cut the Rope: Play Forever (ссылка); абстрактной системы дизайна игр Ludi, которая сгенерировала настольную игру Yavalath (ссылка); и моего собственного автоматизированного помощника Evolver для балансировки мобильной игры City Conquest (ссылка).
Моделирование решений поможет нам сделать ещё несколько шагов к такому уровню поддержки и позволит начать дополнять и расширять собственный интеллект дизайнеров с помощью автоматизированных инструментов. И если у нас есть выбор: иметь или не иметь инструменты, зачем выбирать «не иметь»?
Главное — не электронные таблицы, главное — это модели
Эта серия статей написана для дизайнеров — то есть для всех дизайнеров, вне зависимости от того, какой опыт у них имеется: художественный, программный, опыт создания сторителлинга или настольных игр. Поэтому мы не будем усложнять и обещаем следующее:
- Никакого кода. В статьях не будет абсолютно никакого кода и мы будем иллюстрировать все примеры в Microsoft Excel с помощью встроенного инструмента Solver («Поиск решения»). Однако важно заметить, что эта серия не об электронных таблицах или Excel, а про моделирование и оптимизацию решений. Каждый шаг, который мы сделаем в этой серии, можно так же просто (а иногда и ещё проще) выполнить на любом языке высокого уровня.
- Никакой математики (или, по крайней мере, ничего сложного). Мы стремимся сделать эту серию свободной от математики и не будем использовать ничего, кроме простейших арифметических операций: сложения, вычитания, умножения, деления и иногда вычисления квадратного корня. Греческие буквы будут под строгим запретом.
- Никаких четырёхмерных электронных таблиц; мы будем пользоваться только двухмерными.
Если вы дизайнер, то эта серия статей даст вам все инструменты, необходимые для самостоятельного создания моделей решений без необходимости написания кода вами или программистами. Если вы программист, то серия даст вам достаточно прямолинейную инструкцию по программированию собственных моделей решений на любом ЯВУ, чтобы вы могли строить собственные модели решений, или с нуля, или на основе шаблона, который уже используется в Solver и в Excel.
Эти статьи должны стать всего лишь отправной точкой, чтобы вы могли взять представленные здесь концепции и выбрать самостоятельно: реализовать ли их в Excel, выбрать ли другой инструмент оптимизации, или попробовать построить собственный солвер на языке высокого уровня. Электронные таблицы — это надёжный фундамент для начала, но такие модели решений вероятнее всего станут только вашим трамплином к более богатым и сложным моделям, интегрируемым в архитектуру вашей игры.
Пояснения
Прежде чем мы заберёмся слишком далеко в моделировании решений, нужно дать некоторые пояснения. Моделирование и оптимизация решений не создают никакой завершённой системы для дизайна игры, и мы не будем утверждать ничего подобного. Полезно смотреть на них как на инструмент, помогающий в некоторых аспектах процесса дизайна, и как любой инструмент, он имеет множество ограничений.
Вот некоторые из ограничений, о которых вам нужно знать:
- Их легко использовать неверно. Как и любой другой инструмент, модели решений можно использовать неправильно или несоответствующим образом, а неполная или ошибочная модель решений может привести вас к неверным выводам. Как и в случае с ПО, чем больше становится модель решений, тем больше вероятность наличия в ней ошибок. Кроме того, очень просто ошибочно интерпретировать то, что сообщает вам модель, или построить неполную модель, которая неточно моделирует решение, которое вам нужно принять.
- Они сложны (иногда). Некоторые задачи дизайна слишком сложны, чтобы их можно было при таком подходе смоделировать на практике. Во многих задачах есть слишком много «подвижных частей», или они слишком сильно интегрированы с другими аспектами игры, чтобы их можно было качественно представить в виде отдельной электронной таблицы Excel. В таких случаях приходится принимать решение или о моделировании только части системы (что в результате может привести к неверной/неточной модели), или об интеграции полной модели в саму игру (что может потребовать много усилий), или о полном отказе от моделирования.
- Смоделировать можно не всё. Модели решений не могут сообщить вам, будет ли что-то увлекательным, эстетически приятным, «правильным» или дающим пользователю удобный и доступный интерфейс. Нет общего способа представления таких субъективных и эстетических аспектов в виде дискретной модели. Это значит, что есть чёткие границы использования моделирования решений, и что они гораздо полезнее для дизайна систем и оптимизации механик/динамики, чем для эстетики.
- Они имеют ограничения. Все оптимизаторы имеют свои ограничения, в том числе и применяемый нами Excel Solver, и вполне возможно создать модели решений, имеющие правильные решения, но при этом настолько сложные, что никакой инструмент оптимизации не сможет их найти. В случае достаточно больших неограниченных входящих значений задача может перерасти способности Solver в поиске каждой возможной комбинации входящих значений, и вместо этого ему придётся положиться на различные способы оптимизации. Как мы увидим в этой серии статей, можно упрощать выражения моделей, чтобы «Поиску решений» было проще их обрабатывать. Разработчик Solver (Frontline) предлагает более мощный солвер для более объёмных задач, но совершенно точно можно создать модели, которые Solver решить неспособен.
- Они не гарантируют оптимальности. Вследствие того, что мы работаем со сложными моделями, невозможно быть на 100% уверенными, что мы нашли оптимальное решение. Иногда нам приходится остановиться на втором по оптимальности: мы потратим больше времени на оптимизацию или начнём с нуля и оптимизируем заново, чтобы мы с высокой степенью уверенностью могли бы сказать, что нашли или оптимальное, или очень близкое к оптимальному решение.
Последнее и самое важное:
- Нам нужно убедиться, что модель занимается нужными задачами. Не все задачи достаточно важны, чтобы потребовались такие усилия, нам нужно точно знать свои приоритеты и избегать излишнего сосредоточения на оптимизации бесполезных задач и игнорирования других, более крупных, которые могут оказаться гораздо важнее.
Говоря упрощённо, чтобы моделирование решений было полезным, должны удовлетворяться некоторые условия. Мы должны иметь возможность встроить рассматриваемое решение в некую дискретную модель, и выразить результат решения в виде одного значения. Другими словами, мы должны иметь возможность выразить с помощью модели решений конечное множество входящих данных в одном выходном значении таким образом, чтобы минимизация или максимизация выходного значения давало нам улучшенное решение.
В случаях, когда существуют субъективные аспекты, которые невозможно встроить в эту модель, например, эстетические аспекты или аспекты usability/играбельности, нам потребуется или чётко отделить их от модели решений, или использовать моделирование решений как первый проход, или просто полностью отказаться от моделирования решений.
Чтобы мы могли моделировать решения в электронной таблице, нужно также ограничить сложность модели. Если наша игра выполняет нечто очень сложное, нам, возможно, и не удастся воссоздать эту сложность в Excel. Однако необходимо учитывать, что это ограничение только мощности моделей, которые можно построить в Excel, а не самих моделей решений. В собственном игровом движке мы можем строить намного более мощные солверы, и я надеюсь, что данная серия статей вдохновит вас именно на это.
С другой стороны, все эти ограничения вряд ли делают моделирование решений бесполезным. Даже в случае, когда задача слишком сложна для полной оптимизации в модели решений, эта модель всё равно может помочь нам подобрать множество компонентов дизайна, гораздо более близких к правильной конфигурации, а также найти и отладить многие базовые задачи ещё на ранних этапах разработки.
И даже когда модель решений не может найти оптимальное решение задачи, или потому что задача слишком сложна, или потому что она требует эстетического подхода и других субъективных человеческих факторов, она всё равно может помочь сузить границы решения, позволяя исключить тупики и иными способами снизить сложность задачи.
Наконец, даже если вы решите не использовать моделирование решений, не пытаться оптимизировать электронные таблицы или создавать собственные солверы, понимание моделирования решений всё равно поможет вам изменить взгляд на принятие дизайнерских решений.
Эта серия статей является исследованием. Мы рассмотрим множество примеров задач игрового дизайна и исследуем способы их моделирования и оптимизации, предоставленные нам мощными инструментами дизайна. Вы можете быть скептичными или решить вовсе не использовать оптимизации, но я надеюсь, что вы будете следить за нашими исследованиями и узнаете, чем мы закончим серию.
Заключение
В конце концов, мы хотим создавать дизайн правильно.
Многие вопросы дизайна субъективны, у них нет «правильных» или «неверных» ответов. Но в некоторых случаях они несомненно есть. И в таких случаях мы должны знать, как получить правильный ответ, или по крайней мере понять, как взяться за определение «правильного» ответа и искать, существует ли его решение.
Моделирование и оптимизация решений — это мощные инструменты, которые помогают нам во многих случаях. Я считаю, что такие инструменты должны находиться в инструментарии каждого дизайнера. Приспособившись к ним, вы поймёте, что у этих инструментов есть огромный нереализованный потенциал в более быстром и надёжном исследовании тёмной комнаты гейм-дизайна. В серии наших статей мы покажем, насколько много применений он имеет.
Часть 2. Основы оптимизации и развёртывание симуляции
Электронную таблицу для этой статьи можно скачать здесь.
Подготовка модели решений
Теперь, когда мы рассказали о моделях решений, объяснили, чем они полезны и перечислили некоторые их ограничения, нам хотелось бы проиллюстрировать базовые концепции простым примером.
Но прежде чем мы это сделаем, нужно ввести некоторые правила, касающиеся структуры и формата. Как и в случае с кодом, если не быть аккуратными, электронные таблицы могут быстро превратиться в хаос.
Если говорить упрощённо, то в наших электронных таблицах будет четыре типа ячеек:
- Решение — эти ячейки содержат переменные, которые мы пытаемся оптимизировать — другими словами, мы заставим оптимизатор попытаться найти наилучшие значения для этих ячеек. В этих ячейках мы можем начать с 0 или какого-то другого приемлемого значения по умолчанию, а затем заставить оптимизатор вставить правильные значения. В большинстве случаев мы также ограничим их определённым интервалом, например минимальным и максимальным значениями, а в некоторых случаях целыми или двоичными значениями. Ради согласованности и удобства чтения ячейки решений всегда будут жёлтыми и иметь чёрную рамку.
- «Заданное значение» — значения этих ячеек указываются непосредственно в условиях задачи. Например, если задача говорит нам, что леденец Tootsie Pop весит 17 грамм и каждый раз мы слизываем с него 0,25 грамм, то эти две ячейки будут «заданными значениями». Такие ячейки мы обозначим синим.
- «Вычисление» — значения этих ячеек вычисляются из других ячеек электронной таблицы, которые не подпадают ни под какие другие категории. Мы сделаем их серыми.
- «Цель» (или «выход») — это ячейка, значение которой мы стремимся минимизировать (или максимизировать) при выполнении оптимизатора. В наших примерах всегда будет только одна ячейка цели, она всегда имеет оранжевый цвет и чёрный контур. (Примечание: существуют более мощные солверы, поддерживающие работу с несколькими целями, но для наших статей это будет слишком сложно.)
Когда мы запустим оптимизатор (инструмент Solver («Поиск решений»), встроенный в Microsoft Excel), он просто посмотрит на указанную нами ячейку цели, а затем попытается изменять переменные решений, однако он может (в пределах заданных нами ограничений) или минимизировать, или максимизировать значение этой ячейки цели (любой, которую мы укажем).
Solver почти ничего не знает о вычислениях, происходящих внутри, или о связях между ячейками решений и ячейками целей; он просто выполняет один из нескольких доступных ему алгоритмов, пытаясь минимизировать или максимизировать значение ячейки цели с помощью поиска возможных значений ячеек решений. Такие алгоритмы («Simplex LP», «GRG Nonlinear», «Evolutionary») спроектированы так, что они гораздо умнее исследования всех возможных вариантов переменных решений грубым перебором, и очень часто находят ответы на серьёзные задачи с удивительной эффективностью.
Например, если бы мы хотели узнать, сколько раз нужно лизнуть, чтобы добраться до середины Tootsie Pop, то могли бы использовать подобную электронную таблицу:
Мы можем попросить Excel Solver решить эту задачу, приказав ему минимизировать ячейку цели «Mass remaining on Tootsie Pop» («масса оставшейся Tootsie Pop»), и он бы быстро с помощью экспериментов определил бы, что значение жёлтой ячейки решения, дающее такой результат («Сколько раз лизнуть, чтобы добраться до середины Tootsie Pop») равно 68.
Разумеется, так делать немного глупо, потому что из постановки задачи понятно, что ответ будет 17/0,25=68. Нет смысла запускать оптимизатор для решения задачи, которую можно решить простой арифметикой.
Однако на практике большинство задач, с которыми мы сталкиваемся, не будут иметь простых математических решений. У них будет множество переменных решений, которые ведут к цели неочевидными путями, и сопоставление переменных решений и вывода будет слишком сложной операцией для вычислений математических уравнению вручную (и повторюсь, что в этой серии мы будем старательно избегать сложной математики).
Мы сосредоточимся на описании задач, а всю сложную работу оставим Solver.
Пример 1: налоги
В нашей первой реальной модели решений мы покажем пример определения оптимальной налоговой ставки. Никто не любит налоги, но в данном случае мы будем не платить, а получать налоги; надеюсь, это снизит ваши мучения.
Представьте, что мы создаём 4X-стратегию, похожую на Sid Meier’s Civilization. Мы находимся в процессе создания городов, имеющих определённый уровень недовольства, зависящий от их размера. «Недовольные» жители по сути не настроены на сотрудничество, и мы не получаем от них доходов. Также мы можем попытаться получить деньги с городов, изменяя налоговую ставку каждого города, но при увеличении налоговой ставки уровень неудовлетворённости будет расти экспоненциально, поэтому очень высокие налоги становятся контрпродуктивными.
Допустим также, что мы можем указывать налоговую ставку с инкрементом 10% в интервале значений от 0% до 50%. Вот скриншот, на котором показана похожая система из классической 4X-стратегии Master of Orion 2:
Как дизайнеры, мы хотим задать простой вопрос: какой будет оптимальная налоговая ставка в общем случае?
Это должна быть простая задача, ведь существует всего 6 допустимых значений налоговой ставки. Мы просто можем протестировать каждое из 6 значений вручную, найти то, которое даёт нам наибольший доход, и на этом считать задачу решённой!
(На самом деле, вероятно, можно найти математическое уравнение для решения этой задачи, как и в примере с Tootsie Pop, но это будет контрпродуктивно, потому что мы подготавливаем эту модель, чтобы она выросла в более сложную, которую невозможно будет решить с помощью уравнений. К тому же, в этой серии статей мы избегаем математики.)
Давайте начнём с того, что опишем задачу следующим образом:
- У нас есть город размером 12 (что обозначает 12 миллионов людей). Эти люди представлены как 12 отдельных «граждан».
- Каждый гражданин в любой момент времени может быть доволен или недоволен.
- Довольные граждане платят в виде налогов (налоговую ставку x 10) (то есть, например, налоговая ставка 20% даёт нам 2 единицы валюты в налоговых доходах на каждого довольного гражданина).
- Недовольные граждане не платят налогов.
- В городе есть 3 недовольных граждан, которые остаются недовольными вне зависимости от налоговой ставки.
- Дополнительное количество граждан становится недовольным на основании следующей формулы: (Население) x ((Налоговая ставка) x (Налоговая ставка)) x 3.5, значение округляется вниз до ближайшего целого числа. Для нашего города размером 12, это даст нам 0 дополнительных недовольных граждан при ставках 0% и 10%, 1 дополнительного недовольного гражданина при ставке 20%, 3 дополнительных недовольных граждан при ставке 30%, 6 — при ставке 40%, и 10 — при ставке 50%.
Всё просто, правда?
Мы опишем это в прикреплённой к статье электронной таблице следующим образом:
Вы можете заметить, что мы задаём жёлтую ячейку решения (Tax Level (0-5)) как косвенный способ указания налоговой ставки. Вместо указания налоговой ставки непосредственно в ячейке решения, ячейка вычислений Tax Rate берёт число Tax Level из ячейки решения и умножает его на 10%. Есть логичная причина делать это косвенно, и мы скоро это увидим.
Теперь мы можем экспериментировать и подставить все возможные значения уровня налогов. Можно просто ввести в ячейку Tax Level каждую из цифр от 0 до 5, и получить следующее:
Как видите, существует оптимальное значение налоговой ставки: 30%, которое максимизирует доход от налогов, давая 18 единиц валюты.
Давайте автоматизируем систему!
Это конечно здорово, но что, если у нас будет больше, чем шесть вариантов? Что, если существуют сотни возможных значений налоговой ставки или нам нужно будет изменять и другие переменные решений? Всё станет слишком сложно для тестирования значений вручную.
Как мы увидим, именно для этого и используется Solver.
Для начала мы сбросим значение ячейки Tax Level до нуля. Затем перейдём во вкладку Data («Данные») Excel и увидим в правой части ленты, в разделе Analysis («Анализ»), кнопку Solver («Поиск решения»).
Если вы её не видите, то зайдите в Options («Параметры») Excel, выберите категорию Add-Ins («Надстройки»), убедитесь, что в раскрывающемся списке Manage («Управление») выбрано Excel Add-Ins («Надстройки Excel»), нажмите Go («Перейти…») и убедитесь, что поставлен флажок Solver Add-in («Поиск решения»).
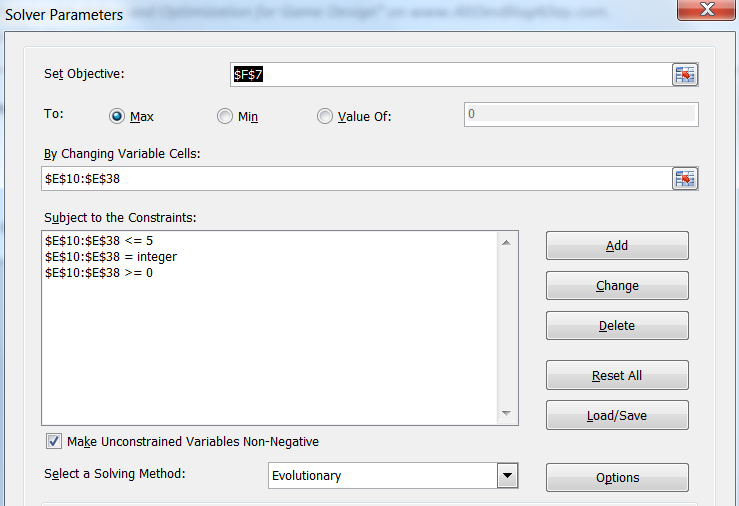
После нажатия на кнопку Solver («Поиск решения») вы должны увидеть похожее диалоговое окно.
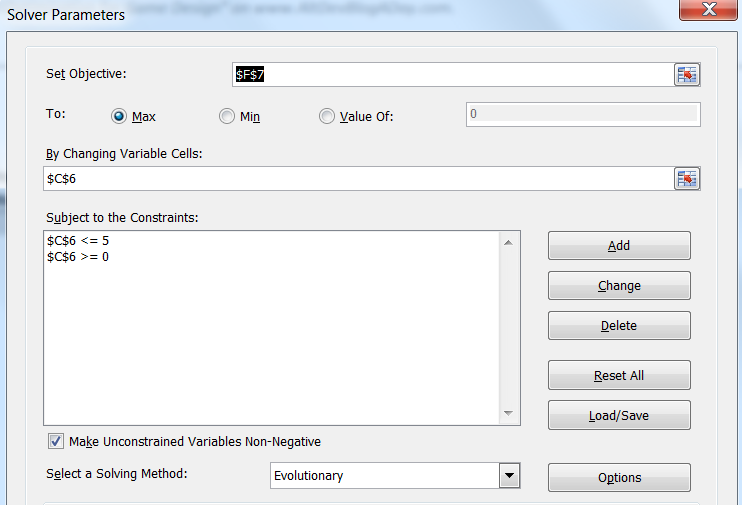
Давайте теперь рассмотрим все этапы настройки диалогового окна Solver.
В поле «Set Objective» («Оптимизировать целевую функцию») мы укажем то, что нужно оптимизировать. В данном случае мы пытаемся получить как можно больший доход от налогов, поэтому выберем оранжевую ячейку цели, которая обозначает доход от налогов, а затем нажмём на «To: Max» («До: Максимум») в списке радиокнопок.
В разделе «By Changing Variable Cells» («Изменяя ячейки переменных») выберем ячейки, которые «Поиск решений» должен вычислить. Нам нужно определить оптимальную налоговую ставку, поэтому выбираем жёлтую ячейку решения (Tax Level (0-5)). Если всё получится правильно, то в результате этой ячейке будет присвоено значение 3, соответствующее налоговой ставке 30%, оптимальность которой мы уже определили при вычислениях вручную.
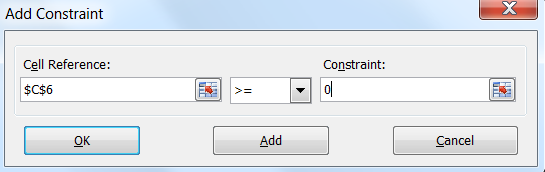
Наконец, нам нужно добавить несколько ограничений. По сути, ограничения являются условиями для любых ячеек нашей модели решений, и Excel Solver сосредоточится только на тех решениях, которые удовлетворяют указанным ограничениям. Такие ограничения могут ограничивать определённые ячейки (обычно ячейки решений и ячейки вычислений) заданными минимальным и/или максимальным значениями, и/или заставлять Solver обрабатывать их как целые или двоичные переменные (0 или 1). Ограничения невероятно полезны для создания корректной модели, которой будет ограничен.
Solver требует хотя бы несколько ограничений, позволяющих ему определить границы ячеек решений — другими словами, минимальное и максимальное значения для каждой ячейки. Чтобы добавить ограничение, нужно нажать на кнопку Add («Добавить») справа, после чего откроется следующее диалоговое окно:
Мы добавим два ограничения, одно для того, чтобы ячейка решения Tax Level удовлетворяла условию >=0, и ещё одно, чтобы ячейка решения была <= 5. Затем выберем в списке Solving Method («Выберите метод решения») значение Evolutionary («Эволюционный поиск решения») и нажмём на Solve («Найти решение»).
Поработав примерно 30 секунд, Solver выдаст нам подобный ответ:
Ой-ёй, возникала проблема. Solver получил верную сумму дохода, но уровень налогов неправильный. Игрок может задавать налоги только с инкрементом в 10%, но Solver очевидно задаёт дробные налоговые ставки, чего игрок сделать не сможет.
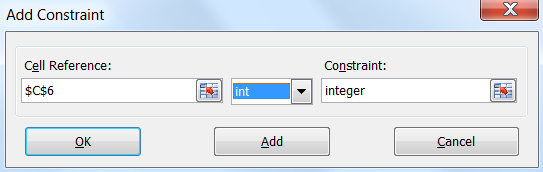
Решить проблему можно, ограничив значения ячейки налоговой ставки только целыми числами. Оно может быть равно только 0, 1, 2, 3, 4 или 5, но без промежуточных значений.
К счастью, в Solver этого можно довольно легко добиться. Откройте Solver, нажмите кнопку Add («Добавить»), выберите ячейку решения Tax Level, а затем выберите в раскрывающемся списке посередине ограничение int («цел»):
Теперь снова запустим Solver и получим следующее:
Идеально! Приложив незначительные усилия, мы получили в Solver правильный ответ. Как мы скоро увидим, при увеличении масштаба задач объём выполняемой за нас инструментом работы значительно превышает время, потраченное на его настройку.
Растущий город
Давайте теперь расширим задачу, слегка усложнив модель города.
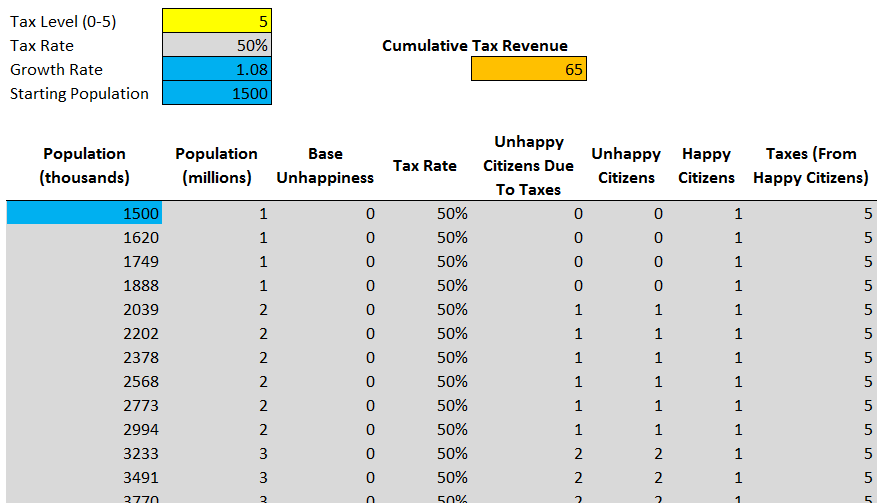
В любой 4X-стратегии города (или планеты, или колонии, или другие населяемые единицы) со временем растут. Мы допустим, что город имеет постоянный прирост в 8% за ход, начиная с 1500 тысяч (1,5 миллиона) горожан, и увеличиваясь до размера в 12 миллионов жителей. Теперь наша электронная таблица будет выглядеть так:
Каждая новая последующая строка таблицы описывает один ход игры.
Также мы изменили вычисления базового уровня недовольства. Теперь он вычисляется как одна вторая от базового уровня населения (в миллионах), округлённая в меньшую сторону. Благодаря этому базовое недовольство будет равно 0, пока город не дорастёт до размера 4, после чего оно будет линейно расти с увеличением размера города.
Как и раньше, мы можем поэкспериментировать с уровнями налогов вручную, изменяя значения Tax Level. Мы получим 0, 102, 190, 222, 144 и 65 единиц валюты в доходах от налогов, при каждом из уровней налогов от 0% до 50%.
И мы снова можем заставить Solver решать эту задачу; он быстро определит, что оптимальная налоговая ставка как и раньше равна 30%, что даёт нам доход в 222 единиц валюты. Вот, как выглядит диалоговое окно Solver:
Переменные налоговые ставки
Но, разумеется, игрок не будет играть таким образом. Наш симулированный «город» задаёт одну налоговую ставку и сохраняет её одинаковой для каждого хода игры. Но настоящий игрок может налоговую ставку в любой момент, и ему часто нужно будет настраивать её, потому что его город растёт и обстоятельства меняются.
Разве не здорово будет, если мы сможем не просто определять единую оптимальную налоговую ставку, но и вычислять оптимальное значение в каждом ходе?
Она мгновенно будет сообщать нам, как игрок может наилучшим образом настроить налоги.
И оказывается, что это можно сделать! Уже настроив модель решений правильным образом, мы можем реализовать это невероятно просто.
Самое большое отличие заключается в том, что нам нужно убрать ячейку решения Tax Level (0-5) и заменить её целым столбцом ячеек уровней налогов, как показано ниже.
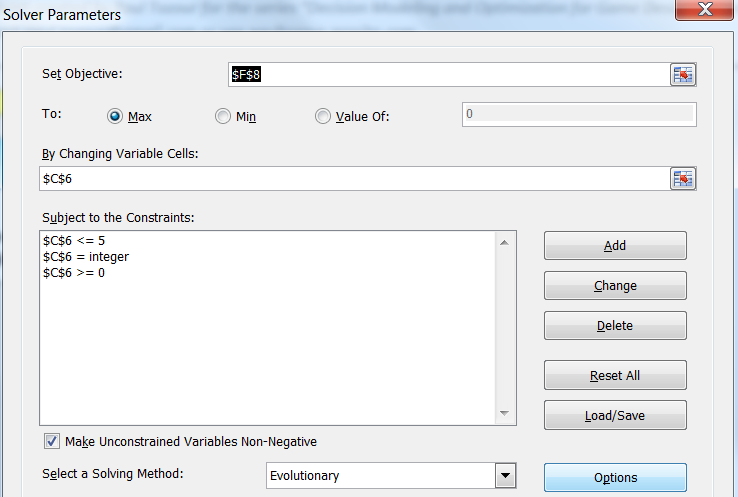
Теперь вместо того, чтобы заставлять Solver оптимизировать отдельную ячейку, мы прикажем ему оптимизировать весь столбец Tax Level. Вот как будет выглядеть диалоговое окно Solver — можно заметить, что оно практически такое же, как и раньше, только вместо одной ячейки переменные и ограничения теперь представляют целый диапазон ячеек столбца Tax Level.
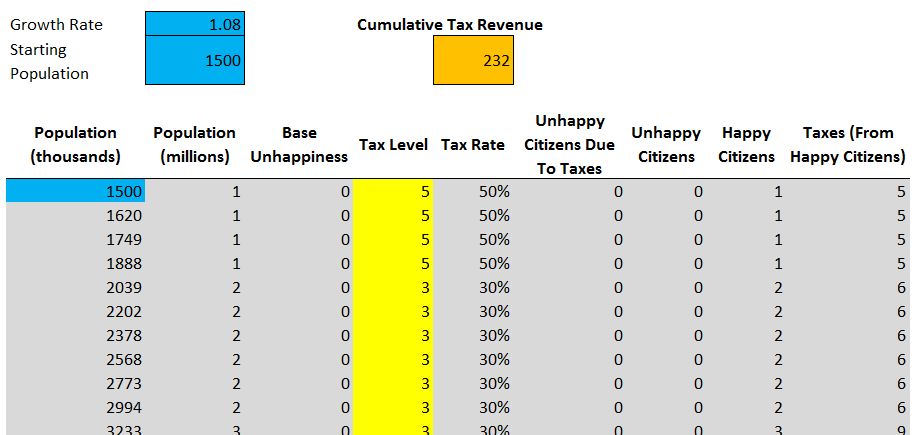
Solver и в самом деле доказывает, что изменение налоговой ставки изменяет результаты — кумулятивный доход теперь составил 232 единиц валюты. По сравнению с одинаковой налоговой ставкой рост составляет всего 5% процентов (222 против 232 единиц), но он всё равно значим, потому что мы знаем, что некоторые игроки смогут его достичь.
Приглядевшись к полученному Solver решению, можно увидеть, что оно начинается с налоговой ставки 50%, потому что город размером 1 не содержит достаточного количества населения для генерации недовольства. В процессе роста города инструмент изменяет в каждом ходу налоговую ставку в интервале от 20% до 30%, в зависимости от того, какая из них принесёт больший доход.
Электронную таблицу для этого примера можно скачать здесь; в ней три этапа этого примера разделены на отдельные листы электронной таблицы (одинаковый налог для города с постоянным населением, одинаковый налог для растущего города и изменяемая налоговая ставка для растущего города).
Заключение
Найденное нами решение показывает нечто интересное: дискретная природа нашего игрового симулятора, представляющая произвольное группирование миллионов людей как дискретных «граждан», которые могут иметь одно или два дискретных состояний довольства, вносит в модель характерные особенности. Хоть самой игре на каком-то уровне потребуется такая дискретизация ради доступности и играбельности, умные и хитрые игроки смогут эксплуатировать эту искусственную дробность для получения преимуществ над игроками, которые не хотят заморачиваться с уровнями налогов в каждом ходе.
Такая ситуация приводит к интересному вопросу: этого ли мы хотим? Заставляет ли механика игроков считать, что для игры им нужно в каждом ходу заниматься микроменеджментом уровней налогов? И хотим ли мы допустить, чтобы нацеленные на победу игроки (power gamers) могли обыгрывать систему таким образом; соответствует ли такой хитрости получаемый ими выигрыш в 5%?
На эти вопросы я не могу ответить. В конце концов, вы являетесь дизайнером, задающим цели дизайна, поэтому вам решать, соответствует ли такой уровень эксплуатации систем целям, которым вы поставили перед игрой.
Разумеется, эта модель — всего лишь голый каркас. В реальной 4X-стратегии игроки могут принимать всевозможные решения о том, как развивать город, строить здания и вносить другие изменения, влияющие на рост города, довольство, доходы от налогов и продуктивность.
В одной из будущих статей цикла мы построим похожую, но гораздо более сложную модель целой планетарной колонии в игре, напоминающей Master of Orion 2. Этот пример будет гораздо более изощрённым, потому что мы сможем принимать в каждом ходу решения, которые будут в дальнейшем влиять на все эти параметры, такие как рост и продуктивность, то есть каждое решение будет иметь последствия, влияющие на последующие решения. Однако мы всё же убедимся, что эволюционный оптимизатор инструмента Solver способен справиться с этой задачей.
В следующей статье мы выполним своё обещание и оптимизируем покупку оружия для SuperTank в примере из вводной статьи.
Страницы работы
Содержание работы
Федеральное агентство по образованию
Новосибирский государственный университет
экономики и управления
Кафедра ЭММ и П
Лабораторная
работа №4
по курсу экономико-математических методов, на тему:
«Решение матричных игр в среде EXCEL»
Выполнила студентка гр.4046
Желтова Е.А.
Проверил: Доцент кафедры
ЭММиП Савиных В.Н.
Новосибирск,2006
План лабораторной работы.
- Составление
моделей, отражающих интересы игроков. - Решение моделей,
отражающих интересы игроков, как задачи ЛП в среде EXCEL. - Анализ
результатов расчетов и их экономическая интерпретация.
- Составление
моделей, отражающих интересы игроков.
Графический анализ матричной игры
Для второго игрока смешанной стратегией будит вектор Q=(q1,q2,q3,q4)
0<=qj<=1
j=1,2,3,4.
q1+q2+q3+q4=1
Тогда средний выигрыш первого игрока:
1-й ход: 4q1-7q2+5q3-7q4<=V
2-й ход: -4q1+7q2-11q3+8q4<=V
V->min
Для первого игрока смешанной стратегией будит вектор P=(p1,p2)
0<=pi<=1
i=1,2.
p1+p2=1
Тогда средний выигрыш первого игрока:
1-й ход: 4p1-4p2>=V
2-й ход: -7p1+7p2>=V
3-й ход: 5p1-11p2>=V
4-й ход: -7p1+8p2>=V
V-> max
Задача оптовой закупки при неопределенности розничной
продажи
Для второго игрока смешанной стратегией будит вектор
Q=(q1,q2)
0<=qj<=1
j=1;2
q1+q2=1
Тогда средний выигрыш первого игрока:
1-й ход: 580q1-2287,2q2<=V
2-й ход: -2287,2q1+1284q2<=V
V->min
Для первого игрока смешанной стратегией будит вектор
P=(p1,p2)
0<=pi<=1
i=1;2
p1+p2=1
Тогда средний выигрыш первого игрока:
580p1-2287,2p2>=V
-2287,2p1+1284p2>=V
V->max
Задача выбора структуры посевов
2.Решение моделей, отражающих интересы игроков, как задачи ЛП в среде EXCEL.
В EXCEL задача составляется на двух листах. На первом отражены
интересы второго игрока, а на втором- первого. На первом листе в ячейки B4:F4 заносятся значения, равные 1. Следующая строка- это нижняя граница,
равная 0, а следующая строка- верхняя граница, равная 1. В ячейки B8:F10 заносятся ограничения модели. В левую часть заносится формула сумма
произведений. В правую часть в первом ограничении заносится 1, в остальные два-
0. Знак в первом ограничении =, а в остальных- <=. Целевая функция на
минимум.
На втором листе в ячейки B4:D4 заносятся 1. Также пишется верхняя и нижняя граница. В
ячейки B8:C12 заносятся 5 ограничений модели. Левая и правая части аналогичны
первому листу. Знак первого ограничения- =, а остальные- >=. Целевая функция на максимум.
Для
составления компьютерного аналога математической модели используется
надстройка «поиск решений». Для вызова окна надстройки необходимо обратиться в
меню сервис/поиск решений.
Для
запуска вычислительного процесса необходимо нажать кнопку ВЫПОЛНИТЬ, после чего
в случае верного решения появляется окно «Результаты поиска решения». При этом
на рабочем листе происходят соответствующие изменения найдены оптимальные
значения переменных, в целевой ячейке – минимальное значение целевой функции, а
на втором листе- максимальное. Внизу экрана появился корешок – отчет по
результатом.
3.Анализ результатов
расчетов, и их экономическая интерпретация.
Графический
анализ матричной игры
P=(0,6; 0,4)
Это означает, что
первый игрок должен делать 1-й ход с вероятностью 0,6, а 2-й с вероятностью
0,4.
V=-1,4 — это означает, что первый игрок проиграет второму
1,4 ед. , и это будет его минимальный проигрыш.
Q=(0; 0,533; 0,467; 0)
Это означает, что
второй игрок должен делать 2-й ход с вероятностью 0,533, 3-й ход с вероятностью
0,467, а первым и четвертым он не должен пользоваться
V=-1,4 – это означает, что второй игрок выиграет 1,4 ед. ,
и это будет его минимальный выигрыш.
Задача
оптовой закупки при неопределенности розничной продажи
P=(0,5547; 0,4353)
Это означает, что
фирма будет рассчитывать на дождь с вероятностью 0,5547, а на солнце с
вероятностью 0,4353.
V= -697 – это означает, что фирма потерпит убытки в
размере 697 рублей, и это будит ее минимальный проигрыш.
Q=(0,5547; 0,4353)
Это означает, что
дождь будит с вероятностью 0,5547, а солнце с вероятностью 0,4353.
Задача
выбора структуры посевов
Приложение
Графический
анализ матричной игры
Лист 1
Похожие материалы
- Решение задач транспортного типа в среде EXCEL
- Анализ пары взаимодвойственных задач в среде EXCEL
- Решение задач целочисленного и нелинейного программирования в среде EXCEL
Информация о работе
Тип:
Отчеты по лабораторным работам
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
Практическая работа по моделированию игр «Чет или нечет?» и «Кубики». Показывает возможность использования генератора случайных чисел в Excel и функции СЧЕТЕСЛИ на примере этих игр.
Описание разработки
1. Игра «Чет или нечет» (вариант 1)
Правила игры: играющий в ответ на появляющийся на экране вопрос «Чет (2) или нечет (1)?» прогнозирует появление одного из 2 случайных чисел: 1 или 2.
После ввода пользователем ответа в ячейку B2 случайным образом генерирует одно из указанных чисел, которое выводится в ячейке В3, и определяется результат прогноза («Верно» или «Неверно»).
Решение:
В ячейку В3 введите формулу: =1 + ЦЕЛОЕ(СЛЧИС()*2), а в ячейку В4 — формулу: = ЕСЛИ(В2 = В3; ”Верно”;”Неверно”).
Однако, при таком оформлении листа еще до ввода играющим своего мнения в ячейку В2 проявятся 2 недостатка:
- В ячейке В3 будет выводиться какое-то число, нужно чтобы оно появлялось только после ввода значения в ячейку В2. Это можно сделать, используя функцию ЕПУСТО: =ЕСЛИ(ЕПУСТО(B2);» «;1+ЦЕЛОЕ(СЛЧИС()*2))
- В ячейке В4 будет выводиться ответ «Неверно», что некорректно. Чтобы устранить этот недостаток, здесь также следует применить функцию ЕПУСТО:
=ЕСЛИ(ЕПУСТО(B2);»»;ЕСЛИ(B2=B3;»Верно»;»Неверно»))
Теперь ответы в ячейке будут появляться только при наличии чисел в ячейке В2.
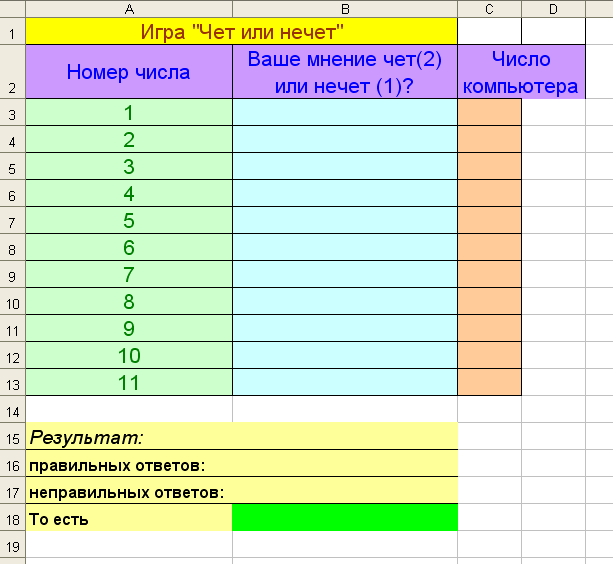
2. Игра «Чет или нечет» (вариант 2)
Правила игры. Играющий дожжен спрогнозировать 11 случайных чисел 1 или 2 (ячейки В3:В13), после чего в ячейках С3:С13 появляются числа, сгенерированные компьютером, а также определяется результат игры.
В ячейке В18 должен быть выведен текст «Вы выиграли!» или «Выиграл компьютер!» (ничьей быть не может). Текст в ячейках А15:А18 и В16:В18 должен выводиться только после заполнения играющим ячейки В13 и исчезать после ее очистки. Необходимые формулы оформите самостоятельно.
*Для подсчета количества правильных и неправильных ответов можно использовать функцию СЧЕТЕСЛИ.
3. Игра «Кубики»
Игра моделирует бросание игрального кубика каждым из 2 участников, после чего определяется результат:
Результат выводится в ячейке В6 в виде «Выиграл Петя» или «Выиграл Вася» или «ничья». Число в ячейке В3 и текст в ячейках А3 и А4 должны выводиться только после ввода имени первого игрока, а число В5 и текст в ячейках А5, А6, В6 – только после ввода имени второго игрока.
4. Смоделировать игру «Кубики» для трех игроков.
Содержимое разработки
11 класс
Практическая работа
«Моделирование простейших игр в Excel»
-
Игра «Чет или нечет» (вариант 1)
Правила игры: играющий в ответ на появляющийся на экране вопрос «Чет (2) или нечет (1)?» прогнозирует появление одного из 2 случайных чисел: 1 или 2.
После ввода пользователем ответа в ячейку B2 случайным образом генерирует одно из указанных чисел, которое выводится в ячейке В3, и определяется результат прогноза («Верно» или «Неверно»).
Решение:
В ячейку В3 введите формулу: =1 + ЦЕЛОЕ(СЛЧИС()*2), а в ячейку В4 — формулу: = ЕСЛИ(В2 = В3; ”Верно”;”Неверно”).
Однако, при таком оформлении листа еще до ввода играющим своего мнения в ячейку В2 проявятся 2 недостатка:
-
В ячейке В3 будет выводиться какое-то число, нужно чтобы оно появлялось только после ввода значения в ячейку В2. Это можно сделать, используя функцию ЕПУСТО: =ЕСЛИ(ЕПУСТО(B2);» «;1+ЦЕЛОЕ(СЛЧИС()*2))
-
В ячейке В4 будет выводиться ответ «Неверно», что некорректно. Чтобы устранить этот недостаток, здесь также следует применить функцию ЕПУСТО:
=ЕСЛИ(ЕПУСТО(B2);»»;ЕСЛИ(B2=B3;»Верно»;»Неверно»))
Теперь ответы в ячейке будут появляться только при наличии чисел в ячейке В2.
-
Игра «Чет или нечет» (вариант 2)
Правила игры. Играющий дожжен спрогнозировать 11 случайных чисел 1 или 2 (ячейки В3:В13), после чего в ячейках С3:С13 появляются числа, сгенерированные компьютером, а также определяется результат игры.
В ячейке В18 должен быть выведен текст «Вы выиграли!» или «Выиграл компьютер!» (ничьей быть не может). Текст в ячейках А15:А18 и В16:В18 должен выводиться только после заполнения играющим ячейки В13 и исчезать после ее очистки. Необходимые формулы оформите самостоятельно.
*Для подсчета количества правильных и неправильных ответов
можно использовать функцию СЧЕТЕСЛИ.
-
Игра «Кубики»
Игра моделирует бросание игрального кубика каждым из 2 участников, после чего определяется результат:
Результат выводится в ячейке В6 в виде «Выиграл Петя» или «Выиграл Вася» или «ничья». Число в ячейке В3 и текст в ячейках А3 и А4 должны выводиться только после ввода имени первого игрока, а число В5 и текст в ячейках А5, А6, В6 – только после ввода имени второго игрока.
-
Смоделировать игру «Кубики» для трех игроков.
-80%
Похожие файлы
-
Урок по моделированию
-
Применение кейс-технологии на уроках информатики
-
Рабочая программа Информатика и ИКТ для 8 класса по учебнику Н. В. Макаровой
ПРАКТИЧЕСКАЯ
РАБОТА №11
Моделирование
случайных процессов в Microsoft Excel
Упражнение 1. ВЕРОЯТНОСТНАЯ МОДЕЛЬ
Цель: Создание
вероятностной модели в электронных таблицах, знакомство с функцией для
генерации случайного числа.
Задание 1. Студенту для
поездки подходит 2 маршрута автобуса. У одного автобуса интервал 10 мин, у
другого — 15 мин. Определить среднее время ожидания и построить в одной системе
координат:
1) график времени ожидания за каждый день года,
2) график среднего времени ожидания для каждого дня
года.
Обоснование задачи. Так как
на остановку студент приходит по-разному, то время ожидания до прибытия
каждого из автобусов будет каждый раз меняться и будет являться случайной
величиной.
СЛУЧАЙНАЯ ВЕЛИЧИНА, СЛУЧАЙНАЯ ПЕРЕМЕННАЯ [random
value, random variable] — всякая наблюдаемая величина, изменяющаяся при
повторении условий, в которых она возникает.
ВЕРОЯТНОСТНАЯ МОДЕЛЬ – это модель, которая содержит
случайные элементы. Таким образом, при задании на входе модели некоторой совокупности
значений, на ее выходе могут получаться различающиеся между собой результаты в
зависимости от действия случайного фактора. Вероятностные модели базируются на
использовании больших серий испытаний со случайными параметрами, причем
точность полученных результатов зависит от количества проведенных опытов.
Для генерации случайной величины в Microsoft Excel
требуется в ячейку ввести формулу =СЛЧИС(). Эта функция возвращает
случайное число из диапазона [0;1).
Чтобы получить случайное вещественное число из
диапазона [0;а), можно использовать следующую формулу: =СЛЧИС()*a.
Если требуется получить случайное вещественное число
между a и b, можно использовать следующую формулу: =СЛЧИС()*(b-a)+a.
Порядок
выполнения.
1. Постройте
в Microsoft Excel таблицу
вида
2. Внесите в
таблицу исходные данные
a –
интервал ожидания 1 автобуса, а=10 минутам;
b –
интервал ожидания 2 автобуса, b=15 минутам;
d – количество
дней в исследуемом периоде (в году) d=365.
3. Заполните
расчетную таблицу формулами в соответствии с математической моделью, используя
абсолютную и относительную адресацию в формулах.
w1 – время
ожидания 1 автобуса (случайное число на отрезке [0;а]);
w2 – время
ожидания 2 автобуса ( случайное число на отрезке [0;b]);
x – время
ожидания за текущий день,
x = min (w1, w2)
t’ср– среднее
время ожидания на текущий день, за n – кол-во дней, для которых
среднее подсчитано;
tср – среднее
время ожидания за год
tср = (x1+x2+…+xn ) / d
4.
Вычислите
время все параметры на исследуемый период (Скопируйте, если это нужно, формулы
вниз на все дни года, используя маркер заполнения)
5.
Построить
на одной диаграмме два графика по заданию (для x и t’ср)
на отдельном листе.
Задание 2. Используя
модель, построенную для решения задачи, определить
·
среднее
время ожидания, если ожидание 1 автобуса 10 мин, 2 автобуса — 60 мин
·
каково
среднее время ожидания, если интервалы автобусов совпадают?
Упражнение
2. БРОСАНИЕ МОНЕТЫ
Цель: моделируя
возможные игровые ситуации (варьируя ставки в данной игре) выяснить, какая
тактика чаще приводит к результату (положительному или отрицательному)
Задание 3. У вас есть 10
монет. Вы хотите увеличить свой капитал в два раза, испытав заодно и свою
судьбу. Суть игры проста, играя с маклером, вы делаете ставку и бросаете
монету. Если выпадет «орел», маклер выдает вам сумму вашей ставка, в противном
случае – вы ему отдаете сумму. Ставка может быть любой от 1 до 10 монет. Вы
можете назначить самую большую ставку в 10 монет, и тогда за один бросок
выяснится, «сорвали» ли вы банк или, наоборот, обанкротились. Опытные игроки
действуют более осторожно, начиная с маленькой ставки.
Удвоение начального капитала или банкротство приводит
к незамедлительному прекращению этого сеанса игры и расчету. Игра может
продолжиться по вашему усмотрению.
Имитировать результат падения монеты можно с помощью
функции СЛЧИС(). Поскольку вероятность выпадения той или иной стороны 50%,то,
если СЛЧИС()<0,5, то результат «орел» (1), в противном случает – «решка»
(0).
Формула
падения монеты при броске имеет следующий вид:
Бросок
= ЕСЛИ (СЛЧИС()<0,5; 1; 0)
Здесь
«1» на выходе функции означает, что игрок угадал, то есть выпал «орел», а «0» —
не угадал, то есть выпала «решка».
Формула
изменения наличности игрока:
Наличность=
ЕСЛИ(Бросок=1; Наличность+Ставка; Наличность-Ставка)
Формула
определения выигрыша:
Выигрыш=ЕСЛИ(Наличность<2*Начальный
капитал; «-»; «банк»)
Здесь
выдается сообщение «банк» при увеличении наличности вдвое или больше, что
является условием прекращением игры.
Функция
определения проигрыша:
Проигрыш=ЕСЛИ(Наличность>0;
«-»; «банкрот»)
Здесь
выдается сообщение «банкрот» по окончании наличности, что так же является
условием прекращения игры.
Порядок
выполнения работы
1. Создайте в
Microsoft Excel таблицу
вида:
2. Ввести
расчетные данные
3. Провести
следующие исследования
·
Исследовать
выпадения «орла» и «решки» в течение сеанса игры
·
Собрать
статистические данные о выигрыше и проигрыше в течение 10-20 сеансов игры с различными
значениями ставок и исследовать их.
4. Ответьте
на вопросы
·
Кто
чаще выигрывает: казино или игрок?
·
Сколько
в среднем надо сделать бросков до окончания игры?
Упражнение
3. ИГРА В КОСТИ
Цель: Создание игровой
модели, основанной на случайных событиях
Задание 4. Два игрока
бросают по две игральные кости. Сумма очков, выпавших на двух игровых костях,
накапливается. Игра прекращается, когда один из игроков достигает суммы 101.
Игра повторяется до трех побед.
Математическая модель складывается из следующих
рассуждений.
На игровой кости имеется 6 граней с количеством точек
от 1 до 6.
Модель, имитирующая бросание двух костей одним
игроком:
К1=ЦЕЛОЕ (1+6*СЛЧИС())
К2=ЦЕЛОЕ (1+6*СЛЧИС())
Случайные значения суммируются. Суммы бросков по
каждому игроку накапливаются в отдельных столбцах СУММА ПЕРВОГО и СУММА ВТОРОГО
и анализируются после каждого броска в столбце РЕЗУЛЬТАТ
ЕСЛИ (ИЛИ («Сумма первого»>101; «Сумма второго»>101);
«конец игры»; «-»)
Здесь, когда обе суммы меньше 101, в столбце
записывается «-»,а при превышении хотя бы одним игроком порога в столбце
записывается «конец игры». Кто победил, можно определить по соседним столбцам.
Игра прекращается при проявлении сообщения «конец
игры» в столбце РЕЗУЛЬТАТ
Создайте таблицу вида
Заполнить самостоятельно по предложенному материалу,
используя абсолютные и относительные ссылки.
Вопросы:
·
Как
части в нашей жизни происходят случайные процессы?
·
Все
ли случайные процессы можно смоделировать на компьютере?
·
Помогают
ли построенные модели для выбора в жизни?
Литература:
1. Дегтярева
И. Ю. Моделирование процессов. Вероятностные модели [текст] URL: http://www.metod-kopilka.ru/page-2-2-6-11.html
2. Информатика
и ИКТ. Задачник по моделированию. Базовый уровень /Под ред.
Н.В. Макаровой. – Питер. 2007. – 192 с.
Вам бывает скучно на работе? Часто сидите два-три дня без единого намёка на трудовую деятельность и пытаетесь ее имитировать, а руководство так и ждет ошибки с вашей стороны?
Теперь этого можно будет избежать, ведь в разработке находится пошаговая RPG в стиле Dragon Quest на NES для офисного приложения Excel.
Конечно, идея не нова. В Excel и раньше делали разнообразные игры (даже полноценный шутер). Но если вы читали мои предыдущие статьи, то поймёте, что создавать троллейбусы из батонов белого (или чёрного) хлеба — мое небольшое хобби.
Перейдём же к делу
На данный момент готова альфа-версия графического движка и редактор карт. С вероятностью в 99% они будут дорабатываться в процессе разработки.
Сперва немного расскажу о некоторых технических характеристиках.
1. Скорее всего в игре будет использоваться событийная модель, а не циклическая, ведь для пошаговой стратегии цикл не так уж и важен. Это будет зависеть от того, как быстро Excel справится с рендером одного кадра. Минус такого подхода заключается в том, что написать какой-нибудь платформер на этой основе не получится. В любом случае я попробую оба варианта.
2. Все текстуры имеют размер 16*16 пикселей. Палитра состоит всего из 56 цветов (стандартный размер палитры Excel). В качестве основы я взял палитру NES.
3. Текстуры я рисую в программе Aseprite, а в Excel из. bmp перевожу с помощью небольшого, написанного на VBA софта, который нашел в интернете.
4. Бэкграунд состоит из тайлов, спрайты же привязаны к системе координат.
Графический движок
Карта уровня представляет собой двумерный массив с кодовым обозначением тайла в формате «XXXY», где XXX — номер текстуры по порядку, Y — значение, указывающее на то, можно ли пройти сквозь тайл. Вторая функция пока что не реализована.
Спрайты хранятся в отдельном массиве в формате: координата X, координата Y, порядковый номер спрайта, тип спрайта и тэг. Два последних значения пока не используются.
Для создания графического движка сперва необходимо инициализировать различные переменные. Часть из них хранится на отдельном листе, а в коде я сделал их публичными (знаю, что так нельзя):
— высота и ширина игрового экрана;
— диапазон игрового экрана;
— массив игрового экрана для рендеринга;
— размер одной текстуры;
— координаты камеры;
— координаты игрока;
— номер уровня;
— карта тайлов и координаты спрайтов;
— массив спрайтов, тайлов и спрайтов игрока.
Все текстуры хранятся на отдельном листе с отображением индексов цветов палитры.
Так как это только первая версия движка, нажатие на «Новую игру» тут же запускает метод fillWithTextures (процесс создания массива цифровых значений цвета).
‘##########ЯДРО ГРАФИЧЕСКОГО ДВИЖКА##########
Sub fillWithTextures()
Dim cntRow As Integer, cntCol As Integer, pixOffsetX As Double, pixOffsetY As Double, _
mapBlockX As Integer, mapBlockY As Integer, texXOffset As Integer, texYOffset As Integer, _
texNumber As Integer, arrBlockTex() As Variant
Dim cntSprites As Integer, spriteOffsetX As Integer, spriteOffsetY As Integer, _
spriteNumber As Integer
ReDim arrRender(main.screenH, main.screenW)
For cntRow = 1 To main.screenH
For cntCol = 1 To main.screenW
‘Считаем смещение пикселя экрана относительно координат камеры
pixOffsetX = main.cameraX + cntCol
pixOffsetY = main.cameraY + cntRow
‘считаем спрайты
For cntSprites = 1 To UBound(arrMapSprites(), 1)
‘считаем смещение спрайта относительно пикселя
spriteOffsetX = pixOffsetX — arrMapSprites(cntSprites, 1)
spriteOffsetY = pixOffsetY — arrMapSprites(cntSprites, 2)
‘если пиксель содержит спрайт
If spriteOffsetX >= 0 And spriteOffsetY >= 0 And spriteOffsetX + pixOffsetX < pixOffsetX + main.blockSize _
And spriteOffsetY + pixOffsetY < pixOffsetY + main.blockSize Then
‘если элемент спрайта не пуст
If arrSprites((spriteOffsetY + blockSize * arrMapSprites(cntSprites, 3)) + 1, spriteOffsetX + 1) <> 0 Then
arrRender(cntRow, cntCol) = arrSprites((spriteOffsetY + blockSize * arrMapSprites(cntSprites, 3)) + 1, spriteOffsetX + 1)
End If
End If
Next
‘рисуем тайлы
If (pixOffsetX > 0 And pixOffsetX < main.mapWidth) And _
(pixOffsetY > 0 And pixOffsetY < main.mapHeight) Then
‘расчет тайла, в который входит пиксель
mapBlockX = WorksheetFunction.RoundUp(pixOffsetX / main.blockSize, 0)
mapBlockY = WorksheetFunction.RoundUp(pixOffsetY / main.blockSize, 0)
‘определяем номер текстуры
texNumber = arrMapTiles(mapBlockY, mapBlockX)
‘Определение цвета текстуры для пикселя
texXOffset = getTexOffset(pixOffsetX) + 1
texYOffset = getTexOffset(pixOffsetY) + 1
If arrMapTiles(mapBlockY, mapBlockX) <> «» And arrTiles(texNumber * _
main.blockSize + texYOffset, texXOffset) <> «» And arrRender(cntRow, cntCol) = «» Then
arrRender(cntRow, cntCol) = arrTiles(texNumber * main.blockSize + texYOffset, texXOffset)
End If
End If
Next
Next
End Sub
Первым делом происходит поиск спрайтов, которые нужно отрисовать. Для этого программа проверяет каждый «пиксель» игрового экрана, считает смещение этого пикселя относительно стартовых координат камеры, а также смещение относительно всех спрайтов на уровне. Если смещение «пикселя» относительно спрайта по каждой оси равно от 0 до 15 (так как размер текстуры 16*16), берётся индекс нужного цвета из массива спрайтов.
Вторым пунктом программа на основе смещения относительно координат камеры высчитывает позицию «пикселей» на карте тайлов. Когда нужный тайл найден, программа с помощью функции getTextOffset возвращает индекс цвета пикселя из массива тайлов.
‘Возвращает координату текстуры
Function getTexOffset(dCoordinate As Double) As Integer
getTexOffset = (dCoordinate — 1) Mod main.blockSize
End Function
Почему сперва происходит проверка спрайтов, а затем тайлов?
Все просто. Программа просто не трогает те «пиксели», которые уже закрашены спрайтами, что влияет на производительность в лучшую строну.
P.S. На следующий день я понял, что проверка условия «закрашенности» спрайтами должна производиться в начале. Тогда это повлияет на производительность. Привет, оптимизация.
Вторая проблема — это проверка спрайтов для каждого пикселя экрана. Предположим, что на уровне находится 40 спрайтов. При размере экрана 96*64 = 6144 пикселей количество итераций цикла достигает 6144 * 40 = 245760. Если пойти другим путём и проверять спрайты не для каждого пикселя, а по условию нахождения в поле зрения камеры, то количество итераций не превысит 40*16*16 = 10240. Эта проблема решается быстро.
Создание игрока и рендеринг изображения
Для того, чтобы поместить спрайт игрока в рендер-массив нужно посчитать смещение спрайта относительно координат камеры.
Sub renderPlayer(imagePose As Integer)
Dim offsetX As Double, offsetY As Double, cntRow As Integer, _
cntCol As Integer
‘Считаем смещение относительно координат камеры
offsetX = main.playerX — main.cameraX
offsetY = main.playerY — main.cameraY
‘Если игрок не находится за пределами камеры
If offsetX >= 0 And offsetY >= 0 And _
offsetX < main.cameraX + main.screenW And _
offsetY < main.cameraY + main.screenH Then
For cntRow = 0 To main.blockSize — 1
For cntCol = 0 To main.blockSize — 1
‘Если пиксель текстуры заполнен
If main.arrPlayerSpr((cntRow + 1) + (imagePose * main.blockSize), cntCol + 1) <> 0 Then
‘Если пиксель не заходит за пределы камеры
If cntRow + main.playerY <= main.screenH + main.cameraY And cntCol + main.playerX <= main.screenW + main.cameraX Then
arrRender(offsetY + cntRow, offsetX + cntCol) = main.arrPlayerSpr((cntRow + 1) + (imagePose * main.blockSize), cntCol + 1)
End If
End If
Next
Next
End If
End Sub
Аргумент imagePose будет использоваться для имитации поворота игрока при движении.
В конце-концов рендер-массив готов, поэтому вызываем последнюю процедуру, которая рисует сформированный кадр на игровом поле. Ее я показывать не буду, потому что она очень сырая и будет дорабатываться.
Будут дорабатываться и текущие процедуры, потому что на данный момент быстродействие немного хромает и реализовать упомянутую циклическую модель в данный момент проблематично.
Вот, что получается в итоге:
На этом можно пока закончить. Надеюсь, что из ваших глаз не пошла кровь от «лучшего в мире» языка программирования и попыток написать что-то осмысленное.
В любом случае жду критику и советы. Всегда интересно послушать, что скажут люди.
Немного саморекламы
Я создал паблик ВКонтакте, куда буду выкладывать свои мысли, алгоритмы, код, ссылки на эти статьи и конечно мемасики:) Если вам интересно наблюдать за разработкой игр и разных странных вещей, добро пожаловать.