Развлекая — поучай.
(Гораций)
Если вы уже имели какой-то опыт программирования в прошлой жизни (привет, Basic, Pascal и т.д.), то, скорее всего, уже прошли этап «игрописательства». Однако, тряхнуть стариной и размять мозги вполне можно. Если же вы никогда не программировали игр, то никогда не поздно начать этот весьма увлекательный процесс. Всё, что нам потребуется — это Excel (любой версии) и 15-20 минут времени для начала.
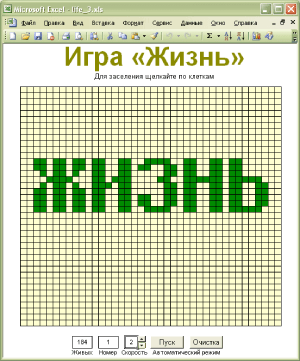
Тренироваться будем на известной в узких кругах программистов игре «Жизнь» (Life). Её придумал британский математик Джон Конвей еще в 1970 году на основе работ легендарного Джона фон Неймана — прадедушки всех современных компьютеров. Если вы не сталкивались с ней раньше — не проблема, правила можно объяснить за полминуты:
-
Игра идет на большом (иногда даже бесконечном) поле в клеточку («вселенной»). Как вы понимаете, Excel для такого подходит идеально
-
В один момент времени каждая клетка может быть в двух состояниях — живой (обозначим её каким-нибудь значком или просто единичкой) или же мертвой (пустой). Начальное состояние всех клеток в игре называют первым поколением.
-
Если брать блок клеток 3х3 с текущей клеткой в середине, то вокруг неё оказывается 8 клеток-соседей. Дальнейшая судьба клетки зависит от того, сколько именно живых клеток (N) окажется в этой окружающей области. Вариантов несколько:
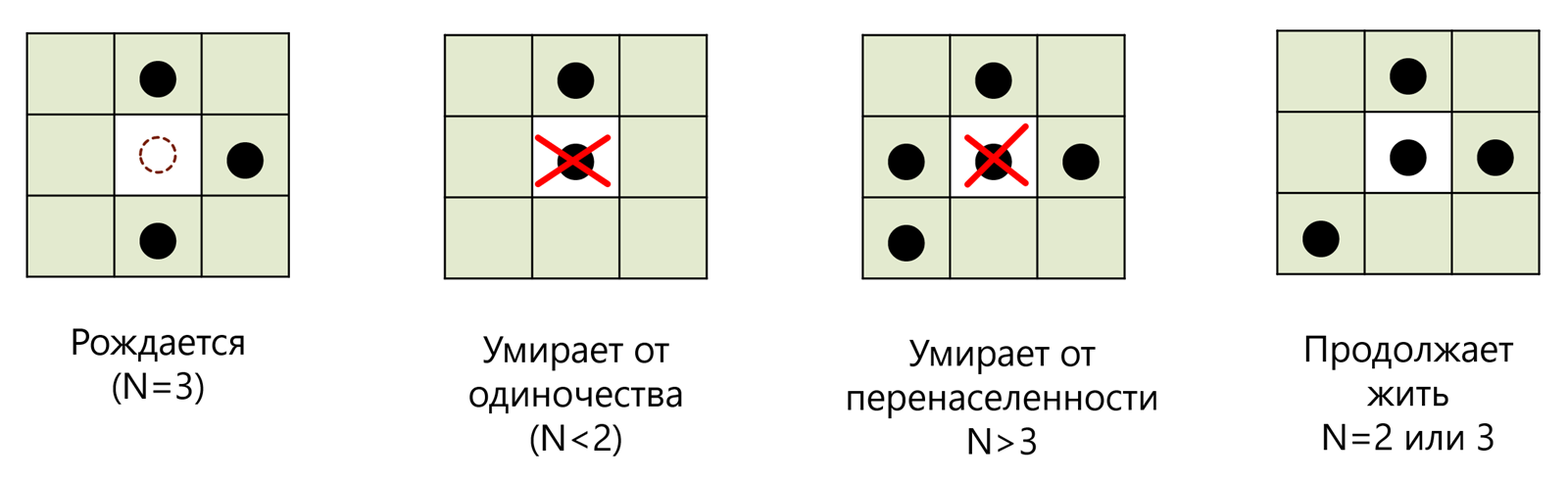
- Если клетка была пустая (мертвая), но у нее есть ровно 3 живых соседа, то в ней зарождается жизнь.
- Если клетка живая, но у неё меньше 2 соседей, то она умирает от одиночества.
- Если клетка живая, но у неё больше 3 соседей, то она умирает от перенаселения.
- Если клетка живая и у нее 2-3 соседа, то клетка продолжает жить.
Вот, собственно, и все правила. Можно даже сказать, что всё это неправильно называть игрой, т.к. здесь нет соперников в привычном понимании. Вы расставляете первое поколение, запускаете процесс и затем просто наблюдаете за развитием вашей «колонии» на протяжении нескольких поколений.
Однако, не стоит недооценивать обманчивую простоту этой логики — количество комбинаций, сценариев игры и многообразие фигур в такой игровой вселенной поражает своим разнообразием и поистине бесконечно. В математике подобные модели называют клеточными автоматами. А самое интересное, что реализовать подобную модель можно в любой версии Excel буквально на 20 строчках кода.
Поехали.
Шаг 1. Готовим игровое пространство
Создадим в новой книге три листа:
- game — это будет основной листы игры, где мы будем наблюдать за развитием нашей «колонии»
- next — этот лист будет формировать следующее поколение, которое затем придет на смену текущему
- start — на этом листе мы будем задавать начальную конфигурацию, т.е. первое поколение в нашей игре
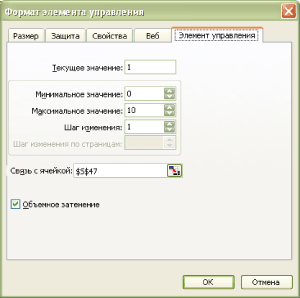
На каждом листе (можно выделить их заранее, удерживая клавишу Shift или Ctrl, чтобы не повторять трижды одни и те же действия), разметим игровое поле размером, допустим, 30 на 30 ячеек. Впоследствии размер поля можно будет подправить в соответствии с вашими аппетитами и мощью вашего ПК:
На листе start разметим с помощью единичек первое поколение любым желаемым образом:
Шаг 2. Пишем макрос
Теперь пришла пора расчехлить наш VBA и написать макрос, который и будет делать всю работу, а именно:
- Копировать первое поколение с листа start на лист game.
- Проходить по ячейкам игрового поля на листе game и проверять окружающих соседей (блок 3х3) для каждой из них.
- В зависимости от результатов проверки помечать на листе следующего поколения next ту же ячейку как живую (1) или мертвую (пусто).
- Копировать получившееся новое поколение с листа next вместо текущего на листы игры game.
- Повторять пункты 2-4 несколько раз, сменяя одно поколение другим и отображая на экране изменения в нашей «колонии».
Для начала откроем редактор Visual Basic на вкладке Разработчик (Developer). Если такой вкладки не видно, то её нужно будет сначала отобразить через Файл — Параметры — Настройка ленты (File — Options — Customize Ribbon), включив соответствующий флажок.
В открывшемся окне редактора создадим новый модуль с помощью команды меню Insert — Module, а затем скопируем и вставим туда код нашего макроса:
Sub Life()
Dim cell As Range, n As Integer, i As Integer
Set rGame = Worksheets("Game").Range("B2:AE31")
Set rStart = Worksheets("Start").Range("B2:AE31")
Set rNext = Worksheets("Next").Range("B2:AE31")
Set wNext = Worksheets("Next")
rStart.Copy Destination:=rGame
For i = 1 To 50
rNext.ClearContents
For Each cell In rGame.Cells
n = WorksheetFunction.CountA(cell.Offset(-1, -1).Resize(3, 3)) - cell.value
If cell = "" And n = 3 Then wNext.Cells(cell.Row, cell.Column) = 1
If cell = 1 And (n = 2 Or n = 3) Then wNext.Cells(cell.Row, cell.Column) = 1
If cell = 1 And (n < 2 Or n > 3) Then wNext.Cells(cell.Row, cell.Column) = ""
Next cell
rNext.Copy Destination:=rGame
Next i
End Sub
Теперь давайте разберем его построчно для понятности:
Поскольку в коде нам придется несколько раз ссылаться и много раз работать с диапазонами игрового пространства (B2:AE31) на каждом из трёх листов книги, то имеет смысл сразу оформить их как переменные. Это делается в блоке:
Set rGame = Worksheets("Game").Range("B2:AE31")
Set rStart = Worksheets("Start").Range("B2:AE31")
Set rNext = Worksheets("Next").Range("B2:AE31")
Заодно мы создаем ещё и переменную wNext, которая ссылается на весь лист next целиком — это нам тоже пригодится в будущем:
Set wNext = Worksheets("Next")
Затем, перед началом игры, мы должны перенести первое поколение с листа start на лист game. Это выполяется командой прямого копирования с использованием уже созданных переменных:
rStart.Copy Destination:=rGame
Поскольку мы хотим прокрутить в нашей игре не одно, а несколько (например, 50 для начала) поколений, то дальнейшие действия заключены в цикл:
For i = 1 to 50 ... Next i
А внутри этого цикла мы, во-первых, сначала очищаем рабочее пространство на листе next для формирования следующего поколения:
rNext.ClearContents
А, во-вторых, запускаем вложенный цикл прохода по всем ячейкам игровой вселенной на листе game, чтобы проверить каждую из них — это реализовано циклом прохода по коллекции:
For Each cell in rGame.Cells ... Next cell
Ссылка на очередную проверяемую ячейку будет храниться в переменной cell. Для этой ячейки нам нужно сначала построить окрестность 3х3 с ней в середине. Это выполняется с помощью конструкции:
cell.Offset(-1, -1).Resize(3, 3)
Здесь метод Offset(-1,-1) виртуально сдвигает текущую проверяемую ячейку на одну строку вверх и на один столбец влево, а потом метод Resize(3,3) опять же виртуально растягивает эту одну ячейку до новых размеров 3 на 3:

Чтобы посчитать количество заполненных ячеек в полученной окрестности применяется функция рабочего листа СЧЁТЗ (COUNTA), которую в VBA можно вызвать с помощью объекта WorksheetFunction. Таким образом количество живых соседей в окружающей текущую ячейку области 3 на 3 мы получаем выражением (не забыв вычесть из полученного количества текущую ячейку):
n = WorksheetFunction.CountA(cell.Offset(-1, -1).Resize(3, 3)) - WorksheetFunction.CountA(cell)
Дальше нам нужно проверить полученное количество соседей и пометить на листе следующего поколения текущую ячейку как живую или мертвую, согласно правилам игры. Это выполняет блок из трёх проверок:
If cell = "" And n = 3 Then wNext.Cells(cell.Row, cell.Column) = 1 If cell = 1 And (n = 2 Or n = 3) Then wNext.Cells(cell.Row, cell.Column) = 1 If cell = 1 And (n < 2 Or n > 3) Then wNext.Cells(cell.Row, cell.Column) = ""
Когда цикл прохода по ячейкам будет завершен, то сформированное следующее поколение с листа next нужно скопировать на место текущего на листе game — делаем это уже знакомой конструкцией:
rNext.Copy Destination:=rGame
Вот, собственно, и вся логика.
Осталось вернуться в Excel на лист game, запустить нашу игру через вкладку Разработчик — Макросы (Developer — Macro) и насладиться процессом развития нашей колонии:
Ссылки по теме
- Что такое макросы и как их программировать в Microsoft Excel
- Справочник по игре «Жизнь» — сайт LifeWiki
Геймификация жизни в Экселе: как я перестал прокрастинировать при помощи нескольких формул
Здравствуйте, я зависим от игр. И нет, фантастические миры, приключения, интриги меня никогда не увлекали. Затягивала сама механика, обманчивое ощущение прогресса от прокачки персонажа, комбинации перков. Каждый раз, когда шкала уровня наполняется, я физически чувствую удовлетворение. Однако в какой-то момент я решил, что лучше обуздать суперстимулы, чем быть им покорным. В итоге это привело к тому, к чему привело. Игра на основе моей жизни, где прокачка осуществляется в зависимости от дел, которые меня развивают. Сначала это была простенькая табличка, где мною вручную вбивались достижения, но вскоре система из обычного калькулятора превратилась в полноценную РПГ с крафтом, характеристиками, бустами, квестами и длинными (и не очень) формулами. Велл cum, я покажу, как у меня всё устроено!
Левелинг
По сути вся игра – адская смесь формул TES, Fallout и HM&M. Из последней, например, взята формула значений количества опыта для следующего уровня.
Навыки отчасти копируют систему TES V: Skyrim. Три группы по 6 в каждой, только в моём случае это умственная работа, физическая работа, творческая работа. Например, в первую группу входят такие параметры, как посещённые лекции, прочитанные доклады, количество написанного текста, количество прочитанного теста (нехудожественного, для художки есть аналогичный навык в творческой группе), занятия репетиторством и кодовые проекты. Разумеется, у каждого навыка разный вес, поскольку затраченные усилия на одну единицу в каждом навыке разные. Визуально это выглядит следующим образом (ячейка выделяется зелёным, когда значение равно или превышает значение этой ячейки, что позволяет автоматически визуализировать прогресс)
Крафт
Просто смотреть на то, как ячейки зеленеют, согласитесь, скучно. Поэтому я придумал систему, при которой можно ввести некий элемент случайности и при этом же прокачиваться. Крафтить полезные предметы можно из ресурсов, которые добываются с долей вероятности при работе над каким-то навыком. В разных группах навыков можно получить разные ресурсы. Формула доли вероятности выглядит таким образом: =ЦЕЛОЕ(((O29*0,01+$K$34/2-AL40/2+N36^1,25*0,01)*100)-O28*10*AL41), где O29 – бонусый элемент, высчитываемый как количество раз без длительных перерывов в степени 1,1 (необходимо для поощрения регулярности прокачки навыка), K34 – доля группы навыков по отношению ко всем трём группам навыков (чем больше ты прокачиваешься в одной группе, тем выше вероятность), N36 – количество очков, влияющих на вероятность нахождения любых ресурсов, остальные ячейки – это перки, усиливающие вероятность получения одних ресурсов и ослабляющие вероятность других.
С помощью крафта можно создать предметы, усиливающие другие значения, но ослабляющие другие. При усиленной прокачки одного из навыков можно усилить положительный коэффициент и ослабить отрицательный.
S.P.E.C.I.A.L.? А может, ИСКХВ?
Предыдущие модификации не отражали самого главного элемента РПГ – отыгрыша. Во многом меня как игрока определяло то, какую именно группу навыков я прокачиваю. И в случае крафта это также учитывалось: одна группа позволяла быстрее открывать новые способности, другая усиливала коэффициент способностей, третья позволяла частично или полностью ослабить негативный эффект способности. Однако система не была гибкой, не было ощущения, что прокачкой занимаюсь лично я, более того, хотелось, чтобы уровень тоже играл какую-то роль.
И тут я понял, что для отыгрыша подойдёт система дополнительных перков и их прокачка на каждом последующем уровне. Интеллект, Сила и Красноречие отвечают за три группы навыков соответственно, дополнительно усиливая связанные с ними бонусы и коэффициенты. Показатель Харизмы влияет на цены, Восприятия – на вероятность найти предметы для крафта и сам крафт (например, в середине есть перк на шанс создать два предмета из одних и тех же материалов). Всё и сразу прокачать не получится – максимальный уровень: 40, перков около сотни, и каждый из них полезен в разных ситуациях.
Помогает ли это?
Да, я использую эту систему уже больше года. Пока у меня не получалось вести одну и ту же игру дольше трёх-четырёх месяцев, но такие результаты – тоже результаты. Влияет ли это на выбор одной деятельности в обход другой? Я бы не сказал. Пишу это, и только сейчас понимаю, что получу опыт за написание этого текста в одном из творческих навыков. Я раскрыл далеко не все формулы и особенности, но, думаю, общая механика должна быть понятна. Это мой эксперимент, к которому я отношусь с известной долей рофла, так что не спешите записывать меня в шизов. Впрочем, я занимаюсь какими-то развивающими меня делами вместо игор, так что, судя по всему, сейчас это и правда мне помогает. Посмотрим, что будет дальше!
Сначала правила:
«Каждая клетка на плоскости может находиться в двух состояниях: быть живой или быть мёртвой. Клетка имеет восемь соседей. Распределение живых клеток в начале игры называется первым поколением. Каждое следующее поколение рассчитывается на основе предыдущего по таким правилам:
- пустая (мёртвая) клетка, рядом с которой ровно три живые клетки, оживает;
- если у живой клетки есть две или три живые соседки, то эта клетка продолжает жить; в противном случае (если соседей меньше двух или больше трёх) клетка умирает (от «одиночества» или от «перенаселённости»).
Игрок не принимает прямого участия в игре, а лишь расставляет начальную конфигурацию «живых» клеток, которые затем взаимодействуют согласно правилам уже без его участия.»
Более подробно можно прочитать на Википедии (ссылка).
Попробуем реализовать эту игру в Excel без использования VBA.
Так как вычисления производятся поэтапно, необходимо отключить автоматический пересчет таблиц. Заходим в пункт меню
«Сервис»
—
«Параметры»
, переходим на вкладку
«Вычисления»
.
Дальше выбираем пункт вычисления
«вручную»
, ставим галочку
«итерации»
, указываем
«предельное число итераций»
равным 1. Щелкаем ОК.
Для начала делаем ширину столбцов и высоту строк одинаковой, к примеру 20 пикселей. Как это сделать описано в заметке Квадратные ячейки в Excel.
Нам нужно будет 2 таблицы. Выделяем область B2:AA27, обводим ее границей, затем копируем и вставляем на область B35:AA60. Пусть Таблица 1 — сверху, а Таблица 2 — снизу.
Живая клетка будет содержать значение 1, мертвая — пустая.
Создаем именованную формулу, которая суммирует 8 ячеек, расположенных вокруг данной:
- Активизируем ячейку B2.
- Выбираем меню «Вставка» — «Имя» — «Присвоить».
- В поле Имя пишем Суммавокруг.
- В поле Формула пишем =!A34+!B34+!C34+!C35+!C36+!B36+!A36+!A35
Теперь если мы в ячейке B2 напишем =Суммавокруг, то получим сумму вокруг ячейки B35, если в ячейке B3 напишем =Суммавокруг, то получим сумму вокруг ячейки B36 и т.д.
Вычисление будут проходить так. В Таблицу 2 забиваем исходное положение, щелкаем F9 (вычислить) и Excel производит расчет в Таблице 1 на основании Таблицы 2 и копирует Таблицу 1 в Таблицу 2.
Чтобы определить, когда в Таблице 2 выводятся исходные данные, а когда копируются из Таблицы 1, присвоим ячейке B31 имя флаг. Если там 1, то выводим исходные данные, если 0, то копируем из Табл. 1.
Приступим к заполнению таблиц.
Выделяем Таблицу 1 и в строке формул пишем (на основании правил игры)
=ЕСЛИ(ИЛИ(Суммавокруг<2;Суммавокруг>3);0;ЕСЛИ(Суммавокруг=3;1;B35))
и щелкаем Ctrl + Enter, чтобы заполнить сразу все ячейки.
Выделяем Таблицу 2 и в строке формул пишем =ЕСЛИ(флаг;0;A2) и щелкаем Ctrl + Enter, чтобы заполнить сразу все ячейки.
Чтобы нули не выводились заходим в пункт меню
«Сервис»
—
«Параметры»
, переходим на вкладку
«Вид»
и снимаем галочку с пункта «
нулевые значения
«.
Но пока у нас исходное положение не содержит «живых» клеток. Чтобы «оживить» клетку, необходимо в формуле, которая в ячейке поменять 0 на 1, но делать это нужно только в Таблице 2. Можно выбрать сразу несколько клеток (выбираем их, удерживая клавишу Ctrl), затем в строке формул меняем 0 на 1 и щелкаем Ctrl + Enter.
Как с этим работать:
- Пишем в ячейке флаг значение 1, т.е. переходим к исходному положению.
- Выделяем Таблицу 2 и в строке формул пишем =ЕСЛИ(флаг;0;A2) и щелкаем Ctrl + Enter. Таким образом мы обнуляем исходные данные.
- Выделяем нужные нам ячейки в Таблице 2 и в строке формул меняем 0 на 1 и щелкаем Ctrl + Enter. Таким образом мы формируем первоначальную позицию.
- Пишем в ячейке флаг значение 0, т.е. запускаем эволюцию.
- Щелкаем F9 (вычислить), чтобы переходить к следующему поколению.
Для большей наглядности сделаем следующее.
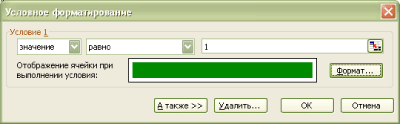
Выделяем все ячейки Таблицы 2. Переходим в пункт меню
«Формат»
—
«Условное форматирование»
. Задаем условие равно 1 и выбираем
«Формат»
красный шрифт и красная заливка.
Теперь Таблицу 1 можно скрыть и работать только с Таблицей 2.
Результат














Презентацию на тему «Реализация и изучение игры «Жизнь» в среде электронных таблиц (MS Ecxel)»
(11 класс)
можно скачать абсолютно бесплатно на нашем сайте. Предмет
проекта: Информатика. Красочные слайды и иллюстрации помогут вам
заинтересовать своих одноклассников или аудиторию.
Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад — нажмите на
соответствующий текст под плеером. Презентация
содержит 13 слайд(ов).
Слайды презентации
Слайд 1
Реализация и изучение игры «Жизнь» в среде электронных таблиц (MS Ecxel)
Докладчик: Посевина А.Д. Номинация: математика
Электросталь, 2010 г.
Слайд 2
Происхождение
1940 г. Родоначальник идеи Джон фон Нейман. Попытка создания гипотетической машины, которая может воспроизводить себя сама.
1970 г. Первая публикация правил игры «Жизнь» в журнале Scientific American Джоном Конвеем. Предложена более простая математическая модель на основе идей Джона фон Неймана.
Слайд 3
Правила игры «Жизнь»
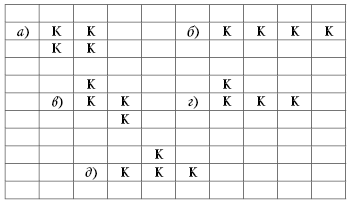
Место действия- разбитая на ячейки поверхность Каждая клетка поверхности может находиться в двух состояниях (мертвая или живая) Клетка имеет 8 соседей Начальное количество клеток(первое поколение) задаётся Мёртвая клетка, рядом с которой 3 живые клетки оживает Если вокруг живой клетки стоят 2,3 живые клетки-соседки, она продолжает жить. Если вокруг живой клетки стоят больше 3-х живых клеток или меньше 2-х, то клетка умирает. Популяцией в нашей игре называется квадрат (минимальный размер 3*3 клеток)
Слайд 4
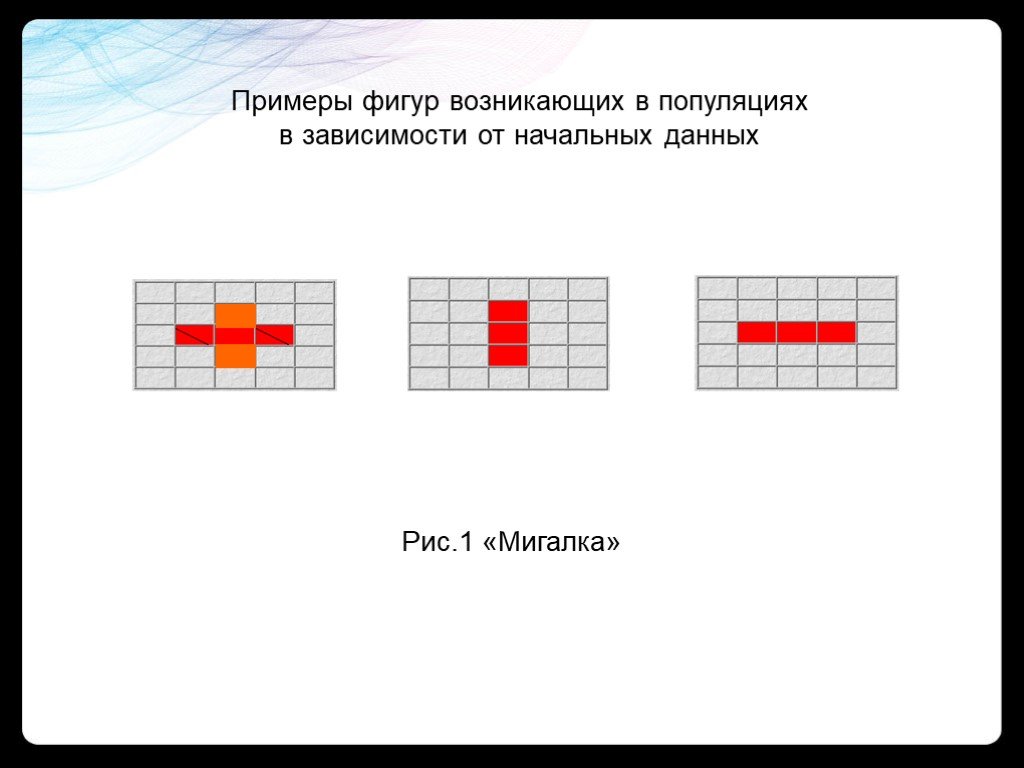
Рис.1 «Мигалка»
Примеры фигур возникающих в популяциях в зависимости от начальных данных
Слайд 5
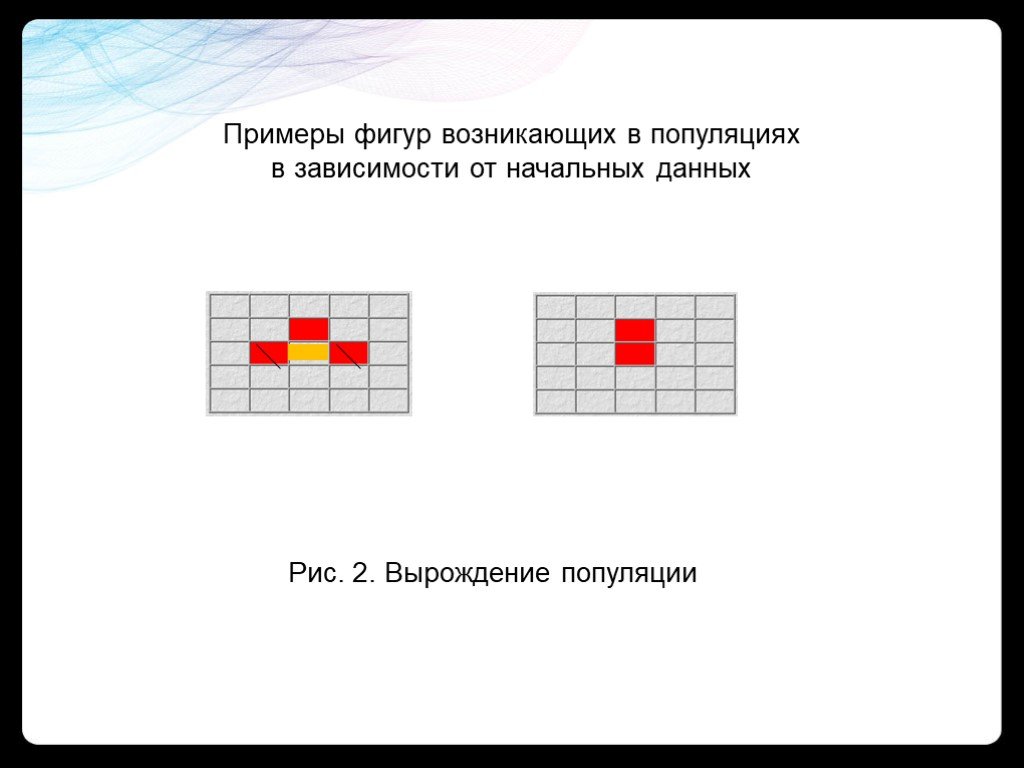
Рис. 2. Вырождение популяции
Слайд 7
Классификация фигур: устойчивые фигуры; периодические фигуры; двигающиеся фигуры; пожиратели и др.
Слайд 8
Формула №1расчета выживаемости для живой клетки расположенной в ячейке С3: ЕСЛИ(ИЛИ((B1+B3+A1+A2+A3+C1+C2+C3)>3;(CB211+B3+AC2+C3)
Слайд 9
Формула №3 проверки мертвая или живая клетка в ячейке B4: ЕСЛИ(B4=1;»Живая»; «Мертвая») Подставим формулу №1 и №2 в формулу №3, получим формулу №4. Формула №4 вычисления состояния клетки в последующей популяции в зависимости от того клетка ячейке B4 мертвая или живая и количества живых соседей: ЕСЛИ(B4=1;ЕСЛИ(ИЛИ((B1+B3+A1+A2+A3+C1+C2+C3)>3; (CB211+B3+A1+A2+A3+C1+C2+C3)
Слайд 10
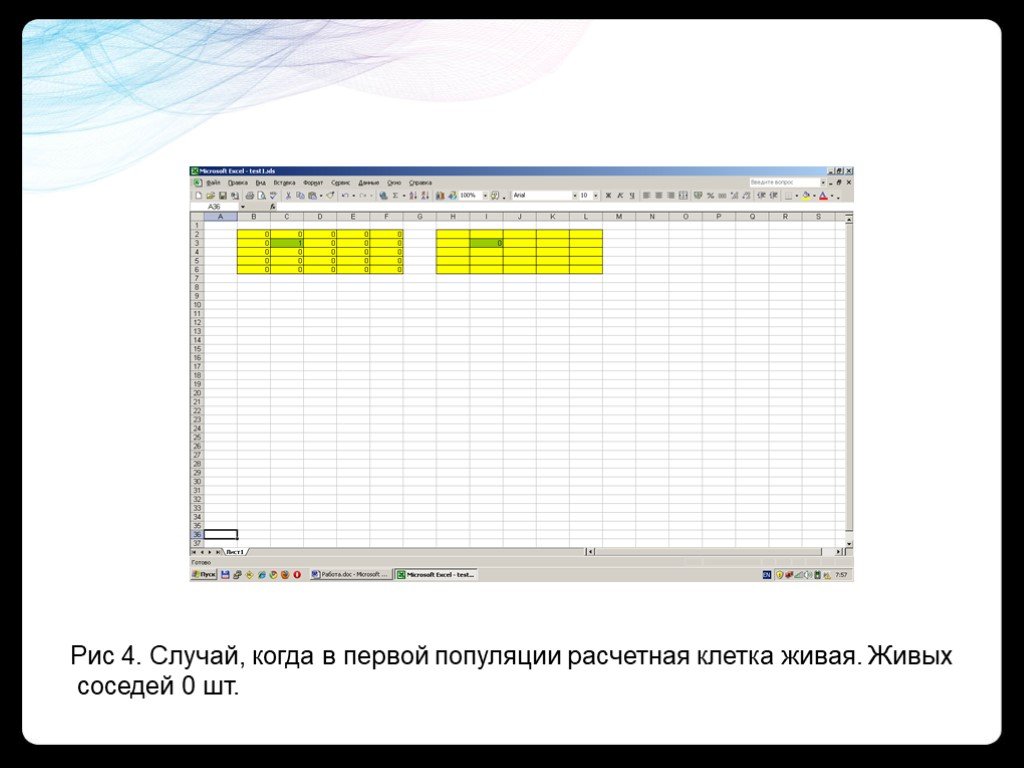
Рис 4. Случай, когда в первой популяции расчетная клетка живая. Живых соседей 0 шт.
Слайд 11
Науки на которые повлияло развитие игры «Жизнь»
Разделы математики и информатики: теория автоматов, теория алгоритмов, теория игр, алгебра и теория чисел, теория вероятностей, комбинаторика и теория графов, фрактальная геометрия, вычислительная математика. «Нематематические» дисциплины: кибернетика, химия, биология, астрономия, физика твёрдого тела, квантовая физика, наномеханика, электротехника, социология, теология, философия.
классификация фигур: устойчивые фигуры, периодические фигуры, двигающиеся фигуры, пожиратели и др.
Слайд 12
Выводы и заключения
Рассмотренная реализация имеет ряд недостатков: невозможный расчёт большого количества популяций, ограниченная численность популяций (в нашем случае 25 элементов), трудоёмкость и ненадежность реализации. Практическая ценность: данная работа может быть использована в качестве лабораторного практикума на уроках математики или информатики по соответствующей теме.
Слайд 13
Спасибо за внимание!
Список похожих презентаций

Электронная таблица MS Excel
Табличное представление данных. 1. Таблицы состоят из столбцов и строк. 2. Элементы данных записываются на пересечении строк и столбцов. Любое пересечение …

Таблицы в MS Word
Примечание: Данная презентация является адаптированной программой для учащихся с нарушением слуха. Цели: Обучающие: обеспечить усвоение учащимися …


Базы данных в электронных таблицах
Цели урока. На этом уроке вы узнаете понятие базы данных и ее назначение; научитесь осуществлять поиск и сортировку данных, выводить на экран компьютера …

Макросы в электронных таблицах
1.Visual Basic для приложений. Язык объектно-ориентированного программирования Visual Basic for Applications (VBA) предназначен для разработки приложений …

Базы данных в электронных таблицах
По данным электронной таблицы определите значение ячейки С1. Дана таблица:. Дан фрагмент электронной таблицы. Определите значение ячейки F8. Дан фрагмент …

Электронная таблица MS Excel
План. MS EXCEL. Microsoft Excel (также иногда называется Microsoft Office Excel) —программа для работы с электронными таблицами, созданная корпорацией …

Деловая графика в электронных таблицах
Цель урока:. Изучить графические возможности табличного процессора Excel; Научиться строить диаграммы различного типа с помощью табличного процессора; …

Графические возможности MS Word
Понятие векторной графики. В отличии от растровой графики, в которой для создания изображений используются большие массивы отдельных точек, в векторной …
Конспекты

Вычисления в таблицах MS Word
Автор:. Медведева Людмила Николаевна, учитель информатики. Государственное бюджетное общеобразовательное учреждение Самарской области средняя общеобразовательная …
Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих
вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно). - Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно
просто читать информацию со слайдов, ее аудитория может прочитать и сама. - Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста
позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая
информация, остальное лучше рассказать слушателям устно. - Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет
сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для
этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации,
а также правильно подобрать сочетание фона и текста. - Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете
первым, как закончите презентацию. Все приходит с опытом. - Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его
выступления. - Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете
меньше волноваться.
Материал подготовили:
А.А. Дуванов, г.
Переславль-Залесский, — реализация на языке Javascript;
Д.М. Златопольский, Москва, — реализации
на Школьном алгоритмическом языке, Pascal, QBasic;
А.Н. Комаровский, г. Россошь,
Воронежская область, — реализация в Excel;
С.Л. Островский, Москва, — идея,
реализация в Flash;
А.В. Паволоцкий, Москва, — реализация
на Delphi;
А.И. Сенокосов, г. Екатеринбург, — вводный
текст.
Исходные коды всех примеров
размещены на странице http://inf.1september.ru/lifegame/.
Что наша «Жизнь»? Игра!
Одной из легенд раннего
программирования по праву является игра,
придуманная американским математиком Джоном
Хортоном Конуэем (другой вариант русского
произношения фамилии — Конвей). Вот уже
несколько десятков лет она привлекает к себе
пристальное внимание. Созданы десятки программ,
реализующих эту игру чуть ли не на всех типах
компьютеров, написаны тысячи статей, сотни
сайтов в Интернете посвящены этой игре.
В свое время она была настолько
популярной среди программистов, что съела немало
их рабочего времени и машинного времени первых
суперкомпьютеров.
Вообще-то большая часть работ Конуэя
относится к области чистой математики, но, помимо
серьезных исследований, он увлекается также
занимательной математикой. Настоящая же статья
посвящена самому знаменитому детищу Конуэя —
игре, которую сам Конуэй назвал “Жизнь”.
Для игры “Жизнь” вам не понадобится
партнер — в нее можно играть и одному.
Возникающие в процессе игры ситуации очень
похожи на реальные процессы, происходящие при
зарождении, развитии и гибели колоний живых
организмов. По этой причине “Жизнь” можно
отнести к категории так называемых
“моделирующих игр” — игр, которые в той или иной
степени имитируют процессы, происходящие в
реальной жизни. Уже довольно давно никто не
играет в эту игру без использования компьютера,
хотя это вполне возможно. Для этого понадобилась
бы довольно большая доска, разграфленная на
клетки, и много плоских фишек двух цветов
(например, просто несколько наборов обычных
шашек небольшого диаметра или одинаковых
пуговиц двух цветов). Можно также
воспользоваться доской для игры в го, но тогда
вам придется раздобыть маленькие плоские шашки,
которые свободно умещаются в ячейках этой доски.
(Обычные камни для игры в го не годятся, потому
что они не плоские.) Можно также рисовать ходы на
бумаге, но значительно проще, особенно для
начинающих, играть, переставляя фишки или шашки
на доске.
Основная идея игры состоит в том,
чтобы, начав с какого-нибудь простого
расположения фишек (организмов), расставленных
по различным клеткам доски, проследить за
эволюцией исходной позиции под действием
“генетических законов” Конуэя, которые
управляют рождением, гибелью и выживанием фишек.
Конуэй тщательно подбирал свои правила и долго
проверял их “на практике”, добиваясь, чтобы
поведение популяции было достаточно интересным,
а главное, непредсказуемым.
Каждая клетка на бесконечном во все
стороны поле имеет ровно восемь соседей.
Рождаются и погибают клетки по следующим
правилам:
1. Если фишка имеет четырех или
более соседей, то она умирает от
перенаселенности (с этой клетки снимается фишка).
2. Если фишка не имеет соседей или
имеет ровно одного соседа, то она умирает от
нехватки общения.
3. Если клетка без фишки имеет ровно
трех соседей, то в ней происходит рождение (на
клетку кладется фишка).
4. Если не выполнено ни одно из
перечисленных выше условий, состояние клетки не
изменяется.
Игра эта пошаговая, и за один шаг игры
со всеми клетками поля одновременно происходят
(или не происходят) изменения, описанные тремя
вышеуказанными правилами.
На бумаге (или на экране) играют в эту
игру так: рисуют какую-нибудь колонию
закрашенных клеток, а затем шаг за шагом
прослеживают ее эволюцию.
Давайте для начала поучимся играть
сами.
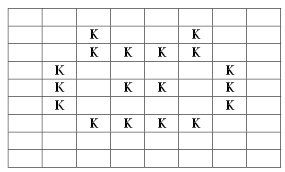
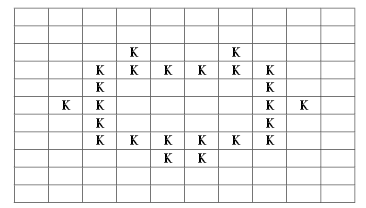
Итак, исходная колония клеток выглядит
следующим образом (см. рис. 1):
Рис. 1. Колония клеток в игре
“Жизнь”, носящая название “Чеширский кот”.
В исходной конфигурации легко просматриваются
ушки и глазки
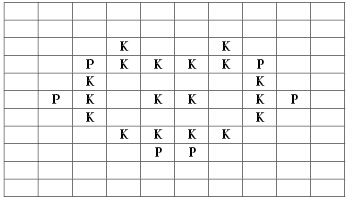
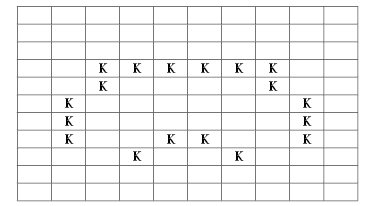
Давайте теперь буквами “Р” отметим те
пустые клетки, на которых произойдет рождение
новых закрашенных клеток. Напомним, что это такие
пустые клетки, которые имеют ровно трех
закрашенных соседей:
Рис. 2. Колония клеток с отмеченными
“новорожденными” клетками
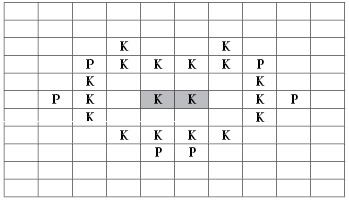
Теперь заштрихуем те старые клетки,
которые должны погибнуть. Напомним, что это такие
закрашенные плитки, которые имеют либо меньше
двух закрашенных соседей, либо больше трех. При
расчетах, разумеется, не надо принимать во
внимание клеточки, отмеченные буквой “Р”, — на
них процесс рождения еще не закончился:
Рис. 3. Колония клеток с отмеченными
клетками, которые должны погибнуть
И, наконец, уберем с заштрихованных
полей плитки, а поля, отмеченные буквой “Р”,
отметим буквой “К”:
Рис. 4. Колония клеток “Чеширский
кот” на втором шаге игры. Глазки закрылись, зато
морда стала шире, и это уже точно кот, а не кошечка
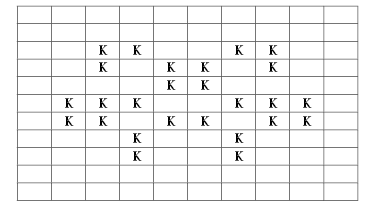
Повторяя этот процесс cнова и снова, мы
должны получить следующие конфигурации:
Рис. 5. “Чеширский кот” на третьем
шаге. Появился во всей красе, только ушки слегка
обвисли
Рис. 6. “Чеширский кот” на
четвертом шаге игры. Морда с усиками
Надеемся, что для вас не составит труда
проследить эволюцию этой колонии клеток до
самого конца.
Добавим, что конфигурация, по которой
мы учились играть, была открыта К.Р. Томпкинсом из
Короны, штат Калифорния.
Начав игру, вы сразу заметите, что
популяция непрестанно претерпевает необычные,
нередко очень красивые и всегда неожиданные
изменения. Иногда первоначальная колония
организмов постепенно вымирает, т.е. все фишки
исчезают, однако произойти это может не сразу, а
лишь после того, как сменится очень много
поколений. В большинстве своем исходные
конфигурации либо переходят в устойчивые
(последние Конуэй называет “любителями
спокойной жизни”) и перестают изменяться, либо
навсегда переходят в колебательный режим. При
этом конфигурации, не обладавшие в начале игры
симметрией, обнаруживают тенденцию к переходу в
симметричные формы. Обретенные свойства
симметрии в процессе дальнейшей эволюции не
утрачиваются, а симметрия конфигурации может
лишь обогащаться.
После первых, достаточно бессистемных,
попыток проследить эволюцию какой-либо колонии
можно перейти к более осмысленным действиям,
продемонстрировав ученикам основы научного
мышления.
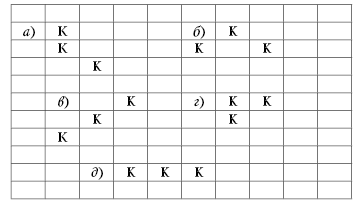
Можно, скажем, проследить эволюцию
всех возможных “триплетов” — комбинаций из
трех клеток. Выживает триплет лишь в том случае,
если по крайней мере одна фишка граничит с двумя
занятыми клетками. Пять триплетов, не исчезающих
на первом же ходу, изображены на рис. 7. (При
этом ориентация триплетов, т.е. как они
расположены на плоскости — прямо, “вверх
ногами” или косо, не играет никакой роли.) Первые
три конфигурации (а, б, в) на втором
ходу погибают. Относительно конфигурации в
заметим, что любой диагональный ряд фишек, каким
бы длинным он ни оказался, с каждым ходом теряет
стоящие на его концах фишки и в конце концов
совсем исчезает. Скорость, с которой шахматный
король перемещается по доске в любом
направлении, Конуэй называет “скоростью света”.
Пользуясь этой терминологией, можно сказать, что
любой диагональный ряд фишек распадается с
концов со скоростью света.
Рис. 7. Эволюция пяти триплетов
Конфигурация г на втором ходу
превращается в устойчивую конфигурацию —
“блок” (квадрат размером 2 ґ 2).
Конфигурация д служит простейшим примером
так называемых “флип-флопов” (кувыркающихся
конфигураций, возвращающихся в исходное
состояние через каждые два хода). При этом она
попеременно превращается то в вертикальный, то в
горизонтальный ряд из трех фишек. Конуэй
называет этот триплет “мигалкой”.
На рис. 8 изображены пять тетрамино
(четыре клетки, из которых состоит элемент
тетрамино, связаны между собой ходом ладьи). Как
вы уже видели (если довели до конца эволюцию
“Чеширского кота”), квадрат а относится к
категории “любителей спокойной жизни”.
Конфигурации б и в после второго хода
превращаются в устойчивую конфигурацию,
называемую “ульем”. Отметим попутно, что
“ульи” возникают в процессе игры довольно
часто. Тетрамино, обозначенное буквой г,
также превращается в улей, но на третьем ходу.
Особый интерес представляет тетрамино д,
которое после девятого хода распадается на
четыре отдельные “мигалки”. Вся конфигурация
носит название “навигационные огни”, или
“светофоры”. “Светофоры” относятся к разряду
флип-флопов и возникают в игре довольно часто.
Рис. 8. Пять видов тетрамино
Предоставляем читателю
самостоятельно поэкспериментировать на досуге с
двенадцатью фигурами пентамино (фигуры,
состоящие из пяти фишек, связанных между собой
так, что их клетки можно обойти ходом ладьи) и
посмотреть, во что они превращаются. Оказывается,
что пять из них на пятом ходу погибают, две быстро
переходят в устойчивые конфигурации из семи
фишек, а четыре после небольшого числа ходов
превращаются в “навигационные огни”.
Единственным исключением в этом смысле является
элемент пентамино, имеющий форму буквы r (рис.
9), превращения которого заканчиваются не столь
быстро (превращения конфигурации считаются
исчерпанными, если та исчезает, переходит в
устойчивую конфигурацию или начинает
периодически пульсировать).
Рис. 9. r-пентамино
Конуэй проследил развитие r-образного
пентамино вплоть до четыреста шестидесятого
хода, после которого данная конфигурация
распалась на множество “глайдеров”. Конуэй
пишет, что “от фигуры осталось множество мертвых
(не изменяющихся) обломков и лишь несколько малых
областей, в которых все еще теплилась жизнь, так
что отнюдь не очевидно, что процесс эволюции
должен происходить бесконечно долго”.
Одним из самых замечательных открытий
Конуэя следует считать конфигурацию из пяти
фишек под названием “глайдер”, изображенную на рис.
10. После второго хода “глайдер” немного
сдвигается и отражается относительно диагонали.
В геометрии такой тип симметрии называется
“скользящим отражением”, отсюда же и происходит
название фигуры.
В результате двух последующих ходов “глайдер”
“выходит из пике”, ложится на прежний курс и
сдвигается на одну клетку вправо и на одну клетку
вниз относительно начальной позиции. Выше уже
отмечалось, что скорость шахматного короля в
игре “Жизнь” принято называть скоростью света.
Выбор Конуэя пал именно на этот термин из-за того,
что в изображенной им игре большие скорости
просто не достигаются. Ни одна конфигурация не
воспроизводит себя достаточно быстро, чтобы
двигаться с подобной скоростью. Конуэй также
доказал, что максимальная скорость по диагонали
составляет одну четверть скорости света.
Поскольку “глайдер” воспроизводит сам себя
после четырех ходов и при этом опускается на одну
клетку по диагонали, то говорят, что он скользит
по полю со скоростью, равной одной четвертой
скорости света.
Рис. 10. “Глайдер?”
Конуэй также показал, что скорость
любой конечной фигуры, перемещающейся по
вертикали или по горизонтали на свободные
клетки, не может превышать половину скорости
света. Сумеет ли читатель самостоятельно найти
достаточно простую фигуру, которая движется с
такой скоростью? Напомним, что скорость движения
определяется дробью, в знаменателе которой стоит
число ходов, необходимых для воспроизведения
фигуры, а в числителе — число клеток, на которое
она при этом смещается. Например, если
какая-нибудь фигура за каждые четыре хода
передвигается на две клетки по вертикали или по
горизонтали, повторяя свою форму и ориентацию, то
скорость такой фигуры будет равна половине
скорости света. Надо сказать, что поиски
перемещающихся по доске фигур — дело
чрезвычайно сложное. Конуэю известны всего
четыре такие конфигурации, которые он называет
“космическими кораблями”. В их число входит уже
известный нам “глайдер”. (“Глайдер” считается
“космическим кораблем” легчайшего веса, потому
что все остальные корабли состоят из большего
числа фишек.)
Конуэй исследовал эволюцию всех
горизонтальных рядов из N фишек вплоть до N
= 20. Мы уже знаем, что происходит при N 4. Ряд из пяти фишек
переходит в “навигационные огни”, ряд из шести
фишек исчезает, из семи фишек получается
“пасека”, из восьми — четыре “улья” и четыре
“блока”, девять фишек превращаются в два
комплекта “навигационных огней”, а ряд,
состоящий из десяти фишек, переходит в
“пентадекатлон” — периодически
воспроизводящую себя конфигурацию с периодом,
равным 15. Ряд из одиннадцати фишек
эволюционирует, превращаясь в две “мигалки”;
двенадцать фишек в конце концов переходят в два
“улья”, а тринадцать — снова в две “мигалки”.
Если ряд состоит из 14 или 15 фишек, то он полностью
исчезает, а если фишек 16, то получается большой
набор “навигационных огней”, состоящий из
восьми “мигалок”. Эволюция ряда из 17 фишек
завершается возникновением четырех “блоков”;
ряды, состоящие из 18 или 19 фишек, также полностью
исчезают с доски, и, наконец, эволюция ряда из 20
фишек завершается появлением двух “блоков”.
Реализация игры “Жизнь” в различных
средах и на различных языках
В этом разделе приведено множество
реализаций игры “Жизнь”. Мы не ставили цель
алгоритмически унифицировать их — это было бы
просто скучно! Реализации писали различные
авторы, и каждая из них несет специфический
отпечаток не только “своей” среды и “своего”
языка, но и авторского стиля. Вместе с тем,
разумеется, во всех приведенных примерах
реализована одна и та же “Жизнь” — с ее
классическими правилами. В качестве поля всюду
используется или тор, посредством которого
моделируется “бесконечное” поле — верхняя
граница поля склеена с нижней, левая — с правой,
или конечное поле, в крайних строках и столбцах
которого фишки находиться не могут.
Жизнь в стиле КуМир 1 (Школьный
алгоритмический язык)
Игровое поле с фишками будем
моделировать в виде квадратного двумерного
массива с элементами символьного типа. Имя этого
массива — поле, а размер — размер (J). На поле и
в соответствующем массиве фишки будем
изображать в виде символа “*”.
Для подсчета числа соседних фишек для
клетки с координатами (i, j) создадим
функцию СчетчикСоседей:
алг цел
СчетчикСоседей(арг цел i, j)
нач цел счетчик, ii, jj
счетчик := 0
нц для ii от i — 1 до i + 1
нц для jj от j — 1 до j + 1
если поле[ii, jj] = «*»
то
счетчик := счетчик + 1
все
кц
кц
|Исключаем из подсчета фишку в
клетке с координатами (i, j)
если поле[i, j] = «*»
то
счетчик := счетчик — 1
все
знач := счетчик |Значение функции
кон
Значения числа соседних фишек
для всех клеток игрового поля будем хранить в
массиве с именем ВсегоСоседей.
Примем, что в крайних строках и
столбцах массива (поля) фишки находиться не
могут, поэтому процедура заполнения этого
массива будет выглядеть так:
алг
ЗаполнениеМассиваВсегоСоседей
нач цел i, j
нц для i от 2 до размер — 1
нц для j от 2 до размер — 1
ВсегоСоседей[i, j] := СчетчикСоседей(i, j)
кц
кц
кон
По значениям элементов массива ВсегоСоседей можно сформировать
новое поколение фишек (новую ситуацию на игровом
поле). Соответствующая процедура имеет вид:
алг НовоеПоколение
нач цел i, j, всего
|Заполняем массив ВсегоСоседей
ЗаполнениеМассиваВсегоСоседей
|Меняем ситуацию на игровом поле
нц для i от 2 до размер — 1
нц для j от 2 до размер — 1
|Чтобы многократно не использовать
значение ВсегоСоседей[i, j],
|применим величину «всего»
всего := ВсегоСоседей[i, j]
если всего = 0 или всего = 1 или
всего > 3
то |Гибель
поле[i, j] := » »
все
если всего = 3
то |Рождение или выживание
поле[i, j] := «*»
все
кц
кц
ВыводПоколения
кон
— где
ВыводПоколения — процедура вывода на экран
всех элементов массива поле:
алг ВыводПоколения
нач цел i, j
нц для i от 1 до размер
нц для j от 1 до размер
вывод поле[i, j]
кц
вывод нс
кц
кон
Обсудим теперь, как задавать
исходную ситуацию. Поскольку в школьном
алгоритмическом языке для ввода данных нет
возможности (пока?) использовать мышь и клавиши
управления курсором, то поступим так. Каждую
строку игрового поля будем задавать как
строковую величину, у которой символ “*”,
находящийся на том или ином месте, соответствует
фишке. Ввод будем проводить в квадратную область,
расположенную в центре игрового поля. Размер
соответствующего квадрата обозначим — длина. Это значит, для ввода
можно использовать одномерный массив длина из элементов строкового
типа. Имя этого массива — поле_ввода.
Пример ввода для случая длина
= 6 показан на рис. К1 (ему соответствует
конфигурация, представленная на рис. К2).
Рис. К1
Внимание! В программах на школьном
алгоритмическом языке (только) при вводе
строковых величин начальные и конечные пробелы
не учитываются, поэтому приходится для пустых
клеток вводить любые другие символы.
Рис. К2
С учетом сказанного и приведенного
рисунка начальный фрагмент процедуры ввода
исходной ситуации на игровом поле оформляется
следующим образом:
алг
ВводИсходнойКонфигурации
нач лит таб поле_ввода[1:длина], цел
i, j, лит строка
вывод нс, «Задайте исходную
конфигурацию»
вывод нс, » «
нц для i от 1 до длина
вывод i
кц
вывод нс
нц для i от 1 до длина
вывод i, «-й ряд «
ввод поле_ввода[i]
кц
…
После ввода всех строк их надо
учесть в массиве поле:
…
|Учитываем введенные строки в массиве
поле
нц для i от 1 до длина
|Запоминаем i-ю строку в переменной
строка
строка := поле_ввода[i]
|Рассматриваем каждый символ
нц для j от 1 до длина
|Если j-й символ — «*»,
если строка[j]=»*»
то
|то записываем его в
|соответствующую позицию поля
поле[div(размер — длина, 2) + i, div(размер —
длина, 2) + j] := «*»
все
кц
кц
кон
Используя созданные процедуры ВводИсходнойКонфигурации и ВыводПоколения, можем оформить
процедуру, которая заполняет и выводит на экран
исходное состояние в игре:
алг
ИсходнаяКонфигурация
нач цел i, j
|Заполняем все элементы
|массива поле пробелами
нц для i от 1 до размер
нц для j от 1 до размер
поле[i, j] := » »
кц
кц
ВводИсходнойКонфигурации
ВыводПоколения
кон
Основная программа,
моделирующая игру, записывается очень кратко:
цел размер, длина
размер := …
длина := …
сим таб поле[1:размер, 1:размер]
цел таб ВсегоСоседей[1:размер,
1:размер]
алг Игра «Жизнь»
нач
ИсходнаяКонфигурация
нц 500 раз
НовоеПоколение
кц
кон
В ней величины размер
и длина и массивы поле и ВсегоСоседей
описаны как общие (глобальные). Подразумевается,
что для прекращения просмотра необходимо нажать
клавишу .
Усовершенствование программы
Изменим программу таким образом,
чтобы в случае достижения устойчивой
конфигурации или “гибели” всех фишек
выполнение программы прекращалось и на экран
выводилось соответствующее сообщение.
Для контроля за достижением
устойчивой конфигурации следует запоминать
каждое состояние игрового поля и сравнивать с
ним состояние для следующего поколения.
Предыдущее состояние будем хранить в массиве пред_поле. Заполнять этот массив
будем в процедуре НовоеПоколение
перед сменой обстановки на игровом поле:
алг НовоеПоколение
нач цел i, j, всего
|Заполняем массив ВсегоСоседей
ЗаполнениеМассиваВсегоСоседей
|Записываем поле в пред_поле
нц для i от 1 до размер
нц для j от 1 до размер
пред_поле[i, j] := поле[i, j]
кц
кц
|Меняем ситуацию на игровом поле
… (см. выше)
— а для получения информации о том,
что достигнута устойчивая конфигурация или все
фишки “погибли”, создадим функцию Проверка,
возвращающую число — “код” достигнутой
конфигурации:
— если все фишки “погибли”, то 0;
— если достигнута устойчивая
конфигурация, то 1;
— иначе — 2.
В функции Проверка
используем следующие основные величины:
— число_фишек
— общее число фишек на поле (если оно равно нулю,
то, увы…);
— совпад —
число элементов массива поле,
значения которых совпадают со значениями
соответствующих элементов массива пред_поле (см. чуть выше).
алг цел Проверка
нач цел i, j, число_фишек совпадает
|Подсчитываем значения величин
число_фишек := 0; совпад := 0
нц для i от 2 до размер — 1
нц для j от 2 до размер — 1
если поле[i, j] = «*»
то
число_фишек := число_фишек + 1
все
если поле[i, j] = пред_поле[i, j]
то
совпад := совпад + 1
все
кц
кц
если число_фишек = 0
то
знач := 0 |Значение функции
иначе
если совпад = (размер — 2) * (размер
— 2)
то
знач := 1
иначе
знач := 2
все
все
кон
В новом варианте основной
программы:
— используем также величину номер — отслеживающую номер
нового поколения фишек (значение этой величины
будем выводить после наступления двух указанных
выше ситуаций);
— применим оператор цикла с
постусловием (условие окончания его работы: Проверка = 0 или Проверка = 1 или
номер > 500).
Итак, новый вариант:
алг Игра «Жизнь»
нач цел номер
ИсходнаяКонфигурация
номер := 0
нц
номер := номер + 1
НовоеПоколение
кц при Проверка = 0 или Проверка
= 1 или номер > 500
если Проверка = 0
то
вывод нс, «Жизни нет — все фишки
погибли! «
вывод «Номер поколения «,
номер
все
если Проверка = 1
то
вывод нс, «Получена устойчивая
конфигурация! «
|Будем считать, что она получена
|в предыдущем поколении
вывод «Номер поколения «,
номер — 1
все
кон
Пример работы программы
приведен на рис. К3.
Рис. К3
Еще одно усовершенствование
Зафиксируем факт появления
периодической смены конфигураций (“пульсации”).
Для этого нужно хранить все поколения в массиве,
т.е. придется использовать трехмерный массив.
Пусть имя этого массива — поколения,
а его описание будет следующим:
сим таб поколения[0:300,
1:размер, 1:размер]
Поскольку первый индекс этого
массива есть номер поколения, то величину номер опишем как общую
(глобальную). Каждое новое поколение после его
формирования будем записывать в массив:
алг НовоеПоколение
…
|Увеличиваем номер поколения
номер := номер + 1
|Записываем новую конфигурацию
|в массив поколения
нц для i от 1 до размер
нц для j от 1 до размер
поколения[номер, i, j] := поле[i, j]
кц
кц
…
В массив поколения
следует записать также и исходную конфигурацию:
алг
ИсходнаяКонфигурация
нач цел i, j
ВводИсходнойКонфигурации
|Записываем исходную конфигурацию в
массив поколения
нц для i от 1 до размер
нц для j от 1 до размер
поколения[0, i, j] := поле[i, j]
кц
кц
ВыводПоколения
кон
Проверку того факта, что
полученное состояние массива поле
совпадает с некоторым k-м
элементом массива поколения,
можно провести с помощью следующего фрагмента
программы:
i := 2; |Номер проверяемой
строки
совпадает := да
нц пока i <= размер — 1 и
совпадает
j := 2 |Индекс столбца
нц пока j <= размер — 1 и
совпадает
если поле[i, j] <> поколения[k, i, j]
то
|k-е поколение отличается
совпадает := нет
иначе
|Переходим к его следующему столбцу
j := j + 1
все
кц
|Если k-е поколение пока не
отличается,
если совпадает
то
|переходим к его следующей строке
i := i + 1
все
кц
— где совпадает —
величина логического типа, определяющая,
совпадают ли сравниваемые массивы.
С использованием этого фрагмента
оформим процедуру, определяющую наступление
пульсации:
алг Проверка2
нач цел i, j, k, лог
найдено_поколение, совпадает
если номер > 1 |Только при этом
проводим проверку
то
k := номер — 2
найдено_поколение := нет
нц пока k >= 0 и не
найдено_поколение
|Проверяем k-е поколение
i := 2; |Номер проверяемой строки
… (см. фрагмент выше)
кц
найдено_поколение := совпадает
если не найдено_поколение
то
|Повторяющееся поколение пока не
найдено
|Проверяем «следующее» поколение
k := k — 1
все
кц
если найдено_поколение
то
вывод нс, «Получена
периодичность. «
вывод «Период равен «, номер —
k
все
все
кон
Комментарии
1. найдено_поколение
— величина логического типа, определяющая,
найдено ли поколение, совпадающее с новым.
2. Проверку проводим, начиная с
поколения номер 2 и “пятясь” назад.
В окончательном (?) варианте 2
основной программы оператор цикла будет
выглядеть так:
нц
НовоеПоколение
Проверка2
кц при Проверка = 0 или
Проверка=1
Жизнь в стиле Паскаль
Игровое поле с фишками будем
моделировать в виде двумерного массива с
элементами символьного типа. Имя этого массива —
field, а размеры:
— число строк — height;
— число столбцов — width.
Примем следующие размеры:
width = 80;
height = 24.
На поле и в соответствующем массиве
фишки будем изображать в виде символа “*”.
Другие используемые массивы:
TotalNeighbours — для
хранения числа соседних фишек для всех клеток
игрового поля;
prevfield — для хранения
предыдущего поколения;
generations — для хранения
всех поколений фишек.
Основные процедуры и функции здесь
аналогичны описанным применительно к школьному
алгоритмическому языку. Приведем
соответствующие варианты на языке Паскаль.
1. Функция для подсчета числа соседних
фишек для клетки с координатами (i,
j):
Function CountNeighbours(i, j: byte):
byte;
var count, ii, jj: byte;
begin
count := 0;
for ii := i — 1 to i + 1 do
for jj := j — 1 to j + 1 do
if field[ii, jj] = ‘*’
then count := count + 1;
{Исключаем из подсчета фишку в клетке с
координатами (i, j)}
if field[i, j] = ‘*’
then count := count — 1;
{Значение функции}
CountNeighbours := count
end;
2. Процедура заполнения массива TotalNeighbours со значениями числа
соседних фишек для всех клеток игрового поля:
Procedure FillArrayTotalNeighbours;
var i, j: byte;
Function CountNeighbours(i, j: byte): byte;
begin
… (см. чуть выше)
end;
begin {Procedure FillArrayTotalNeighbours}
{Примем, что в крайних строках и
столбцах массива (поля) фишки находиться не
могут}
for i := 2 to height — 1 do
for j := 2 to width — 1 do
TotalNeighbours[i, j] := CountNeighbours(i, j)
end;
3. Процедура вывода на экран всех
элементов массива field:
Procedure PrintGeneration;
var i, j: byte;
begin
GotoXY(1, 1);
for i := 1 to height do
for j := 1 to width do write(field[i, j])
end;
4. Процедура формирования и вывода
на экран нового поколения фишек (новой ситуации
на игровом поле):
Procedure NewGeneration;
var i, j, total: byte;
begin
{Заполняем массив TotalNeighbours}
FillArrayTotalNeighbours;
{Записываем массив field в prevfield}
for i := 1 to height do
for j := 1 to width do
prevfield[i, j] := field[i, j];
{Меняем ситуацию на игровом поле}
for i := 2 to height — 1 do
for j := 2 to width — 1 do
begin
{Чтобы многократно не использовать
значение TotalNeighbours[i, j],
применим величину total}
total := TotalNeighbours[i, j];
if (total = 0) or (total = 1) or (total > 3)
then {Гибель фишки} field[i, j] := ‘ ‘;
if total = 3
then {Рождение или выживание} field[i, j] :=
‘*’
end;
{Увеличиваем номер поколения}
number := number + 1;
{Записываем новую конфигурацию в
массив generations}
for i := 1 to height do
for j := 1 to width do
generations[number, i, j] := field[i, j];
{Выводим новое поколение на экран}
PrintGeneration
end;
5. Функция, с помощью которой можно
зафиксировать факт гибели всех фишек или
достижения устойчивой конфигурации:
Function Control: byte;
var ident, sum_fish: word;
{sum_fish — общее число фишек на поле,
ident — число элементов массива field,
значения которых совпадают со значениями
соответствующих элементов массива
prevfield}
i, j: byte;
begin
ident := 0; sum_fish := 0;
for i := 2 to height — 1 do
for j := 2 to width — 1 do
begin
{Подсчет числа фишек на поле}
if field[i, j] = ‘*’
then sum_fish := sum_fish + 1;
{Подсчет числа фишек, совпадающих с
предыдущим поколением}
if field[i, j] = prevfield[i, j]
then ident := ident + 1
end;
{Значение функции}
if sum_fish = 0
then Control := 0 {Все фишки погибли}
else
if ident = (height — 2) * (width — 2)
then {Устойчивая конфигурация}
Control := 1
else Control := 2
end;
6. Процедура, определяющая
наступление пульсации (периодического появления
тех или иных поколений фишек):
Procedure Control2;
var find, same: boolean;
{find — величина, определяющая, найдено
ли поколение, совпадающее с новым,
same — величина, определяющая, совпадают
ли сравниваемые массивы}
i, j: byte; k: integer;
begin
if number > 1 {Только при этом проводим
проверку}
then
begin
k := number — 2;
{Проверку проводим, начиная с
поколения номер 2 и «пятясь» назад}
find := false;
while (k >= 0) and not find do
begin
{Проверяем k-е поколение}
i := 2; same := true;
while (i <= height — 1) and same do
begin
j := 2; {индекс столбца}
while (j <= width — 1) and same do
if field[i, j] <> generations[k, i, j]
then
{k-е поколение отличается}
same := false
else
{Переходим к следующему элементу
строки}
j := j + 1;
{Если k-е поколение пока не отличается,}
if same then
{переходим к его следующей строке}
i := i + 1
end;
find := same;
if not find then
{Повторяющееся поколение пока не
найдено. Проверяем «следующее» поколение}
k := k — 1;
end; {while (k >= 0) and not find}
if find then
write(‘Получена периодичность. Период
равен ‘, number — k)
end {if number > 1}
end;
Теперь о важном отличии. В
программе на Паскале можно обеспечить ввод
исходной конфигурации непосредственно на
экране, перемещая текстовый курсор в любом
направлении с помощью клавиш со стрелками. Для
того чтобы в том или ином месте разместить/убрать
фишку, следует нажать клавишу “Пробел”.
Отслеживание нажатой клавиши происходит с
помощью функции readkey. Вся
процедура ввода исходной конфигурации в игровое
поле и в массив field имеет вид:
Procedure InputInitial;
var c: char; i, j: byte;
begin
clrscr;
{Выводим подсказки}
GotoXY(7,9); write(‘Создайте первоначальную
конфигурацию’);
GotoXY(7,11); write(‘Перемещение курсора
осуществляется с помощью клавиш со стрелками’);
GotoXY(7,12); write(‘Можно использовать клавиши
<Home>, <End>, <PageDown>
и <PageUp>’);
GotoXY(7,13); write(‘Для установки (удаления)
фишки нажмите клавишу «Пробел»‘);
GotoXY(7,14); write(‘Для завершения
редактирования — нажмите клавишу «Enter»‘);
GotoXY(7,16); write(‘Для начала создания —
нажмите любую клавишу’);
{Ждем нажатия любой клавиши}
repeat until keypressed;
{Начальное состояние массива field}
for i := 1 to height do
for j := 1 to width do field[i, j] := ‘ ‘;
clrscr;
repeat {Начало редактирования
обстановки}
c := readkey;
case c of
#75 {Клавиша «Стрелка влево»}:
GotoXY(WhereX — 1, WhereY);
#77 {Клавиша «Стрелка вправо»}:
GotoXY(WhereX + 1, WhereY);
#72 {Клавиша «Стрелка вверх»}:
GotoXY(WhereX, WhereY — 1);
#80 {Клавиша «Стрелка вниз»}:
GotoXY(WhereX, WhereY + 1);
#71 {Клавиша <Home>}: GotoXY(2, WhereY);
#79 {Клавиша <End>}: GotoXY(width — 1, WhereY);
#73 {Клавиша <PageUp>}: GotoXY(WhereX, 2);
#81 {Клавиша <PageDown>}: GotoXY(WhereX, height — 1);
#32 {Клавиша «Пробел»}:
if (WhereX > 1) and (WhereX < width) and
(WhereY > 1) and (WhereY < height)
then if field[WhereY, WhereX] = ‘*’
then
begin
field[WhereY, WhereX] := ‘ ‘;
write(‘ ‘)
end
else
begin
field[WhereY, WhereX] := ‘*’;
write(‘*’)
end
end; {case}
until c = #13
end;
Используя эту процедуру как
вспомогательную, можем создать процедуру,
которая формирует и выводит на экран исходную
конфигурацию:
Procedure Initial;
var i, j: byte;
begin
InputInitial;
{Записываем исходную конфигурацию в
массив generations}
for i := 1 to height do
for j := 1 to width do
generations[0, i, j] := field[i, j];
Выводим ее}
PrintGeneration
end;
Раздел описаний и основная часть
программы имеют вид:
Uses CRT;
const width = 80; height = 24;
var
field, prevfield: array [1..height, 1..width] of char;
TotalNeighbours: array [1..height, 1..width] of word;
generations: array [0..300 3, 1..height, 1..width] of char;
number, pause: word;
speed: byte;
c: char;
begin
clrscr;
write(‘Задайте скорость смены поколений
‘);
write(‘(целое число от 1 до 5)’);
readln(speed);
case speed of
1: pause := … ; {Значения подбираются в
зависимости от быстродействия компьютера}
2: pause := … ;
3: pause := … ;
4: pause := … ;
5: pause := … ;
end;
clrscr;
Initial;
number := 0;
repeat
Delay(pause);
NewGeneration;
Control2;
until (Control = 0) or (Control = 1) or
keypressed;
GotoXY(1, 25);
if Control = 0
then writeln(‘Жизни нет — все фишки
погибли! Номер поколения: ‘, number);
if Control = 1
then write(‘Получена устойчивая
конфигурация! ‘;
{Будем считать, что она получена в
предыдущем поколении}
writeln(‘Номер поколения: ‘, number — 1);
repeat until keypressed
end.
Подразумевается, что для
прекращения просмотра и для окончания работы
программы необходимо нажать любую клавишу.
В заключение приведем несколько
возможных усовершенствований программы:
— задание и использование цвета фишек
и цвета игрового поля;
— использование в качестве фишек
других символов;
— смена поколений на экране только
после нажатия любой клавиши;
— вывод на экран номера поколения.
Жизнь в стиле Бейсик (QBasic)
Игровое поле с фишками будем
моделировать в виде двумерного массива с
элементами строкового типа фиксированной длины
(один символ). Имя этого массива — field,
а размеры:
— число строк — height;
— число столбцов — wid.
На поле и в массиве field
фишки будем изображать в виде символа “*”.
Другие используемые массивы:
totalneighbours — для
хранения числа соседних фишек для всех клеток
игрового поля;
prevfield — для хранения
предыдущего поколения;
generations — для хранения
всех поколений фишек.
Основные процедуры и функции,
используемые в программе, аналогичны описанным
применительно к школьному алгоритмическому
языку. Приведем соответствующие варианты на
языке Бейсик.
1. Функция для подсчета числа соседних
фишек для клетки с координатами (i,
j):
FUNCTION CountNeighbours (i AS
INTEGER, j AS INTEGER)
DIM count AS INTEGER, ii AS INTEGER, jj AS
INTEGER
count = 0
FOR ii = i — 1 TO i + 1
FOR jj = j — 1 TO j + 1
IF field(ii, jj) = «*» THEN
count = count + 1
END IF
NEXT jj
NEXT ii
‘Исключаем из подсчета фишку в клетке с
координатами (i, j)
IF field(i, j) = «*» THEN
count = count — 1
END IF
CountNeighbours = count
END FUNCTION
2. Процедура заполнения массива totalneighbours со значениями числа
соседних фишек для всех клеток игрового поля:
SUB FillArrayTotalNeighbours
DIM i AS INTEGER, j AS INTEGER
‘Примем, что в крайних строках и
столбцах массива (поля) фишки находиться не могут
FOR i = 2 TO height — 1
FOR j = 2 TO wid — 1
TotalNeighbours(i, j) = CountNeighbours(i, j)
NEXT j
NEXT i
END SUB
3. Процедура вывода на экран всех
элементов массива field:
SUB PrintGeneration
DIM i AS INTEGER, j AS INTEGER
LOCATE 1, 1
FOR i = 1 TO height
FOR j = 1 TO wid
PRINT field(i, j);
NEXT j
NEXT i
END SUB
4. Процедура формирования и
вывода на экран нового поколения фишек (новой
ситуации на игровом поле):
SUB NewGeneration
DIM i AS INTEGER, j AS INTEGER, total AS
INTEGER
‘Заполняем массив TotalNeighbours
CALL FillArrayTotalNeighbours
‘Записываем массив field в prevfield
FOR i = 1 TO height
FOR j = 1 TO wid
prevfield(i, j) = field(i, j)
NEXT j
NEXT i
‘Меняем ситуацию на игровом поле
FOR i = 2 TO height — 1
FOR j = 2 TO wid — 1
‘Чтобы многократно не использовать
значение totalneighbours(i, j),
‘применим величину total
total = totalneighbours(i, j)
IF total = 0 OR total = 1 OR total > 3 THEN
‘Гибель фишки
field(i, j) = » «
END IF
IF total = 3 THEN
‘Рождение или выживание
field(i, j) = «*»
END IF
NEXT j
NEXT i
‘Записываем новую конфигурацию в
массив generations
FOR i = 1 TO height
FOR j = 1 TO wid
generations(number, i, j) = field(i, j)
NEXT j
NEXT i
‘Выводим новое поколение на экран
CALL PrintGeneration
END SUB
5. Функция, с помощью которой
можно зафиксировать факт гибели всех фишек или
достижения устойчивой конфигурации:
FUNCTION Control!
DIM i AS INTEGER, j AS INTEGER,
DIM sum AS INTEGER, ident AS INTEGER
‘sum — общее число фишек на поле,
‘ident — число элементов массива field,
‘значения которых совпадают со
значениями соответствующих элементов массива
prevfield
ident = 0
sum = 0
FOR i = 2 TO height — 1
FOR j = 2 TO wid — 1
‘Подсчет числа фишек на поле
IF field(i, j) = «*» THEN
sum = sum + 1
END IF
‘Подсчет числа фишек, совпадающих с
предыдущим поколением
IF field(i, j) = prevfield(i, j) THEN
ident = ident + 1
END IF
NEXT j
NEXT i
‘Значение функции:
IF sum = 0 THEN
‘Все фишки погибли
Control = 0
ELSE
IF ident = (height — 2) * (wid — 2) THEN
‘Устойчивая конфигурация
Control = 1
ELSE
Control = 2
END IF
END IF
END FUNCTION
6. Процедура, определяющая
наступление пульсации (периодического появления
тех или иных поколений фишек):
SUB Control2
DIM AS INTEGER i, AS INTEGER j, AS INTEGER
k,
DIM find AS INTEGER, same AS INTEGER
‘find — величина, определяющая,
‘найдено ли поколение, совпадающее с
новым
‘same — величина, определяющая,
‘совпадают ли сравниваемые массивы
IF number > 1 THEN
‘Только при этом проводим проверку
k = number — 2
find = 0
‘Проверку проводим, начиная с
поколения номер 2 и «пятясь» назад}
WHILE k >= 0 AND find = 0
‘Проверяем k-е поколение
i = 2: same = 1
WHILE i <= height — 1 AND same = 1
j = 2 ‘Индекс столбца
WHILE j <= wid — 1 AND same = 1
IF field(i, j) <> generations(k, i, j) THEN
‘k-е поколение отличается
same = 0
ELSE
‘Переходим к следующему элементу
строки
j = j + 1
END IF
WEND
‘Если k-е поколение пока не
отличается,
IF same THEN
‘переходим к его следующей строке
i = i + 1
END IF
WEND
find = same
IF find = 0 THEN
‘Повторяющееся поколение пока не
найдено.
‘Проверяем «следующее» поколение
k = k — 1
END IF
WEND
IF find = 1 THEN
PRINT «Получена периодичность.
Период равен «; number — k
END IF
END IF ‘IF number > 1
END SUB
7. Процедура ввода исходной
конфигурации. Последняя вводится путем нажатия
клавиши “Пробел” в том или ином месте экрана.
Текстовый курсор можно перемещать в любом
направлении с помощью клавиш со стрелками, а
также клавиш Home, ,
и
. Отслеживание нажатой
клавиши происходит с помощью функции INKEY$,
возвращающей одно- или двухбайтную строку. Вся
процедура ввода исходной конфигурации в игровое
поле и в массив field имеет вид:
SUB InputInitial
DIM i AS INTEGER, j AS INTEGER
DIM c$
CLS
‘Выводим подсказки
LOCATE 9, 7: PRINT «Создайте
первоначальную конфигурацию»
LOCATE 11, 7: PRINT «Перемещение
курсора осуществляется с помощью клавиш со
стрелками»
LOCATE 12, 7: PRINT «Можно
использовать клавиши <Home>, <End>, <PageDown> и
<PageUp>»
LOCATE 13, 7: PRINT «Для установки
(удаления) фишки нажмите клавишу «Пробел»»
LOCATE 14, 7: PRINT «Для завершения
редактирования — нажмите клавишу <Enter>»
LOCATE 17, 7: PRINT «Для начала
создания — нажмите любую клавишу»
‘Ждем нажатия любой клавиши
DO
LOOP UNTIL INKEY$ <> «»
‘Начальное состояние массива field
FOR i = 1 TO height
FOR j = 1 TO wid
field(i, j) = » «
NEXT j
NEXT i
CLS
‘Начало редактирования обстановки
‘Размещаем курсор в центре экрана и
показываем его
LOCATE 12, 40, 1
DO
c$ = INKEY$
IF LEN(c$) = 1 THEN ‘c$ содержит символ,
распознаваемый по ASCII-коду.
‘Если нажата клавиша «Пробел»
IF ASC(c$) = 32 THEN
IF POS(0) > 1 AND POS(0) < wid AND
CSRLIN > 1 AND CSRLIN < height THEN
IF field(CSRLIN, POS(0)) = «*» THEN
field(CSRLIN, POS(0)) = » «
PRINT » «;
ELSE
field(CSRLIN, POS(0)) = «*»
PRINT «*»;
END IF
END IF
END IF
ELSE ‘ LEN(c$) = 2
‘Нажаты клавиши управления курсором
или специальные клавиши, в т.ч. <Enter>
‘Клавишу можно распознать по второму
символу
SELECT CASE RIGHT$(c$, 1)
CASE CHR$(72)
‘Клавиша «Стрелка вверх»
IF CSRLIN > 1 THEN
LOCATE CSRLIN — 1, POS(0), 1
END IF
CASE CHR$(80)
‘Клавиша «Стрелка вниз»
IF CSRLIN < height THEN
LOCATE CSRLIN + 1, POS(0), 1
END IF
CASE CHR$(75)
‘Клавиша «Стрелка влево»
IF POS(0) > 1 THEN
LOCATE CSRLIN, POS(0) — 1, 1
END IF
CASE CHR$(77)
‘Клавиша «Стрелка вправо»
IF POS(0) < wid — 1 THEN
LOCATE CSRLIN, POS(0) + 1, 1
END IF
CASE CHR$(73)
‘Клавиша <Home>
IF POS(0) > 1 THEN
LOCATE CSRLIN, 2, 1
END IF
CASE CHR$(79)
‘Клавиша <End>
IF POS(0) > 1 THEN
LOCATE CSRLIN, wid — 1, 1
END IF
CASE CHR$(71)
‘Клавиша <PageUp>
IF CSRLIN < height THEN
LOCATE 2, POS(0), 1
END IF
CASE CHR$(81)
‘Клавиша <PageDown>
IF CSRLIN < height THEN
LOCATE height — 1, POS(0), 1
END IF
END SELECT
END IF ‘IF LEN(c$) = 1
‘Окончание редактирования — клавиша
<Enter>
LOOP UNTIL RIGHT$(c$, 1) = CHR$(13)
END SUB
Используя эту процедуру как
вспомогательную, можем создать процедуру,
которая формирует и выводит на экран исходную
конфигурацию:
SUB Initial
DIM i AS INTEGER, j AS INTEGER
‘Формируем исходную конфигурацию
CALL InputInitial
‘Записываем ее в массив generations
FOR i = 1 TO height
FOR j = 1 TO wid
generations(0, i, j) = field(i, j)
NEXT j
NEXT i
‘и выводим на экран
CALL PrintGeneration
END SUB
Раздел описаний глобальных
величин и массивов и основная часть программы
имеют вид:
DIM SHARED wid, height
wid = 80: height = 24
DIM SHARED field2(1 TO height, 1 TO wid) AS STRING * 1
DIM SHARED prevfield(1 TO height, 1 TO wid) AS STRING * 1
DIM SHARED TotalNeighbours(1 TO height, 1 TO wid) AS INTEGER
DIM SHARED generations(0 TO 300, 1 TO height, 1 TO
wid) AS STRING * 1
DIM SHARED number AS INTEGER, speed AS INTEGER,
pause AS INTEGER
PRINT «Задайте скорость смены
поколений «
INPUT «(целое число от 1 до 5) «, speed
SELECT CASE speed
‘Значения величины pause влияют на
длительность паузы между сменой поколений
‘и подбираются в зависимости от
быстродействия компьютера
CASE 1
pause = …
CASE 2
pause = …
CASE 3
pause = …
CASE 4
pause = …
CASE 5
pause = …
END SELECT
number = 0
CALL Initial
DO
FOR i = 1 TO pause ‘Пауза
NEXT i
number = number + 1
CALL NewGeneration
CALL Control2
LOOP UNTIL Control = 0 OR Control = 1 OR
INKEY$ <> «»
LOCATE 24, 1
IF Control = 0 THEN
PRINT «Жизни нет — все фишки погибли!
Номер поколения: «; number
END IF
IF Control = 1 THEN
PRINT «Получена устойчивая
конфигурация! «;
‘Будем считать, что она получена в
предыдущем поколении
PRINT «Номер поколения: «; number — 1
END IF
END
Жизнь в стиле Excel
Реализация игры “Жизнь” в
электронных таблицах, имеющих мощный потенциал
математического моделирования, вероятно, проще,
чем это позволяют другие приложения или
инструментальные средства, при этом возможны
различные варианты как представления самих
поколений, так и организации их смены.
Прежде всего, нам почти не придется
организовывать среду обитания, так как клеток на
рабочем листе электронных таблиц изобилие.
Правда, сама игра обычно предполагает
безграничность пространства исполнения, и ее мы
несколько позже организуем, а пока будем
довольствоваться диапазоном, например, 40 х 40 ячеек (размеры в данном случае
существенной роли не играют, а форма может быть и
прямоугольной).
Далее рассматривается технология
создания игры в среде Microsoft Office Excel 2003, однако
готовый проект работает как в более ранних
версиях, так и в более поздней. Для реализации
проекта в Excel 2007 следует, обратившись по адресу: Кнопка
Office — Параметры Excel — Настройка — Выбрать
команды из… — Команды не на ленте, затем
добавить: “Кнопка (элемент управления)” и
“Счетчик (элемент управления)”, а также сделать
поправку на изменение интерфейса в плане
размещения на ленте условного форматирования на
вкладке “Главная” и работы с макросами на
вкладке “Вид”.
Более того, используя описанную
технологию, можно выполнить предлагаемый проект
даже в OpenOffice.org Calc, правда, текст макросов там
может несколько отличаться от приведенных.
Первое приближение
Арена жизни
Чтобы обеспечить обозримость
развития будущих “цивилизаций”, модифицируем
клеточное пространство рабочего листа, приведя
его к виду, близкому к разлиновке листа школьной
тетради в клетку. Для этого выделим весь рабочий
лист и, кликнув правой кнопкой мыши на заголовках
столбцов, установим их ширину равной 1 символу.
Проделав ту же операцию на заголовках строк,
зададим высоту в 8,5 пунктов. Желательно сразу же,
не снимая выделения, решить вопрос и с размером
шрифта, определив его равным 8 пунктам.
Основные события у нас будут
разворачиваться на квадратной “арене” в
диапазоне C5:AP44, поэтому выделим его
и установим внутренние и внешние границы. Сразу
же, не снимая выделения, скопируем полученную
заготовку и, отступив вправо (можно и вниз),
вставим содержимое буфера обмена напротив
оригинала, допустим, в диапазон AU5:CH44.
Этому полю мы отведем роль “родильного
отделения”, в котором будет появляться новое
поколение клеточной “жизни”.
Для начала все клетки основного поля
заполним нулями, означающими, что “жизнь” в них
отсутствует. Временно, пока мы не решили вопрос с
безграничностью, клетки внешнего периметра
“арены” также заполним нулями, тем более что
“жизни” там нет и пока не предвидится.
Думаю, вы уже догадались, что
олицетворять жизнь в клетках будут единицы. А для
заселения нашей, пока еще не обитаемой,
“планеты” придется эти единички “сеять” с
помощью клавиатуры и мышки. Позже эту заботу мы
постараемся облегчить, а пока не будем опережать
события.
Правила игры
Настало время заняться
правилами игры. Напомним их:
1. Правило выживания. Каждая клетка,
у которой имеются две или три “живых” соседних,
выживает и переходит в следующее поколение.
2. Правило рождения. Если число
“живых” клеток, с которыми граничит какая-либо
пустая клетка, равно трем, то на ней происходит
рождение нового организма.
3. Правило гибели. Каждая клетка, у
которой оказывается более трех “живых”
соседних, погибает от перенаселения. Каждая
клетка, вокруг которой свободны все клетки или
“жива” только одна, погибает от одиночества.
Попробуем сформулировать их на
алгоритмическом языке. Сначала нам надо
определиться, “живой” или “мертвой” является
та или иная клетка. Далее решаем вопрос: жить ли
ей далее или отойти в мир иной. Считаем сумму
единиц всех клеток диапазона, размером 3 х 3, в котором данная клетка является
центральной и, с учетом того, что в первом случае
в ней стоит “1”, налагаем на сумму условие быть
больше двух, но меньше пяти, а во втором —
проверяем равенство трем.
если клетка живая
то
если сумма > 2 и сумма < 5
то жить
иначе погибнуть
все
иначе
если сумма = 3
то жить
иначе погибнуть
все
все
Разобравшись в структуре
приведенной части алгоритма, несложно
переложить ее на язык формул электронных таблиц.
Переместимся в верхнюю левую ячейку
ранее созданного поля “роддома” и введем в нее
формулу, реализующую правила игры:
=ЕСЛИ(C5=1;ЕСЛИ(И(СУММ(B4:D6)>2;СУММ(B4:D6)<5);1;0);ЕСЛИ(СУММ(B4:D6)=3;1;0))
Скопируем ее и, выделив весь
диапазон поля для формирования “поколения Next”,
вставим.
Задачу в общих чертах можно считать
решенной. Теперь, расставив единички на основном
поле и “заселив” тем самым “жизнь”, можно сразу
же на дополнительном поле видеть новое
поколение. Чтобы вывести его на “арену”,
поступим следующим образом: выделим и скопируем
все ячейки поля с “молодняком” и,
переместившись в верхнюю левую клетку основного
поля, выполним в главном меню: Правка —
Специальная вставка… — и в диалоговом окне
выберем переключателем “значения”. Круг
замкнулся. Теперь “арена” занята вторым
поколением, а в “родильном отделении” ждет
своей очереди следующее.
Второе приближение
Сворачиваем тор
Настала очередь решения
проблемы безграничности. Представим себе поле,
на котором разворачиваются основные события, в
виде эластичного листа. Свернем лист в трубку,
для чего состыкуем его верхний и нижний края, а
затем согнем трубку в кольцо и “склеим” ее
концы. Получившийся в результате тор и есть та
самая безграничная поверхность, на которой
обычно реализуется игра “Жизнь”.
Операцию стыковки и склейки выполним в
три этапа:
— Поместим курсор в ячейку C4
на внешней стороне основного поля и, введя с
клавиатуры знак равенства, сделаем ссылку на
клетку C44 — первую слева в
последней строке “арены”. Затем, схватившись за
маркер автозаполнения, протянем ее вправо до
последней ячейки. Склеивание верха и низа
завершим аналогичными действиями: выделив
ячейку С45, поместим в нее формулу =C5, которую протянем в ту же сторону
до ячейки AP45.
— На следующем этапе склеим левую и
правую стороны образовавшегося цилиндра.
Сначала через протягивание вниз формулы =AP45 из ячейки B5 на
внешней левой стороне основного поля, затем
формулы =C5 из ячейки AQ5.
— В завершение в четыре шага состыкуем
вершины вводом во внешние угловые ячейки ссылок
на диагонально противоположные угловые клетки
“арены”, связав: B4 с AP44,
AQ4 с C44, AQ45 с C5 и, наконец, B45 с AP5.
Наша “арена” превратилась в
воображаемый тор, но “нулики” по периметру, да и
в самом поле не очень ее украшают.
Рис. E1. «Склеиваем» стороны и
вершины
Сначала займемся периферией. Здесь
видится по крайней мере два варианта решения:
скрыть соответствующие строки и столбцы,
соприкасающиеся с внешними сторонами основного
поля, или выбрать цвет шрифта в этих ячейках
таким же, как и фон, то есть белым. Первый вариант
предпочтительнее, так как гарантирует от
случайных изменений содержимого. Есть и третий
вариант, но о нем несколько позже.
Визуализация
Что-то уж слишком скромно
смотрятся единички “жизни” на фоне зануленной
“пустыни”. Хорошо бы проявления “жизни”
сделать более заметными, а “пустыню” не такой
пестрой. Прежде всего расправимся с засильем
нуликов. Выделив весь диапазон основного поля,
окрасим ячейки в какой-либо желтый оттенок (под
цвет пустыни), а заодно выберем тот же цвет для
шрифта. Теперь замаскировались не только нулики,
но и единички. Не спешите снимать выделение.
Чтобы “жизнь” выглядела подобающим образом,
воспользуемся условным форматированием: Формат
— Условное форматирование… В открывшемся
диалоговом окне выбираем в списках “значение”,
“равно”, затем в следующее поле заносим единицу
и на вкладке Шрифт диалогового окна Формат
ячеек (кнопка Формат) выбираем цвет зеленый
и на вкладке Вид для заливки ячеек указываем
тот же цвет.
Рис. E2. Задаем условный формат ячеек
Наша “арена” сразу же преобразилась.
Теперь на неброском фоне “пустыни” ярко
зазеленели ростки “жизни”.
Борьба с рутиной
Но не все так хорошо, как бы
хотелось. Как акт первоначального заселения, так
и процедура переноса из “роддома” на “арену”
однообразны и затратны по времени. Хорошо бы их
усовершенствовать. Для автоматизации рутинных
операций в MS Excel есть такое мощное средство, как
макросы.
Щелчком правой кнопки мыши на любой из
верхних панелей вызовем контекстное меню и
отобразим панель Visual Basic.
Нажав на кнопку — Записать макрос, выполним
копирование диапазона, соответствующего
“родильному отделению”, и, переместившись в
левую верхнюю клетку основного поля, вставим его
через меню Правка — Специальная вставка… —
“значения”. Сразу же после этого завершим
создание макроса кликом по появившейся вместо
предыдущей кнопке — Остановить запись.
Теперь для вызова на “арену”
очередного поколения будем щелкать по кнопке — Выполнить
макрос и в диалоговом окне Макрос, выбрав
нужную строку, нажимать кнопку Выполнить или,
через кнопку Параметры, назначив для запуска
только что созданного макроса сочетание клавиш,
использовать эту возможность.
Рис. E3. Выполняем макрос
Последний прием требует меньше
действий и выглядит предпочтительнее. Но можно
уменьшить хлопоты и без использования
клавиатуры, сократив их до щелчка по кнопке. Для
этого, открыв контекстное меню на любой из
панелей, отобразим панель Формы. Щелкнем на
ней по элементу — Кнопка и, перейдя на рабочий лист,
создадим под основным полем протягиванием
вправо-вниз при нажатой левой кнопке мыши
изображение нужного нам элемента подходящего
размера. При отпускании кнопки мыши появляется
диалоговое окно Назначить макрос объекту, в
котором уже выделен единственный пока макрос.
Нам остается только нажать кнопку ОК.
Рис. E4. Выбираем кнопку
Выполнив двойной щелчок по кнопке,
изменим надпись на ней на Шаг и с помощью
угловых и боковых маркеров установим подходящие
размеры.
Новые проблемы
Сняв выделение с кнопки щелчком
в любой ячейке рабочего листа, испытаем систему
усовершенствованного вывода молодняка в
“свет”. Пощелкав по кнопке Шаг и с
удовлетворением восприняв достигнутый
положительный результат снижения трудоемкости,
отмечаем ряд недостатков:
— что-то застлалась легкой мглой
“арена” жизни;
— а еще сквозь пелену проглядывают
нулики и единички;
— к тому ж пелена эта мигает при
выполнении макроса;
— да и вокруг “роддома” отвлекающе
мерцают “муравьи” пунктирного выделения.
От пелены, а следовательно, и от
демаскировки нуликов можно было бы избавиться,
если копирование заменить последовательным
присваиванием значений из массива
дополнительного поля в соответствующие клетки
“арены”. Однако практическая проверка такой
идеи показала, что в этом случае использование
вложенных циклов по строкам и столбцам
значительно сокращает скорость смены поколений
и заметно портит зрительный эффект. Жизнь не
бывает безоблачной, так что с пеленой предлагаю
смириться или, если вы предложите другие
эффектные способы, буду рад о них от вас узнать.
Маскировка
Для решения проблемы
демаскировки воспользуемся ранее заявленным
третьим вариантом, который потребует от нас
кардинальных преобразований:
— Откажемся от нуликов. Если в
клетке нет “жизни”, так пусть же признаком этого
будет пустота, то есть отсутствие данных в ячейке
или пустой текст “”. Чтобы одним выстрелом убить
сразу двух зайцев, поступим следующим образом:
включим запись макросов, выделим весь диапазон
“арены” жизни, нажмем клавишу на клавиатуре и остановим запись
макроса. Так как процедуру очистки основного
поля в процессе игры придется выполнять
неоднократно, то неплохо бы привязать только что
созданный макрос к соответствующей кнопке
“Очистка”, применив ранее приведенную
технологию ее создания и обработки.
— Может, это и кощунство, но заселять
в клетки будем пробелы, они-то уж точно не будут
просматриваться сквозь пелену выделения.
— Электронные таблицы предоставляют
огромный арсенал различных функций, так что не
стоит зацикливаться на суммировании единичек.
Для решения нашей задачи воспользуемся
функцией “СЧЁТЕСЛИ(диапазон;критерий)”,
в связи с чем внесем коррективы в формулу первой
ячейки верхнего ряда “родильного отделения”.
Теперь она будет выглядеть так:
=ЕСЛИ(C5=»
«;ЕСЛИ(И(СЧЁТЕСЛИ(B4:D6;»
«)>2;СЧЁТЕСЛИ(B4:D6;» «)<5);»
«;»»);ЕСЛИ(СЧЁТЕСЛИ(B4:D6;» «)=3;»
«;»»))
Скопируем ее и, выделив весь
диапазон дополнительного поля, вставим.
Следует отметить еще один
положительный эффект произведенных
преобразований — поле “родильного отделения”
также очистилось от нулей и единиц.
После автоматизации процесса переноса
поколений надобность следить за обоими полями
отпала. Теперь можно обеспечить таинство
рождения нового поколения. Попытка скрыть
столбцы, содержащие дополнительное поле,
приводит к частичному результату, так как от
“бегущих муравьев” этим способом избавиться не
удается, и они по-прежнему мельтешат,
предательски выдавая место зарождения “жизни”.
Придется “родильное отделение”
переместить с глаз подальше за пределы экрана
вправо или вниз. Для этого, выделив диапазон,
включающий “роддом”, вырежем его и,
переместившись (например, в ячейку HC5),
вставим или, схватившись за край выделения,
перетянем его на новое место. Для надежности
соответствующие столбцы лучше всего скрыть.
Минимизация
Естественно, что сразу же после
произведенных преобразований необходимо внести
коррективы и в макрос переноса поколений.
Для этого щелчком по значку панели Visual Basic или
сочетанием клавиш
+ F11 перейдем в окно редактора макросов, где в
окне проводника проекта Project двойным кликом
по строке Module1 откроем окно кода ранее
записанных нами макросов и минимизируем их,
откорректировав до вида:
Sub Макрос1()
Range(«HC5:IP44»).Copy
Range(«C5»).PasteSpecial Paste := xlPasteValues
Range(«A1»).Select
End Sub
Sub Макрос2()
Range(«C5:AP44»).ClearContents
End Sub
Проверив действие клеточного
автомата после внедрения рационализаторских
предложений, убеждаемся, что большая часть
изъянов устранена и задачу можно считать
решенной во втором приближении, но пока что в
нашей игре самой неудобной составляющей
является процесс заселения первого поколения.
Хорошо бы усовершенствовать и эту процедуру.
Третье приближение
Начинаем программировать
Мы уже приобрели некоторый опыт
создания, редактирования макросов и подключения
их к кнопкам для исполнения. Если у вас не вызвали
особых затруднений ранее рассмотренные
действия, а желание довести начатую работу до
совершенства не иссякло, смело бросаемся в
пучины программирования в среде VBA.
Перейдем в редактор Visual Basic и в поле
проводника проекта двойным щелчком по строке Лист1(Лист1)
откроем страницу для записи и редактирования
программного кода, относящегося к данному
рабочему листу. Открыв левый список в верхней
части этой страницы, выберем Worksheet, а в правом
списке — SelectionChange (выбор или изменение).
Дополним появившуюся заготовку событийной
процедуры, запускающейся при выделении или
изменении значения какой-либо ячейки листа, так
чтобы она приобрела следующий вид:
Private Sub Worksheet_SelectionChange(ByVal
Target As Range)
r = Selection.Cells.Row
c = Selection.Cells.Column
z = r > 4 And r < 45 And c > 2 And c < 43
If z Then
If Cells(r, c) = «» Then
Cells(r, c) = » «
Else
Cells(r, c) = «»
End If
End If
End Sub
Здесь переменной r
присваивается номер строки выделенной ячейки, а
переменной с — номер ее
столбца. Затем формируем условие попадания в
основное поле и его логическое значение
присваиваем переменной z. Если
ячейка выделена в пределах “арены”, то, если до
этого там было пусто, в нее заносится пробел,
иначе клетка очищается присвоением пустого
текста.
Переключившись в окно MS Excel и пощелкав
мышкой в пределах основного диапазона,
убеждаемся, что процедура заселения первого
поколения теперь заметно упростилась. Однако,
как это нередко бывает, новые идеи несут с собой
не только новые решения, но и новые проблемы. Не
обошлось без неприятных сюрпризов и в данном
случае. Щелкая по кнопке “Шаг”, замечаем, что
клетка в верхнем левом углу “арены”, вопреки
всем правилам игры, “ожила” на втором шаге и,
вопреки правилам Конвея, продолжает свое
существование в этом статусе в последующих
поколениях.
А чего мы хотим?
Не пора ли нам перестать “ходить
вокруг да около”, а взяться за дело всерьез и
создать действительно полноценный продукт? Для
начала определимся, а чего бы такого, кроме
устранения уже отмеченных недостатков, нам
недостает?
Хорошо бы, наряду с пошаговым, иметь и
автоматический режим смены поколений, чтобы
щелкнул разок — и наблюдай беззаботно, как
разворачиваются события на “арене”, а в случае
чего остановил исторический процесс, вмешался в
ситуацию, и пускай снова плодится клеточная
“жизнь”. Если же в каком-то поколении она
вырождается, то игра должна заканчиваться.
Неплохо бы иметь возможность
регулировать скорость смены поколений, а также
знать, в каком поколении возникла та или иная
конфигурация с расселением или произведена
остановка, каково количество “живых” клеток на
том или ином этапе?
Займемся интерфейсом
Сначала спланируем интерфейс.
Последовательно выделим и объединим диапазоны: K47:M48, O47:Q48 и S47:T48,
— отформатировав в виде сплошной тонкой линии их
внешние границы.
Рис. E6. Организация интерфейса
В первый диапазон внесем формулу: =СЧЁТЕСЛИ(C5:AP44;» «), которая будет
подсчитывать количество “живых” клеток на
арене в том или ином поколении. Сразу же в ячейку W47 впишем связанную с этим диапазоном
формулу для вывода предупреждающего сообщения: =ЕСЛИ(K47=0;»Жизнь отсутствует»;»»).
Следующий диапазон будет предназначен
для вывода порядкового номера очередного
поколения. Эти сведения будут заполняться
программным способом.
Третий диапазон предназначен для
отображения скорости смены поколений в секунду.
Для регулировки скорости воспользуемся
счетчиком, который, по аналогии с кнопками,
создадим с помощью панели Формы щелчком по
соответствующему элементу и протяжкой на
рабочем листе при нажатой левой кнопке мыши.
Подогнав размеры и разместив изображение
счетчика справа от диапазона S47:T48,
вызовем через контекстное меню диалоговое окно Формат
объекта, где на вкладке Элемент управления
установим:
Текущее значение: 1.
Минимальное значение: 0.
Максимальное значение: 10.
Шаг изменения: 1.
Связь с ячейкой: $S$47.
Отметим флажок “Объемное затенение”.
Рис. E7. Настройка счетчика
В ячейке AB49 поместим
формулу для вывода сообщения о текущем рабочем
режиме — пошаговом — в случае нулевой скорости
или автоматическом:
=СЦЕПИТЬ(ЕСЛИ(S47=0;”Пошаговый”;”Автоматический”);”
режим”)
Совершенствуем макросы
Завершив работу над интерфейсом,
переключимся в редактор Visual Basic. Открыв
программный код модуля, скопируем ранее
записанные макросы переноса и очистки и, перейдя
в окно кода рабочего листа с событийной
процедурой, которая помогала нам щедро рассыпать
пробелы по “арене”, вставим. Теперь через
контекстное меню модуль можно удалить, так как
для осуществления наших замыслов будет
достаточно страницы кода первого листа рабочей
книги.
Первым делом отредактируем ранее
созданные макросы. Макрос1 переименуем и,
удалив строку выделения ячейки, заменим ее
команду срабатывания счетчика поколений в
ячейке O47.
Sub Новое_поколение()
Range(«HC5:IP44»).Copy
Range(«C5:AP44»).PasteSpecial Paste := xlPasteValues
Range(«O47») = Range(«O47») + 1
End Sub
“Макрос2” также переименуем и
дополним еще двумя строками.
Sub Очистка()
Range(«C5:AP44»).ClearContents ‘Очистка
диапазона
Range(«O47») = 0 ‘Сброс счетчика
поколений
Call Стоп ‘Вызов процедуры «Стоп»
End Sub
Упомянутую здесь процедуру
“Стоп” создадим позже. Естественно, что после
переименования подпрограммы придется выполнить
переподключение ее к кнопке “Очистка”. Для
этого вызовем на ней контекстное меню, выберем
строку Назначить макрос…, найдем и выделим в
списке Лист1.Очистка и нажмем кнопку OK.
Рис. E8. Подключение макроса к кнопке
В событийную процедуру заселения
жизни в выбранные ячейки добавим дополнительные
условия выполнения, учитывающие рабочий режим и
фактор времени (чтобы не выделялась клетка в
верхнем левом углу основного поля при остановке).
Определим не только номера строки и столбца
активной ячейки, но и адрес всего диапазона
выделения, чтобы командой присваивания пробелов
или пустого текста иметь возможность одним
движением его заселять или очищать. Кроме того,
значение счетчика поколений в ячейке O47
устанавливаем на единицу. В окончательном
варианте подпрограмма имеет вид:
Sub Worksheet_SelectionChange(ByVal Target As
Range)
If Timer > t + 1 And m <> 2 Then
ad = Selection.Cells.Address()
r = Selection.Cells.Row
c = Selection.Cells.Column
z = r > 4 And r < 45 And c > 2 And c < 43
If z Then
If Cells(r, c) = «» Then
Range(ad) = « «
Else
Range(ad) = «»
End If
Range(«O47») = 1
End If
Range(«S47»).Select
End If
End Sub
Вводим переменные
Закончив редактирование,
займемся необходимыми дополнениями. Откроем
левый список в верхней части страницы и выберем
строку (General). Оказавшись над ранее созданными
подпрограммами в зоне объявления общих для всех
процедур данного листа переменных, сделаем
следующие записи:
Dim f As Boolean ‘Флаг пуска
Dim t As Single ‘Время прерывания
Dim m As Integer ‘Маркер режима
Эти переменные мы объявили, чтобы
упростить процедуру передачи параметров, так как
они будут использоваться в нескольких
подпрограммах. Остальные локальные переменные
можно не объявлять. В последних версиях Visual Basic.Net
такие вольности, конечно, недопустимы, но VBA,
встроенный в приложения Microsoft Office, относится к
этому довольно лояльно. Логическая переменная f будет сигнализировать, нажата ли
кнопка “Пуск” или нет, а значение маркера m будет указывать, какой из
режимов действует в данный момент: пошаговый,
пуск-авто или стоп-авто.
Входим в режим
Для определения режима и смены
надписей на первой кнопке запишем следующую
процедуру:
Sub Режим()
ActiveSheet.Shapes(1).Select
If Range(«S47») = 0 Then
f = False
m = 1
Selection.Characters.Text = «Шаг»
Else
If f Then
m = 2
Selection.Characters.Text = «Стоп»
Else
m = 3
Selection.Characters.Text = «Пуск»
End If
End If
Range(«S47»).Select
End Sub
В этой подпрограмме, выделив
первую кнопку 4, определяем значение
скорости в ячейке S47. Если оно равно
нулю, то сбрасываем флаг пуска, задаем значение
маркера равное единице и на кнопке делаем
надпись “Шаг”. Если же скорость отлична от нуля,
то есть выбран авторежим, то при запущенной игре
(режим “два”) на кнопке делаем надпись “Стоп”
для последующего останова. В противном случае
устанавливаем третий режим и готовим кнопку к
пуску.
Для самой кнопки создадим следующую
подпрограмму, которую подключим к ней по
вышеописанной технологии.
Sub Пуск_Стоп()
Call Режим ‘Вызов процедуры «Режим»
Select Case m ‘Выбор по значению маркера m
Case 1: Call Шаг ‘При m = 1 вызов процедуры
«Шаг»
Case 2: Call Стоп ‘При m = 2 вызов процедуры
«Стоп»
Case 3: Call Пуск ‘При m = 3 вызов процедуры
«Пуск»
End Select ‘Конец выбора
End Sub
Процедуры “Шаг”, “Пуск” и
“Стоп” запишем отдельно:
Sub Шаг()
t = Timer ‘Фиксируем время
Call Новое_поколение ‘Вызов процедуры
«Новое_поколение»
End Sub
Sub Пуск()
f = True ‘Флаг пуска установить
Call Режим ‘Вызов процедуры «Режим»
Call Таймер ‘Вызов процедуры
«Таймер»
End Sub
Sub Стоп()
t = Timer ‘Фиксируем время
f = False ‘Флаг пуска сбросить
Call Режим ‘Вызов процедуры «Режим»
End Sub
Набираем скорость
Осталась последняя процедура
задержки времени смены поколений, которая
работает, пока включен режим “2”. Определив
текущее время и добавив к нему промежуток,
вычисленный на основе установленного в ячейке S47 значения скорости, вызывается
подпрограмма Новое_поколение.
Затем по значению счетчика “живых” клеток в
ячейке K47 проверяется, не
прекратилась ли “жизнь” на площадке? Если “да”,
то вызывается процедура остановки. Для
осуществления задержки времени используется
цикл “пока”, действующий до истечения
временного промежутка, в теле которого
проверяется наличие системных событий.
Sub Таймер()
Do While m = 2
t = Timer + (11 — Range(«S47»)) / 10
Call Новое_поколение
If Range(«K47») = 0 Then Call Стоп
Do While Timer < t
DoEvents
Loop
Loop
End Sub
Экспериментируйте
Отладив код игры, убеждаемся, что
наши труды не были напрасны. Значительно снижены
затраты на отвлекающие моменты, и теперь можно
сосредоточиться на самой игре. Необходимо
отметить, что это не только забава, но и площадка
для серьезных исследований. Закономерности и
процессы, происходящие во время игры, имеют свои
аналоги и продолжения в ряде наук, начиная от
кибернетики и кончая теологией. Проблемам,
затронутым в ней, посвящено множество научных
публикаций в области математики и информатики.
Рис. E9. Окончательный вариант игры
Вместе с тем, несмотря на то что самой
игре вот уже сорок лет, она продолжает привлекать
пытливые умы своей непредсказуемостью,
завораживающими узорами, удивительными
сюжетами. В ней до сих пор остается еще много
белых пятен, которые ждут своих первопроходцев.
Словом, как сказал Козьма Прутков: “Бросая в воду
камни, смотри на круги, ими образуемые, иначе
такое бросание будет пустым занятием”.
Жизнь в стиле Javascript
Подход к реализации
Рис. JS1
Реализация игры на языке Javascript состоит
из четырех файлов. Основной файл — index.htm.
Скриптовый моторчик игры содержится в
подключаемом файле main.js, стили — в файле main.css.
Еще один подключаемый файл add.js содержит
вспомогательные функции, не имеющие отношения к
алгоритмической сути реализации игры.
Игровое поле в реализации
представлено элементом TABLE,
который строит функция Life.putM().
Каждой клетке (элементу TD)
приписывается идентификатор id,
имя которого содержит координаты клетки в
формате сROW_COL. Здесь:
· c
— латинская буква (идентификатор должен
начинаться с буквы);
· ROW
— число, номер строки;
· _
— знак подчеркивания (разделитель ROW и COL);
· COL
— число, номер столбца.
Например, идентификатор с2_10 относится к клетке,
расположенной во второй строке и десятом столбце
(нумерация с нуля).
Таким образом, построенный
идентификатор позволяет не только получить
доступ к клетке, но и сообщить о ее расположении в
игровой таблице. Перевод координат в
идентификатор выполняет функция Life.getId(row,col),
обратное преобразование — функция Life.getRowCol(id).
Кроме того, каждой клетке (элементу TD) приписан обработчик события onclick — функция Life.click(row,
col). Щелчок внутри TABLE
получается адресным и не требует анализа
экранных координат (можно было бы обойтись одним
общим обработчиком, прикрепив его к TABLE, но тогда не избежать
координатных вычислений).
Жизнью внутри TABLE
управляет стиль background-color,
который задается программно для нужной клетки
(элемента TD) при помощи
свойства style.backgroundColor.
Фон живой клетки окрашивается цветом Life.lifeCell (в разделе констант
прописано #f00 — красный). Для
пустой клетки свойству style.backgroundColor
присваивается значение Life.emptyCell,
которое определено как «»
(пустая строка). Последнее требует пояснений.
Свойство style.backgroundColor
относится к встроенным стилям, то есть к
стилям, которые заданы в самом элементе при
помощи атрибута style.
Несмотря на то что во внешней стилевой таблице
(файл main.css) для TD
прописан стиль background-color:white,
значением свойства style.backgroundColor будет
пустая строка, которая и считается в реализации
признаком пустой клетки.
Проверка if
(element.style.backgroundColor) на пустых клетках будет
провалена, а на “живых” — выдержана (пустая
строка равнозначна значению false).
Построение следующего поколения
Кнопка “Старт” запускает
обработчик Life.startStop, а он, в свою
очередь, инициализирует метод setInterval,
служащий для выполнения действий, повторяющихся
с заданным интервалом времени. Метод setInterval (метод объекта window) имеет следующий формат:
переменная=setInterval(вызов_функции,
число_миллисекунд);
Функция, заданная в качестве
первого аргумента, будет запускаться в
непрерывном цикле через промежуток, указанный во
втором аргументе. Останавливает этот цикл метод clearInterval:
clearInterval(переменная);
Построением следующего поколения
“Жизни” занимается функция Life.generation().
Именно она и запускается в асинхронном цикле,
организуемом при помощи метода setInterval.
Функция Life.generation()
построена по алгоритму, описанному Олегом
Алферовым на сайте www.secoh.ru/msx/life-algorithm-r.html.
Программа поддерживает список живых
клеток и список клеток, которые могут поменять
статус на следующем ходу.
В начале цикла ячейки игрового поля
содержат 0, если соответствующая клетка мертва,
или некоторое большое число (например, 100), если
клетка жива. Список клеток содержит живые клетки
и не содержит мертвых. Список клеток-кандидатов
пуст. Первый шаг: для каждой живой клетки из
первого списка определяются ее соседи (8 клеток) и
увеличиваются на 1 их значения в ячейках игрового
поля. После выполнения этого шага каждая ячейка
игрового поля содержит количество ее живых
соседей. (Для клеток, которые живы на текущем
шаге, — количество соседей плюс 100.)
Кроме того, на первом шаге происходит
добавление во второй список: а) клеток, которые
живы на текущем шаге, и б) всех их соседей,
значения которых равны 0. Это гарантирует, что
будут перечислены все клетки, способные сменить
статус на следующем ходу, а также, что каждая
клетка будет перечислена только один раз.
Очистим первый список. Второй шаг:
для каждой клетки из второго списка, помечаем ее,
как живую (то есть присваиваем соответствующей
ячейке значение 100), если ее значение было 3, 102 или
103. В противном случае — присваиваим 0 (мертвая
клетка). Записываем живые клетки в первый список.
После завершения этой процедуры очищаем второй
список.
Выполнение в цикле приведенных двух
шагов обеспечивает выполнение правил игры
“Жизнь” (проверьте это!) и является самой
быстрой ее реализацией в общем случае.
Детали реализации этого алгоритма
можно проследить по файлу main.js.
index.htm
<!DOCTYPE HTML PUBLIC
«-//W3C//DTD HTML 4.01 Transitional//EN»
«http://www.w3.org/TR/html4/loose.dtd»>
<HTML lang=»ru»>
<HEAD>
<META http-equiv=»Content-Type» content=»text/html;
charset=windows-1251″>
<META http-equiv=»imagetoolbar» content=»no»>
<META http-equiv=»author» content=»А. А.
Дуванов»>
<META http-equiv=»Content-Style-Type»
content=»text/css»>
<LINK rel=»stylesheet» type=»text/css»
href=»main.css»>
<SCRIPT language=»JavaScript»
type=»text/javascript»
src=»main.js»></SCRIPT>
<SCRIPT language=»JavaScript»
type=»text/javascript»
src=»add.js»></SCRIPT>
<TITLE>Жизнь</TITLE>
</HEAD>
<BODY
onload=»preventSelection(document.getElementById(‘mLife’))»>
<H1>Игра Жизнь</H1>
<!— Матрица игры —>
<SCRIPT language=JavaScript
type=»text/javascript»>Life.putM();</SCRIPT>
<!— Управление —>
<FORM>
<INPUT id=»start» type=»button»
value=»Старт»
onclick=»Life.startStop()»>
<INPUT id=»clear» type=»button»
value=»Очистить»
onclick=»Life.clear()»>
<DIV>Номер поколения: <SPAN
id=»time»>0</SPAN></DIV>
</FORM>
</BODY>
</HTML>
main.js
// Игра Жизнь
// ————————————————-
// Пространство имён внутри
глобального объекта Life
// Life — единственное глобальное имя в
этом скрипте
// ————————————————
var Life = {};
// ————————————————-
// Константы
// ———
Life.nRow = 30; // Число строк в игровой
матрице
Life.nCol = 45; // Число столбцов в игровой
матрице
Life.emptyCell = «»; // Пустая клетка
Life.lifeCell = «#f00»; // Живая клетка (цвет
Жизни)
Life.nTick = 1000; // Интервал времени между
поколениями
// Представление на экране
===========================================
// —————————————————
// Построение матрицы на экране
// —————————————————
Life.putM = function()
{
var str = «<TABLE id=’mLife’ cellspacing=0
cellpadding=0>»;
for(var i=0; i<Life.nRow; i++)
{
str += «<TR>»;
for(var j=0; j<Life.nCol; j++)
str += «<TD
onclick=’Life.click(«+i+»,»+j+»)’
id='»+Life.getId(i,j)+»‘> </TD>»;
str += «</TR>»;
}
str += «</TABLE>»;
document.write(str);
};
// Математика ===================================
// ———-
// Первый список ячеек
// Здесь будем хранить живые клетки
// ——————-
Life.list1 = {};
//
// Второй список ячеек (рабочий)
// Здесь будем хранить живые клетки и их
соседей
// ——————-
Life.list2 = {};
// Формат хранения клеток в списках:
// id:значение
// Значение равно 100 для живой клетки, 0
для пустой.
// Во втором списке к значению клетки (к
0 или к 100) будем добавлять
// количество ее соседей.
// Имя клетки совпадает с её
идентификатором id в TABLE и
// строится по формуле сROW_COL
// Здесь:
// c — латинская буква (идентификатор
должен начинаться с буквы)
// ROW — число, номер строки
// _ — знак подчеркивания (разделитель ROW
и COL)
// COL — число, номер столбца
// Идентификатор строит функция id =
Life.getId(row,col) — см. ниже
// —————————————————-
// Вернуть/установить стиль background-color
клетки (элемент TD)
// ——————————————————
Life.CellStatus = function(row, col, status)
{
var st = document.getElementById(Life.getId(row, col)).style;
if (arguments.length > 2) st.backgroundColor = status;
return st.backgroundColor;
};
//——————————————————
// Изменить статус клетки.
// Для живой клетки:
// * сбросить стиль background-color (Life.emptyCell)
// * удалить клетку из Life.list1
// Для пустой клетки:
// * установить стиль background-color (Life.lifeCell)
// * добавить клетку в Life.list1
// ——————————————————
Life.changeCellStatus = function(row, col)
{
var id = Life.getId(row, col);
var st = document.getElementById(id).style;
if (st.backgroundColor)
{
st.backgroundColor = Life.emptyCell; // сбросить фон
delete Life.list1[id]; // удалить клетку из Life.list1
}
else
{
st.backgroundColor = Life.lifeCell; // установить фон
Life.list1[id] = 100; // добавить клетку в Life.list1
}
};
// —————————————————
// Обработка нажатия кнопки Старт/Стоп
// —————————————————
Life.start = true; // На кнопке Старт/Стоп
надпись Старт?
Life.timer; // Таймер
Life.time; // Счетчик поколений
Life.startStop = function()
{
Life.start = !Life.start;
document.getElementById(«start»).value = Life.start ?
«Старт» : «Стоп»;
if(Life.start) clearInterval(Life.timer); // остановить
игру
else // запустить игру
{
Life.time = 0;
// Запускать смену поколений через
каждые Life.nTick
Life.timer = setInterval(Life.generation, Life.nTick);
}
};
// ————————————————
// Построение следующего поколения
// Алгоритм описан Олегом Алферовым на
сайте
// http://www.secoh.ru/msx/life-algorithm-r.html
// ————————————————
Life.generation = function()
{
// Копировать список 1 в список 2
for(var cell in Life.list1) Life.list2[cell] = Life.list1[cell];
// Соседи живых клеток заносятся в
список 2 и их значения увеличиваются на 1.
// После выполнения этого шага каждая
клетка в Life.list2 содержит
// количество ее живых соседей. (Для
клеток, которые живы на текущем
// шаге, — количество соседей плюс 100.)
for(var cell in Life.list1)
{
var list = Life.listNear(cell); // список соседей
клетки cell
// Добавить в список Life.list2 те ячейки из
list, которых там нет,
// если ячейка уже есть, увеличить ее
значение (число соседей) на 1
for(var k in list) Life.list2[k] = Life.list2[k] ? (Life.list2[k]+1) :
1;
// Удалить ячейку из первого списка
delete Life.list1[cell];
}
// Работа со вторым списком (первый
список сейчас пуст)
for(var cell in Life.list2)
{
// Преобразуем значения во втором
списке:
// 3, 102, 103 заменить на 100 (живые клетки в
следующем поколении)
// заменить на 0 в остальных случаях
(погибшие клетки)
Life.list2[cell] = (Life.list2[cell] == 3 ||
Life.list2[cell] == 102 ||
Life.list2[cell] == 103) ? 100 : 0;
// Если 100, то добавить в первый список и
покрасить на экране,
// в противном случае сбросить окраску.
var ob = Life.getRowCol(cell); // получить координаты
клетки
if (Life.list2[cell] == 100)
{
Life.list1[cell] = 100;
Life.CellStatus(ob.row,ob.col,Life.lifeCell);
}
else Life.CellStatus(ob.row,ob.col,Life.emptyCell);
// Удалить элемент из второго списка.
delete Life.list2[cell];
}
// Поколение построено.
// Сейчас список Life.list2 пуст, а в списке
Life.list1 собраны
// живые клетки. Все готово к построению
следующего поколения.
// Вывести номер поколения на экран
document.getElementById(«time»).innerHTML = ++Life.time;
};
// —————————————————
// Построение списка соседей данной
клетки (8 клеток):
// 2 1 3
// 4 * 5 (схема соседей клетки *)
// 7 6 8
// —————————————————
Life.listNear = function(cell)
{
var list = {}; // здесь будем формировать
список соседей клетки cell
var row, col; // здесь будем формировать
координаты соседей
// Получить координаты для исходной
клетки
var ob = Life.getRowCol(cell);
// Соседи в строке выше
row = ob.row-1;
if(row < 0) row = Life.nRow-1; // учитываем, что
среда — тор
col = ob.col;
list[Life.getId(row, col)] = 1; // клетка 1 (по схеме
соседей)
col = ob.col-1;
if(col < 0) col = Life.nCol-1; // учитываем, что
среда — тор
list[Life.getId(row, col)] = 1; // клетка 2 (по схеме
соседей)
col = ob.col+1;
if(col >= Life.nCol) col = 0; // учитываем, что
среда — тор
list[Life.getId(row, col)] = 1; // клетка 3 (по схеме
соседей)
// Соседи в той же строке
row = ob.row;
col = ob.col-1;
if(col < 0) col = Life.nCol-1; // учитываем, что
среда — тор
list[Life.getId(row, col)] = 1; // клетка 4 (по схеме
соседей)
col = ob.col+1;
if(col >= Life.nCol) col = 0; // учитываем, что
среда — тор
list[Life.getId(row, col)] = 1; // клетка 5 (по схеме
соседей)
// Соседи в строке ниже
row = ob.row+1;
if(row >= Life.nRow) row = 0 // учитываем, что
среда — тор
col = ob.col;
list[Life.getId(row, col)] = 1; // клетка 6 (по схеме
соседей)
col = ob.col-1;
if(col < 0) col = Life.nCol-1; // учитываем, что
среда — тор
list[Life.getId(row, col)] = 1; // клетка 7 (по схеме
соседей)
col = ob.col+1;
if(col >= Life.nCol) col = 0; // учитываем, что
среда — тор
list[Life.getId(row, col)] = 1; // клетка 8 (по схеме
соседей)
return list; // возвращаем список
}
// ———————————————
// Очистить среду
// ———————————————
Life.clear = function()
{
if(!Life.start) return;
// Каждой живой клетке присвоим статус
«пустая»
// и удалим ее из списка Life.list1
for(var cell in Life.list1)
{
var ob = Life.getRowCol(cell);
Life.CellStatus(ob.row,ob.col,Life.emptyCell);
delete Life.list1[cell];
}
// Вывести номер поколения
Life.time = 0;
document.getElementById(«time»).innerHTML = Life.time;
};
// Обработка щелчка в матрице
========================================
//
Life.click = function(row, col)
{
if(!Life.start) return;
Life.changeCellStatus(row, col);
};
// Вспомогательные функции
===========================================
// ———————————————
// Вернуть координаты ячейки по ее
идентификатору
// ———————————————
Life.getRowCol = function(id)
{
var ob = {};
var d = id.indexOf(«_»);
ob.row = parseInt(id.substring(1, d));
ob.col = parseInt(id.substring(d+1));
return ob;
};
// —————————————-
// Вернуть идентификатор по
координатам ячейки
// —————————————
Life.getId = function(row, col)
{
return «c»+row+»_»+col;
};
Жизнь в стиле Flash
Интерфейс и элементы управления
Традиционный минимальный
интерфейс “Жизни” состоит из клетчатого поля
(размерность задается константой в коде) и трех
кнопок: “Старт”, “Стоп” и “Очистить”.
Рис. F1. Поле игры
Клетчатое поле строится из
экземпляров символа onecell —
MovieClip, имеющего два кадра-состояния,
соответствующих “пустой” и “живой” клетке. В
каждом кадре содержится единственная команда stop().
Библиотека проекта показана на
рисунке.
Рис. F2. Библиотека проекта
Кнопки “Старт” и “Стоп” имеют
одинаковые размеры и координаты — в каждый
момент времени видна только одна из них.
Реализация
Весь код размещается в первом и
единственном кадре главной сцены.
//Размер поля в клетках
(NxN) определяется константой
var N=20;
//В зависимости от размера поля
вычисляем размер родной клетки
var W=Math.round(Stage.height/N)-1;
var s=[]; //Текущее поколение
var s1=[]; //Следующее поколения
var cells=[]; //Массив из клеток — MovieClip’ов
var states=[«dead»,»alive»]; //Метки
кадров в клетке
var life=false; //Флаг: идет процесс или нет
bstop._visible=false; //Начальное состояние:
спрятать кнопку «Стоп»
//Создаем поле
for(i=0;i<N;i++) {
s[i]=[];s1[i]=[];cells[i]=[];
for (j=0;j<N;j++) {
s[i][j]=0;
cells[i][j]=attachMovie(«cell»,»cell»+i+»_»+j,i*N+j,
{_width:W,
_height:W,
_x:j*(W+1),
_y:i*(W+1),r:i,c:j});
cells[i][j].onRelease=function() {
//Каждая клетка реагирует на нажатие —
изменяет
//соответствующее ей значение в
массиве s
s[this.r][this.c]=(s[this.r][this.c]+1)%2;
}
cells[i][j].onEnterFrame=function() {
//В каждый момент времени клетка
проверяет
//свое состояние и переходит в
соответствующий кадр
this.gotoAndStop(states[s[this.r][this.c]]);
}
}
}
function around(i,j) {
//Количество соседей у клетки (i,j)
ret=0;
for(di=-1;di<2;di++)
for(dj=-1;dj<2;dj++)
if ((di!=0)||(dj!=0)) ret+=s[(i+di+N)%N][(j+dj+N)%N];
return ret;
}
function cycle() {
//Основная функция — один шаг
«Жизни»
//В массиве s1 сформируем следующее
поколение
for (i=0;i<N;i++)
for(j=0;j<N;j++) {
if ((s[i][j]==0)&&(around(i,j)==3))
s1[i][j]=1; //На этом месте родится клетка
else if
((s[i][j]==1)&&((around(i,j)<2)||(around(i,j)>3)))
s1[i][j]=0; //На этом месте клетка погибнет
else
s1[i][j]=s[i][j]; //Состояние клетки не
изменится
}
//Сделаем будущее настоящим
for (i=0;i<N;i++)
for (j=0;j<N;j++)
s[i][j]=s1[i][j];
}
bstart.onRelease=function() {
//По нажатию на кнопку «Старт»
будем по таймеру вызывать
//функцию cycle()
life=true;
lifeInterval=setInterval(cycle,100);
this._visible=false;
bstop._visible=true;
}
bstop.onRelease=function() {
//Кнопка «Стоп» отменяет вызов
функции cycle()
life=false;
clearInterval(lifeInterval);
this._visible=false;
bstart._visible=true;
}
bclear.onRelease=function() {
//Очищаем поле
for (i=0;i<N;i++)
for (j=0;j<N;j++)
s[i][j]=0;
}
Жизнь в стиле Delphi
Рис. D1. Интерфейс реализации на
Delphi
Окно программы состоит из пяти
областей:
1. Собственно игровое поле (таблица
на рис. D1 справа).
2. Область в левом верхнем углу, в
которой задаются размеры игрового поля (имеется
ограничение в 50 строк и 100 столбцов) и цвет,
которым закрашивается клетка, если она “живая”.
3. Область “Скорость популяции”, в
которой можно изменять скорость появления
следующей популяции игры.
4. Основная панель управления,
содержащая три кнопки:
· “Очистить” — при
нажатии на нее игровое поле очищается и игра
возвращается к первой популяции;
· “Следующий шаг” —
позволяет играть в “ручном” режиме. При нажатии
происходит переход к следующей популяции;
· “Старт/стоп” —
кнопка, которая запускает автоматический расчет
популяций или прекращает его.
5. Статус — панель внизу окна, в
которую выводится информация о номере текущей
популяции.
Фактически в программе имеются два
игровых поля: логическое — целочисленная
матрица GameField, элементы которой
могут принимать значения 0 или 1, и визуальное —
объект класса TDrawGrid LifeGrid. Для LifeGrid
описан метод LifeGridDrawCell,
который по значению элемента в GameField
закрашивает клетку в нужный цвет. Кроме того, для LifeGrid определены методы LifeGridMouseDown, LifeGridMouseUp
и LifeGridMouseMove, которые позволяют
расставлять первоначальную популяцию. Например,
можно нажать кнопку мыши и двигать ей по игровому
полю. Там, где “проехала” мышь, клетки будут
помечены. Если проехать по помеченной клетке
второй раз, то она вернется в предыдущее
состояние.
Для того чтобы вычислить следующее
состояние, определен метод GetNextGen.
В цикле пробегаем по всему игровому полю (GameField), для каждой клетки с помощью
метода CalcNeib получаем
количество соседей (причем не забываем, что мы
двигаемся по тору) и формируем новое игровое
поле.
Для организации автоматического
вычисления популяции используется таймер LifeTimer, для которого определен метод
LifeTimerTimer. В этом методе
вычисляется новое игровое поле, а затем
вызывается метод LifeGrid.Refresh, который обновляет
визуальное игровое поле. Аналогичные действия
происходят и при нажатии на кнопку “Следующий
шаг”.
При вычислении каждой следующей
популяции увеличивается счетчик, значение
которого выводится в StatusBar.
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls,
Forms,
Dialogs, ExtCtrls, Grids, StdCtrls, Spin, Buttons, ComCtrls;
const
MaxGrid = 100; //Максимальный размер поля
type
TMainForm = class(TForm)
Panel1: TPanel;
Panel2: TPanel;
Panel3: TPanel;
LifeGrid: TDrawGrid; //Игровое поле
GroupBox1: TGroupBox;
Splitter1: TSplitter;
Label1: TLabel;
Label2: TLabel;
CellColorBox: TColorBox; //Цвет, которым будет
закрашиваться поле
Label3: TLabel;
WSizeEdit: TSpinEdit; //Размер игрового поля по
горизонтали
HSizeEdit: TSpinEdit; //Размер игрового поля по
вертикали
StartBtn: TBitBtn; //Кнопка старт/стоп,
запускающая игру
ClearBtn: TBitBtn; //Кнопка, очищающая игровое
поле
NextBtn: TBitBtn;
LifeTimer: TTimer;
StatusBar: TStatusBar;
GroupBox2: TGroupBox;
TrackBar1: TTrackBar;
Label4: TLabel;
Label5: TLabel;
procedure TrackBar1Change(Sender: TObject);
procedure LifeTimerTimer(Sender: TObject);
procedure StartBtnClick(Sender: TObject);
procedure NextBtnClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure LifeGridMouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
procedure LifeGridMouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
procedure LifeGridMouseDown(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
procedure CellColorBoxChange(Sender: TObject);
procedure ClearBtnClick(Sender: TObject);
procedure LifeGridDrawCell(Sender: TObject; ACol, ARow: Integer;
Rect: TRect; State: TGridDrawState); //Кнопка
пошагового прохода
//Обработка события на изменение
значения в HSizeEdit
procedure HSizeEditChange(Sender: TObject);
//Обработка события на изменение
значения в WSizeEdit
procedure WSizeEditChange(Sender: TObject);
private
// Матрица, описывающая игровое поле: 0
— мертвая клетка, 1 — живая
GameField: Array [0..MaxGrid+1, 0..MaxGrid+1] of 0..1;
MouseDownFlag: Boolean; //Флаг, говорящий о том,
//нажата ли клавиша мыши
OldC, OldR: Integer; // переменные, необходимые
для вычисления клетки
// по координатам мыши
GenCount: Integer; //Счетчик популяций
function CalcNeib(i, j: Integer): Integer; //Посчитать
соседей клетки
//с координатами i и j
procedure GetNextGen; // Получить следующую
популяцию.
public
{ Public declarations }
end;
var
MainForm: TMainForm;
implementation
{$R *.dfm}
procedure TMainForm.CellColorBoxChange(Sender: TObject);
begin
//Перерисуем игровое поле при
изменении цвета
LifeGrid.Refresh;
end;
// Обработка очистки игрового поля
procedure TMainForm.ClearBtnClick(Sender: TObject);
var
i, j: Integer;
begin
//Очищаем матрицу игрового поля
for i := 1 to MaxGrid do
for j := 1 to MaxGrid do GameField[i,j] := 0;
//Обновляем визуальное игровое поле
LifeGrid
LifeGrid.Refresh;
GenCount := 0; //Обнулим счетчик популяций
StatusBar.SimpleText := ‘Популяция: 0’;
end;
procedure TMainForm.FormCreate(Sender: TObject);
var
i, j: Integer;
begin
//Очистим игровое поле
//Очищаем матрицу игрового поля
for i := 1 to MaxGrid do
for j := 1 to MaxGrid do GameField[i,j] := 0;
MouseDownFlag := false;
GenCount := 0; //Обнулим счетчик популяций
StatusBar.SimpleText := ‘Популяция: 0’;
end;
// Изменение количества столбцов
игрового поля
procedure TMainForm.HSizeEditChange(Sender: TObject);
begin
//Для установки количества строк
игрового поля
//берем значение из HSizeEdit
LifeGrid.ColCount := HSizeEdit.Value;
end;
// Изменение количества строк игрового
поля
procedure TMainForm.WSizeEditChange(Sender: TObject);
begin
//Для установки количества столбцов
игрового поля
//берем значение из WSizeEdit
LifeGrid.RowCount := WSizeEdit.Value;
end;
//Перерисовка игрового поля в
соответствии с матрицей
procedure TMainForm.LifeGridDrawCell(Sender: TObject;
ACol, ARow: Integer;
Rect: TRect; State: TGridDrawState);
var
cl: TColor;
begin
//При перерисовке LifeGrid’а смотрим на
значение элемента
//матрицы GameField с координатами ACol, ARow и
если там 1, то
//закрашиваем ее в цвет CellColorBox, в
противном случае —
//в цвет clWindow
if GameField[ARow+1, ACol+1] = 1 then cl := CellColorBox.Selected
else cl := clWindow;
with LifeGrid.Canvas do
begin
Brush.Color := cl;
Brush.Style := bsSolid;
Pen.Color := cl;
FillRect(Rect);
end;
end;
procedure TMainForm.LifeGridMouseDown(Sender: TObject;
Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
begin
//устанавливаем флаг нажатой кнопки
мыши в истину
MouseDownFlag := true;
OldC := -1;
OldR := -1;
end;
procedure TMainForm.LifeGridMouseMove(Sender: TObject;
Shift: TShiftState;
X, Y: Integer);
var
NewC, NewR: Integer;
begin
// Обрабатываем движение мыши, если
была нажата клавиша
if MouseDownFlag then
begin
//Определяем клетку, по которой был
клик, и для этой клетки
//меняем значение в GameField на
противоположное
LifeGrid.MouseToCell(X, Y, NewC, NewR);
// Изменяем ситуацию на поле, если мы
попали в клетку, отличную
// от предыдущей, поскольку мы можем
двигать мышью медленно
if (NewR<>OldR) Or (NewC<>OldC) then
begin
GameField[NewR+1, NewC+1] := (GameField[NewR+1, NewC+1] + 1) mod 2;
LifeGrid.Refresh;
OldC := NewC;
OldR := NewR;
end;
end;
end;
procedure TMainForm.LifeGridMouseUp(Sender: TObject;
Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
begin
//устанавливаем флаг нажатой кнопки
мыши в ложь
MouseDownFlag := false;
end;
procedure TMainForm.LifeTimerTimer(Sender: TObject);
// Создание мультипликации из жизни
begin
// Рассчитаем следующую популяцию
GetNextGen;
// Обновим поле
LifeGrid.Refresh;
// Увеличим счетчик популяций и обновим
статусбар
Inc(GenCount);
StatusBar.SimpleText := ‘Популяция: ‘ + IntToStr(GenCount);
end;
procedure TMainForm.NextBtnClick(Sender: TObject);
//Обработаем нажатие на кнопку
следующая популяция
begin
// Рассчитаем следующую популяцию
GetNextGen;
// Обновим поле
LifeGrid.Refresh;
// Увеличим счетчик популяций и обновим
статусбар
Inc(GenCount);
StatusBar.SimpleText := ‘Популяция: ‘ + IntToStr(GenCount);
end;
procedure TMainForm.StartBtnClick(Sender: TObject);
// Запуск и остановка таймера
begin
if StartBtn.Caption = ‘Старт’ then
begin
StartBtn.Caption := ‘Стоп’;
LifeTimer.Enabled := true;
NextBtn.Enabled := False;
end
else
begin
StartBtn.Caption := ‘Старт’;
LifeTimer.Enabled := false;
NextBtn.Enabled := true;
end;
end;
procedure TMainForm.TrackBar1Change(Sender: TObject);
begin
// Установка таймера
LifeTimer.Interval := TrackBar1.Position;
end;
function TMainForm.CalcNeib(i: Integer; j: Integer): Integer;
// Считаем соседей клетки с учетом того,
что поверхность моделирует тор
var
left, top, right, bottom: Integer;
begin
if (j<>1) then left := j — 1
else left := HSizeEdit.Value;
if (j<>HSizeEdit.Value) then right := j + 1
else right := 1;
if (i<>1) then top := i — 1
else top := WSizeEdit.Value;
if (i<>WSizeEdit.Value) then bottom := i + 1
else bottom := 1;
Result := GameField[top, left] + GameField[top, j] +
GameField[top, right] +
GameField[i, left] + GameField[i, right] +
GameField[bottom, left] + GameField[bottom, j] +
GameField[bottom, right];
end;
procedure TMainForm.GetNextGen;
// Проходим по матрице GameField и для
каждой клетки вычисляем
// новое значение по правилам игры
var
s, i, j: Integer;
NewGameField: Array [0..MaxGrid+1, 0..MaxGrid+1] of 0..1;
begin
// сформируем новое игровое поле
for i := 1 to WSizeEdit.Value do
for j := 1 to HSizeEdit.Value do
begin
s := CalcNeib(i, j); //Посчитали соседей
// Если у пустой клетки 3 соседа, то в ней
«зарождается жизнь»
if (GameField[i, j] = 0) And (s = 3) then NewGameField[i, j] := 1
else NewGameField[i, j] := 0;
if (GameField[i, j] = 1) then
begin
if (s = 2) or (s = 3) then NewGameField[i, j] := 1
else NewGameField[i, j] := 0;
end;
end;
// перенесем новое игровое поле в
старое
for i := 1 to WSizeEdit.Value do
for j := 1 to HSizeEdit.Value do GameField[i, j] := NewGameField[i, j];
end;
end.
1 Использована новая версия
системы КуМир (см. “Информатику” № 6/2009).
2 Конечно, можно провести и
другие усовершенствования.
3 При использовании систем
программирования Borland Pascal и Turbo Pascal первый размер
массива generations должен
быть уменьшен.
4 Может случиться, что у вас номер
кнопки будет иным. Для определения номера
необходимо отобразить панель Рисование,
щелкнуть на ней по значку со стрелкой, похожей на
указатель мыши Выбор объектов, затем
выделить кнопку, и в
начале строки формул в поле адреса отобразятся
имя и номер объекта.