Модель по информатике на excel - Word и Excel - помощь в работе с программами

Ярославский областной
институт повышения квалификации

педагогических и руководящих
работников образования

Творческая работа

“Задачи по моделированию

в среде Excel”

Учителя информатики

средней школы № 58

г.Ярославля

Горбачевой Александры Николаевны

Научный руководитель:

проректор ИПК, руководитель ЦИТ

Смирнова Алевтина Николаевна,

методист ЦИТ ИПК

Потехин Николай Владимирович

г. Ярославль, 2000
Содержание

1. Введение
…………………………………………………………………………………………………….
3
1.1 Психолого-педагогические особенности изучения темы

“Моделирования” в школьном курсе
информатики

1.2 Обязательный
минимум содержания образования по теме

“Моделирование
и формализация”

1.3
Требования к уровню подготовки выпускников по теме

“Моделирование
и формализация”

2. Основные понятия моделирования
……………………………………………….……………. 7

3. Основные этапы моделирования
…………………………………………………..……………. 10

4. Метод математических моделей
………………………………………………….…………….. 13

5. Задачи по моделированию из
различных предметных областей ……….…………. 16

5.1 “Экономика”
……………………………………………………………………… 16
5.2 “Астрономия” ……………………………………………………………………. 24
5.3. “Физика” ………………………………………………………………………… 27
5.4 “Экология” ……………………………………………………………………….. 31
5.5 “Биология” ……………………………………………………………………….. 38

5.6 “География”
……………………………………………………………………… 44

6. Заключение …………………………………………………………………………… 45

7. Список литературы
………………………………………………………………….. 46

8. Приложение
………………………………………………………………………….. 47

1. Введение

1.1 Психолого-педагогические
особенности изучения темы “Моделирования” в школьном курсе информатики

Наиболее важные и
значимые общеобразовательные цели информатики и информатизации — установление и
усиление межпредметных связей, создание условий для восприятия и понимания
информационных процессов в обществе, природе, познании — формирование у
учащихся информационной картины мира.

Современное образование
требует преодоления разрозненности учебных предметов. Каждой научной дисциплине
свойственно свое особое сочетание формализованных и неформализованных методов
моделирования явлений, процедур доказательства и объяснения, и лишь информатика
легко преодолевает межпредметные границы, обогащает все области научного
познания.

Проблема взаимосвязи
школьных дисциплин — математики, информатики, физики, биологии и др. — является
одной из актуальных проблем современной дидактики, психологии и методики преподавания.
Решение задач — конкретных моделей явлений — на уроках информатики является
одним из мощных способов реализации межпредметных связей информатики и других
наук.

Человек издавна
использует моделирование для исследования объектов, процессов, явлений в
различных областях. Результаты этих исследований служат для определения и
улучшения характеристик реальных объектов и процессов; для понимания сути
явлений и выработки умения приспосабливаться или управлять ими; для
конструирования новых объектов или модернизации старых. Моделирование помогает
человеку принимать обоснованные и продуманные решения, предвидеть последствия
своей деятельности.

Компьютерное
моделирование учебных и реальных объектов, ситуаций и процессов в математике,
физике, химии, биологии, экологии ставит учащегося в активную позицию
исследователя, позволяет самостоятельно открывать законы и явления.

Развитие навыков
построения моделей способствует решению задачи, имеющей общеобразовательную
ценность, а именно развитию системного и логического мышления. Ведь процесс
построения моделей требует помимо специальных знаний еще и особым образом
развитого мышления.

Решение задач по
моделированию процессов и явлений развивает мыслительную деятельность учащихся.

Под развитием мышления
учащихся в процессе обучения психологи понимают формирование и
совершенствование всех видов, форм и операций мышления, выработку умений и
навыков по применению законов мышления в познавательной и учебной деятельности,
а также умений осуществлять перенос приемов мыслительной деятельности из одной
области знаний в другую.

Таким образом, развитие
мышления включает в себя:

1. Развитие всех видов мышления
(наглядно-действенного, наглядно-образного, абстрактно-логического) и
одновременно стимуляцию процесса перерастания их из одного вида в другой.

2. Формирование и
совершенствование мыслительных операций.

3. Развитие умений:

·
выделять
существенные свойства предметов и абстрагировать их от несущественных;

·
находить
главные связи и отношения предметов и явлений реального мира;

·
делать
правильные выводы из фактов и проверять их;

·
доказывать
истинность своих суждений и опровергать ложные умозаключения;

·
раскрывать
сущность основных форм правильных умозаключений (индукции, дедукции и по
аналогии);

·
излагать
свои мысли определенно, последовательно, непротиворечиво и обоснованно.

4. Выработку умения осуществлять
перенос операций и приемов мышления из одной области знания в другую;
прогнозирование развития явлений и умение делать выводы.

5. Совершенствование умений и
навыков по применению законов и требований формальной и диалектической логики в
учебной и во внеучебной познавательной деятельности учащихся.

По мнению психологов
схема решения мыслительных задач выглядит следующим образом:

Условия возникновения	Процесс	Приемы	Результат	Формы реализации

		Анализ		Суждения

Проблемная	Мышление	Синтез	Продукт	Понятия

ситуация		Сравнение	мышления	Умозаключения

		Обобщение

В процессе построения
модели учащиеся, отталкиваясь от общей формулировки задачи, выделяют
существенные части моделируемой системы, исследуют свойства этих объектов,
находят связи между ними, проводят компьютерные эксперименты и анализируют
результаты моделирования. Практически все перечисленные выше процессы мыслительной
деятельности прослеживаются при решении задач на составление моделей.

Умение выделять
необходимую информацию и организовывать ее в структуру — важнейшее качество человеческого
интеллекта.

1.2 Обязательный минимум
содержания образования

по теме “Моделирование и
формализация”

Моделирование как метод познания. Материальные и
информационные модели. Объектно-ориентированное информационное моделирование.
Формализация. Основные типы информационных моделей (табличные, иерархические,
сетевые). Исследование информационных моделей на компьютере.

1.3 Требования к уровню
подготовки выпускников

по теме “Моделирование и
формализация”

Учащиеся должны:

·
уметь
характеризовать сущность моделирования;

·
уметь
характеризовать сущность формализации;

·
знать о
существовании множества моделей для одного и того же объекта;

·
уметь
строить простейшие информационные модели;

·
знать
этапы информационной технологии решения задач с использованием компьютера.

2. Основные понятия моделирования

Понятие модели

Модель —
это некоторое упрощенное подобие реального объекта, явления или процесса.

Модель — это такой
материальный или мысленно представляемый объект, который замещает
объект-оригинал с целью его исследования, сохраняя некоторые важные для данного
исследования типичные черты и свойства оригинала.

Хорошо построенная
модель, как правило, доступнее для исследования, чем реальный объект (например,
такой, как экономика страны, Солнечная система и т.п.). Другое, не менее важное
назначение модели состоит в том, что с ее помощью выявляются наиболее
существенные факторы, формирующие те или иные свойства объекта. Модель также
позволяет учиться управлять объектом, что важно в тех случаях, когда
экспериментировать с объектом бывает неудобно, трудно или невозможно (например,
когда эксперимент имеет большую продолжительность или когда существует риск
привести объект в нежелательное или необратимое состояние).

Таким образом, можно сделать
вывод, что модель необходима для того, чтобы:

·
понять,
как устроен конкретный объект — каковы его структура, основные свойства, законы
развития и взаимодействия с окружающим миром;

·
научиться
управлять объектом или процессом и определить наилучшие способы управления при
заданных целях и критериях (оптимизация);

·
прогнозировать
прямые и косвенные последствия реализации заданных способов и форм воздействия
на объект, процесс.

Структура — это определенный способ
объединения элементов, составляющих единый сложный объект.

Система — это сложный объект,
представляющий собой совокупность взаимосвязанных элементов, объединенных в
некоторую структуру.

В учебнике “Информатика 9
класс” Н.В.Макаровой предложена следующая классификация моделей.

1. Классификация по области использования

Модели

Учебные

Опытные

Научно-технические

Игровые

Имитационные

Учебные: наглядные пособия,
различные тренажеры, обучающие программы.

Опытные: уменьшенные или увеличенные
копии исследуемого объекта для дальнейшего его изучения (модели корабля,
автомобиля, самолета, гидростанции).

Научно-технические модели создают для
исследования процессов и явлений (стенд для проверки телевизоров; синхротрон —
ускоритель электронов и др.).

Игровые: военные, экономические,
спортивные, деловые игры.

Имитационные: отражают реальность с той
или иной степенью точности (испытание нового лекарственного средства в ряде
опытах на мышах; эксперименты по внедрению в производство новой технологии).

2.
Классификация с учетом фактора времени

	Модели


Статические		Динамические

Статическая модель — модель объекта в данный момент
времени.

Динамическая модель позволяет увидеть изменения объекта во времени.

3.
Классификация по способу представления

Модели

Материальные

Информационные

Знаковые

Вербальные

Компьютерные

Некомпьютерные

Материальная модель — это физическое подобие
объекта. Они воспроизводят геометрические и физические свойства оригинала
(чучела птиц, муляжи животных, внутренних органов человеческого организма,
географические и исторические карты, схема солнечной системы).

Информационная модель — это совокупность
информации, характеризующая свойства и состояния объекта, процесса, явления, а
также взаимосвязь с внешним миром.

Любая информационная
модель содержит лишь существенные сведения об объекте с учетом той цели, для
которой она создается. Информационные модели одного и того же объекта,
предназначенные для разных целей, могут быть совершенно разными.

Вербальная модель — информационная модель в
мысленной или разговорной форме.

Знаковая модель — информационная модель,
выраженная специальными знаками, т.е. средствами любого формального языка.
Знаковые модели — это рисунки, тексты, графики, схемы, таблицы …

Компьютерная модель — модель, реализованная
средствами программной среды.

Прежде чем построить
модель объекта (явления, процесса), необходимо выделить составляющие его
элементы и связи между ними (провести системный анализ) и “перевести”
полученную структуру в какую-либо заранее определенную форму — формализовать
информацию.

Формализация — это процесс выделения и перевода
внутренней структуры предмета, явления или процесса в определенную
информационную структуру — форму.

Процесс построения модели
называется моделированием.

3. Основные этапы моделирования

Моделирование —
творческий процесс. Заключить его в формальные рамки очень трудно. В наиболее
общем виде его можно представить поэтапно в следующем виде.

I этап. Постановка задачи Описание задачи Цель моделирования Анализ объекта

II этап. Разработка модели Информационная модель Знаковая модель Компьютерная модель

III этап. Компьютерный эксперимент

IV этап. Анализ результатов моделирования

Результаты соответствуют цели	Результаты не соответствуют цели

Каждый раз при решении
конкретной задачи такая схема может подвергаться некоторым изменениям: какой-то
блок может быть убран или усовершенствован. Все этапы определяются поставленной
задачей и целями моделирования.

I этап. Постановка
задачи

Под задачей в самом общем
смысле понимается некая проблема, которую надо решить. Главное — определить
объект моделирования и понять, что собой должен представлять результат.

По характеру постановки
все задачи можно разделить на две основные группы. К первой группе можно
отнести задачи, в которых требуется исследовать, как изменяется характеристика
объекта при некотором воздействии на него. Такую постановку задачи принято
называть “что будет, если…”. Вторая группа задач имеет такую обобщенную
формулировку: какое надо произвести воздействие на объект, чтобы его параметры
удовлетворяли некоторому заданному условию? Такая постановка задачи часто
называется “как сделать, чтобы…”.

Цели моделирования
определяются расчетными параметрами модели. Чаще всего это поиск ответа на
вопрос, поставленный в формулировке задачи.

Далее переходят к
описанию объекта или процесса. На этой стадии выявляются факторы, от которых
зависит поведение модели. При моделировании в электронных таблицах учитывать
можно только те параметры, которые имеют количественные характеристики.

Иногда задача может быть
уже сформулирована в упрощенном виде, и в ней четко поставлены цели и
определены параметры модели, которые надо учесть.

При анализе объекта
необходимо ответить на следующий вопрос: можно ли исследуемый объект или
процесс рассматривать как единое целое или же это система, состоящая из более
простых объектов? Если это единое целое, то можно перейти к построению
информационной модели. Если система — надо перейти к анализу объектов, ее
составляющих, определить связи между ними.

II этап. Разработка
модели

По результатам анализа
объекта составляется информационная модель. В ней детально описываются
все свойства объекта, их параметры, действия и взаимосвязи.

Далее информационная
модель должна быть выражена в одной из знаковых форм. Учитывая, что мы будем
работать в среде электронных таблиц, то информационную модель необходимо
преобразовать в математическую. На основе информационной и
математической моделей составляется компьютерная модель в форме таблиц,
в которой выделяются три области данных: исходные данные, промежуточные
расчеты, результаты. Исходные данные вводятся “вручную”. Расчеты, как промежуточные,
так и окончательные, проводятся по формулам, записанным по правилам электронных
таблиц.

III этап. Компьютерный
эксперимент

Чтобы дать жизнь новым конструкторским
разработкам, внедрить новые технические решения в производство или проверить
новые идеи, нужен эксперимент. В недалеком прошлом такой эксперимент можно было
провести либо в лабораторных условиях на специально создаваемых для него
установках, либо на натуре, т.е. на настоящем образце изделия, подвергая его
всяческим испытаниям. Это требует больших материальных затрат и времени. В
помощь пришли компьютерные исследования моделей. При проведении компьютерного
эксперимента проверяют правильность построения моделей. Изучают поведение
модели при различных параметрах объекта. Каждый эксперимент сопровождается
осмыслением результатов. Если результаты компьютерного эксперимента
противоречат смыслу решаемой задачи, то ошибку надо искать в неправильно выбранной
модели или в алгоритме и методе ее решения. После выявления и устранения ошибок
компьютерный эксперимент повторяется.

IV этап. Анализ
результатов моделирования

Заключительный этап
моделирования — анализ модели. По полученным расчетным данным проверяется,
насколько расчеты отвечают нашему представлению и целям моделирования. На этом
этапе определяются рекомендации по совершенствованию принятой модели и, если
возможно, объекта или процесса.

4. Метод математических
моделей

Если попытаться одной
фразой ответить на вопрос: ”Каким образом современная математика применяется к
изучению физических, астрономических, биологических, экономических,
гуманитарных и других явлений?”, то ответ будет таким: ”С помощью построения и
анализа математических моделей изучаемого явления”. Что же такое математическая
модель?

Под математической
моделью понимают систему математических соотношений — формул, уравнений
неравенств и т.д., отражающих существенные свойства объекта или процесса.

При построении
математических моделей далеко не всегда удается найти формулы, явно выражающие
искомые величины через исходные данные. В таких случаях используются
математические модели, позволяющие дать ответы той или иной степени точности.

Изучение явлений с
помощью математических моделей называется математическим моделированием. Схематически
процесс математического моделирования представлен в следующей таблице:

Явление

внешнего мира

Его приближенное описание. Запись основных свойств и
соотношений между ними на математическом языке, формулировка основных
математических задач

Решение математических задач, исследование решений

Выводы, новые свойства изучаемого явления, прогнозы,
сравнение с известными результатами

Уточнение модели

Хорошо построенная
математическая модель обладает удивительным свойством: ее изучение дает новые,
неизвестные ранее знания об изученном объекте или явлении.

П р и м е р 1. В 1846
г. Французский астроном У.Ж.Ж.Леверье (1811-1877) открыл новую планету
Солнечной системы и назвал ее Нептуном. Открытие этой планеты было сделано
чисто математически, путем вычислений, так сказать, “на кончике пера”.
Анализируя созданную И.Кеплером и И.Ньютоном модель движения планет Солнечной
системы, ученые обнаружили, что фактическая траектория движения планеты Уран
отклонялась от теоретически вычисляемого движения. Ж.Леверье предположил, что
”возмутителем порядка” является неизвестная планета, которая воздействует на
планету Уран. Пользуясь моделью Солнечной системы, он определил массу и закон
движения новой планеты, так что все противоречия и движения планеты Уран были
сняты.

Немецкий астроном
И.Г.Галле в 1846 г. наблюдал новую планету в точно указанном Леверье месте.

Аналогичным методом,
благодаря использованию расхождения теоретически вычисленной траектории Нептуна
с наблюдаемой, в 1930 г. была открыта еще одна планета Солнечной системы,
названная Плутоном.

П р и м е р 2. Знаменитый
английский физик Дж. К. Максвелл (1831 — 1879), изучая построенную им
математическую модель классической электродинамики, из анализа уравнений модели
предсказал существование электромагнитных волн, которые позднее были
экспериментально обнаружены немецким физиком Г.Р.Герцем (1857 — 1894).

П р и м е р 3. Русский
ученый А.А.Фридман (1888 — 1925), анализируя уравнения общей теории относительности,
составленные А.Эйнштейном (1879 — 1955), в 1922
г. обнаружил, что кроме решений, не зависящих от времени, уравнения
А.Эйнштейна имеют еще и другие решения, которые от времени зависят. Это привело
к открытию того, что Вселенная расширяется и сжимается, т.е. пульсирует.
Представление о пульсировании Вселенной стало основой всей современной космологии.

Математические модели, с
помощью которых исследование явлений внешнего мира сводится к решению
математических задач, занимают ведущее место среди других методов исследования
и позволяют не только объяснить наблюдаемые явления, как это было, например, с
движением планеты Уран, но и заглянуть туда, где еще в принципе не могло быть
опытных, экспериментальных данных. Именно так было при проведении первых
атомных и водородных взрывов. И это еще не все. Существуют сферы человеческой
деятельности, где проведение экспериментов, получение экспериментальных
результатов принципиально не возможны!

Например, невозможно
экспериментировать над озоновым слоем Земли. Невозможно определить меру
антропогенного воздействия на ноосферу, достаточную для ее разрушения, —
неизвестно, найдется ли в этом случае на Земле место для человечества.

Развитие математического
аппарата и внедрение мощных современных компьютеров позволили математическому
моделированию, успешно зарекомендовавшему себя в технике, физике, астрономии и
космологии, проникнуть сегодня практически во все области человеческой
деятельности — в экономику и биологию, экологию и лингвистику, медицину и
психологию, историю, социологию и т.д. По мере усложнения объектов
исследования, роль математических моделей изучаемых явлений существенно
возрастает. Появляется целая иерархия математических моделей, каждая из которых
описывает изучаемое явление глубже, полнее, всестороннее.

5. Задачи по моделированию из различных предметных
областей

5.1 Экономика

Задача 1

Машиностроительный завод, реализуя
продукцию по договорным ценам, получил определенную выручку, затлатив на
производство некоторую сумму денег. Определить отношение чистой прибыли к вложенным
средствам.

Постановка задачи

Цель моделирования —
исследовать процесс производства и реализации продукции с целью получения
наибольшей чистой прибыли. Пользуясь экономическими формулами найти отношение
чистой прибыли к вложенным средствам.

Чистая прибыль — это
прибыль после уплаты налога. При расчете налога на прибыль необходимо учитывать
его зависимость от уровня рентабельности. Примем, если уровень рентабельности
не превышает 50%, то с прибыли предприятия взимается налог в 32%. Если же
уровень рентабельности превышает 50%, то с соответствующей суммы прибыли налог
взимается в размере 75%.

Объектом моделирования
является процесс производства и реализации некоторой продукции.

Разработка модели

Основными параметрами объекта
моделирования являются: выручка, себестоимость, прибыль, рентабельность, налог
с прибыли.

Исходные данные:

выручка B;

затраты (себестоимость) S.

Другие параметры найдем, используя
основные экономические зависимости. Значение прибыли определяется как разность
между выручкой и себестоимостью P=B-S.

Рентабельность r вычисляется по
формуле: .

Прибыль, соответствующая предельному
уровню рентабельности 50%, составляет 50% от себестоимости продукции S, т.е.
S*50/100=S/2, поэтому налог с прибыли N определяется следующим образом:

если r<=50, то
N=P*32/100 р., иначе N=S/2*32/100+(P-S/2)*75/100.

Чистая прибыль Р_ч=Р-N.

И, наконец, результат решения этой
задачи — отношение чистой прибыли к вложенным средствам q= Р_ч/S.

Так выглядит электронная таблица в
формате отображения формул:

	A.	B.
1.	Рентабельность производства
2.	Исходные данные
3.	Выручка (р.)
4.	Себестоимость (р.)
5.
6.	Прибыль (р.)	=B2-B3
7.	Рентабельность (%)	=B4/B3*100
8.	Налог (р.)	=ЕСЛИ(B7<=50;B60,32;B4/20,32+(B6-B4/2)*0,75)
9.	Чистая прибыль (р.)	=B4-B6
10.	Отношение чистой прибыли к вложенным средствам	=B7/B3

Компьютерный эксперимент

1.
Ввести в
компьютерную модель исходные данные.
Например: B=3000; S=2000.

2. Исследовать, как изменяется
отношение чистой прибыли к вложенным средствам, если менять только выручку,
оставляя постоянной себестоимость.

3. Исследовать, как изменяется
отношение чистой прибыли к вложенным средствам, если менять только
себестоимость, оставляя постоянной выручку.

4.
Как
измениться модель, если налог вычисляется следующим образом:

рентабельность	<=30%	от 30 до 70%	>70%
налог	20%	40%	60%

Изменится
только формула в ячейке B8.

Налог (р.)

=ЕСЛИ(B7<=30;
B6*0,2;ЕСЛИ(B7<=70; B6*0,4; B6*0,6))

Анализ результатов

Полученная модель
позволяет в зависимости от рентабельности определять налог с прибыли,
автоматически пересчитывать размер чистой прибыли, находить отношение чистой
прибыли к вложенным средствам.

Проведенный компьютерный
эксперимент показывает, что отношение чистой прибыли к вложенным средствам
увеличивается при увеличении выручки и уменьшается при увеличении себестоимости
продукции.

Задача 2

Леспромхоз ведет заготовку деловой
древесины. Известен ее первоначальный объем, ежегодный естественный прирост, а
также годовой план заготовки. Какой объем деловой древесины на данной территории
будет через год, через 2 года и т.д. — до тех пор, пока этот объем не станет
меньше минимально допустимого значения.

Постановка задачи

Цель моделирования —
показать динамику изменения объема деловой древесины, определить время до
которого эти изменения будут происходить.

Объектом моделирования
является процесс ежегодного изменения количества деловой древесины.

Количество деловой
древесины в каждый следующий год вычисляется по количеству древесины
предыдущего года до тех пор пока этот объем не станет меньше минимально
допустимого значения (23000 м³).

Разработка модели

Допустим, исходные данные принимают
следующие значения:

первоначальный объем V (м³)
— 120000;

ежегодный прирост p (%)
— 5,5;

годовой план заготовки R
(м³) — 9500;

миним. допустимое значение
(м³) — 23000.

Результатом является объем древесины через 1, 2, 3, … года.

Объем древесины в каждом следующем
году вычисляется по формуле:

V_i+1 = V_i + V_i*p/100-R

Так выглядит электронная таблица в
режиме отображения формул:

	A.	B.
1.	Задача о заготовке древесины
2.	Исходные данные:
3.	Первоначальный объем (м³)	120000
4.	Ежегодный прирост (%)	5,5
5.	Годовой план заготовки (м³)	9500
6.	Миним. допустимое значение (м³)	23000
7.		Объем древесины (м³)
8.	Через 1 год	=B3+B3*B4/100-B5
9.	2	=B8+B8*$B$4/100-$B$5
10.	3	=B9+B9*$B$4/100-$B$5

Формулу
копируем.

….

27.

=B26+B26*$B$4/100-$B$5

Вычислительный эксперимент

1. Введите значения исходных
данных и проследите динамику ежегодного изменения количества древесины,
построив график.

2. Разработайте план
использования древесины, так, чтобы данный процесс продолжался в течение 25
лет. (Изменяя значения R.)

	A.	B.
1.	Задача о заготовке древесины
2.	Исходные данные:
3.	Первоначальный объем (м³)	120000
4.	Ежегодный прирост (%)	5,5
5.	Годовой план заготовки (м³)	9500
6.	Миним. допустимое значение (м³)	23000
7.		Объем древесины (м³)
8.	Через 1 год	117100
9.	2	114041
10.	3	110813
11.	4	107407
12.	5	103815
13.	6	100025
14.	7	96026
15.	8	91807
16.	9	87357
17.	10	82661
18.	11	77708
19.	12	72482
20.	13	66968
21.	14	61152
22.	15	55015
23.	16	48541
24.	17	41710
25.	18	34505
26.	19	26902
27.	20	18882

Анализ результатов

В результате эксперимента, видим, что
процесс ежегодного изменения количества деловой древесины будет происходить в
течение 19 лет (до тех пор, пока ее объем не будет меньше минимально
допустимого значения V<23000 м³).

Задача 3

Фирма выпускает прогулочные и
спортивные велосипеды. Ежемесячно сборочный цех способен собрать не более 600
прогулочных и не более 300 спортивных велосипедов. Качество каждого велосипеда
проверяется на двух стендах А и В. Каждый прогулочный велосипед проверяется 0,3
ч на стенде А и 0,1 ч — на стенде В, а каждый спортивный велосипед проверяется
0,4 ч на стенде А и 0,3 ч — на стенде В. По технологическим причинам стенд А не
может работать более 240 ч в месяц, а стенд В — более 120 ч в месяц. Реализация
каждого прогулочного велосипеда приносит фирме доход в 50 руб., а каждого
спортивного — 90 руб. Сколько прогулочных и сколько спортивных велосипедов
должна ежемесячно выпускать фирма, чтобы ее прибыль была наибольшей? [3]

Постановка задачи

Цель моделирования —
составить такой производственный план, который обеспечит максимальную прибыль.

Объект моделирования —
процесс производства и реализации велосипедов

Разработка модели

Исходные данные:

x — количество прогулочных
велосипедов, выпускаемых ежемесячно фирмой;

y — количество спортивных
велосипедов.

Занятость стенда А составляет
0,3х+0,4y, что не должно превышать 240 ч.

Занятость стенда В составляет
0,1х+0,3y, что не должно превышать 120 ч.

Прибыль фирмы составляет S=50х+90у
(руб.)

Итак, мы пришли к следующей модели:
необходимо найти целые значения х и у, удовлетворяющие системе неравенств.

0,3х+0,4y £ 240 О1

0,1х+0,3y £ 120 О2

0 £ x £ 600 О3

0 £ y £ 300 О4

и такие, чтобы прибыль
S=50х+90у была наибольшей.

Таким образом, задача нахождения
наилучшего производственного плана свелась к задаче определения максимального
значения функции S(x,y) при заданных ограничениях. (Такие задачи называются
задачами условной оптимизации)

Электронная таблица в режиме
отображения формул выглядит следующим образом:

	A.	B.
1.	Задача планирования
2.	Исходные данные
3.	х
4.	у
5.	Ограничения
6.		=0,3B3+0,4B4
7.		=0,1B3+0,3B4
8.	Результат	Прибыль
9.		=50B3+90B4

Компьютерный эксперимент

В среде электронных таблиц существует
возможность автоматического поиска максимального (минимального) значения
функции. Для этого:

1. введите значения исходных
данных в ячейки В3 и В4 — любые целые числа, учитывая ограничения О3 и О4;

2. выберите команду
[Сервис-Поиск решения…];

3. в появившемся диалоговом окне
введите адрес ячейки, где содержится формула (функция для оптимизации);

4. укажите цель оптимизации
(максимальное значение);

5. введите диапазон ячеек,
посредством изменения значений которых будет достигнуто оптимальное значение
целевой функции;

6. введите все ограничения.

Результат выполнения выглядит так:

	A.	B.
1.	Задача планирования
2.	Исходные данные
3.	х	480
4.	у	240
5.	Ограничения
6.		240
7.		120
8.	Результат	Прибыль
9.		45600

Анализ результатов

Значения, находящиеся в ячейках В3,
В4 являются оптимальными для получения максимальной прибыли.

Продолжите компьютерный эксперимент

1. Что будет, если по
технологическим причинам возможность работы стенда В уменьшится до 100 ч. в
месяц.

2. Что будет, если доход от
реализации каждого прогулочного велосипеда увеличится до 60 руб.

3. Что будет, если проверку
спортивного велосипеда на стенде А ограничить до 0,3ч

Задача 4

В городе имеются два склада муки и
два хлебозавода. Ежедневно с первого склада вывозится 50 т муки, со второго —
70 т. Эта мука доставляется на хлебозаводы, причем первый получает 40 т, второй
— 80 т. Допустим, что перевозка одной тонны муки с первого склада на первый
завод составляет 120 руб., с первого склада на второй завод — 160 руб., со
второго склада на первый завод — 80 руб. и со второго склада на второй завод —
100 руб. Как нужно спланировать перевозки, чтобы их общая стоимость за один
день была минимальной? [13]

Задача 5

Для полива трех полей колхоз
использует насосную станцию. На первое поле требуется подать не менее 200
кубометров воды в сутки, на второе — не менее 300, на третье — не менее 350.
Колхоз имеет право расходовать не более 1200 кубометров воды в сутки. Стоимость
подачи одного кубометра воды на первое поле — 1570 руб., на второе поле — 1720
руб., на третье — 1930 руб. Сколько кубометров воды надо подать на каждое поле,
чтобы затраты были наименьшими? [13]

5.2 Астрономия

Задача 1

Определите скорость движения планет
по орбите. Для этого составьте компьютерную модель Солнечной системы.

Постановка задачи

Цель моделирования —
определить скорость движения планет по орбите.

Объект моделирования — Солнечная
система, элементами которой являются планеты. Внутреннее строение планет в
расчет не принимается. Будем рассматривать планеты как элементы, обладающие
следующими характеристиками:

название;

R — удаленность от Солнца (в
астрономических единицах;

астроном. ед. — среднее
расстояние от Земли до Солнца);

t — период обращения вокруг Солнца (в
годах);

V — скорость движения по орбите
(астр.ед./год), предполагая, что планеты

движутся вокруг Солнца по
окружностям с постоянной скоростью.

Разработка модели

Исходные данные:

R — расстояние от планеты до Солнца,

t — период обращения планеты вокруг
Солнца.

Т.к. планеты движутся вокруг Солнца
по окружностям с постоянной скоростью, значение скорости найдем по формуле:

, (1)

Данную модель реализуем в среде
электронных таблиц. Диапазон ячеек D3:D11 содержат формулы. Так выглядит
таблица в формате отображения формул:

	A.	B.	C.	D.
1.	Модель Солнечной системы
2.	Планета	Расстояние от Солнца (астр.ед.)	Период обращения вокруг Солнца (год)	Скорость движения по орбите (астр.ед./год)
3.	Меркурий	0,387	0,24	=2ПИ()B3/C3
4.	Венера	0,723	0,62	=2* ПИ()*B4/C4
5.	Земля	1,000	1,00	=2* ПИ()*B5/C5
6.	Марс	1,524	1,88	=2* ПИ()*B6/C6
7.	Юпитер	5,203	11,86	=2* ПИ()*B7/C7
8.	Сатурн	9,539	29,46	=2* ПИ()*B8/C8
9.	Уран	19,18	84,02	=2* ПИ()*B9/C9
10.	Нептун	30,07	164,79	=2* ПИ()*B10/C10
11.	Плутон	39,44	247,7	=2* ПИ()*B11/C11

Компьютерный эксперимент

1. Выполните расчеты по формулам.

	A.	B.	C.	D.
1.	Модель Солнечной системы
2.	Планета	Расстояние от Солнца (астр.ед.)	Период обращения вокруг Солнца (год)	Скорость движения по орбите (астр.ед./год)
3.	Меркурий	0,387	0,24	10,132
4.	Венера	0,723	0,62	7,327
5.	Земля	1,000	1,00	6,283
6.	Марс	1,524	1,88	5,093
7.	Юпитер	5,203	11,86	2,756
8.	Сатурн	9,539	29,46	2,034
9.	Уран	19,18	84,02	1,434
10.	Нептун	30,07	164,79	1,147
11.	Плутон	39,44	247,7	1,000

2. Вычислите скорость движения
планет по орбите в км/ч и постройте график в виде столбчатой диаграммы для
скоростей.

В данной модели формула (1)
будет иметь вид:

(1 астрономическая единица = 150 млн.
км.)

Анализ результатов

1. Проанализируйте результаты
расчетов. Можно ли утверждать, что планеты, находящиеся ближе к Солнцу имеют
большую скорость движения по орбите?

2. Представленная модель Солнечной
системы является статической. При построении этой модели мы пренебрегали
изменениями расстояния от планет до Солнца во время их движения по орбите.
Чтобы знать, какая планета дальше и каковы примерные соотношения между
расстояниями, этой информации вполне достаточно. Если же мы хотим определить
расстояние между Землей и Марсом, то пренебрегать временными изменениями
нельзя, и здесь придется использовать уже динамическую модель.

5.3 Физика

Задача 1

При подъеме в гору “заглох” мотор у
машины. Остановится ли машина на горе или же она будет скатываться вниз.

Постановка задачи

Цель моделирования —
пользуясь знакомыми физическими законами движения тела под действием нескольких
сил, исследовать данную ситуацию при различных значениях исходных данных.

Объектом моделирования
является система, состоящая из двух компонентов: машина и дорога.

Разработка модели

Необходимо рассмотреть силы,
действующие на машину в данной системе.

Fтр

Fт a

_ _

На машину действуют три силы: сила
тяжести Fт=mg, сила трения Fтр и сила реакции опоры N.

По I закону Ньютона тело находится в
состоянии покоя или движется прямолинейно и равномерно, если равнодействующая
всех приложенных к телу сил равна нулю, т.е. F=0.
_ _ _

II закон Ньютона в векторной форме
записывается так: Fт+N+Fтр=0.

Запишем его в скалярной форме, для
этого рассмотрим проекции сил

на ось x:

на ось y:

(Fт)_х=m*g*sina;

N_x=0;

(Fтр)_х=-Fтр

Уравнение: m*g*sina-Fтр=0

(Fт)_y=-m*g*cosa;

N_y=N;

(Fтр)_y=0

Уравнение: -m*g*cosa+N=0

Fтр=
m*g*sina

N= m*g*cosa

Так как Fтр=m*N, то m*g*sina=m* m*g*cosa

sina=m* cosa

tga=m

Итак, если tga>m, то машина стоит на месте, в
противном случае она будет скатываться вниз.

Исходными данными
являются:

m — коэффициент трения, 0<m<1;

a — угол наклона, 0<a<90. Так как в электронной
таблице Excel функция tg находит значение tg от угла, выраженного в радианах,
то при записи формулы предусмотрим перевод градусной меры угла в радианную.

Так выглядит таблица в формате
отображения формул:

	A.	B.
1.	Задача о дорожном происшествии
2.	Исходные данные:
3.	m
4.	a (град.)
5.	Результат	=ЕСЛИ(TAN(B4*ПИ()/180)> B3;”Поедет”;”Стоит на горе”)

Компьютерный эксперимент

1.
Введите в
компьютерную модель исходные данные.
(Например: m=0,5; a=12)

2. Найти такой коэффициент
трения при котором машина поедет с горы (при данном угле).

3. Найти такой угол при котором
машина будет стоять на горе (при данном коэффициенте трения).

4. Каков будет результат, если
силой трения пренебречь.

Анализ результатов

Интересно заметить, что в
построенной модели результат не зависит ни от массы автомобиля, ни от ускорения
свободного падения.

Задача 2

На заданном
расстоянии от пушки находится стена. Известны угол наклона пушки и начальная
скорость снаряда. Попадет ли снаряд в стену?[5]

Постановка задачи

Цель моделирования —
пользуясь знакомыми физическими законами движения тела, брошенного под углом к
горизонту, исследовать данную ситуацию при различных значениях исходных данных.

Объектом моделирования
является система, состоящая из двух компонентов: снаряд, брошенный под углом к
горизонту, и стена. Подобрать начальную скорость и угол бросания так, чтобы
брошенное тело (снаряд) достигло цели.

Разработка модели

Снаряд считаем материальной точкой.

Сопротивлением воздуха и размерами
пушки пренебрегаем.

Исходные данные:

a — угол наклона пушки, 0<a<90 градусов;

V — начальная скорость снаряда (м/с),
0<V<1000;

S — расстояние от пушки до стены (м),
S>0;

h — высота стены (м), h>0.

Результатом является одно из
сообщений: “Снаряд попал в стену”, “Снаряд не попал в стену”.

Для определения попадания
снаряда в стену надо найти высоту L снаряда на расстоянии S от пушки: ведь
попадание снаряда в стену означает, что 0<L<h. Перемещение снаряда по
горизонтали и вертикали:

x=V*t*cosa

y=V*t*sina-g*t²/2, где
g-ускорение свободного падения (9,8 м/с²).

Определим, сколько времени
понадобится снаряду, чтобы преодолеть расстояние S:

t=S/( V*cosa).

Подставив это значение t в выражение
для y, получим значение:

L=S*tga-g*S²/(2*V²*cos²a).

Если L<0, то снаряд до стены не
долетит. Если L>h, то снаряд перелетит через стену.

Так выглядит электронная таблица в
формате отображения формул:

	A.	B.
1.	Полет снаряда
2.	Исходные данные:
3.	a (град.)	35
4.	V	180
5.	S	3000
6.	h	6
7.	g	9,8
8.	a (радианы)	=B3*ПИ()/180
9.	L	=B5TAN(B8)-B7B5^2/(2B4^2(COS(B8))^2)
10.	Результат	=ЕСЛИ(И(B9>0;B9<B6);»Попал»;»Не попал»)

Компьютерный эксперимент

1.
Введите
значения исходных данных:
Например: a=35; V=180; S=3000; h=6; g=9.8 и проанализируйте результат.
(Результат “Не попал”)

2.
Найти
такой угол наклона пушки, не изменяя другие параметры системы, при котором
снаряд попадет в цель. (Результат a=32.6; a=32.7)

3.
Найти
такую скорость снаряда, не изменяя другие параметры системы, при котором снаряд
попадет в цель. (Результат V=177)

4. Усовершенствуйте модель таким
образом, чтобы результатом являлось одно из сообщений: “Снаряд попал в стену”,
“Недолет”, “Перелет”.

Анализ результатов

Данная компьютерная
модель позволяет проводить вычислительный эксперимент, взамен физическому.
Меняя значения исходных данных, можно видеть все изменения происходящие в
системе, производить расчет на поражение цели в зависимости от угла наклона
пушки и скорости снаряда.

Задача 3

Две моторные лодки равномерно
двигались по реке в направлении к озеру, в которое река впадает. Поравнявшись,
они начали двигаться равноускоренно. Какая из лодок раньше дойдет до озера? [11]

5.4 Экология

Задача 1

Представьте себе, что на Земле
останется только один источник пресной воды — озеро Байкал. На сколько лет
Байкал обеспечит население всего мира водой?

Постановка задачи

Цель моделирования —
определить количество лет, в течение которых Байкал обеспечит население всего
мира водой, исследовать построенную модель.

Объектом моделирования
является система, состоящая из двух компонентов: озеро Байкал и население
Земли.

Зная количество воды в
Байкале, численность населения Земли и потребляемость воды на 1 человека, можно
найти на сколько лет ее хватит. При составлении этой модели мы не учитываем
возможные изменения климатических условий. Мы также считаем постоянными численность
населения Земли и потребляемость воды на 1 чел. в день. (Человечество
потребляет на свои нужды огромное количество пресной воды. Основными ее
потребителями являются промышленность, сельское и коммунально-бытовое
хозяйство. Объем потребляемой воды зависит от уровня жизни, составляя от 3 до 700
л на одного человека.)

Разработка модели

Для построения
математической модели определим исходные данные. Обозначим:

V — объем озера Байкал 23000 км³;

N — население Земли 6 млрд. чел.;

p — потребление воды в день на 1
человека (в среднем) 300 л.

Так как 1л. = 1 дм³ воды,
необходимо выполнить перевод V воды озера из км³ в дм³. V
(км³) = V * 10⁹ (м³) = V * 10¹² (дм³)

Результат — количество лет, за
которое население Земли использует воды Байкала, обозначим g. Итак,
g=(V*1000000000000)/(N*p*365)

Так выглядит электронная таблица в
режиме отображения формул:

	A.	B.
1.	Задача об использовании вод Байкала
2.	Исходные данные
3.	V(км³)
4.	N (чел)
5.	p (л)
6.	g (год)	=(B31000000000000)/(B4B5*365)

Компьютерный эксперимент

1.
Введите в
компьютерную модель исходные данные.

	A.	B.
1.	Задача об использовании вод Байкала
2.	Исходные данные
3.	V(км³)	23000
4.	N (чел)	6000000000
5.	p (л)	300
6.	g (год)	35

2. Сколько лет можно будет
пользоваться водами Байкала, если потребляемость воды увеличится до 400
литров на человека?

3. Сколько лет можно будет
пользоваться водами Байкала, если население Земли уменьшится до 5,7 млрд. чел.?

Анализ результатов

Построенная модель позволяет
прогнозировать время использования вод Байкала с учетом потребляемости воды на 1
человека, изменения численности населения всего мира. Данную модель можно
уточнить, учитывая изменения климатических условий.

Задача 2

Известны ежегодные показатели
рождаемости и смертности некоторой популяции. Рассчитайте, до какого возраста
могут дожить особи одного поколения.

Постановка задачи

Цель моделирования —
исследовать изменение численности поколения популяции в зависимости от времени,
определить возраст до которого могут дожить особи одного поколения популяции.

Объектом моделирования
является процесс ежегодного изменения количества одного поколения популяции,
который зависит от рождаемости популяции и ее смертности.

Разработка модели

Так как ежегодная рождаемость
популяции соответствует количеству особей одного поколения в популяции, то
исходными данными являются:

x — количество особей в 1 год;

p — ежегодная смертность (%).

Численность популяции в каждом
следующем году рассчитывается по формуле: x_i+1=x_i — x_i*p/100.
Расчет производим до тех пор, пока значение x_i не станет <1.

Так выглядит электронная таблица в
режиме отображения формул:

	A.	B.
1.	Задача о прогнозировании численности популяции
2.	Исходные данные
3.	смертность (%)
4.	рождаемость
5.	1 год	B4
6.	2 год	=B5-B5*$B$3/100
7.	3 год	=B6-B6*$B$3/100

Формулу копируем.

Компьютерный эксперимент

1. Введите в компьютерную модель
исходные данные p, x (например p=30, x=1000) и проиллюстрируйте зависимость
численности популяции от времени на графике.

Результаты вычислений выглядят
следующим образом:

	A.	B.
1.	Задача о прогнозировании численности популяции
2.	% смертности	30
3.	1 год	1000
4.	2 год	700
5.	3 год	490
6.	4 год	343
7.	5 год	240,1
8.	6 год	168,1
9.	7 год	117,6
10.	8 год	82,4
11.	9 год	57,6
12.	10 год	40,4
13.	11 год	28,2
14.	12 год	19,8
15.	13 год	13,8
16.	14 год	9,7
17.	15 год	6,8
18.	16 год	4,7
19.	17 год	3,3
20.	18 год	2,3
21.	19 год	1,6
22.	20 год	1,1
23.	21 год	0,8
24.	22 год	0,6

Анализ результатов

Результаты эксперимента показывают,
что особи одного поколения данной популяции могут дожить до 20 лет.

Продолжите компьютерный
эксперимент

1.
Какова
должна быть рождаемость популяции, чтобы особи одного поколения доживали до 25
лет при той же смертности. (Результат: x=5000)

2.
Каков
должен быть показатель смертности, чтобы при той же рождаемости (x=1000) особи
одного поколения доживали до 35 лет. (Результат: p=18)

Анализ результатов

Модель показывает, что количество
особей одного поколения всегда уменьшается и стремится к нулю, т.е. приводит к
гибели данного поколения популяции.

Задача 3

Определите, как будет меняться
плотность популяции голубя в течение 5 ближайших лет, если предварительные
наблюдения позволили установить, что ее плотность составляет 130 особей/га. За
период размножения (у голубя раз в году) из одной кладки яиц в среднем выживает
1,3 детенышей. Смертность голубя постоянна, в среднем за год погибает 27% особей.
При увеличении плотности популяции до 300 особей/га и выше смертность составляет
50%.

Постановка задачи

Цель моделирования —
исследовать процесс изменения плотности популяции с учетом ее рождаемости и
смертности.

Объект моделирования —
процесс изменения плотности популяции.

Плотность популяции — это
число особей, приходящаяся на единицу площади или объема жизненного
пространства. Измерением плотности пользуются в тех случаях, когда важнее знать
не конкретную величину популяции в тот или иной момент времени, а ее динамику,
то есть ход изменений численности во времени.

Рождаемость характеризует
способность популяции к увеличению численности за счет размножения особей.
Показатель рождаемости — это число новых особей (также яиц, семян), родившихся
(вылупившихся, отложенных) в популяции за определенный промежуток времени.

Смертность — это
показатель, противоположный рождаемости. Смертность, как и рождаемость,
выражается числом особей, погибших за данный период времени, но чаще в виде
относительной или удельной величины. Такой величиной может быть процент особей,
погибших в единичный отрезок времени.

Разработка модели

Известно начальное значение
плотности популяции.

Плотность популяции к
началу следующего года есть ее плотность к началу данного года плюс рождаемость
и минус смертность.

Рождаемость зависит от
плотности самок и плодовитости. Предположим, что в популяции равное количество
самок и самцов, то, зная плотность популяции, можно определить плотность самок
(плотность самок=1/2 плотности популяции). Плодовитость известна по условию
задачи. Число особей, погибших за год — это процент (смертности) от общей
плотности популяции. Смертность популяции зависит так же и от величины
плотности популяции.

Исходные данные:

плотность популяции (P) — 130 особей/га;

плодовитость — 1,3 детеныша в год.

Остальные показатели рассчитываются
следующим образом:

плотность самок = P/2;

рождаемость (R) = плотность самок *
плодовитость;

смертность (S) = P * удельная
смертность;

где удельная
смертность голубя = 27% в год, если P<300,

в противном
случае она равна 50%;

Плотность популяции в каждом следующем году рассчитывается по
формуле:

P_i+1 = P_i + R_i— S_i.

2. По результатам расчетов,
выделив диапазон ячеек B10:E40, постройте общую диаграмму для трех биоритмов.

Анализ результатов

1. Проанализировав диаграмму,
выберите неблагоприятные дни для участия в спортивных соревнованиях.

2. Выберете дни, когда учебная
деятельность будет наиболее (наименее) успешной.

3. Выберете день для посещения
театра.

4. Определите, есть ли у вас
дважды (трижды) критические дни в этом месяце?

5. Как вы думаете, что будет
показывать график, если сложить все три биоритма? Можно ли по нему что-либо
определить?

6. Сторонники селенобиологической
гипотезы (селенобиология исследует влияние Луны на земные организмы)
утверждают, что периоды многодневных ритмов, зависящие от Луны, не должны были
бы представлять собой точно определенные отрезки времени. По их мнению, Луна
диктует некоторый ритм, который не является таким уж регулярным. В связи с этой
гипотезой продолжительность периода такова: физический период — 23,688437
суток, эмоциональный период — 28,426124 суток и интеллектуальный — 33,163812
суток. [8]

Измените модель биоритмов человека в
соответствии с данной теорией.

5.6
География

Задача 1

Какова будет численность населения
России в 2010 году? [16]

Постановка задачи

Объектом моделирования является
процесс изменения численности населения в зависимости от времени. На этот
процесс влияют многие факторы: экология, состояние медицинского обслуживания,
экономическая ситуация в стране, международная обстановка и многое другое.
Обобщив демографические данные, ученые вывели функцию, выражающую зависимость
численности населения от времени:

f(t)=

где коэффициента a и b для каждого
государства свои,

e основание натурального логарифма.

Эта формула лишь приближенно отражает
реальность. Для нахождения значений коэффициентов a и b можно воспользоваться
статистическим справочником. Взяв из справочника значения f(t) (численность
населения в момент времени t), можно приближенно подобрать a и b так, чтобы
теоретические значения f(t), вычисляемые по формуле, не сильно отличались от
фактических данных в справочнике.

6. Заключение

Тема “Моделирование”
является очень важной в курсе информатики, так как дает учащимся возможность
провести исследовательскую работу, выполнить анализ полученных результатов,
обратить внимание на конечность алгоритма, оценить точность модели, столкнуться
с погрешностью приближенных вычислений, увидеть взаимосвязь различных наук и
дисциплин, получить удовлетворение от выполненной работы.

Использование компьютера
как инструмента учебной деятельности дает возможность переосмыслить
традиционные подходы к изучению многих вопросов естественнонаучных дисциплин,
усилить экспериментальную деятельность учащихся, приблизить процесс обучения к
реальному процессу познания, основанному на технологии моделирования.

Решение задач из
различных областей деятельности человека на компьютере базируются не только на
знаниях учащимися технологии моделирования, но, естественно, и на знаниях
данной предметной области. В связи с этим, предложенные уроки по моделированию
целесообразнее проводить после изучения учащимися материала на
общеобразовательном предмете, учителю информатики необходимо сотрудничать с
учителями разных образовательных областей. Известен опыт проведения бинарных
уроков, т.е. уроков, проводимых учителем информатики совместно с
учителем-предметником.

Предложенные задачи можно
использовать при изучении курса информатики в 9-11 классах.

7. Список литературы

1.
Извозчиков
В.А., Бережной Л.Н., Слуцкий А.М. Межпредметные связи и информатика
(методические рекомендации) — Санкт-Петербург, 1992.

2.
Машбиц
Е.И. Психолого-педагогические проблемы компьютеризации обучения — М.,
Педагогика, 1988.

3.
Симонов
А.С. Экономика на уроках математики. — М., Школа-Пресс, 1999.

4.
Учебник
“Информатика. 9 класс.” под ред. Макаровой Н.В. — Санкт-Петербург, ПИТЕР КОМ,
1999.

5.
Гейн
А.Г., Житомирский В.Г. и др. “Основы информатики и вычислительной техники”
пробный учебник для 10-11 классов средней школы — М., Просвещение, 1992.

6.
Семакин
И., Залогова Л., Русаков С., Шестакова Л. «Информатика” учебник по
базовому курсу — М., ООО Лаборатория Базовых Знаний, 1998.

7.
Гисин
В.Б., Коновалов В.П., “Программно-методический комплекс № 4 по курсу
информатики. Элементы компьютерного моделирования” — М., АО КУДИЦ, 1994.

8.
Дагене
В.А., Григас Г.К., Аугутис К.Ф. “100 задач по программированию”, книга для
учащихся, пер. с лит. — М., Просвещение, 1993.

9.
Криксунов
Е.А., Пасечник В.В., Сидорин А.П. “Экология 9 класс”, учебник для
общеобразовательных учебных заведений — М., Дрофа, 1995.

10.Криксунов Е.А., Королев Ю.Б.,
Пасечник В.В., “Экология 9 класс”, рабочая тетрадь — М., Дрофа, 1996.

11. Кикоин И.К., Кикоин А.К. “Физика. 9
класс”, учебник — М., Просвещение,1990.

12.Петросян В.Г., Газарян Р.М.
Межпредметные связи и решение задач//
Информатика и образование. 1998 №8.

13.Островская Е.М. Моделирование на
компьютере// Информатика и образование. 1998 №7, 8; 1999 №1.

14.Пономарева Е.А. Основные
закономерности развития мышления// Информатика и образование. 1999 №8.

15.Бешенков С.А., Лыскова В.Ю., Матвеева
Н.В., Ракитина Е.А. Формализация и моделирование// Информатика и образование.
1999 №6.

16.Гусева О.Л., Миронова Н.Н. Excel для
Windows. Практические работы// Информатика и образование. 1996 №5.

8. Приложение

Рентабельность и вычисление налогов на прибыль

Любое производство не может
существовать, если оно не получает прибыль. Прибыль является важнейшим показателем
финансовой деятельности предприятия. В экономике рассматривают различные формы
прибыли. Под прибылью будем понимать разность между выручкой и себестоимостью.
Выручкой называются доходы от продажи товаров, а себестоимостью — затраты на их
производство и продажу. Обычно прибыль выражают в денежных единицах.

Обозначим выручку от
реализации продукции через B, себестоимость — через S. Тогда
прибыль P будет равна

P = B — S.

Однако величина прибыли
от продажи некоторого продукта безотносительно к тому, сколько затрачено на его
производство, мало что говорит.

На рисунке показаны три
фирмы, имеющие одинаковый доход D, но совершенно различные затраты, этот
доход обеспечивавшие.

фирма I
фирма II фирма III

Затраты З₁
фирмы I для получения дохода D достаточно велики, у фирмы II — затраты З₂
меньше, чем у фирмы I, а у фирмы III они меньше всех. Очевидно, что фирма III
работает более эффективно, чем фирмы I и II.

Понятие рентабельности
(от нем. rentabel — доходный) и является одним из способов измерения
эффективности деятельности фирмы, отрасли и т.д. за определенный промежуток
времени.

Показателем
рентабельности, или рентабельностью r называют отношение прибыли P
предприятия или фирмы за некоторый промежуток времени к полным затратам
(себестоимости) S за этот же период. Поэтому

или (1)

Если дробь то это значит, что P>S, т.е.
предприятие работает эффективно, окупает не только все издержки производства,
но и получает определенную прибыль на каждый затраченный рубль.

Если же дробь то это говорит о неэффективности фирмы и
необходимости повышения ее рентабельности путем снижения себестоимости,
повышения качества, уменьшения потерь и т.д. Рисунок показывает, что наибольшая
рентабельность у фирмы III, несколько меньше она у фирмы II, и совсем небольшая
у фирмы I.

Как правило,
рентабельность выражается в процентах:

(2)

Изменение показателя
рентабельности характеризует динамику развития производства, прибыльность или
убыточность хозяйственной деятельности фирм, отраслей и т.д. Еще несколько лет
назад уровень рентабельности играл важнейшую роль при определении налога с
прибыли предприятия или фирм, потому что ставка налога на прибыль существенно
зависела от рентабельности. Дело в том, что в условиях дефицита продукции и
отсутствия конкурентности, некоторые предприятия, особенно
предприятия-монополисты, имели возможность установить непомерно высокие цены на
свою продукцию и тем самым значительно увеличить прибыль без крупных вложений в
производство. Увеличение прибыли вело к повышению рентабельности. Чтобы цены не
росли непомерно, государство принимало различные меры и в том числе установило
так называемый предельный уровень рентабельности. Если рентабельность продукции
предприятия превышала установленный предельный уровень, то налог взимался по
повышенной ставке. Так, в 1991-1993 гг. в России был установлен предельный
уровень рентабельности в 50%. Если уровень рентабельности не превышал этого
значения, то с прибыли предприятия взимался налог в 32%. Если же уровень
рентабельности превышал 50%, то с соответствующей суммы прибыли налог взимался
в размере 75%. (Прибыль, соответствующая предельному уровню рентабельности 50%,
составляет 50% от себестоимости продукции S, т.е. S*50/100=S/2.)

Соотношения , или позволяют определить любую из величин r, P
или S, если известны две другие.

Источник

Пример имитационной модели

NOTE:

To change the image on this slide, select the picture and delete it. Then click the Pictures icon in the placeholder to insert your own image.

§26

Информатика, 8 класс

Учитель информатики

Дворецкая Ю.Ю,

Основные темы параграфа

Что такое имитационная модель
Пример имитационного моделирования в электронной таблице

ОПРЕДЕЛЕНИЕ

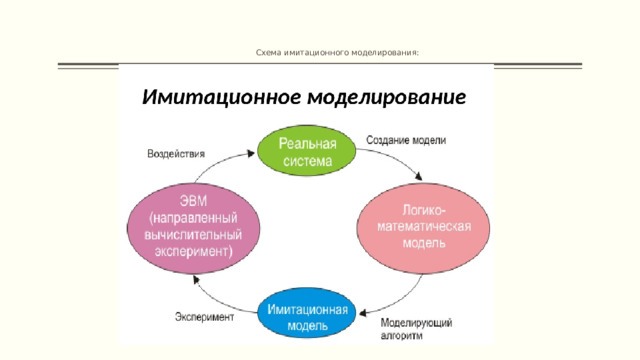
ИМИТАЦИОННАЯ МОДЕЛЬ – это логико-математическое описание объекта, которое может быть использовано для экспериментирования на компьютере в целях проектирования, анализа и оценки функционирования объекта.

Имитационная модель имеет определенную минимальную опорную структуру, которую пользователь может дополнить и расширить с учетом специфики решаемых задач и базовых методов обработки.

ОПРЕДЕЛЕНИЕ

ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ — это метод исследования, при котором изучаемая система заменяется моделью с достаточной точностью описывающей реальную систему и с ней проводятся эксперименты с целью получения информации об этой системе.

Отличие от математического моделирования

имитационное моделирование исследует математические модели в виде алгоритмов , воспроизводящих функционирование исследуемой системы путем последовательного выполнения большого количества элементарных операций .
в имитационных моделях для получения необходимой информации или результатов необходимо осуществлять их «прогон» в отличие от аналитических моделей, которые необходимо «решать».
имитационные модели неспособны формировать свое собственное решение в том виде, в каком это имеет место в аналитических моделях, а могут лишь служить в качестве средства для анализа поведения системы в условиях, которые определяются экспериментатором.

Имитационные модели

В общем виде структуру имитационной модели в математической форме можно представляет следующим образом: ,

где E – результат действия системы;

x i – переменные и параметры, которыми мы можем управлять;

y i – переменные и параметры, которыми мы управлять не можем;

f – функциональная зависимость между x i и y i , которая определяет величину E .

Имитационные модели

Имитационная модель представляет собой комбинацию таких составляющих, как:

компоненты;
переменные;
параметры;
функциональные зависимости;
ограничения;
целевые функции.

Схема имитационного моделирования:

НЕДОСТАТКИ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ:

разработка имитационных моделей требует больших затрат, времени и сил;
любая имитационная модель сложной системы менее объективна, чем аналитическая модель;
результаты имитационного моделирования носят как правило частный характер, поэтому для предоставления обоснованных выводов необходимо провести серии модельных экспериментов.

Пример имитационного моделирования на компьютере

Имитационная модель воспроизводит поведение сложной системы, элементы которой могут вести себя случайным образом. Иначе говоря, поведение которых заранее предсказать нельзя.

Модель – эволюция популяций

Пусть на определенном пространстве случайным образом расселяются живые организмы.
В дальнейшем происходит процесс смены поколений: в каких-то местах расселения жизнь сохраняется, в каких-то исчезает.
Эти процессы протекают в соответствии с законами эволюции (формальными правилами).

Цель моделирования — проследить изменения в расселении живых организмов со сменой поколений.

Имитационные модели

Законы эволюции:

В следующем поколении в пустой ячейке жизнь может либо появиться, либо нет.
В живой ячейке жизнь может либо сохраниться, либо исчезнуть
На состояние данной ячейки влияют ее ближайшие соседи: два соседа слева и два соседа справа.
Если ячейка была живая, и число живых соседей не превышает двух, то в следующем поколении в этой ячейке жизнь сохранится, иначе жизнь исчезнет (погибнет от перенаселения).
Если в ячейке жизни не было, но среди ее соседей есть 1, 2 или 3 живые ячейки, то в следующем поколении в этой ячейке появится жизнь. В противном случае ячейка останется пустой.

Модельное описание процесса эволюции популяции

Следует учитывать, что у ячеек, расположенных у края, число соседей меньше других.
У ячейки номер 2 соседи: 1, 3 и 4.
Но ячейка 1 всегда пустая.
У ячейки номер 3 из четырех соседей живыми могут быть не больше трех (2,4,5).
Аналогичная ситуация у крайних правых ячеек.

Кодирование

Распределение живых организмов по ячейкам будем кодировать последовательностью из нулей и единиц.
Ноль обозначает пустую ячейку , единица — живую .
Например, расселение, отображенное на рис. 4.3, кодируется следующим образом:

00001001000100000000

Имитационные модели

Введем обозначения:

n — номер ячейки,

R (n) — значение двоичного числа, соответствующего этой ячейке в текущем поколении.

В рассматриваемом примере R (5) = R (8) = R (12) = 1 .

Все остальные значения ячеек равны нулю.

Значения кода в n -й ячейке для следующего поколения будем обозначать S ( n ) .

Проанализировав правила эволюции, приходим к следующей формуле:

Если 1 R ( n — 2) + R ( n — 1) + R ( n ) + R ( n + 1) + R ( n + 2) 3, то S ( n ) = 1, иначе S ( n ) = 0.

Имитационные модели

Эта формула работает для значений n от 3 до 18 .

Всегда: S (1) = S (20) = 0 .

Для ячеек с номерами 2 и 19 в данной сумме нужно убрать по одному слагаемому. Но можно поступить иначе: для этого к отрезку добавим по одной фиктивной ячейке справа и слева.

Их номера будут, соответственно, 0 и 21. В этих ячейках, как и в ячейках 1 и 20, всегда будут храниться нули. Тогда написанную формулу можно применять для n от 2 до 19.

Итак, модель построена и формализована.

Имитационные модели

Для реализации применим табличный процессо р.

Моделью жизненного пространства будет строка электронной таблицы.

Первая строка — первое поколение,

вторая строка — второе поколение и т. д.

Тогда номера ячеек будут идентифицироваться именами столбцов таблицы.

Ячейка номер 0 — столбец А,

ячейка 1 — столбец В и т. д.,

ячейка 21 — столбец F.

=1; А1 + В1 + С1 + D1 + Е1 Далее, копируя эту формулу во все остальные ячейки второй строки с D2 по Т2, получаем картину распределения живых организмов во втором поколении. Чтобы получить третье поколение, достаточно скопировать вторую строку (блок С2:Т2) в третью строку (блок СЗ:ТЗ). Так можно продолжать сколько угодно. » width=»640″

В первой строке выставляем единицы в ячейках, заселенных в первом поколении. Это будут ячейки F1, I1, М1 . Незаполненные ячейки по умолчанию приравниваются к нулю.
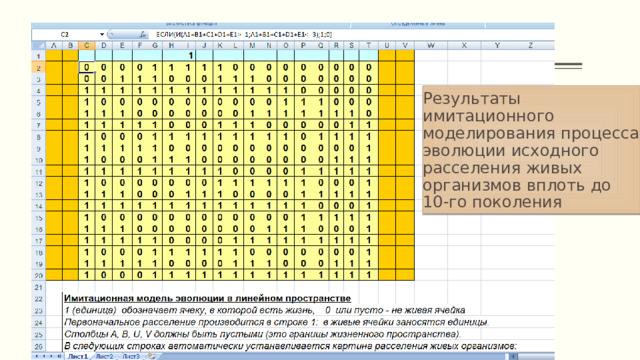
Теперь в ячейки второй строки нужно записать формулы. Сделать это достаточно один раз. Например, в ячейку С2 занести следующую формулу:

ЕСЛИ(И(А1 + В1 + С1 + D1 + Е1 =1; А1 + В1 + С1 + D1 + Е1

Далее, копируя эту формулу во все остальные ячейки второй строки с D2 по Т2, получаем картину распределения живых организмов во втором поколении.
Чтобы получить третье поколение, достаточно скопировать вторую строку (блок С2:Т2) в третью строку (блок СЗ:ТЗ). Так можно продолжать сколько угодно.

Результаты имитационного моделирования процесса эволюции исходного расселения живых организмов вплоть до 10-го поколения

Модель Дж. Конуэя «Жизнь»

В этой модели эволюция популяции живых организмов происходит в двумерном пространстве.

Рассматривается прямоугольная область, разделенная на квадратные ячейки. Тогда у каждой внутренней ячейки имеется 8 соседей. Судьба жизни в ячейке также зависит от состояния соседних клеток.

Но теперь правила эволюции такие:

если клетка живая и в ее окружении более трех живых клеток, то она погибает от перенаселения;

если же живых соседей меньше двух, то она погибает от одиночества.

в пустой клетке в следующем поколении зарождается жизнь, если у нее есть ровно три живых соседа.

Домашнее задание

§26 конспект

Источник

Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа № 15 имени Пяти Героев Советского Союза

Иследовательская работа

Тема:

«Создание и исследование моделей

в электронной таблице Excel»

Секция информатики

Выполнила: Сотникова Полина Андреевна,

ученица 10 «А» класса

Руководитель: Титаренко Алексей Анатольевич,

учитель информатики

г. Хабаровск

2016

Содержание

Актуальность темы…………………………………………………………………………………………………………………3

Введение………………………………………………………………………………………………………………………………..4

Создание информационных моделей…………………………………………………………………………………..5

Формулы в Excel…………………………………………………………………………………………………………………….7

Этапы разработки и исследования моделей………………………………………………………………………..10

Исследование физических моделей в электронных таблицах…………………………………………..11

Исследование биологической модели развития популяций………………………………………………14

Оптимизационное моделирование в экономике…………………………………………………………………17

Заключение…………………………………………………………………………………………………………………………….20

Список использованной литературы…………………………………………………………………………………….21

Актуальность темы

Часто для исследования предметов, процессов и явлений человек создает модели окружающего мира.

Наглядные модели часто используются в процессе обучения. На уроке географии мы изучаем нашу планету используя её модели – карты и глобусы, при изучении химии мы используем модели молекул и кристаллических решеток, изучаем строение человека по анатомическим муляжам скелета и органов на биологии.

Модели играют чрезвычайно важную роль в проектировании и создании различных технических устройств, машин и механизмов, зданий, электрических цепей и т.д. Без предварительного создания чертежей невозможно изготовить даже простую деталь, не говоря уже о сложном механизме. Кроме чертежей,в проектировании часто изготавливают макеты. Разработка электрической схемы обязательно предшествует созданию электрических цепей.

Развитие науки невозможно без создания теоретических моделей (теорий, законов, гипотез), отражающих строение, свойства и поведение реальных объектов. Соответствие теоретических моделей действительности проверяется с помощью опытов и экспериментов.

Все художественное творчество фактически является процессом создания моделей. Например, такой литературный жанр, как басня, переносит реальные отношения между людьми на отношения между животными и фактически создает модели человеческих отношений.

Введение

Моделирование – это метод познания, состоящий в создании и исследовании моделей – неких новых объектов, которые отражают существенные особенности изучаемого объекта, явления или процесса.Модель – это некий новый объект, который отражает существенные особенности изучаемого объекта,явления или процесса. Модели позволяют представить в наглядной форме объекты и процессы, недоступные для непосредственного восприятия (очень большие или очень маленькие объекты, очень быстрые или очень медленные процессы).

Компьютерные модели стали обычным инструментом математического моделирования и применяются в физике, астрофизике, механике, химии, биологии, экономике, социологии, метеорологии, других науках и прикладных задачах в различных областях радиоэлектроники, машиностроения, автомобилестроения и прочих. Компьютерные модели используются для получения новых знаний о моделируемом объекте или для приближенной оценки поведения систем, слишком сложных для аналитического исследования. Компьютерное моделирование является одним из эффективных методов изучения сложных систем. Компьютерные модели проще и удобнее исследовать в силу их возможности проводить вычислительные эксперименты, в тех случаях когда реальные эксперименты затруднены из-за финансовых или физических препятствий или могут дать непредсказуемый результат. Логичность и формализованность компьютерных моделей позволяет определить основные факторы, определяющие свойства изучаемого объекта-оригинала (или целого класса объектов). В частности, моделирование в электронных таблицах может быть использовано для описания ряда объектов, обладающих одинаковыми наборами свойств. С помощью таблиц могут быть построены как статические, так и динамические информационные модели в различных предметных областях, а простота использования программ создания таблиц помогает составлять модели людям без знания сложных языков программирования.

Создание информационных моделей:

Информационные модели отражают различные типы систем объектов, в которых реализуются различные структуры взаимодействия и взаимосвязи между элементами системы. Для отражения систем с различными структурами используются различные типы информационных моделей: табличные, иерархические и сетевые. В программе Excelдоступно создание табличного типа моделей.

Табличные информационные модели:

Одним из наиболее часто используемых типов информационных моделей является прямоугольная таблица, состоящая из столбцов и строк. Такой тип моделей применяется для описания ряда объектов, обладающих одинаковыми наборами свойств.

В табличной информационной модели обычно перечень объектов размещен в ячейках первого столбца таблицы, а значения их свойств – в других столбцах.

С помощью электронной таблицы Excelпостроим таблицу стоимости продуктов. В первом столбце таблицы будет содержаться перечень продуктов, а во втором – интересующее нас свойство (цена).

С помощью специальных инструментов, встроенных в программу Excelможно визуализировать таблицу, представив ее в виде графика или круговой диаграммы. Для этого нужно выделить таблицу, зайти во вкладку «Вставка» и выбрать нужный формат визуализации.

Визуализация круговой диаграммой

Визуализация столбчатой диаграммой

Формулы в Excel

В таблицах Excelможно не только вводить и визуализировать данные, но и производить простые и сложные расчеты над данными.Все это реализуется при помощи формул в ячейках. Формула выполняет вычисления или другие действия с данными в листе.

Порядок ввода формулы

Для начала определим, в какой ячейке должен стоять результат расчета. Затем выделим эту ячейку (нажмем на нее левой кнопкой мышки и ячейка станет активной).

Вводить формулу надо со знака равенства. Это надо для того, чтобы Excel понял, что в ячейку вводится именно формула, а не данные.

Выделим произвольную ячейку, например D1. В строке формул введем =2+3 и нажмем Enter. В ячейке появится результат (5). А в строке формул сверху останется сама формула.

При обработке формулы с большим количеством вычислений, наблюдается определенный приоритет.

В первую очередь выполняются выражения внутри скобок.
Умножение и деление имеют более высокий приоритет чем сложение и вычитание.
Операторы с одинаковым приоритетом выполняются слева направо.

Так, в примере выше, сначала выполняется действие в скобках (5-4=1), потом первое умножение (100*1=100), затем второе умножение (38*2=76), сложение (100+26=126), и в конце вычитание (126-76=50).

Также, можно выполнять действия над числами, содержащимися в ячейках. Для этого, вместо цифр, в формулах нужно использовать ссылки на ячейки – букву латинского алфавита, обозначающую столбец и цифру, обозначающую строку.

Так, в ячейку D3 была введена формула D1+D2. В результате сложились числа,стоящие в ячейках D1(4) и D2(6) и полученный результат – 10 был записан в ячейку D3.

Для складывания нескольких ячеек используется функция СУММ. Для суммирования трех чисел формула запишется следующим образом

Но можно облегчить себе работу и вместо перечисления каждой ячейки записать диапазон, с помощью двоеточия

Истинное значение функции СУММ раскрывается, когда необходимо сложить большое количество ячеек в Excel. В примере ниже требуется просуммировать 12 значений. Функция СУММ позволяет сделать это несколькими щелчками мышью, если же использовать оператор сложения, то провозиться придется долго.

В таблицах Excelможно не только проводить простейшие вычисления над числами, но и возводить в степень, извлекать корень, производить сравнение чисел и многое другое.

Этапы разработки и исследования моделей

Использование компьютера для исследования информационных моделей различных объектов и систем позволяет изучить их изменения в зависимости от значения тех или иных параметров. Процесс разработки моделей и их исследования на компьютере можно разделить на несколько основных этапов.

На первом этапе исследования объекта или процесса обычно строится описательная информационная модель. Такая модель выделяет существенные с точки зрения целей проводимого исследования параметры объекта, а несущественными параметрами пренебрегает.

На втором этапе создается формализованная модель, то есть описательная информационная модель записывается с помощью какого-либо формального языка. В такой модели с помощью формул, уравнений, неравенств и пр. фиксируются формальные соотношения между начальными и конечными значениями свойств объектов, а также накладываются ограничения на допустимые значения этих свойств.

Однако далеко не всегда удается найти формулы, явно выражающие искомые величины через исходные данные. В таких случаях используются приближенные математические методы, позволяющие получать результаты с заданной точностью.

На третьем этапе необходимо формализованную информационную модель преобразовать в компьютерную модель, то есть выразить ее на понятном для компьютера языке. Существуют два принципиально различных пути построения компьютерной модели:

1) построение алгоритма решения задачи и его кодирование на одном из языков программирования;

2) построение компьютерной модели с использованием одного из приложений (электронных таблиц, СУБД и пр.).

В процессе создания компьютерной модели полезно разработать удобный графический интерфейс, который позволит визуализировать формальную модель, а также реализовать интерактивный диалог человека с компьютером на этапе исследования модели.

Четвертый этап исследования информационной модели состоит в проведении компьютерного эксперимента. Если компьютерная модель существует в виде программы на одном из языков программирования, ее нужно запустить на выполнение и получить результаты.

Если компьютерная модель исследуется в приложении, например в электронных таблицах, можно провести сортировку или поиск данных, построить диаграмму или график и так далее.

Пятый этап состоит в анализе полученных результатов и корректировке исследуемой модели. В случае различия результатов, полученных при исследовании информационной модели, с измеряемыми параметрами реальных объектов можно сделать вывод, что на предыдущих этапах построения модели были допущены ошибки или неточности. Например, при построении описательной качественной модели могут быть неправильно отобраны существенные свойства объектов, в процессе формализации могут быть допущены ошибки в формулах и так далее. В этих случаях необходимо провести корректировку модели, причем уточнение модели может проводиться многократно, пока анализ результатов не покажет их соответствие изучаемому объекту.

Исследование физических моделей в электронных таблицах:

Рассмотрим процесс построения и исследования модели на конкретном примере движения тела, брошенного под углом к горизонту.

Задача: В процессе тренировке теннисистов используются автоматы по бросания мячика в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в мишень определенного размера, находящуюся на известном расстоянии.

Качественная описательная модель: Сначала построим качественную описательную модель процесса движения тела с использованием физических объектов, понятия и законов, то есть в данном случае идеализированную модель движения объекта. Из условия задачи можно сформулировать следующие основные предположения:

Мячик мал по сравнению с Землей, поэтому его можно считать материальной точкой;
Изменение высоты мячика мало, поэтому ускорение свободного падения можно считать постоянной величиной g= 9,8 мс и движение по оси ОУ можно считать равноускоренным;
Скорость бросания тела мала, поэтому сопротивлением воздуха можно пренебречь и движение по оси ОХ можно считать равномерным

Формальная модель: Для формализации модели используем известные из курса физики формулы равномерного и равноускоренного движения. При заданных начальной скорости v0 и угле бросания aзначения координат дальности полета х и высоты у от времени можно записать следующими формулами:

X=v0*cos*t;

Y=v0*sinα*t – g*t²/2

Пусть мишень высотой h будет размещаться на расстоянии sот автомата. Из первой формулы выражаем время, которое понадобится мячику, чтобы преодолеть расстояние s:

t = s/(v0*cos2α)

Представляем это значение для tв формулу для у. Получаем l – высоту мячика над землей на расстоянии s:

l = s*tgα – g*s²/(2*v0²*cosα²)

Формализуем теперь условие попадания мячика в мишень. Попадание произойдет, если значение высоты lмячика в мишень. Попадание произойдет, если значение высоты lмячика будет удовлетворять условию в форме неравенства:

0≤l ≤ h

Если l<0, то это означает «недолет», а если l>h, то это означает «перелет».

Создание модели:

Для ввода начальной скорости будем использовать ячейку В1, а для ввода угла – ячейку В2
Введем в ячейки А5:А18 значения времени с интервалом в 0,2 с.
В ячейки В5 и С5 введем формулы:

=$B$1*cos(Радианы($B$2))*А5

=$B$1*sin(РАДИАНЫ($B$2))*A5-4,9*A5*A5

Скопируем формулы в ячейки В6:В18 и С6:С18 соответственно.

Визуализируем модель, построив график зависимости координаты у от координаты х (траекторию движения тела).

Построить диаграмму типа График, в которой используется в качестве категории диапазон ячеек В5:В18, а в качестве значений – диапазон ячеек С5:С18.

Исследование модели: Исследуем модель и определим с заданной точностью 0,1 диапазон изменений угла, который обеспечивает попадание в мишень, находящуюся на расстоянии 30 м и имеющую высоту 1 м, при заданной начальной скорости 18 м/с. Воспользуемся для этого методом Подбор параметра.

Установить для ячеек точность один знак после запятой

Ввести в ячейки B21, B22 и В23 значения расстояния до мишени S = 30 м, начальной скорости Vо = 18 м/с и угла α= 35⁰, а в ячейку В25 – формулу для вычисления высоты мячика над поверхностью для заданных условий:

=B21*TAN(РАДИАНЫ(B23))-(9,81*B21^2)/(2*B22^2*COS(РАДИАНЫ(B23))^2)

Для заданных начальных условий определим углы, которые обеспечивают попадание в мишень на высотах 0 и 1 м.

Выделить ячейку В25 и ввести команду [Сервис-Подбор параметра…]. На появившейся диалоговой панели ввести в поле Значение: наименьшую высоту попадания в мишень ( то есть 0). В поле Изменяя значение ячейки: ввести адрес ячейки, содержащей значение угла (в данном случае $B$23).

В ячейке В23 появится значение 32,6. Повторить процедуру подбора параметра для максимальной высоты попадания в мишень – в ячейке В23 получим значение 36,1.

Таким образом, исследование компьютерной модели в электронных таблицах показало, что существует диапазон значений для угла бросания от 32,6 до 36,1⁰, который обеспечивает попадание в мишень высотой 1 м, находящуюся на расстоянии 30 м, мячиком брошенным со скоростью 18 м/с.

Исследование биологической модели развития популяций

В биологии при исследовании развития биосистем строятся динамические модели изменения численности популяций различных живых существ (бактерий, рыб, животных и пр.) с учетом различных факторов. Взаимовлияние популяций рассматривается в моделях типа «хищник-жертва».

Формальная модель. Изучение динамики численности популяций естественно начать с простейшей модели неограниченного роста, в которой численность популяции ежегодно увеличивается на определенный процент. Математическую модель можно записать с помощью рекуррентной формулы, связывающей численность популяции следующего года с численностью популяции текущего года, с использованием коэффициента роста а:

X(n+1) = a * x(n)

Например, если ежегодный прирост численности популяции составляет 5%, то а = 1,05. В модели ограниченного роста учитывается эффект перенаселенности, связанный с нехваткой питания, болезнями и так далее, который замедляет рост популяции с увеличением ее численности. Введем коэффициент перенаселенности b, значение которого обычно существенно меньше а (b<<а). Тогда коэффициент ежегодного увеличения численности равен (а — b*х(n)) и формула принимает вид:

X(n+1) = (a – b * x(n)) * x(n)

В модели ограниченного роста с отловом учитывается, что на численность популяций промысловых животных и рыб оказывает влияние величина ежегодного отлова. Если величина ежегодного отлова равна с, то формула принимает вид:

X(n+1) = (a – b * x(n)) * x(n) — c

Популяции обычно существуют не изолированно, а во взаимодействии с другими популяциями. Наиболее важным типом такого взаимодействия является взаимодействие между жертвами и хищниками (например, караси-щуки, зайцы-волки и так далее). В модели «хищник-жертва» количество жертв х(n) и количество хищников у(n) связаны между собой. Количество встреч жертв с хищниками можно считать пропорциональным произведению количеств жертв и хищников, а коэффициент f характеризует возможность гибели жертвы при встрече с хищниками. В этом случае численность популяции жертв ежегодно уменьшается на величину f * х(n)* у(n) и формула для расчета численности жертв принимает вид:

X(n+1) = (a – b * x(n)) * x(n) – c – f* x(n) * y(n)

Численность популяции хищников в отсутствие жертв (в связи с отсутствием пищи) уменьшается, что можно описать рекуррентной формулой

Y(n+1) = d* y(n)

где значение коэффициента d < 1 характеризует скорость уменьшения численности популяции хищников. Увеличение популяции хищников можно считать пропорциональной произведению собственно количеств жертв и хищников, а коэффициент е характеризует величину роста численности хищников за счет жертв. Тогда для численности хищников можно использовать

формулу:

y(n+1) = d*y(n) + e*x(n)*y(n)

Компьютерная модель. Построим в электронных таблицах компьютерную модель, позволяющую исследовать численность популяций с использованием различных моделей: неограниченного роста, ограниченного роста, ограниченного роста с отловом и «хищник—жертва».

В ячейки В1 и В6 внести начальные значения численности популяций жертв и хищников.

В ячейки В2:В5 внести значения коэффициентов a, b, cи f, влияющих на изменение численности жертв.

В ячейки В7 и В8 внести значения коэффициентов dи е, влияющих на изменение численности хищников

В столбце Dбудем вычислять численность популяции в соответствии с моделью неограниченного роста, в столбце Е – ограниченного роста, в столбце F–ограниченного роста с отловом, в столбцах Gи H–«хищник-жертва».

В ячейки D1, E1, F1 и G1 внести значения начальной численности популяций жертв, в ячейку Н1 – хищников.

В ячейку D2 внести рекуррентную формулу неограниченного роста =$B$2*D1

В ячейку Е2 внести рекуррентную формулу неограниченного роста =($B$2-$B$3*E1)*E1

В ячейку F2 внести рекуррентную формулу ограниченного роста с отловом =($B$2-$B$3*F1)*F1-$B$4

В ячейку G2 внести рекуррентную формулу изменения количества жертв =($B$2-$B$3*G1)*G1-$B$4-$B$5*G1*H1

В ячейку Н2 внести рекуррентную формулу изменения количества хищников =$B$7*H1+$B$8*G1*H1

Скопировать внесенные формулы в ячейки столбцов командой [Правка-Заполнить-Вниз].

В ячейках столбцов ознакомиться с динамикой изменения численности популяций.

Выделить столбцы данных и построить диаграмму типа График. Появятся графики изменения численности популяций в соответствии с моделями неограниченного роста, ограниченного роста, ограниченного роста с отловом, моделью хищник-жертва.

Исследование модели: Изменяя значения начальных численностей популяций, а также коэффициенты, можно получать различные варианты изменения численности популяций в зависимости от времени.

Оптимизационное моделирование в экономике

В сфере управления сложными системами (например, в экономике) применяется оптимизационное моделирование, в процессе которого осуществляется поиск наиболее оптимального пути развития системы.

Критерием оптимальности могут быть различные параметры; например, в экономике можно стремиться к максимальному количеству выпускаемой продукции, а можно к ее низкой себестоимости. Оптимальное развитие соответствует экстремальному (максимальному или минимальному) значению выбранного целевого параметра.

Развитие сложных систем зависит от множества факторов (параметров), следовательно, значение целевого параметра зависит от множества параметров. Выражением такой зависимости является целевая функция

К = F(X1,X2,…,Xn),

где К — значение целевого параметра; X1,X2,…,Xn — параметры, влияющие на развитие системы.

Цель исследования состоит в нахождении экстремума этой функции и определении значений параметров, при которых этот экстремум достигается. Если целевая функция нелинейна, то она имеет экстремумы, которые находятся определенными методами.

Однако часто целевая функция линейна и, соответственно, экстремумов не имеет. Задача поиска оптимального режима при линейной зависимости приобретает смысл только при наличии определенных ограничений на параметры. Если ограничения на параметры (система неравенств) также имеют линейный характер, то такие задачи являются задачами линейного программирования. (Термин «линейное программирование» в имитационном моделировании понимается как поиск экстремумов линейной функции, на которую наложены ограничения.) Рассмотрим в качестве примера экономического моделирования поиск вариантов оптимального раскроя листов материала на заготовки определенного размера.

Содержательная постановка проблемы. В ходе производственного процесса из листов материала получают заготовки деталей двух типов А и Б тремя различными способами, при этом количество получаемых заготовок при каждом методе различается.

Тип Заготовки	1 способ раскроя	2 способ раскроя	3 способ раскроя
А	10	3	8
Б	3	6	4

Необходимо выбрать оптимальное сочетание способов раскроя, для того чтобы получить 500 заготовок первого типа и 300 заготовок второго типа при расходовании наименьшего количества листов материала.

Формальная модель. Параметрами, значения которых требуется определить, являются количества листов материала, которые будут раскроены различными способами:

Х1 — количество листов, раскроенное способом 1;

Х2 — количество листов, раскроенное способом 2;

Х3 — количество листов, раскроенное способом 3.

Тогда целевая функция, значением которой является количество листов материала, примет вид:

F = Х1+ Х2 + Х3.

Ограничения определяются значениями требуемых количеств заготовок типа А и Б, тогда с учетом количеств заготовок, получаемых различными способами, должны выполняться два равенства: 10Х1+ ЗХ2 + 8Х3 = 500;

ЗХ1 + 6Х2 + 4Х3 = 300.

Кроме того, количества листов не могут быть отрицательными, поэтому должны выполняться неравенства:

X1>= 0; Х2>= 0; Х3 >= 0.

Таким образом, необходимо найти удовлетворяющие ограничениям значения параметров, при которых целевая функция принимает минимальное значение. Компьютерная модель. Будем искать решение задачи путем создания и исследования компьютерной модели в электронных таблицах Excel.

Оптимизационное моделирование

Ячейки В2, С2 и D2 выделить для значений параметров Х1, Х2 и Х3.

В ячейку В4 ввести формулу для вычисления целевой функции:

=В2+С2+D2

В ячейку В7 ввести формулу вычисления количества заготовок типа А:

=10*B2+3*C2+8*D2.

В ячейку В8 ввести формулу вычислений количества заготовок типа Б:

=3*B2+6*C2+4*D2

Исследование модели: Для поиска оптимального набора значений параметров, который соотвествует минимальному значению целевой функции, воспользоваться надстройкой электронных таблиц Поиск решения.

На вкладке Данные нажмите кнопку Поиск решения.
На появившейся диалоговой панели Поиск решения установить:

Адрес целевой ячейки
Вариант оптимизации значения целевой ячейки (максимизация, минимизация или подбор значения)
Адреса ячеек, значения которых изменяются в процессе поиска решения ( в которых хранятся значения параметров)

Ограничения (типа «=» для ячеек, хранящих количество деталей, и типа «≥» для параметров).

Щелкнуть по кнопке Выполнить. В ячейке целевой функции появится значение 69,4, а в ячейках параметров значения 0,11,58.

Таким образом, для изготовления 500 деталей А и 300 деталей Б требуется 71 лист материала, при этом 12 листов нужно раскроить по второму, а 59 по третьему способу.

Заключение

Моделирование глубоко проникает в теоретическое мышление. Более того, развитие любой науки в целом можно трактовать — в весьма общем, но вполне разумном смысле, — как «теоретическое моделирование». Важная познавательная функция моделирования состоит в том, чтобы служить импульсом, источником новых теорий. Нередко бывает так, что теория первоначально возникает в виде модели, дающей приближённое, упрощённое объяснение явления, и выступает как первичная рабочая гипотеза, которая может перерасти в «предтеорию» — предшественницу развитой теории. При этом в процессе моделирования возникают новые идеи и формы эксперимента, происходит открытие ранее неизвестных фактов. Такое «переплетение» теоретического и экспериментального моделирования особенно характерно для развития физических теорий.

Моделирование — не только одно из средств отображения явлений и процессов реального мира, но и — несмотря на описанную выше его относительность — объективный практический критерий проверки истинности наших знаний, осуществляемой непосредственно или с помощьюустановления их отношения с другой теорией, выступающей в качестве модели, адекватность которой считается практически обоснованной. Применяясь в органическом единстве с другими методами познания, моделирование выступает как процесс углубления познания, его движения от относительно бедных информацией моделей к моделям более содержательным, полнее раскрывающим сущность исследуемых явлений действительности.

В своем проекте я показала, как использовать электронные таблицы Excelдля моделирования и анализа созданных моделей.

Список использованной литературы

Н. Угринович «Информатика и информационные технологии»
Н. Угринович «Информатика и ИКТ»
http://on-line-teaching.com/excel/lsn003.html
http://www.excel-office.ru/formulivexcel/formulivexcel

Источник

Модель данных позволяет интегрировать данные из нескольких таблиц, эффективно создавая реляционный источник данных в книге Excel. В Excel модели данных используются прозрачно, предоставляя табличные данные, используемые в сводных таблицах и сводных диаграммах. Модель данных визуализируются как коллекция таблиц в списке полей, и в большинстве раз вы даже не узнаете, что она существует.

Прежде чем приступить к работе с моделью данных, необходимо получить некоторые данные. Для этого мы будем использовать интерфейс Get & Transform (Power Query), поэтому вам может потребоваться выполнить шаг назад и посмотреть видео, или следуйте нашему руководству по обучению по get & Transform и Power Pivot.

Где есть Power Pivot?

Excel 2016 & Excel для Microsoft 365 — Power Pivot включен в ленту.
Excel 2013 — Power Pivot входит в Office профессиональный плюс Excel 2013, но не включен по умолчанию. Дополнительные сведения о запуске надстройки Power Pivot для Excel 2013.
Excel 2010 — скачайте надстройку Power Pivot, а затем установите надстройку Power Pivot.

Где находится get & Transform (Power Query)?

Excel 2016 & Excel для Microsoft 365 . Get & Transform (Power Query) интегрировано с Excel на вкладке «Данные«.
Excel 2013 — Power Query — это надстройка, которая входит в Excel, но ее необходимо активировать. Перейдите к разделу «Параметры >» > надстроек, а затем в раскрывающемся списке «Управление» в нижней части панели выберите com-надстройки > Go. Проверьте microsoft Power Query Excel, а затем ОК, чтобы активировать его. На Power Query будет добавлена вкладка Power Query.
Excel 2010 — скачивание и установка Power Query надстройки.. После активации на ленту Power Query вкладки.

Начало работы

Сначала необходимо получить некоторые данные.

В Excel 2016 и Excel для Microsoft 365 используйте data >Get & Transform Data > Get Data > Get Data to import data from any number of external data sources, such as a text file, Excel workbook, website, Microsoft Access, SQL Server, or another relational database that contains multiple related tables.

В Excel 2013 и 2010 перейдите к Power Query >получения внешних данных и выберите источник данных.
Excel предложит выбрать таблицу. Если вы хотите получить несколько таблиц из одного источника данных, установите флажок «Включить выбор нескольких таблиц «. При выборе нескольких таблиц Excel автоматически создает модель данных.

Примечание: В этих примерах мы используем книгу Excel с вымышленными сведениями о классах и оценках учащихся. Вы можете скачать пример книги модели данных учащихся и следовать инструкциям. Вы также можете скачать версию с готовой моделью данных..
Выберите одну или несколько таблиц и нажмите кнопку «Загрузить «.

Если необходимо изменить исходные данные, можно выбрать параметр «Изменить «. Дополнительные сведения см. в статье «Общие сведения Редактор запросов (Power Query)».

Теперь у вас есть модель данных, которая содержит все импортированные таблицы, и они будут отображаться в списке полей сводной таблицы.

Примечания:

Модели создаются неявно, когда вы импортируете в Excel несколько таблиц одновременно.
Модели создаются явно, если вы импортируете данные с помощью надстройки Power Pivot. В надстройке модель представлена в макете с вкладками, аналогичном Excel, где каждая вкладка содержит табличные данные. Дополнительные сведения об импорте данных с помощью надстройки Power Pivotсм. в статье «Получение данных с помощью SQL Server данных».
Модель может содержать одну таблицу. Чтобы создать модель на основе только одной таблицы, выберите таблицу и нажмите кнопку Добавить в модель данных в Power Pivot. Это может понадобиться в том случае, если вы хотите использовать функции Power Pivot, например отфильтрованные наборы данных, вычисляемые столбцы, вычисляемые поля, ключевые показатели эффективности и иерархии.
Связи между таблицами могут создаваться автоматически при импорте связанных таблиц, у которых есть связи по первичному и внешнему ключу. Excel обычно может использовать импортированные данные о связях в качестве основы для связей между таблицами в модели данных.
Советы по сокращению размера модели данных см. в статье «Создание модели данных, оптимизированной для памяти, с помощью Excel и Power Pivot».
Дополнительные сведения см. в руководстве по импорту данных в Excel и созданию модели данных.

Создание связей между таблицами

Следующим шагом является создание связей между таблицами, чтобы вы могли извлекать данные из любой из них. Каждая таблица должна иметь первичный ключ или уникальный идентификатор поля, например идентификатор учащегося или номер класса. Самый простой способ — перетащить эти поля, чтобы подключить их в представлении схемы Power Pivot.

Перейдите в power Pivot > Manage.
На вкладке « Главная» выберите » Представление схемы».
Будут отображены все импортированные таблицы, и может потребоваться некоторое время, чтобы изменить их размер в зависимости от количества полей в каждой из них.
Затем перетащите поле первичного ключа из одной таблицы в следующую. В следующем примере показано представление схемы таблиц учащихся.

Мы создали следующие ссылки:
- tbl_Students | Идентификатор учащегося > tbl_Grades | Идентификатор учащегося
  
  Другими словами, перетащите поле «Идентификатор учащегося» из таблицы «Учащиеся» в поле «Идентификатор учащегося» в таблице «Оценки».
- tbl_Semesters | Идентификаторы > tbl_Grades | Семестр
- tbl_Classes | Номер класса > tbl_Grades | Номер класса
Примечания:
- Имена полей не обязательно должны совпадать для создания связи, но они должны быть одинаковыми типами данных.
- Соединители в представлении схемы имеют «1» с одной стороны, а «*» — с другой. Это означает, что между таблицами существует связь «один ко многим», которая определяет, как данные используются в сводных таблицах. См. дополнительные сведения о связях между таблицами в модели данных.
- Соединители указывают только на наличие связи между таблицами. На самом деле они не показывают, какие поля связаны друг с другом. Чтобы просмотреть ссылки, перейдите в раздел Power Pivot > Manage > Design > Relationships > Управление связями. В Excel можно перейти к разделу «>данных».

Создание сводной таблицы или сводной диаграммы с помощью модели данных

Книга Excel может содержать только одну модель данных, но эта модель может содержать несколько таблиц, которые можно многократно использовать в книге. Вы можете добавить дополнительные таблицы в существующую модель данных в любое время.

В Power Pivotперейдите к разделу » Управление».
На вкладке « Главная» выберите сводную таблицу.
Выберите место размещения сводной таблицы: новый лист или текущее расположение.
Нажмите кнопку «ОК», и Excel добавит пустую сводную таблицу с областью списка полей справа.

Затем создайте сводную таблицу или сводную диаграмму. Если вы уже создали связи между таблицами, можно использовать любое из их полей в сводной таблице. Мы уже создали связи в образце книги модели данных учащихся.

Добавление имеющихся несвязанных данных в модель данных

Предположим, вы импортировали или скопировали много данных, которые вы хотите использовать в модели, но не добавили их в модель данных. Принудительно отправить новые данные в модель очень просто.

Начните с выбора любой ячейки в данных, которые необходимо добавить в модель. Это может быть любой диапазон данных, но лучше всего использовать данные, отформатированные в виде таблицы Excel .
Добавьте данные одним из следующих способов.
Щелкните Power Pivot > Добавить в модель данных.
Выберите Вставка > Сводная таблица и установите флажок Добавить эти данные в модель данных в диалоговом окне «Создание сводной таблицы».

Диапазон или таблица будут добавлены в модель как связанная таблица. Дополнительные сведения о работе со связанными таблицами в модели см. в статье Добавление данных с помощью связанных таблиц Excel в Power Pivot.

Добавление данных в таблицу Power Pivot данных

В Power Pivot невозможно добавить строку в таблицу, введя текст непосредственно в новой строке, как это можно сделать на листе Excel. Но можно добавить строки , скопируйте и вставьте или обновите исходные данные и обновите модель Power Pivot.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

См. также

Ознакомьтесь & по преобразованию и обучению Power Pivot

Общие сведения о редакторе запросов (Power Query)

Создание модели данных, оптимизированной для памяти, с помощью Excel и Power Pivot

Руководство. Импорт данных в Excel и создание модели данных

Определение источников данных, используемых в модели данных книги

Связи между таблицами в модели данных

Источник

Тип урока: Урок – исследование возможностей табличного процессора.

Вид урока: Коммуникативно-исследовательский.

Ведущий метод: беседа.

Комплексная цель урока:

ОБРАЗОВАТЕЛЬНАЯ.

Использование полученных знаний и умение применить полученные знания при изучении табличного процессора.

ВОСПИТАТЕЛЬНАЯ.

Воспитать умение слушать, дискутировать, излагать свои мысли, помогать друг другу.

РАЗВИВАЮЩАЯ.

Развитие навыков ассоциативного и логического мышления, зрительной памяти и внимания.
Формирование навыков восприятия и осмысливания информации и соответствующей адекватной реакции на нее.

ИССЛЕДОВАТЕЛЬСКАЯ.

Определение уровня восприятия, усвоения новых знаний и умение применить их на практике.

Предварительная подготовка учащихся:

Ученики должны знать и уметь пользоваться табличным процессором EXCEL.

Технические средства обучения:

— компьютеры

— видеопректор.

СТРУКТУРА УРОКА

Организационный момент…………………………………………………………3 мин.
Повторение пройденного материала………………………………………….6 мин.
Выполнение практических заданий………………………………………..22 мин.
Домашнее задание…………………………………………………………………….2 мин.
Релакс………………………………………………………………………………………3 мин.
Подведение итогов урока………………………………………………………….4 мин.

Ход урока

I. Организационный момент

II. Повторение пройденного материала в 8 классе

Для начала вам вспомнить то что мы проходили с вами в прошлом учебном году. Повторить интерфейс табличного процессора.

Ваша работа состоит из трех заданий. Нам необходимо вспомнить все способы запуска программы, интерфейс и способы завершения работы с табличным процессором.

(На экране интерфейс программы, ученики вспоминают и заносят в папки исследователя соответствующие данные).

Какие данные можно заносить в ячейки?

Как узнать адрес ячейки? С чего необходимо начать запись формулы?

III. Выполнение практических заданий

Задача №1. Представьте себе, что на Земле останется только один источник пресной воды- озеро Байкал. На сколько лет озеро Байкал обеспечит население всего мира водой?

Разработка модели.

Для построения математической модели определим исходные данные. Обозначим:

V – объем озера Байкал – 23000 км³;

N – население Земли – 6 млрд. человек;

р – потребление воды в среднем на 1 человека в день – 300 л.

Т.к. 1 л = 1 дм³ воды, необходимо выполнить перевод V воды озера из км³ в дм³,

V (км³)= V* 10⁹ (м³) = V * 10¹² (дм³)

Результат — количество лет, за которое население Земли использует воды озера Байкала,

— обозначим g.

Итак, g = (V* 1000000000000)/( N*р*365).

Так выглядит электронная таблица.

	А	B
1	Задача об использовании вод Байкала
2	Исходные данные:
3	V (км³)
4	N (чел.)
5	Р(л)
6	g год	=(ВЗ1000000000000)/(В4В5*365)
7

Компьютерный эксперимент.

Выполнение задания на компьютере в Microsoft Office Excel.

Дополнительные вопросы:

2. Сколько лет можно будет пользоваться водами Байкала, если потребление воды увеличится до 400 л на человека?

3.Сколько лет можно будет пользоваться водами Байкала, если население Земли уменьшится до 5,7 млрд. человек?

Задача№2. Сколько стоят билеты на самолет в разные страны в долларах?

Стоимость авиабилетов на самолёты
Курс $	30,23
	Цена в р.	Цена в $
Анталия	7735
Стамбул(Турция)	6000
Варна(Болгария)	8600
Прага(Чехия)	10678
Франкфурт(Германия)	5000

Выбор за вами. К примеру, я хочу сейчас перенестись на берег Белого моря…в Турцию, но знаете, говорят там сильно развита преступность и нам надо быть готовым к тому, чтобы быть бдительным, а в случае чего самому смочь раскрыть преступление, и в этом нам тоже поможет Электронные таблицы Эксель. (именно этой программой пользуется криминалисты-эксперты).

Задача №3.

На месте совершения преступления вы обнаружели след от обуви. Есть пара свидетелей, которые утверждают, что это был молодой человек — лет 26-28, не больше… наша задача собрать как можно больше информации о человеке, совершившем преступление.

Примечание: По следу (отпечатку обуви) можно узнать: рост человека; определить длину шага; создать модель человека. Если известен примерный возраст, то рассчитать идеальную массу.

Рост = (( длина ступни — 15)*100)/15,8

Длина шага = длина ступни * 3

Ширина ступни = Рост / 18

Длина пятки = Рост / 27

Голова = Рост / 8

Идеальная масса = ((Рост * 3) / 10 — 450 + Возраст) * 0,25 + 45

Я вам сейчас раздам образцы следов преступников, а вы попробуйте определить их основные параметры и помочь следствию.

Подведение итогов.

Сегодня мы еще раз убедились в многофункциональности и необходимости такой непростой, на первый взгляд программы M.Exsel. Спасибо вам за урок, надеюсь что полученные знания вы будете применять и дальше в своих профессиях.

Источник