Модель ограниченного роста excel

Уроки 13 — 16
§1.5. Биологические модели развития популяций

Содержание урока

1.5.1. Информационные модели развития популяций

1.5.2. Компьютерные модели развития популяций на языке Visual Basic

1.5.3. Компьютерные модели развития популяций на языке Turbo Delphi

1.5.4. Компьютерные модели развития популяций в электронных таблицах

Компьютерная модель «Численность популяций» в электронных таблицах

1.5.4. Компьютерные модели развития популяций в электронных таблицах

Компьютерная модель «Численность популяций» в электронных таблицах

Построим в электронных таблицах компьютерную модель, позволяющую исследовать численность популяций с использованием различных моделей: неограниченного роста, ограниченного роста, ограниченного роста с отловом и «жертва-хищник».

1. В ячейки В2 и В7 ввести начальные значения численности популяций жертв и хищников. Для простоты примем начальные количества жертв X1 и хищников Y1 за единицу (рис. 1.25).

Рис. 1.25. Ввод начальных значений

В ячейки ВЗ:В6 ввести значения коэффициентов а, b, с и f, влияющих на изменение численности жертв.

В ячейки В8 и В9 внести значения коэффициентов d и g, влияющих на изменение численности хищников.

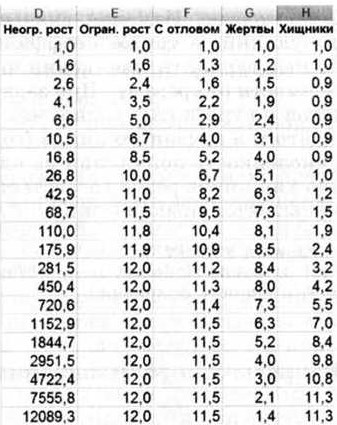
В столбце D будем вычислять численность популяции в соответствии с моделью неограниченного роста, в столбце Е — ограниченного роста, в столбце F — ограниченного роста с отловом, в столбцах G и Н численность популяций жертв и хищников.

2. В ячейки D2, Е2, F2, G2 и Н2 внести значения начальной численности популяций.

В ячейку D3 внести рекуррентную формулу неограниченного роста =$B$3*D2.
В ячейку ЕЗ внести рекуррентную формулу ограниченного роста =($В$3-$В$4*Е2)*Е2.
В ячейку F3 внести рекуррентную формулу ограниченного роста с отловом =($B$3-$B$4*F2)*F2-$B$5.
В ячейку G3 внести рекуррентную формулу роста жертв =($B$3-$B$4*G2)*G2-$B$5-$B$6*G2*H2.
В ячейку НЗ внести рекуррентную формулу роста хищников =$B$8*H2+$B$9*G2*H2.

3. Скопировать внесенные формулы в ячейки столбцов командами [Правка-Заполнить-Вниз].

В ячейках столбцов ознакомиться с динамикой изменения численности популяций (рис. 1.26).

Рис. 1.26. Динамика изменения численности популяций

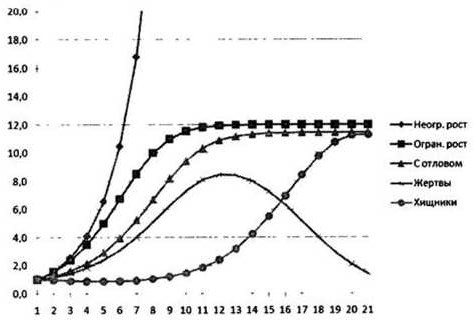
Для визуализации компьютерной модели построим графики изменения популяций с течением времени.

4. Выделить столбцы данных D, Е, F, G, Н и построить диаграмму типа График.

Появятся графики изменения численности популяций в соответствии с моделями неограниченного роста, ограниченного роста, ограниченного роста с отловом, количества жертв и хищников в модели «жертва-хищник» (рис. 1.27).

Рис. 1.27. Графики изменения численности популяций

Следующая страница Исследование модели

Cкачать материалы урока

Источник

Уроки 15 — 18
Модели ограниченного и неограниченного роста
(§10. Математические модели в биологии)

Содержание урока

Модель неограниченного роста

Модель неограниченного роста

Многие идеи в области моделирования были предложены биологами. Достаточно вспомнить, что родоначальником общей теории систем (системного подхода) был биолог Людвиг фон Берталанфи. В этом параграфе мы познакомимся с моделями некоторых биологических систем.

Одна из задач, которые решают биологи, — изучение изменения численности животных в некоторой области. Обычно их пересчитывают раз в год, поэтому модель изменения численности получается дискретной — с её помощью можно определить численность с интервалом 1 год.

Обозначим через N₀ начальную численность, а через N_i — численность в i-й год с момента начала наблюдений. Количество родившихся и умерших животных пропорционально численности, поэтому годовой прирост равен k_p • N_i — k_c • N_i, где k_p и k_c — коэффициенты рождаемости и смертности. Тогда количество животных в (i + 1)-й год может быть вычислено через их количество N_i в предыдущему году:

где К = kp — k_c — коэффициент прироста. Это и есть математическая модель развития популяции («населения») животных. Коэффициенты k_p и k_c (так же как и другие коэффициенты в рассматриваемых далее моделях) обычно определяются экспериментально.

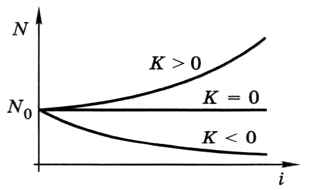
При К = 0 (рождаемость равна смертности) количество животных не меняется, при К 0 (k_p > k_c) их число бесконечно увеличивается (рис. 2.14).

Поэтому эту модель называют моделью неограниченного роста.

Английский учёный и экономист Томас Мальтус использовал её для описания роста населения Земли, поэтому эту модель иногда называют моделью Мальтуса.

Недостаток этой модели в том, что она не учитывает ограниченность ресурсов (например, пищи), влияние других видов и изменяющихся природных условий, из-за которых изменяются коэффициенты рождаемости и смертности. Поэтому модель Мальтуса адекватна только при небольших интервалах наблюдения.

Следующая страница Модель ограниченного роста

Cкачать материалы урока

Источник

Лабораторные работы по моделированию в Excel

Лабораторная работа № 1

Модель неограниченного роста

Цель работы: Используя компьютерную модель неограниченного роста исследовать прирост массы живых организмов с течением времени.

Ø прирост массы живых организмов за единицу времени пропорционален уже их имеющейся массе;

Ø регулятором прироста выступает окружающая среда;

Ø коэффициент размножения постоянен

Ø начальная масса живых организмов М(0) = 1 т;

Ø коэффициент размножения k:

Связь между параметрами модели задается соотношением:

1) Определить, через сколько лет масса растений в различных природных зонах превысит 100 т;

2) Определить, через сколько лет масса растений в различных природных зонах превысит 1000 т, 10000 т (т.е. произойдет ее «удесятерение») ;

3) Построить график зависимости массы растений от числа прошедших лет (для каждой природной зоны);

4) Определить, через сколько лет масса растений в различных природных зонах превысит

массу Земли (5 976 000 000 000 000 000 000 т).

Коэффициент размножения k

Начальная масса М(0)

Масса через 1 год

Масса через 2 года

1. Загрузите электронную таблицу Excel и занесите в таблицу 2 исходные данные (они выделены цветом) и формулы.

2. Измените формулы в блоке ячеек C 4: D 5 с учетом того, что номер строки в адресах некоторых ячеек должен быть абсолютным (неизменным при копировании в последующие строки).

3. Занесите формулы в ячейки Е4 и F 4.

Подготовленную таблицу в режиме отображения формул приложите к отчету.

4. Последовательно скопируйте блок ячеек В4: F 4 в последующие строки. Копирование прекратить, как только во всех четырех столбцах C , D , E и F возникнут числа, большие 100.

Для каждой природной зоны определите, через сколько лет масса растений превысит 100 т. Результаты запишите в отчет.

5. С помощью электронной таблицы вычислить, через сколько лет масса растений в различных природных зонах превысит 1000 т и 10000 т.

Результаты запишите в отчет. Для каждой природной зоны сделайте вывод о времени, необходимом для увеличения массы растений в 10 раз.

6. С помощью электронной таблицы вычислить, через сколько лет масса растений в различных природных зонах превысит массу Земли, равную 5 976 000 000 000 000 000 000 т.

Результаты запишите в отчет. Для каждой природной зоны сделайте вывод о времени, когда масса растений превысит массу Земли.

7. С помощью электронной таблицы для каждой природной зоны построить график зависимости массы растений от числа прошедших лет.

Таблицу в режиме отображения значений и графики приложите к отчету.

Лабораторная работа № 2

Модель ограниченного роста

Цель работы: Используя компьютерную модель ограниченного роста исследовать прирост массы живых организмов с течением времени.

Ø прирост массы живых организмов за единицу времени пропорционален уже их имеющейся массе;

Ø существует некоторое предельное значение массы живых организмов;

Ø коэффициент прироста массы живых организмов за единицу времени пропорционален разности между максимально возможным значением массы и массой, имеющейся к данному моменту времени.

Ø начальная масса живых организмов М(0) = 1 т;

Ø предельное значение массы живых организмов L = 11000 т.

Ø коэффициент пропорциональности a в формуле для коэффициента прироста;

Связь между параметрами модели задается соотношением:

1) Определить, через сколько лет масса растений в различных природных зонах превысит 100 т;

2) Определить, через сколько лет масса растений в различных природных зонах превысит 1000 т; 10 000 т (т.е. произойдет ее «удесятерение»)

3) Построить график зависимости массы растений от числа прошедших лет (для каждой природной зоны);

1. Загрузите электронную таблицу Excel и занесите в таблицу исходные данные (они выделены цветом) и формулы:

Коэффициент размножения k

Предельное значение массы L

Начальная масса М(0)

Масса через 1 год

Масса через 2 года

2. Измените формулы в блоке ячеек C4:D5 с учетом того, что номер строки в адресах некоторых ячеек должен быть абсолютным (неизменным при копировании в последующие строки).

Подготовленную таблицу в режиме отображения формул приложите к отчету.

3. Последовательно скопируйте блок ячеек В4:F4 в последующие строки. Копирование прекратить, как только во всех четырех столбцах C, D, E и F возникнут числа, большие 100.

Результаты занесите в отчет. Сравните с результатами предыдущей практической работы и сделайте выводы.

4. С помощью электронной таблицы вычислить, через сколько лет масса растений в различных природных зонах превысит 1000 т и 10000.

Результаты занесите в отчет. Сравните с результатами предыдущей практической работы и сделайте выводы.

5. С помощью электронной таблицы для каждой природной зоны построить график зависимости массы растений от числа прошедших лет.

Таблицу в режиме отображения значений и графики приложите к отчету.

Лабораторная работа № 3

Границы адекватности модели неограниченного роста

Цель работы : Найти границы адекватности модели неограниченного роста.

Предположения и параметры моделей:

Всякая модель имеет ограниченную область адекватности, и за пределами этой области она перестает удовлетворительно отражать свойства моделируемого объекта. Модель неограниченного роста остается адекватной, пока масса живых организмов достаточно мала по сравнению с предельно допустимой массой этих организмов в данных природных условиях.

Параметры модели неограниченного роста : начальная масса М(0), коэффициент прироста k, предельное значение массы L , число лет n, масса живых организмов через n лет М( n ); связь между параметрами модели определяется формулой:

Параметры модели ограниченного роста: начальная масса М_о(0), коэффициент прироста k, число лет n, масса живых организмов через n лет М_о( n ); связь между параметрами модели определяется формулой:

Поскольку М_о(0)= М(0), то нетрудно подсчитать, что М_о(1)= М(1), но вот уже М_о(2)

Экспериментально установлено, что предельное значение массы L образует геометрическую прогрессию относительно границы адекватности n, т.е. L = b × 2 n -1 , где b – некоторый коэффициент.

Компьютерные эксперименты показали, что моделью неограниченного роста можно пользоваться с уровнем погрешности в 10% при выполнении условия L ³ 8 × (1+ k ) n -1 . Выражение для n полученное при решении показательного неравенства, показывает, как долго можно пользоваться моделью неограниченного роста при заданных (предельного уровня массы живых организмов) и (коэффициента ежегодного прироста):

1) Найти границу адекватности n при k =1,8 и L =11000.

2) Исследовать, как граница адекватности n зависит от величины k ( L =11000; k =1,8; 1,2; 1)

3) Исследовать, как граница адекватности n зависит от величины L (k=1; L= 5500; 11000; 22000; 44000)

4) Исследовать, как коэффициент b зависит от k ( L =5000; k =1; 1,2; 1,5; 2)

1. Загрузите электронную таблицу Excel и занесите в таблицу исходные данные и формулы (при занесении формулы в ячейку Е2 используйте функцию).

Источник

§ 10. Моделирование динамики численности популяций

Сайт:	Профильное обучение
Курс:	Информационные технологии. 11 класс (Базовый уровень)
Книга:	§ 10. Моделирование динамики численности популяций
Напечатано::	Гость
Дата:	Понедельник, 20 Март 2023, 12:45

Оглавление

10.1. Основные понятия

Популяция — это совокупность особей одного вида, которая занимает определенное пространство, относительно изолирована и способна к самовоспроизведению.

Популяции образуют самые разнообразные организмы (пример 10.1).

Среди характеристик популяции выделяют численность, плотность, пространственное распределение, структуру (возрастной и половой состав), показатели рождаемости и смертности. Нас будет интересовать динамика численности популяции, т.е. изменение численности популяции во времени (пример 10.2).

Наблюдения за популяциями проводят в равноотстоящие моменты времени. Длительность промежутка времени между моментами наблюдений назовем периодичностью наблюдений .

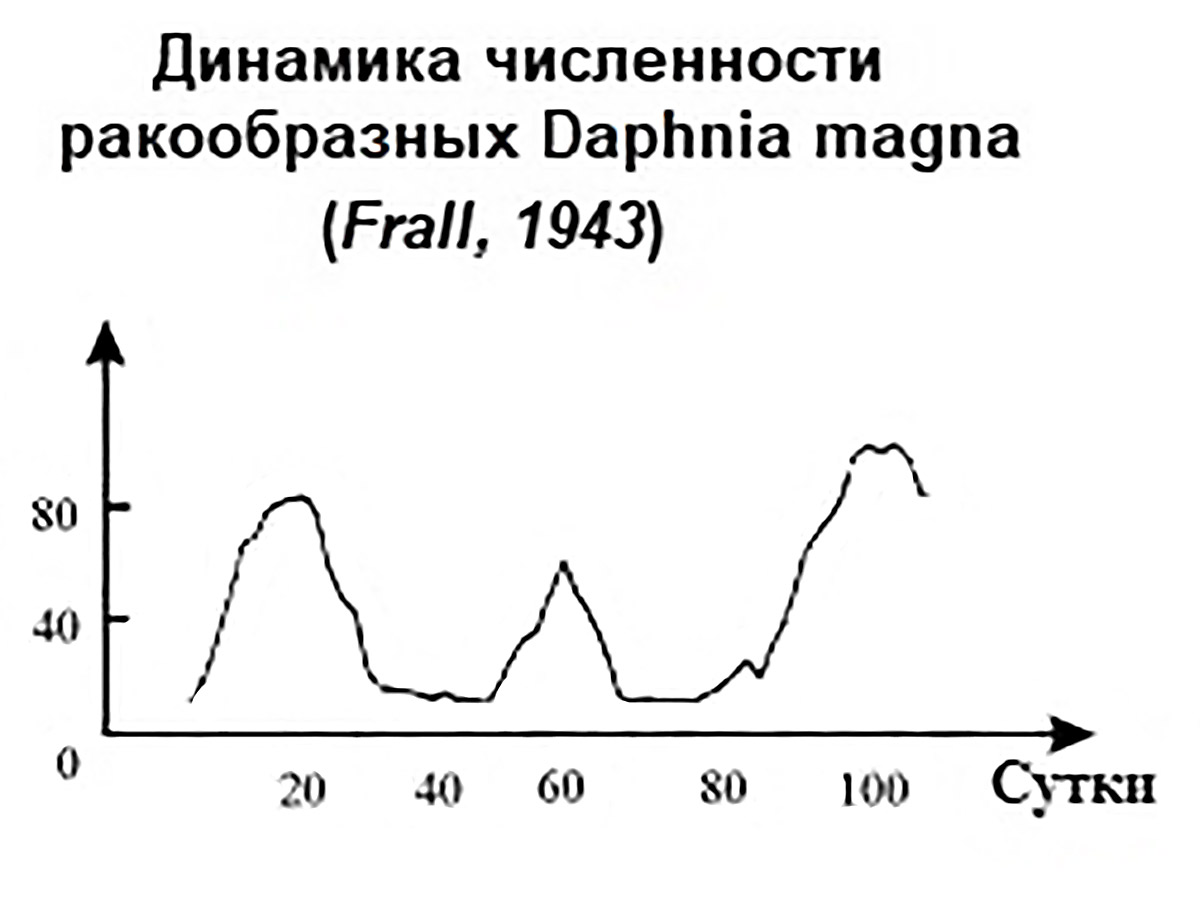
Периодичность наблюдений зависит от скорости роста популяции и может быть равна 1 году, 1 суткам, 1 часу (см. пример 10.2).

Для описания динамики численности популяций ученые используют несколько математических моделей.

Для одной популяции используются:

— модель неограниченного роста;
— модель ограниченного роста ;
— модель с критической численностью ;
— модель с отловом .

Для двух популяций используются модели взаимодействия двух видов. Среди них модель «хищник-жертва», модель конкуренции двух видов за ресурсы питания, модели взаимовыгодного взаимодействия (симбиоза).

Пример 10.1. Популяции могут составлять бактерии, рыбы, ракообразные, киты, птицы, звери.

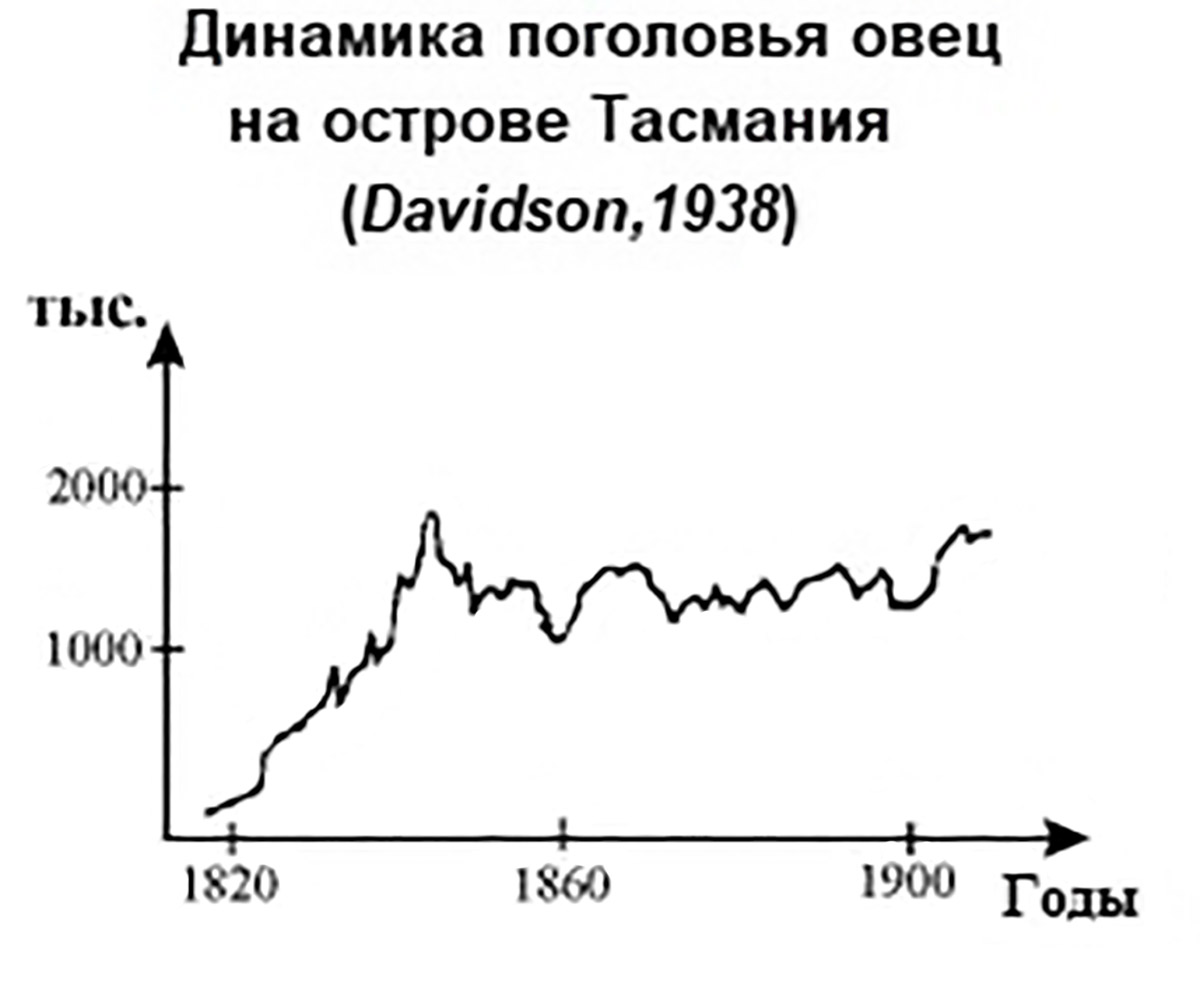
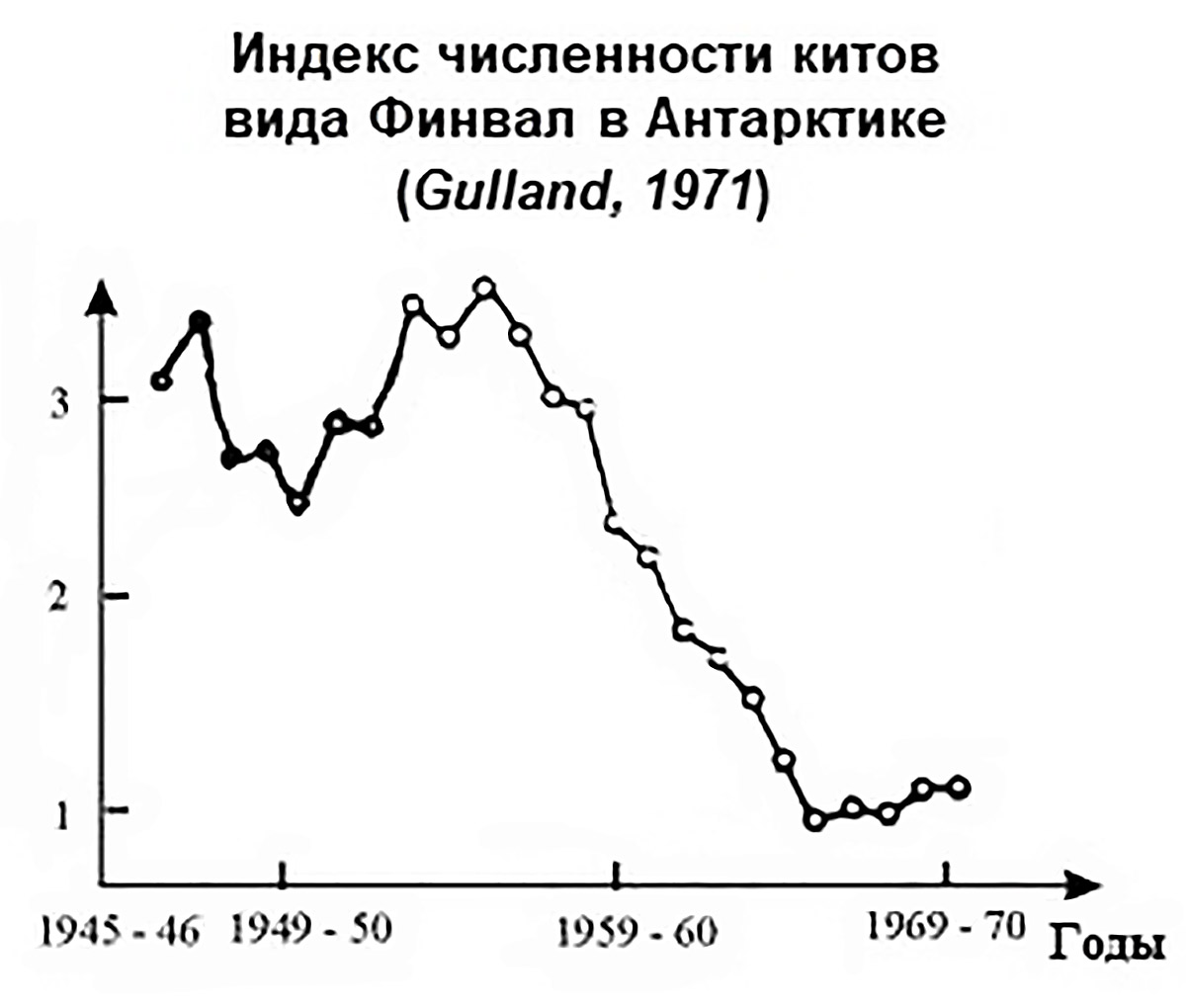
Пример 10.2. Наблюдения за численностью различных популяций ученые ведут уже очень давно. Поэтому хорошо известно, что численность популяции во времени может расти, меняться циклически и падать.

10.2. Модель неограниченного роста

Модель неограниченного роста является классической математической моделью дина­мики численности популяции (пример 10.3).

Если обозначить численность популяции в момент времени t через x(t), а скорость роста этой численности через v(t), то модель неограниченного роста выражается уравнением:

где a — коэффициент естественного прироста.

Коэффициент естественного прироста подсчитывается на основе наблюдений за численностью популяции (пример 10.4).

Чтобы построить график решения урав­нения, воспользуемся методом дискретизации времени с шагом t. Пусть начальный момент t₀ = 0, последующие моменты t₁, t₂, t₃, … и скорость v(t) меняется только в эти моменты времени. Тогда значения x(t_{i +1}) и x(t_i ) связаны равенством

а с учетом уравнения неограниченного роста получаем

Будем считать, что шаг времени t = 1 и совпадает с периодичностью наблюдений (1 год, 1 сутки или 1 час). Тогда t_i = i и последняя формула получает вид

Расчеты по таким формулам удобно проводить в электронных таблицах. При i = 0 из формулы модели получаем основную формулу расчетной модели в электронных таблицах:

x(1) = (1 + а )x(0).

Пример 10.3. Модель была предложена английским священником и ученым Томасом Робертом Мальтусом в 1798 г.

Он первым обратил внимание на то, что рост численности популяции может сильно опережать рост ресурсов для ее питания. На этом основании для человеческой популяции он сделал вывод о неизбежности войн за ресурсы питания, наступления хаоса и голода.

Пример 10.4. Коэффициент естественного прироста — это отношение численности прироста за период наблюдения к численности популяции на начало периода.

Например, если численность популяции в 3000 особей за год выросла на 150 особей, то коэффициент естественного прироста равен

Интересно, что в модели популяция с коэффициентом прироста 0,05 удваивает свою численность через каждые 14 лет.

Если в популяции рождаемость равна смертности, то коэффициент естественного прироста равен нулю и численность популяции остается без изменения.

10.3. Модель ограниченного роста

Наблюдения показали, что модель неограниченного роста справедлива только на ограниченных промежутках времени. Постоянный неограниченный рост популяции невозможен, прежде всего, из-за конкуренции внутри популяции за ресурсы питания.

Осознание этого фактора привело к созданию математической модели ограниченного роста (пример 10.5).

В обозначениях предыдущего пункта модель ограниченного роста выражается уравнением:

где a — коэффициент естественного прироста;

b — коэффициент смертности от вну­тривидовой конкуренции (пример 10.6).

Еще раз используем метод дискретизации времени с формулой

Откуда при i = 0 получим расчетную формулу для электронных таблиц

x(1) = x(0) + ( a – bx(0))x(0).

Пример 10.5. Модель ограниченного роста предложил в 1848 г. бельгийский математик Пьер Франсуа Ферхюльст.

Идея Ферхюльста состояла в том, что любая популяция, развиваясь, достигает своей максимальной численности, зависящей от факторов внешней среды.

Пример 10.6. Коэффициенты a и b математической модели ограниченного роста определяют максимальную численность популяции как величину, равную дроби . А выражение a — bx(t) можно понимать как переменный коэффициент прироста.

10.4. Модель с критической численностью

Существуют популяции, численность которых не может опускаться ниже некоторой критической численности. Иначе популяция погибает (пример 10.7).

Математическая модель ограниченного роста, учитывающая наименьшую критическую численность, в обозначениях предыдущей модели имеет вид:

где L — критическая численность популяции.

С использованием метода дискретизации времени о сновная формула расчетной модели получает вид

x(1) = x(0) + ( a – bx(0)) · (x(0) – L).

Пример 10.7. Причина гибели популяции в том, что из-за ее малочисленности половозрелые особи популяции не находят друг друга в брачный сезон. Величина наименьшей критической численности различна для разных популяций.

По наблюдениям биологов для ондатр критическая численность равна всего лишь одной паре особей на тысячу квадратных километров. А вот для американского странствующего голубя наименьшая критическая численность равна сотням тысяч особей.

10.5. Модель с критической численностью и с отловом

Рассматриваемая модель описывает динамику численности популяции промысловой рыбы с критической численностью и с учетом ее промышленной добычи (пример 10.8).

Оставляем в силе предположения предыдущих пунктов параграфа. Если объем регулярной добычи рыбы составляет Z особей популяции за время
t = 1, то основная формула расчетной модели получит вид

x(1) = x(0) + ( a – bx(0))·(x(0) – L) – Z.

Пример 10.8. В океанах, морях, реках и озерах мира обитает более 30 тыс. видов рыб. Примерно 10% от этого числа составляют промысловые рыбы.

Рыбой обеспечивается примерно одна шестая мировой потребности человечества в белке, что привело к сокращению ее запасов. Так, например, промысловые запасы трески, хека, морского окуня и камбалы в северной части Атлантики за последние годы сократились на 95 %.

10.6. Создание компьютерной модели динамики численности популяций

В электронных таблицах создадим комплексную компьютерную модель динамики численности четырех популяций, рассмотренных в п. 10.2—10.5 (пример 10.9).

Для расчета численности популяции с неограниченным ростом используем формулу п. 10.2

Для популяции с ограниченным ростом используем формулу п. 10.3

Для популяции с минимальной критической численностью используем формулу п. 10.4

Для популяции с критической численностью и отловом используем формулу п. 10.5

В исходных данных нужно задать значения параметров, записанных в правых частях этих формул (пример 10.9).

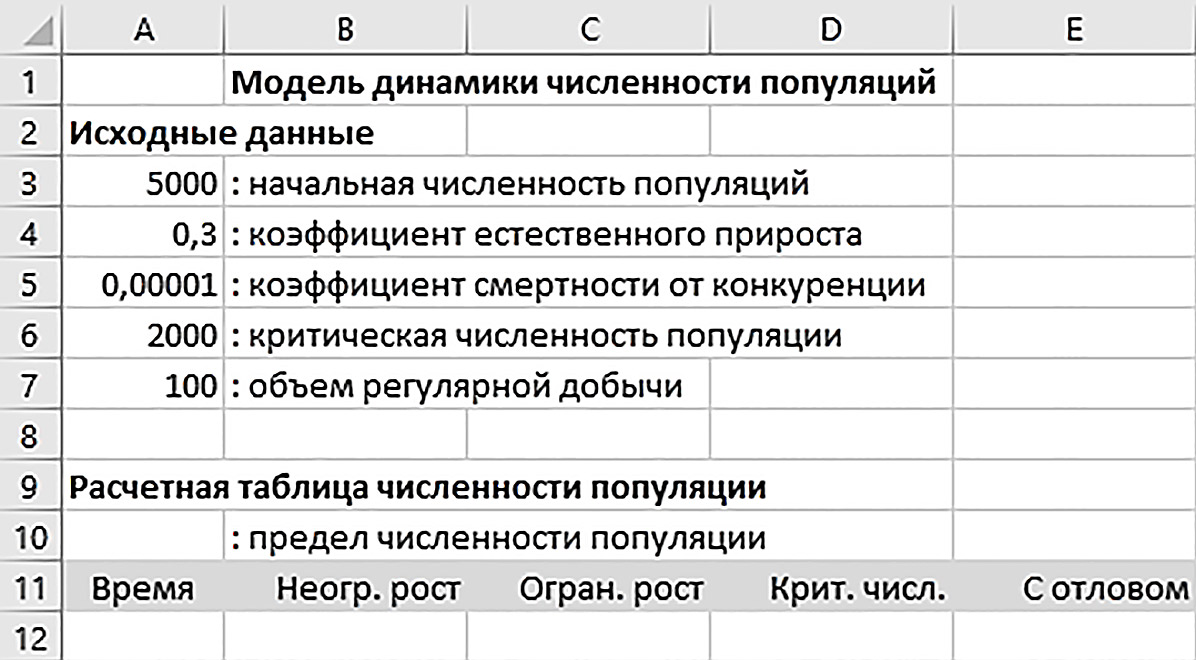
Данные компьютерной расчетной модели разместим по схеме примера 10.10.

В ячейки B12:E12 вводим формулу

В следующей строке

В ячейки B13:E13 нужно ввести правые части четырех расчетных формул. Значение x(0) для формулы в каждом столбце берется из предыдущей строки.

Формулы моделей требуют доработки (пример 10.11). Формулами диапазона A13:E13 таблица заполняется вниз до строки 47 включительно. Затем надо вывести на лист диаграмму с четырьмя графиками моделей.

Выделяется диапазон A12:E47 в расчетной таблице и на лист рабочей книги вставляется диаграмма Точечная ( — Точечная с гладкими кривыми). Вводится название диаграммы «Динамика численности популяций». В нижнюю часть диаграммы выводится Легенда (пример 10.12).

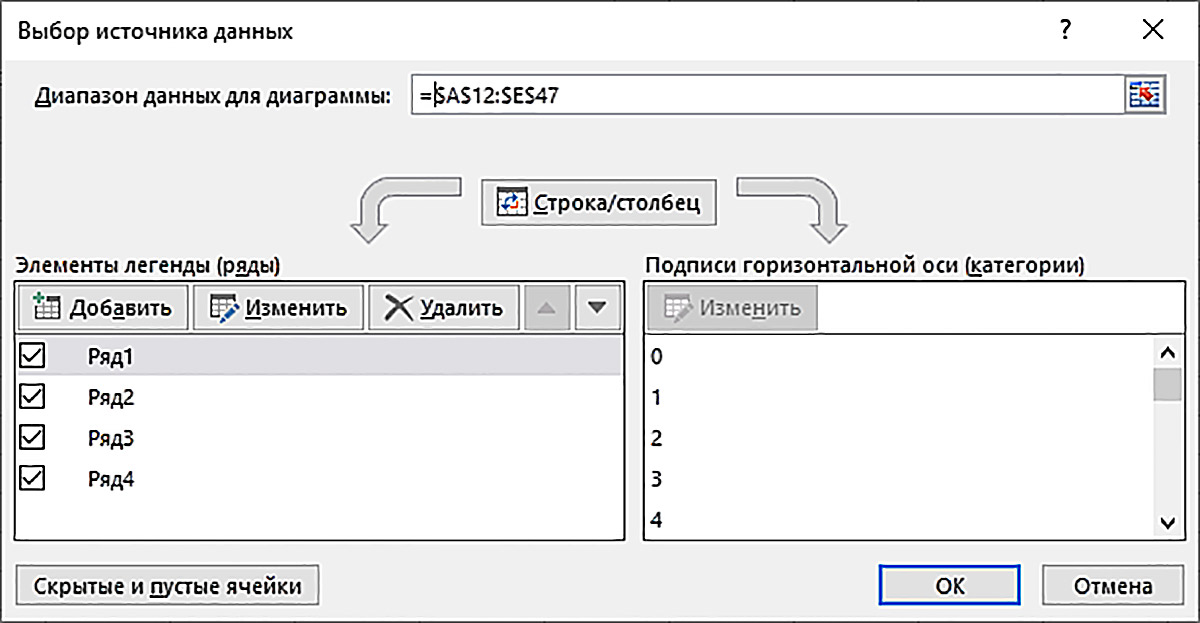
Осталось поменять имена элементов Диаграммы. Щелкаем по диаграмме правой клавишей мыши и в контекстном меню выбираем пункт Выбрать данные … . Появляется диалоговое окно Выбор источника данных (пример 10.13).

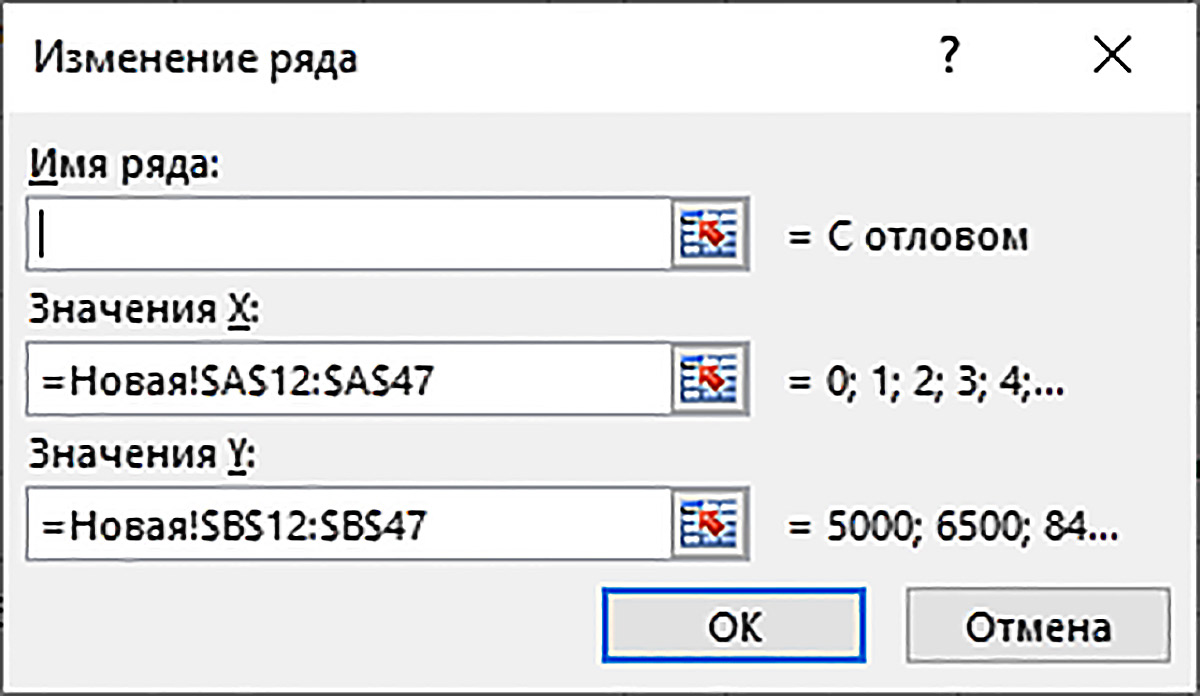
В диалоговом окне слева выделяем строку Ряд1 и щелкаем по кнопке Изменить. Появляется диалоговое окно Изменение ряда (пример 10.14).

В верхнее поле Имя ряда: щелчком по ячейке B11 вводим ссылку на заголовок второго столбца. Щелкаем кнопку OK. Имена остальных рядов изменяем аналогично.

[1] Знак показывает место разрыва длинной формулы здесь, в электронном приложении. При вводе в ячейку таблицы формула в этом месте разрываться не должна.

Пример 10.9. Исходные данные компьютерной модели должны включать:

* численность x(0), начальную для всех четырех популяций;
* значение коэффициента a естествен­ного прироста;
* значение коэффициента b смертности от конкуренции;
* минимальную критическую числен­ность L популяции;
* объем Z регулярной добычи.

Пример 10.10. Комплексная компьютерная модель динамики численности популяций должна включать раздел Исходные данные и Расчетную таблицу.

Используем следующую схему размещения данных:

Ширину столбцов B:E установим равной 13, для заголовков этих столбцов в расчетной таблице установим выравнивание вправо.

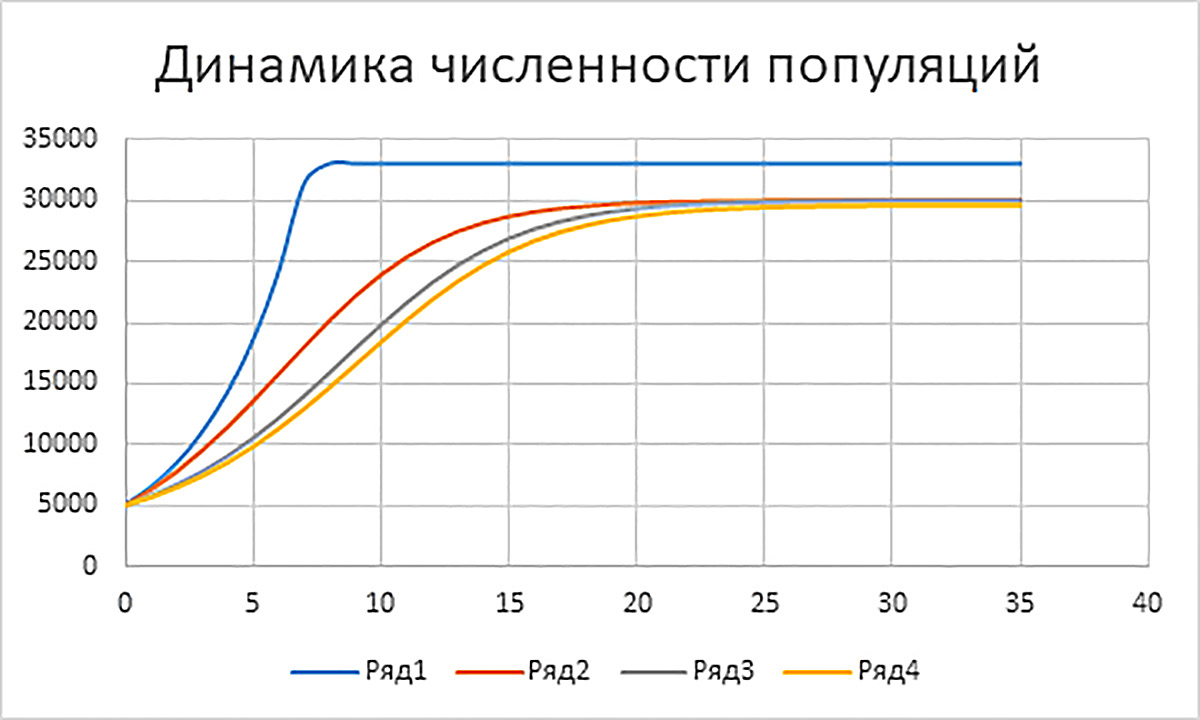
Пример 10.11. Численность популяции в модели неограниченного роста растет очень быстро. Поэтому ограниченные численности остальных трех популяций на совместной диаграмме становятся практически незаметными.

Чтобы избежать такого эффекта, искусственно ограничим численность в первой модели величиной

пользуясь тем, что в ячейке A10 вычислен предел численности популяции с ограниченным ростом.

Для построения ограничения используем функцию ЕСЛИ() и в ячейку B13 вместо формулы модели неограниченного роста ФОРМН введем новую формулу по схеме

Формулы остальных трех моделей в ячейках расчетной таблицы могут выдавать отрицательные значения численности популяций, что нарушает адекватность.

Поэтому вместо формул ФОРМ этих моделей в ячейки С13:E13 введем новые формулы по схеме

=ЕСЛИ(ФОРМ>0; ФОРМ; 0)

Пример 10.12. Диаграмма с графиками компьютерной модели:

Пример 10.13. Диалоговое окно Выбор источника данных:

Пример 10.14. Диалоговое окно Изменение ряда:

10.7. Добавление интерактивных флажков

Работать сразу с четырьмя графиками на диаграмме не всегда удобно, поэтому добавим в компьютерную модель интерактивные флажки для выключения графиков на диаграмме. Работу с флажками обеспечивает вкладка Разработчик (пример 10.15).

Для вывода флажка на лист на вкладке Разработчик в группе Элементы управления выбирают инструмент Вставить, а на его панели выбирают элемент управления формы Флажок (пример 10.16).

После выбора щелчком элемента Флажок указатель мыши получает вид креста. Этим указателем мыши с нажатой левой кнопкой повторяют контур ячейки B8 вспомогательным прямоугольником (подобно рисованию прямоугольника в графическом редакторе Paint).

После отпускания кнопки мыши на ячейке B8 появляется флажок в форме квадрата с названием по умолчанию. Флажок помещен в рамку с маркерами (пример 10.17).

Название флажка по умолчанию надо удалить (пример 10.18).

Флажок является графическим элементом, располагается поверх ячеек, и выделенный флажок можно перетаскивать по таблице.

Флажок нужно аккуратно перетащить на ячейку B11 так, чтобы его квадрат размещался перед заголовком столбца (пример 10.19). В остальные ячейки с заголовками столбцов нужно вывести копии флажка (пример 10.20).

Состояние флажка можно вывести в ячейку таблицы в виде значений ИСТИНА (флажок включен) и ЛОЖЬ (флажок выключен). Состояние первого флажка нужно вывести в ячейку B8 (пример 10.21). Щелчок по флажку теперь выводит галочку в квадрат и меняет значение связанной с флажком ячейки B8. Остальные флажки надо связать с ячейками C8:E8.

Осталось изменить формулы в строке 12 таблицы. В ячейку B12 вводим формулу

Здесь #Н/Д — это искусственная ошибка, которая не позволит построить график.

Формулой ячейки B12 заполняется вправо диапазон C12:E12. Теперь щелчки по флажкам выключают и включают графики на диаграмме.

Значения состояний флажков в строке 8 можно сделать невидимыми, если в диапазоне B8:E8 установить белый цвет шрифта.

Пример 10.15. Вкладка Разработчик выводится на экран командой:

в Excel 2007 Офис → Параметры Excel → Отобразить вкладку Разработчик на ленте;

в Excel 2010+ Файл → Параметры → Настройка ленты и в правом поле включить флаг у пункта Разрабочик.

Настройка завершается кнопкой OK.

Пример 10.16. Панель инструмента Вставить, на которой стрелкой указан верхний элемент Флажок для вставки.

Пример 10.17. Флажок с названием по умолчанию в рамке.

Рамка означает, что флажок выделен. При необходимости флажок выделяется щелчком правой клавишей мыши.

Пример 10.18. По названию выделенного флажка щелкают, в рамке появляется текстовый курсор. Название флажка удаляют. Затем по флажку щелкают правой клавишей мыши и в новом меню выбирают пункт Завершить изменение текста.

Пример 10.19. Флажок установлен на ячейку B11.

Пример 10.20. Нажимаем клавишу Ctrl клавиатуры и устанавливаем указатель мыши на рамку выделенного флажка так, чтобы указатель получил вид стрелки с плюсом .

Перетаскиваем и устанавливаем флажок-копию на другую ячейку. Аналогично устанавливаем остальные два флажка.

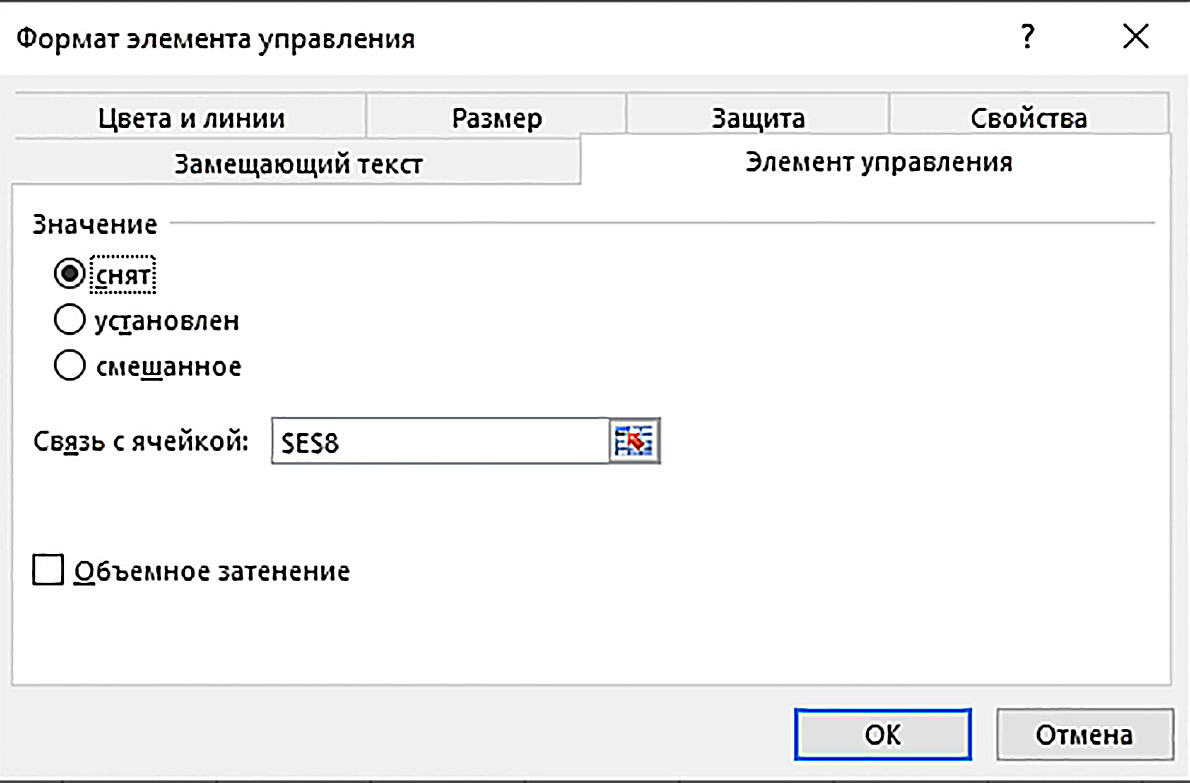
Пример 10.21. Щелкаем по флажку правой клавишей мыши и в меню выбираем пункт Формат объекта … .

Появляется диалоговое окно:

На вкладке Элемент управления в поле Связь с ячейкой: вводим B8. Объемное затенение — по желанию. Операция завершается щелчком по кнопке OK.

Упражнения

1. Повторите на компьютере рассмотренное в параграфе построение комплексной компьютерной модели динамики численности популяций. Введите в модель исходные данные, приведенные на схеме примера 10.10. Для ячеек расчетной таблицы следует задать формат Числовой с числом десятичных знаков 0 (целые числа).

Проверьте адекватность модели сравнением данных ее строки 47 со следующими выверенными данными

2. В модели динамики численности популяций с исходными данными примера 10.10 оставьте включенными графики моделей неограниченного и ограниченного роста. Увеличивая постепенно начальную численность популяций от 5000 до 25000 с шагом 5000, проанализируйте взаимное положение двух графиков.

3. В модели динамики численности популяций с исходными данными примера 10.10 оставьте включенными графики модели ограниченного роста и модели с критической численностью. Уменьшая постепенно начальную численность популяций от 3000 до 1600 с шагом 200, проанализируйте положение графиков и объясните их поведение.

4. В модели динамики численности популяций с исходными данными примера 10.10 оставьте включенными графики модели с критической численностью и модели с отловом. Постепенно увеличивая объем регулярной добычи от 100 до 1200 с шагом 100, опишите поведение графика модели с отловом. Найдите максимальное значение объема отлова, при котором популяция еще может восстановиться.

Источник