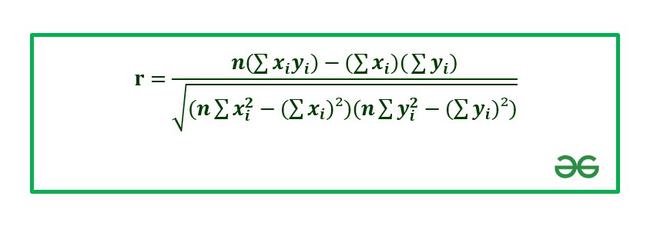Модель корреляции в excel - Word и Excel - помощь в работе с программами

Содержание

Суть корреляционного анализа
Расчет коэффициента корреляции
- Способ 1: определение корреляции через Мастер функций
- Способ 2: вычисление корреляции с помощью пакета анализа
Вопросы и ответы

Корреляционный анализ – популярный метод статистического исследования, который используется для выявления степени зависимости одного показателя от другого. В Microsoft Excel имеется специальный инструмент, предназначенный для выполнения этого типа анализа. Давайте выясним, как пользоваться данной функцией.

Суть корреляционного анализа

Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.

Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.

Расчет коэффициента корреляции

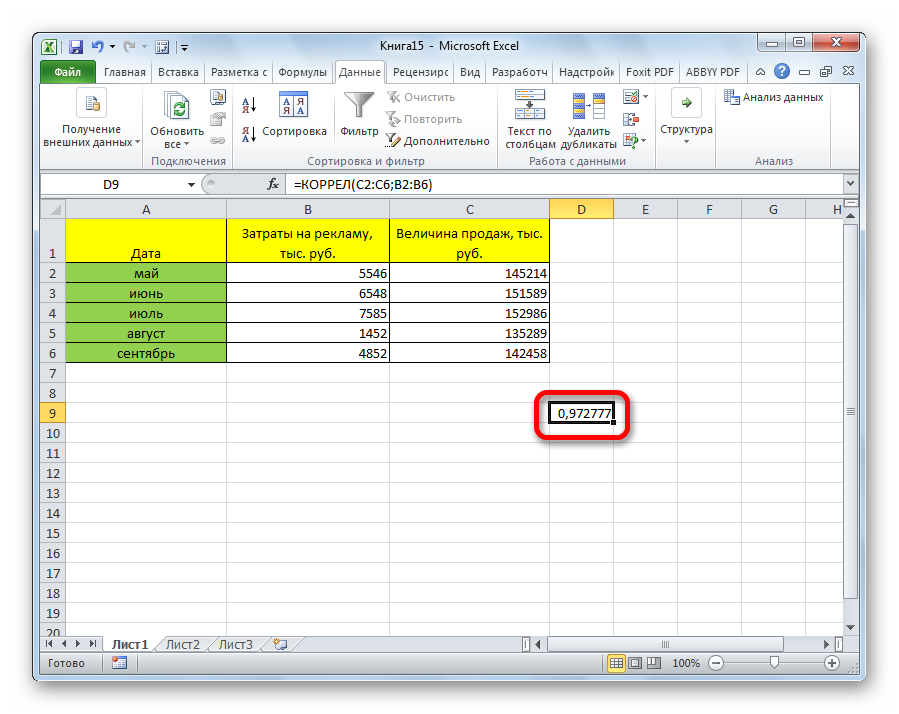
Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.

Способ 1: определение корреляции через Мастер функций

Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).

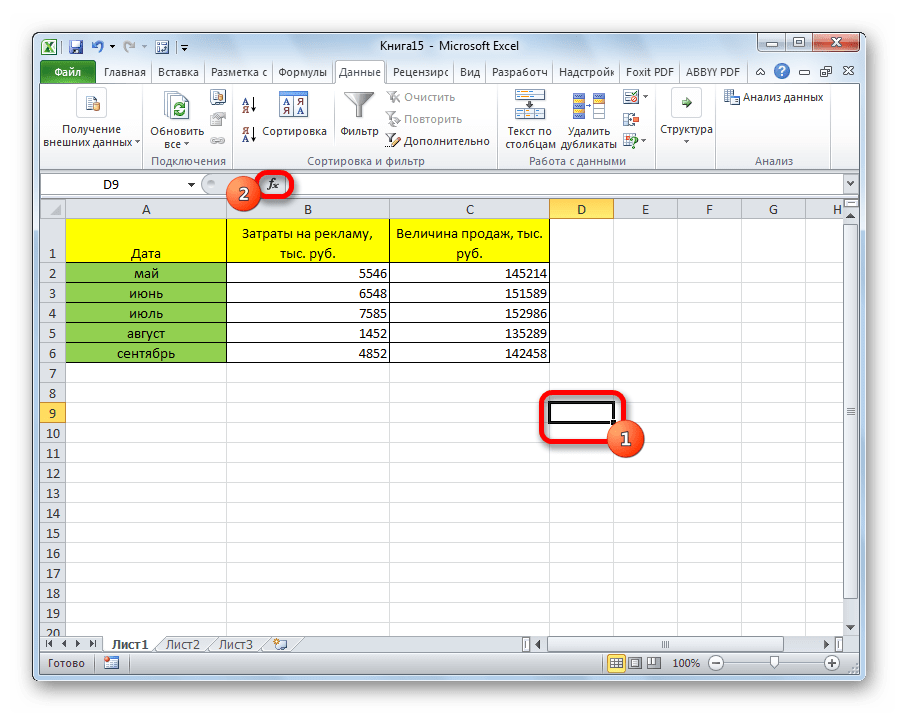
Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.

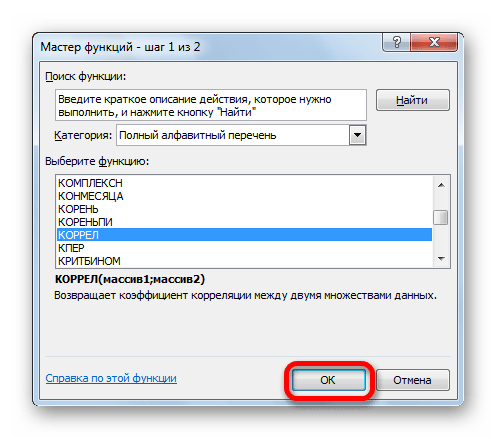
В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».

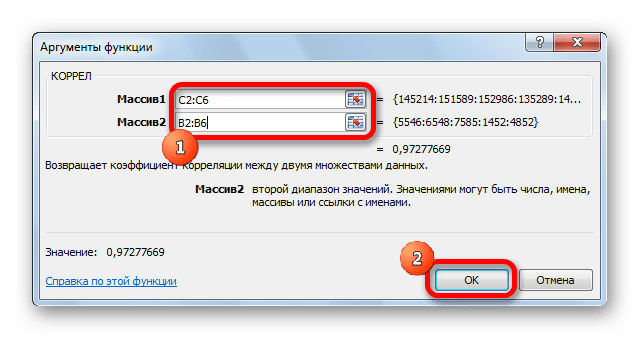
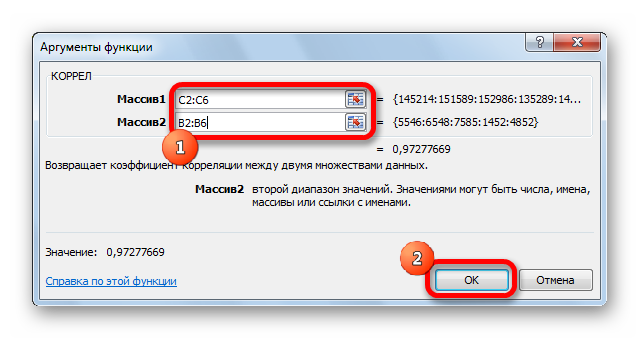
Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.
В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.

Жмем на кнопку «OK».

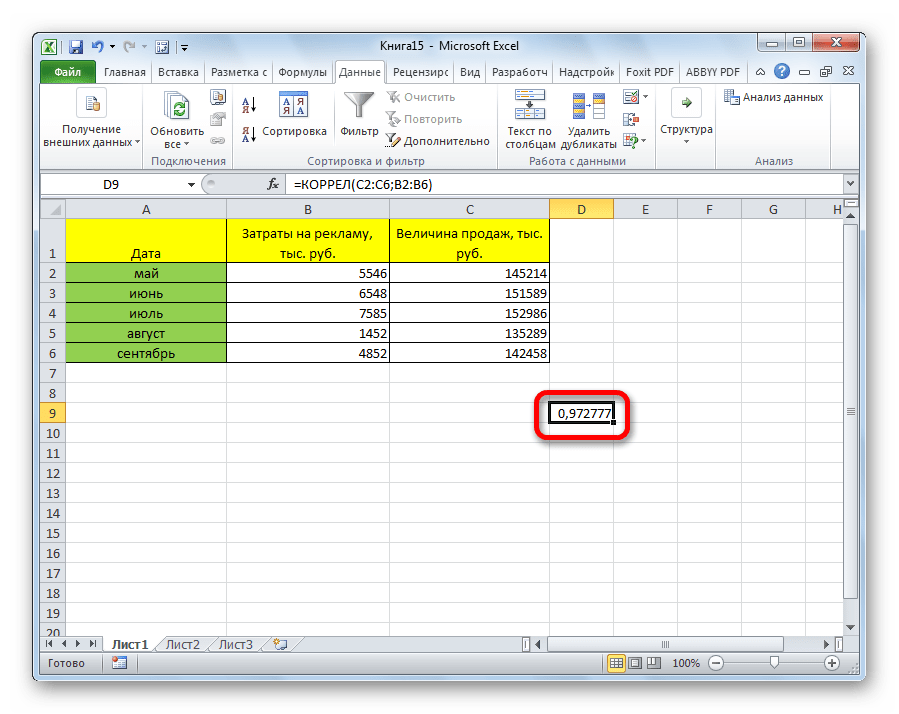
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.

Способ 2: вычисление корреляции с помощью пакета анализа

Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.

Переходим во вкладку «Файл».

В открывшемся окне перемещаемся в раздел «Параметры».

Далее переходим в пункт «Надстройки».

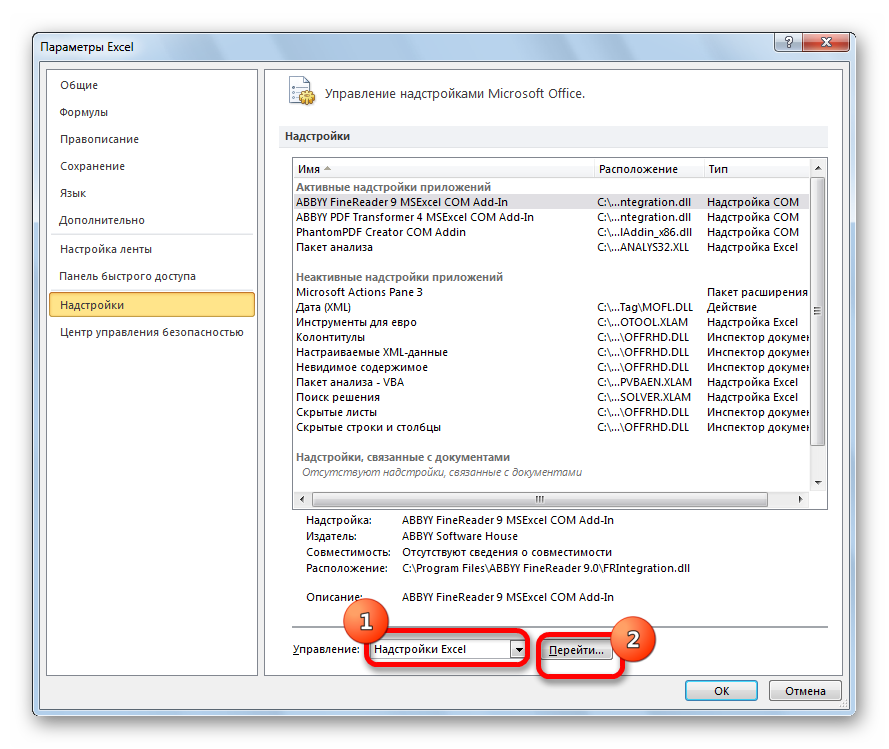
В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».

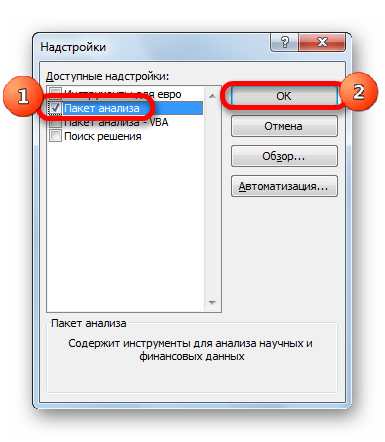
В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».

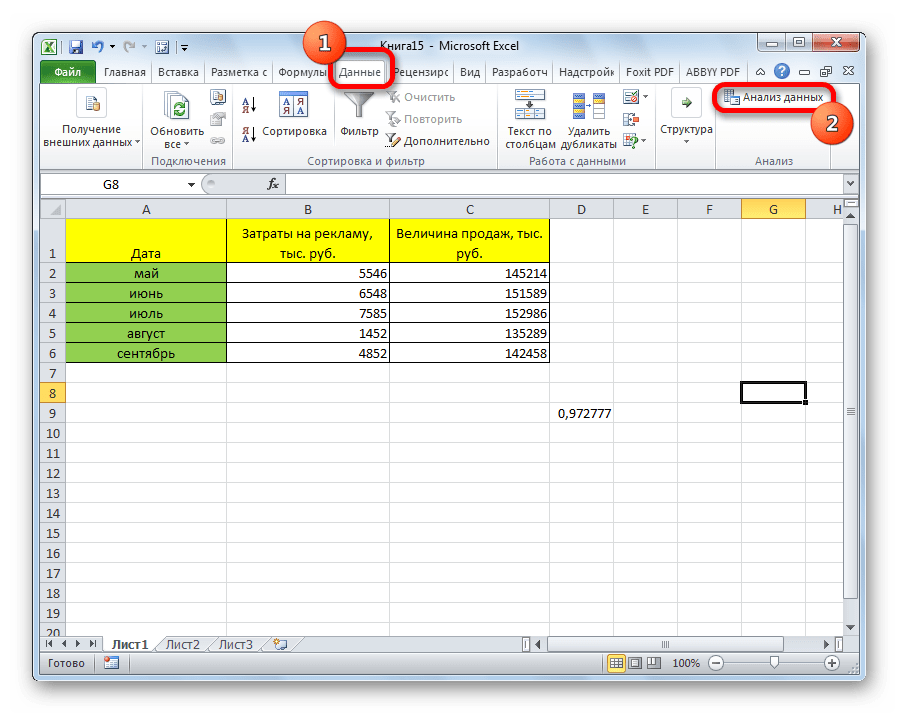
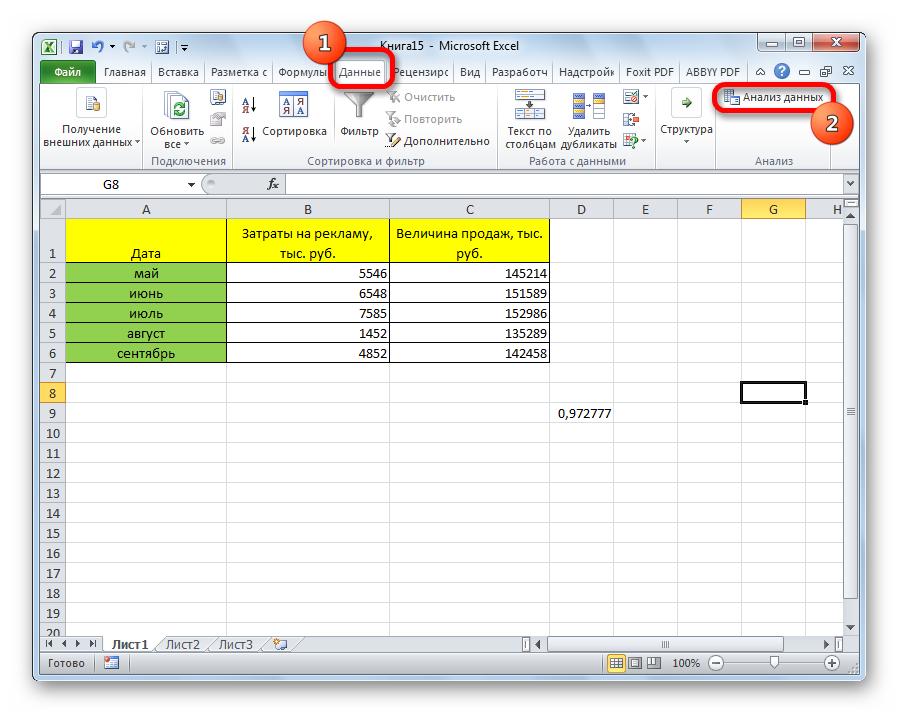
После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.

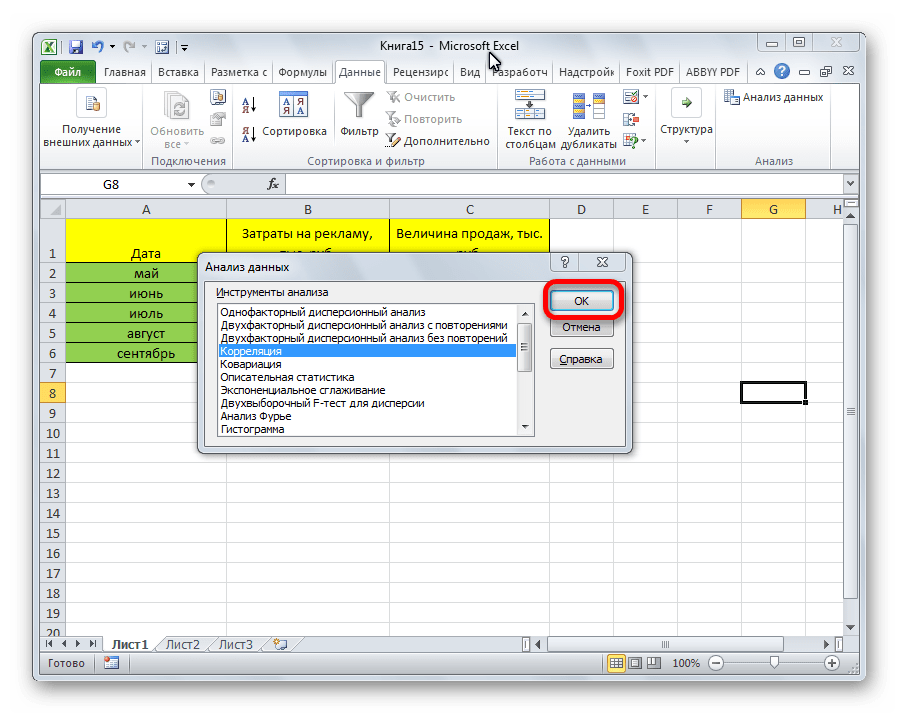
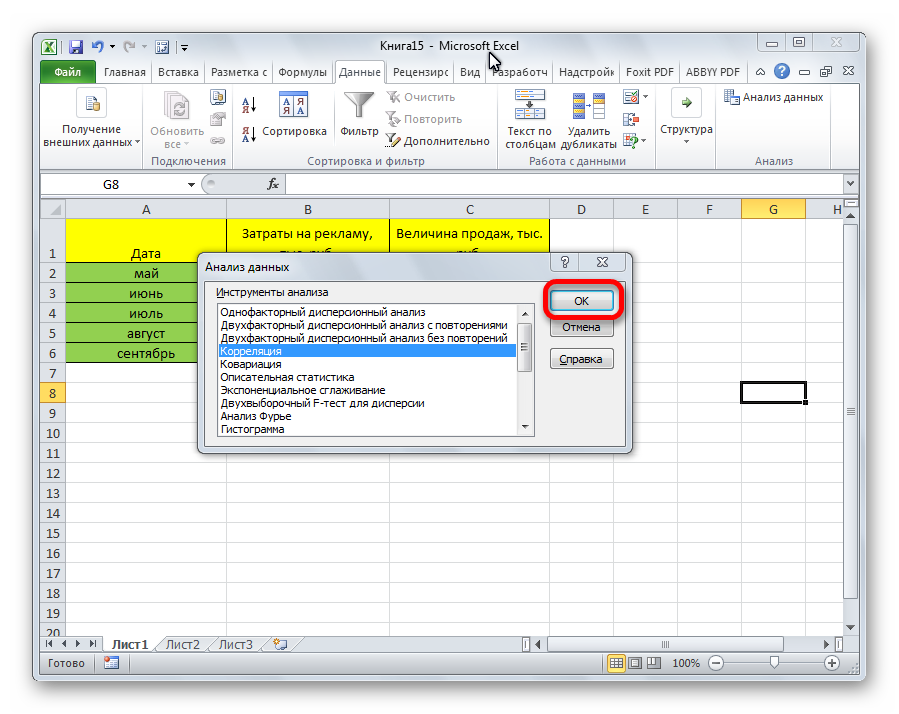
Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».

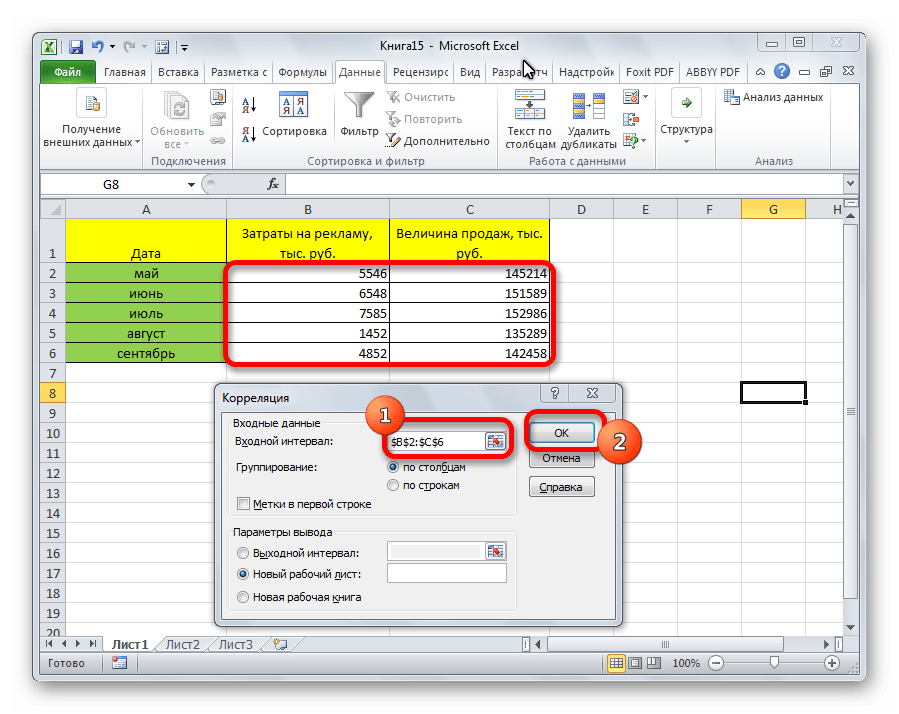
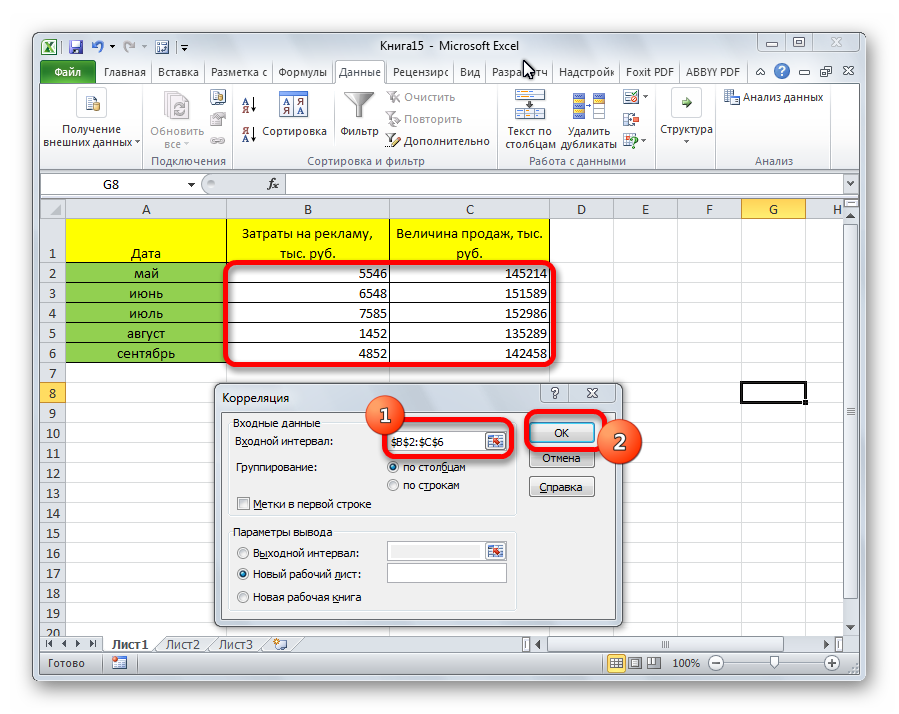
Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».
Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».

В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).

Когда все настройки установлены, жмем на кнопку «OK».

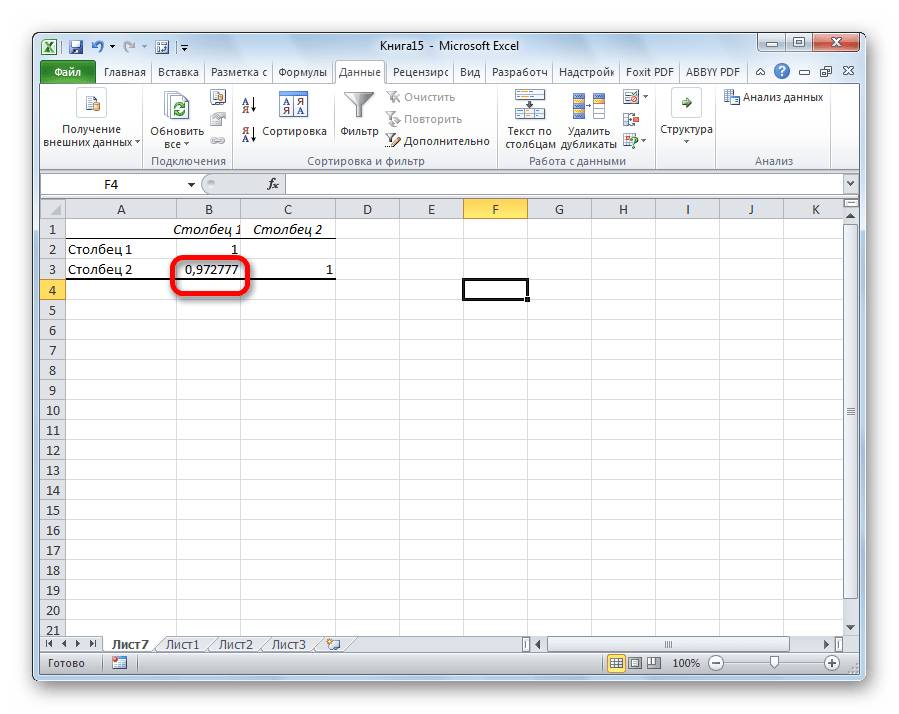
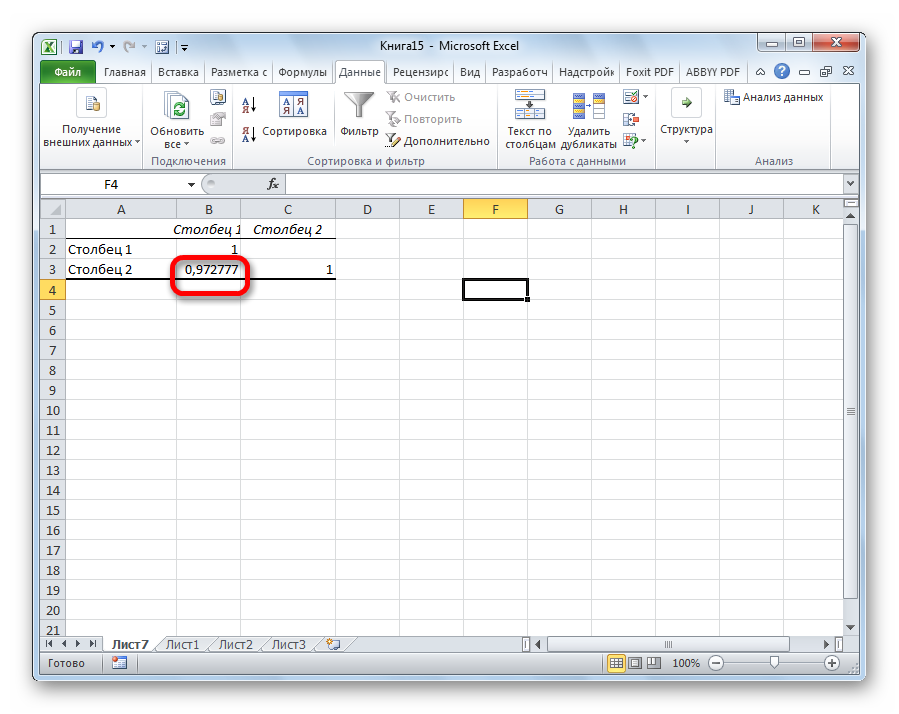
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.

Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.

Еще статьи по данной теме:

Помогла ли Вам статья?

Источник

Correlation basically means a mutual connection between two or more sets of data. In statistics bivariate data or two random variables are used to find the correlation between them. Correlation coefficient is generally the measurement of correlation between the bivariate data which basically denotes how much two random variables are correlated with each other.

If the correlation coefficient is 0, the bivariate data are not correlated with each other.

If the correlation coefficient is -1 or +1, the bivariate data are strongly correlated with each other.

r=-1 denotes strong negative relationship and r=1 denotes strong positive relationship.

In general, if the correlation coefficient is close to -1 or +1 then we can say that the bivariate data are strongly correlated to each other.

The correlation coefficient is calculated using Pearson’s Correlation Coefficient which is given by :

where,

r : Correlation coefficient
 : Values of the variable x.
 : Values of the variable y.
n : Number of samples taken in the data set.
Numerator : Covariance of x and y.
Denominator : Product of Standard Deviation of x and Standard Deviation of y.

In this article we are going to discuss how to make correlation charts in Excel using suitable examples.

Example 1 : Consider the following data set :

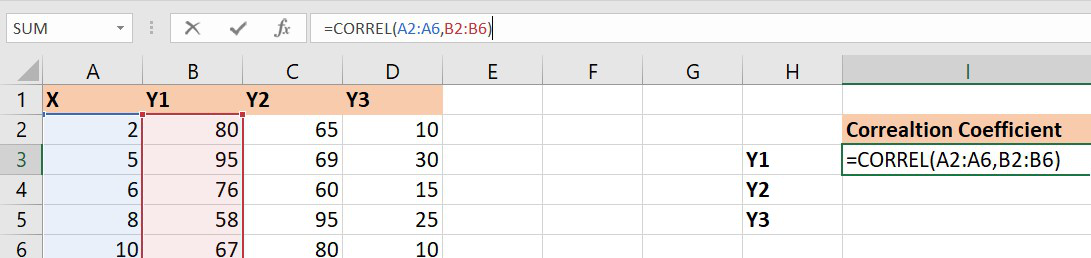
FINDING CORRELATION COEFFICIENT IN EXCEL

In Excel to find the correlation coefficient use the formula :

=CORREL(array1,array2)
array1 : array of variable x
array2: array of variable y

To insert array1 and array2 just select the cell range for both.

1. Let’s find the correlation coefficient for the variables and X and Y1.

array1 : Set of values of X. The cell range is from A2 to A6.

array2 : Set of values of Y1. The cell range is from B2 to B6.

Similarly, you can find the correlation coefficients for (X , Y2) and (X , Y3) using the Excel formula.

Finally, the correlation coefficients are as follows :

From the above table we can infer that :

X and Y1 has negative correlation coefficient.

X and Y2 has positive correlation coefficient.

X and Y3 are not correlated as the correlation coefficient is almost zero.

Correlation Chart in Excel:

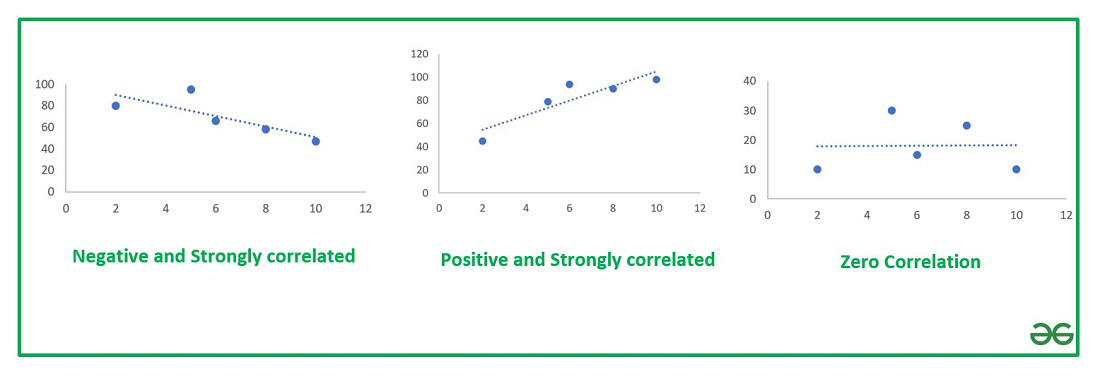
A scatter plot is mostly used for data analysis of bivariate data. The chart consists of two variables X and Y where one of them is independent and the second variable is dependent on the previous one. The chart is a pictorial representation of how these two data are correlated with each other. Three cases are possible on the basis of the value of the correlation coefficient, R as shown below :

Types of Correlation Chart

Example 2: Consider the following data set :

The correlation coefficients for the above data set are :

The steps to plot a correlation chart are :

Select the bivariate data X and Y in the Excel sheet.
Go to Insert tab on the top of the Excel window.
Select Insert Scatter or Bubble chart. A pop-down menu will appear.
Now select the Scatter chart.

Now, we need to add a linear trendline in the scatter plot to show the correlation between the bivariate data. In order to do so, select the chart and from the top right corner click on the “+” button and then check the box of Trendline.

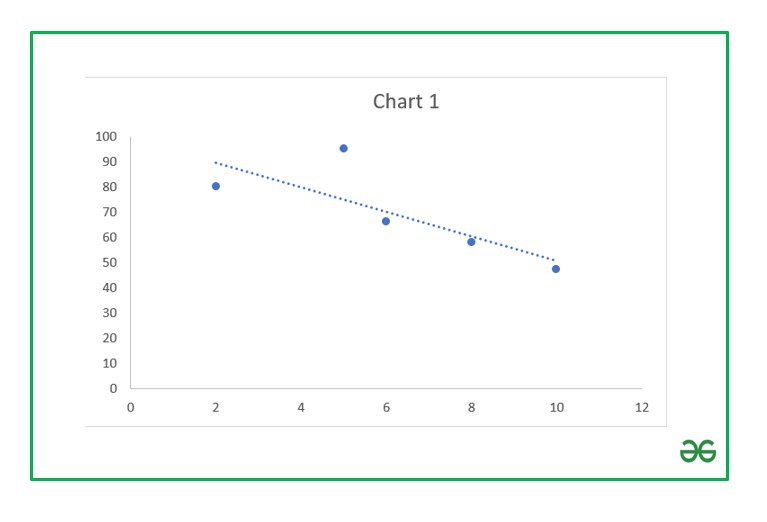
The trendline is now added and our correlation chart is now ready.

Negative relationship chart

Now you can format the Trendline by selecting and clicking on the “Format Trendline” option. A dialog box will open where you can change the type and color of the trendline and also show the value in the chart.

You can further format the above chart by making it more interactive by changing the “Chart Styles”, adding suitable “Axis Titles”, “Chart Title”, “Data Labels”, changing the “Chart Type” etc. It can be done using the “+” button in the top right corner of the Excel chart.

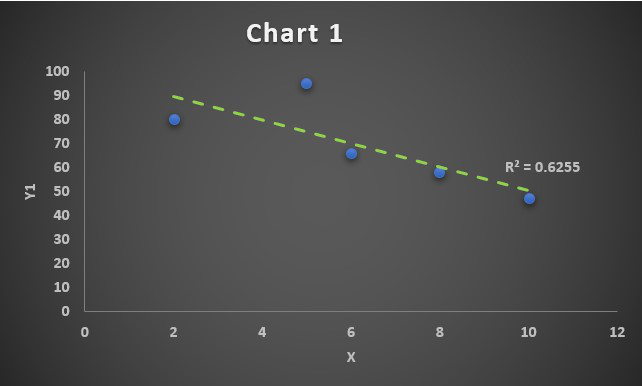
Finally, after all the modification the charts look like :

Correlation Chart 1

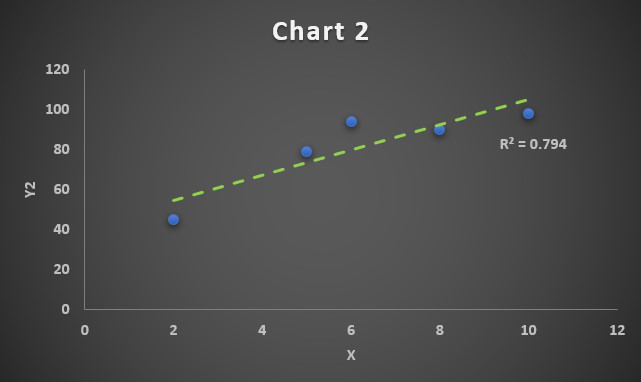
Since the correlation coefficient is R=-0.79, we have obtained a negative correlated chart. The linear trendline will grow downwards.

Correlation Chart 2

Since the correlation coefficient is R=0.89, we have obtained a positive correlated chart. The linear trendline will grow upwards.

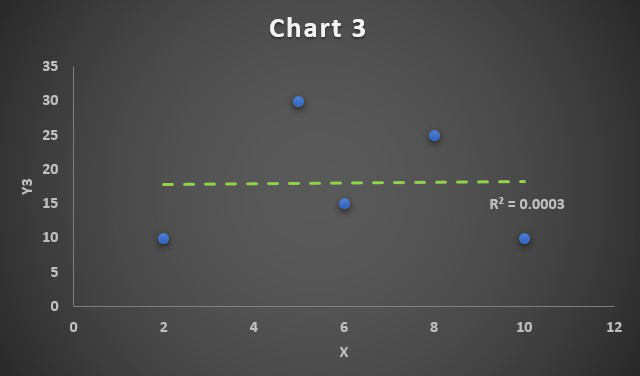
Correlation Chart 3

Since the correlation coefficient is R=0.01, which is approximately 0, so we have obtained a zero correlated chart. The linear trendline will be a straight line parallel to X-axis and it implies the bivariate data X and Y3 are not correlated to each other.

Источник

Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.

Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.

Регрессионный анализ в Excel

Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.

Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.

Регрессия бывает:

линейной (у = а + bx);
параболической (y = a + bx + cx²);
экспоненциальной (y = a * exp(bx));
степенной (y = a*x^b);
гиперболической (y = b/x + a);
логарифмической (y = b * 1n(x) + a);
показательной (y = a * b^x).

Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.

Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.

Модель линейной регрессии имеет следующий вид:

У = а₀ + а₁х₁ +…+а_кх_к.

Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.

В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).

В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».

Активируем мощный аналитический инструмент:

Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».

Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.

Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.

После активации надстройка будет доступна на вкладке «Данные».

Теперь займемся непосредственно регрессионным анализом.

Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».

Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.

После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).

В первую очередь обращаем внимание на R-квадрат и коэффициенты.

R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».

Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.

Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.

Корреляционный анализ в Excel

Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.

Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.

Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.

Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.

Для нахождения парных коэффициентов применяется функция КОРРЕЛ.

Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.

Ставим курсор в любую ячейку и нажимаем кнопку fx.

В категории «Статистические» выбираем функцию КОРРЕЛ.
Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
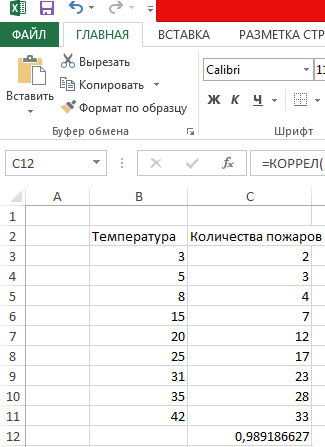
Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.

Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).

Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.

Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:

Корреляционно-регрессионный анализ

На практике эти две методики часто применяются вместе.

Пример:

Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.

Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».

Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».

Жмем «Закрыть».

Теперь стали видны и данные регрессионного анализа.

Источник

Excel – это эффективный инструмент для статистической обработки данных. И определение корреляций является очень важной составляющей этого процесса. Программа имеет весь необходимый инструментарий для осуществления расчетов такого плана. Сегодня мы более детально разберемся, что нам нужно для осуществления анализа этого типа.

Содержание

Что представляет собой корреляционный анализ
Корреляционный анализ в Excel — 2 способа
Как рассчитать коэффициент корреляции
Способ 1. Определение корреляции с помощью Мастера Функций
Способ 2. Вычисление корреляции с помощью пакета анализа
Как построить поле корреляции в Excel
Диаграмма рассеивания. Поле корреляции

Что представляет собой корреляционный анализ

Простыми словами, корреляция – это связь между двумя явлениями. В свою очередь, под корреляционным анализом подразумевают выявление этой связи. Очень частое утверждение гласит, что корреляция – это зависимость между разными объектами, но на деле это неточное определение. Ведь существует множество изображений, которые показывают связь между явлениями, которые никак не могут быть зависимы друг от друга или одного третьего фактора, который влияет на них.

Для определения зависимости используется другой тип анализа, который называется регрессионным.

Величина, определяющая степень выраженности взаимосвязи, называется коэффициентом корреляции. Это единственная величина, которая рассчитывается корреляционным анализом по сравнению с регрессионным. Возможные вариации коэффициента корреляции могут быть в пределах от -1 до 1. Если это число положительное, взаимосвязь между динамикой изменения значений прямая. Если же отрицательное, то увеличение числа 1 приводит к аналогичному уменьшению числа 2. Если число меньше единицы по модулю, то корреляция неполная. Например, увеличение числа 1 на единицу приводит к увеличению числа 2 на 0,5. В таком случае коэффициент корреляции составляет 0,5. Если же коэффициент корреляции составляет 0, то взаимосвязи между двумя переменными нет.

Интересный факт: корреляции делятся на истинные и ложные. То есть, иногда то, что графики идут в одинаковом направлении, может быть чистой случайностью, а не закономерным следствием воздействия одной переменной на другую или влияния общего фактора на обе переменные. В узких кругах довольно популярны картинки, где коррелируют между собой абсолютно не связанные явления. Вот некоторые примеры:

Количество человек, которые стали утопленниками в бассейнах, четко коррелирует с количеством фильмов, в которых Николас Кейдж был актером.
Количество съеденной моцареллы и количество человек, которые получили докторскую степень, также коррелирует на протяжении 2000-2009 годов. Наверно, действительно, моцарелла как-то влияет на мозг и стимулирует желание совершать научные открытия.
Почти во всех случаях средний возраст женщин, которые получили статус «Мисс Америка» коррелирует с количеством людей, которые погибли от нахождения в горячем паре.
Число людей, которое погибло в результате дорожно-транспортного происшествия, четко коррелирует с количеством сметаны, которое съедают люди.
Мало кто знает, что чем больше курятины человек ест, тем больше сырой нефти импортируется в мире. Правда, это тоже пример ложной корреляции. Кстати, импорт сырой нефти родом из Норвегии тесно связано с количеством людей, которые погибли в результате столкновения автомобиля с поездом. Причем в этом случае корреляция почти 100 процентов.
А еще маргарин негативно влияет на статистику разводов. Чем больше людей, которые проживали в штате Мэн, потребляли маргарина, тем выше была частота разводов. Правда, здесь еще может быть рациональное зерно. Ведь частота потребления маргарина имеет обратную корреляцию с экономическим положением в семье. В свою очередь, плохое экономическое положение в семье имеет непосредственную связь с количеством разводов. И это уже доказано научно. Так что кто знает, может, эта корреляция и не является такой ложной. Правда, никто этого не перепроверял.
Количество денег, которое правительство США тратит на развитие науки, космоса и технологий, имеет тесную связь с количеством самоубийств, проведенных в форме повешения или удушения.

Ну и наконец, еще один пример ложной корреляции – чем больше сыра люди едят, тем больше людей умирает из-за того, что они запутываются в своих простынях.

Поэтому несмотря на то, что корреляция является эффективным статистическим инструментом, нужно учиться отфильтровывать истинные взаимосвязи между явлениями и ложные. Иначе исследование может получить такие интересные результаты. А теперь переходим непосредственно к тому, как проводить корреляционный анализ в Excel.

Корреляционный анализ в Excel — 2 способа

Вычисление коэффициента корреляции осуществляется двумя способами. Первый – это использование Мастера функций, который позволяет ввести формулу КОРРЕЛ. Второй инструмент – это пакет анализа, требующий отдельной активации.

Как рассчитать коэффициент корреляции

Давайте продемонстрируем механизм получения коэффициента корреляции на реальном кейсе. Допустим, у нас есть таблица с информацией о суммах продаж и рекламу. Нам нужно понять, в какой степени количество продаж и количество денег, которые были использованы на продвижение, взаимосвязаны.

Способ 1. Определение корреляции с помощью Мастера Функций

Функция КОРРЕЛ – один из самых простых методов, как можно реализовать поставленную задачу. В своем общем виде этот оператор имеет следующий вид: КОРРЕЛ(массив1;массив2). Как же ее ввести? Для этого нужно осуществлять следующие действия:

С помощью левой кнопки мыши выделяем ту ячейку, в которой будет находиться получившийся коэффициент корреляции. После этого находим слева от строки формул кнопку fx, которая откроет инструмент ввода функций.
Далее выбираем категорию «Полный алфавитный перечень», в котором ищем функцию КОРРЕЛ. Как видно из названия категории, все названия функций располагаются в алфавитном порядке.
Далее открывается окно ввода параметров функции. У нас два основных аргумента, каждый из которых являет собой массив данных, которые сравниваются между собой. В поле «Массив 1» указываем координаты первого диапазона, а в поле «Массив 2» – адрес второго диапазона. Для ввода данных массива, используемого для расчета, достаточно выделить нажать левой кнопкой мыши по соответствующему полю и выделить правильный диапазон.
После того, как мы введем данные в аргументы, нажимаем кнопку «ОК», чем подтверждаем совершенные действия.

После выполнения описанных выше шагов мы видим в ячейке, выбранной нами на первом этапе, коэффициент корреляции. В нашем примере он составляет 0,97, что указывает на очень сильно выраженную взаимосвязь между данными двух диапазонов.

Способ 2. Вычисление корреляции с помощью пакета анализа

Также довольно неплохой инструмент для определения корреляции между двумя диапазонами – пакет анализа. Но перед тем, как его использовать, нам надо его включить. Для этого выполняем следующие действия:

Нажимаем на кнопку «Файл», которая находится в левом верхнем углу сразу возле вкладки «Главная».
После этого открываем раздел с настройками.
В меню слева переходим в предпоследний пункт, озаглавленный, как «Надстройки». Делаем левый клик по соответствующей надписи.
Открывается окно управления надстройками. Нам нужно переключить поле ввода, находящееся внизу, на пункт «Надстройки Excel» и нажать на «Перейти». Если это поле уже находится в таком положении, то не выполняем никаких изменений.
Затем включаем пакет анализа в настройках. Для этого ставим соответствующую галочку и нажимаем на кнопку «ОК».

Все, теперь наша надстройка включена. Теперь мы во вкладке «Данные» можем увидеть кнопку «Анализ данных». Если она появилась, то мы все сделали правильно. Нажимаем на нее.

Появляется перечень с выбором разных способов анализа информации. Нам следует выбрать пункт «Корреляция» и нажать на «ОК».

Затем нам нужно ввести настройки. Основное отличие этого метода от предыдущего заключается в том, что нам нужно вводить полностью диапазон, а не разрывать его на две части. В нашем случае, это информация, указанная в двух столбцах «Затраты на рекламу» и «Величина продаж».

Не вносим никаких изменений в параметр «Группирование». По умолчанию выставлен пункт «По столбцам», и он правильный. Эта настройка определяет, каким образом программа будет разбивать данные. Если же наши данные были бы представлены в двух рядах, то надо было бы изменить этот пункт на «По строкам».

В настройках вывода уже стоит пункт «Новый рабочий лист». То есть, информация о корреляции будет располагаться на отдельном листе. Пользователь может настроить место самостоятельно с помощью соответствующего переключателя – на текущий лист или в отдельный файл. Проверяем, все ли настройки были введены правильно. Если да, подтверждаем свои действия нажатием на клавишу «ОК».

Поскольку мы оставили поле с данными о том, куда будут выводиться результаты, таким, каким оно было, мы переходим на новый лист. На нем можно найти коэффициент корреляции. Конечно, он такой же самый, как был в предыдущем методе – 0,97. Причина этого в том, что вычисления производятся одинаковые, исходные данные мы также не меняли. Просто разными методами, но не более.

Таким образом, Эксель дает сразу два метода осуществления корреляционного анализа. Как вы уже понимаете, в результате вычислений итог получится таким же. Но каждый пользователь может выбрать тот метод расчета, который ему больше всего подходит.

Как построить поле корреляции в Excel

Итак, давайте теперь разберемся, как построить поле корреляции. Для начала нужно разобраться, что это вообще такое. Под корреляционным полем подразумевается фактически график корреляции. Главное требование к такой диаграмме – каждая точка должна соответствовать единице совокупности. Поле корреляции поможет установить более глубокие связи и проанализировать данные более качественно. Для начала нам нужно найти коэффициент корреляции между двумя диапазонами, используя функцию КОРРЕЛ.

После того, как мы это сделали, мы теперь можем сделать поле корреляции. Для этого выполняем следующие действия:

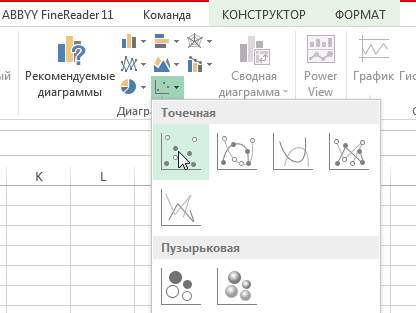
Переходим во вкладку «Вставка» и там находим вариант диаграммы «точечный график».
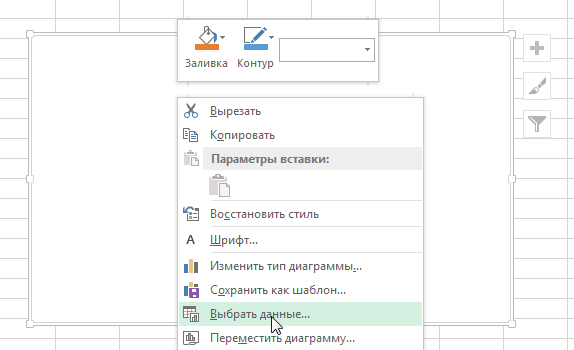
После того, как мы его добавили, нажимаем по будущему полю корреляции правой кнопкой мыши и вызываем контекстное меню. Далее нажимаем на «Выбрать данные».
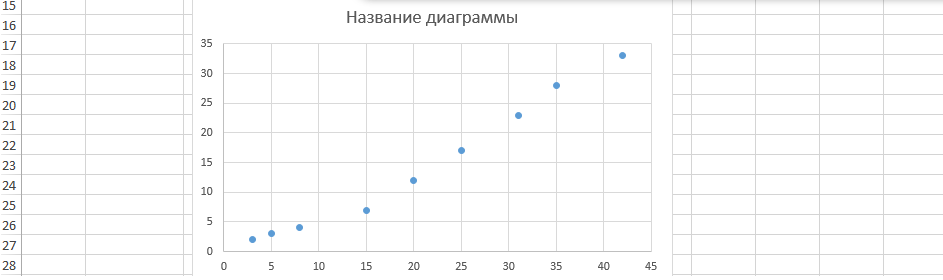
Далее выбираем наш диапазон в качестве источника данных. После этого подтверждаем свои действия нажатием клавиши ОК. Все остальные действия программа выполнит самостоятельно.

Этот график можно построить не только на основе корреляции, определенной через функцию КОРРЕЛ.

Диаграмма рассеивания. Поле корреляции

До сих пор часть пользователей сидит на старой версии Word. Как построить корреляционное поле в этом случае? Для этого существует специальный инструмент, который называется мастером диаграмм. Найти его можно на панели инструментов по специфическому изображению диаграммы. Если навести на эту иконку мышкой, то появится всплывающая подсказка, которая поможет нам убедиться в том, что это действительно мастер диаграмм.

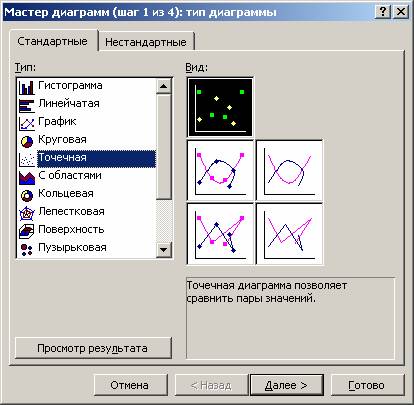
После этого появится диалоговое окно, в котором нам надо выбрать точечный тип диаграммы. Видим, что логика действий в старых версиях офисного пакета в целом остается той же самой, просто немного другой интерфейс. Немного правее мы можем увидеть, как будет выглядеть точечная диаграмма и выбрать подходящий вид, а также прочитать описание этого типа диаграммы. После этого нажимаем на кнопку «Далее».

Затем выбираем диапазон данных, и наша линия появляется. После этого можно добавить линию регрессии к графику. Для этого необходимо сделать клик правой кнопкой мыши по одной из точек и в появившемся перечне найти «Добавить линию тренда» и сделать клик по этому пункту.

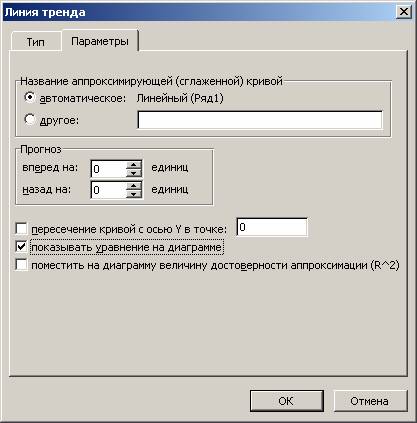
Далее выставляем настройки. Нас интересует тип «Линейная», а в окне параметров нужно поставить флажок «Показывать уравнение на диаграмме».

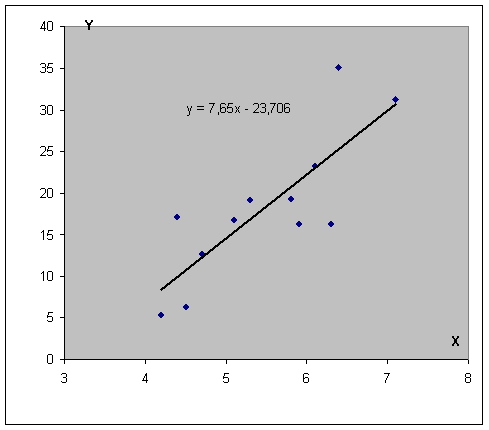
После подтверждения действий у нас появится что-то типа такого графика.

Как видим, возможных вариантов построения может быть огромное количество.

Оцените качество статьи. Нам важно ваше мнение:

Источник

2 способа корреляционного анализа в Microsoft Excel

Суть корреляционного анализа

Расчет коэффициента корреляции

Способ 1: определение корреляции через Мастер функций

«Вставить функцию»

Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.

В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.

Способ 2: вычисление корреляции с помощью пакета анализа

«Файл»

В открывшемся окне перемещаемся в раздел «Параметры».

Далее переходим в пункт «Надстройки».

В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».

В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».

После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.

Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».

Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».

Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».

В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).

Когда все настройки установлены, жмем на кнопку «OK».

Отблагодарите автора, поделитесь статьей в социальных сетях.

Корреляционно-регрессионный анализ в Excel: инструкция выполнения

Регрессионный анализ в Excel

линейной (у = а + bx);
параболической (y = a + bx + cx 2 );
экспоненциальной (y = a * exp(bx));
степенной (y = a*x^b);
гиперболической (y = b/x + a);
логарифмической (y = b * 1n(x) + a);
показательной (y = a * b^x).

Модель линейной регрессии имеет следующий вид:

Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.

Активируем мощный аналитический инструмент:

Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.

После активации надстройка будет доступна на вкладке «Данные».

Теперь займемся непосредственно регрессионным анализом.

Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).

В первую очередь обращаем внимание на R-квадрат и коэффициенты.

Корреляционный анализ в Excel

Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.

Для нахождения парных коэффициентов применяется функция КОРРЕЛ.

Ставим курсор в любую ячейку и нажимаем кнопку fx.

В категории «Статистические» выбираем функцию КОРРЕЛ.
Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.

Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:

Корреляционно-регрессионный анализ

На практике эти две методики часто применяются вместе.

Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
Жмем «Закрыть».

Теперь стали видны и данные регрессионного анализа.

Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel

По территориям региона приводятся данные за 200Х г.

1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.

2. Рассчитайте параметры уравнения линейной регрессии

3. Оцените тесноту связи с помощью показателей корреляции и детерминации.

4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.

5. Оцените с помощью средней ошибки аппроксимации качество уравнений.

6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.

7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости .

8. Оцените полученные результаты, выводы оформите в аналитической записке.

Решим данную задачу с помощью Excel.

1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.

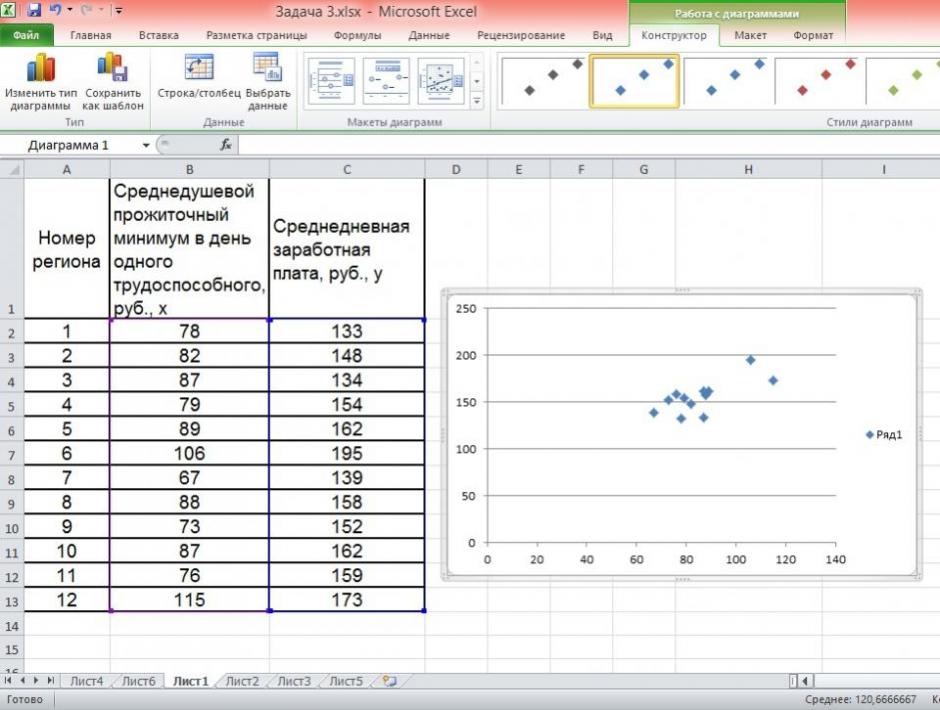
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.

Выделите область ячеек, содержащую данные.

Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.

Рисунок 1 Построение поля корреляции

Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.

2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.

1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
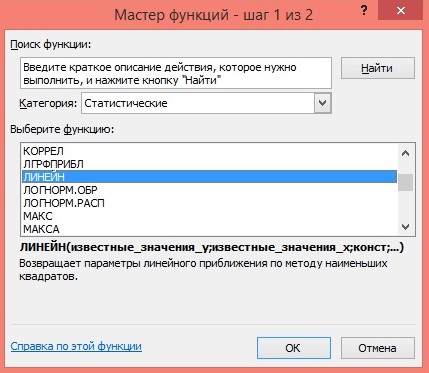
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;

Рисунок 2 Диалоговое окно «Мастер функций»

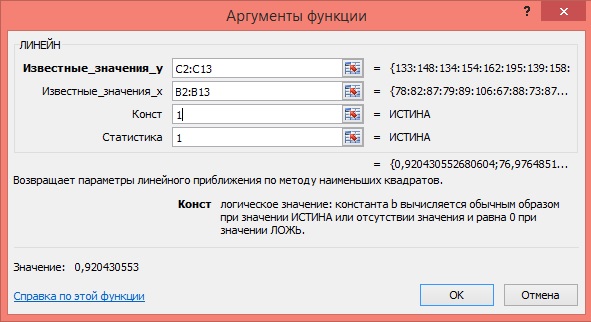
5) Заполните аргументы функции:

Известные значения у – диапазон, содержащий данные результативного признака;

Известные значения х – диапазон, содержащий данные факторного признака;

Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;

Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.

Щёлкните по кнопке ОК;

Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН

6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу , а затем на комбинацию клавиш + + .

Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:

Основы регрессионного анализа для инвесторов. Построение модели в Excel

Представляем вашему вниманию статистический метод расчета справедливой стоимости акций. Речь идет о регрессионном анализе. Незаменимую помощь в процессе исследования окажет обычный Excel.

Что такое регрессия

Регрессионный анализ является статистическим методом исследования. Он позволяет оценить зависимость одной (зависимой) переменной от других (независимых) переменных. Самой простой является линейная регрессия. Ее формула такова:

Y = a0 + a1x1 + … + anxn

где Y — зависимая переменная,
x — независимые переменные, влияющие на нее,
a — коэффициенты регрессии.

Зависимой переменной может выступать цена актива. Возможные влияющие факторы — цены других активов, финансовые и макропоказатели и т.д. В нашем случае считать будем теоретическую (расчетную) условно справедливую стоимость акций, зависящую от цен на другие активы.

Важно, чтобы независимых переменных было не слишком мало, но и не слишком много. Влияющие переменные стоит отбирать из экономических соображений, руководствуясь здравым смыслом. В идеале их нужно тестировать на мультиколлинеарность и т.д., но наш обзор посвящен базовым принципам регрессионного анализа. Статистическую значимость модели поможет оценить показатель R2 (R — квадрат), о нем речь пойдет дальше.

Если фактическая цена бумаги заметно отклоняется от расчетной, появляется повод для дополнительного анализа. Стоит также смотреть на техническую картину, мультипликаторы, общерыночную ситуацию. Существуют также методы финансового моделирования, носящие фундаментальный подход, в частности, модели дисконтирования денежных потоков (DCF) и модели дисконтирования дивидендов (DDM).

Пример расчетов в Excel и выводы

В качестве примера возьмем акции американского нефтегазового гиганта Exxon Mobil (XOM). Модель будет упрощенной и учебной и не является рекомендацией для осуществления операций с бумагами, ситуацию нужно смотреть в комплексе.

Независимыми переменными у нас выступят фьючерсы на американскую нефть WTI (склеенные фронтальные контракты) и индекс S&P 500. Логика проста — бизнес компании зависит от цен на нефть, а поведение акций в теории должно быть связано в общерыночной ситуацией.

Шаг 1. Выкачиваем в Excel котировки XOM, SPX и CL1. Данные возьмем за пять лет. Так как на более длительных периодах наблюдалась разная структурная ситуация на нефтяном рынке. Возьмем статистику в недельной разбивке, будет 262 наблюдения.

Шаг 2. Активируем настройку регрессионного анализа. Открываем раздел Файл. Переходим на вкладку Параметры Excel — Надстройки. Внизу появившегося окна будет вкладка Управление, где стоит параметр Надстройки Excel, жмем — Перейти.

Выбираем опцию Пакет анализа.

Готово. Результат появится в разделе Данные — Анализ данных.

Шаг 3. Строим регрессию. При клике на Анализ данных появится меню с опциями функционала для анализа. Выбираем Регрессия.

Заполняем окна по аналогии со схемой, используя ранее выгруженные данные по активам.

На выходе получаем вот такие данные.

Шаг 4. Интерпретация. Статистических показателей много. Не вдаваясь в теорию, наиболее интересными являются значения коэффициентов регрессии и показатель R2.

Наша модель будет иметь следующий вид:

Цена акций Exxon Mobil = $96,2 + 0,28*WTI — 0,01*S&P 500

R — квадрат равен 0,61. Показатель показывает, насколько значение зависимой переменной определяется значениями независимых переменных. Речь идет о статистической значимости модели. Модель является очень хорошей, если R2 превышает 0,8, и при этом сама модель имеет экономическое обоснование. В нашем случае все не настолько идеально, но все же выше 0,5, поэтому модель можно использовать.

Отмечу, что в процессе подготовки материала делались расчеты не только за пять лет, но и за 10, и за три года, также WTI заменялась на Brent. Итоговый вариант был выбран в связи с наибольшим значением R2.

Шаг 5. Применение. Рассчитаем в Excel теоретические значения акций Exxon за весь использовавшийся для построения модели период (5 лет).

Построим линейную диаграмму, на которой будут представлены динамика фактической цены и расчетной цены акций. Заметно, что расхождения между двумя величинами редко носили слишком серьезный характер. По состоянию на 06.06.2019 фактическая цена акций составила $74,2, а теоретическая — $76,7. Исходя из этого, критерия бумаги вполне справедливо оценены рынком. Однако это только один, причем упрощенный подход. Ситуацию нужно рассматривать в комплексе. К примеру, медианный таргет аналитиков на 12 месяцев равен $84. Это усредненный показатель результатов моделей фундаментальной оценки, предполагающий заметный потенциал роста.

Корреляционный анализ

Дополним нашу регрессию корреляционным анализом. Корреляция означает зависимость одного показателя от другого. Коэффициент корреляции — показатель взаимосвязи (в нашем случае финансовых активов).

Строим корреляционную матрицу. В том же разделе Анализ данных выбираем опцию Корреляция. Заполняем окно, как показано ниже, с учетом котировок наших активов.

На выходе получаем корреляционную матрицу. На ней видно, что цена Exxon положительно связана с WTI (коэффициент корреляции = 0,55) и отрицательно зависит от динамики индекса S&P 500 (коэффициент корреляции = -0,48).

Так что Exxon — это преимущественно нефтяная история, зачастую не совпадающая по динамике с широким рынком. Это можно заметить на графике трех активов с 2010 г. Ситуация стала такой с 2014 г., когда рынок нефти обвалился из-за структурных сдвигов. На нашей выборке за 5 лет корреляция между WTI и S&P 500 равна 0,13, то есть несущественна.

Построение графика простой регрессии

Расскажем об еще одном регрессионном функционале Excel. Программа позволяет построить график линейной регрессии. Правда доступно это лишь при наличии одной независимой переменной. В нашем случае ею будет нефть, так как она в большей мере объясняет движения акций Exxon — коэффициент регрессии равен 0,28 против (-0,01) у S&P 500.

Строим точечную диаграмму по XOM и WTI за 5 лет. Получаем поле корреляции. Щелкаем по любой из точек на диаграмме и меню левой кнопки мыши выбираем Добавить линию тренда.

В окне выбираем линейную линию тренда, ставим галочки напротив Показывать уравнение и Поместить на диаграмму R2.

В итоге получим такую схему зависимости Exxon (y) от WTI (x). В нашем случае модель не является статистически значимой — R-квадрат равен лишь 0,3.

Как еще использовать корреляционно-регрессионный анализ

В архивах раздела Обучение БКС Экспресс есть материалы на эту тему.

Отмечу, что наш материал носил ознакомительный характер. В регрессионные модели можно вносить макроэкономические, финансовые и прочие показатели. В идеале, независимые переменные нужно тестировать на ряд факторов. Наш обзор — это пример «мгновенной и грубой» оценки. В любом случае, выводы, полученные в результате регрессионного моделирования, стоит комбинировать с другими подходами к инвестиционному анализу.

БКС Брокер

пополни брокерский счёт без комиссии

С карты любого банка
Прямо на сайте
Без комиссии

Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel

По территориям региона приводятся данные за 200Х г.

1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.

2. Рассчитайте параметры уравнения линейной регрессии

3. Оцените тесноту связи с помощью показателей корреляции и детерминации.

5. Оцените с помощью средней ошибки аппроксимации качество уравнений.

6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.

8. Оцените полученные результаты, выводы оформите в аналитической записке.

Решим данную задачу с помощью Excel.

Выделите область ячеек, содержащую данные.

Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.

Рисунок 1 Построение поля корреляции

Рисунок 2 Диалоговое окно «Мастер функций»

5) Заполните аргументы функции:

Известные значения у – диапазон, содержащий данные результативного признака;

Известные значения х – диапазон, содержащий данные факторного признака;

Щёлкните по кнопке ОК;

Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН

Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:

Источник

Суть корреляционного анализа

Расчет коэффициента корреляции

Способ 1: определение корреляции через Мастер функций

Способ 2: вычисление корреляции с помощью пакета анализа

Еще статьи по данной теме:

Помогла ли Вам статья?

FINDING CORRELATION COEFFICIENT IN EXCEL

Correlation Chart in Excel:

Регрессионный анализ в Excel

Корреляционный анализ в Excel

Корреляционно-регрессионный анализ

Что представляет собой корреляционный анализ

Корреляционный анализ в Excel — 2 способа

Как рассчитать коэффициент корреляции

Способ 1. Определение корреляции с помощью Мастера Функций

Способ 2. Вычисление корреляции с помощью пакета анализа

Как построить поле корреляции в Excel

Диаграмма рассеивания. Поле корреляции

2 способа корреляционного анализа в Microsoft Excel

Суть корреляционного анализа

Расчет коэффициента корреляции

Способ 1: определение корреляции через Мастер функций

Способ 2: вычисление корреляции с помощью пакета анализа

Корреляционно-регрессионный анализ в Excel: инструкция выполнения

Регрессионный анализ в Excel

Корреляционный анализ в Excel

Корреляционно-регрессионный анализ

Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel

Основы регрессионного анализа для инвесторов. Построение модели в Excel

пополни брокерский счёт без комиссии

Последние новости

Рекомендованные новости

Итоги торгов. Возобновили опережающие темпы роста, несмотря на санкционные риски

Система объявила о продаже доли в Детском Мире

Топ 5 самых популярных ETF

Крупнейший фондовый рынок Азии терпит бедствие

Все указывает на продолжение коррекции на следующей неделе

Ставки по депозитам в России опустились ниже 6,2%

Рынок США. ФРС перестраховывается

Несмотря на снижение нефти, рубль укрепляется на фоне роста ОФЗ и развивающихся валют

Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel