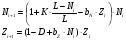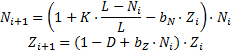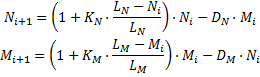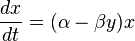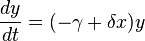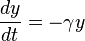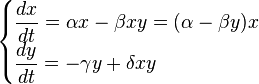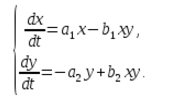Модель хищникжертва
|
Единственный в мире Музей Смайликов |
|
Подборка по базе: структурная модель программы развития (2).doc, “3D модельдеу программалары9.docx, Курсы нысандарды байыпты модельдеуге (1).docx, Доскин 2МСиСПРсН заоч. Модель семейного равенства.docx, Отчет ПЗ 4.1 Модель угроз безопасности ПДн (2022) КОНЕВЕЦ .docx, эмблема модельер.docx, Практическая работа № 2 «Региональная модель методического сопро, Бизнес модель социальное предпринимательство.pdf, Бюрократическая модель организации Макса Вебера.docx, ОТКРЫТАЯ СИСТЕМА и МОДЕЛЬ OSI.doc
-
Модель «хищник-жертва»
Для выполнения работы откройте файл-заготовку ХищникЖертва.xls.
Выполните моделирование биологической системы «щуки-караси»
где 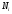
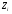
при следующих значениях параметров:
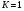
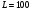
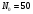
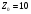
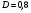
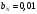
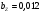
Постройте на одном поле графики изменения численности карасей и щук в течение 30 периодов моделирования.
Ответьте на следующие вопросы:
-
Сколько карасей и щук живут в водоеме в состоянии равновесия?
Ответ:
N=100 Z=100
-
Что влияет на количество рыб в состоянии равновесия: начальная численность хищников и жертв или значения коэффициентов модели?
Ответ:
Значения коэффициентов модели
-
На что влияет начальная численность хищников и жертв?
Ответ:
На количество периодов требующихся для накопления L
- Подберите значения коэффициентов, при которых модель становится неадекватна.
Ответ:
- Подберите значения коэффициентов, при которых щуки вымирают, а численность карасей достигает предельно возможного значения. Как вы можете объяснить это с точки зрения биологии?
Ответ:
Замуление водоема
Глава 2.
Моделирование
Практические работы
Практическая работа № 6.
Моделирование работы процессора
1.
Напишите программу, которая моделирует работу процессора. Процессор
имеет 4 регистра, они обозначаются R0, R1, R2 и R3. Все команды состоят из трех
десятичных цифр: код операции, номер первого регистра и номер второго регистра
(или число от 0 до 9). Коды команд и примеры их использования приведены в
таблице:
|
Код |
Описание |
Пример |
Псевдокод |
|
1 |
запись |
128 |
R2 := |
|
2 |
копирование |
203 |
R3 := R0 |
|
3 |
сложение |
331 |
R1 := |
|
4 |
вычитание |
431 |
R1 := R1 – |
Обратите внимание,
что результат записывается во второй регистр. Команды вводятся
последовательно как символьные строки. После ввода каждой строки программа
показывает значения всех регистров.
2.
*Добавьте в систему команд умножение, деление и логические операции c
регистрами – «И», «ИЛИ», «исключающее ИЛИ».
3.
*Добавьте в систему команд логическую операцию «НЕ». Подумайте, как
можно использовать второй регистр.
4.
*Сделайте так, чтобы в команде с кодом 1 можно было использовать
шестнадцатеричные значения констант (0-9, A-F).
5.
Добавьте обработку ошибок типа «неверная команда», «неверный номер
регистра», «деление на ноль».
6.
*Добавьте команду «СТОП», которая прекращает работу программы. Введите
строковый массив, моделирующий память, и запишите в него программу –
последовательность команд. Ваша программа должна последовательно выполнять эти
команды, выбирая их из «памяти», пока не встретится команда «СТОП».
7.
**Подумайте, как можно было бы организовать условный переход: перейти на
N байт вперед (или назад), если результат последней операции – ноль.
Практическая
работа № 7.
Моделирование движения
1.
Парашютист массой 90 кг разгоняется в свободном падении до скорости
10 м/с и на высоте 50 м раскрывает парашют, площадь которого 55 м2.
Коэффициент сопротивления парашюта равен 0,9. Выполните следующие задания:
·
постройте графики изменения скорости и высоты полета в течение
первых 4 секунд;
·
определите, с какой скоростью приземлится парашютист?
2.
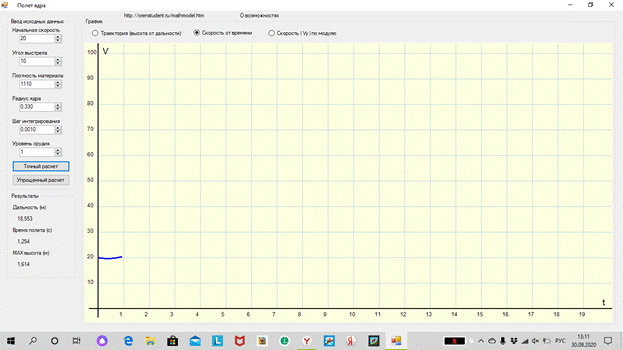
Напишите программу, которая моделирует полет мяча, брошенного
вертикально вверх, при
мм,
г,
м/с,
с.
Остальные
необходимые данные есть в тексте § 9. Выполните следующие задания:
· определите
время полета, максимальную высоту подъема мяча и скорость в момент приземления;
·
вычислите время полета и максимальную высоту подъема мяча,
используя модель движения без сопротивления воздуха:
|
без учёта сопротивления |
с учётом сопротивления |
|
|
Время полета, с |
1,207 |
0,928 |
|
Максимальная высота, м |
1,823 |
1,647 |
|
Дальность, м |
18,485 |
18,289 |
·
с помощью табличного процессора постройте траекторию движения
мяча, а также графики изменения скорости, ускорения и силы сопротивления;
·
уменьшите шаг до 0,01 с и повторите моделирование; сделайте
выводы по поводу выбора шага в данной задаче.
Ответ:
3.
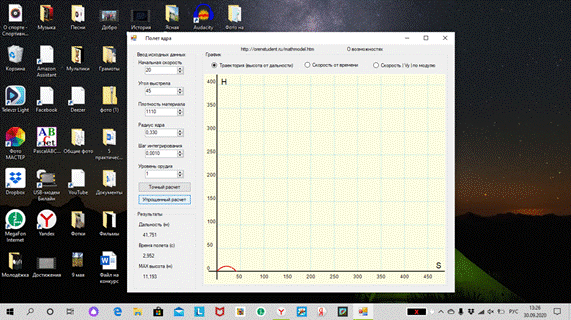
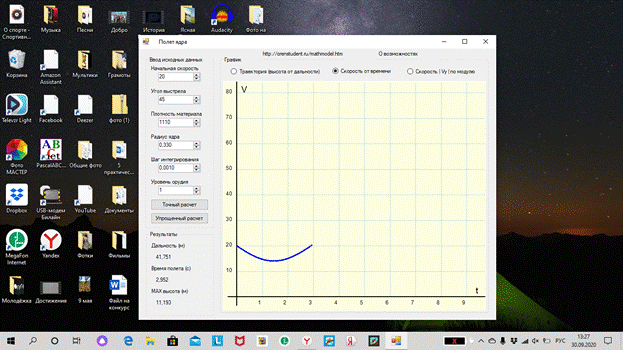
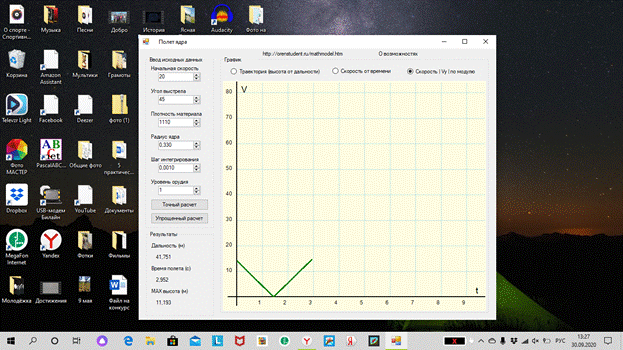
*Выполните моделирование движения мяча, брошенного под углом 45° к
горизонту:
·
определите время полета, максимальную высоту и дальность полета
мяча, скорость в момент приземления;
|
без учёта сопротивления |
с учётом сопротивления |
|
|
Время полета, с |
2,952 |
2,720 |
|
Максимальная высота, м |
11,193 |
10,950 |
|
Дальность полета, м |
41,751 |
41,413 |
Практическая
работа № 8.
Моделирование популяции животных
Для
выполнения работы откройте файл-заготовку Популяция.xls.
1.
Постройте графики изменения численности популяции животных для моделей
ограниченного и неограниченного роста при ,
и
в течение первых 15 периодов.
2.
Используя модель ограниченного роста из предыдущей задачи, выполните следующие
задания:
·
определите количество животных в состоянии равновесия по
результатам моделирования; зависит ли оно от начальной численности?
Ответ:
От
начальной численности в данный момент ничего не зависит, т.к это неизменяемая
величина, а численность животных зависит от периода времени.
·
определите, на что влияет начальная численность животных;
Ответ:
Все будет зависеть от
кормовой базы, от наличия хищников, от паразитов, от болезней в популяции, от
разветвленных пищевых сетей.
·
*определите максимально допустимый отлов теоретически, из модели
ограниченного роста с отловом; сравните это значение с результатами
моделирования
Ответ:
Практическая
работа № 9.
Моделирование эпидемии
Для
выполнения работы откройте файл-заготовку Эпидемия.xls.
При эпидемии гриппа число больных
изменяется по формуле
,
где – количество заболевших в -й день,
а – количество выздоровевших в тот же
день. Число заболевших рассчитывается согласно модели ограниченного роста:
,
где –
общая численность жителей, – коэффициент роста и
– число переболевших (тех, кто уже
переболел и выздоровел, и поэтому больше не заболеет):
.
Считается, что в начале эпидемии
заболел 1 человек, все заболевшие выздоравливают через 7 дней и больше не
болеют.
Выполните моделирование развития эпидемии при и
до
того момента, когда количество больных станет равно нулю. Постройте график
изменения количества больных.
Ответьте на следующие вопросы:
1.
Когда закончится эпидемия?
Ответ:
Когда
количество выздоровевших в сутки начнёт превышать количество заболевших за
сутки.
2.
Сколько человек переболеет, а сколько вообще не заболеет гриппом?
Ответ:
В
данный момент переболело 283 человека, т.е приблизительно 1/3 всего населения,
возможно, что всего переболеет 2/3 населения, а 1/3 населения вовсе не
заболеет, на это влияют такие факторы, как: отсутствие контакта с заболевшими,
крепкий иммунитет, профилактика и т.д
3.
Каково максимальное число больных в один день?
Ответ:
65
4.
Изменяя коэффициент , определите, при каких
значениях модель явно перестает быть
адекватной.
Ответ:
При
отрицательных числах, при нуле и единице.
Практическая
работа № 10.
Модель «хищник-жертва»
Для
выполнения работы откройте файл-заготовку ХищникЖертва.xls.
Выполните моделирование
биологической системы «щуки-караси»
где – численность карасей
– численность щук
при следующих
значениях параметров:
–
коэффициент прироста карасей;
– предельная численность карасей;
– начальная численность карасей;
– начальная численность щук;
–
коэффициент смертности щук без пищи;
и
– коэффициенты модели.
Постройте на
одном поле графики изменения численности карасей и щук в течение 10 периодов
моделирования.
Ответьте на следующие вопросы:
1.
Что влияет на количество рыб в состоянии равновесия: начальная
численность хищников и жертв или значения коэффициентов модели?
Ответ:
Наибольшую
роль играет начальная численность животных.
2.
На что влияет начальная численность хищников и жертв?
Ответ:
В
основном на численность вида в определенный период.
3.
Подберите значения коэффициентов, при которых модель становится
неадекватна.
Ответ:
При
нуле и при отрицательных значениях.
Практическая
работа № 10а.
Модель «две популяции»
Для
выполнения работы откройте файл-заготовку ДвеПопуляции.xls.
Белки и бурундуки живут в одном
лесу и едят примерно одно и то же (конкурируют за пищу). Модель, описывающая
изменение численности двух популяций, имеет вид:
Здесь и
– численность белок и бурундуков;
и
– их максимальные численности;
и
– коэффициенты прироста;
и
– коэффициенты взаимного влияния.
Выполните моделирование изменения
численности двух популяций в течение 10 периодов при ,
,
,
,
и
. Постройте графики изменения
численности обеих популяций на одном поле.
Ответьте на следующие вопросы:
1.
Является ли эта модель системной? Почему?
Ответ:
Нет,
т.к система представляет собой определённые цели и задачи, а в нашей модели это
не прослеживается
2.
Какова численность белок и бурундуков в состоянии равновесия?
Ответ:
Различна,
отличие составляет несколько десятков
3.
Что влияет на состояние равновесия?
Ответ:
Среда
обитания животных, наличие корма, конкуренция — это самые основные черты,
влияющие на состояние равновесия.
4.
На что влияет начальная численность животных?
Ответ:
На количество животных в различные периоды времени.
Практическая
работа № 11.
Саморегуляция
Для
выполнения работы откройте файл-заготовку Саморегуляция.xls.
Биологи выяснили, что для каждого
вида животных существует некоторая минимальная численность популяции, которая
необходима для выживания этой колонии. Это может быть одна пара животных
(например, для ондатр) или даже тысячи особей (для американских почтовых
голубей). Если количество животных становится меньше этого минимального
значения, популяция вымирает. Для этого случая предложена следующая модель
изменения численности:
, (*)
Эта модель отличатся от модели
ограниченного роста только дополнительным множителем , где
и
– некоторые числа (параметры),
смысл которых вам предстоит выяснить.
1.
Выполните моделирование для 30 периодов при следующих значениях
параметров модели:
Сравните
результаты, которые дают модель классическая модель ограниченного роста и
модель (*). Сделайте выводы и опишите, в чём проявляется саморегуляция для этих
моделей.
Ответ:
2.
Постепенно увеличивая коэффициент от 0 до 500, выясните с помощью
моделирования, как влияет этот коэффициент на саморегуляцию.
Ответ:
3.
Через 10 периодов в результате изменения природных условия число
животных уменьшилось до 400 (то есть, ). Выполните моделирование при этих
условиях и опишите, как работает саморегуляция и чем отличается поведение двух
сравниваемых моделей.
Ответ:
4.
Повторите моделирование п. 3 при и сделайте аналогичные выводы:
Ответ:
5.
Экспериментируя с моделями, найдите минимальную численность популяции , при которой она выживает в
соответствии с моделью (*).
Ответ:
6.
Сделайте выводы о смысле коэффициента в
модели (*).
Ответ:
7.
Сравните свойства саморегуляции для модели ограниченного роста и модели
(*).
Ответ:
Практическая
работа № 12.
Моделирование работы банка
Для моделирования
обслуживания клиентов в банке предложена следующая модель:
·
за 1 минуту в банк входит случайное число клиентов, от 0 до (распределение равномерное);
·
на обслуживание клиентов требуется от до
минут; время обслуживания
определяется
для каждой рабочей минуты случайным образом (распределение равномерное);
·
моделирование выполняется для интервала времени ,
равного 8-часам (рабочая смена).
·
число клиентов, находящихся в помещении банка, вычисляется по
формуле
где
– количество клиентов, вошедших за
-ую минуту, а – количество клиентов, обслуженных
за это время;
·
если кассир обслуживает клиента за минут,
то можно считать, что за 1 минуту он сделает часть работы, равную ; если предположить, что скорость
работы кассиров одинакова, то касс за 1 минуту
обслужат клиентов;
·
если считать, что клиентов равномерно
распределяются по кассам, так что средняя длина
очереди равна , а среднее время ожидания в
течение этой минуты равно
·
достаточным считается число касс, при которых среднее время
ожидания превышает установленный предел
не
более, чем 5% рабочего времени в течение дня.
Используя эту
вероятностную модель работы банка, напишите программу, с помощью которой
определите минимальное необходимое количество касс при следующих исходных
данных:
,
,
,
.
begin
Pmax:=4;
Tmin:=1;
Tmax:=9;
L:=480;
M:=15;
N:=0;
count:=0;
from ; random ;import ;random; randint;
for i : integer:=range(L) to
P=randint(0.Pmax)do;
T;Tmin ; random(); (Tmax — Tmin);
R ; round(K / T);
N+= P-R;
if N < 0 then N;0:
dT; N ; K ; T;
if dT > M then count += 1;
end.
Дополнительное задание.
Практическая работа №4
Задача. Биологические модели развития популяции. Модель типа «хищник – жертва».
Описание задачи. 1.Построить модель неограниченного роста, в которой численность популяции ежегодно увеличивается на определенный процент.
Математическая модель: xn+1=a*xn, a-коэффициент роста.
2.Модель ограниченного роста – учитывается эффект перенаселенности, связанный с нехваткой питания, болезнями, т.д., который замедляет увеличение численности.
Xn+1=(a-b*xn)*xn, b-коэффициент перенаселенности
3. Модель ограниченного роста с отловом. Учитывается, что на численность популяций промысловых животных оказывает влияние величина ежегодного отлова.
x n+1=(a-b*xn)*xn-c.
4. В модели «хищник – жертва» количество жертв Xn и количество хищников yn связаны между собой.
Xn+1=(a-b*xn)*xn-c-f*xn*yn, где f- возможность гибели жертвы при встрече с хищниками.
Yn+1=d*yn+e*xn*yn, где d- скорость уменьшения популяции хищников, е- характеризует величину роста численности хищников за счет жертв.
Компьютерная модель
1. В ячейки В1 и В6 внести начальные значения численности популяций жертв и хищников.
В ячейки В2:В5 внести значения коэффициентов a,b,c,f, влияющие на изменение численности жертв. В ячейки В7 и В8 внести значения коэффициентов d,e, влияющих на изменение численности хищников.
В столбце D будем вычислять численность популяции в соответствии с моделью неограниченного роста, в столбце Е – ограниченного роста, в столбце F- ограниченного роста с отловом, в столбцах G,H- «хищник – жертва».
2. В ячейки D1,E1,F1,G1 внести значения начальной численности популяций жертв, в ячейку Н1-хищников. В ячейку D2 внести рекуррентную формулу ограниченного роста =$B$2*D1
В ячейку E2 внести рекуррентную формулу ограниченного роста =($B$2-$B$3*E1)*E1
В ячейку F2 внести рекуррентную формулу ограниченного роста с отловом =($B$2-$B$3*F1)*F1-$B$4
В ячейку G2 внести рекуррентную формулу изменения количества жертв =($B$2-$B$3*G1)*G1-$B$4-$B$5*G1*H1
В ячейку Н2 внести рекуррентную формулу изменения количества хищников =$B$7*H1+$B$8*G1*H1
3. Скопировать внесенные формулы в ячейки столбцов
Ознакомиться с динамикой изменения численности популяций.
Построить график изменения популяций с течением времени( построить диаграмму типа График).
Изменяя значения начальных численностей популяций, а также коэффициенты, получить различные варианты изменения численности популяций в зависимости от времени.
Начальные данные. x1=1.5
a=1.1
b=0.03
c=0.03
f=0.04
y1=1
d=0.9
e=0.05
Модель клеточного автомата, реализованная средствами VBA в Excel (с использованием модуля класса)
В таблице произвольного размера клетки могут быть в трех состояниях: пустая (без цвета), травоядное (зеленый цвет ячейки), хищник (красный цвет ячейки).
Поведение системы характеризуется следующими параметрами:
- особь может переместиться на любую клетку, имеющую с данной общую сторону. Направление выбирается случайно из возможных свободных.
- особь может оставить потомство в той клетке, из которой она переместилась. Потомство появляется периодически, период является параметром.
- если особь является «хищной», то она может поглотить свою жертву, при этом перемещаясь на место жертвы.
- особь живет ограниченное количество времени, называемое временем жизни особи – так же параметр.
- если «хищная» особь не находит себе пищи в течение определенного времени (называемого временем голодной смерти), то она погибает.
- время голодной смерти является параметром.
Для запуска программы нажмите зелёную кнопку.
Предварительно вы можете изменить параметры в желтых ячейках.
Михаил Витер
Эксперт по предмету «Информационные технологии»
Задать вопрос автору статьи
Часто представители одного вида (популяции) питаются представителями другого вида.
Модель Лотки – Вольтерры – модель взаимного существования двух популяций типа «хищник – жертва».
Названа в честь авторов модели – Лотка и Вольтерра, которые представили уравнения модели независимо друг от друга. Довольно распространенным является неправильное название – модель Лотки – Вольтерра.
Впервые модель «хищник – жертва» была получена А. Лоткой в 1925 году, который использовал ее для описания динамики взаимодействующих биологических популяций. В 1926 году независимо от Лотки аналогичные (к тому же более сложные) модели были разработаны итальянским математиком В. Вольтерра, глубокие исследования которого в области экологических проблем заложили фундамент математической теории биологических сообществ или т. н. математической экологии.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
В математической форме предложенная система уравнений имеет вид:
где x – количество жертв, y – количество хищников, t – время, α, β, γ, δ – коэффициенты, которые отражают взаимодействия между популяциями.
Уравнения используются для моделирования системы «хищник – жертва», «паразит – хозяин», конкуренции и других видов взаимодействия между двумя видами.
Постановка задачи
Рассмотрим закрытое пространство, в котором существуют две популяции – травоядные («жертвы») и хищники. Считается, что животных не ввозят и не вывозят и что еды для травоядных животных достаточно. Тогда уравнение изменения числа жертв (только жертв) примет вид:
«Модель «хищник-жертва»» 👇
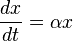
где $α$ – коэффициент рождаемости жертв,
$x$– размер популяции жертв,
$frac{dx}{dt}$ – скорость прироста популяции жертв.
Когда хищники не охотятся, они могут вымирать, значит, уравнение для количества хищников (только хищников) примет вид:
,
где $γ$ – коэффициент убыли хищников,
$y$ – размер популяции хищников,
$frac{dy}{dt}$ – скорость прироста популяции хищников.
При встрече хищников и жертв (частота встреч прямо пропорциональна произведению ) хищники уничтожают жертв с коэффициентом , сытые хищники могут воспроизводить потомство с коэффициентом . Таким образом, система уравнений модели примет вид:
Решение задачи
Построим математическую модель совместного существования двух биологических популяций типа «хищник – жертва».
Пусть две биологические популяции совместно обитают в изолированной среде. Среда является стационарной и обеспечивает в неограниченном количестве всем необходимым для жизни один из видов – жертвы. Другой вид – хищник – также обитает в стационарных условиях, но питается только жертвами. В роли хищников могут выступать коты, волки, щуки, лисы, а в роли жертв – куры, зайцы, караси, мыши соответственно.
Для определенности рассмотрим в роли хищников – котов, а в роли жертв – кур.
Итак, куры и коты живут в некотором изолированном пространстве – хозяйственном дворе. Среда предоставляет курам питание в неограниченном количестве, а коты питаются только курами. Обозначим через
$х$ – количество кур,
$у$ – количество котов.
Со временем количество кур и котов меняется, но будем считать $х$ и $у$ непрерывными функциями от времени t. Назовем пару чисел $х, у)$ состоянием модели.
Найдем каким образом изменяется состояние модели $(х, у).$
Рассмотрим $frac{dx}{dt}$ – скорость изменения количества кур.
Если котов нет, то количество кур возрастает и тем быстрее, чем больше кур. Будем считать зависимость линейной:
$frac{dx}{dt} a_1 x$,
$a_1$ – коэффициент, который зависит только от условий жизни кур, их естественной смертности и рождаемости.
$frac{dy}{dt}$ – скорость изменения количества котов (если нет кур), зависит от количества котов y.
Если кур нет, то количество котов уменьшается (у них нет пищи) и они вымирают. Будем считать зависимость линейной:
$frac{dy}{dt} — a_2 y$.
В экосистеме скорость изменения количества каждого вида также будем считать пропорциональным его количеству, но только с коэффициентом, зависящим от количества особей другого вида. Так, для кур этот коэффициент уменьшается с увеличением количества котов, а для котов возрастает с увеличением количества кур. Будем считать зависимость также линейной. Тогда получим систему дифференциальных уравнений:
Данная система уравнений называется моделью Вольтерра-Лотки.
a1, a2, b1, b2 – числовые коэффициенты, которые называют параметрами модели.
Как видно, характер изменения состояния модели (x, y) определяется значениями параметров. Изменяя данные параметры и решая систему уравнений модели, можно исследовать закономерности изменения состояния экологической системы.
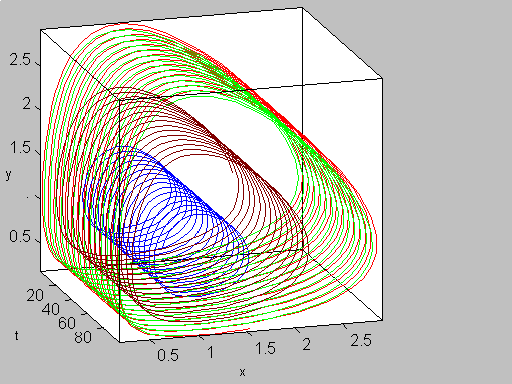
С помощью программы MATLAB система уравнений Лотки-Вольтерра решается следующим образом:
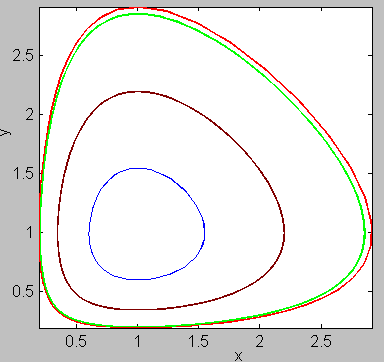
На рис. 1 представлено решение системы. В зависимости от начальных условий решения разные, чему отвечают разные цвета траекторий.
На рис. 2 представлены те же решения, но с учетом оси времени t (т.е. наблюдается зависимость от времени).
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме


 Скачать 27.74 Kb.
Скачать 27.74 Kb.