Цель
работы: освоить приемы решения обыкновенных
дифференциальных уравнений с помощью
Excel,
провести их параметрические исследования
и познакомиться с функциями ВПР, СМЕЩ,
ПОИСКПОЗ.
Развитие
финансовой пирамиды во многом напоминает
развитие эпидемии, когда число заболевших
(купивших акции) в конкретный день
пропорционально числу больных в городе
(числу проданных акций) n,
перемноженному на число еще не переболевших
(не купивших акции) Mn.
В случае эпидемии коэффициент
пропорциональности зависит от мер
профилактики. В случае финансовой
пирамиды этот коэффициент (назовем его
коэффициентом ажиотажа КА)
зависит от уровня инфляции, рекламы,
наличия других параллельных пирамид,
от срока, прошедшего с момента шумного
краха предыдущей пирамиды, и т.д.
Тогда
процесс можно описать обыкновенным
дифференциальным уравнением
.
Применяя
к этому уравнению разностную схему
Эйлера, имеем
.
При
t=1
(один день) получаем формулу для
определения числа акций SNKD+1,
купленных жителями на
(D+1)-й
день (предположим, что один житель
покупает одну акцию):
SNKD+1
=
SNKD
+ NKD+1,
где
NKD+1
= KA×(MSNKD)×SNKD
– общее число купивших акции в
день D+1,
M
число жителей в городе.
За
волной купивших акции идет волна желающих
их сдать (продать)
вернуть свои «кровные» и причитающиеся
дивиденды. Будем считать, что волна
продающих акции отстает от волны их
купивших на число дней Т.
Тогда
число акций, проданных жителями в день
D,
можно подсчитать по формуле
0,
если D £
T,
NKD–T
, если D > T.
Количество
денег на счету организаторов пирамиды
завтра (ПD+1)
можно выразить через количество денег
сегодня (ПD),
если известен курс акций и количество
покупок NKD
и продаж NPD
акций населением.
Пусть
динамика изменения курсов продажи и
покупки рублевых акций выражается
таблицей 11.1:
Таблица
11.1 – Курс покупки-продажи акций населению
|
Дни, |
1 |
2 |
3 |
¼ |
51 |
¼ |
365 |
¼ |
|
Курс |
1,05 |
1,07 |
1,09 |
¼ |
2,05 |
¼ |
8,33 |
¼ |
|
Курс |
1,00 |
1,02 |
1,04 |
¼ |
2,00 |
¼ |
8,28 |
¼ |
Тогда
с учетом ежедневного дохода организатора
пирамиды (S
процентов от суммы в кассе) и затрат на
организацию пирамиды R
(налоги, оплата текущих расходов, реклама
и т.п.) имеем1:
ПD+1=ПD
+ NKD×K(D)
– NPD×P(D)
– ПD×S/100
– R.
Задание
1. Построить
таблицу, состоящую из следующих граф
(столбцов): День;
Курс продаж; Продано в день; Продано
всего; Курс покупки; Куплено в день;
Куплено всего; Сумма в кассе; Доход в
день; Доход всего.
Исходные данные использовать с абсолютной
адресацией, выбирая их из Таблицы
исходных данных.
Сдвиг волны «покупка-продажа» задать
программно с помощью функций Excel
из категории Ссылки
и массивы,
например, СМЕЩ
или
ВПР, используя
их как аргумент функции
ЕСЛИ.
Функция
СМЕЩ
возвращает ссылку на ячейку или диапазон
ячеек, отстоящие от ячейки или диапазона
ячеек на заданное число строк и столбцов.
Возвращаемая ссылка может быть как
отдельной ячейкой, так и диапазоном
ячеек. Можно задавать количество
возвращаемых строк и столбцов.
Синтаксис
функции:
СМЕЩ(ссылка;смещ_по_стр;смещ_по_столбц;выс;шир)
Ссылка
– это ссылка на ячейку или на диапазон
смежных ячеек, от которых вычисляется
смещение, в противном случае функция
СМЕЩ
возвращает значение ошибки #ЗНАЧ!.
Смещ_по_стр
– это количество строк, которые нужно
отсчитать вверх или вниз, так чтобы
верхняя
левая ячейка
результата ссылалась на это место. Если
значение положительное, то отсчитывается
ниже начальной ссылки, если отрицательное,
то выше начальной ссылки.
Смещ_по_столбц
– это количество столбцов, которые
нужно отсчитать влево или вправо, так
чтобы верхняя
левая ячейка
результата ссылалась на это место. Если
значение положительное, то отсчет
ведется вправо от начальной ссылки,
если отрицательное, то влево от начальной
ссылки.
Выс
– это высота (число строк) возвращаемой
ссылки. Высота должна быть положительным
числом.
Шир
– это ширина (число столбцов) возвращаемой
ссылки. Ширина должна быть положительным
числом.
Если
высота или ширина опущена, то предполагается,
что используется такая же высота или
ширина как в аргументе Ссылка.
Функция
ВПР
ищет значение в крайнем левом столбце
таблицы и возвращает значение в той же
строке из указанного столбца таблицы1.
Синтаксис
функции:
ВПР(иск_знач;таблица;номер_столбца;интерв_просмотр)
Иск_знач
– это значение, которое должно быть
найдено в первом столбце массива.
Иск_знач
может быть значением, ссылкой или
текстовой строкой.
Таблица
– это таблица с информацией, в которой
ищутся данные. Можно использовать ссылку
на интервал или имя интервала. Значения
в первом столбце таблицы могут быть
текстом, числами или логическими
значениями. Регистр не учитывается
(т.е. строчные и заглавные буквы не
различаются).
Номер_столбца
– это номер столбца, в котором должно
быть найдено соответствующее значение.
Если номер_столбца
меньше 1, то функция ВПР
возвращает значение ошибки #ЗНАЧ!; если
номер_столбца
больше, чем количество столбцов в
таблице, то функция ВПР
возвращает значение ошибки #ССЫЛ!.
Интерв_просмотр
– это логическое значение, которое
определяет, нужно ли, чтобы ВПР
искала точное или приближенное
соответствие. Если этот аргумент имеет
значение ИСТИНА
или опущен, то возвращается приблизительно
соответствующее значение (наибольшее
значение, которое меньше, чем иск_знач).
Если этот аргумент имеет значение ЛОЖЬ,
то функция ВПР
ищет точное соответствие. Если таковое
не найдено, то возвращается значение
ошибки #Н/Д. Кроме того, если параметр
интерв_просмотр
имеет значение ИСТИНА,
то значения в первом столбце таблицы
должны быть расположены в возрастающем
порядке, в противном случае функция ВПР
может выдать неправильный результат.
Если интерв_просмотр
имеет значение ЛОЖЬ,
то таблица не обязана быть сортированной.
Примечание.
Для удобства работы с таблицей
рекомендуется использовать одновременный
просмотр двух частей листа.
Для
того, чтобы разбить лист на две части,
наведите указатель на узкую полоску,
расположенную в верхней части вертикальной
полосы прокрутки или в правой части
горизонтальной полосы прокрутки (см.
рис.). Когда указатель примет вид
двунаправленной стрелки, перетащите
его вниз (или влево). Так как при выполнении
данной лабораторной работы таблица
вытянута вниз, то имеет смысл поставить
полосу разделения сразу за заголовками
таблицы, чтобы постоянно держать их
перед глазами при прокрутке строк
таблицы.
2. Построить
в одной системе координат графики
изменения количества денег в кассе Пи изменения суммарных доходов организатора
пирамидыД, взяв реальный диапазон
дней.
3. Определить
сумму максимального дохода организатора
пирамиды ДMAX
и день ее достижения DMAX,
используя при этом функции Excel
МАКС
и ПОИСКПОЗ.
Функция
ПОИСКПОЗ
возвращает относительное положение
(позицию) элемента массива, который
соответствует заданному значению
указанным образом1.
Синтаксис
функции:
ПОИСКПОЗ(иск_знач,интервал,тип_сопост)
Иск_знач
– это значение, которое сопоставляется
со значениями в аргументе интервал.
Может быть значением (числом, текстом
или логическим значением) или ссылкой
на ячейку, содержащую число, текст или
логическое значение.
Интервал
– это непрерывный интервал ячеек,
возможно содержащих искомые значения.
Интервал
может быть массивом или ссылкой на
массив.
Тип_сопост
– это число -1, 0 или 1. Если тип_сопост
равен 1 или опущен, то функция находит
наибольшее значение, которое равно или
меньше, чем иск_знач.
Интервал
должен быть упорядочен по возрастанию.
Если тип_сопост
равен 0, то функция находит первое
значение, которое в точности равно
аргументу иск_знач.
Интервал
может быть в любом порядке. Если тип_сопост
равен -1, то функция находит наименьшее
значение, которое равно и больше чем
иск_знач.
Интервал
должен быть упорядочен по убыванию.
Использование
этой функции для решения поставленной
задачи облегчается тем, что номер строки
в таблице в точности соответствует дню.
4. Любое
дело требует начальных расходов, иногда
весьма существенных. С помощью сервисного
средства Excel
Подбор
параметра подобрать
такое минимальное значение начального
капитала П1MIN,
которое бы позволило не уйти в отрицательную
сумму в кассе на начальном этапе развития
пирамиды.
Указание.
Найти предварительно локальный минимум
функции Сумма в кассе на начальном
участке строительства пирамиды (в
диапазоне дней от D=1
до DMAX).
5. Изменяя
исходные данные, проследить за изменением
дохода организатора (в каждом варианте
изменять только один параметр!). Результаты
исследований оформить на новом листе
в виде таблицы параметрического
исследования модели (табл. 11.2). Можно
использовать Диспетчер сценариев.
Сделать выводы.
Таблица
11.2 – Параметрическое исследование
модели
|
Изменяемый параметр |
Увеличиваем |
Уменьшаем |
||||
|
Значение |
День |
Доходы |
Значение |
День |
Доходы |
|
|
M KA … |
Исходные
данные для расчета.
Число
жителей в городе M=1000000.
Коэффициент
ажиотажа КА=0,0000001.
Ежедневные
расходы (руб.) R=1200.
Время
между покупкой и продажей акции (дни)
Т=50.
Норма
прибыли (ежедневный процент от суммы в
кассе) S=3.
Состояние
на первый день:
начальный
капитал (руб.) П1=100000;
число
купивших акции в первый день NK1=100.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
11.05.2015211.06 Кб22mss_labN5.docx
Здравствуйте, имеется лабораторная » Моделирование финансовой пирамиды «. Одно из заданий: «6. Последовательно изменяя исходные данные сначала в сторону увеличения, затем в сторону уменьшения (например, в два раза), проследить за изменением суммы на счете и прибыли организаторов пирамиды. Не забывайте контролировать значение локального минимума суммы на счете – оно не должно быть отрицательным! Если это произошло, с помощью Подбора параметра изменить другое исходное данное так, чтобы обеспечить неотрицательное значение локального минимума.» В ячейке «число жителей /2» раньше стояло число «500 000». Как с помощью подбора параметра могло получиться число «827 925»? Помогите пожалуйста! Работу приложил.
Изменено: drujinin272 — 23.09.2019 17:11:36
Математическое моделирование устойчивости финансовых пирамид +9
Программирование, Python
Рекомендация: подборка платных и бесплатных курсов Java — https://katalog-kursov.ru/
Чарльз Понци – создатель первой финансовой пирамиды
В данной статье мы увидим как создаются, счастливо живут, и умирают финансовые пирамиды.
Финансовая пирамида в классическом понимании этого слова (деньги предыдущим «вкладчикам» выплачиваются за счет следующих) была придумана Чарльзом Понци, в 1919 году им была создана финансовая пирамида и в 1920 году «предприятие» закрылось. Сколько «вкладчиков» может быть у финансовой пирамиды? У финансовой пирамиды может быть 15 млн «вкладчиков» (финансовая пирамида созданная Сергеем Мавроди, 1994 год). Сколько по времени может просуществовать финансовая пирамида? Финансовая пирамида Бернарда Мэддофа работала 17 лет (с 1991 по 2008), при этом «вкладчикам» казалось что они вкладывают деньги в инвестиционный фонд, так как «предприятие» заявляло доходность 12% в год и по уровню доходности не отличалось от других инвестиционных фондов.
Давайте проверим устойчивость финансовой пирамиды с помощью математического моделирования.
Как будем создавать математическую модель? На языке программирования питон. Что нужно чтобы создать математическую модель финансовой пирамиды? Ну для начала нужно формализовать как она будет работать.
Вот пример того как может выглядеть финансовая пирамида.
Есть основатель, он получает прибыль от финансовой пирамиды. Есть «вкладчики», они заводят «счет» в финансовой пирамиде (в нашем случае это будет случайная сумма от 1 $ до 100 $, случайная сумма – целое, не дробное число). Каждый день «вкладчикам» выплачивается процент прибыли с их суммы (в нашем случае 1% в день). Также допустим что в финансовой пирамиде есть 2 счета: 1-й – это счет основателя, 2-й – это основной счет для финансовой деятельности (из него выплачиваются проценты «вкладчикам»). Допустим что каждый день основатель берет 9% от основного счета и переводит себе на счет (ну ему же нужны деньги). Ну и собственно, формула роста числа вкладчиков: допустим что число вкладчиков увеличивается на 10% в день. Поскольку число вкладчиков – целое, то для прироста на 1 человека в день нам нужно 10 человек, для этого первые 10 дней запрограммируем рост числа вкладчиков не как 10% в день, а на 1 человека в день. Матмодель будет работать пока число «вкладчиков» меньше 500000 (можно смоделировать для любого числа которое сможет рассчитать ваш компьютер, но больше 500000 у меня компьютер уже начинает медленно обрабатывать информацию). Матмоделирование будет происходить по дням.
Код математической модели:
import random
def pay_percents(deposits, gathered_money):
for deposit in deposits:
gathered_money -= deposit / 100
return gathered_money
day = 0
deposits = []
investors_count = 0
gathered_money = 0
organizer_account = 0
while investors_count < 10: # gather first 10 'investors'
investors_count += 1
new_investor_money = random.randint(1, 100)
gathered_money += new_investor_money
if day != 0:
gathered_money = pay_percents(deposits, gathered_money)
deposits.append(new_investor_money)
organizer_account += 0.09 * gathered_money # pay to organizer (replenish organizer's account)
gathered_money -= 0.09 * gathered_money # pay to organizer (take money from gathered money)
day += 1
print('day =', day)
print('money in scheme =', gathered_money)
print('investors count =', investors_count)
print('---') # for better viewing results
while investors_count < 500000:
new_wave_investors_count = int(0.1 * investors_count)
for _ in range(0, new_wave_investors_count):
new_investors_money = random.randint(1, 100)
deposits.append(new_investors_money)
gathered_money += new_investors_money
gathered_money = pay_percents(deposits[:investors_count], gathered_money)
investors_count += new_wave_investors_count
organizer_account += 0.09 * gathered_money # pay to organizer (replenish organizer's account)
gathered_money -= 0.09 * gathered_money # pay to organizer (take money from gathered money)
day += 1
print('day =', day)
print('money in scheme =', gathered_money)
print('investors count =', investors_count)
print('---')
print('organizer account money =', organizer_account)
print('money in scheme =', gathered_money)
print('investors count =', investors_count)
Ну что же, вот результаты:
Красный график — счет основателя, черный график – основной счет пирамиды
Срок работы пирамиды — 129 дней, количество «вкладчиков» – 521893 человек. Пирамида принесла нам 23 млн $ за 129 дней. 23 млн $ за 4 месяца, неплохо.
При этом на 129 день пирамида не развалилась, то есть эти 129 дней она была устойчивой. Почему так произошло? Ну матмодель описывает идеальный случай, и в реальности не факт, что прирост «вкладчиков» первые 10 дней составлял бы 1 человек в день, а после 10 дней составлял бы 10% в день. Вообще срок жизни финансовой пирамиды определяется только 2-мя величинами: процентом, который выплачивается вкладчикам, и формулой прироста новых вкладчиков.
Из определения работы финансовой пирамиды известно, что она развалится в любом случае, так как конечно число людей на Земле.
Постойте. Население Земли постоянно увеличивается, то есть не является постоянным. Что если финансовая пирамида охватит весь мир, и при этом будет учитываться рост населения Земли.
Делаем математическую модель.
На этот раз изменим правила работы финансовой пирамиды. У нас как и раньше есть основатель финансовой пирамиды, и он как и раньше берет 9% в день от общего счета финансовой пирамиды. Но моделирование случайной суммы вклада мы заменим на постоянную сумму которую будет вносить «среднестатистический» житель Земли. Также будем считать что «среднестатистический» житель Земли получает «среднестатистическую» заработную плату на Земле. И «среднестатистический» житель Земли если у него уже есть «депозит», при получении заработной платы обязательно внесет еще один «вклад», на ту же самую фиксированную сумму. В общем, мы будем моделировать ситуацию, при которой человек относит все свои свободные средства при получении заработной платы в финансовую пирамиду. Формула прироста «вкладчиков» будет такая: первые 10 дней – 1 человек в день, далее 10% в день от текущего числа «вкладчиков», а когда мы упремся в число людей на Земле, которое способно сделать «вклад», то уже будет учитываться прирост населения Земли в день, и в этот период времени прирост «вкладчиков» будет соответствовать максимально возможному числу «вкладчиков» которые способны внести «депозит».
Давайте сделаем некоторые допущения.
Допустим что «среднестатистический» житель Земли, который получает «среднестатистическую» заработную плату, получает ее 1 раз каждые 30 дней.
Теперь нужно определить «среднестатистическую» заработную плату на Земле.
Таблица среднестатистических заработных плат за 2018 год по странам
В таблице 160 стран.
Средняя заработная плата на Земле = складываем все заработные платы, а потом делим получившееся число на 160 = 876$
Итак, у нас есть средняя заработная плата на Земле. Но «среднестатистический» житель Земли не будет относить все свою заработную плату в финансовую пирамиду, он будет относить только свободные средства которые остаются от заработной платы. Свободными средствами будем считать заработную плату минус расходы на еду и минус различные налоги.
Будем считать что «среднестатистический» житель Земли тратит в месяц 22% от своей заработной платы на еду и 13% на различные налоги.
Внести «депозит» может только работающий житель Земли. Будем считать что количество работающих жителей Земли составляет 47% от всего населения Земли. Также будем учитывать, что когда мы упремся в число людей на Земле которое способно сделать «вклад», то будет учитываться прирост населения Земли в день, и в этот период времени будут приниматься «вклады» только от работающих людей, то есть 47% от числа людей, на которое увеличивается население Земли в день.
Теперь нужно определить прирост населения Земли в день.
В 2017 году население Земли составляло 7.5 млрд человек. В 2018 году население Земли составляло 7.6 млрд человек.
Будем считать что 1 января 2019 года (начальный день моделирования финансовой пирамиды) население Земли составляло 7.7 млрд человек. Также допустим, что население Земли увеличивается на 273973 ((7.7 млрд – 7.6 млрд)/365 дней) человека в день, и учтем что население Земли растет на 1,1% в год или на 0.0030136986% в день.
Теперь учтены все нужные параметры, можно делать математическую модель.
day = 0
investors_count = 0
investors_accounts = 0
average_salary = 876
tax = 13
meal = 22
gathered_money = 0
organizer_account = 0
previous_investors_count = 0
payment_per_month = average_salary - (average_salary / 100 * tax) - (average_salary / 100 * meal)
earth_population = 7700000000
people_per_day = 273973
while investors_accounts < 10: # gather first 10 'investors'
people_per_day += int(people_per_day / 100 * 0.0030136986)
earth_population += people_per_day
gathered_money += payment_per_month
if day != 0:
gathered_money -= investors_accounts * 0.01 * payment_per_month # pay to 'investors'
organizer_account += 0.09 * gathered_money # pay to organizer (replenish organizer's account)
gathered_money -= 0.09 * gathered_money # pay to organizer (take money from gathered money)
investors_count += 1
investors_accounts += 1
day += 1
print('day =', day)
print('organizer account =', organizer_account)
print('gathered money =', gathered_money)
print('investors count =', investors_count)
print('investors accounts =', investors_accounts)
print('---') # for better viewing results
while gathered_money > 0:
people_per_day += int(people_per_day * 0.0030136986)
earth_population += people_per_day
day += 1
if investors_count <= (0.47 * earth_population):
new_wave_investors_count = int(0.1 * investors_accounts)
else:
new_wave_investors_count = int(0.47 * people_per_day)
if day % 30 == 0:
previous_investors_count = investors_count
if day // 30 > 1:
investors_count += new_wave_investors_count
new_investors_money = payment_per_month * new_wave_investors_count
gathered_money += new_investors_money + previous_investors_count * payment_per_month
organizer_account += 0.09 * gathered_money # pay to organizer (replenish organizer's account)
gathered_money -= 0.09 * gathered_money # pay to organizer (take money from gathered money)
gathered_money -= investors_accounts * 0.01 * payment_per_month # pay to 'investors'
investors_accounts += new_wave_investors_count + previous_investors_count
else:
investors_count += new_wave_investors_count
new_investors_money = payment_per_month * new_wave_investors_count
gathered_money += new_investors_money
organizer_account += 0.09 * gathered_money # pay to organizer (replenish organizer's account)
gathered_money -= 0.09 * gathered_money # pay to organizer (take money from gathered money)
gathered_money -= investors_accounts * 0.01 * payment_per_month # pay to 'investors'
investors_accounts += new_wave_investors_count
else:
investors_count += new_wave_investors_count
new_investors_money = payment_per_month * new_wave_investors_count
gathered_money += new_investors_money
organizer_account += 0.09 * gathered_money # pay to organizer (replenish organizer's account)
gathered_money -= 0.09 * gathered_money # pay to organizer (take money from gathered money)
gathered_money -= investors_accounts * 0.01 * payment_per_month # pay to 'investors'
investors_accounts += new_wave_investors_count
print('day =', day)
print('organizer account =', organizer_account)
print('gathered money =', gathered_money)
print('investors count =', investors_count)
print('investors accounts =', investors_accounts)
print('---')
Вот результаты:
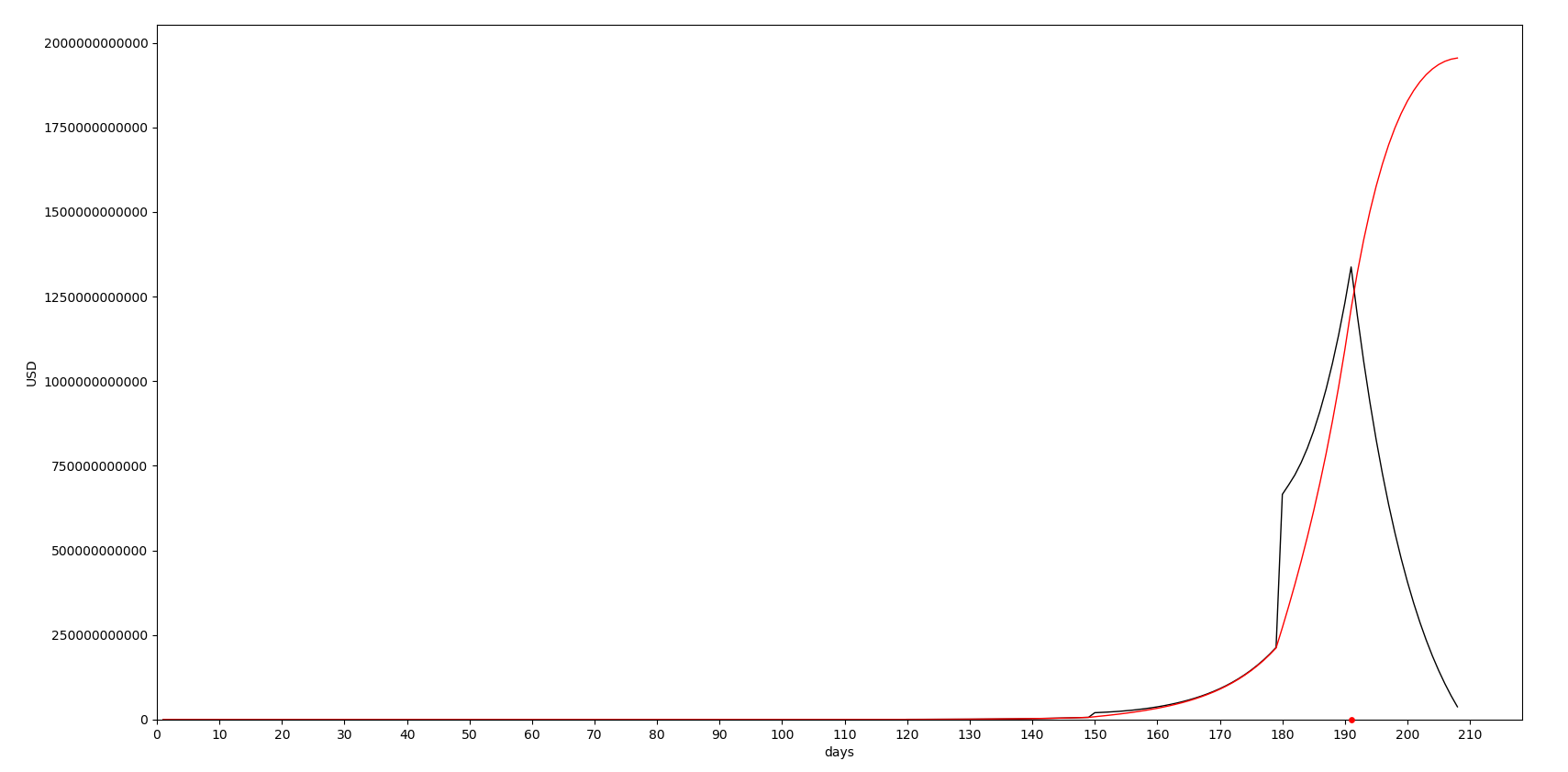
Красный график — счет основателя, черный график — основной счет пирамиды. Красной точкой (на оси days) показан день, когда «предприятие» нужно закрывать.
График количества «инвесторов»
На 209 день денег в пирамиде будет недостаточно для выплаты денег предыдущим «вкладчикам».
Сумма организатора + деньги в пирамиде составляют максимум на 191 день работы пирамиды, на 191 день количество «вкладчиков» будет составлять 3,8 млрд человек. У «пирамидостроителей» есть свои «тонкости» работы, они заключаются не в том чтобы подольше выплачивать процент «вкладчикам», а в том чтобы закрыть «предприятие» в момент времени, когда сумма средств у «пирамидостроителя» будет максимальна. Под суммой средств подразумевается личный счет «пирамидостроителя» + деньги в пирамиде. Соответственно в данном случае мировой пирамиды организатору нужно ретироваться как минимум на Луну (на Земле то его уже все знают) на 191 день работы пирамиды. Жаль что 2 трлн $ на Луне потратить негде.
Уважаемые посетители!
Скачивайте бесплатно данную финансовую модель со всеми действующими, открытыми формулами ниже в серой рамке, причем как в заполненном виде, для примера заполнения,
так и в незаполненном.
Идентификационный номер этой финмодели: IDFM-100010
Если у Вас нет желания тратить много времени на внесение данных Вашего проекта в условия модели и
плюс к тому Ваш бюджет на создание финансовой модели позволяет, то можем предложить Вам за сравнительно небольшие деньги
воспользоваться услугой заполнения финмодели Вашими данными в нашем
Маркетплейсе финансовых моделей P&L.RU,
либо подписавшись на платный Тариф 2 после регистрации
Смотрите обучающую видео-методологию с нашего Ютуб-канала о том, как прописать действующие формулы данной финансовой модели в EXCEL:
Используйте этот видео-ролик в качестве инструкции для заполнения и корректировок финансовой модели.
Онлайн-версию этой финмодели смотрите здесь:
перейти в онлайн-модель
Описание характеристик финансовой экспресс-модели от 5 параметров:
- Простейшая финмодель для быстрого расчета Вашего бизнес-проекта — носит универсальный характер;
- Данная финмодель помимо представления в EXCEL, имеет онлайн-реализацию;
- Горизонт моделирования неограничен и периодизация может быть ежемесячной, ежеквартальной или ежегодной;
- Доходная часть задается в денежном представлении с динамикой в виде прироста по правилам линейной прогрессии, начинающейся с заданной суммы дохода в начальный период;
- Себестоимость задается через процент рентабельности (маржинальности);
- Переменные расходы задаются единым процентом от дохода;
- Постоянные расходы задаются единой суммой за период.
Успехов Вам в создании финмодели Вашего проекта!
Еще финмодели:
Двуязычная финмодель от 5 параметров со сценариями
Наше обучающее видео
Rutube:
Финансовая модель поколения 4.0
Rutube:
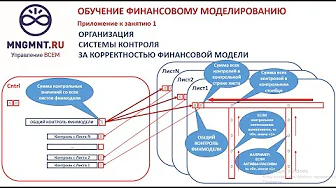
Система контроля за корректностью финмодели в EXCEL
Rutube:
Простая финмодель от 10 параметров и с расчетом IRR, NPV, PBP, ROI и т.п.
Rutube:
Баланс, прибыль, деньги и финотчеты BS PL CF
Rutube:
Организация системы управленческого учета в EXCEL
Rutube:
Курс обучения финансовому моделированию в Excel. Часть1
Вконтакте:
Финансовая модель поколения 4.0
Вконтакте:
Система контроля за корректностью финмодели в EXCEL
Вконтакте:
Простая финмодель от 10 параметров и с расчетом IRR, NPV, PBP, ROI и т.п.
Вконтакте:
Баланс, прибыль, деньги и финотчеты BS PL CF
Вконтакте:
Организация системы управленческого учета в EXCEL
Вконтакте:
Курс обучения финансовому моделированию в Excel. Часть1
YouTube:
Финансовая модель поколения 4.0
YouTube:
Система контроля за корректностью финмодели в EXCEL
YouTube:
Простая финмодель от 10 параметров и с расчетом IRR, NPV, PBP, ROI и т.п.
YouTube:
Баланс, прибыль, деньги и финотчеты BS PL CF
YouTube:
Организация системы управленческого учета в EXCEL
YouTube:
Курс обучения финансовому моделированию в Excel. Часть1
С НАМИ ЭФФЕКТИВНЕЕ!