Модель данных позволяет интегрировать данные из нескольких таблиц, эффективно создавая реляционный источник данных в книге Excel. В Excel модели данных используются прозрачно, предоставляя табличные данные, используемые в сводных таблицах и сводных диаграммах. Модель данных визуализируются как коллекция таблиц в списке полей, и в большинстве раз вы даже не узнаете, что она существует.
Прежде чем приступить к работе с моделью данных, необходимо получить некоторые данные. Для этого мы будем использовать интерфейс Get & Transform (Power Query), поэтому вам может потребоваться выполнить шаг назад и посмотреть видео, или следуйте нашему руководству по обучению по get & Transform и Power Pivot.
Где есть Power Pivot?
-
Excel 2016 & Excel для Microsoft 365 — Power Pivot включен в ленту.
-
Excel 2013 — Power Pivot входит в Office профессиональный плюс Excel 2013, но не включен по умолчанию. Дополнительные сведения о запуске надстройки Power Pivot для Excel 2013.
-
Excel 2010 — скачайте надстройку Power Pivot, а затем установите надстройку Power Pivot.
Где находится get & Transform (Power Query)?
-
Excel 2016 & Excel для Microsoft 365 . Get & Transform (Power Query) интегрировано с Excel на вкладке «Данные«.
-
Excel 2013 — Power Query — это надстройка, которая входит в Excel, но ее необходимо активировать. Перейдите к разделу «Параметры >» > надстроек, а затем в раскрывающемся списке «Управление» в нижней части панели выберите com-надстройки > Go. Проверьте microsoft Power Query Excel, а затем ОК, чтобы активировать его. На Power Query будет добавлена вкладка Power Query.
-
Excel 2010 — скачивание и установка Power Query надстройки.. После активации на ленту Power Query вкладки.
Начало работы
Сначала необходимо получить некоторые данные.
-
В Excel 2016 и Excel для Microsoft 365 используйте data >Get & Transform Data > Get Data > Get Data to import data from any number of external data sources, such as a text file, Excel workbook, website, Microsoft Access, SQL Server, or another relational database that contains multiple related tables.
В Excel 2013 и 2010 перейдите к Power Query >получения внешних данных и выберите источник данных.
-
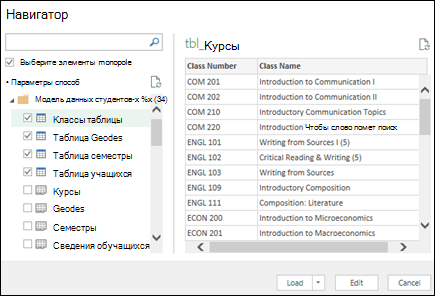
Excel предложит выбрать таблицу. Если вы хотите получить несколько таблиц из одного источника данных, установите флажок «Включить выбор нескольких таблиц «. При выборе нескольких таблиц Excel автоматически создает модель данных.
Примечание: В этих примерах мы используем книгу Excel с вымышленными сведениями о классах и оценках учащихся. Вы можете скачать пример книги модели данных учащихся и следовать инструкциям. Вы также можете скачать версию с готовой моделью данных..
-
Выберите одну или несколько таблиц и нажмите кнопку «Загрузить «.
Если необходимо изменить исходные данные, можно выбрать параметр «Изменить «. Дополнительные сведения см. в статье «Общие сведения Редактор запросов (Power Query)».
Теперь у вас есть модель данных, которая содержит все импортированные таблицы, и они будут отображаться в списке полей сводной таблицы.
Примечания:
-
Модели создаются неявно, когда вы импортируете в Excel несколько таблиц одновременно.
-
Модели создаются явно, если вы импортируете данные с помощью надстройки Power Pivot. В надстройке модель представлена в макете с вкладками, аналогичном Excel, где каждая вкладка содержит табличные данные. Дополнительные сведения об импорте данных с помощью надстройки Power Pivotсм. в статье «Получение данных с помощью SQL Server данных».
-
Модель может содержать одну таблицу. Чтобы создать модель на основе только одной таблицы, выберите таблицу и нажмите кнопку Добавить в модель данных в Power Pivot. Это может понадобиться в том случае, если вы хотите использовать функции Power Pivot, например отфильтрованные наборы данных, вычисляемые столбцы, вычисляемые поля, ключевые показатели эффективности и иерархии.
-
Связи между таблицами могут создаваться автоматически при импорте связанных таблиц, у которых есть связи по первичному и внешнему ключу. Excel обычно может использовать импортированные данные о связях в качестве основы для связей между таблицами в модели данных.
-
Советы по сокращению размера модели данных см. в статье «Создание модели данных, оптимизированной для памяти, с помощью Excel и Power Pivot».
-
Дополнительные сведения см. в руководстве по импорту данных в Excel и созданию модели данных.
Создание связей между таблицами
Следующим шагом является создание связей между таблицами, чтобы вы могли извлекать данные из любой из них. Каждая таблица должна иметь первичный ключ или уникальный идентификатор поля, например идентификатор учащегося или номер класса. Самый простой способ — перетащить эти поля, чтобы подключить их в представлении схемы Power Pivot.
-
Перейдите в power Pivot > Manage.
-
На вкладке « Главная» выберите » Представление схемы».
-
Будут отображены все импортированные таблицы, и может потребоваться некоторое время, чтобы изменить их размер в зависимости от количества полей в каждой из них.
-
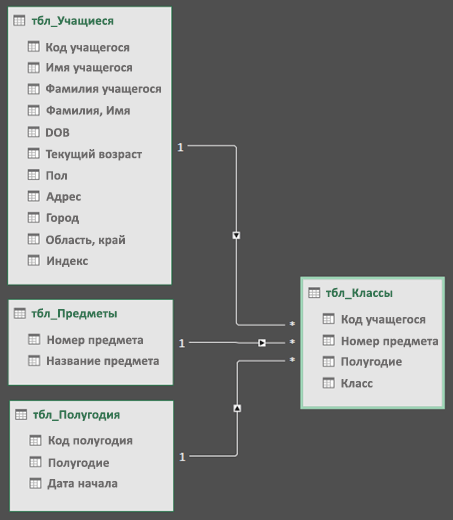
Затем перетащите поле первичного ключа из одной таблицы в следующую. В следующем примере показано представление схемы таблиц учащихся.
Мы создали следующие ссылки:
-
tbl_Students | Идентификатор учащегося > tbl_Grades | Идентификатор учащегося
Другими словами, перетащите поле «Идентификатор учащегося» из таблицы «Учащиеся» в поле «Идентификатор учащегося» в таблице «Оценки».
-
tbl_Semesters | Идентификаторы > tbl_Grades | Семестр
-
tbl_Classes | Номер класса > tbl_Grades | Номер класса
Примечания:
-
Имена полей не обязательно должны совпадать для создания связи, но они должны быть одинаковыми типами данных.
-
Соединители в представлении схемы имеют «1» с одной стороны, а «*» — с другой. Это означает, что между таблицами существует связь «один ко многим», которая определяет, как данные используются в сводных таблицах. См. дополнительные сведения о связях между таблицами в модели данных.
-
Соединители указывают только на наличие связи между таблицами. На самом деле они не показывают, какие поля связаны друг с другом. Чтобы просмотреть ссылки, перейдите в раздел Power Pivot > Manage > Design > Relationships > Управление связями. В Excel можно перейти к разделу «>данных».
-
Создание сводной таблицы или сводной диаграммы с помощью модели данных
Книга Excel может содержать только одну модель данных, но эта модель может содержать несколько таблиц, которые можно многократно использовать в книге. Вы можете добавить дополнительные таблицы в существующую модель данных в любое время.
-
В Power Pivotперейдите к разделу » Управление».
-
На вкладке « Главная» выберите сводную таблицу.
-
Выберите место размещения сводной таблицы: новый лист или текущее расположение.
-
Нажмите кнопку «ОК», и Excel добавит пустую сводную таблицу с областью списка полей справа.
Затем создайте сводную таблицу или сводную диаграмму. Если вы уже создали связи между таблицами, можно использовать любое из их полей в сводной таблице. Мы уже создали связи в образце книги модели данных учащихся.
Добавление имеющихся несвязанных данных в модель данных
Предположим, вы импортировали или скопировали много данных, которые вы хотите использовать в модели, но не добавили их в модель данных. Принудительно отправить новые данные в модель очень просто.
-
Начните с выбора любой ячейки в данных, которые необходимо добавить в модель. Это может быть любой диапазон данных, но лучше всего использовать данные, отформатированные в виде таблицы Excel .
-
Добавьте данные одним из следующих способов.
-
Щелкните Power Pivot > Добавить в модель данных.
-
Выберите Вставка > Сводная таблица и установите флажок Добавить эти данные в модель данных в диалоговом окне «Создание сводной таблицы».
Диапазон или таблица будут добавлены в модель как связанная таблица. Дополнительные сведения о работе со связанными таблицами в модели см. в статье Добавление данных с помощью связанных таблиц Excel в Power Pivot.
Добавление данных в таблицу Power Pivot данных
В Power Pivot невозможно добавить строку в таблицу, введя текст непосредственно в новой строке, как это можно сделать на листе Excel. Но можно добавить строки , скопируйте и вставьте или обновите исходные данные и обновите модель Power Pivot.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Ознакомьтесь & по преобразованию и обучению Power Pivot
Общие сведения о редакторе запросов (Power Query)
Создание модели данных, оптимизированной для памяти, с помощью Excel и Power Pivot
Руководство. Импорт данных в Excel и создание модели данных
Определение источников данных, используемых в модели данных книги
Связи между таблицами в модели данных
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Любому бизнесу интересно заглянуть в будущее и правильно ответить на вопрос: «А сколько денег мы заработаем за следующий период?» Ответить на такого рода вопросы позволяют различные методики прогнозирования. В данной статье мы с вами рассмотрим несколько таких методик и произведем все необходимые расчеты в Excel. Еще больше про анализ данных в Excel мы рассказываем на нашем открытом курсе «Аналитика в Excel».
Постановка задачи
Исходные данные
Для начала, давайте определимся, какие у нас есть исходные данные и что нам нужно получить на выходе. Фактически, все что у нас есть, это некоторые исторические данные. Если мы говорим о прогнозировании продаж, то историческими данными будут продажи за предыдущие периоды.
Примечание. Собранные в разные моменты времени значения одной и той же величины образуют временной ряд. Каждое значение такого временного ряда называется измерением. Например: данные о продажах за последние 5 лет по месяцам — временной ряд; продажи за январь прошлого года — измерение.
Составляющие прогноза
Следующий шаг: давайте определимся, что нам нужно учесть при построении прогноза. Когда мы исследуем наши данные, нам необходимо учесть следующие факторы:
- Изменение нашей пронозируемой величины (например, продаж) подчиняется некоторому закону. Другими словами, в временном ряде можно проследить некую тенденцию. В математике такая тенденция называется трендом.
- Изменение значений в временном ряде может зависить от промежутка времени. Другими словами, при построении модели необходимо будет учесть коэффициент сезонности. Например, продажи арбузов в январе и августе не могут быть одинаковыми, т.к. это сезонный продукт и летом продажи значительно выше.
- Изменение значений в временном ряде периодически повторяется, т.е. наблюдается некоторая цикличность.
Эти три пункта в совокупность образуют регулярную составляющую временного ряда.
Примечание. Не обязательно все три элемента регулярной составляющей должны присутствовать в временном ряде.
Однако, помимо регулярной составляющей, в временном ряде присутствует еще некоторое случайное отклонение. Интуитивно это понятно – продажи могут зависеть от многих факторов, некоторые из которых могут быть случайными.
Вывод. Чтобы комплексно описать временной ряд, необходимо учесть 2 главных компонента: регулярную составляющую (тренд + сезонность + цикличность) и случайную составляющую.
Виды моделей
Следующий вопрос, на который нужно ответить при построении прогноза: “А какие модели временного ряда бывают?”
Обычно выделяют два основных вида:
- Аддитивная модель: Уровень временного ряда = Тренд + Сезонность + Случайные отклонения
- Мультипликативная модель: Уровень временного ряда = Тренд X Сезонность X Случайные отклонения
Иногда также выделают смешанную модель в отдельную группу:
- Смешанная модель: Уровень временного ряда = Тренд X Сезонность + Случайные отклонения
С моделями мы определились, но теперь возникает еще один вопрос: «А когда какую модель лучше использовать?»
Классический вариант такой:
— Аддитивная модель используется, если амплитуда колебаний более-менее постоянная;
— Мультипликативная – если амплитуда колебаний зависит от значения сезонной компоненты.
Пример:

Решение задачи с помощью Excel
Итак, необходимые теоретические знания мы с вами получили, пришло время применить их на практике. Мы будем с вами использовать классическую аддитивную модель для построения прогноза. Однако, мы построим с вами два прогноза:
- с использованием линейного тренда
- с использованием полиномиального тренда
Во всех руководствах, как правило, разбирается только линейный тренд, поэтому полиномиальная модель будет крайне полезна для вас и вашей работы!
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Модель с линейным трендом
Пусть у нас есть исходная информация по продажам за 2 года:

Учитывая, что мы используем линейный тренд, то нам необходимо найти коэффициенты уравнения
y = ax + b
где:
- y – значения продаж
- x – номер периода
- a – коэффициент наклона прямой тренда
- b – свободный член тренда
Рассчитать коэффициенты данного уравнения можно с помощью формулы массива и функции ЛИНЕЙН. Нам необходимо будет сделать следующую последовательность действий:
- Выделяем две ячейки рядом
- Ставим курсор в поле формул и вводим формулу =ЛИНЕЙН(C4:C27;B4:B27)
- Нажимаем Ctrl+Shift+Enter, чтобы активировать формулу массива
На выходе мы получили 2 числа: первое — коэффициент a, второе – свободный член b.

Теперь нам нужно рассчитать для каждого периода значение линейного тренда. Сделать это крайне просто — достаточно в полученное уравнение подставить известные номера периодов. Например, в нашем случае, мы прописываем формулу =B4*$F$4+$G$4 в ячейке I4 и протягиваем ее вниз по всем периодам.

Нам осталось рассчитать коэффициент сезонности для каждого периода. Учитывая, что у нас есть исторические данные за два года, разумно будет учесть это при расчете. Можем сделать следующим образом: в ячейке J4 прописываем формулу =(C4+C16)/СРЗНАЧ($C$4:$C$27)/2 и протягиваем вниз на 12 месяцев (т.е. до J15).

Что нам это дало? Мы посчитали, сколько суммарно продавалось каждый январь/каждый февраль и так далее, а потом разделили это на среднее значение продаж за все два периода.
То есть мы выяснили, как продажи двух январей отклонялись от средних продаж за два года, как продажи двух февралей отклонялись и так далее. Это и дает нам коэффициент сезонности. В конце формулы делим на 2, т.к. в расчете фигурировало 2 периода.
Примечание. Рассчитали только 12 коэффициентов, т.к. один коэффициент учитывает продажи сразу за 2 аналогичных периода.
Итак, теперь мы на финишной прямой. Нам осталось рассчитать тренд для будущих периодов и учесть коэффициент сезонности для них. Давайте амбициозно построим прогноз на год вперед.
Сначала создаем столбец, в котором прописываем номера будущих периодов. В нашем случае нумерация начинается с 25 периода.
Далее, для расчета значения тренда просто прописываем уже известную нам формулу =L4*$F$4+$G$4 и протягиваем вниз на все 12 прогнозируемых периодов.
И последний штрих — умножаем полученное значение на коэффициент сезонности. Вуаля, это и есть итоговый ответ в данной модели!
Модель с полиномиальным трендом
Конструкция, которую мы только что с вами построили, достаточно проста. Но у нее есть один большой минус — далеко не всегда она дает достоверные результаты.
Посмотрите сами, какая модель более точно аппроксимирует наши точки — линейный тренд (прямая зеленая линия) или полиномиальный тренд (красная кривая)? Ответ очевиден. Поэтому сейчас мы с вами и разберем, как построить полиномиальную модель в Excel.
Пусть все исходные данные у нас будут такими же. Для простоты модели будем учитывать только тренд, без сезонной составляющей.
Для начала давайте определимся, чем полиномиальный тренд отличается от обычного линейного. Правильно — формой уравнения. У линейного тренда мы разбирали обычный график прямой:

У полиномиального тренда же уравнение выглядит иначе:

где конечная степень определяется степенью полинома.
Т.е. для полинома 4 степени необходимо найти коэффициенты уравнения:

Согласитесь, выглядит немного страшно. Однако, ничего страшного нет, и мы с легкостью можем решить эту задачку с помощью уже известных нам методов.
- Ставим в ячейку F4 курсор и вводим формулу =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4});1;1). Функция ЛИНЕЙН позволяет произвести расчет коэффициентов, а с помощью функции ИНДЕКС мы вытаскиваем нужный нам коэффициент. В данном случае за выбор коэффициента отвечает самый последний аргумент. У нас стоит 1 — это коэффициент при самой высокой степени (т.е. при 4 степени, коэффициент). Кстати, узнать о самых полезных математических формулах Excel можно в нашем бесплатном гайде «Математические функции Excel».
- Аналогично прописываем формулу =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4});1;2) в ячейке ниже.
- Делаем такие же действия, пока не найдем все коэффициенты.
Кстати говоря, мы можем легко сами себя проверить. Давайте построим график наших продаж и добавим к нему полиномиальный тренд.
- Выделяем столбец с продажами
- Выбираем «Вставка» → «График» → «Точечный» → «Точечная диаграмма»
- Нажимаем на любую точку графика правой кнопкой мыши и выбираем «Добавить линию тренда»
- В открывшемся справа меню выбираем «Полиномиальная модель», меняем степень на 4 и ставим галочку на «Показывать уравнение на диаграмме»
Теперь вы наглядно можете видеть, как рассчитанный тренд аппроксимирует исходные данные и как выглядит само уравнение. Можно сравнить уравнение на графике с вашими коэффициентами. Сходится? Значит сделали все верно!
Помимо всего прочего, вы можете сразу оценить точность аппроксимации (не полностью, но хотя бы первично). Это делается с помощью коэффициента R^2. Тут у вас снова есть два пути:
- Вы можете вывести коэффициент на график, поставив галочку «Поместить на диаграмму величину достоверности аппроксимации»
- Вы можете рассчитать коэффициент R^2 самостоятельно по формуле =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4};;1);3;1)
Заключение
Мы с вами подробно разобрали вопрос прогнозирования — изучили необходимые термины и виды моделей, построили аддитивную модель в Excel с использованием линейного и полиномиального тренда, а также научились отображать результаты своих вычислений на графиках. Все это позволит вам эффективно внедрять полученные знания на работе, усложнять существующие модели и уточнять прогнозы. Чем большим количеством методов и инструментов вы будете владеть, тем выше будет ваш профессиональный уровень и статус на рынке труда.
Если вас интересуют еще какие-то модели прогнозирования — напишите нам об этом, и мы постараемся осветить эти темы в дальнейших своих статьях! Или запишитесь на курс «Excel Academy» от SF Education, где мы рассказываем про возможности Excel, необходимые для анализа.
Автор: Алексанян Андрон, эксперт SF Education
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Блог SF Education
Data Science
5 примеров экономии времени в Excel
Что для работодателя главное в сотруднике? Добросовестность, ответственность, профессионализм и, конечно же, умение пользоваться отведенным временем! Предлагаем познакомиться с очень нужными, на наш взгляд,…
Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа № 15 имени Пяти Героев Советского Союза
Иследовательская работа
Тема:
«Создание и исследование моделей
в электронной таблице Excel»
Секция информатики
Выполнила: Сотникова Полина Андреевна,
ученица 10 «А» класса
Руководитель: Титаренко Алексей Анатольевич,
учитель информатики
г. Хабаровск
2016
Содержание
Актуальность темы…………………………………………………………………………………………………………………3
Введение………………………………………………………………………………………………………………………………..4
Создание информационных моделей…………………………………………………………………………………..5
Формулы в Excel…………………………………………………………………………………………………………………….7
Этапы разработки и исследования моделей………………………………………………………………………..10
Исследование физических моделей в электронных таблицах…………………………………………..11
Исследование биологической модели развития популяций………………………………………………14
Оптимизационное моделирование в экономике…………………………………………………………………17
Заключение…………………………………………………………………………………………………………………………….20
Список использованной литературы…………………………………………………………………………………….21
2
Актуальность темы
Часто для исследования предметов, процессов и явлений человек создает модели окружающего мира.
Наглядные модели часто используются в процессе обучения. На уроке географии мы изучаем нашу планету используя её модели – карты и глобусы, при изучении химии мы используем модели молекул и кристаллических решеток, изучаем строение человека по анатомическим муляжам скелета и органов на биологии.
Модели играют чрезвычайно важную роль в проектировании и создании различных технических устройств, машин и механизмов, зданий, электрических цепей и т.д. Без предварительного создания чертежей невозможно изготовить даже простую деталь, не говоря уже о сложном механизме. Кроме чертежей,в проектировании часто изготавливают макеты. Разработка электрической схемы обязательно предшествует созданию электрических цепей.
Развитие науки невозможно без создания теоретических моделей (теорий, законов, гипотез), отражающих строение, свойства и поведение реальных объектов. Соответствие теоретических моделей действительности проверяется с помощью опытов и экспериментов.
Все художественное творчество фактически является процессом создания моделей. Например, такой литературный жанр, как басня, переносит реальные отношения между людьми на отношения между животными и фактически создает модели человеческих отношений.
3
Введение
Моделирование – это метод познания, состоящий в создании и исследовании моделей – неких новых объектов, которые отражают существенные особенности изучаемого объекта, явления или процесса.Модель – это некий новый объект, который отражает существенные особенности изучаемого объекта,явления или процесса. Модели позволяют представить в наглядной форме объекты и процессы, недоступные для непосредственного восприятия (очень большие или очень маленькие объекты, очень быстрые или очень медленные процессы).
Компьютерные модели стали обычным инструментом математического моделирования и применяются в физике, астрофизике, механике, химии, биологии, экономике, социологии, метеорологии, других науках и прикладных задачах в различных областях радиоэлектроники, машиностроения, автомобилестроения и прочих. Компьютерные модели используются для получения новых знаний о моделируемом объекте или для приближенной оценки поведения систем, слишком сложных для аналитического исследования. Компьютерное моделирование является одним из эффективных методов изучения сложных систем. Компьютерные модели проще и удобнее исследовать в силу их возможности проводить вычислительные эксперименты, в тех случаях когда реальные эксперименты затруднены из-за финансовых или физических препятствий или могут дать непредсказуемый результат. Логичность и формализованность компьютерных моделей позволяет определить основные факторы, определяющие свойства изучаемого объекта-оригинала (или целого класса объектов). В частности, моделирование в электронных таблицах может быть использовано для описания ряда объектов, обладающих одинаковыми наборами свойств. С помощью таблиц могут быть построены как статические, так и динамические информационные модели в различных предметных областях, а простота использования программ создания таблиц помогает составлять модели людям без знания сложных языков программирования.
4
Создание информационных моделей:
Информационные модели отражают различные типы систем объектов, в которых реализуются различные структуры взаимодействия и взаимосвязи между элементами системы. Для отражения систем с различными структурами используются различные типы информационных моделей: табличные, иерархические и сетевые. В программе Excelдоступно создание табличного типа моделей.
Табличные информационные модели:
Одним из наиболее часто используемых типов информационных моделей является прямоугольная таблица, состоящая из столбцов и строк. Такой тип моделей применяется для описания ряда объектов, обладающих одинаковыми наборами свойств.
В табличной информационной модели обычно перечень объектов размещен в ячейках первого столбца таблицы, а значения их свойств – в других столбцах.
С помощью электронной таблицы Excelпостроим таблицу стоимости продуктов. В первом столбце таблицы будет содержаться перечень продуктов, а во втором – интересующее нас свойство (цена).
С помощью специальных инструментов, встроенных в программу Excelможно визуализировать таблицу, представив ее в виде графика или круговой диаграммы. Для этого нужно выделить таблицу, зайти во вкладку «Вставка» и выбрать нужный формат визуализации.
5
Визуализация круговой диаграммой
Визуализация столбчатой диаграммой
6
Формулы в Excel
В таблицах Excelможно не только вводить и визуализировать данные, но и производить простые и сложные расчеты над данными.Все это реализуется при помощи формул в ячейках. Формула выполняет вычисления или другие действия с данными в листе.
Порядок ввода формулы
Для начала определим, в какой ячейке должен стоять результат расчета. Затем выделим эту ячейку (нажмем на нее левой кнопкой мышки и ячейка станет активной).
Вводить формулу надо со знака равенства. Это надо для того, чтобы Excel понял, что в ячейку вводится именно формула, а не данные.
Выделим произвольную ячейку, например D1. В строке формул введем =2+3 и нажмем Enter. В ячейке появится результат (5). А в строке формул сверху останется сама формула.
При обработке формулы с большим количеством вычислений, наблюдается определенный приоритет.
- В первую очередь выполняются выражения внутри скобок.
- Умножение и деление имеют более высокий приоритет чем сложение и вычитание.
- Операторы с одинаковым приоритетом выполняются слева направо.
7
Так, в примере выше, сначала выполняется действие в скобках (5-4=1), потом первое умножение (100*1=100), затем второе умножение (38*2=76), сложение (100+26=126), и в конце вычитание (126-76=50).
Также, можно выполнять действия над числами, содержащимися в ячейках. Для этого, вместо цифр, в формулах нужно использовать ссылки на ячейки – букву латинского алфавита, обозначающую столбец и цифру, обозначающую строку.
Так, в ячейку D3 была введена формула D1+D2. В результате сложились числа,стоящие в ячейках D1(4) и D2(6) и полученный результат – 10 был записан в ячейку D3.
Для складывания нескольких ячеек используется функция СУММ. Для суммирования трех чисел формула запишется следующим образом
Но можно облегчить себе работу и вместо перечисления каждой ячейки записать диапазон, с помощью двоеточия
Истинное значение функции СУММ раскрывается, когда необходимо сложить большое количество ячеек в Excel. В примере ниже требуется просуммировать 12 значений. Функция СУММ позволяет сделать это несколькими щелчками мышью, если же использовать оператор сложения, то провозиться придется долго.
8
В таблицах Excelможно не только проводить простейшие вычисления над числами, но и возводить в степень, извлекать корень, производить сравнение чисел и многое другое.
9
Этапы разработки и исследования моделей
Использование компьютера для исследования информационных моделей различных объектов и систем позволяет изучить их изменения в зависимости от значения тех или иных параметров. Процесс разработки моделей и их исследования на компьютере можно разделить на несколько основных этапов.
На первом этапе исследования объекта или процесса обычно строится описательная информационная модель. Такая модель выделяет существенные с точки зрения целей проводимого исследования параметры объекта, а несущественными параметрами пренебрегает.
На втором этапе создается формализованная модель, то есть описательная информационная модель записывается с помощью какого-либо формального языка. В такой модели с помощью формул, уравнений, неравенств и пр. фиксируются формальные соотношения между начальными и конечными значениями свойств объектов, а также накладываются ограничения на допустимые значения этих свойств.
Однако далеко не всегда удается найти формулы, явно выражающие искомые величины через исходные данные. В таких случаях используются приближенные математические методы, позволяющие получать результаты с заданной точностью.
На третьем этапе необходимо формализованную информационную модель преобразовать в компьютерную модель, то есть выразить ее на понятном для компьютера языке. Существуют два принципиально различных пути построения компьютерной модели:
1) построение алгоритма решения задачи и его кодирование на одном из языков программирования;
2) построение компьютерной модели с использованием одного из приложений (электронных таблиц, СУБД и пр.).
В процессе создания компьютерной модели полезно разработать удобный графический интерфейс, который позволит визуализировать формальную модель, а также реализовать интерактивный диалог человека с компьютером на этапе исследования модели.
Четвертый этап исследования информационной модели состоит в проведении компьютерного эксперимента. Если компьютерная модель существует в виде программы на одном из языков программирования, ее нужно запустить на выполнение и получить результаты.
Если компьютерная модель исследуется в приложении, например в электронных таблицах, можно провести сортировку или поиск данных, построить диаграмму или график и так далее.
Пятый этап состоит в анализе полученных результатов и корректировке исследуемой модели. В случае различия результатов, полученных при исследовании информационной модели, с измеряемыми параметрами реальных объектов можно сделать вывод, что на предыдущих этапах построения модели были допущены ошибки или неточности. Например, при построении описательной качественной модели могут быть неправильно отобраны существенные свойства объектов, в процессе формализации могут быть допущены ошибки в формулах и так далее. В этих случаях необходимо провести корректировку модели, причем уточнение модели может проводиться многократно, пока анализ результатов не покажет их соответствие изучаемому объекту.
10
Исследование физических моделей в электронных таблицах:
Рассмотрим процесс построения и исследования модели на конкретном примере движения тела, брошенного под углом к горизонту.
Задача: В процессе тренировке теннисистов используются автоматы по бросания мячика в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в мишень определенного размера, находящуюся на известном расстоянии.
Качественная описательная модель: Сначала построим качественную описательную модель процесса движения тела с использованием физических объектов, понятия и законов, то есть в данном случае идеализированную модель движения объекта. Из условия задачи можно сформулировать следующие основные предположения:
- Мячик мал по сравнению с Землей, поэтому его можно считать материальной точкой;
- Изменение высоты мячика мало, поэтому ускорение свободного падения можно считать постоянной величиной g= 9,8 мс и движение по оси ОУ можно считать равноускоренным;
- Скорость бросания тела мала, поэтому сопротивлением воздуха можно пренебречь и движение по оси ОХ можно считать равномерным
Формальная модель: Для формализации модели используем известные из курса физики формулы равномерного и равноускоренного движения. При заданных начальной скорости v0 и угле бросания aзначения координат дальности полета х и высоты у от времени можно записать следующими формулами:
X=v0*cos*t;
Y=v0*sinα*t – g*t²/2
Пусть мишень высотой h будет размещаться на расстоянии sот автомата. Из первой формулы выражаем время, которое понадобится мячику, чтобы преодолеть расстояние s:
t = s/(v0*cos2α)
Представляем это значение для tв формулу для у. Получаем l – высоту мячика над землей на расстоянии s:
l = s*tgα – g*s²/(2*v0²*cosα²)
Формализуем теперь условие попадания мячика в мишень. Попадание произойдет, если значение высоты lмячика в мишень. Попадание произойдет, если значение высоты lмячика будет удовлетворять условию в форме неравенства:
0≤l ≤ h
Если l<0, то это означает «недолет», а если l>h, то это означает «перелет».
Создание модели:
- Для ввода начальной скорости будем использовать ячейку В1, а для ввода угла – ячейку В2
- Введем в ячейки А5:А18 значения времени с интервалом в 0,2 с.
- В ячейки В5 и С5 введем формулы:
11
=$B$1*cos(Радианы($B$2))*А5
=$B$1*sin(РАДИАНЫ($B$2))*A5-4,9*A5*A5
- Скопируем формулы в ячейки В6:В18 и С6:С18 соответственно.
Визуализируем модель, построив график зависимости координаты у от координаты х (траекторию движения тела).
- Построить диаграмму типа График, в которой используется в качестве категории диапазон ячеек В5:В18, а в качестве значений – диапазон ячеек С5:С18.
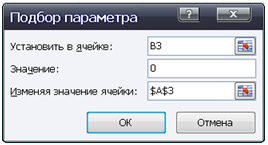
Исследование модели: Исследуем модель и определим с заданной точностью 0,1 диапазон изменений угла, который обеспечивает попадание в мишень, находящуюся на расстоянии 30 м и имеющую высоту 1 м, при заданной начальной скорости 18 м/с. Воспользуемся для этого методом Подбор параметра.
- Установить для ячеек точность один знак после запятой
12
- Ввести в ячейки B21, B22 и В23 значения расстояния до мишени S = 30 м, начальной скорости Vо = 18 м/с и угла α= 35⁰, а в ячейку В25 – формулу для вычисления высоты мячика над поверхностью для заданных условий:
=B21*TAN(РАДИАНЫ(B23))-(9,81*B21^2)/(2*B22^2*COS(РАДИАНЫ(B23))^2)
Для заданных начальных условий определим углы, которые обеспечивают попадание в мишень на высотах 0 и 1 м.
- Выделить ячейку В25 и ввести команду [Сервис-Подбор параметра…]. На появившейся диалоговой панели ввести в поле Значение: наименьшую высоту попадания в мишень ( то есть 0). В поле Изменяя значение ячейки: ввести адрес ячейки, содержащей значение угла (в данном случае $B$23).
- В ячейке В23 появится значение 32,6. Повторить процедуру подбора параметра для максимальной высоты попадания в мишень – в ячейке В23 получим значение 36,1.
Таким образом, исследование компьютерной модели в электронных таблицах показало, что существует диапазон значений для угла бросания от 32,6 до 36,1⁰, который обеспечивает попадание в мишень высотой 1 м, находящуюся на расстоянии 30 м, мячиком брошенным со скоростью 18 м/с.
13
Исследование биологической модели развития популяций
В биологии при исследовании развития биосистем строятся динамические модели изменения численности популяций различных живых существ (бактерий, рыб, животных и пр.) с учетом различных факторов. Взаимовлияние популяций рассматривается в моделях типа «хищник-жертва».
Формальная модель. Изучение динамики численности популяций естественно начать с простейшей модели неограниченного роста, в которой численность популяции ежегодно увеличивается на определенный процент. Математическую модель можно записать с помощью рекуррентной формулы, связывающей численность популяции следующего года с численностью популяции текущего года, с использованием коэффициента роста а:
X(n+1) = a * x(n)
Например, если ежегодный прирост численности популяции составляет 5%, то а = 1,05. В модели ограниченного роста учитывается эффект перенаселенности, связанный с нехваткой питания, болезнями и так далее, который замедляет рост популяции с увеличением ее численности. Введем коэффициент перенаселенности b, значение которого обычно существенно меньше а (b<<а). Тогда коэффициент ежегодного увеличения численности равен (а — b*х(n)) и формула принимает вид:
X(n+1) = (a – b * x(n)) * x(n)
В модели ограниченного роста с отловом учитывается, что на численность популяций промысловых животных и рыб оказывает влияние величина ежегодного отлова. Если величина ежегодного отлова равна с, то формула принимает вид:
X(n+1) = (a – b * x(n)) * x(n) — c
Популяции обычно существуют не изолированно, а во взаимодействии с другими популяциями. Наиболее важным типом такого взаимодействия является взаимодействие между жертвами и хищниками (например, караси-щуки, зайцы-волки и так далее). В модели «хищник-жертва» количество жертв х(n) и количество хищников у(n) связаны между собой. Количество встреч жертв с хищниками можно считать пропорциональным произведению количеств жертв и хищников, а коэффициент f характеризует возможность гибели жертвы при встрече с хищниками. В этом случае численность популяции жертв ежегодно уменьшается на величину f * х(n)* у(n) и формула для расчета численности жертв принимает вид:
X(n+1) = (a – b * x(n)) * x(n) – c – f* x(n) * y(n)
Численность популяции хищников в отсутствие жертв (в связи с отсутствием пищи) уменьшается, что можно описать рекуррентной формулой
Y(n+1) = d* y(n)
где значение коэффициента d < 1 характеризует скорость уменьшения численности популяции хищников. Увеличение популяции хищников можно считать пропорциональной произведению собственно количеств жертв и хищников, а коэффициент е характеризует величину роста численности хищников за счет жертв. Тогда для численности хищников можно использовать
14
формулу:
y(n+1) = d*y(n) + e*x(n)*y(n)
Компьютерная модель. Построим в электронных таблицах компьютерную модель, позволяющую исследовать численность популяций с использованием различных моделей: неограниченного роста, ограниченного роста, ограниченного роста с отловом и «хищник—жертва».
- В ячейки В1 и В6 внести начальные значения численности популяций жертв и хищников.
В ячейки В2:В5 внести значения коэффициентов a, b, cи f, влияющих на изменение численности жертв.
В ячейки В7 и В8 внести значения коэффициентов dи е, влияющих на изменение численности хищников
В столбце Dбудем вычислять численность популяции в соответствии с моделью неограниченного роста, в столбце Е – ограниченного роста, в столбце F–ограниченного роста с отловом, в столбцах Gи H–«хищник-жертва».
- В ячейки D1, E1, F1 и G1 внести значения начальной численности популяций жертв, в ячейку Н1 – хищников.
В ячейку D2 внести рекуррентную формулу неограниченного роста =$B$2*D1
В ячейку Е2 внести рекуррентную формулу неограниченного роста =($B$2-$B$3*E1)*E1
В ячейку F2 внести рекуррентную формулу ограниченного роста с отловом =($B$2-$B$3*F1)*F1-$B$4
В ячейку G2 внести рекуррентную формулу изменения количества жертв =($B$2-$B$3*G1)*G1-$B$4-$B$5*G1*H1
В ячейку Н2 внести рекуррентную формулу изменения количества хищников =$B$7*H1+$B$8*G1*H1
- Скопировать внесенные формулы в ячейки столбцов командой [Правка-Заполнить-Вниз].
В ячейках столбцов ознакомиться с динамикой изменения численности популяций.
15
- Выделить столбцы данных и построить диаграмму типа График. Появятся графики изменения численности популяций в соответствии с моделями неограниченного роста, ограниченного роста, ограниченного роста с отловом, моделью хищник-жертва.
Исследование модели: Изменяя значения начальных численностей популяций, а также коэффициенты, можно получать различные варианты изменения численности популяций в зависимости от времени.
16
Оптимизационное моделирование в экономике
В сфере управления сложными системами (например, в экономике) применяется оптимизационное моделирование, в процессе которого осуществляется поиск наиболее оптимального пути развития системы.
Критерием оптимальности могут быть различные параметры; например, в экономике можно стремиться к максимальному количеству выпускаемой продукции, а можно к ее низкой себестоимости. Оптимальное развитие соответствует экстремальному (максимальному или минимальному) значению выбранного целевого параметра.
Развитие сложных систем зависит от множества факторов (параметров), следовательно, значение целевого параметра зависит от множества параметров. Выражением такой зависимости является целевая функция
К = F(X1,X2,…,Xn),
где К — значение целевого параметра; X1,X2,…,Xn — параметры, влияющие на развитие системы.
Цель исследования состоит в нахождении экстремума этой функции и определении значений параметров, при которых этот экстремум достигается. Если целевая функция нелинейна, то она имеет экстремумы, которые находятся определенными методами.
Однако часто целевая функция линейна и, соответственно, экстремумов не имеет. Задача поиска оптимального режима при линейной зависимости приобретает смысл только при наличии определенных ограничений на параметры. Если ограничения на параметры (система неравенств) также имеют линейный характер, то такие задачи являются задачами линейного программирования. (Термин «линейное программирование» в имитационном моделировании понимается как поиск экстремумов линейной функции, на которую наложены ограничения.) Рассмотрим в качестве примера экономического моделирования поиск вариантов оптимального раскроя листов материала на заготовки определенного размера.
Содержательная постановка проблемы. В ходе производственного процесса из листов материала получают заготовки деталей двух типов А и Б тремя различными способами, при этом количество получаемых заготовок при каждом методе различается.
|
Тип Заготовки |
1 способ раскроя |
2 способ раскроя |
3 способ раскроя |
|
А |
10 |
3 |
8 |
|
Б |
3 |
6 |
4 |
Необходимо выбрать оптимальное сочетание способов раскроя, для того чтобы получить 500 заготовок первого типа и 300 заготовок второго типа при расходовании наименьшего количества листов материала.
Формальная модель. Параметрами, значения которых требуется определить, являются количества листов материала, которые будут раскроены различными способами:
Х1 — количество листов, раскроенное способом 1;
Х2 — количество листов, раскроенное способом 2;
Х3 — количество листов, раскроенное способом 3.
Тогда целевая функция, значением которой является количество листов материала, примет вид:
17
F = Х1+ Х2 + Х3.
Ограничения определяются значениями требуемых количеств заготовок типа А и Б, тогда с учетом количеств заготовок, получаемых различными способами, должны выполняться два равенства: 10Х1+ ЗХ2 + 8Х3 = 500;
ЗХ1 + 6Х2 + 4Х3 = 300.
Кроме того, количества листов не могут быть отрицательными, поэтому должны выполняться неравенства:
X1>= 0; Х2>= 0; Х3 >= 0.
Таким образом, необходимо найти удовлетворяющие ограничениям значения параметров, при которых целевая функция принимает минимальное значение. Компьютерная модель. Будем искать решение задачи путем создания и исследования компьютерной модели в электронных таблицах Excel.
Оптимизационное моделирование
- Ячейки В2, С2 и D2 выделить для значений параметров Х1, Х2 и Х3.
В ячейку В4 ввести формулу для вычисления целевой функции:
=В2+С2+D2
В ячейку В7 ввести формулу вычисления количества заготовок типа А:
=10*B2+3*C2+8*D2.
В ячейку В8 ввести формулу вычислений количества заготовок типа Б:
=3*B2+6*C2+4*D2
Исследование модели: Для поиска оптимального набора значений параметров, который соотвествует минимальному значению целевой функции, воспользоваться надстройкой электронных таблиц Поиск решения.
- На вкладке Данные нажмите кнопку Поиск решения.
- На появившейся диалоговой панели Поиск решения установить:
- Адрес целевой ячейки
- Вариант оптимизации значения целевой ячейки (максимизация, минимизация или подбор значения)
- Адреса ячеек, значения которых изменяются в процессе поиска решения ( в которых хранятся значения параметров)
18
- Ограничения (типа «=» для ячеек, хранящих количество деталей, и типа «≥» для параметров).
- Щелкнуть по кнопке Выполнить. В ячейке целевой функции появится значение 69,4, а в ячейках параметров значения 0,11,58.
Таким образом, для изготовления 500 деталей А и 300 деталей Б требуется 71 лист материала, при этом 12 листов нужно раскроить по второму, а 59 по третьему способу.
19
Заключение
Моделирование глубоко проникает в теоретическое мышление. Более того, развитие любой науки в целом можно трактовать — в весьма общем, но вполне разумном смысле, — как «теоретическое моделирование». Важная познавательная функция моделирования состоит в том, чтобы служить импульсом, источником новых теорий. Нередко бывает так, что теория первоначально возникает в виде модели, дающей приближённое, упрощённое объяснение явления, и выступает как первичная рабочая гипотеза, которая может перерасти в «предтеорию» — предшественницу развитой теории. При этом в процессе моделирования возникают новые идеи и формы эксперимента, происходит открытие ранее неизвестных фактов. Такое «переплетение» теоретического и экспериментального моделирования особенно характерно для развития физических теорий.
Моделирование — не только одно из средств отображения явлений и процессов реального мира, но и — несмотря на описанную выше его относительность — объективный практический критерий проверки истинности наших знаний, осуществляемой непосредственно или с помощьюустановления их отношения с другой теорией, выступающей в качестве модели, адекватность которой считается практически обоснованной. Применяясь в органическом единстве с другими методами познания, моделирование выступает как процесс углубления познания, его движения от относительно бедных информацией моделей к моделям более содержательным, полнее раскрывающим сущность исследуемых явлений действительности.
В своем проекте я показала, как использовать электронные таблицы Excelдля моделирования и анализа созданных моделей.
20
Список использованной литературы
- Н. Угринович «Информатика и информационные технологии»
- Н. Угринович «Информатика и ИКТ»
- http://on-line-teaching.com/excel/lsn003.html
- http://www.excel-office.ru/formulivexcel/formulivexcel
21
Преимущества сводной по Модели Данных
При построении сводной таблицы в Excel в первом же диалоговом окне, где нас просят задать исходный диапазон и выбрать место для вставки сводной, есть внизу неприметная, но очень важная галочка — Добавить эти данные в Модель Данных (Add this data to Data Model) и, чуть выше, переключатель Использовать модель данных этой книги (Use Data Model of this workbook):
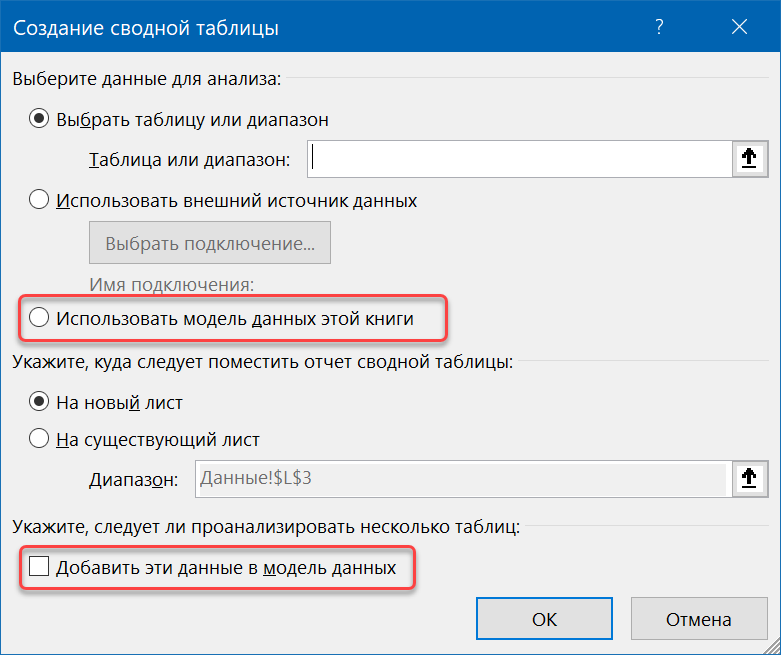
К сожалению, очень многие даже давно знакомые со сводными таблицами и успешно применяющие их в работе пользователи, порой не очень понимают смысл этих опций и никогда их не используют. И зря. Ведь создание сводной по Модели Данных даёт нам несколько очень важных преимуществ по сравнению с классической сводной таблицей Excel.
Однако, перед тем, как рассматривать эти «плюшки» вблизи, давайте сначала разберёмся с тем, что такое, собственно, эта Модель Данных?
Что такое Модель Данных
Модель Данных (сокращенно — МД или DM=Data Model) — это специальная область внутри файла Excel, куда можно где можно хранить табличные данные — одну или несколько таблиц связанных, при желании, между собой. По сути, это маленькая база данных (OLAP-куб), встроенная внутрь книги Excel. По сравнению с классическим хранением данных в виде обычных (или умных) таблиц на листах самого Excel, у Модели Данных есть несколько серьезных преимуществ:
- Размер таблиц может достигать 2 млрд. строк, а на лист Excel вмещается чуть больше 1 млн.
- Не смотря на гигантские размеры, обработка таких таблиц (фильтрация, сортировка, вычисления по ним, построение сводных и т.д.) выполняются очень быстро — гораздо быстрее, чем в самом Excel.
- С данными в Модели можно производить дополнительные (при желании — весьма сложные) вычисления с помощью встроенного языка DAX.
- Вся информация, загруженная в Модель Данных, очень сильно сжимается с помощью специального встроенного архиватора и весьма умеренно увеличивает размер исходного Excel-файла.
Управлением Моделью и вычислениями по ней занимается специальная встроенная в Microsoft Excel надстройка — Power Pivot, о которой я уже писал. Чтобы её включить, на вкладке Разработчик нажмите кнопку Надстройки COM (Developer — COM Add-ins) и поставьте соответствующую галочку:
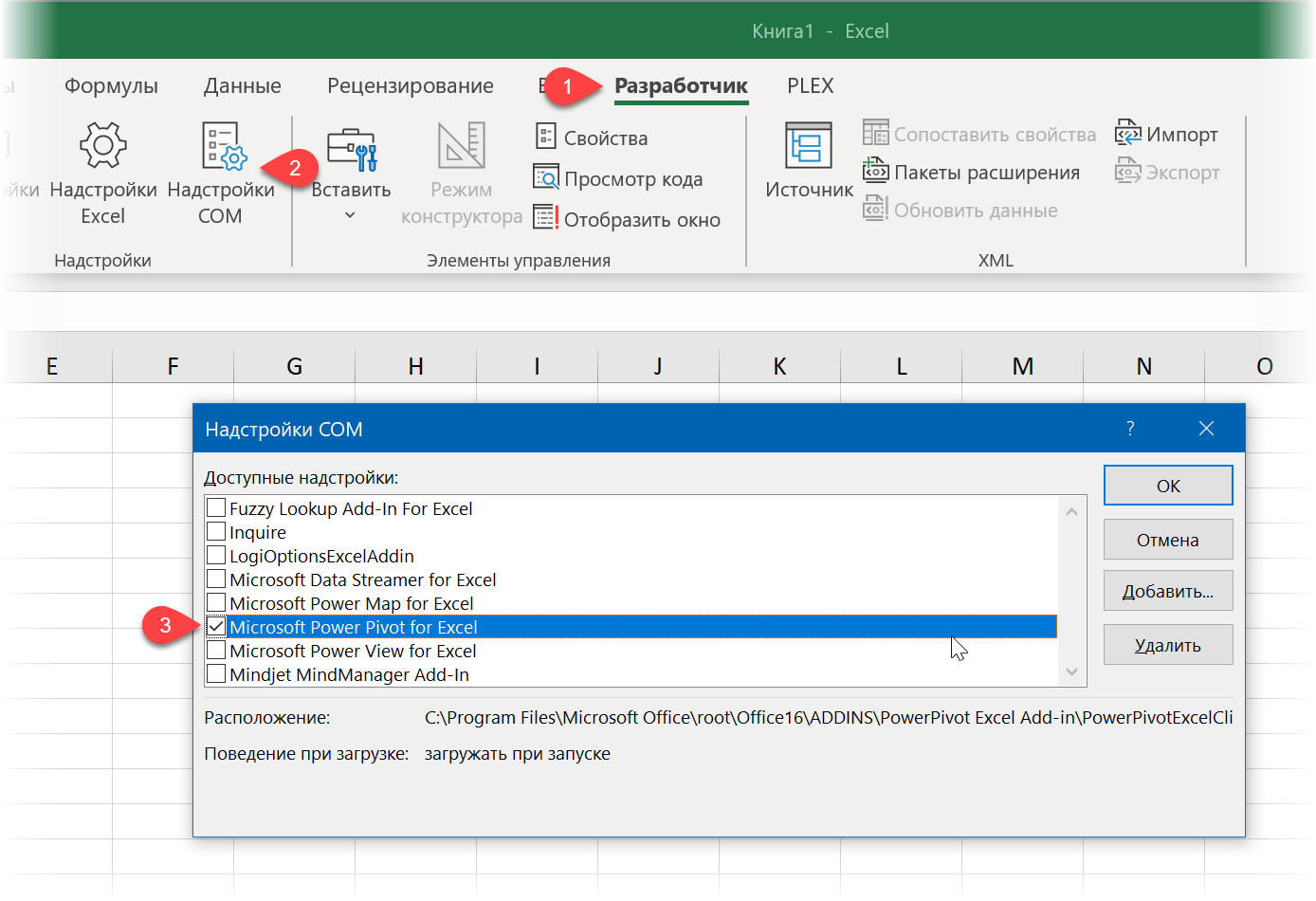
Если вкладки Разработчик (Developer) у вас на ленте не видно, то включить её можно через Файл — Параметры — Настройка ленты (File — Options — Customize Ribbon). Если же в показанном выше окне в списке COM-надстроек у вас нет Power Pivot, то значит она не входит в вашу версию Microsoft Office 
На появившейся вкладке Power Pivot будет большая салатового цвета кнопка Управление (Manage), нажатие на которую и откроет поверх Excel окно Power Pivot, где мы и увидим содержимое Модели Данных текущей книги:
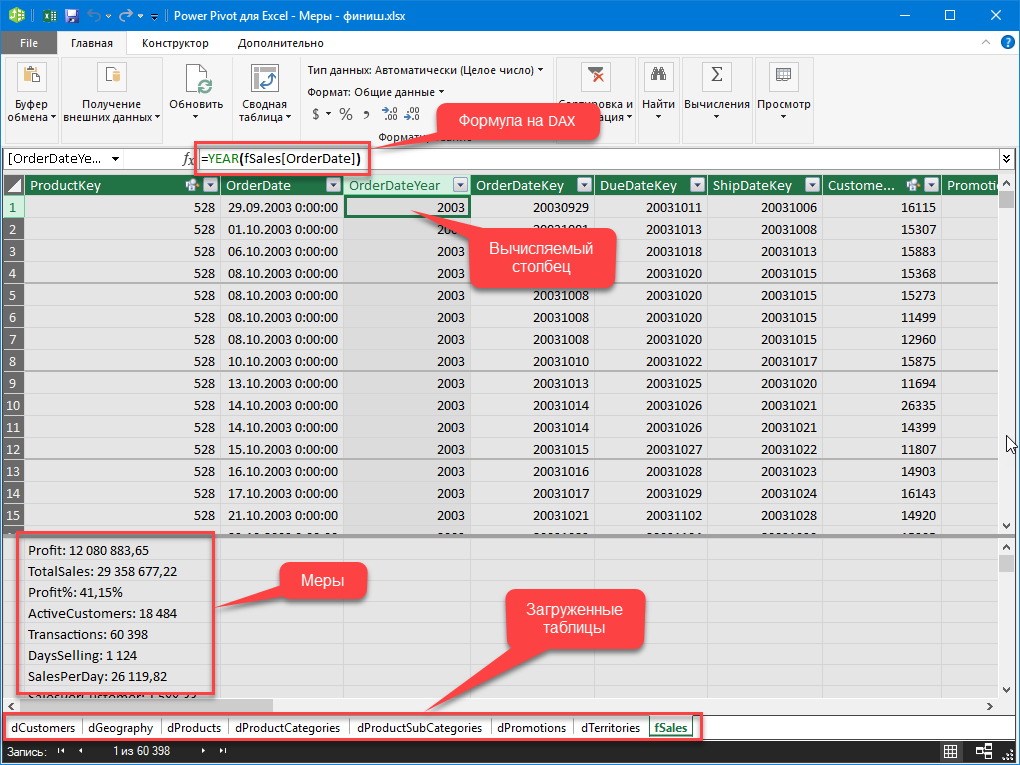
Важное замечание по ходу: книга Excel может содержать только одну Модель Данных.
Грузим таблицы в Модель Данных
Для загрузки данных в Модель сначала превращаем таблицу в динамическую «умную» сочетанием клавиш Ctrl+T и даём ей понятное имя на вкладке Конструктор (Design). Это обязательный этап.
Затем можно использовать любой из трех способов, на выбор:
- Жмём кнопку Добавить в модель (Add to Data Model) на вкладке Power Pivot на вкладке Главная (Home).
- Выбираем команды Вставка — Сводная таблица (Insert — Pivot Table) и включаем флажок Добавить эти данные в Модель данных (Add this data to Data Model). В этом случае по загруженным в Модель данным сразу строится ещё и сводная таблица.
- На вкладке Данные (Data) жмём на кнопку Из таблицы/диапазона (From Table/Range), чтобы загрузить нашу таблицу в редактор Power Query. Этот путь самый долгий, но, при желании, здесь можно произвести дополнительную зачистку данных, правки и всяческие трансформации, в которых Power Query очень силён.
Затем причёсанные данные выгружаются в Модель командой Главная — Закрыть и загрузить — Закрыть и загрузить в… (Home — Close&Load — Close&Load to…). В открывшемся окне выбираем вариант Только создать подключение (Only create connection) и, главное, ставим галочку Добавить эти данные в Модель данных (Add this data to Data Model).
Строим сводную по Модели Данных
Чтобы построить сводную Модели Данных можно использовать любой из трёх подходов:
- Нажать кнопку Сводная таблица (Pivot Table) в окне Power Pivot.
- Выбрать в Excel команды Вставка — Сводная таблица и переключиться в режим Использовать модель данных этой книги (Insert — Pivot Table — Use this workbook’s Data Model).
- Выбираем команды Вставка — Сводная таблица (Insert — Pivot Table) и включаем флажок Добавить эти данные в Модель данных (Add this data to Data Model). Текущая «умная» таблица будет загружена в Модель и по всей Модели будет построена сводная таблица.
Теперь, когда мы разобрались с тем, как загружать данные в Модель Данных и строить по ним сводную, давайте изучем те выгоды и преимущества, которые нам это даёт.
Преимущество 1. Связи между таблицами без помощи формул
Обычная сводная может быть построена только по данным из одной исходной таблицы. Если же у вас их несколько, например, продажи, прайс, справочник по клиентам, реестр договоров и т.д., то сначала придется собирать данные из всех таблиц в одну с помощью функций типа ВПР (VLOOKUP), ИНДЕКС (INDEX), ПОИСКПОЗ (MATCH), СУММЕСЛИМН (SUMIFS) и им подобных. Это долго, муторно и вгоняет ваш Excel в «задумчивость» при большом количестве данных.
В случае сводной по Модели Данных всё гораздо проще. Достаточно один раз настроить связи между таблицами в окне Power Pivot — и дело в шляпе. Для этого на вкладке Power Pivot жмём кнопку Управление (Manage) и затем в появившемся окне — кнопку Представление диаграммы (Diagram View). Останется перетащить общие (ключевые) названия столбцов (поля) между таблицами, чтобы создать связи:
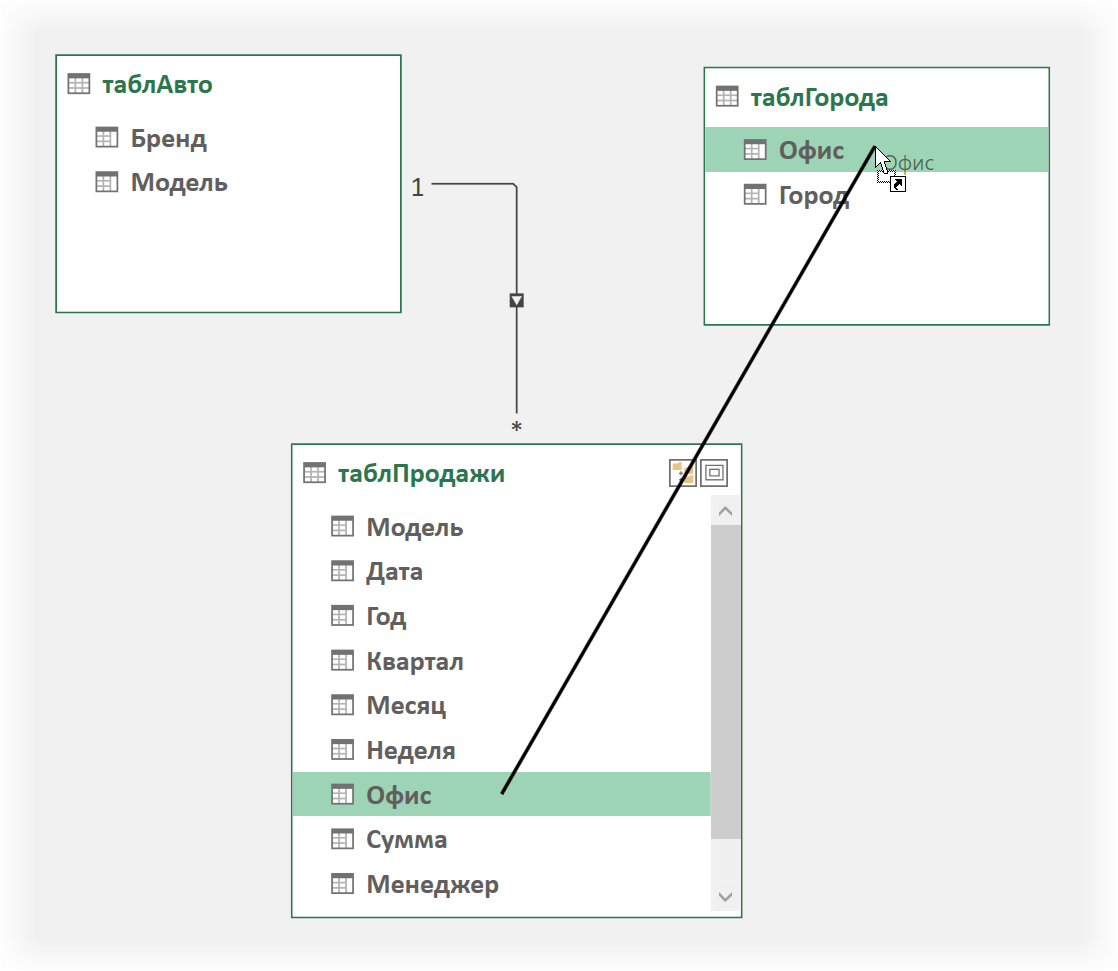
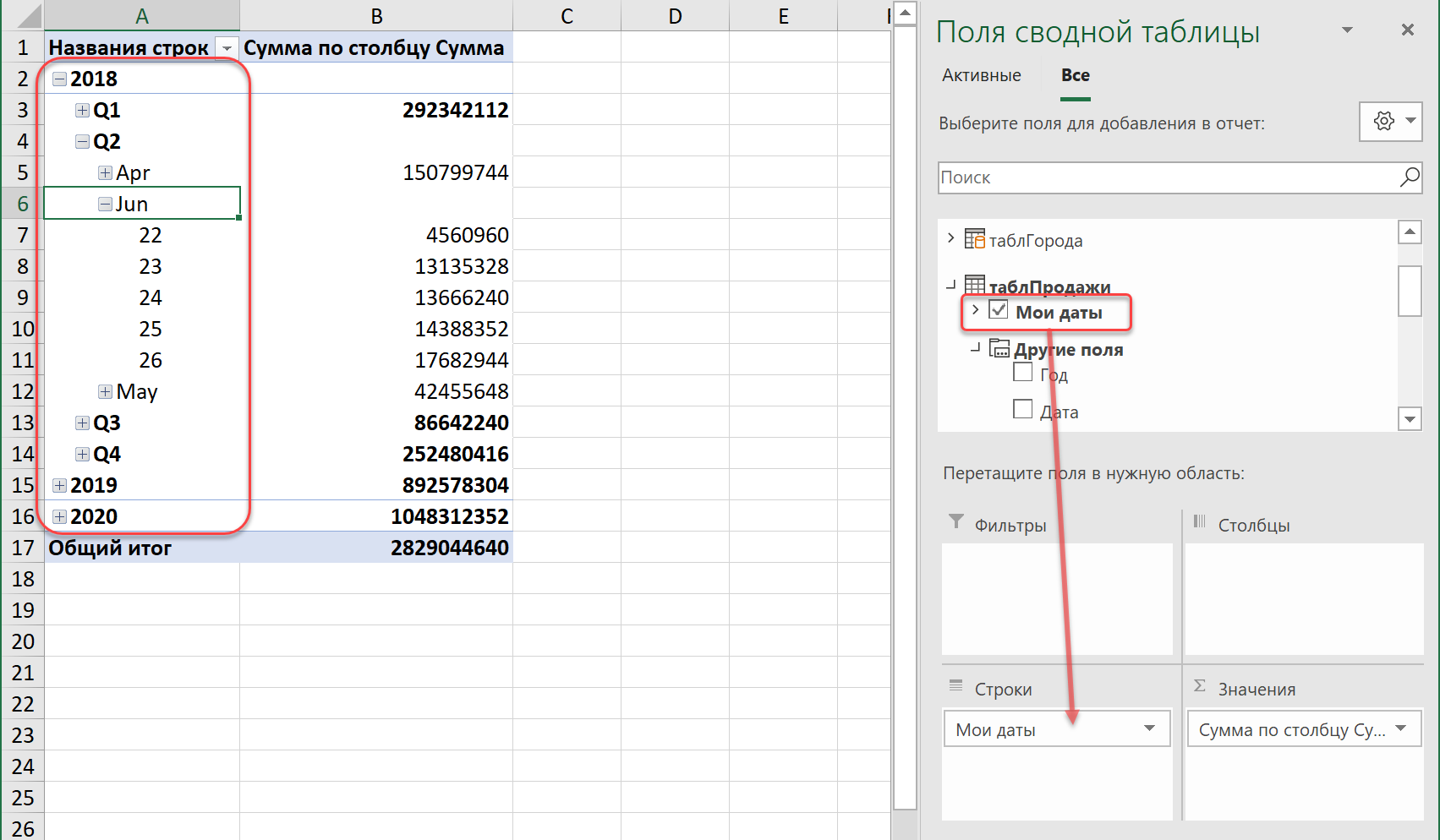
После этого в сводной по Модели Данных можно закидывать в области сводной (строки, столбцы, фильтры, значения) любые поля из любых связанных таблиц — всё будет связываться и подсчитываться уже автоматически:
Преимущество 2. Подсчёт количества уникальных значений
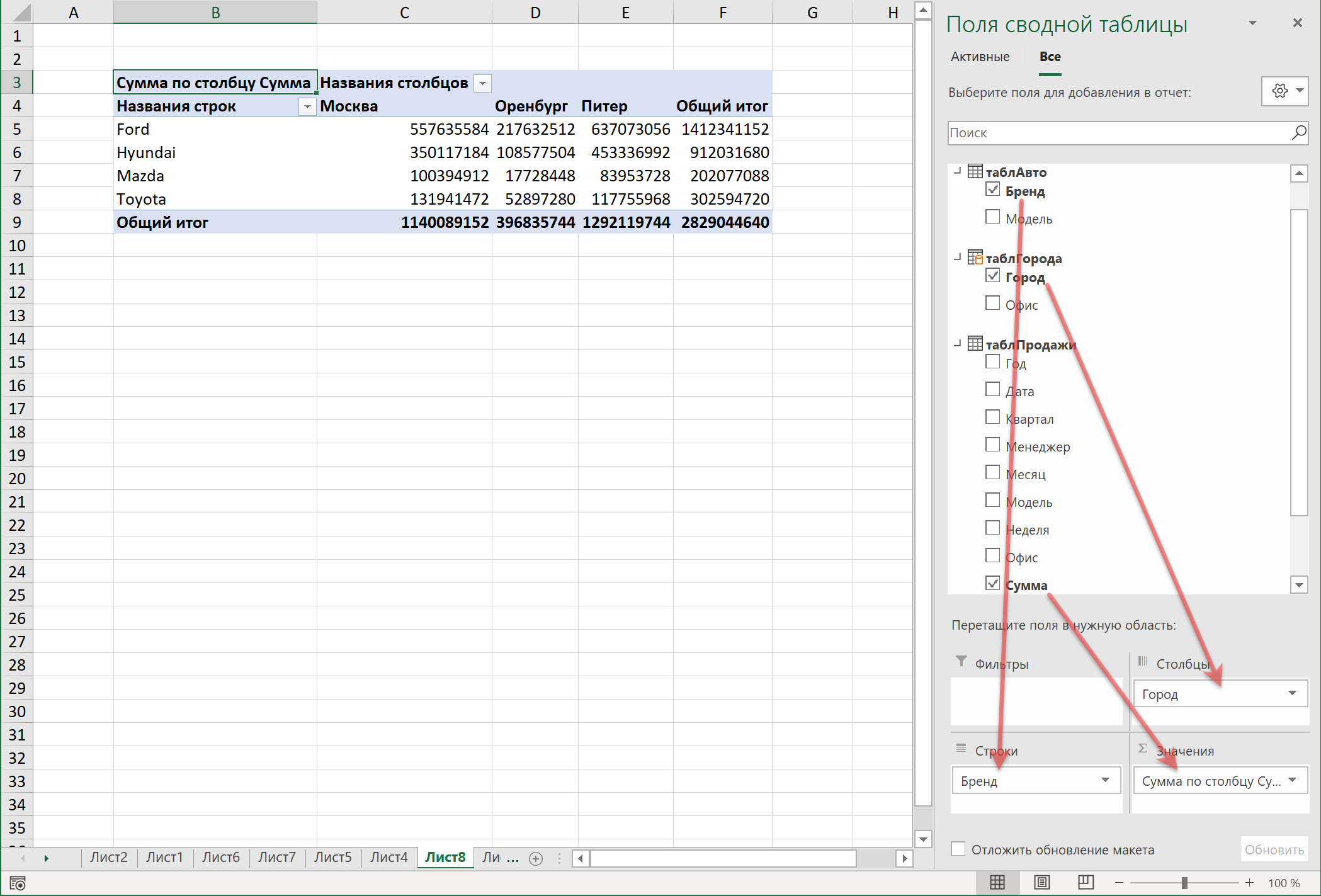
Обычная сводная таблица даёт нам возможность выбрать одну из нескольких встроенных функций расчёта: сумму, среднее, количество, минимум, максимум и т.д. В сводной по Модели Данных к этому стандартному списку добавляется весьма полезная функция подсчёта количества уникальных (неповторяющихся значений). С её помощью, например, можно легко посчитать количество уникальных наименований товаров (ассортимент), который мы продаём в каждом городе.
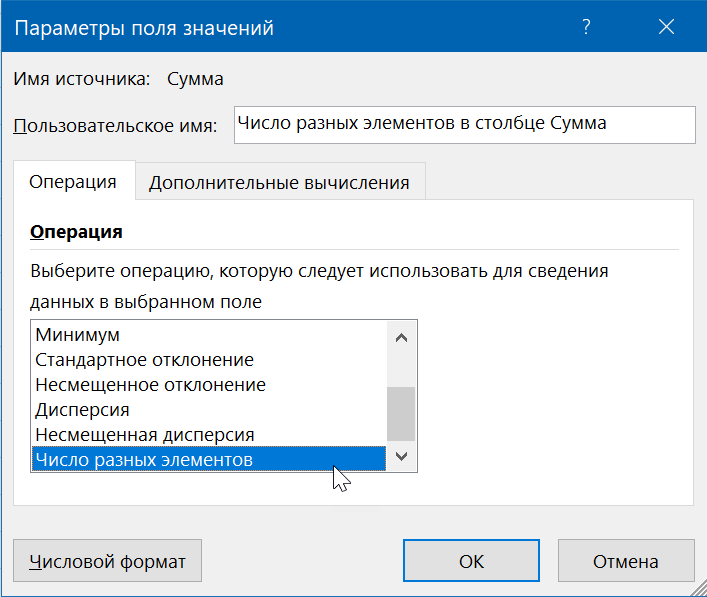
Щёлкаем правой кнопкой мыши по полю — команда Параметры полей значений и на вкладке Операция выбираем Число разных элементов (Distinct count):
Преимущество 3. Свои формулы на языке DAX
Иногда в сводных таблицах приходится выполнять различные дополнительные вычисления. В обычных сводных это делается с помощью вычисляемых полей и объектов, а сводной по Модели Данных для этого используются меры на специальном языке DAX (DAX = Data Analysis Expressions).
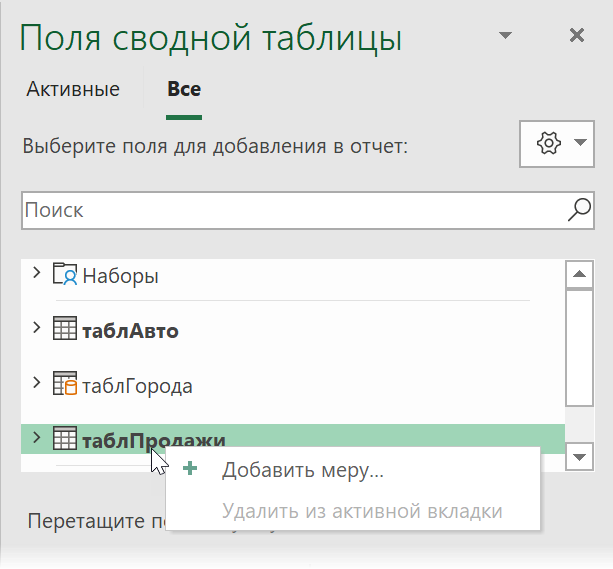
Для создания меры выберите на вкладке Power Pivot команду Меры — Создать меру (Measures — New measure) или просто щёлкните правой кнопкой мыши по таблице в списке полей сводной и выберите Добавить меру (Add measure) в контекстном меню:
В открывшемся окне задаём:
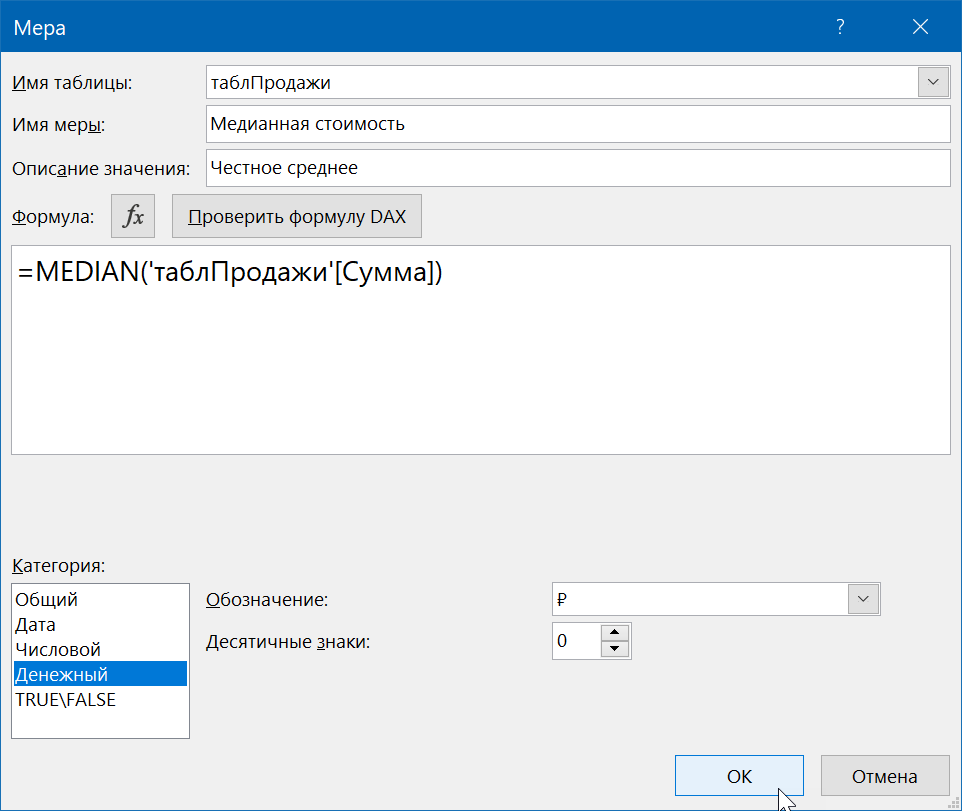
- Имя таблицы, где созданная мера будет храниться.
- Название меры — любое понятное вам имя для нового поля.
- Описание — по желанию.
- Формула — самое главное, т.к. здесь мы либо вручную вписываем, либо жмём на кнопку fx и выбираем из списка функцию DAX, которая должна вычислять результат, когда мы потом забросим нашу меру в область Значений.
- В нижней части окна можно сразу задать для меры числовой формат в списке Категория.
Язык DAX не всегда прост для понимания, т.к. оперирует не отдельными значениями, а целыми столбцами и таблицами, т.е. требует некоторой перестройки мышления после классических формул Excel. Однако же, оно того стоит, ибо мощь его возможностей при обработке больших объемов данных трудно переоценить.
Преимущество 4. Свои иерархии полей
Часто при создании типовых отчётов приходится забрасывать в сводные таблицы одни и те же комбинации полей в заданной последовательности, например Год-Квартал-Месяц-День, или Категория-Товар, или Страна-Город-Клиент и т.п. В сводной по Модели Данных эта проблема легко решается созданием собственных иерархий — пользовательских наборов полей.
В окне Power Pivot переключитесь в режим диаграммы кнопкой Представление диаграммы на вкладке Главная (Home — Diagram View), выделите с Ctrl нужные поля и щёлкните по ним правой кнопкой мыши. В контекстном меню будет команда Создать иерархию (Create hierarchy):
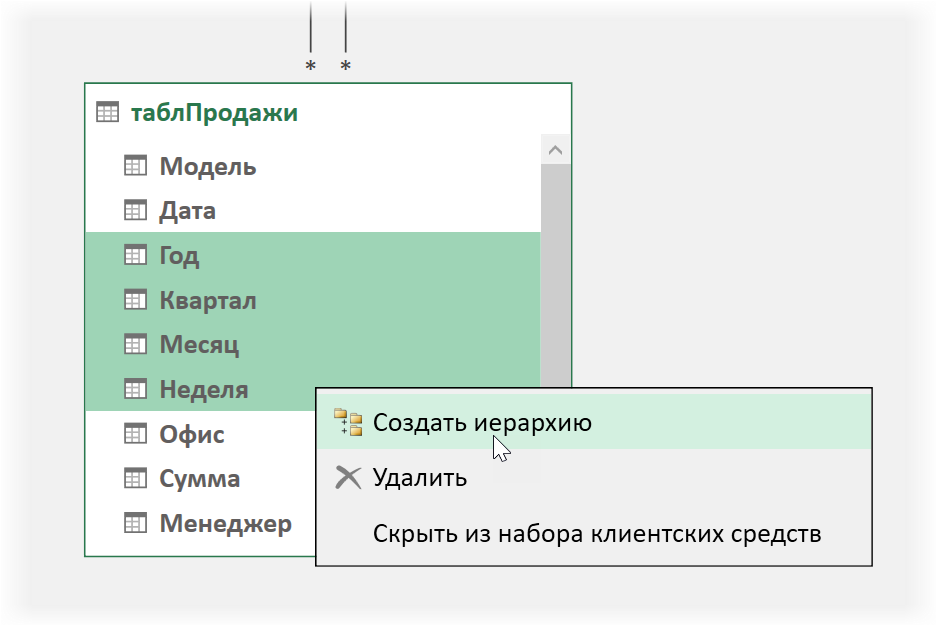
Созданную иерархию можно переименовать и перетащить в неё мышью требуемые поля, чтобы потом в одно движение забрасывать их в сводную:
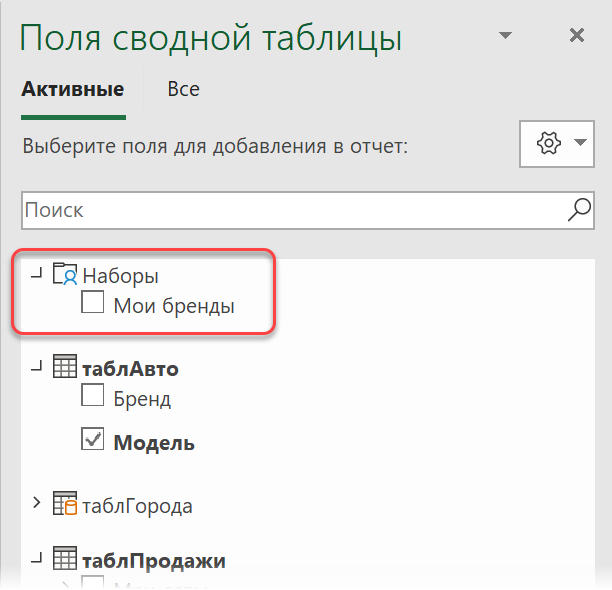
Преимущество 5. Свои наборы элементов
Продолжая идею предыдущего пункта, в сводной по Модели Данных можно создавать ещё и свои наборы элементов для каждого поля. Например, из всего списка городов можно легко сделать набор только из тех, которые входят в зону вашей ответственности. Или собрать в специальный набор только своих клиентов, свои товары и т.п.
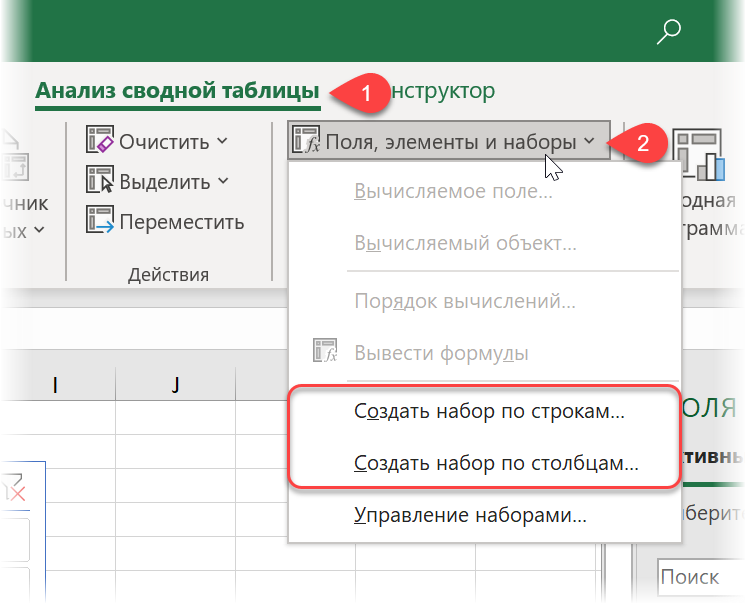
Для этого на вкладке Анализ сводной таблицы в выпадающем списке Поля, элементы и наборы есть соответствующие команды (Analyze — Fields, Items & Sets — Create set based on row/column items):
В открывшемся окне можно выборочно удалить, добавить или поменять положение любых элементов и сохранить получившийся набор под новым именем:
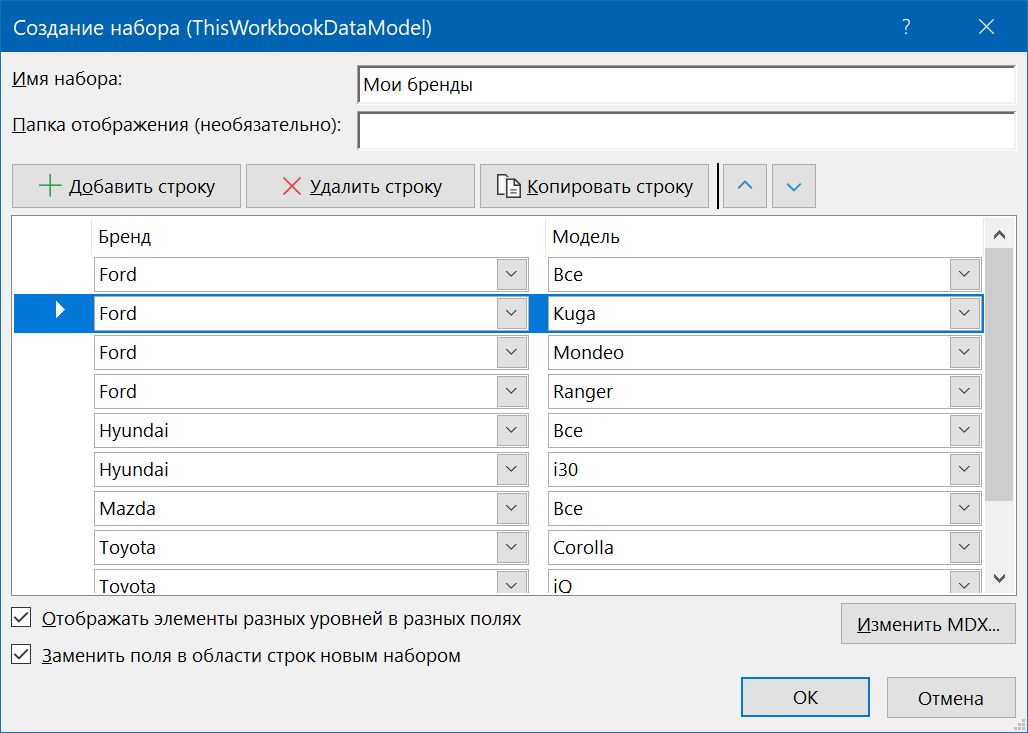
Все созданные наборы будут отображаться в панели полей сводной таблицы в отдельной папке, откуда их можно свободно перетаскивать в области строк и столбцов любой новой сводной таблицы:
Преимущество 6. Выборочное скрытие таблиц и столбцов
Это хоть и небольшое, но весьма приятное в некоторых случаях преимущество. Щёлкнув правой кнопкой мыши по названию поля или по ярлычку таблицы в окне Power Pivot, можно выбрать команду Скрыть из набора клиентских средств (Hide from Client Tools):
Скрытый столбец или таблица пропадут из панели со списком полей сводной таблицы. Очень удобно, если вам требуется скрыть от пользователя некоторые вспомогательные столбцы (например, расчетные или столбцы с ключевыми значениями для создания связей) или даже целые таблицы.
Преимущество 7. Продвинутый drill-down
Если в обычной сводной таблице сделать двойной щелчок левой кнопкой мыши по любой ячейке в области значений, то Excel выводит на отдельном листе копию фрагмента исходных данных, которые участвовали в расчёте этой ячейки. Это очень удобная штука, официально называющаяся Drill-down (на русском обычно говорят «провалиться»).
В сводной по Модели Данных этот удобный инструмент работает более тонко. Встав на любую интересующую нас ячейку с результатом, можно щёлкнуть по всплывающему рядом значку с лупой (он называется Экспресс-тенденции) и выбрать затем любое интересующее вас поле в любой связанной таблице:
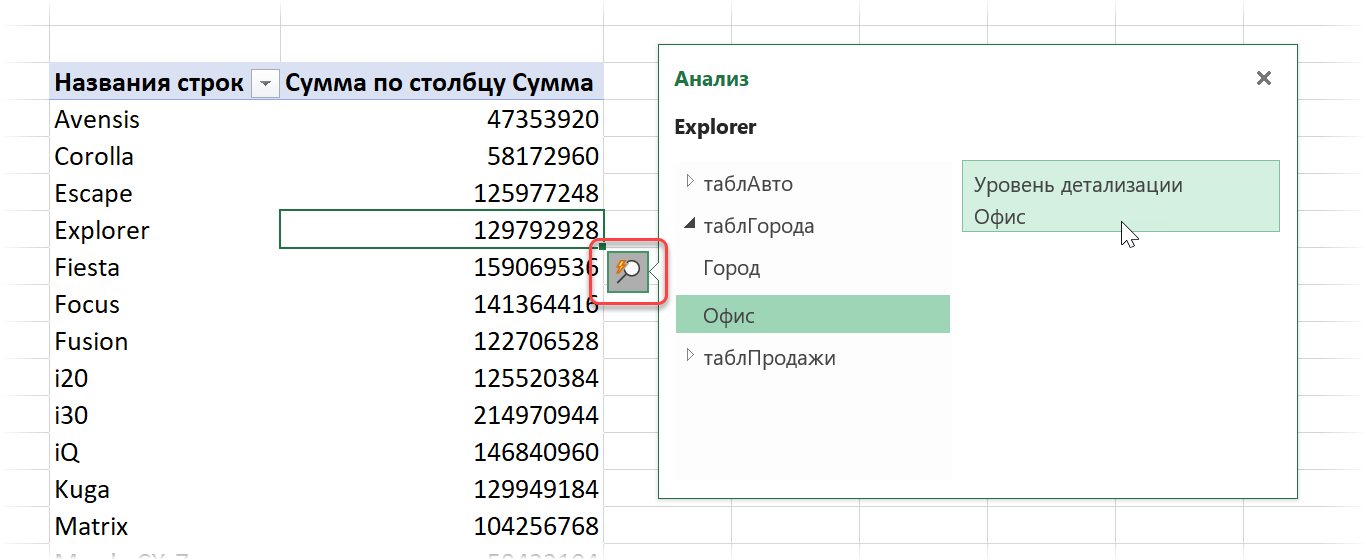
После этого текущее значение (Модель = Explorer) уйдет в область фильтра, а сводная будет построена уже по офисам:
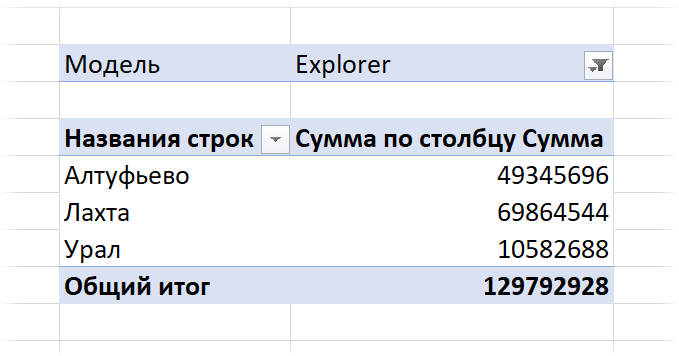
Само-собой, такую процедуру можно повторять многократно, последовательно углубляясь в ваши данные в интересующем вас направлении.
Преимущество 8. Преобразование сводной в функции кубов
Если выделить любую ячейку в сводной по Модели Данных и выбрать затем на вкладке Анализ сводной таблицы команду Средства OLAP — Преобразовать в формулы (Analyze — OLAP Tools — Convert to formulas), то вся сводная будет автоматически преобразована в формулы. Теперь значения полей в области строк-столбцов и результаты в области значений будут извлекаться из Модели Данных с помощью специальных функций кубов: КУБЗНАЧЕНИЕ и КУБЭЛЕМЕНТ:
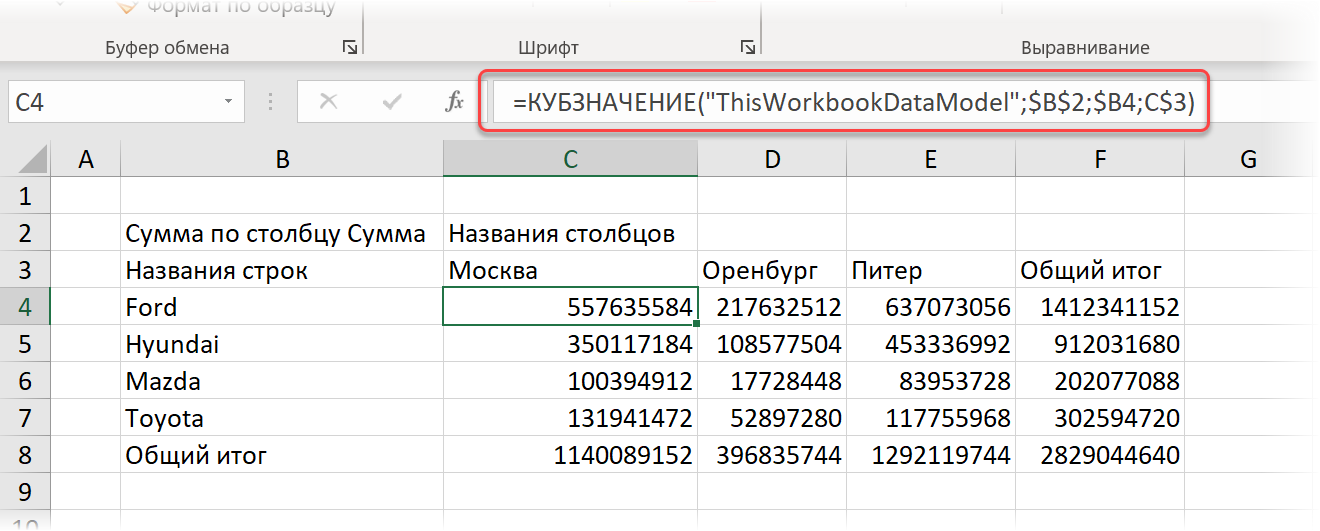
Технически, это означает, что теперь мы имеем дело не со сводной, а с несколькими ячейками с формулами, т.е. спокойно можем делать с нашим отчетом любые преобразования недоступные в сводных, например, вставлять в середину отчета новые строки или столбцы, делать внутри сводной любые доп.вычисления, оформлять их любым желаемым образом и т.д.
При этом связь с исходными данными, само-собой, остается и в будущем эти формулы будут обновляться при изменении источников. Красота!
Ссылки по теме
- План-факт анализ в сводной таблице с Power Pivot и Power Query
- Сводная по таблице с многострочной шапкой
- Создание базы данных в Excel с помощью Power Pivot
Пример имитационной модели
NOTE:
To change the image on this slide, select the picture and delete it. Then click the Pictures icon in the placeholder to insert your own image.
§26
Информатика, 8 класс
Учитель информатики
Дворецкая Ю.Ю,
1
Основные темы параграфа
- Что такое имитационная модель
- Пример имитационного моделирования в электронной таблице
ОПРЕДЕЛЕНИЕ
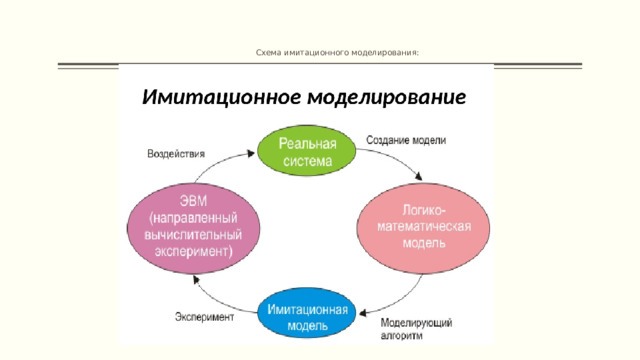
ИМИТАЦИОННАЯ МОДЕЛЬ – это логико-математическое описание объекта, которое может быть использовано для экспериментирования на компьютере в целях проектирования, анализа и оценки функционирования объекта.
Имитационная модель имеет определенную минимальную опорную структуру, которую пользователь может дополнить и расширить с учетом специфики решаемых задач и базовых методов обработки.
ОПРЕДЕЛЕНИЕ
- ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ — это метод исследования, при котором изучаемая система заменяется моделью с достаточной точностью описывающей реальную систему и с ней проводятся эксперименты с целью получения информации об этой системе.
Отличие от математического моделирования
- имитационное моделирование исследует математические модели в виде алгоритмов , воспроизводящих функционирование исследуемой системы путем последовательного выполнения большого количества элементарных операций .
- в имитационных моделях для получения необходимой информации или результатов необходимо осуществлять их «прогон» в отличие от аналитических моделей, которые необходимо «решать».
- имитационные модели неспособны формировать свое собственное решение в том виде, в каком это имеет место в аналитических моделях, а могут лишь служить в качестве средства для анализа поведения системы в условиях, которые определяются экспериментатором.
Имитационные модели
В общем виде структуру имитационной модели в математической форме можно представляет следующим образом: ,
где E – результат действия системы;
x i – переменные и параметры, которыми мы можем управлять;
y i – переменные и параметры, которыми мы управлять не можем;
f – функциональная зависимость между x i и y i , которая определяет величину E .
Имитационные модели
Имитационная модель представляет собой комбинацию таких составляющих, как:
- компоненты;
- переменные;
- параметры;
- функциональные зависимости;
- ограничения;
- целевые функции.
Схема имитационного моделирования:
НЕДОСТАТКИ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ:
- разработка имитационных моделей требует больших затрат, времени и сил;
- любая имитационная модель сложной системы менее объективна, чем аналитическая модель;
- результаты имитационного моделирования носят как правило частный характер, поэтому для предоставления обоснованных выводов необходимо провести серии модельных экспериментов.
Пример имитационного моделирования на компьютере
Имитационная модель воспроизводит поведение сложной системы, элементы которой могут вести себя случайным образом. Иначе говоря, поведение которых заранее предсказать нельзя.
Модель – эволюция популяций
- Пусть на определенном пространстве случайным образом расселяются живые организмы.
- В дальнейшем происходит процесс смены поколений: в каких-то местах расселения жизнь сохраняется, в каких-то исчезает.
- Эти процессы протекают в соответствии с законами эволюции (формальными правилами).
Цель моделирования — проследить изменения в расселении живых организмов со сменой поколений.
Имитационные модели
Законы эволюции:
- В следующем поколении в пустой ячейке жизнь может либо появиться, либо нет.
- В живой ячейке жизнь может либо сохраниться, либо исчезнуть
- На состояние данной ячейки влияют ее ближайшие соседи: два соседа слева и два соседа справа.
- Если ячейка была живая, и число живых соседей не превышает двух, то в следующем поколении в этой ячейке жизнь сохранится, иначе жизнь исчезнет (погибнет от перенаселения).
- Если в ячейке жизни не было, но среди ее соседей есть 1, 2 или 3 живые ячейки, то в следующем поколении в этой ячейке появится жизнь. В противном случае ячейка останется пустой.
Модельное описание процесса эволюции популяции
- Следует учитывать, что у ячеек, расположенных у края, число соседей меньше других.
- У ячейки номер 2 соседи: 1, 3 и 4.
- Но ячейка 1 всегда пустая.
- У ячейки номер 3 из четырех соседей живыми могут быть не больше трех (2,4,5).
- Аналогичная ситуация у крайних правых ячеек.
Кодирование
- Распределение живых организмов по ячейкам будем кодировать последовательностью из нулей и единиц.
- Ноль обозначает пустую ячейку , единица — живую .
- Например, расселение, отображенное на рис. 4.3, кодируется следующим образом:
00001001000100000000
Имитационные модели
Введем обозначения:
n — номер ячейки,
R (n) — значение двоичного числа, соответствующего этой ячейке в текущем поколении.
В рассматриваемом примере R (5) = R (8) = R (12) = 1 .
Все остальные значения ячеек равны нулю.
Значения кода в n -й ячейке для следующего поколения будем обозначать S ( n ) .
Проанализировав правила эволюции, приходим к следующей формуле:
Если 1 R ( n — 2) + R ( n — 1) + R ( n ) + R ( n + 1) + R ( n + 2) 3, то S ( n ) = 1, иначе S ( n ) = 0.
Имитационные модели
Эта формула работает для значений n от 3 до 18 .
Всегда: S (1) = S (20) = 0 .
Для ячеек с номерами 2 и 19 в данной сумме нужно убрать по одному слагаемому. Но можно поступить иначе: для этого к отрезку добавим по одной фиктивной ячейке справа и слева.
Их номера будут, соответственно, 0 и 21. В этих ячейках, как и в ячейках 1 и 20, всегда будут храниться нули. Тогда написанную формулу можно применять для n от 2 до 19.
Итак, модель построена и формализована.
Имитационные модели
Для реализации применим табличный процессо р.
Моделью жизненного пространства будет строка электронной таблицы.
Первая строка — первое поколение,
вторая строка — второе поколение и т. д.
Тогда номера ячеек будут идентифицироваться именами столбцов таблицы.
Ячейка номер 0 — столбец А,
ячейка 1 — столбец В и т. д.,
ячейка 21 — столбец F.

- В первой строке выставляем единицы в ячейках, заселенных в первом поколении. Это будут ячейки F1, I1, М1 . Незаполненные ячейки по умолчанию приравниваются к нулю.
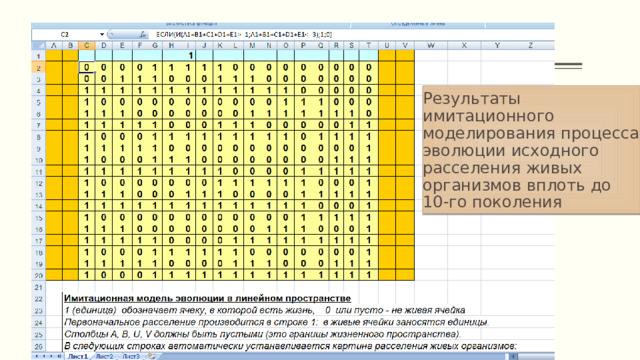
- Теперь в ячейки второй строки нужно записать формулы. Сделать это достаточно один раз. Например, в ячейку С2 занести следующую формулу:
ЕСЛИ(И(А1 + В1 + С1 + D1 + Е1 =1; А1 + В1 + С1 + D1 + Е1
- Далее, копируя эту формулу во все остальные ячейки второй строки с D2 по Т2, получаем картину распределения живых организмов во втором поколении.
- Чтобы получить третье поколение, достаточно скопировать вторую строку (блок С2:Т2) в третью строку (блок СЗ:ТЗ). Так можно продолжать сколько угодно.
Результаты имитационного моделирования процесса эволюции исходного расселения живых организмов вплоть до 10-го поколения
Модель Дж. Конуэя «Жизнь»
В этой модели эволюция популяции живых организмов происходит в двумерном пространстве.
Рассматривается прямоугольная область, разделенная на квадратные ячейки. Тогда у каждой внутренней ячейки имеется 8 соседей. Судьба жизни в ячейке также зависит от состояния соседних клеток.
Но теперь правила эволюции такие:
- если клетка живая и в ее окружении более трех живых клеток, то она погибает от перенаселения;
- если же живых соседей меньше двух, то она погибает от одиночества.
- в пустой клетке в следующем поколении зарождается жизнь, если у нее есть ровно три живых соседа.
Домашнее задание
§26 конспект
Дмитрий Михайлович Беляев
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Определение 1
Моделирование — это изучение какого-либо явления, процесса или системы объектов посредством формирования и исследования их моделей.
Введение
В системах, связанных с экономикой, руководящим работникам необходимо постоянно принимать решения следующих категорий:
- Стратегические решения.
- Тактические решения.
- Оперативные решения.
Если принимаемые решения обладают низким интеллектуальным уровнем, то простота представления реальных ситуаций обычно ведёт к неточностям при выработке прогнозов, а, кроме того, к убыткам и добавочным финансовым потерям. Чтобы избежать возникновения подобных ситуаций и обеспечить устойчивое экономическое положение, существуют разнообразные системы поддержки выработки решений, усовершенствование которых превращается в наиболее актуальную проблему при наличии жёсткой конкуренции.
Существенным условием для таких программ считается возможность имитации вырабатываемых решений, апробации вероятных коррекций в экономической системе, появляющихся в результате влияния разных факторов, то есть нахождение ответа на вопрос типа, «что случится, если…». Это позволит существенно сократить риски от осуществления решений и сэкономить ресурсы, чтобы достичь поставленной цели.
Такие возможности предоставляют имитационные модели, которые обладают следующим набором качеств:
- Возможность регулировать уровень сложности модели.
- Присутствие случайных факторов.
- Возможность описать процесс, развивающийся по времени.
- Обязательное использование электронной вычислительной машины.
Имитационные модели предназначаются для того, чтобы оценить варианты намечаемых коррекций, обладать игровой формой для обучения работников, визуально отобразить работу исследуемого объекта во времени и так далее. Реализовать модели можно при помощи универсальных языков программирования, к примеру,Pascal, Basic, пакетов прикладных программ, таких как,Excel, MathCAD, и так далее. Выбор конкретного метода моделирования определяется сложностью задачи, наличием необходимых ресурсов и так далее.
«Моделирование в Excel» 👇
Однако имитационное моделирование применяется экономистами и другими специалистами только в малом проценте случаев, в которых можно было бы при помощи моделей поиметь важную для выработки решений информацию.Причина этого явления кроется в отсутствии инструкций по проведению имитационного моделирования при помощи общеизвестного и доступного инструментария, а именно, пакетов прикладного программного обеспечения, такого как Excel и MathCAD, которые могут обеспечить простую платформу для моделирования.Поэтому примеры формирования имитационных моделей при помощи, например, приложения Excel, помогают их широкому распространению в кругу работников, не владеющих языками моделирования и методиками, имеющимися в средах моделирования.
Электронные таблицы Excel как инструмент формирования имитационных моделей
Имитационное моделирование при помощи табличного процессора является отдельным направлением, имеющем свои особенности. Применение таких систем позволяет лучше понять происходящие процессы, в сравнении с использованием специализированных программ, обладающих высокой стоимостью и требующих много времени для их освоения, а также не позволяющих увидеть применяемые механизмы. Например, специалисты полагают, что имитация при помощи таблиц Excel позволяет лучше представить работу систем массового обслуживания, чем даже теория очередей, а также помогает в развитии интуиции, предоставляет даже не знающим программирования пользователям опыт формирования разных моделей. Специалисты предлагают следующие этапы обучения моделированию в Excel:
- Базовые понятия.
- Введение в теорию вероятности и статистику.
- Процесс имитационного моделирования в ручном режиме.
- Имитационное моделирование при помощи электронных таблиц.
- Генерирование случайных чисел.
- Осуществление анализа исходных данных.
- Осуществление анализа итогов моделирования.
При формировании моделей в Excelприменяются следующие главные подходы к осуществлению имитации:
- Подход, который ориентирован на события.
- Подход, имеющий ориентацию на процессы.
- Подход, направленный на сканирование активностей.
Первый подход служит для описания изменений в системе, которые происходят при совершении любого случайного события, например, получение заявки, завершение обслуживания. При его формировании при помощи электронных таблиц обычно применяется одна строчка для каждого события.
Если используется подход, ориентированный на процесс, то выполняется моделирование очерёдности событий для каждой заявки, и чтобы его реализовать, применяется одна строчка для каждого требования (используется при моделировании систем массового обслуживания).
Сканирование активностей состоит в описании действий, возникающих в системе за фиксированный временной интервал (день, неделя, месяц, год), и при его осуществлении, как правило, применяется одна строчка для каждого отрезка времени. К примеру, это может быть моделирование системы управления запасами.
Использование программного пакета MSExcelобладает следующими преимуществами:
- В составе пакета Excelесть значительное число встроенных функций из области математики, статистики и других областей, включая возможность генерации случайных значений.
- Excelдаёт возможность сохранять информацию и иметь к ней доступ.
- Программный пакетExcelпозволяет строить графики и диаграммы.
- Программный пакет Excel обладает встроенным языкомVBA (VisualBasicforApplication).
- Программный пакет Excelшироко распространён среди специалистов, то есть имеется на компьютере практически у всех.
- Наличие возможности экспорта информационных данных в иные программные приложения.
Помимо этих достоинств, возможен просмотр любой формулы, занесённой в ячейку таблицы, что увеличивает уровень доверия к итогам моделирования.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Цели мероприятия:
1. Дидактические:
- рассмотрение этапов информационного моделирования на примере решения
конкретных задач; - закрепление навыков работы в MS Excel;
- установление межпредметных связей: информатики и математики.
2. Развивающие:
- развитие познавательного интереса, воображения;
- развитие умений применять знания на практике.
3. Воспитательные:
- расширение научного кругозора;
- воспитание самостоятельности в работе.
Учебно-методическое обеспечение: презентация (Презентация),
ПО MS Excel, ПО MS PowerPoint, методические указания.
Оборудование: мультимедийная установка, персональные компьютеры.
Ход конференции
Преподаватель: Межпредметное значение информатики в значительной
степени проявляется именно через внедрение компьютерного моделирования в
различные научные и прикладные области: математику и физику, технику, биологию и
медицину, экономику, управление и многие другие. С помощью компьютерного
моделирования решаются многие научные и производственные задачи. Гибким
инструментом для компьютерного моделирования является MS Excel.
Возможности электронных таблиц Microsoft Excel весьма многогранны. Всем
известно, что Excel является мощным вычислительным инструментом, позволяющим
производить простые и сложные расчеты в различных областях человеческой
деятельности: математике, физике, инженерных науках, экономике, технологии. На
этом уроке мы рассмотрим использование электронных таблиц для решения
математических задач и уравнений.
Теоретическая часть
Преподаватель: Рассмотрим этапы информационного моделирования.
1. Модель задачи.
Пусть вам надо решить какую-либо задачу, и вы хотите воспользоваться для
этого помощью компьютера. С чего начать? Прежде всего, нужно разобраться, что
дано, что требуется получить, как связаны исходные данные и результаты.
Предположения, которые позволяют в море информации об изучаемом явлении или
объекте определить исходные данные, понять, что будет служить результатом и
какова связь между исходными данными и результатом, называют моделью задачи.
(Презентация. Слайд 2)
2. Понятие математической модели.
В моделировании есть два различных пути. Во-первых, это использование
натурных моделей. Но если модель должна отображать реальность в абстрактной
форме, то в таком случае всегда привлекаются средства математики, и мы имеем
дело с математической моделью.
Математическая модель выражает существенные признаки объекта или процесса
языком уравнений и других математических средств. (Презентация. Слайд 3)
Собственно говоря, в историческом аспекте сама математика обязана своим
существованием тому, что пыталась отражать, т.е. моделировать, на своем
специфическом языке закономерности окружающего мира.
Под математической моделью понимают систему математических соотношений –
формул, уравнений, неравенств и т.д., отражающих существенные свойства объекта
или процесса. (Презентация. Слайд 3)
Математическое моделирование в наше время гораздо более всеобъемлющее, нежели
моделирование натурное. Математический аппарат для моделирования объектов и
процессов реального мира ученые использовали очень давно, но огромный толчок
математическому моделированию дало появление ЭВМ, которые сегодня помогают в
этой деятельности. Использование математического моделирования – это самый общий
метод научных исследований.
Простой пример. Представьте, что нужно определить площадь поверхности
письменного стола. Как обычно поступают в таком случае? Измеряют длину и ширину
стола, а затем перемножают полученные числа. Это фактически означает, что
реальный объект – поверхность стола – заменяется абстрактной математической
моделью – прямоугольником. Площадь этого прямоугольника и считается искомой
величиной.
Как видно, из всех свойств стола мы выделили три: форму поверхности
(прямоугольник) и длины двух сторон. Для нас не важны ни цвет стола, ни
материал, из которого он сделан, ни то, как стол используется. (Если бы мы
решали другую задачу о столе, например, сколько стоит его изготовление, то
возможно, для нас важна была бы как раз эта информация.) (Презентация. Слайд 4)
Предположив, что поверхность стола – прямоугольник, мы легко указываем
исходные данные и находим результат. Они связаны соотношение S = a * b.
(Презентация. Слайд 5)
Сделанное предположение позволило «перевести» нашу задачу на язык чисел: и
исходные данные, и результат – числа, а соотношение между ними задается
математической формулой.
Анализировать математические модели проще и быстрее, чем экспериментально
определять поведение реального объекта. Кроме того, анализ математической модели
позволяет выделить наиболее существенные свойства данного объекта (процесса), на
которые надо обратить внимание при принятии решения.
3. Этапы решения задач на компьютере.
1 этап. Постановка задачи – точная формулировка условий и целей
решения, описание наиболее существенных свойств объекта. (Презентация. Слайд 6)
2 этап. Построение математической модели – описание наиболее
существенных свойств объекта с помощью математических формул. (Презентация.
Слайд 6)
3 этап. Создание компьютерной модели – выражение математической модели
на понятном для компьютера языке. Существуют два принципиально различных пути
построения компьютерной модели:
- Построение алгоритма решения задачи и его кодирование на одном из языков
программирования. - Построение компьютерной модели и использованием ПО компьютера
(приложений Windows – электронных таблиц, СУБД и пр.). (Презентация. Слайд
7)
4 этап. Проведение компьютерного эксперимента (исследование модели) –
если компьютерная модель существует в виде программы на одном из языков
программирования, то её нужно запустить на выполнение и получить результаты;
если компьютерная модель исследуется в приложении, например, в электронных
таблицах, можно провести сортировку или поиск данных, построить диаграмму или
график и т.д. (Презентация. Слайд 
5 этап. Анализ полученных результатов и корректировка модели – в
случае различия результатов, полученных при исследовании модели, с измеряемыми
параметрами реальных объектов можно сделать вывод, что на предыдущих этапах
построения модели были допущены ошибки или неточности. В этом случае необходимо
провести корректировку модели, причём уточнение модели может проводиться
многократно, пока анализ результатов не покажет их соответствие изучаемому
объекту. (Презентация. Слайд 9)
Рассмотрим конкретные задачи математического моделирования. Для этого будем
использовать приложение Windows – электронные таблицы MS Excel. Для этих целей в
Excel имеется много возможностей: вычисление по формулам, построение диаграмм и
графиков, поиск решения, подбор параметра и т.д.
Практическая часть
Студент 1:
Задача 1. Необходимо покрасить краской стены кухни. Сколько
потребуется банок краски, если известно, что
- размеры кухни 405 × 310 × 285 см;
- 88% площади стен занимает кафельная плитка;
- 1 банка краски предназначена для покраски площади 5 м2?
(Презентация. Слайд 10)
Решение.
Постановка задачи.
Дано:
a = 405 см – длина комнаты,
b = 310 см – ширина комнаты,
c = 285 см – высота комнаты,
1 – 0,88 = 0,12 – часть комнаты для покраски (без кафеля),
5 м2 – площадь покраски при использовании 1 банки краски.
Найти: необходимое для покраски стен кухни количество банок краски.
(Презентация. Слайд 11)
Математическая модель.
Sстен с кафелем =2(a + b)c.
Sстен для покраски = 2(a + b)c * 0,12.
Чтобы определить, сколько потребуется банок краски, надо площадь для покраски
разделить на 5 м2, т. е. Sстен для покраски /5 и результат
округлить до целых.
Моделирование в среде ЭТ.
Заносим данные задачи в электронную таблицу, вводим формулы.
Электронная таблица в режиме отображения формул. (Приложение
1. Презентация. Слайд 12)
Электронная таблица в режиме отображения значений. (Приложение
2. Презентация. Слайд 13)
С помощью MS Excel мы определили, что для покраски стен кухни необходима 1 банка
краски.
Студент 2:
Задача 2. Через иллюминатор корабля требуется вытащить сундук с
драгоценностями. Удастся ли это сделать?
Решение.
Постановка задачи.
Иллюминатор корабля имеет форму круга. Будем считать, что сундук имеет форму
параллелепипеда. Чтобы вытащить сундук, необходимо, чтобы диаметр иллюминатора
был больше любой из трех диагоналей поверхности сундука. (Презентация. Слайд 14)
Математическая модель.
Пусть r – радиус иллюминатора,
a, b, c – размеры сундука,
d1, d2, d3 – диагонали боковых поверхностей сундука. (Презентация. Слайд 15)
Сундук можно вытаскивать через иллюминатор одной из трех боковых граней,
следовательно, достаточно, чтобы диагональ иллюминатора оказалась меньше одной
из трех диагоналей сундука, т.е. должно быть истинно хотя бы одно из условий:
ЕСЛИ((2*R>КОРЕНЬ(a^2+b^2));1;0)
ЕСЛИ((2*R>КОРЕНЬ(a^2+c^2));1;0)
ЕСЛИ((2*R>КОРЕНЬ(с^2+b^2));1;0)
(Презентация. Слайд 16)
Моделирование в среде ЭТ.
Заносим данные задачи в электронную таблицу, вводим формулы.
Электронная таблица в режиме отображения формул. (Приложение
3. Презентация. Слайд 17)
Электронная таблица в режиме отображения значений. (Приложение
4.Презентация. Слайд 18)
Компьютерный эксперимент.
В электронной таблице находим сумму трех условий. Если сумма равна 0, делаем
вывод «Сокровища недоступны», иначе «Сокровища доступны» (Слайд 19 Презентация).
Студент 3:
Задача 3. Решить уравнение х4-4х3-10х2+37х-14=0 (Слайд 20
Презентация).
Решение.
Необходимо построить график функции у = х4 – 4х3 – 10х2
+ 37х – 14. Точки пересечения графика с осью Х будут решениями данного
уравнения. Составляем в MS Excel таблицу значений функции. (Приложение
5. Презентация. Слайд 21)
Построим график функции (диаграмму). (Приложение 5.
Презентация. Слайд 22)
Мы видим, что график четырежды пересекает ось ОХ, значит уравнение х4
– 4х3 – 10х2 + 37х –14 = 0 имеет четыре корня.
Из таблицы и графика можно определить промежутки, в которых находятся корни
этого уравнения:
х1
[–3,5; –3], х2
[0; 0,5], х3
[2; 2,5], х4
[4,5; 5].
(Презентация. Слайд 23)
Затем с помощь анализа «что-если»/Подбор параметра можно
уточнить значения корней. Для этого следует активизировать ячейку со значением
функции у = 55,56, соответствующим значению аргумента х = -3,5, или ячейку со
значением у = -26, соответствующим х = -3, и выполнить команду Данные/группа
Работа с данными/Анализ «что-если»/Подбор параметра. Появится
одноименное диалоговое окно с тремя строками (Слайд 23 Презентация).
В первой строке указан адрес выбранного значения функции. Во второй нужно
установить курсор и занести подбираемое значение функции, указанное в правой
части данного уравнения (в нашем случае – число 0). А затем, установив курсор в
третьей строке, надо щелкнуть мышью на ячейке с соответствующим значением
аргумента, чтобы получить абсолютное значение этого адреса, затем щелкнуть ОК.
Аналогично проверяются корни из других промежутков.
Из результирующей таблицы выбираем корни уравнения. (Приложение
5. Презентация. Слайд 24)
Преподаватель: С особым вниманием следует применять этот способ для
решения уравнений, у которых графики функции не являются так называемыми
«гладкими» кривыми. Это касается, прежде всего, шага изменения аргумента при
построении графика соответствующей функции: он не должен быть слишком большим,
чтобы не пропустить значения некоторых корней.
Поясним это на примере решения уравнения.
Студент 4:
Задача 4. Решить уравнение log2(x(1 – x)) – sin(π/x) + 2 =
0, область определения которого: x принадлежит промежутку (0;1). (Презентация.
Слайд 25)
Решение.
Если построить график соответствующей функции в области ее определения с
шагом h = 0,04, то получится один результат (Приложение 6.
Презентация. Слайд 27), но если построить тот же график с меньшим шагом h =
0,01, то мы получим иной результат. (Приложение 6.
Презентация. Слайд 27) Сравнение этих графиков показывает, что в первом случае
из-за слишком большого шага «потеряны» два первых корня. Всего же
рассматриваемое уравнение имеет шесть корней, которые уточняются с помощью
Подбора параметра. (Презентация. Слайд 28)
Вывод. (Презентация. Слайд 29)
- С помощью электронных таблиц MS Excel можно решать математические задачи
и уравнения. - При этом отрабатываются навыки работы в электронных таблицах, а именно:
оформление таблицы, работа с формулами, построение диаграмм.
Литература:
- О.К. Мясникова. Моделирование и формализация в курсе информатики. //
Информатика и образование, №11-2003. - В.П. Кудинов. Решение уравнений с помощью MS Excel. // Информатика и
образование, №3-2004. - Информатика и информационные технологии. Учебник для 10-11 классов /
Н.Д. Угринович. – М.:Бином. Лаборатория знаний, 2003.
Финансовая модель — это функциональный инструмент, который поможет оперативно просчитать влияние различных факторов и изменений на результаты работы и финансовое состояние организации. За счёт формул и уравнений расчётов после изменения исходных данных все зависимые характеристики, будут пересчитаны программой автоматически.
Для финансового моделирования наиболее удобен и доступен формат Excel. Использовать его могут как бухгалтеры, так и руководители различных уровней.
Набор показателей для финансовой модели зависит от специфики деятельности организации. Основных групп, как правило, четыре:
- активы — имущество, принадлежащее организации;
- пассивы — обязательства;
- финансовые потоки — различные денежные поступления и платежи;
- доходы и расходы.
Результаты расчётов можно представить в виде баланса, отчётов о доходах и расходах и о движении денежных средств (по состоянию на определённую дату).
Алгоритм построения финансовой модели
Начните финансовое моделирование в Excel с создания простой модели. Из внешних параметров можно, например, взять стоимость продукции и спрос на неё. Например, в качестве внутренних показателей можно взять размер выручки и затрат. На первом этапе количество элементов может быть минимальным, а особой точностью можно пренебречь. Основная цель — установить рабочие взаимосвязи для автоматического пересчёта. Далее модель можно развивать, детализировать и усложнять.
Рассмотрим пример простого моделирования в Excel с небольшим количеством ключевых переменных. Для каждой таблицы необходимо отвести отдельную страницу.
1. Задаём исходные параметры
Попробуем спрогнозировать выручку. За основу можно взять план реализации товаров или услуг за год. Размер выручки на первом этапе можно округлить или указать приблизительные данные (рисунок 1).
Рисунок 1 — План реализации услуг (тыс.руб.)

Выручка рассчитывается как сумма услуг.
2. Определяем переменные затраты
В качестве переменных введём затраты на заработную плату сотрудникам. Допустим, она зависит от объёма реализованных услуг и составляет 25% от выручки. Зарплата рассчитывается помесячно как произведение коэффициента 0,25 (25/100) и плана продаж на конкретный месяц.
Расходы на аренду и управление внесём как фиксированные значения.
Например, чтобы посчитать зарплату за январь, берём план реализации на январь и умножаем на коэффициент
151 * 0,25 = 38 тыс. руб.
В Excel прописываем формулу: fx = 0,25*название страницы с таблицей по плану реализации!B8
Общий размер планируемых затрат будет равен сумме зарплаты, аренды и управленческих расходов (рисунок 2).
Рисунок 2 — План затрат

3. Составляем план доходов и расходов
Обратите внимание на строки «операционные доходы» и «операционные расходы» (рисунок 3). Чтобы их заполнить, потребуется прописать ссылки на соответствующие ячейки функциональных планов.
Рисунок 3 — План доходов и расходов, тыс. руб.

Так, операционные доходы будут равны суммам от услуг 1-4. Например, чтобы рассчитать операционный доход за январь, складываем 15+30+46+60. Получаем 151 тыс. руб.
В формулу прописываем: fх =СУММ(B5:B8)
Числовые значения по услугам прописываем ссылками на ячейки таблицы «План реализации услуг».
Графа «Итого» считается как сумма ячеек с B4 по M4
fх =СУММ(B4:M4)
Аналогично рассчитываются операционные расходы. Данные синхронизируем с таблицей «План затрат».
Операционная прибыль рассчитывается как разность операционные доходы — операционные расходы.
Например, операционная прибыль за январь равна: 151 — 96 = 55 тыс. руб.
Рентабельность рассчитывается как отношение операционной прибыли к операционному доходу помноженное на 100.
За январь получаем: 55/151*100 = 36,69%
fх = B13/B4*100
Обратите внимание, что итоговая рентабельность рассчитывается не как сумма за предыдущие месяцы, а как отношение итоговой операционной прибыли к итоговому операционному доходу.
Прибыль нарастающим итогом — это прибыли (убытки) за прошлый и текущий отчётные периоды. В январе мы берём данные операционной прибыли, равные 55 тысячам рублей. В феврале прибавляем 58 тысяч. Получаем 113 тысяч рублей. В марте прибавляем ещё 64 тысячи. Получаем 176 тысяч. И так суммируем по каждому месяцу.
В нашем финансовом плане прибыль нарастающим итогом за февраль будет прописываться формулой: fх=B15+C13
4. Составляем план движения денежных средств
Допустим, что в организации осуществляется только операционная деятельность, без капитальных вложений и заёмных средств. Также для упрощения исключим дебиторскую задолженность, допустив что время оплаты и время оказания услуг совпадают.
Платежи по заработной плате и аренде происходят в месяце, следующем за месяцем их начисления, а управленческие расходы — в месяц их осуществления (рисунок 4).
Рисунок 4 — План движения денежных средств, тыс. руб.

Платежи по операционной деятельности рассчитываются, как сумма зарплата + аренда + управленческие расходы.
Сальдо по операционной деятельности — это разность поступлений по операционной деятельности и платежей по операционной деятельности.
Сальдо операционной деятельности за январь будет равно: 151 — 38 = 113 тысяч рублей.
Сальдо на конец периода рассчитывается как сумма сальдо на начало периода и сальдо по операционной деятельности. Если принять сальдо на начало января равное 10 тысячам рублей, сальдо на конец периода будет равно 123 тысячам рублей.
5. Делаем прогнозный баланс
На основании плана доходов и расходов и плана движения денежных средств можно построить прогнозный баланс. Начальные остатки нужно взять из баланса предыдущего периода. Допустим, что все они равны 10 тысячам рублей (рисунок 5).
Рисунок 5 — Прогнозный баланс, тыс. руб.

В графу «денежные средства» подставляем значение сальдо на конец периода предыдущего месяца. Так, денежные средства за февраль = 123 тысячам рублей.
Активы будут равны сумме: денежные средства + основные средства + дебиторская задолженность.
Кредиторская задолженность рассчитывается: кредиторская задолженность предыдущего периода + планируемые затраты на заработную плату и аренду предыдущего месяца — планируемы движения денежных средств по зарплате и аренде предыдущего месяца.
Так, кредиторская задолженность на 1 февраля составит 58 тысяч рублей
0+38+20-0-0.
Капитал = капитал за предыдущий период + операционная прибыль предыдущего периода.
Капитал на 1 февраля составляет 65 тысяч рублей. 10+55.
Пассив — это сумма капитала и кредиторской задолженности
Обратите внимание, что дебиторская задолженность будет рассчитываться как дебиторская задолженность за предыдущую дату + отгрузка периода — поступление денежных средств.
Далее финансовую модель можно детализировать. Например, разбить по видам управленческие расходы, расписать зарплаты по сотрудникам, детализировать план продаж.
Финансовую модель можно корректировать, заменять плановые данные фактическими, отслеживать риски и контролировать финансовые результаты.
Узнайте больше о финансовом моделировании в Excel и прогнозировании финансового состояния бизнеса на семинаре в Учебном центре «Финконт».