The forecasting approach is exactly as described in Real Statistics ARMA Data Analysis Tool. The only difference now is that we need to account for the differencing.
Example 1: Find the forecast for the next five terms in the time series from Example 1 of Real Statistics ARMA Data Analysis Tool based on the ARIMA(2,1,1) model without constant term.
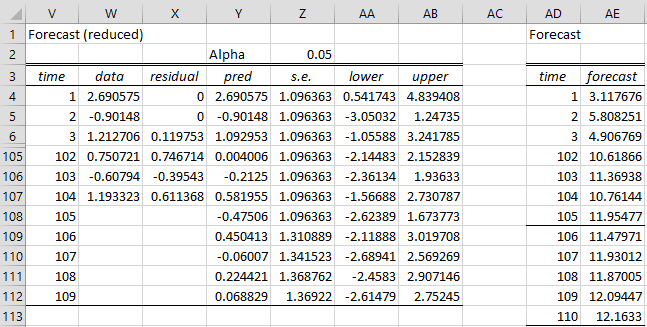
Figure 1 – Forecast for ARIMA(2,1,1) model
The table on the left side is calculated exactly as in Figure 3 of Real Statistics ARMA Data Analysis Tool. The right side undoes the differencing. E.g. Cell AD4 contains the formula =B4 (with reference to the data in Figure 1 of Calculating ARIMA Model Coefficients). Cell AD109 contains the formula =X108+AD108.
Note that if you had not assumed that there was no constant term, cell AD109 would contain the formula =X108+AD108+J$6. If Differences is 2, then AD109 would contain the formula =X107+2*AD108-AD107+J$6.
This tutorial will help you set up and interpret an ARIMA — Autoregressive Integrated Moving Average — model in Excel using the XLSTAT software.
Dataset to fit an ARIMA model to a time series
The data have been obtained in [Box, G.E.P. and Jenkins, G.M. (1976). Time Series Analysis: Forecasting and Control. Holden-Day, San Francisco], and correspond to monthly international airline passengers (in thousands) from January 1949 to December 1960.
We notice on the chart, that there is a global upward trend, that every year a similar cycle starts, and that the variability within a year seems to increase over time. Before we fit the ARIMA model, we need to stabilize the variability. To do that, we transform the series using a log transformation. We can see on the chart below that the variability is reduced.
We can now fit an ARIMA(0,1, 1)(0,1,1)12 model which seems to be appropriate to remove the trend effect and the yearly seasonality of the data.
Setting up the fitting of an ARIMA model to a time series
-
Open XLSTAT
-
Select the XLSTAT / Time Series Analysis / ARIMA command. Once you’ve clicked on the button, the ARIMA dialog box will appear.
-
Select the data on the Excel sheet. In the Times series field you can now select the Log(Passengers) data.
-
Activate the Center option because we want XLSTAT to automatically center the series before optimizing the ARIMA model.
-
Define the type of ARIMA model by entering the value of the (p,d,q)(P,D,Q)s orders. The period of the series is set to 12, because it seems the cycles are repeated every year (12 months).
-
Activate the Series labels the first row of the selected data contains the header of the variable.
-
In the validation tab, enter 12 so that the last 12 values are not used to fit the model, but only to validate the model.
-
Click OK to launch the computations.
Interpreting the results of an ARIMA model fitting to a time series
After the summary statistics of the series, a table displays the various criteria that allow to evaluate the quality of the fit, and to compare the fit of this model with other models (if available).
The next table displays the parameters of the model. We notice that both the MA(1) and SMA(1) parameters are significantly different from 0 as the 95% confidence interval does not include 0. The confidence intervals are computed using the Hessian after optimization which is what other software usually display, and using an asymptotical method. The constant of the model is fixed as it comes from the removal of the mean.
The ARIMA model writes:
Y(t) = 0.000+Z(t-1)-0.348.Z(t-1)-0.562.Z(t-12)+0.195*Z(t-13) where Z(t) is a white noise N(0, 0.001) Y(t)=(1-B)(1-B12)X(t), and X(t) is the input series.
The forecasting equation for the X(t) series is given by: X(t+1) = Y(t+1)+X(t)+X(t-11)-X(t-12)
A table gives the values of the original series, and the smoothed series (the predictions). Because of the constraints of the model, predictions are not available for the 13 first observations (the predictions are replaced by the values of the input series). Notice that a time variable «T» has been created to facilitate the graphical representation. For the last 12 observations predictions have been computed in validation mode and a confidence range is available. We notice that almost all residuals (in red) are negative. This means that in forecasting mode the model overestimates the traffic.
On the chart below, we can visually see that the predictions (Validation) are very close to the data.
Was this article useful?
- Yes
- No
Три подхода к прогнозированию продаж чего угодно
Заглядываем в будущее при помощи статистики
Качественные прогнозы приносят деньги
Из знания уровня будущих продаж предприниматели могут извлечь значительную выгоду: направить оборотные средства на более востребованные SKU, избежать упущенной выгоды, сократить долю просроченных и невостребованных товаров.
Методология прогнозирования экспортных продаж нефти и булочек в районном кафе будет отличаться, но в обоих случаях можно построить точные прогнозы при помощи Excel или специального статистического П.О.
Хотите систематизировать свои знания по аналитике?
Встречайте «Анализ данных для хулиганов» ✨
Нескучное онлайн пособие о том, как создавать великолепные продукты и эффективно управлять маркетингом на основе данных
Три подхода
Все модели можно разделить на три типа:
а) Простые и наивные методы. К ним относится простая экстраполяция на основе среднего значения или темпа прироста, подбор коэффициентов сезонности или продолжение тренда. Эти методы подходят для быстрого прогноза «на коленке».
б) Модели класса ARIMA. Особенности временных рядов заключается в том, что прошлые значения связаны с текущими и будущими. Для краткосрочного прогнозирования рядов с устойчивой структурой достаточно данных о продажах в прошлых периодах.
в) Математическое моделирование. Используются в случаях когда прогнозируемая переменная сильно зависит от внешних факторов: погода, ключевая ставка ЦБ, рекламный бюджет, уровень цен…
Подходы можно комбинировать для улучшения точности прогноза.
ОПРЕДЕЛЕНИЕ
Временной ряд (динамический ряд) — это значение признака, измеренного в хронологическом порядке через постоянные временные промежутки.
Главная особенность динамических рядов в том, что они являются зависимыми. Предыдущие показатели связаны с текущими и будущими, а сам ряд можно разложить на компоненты:
- тренд;
- сезонность;
- цикличность;
- случайные отклонения.
Визуализация
Порой хороший график приносит больше пользы, чем самые сложные модели. В любом случае перед тем как прогнозировать любые динамические ряды их необходимо изучить визуально.
- Посмотрим на ряд при помощи обычного линейного графика. Скользящее среднее или экспоненциальное сглаживание помогают выявить тенденции среди шума.
Сглаживание динамического ряда при помощи скользящей средней
2. Графическая декомпозиция недоступна в Excel, зато гарантированно присутствует в любом статистическом пакете. С ее помощью ряд раскладывается на компоненты.
В данном случае график подсказывает исследователю, что продажи товара Х имеют не только ярко выраженную сезонность, но и стабильную цикличность в рамках недели.
Декомпозиция динамического ряда
3. Коррелограмма — это график автокорреляций. Он помогает понять как значения ряда связаны со своими же значениями в прошлом. Лаг отражает степень запаздывания. Значимый коэффициент корреляции для лагов 7 и 14 также намекает на недельную цикличность.
Модели класса ARIMA
Согласно теореме Вальда любой
стационарный
ряд может быть описан моделью ARMA.
AR – это модель авторегрессии порядка p. Обычное регрессионное уравнение в котором будущие значения ряда линейно зависят от предыдущих.
MA – модель скользящего среднего порядка q. Функция при которой значение в каждой точке ряда равно среднему значению n соседних точек.
СПРАВКА.
ARIMA – расширение моделей ARMA для нестационарных временных рядов.
SARMA / SARIMA – расширение для рядов с сезонной составляющей.
SARIMAX – расширение, позволяющее включить внешнюю регрессионную составляющую.
Стационарный ряд
– это ряд, в котором отсутствует автокорреляция, а среднее и дисперсия не меняются со временем.
Перед тем, как применять модель необходимо позаботиться о стационарности динамического ряда.
Ряд приводят к стационарности взятием последовательных разностей (вместо исходных 3,5,5,4,8 получится 2,0,-1,4) или преобразованием Бокса-Кокса. Стабилизировать дисперсию помогает логарифмирование.
Чтобы убедиться, что мы все сделали правильно применяем формальные тесты:
СПРАВКА. Критерий Льюнга-Бокса — критерий для выявления автокоррелированности временных рядов.
Критерий KPSS (KPSS test) — критерий для проверки на стационарность (Hо = ряд стационарен).
Критерий Дики-Фулера — критерий для проверки на стационарность (Но = ряд нестационарен).
Отлично! Теперь нужно подобрать параметры p и q. Это можно сделать вручную, на основе крупнейших лагов автокорреляционной функции ACF и PACF или воспользоваться чудо-функцией
auto.arima
из библиотеки Forecast для R.
Прогнозирование временных рядов в R
Лучшая модель подбирается с помощью AIC. Модель с самым низким значением информационного критерия Акаике (не несет абсолютную оценку, используется только для сравнения моделей между собой) нужно проверить на адекватность путем анализа остатков (разницы между фактическими и прогнозными значениями).
Нужно убедиться, что остатки:
- имеют низкое абсолютное значение, в них отсутствует тренд и циклы;
- распределены нормально со средним ~0;
- отсутствует автокорреляция (смотрим коррелограмму и тесты «Box-Pierce» «Ljung-Box»).
Если хотя бы что-то не так — значит модель описала не всю структуру и качество можно улучшать. Возвращаемся назад для подбора лучших параметров или преобразования исходных данных.
Анализ временных рядов в R
Install.packages("forecast"); Install.packages("tseries") #устанавливаем полезные расширения
library(forecast); library(tseries) #задействуем их
my_time_series <- ts(data$sales, frequency = 7) #кодируем числовой вектор, как временной ряд
my_time_series <- tsclean(my_time_series) #автоматическая замена выбросов и пропущенных значений
plot(my_time_series) #визуализация
plot(decompose(my_time_series)) #график декомпозиции ряда
acf(my_time_series) #построение коррелограммы
fit <- auto.arima(my_time_series) #автоматический подбор модели и оптимальных параметров
fit #модель
tsdisplay(residuals(fit)) #графический анализ остатков
Box.test(residuals(fit)) #формальный тест скоррелированности остатков
my_forecast <- forecast(fit, h=3) #прогноз на 3 периода вперед
plot(forecast(fit, h=3)) #визуализация прогноза с доверительным интервалом
- - - - -
#другие полезные функции:
ets() #экспоненциальное сглаживание
BoxCox() #преобразование Бокса-Кокса
adf.test() #проверка стационарности (тест Дики-Фуллера)
Математическое моделирование
Пример регресионной модели прогнозирования продаж
Некоторые динамические ряды не имеют устойчивой структуры и сильно зависят от влияния внешних факторов (например: погода, рекламный бюджет). В таких случаях целесообразно применить математическое моделирование. Подойдет простая регрессия, нейронные сеточки, случайные леса, ближайшие соседи, SVM или ансамбль из всех перечисленных (зависит от типа, распределения и объема исходных данных).
Алгоритмы будут сопоставлять весь массив входных данных (предикторов) и соответствующих значений целевой переменной (т.е. уровня продаж). Такой процесс называется «обучением». Методы машинного обучения как бы обобщают полученный опыт для ответов на новые вопросы. Гиперпараметры подгоняются так, чтобы ошибка прогнозов была минимальной.
Пример исходных данных для прогнозирования продаж
Выбор алгоритмов их их параметров оказывают большое влияние на точность прогнозов, но определяющую роль играет набор признаков, т.е. состав переменных на которых будет будет обучаться алгоритм. При выборе признаков руководствуются физическими ограничениями, так как не все получается оцифровать и измерить (или сделать это за приемлемую цену).
Специалист из предметной области определяет набор данных, которые необходимо получить и использовать для моделирования. Если таких данных много в уже оцифрованном виде, то применяются математические методы селекции: корреляция (correlation), хи-квадрат (chi-square), мера энтропии (Informaition gain), индекс Джини (GINI index), расчет уменьшения предсказательной способности при исключении переменной, рекурсивное разбиение (Recursive partitioning), сети векторного квантования (Learning Vector Quantization) и др.
Перечислим полезные лайфхаки:
- Цикличность можно закодировать категориальным фактором (день недели или месяца) или числовой переменной, которая отражает средний уровень целевой переменной за этот период.
- Погоду, курсы валют и ставки ЦБ можно получать напрямую через API или скрапингом. Благодаря этому ваша модель будет работать без ручного обогащения новыми данными.
- Результаты прогноза по ARIMA-моделям могут быть поданы на вход другим алгоритмам для дальнейшего сокращения остатков.
Заключение
Чтобы быстро прикинуть продажи в следующей неделе / месяце / году воспользуйтесь одним из наивных методов.
Для краткосрочного прогнозирования временных рядов с устойчивой структурой подходят модели класса ARIMA.
Для долгосрочного моделирования сложных и зависимых от внешних факторов процессов используйте модели машинного обучения.
Хотите систематизировать свои знания по аналитике?
Встречайте «Анализ данных для хулиганов»
Онлайн пособие о том, как создавать великолепные продукты и эффективно управлять маркетингом на основе данных⚡
Методики / Фреймворки / Шаблоны для скачивания
Introduction
XLMiner facilitates the analysis of datasets via the use of trend discovery techniques (autocorrelation and partial autocorrelation) and comprehensive modeling methods (ARIMA and exponential smoothing).
ARIMA — AutoRegressive Integrated Moving-Average model — is one of the most popular modeling methods used in time series forecasting, due largely to its focus on using data autocorrelation techniques to achieve high-quality models. XLMiner fully utilizes all aspects of ARIMA implementation, including variable selections, seasonal / non-seasonal parameter definitions, and advanced options such as iteration maximums, output, and forecast options.
ARIMA Modeling in XLMiner
An ARIMA model is a regression-type model that includes autocorrelation. When estimating ARIMA coefficients, the basic assumption is that the data is stationary; meaning, the trend or seasonality cannot affect the variance. This is generally not true. In order to achieve stationary data, XLMiner needs to apply differencing: ordinary, seasonal, or both.
After XLMiner fits the model, various results will be available. The quality of the model can be evaluated by comparing the time plot of the actual values with the forecasted values. If both curves are close, then it can be assumed that the model is a good fit. The model should expose any trends and seasonality, if any exist.
Next an analysis of the residuals should convey whether or not the model is a good fit: random residuals means that the model is accurate, but if the residuals exhibit a trend then the model may be inaccurate. Fitting an ARIMA model with parameters (0,1,1) will give the same results as exponential smoothing, while using the parameters (0,2,2) will give the same results as double exponential smoothing.
How to Access ARIMA Settings in Excel
- Launch Excel.
- In the toolbar, click XLMINER PLATFORM.
- In the ribbon, click ARIMA.
- In the drop-down menu, select ARIMA Model.
For usability information, please reference Using Time Series and/or the XLMiner Online Help.
ARIMA Model Summary
- ARIMA: AutoRegressive Integrated Moving Average.
- Forecasting model used in time-series analysis.
- ARIMA Parameter Syntax: ARIMA (p,d,q) where p = the number of auto-regressive terms, d = the number of non-seasonal differences, and q = the number of moving average terms.
Resources
- Time Series Example: View an example of how an ARIMA model can be applied.
- Using Time Series: How to use time series analysis functionality within XLMiner.
- Smoothing Models: How smoothing techniques can be applied to time series forecasting models.
- XLMiner Online Help: Help system covering functionality within the XLMiner module.
Box-Jenkins ARIMA in Excel with UNISTAT
The UNISTAT statistics add-in extends Excel with Box-Jenkins ARIMA capabilities.
For further information visit UNISTAT User’s Guide section 9.1. Box-Jenkins ARIMA.
Here we provide a sample output from the UNISTAT Excel statistics add-in for data analysis.
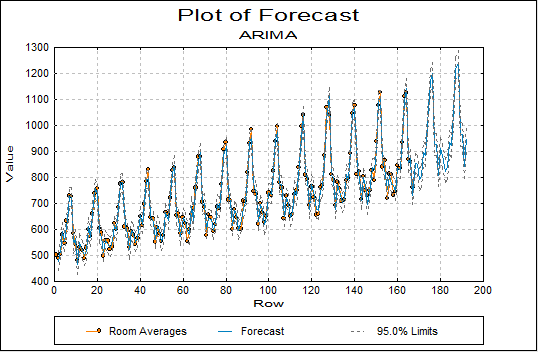
ARIMA: Forecasting
Forecast Table: Room Averages
Forecasts with Origin at 168
| Row | Forecast | Lower 95% | Upper 95% |
|---|---|---|---|
| 169 | 848.4627 | 812.5347 | 884.3908 |
| 170 | 790.4152 | 748.5739 | 832.2565 |
| 171 | 802.9863 | 761.1450 | 844.8277 |
| 172 | 897.2505 | 855.4092 | 939.0918 |
| 173 | 884.6228 | 842.7815 | 926.4642 |
| 174 | 1004.5412 | 962.6999 | 1046.3826 |
| 175 | 1172.1330 | 1130.2917 | 1213.9743 |
| 176 | 1198.5591 | 1156.7178 | 1240.4004 |
| 177 | 926.1231 | 884.2818 | 967.9644 |
| 178 | 926.0101 | 884.1688 | 967.8514 |
| 179 | 806.3858 | 764.5445 | 848.2271 |
| 180 | 911.1494 | 869.3081 | 952.9907 |
| 181 | 882.9764 | 838.7358 | 927.2169 |
| 182 | 824.0693 | 779.0048 | 869.1338 |
| 183 | 837.2795 | 792.2150 | 882.3440 |
| 184 | 934.0786 | 889.0141 | 979.1431 |
| 185 | 921.2332 | 876.1687 | 966.2976 |
| 186 | 1044.2033 | 999.1388 | 1089.2677 |
| 187 | 1216.0144 | 1170.9499 | 1261.0788 |
| 188 | 1243.1172 | 1198.0528 | 1288.1817 |
| 189 | 963.8793 | 918.8148 | 1008.9438 |
| 190 | 963.7683 | 918.7039 | 1008.8328 |
| 191 | 841.1561 | 796.0916 | 886.2206 |
| 192 | 948.5402 | 903.4758 | 993.6047 |
ARIMA: Fit Model
Model Results
| Parameter | Estimate | Standard Error | t Ratio |
|---|---|---|---|
| (AR) P(1) | 0.5490 | 0.0292 | 18.7748 |
| (MA) Q(1) | 0.5969 | 0.0284 | 20.9931 |
| (SAR) Ps(1) | 1.0250 | 0.0099 | 103.7169 |
| (SMA) Qs(1) | 0.6250 | 0.0430 | 14.5430 |
| Number of Iterations | 22 (Converged) |
|---|---|
| Number of Backforecasts | 24 |
| Seasonal Period | 12 |
Parameter Covarience
| (AR) P(1) | (MA) Q(1) | (SAR) Ps(1) | (SMA) Qs(1) | |
|---|---|---|---|---|
| (AR) P(1) | 0.0009 | -0.0001 | 0.0001 | 0.0008 |
| (MA) Q(1) | -0.0001 | 0.0008 | 0.0001 | 0.0007 |
| (SAR) Ps(1) | 0.0001 | 0.0001 | 0.0001 | 0.0003 |
| (SMA) Qs(1) | 0.0008 | 0.0007 | 0.0003 | 0.0018 |
Parameter Correlation
| (AR) P(1) | (MA) Q(1) | (SAR) Ps(1) | (SMA) Qs(1) | |
|---|---|---|---|---|
| (AR) P(1) | 1.0000 | -0.1771 | 0.3616 | 0.6459 |
| (MA) Q(1) | -0.1771 | 1.0000 | 0.3090 | 0.6118 |
| (SAR) Ps(1) | 0.3616 | 0.3090 | 1.0000 | 0.6802 |
| (SMA) Qs(1) | 0.6459 | 0.6118 | 0.6802 | 1.0000 |
Residual Autocorrelations
() Two Standard Error Limits
| Lag | Correlation | Standard Error |
-1.0000 1.0000 |
|---|---|---|---|
| 1 | -0.3762 | 0.0798 |
******(**** ) |
| 2 | 0.1995 | 0.0795 |
( ***)* |
| 3 | -0.3327 | 0.0793 |
*****(**** ) |
| 4 | 0.0968 | 0.0790 |
( ***) |
| 5 | -0.2434 | 0.0788 |
**(**** ) |
| 6 | 0.1446 | 0.0785 |
( **** |
| 7 | -0.0753 | 0.0782 |
( *** ) |
| 8 | 0.1267 | 0.0780 |
( **** |
| 9 | -0.1371 | 0.0777 |
***** ) |
| 10 | 0.0799 | 0.0774 |
( ** ) |
| 11 | -0.0426 | 0.0772 |
( *** ) |
| 12 | 0.0797 | 0.0769 |
( ** ) |
| 13 | 0.0177 | 0.0766 |
( * ) |
| 14 | 0.0482 | 0.0763 |
( ** ) |
| 15 | -0.0214 | 0.0761 |
( ** ) |
| 16 | -0.0176 | 0.0758 |
( ** ) |
| 17 | 0.0434 | 0.0755 |
( ** ) |
| 18 | -0.2533 | 0.0752 |
***(**** ) |
| 19 | 0.1797 | 0.0750 |
( ***)* |
| 20 | -0.0784 | 0.0747 |
( *** ) |
| 21 | 0.1364 | 0.0744 |
( **** |
| 22 | -0.1768 | 0.0741 |
*(**** ) |
| 23 | 0.1528 | 0.0738 |
( **** |
| 24 | -0.1589 | 0.0736 |
***** ) |
| 25 | 0.1915 | 0.0733 |
( ***)* |
Ljung-Box Statistic
| Lag | Ljung Box | DoF | Prob |
|---|---|---|---|
| 6 | 60.5684 | 2 | 0.0000 |
| 12 | 69.6972 | 8 | 0.0000 |
| 18 | 81.9477 | 14 | 0.0000 |
| 25 | 113.6225 | 21 | 0.0000 |
ARIMA
Auto Correlations: Room Averages
() Two Standard Error Limits
| Lag | Correlation | Standard Error |
-1.0000 1.0000 |
|---|---|---|---|
| 1 | 0.0190 | 0.0774 |
( * ) |
| 2 | -0.0201 | 0.0774 |
( ** ) |
| 3 | -0.2507 | 0.0774 |
***(**** ) |
| 4 | -0.0031 | 0.0822 |
( ** ) |
| 5 | -0.2540 | 0.0822 |
**(***** ) |
| 6 | 0.0029 | 0.0867 |
( * ) |
| 7 | -0.2378 | 0.0867 |
*(***** ) |
| 8 | 0.0042 | 0.0906 |
( * ) |
| 9 | -0.2221 | 0.0906 |
*(***** ) |
| 10 | -0.0156 | 0.0938 |
( ** ) |
| 11 | 0.0232 | 0.0938 |
( * ) |
| 12 | 0.9027 | 0.0938 |
( ****)****************** |
| 13 | 0.0270 | 0.1362 |
( * ) |
| 14 | -0.0147 | 0.1363 |
( ** ) |
| 15 | -0.2332 | 0.1363 |
(******* ) |
| 16 | 0.0039 | 0.1386 |
( * ) |
| 17 | -0.2282 | 0.1386 |
(******* ) |
| 18 | -0.0096 | 0.1409 |
( ** ) |
| 19 | -0.2142 | 0.1409 |
(******* ) |
| 20 | -0.0021 | 0.1428 |
( ** ) |
| 21 | -0.2007 | 0.1428 |
( ****** ) |
| 22 | -0.0241 | 0.1445 |
( ** ) |
| 23 | 0.0319 | 0.1445 |
( * ) |
| 24 | 0.8186 | 0.1446 |
( *******)************* |
| 25 | 0.0353 | 0.1701 |
( * ) |
Partial Autocorrelations: Room Averages
() Two Standard Error Limits
| Lag | Correlation | Standard Error |
-1.0000 1.0000 |
|---|---|---|---|
| 1 | 0.0190 | 0.0774 |
( * ) |
| 2 | -0.0204 | 0.0774 |
( ** ) |
| 3 | -0.2501 | 0.0774 |
***(**** ) |
| 4 | 0.0052 | 0.0774 |
( * ) |
| 5 | -0.2807 | 0.0774 |
***(**** ) |
| 6 | -0.0595 | 0.0774 |
( *** ) |
| 7 | -0.3066 | 0.0774 |
****(**** ) |
| 8 | -0.1798 | 0.0774 |
*(**** ) |
| 9 | -0.4166 | 0.0774 |
*******(**** ) |
| 10 | -0.5227 | 0.0774 |
*********(**** ) |
| 11 | -0.7529 | 0.0774 |
***************(**** ) |
| 12 | 0.5100 | 0.0774 |
( ***)********* |
| 13 | -0.1686 | 0.0774 |
*(**** ) |
| 14 | -0.1999 | 0.0774 |
*(**** ) |
| 15 | -0.0377 | 0.0774 |
( ** ) |
| 16 | -0.1073 | 0.0774 |
(**** ) |
| 17 | 0.0794 | 0.0774 |
( ** ) |
| 18 | -0.0910 | 0.0774 |
(**** ) |
| 19 | 0.0306 | 0.0774 |
( * ) |
| 20 | -0.0060 | 0.0774 |
( ** ) |
| 21 | -0.0172 | 0.0774 |
( ** ) |
| 22 | -0.0207 | 0.0774 |
( ** ) |
| 23 | -0.0014 | 0.0774 |
( ** ) |
| 24 | 0.0452 | 0.0774 |
( ** ) |
| 25 | -0.0021 | 0.0774 |
( ** ) |