Мода вариационного ряда в excel - Word и Excel - помощь в работе с программами

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

Предположим, что вы хотите узнать наиболее распространенное количество видов птицы в образце видов птицы на критической заболоченой за 30-летней период времени или узнать наиболее часто посещаемые телефонные вызовы в центре поддержки по телефону в некритовые часы. Для вычисления режима группы чисел используйте функцию РЕЖИМ.

Режим возвращает наиболее часто повторяющийся (повторяющийся) значение в массиве или диапазоне данных.

Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.

Дополнительные сведения о новых функциях см. в разделах Функция МОДА.НСК и Функция МОДА.ОДН.

Синтаксис

МОДА(число1;[число2];…)

Аргументы функции МОДА описаны ниже.

Число1 Обязательный. Первый числовой аргумент, для которого требуется вычислить моду.
Число2… Необязательный. От 1 до 255 числовых аргументов, для которых вычисляется мода. Вместо аргументов, разделенных точкой с запятой, можно воспользоваться массивом или ссылкой на массив.

Замечания

Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения игнорируются; ячейки, содержащие нулевые значения, учитываются.
Аргументы, которые являются значениями ошибки или текстами, не преобразуемыми в числа, приводят к возникновению ошибок.
Если множество данных не содержит одинаковых данных, функция МОДА возвращает значение ошибки #Н/Д.

Функция МОДА измеряет центральную тенденцию, которая является центром множества чисел в статистическом распределении. Существует три наиболее распространенных способа определения центральной тенденции:

Среднее значение — это среднее арифметическое, которое вычисляется путем сложения набора чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.
Мода — это число, наиболее часто встречающееся в данном наборе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.

При симметричном распределении множества чисел все три значения центральной тенденции будут совпадать. При смещенном распределении множества чисел значения могут быть разными.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные
5,6
4
4
3
2
4
Формула	Описание	Результат
=МОДА(A2:A7)	Мода или наиболее часто встречающееся число	4

Нужна дополнительная помощь?

Источник

Загрузить PDF

Microsoft Excel выполняет ряд статистических функций, в их числе – подсчет среднего значения, медианы и моды. В то время как среднее значение (среднее арифметическое группы чисел) и медиана (число, которое является серединой группы) используются чаще, мода – наиболее часто встречающееся число в наборе чисел – тоже считается довольно полезной функцией. Она пригодится, например, чтобы использовать наиболее частую числовую оценку для определения эффективности метода обучения. Вот как рассчитывать моду с помощью Excel.

1

Введите каждое число в отдельную ячейку. Для соблюдения принципа преемственности, вводите значения по порядку – в строку или в столбец – но для удобства столбец предпочтительнее.
2
Введите функцию MODE в ячейку, в которой вы хотите увидеть результат. Формат функции следующий: «=MODE(Cx:Dy)», где C и D представляют букву столбца первой и последней ячейки набора чисел, а х и y – номер первой и последней строки набора чисел (хотя в этом примере используются разные буквы, вы будете использовать одну и ту же букву столбца для первой и последней ячейки, если будете вводить данные в столбец или тот же номер строки при вводе данных в строку).
- Вы также можете указать каждую ячейку отдельно (до 255 ячеек), как в «=MODE(A1, A2, A3)», но рекомендуется делать это только тогда, если у вас очень мало данных и вы не планируете их добавлять в будущем. Можно использовать функцию с константами, например «=MODE(4,4,6)», но в этом случае нужно будет редактировать функцию каждый раз, когда вы захотите найти другую моду.
- Для выделения в наборе чисел возможно отформатировать ячейку на отображение моды жирным шрифтом или курсивом.
3
Посчитайте и отобразите результаты. Обычно в Excel это происходит автоматически, но если вы изменили его настройки на ручное вычисление, нажмите F9 для отображения моды.
- Для набора данных 10, 7, 9, 8, 7, 0 и 4, введенных в ячейки с 1 по 8 колонки А, функция =MODE(A1:A8) отобразит результат 7, так как 7 появляется в наборе данных чаще других чисел.
- Если в наборе данных имеется более одного числа, которое квалифицируется в качестве моды (например, 7 и 9 появляются дважды, а все остальные числа – по одному разу), то первое по списку число моды и будет результатом. Если ни одно значение не появляется чаще других, функция MODE отобразит сообщение об ошибке #N/A.
- Функция MODE доступна во всех версиях Excel, включая Excel 2010, который включает ее для совместимости с электронными таблицами, созданными в более ранних версиях. Excel 2010 использует функцию MODE.SNGL, которая, за исключением синтаксиса (=MODE.SNGL(Cx:Dy)), работает фактически так же, как и функция MODE в более ранних версиях Excel.
Реклама

1

Введите каждое число в наборе данных в отдельную ячейку.
2

Выберите диапазон ячеек, равный количеству мод, которые вы хотите найти в наборе данных. Если вы хотите найти три моды, выберите три ячейки. В противном случае, вы увидите количество мод, равное количеству выбранных ячеек.
3
Введите функцию MODE.MULT в панель формул. Формат функции MODE.MULT следующий: «=MODE.MULT(Cx:Dy),» где C и D отображают букву колонки первой и последней ячеек диапазона, а x и y – число первой и последней строки (как и с функцией MODE, обычно данные вводят в ячейки одного столбца и используют при этом одну букву столбца для первой и последней диапазона или же в ячейки одной строки с использованием того же номера строки для первой и последней ячеек диапазона).
- MODE.MULT также можно использовать с указанием отдельных ячеек или констант в скобках, но любой из этих вариантов следует использовать только с небольшим набором данных, которые вы не планируете менять.
4

Используйте сочетание клавиш control+shift+enter для отображения результата в виде массива, в противном случае, он будет выведен так же, как и с функцией MODE.SNGL. Если вы изменили настройки на ручное вычисление, нажмите F9, чтобы увидеть результат.
5

В отличие от MODE.SNGL, функция MODE.MULT показывает несколько результатов. Для набора данных 2,1,3,4,3,2,1,7,1,2,3,8, введенных в ячейки с 1 по 12 колонки A, формула =MODE.MULT(A1:A12) отобразит моды 1, 2 и 3, так как каждое число появляется в ряде данных три раза.
6

Если ни одно число в ряде данных не появляется чаще других, функция MODE.MULT отобразит сообщение об ошибке «#N/A».
7

Функция MODE.MULT доступна только в Microsoft Excel 2010.

Реклама

Советы

При добавлении новых чисел в набор данных проверяйте формулу, чтобы убедиться в правильности указания первой и последней ячеек набора данных. Если вы вставите строки перед начальным первым номером в наборе и введете в них данные, нужно отредактировать в теле функции первый номер ячейки в диапазоне. Если вы вставите строки и заполните их данными после последнего числа ряда данных – отредактируйте функцию, изменив последнюю ячейку. Если вы вставите строки в середину, диапазон ячеек изменится автоматически.

Предупреждения

Использование формулы MODE.MULT для одновременного поиска большого количества мод может замедлить работу вашего компьютера, если ему не хватает достаточного количества памяти и вычислительной мощности.

Об этой статье

Эту страницу просматривали 33 230 раз.

Была ли эта статья полезной?

Источник

В статистике есть целый набор показателей, которые характеризуют центральную тенденцию. Выбор того или иного индикатора в основном зависит от характера данных, целей расчетов и его свойств.

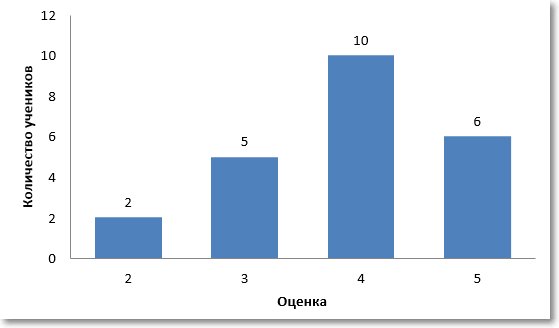
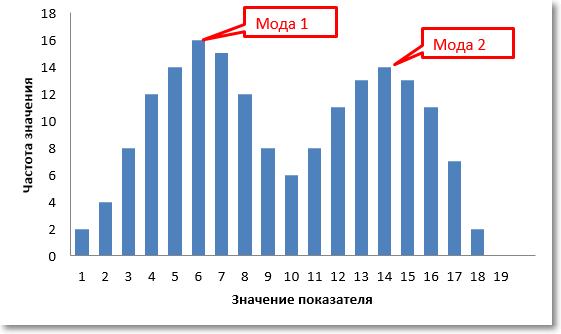
Что подразумевается под характером данных? Прежде всего, мы говорим о количественных данных, которые выражены в числах. Но набор числовых данных может иметь разное распределение. Под распределением понимаются частоты отдельных значений. К примеру, в классе из 23 человек 2 школьника написали контрольную работу на двойку, 5 – на тройку, 10 – на четверку и 6 – на пятерку. Это и есть распределение оценок. Распределение очень наглядно можно представить с помощью специальной диаграммы – гистограммы. Для данного примера получится следующая гистограмма.

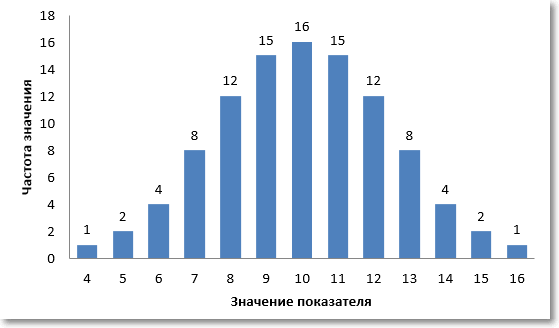
Во многих случаях количество уникальных значений намного больше, а распределение похоже на нормальное. Ниже приведена примерная иллюстрация нормального распределения случайных чисел.

Итак, центральная тенденция. Если частоты анализируемых значений распределены по нормальному закону, то есть симметрично вокруг некоторого центра, то центральная тенденция определяется вполне однозначно – это есть тот самый центр, и математически он соответствует средней арифметической.

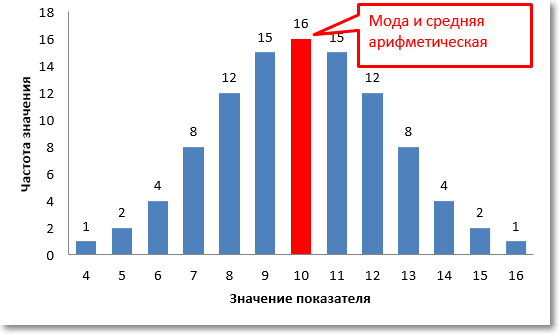
Как нетрудно заметить, в этом же центре находится и максимальная частота значений. То есть при нормальном распределении центральная тенденция есть не только средняя арифметическая, но и максимальная частота, которая в статистике называется модой или модальным значением.

На диаграмме оба значения центральной тенденции совпадают и равны 10.

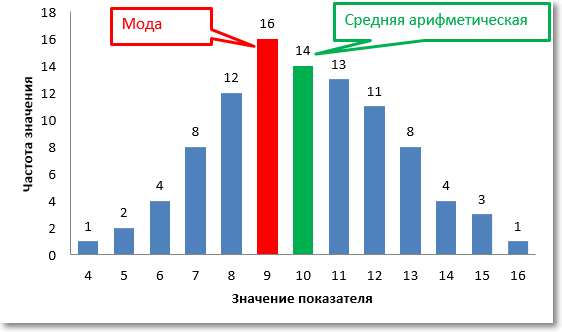
Но такое распределение встречается далеко не всегда, а при малом числе данных – совсем редко. Чаще бывает так, что частоты распределяются асимметрично. Тогда мода и среднее арифметическое не будут совпадать.

На рисунке выше среднее арифметическое по-прежнему составляет 10, а вот мода уже равна 9. Что в таком случае считать значением центральной тенденции? Ответ зависит от поставленных целей анализа. Если интересует уровень, сумма отклонений от которого равна нулю со всеми вытекающим отсюда свойствами и последствиями, то это средняя арифметическая. Если нужно максимально частое значение, то это мода.

Итак, зачем нужна мода? Приведу пару примеров. Экономист планово-экономического отдела обувной фабрики интересуется, какой размер обуви пользуется наибольшим спросом. Средний размер обуви, скорее всего, здесь не подойдет, тем более, что число может получится дробным. А вот мода – как раз нужный показатель.

Расчет моды

Теперь посмотрим, как рассчитать моду. Мода – это то значение в анализируемой совокупности данных, которое встречается чаще других, поэтому нужно посмотреть на частоты значений и отыскать максимальное из них. Например, в наборе данных 3, 4, 6, 7, 3, 5, 3, 4 модой будет значение 3 – повторяется чаще остальных. Это в дискретном ряду, и здесь все просто. Если данных много, то моду легче всего найти с помощью соответствующей гистограммы. Бывает так, что совокупность данных имеет бимодальное распределение.

Без диаграммы очень трудно понять, что в данных не один, а два центра. К примеру, на президентских выборах предпочтения сельских и городских жителей могут отличаться. Поэтому распределение доли отданных голосов за конкретного кандидата может быть «двугорбым». Первый «горб» – выбор городского населения, второй – сельского.

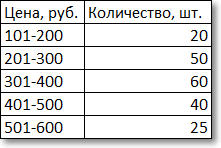
Немного сложнее с интервальными данными, когда вместо конкретных значений имеются интервалы. В этом случае говорят о модальном интервале (при анализе доходов населения, например), то есть интервале, частота которого максимальна относительно других интервалов. Однако и здесь можно отыскать конкретное модальное значение, хотя оно будет условным и примерным, так как нет точных исходных данных. Представим, что есть следующая таблица с распределением цен.

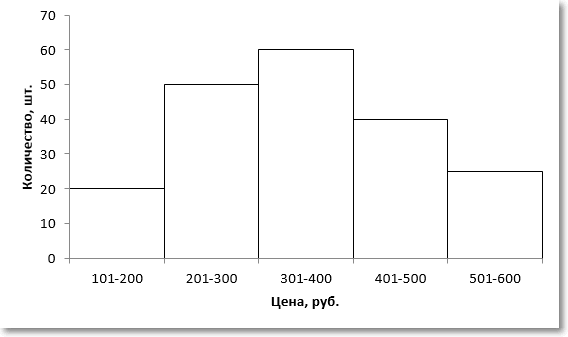
Для наглядности изобразим соответствующую диаграмму.

Требуется найти модальное значение цены.

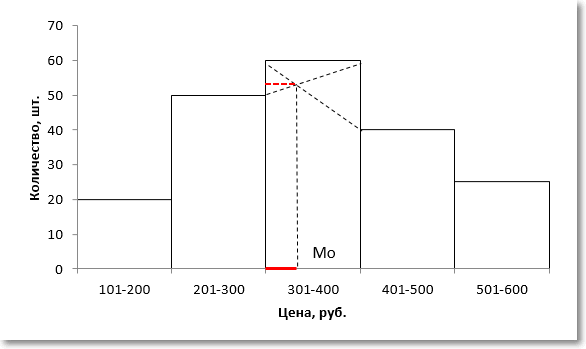
Вначале нужно определить модальный интервал, который соответствует интервалу с наибольшей частотой. Найти его так же легко, как и моду в дискретном ряду. В нашем примере это третий интервал с ценой от 301 до 400 руб. На графике – самый высокий столбец. Теперь нужно определить конкретное значение цены, которое соответствует максимальному количеству. Точно и по факту сделать это невозможно, так как нет индивидуальных значений частот для каждой цены. Поэтому делается допущение о том, что интервалы выше и ниже модального в зависимости от своей частоты имеют разные вес и как бы перетягивают моду в свою сторону. Если частота интервала следующего за модальным больше, чем частота интервала перед модальным, то мода будет правее середины модального интервала и наоборот. Давайте еще раз посмотрим на рисунок, чтобы понять формулу, которую я напишу чуть ниже.

На рисунке отчетливо видно, что соотношение высоты столбцов, расположенных слева и справа от модального определяет близость моды к левому или правому краю модального интервала. Задача по расчету модального значения состоит в том, чтобы найти точку пересечения линий, соединяющих модальный столбец с соседними (как показано на рисунке пунктирными линиями) и нахождении соответствующего значения признака (в нашем примере цены). Зная основы геометрии (7-й класс), по данному рисунку нетрудно вывести формулу расчета моды в интервальном ряду.

Формула моды имеет следующий вид.

Где Мо – мода,

x₀ – значение начала модального интервала,

h – размер модального интервала,

f_Мо – частота модального интервала,

f_Мо-1 – частота интервала, находящего перед модальным,

f_Мо1 – частота интервала, находящего после модального.

Второе слагаемое формулы моды соответствует длине красной линии на рисунке выше.

Рассчитаем моду для нашего примера.

Таким образом, мода интервального ряда представляет собой сумму, состоящую из значения начального уровня модального интервала и отрезка, который определяется соотношением частот ближайших интервалов от модального.

Расчет моды в Excel

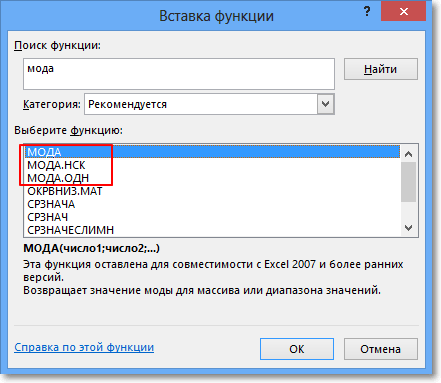
В настоящее время большинство вычислений делается в MS Excel, где для расчета моды также предусмотрена специальная функция. В Excel 2013 я таких нашел ажно 3 штуки.

МОДА – пережиток старых изданий Excel. Функция оставлена для совмещения со старыми версиями.

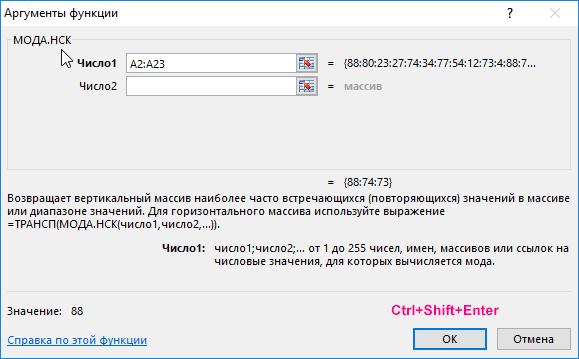
МОДА.ОДН – рассчитывает моду по заданным значениям. Здесь все просто. Вставили функцию, указали диапазон данных и «Ок».

МОДА.НСК – позволяет рассчитать сразу несколько модальных значений (одинаковых максимальных частот) для одного ряда данных, если они есть. Функцию нужно вводить как формулу массива, перед этим выделив количество ячеек равное количеству требуемых модальных значений. Иногда действительно модальных значений может быть несколько. Однако для этих целей предварительно лучше посмотреть на диаграмму распределения.

Моду для интервальных данных одной функцией в Excel рассчитать нельзя. То есть такая функция в готовом виде не предусмотрена. Придется прописывать вручную.

Следующая статья посвящена медиане.

До встречи на statanaliz.info.

Поделиться в социальных сетях:

Источник

Для различных аналитических целей часто требуется получить средний уровень различных показателей: средний возраст, средняя зарплата и т.д. Первое, что приходит на ум – это найти простое среднее арифметическое. Но всегда ли это правильно? В этой статье разберемся, что такое медиана, среднее арифметическое и мода. А также научимся считать их в Excel.

Среднее арифметическое
Медиана – чем отличается от среднего значения
Что лучше – медиана или среднее значение
Что такое мода
Средневзвешенное значение

Среднее арифметическое

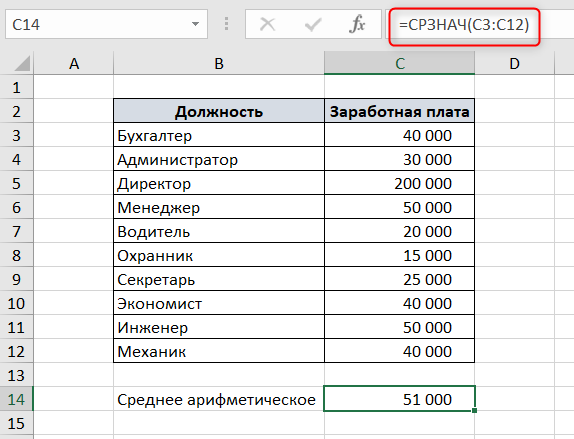
Среднее арифметическое значение – это сумма всех элементов выборки, поделенная на количество этих элементов.

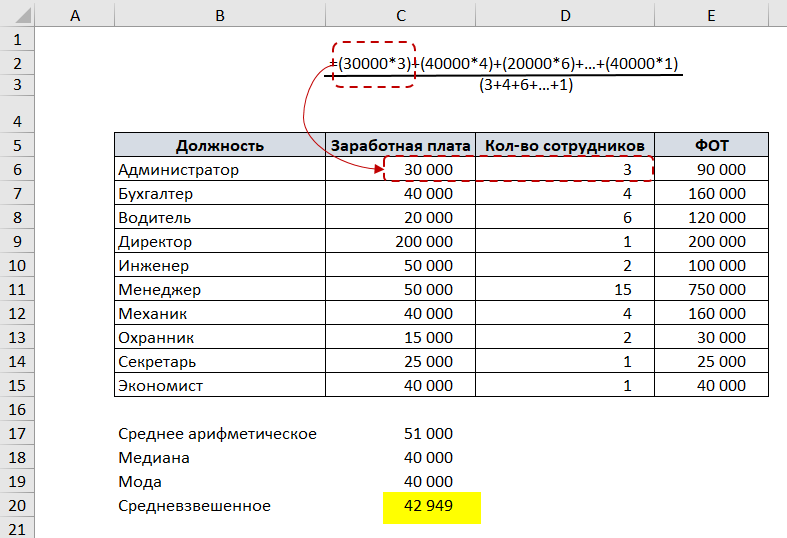
Например, есть список должностей и заработных плат. Чтобы посчитать среднюю заработную плату в Excel, воспользуемся функцией СРЗНАЧ.

Медиана – чем отличается от среднего значения

Медиана – это середина набора чисел, отсортированного по возрастанию.

Другими словами, 50% наблюдений ниже медианы и 50% наблюдений выше медианы. Медиана всегда равно удалена от начала и от конца набора чисел.

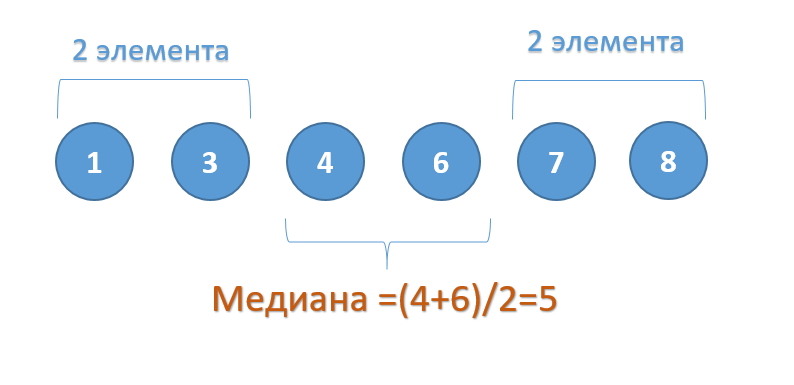
Если набор чисел состоит из нечетного количества элементов, то медианой будет число, которое находится в середине.

Если набор чисел состоит из четного числа элементов, то медиана будет равна среднему арифметическому между двумя центральными элементами списка.

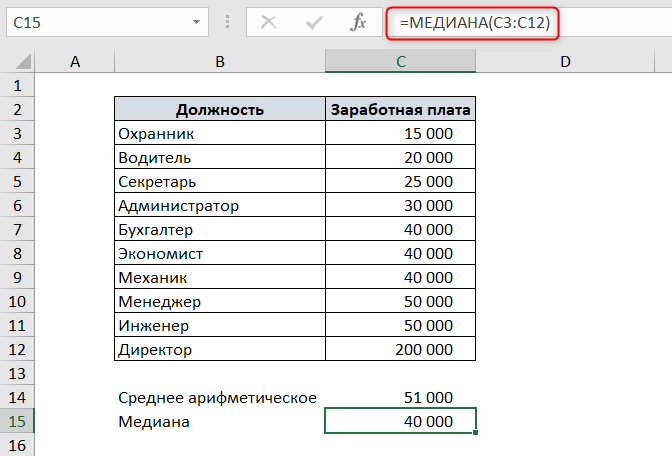
Чтобы наглядно увидеть, чем отличается медиана от среднеарифметического значения на нашем первом примере с зарплатой, отсортируем список по возрастанию.

Поскольку в списке 10 элементов – четное количество – то медианой будет среднее арифметическое 5 и 6 элементов.

Чтобы посчитать медиану в Excel, воспользуемся функцией МЕДИАНА. В качестве аргументов функция принимает числовые значения ряда данных.

Как видите, медиана не равна среднему значению.

Что лучше – медиана или среднее значение

На этот вопрос однозначного ответа нет, все зависит от целей вашего анализа.

Основные отличия медианы от среднего арифметического:

Медиана в отличие от среднего арифметического игнорирует выбросы данных (выбросы – это значения, которые значительно отличаются от основного массива выборки).

Рассмотрим пример:

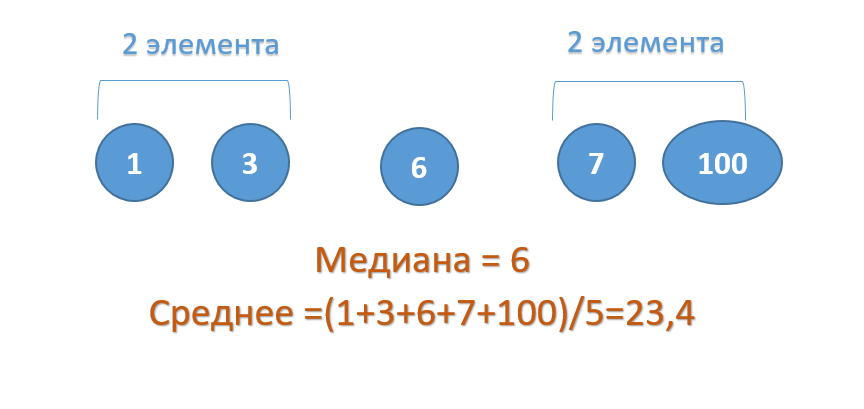
В данном примере число 100 – это выброс, т.к. оно значительно отличается от основной других чисел в ряду. И при расчете среднего арифметического это число 100 исказило среднее – оно стало значительно больше остальных чисел.

Медиана же останется неизменной, даже если вместо 100 мы укажем 1000, т.к. середина ряда все равно будет число 6.

Это свойство медианы – игнорировать выбросы – особенно полезно, когда нужно посчитать среднюю зарплату или средний возраст. В целом, медиана более точно определяет середину выборки, чем среднее арифметическое, поскольку устойчива к искажениям.

Свойство медианы игнорировать выбросы, на самом деле, не всегда полезно. Оно может скрыть из виду важные моменты, тогда как среднее арифметическое, завысив или занизив среднее, поможет обратить на них внимание.

В нашем примере с заработной платой среднее арифметическое заработных плат выше, чем медиана. Это может обратить внимание на то, что одна из заработных плат (в данном случае – директора) сильно отличается от заработных плат других сотрудников.

Если ряд данных имеет нормальное или близкое к нормальному распределение, то медиана или среднее значение будут равны или близки друг к другу.
Если среднее значение больше медианы, то распределение положительно искажено (т.е. имеет выбросы в сторону больших значений). И наоборот, если среднее значение меньше медианы, то выборка отрицательно искажена (преобладают меньшие значения).

Что такое мода

Мода – это наиболее часто встречающееся значение выборки.

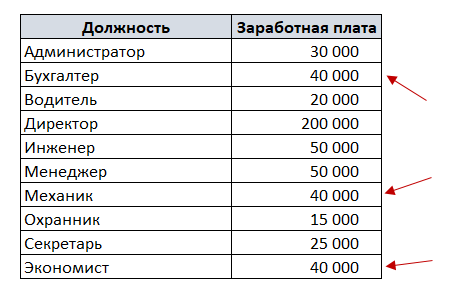
В нашем примере мода – это заработная плата 40000, т.к. это значение встречается 3 раза, в то время, как остальные значения – один или два раза.

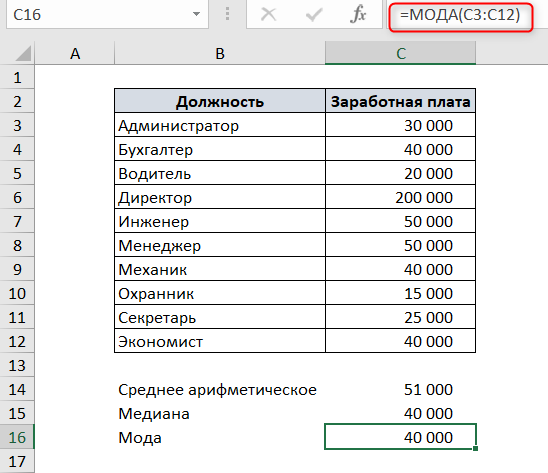
Чтобы посчитать моду в Excel, используем функцию МОДА.

Для чего считать моду? Пример использования моды на коммерческом предприятии: для планирования производства обуви необходимо определить размер, который наиболее часто приобретают покупатели.

Средневзвешенное значение

Средневзвешенное значение отличается от среднего арифметического тем, что каждому элементу ряда присваивается «вес» — или как бы «значимость» его в ряду.

Для того, что определить средневзвешенное, сумма элементов ряда, умноженная на их «вес», делится на количество элементов.

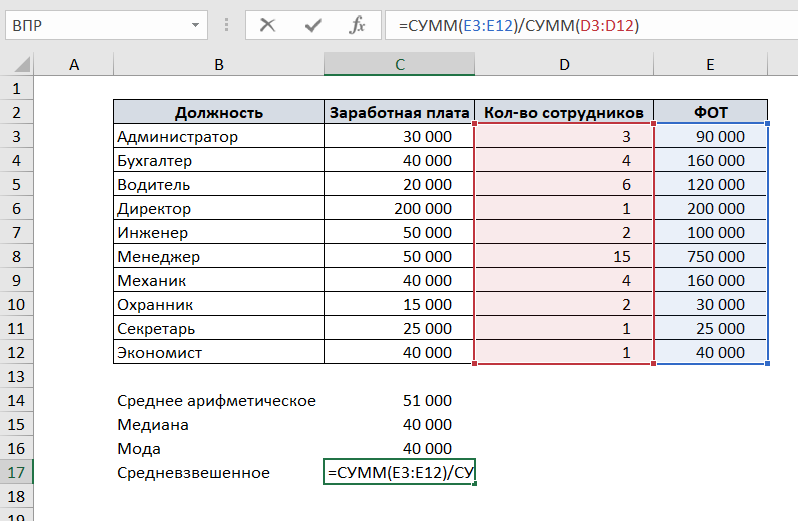
Рассмотрим на том же примере с зарплатой. Добавим к таблице два столбца: количество сотрудников и ФОТ (в этом столбце умножим заработную плату одного сотрудника на количество сотрудников).

Чтобы посчитать средневзвешенную заработную плату, разделим сумму всех зарплат сотрудников на сумму количества сотрудников.

Таким образом, зарплату каждого сотрудника мы «взвесили» на количество сотрудников каждой должности.

Если разложить формулу средневзвешенного подобно, то получается:

Для данного примера медиана, среднее арифметическое, средневзвешенное и мода отличаются.

Таким образом, в этом статье мы разобрались, что такое медиана, среднее арифметическое и мода и узнали, при помощи каких функций их можно посчитать в Excel.

Сообщество Excel Analytics | обучение Excel

Канал на Яндекс.Дзен

Вам может быть интересно:

Источник

Excel функция МОДА (MODE)

Microsoft Excel функция МОДА возвращает наиболее часто встречающееся число из набора чисел.
Эта функция была заменена функциями МОДА.ОДН и МОДА.НСК, начиная с Excel 2010.
Функция МОДА — это встроенная в Excel функция, которая относится к категории статистических функций.
Её можно использовать как функцию рабочего листа (WS) в Excel.
Как функцию рабочего листа, функцию МОДА можно ввести как часть формулы в ячейке рабочего листа.

Синтаксис

Синтаксис функции МОДА в Microsoft Excel:

Аргументы или параметры

Возвращаемое значение

Функция МОДА возвращает числовое значение.
Если все числовые значения в диапазоне уникальны, функция МОДА возвращает ошибку #Н/Д.
Если текстовое значение, такое как «A», вводится в качестве параметра, функция МОДА вернет #ЗНАЧ!
Если ссылка на диапазон или ячейку содержит нечисловые значения, такие как текстовые значения, логические значения или пустые ячейки, эти значения будут проигнорированы.

Примечание

См. также функции МОДА.ОДН и МОДА.НСК.

Применение

Excel для Office 365, Excel 2019, Excel 2016, Excel 2013, Excel 2011 для Mac, Excel 2010, Excel 2007, Excel 2003

Тип функции

Функция рабочего листа (WS)

Пример (как функция рабочего листа)

Рассмотрим несколько примеров функции МОДА, чтобы понять, как использовать Excel функцию МОДА как функцию рабочего листа в Microsoft Excel:

На основании, приведенной выше электронной таблицы Excel могут быть возвращены следующие примеры МОДА:

Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел. Модой ряда чисел называется число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды, а может не иметь моды совсем. Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.

Как найти моду в ряду распределения?

Для интервального ряда мода определяется по формуле: Mo=XMo+hMo⋅fMo−fMo−1(fMo−fMo−1)+(fMo−fMo+1), XMo — левая граница модального интервала, hMo — длина модального интервала, fMo−1 — частота премодального интервала, fMo — частота модального интервала, fMo+1 — частота послемодального интервала.

Как рассчитать медиану в Excel?

Для определения медианы в MS EXCEL существует одноименная функция МЕДИАНА() , английский вариант MEDIAN(). Медиана не обязательно совпадает со средним значением (mean, average) в выборке . Совпадение имеет место только в том случае, если значения в выборке распределены симметрично относительно среднего .

Как определить моду в статистике пример?

Мода – это то значение в анализируемой совокупности данных, которое встречается чаще других, поэтому нужно посмотреть на частоты значений и отыскать максимальное из них. Например, в наборе данных 3, 4, 6, 7, 3, 5, 3, 4 модой будет значение 3 – повторяется чаще остальных. Это в дискретном ряду, и здесь все просто.

Как найти моду графически?

Моду и медиану в интервальном ряду можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который является в данном случае модальным. Затем правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника.

Как рассчитывается медиана?

Медианой ряда чисел (медианой числового ряда) называется число, стоящее посередине упорядоченного по возрастанию ряда чисел — в случае, если количество чисел нечётное. Если же количество чисел в ряду чётно, то медианой ряда является полусумма двух стоящих посередине чисел упорядоченного по возрастанию ряда.

Как найти медиану в ряду распределения?

(Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле: Ме = (n(число признаков в совокупности) + 1)/2, в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).

Чем является медиана в ряду распределения?

Медиана — это такое значение признака, которое разделяет ранжированный ряд распределения на две равные части — со значениями признака меньше медианы и со значениями признака больше медианы. Для нахождения медианы, нужно отыскать значение признака, которое находится на середине упорядоченного ряда.

Что такое медиана в ряду чисел?

Медиа́на (от лат. mediāna «середина») набора чисел — число, которое находится в середине этого набора, если его упорядочить по возрастанию, то есть такое число, что половина из элементов набора не меньше него, а другая половина не больше.

Что такое медиана в Excel?

Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4. Мода — это число, наиболее часто встречающееся в данном наборе чисел.

Как рассчитать дисперсию в Excel?

Для распределений, представленных в MS EXCEL , дисперсию можно вычислить аналитически, как функцию от параметров распределения. Например, для Биномиального распределения дисперсия равна произведению его параметров: n*p*q. Примечание : Дисперсия, является вторым центральным моментом , обозначается D[X], VAR(х), V(x).

Как найти медиану по выборке?

Для удобства нахождения медианы сначала нужно отсортировать выборку в возрастающем или убывающем порядке . Тогда элемент, стоящий ровно посередине, будет медианой.

Что такое мода и медиана в статистике?

В статистике модой называется величина признака (варианта), которая чаще всего встречается в данной совокупности. Медианой в статистике называется варианта, которая находится в середине вариационного ряда. Медиана делит ряд пополам. Обозначают медиану символом.

Как определить медианное значение?

Медиану рассчитывают по определенному правилу. Для начала (после ранжирования данных) находят медианный интервал. Это такой интервал, через который проходит искомое медианное значение. Определяется с помощью накопленной доли ранжированных интервалов.

Что такое мода в математике?

Мода — значение во множестве наблюдений, которое встречается наиболее часто. Иногда в совокупности встречается более чем одна мода (например: 2, 6, 6, 6, 8, 9, 9, 9, 10; мода = 6 и 9). Из структурных средних величин только мода обладает таким уникальным свойством. .

Как найти моду в excel

Здравствуйте, друзья. В этой статье расскажу, как в Эксель получить наиболее часто использующееся число в массиве. Для этого применяем формулу МОДА:

В примере выше есть ведомость оценок для учеников 1-3 классов. С помощью функции МОДА мы узнали, что наибольшее количество участников получили в этом списке четвёрку.

МОДА принимает в качестве аргумента:

Ссылку на диапазон
Массив значений
Именованный диапазон
Перечень чисел, массивов, диапазонов через точку с запятой

Функция игнорирует ячейки с текстом, логическими значениями, пустые. Если она не может определить наиболее часто встречающееся значение – выводит ошибку #Н/Д. Чтобы ее перехватить, можете использовать функцию-обработчик.

В последних версиях Excel, разработчики пометили функцию МОДа, как устаревшую. Вместо нее предлагают использовать:

МОДА.ОДН( массив ) – оптимизированный аналог МОДЫ
МОДА.НСК( массив ) – выводит список из наиболее частотных цифр, содержащихся в массиве

Используются эти функции так же само, однако более оптимальны с точки зрения внутреннего кода.

Как найти моду в экселе?

Мода это цифра (число) чаще всего повторяющаяся в наборе цифр (чисел) в экселе (если имеется ввиду продукт microsoft excel) существует такая функция. В нужной Вам ячейке неубходимо указать «=МОДА(:)» а вместо знака ** выделить диапазон чисел из которых вы ищете.

Пример: =МОДА(А1:А101). На указанной Вами ячейке программа найдёт моду числ в ячейках от a1 до a101.

Желаю удачи в познании экселя!

Актуальный вопрос на самом деле. Итак, чтобы нам это сделать необходимо : ввести функцию «MODE» в ячейку, в которой мы хотим увидеть итоговый результат. Формат функции следующий: «=MODE(Cx:Dy)», где C и D являются — столбца первой и последней ячейки набора чисел,а вот х и y – это номер первой и последней строки набора чисел.Это, как правило, можно и посчитать в автоматическом режиме , написав просто » мода» в русскоязычном экселе ( пишите мода и выделяете тот столбец, то есть признак, который вы и хотите посчитать).

Источник

Для вычисления моды выборки в MS EXCEL существует специальная функция

МОДА()

. Вычислим моду для заданного распределения случайной величины.

Мода

, наряду со

средним значением

медианой

, является показателем, характеризующим типичное или «центральное» значение в

выборке

(массиве, множестве чисел).

Мода

– это наиболее часто встречающееся (повторяющееся) значение в

выборке

. Для вычисления

моды

в MS EXCEL используется функция

МОДА()

, английский вариант MODE(). Вычисление

моды выборки

подробно рассмотрено в статье

Описательная статистика в MS EXCEL

. В этой статье сосредоточимся на вычислении моды для заданного распределения непрерывной случайной величины.

Мода распределения непрерывной случайной величины

Чтобы определить

моду

распределения

непрерывной случайной величины

необходимо вычислить максимум соответствующей

функции плотности распределения

Примечание

: Подробнее о

функции плотности распределения

см. статью

Функция распределения и плотность вероятности в MS EXCEL

В статье о

распределениях MS EXCEL

приведены ссылки на распределения, для которых в MS EXCEL существуют специальные функции (

Нормальное распределение

Гамма-распределение

Экспоненциальное

и др.). Используя эти функции в MS EXCEL можно вычислить

моду

соответствующего распределения.

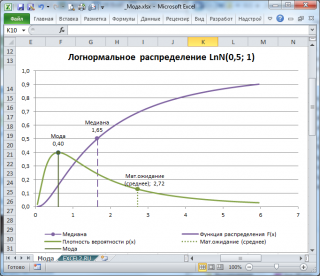
В качестве примера вычислим

моду

для

Логнормального распределения

(см.

файл примера

).

С помощью функции

ЛОГНОРМ.РАСП()

построим график

Функции распределения и плотности вероятности

.

Настроим

Поиск решения

, чтобы вычислить значение случайной величины (х), при котором

функция плотности вероятности

достигает максимума, т.е. вычислим

моду

.

Целевую функцию

=ЛОГНОРМ.РАСП(P8;B8;B9;ЛОЖЬ)

разместим в ячейке

P9

. Эта функция с 4-м аргументом равным ЛОЖЬ вернет

плотность вероятности

. Нам нужно найти значение

x

(первый аргумент функции

ЛОГНОРМ.РАСП()

), при котором значение целевой функции максимально. Найденное значение

х

и будет

модой

.

В ячейках

B8

и

B9

введем параметры

Логнормального распределения

. В ячейке

P8

разместим значение

х

— переменную, которую

Поиск решения

будет изменять, чтобы максимизировать целевую функцию.

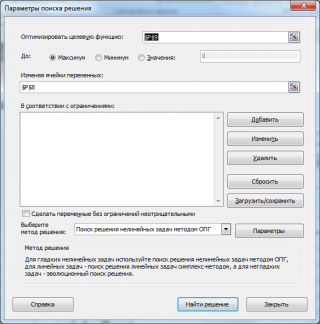
Диалоговое окно для настройки

Поиска решения

будет выглядеть так (в MS EXCEL 2010):

После нажатия кнопки

Найти решение

Поиск решения

подберет значение в ячейке

P8

, при котором результат формулы

=ЛОГНОРМ.РАСП(P8;B8;B9;ЛОЖЬ)

примет максимальное значение. Чтобы найти

моду

для

Логнормального распределения

с другими параметрами, измените их в ячейках

B8

и

B9

, а затем перезапустите

Поиск решения

.

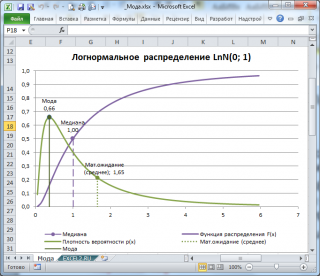
Найденное значение моды можно сравнить со значением моды, вычисленным аналитически с помощью формулы

=EXP(B8-B9*B9)

. Аналогичным образом можно вычислить моду для других распределений. Для этого нужно заменить целевую функцию. Например, для

нормального распределения

используйте функцию

=НОРМ.РАСП(P8;B8;B9;ЛОЖЬ)

.

Источник

Содержание

— Как вычислить моду?
— Как найти моду в ряду распределения?
— Как рассчитать медиану в Excel?
— Как определить моду в статистике пример?
— Как найти моду графически?
— Как рассчитывается медиана?
— Как найти медиану в ряду распределения?
— Чем является медиана в ряду распределения?
— Что такое медиана в ряду чисел?
— Что такое медиана в Excel?
— Как рассчитать дисперсию в Excel?
— Как найти медиану по выборке?
— Что такое мода и медиана в статистике?
— Как определить медианное значение?
— Что такое мода в математике?

Выберите диапазон ячеек, равный количеству мод, которые вы хотите найти в наборе данных. Если вы хотите найти три моды, выберите три ячейки. В противном случае, вы увидите количество мод, равное количеству выбранных ячеек. Введите функцию MODE.

Как вычислить моду?

Как найти моду в ряду распределения?

Как определить моду в статистике пример?

Как найти моду графически?

Как рассчитывается медиана?

Как найти медиану в ряду распределения?

Чем является медиана в ряду распределения?

Что такое медиана в ряду чисел?

Что такое медиана в Excel?

Как рассчитать дисперсию в Excel?

Как найти медиану по выборке?

Для удобства нахождения медианы сначала нужно отсортировать выборку в возрастающем или убывающем порядке {2,5,7,8,10}. Тогда элемент, стоящий ровно посередине, будет медианой.

Что такое мода и медиана в статистике?

Как определить медианное значение?

Что такое мода в математике?

Интересные материалы:

Нужно ли менять старый советский номер?
Нужно ли замазывать номер машины на фото?
Откуда номер телефона 499?
Почему +7 в номере?
Почему Авито скрывает номера?
Почему Gmail просит номер телефона?
Почему говорят что номер набран неправильно?
Почему говорит неправильно набран номер мтс?
Почему говорит номер не существует?
Почему когда я звоню на телефон мне говорят неправильно набран номер?

Источник

17 авг. 2022 г.
читать 2 мин

Вы можете использовать следующие формулы, чтобы найти среднее значение, медиану и моду набора данных в Excel:

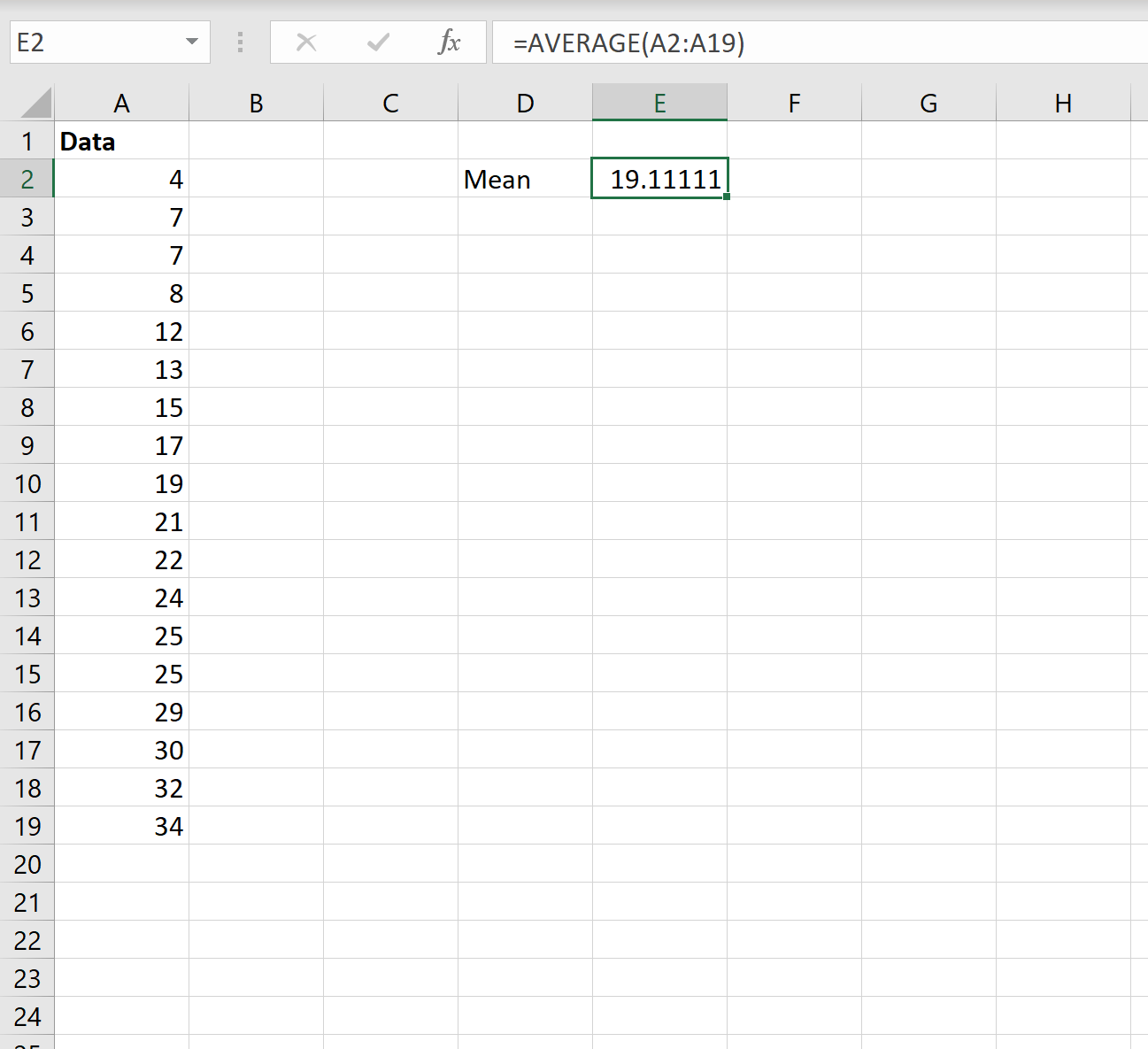
=AVERAGE( A1:A10 )

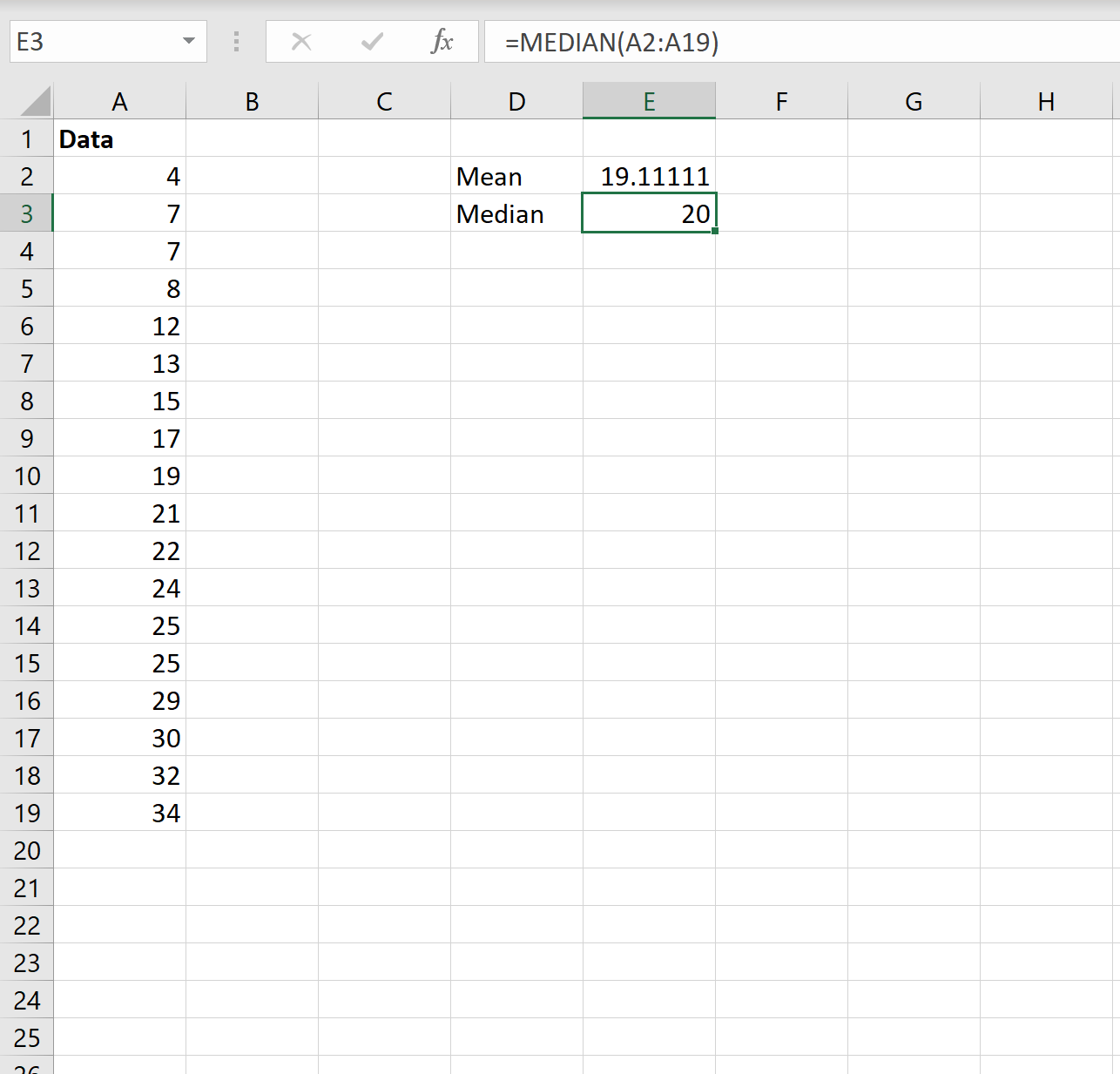
=MEDIAN( A1:A10 ) 

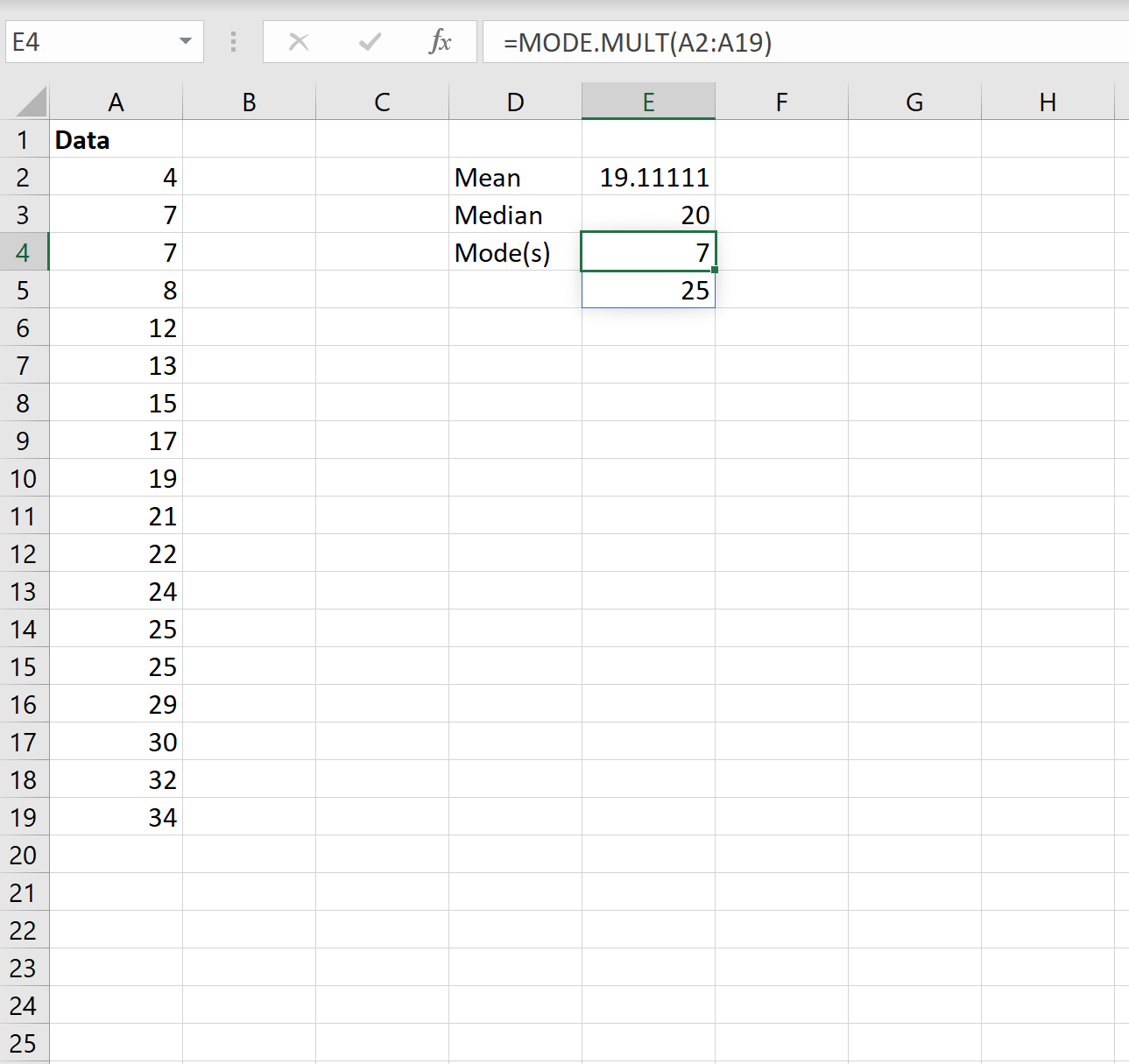
=MODE.MULT( A1:A10 )

Стоит отметить, что каждая из этих формул просто игнорирует нечисловые или пустые значения при расчете этих показателей для диапазона ячеек в Excel.

В следующих примерах показано, как использовать эти формулы на практике со следующим набором данных:

Пример: нахождение среднего значения в Excel

Среднее значение представляет собой среднее значение в наборе данных.

На следующем снимке экрана показано, как рассчитать среднее значение набора данных в Excel:

Среднее значение получается 19,11 .

Пример: поиск медианы в Excel

Медиана представляет собой среднее значение в наборе данных, когда все значения расположены от наименьшего к наибольшему.

На следующем снимке экрана показано, как рассчитать медиану набора данных в Excel:

Медиана получается 20 .

Пример: поиск режима в Excel

Мода представляет значение, которое чаще всего встречается в наборе данных. Обратите внимание, что набор данных может не иметь режима, иметь один режим или несколько режимов.

На следующем снимке экрана показано, как рассчитать режим(ы) набора данных в Excel:

Моды оказываются 7 и 25.Каждое из этих значений встречается в наборе данных дважды, что встречается чаще, чем любое другое значение.

Примечание. Если вместо этого вы используете функцию =MODE() , она вернет только первый режим. Для этого набора данных будет возвращено только значение 7. По этой причине всегда рекомендуется использовать функцию =MODE.MULT() , если в наборе данных окажется более одной моды.

Дополнительные ресурсы

Как рассчитать межквартильный диапазон (IQR) в Excel
Как рассчитать средний диапазон в Excel
Как рассчитать стандартное отклонение в Excel

Написано

Замечательно! Вы успешно подписались.

Добро пожаловать обратно! Вы успешно вошли

Вы успешно подписались на кодкамп.

Срок действия вашей ссылки истек.

Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.

Успех! Ваша платежная информация обновлена.

Ваша платежная информация не была обновлена.

Источник

Функция МОДА в Excel выполняет поиск повторяющихся либо наиболее часто встречающихся элементов в массиве или значений в диапазоне данных и возвращает эти значения.

Функция МОДА.НСК выполняет поиск наиболее встречающихся значений среди диапазона данных или элементов массива и возвращает вертикальный массив этих значений.

Функция МОДА.ОДН находит наиболее встречающееся значение в массиве или диапазоне данных и возвращает данное значение.

Примеры использования функций МОДА в Excel

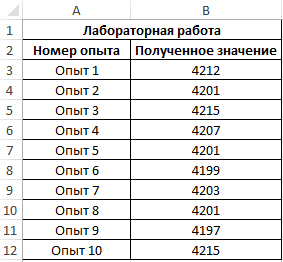
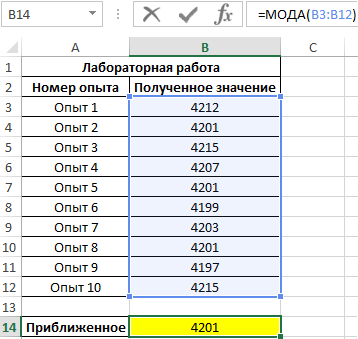
Пример 1. В ходе лабораторной работы эмпирическим путем были получены несколько значений одной и той же физической величины. Для расчета ее приближенного значения было решено определить моду из диапазона полученных значений. Ниже рассмотрим, как найти моду в Excel.

Таблица данных:

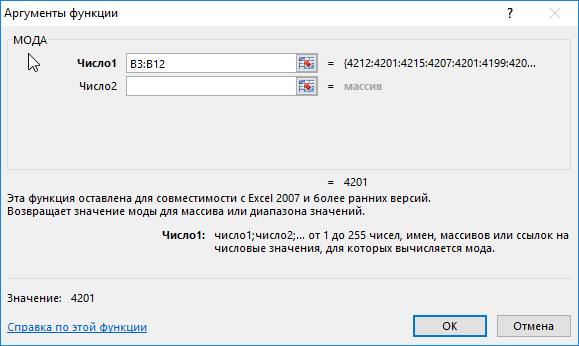
Для определения наиболее часто встречаемого значения используем формулу:

Описание аргументов:

B3:B12 – массив значений, в котором необходимо определить наиболее повторяющееся значение.

Результат вычислений:

Пример использования функции МОДА.НСК в Excel

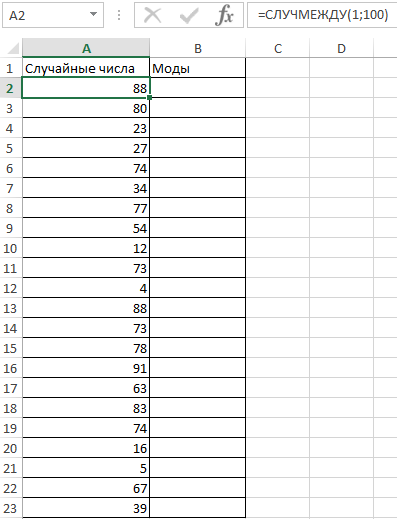
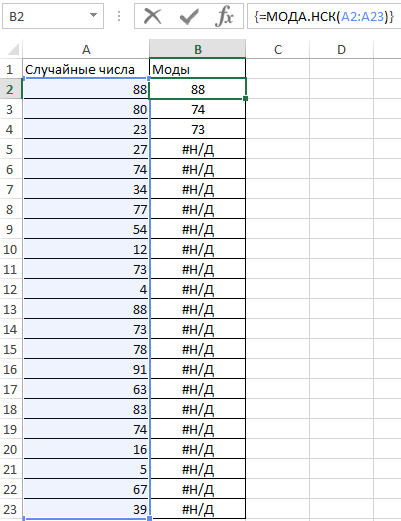
Пример 2. В ряде числовых значений, полученном в результате работы генератора случайных чисел, необходимо определить повторяющиеся числа. Теперь смотрим как посчитать моду в Excel.

Заполним столбец «Случайные числа» с использованием функции СЛУЧМЕЖДУ(1;100), то есть случайными числами из диапазона от 1 до 100:

Примечание: функция СЛУЧМЕЖДУ выполняет пересчет полученных случайных значений при каждом вводе нового значения в любую ячейку, поэтому значения в столбце A2 на разных изображениях могут отличаться.

Выделим диапазон ячеек B2:B23 и введем формулу:

Для ввода формулы используем комбинацию клавиш Ctrl+Shift+Enter, чтобы функция была выполнена в массиве. В результате получим:

В указанном диапазоне случайных чисел повторяются значения 48, 47 и 53. Поскольку остальные числа являются уникальными, для ячеек B5:B23 сгенерирован код ошибки #Н/Д (то есть, формула не нашла запрашиваемое значение).

Пример работы с функцией МОДА.ОДН в Excel

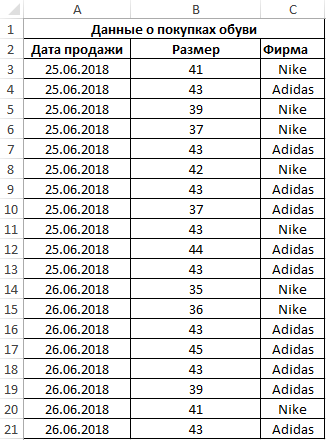
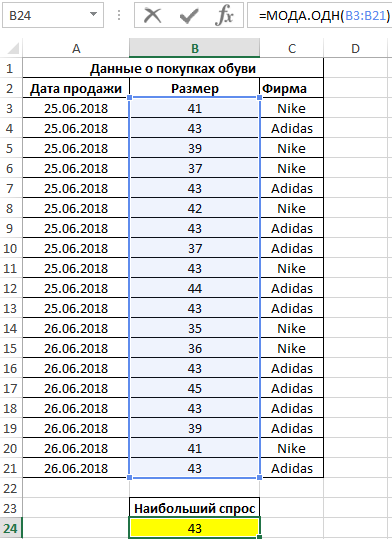
Пример 3. Поставщик обувного магазина поинтересовался у владельца, какой размер обуви пользуется наибольшим спросом. Экономист просмотрел данные из таблицы покупок и практически сразу дал ответ. Как ему это удалось?

Таблица данных о покупках:

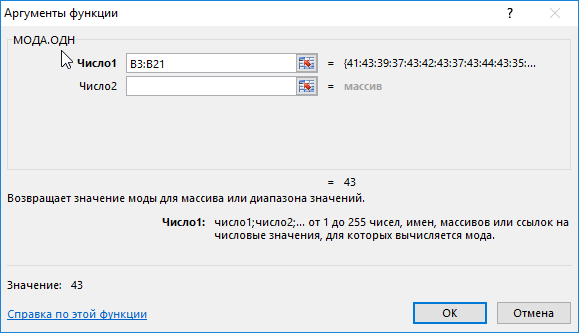
Как вычислить моду в Excel? Для определения размера, который пользуется наибольшим спросом, использована формула моды:

Полученный результат:

Примечание: в отличие от среднего арифметического значения (для данного примера – примерно 41), мода определяет наиболее часто встречаемое событие в диапазоне событий. Ее рационально использовать для решения статистических задач, связанных с анализом нормально распределенных данных.

Функции МОДА, МОДА.НСК и МОДА.ОДН в Excel и особенности их использования

Функция МОДА имеет следующие аргументы:

число 1 – обязательный для заполнения аргумент, характеризующий первое числовое значение, для которого необходимо определить моду.
[число 2] и последующие аргументы являются необязательными для заполнения и характеризуют последующие числовые значения, для которых требуется найти значение моды.

Аргументы модификации функции имеют одинаковый смысл.

Примечания 1:

Максимальное количество аргументов в рассматриваемых функциях – не более 255.
Вместо аргументов типа число 1; число 2;…;число n можно указывать массив значений или ссылку на диапазон ячеек.
В качестве аргументов принимаются объекты данных следующих типов: имена, которые содержат числа, массивы числовых значений и ссылки.
Все рассматриваемые функции для определения моды игнорируют пустые, логические значения и текстовые строки, содержащиеся в диапазоне значений, переданном в качестве аргумента.
Если все элементы массива или диапазона чисел, переданных в качестве аргументов для всех трех функций являются уникальными (повторяющиеся значения отсутствуют), результатом работы данных функций будет являться код ошибки #Н/Д.
Если функция МОДА.НСК была использована в качестве обычной функции, будет возвращено единственное значение моды. Для отображения нескольких мод необходимо выделить диапазон ячеек, ввести формулу и ее аргументы, использовать сочетание клавиш Ctrl+Shift+Enter для вывода массива вычисленных результатов.

Примечание 2: функция МОДА была разработана для ранних версий Excel и пока поддерживается новыми версиями программы, однако в последующих версиях поддержка данной функции может быть отменена. Вместо данной функции предлагается использование двух ее аналогов, которые будут рассмотрены ниже.

Примечания 3:

Для возврата горизонтального массива наиболее встречающихся значений следует использовать запись вида ТРАНСП(МОДА.НСК(число 1; число 2;…;число n).
МОДА.НСК принадлежит к классу формул массива и может возвращать как одну, так и несколько мод. Для записи в качестве формулы массива необходимо использовать сочетание клавиш Ctrl+Shift+Enter.

Примечание 4: функции МОДА и МОДА.ОДН определяют центральную тенденцию множества чисел в статическом распределении способом определения моды (существуют еще два распространенных способа: поиск среднего значения и медианы), то есть путем поиска элемента, значение которого наиболее часто встречается в определенном наборе чисел.

Источник