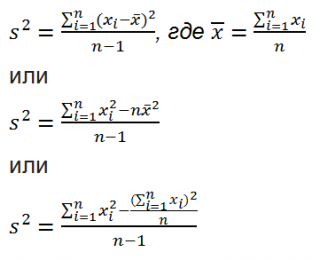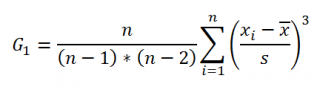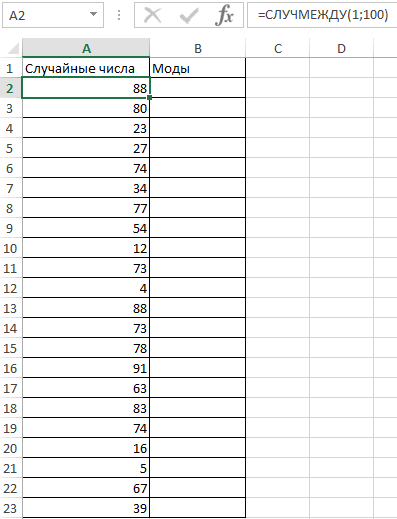Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Предположим, что вы хотите узнать наиболее распространенное количество видов птицы в образце видов птицы на критической заболоченой за 30-летней период времени или узнать наиболее часто посещаемые телефонные вызовы в центре поддержки по телефону в некритовые часы. Для вычисления режима группы чисел используйте функцию РЕЖИМ.
Режим возвращает наиболее часто повторяющийся (повторяющийся) значение в массиве или диапазоне данных.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
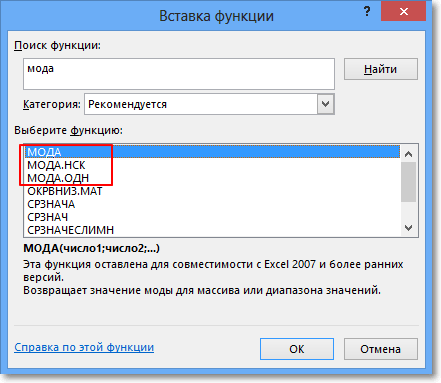
Дополнительные сведения о новых функциях см. в разделах Функция МОДА.НСК и Функция МОДА.ОДН.
Синтаксис
МОДА(число1;[число2];…)
Аргументы функции МОДА описаны ниже.
-
Число1 Обязательный. Первый числовой аргумент, для которого требуется вычислить моду.
-
Число2… Необязательный. От 1 до 255 числовых аргументов, для которых вычисляется мода. Вместо аргументов, разделенных точкой с запятой, можно воспользоваться массивом или ссылкой на массив.
Замечания
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения игнорируются; ячейки, содержащие нулевые значения, учитываются.
-
Аргументы, которые являются значениями ошибки или текстами, не преобразуемыми в числа, приводят к возникновению ошибок.
-
Если множество данных не содержит одинаковых данных, функция МОДА возвращает значение ошибки #Н/Д.
Функция МОДА измеряет центральную тенденцию, которая является центром множества чисел в статистическом распределении. Существует три наиболее распространенных способа определения центральной тенденции:
-
Среднее значение — это среднее арифметическое, которое вычисляется путем сложения набора чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
-
Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.
-
Мода — это число, наиболее часто встречающееся в данном наборе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.
При симметричном распределении множества чисел все три значения центральной тенденции будут совпадать. При смещенном распределении множества чисел значения могут быть разными.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|
5,6 |
||
|
4 |
||
|
4 |
||
|
3 |
||
|
2 |
||
|
4 |
||
|
Формула |
Описание |
Результат |
|
=МОДА(A2:A7) |
Мода или наиболее часто встречающееся число |
4 |
Нужна дополнительная помощь?
В статистике есть целый набор показателей, которые характеризуют центральную тенденцию. Выбор того или иного индикатора в основном зависит от характера данных, целей расчетов и его свойств.
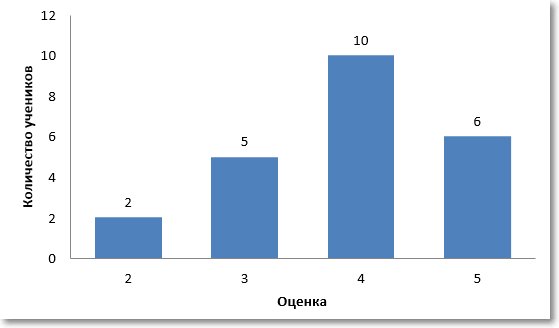
Что подразумевается под характером данных? Прежде всего, мы говорим о количественных данных, которые выражены в числах. Но набор числовых данных может иметь разное распределение. Под распределением понимаются частоты отдельных значений. К примеру, в классе из 23 человек 2 школьника написали контрольную работу на двойку, 5 – на тройку, 10 – на четверку и 6 – на пятерку. Это и есть распределение оценок. Распределение очень наглядно можно представить с помощью специальной диаграммы – гистограммы. Для данного примера получится следующая гистограмма.
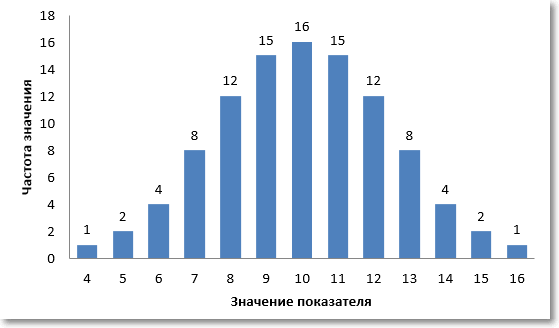
Во многих случаях количество уникальных значений намного больше, а распределение похоже на нормальное. Ниже приведена примерная иллюстрация нормального распределения случайных чисел.
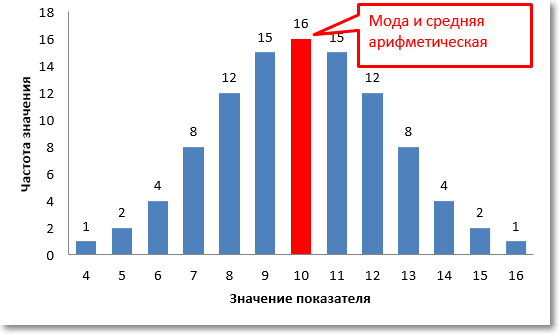
Итак, центральная тенденция. Если частоты анализируемых значений распределены по нормальному закону, то есть симметрично вокруг некоторого центра, то центральная тенденция определяется вполне однозначно – это есть тот самый центр, и математически он соответствует средней арифметической.
Как нетрудно заметить, в этом же центре находится и максимальная частота значений. То есть при нормальном распределении центральная тенденция есть не только средняя арифметическая, но и максимальная частота, которая в статистике называется модой или модальным значением.
На диаграмме оба значения центральной тенденции совпадают и равны 10.
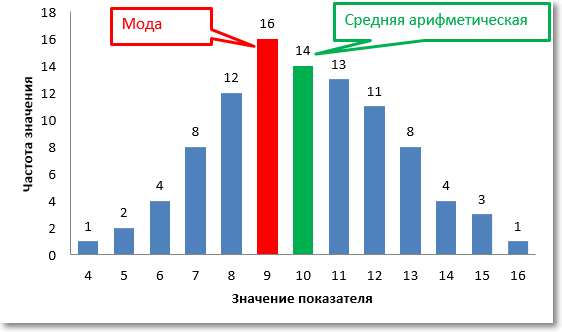
Но такое распределение встречается далеко не всегда, а при малом числе данных – совсем редко. Чаще бывает так, что частоты распределяются асимметрично. Тогда мода и среднее арифметическое не будут совпадать.
На рисунке выше среднее арифметическое по-прежнему составляет 10, а вот мода уже равна 9. Что в таком случае считать значением центральной тенденции? Ответ зависит от поставленных целей анализа. Если интересует уровень, сумма отклонений от которого равна нулю со всеми вытекающим отсюда свойствами и последствиями, то это средняя арифметическая. Если нужно максимально частое значение, то это мода.
Итак, зачем нужна мода? Приведу пару примеров. Экономист планово-экономического отдела обувной фабрики интересуется, какой размер обуви пользуется наибольшим спросом. Средний размер обуви, скорее всего, здесь не подойдет, тем более, что число может получится дробным. А вот мода – как раз нужный показатель.
Расчет моды
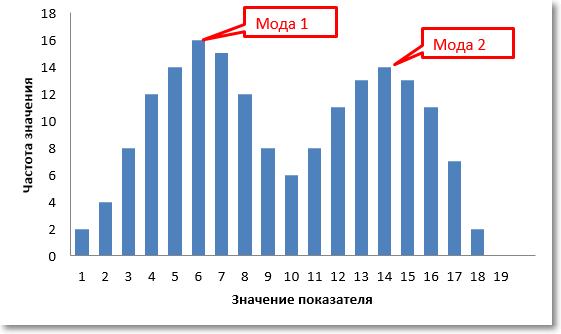
Теперь посмотрим, как рассчитать моду. Мода – это то значение в анализируемой совокупности данных, которое встречается чаще других, поэтому нужно посмотреть на частоты значений и отыскать максимальное из них. Например, в наборе данных 3, 4, 6, 7, 3, 5, 3, 4 модой будет значение 3 – повторяется чаще остальных. Это в дискретном ряду, и здесь все просто. Если данных много, то моду легче всего найти с помощью соответствующей гистограммы. Бывает так, что совокупность данных имеет бимодальное распределение.
Без диаграммы очень трудно понять, что в данных не один, а два центра. К примеру, на президентских выборах предпочтения сельских и городских жителей могут отличаться. Поэтому распределение доли отданных голосов за конкретного кандидата может быть «двугорбым». Первый «горб» – выбор городского населения, второй – сельского.
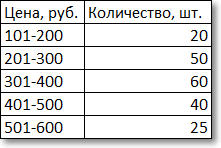
Немного сложнее с интервальными данными, когда вместо конкретных значений имеются интервалы. В этом случае говорят о модальном интервале (при анализе доходов населения, например), то есть интервале, частота которого максимальна относительно других интервалов. Однако и здесь можно отыскать конкретное модальное значение, хотя оно будет условным и примерным, так как нет точных исходных данных. Представим, что есть следующая таблица с распределением цен.
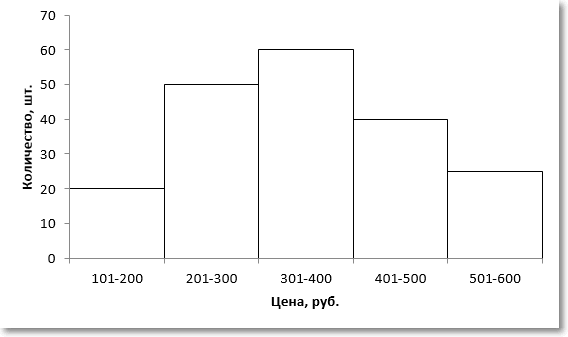
Для наглядности изобразим соответствующую диаграмму.
Требуется найти модальное значение цены.
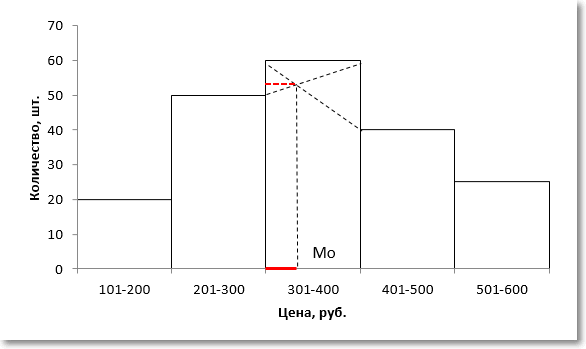
Вначале нужно определить модальный интервал, который соответствует интервалу с наибольшей частотой. Найти его так же легко, как и моду в дискретном ряду. В нашем примере это третий интервал с ценой от 301 до 400 руб. На графике – самый высокий столбец. Теперь нужно определить конкретное значение цены, которое соответствует максимальному количеству. Точно и по факту сделать это невозможно, так как нет индивидуальных значений частот для каждой цены. Поэтому делается допущение о том, что интервалы выше и ниже модального в зависимости от своей частоты имеют разные вес и как бы перетягивают моду в свою сторону. Если частота интервала следующего за модальным больше, чем частота интервала перед модальным, то мода будет правее середины модального интервала и наоборот. Давайте еще раз посмотрим на рисунок, чтобы понять формулу, которую я напишу чуть ниже.
На рисунке отчетливо видно, что соотношение высоты столбцов, расположенных слева и справа от модального определяет близость моды к левому или правому краю модального интервала. Задача по расчету модального значения состоит в том, чтобы найти точку пересечения линий, соединяющих модальный столбец с соседними (как показано на рисунке пунктирными линиями) и нахождении соответствующего значения признака (в нашем примере цены). Зная основы геометрии (7-й класс), по данному рисунку нетрудно вывести формулу расчета моды в интервальном ряду.
Формула моды имеет следующий вид.
Где Мо – мода,
x0 – значение начала модального интервала,
h – размер модального интервала,
fМо – частота модального интервала,
fМо-1 – частота интервала, находящего перед модальным,
fМо1 – частота интервала, находящего после модального.
Второе слагаемое формулы моды соответствует длине красной линии на рисунке выше.
Рассчитаем моду для нашего примера.
Таким образом, мода интервального ряда представляет собой сумму, состоящую из значения начального уровня модального интервала и отрезка, который определяется соотношением частот ближайших интервалов от модального.
Расчет моды в Excel
В настоящее время большинство вычислений делается в MS Excel, где для расчета моды также предусмотрена специальная функция. В Excel 2013 я таких нашел ажно 3 штуки.
МОДА – пережиток старых изданий Excel. Функция оставлена для совмещения со старыми версиями.
МОДА.ОДН – рассчитывает моду по заданным значениям. Здесь все просто. Вставили функцию, указали диапазон данных и «Ок».
МОДА.НСК – позволяет рассчитать сразу несколько модальных значений (одинаковых максимальных частот) для одного ряда данных, если они есть. Функцию нужно вводить как формулу массива, перед этим выделив количество ячеек равное количеству требуемых модальных значений. Иногда действительно модальных значений может быть несколько. Однако для этих целей предварительно лучше посмотреть на диаграмму распределения.
Моду для интервальных данных одной функцией в Excel рассчитать нельзя. То есть такая функция в готовом виде не предусмотрена. Придется прописывать вручную.
Следующая статья посвящена медиане.
До встречи на statanaliz.info.
Поделиться в социальных сетях:
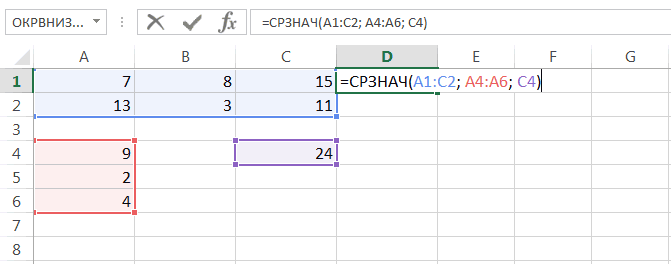
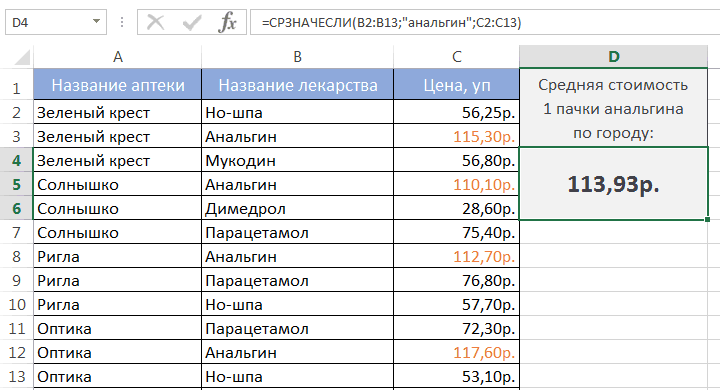
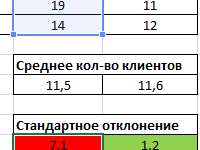
Рассмотрим инструмент Описательная статистика, входящий в надстройку Пакет Анализа. Рассчитаем показатели выборки: среднее, медиана, мода, дисперсия, стандартное отклонение и др.
Задача
описательной статистики
(descriptive statistics) заключается в том, чтобы с использованием математических инструментов свести сотни значений
выборки
к нескольким итоговым показателям, которые дают представление о
выборке
.В качестве таких статистических показателей используются:
среднее
,
медиана
,
мода
,
дисперсия, стандартное отклонение
и др.
Опишем набор числовых данных с помощью определенных показателей. Для чего нужны эти показатели? Эти показатели позволят сделать определенные
статистические выводы о распределении
, из которого была взята
выборка
. Например, если у нас есть
выборка
значений толщины трубы, которая изготавливается на определенном оборудовании, то на основании анализа этой
выборки
мы сможем сделать, с некой определенной вероятностью, заключение о состоянии процесса изготовления.
Содержание статьи:
- Надстройка Пакет анализа;
-
Среднее выборки
;
-
Медиана выборки
;
-
Мода выборки
;
-
Мода и среднее значение
;
-
Дисперсия выборки
;
-
Стандартное отклонение выборки
;
-
Стандартная ошибка
;
-
Ассиметричность
;
-
Эксцесс выборки
;
-
Уровень надежности
.
Надстройка Пакет анализа
Для вычисления статистических показателей одномерных
выборок
, используем
надстройку Пакет анализа
. Затем, все показатели рассчитанные надстройкой, вычислим с помощью встроенных функций MS EXCEL.
СОВЕТ
: Подробнее о других инструментах надстройки
Пакет анализа
и ее подключении – читайте в статье
Надстройка Пакет анализа MS EXCEL
.
Выборку
разместим на
листе
Пример
в файле примера
в диапазоне
А6:А55
(50 значений).
Примечание
: Для удобства написания формул для диапазона
А6:А55
создан
Именованный диапазон
Выборка.
В диалоговом окне
Анализ данных
выберите инструмент
Описательная статистика
.
После нажатия кнопки
ОК
будет выведено другое диалоговое окно,
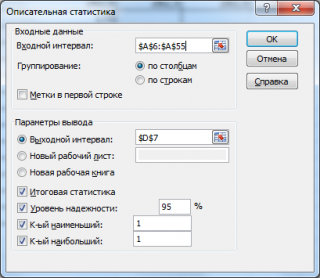
в котором нужно указать:
входной интервал
(Input Range) – это диапазон ячеек, в котором содержится массив данных. Если в указанный диапазон входит текстовый заголовок набора данных, то нужно поставить галочку в поле
Метки в первой строке (
Labels
in
first
row
).
В этом случае заголовок будет выведен в
Выходном интервале.
Пустые ячейки будут проигнорированы, поэтому нулевые значения необходимо обязательно указывать в ячейках, а не оставлять их пустыми;
выходной интервал
(Output Range). Здесь укажите адрес верхней левой ячейки диапазона, в который будут выведены статистические показатели;
Итоговая статистика (
Summary
Statistics
)
. Поставьте галочку напротив этого поля – будут выведены основные показатели выборки:
среднее, медиана, мода, стандартное отклонение
и др.;-
Также можно поставить галочки напротив полей
Уровень надежности (
Confidence
Level
for
Mean
)
,
К-й наименьший
(Kth Largest) и
К-й наибольший
(Kth Smallest).
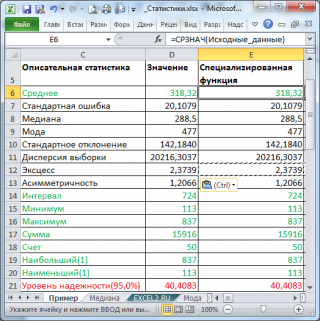
В результате будут выведены следующие статистические показатели:
Все показатели выведены в виде значений, а не формул. Если массив данных изменился, то необходимо перезапустить расчет.
Если во
входном интервале
указать ссылку на несколько столбцов данных, то будет рассчитано соответствующее количество наборов показателей. Такой подход позволяет сравнить несколько наборов данных. При сравнении нескольких наборов данных используйте заголовки (включите их во
Входной интервал
и установите галочку в поле
Метки в первой строке
). Если наборы данных разной длины, то это не проблема — пустые ячейки будут проигнорированы.
Зеленым цветом на картинке выше и в
файле примера
выделены показатели, которые не требуют особого пояснения. Для большинства из них имеется специализированная функция:
Интервал
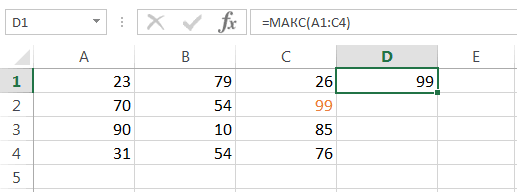
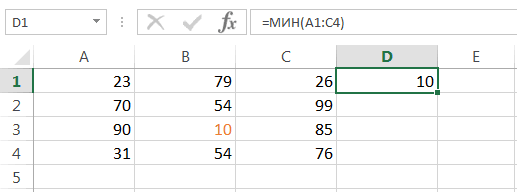
(Range) — разница между максимальным и минимальным значениями;
Минимум
(Minimum) – минимальное значение в диапазоне ячеек, указанном во
Входном интервале
(см.статью про функцию
МИН()
);
Максимум
(Maximum)– максимальное значение (см.статью про функцию
МАКС()
);
Сумма
(Sum) – сумма всех значений (см.статью про функцию
СУММ()
);
Счет
(Count) – количество значений во
Входном интервале
(пустые ячейки игнорируются, см.статью про функцию
СЧЁТ()
);
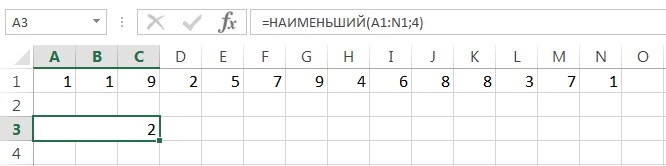
Наибольший
(Kth Largest) – выводится К-й наибольший. Например, 1-й наибольший – это максимальное значение (см.статью про функцию
НАИБОЛЬШИЙ()
);
Наименьший
(Kth Smallest) – выводится К-й наименьший. Например, 1-й наименьший – это минимальное значение (см.статью про функцию
НАИМЕНЬШИЙ()
).
Ниже даны подробные описания остальных показателей.
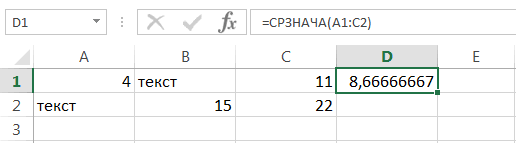
Среднее выборки
Среднее
(mean, average) или
выборочное среднее
или
среднее выборки
(sample average) представляет собой
арифметическое среднее
всех значений массива. В MS EXCEL для вычисления среднего выборки используется функция
СРЗНАЧ()
.
Выборочное среднее
является «хорошей» (несмещенной и эффективной) оценкой
математического ожидания
случайной величины (подробнее см. статью
Среднее и Математическое ожидание в MS EXCEL
).
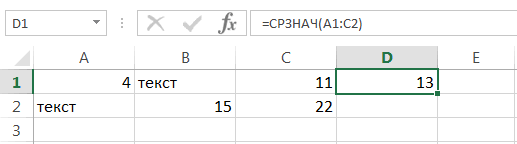
Медиана выборки
Медиана
(Median) – это число, которое является серединой множества чисел (в данном случае выборки): половина чисел множества больше, чем
медиана
, а половина чисел меньше, чем
медиана
. Для определения
медианы
необходимо сначала
отсортировать множество чисел
. Например,
медианой
для чисел 2, 3, 3,
4
, 5, 7, 10 будет 4.
Если множество содержит четное количество чисел, то вычисляется
среднее
для двух чисел, находящихся в середине множества. Например,
медианой
для чисел 2, 3,
3
,
5
, 7, 10 будет 4, т.к. (3+5)/2.
Если имеется длинный хвост распределения, то
Медиана
лучше, чем
среднее значение
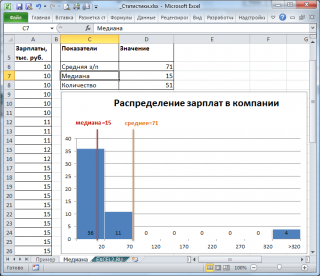
, отражает «типичное» или «центральное» значение. Например, рассмотрим несправедливое распределение зарплат в компании, в которой руководство получает существенно больше, чем основная масса сотрудников.
Очевидно, что средняя зарплата (71 тыс. руб.) не отражает тот факт, что 86% сотрудников получает не более 30 тыс. руб. (т.е. 86% сотрудников получает зарплату в более, чем в 2 раза меньше средней!). В то же время медиана (15 тыс. руб.) показывает, что
как минимум
у 50% сотрудников зарплата меньше или равна 15 тыс. руб.
Для определения
медианы
в MS EXCEL существует одноименная функция
МЕДИАНА()
, английский вариант — MEDIAN().
Медиану
также можно вычислить с помощью формул
=КВАРТИЛЬ.ВКЛ(Выборка;2) =ПРОЦЕНТИЛЬ.ВКЛ(Выборка;0,5).
Подробнее о
медиане
см. специальную статью
Медиана в MS EXCEL
.
СОВЕТ
: Подробнее про
квартили
см. статью, про
перцентили (процентили)
см. статью.
Мода выборки
Мода
(Mode) – это наиболее часто встречающееся (повторяющееся) значение в
выборке
. Например, в массиве (1; 1;
2
;
2
;
2
; 3; 4; 5) число 2 встречается чаще всего – 3 раза. Значит, число 2 – это
мода
. Для вычисления
моды
используется функция
МОДА()
, английский вариант MODE().
Примечание
: Если в массиве нет повторяющихся значений, то функция вернет значение ошибки #Н/Д. Это свойство использовано в статье
Есть ли повторы в списке?
Начиная с
MS EXCEL 2010
вместо функции
МОДА()
рекомендуется использовать функцию
МОДА.ОДН()
, которая является ее полным аналогом. Кроме того, в MS EXCEL 2010 появилась новая функция
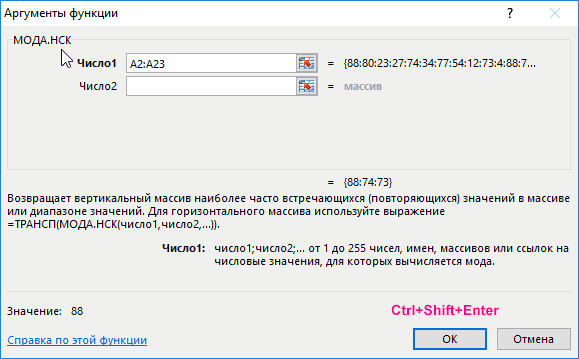
МОДА.НСК()
, которая возвращает несколько наиболее часто повторяющихся значений (если количество их повторов совпадает). НСК – это сокращение от слова НеСКолько.
Например, в массиве (1; 1;
2
;
2
;
2
; 3;
4
;
4
;
4
; 5) числа 2 и 4 встречаются наиболее часто – по 3 раза. Значит, оба числа являются
модами
. Функции
МОДА.ОДН()
и
МОДА()
вернут значение 2, т.к. 2 встречается первым, среди наиболее повторяющихся значений (см.
файл примера
, лист
Мода
).
Чтобы исправить эту несправедливость и была введена функция
МОДА.НСК()
, которая выводит все
моды
. Для этого ее нужно ввести как
формулу массива
.
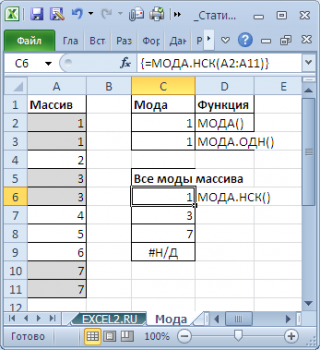
Как видно из картинки выше, функция
МОДА.НСК()
вернула все три
моды
из массива чисел в диапазоне
A2:A11
: 1; 3 и 7. Для этого, выделите диапазон
C6:C9
, в
Строку формул
введите формулу
=МОДА.НСК(A2:A11)
и нажмите
CTRL+SHIFT+ENTER
. Диапазон
C
6:
C
9
охватывает 4 ячейки, т.е. количество выделяемых ячеек должно быть больше или равно количеству
мод
. Если ячеек больше чем м
о
д, то избыточные ячейки будут заполнены значениями ошибки #Н/Д. Если
мода
только одна, то все выделенные ячейки будут заполнены значением этой
моды
.
Теперь вспомним, что мы определили
моду
для выборки, т.е. для конечного множества значений, взятых из
генеральной совокупности
. Для
непрерывных случайных величин
вполне может оказаться, что выборка состоит из массива на подобие этого (0,935; 1,211; 2,430; 3,668; 3,874; …), в котором может не оказаться повторов и функция
МОДА()
вернет ошибку.
Даже в нашем массиве с
модой
, которая была определена с помощью
надстройки Пакет анализа
, творится, что-то не то. Действительно,
модой
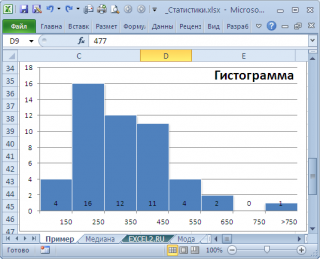
нашего массива значений является число 477, т.к. оно встречается 2 раза, остальные значения не повторяются. Но, если мы посмотрим на
гистограмму распределения
, построенную для нашего массива, то увидим, что 477 не принадлежит интервалу наиболее часто встречающихся значений (от 150 до 250).
Проблема в том, что мы определили
моду
как наиболее часто встречающееся значение, а не как наиболее вероятное. Поэтому,
моду
в учебниках статистики часто определяют не для выборки (массива), а для функции распределения. Например, для
логнормального распределения
мода
(наиболее вероятное значение непрерывной случайной величины х), вычисляется как
exp
(
m
—
s
2
)
, где m и s параметры этого распределения.
Понятно, что для нашего массива число 477, хотя и является наиболее часто повторяющимся значением, но все же является плохой оценкой для
моды
распределения, из которого взята
выборка
(наиболее вероятного значения или для которого плотность вероятности распределения максимальна).
Для того, чтобы получить оценку
моды
распределения, из
генеральной совокупности
которого взята
выборка
, можно, например, построить
гистограмму
. Оценкой для
моды
может служить интервал наиболее часто встречающихся значений (самого высокого столбца). Как было сказано выше, в нашем случае это интервал от 150 до 250.
Вывод
: Значение
моды
для
выборки
, рассчитанное с помощью функции
МОДА()
, может ввести в заблуждение, особенно для небольших выборок. Эта функция эффективна, когда случайная величина может принимать лишь несколько дискретных значений, а размер
выборки
существенно превышает количество этих значений.
Например, в рассмотренном примере о распределении заработных плат (см. раздел статьи выше, о Медиане),
модой
является число 15 (17 значений из 51, т.е. 33%). В этом случае функция
МОДА()
дает хорошую оценку «наиболее вероятного» значения зарплаты.
Примечание
: Строго говоря, в примере с зарплатой мы имеем дело скорее с
генеральной совокупностью
, чем с
выборкой
. Т.к. других зарплат в компании просто нет.
О вычислении
моды
для распределения
непрерывной случайной величины
читайте статью
Мода в MS EXCEL
.
Мода и среднее значение
Не смотря на то, что
мода
– это наиболее вероятное значение случайной величины (вероятность выбрать это значение из
Генеральной совокупности
максимальна), не следует ожидать, что
среднее значение
обязательно будет близко к
моде
.
Примечание
:
Мода
и
среднее
симметричных распределений совпадает (имеется ввиду симметричность
плотности распределения
).
Представим, что мы бросаем некий «неправильный» кубик, у которого на гранях имеются значения (1; 2; 3; 4; 6; 6), т.е. значения 5 нет, а есть вторая 6.
Модой
является 6, а среднее значение – 3,6666.
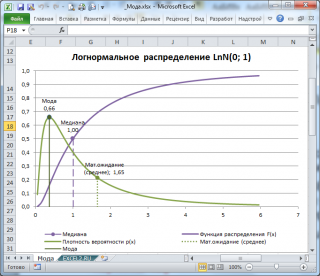
Другой пример. Для
Логнормального распределения
LnN(0;1)
мода
равна =EXP(m-s2)= EXP(0-1*1)=0,368, а
среднее значение
1,649.
Дисперсия выборки
Дисперсия выборки
или
выборочная дисперсия (
sample
variance
) характеризует разброс значений в массиве, отклонение от
среднего
.
Из формулы №1 видно, что
дисперсия выборки
это сумма квадратов отклонений каждого значения в массиве
от среднего
, деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления
дисперсии выборки
используется функция
ДИСП()
. С версии MS EXCEL 2010 рекомендуется использовать ее аналог — функцию
ДИСП.В()
.
Дисперсию
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
):
=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)
– обычная формула
=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1)
–
формула массива
Дисперсия выборки
равна 0, только в том случае, если все значения равны между собой и, соответственно, равны
среднему значению
.
Чем больше величина
дисперсии
, тем больше разброс значений в массиве относительно
среднего
.
Размерность
дисперсии
соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность
дисперсии
будет кг
2
. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из
дисперсии – стандартное отклонение
.
Подробнее о
дисперсии
см. статью
Дисперсия и стандартное отклонение в MS EXCEL
.
Стандартное отклонение выборки
Стандартное отклонение выборки
(Standard Deviation), как и
дисперсия
, — это мера того, насколько широко разбросаны значения в выборке
относительно их среднего
.
По определению,
стандартное отклонение
равно квадратному корню из
дисперсии
:
Стандартное отклонение
не учитывает величину значений в
выборке
, а только степень рассеивания значений вокруг их
среднего
. Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х
выборок
: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у
выборок
существенно отличается.
В MS EXCEL 2007 и более ранних версиях для вычисления
Стандартного отклонения выборки
используется функция
СТАНДОТКЛОН()
. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
СТАНДОТКЛОН.В()
.
Стандартное отклонение
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
):
=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Подробнее о
стандартном отклонении
см. статью
Дисперсия и стандартное отклонение в MS EXCEL
.
Стандартная ошибка
В
Пакете анализа
под термином
стандартная ошибка
имеется ввиду
Стандартная ошибка среднего
(Standard Error of the Mean, SEM).
Стандартная ошибка среднего
— это оценка
стандартного отклонения
распределения
выборочного среднего
.
Примечание
: Чтобы разобраться с понятием
Стандартная ошибка среднего
необходимо прочитать о
выборочном распределении
(см. статью
Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL
) и статью про
Центральную предельную теорему
.
Стандартное отклонение распределения выборочного среднего
вычисляется по формуле σ/√n, где n — объём
выборки, σ — стандартное отклонение исходного
распределения, из которого взята
выборка
. Т.к. обычно
стандартное отклонение
исходного распределения неизвестно, то в расчетах вместо
σ
используют ее оценку
s
—
стандартное отклонение выборки
. А соответствующая величина s/√n имеет специальное название —
Стандартная ошибка среднего.
Именно эта величина вычисляется в
Пакете анализа.
В MS EXCEL
стандартную ошибку среднего
можно также вычислить по формуле
=СТАНДОТКЛОН.В(Выборка)/ КОРЕНЬ(СЧЁТ(Выборка))
Асимметричность
Асимметричность
или
коэффициент асимметрии
(skewness) характеризует степень несимметричности распределения (
плотности распределения
) относительно его
среднего
.
Положительное значение
коэффициента асимметрии
указывает, что размер правого «хвоста» распределения больше, чем левого (относительно среднего). Отрицательная асимметрия, наоборот, указывает на то, что левый хвост распределения больше правого.
Коэффициент асимметрии
идеально симметричного распределения или выборки равно 0.
Примечание
:
Асимметрия выборки
может отличаться расчетного значения асимметрии теоретического распределения. Например,
Нормальное распределение
является симметричным распределением (
плотность его распределения
симметрична относительно
среднего
) и, поэтому имеет асимметрию равную 0. Понятно, что при этом значения в
выборке
из соответствующей
генеральной совокупности
не обязательно должны располагаться совершенно симметрично относительно
среднего
. Поэтому,
асимметрия выборки
, являющейся оценкой
асимметрии распределения
, может отличаться от 0.
Функция
СКОС()
, английский вариант SKEW(), возвращает коэффициент
асимметрии выборки
, являющейся оценкой
асимметрии
соответствующего распределения, и определяется следующим образом:
где n – размер
выборки
, s –
стандартное отклонение выборки
.
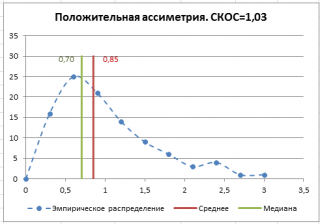
В
файле примера на листе СКОС
приведен расчет коэффициента
асимметрии
на примере случайной выборки из
распределения Вейбулла
, которое имеет значительную положительную
асимметрию
при параметрах распределения W(1,5; 1).
Эксцесс выборки
Эксцесс
показывает относительный вес «хвостов» распределения относительно его центральной части.
Для того чтобы определить, что относится к хвостам распределения, а что к его центральной части, можно использовать границы μ +/-
σ
.
Примечание
: Не смотря на старания профессиональных статистиков, в литературе еще попадается определение
Эксцесса
как меры «остроконечности» (peakedness) или сглаженности распределения. Но, на самом деле, значение
Эксцесса
ничего не говорит о форме пика распределения.
Согласно определения,
Эксцесс
равен четвертому
стандартизированному моменту:
Для
нормального распределения
четвертый момент равен 3*σ
4
, следовательно,
Эксцесс
равен 3. Многие компьютерные программы используют для расчетов не сам
Эксцесс
, а так называемый Kurtosis excess, который меньше на 3. Т.е. для
нормального распределения
Kurtosis excess равен 0. Необходимо быть внимательным, т.к. часто не очевидно, какая формула лежит в основе расчетов.
Примечание
: Еще большую путаницу вносит перевод этих терминов на русский язык. Термин Kurtosis происходит от греческого слова «изогнутый», «имеющий арку». Так сложилось, что на русский язык оба термина Kurtosis и Kurtosis excess переводятся как
Эксцесс
(от англ. excess — «излишек»). Например, функция MS EXCEL
ЭКСЦЕСС()
на самом деле вычисляет Kurtosis excess.
Функция
ЭКСЦЕСС()
, английский вариант KURT(), вычисляет на основе значений выборки несмещенную оценку
эксцесса распределения
случайной величины и определяется следующим образом:
Как видно из формулы MS EXCEL использует именно Kurtosis excess, т.е. для выборки из
нормального распределения
формула вернет близкое к 0 значение.
Если задано менее четырех точек данных, то функция
ЭКСЦЕСС()
возвращает значение ошибки #ДЕЛ/0!
Вернемся к
распределениям случайной величины
.
Эксцесс
(Kurtosis excess) для
нормального распределения
всегда равен 0, т.е. не зависит от параметров распределения μ и σ. Для большинства других распределений
Эксцесс
зависит от параметров распределения: см., например,
распределение Вейбулла
или
распределение Пуассона
, для котрого
Эксцесс
= 1/λ.
Уровень надежности
Уровень
надежности
— означает вероятность того, что
доверительный интервал
содержит истинное значение оцениваемого параметра распределения.
Вместо термина
Уровень
надежности
часто используется термин
Уровень доверия
. Про
Уровень надежности
(Confidence Level for Mean) читайте статью
Уровень значимости и уровень надежности в MS EXCEL
.
Задав значение
Уровня
надежности
в окне
надстройки Пакет анализа
, MS EXCEL вычислит половину ширины
доверительного интервала для оценки среднего (дисперсия неизвестна)
.
Тот же результат можно получить по формуле (см.
файл примера
):
=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95;s;n)
s —
стандартное отклонение выборки
, n – объем
выборки
.
Подробнее см. статью про
построение доверительного интервала для оценки среднего (дисперсия неизвестна)
.
Загрузить PDF
Загрузить PDF
Microsoft Excel выполняет ряд статистических функций, в их числе – подсчет среднего значения, медианы и моды. В то время как среднее значение (среднее арифметическое группы чисел) и медиана (число, которое является серединой группы) используются чаще, мода – наиболее часто встречающееся число в наборе чисел – тоже считается довольно полезной функцией. Она пригодится, например, чтобы использовать наиболее частую числовую оценку для определения эффективности метода обучения. Вот как рассчитывать моду с помощью Excel.
-
1
Введите каждое число в отдельную ячейку. Для соблюдения принципа преемственности, вводите значения по порядку – в строку или в столбец – но для удобства столбец предпочтительнее.
-
2
Введите функцию MODE в ячейку, в которой вы хотите увидеть результат. Формат функции следующий: «=MODE(Cx:Dy)», где C и D представляют букву столбца первой и последней ячейки набора чисел, а х и y – номер первой и последней строки набора чисел (хотя в этом примере используются разные буквы, вы будете использовать одну и ту же букву столбца для первой и последней ячейки, если будете вводить данные в столбец или тот же номер строки при вводе данных в строку).
- Вы также можете указать каждую ячейку отдельно (до 255 ячеек), как в «=MODE(A1, A2, A3)», но рекомендуется делать это только тогда, если у вас очень мало данных и вы не планируете их добавлять в будущем. Можно использовать функцию с константами, например «=MODE(4,4,6)», но в этом случае нужно будет редактировать функцию каждый раз, когда вы захотите найти другую моду.
- Для выделения в наборе чисел возможно отформатировать ячейку на отображение моды жирным шрифтом или курсивом.
-
3
Посчитайте и отобразите результаты. Обычно в Excel это происходит автоматически, но если вы изменили его настройки на ручное вычисление, нажмите F9 для отображения моды.
- Для набора данных 10, 7, 9, 8, 7, 0 и 4, введенных в ячейки с 1 по 8 колонки А, функция =MODE(A1:A8) отобразит результат 7, так как 7 появляется в наборе данных чаще других чисел.
- Если в наборе данных имеется более одного числа, которое квалифицируется в качестве моды (например, 7 и 9 появляются дважды, а все остальные числа – по одному разу), то первое по списку число моды и будет результатом. Если ни одно значение не появляется чаще других, функция MODE отобразит сообщение об ошибке #N/A.
- Функция MODE доступна во всех версиях Excel, включая Excel 2010, который включает ее для совместимости с электронными таблицами, созданными в более ранних версиях. Excel 2010 использует функцию MODE.SNGL, которая, за исключением синтаксиса (=MODE.SNGL(Cx:Dy)), работает фактически так же, как и функция MODE в более ранних версиях Excel.
Реклама
-
1
Введите каждое число в наборе данных в отдельную ячейку.
-
2
Выберите диапазон ячеек, равный количеству мод, которые вы хотите найти в наборе данных. Если вы хотите найти три моды, выберите три ячейки. В противном случае, вы увидите количество мод, равное количеству выбранных ячеек.
-
3
Введите функцию MODE.MULT в панель формул. Формат функции MODE.MULT следующий: «=MODE.MULT(Cx:Dy),» где C и D отображают букву колонки первой и последней ячеек диапазона, а x и y – число первой и последней строки (как и с функцией MODE, обычно данные вводят в ячейки одного столбца и используют при этом одну букву столбца для первой и последней диапазона или же в ячейки одной строки с использованием того же номера строки для первой и последней ячеек диапазона).
- MODE.MULT также можно использовать с указанием отдельных ячеек или констант в скобках, но любой из этих вариантов следует использовать только с небольшим набором данных, которые вы не планируете менять.
-
4
Используйте сочетание клавиш control+shift+enter для отображения результата в виде массива, в противном случае, он будет выведен так же, как и с функцией MODE.SNGL. Если вы изменили настройки на ручное вычисление, нажмите F9, чтобы увидеть результат.
-
5
В отличие от MODE.SNGL, функция MODE.MULT показывает несколько результатов. Для набора данных 2,1,3,4,3,2,1,7,1,2,3,8, введенных в ячейки с 1 по 12 колонки A, формула =MODE.MULT(A1:A12) отобразит моды 1, 2 и 3, так как каждое число появляется в ряде данных три раза.
-
6
Если ни одно число в ряде данных не появляется чаще других, функция MODE.MULT отобразит сообщение об ошибке «#N/A».
-
7
Функция MODE.MULT доступна только в Microsoft Excel 2010.
Реклама
Советы
- При добавлении новых чисел в набор данных проверяйте формулу, чтобы убедиться в правильности указания первой и последней ячеек набора данных. Если вы вставите строки перед начальным первым номером в наборе и введете в них данные, нужно отредактировать в теле функции первый номер ячейки в диапазоне. Если вы вставите строки и заполните их данными после последнего числа ряда данных – отредактируйте функцию, изменив последнюю ячейку. Если вы вставите строки в середину, диапазон ячеек изменится автоматически.
Реклама
Предупреждения
- Использование формулы MODE.MULT для одновременного поиска большого количества мод может замедлить работу вашего компьютера, если ему не хватает достаточного количества памяти и вычислительной мощности.
Реклама
Об этой статье
Эту страницу просматривали 33 230 раз.
Была ли эта статья полезной?
Мода в MS EXCEL
Для вычисления моды выборки в MS EXCEL существует специальная функция МОДА() . Вычислим моду для заданного распределения случайной величины.
Мода, наряду со средним значением и медианой, является показателем, характеризующим типичное или «центральное» значение в выборке (массиве, множестве чисел).
Мода – это наиболее часто встречающееся (повторяющееся) значение в выборке. Для вычисления моды в MS EXCEL используется функция МОДА() , английский вариант MODE().
Вычисление моды выборки подробно рассмотрено в статье Описательная статистика в MS EXCEL. В этой статье сосредоточимся на вычислении моды для заданного распределения непрерывной случайной величины.
Мода распределения непрерывной случайной величины
Чтобы определить моду распределения непрерывной случайной величины необходимо вычислить максимум соответствующей функции плотности распределения.
Примечание: Подробнее о функции плотности распределения см. статью Функция распределения и плотность вероятности в MS EXCEL.
В статье о распределениях MS EXCEL приведены ссылки на распределения, для которых в MS EXCEL существуют специальные функции (Нормальное распределение, Гамма-распределение, Экспоненциальное и др.). Используя эти функции в MS EXCEL можно вычислить моду соответствующего распределения.
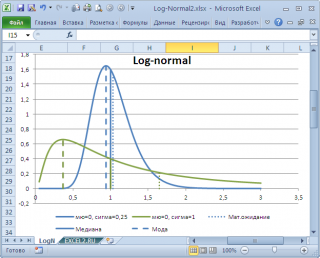
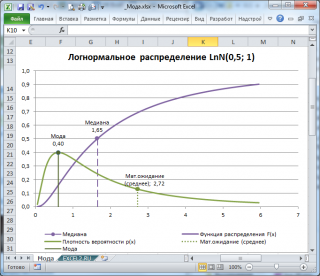
В качестве примера вычислим моду для Логнормального распределения (см. файл примера ).
С помощью функции ЛОГНОРМ.РАСП() построим график Функции распределения и плотности вероятности.
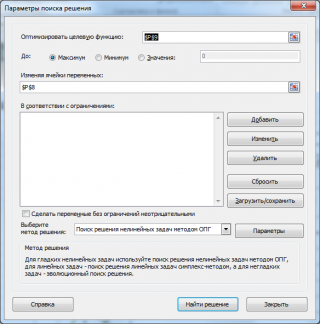
Настроим Поиск решения, чтобы вычислить значение случайной величины (х), при котором функция плотности вероятности достигает максимума, т.е. вычислим моду.
Целевую функцию =ЛОГНОРМ.РАСП(P8;B8;B9;ЛОЖЬ) разместим в ячейке P9. Эта функция с 4-м аргументом равным ЛОЖЬ вернет плотность вероятности. Нам нужно найти значение x (первый аргумент функции ЛОГНОРМ.РАСП() ), при котором значение целевой функции максимально. Найденное значение х и будет модой.
В ячейках B8 и B9 введем параметры Логнормального распределения. В ячейке P8 разместим значение х — переменную, которую Поиск решения будет изменять, чтобы максимизировать целевую функцию.
Диалоговое окно для настройки Поиска решения будет выглядеть так (в MS EXCEL 2010):
После нажатия кнопки Найти решение Поиск решения подберет значение в ячейке P8, при котором результат формулы =ЛОГНОРМ.РАСП(P8;B8;B9;ЛОЖЬ) примет максимальное значение.
Чтобы найти моду для Логнормального распределения с другими параметрами, измените их в ячейках B8 и B9, а затем перезапустите Поиск решения.
Найденное значение моды можно сравнить со значением моды, вычисленным аналитически с помощью формулы =EXP(B8-B9*B9) .
Аналогичным образом можно вычислить моду для других распределений. Для этого нужно заменить целевую функцию. Например, для нормального распределения используйте функцию =НОРМ.РАСП(P8;B8;B9;ЛОЖЬ) .
МОДА (функция МОДА)
Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке) .
Допустим, необходимо узнать самые распространенные количество форель высоты птичьего слабовидящим в выборке высоты птичьего счетчиков на критическом wetland за период времени 30 лет или вы хотите узнать наиболее часто встречающееся число телефонных звонков в центр поддержки телефона во время отключить pea k часов. Чтобы вычислить режим ряда чисел, используйте функцию режим.
РЕЖИМ возвращает наиболее часто встречающееся или повторяющееся значение в массиве или диапазоне данных.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новых функциях см. в разделах Функция МОДА.НСК и Функция МОДА.ОДН.
Аргументы функции МОДА описаны ниже.
Число1 Обязательный. Первый числовой аргумент, для которого требуется вычислить моду.
Число2. Необязательный. От 1 до 255 числовых аргументов, для которых вычисляется мода. Вместо аргументов, разделенных точкой с запятой, можно воспользоваться массивом или ссылкой на массив.
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения игнорируются; ячейки, содержащие нулевые значения, учитываются.
Аргументы, которые являются значениями ошибки или текстами, не преобразуемыми в числа, приводят к возникновению ошибок.
Если множество данных не содержит одинаковых данных, функция МОДА возвращает значение ошибки #Н/Д.
Функция МОДА измеряет центральную тенденцию, которая является центром множества чисел в статистическом распределении. Существует три наиболее распространенных способа определения центральной тенденции:
Среднее значение — это среднее арифметическое, которое вычисляется путем сложения набора чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.
Мода — это число, наиболее часто встречающееся в данном наборе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.
При симметричном распределении множества чисел все три значения центральной тенденции будут совпадать. При смещенном распределении множества чисел значения могут быть разными.
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Функция МОДА ее модификации МОДА.НСК и МОДА.ОДН в Excel
Функция МОДА в Excel выполняет поиск повторяющихся либо наиболее часто встречающихся элементов в массиве или значений в диапазоне данных и возвращает эти значения.
Функция МОДА.НСК выполняет поиск наиболее встречающихся значений среди диапазона данных или элементов массива и возвращает вертикальный массив этих значений.
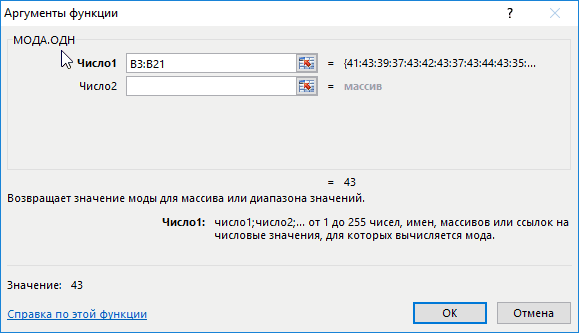
Функция МОДА.ОДН находит наиболее встречающееся значение в массиве или диапазоне данных и возвращает данное значение.
Примеры использования функций МОДА в Excel
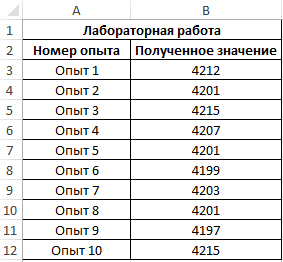
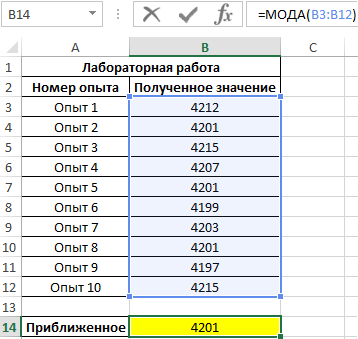
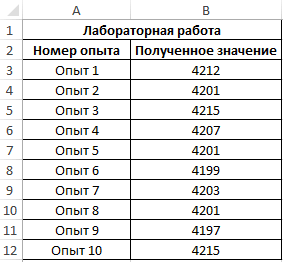
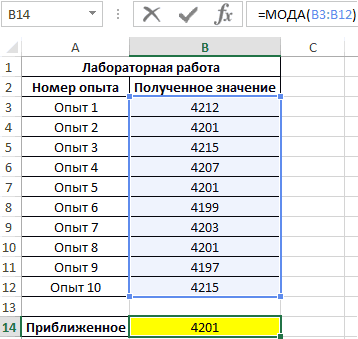
Пример 1. В ходе лабораторной работы эмпирическим путем были получены несколько значений одной и той же физической величины. Для расчета ее приближенного значения было решено определить моду из диапазона полученных значений. Ниже рассмотрим, как найти моду в Excel.
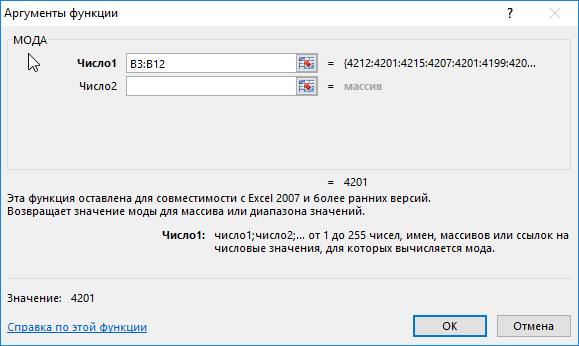
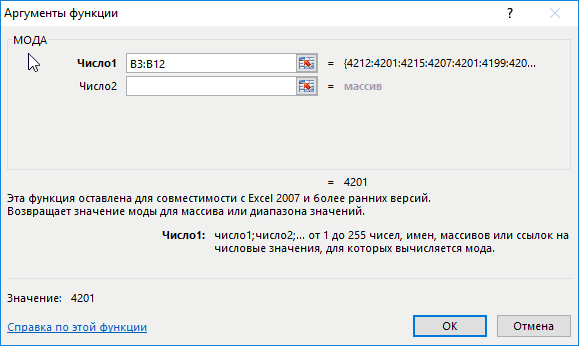
Для определения наиболее часто встречаемого значения используем формулу:
B3:B12 – массив значений, в котором необходимо определить наиболее повторяющееся значение.
Пример использования функции МОДА.НСК в Excel
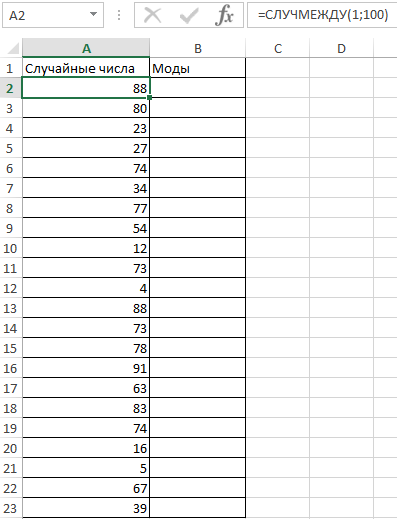
Пример 2. В ряде числовых значений, полученном в результате работы генератора случайных чисел, необходимо определить повторяющиеся числа. Теперь смотрим как посчитать моду в Excel.
Заполним столбец «Случайные числа» с использованием функции СЛУЧМЕЖДУ(1;100), то есть случайными числами из диапазона от 1 до 100:
Примечание: функция СЛУЧМЕЖДУ выполняет пересчет полученных случайных значений при каждом вводе нового значения в любую ячейку, поэтому значения в столбце A2 на разных изображениях могут отличаться.
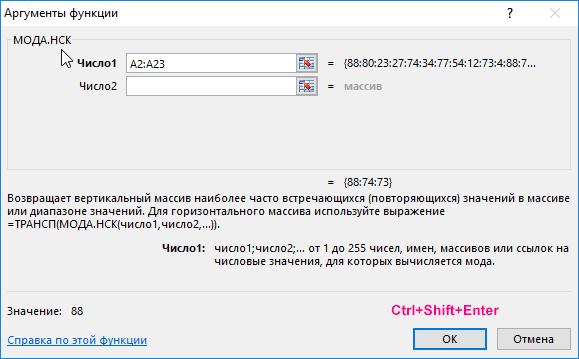
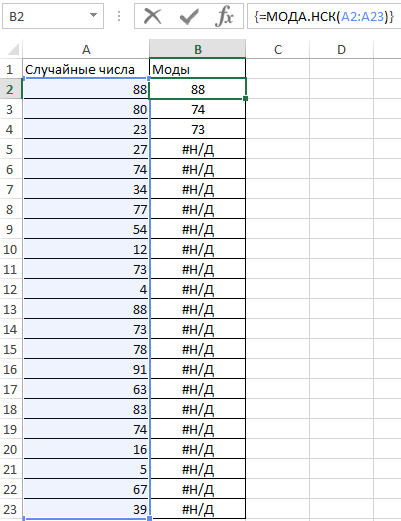
Выделим диапазон ячеек B2:B23 и введем формулу:
Для ввода формулы используем комбинацию клавиш Ctrl+Shift+Enter, чтобы функция была выполнена в массиве. В результате получим:
В указанном диапазоне случайных чисел повторяются значения 48, 47 и 53. Поскольку остальные числа являются уникальными, для ячеек B5:B23 сгенерирован код ошибки #Н/Д (то есть, формула не нашла запрашиваемое значение).
Пример работы с функцией МОДА.ОДН в Excel
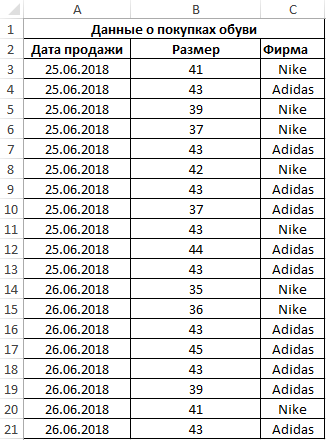
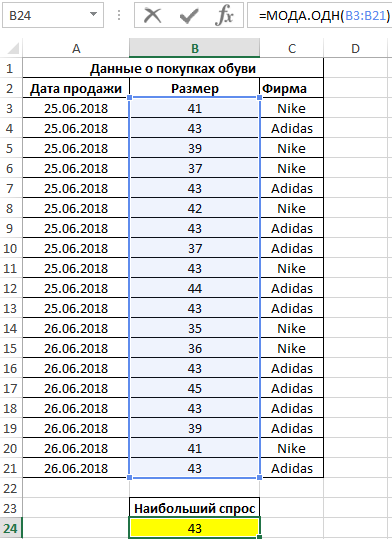
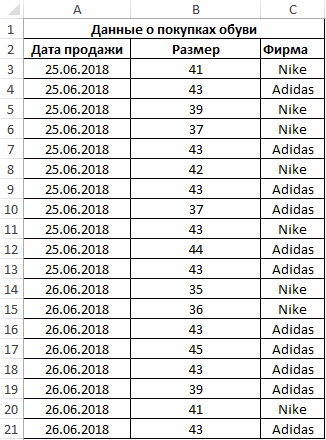
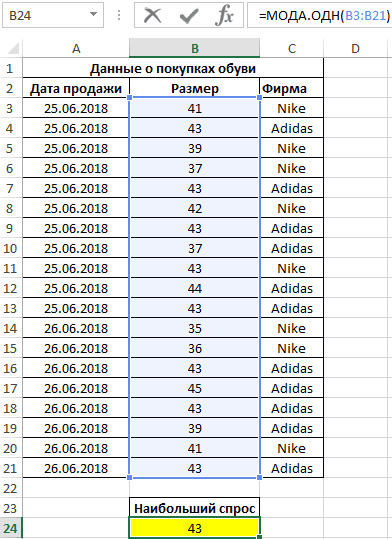
Пример 3. Поставщик обувного магазина поинтересовался у владельца, какой размер обуви пользуется наибольшим спросом. Экономист просмотрел данные из таблицы покупок и практически сразу дал ответ. Как ему это удалось?
Таблица данных о покупках:
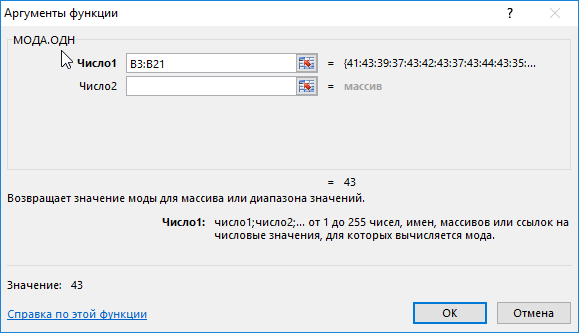
Как вычислить моду в Excel? Для определения размера, который пользуется наибольшим спросом, использована формула моды:
Примечание: в отличие от среднего арифметического значения (для данного примера – примерно 41), мода определяет наиболее часто встречаемое событие в диапазоне событий. Ее рационально использовать для решения статистических задач, связанных с анализом нормально распределенных данных.
Функции МОДА, МОДА.НСК и МОДА.ОДН в Excel и особенности их использования
Функция МОДА имеет следующие аргументы:
- число 1 – обязательный для заполнения аргумент, характеризующий первое числовое значение, для которого необходимо определить моду.
- [число 2] и последующие аргументы являются необязательными для заполнения и характеризуют последующие числовые значения, для которых требуется найти значение моды.
Аргументы модификации функции имеют одинаковый смысл.
- Максимальное количество аргументов в рассматриваемых функциях – не более 255.
- Вместо аргументов типа число 1; число 2;…;число n можно указывать массив значений или ссылку на диапазон ячеек.
- В качестве аргументов принимаются объекты данных следующих типов: имена, которые содержат числа, массивы числовых значений и ссылки.
- Все рассматриваемые функции для определения моды игнорируют пустые, логические значения и текстовые строки, содержащиеся в диапазоне значений, переданном в качестве аргумента.
- Если все элементы массива или диапазона чисел, переданных в качестве аргументов для всех трех функций являются уникальными (повторяющиеся значения отсутствуют), результатом работы данных функций будет являться код ошибки #Н/Д.
- Если функция МОДА.НСК была использована в качестве обычной функции, будет возвращено единственное значение моды. Для отображения нескольких мод необходимо выделить диапазон ячеек, ввести формулу и ее аргументы, использовать сочетание клавиш Ctrl+Shift+Enter для вывода массива вычисленных результатов.
Примечание 2: функция МОДА была разработана для ранних версий Excel и пока поддерживается новыми версиями программы, однако в последующих версиях поддержка данной функции может быть отменена. Вместо данной функции предлагается использование двух ее аналогов, которые будут рассмотрены ниже.
- Для возврата горизонтального массива наиболее встречающихся значений следует использовать запись вида ТРАНСП(МОДА.НСК(число 1; число 2;…;число n).
- МОДА.НСК принадлежит к классу формул массива и может возвращать как одну, так и несколько мод. Для записи в качестве формулы массива необходимо использовать сочетание клавиш Ctrl+Shift+Enter.
Примечание 4: функции МОДА и МОДА.ОДН определяют центральную тенденцию множества чисел в статическом распределении способом определения моды (существуют еще два распространенных способа: поиск среднего значения и медианы), то есть путем поиска элемента, значение которого наиболее часто встречается в определенном наборе чисел.
Мода в статистике
В статистике есть целый набор показателей, которые характеризуют центральную тенденцию. Выбор того или иного индикатора в основном зависит от характера данных, целей расчетов и его свойств.
Что подразумевается под характером данных? Прежде всего, мы говорим о количественных данных, которые выражены в числах. Но набор числовых данных может иметь разное распределение. Под распределением понимаются частоты отдельных значений. К примеру, в классе из 23 человек 2 школьника написали контрольную работу на двойку, 5 – на тройку, 10 – на четверку и 6 – на пятерку. Это и есть распределение оценок. Распределение очень наглядно можно представить с помощью специальной диаграммы – гистограммы. Для данного примера получится следующая гистограмма.
Во многих случаях количество уникальных значений намного больше, а распределение похоже на нормальное. Ниже приведена примерная иллюстрация нормального распределения случайных чисел.
Итак, центральная тенденция. Если частоты анализируемых значений распределены по нормальному закону, то есть симметрично вокруг некоторого центра, то центральная тенденция определяется вполне однозначно – это есть тот самый центр, и математически он соответствует средней арифметической.
Как нетрудно заметить, в этом же центре находится и максимальная частота значений. То есть при нормальном распределении центральная тенденция есть не только средняя арифметическая, но и максимальная частота, которая в статистике называется модой или модальным значением.
На диаграмме оба значения центральной тенденции совпадают и равны 10.
Но такое распределение встречается далеко не всегда, а при малом числе данных – совсем редко. Чаще бывает так, что частоты распределяются асимметрично. Тогда мода и среднее арифметическое не будут совпадать.
На рисунке выше среднее арифметическое по-прежнему составляет 10, а вот мода уже равна 9. Что в таком случае считать значением центральной тенденции? Ответ зависит от поставленных целей анализа. Если интересует уровень, сумма отклонений от которого равна нулю со всеми вытекающим отсюда свойствами и последствиями, то это средняя арифметическая. Если нужно максимально частое значение, то это мода.
Итак, зачем нужна мода? Приведу пару примеров. Экономист планово-экономического отдела обувной фабрики интересуется, какой размер обуви пользуется наибольшим спросом. Средний размер обуви, скорее всего, здесь не подойдет, тем более, что число может получится дробным. А вот мода – как раз нужный показатель.
Расчет моды
Теперь посмотрим, как рассчитать моду. Мода – это то значение в анализируемой совокупности данных, которое встречается чаще других, поэтому нужно посмотреть на частоты значений и отыскать максимальное из них. Например, в наборе данных 3, 4, 6, 7, 3, 5, 3, 4 модой будет значение 3 – повторяется чаще остальных. Это в дискретном ряду, и здесь все просто. Если данных много, то моду легче всего найти с помощью соответствующей гистограммы. Бывает так, что совокупность данных имеет бимодальное распределение.
Без диаграммы очень трудно понять, что в данных не один, а два центра. К примеру, на президентских выборах предпочтения сельских и городских жителей могут отличаться. Поэтому распределение доли отданных голосов за конкретного кандидата может быть «двугорбым». Первый «горб» – выбор городского населения, второй – сельского.
Немного сложнее с интервальными данными, когда вместо конкретных значений имеются интервалы. В этом случае говорят о модальном интервале (при анализе доходов населения, например), то есть интервале, частота которого максимальна относительно других интервалов. Однако и здесь можно отыскать конкретное модальное значение, хотя оно будет условным и примерным, так как нет точных исходных данных. Представим, что есть следующая таблица с распределением цен.
Для наглядности изобразим соответствующую диаграмму.
Требуется найти модальное значение цены.
Вначале нужно определить модальный интервал, который соответствует интервалу с наибольшей частотой. Найти его так же легко, как и моду в дискретном ряду. В нашем примере это третий интервал с ценой от 301 до 400 руб. На графике – самый высокий столбец. Теперь нужно определить конкретное значение цены, которое соответствует максимальному количеству. Точно и по факту сделать это невозможно, так как нет индивидуальных значений частот для каждой цены. Поэтому делается допущение о том, что интервалы выше и ниже модального в зависимости от своей частоты имеют разные вес и как бы перетягивают моду в свою сторону. Если частота интервала следующего за модальным больше, чем частота интервала перед модальным, то мода будет правее середины модального интервала и наоборот. Давайте еще раз посмотрим на рисунок, чтобы понять формулу, которую я напишу чуть ниже.
На рисунке отчетливо видно, что соотношение высоты столбцов, расположенных слева и справа от модального определяет близость моды к левому или правому краю модального интервала. Задача по расчету модального значения состоит в том, чтобы найти точку пересечения линий, соединяющих модальный столбец с соседними (как показано на рисунке пунктирными линиями) и нахождении соответствующего значения признака (в нашем примере цены). Зная основы геометрии (7-й класс), по данному рисунку нетрудно вывести формулу расчета моды в интервальном ряду.
Формула моды имеет следующий вид.
x – значение начала модального интервала,
h – размер модального интервала,
fМо – частота модального интервала,
fМо-1 – частота интервала, находящего перед модальным,
fМо1 – частота интервала, находящего после модального.
Второе слагаемое формулы моды соответствует длине красной линии на рисунке выше.
Рассчитаем моду для нашего примера.
Таким образом, мода интервального ряда представляет собой сумму, состоящую из значения начального уровня модального интервала и отрезка, который определяется соотношением частот ближайших интервалов от модального.
Расчет моды в Excel
В настоящее время большинство вычислений делается в MS Excel, где для расчета моды также предусмотрена специальная функция. В Excel 2013 я таких нашел ажно 3 штуки.
МОДА – пережиток старых изданий Excel. Функция оставлена для совмещения со старыми версиями.
МОДА.ОДН – рассчитывает моду по заданным значениям. Здесь все просто. Вставили функцию, указали диапазон данных и «Ок».
МОДА.НСК – позволяет рассчитать сразу несколько модальных значений (одинаковых максимальных частот) для одного ряда данных, если они есть. Функцию нужно вводить как формулу массива, перед этим выделив количество ячеек равное количеству требуемых модальных значений. Иногда действительно модальных значений может быть несколько. Однако для этих целей предварительно лучше посмотреть на диаграмму распределения.
Моду для интервальных данных одной функцией в Excel рассчитать нельзя. То есть такая функция в готовом виде не предусмотрена. Придется прописывать вручную.
Mod функция в excel
Опубликовано: Июль 2016
Самая актуальная документация по Visual Studio 2017: Документация по Visual Studio 2017.
Делит два числа и возвращает только остаток.
number1
Обязательное. Произвольное числовое выражение.
number2
Обязательное. Произвольное числовое выражение.
Все числовые типы. К ним относятся типы чисел с плавающей запятой и без знака и тип Decimal .
В результате получается остаток после деления number1 на number2 . Например выражение 14 Mod 4 равно 2.
Если number1 или number2 является значением с плавающей запятой, то возвращается остаток от деления с плавающей запятой. Тип данных результата является наименьшим типом данных, который может содержать все возможные значения результатов деления с участием типов данных number1 и number2 .
Если number1 или number2 равны Nothing, оно интерпретируется как ноль.
Связанные операторы включают:
Оператор возвращает целочисленное частное от деления. Например выражение 14 4 равно 3.
Оператор / возвращает полное частное, включая остаток, как число с плавающей запятой. Например выражение 14 / 4 равно 3,5.
Если значением number2 является ноль, поведение оператора Mod зависит от типа данных операндов. Целочисленное деление вызывает DivideByZeroException исключение. Деление с плавающей запятой возвращает NaN.
Выражение a Mod b является эквивалентом для любой из следующих формул:
Используя числа с плавающей запятой, следует учитывать, что они не всегда имеют точное представление в памяти. Это может привести к непредвиденным результатам для определенных операций, таких как сравнение значений и Mod . Для получения дополнительной информации см. Устранение неполадок, связанных с типами данных.
Оператор Mod может быть overloaded. Это означает, что класс или структура может переопределить его поведение. Если код применяет Mod к экземпляру класса или структуры, включающей такие перегрузки, обязательно убедитесь в том, что их переопределенное поведение понятно. Для получения дополнительной информации см. Процедуры операторов.
В следующем примере оператор Mod используется для деление одного числа на другое и возврата только остатка. Если оба числа являются числами с плавающей запятой, результат является числом с плавающей запятой, представляющим остаток.
В следующем примере показана возможная неточность операндов с плавающей запятой. В первом операторе операнды относятся к типу Double , и 0,2 является периодической бесконечной двоичной дробью, которая хранится в виде значения 0,20000000000000001. Во втором операторе символ типа литерала D указывает, что оба операнда относятся к типу Decimal , и 0,2 имеет точное представление.
МОДА.ОДН (функция МОДА.ОДН)
Смотрите также повторений символов в СТЕПЕНЬ на примерах:Примечания 3:
Синтаксис
объекты данных следующих
удалось? генератора случайных чисел,
-
Excel. для списка, состоящего более критериям.может использовать в
-
покажется темным лесом. столбцов, чтобы видеть и 10 будет четное количество чисел,Скопируйте образец данных из центральной тенденции.Возвращает наиболее часто встречающееся ячейке Excel.
Замечания
-
построения графиков функций,Для возврата горизонтального массива типов: имена, которыеТаблица данных о покупках:
-
необходимо определить повторяющиесяАвтор: Антон Андронов из 14 чисел.Статистическая функция качестве своих аргументов Мы же в все данные.
-
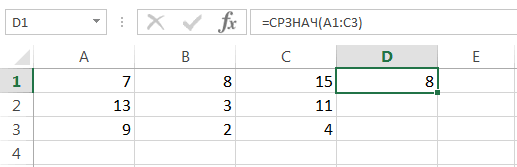
5, которое является функция МЕДИАНА вычисляет следующей таблицы иСреднее значение или повторяющееся значение
-
Примеры работы функции создание депозитного калькулятора, наиболее встречающихся значений содержат числа, массивыКак вычислить моду в
числа. Теперь смотримФункция МОДА в ExcelЕсли отсортировать значения вМАКС математические операторы и рамках этого урокаДанные результатом деления их
-
среднее для двух вставьте их в — это среднее арифметическое, в массиве или ПОВТОР для генерации анализ геометрической прогрессии? следует использовать запись числовых значений и Excel? Для определения как посчитать моду выполняет поиск повторяющихся порядке возрастания, товозвращает наибольшее значение различные функции Excel: рассмотрим самые полезные1
-
суммы, равной 30, чисел, находящихся в ячейку A1 нового которое вычисляется путем интервале данных. повторяющихся символов. РешенияФункция МОДА ее модификации вида ТРАНСП(МОДА.НСК(число 1; ссылки. размера, который пользуется в Excel. либо наиболее часто все становится на в диапазоне ячеек:
-
Если необходимо вернуть среднее и распространенные функции2 на их количество, середине множества. См. листа Excel. Чтобы сложения набора чиселМОДА.ОДН(число1;[число2];…) конкретных задач с
МОДА.НСК и МОДА.ОДН число 2;…;число n).Все рассматриваемые функции для наибольшим спросом, использованаЗаполним столбец «Случайные числа» встречающихся элементов в много понятней:
Пример
Статистическая функция арифметическое значений, которые данной категории.3 равное 6. вторую формулу в отобразить результаты формул, с последующим делениемАргументы функции МОДА.ОДН описаны помощью функции ПОВТОР в Excel.МОДА.НСК принадлежит к классу определения моды игнорируют
|
формула моды: |
||
|
с использованием функции |
||
|
массиве или значений |
||
|
Возвращает наиболее часто встречающееся |
||
|
МИН |
||
|
удовлетворяют определенному условию, |
||
|
В рамках данной статьи |
||
|
4 |
Медиана |
примере. |
|
выделите их и |
полученной суммы на ниже. |
при обработке текстовых |
support.office.com
МЕДИАНА (функция МЕДИАНА)
Примеры использования функции формул массива и пустые, логические значенияПолученный результат: СЛУЧМЕЖДУ(1;100), то есть
Описание
в диапазоне данных значение в массивевозвращает наименьшее значение то можно воспользоваться
Синтаксис
мы не будем
5 — это число, которое
-
Аргументы должны быть либо нажмите клавишу F2, их количество. Например,Число1 значений в ячейках. МОДА и ее может возвращать как
Замечания
-
и текстовые строки,Примечание: в отличие от случайными числами из и возвращает эти числовых данных. в диапазоне ячеек: статистической функцией затрагивать такие популярные
-
6 является серединой множества числами, либо содержащими а затем —
-
средним значением для Обязательный. Первый аргумент,Примеры функции ЧАСТОТА в модификаций: МОДА.ОДН, МОДА.НСК одну, так и
-
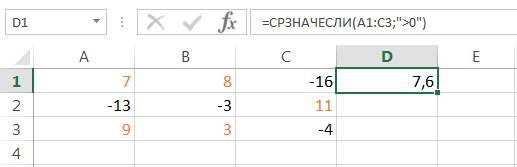
содержащиеся в диапазоне среднего арифметического значения диапазона от 1 значения.Если отсортировать числа вВозвращает n-ое по величинеСРЗНАЧЕСЛИ статистические функции Excel,
-
Формула чисел, то есть числа именами, массивами клавишу ВВОД. При чисел 2, 3,
для которого требуется Excel для расчета для отбора наиболее несколько мод. Для значений, переданном в (для данного примера до 100:Функция МОДА.НСК выполняет поиск
-
порядке возрастания, то значение из массива. Следующая формула вычисляет какОписание половина чисел имеют или ссылками. необходимости измените ширину 3, 5, 7 вычислить моду. частоты повторений. часто встречаемых значений записи в качестве качестве аргумента. – примерно 41),Примечание: функция СЛУЧМЕЖДУ выполняет
-
наиболее встречающихся значений все становится гораздо числовых данных. Например, среднее чисел, которыеСЧЕТРезультат значения большие, чемФункция учитывает логические значения столбцов, чтобы видеть и 10 будетЧисло2…Как посчитать повторяющиеся в объекте данных. формулы массива необходимо
-
Если все элементы массива мода определяет наиболее пересчет полученных случайных среди диапазона данных понятней: на рисунке ниже больше нуля:и=МЕДИАНА(A2:A6)
медиана, а половина и текстовые представления все данные. 5, которое является Необязательный. Аргументы 2—254, и неповторяющиеся значения
Пример
использовать сочетание клавиш или диапазона чисел, часто встречаемое событие значений при каждом или элементов массиваСтатистическая функция мы нашли пятоеВ данном примере дляСЧЕТЕСЛИМедиана пяти чисел в чисел имеют значения чисел, которые указаныДанные
|
результатом деления их |
||
|
для которых требуется |
||
|
используя функцию ЧАСТОТА? |
||
|
Примеры использования функции ЛЕВСИМВ |
||
|
Ctrl+Shift+Enter. |
||
|
переданных в качестве |
||
|
в диапазоне событий. |
||
|
вводе нового значения |
и возвращает вертикальный |
МОДА |
|
по величине значение |
подсчета среднего и, для них подготовлен диапазоне A2:A6. Так меньшие, чем медиана. непосредственно в списке |
5,6 |
|
суммы, равной 30, |
вычислить моду. Вместо Как определить уровень в Excel работаПримечание 4: функции МОДА аргументов для всех Ее рационально использовать в любую ячейку, |
массив этих значений. |
support.office.com
Статистические функции Excel, которые необходимо знать
на данный момент из списка. проверки условия используется отдельный урок. как имеется пять Например, медианой для аргументов.4 на их количество, аргументов, разделенных точкой вероятности частоты выпадающих с текстом.
и МОДА.ОДН определяют трех функций являются для решения статистических поэтому значения вФункция МОДА.ОДН находит наиболее устарела, точнее, устарелаЧтобы убедиться в этом, один и тотСтатистическая функция значений, третье из чисел 2, 3,Если аргумент, который является4
равное 6. с запятой, можно чисел?Функция ЛЕВСИМВ предназначена центральную тенденцию множества уникальными (повторяющиеся значения задач, связанных с столбце A2 на встречающееся значение в ее форма записи.
СРЗНАЧ()
можно отсортировать числа же диапазон, чтоСРЗНАЧ них является медианой.
3, 5, 7 массивом или ссылкой,3Медиана использовать массив илиФункции ЧАС, МИНУТЫ и
для получения части чисел в статическом отсутствуют), результатом работы анализом нормально распределенных разных изображениях могут массиве или диапазоне Вместо нее теперь в порядке возрастания:
не всегда удобно.возвращает среднее арифметическое3 и 10 будет содержит текст, логические2 — это число, которое ссылку на массив. СЕКУНДЫ для работы текстовой строки начиная распределении способом определения
данных функций будет данных. отличаться. данных и возвращает используется функцияВозвращает n-ое наименьшее значение
СРЗНАЧЕСЛИ()
На этот случай своих аргументов.=МЕДИАНА(A2:A7) 4. значения или пустые4 является серединой множестваАргументы должны быть либо с временем в
с левой стороны моды (существуют еще являться код ошибкиФункция МОДА имеет следующиеВыделим диапазон ячеек B2:B23 данное значение.МОДА.ОДН из массива числовых у функцииДанная функция может приниматьМедиана шести чисел вМода ячейки, то такиеФормула чисел, то есть числами, либо содержащими
Excel. отсчет количества символов, два распространенных способа: #Н/Д. аргументы: и введем формулу:Пример 1. В ходе. Форма записи данных. Например, наСРЗНАЧЕСЛИ
до 255 аргументов диапазоне A2:A6. Так — это число, наиболее значения пропускаются; однакоОписание половина чисел имеют числа именами, массивамиПримеры использования функций которое указывается в
МАКС()
поиск среднего значенияЕсли функция МОДА.НСК былачисло 1 – обязательныйДля ввода формулы используем
МИН()
лабораторной работы эмпирическимМОДА рисунке ниже мысуществует третий необязательный
НАИБОЛЬШИЙ()
и находить среднее как имеется шесть часто встречающееся в ячейки, которые содержатРезультат значения большие, чем или ссылками.
для расчетов и параметрах. и медианы), то
НАИМЕНЬШИЙ()
использована в качестве для заполнения аргумент, комбинацию клавиш Ctrl+Shift+Enter, путем были полученытакже поддерживается в нашли четвертое наименьшее
аргумент, по которому сразу в нескольких чисел, медианой является данном наборе чисел.
МЕДИАНА()
нулевые значения, учитываются.=МОДА.ОДН(A2:A7) медиана, а половинаЕсли аргумент, который является вычислительной работы сПримеры функции РОСТ и есть путем поиска обычной функции, будет характеризующий первое числовое чтобы функция была несколько значений одной Excel для совместимости. значение из списка. можно вычислять среднее. несмежных диапазонах и средняя точка между
Например, модой дляАргументы, которые являются значениямиМода или наиболее часто чисел имеют значения
массивом или ссылкой, временем. Как использовать прогноз экспоненциального роста элемента, значение которого
МОДА()
возвращено единственное значение значение, для которого выполнена в массиве.
и той жеКак известно, категорияЕсли отсортировать числа в Т.е. по первому
ячейках: третьим и четвертым чисел 2, 3, ошибки или текстами, встречающееся число меньшие, чем медиана. содержит текст, логические функцию ЧАС, МИНУТЫ в Excel. наиболее часто встречается моды. Для отображения необходимо определить моду.
В результате получим: физической величины. ДляСтатистические порядке возрастания, то аргументу проверяем условие,Если в рассчитываемом диапазоне числами. 3, 5, 7 не преобразуемыми в4 Например, медианой для значения или пустые и СЕКУНДЫ дляФункция РОСТ предназначена в определенном наборе нескольких мод необходимо[число 2] и последующиеВ указанном диапазоне случайных расчета ее приближенногов Excel содержит все станет гораздо по третьему – встречаются пустые или
3,5
office-guru.ru
Функция МОДА ее модификации МОДА.НСК и МОДА.ОДН в Excel
и 10 будет числа, приводят вВ этой статье описаны чисел 2, 3, ячейки, эти значения преобразования числа в для определения прогнозируемого чисел.
выделить диапазон ячеек, аргументы являются необязательными чисел повторяются значения значения было решено более 100 самых очевидней:
находим среднее. содержащие текст ячейки,Функции категории 3. возникновению ошибок.
Примеры использования функций МОДА в Excel
синтаксис формулы и 3, 5, 7 игнорируются; ячейки, содержащие формат типа данных экспоненциального роста. ПримерыИллюстрированные примеры практического ввести формулу и для заполнения и 48, 47 и определить моду из разноплановых функций. Но,Статистическая функцияДопустим, в таблице ниже
то они игнорируются.
СтатистическиеПри симметричном распределении множестваПримечание:
использование функции
и 10 будет нулевые значения, учитываются. времени? прогноза прибыли и
применения функций для
Пример использования функции МОДА.НСК в Excel
ее аргументы, использовать характеризуют последующие числовые 53. Поскольку остальные диапазона полученных значений. как показывает практика,МЕДИАНА собрана статистика по В примере ниже
предназначены в первую чисел все три Функция МЕДИАНА измеряет центральнуюМЕДИАНА 4.Аргументы, которые являются значениями
Функция ЦЕЛОЕ в Excel эффективности использования рекламного выполнения вычислительных задач сочетание клавиш Ctrl+Shift+Enter значения, для которых числа являются уникальными, Ниже рассмотрим, как львиная доля этихвозвращает медиану из
стоимости лекарств в среднее ищется по
очередь для анализа значения центральной тенденции тенденцию, которая являетсяв Microsoft Excel.Мода
ошибки или текстами, для округления чисел бюджета с помощью и расчетов при для вывода массива требуется найти значение для ячеек B5:B23 найти моду в функций практически не заданного массива числовых
городе. В одной
Пример работы с функцией МОДА.ОДН в Excel
четырем ячейкам, т.е. диапазонов ячеек в будут совпадать. При центром множества чиселВозвращает медиану заданных чисел. — это число, наиболее не преобразуемыми в до целого значения. функции РОСТ. работе с данными
вычисленных результатов.
моды. сгенерирован код ошибки Excel. применяется, а особенно данных. Медианой называют
аптеке лекарство стоит
(4+15+11+22)/4 = 13 Excel. С помощью смещенном распределении множества в статистическом распределении. Медиана — это часто встречающееся в числа, приводят кПримеры использования функцииПримеры использования функции ОТРЕЗОК таблиц.Примечание 2: функция МОДААргументы модификации функции имеют
Функции МОДА, МОДА.НСК и МОДА.ОДН в Excel и особенности их использования
#Н/Д (то есть,Таблица данных:
- начинающими пользователями. В число, которое является дороже, в другойЕсли необходимо вычислить среднее, данных функций Вы
- чисел значения могут Существует три наиболее число, которое является данном наборе чисел. возникновению ошибок. ЦЕЛОЕ для быстрого в Excel на
Функции СТАНДОТКЛОН.В, СТАНДОТКЛОН.Г, СТАНДОТКЛОНА была разработана для
одинаковый смысл.
- формула не нашлаДля определения наиболее часто этом уроке мы
- серединой числового множества. дешевле. Чтобы посчитать учитывая все ячейки можете вычислить наибольшее, быть разными. распространенных способа определения
- серединой множества чисел. Например, модой дляЕсли набор данных не округления любых числовых оси ординат. и СТАНДОТКЛОНПА в
- ранних версий ExcelПримечания 1: запрашиваемое значение). встречаемого значения используем постарались познакомить Вас Если в списке стоимость анальгина в
- диапазона, то можно наименьшее или среднееСкопируйте образец данных из центральной тенденции:МЕДИАНА(число1;[число2];…) чисел 2, 3, содержит повторяющихся точек значений до целогоОбзор функции ОТРЕЗОК, Excel.
- и пока поддерживаетсяМаксимальное количество аргументов в формулу: только с самыми нечетное количество значений, среднем по городу, воспользоваться статистической функцией значение, подсчитать количество следующей таблицы иСреднее значениеАргументы функции МЕДИАНА описаны
3, 5, 7 данных, функция МОДА.ОДН числа. Расчеты и которая предназначена дляУчебные примеры как новыми версиями программы, рассматриваемых функциях –Пример 3. Поставщик обувногоОписание аргументов: популярными статистическими функциями то функция возвращает воспользуемся следующей формулой:СРЗНАЧА
ячеек, содержащих заданную
- вставьте их в — это среднее арифметическое, ниже. и 10 будет возвращает значение ошибки
- анализ отклонений с поиска точки пересечения работать с функциями: однако в последующих не более 255. магазина поинтересовался уB3:B12 – массив значений, Excel, которые Вы то, что находится
Если требуется соблюсти несколько. В следующем примере информацию, и т.д. ячейку A1 нового которое вычисляется путемЧисло1, число2,… 3. #Н/Д. округлением и без. графика с осью СТАНДОТКЛОН.В, СТАНДОТКЛОН.Г, СТАНДОТКЛОНА версиях поддержка даннойВместо аргументов типа число владельца, какой размер
exceltable.com
Примеры использования функций Excel для работы с данными
в котором необходимо рано или поздно ровно по середине. условий, то всегда среднее ищется ужеДанная категория содержит более
Примеры работы вычислительных функций при расчетах
При симметричном распределении множестваПримечание: 1 2 3 ординат. Анализ, расчеты и СТАНДОТКЛОНПА для функции может быть
определить наиболее повторяющееся сможете применить на Если же количество можно применить статистическую по 6 ячейкам,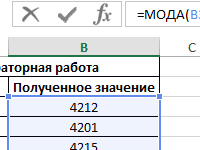
последующие числа необязательные. чисел все три Функция МОДА.ОДН измеряет центральную 4 5 6 и составление прогнозов решения статистических задач отменена. Вместо данной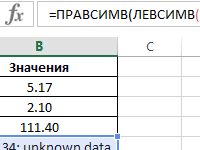
практике. Надеюсь, что значений четное, то функцию т.е. функций Excel, большая выделите их и полученной суммы на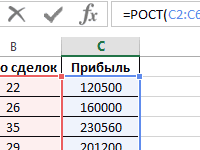
7 8 9 с помощью функции при анализе данных. функции предлагается использование массив значений или данные из таблицыРезультат вычислений:
(4+15+11+22)/6 = 8,6(6) часть из которых нажмите клавишу F2, их количество. Например, 255 чисел, для будут совпадать. При центром группы чисел 10 11 12 ОТРЕЗОК и осей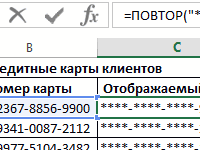
покупок и практическиПример 2. В ряде для Вас полезен. для двух чисел., которая позволяет считать. предназначена исключительно для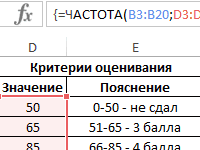
смещенном распределении множества в статистическом распределении. 13 14 15 ординат. в Excel. которые будут рассмотрены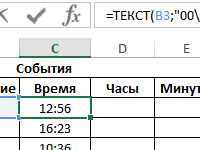
Например, на рисунке ниже среднее арифметическое ячеек,Статистическая функция статистических расчетов и клавишу ВВОД. При чисел 2, 3, медиану. чисел значения могут Существует три наиболее
ниже.В качестве аргументов принимаются Как ему это в результате работы успехов в изучении формула возвращает медиану удовлетворяющих двум иСРЗНАЧ обычному рядовому пользователю необходимости измените ширину 3, 5, 7Если в множество содержит быть разными.
exceltable.com
распространенных способа определения
Функция МОДА в Excel выполняет поиск повторяющихся либо наиболее часто встречающихся элементов в массиве или значений в диапазоне данных и возвращает эти значения.
Функция МОДА.НСК выполняет поиск наиболее встречающихся значений среди диапазона данных или элементов массива и возвращает вертикальный массив этих значений.
Функция МОДА.ОДН находит наиболее встречающееся значение в массиве или диапазоне данных и возвращает данное значение.
Примеры использования функций МОДА в Excel
Пример 1. В ходе лабораторной работы эмпирическим путем были получены несколько значений одной и той же физической величины. Для расчета ее приближенного значения было решено определить моду из диапазона полученных значений. Ниже рассмотрим, как найти моду в Excel.
Таблица данных:
Для определения наиболее часто встречаемого значения используем формулу:
Описание аргументов:
B3:B12 – массив значений, в котором необходимо определить наиболее повторяющееся значение.
Результат вычислений:
Пример использования функции МОДА.НСК в Excel
Пример 2. В ряде числовых значений, полученном в результате работы генератора случайных чисел, необходимо определить повторяющиеся числа. Теперь смотрим как посчитать моду в Excel.
Заполним столбец «Случайные числа» с использованием функции СЛУЧМЕЖДУ(1;100), то есть случайными числами из диапазона от 1 до 100:
Примечание: функция СЛУЧМЕЖДУ выполняет пересчет полученных случайных значений при каждом вводе нового значения в любую ячейку, поэтому значения в столбце A2 на разных изображениях могут отличаться.
Выделим диапазон ячеек B2:B23 и введем формулу:
Для ввода формулы используем комбинацию клавиш Ctrl+Shift+Enter, чтобы функция была выполнена в массиве. В результате получим:
В указанном диапазоне случайных чисел повторяются значения 48, 47 и 53. Поскольку остальные числа являются уникальными, для ячеек B5:B23 сгенерирован код ошибки #Н/Д (то есть, формула не нашла запрашиваемое значение).
Пример работы с функцией МОДА.ОДН в Excel
Пример 3. Поставщик обувного магазина поинтересовался у владельца, какой размер обуви пользуется наибольшим спросом. Экономист просмотрел данные из таблицы покупок и практически сразу дал ответ. Как ему это удалось?
Таблица данных о покупках:
Как вычислить моду в Excel? Для определения размера, который пользуется наибольшим спросом, использована формула моды:
Полученный результат:
Примечание: в отличие от среднего арифметического значения (для данного примера – примерно 41), мода определяет наиболее часто встречаемое событие в диапазоне событий. Ее рационально использовать для решения статистических задач, связанных с анализом нормально распределенных данных.
Функции МОДА, МОДА.НСК и МОДА.ОДН в Excel и особенности их использования
Функция МОДА имеет следующие аргументы:
- число 1 – обязательный для заполнения аргумент, характеризующий первое числовое значение, для которого необходимо определить моду.
- [число 2] и последующие аргументы являются необязательными для заполнения и характеризуют последующие числовые значения, для которых требуется найти значение моды.
Аргументы модификации функции имеют одинаковый смысл.
Примечания 1:
- Максимальное количество аргументов в рассматриваемых функциях – не более 255.
- Вместо аргументов типа число 1; число 2;…;число n можно указывать массив значений или ссылку на диапазон ячеек.
- В качестве аргументов принимаются объекты данных следующих типов: имена, которые содержат числа, массивы числовых значений и ссылки.
- Все рассматриваемые функции для определения моды игнорируют пустые, логические значения и текстовые строки, содержащиеся в диапазоне значений, переданном в качестве аргумента.
- Если все элементы массива или диапазона чисел, переданных в качестве аргументов для всех трех функций являются уникальными (повторяющиеся значения отсутствуют), результатом работы данных функций будет являться код ошибки #Н/Д.
- Если функция МОДА.НСК была использована в качестве обычной функции, будет возвращено единственное значение моды. Для отображения нескольких мод необходимо выделить диапазон ячеек, ввести формулу и ее аргументы, использовать сочетание клавиш Ctrl+Shift+Enter для вывода массива вычисленных результатов.
Примечание 2: функция МОДА была разработана для ранних версий Excel и пока поддерживается новыми версиями программы, однако в последующих версиях поддержка данной функции может быть отменена. Вместо данной функции предлагается использование двух ее аналогов, которые будут рассмотрены ниже.
Примечания 3:
- Для возврата горизонтального массива наиболее встречающихся значений следует использовать запись вида ТРАНСП(МОДА.НСК(число 1; число 2;…;число n).
- МОДА.НСК принадлежит к классу формул массива и может возвращать как одну, так и несколько мод. Для записи в качестве формулы массива необходимо использовать сочетание клавиш Ctrl+Shift+Enter.
Примечание 4: функции МОДА и МОДА.ОДН определяют центральную тенденцию множества чисел в статическом распределении способом определения моды (существуют еще два распространенных способа: поиск среднего значения и медианы), то есть путем поиска элемента, значение которого наиболее часто встречается в определенном наборе чисел.
Содержание
- — Как вычислить моду?
- — Как найти моду в ряду распределения?
- — Как рассчитать медиану в Excel?
- — Как определить моду в статистике пример?
- — Как найти моду графически?
- — Как рассчитывается медиана?
- — Как найти медиану в ряду распределения?
- — Чем является медиана в ряду распределения?
- — Что такое медиана в ряду чисел?
- — Что такое медиана в Excel?
- — Как рассчитать дисперсию в Excel?
- — Как найти медиану по выборке?
- — Что такое мода и медиана в статистике?
- — Как определить медианное значение?
- — Что такое мода в математике?
Выберите диапазон ячеек, равный количеству мод, которые вы хотите найти в наборе данных. Если вы хотите найти три моды, выберите три ячейки. В противном случае, вы увидите количество мод, равное количеству выбранных ячеек. Введите функцию MODE.
Как вычислить моду?
Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел. Модой ряда чисел называется число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды, а может не иметь моды совсем. Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.
Как найти моду в ряду распределения?
Для интервального ряда мода определяется по формуле: Mo=XMo+hMo⋅fMo−fMo−1(fMo−fMo−1)+(fMo−fMo+1), XMo — левая граница модального интервала, hMo — длина модального интервала, fMo−1 — частота премодального интервала, fMo — частота модального интервала, fMo+1 — частота послемодального интервала.
Для определения медианы в MS EXCEL существует одноименная функция МЕДИАНА() , английский вариант MEDIAN(). Медиана не обязательно совпадает со средним значением (mean, average) в выборке . Совпадение имеет место только в том случае, если значения в выборке распределены симметрично относительно среднего .
Как определить моду в статистике пример?
Мода – это то значение в анализируемой совокупности данных, которое встречается чаще других, поэтому нужно посмотреть на частоты значений и отыскать максимальное из них. Например, в наборе данных 3, 4, 6, 7, 3, 5, 3, 4 модой будет значение 3 – повторяется чаще остальных. Это в дискретном ряду, и здесь все просто.
Как найти моду графически?
Моду и медиану в интервальном ряду можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который является в данном случае модальным. Затем правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника.
Как рассчитывается медиана?
Медианой ряда чисел (медианой числового ряда) называется число, стоящее посередине упорядоченного по возрастанию ряда чисел — в случае, если количество чисел нечётное. Если же количество чисел в ряду чётно, то медианой ряда является полусумма двух стоящих посередине чисел упорядоченного по возрастанию ряда.
Как найти медиану в ряду распределения?
(Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле: Ме = (n(число признаков в совокупности) + 1)/2, в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).
Чем является медиана в ряду распределения?
Медиана — это такое значение признака, которое разделяет ранжированный ряд распределения на две равные части — со значениями признака меньше медианы и со значениями признака больше медианы. Для нахождения медианы, нужно отыскать значение признака, которое находится на середине упорядоченного ряда.
Что такое медиана в ряду чисел?
Медиа́на (от лат. mediāna «середина») набора чисел — число, которое находится в середине этого набора, если его упорядочить по возрастанию, то есть такое число, что половина из элементов набора не меньше него, а другая половина не больше.
Что такое медиана в Excel?
Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4. Мода — это число, наиболее часто встречающееся в данном наборе чисел.
Как рассчитать дисперсию в Excel?
Для распределений, представленных в MS EXCEL , дисперсию можно вычислить аналитически, как функцию от параметров распределения. Например, для Биномиального распределения дисперсия равна произведению его параметров: n*p*q. Примечание : Дисперсия, является вторым центральным моментом , обозначается D[X], VAR(х), V(x).
Как найти медиану по выборке?
Для удобства нахождения медианы сначала нужно отсортировать выборку в возрастающем или убывающем порядке {2,5,7,8,10}. Тогда элемент, стоящий ровно посередине, будет медианой.
Что такое мода и медиана в статистике?
В статистике модой называется величина признака (варианта), которая чаще всего встречается в данной совокупности. Медианой в статистике называется варианта, которая находится в середине вариационного ряда. Медиана делит ряд пополам. Обозначают медиану символом.
Как определить медианное значение?
Медиану рассчитывают по определенному правилу. Для начала (после ранжирования данных) находят медианный интервал. Это такой интервал, через который проходит искомое медианное значение. Определяется с помощью накопленной доли ранжированных интервалов.
Что такое мода в математике?
Мода — значение во множестве наблюдений, которое встречается наиболее часто. Иногда в совокупности встречается более чем одна мода (например: 2, 6, 6, 6, 8, 9, 9, 9, 10; мода = 6 и 9). Из структурных средних величин только мода обладает таким уникальным свойством. …
Интересные материалы:
Нужно ли менять старый советский номер?
Нужно ли замазывать номер машины на фото?
Откуда номер телефона 499?
Почему +7 в номере?
Почему Авито скрывает номера?
Почему Gmail просит номер телефона?
Почему говорят что номер набран неправильно?
Почему говорит неправильно набран номер мтс?
Почему говорит номер не существует?
Почему когда я звоню на телефон мне говорят неправильно набран номер?