Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Функция МОБР возвращает обратную матрицу для матрицы, храняной в массиве.
Примечание: Если у вас установлена текущая версия Microsoft 365, можно просто ввести формулу в верхней левой ячейке диапазона вывода и нажать клавишу ВВОД, чтобы подтвердить использование формулы динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.
Синтаксис
МОБР(массив)
Аргументы функции МОБР описаны ниже.
-
Массива Обязательный. Числовой массив с равным количеством строк и столбцов.
Замечания
-
Массив может быть задан как диапазон ячеек, например A1:C3 как массив констант, например {1;2;3: 4;5;6: 7;8;9} или как имя диапазона или массива.
-
Если какие-либо ячейки в массиве пустые или содержат текст, функции МОБР возвращают #VALUE! ошибку «#ВЫЧИС!».
-
МоБР также возвращает #VALUE! если массив не имеет равного числа строк и столбцов.
-
Обратные матрицы, такие как определители, обычно используются для решения систем математических уравнений с несколькими переменными. Произведением матрицы и обратной является матрица удостоверений — квадратный массив, в котором диагональные значения равны 1, а все остальные — 0.
-
В качестве примера вычисления обратной матрицы, рассмотрим массив из двух строк и двух столбцов A1:B2, который содержит буквы a, b, c и d, представляющие любые четыре числа. В таблице приведена обратная матрица для массива A1:B2.
|
Столбец A |
Столбец B |
|
|---|---|---|
|
Строка 1 |
d/(a*d-b*c) |
b/(b*c-a*d) |
|
Строка 2 |
c/(b*c-a*d) |
a/(a*d-b*c) |
-
Функция МОБР производит вычисления с точностью до 16 значащих цифр, что может привести к незначительным ошибкам округления.
-
Некоторые квадратные матрицы невозможно инвертировать и возвращают #NUM! в функции МОБР. Определител непревратимой матрицы 0.
Примеры
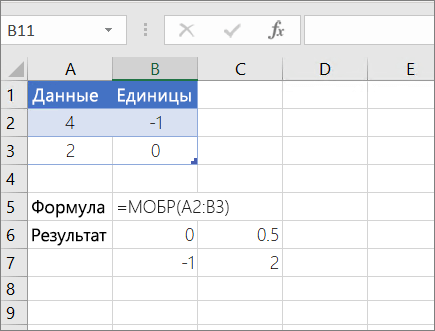
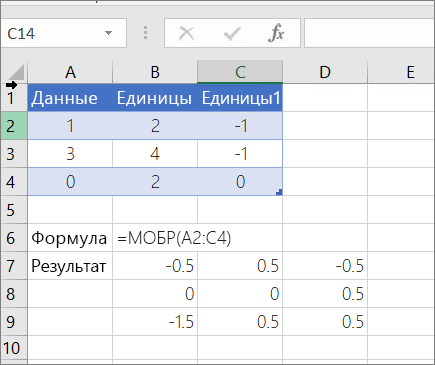
Чтобы указанные выше формулы вычислялись правильно, нужно вводить их в виде формул массивов. После ввода формулы нажмите ввод, если у вас есть текущая Microsoft 365 подписка. в противном случае нажмите CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, возвращается единственный результат.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Нужна дополнительная помощь?
Функция МОБР – это вычислительное определение матрицы. Она возвращает обратную матрицу для матрицы, хранящейся в массиве. Обратные матрицы, как и определители, обычно используются для решения систем уравнений с несколькими неизвестными. Некоторые квадратные матрицы не могут быть обращены: в таких случаях функция МОБР возвращает значение ошибки #ЧИСЛО!. Определитель такой матрицы равен = 0.
Описание использования функции МОБР в Excel
Как использовать функцию МОБР в Excel рассмотрим ниже на примерах. Но сначала ознакомимся как устроена данная функции.
Аргумент функции МОБР – это массив. Он может быть задан как диапазон ячеек, например A1:C3 как массив констант, например {1;2;3:4;5;6:7;8;9} или как имя диапазона или массива. В случае, если хотя бы одна из ячеек массива пуста или содержит текст, функция возвращает значение ошибки #ЗНАЧ!
Массив должен иметь равное количество строк и столбцов. В случае, если они не равны, то функция МОБР также возвращает значение ошибки #ЗНАЧ!
Формулы, которые возвращают массивы, должны быть введены как формулы массива.
Для вывода обратного массива необходимо после выбора диапазона для данной функции нажать комбинацию клавиш Ctrl+Shift+Enter, а не просто Enter.
Функция МОБР производит вычисления с точностью до 16 значащих цифр, что может привести к незначительным ошибкам округления. Рассмотрим применение данной функции на конкретных примерах.
Поиск обратной матрицы в Excel с помощью функции МОБР
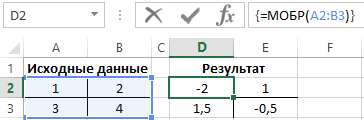
Пример 1. Используя пакет Excel, найти обратную матрицу для матрицы, приведенной в таблице 1.
Таблица 1:
Для решения данной задачи открывает пакет Excel, в произвольной ячейке вводим исходные данные, дальше выбираем функцию МОБР. В качестве массива выбираем диапазон с введенными данными и контролируем полученный результат. В Excel общий вид функции выглядит следующим образом:
Рисунок 1 – Результат расчета.
Как найти валовый показатель по матрице взаимосвязей?
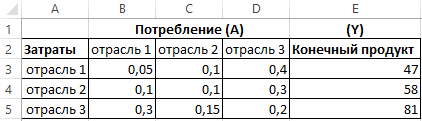
Пример 2. Связь между тремя отраслями представлена матрицей прямых затрат А. Спрос (конечный продукт) задан вектором X. Найти валовой выпуск продукции отраслей Х. Описать используемые формулы, представить распечатку со значениями и с формулами.
Исходные данные приведены на рисунке 2:
Рисунок 2 – Исходные данные.
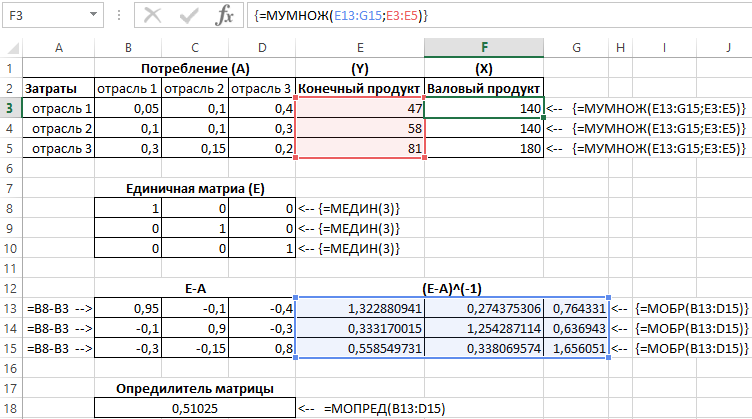
Данная задача связана с определением объема производства каждой из N отраслей, чтобы удовлетворить все потребности в продукции данной отрасли. При этом каждая отрасль выступает и как производитель некоторой продукции и как потребитель своей и произведенной другими отраслями продукции. Задача межотраслевого баланса – отыскание такого вектора валового выпуска X, который при известной матрице прямых затрат обеспечивает заданный вектор конечного продукта Y.
Матричное решение данной задачи:
X = ( E — A )-1 Y
где Е – единична матрица.
Для решения задачи в примере используем следующие 4 функции для работы с матрицами в Excel:
- МОБР – нахождение обратной матрицы.
- МУМНОЖ – умножение матриц.
- МОПРЕД – нахождение определителя матрицы.
- МЕДИН – нахождение единичной матрицы.
Результаты приведены на рисунке 3:
Рисунок 3 – Результат вычислений.
Функция МОБР возвращает ошибку #ЧИСЛО!
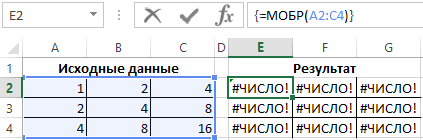
Пример 3. Найти обратную матрицу для матрицы, приведенной в таблице 2.
Таблица 2:
| Исходные данные | ||
| 1 | 2 | 4 |
| 2 | 4 | 8 |
| 4 | 8 | 16 |
Результат решения приведен на рисунке 4. Видно, что определитель данной матрицы равен 0, поэтому функция МОБР выводит в результате значение #ЧИСЛО!.
Рисунок 4 – Окончательный результат.
Содержание
- Выполнение расчетов
- Расчет определителя
- Расчет обратной матрицы
- Вопросы и ответы
Приложение Excel выполняет целый ряд вычислений, связанных с матричными данными. Программа обрабатывает их, как диапазон ячеек, применяя к ним формулы массива. Одно из таких действий – это нахождение обратной матрицы. Давайте выясним, что представляет собой алгоритм данной процедуры.
Выполнение расчетов
Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.
Расчет определителя
Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.
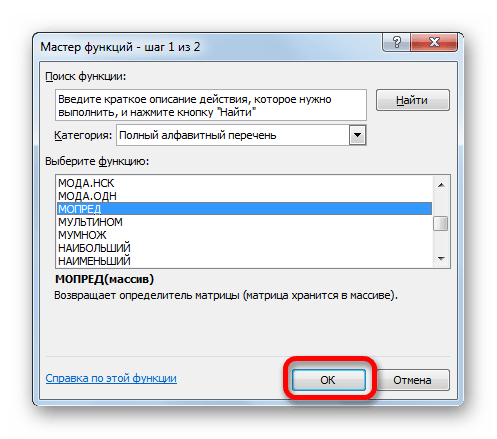
- Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.
- Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
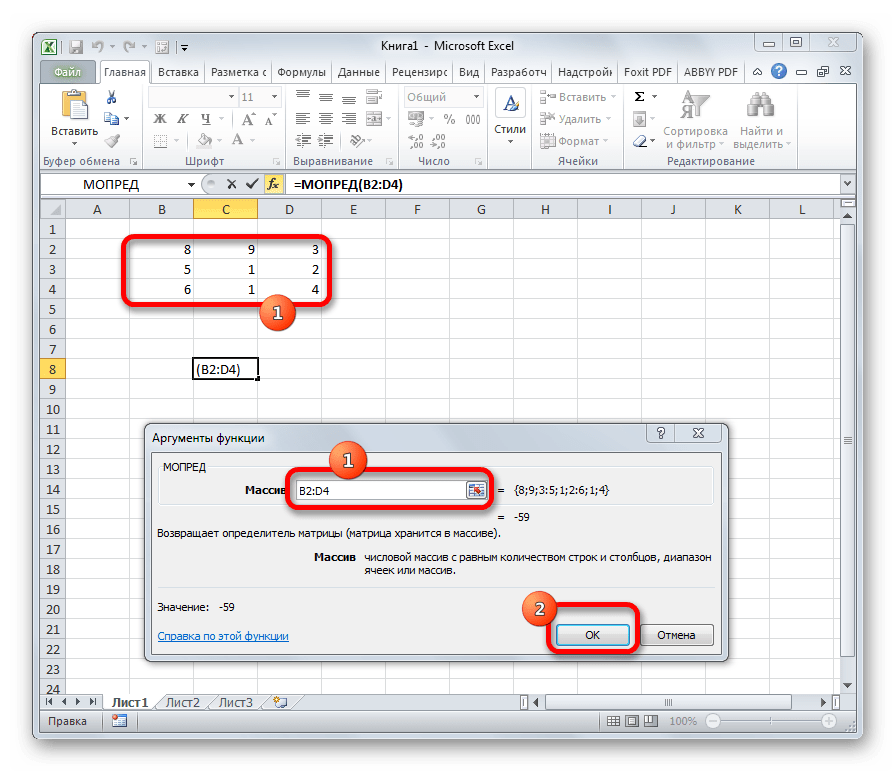
- Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».
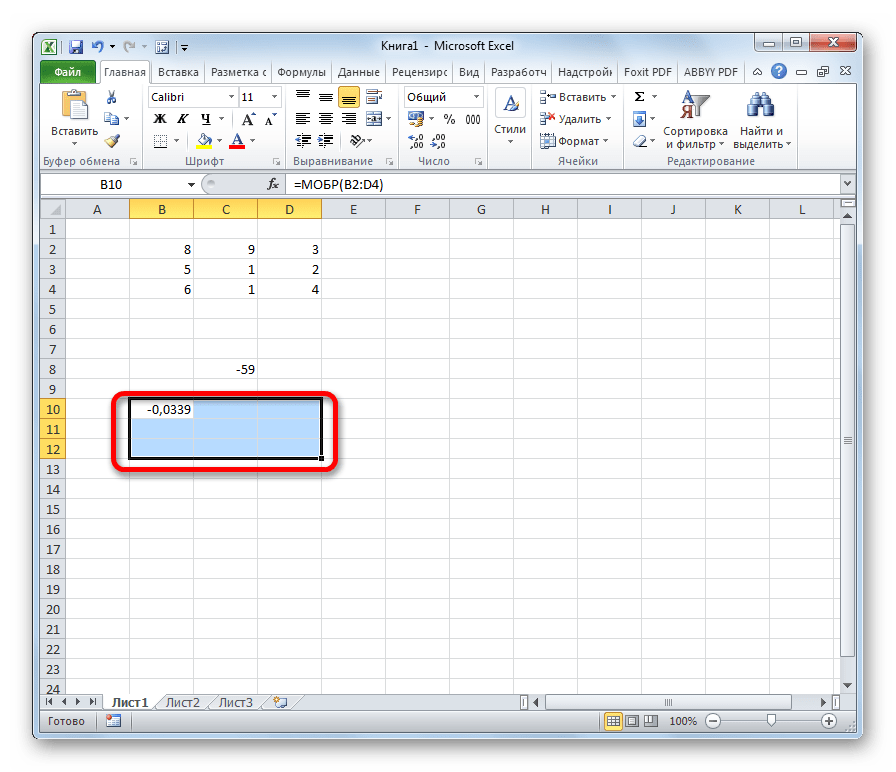
- Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.
Расчет обратной матрицы
Теперь можно преступить к непосредственному расчету обратной матрицы.
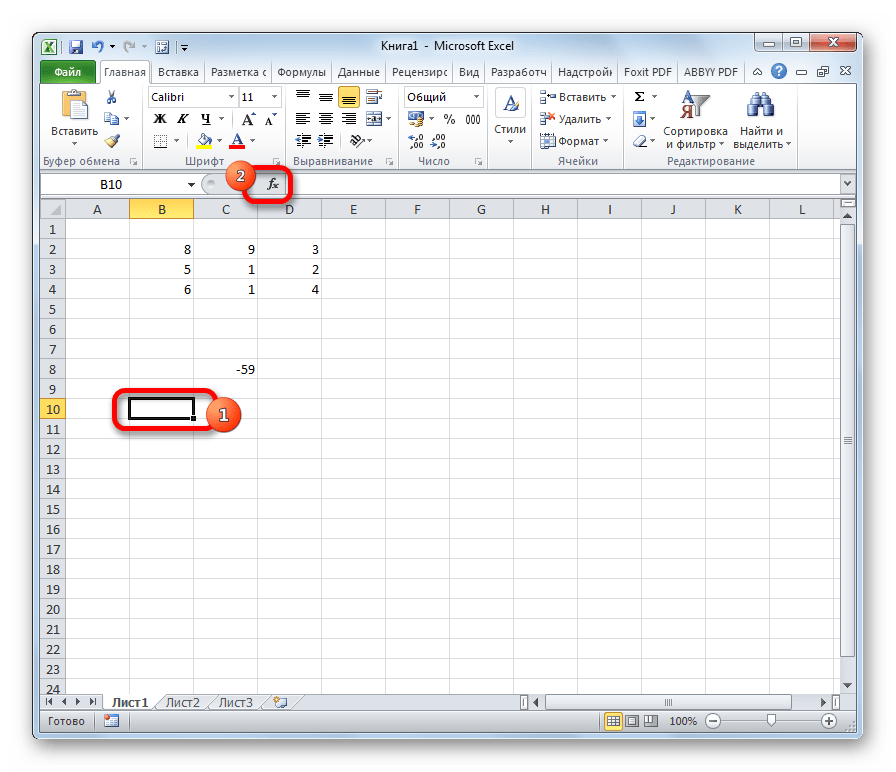
- Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
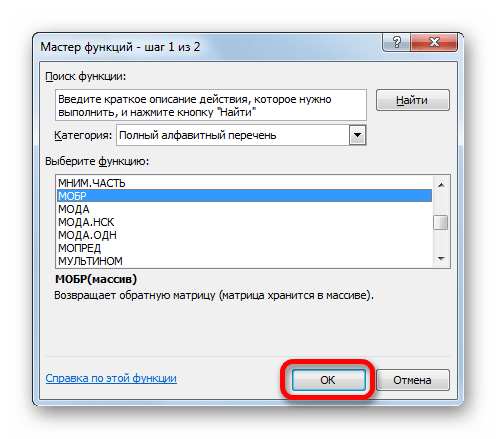
- В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».
- В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».
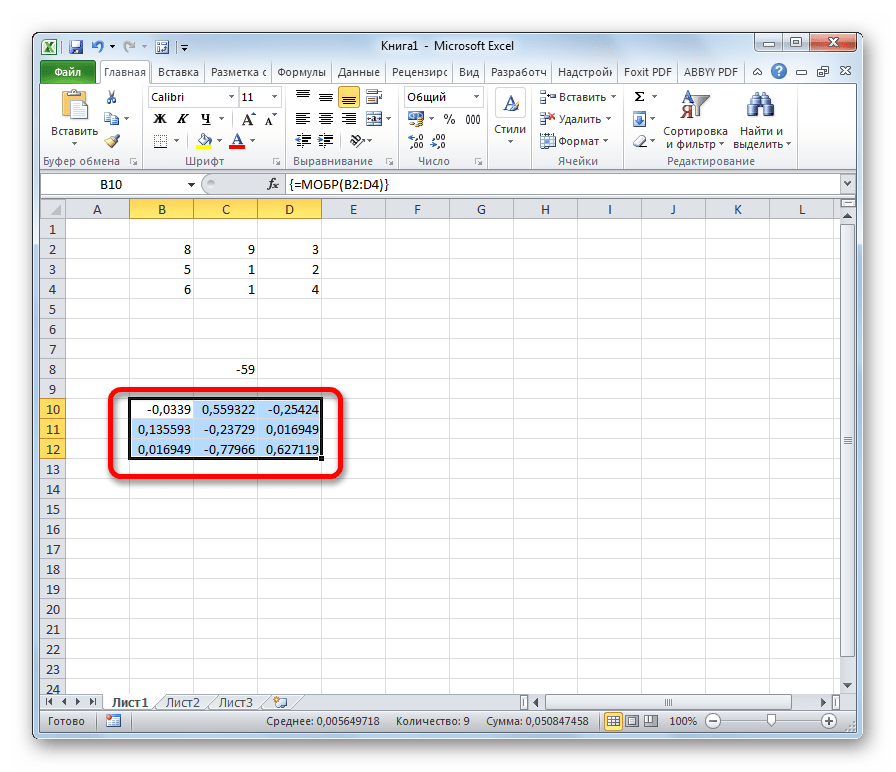
- Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
- Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.
На этом расчет можно считать завершенным.
Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.
Еще статьи по данной теме:
Помогла ли Вам статья?
Для вычисления обратной матрицы в MS EXCEL существует специальная функция
МОБР()
или англ.
MINVERSE
.
Понятие обратной матрицы определено только для квадратных матриц, определитель которых отличен от нуля.
СОВЕТ
: О нахождении определителя матрицы читайте статью
Вычисление определителя матрицы в MS EXCEL
Матрица А
-1
называется обратной для исходной матрицы А порядка n, если
справедливы равенства
А
-1
*А=Е и А*А
-1
=Е, где Е единичная матрица порядка n.
Для вычисления обратной матрицы в MS EXCEL существует специальная функция
МОБР()
.
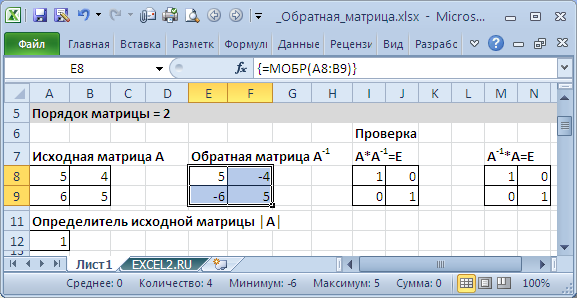
Если элементы исходной матрицы 2 х 2 расположены в диапазоне
А8:В9
, то для получения
транспонированной матрицы
нужно (см.
файл примера
):
-
выделить диапазон 2 х 2, который не пересекается с исходным диапазоном
А8:В9
,
например,
Е8:F9
-
в
Cтроке формул
ввести формулу
=
МОБР
(A8:B9)
и нажать комбинацию клавиш
CTRL+SHIFT+ENTER
, т.е. нужно ввести ее какформулу массива
(формулу можно ввести прямо в ячейку, предварительно нажав клавишу
F2
)
Если матрица большей размерности, то перед вводом формулы нужно выделить соответственно больший диапазон ячеек.
Массив может быть задан не только как интервал ячеек, например
A8:B9
, но и как
массив констант
, например
=МОБР({5;4: 3;2})
. Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией. Массив в этом случае указывается по строкам: например, сначала первая строка 5;4, затем через двоеточие записывается следующая строка 3;2. Элементы отделяются точкой с запятой.
Ссылка на массив также может быть указана как ссылка на
именованный диапазон
.
Некоторые квадратные матрицы не могут быть обращены: в таких случаях функция
МОБР()
возвращает значение ошибки #ЧИСЛО!. Матрицы не могут быть обращены, у которых определитель равен 0.
Если функция
МОБР()
вернула значение ошибки #ЗНАЧ!, то либо число строк в массиве не равно числу столбцов, либо какая-либо из ячеек в массиве пуста или содержит текст. Т.е. функция
МОБР()
пустую ячейку воспринимает не как содержащую 0 (как например, это делает
СУММ()
), а как ошибочное значение.
Вычисление обратной матрицы с помощью матрицы из алгебраических дополнений
СОВЕТ
: Этот раздел стоит читать только продвинутым пользователям MS EXCEL. Кроме того материал представляет только академический интерес, т.к. есть функция
МОБР()
.
В
файле примера
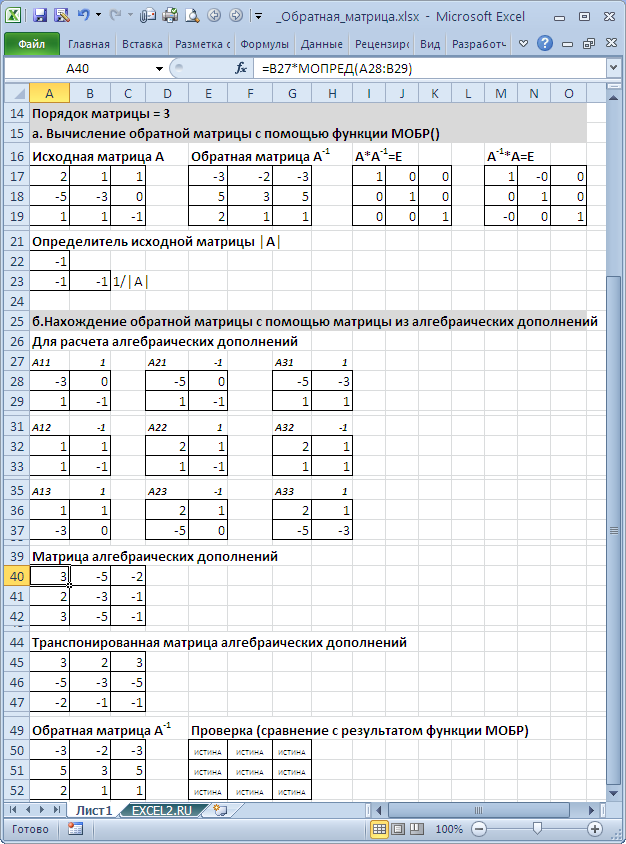
приведен расчет обратной матрицы 3-го порядка через матрицу алгебраических дополнений.
Порядок действий при вычислении обратной матрицы:
-
Вычисляем определитель
матрицы
А
(далее — Det(A)) и убеждаемся, что он отличен от нуля (в противном случае матрица
А
необратима) - Строим матрицу из алгебраических дополнений элементов исходной матрицы
-
Транспонируем матрицу
из алгебраических дополнений
-
Умножаем каждый элемент транспонированной матрицы
из алгебраических дополнений на 1/Det(A) и получаем обратную матрицу
В качестве проверки можно
перемножить исходную и обратную матрицы
. В результате должна получиться единичная матрица.
Функция МОБР возвращает обратную матрицу для матрицы, хранящейся в массиве.
Описание функции МОБР
Возвращает обратную матрицу для матрицы, хранящейся в массиве.
Синтаксис
=МОБР(массив)Аргументы
массив
Обязательный аргумент. Числовой массив с равным количеством строк и столбцов.
Замечания
- Массив может быть задан как диапазон ячеек, например A1:C3 как массив констант, например {1;2;3: 4;5;6: 7;8;9} или как имя диапазона или массива.
- Если хотя бы одна из ячеек массива пуста или содержит текст, функция МОБР возвращает значение ошибки #ЗНАЧ!.
- Функция МОБР также возвращает значение ошибки #ЗНАЧ!, если число строк в массиве не равно числу столбцов.
- Формулы, которые возвращают массивы, должны быть введены как формулы массива.
- Обратные матрицы, как и определители, обычно используются для решения систем уравнений с несколькими неизвестными. Произведение матрицы на ее обратную — это единичная матрица, т. е. квадратный массив, у которого диагональные элементы равны 1, а все остальные — 0.
- В качестве примера вычисления обратной матрицы, рассмотрим массив из двух строк и двух столбцов A1:B2, который содержит буквы a, b, c и d, представляющие любые четыре числа. В таблице приведена обратная матрица для массива A1:B2.
Столбец A Столбец B Строка 1 d/(a*d-b*c) b/(b*c-a*d) Строка 2 c/(b*c-a*d) a/(a*d-b*c) - Функция МОБР производит вычисления с точностью до 16 значащих цифр, что может привести к незначительным ошибкам округления.
- Некоторые квадратные матрицы не могут быть обращены: в таких случаях функция МОБР возвращает значение ошибки #ЧИСЛО!. Определитель такой матрицы равен 0.
Примеры
Для правильной работы формулу нужно ввести в приложении Excel как формулу массива, с помощью клавиш Ctrl+Shift+Enter.
Пример1Пример2
Исходная матрица:
Для нахождения обратной необходимо в одну из ячеек ввести формулу и потом выделить количество ячеек, которое соответсвует первоначальному (для нахождения обратной матрицы количество строк и столбцов должно совпадать) поставить курсор в строку формул и нажать Ctrl+Shift+Enter.
Результат:
Полностью заполненное решение нахождения обратной матрицы выглядит следующим образом:

И скрин с формулами: