Содержание
- Обратная матрица в Excel
- Как найти обратную матрицу в Excel?
- Функция МОБР
- Вычисление обратной матрицы в Microsoft Excel
- Выполнение расчетов
- Расчет определителя
- Расчет обратной матрицы
- Вычисление обратной матрицы в EXCEL
- Вычисление обратной матрицы с помощью матрицы из алгебраических дополнений
- Функция МОБР
- Синтаксис
- Замечания
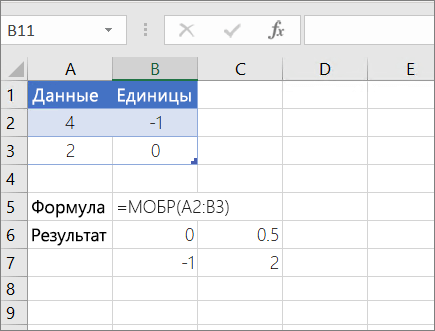
- Примеры
- Дополнительные сведения
- Функция МОПРЕД
- Описание
- Синтаксис
- Замечания
- Пример
Обратная матрица в Excel
Подробно рассмотрим особенности вычисления обратной матрицы в Excel и примеры использования функции МОБР.
В первую очередь освежим в памяти, что обратная матрица — это матрица (записывается как A -1 ), при умножении которой на исходную матрицу (A) дает единичную матрицу (E), другими словами выполняется формула:
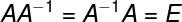
Из определения следует важное свойство, что обратная матрица определена только для квадратных (т.е. число строк и столбцов совпадает) и невырожденных матриц (т.е. определитель отличен от нуля).
Как найти обратную матрицу в Excel?
В отличие от транспонированной матрицы, вычислить обратную матрицу технически несколько сложнее.
Посчитать обратную матрицу можно через построение матриц алгебраических дополнений и определителя исходной матрицы.
Однако сложность вычисления по данному алгоритму имеет квадратичную зависимость от порядка матрицы.
К примеру, для обращения квадратной матрицы 3-го порядка нам необходимо будет дополнительно сделать 9 матриц алгебраических дополнений, транспонировать итоговую созданную матрицу и поэлементно разделить на определитель начальной матрицы, что затрудняет возможность подобного расчета в Excel.
Поэтому воспользуемся стандартной функцией МОБР, которая позволит найти обратную матрицу:
Функция МОБР
Синтаксис и описание функции МОБР в Excel:
МОБР(массив)
Возвращает обратную матрицу (матрица хранится в массиве).
- Массив(обязательный аргумент) — числовой массив, содержащий матрицу с одинаковым числом столбцов и строк.
Рассмотрим расчет обратной матрицы посредством функции МОБР на конкретном примере.
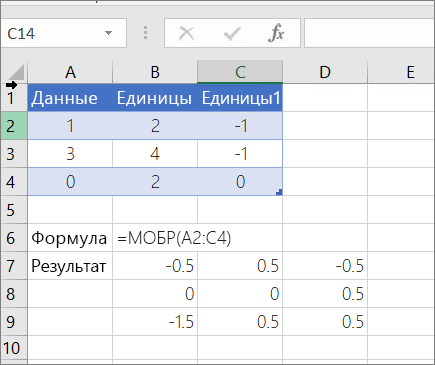
Предположим у нас имеется следующая квадратная матрица 3-го порядка:
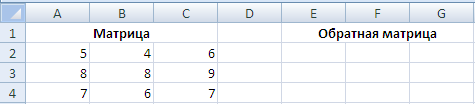
Выделяем диапазон пустых ячеек E2:G4, куда мы в дальнейшем поместим обратную матрицу.
Не снимая выделения ячеек вводим формулу =МОБР(A2:C4) и нажимаем комбинацию клавиш Ctrl + Shift + Ввод для расчета формулы массива по данному диапазону:
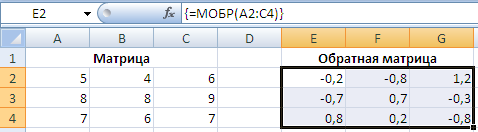
При работе с функцией МОБР могут возникнуть следующие ошибки:
- В том случае, когда исходная матрица является вырожденной (определитель равен нулю), то функция вернет ошибку #ЧИСЛО!;
- Если число строк и столбцов в матрице не совпадает, то функция возвратит ошибку #ЗНАЧ!;
- Функция также вернет ошибку #ЗНАЧ!, если хотя бы один из элементов матрицы является пустым или записан в текстовом виде.
Источник
Вычисление обратной матрицы в Microsoft Excel
Приложение Excel выполняет целый ряд вычислений, связанных с матричными данными. Программа обрабатывает их, как диапазон ячеек, применяя к ним формулы массива. Одно из таких действий – это нахождение обратной матрицы. Давайте выясним, что представляет собой алгоритм данной процедуры.
Выполнение расчетов
Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.
Расчет определителя
Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.
- Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.
Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
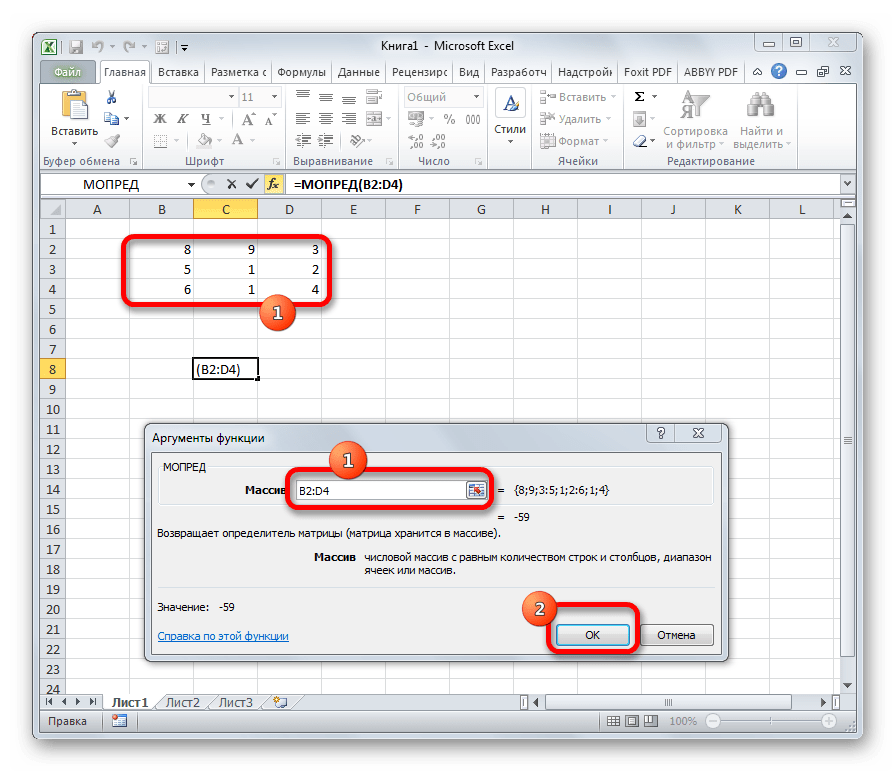
Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».
Расчет обратной матрицы
Теперь можно преступить к непосредственному расчету обратной матрицы.
- Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».
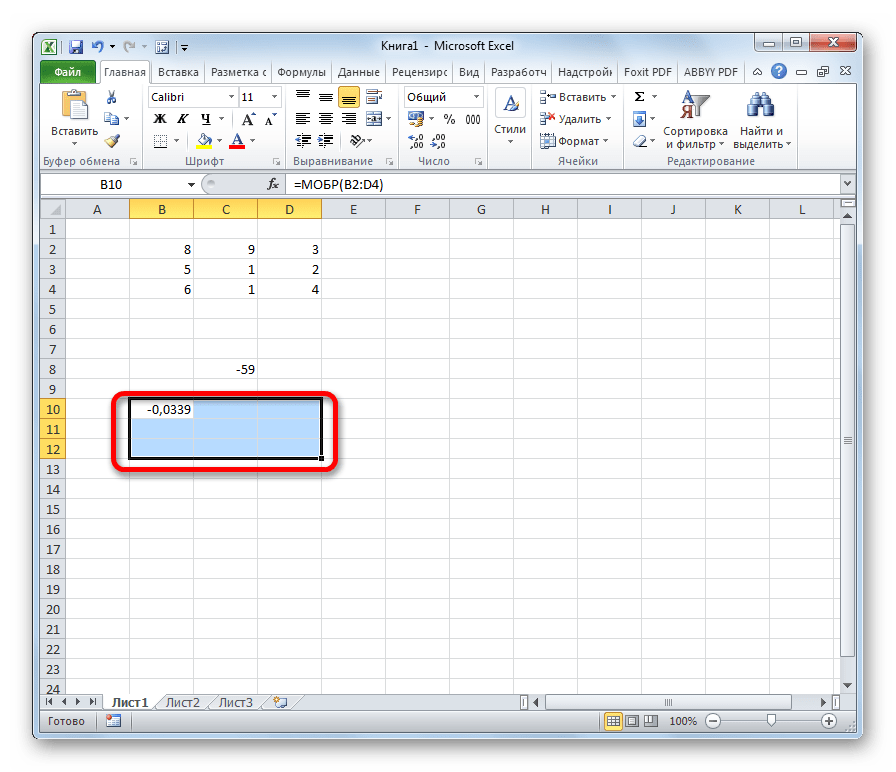
Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
На этом расчет можно считать завершенным.
Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.
Помимо этой статьи, на сайте еще 12333 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Источник
Вычисление обратной матрицы в EXCEL
history 7 декабря 2015 г.
Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР() или англ. MINVERSE .
Понятие обратной матрицы определено только для квадратных матриц, определитель которых отличен от нуля.
СОВЕТ : О нахождении определителя матрицы читайте статью Вычисление определителя матрицы в MS EXCEL
Матрица А -1 называется обратной для исходной матрицы А порядка n, если справедливы равенства А -1 *А=Е и А*А -1 =Е, где Е единичная матрица порядка n.
Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР() .
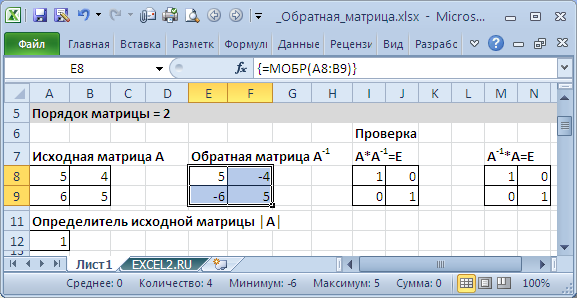
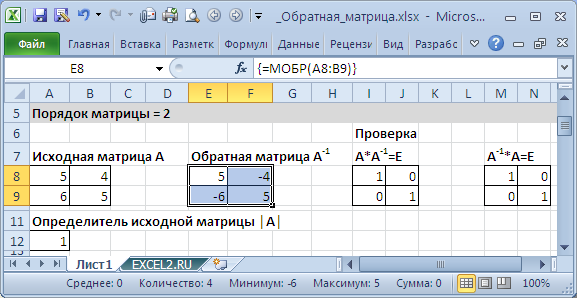
Если элементы исходной матрицы 2 х 2 расположены в диапазоне А8:В9 , то для получения транспонированной матрицы нужно (см. файл примера ):
- выделить диапазон 2 х 2, который не пересекается с исходным диапазоном А8:В9 , например, Е8:F9
- в Cтроке формул ввести формулу = МОБР (A8:B9) и нажать комбинацию клавиш CTRL+SHIFT+ENTER , т.е. нужно ввести ее как формулу массива (формулу можно ввести прямо в ячейку, предварительно нажав клавишу F2 )
Если матрица большей размерности, то перед вводом формулы нужно выделить соответственно больший диапазон ячеек.
Массив может быть задан не только как интервал ячеек, например A8:B9 , но и как массив констант , например =МОБР(<5;4: 3;2>) . Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией. Массив в этом случае указывается по строкам: например, сначала первая строка 5;4, затем через двоеточие записывается следующая строка 3;2. Элементы отделяются точкой с запятой.
Ссылка на массив также может быть указана как ссылка на именованный диапазон .
Некоторые квадратные матрицы не могут быть обращены: в таких случаях функция МОБР() возвращает значение ошибки #ЧИСЛО!. Матрицы не могут быть обращены, у которых определитель равен 0.
Если функция МОБР() вернула значение ошибки #ЗНАЧ!, то либо число строк в массиве не равно числу столбцов, либо какая-либо из ячеек в массиве пуста или содержит текст. Т.е. функция МОБР() пустую ячейку воспринимает не как содержащую 0 (как например, это делает СУММ() ), а как ошибочное значение.
Вычисление обратной матрицы с помощью матрицы из алгебраических дополнений
СОВЕТ : Этот раздел стоит читать только продвинутым пользователям MS EXCEL. Кроме того материал представляет только академический интерес, т.к. есть функция МОБР() .
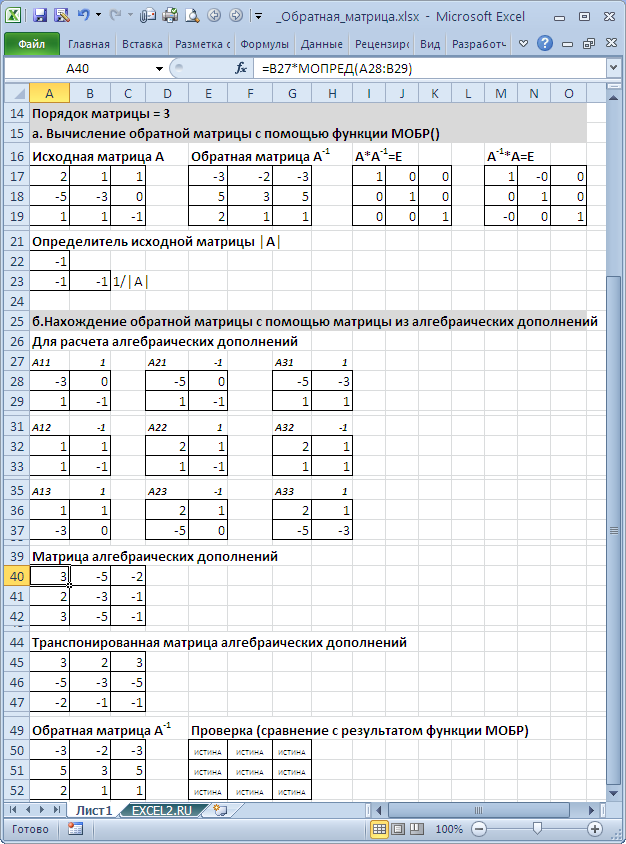
В файле примера приведен расчет обратной матрицы 3-го порядка через матрицу алгебраических дополнений.
Порядок действий при вычислении обратной матрицы:
- Вычисляем определитель матрицы А (далее — Det(A)) и убеждаемся, что он отличен от нуля (в противном случае матрица А необратима)
- Строим матрицу из алгебраических дополнений элементов исходной матрицы
- Транспонируем матрицу из алгебраических дополнений
- Умножаем каждый элемент транспонированной матрицы из алгебраических дополнений на 1/Det(A) и получаем обратную матрицу
В качестве проверки можно перемножить исходную и обратную матрицы . В результате должна получиться единичная матрица.
Источник
Функция МОБР
Функция МОБР возвращает обратную матрицу для матрицы, храняной в массиве.
Примечание: Если у вас установлена текущая версия Microsoft 365, можно просто ввести формулу в верхней левой ячейке диапазона вывода и нажать клавишу ВВОД, чтобы подтвердить использование формулы динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.
Синтаксис
Аргументы функции МОБР описаны ниже.
Массива Обязательный. Числовой массив с равным количеством строк и столбцов.
Замечания
Массив может быть задан как диапазон ячеек, например A1:C3 как массив констант, например <1;2;3: 4;5;6: 7;8;9>или как имя диапазона или массива.
Если какие-либо ячейки в массиве пустые или содержат текст, функции МОБР возвращают #VALUE! ошибку «#ВЫЧИС!».
МоБР также возвращает #VALUE! если массив не имеет равного числа строк и столбцов.
Обратные матрицы, такие как определители, обычно используются для решения систем математических уравнений с несколькими переменными. Произведением матрицы и обратной является матрица удостоверений — квадратный массив, в котором диагональные значения равны 1, а все остальные — 0.
В качестве примера вычисления обратной матрицы, рассмотрим массив из двух строк и двух столбцов A1:B2, который содержит буквы a, b, c и d, представляющие любые четыре числа. В таблице приведена обратная матрица для массива A1:B2.
Функция МОБР производит вычисления с точностью до 16 значащих цифр, что может привести к незначительным ошибкам округления.
Некоторые квадратные матрицы невозможно инвертировать и возвращают #NUM! в функции МОБР. Определител непревратимой матрицы 0.
Примеры
Чтобы указанные выше формулы вычислялись правильно, нужно вводить их в виде формул массивов. После ввода формулы нажмите ввод, если у вас есть текущая Microsoft 365 подписка. в противном случае нажмите CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, возвращается единственный результат.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Источник
Функция МОПРЕД
В этой статье описаны синтаксис формулы и использование MDETERM в Microsoft Excel.
Описание
Возвращает определитель матрицы (матрица хранится в массиве).
Синтаксис
Аргументы функции МОПРЕД описаны ниже.
Массив Обязательный. Числовой массив с равным количеством строк и столбцов.
Замечания
Массив может быть задан как интервал ячеек, например A1:C3, как массив констант, например <1;2;3:4;5;6:7;8;9>, как имя для интервала или массива.
Функция МОПРЕД возвращает значение ошибки #ЗНАЧ! в случаях, указанных ниже.
Если какая-либо ячейка в массиве пуста или содержит текст.
Если количество строк в массиве не равно количеству столбцов.
Определитель матрицы — это число, вычисляемое на основе значений элементов массива. Для массива A1:C3, состоящего из трех строк и трех столбцов, определитель вычисляется следующим образом:
МОПРЕД(A1:C3)
равно A1*(B2*C3-B3*C2) + A2*(B3*C1-B1*C3) + A3*(B1*C2-B2*C1)
Определители матриц обычно используются при решении систем уравнений с несколькими неизвестными.
Функция МОПРЕД производит вычисления с точностью примерно 16 значащих цифр, что может в некоторых случаях приводить к незначительным ошибкам. Например, определитель сингулярной матрицы отличается от нуля на 1E-16.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Источник
Функция МОБР – это вычислительное определение матрицы. Она возвращает обратную матрицу для матрицы, хранящейся в массиве. Обратные матрицы, как и определители, обычно используются для решения систем уравнений с несколькими неизвестными. Некоторые квадратные матрицы не могут быть обращены: в таких случаях функция МОБР возвращает значение ошибки #ЧИСЛО!. Определитель такой матрицы равен = 0.
Описание использования функции МОБР в Excel
Как использовать функцию МОБР в Excel рассмотрим ниже на примерах. Но сначала ознакомимся как устроена данная функции.
Аргумент функции МОБР – это массив. Он может быть задан как диапазон ячеек, например A1:C3 как массив констант, например {1;2;3:4;5;6:7;8;9} или как имя диапазона или массива. В случае, если хотя бы одна из ячеек массива пуста или содержит текст, функция возвращает значение ошибки #ЗНАЧ!
Массив должен иметь равное количество строк и столбцов. В случае, если они не равны, то функция МОБР также возвращает значение ошибки #ЗНАЧ!
Формулы, которые возвращают массивы, должны быть введены как формулы массива.
Для вывода обратного массива необходимо после выбора диапазона для данной функции нажать комбинацию клавиш Ctrl+Shift+Enter, а не просто Enter.
Функция МОБР производит вычисления с точностью до 16 значащих цифр, что может привести к незначительным ошибкам округления. Рассмотрим применение данной функции на конкретных примерах.
Поиск обратной матрицы в Excel с помощью функции МОБР
Пример 1. Используя пакет Excel, найти обратную матрицу для матрицы, приведенной в таблице 1.
Таблица 1:
Для решения данной задачи открывает пакет Excel, в произвольной ячейке вводим исходные данные, дальше выбираем функцию МОБР. В качестве массива выбираем диапазон с введенными данными и контролируем полученный результат. В Excel общий вид функции выглядит следующим образом:
Рисунок 1 – Результат расчета.
Как найти валовый показатель по матрице взаимосвязей?
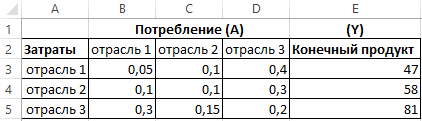
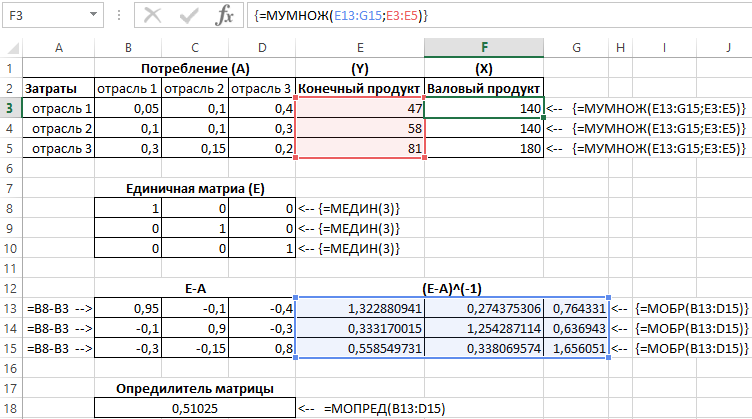
Пример 2. Связь между тремя отраслями представлена матрицей прямых затрат А. Спрос (конечный продукт) задан вектором X. Найти валовой выпуск продукции отраслей Х. Описать используемые формулы, представить распечатку со значениями и с формулами.
Исходные данные приведены на рисунке 2:
Рисунок 2 – Исходные данные.
Данная задача связана с определением объема производства каждой из N отраслей, чтобы удовлетворить все потребности в продукции данной отрасли. При этом каждая отрасль выступает и как производитель некоторой продукции и как потребитель своей и произведенной другими отраслями продукции. Задача межотраслевого баланса – отыскание такого вектора валового выпуска X, который при известной матрице прямых затрат обеспечивает заданный вектор конечного продукта Y.
Матричное решение данной задачи:
X = ( E — A )-1 Y
где Е – единична матрица.
Для решения задачи в примере используем следующие 4 функции для работы с матрицами в Excel:
- МОБР – нахождение обратной матрицы.
- МУМНОЖ – умножение матриц.
- МОПРЕД – нахождение определителя матрицы.
- МЕДИН – нахождение единичной матрицы.
Результаты приведены на рисунке 3:
Рисунок 3 – Результат вычислений.
Функция МОБР возвращает ошибку #ЧИСЛО!
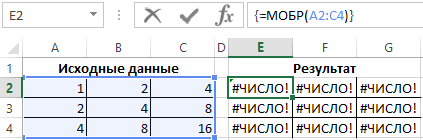
Пример 3. Найти обратную матрицу для матрицы, приведенной в таблице 2.
Таблица 2:
| Исходные данные | ||
| 1 | 2 | 4 |
| 2 | 4 | 8 |
| 4 | 8 | 16 |
Результат решения приведен на рисунке 4. Видно, что определитель данной матрицы равен 0, поэтому функция МОБР выводит в результате значение #ЧИСЛО!.
Рисунок 4 – Окончательный результат.
Содержание
- Выполнение расчетов
- Расчет определителя
- Расчет обратной матрицы
- Вопросы и ответы
Приложение Excel выполняет целый ряд вычислений, связанных с матричными данными. Программа обрабатывает их, как диапазон ячеек, применяя к ним формулы массива. Одно из таких действий – это нахождение обратной матрицы. Давайте выясним, что представляет собой алгоритм данной процедуры.
Выполнение расчетов
Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.
Расчет определителя
Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.
- Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.
- Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
- Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».
- Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.
Расчет обратной матрицы
Теперь можно преступить к непосредственному расчету обратной матрицы.
- Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
- В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».
- В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».
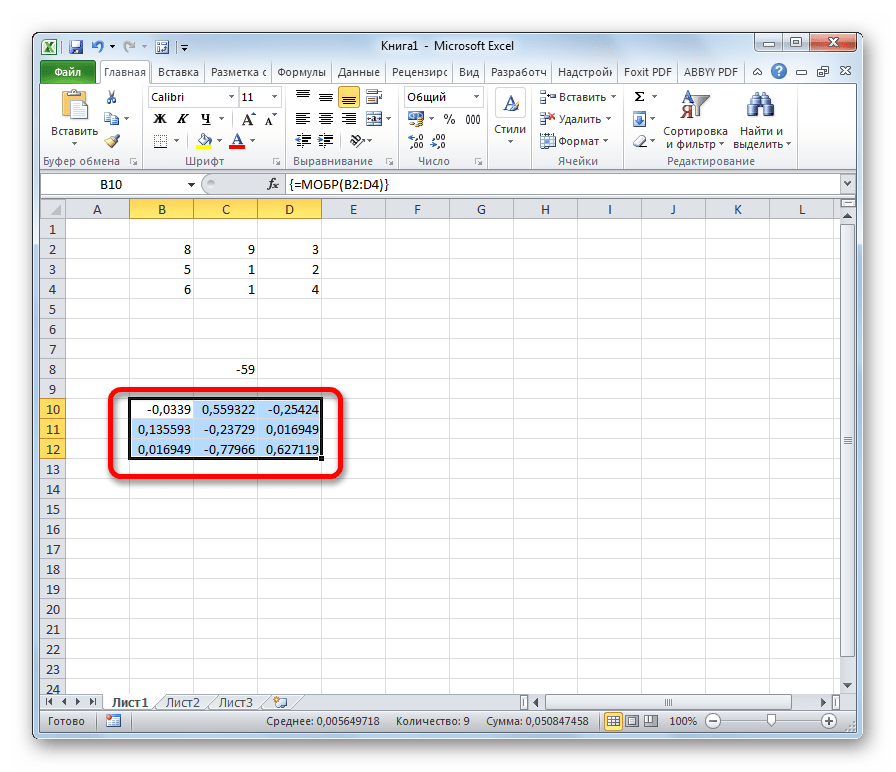
- Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
- Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.
На этом расчет можно считать завершенным.
Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.
Еще статьи по данной теме:
Помогла ли Вам статья?
Excel обладает мощным инструментарием, позволяющим выполнять множество математических, статистических, логических и прочих задач. В программе также можно выполнить такое действие, как нахождение обратной матрицы. Ниже мы на практическом примере рассмотрим, как именно это сделать.
Примечание: Найти обратную матрицу можно только при условии, что исходная является квадратной (количество столбцов и строк одинаковое). К тому же, ее определитель не должен равняться цифре 0.
Этап 1. Вычисляем определитель
В программе данное действие выполняется с помощью функции МОПРЕД.
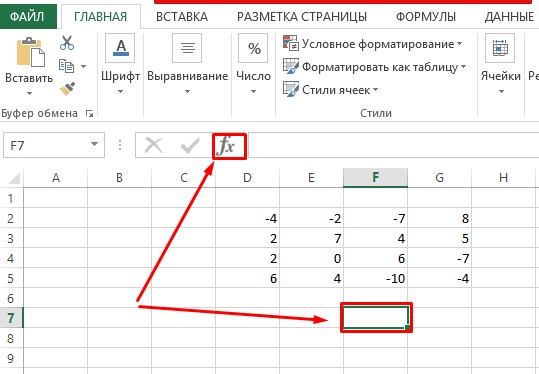
- Переходим в свободную ячейку, в которой планируем производить расчеты, после чего кликаем по кнопке “Вставить функцию” (fx) слева от строки формул.
- В открывшемся окне вставки функций выбираем категорию “Математические”, в которой кликаем по оператору “МОПРЕД”, затем – по кнопке OK.
- В следующем окне нужно заполнить единственный аргумент функции – “Массив”, в значении которого указываем координаты нашей матрицы. Сделать это можно вручную, прописав адреса ячеек, используя клавиши клавиатуры. Либо можно сначала кликнуть внутри области ввода информации, затем зажав левую кнопку мыши выделить диапазон ячеек непосредственно в самой таблице. Когда все готово, нажимаем кнопку OK.
- В выбранной ячейке отобразился результат, а именно, определитель матрицы. С учетом наших данных получилось число 157894, что значит, что у нашей матрицы обратная матрица существует, так как определитель не равен нулю.
Этап 2. Находим обратную матрицу
Итак, после того, как мы вычислили, что определитель матрицы не равен нулю, можно приступить к нахождению обратной.
- Встаем в ячейку, которая станет самым верхним левым элементом новой обратной матрицы. Заходим в окно Вставки функции, нажав на соответствующую кнопку.
- В категории “Математические” выбираем функцию “МОБР”, после чего щелкаем по кнопке OK.
- Аналогично заполнению значения аргумента “Массив” для функции МОПРЕД, рассмотренной в первом разделе, указываем координаты первичной матрицы, после чего нажимаем OK.
- Получаем требуемый результат в выбранной ячейке.
- Чтобы скопировать функцию в другие ячейки, выделяем область, которая совпадает по количеству столбцов и строк с начальной матрицей. Затем нажимаем клавишу F2 на клавиатуре, после чего жмем комбинацию Ctrl+Shift+Enter.
- Все готово. В результате выполненных действий нам удалось найти обратную матрицу.
Заключение
Нахождение обратной матрицы – не такая распространенная математическая задача, как, например, сложение, вычитание, умножение, деление, расчеты с процентами и т.д. Но, если все же возникнет такая потребность, вовсе необязательно делать это вручную на листке бумаги, ведь Эксель позволяет быстро и безошибочно справиться с этой задачей.
history 7 декабря 2015 г.
-
Группы статей
- Матрицы
Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР() или англ. MINVERSE .
Понятие обратной матрицы определено только для квадратных матриц, определитель которых отличен от нуля.
СОВЕТ : О нахождении определителя матрицы читайте статью Вычисление определителя матрицы в MS EXCEL
Матрица А -1 называется обратной для исходной матрицы А порядка n, если справедливы равенства А -1 *А=Е и А*А -1 =Е, где Е единичная матрица порядка n.
Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР() .
Если элементы исходной матрицы 2 х 2 расположены в диапазоне А8:В9 , то для получения транспонированной матрицы нужно (см. файл примера ):
- выделить диапазон 2 х 2, который не пересекается с исходным диапазоном А8:В9 , например, Е8:F9
- в Cтроке формул ввести формулу = МОБР (A8:B9) и нажать комбинацию клавиш CTRL+SHIFT+ENTER , т.е. нужно ввести ее как формулу массива (формулу можно ввести прямо в ячейку, предварительно нажав клавишу F2 )
Если матрица большей размерности, то перед вводом формулы нужно выделить соответственно больший диапазон ячеек.
Массив может быть задан не только как интервал ячеек, например A8:B9 , но и как массив констант , например =МОБР(<5;4: 3;2>) . Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией. Массив в этом случае указывается по строкам: например, сначала первая строка 5;4, затем через двоеточие записывается следующая строка 3;2. Элементы отделяются точкой с запятой.
Ссылка на массив также может быть указана как ссылка на именованный диапазон .
Некоторые квадратные матрицы не могут быть обращены: в таких случаях функция МОБР() возвращает значение ошибки #ЧИСЛО!. Матрицы не могут быть обращены, у которых определитель равен 0.
Если функция МОБР() вернула значение ошибки #ЗНАЧ!, то либо число строк в массиве не равно числу столбцов, либо какая-либо из ячеек в массиве пуста или содержит текст. Т.е. функция МОБР() пустую ячейку воспринимает не как содержащую 0 (как например, это делает СУММ() ), а как ошибочное значение.
Вычисление обратной матрицы с помощью матрицы из алгебраических дополнений
СОВЕТ : Этот раздел стоит читать только продвинутым пользователям MS EXCEL. Кроме того материал представляет только академический интерес, т.к. есть функция МОБР() .
В файле примера приведен расчет обратной матрицы 3-го порядка через матрицу алгебраических дополнений.
Порядок действий при вычислении обратной матрицы:
- Вычисляем определитель матрицы А (далее — Det(A)) и убеждаемся, что он отличен от нуля (в противном случае матрица А необратима)
- Строим матрицу из алгебраических дополнений элементов исходной матрицы
- Транспонируем матрицу из алгебраических дополнений
- Умножаем каждый элемент транспонированной матрицы из алгебраических дополнений на 1/Det(A) и получаем обратную матрицу
В качестве проверки можно перемножить исходную и обратную матрицы . В результате должна получиться единичная матрица.
Обратная матрица в Excel. Как найти обратную матрицу в Эксель в 2 этапа
Обратная матрица – это сложное математическое понятие, для нахождения которой необходимо выполнить множество непростых действий на бумаге. Однако программа Excel решает данную задачу в более короткие сроки и без особых усилий со стороны исполнителя. Давайте разберемся, каким образом можно найти обратную матрицу в несколько этапов на одном из примеров.
Замечание эксперта! Обязательным условием для нахождения обратной матрицы, является соответствие исходных данных квадратной матрице, а определителя нулю.
Находим значение определителя
Чтобы выполнить это действие, необходимо воспользоваться функцией МОПРЕД. Как именно это делается, рассмотрим на примере:
- Записываем квадратную матрицу в любом свободном месте.
- Выбираем свободную ячейку, после чего находим напротив строки формул кнопку «fx» («Вставить функцию») и кликаем по ней ЛКМ.
1
- Должно открыться окно, где в строке «Категория:» останавливаемся на «Математические», а ниже выбираем функцию МОПРЕД. Соглашаемся с выполненными действиями кликнув по кнопке «ОК».
- Далее в открывшемся окне заполняем координаты массива.
Совет! Заполнить адресацию можно одним из двух способов: вручную или кликнув кнопкой мыши в месте ввода информации о массиве и, определив выделением зоны место расположения квадратной матрицы, получить адрес массива автоматически.
- После проверки введенных ручным или автоматическим образом данных жмите «ОК».
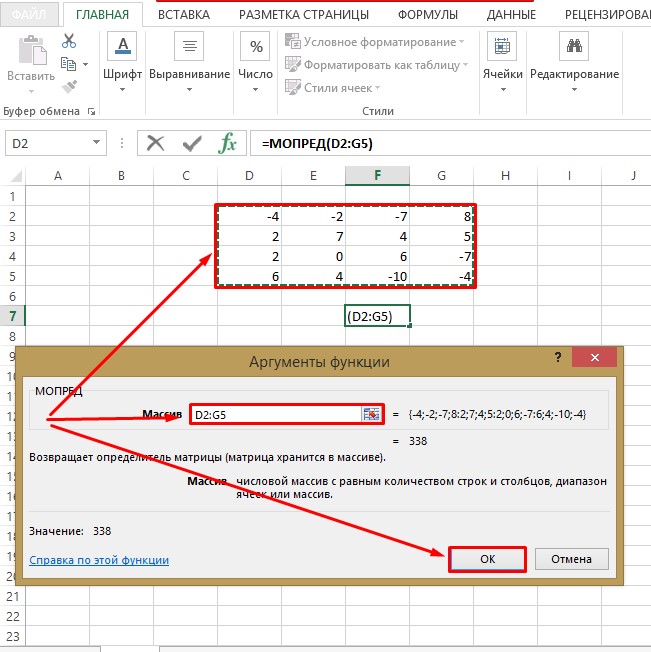
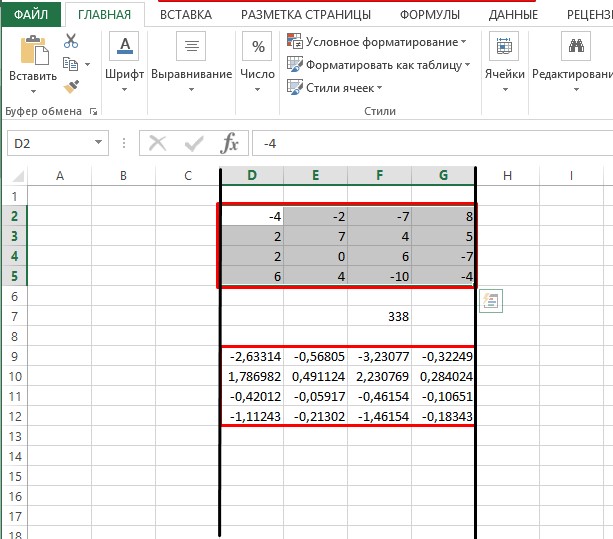
- После всех проведенных манипуляций свободная ячейка должна отобразить определитель матрицы, значение которого понадобится для нахождения обратной матрицы. Как видно по скриншоту, после вычислений получилось число 338, а, следовательно, потому как определитель не равен 0, то обратная матрица существует.
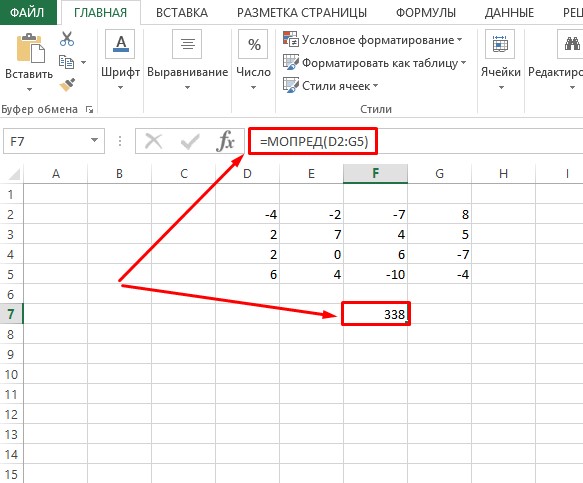
Определяем значение обратной матрицы
Как только вычисление определителя закончено, можно переходить к определению обратной матрицы:
- Выбираем место расположения верхнего элемента обратной матрицы, открываем окно «Вставка функции».
- Выбираем категорию «Математические».
- В расположившихся снизу функциях пролистываем список и останавливаем выбор на МОБР. Кликаем по кнопке «ОК».
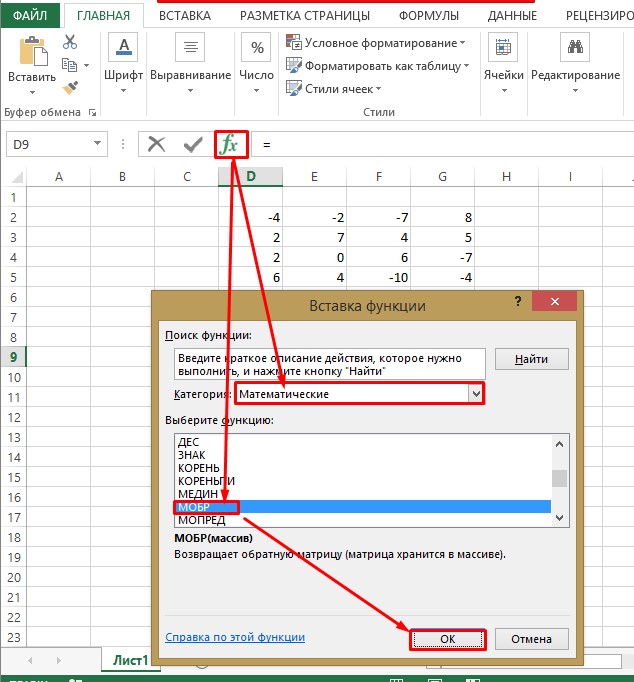
- Аналогично ранее выполняемым действиям при нахождении значений определителя вписываем координаты массива с квадратной матрицей.
- Убеждаемся в правильности выполненных действий и жмем «ОК».
- В выбранной верхней левой ячейке будущей обратной матрицы появится результат.
- Для копирования формулы для нахождения значений в других ячейках используем свободное выделение. Для этого, зажав ЛКМ, растягиваем на всю область будущей обратной матрицы.
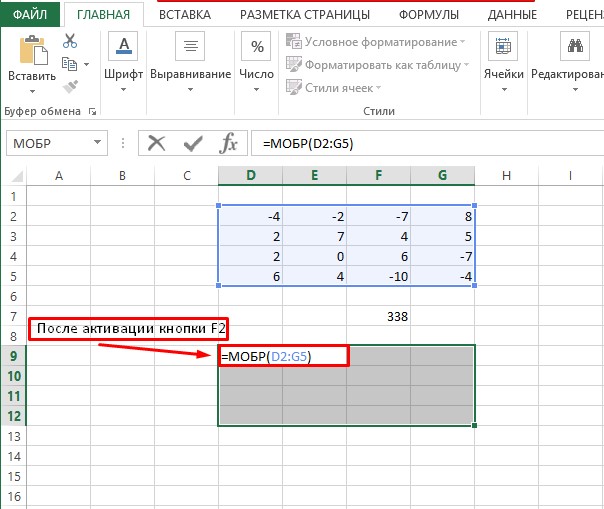
- Жмем на клавиатуре кнопку F2 и переходим к набору комбинации «Ctrl+Shift+Enter». Готово!
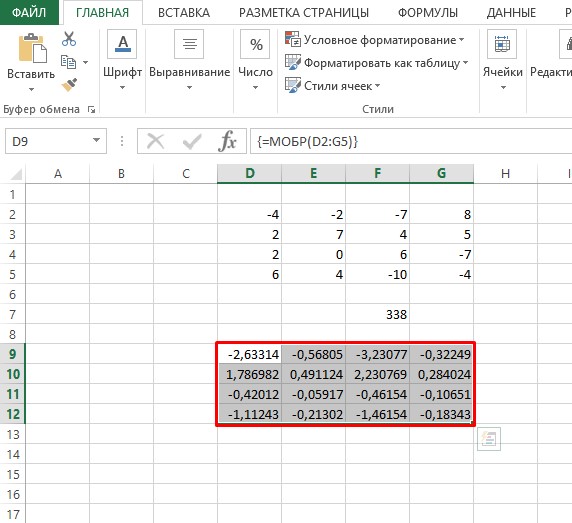
Рекомендация эксперта! Для удобства выполнения действий по нахождению обратной матрицы в таблице Excel расположение массива с квадратной матрицей и выбранная область для ячеек с обратной матрицей должны располагаться на одном уровне по отношению к столбцам. Таким образом будет проще определить границы адресации второго массива. Пример указан на иллюстрации ниже.
7
Сферы использования расчетов с обратной матрицей
Экономика – это область, которая требует проведения постоянных и очень сложных расчетов. Для облегчения используется матричная система расчетов. Нахождение обратной матрицы – это быстрый способ обработки большого объема информации за максимально короткие сроки, конечный результат которого будет представлен в наиболее удобном для восприятия виде.
Другая область применения – это 3D моделирование изображений. Всевозможные программы имеют встроенные инструменты для проведения подобного рода расчетов, что в значительной степени облегчает работу конструкторам при производстве расчетов. Наиболее популярной программой среди 3D моделистов считается Компас-3D.
Существуют и другие сферы деятельности, где можно применить систему расчетов обратной матрицы, но все же основной программой для проведения матричных расчетов можно считать Excel.
Заключение
Нахождение обратной матрицы нельзя назвать такой же распространенной математической задачей, как вычитание, сложение или деление, но если появилась необходимость в ее решении, то все действия могут произведены в табличном процессоре Excel. Если человеческий фактор склонен допускать ошибки, то компьютерная программа выдаст 100% точный результат.
Обратная матрица в Excel
- Введение в обратную матрицу в Excel
Обратная матрица Excel (оглавление)
- Введение в обратную матрицу в Excel
- Примеры обратной матрицы в Excel
Введение в обратную матрицу в Excel
Матрица, для которой вы хотите вычислить обратное значение, должна быть квадратной матрицей. Это означает, что матрица должна иметь одинаковое количество строк и столбцов. Определитель для матрицы не должен быть нулевым. Если оно равно нулю, вы можете найти обратную матрицу. Теоретическая формула для вычисления обратной матрицы A выглядит следующим образом:
| | = Определитель матрицы А.
(прил. A) = присоединенный к матрице A.
Если мы поместим оба эти значения в приведенную выше формулу, мы сможем получить инверсию любой матрицы A. Иногда становится очень утомительно вычислять обратную матрицу. Математики будут рады узнать, есть ли какая-либо функция, которая может работать для них, и вычислить обратную матрицу для них.
Функция MINVERSE для вычисления обратной матрицы
Функция Excel MINVERSE позволяет пользователю вычислять инверсию любой квадратной матрицы, которая имеет ненулевой определитель. Обращенная матрица имеет размер, равный размеру исходной матрицы. Рассчитанная обратная матрица имеет такой же размер, как и исходная матрица.
Синтаксис:
Аргумент:
массив — это массив значений, представляющих матрицу.
В этой статье мы увидим, как вычислить обратную квадратную матрицу.
Примеры обратной матрицы в Excel
Давайте разберемся, как создать обратную матрицу в Excel, на нескольких примерах.
Вы можете скачать этот шаблон обратной матрицы Excel здесь — шаблон обратной матрицы Excel
Пример # 1 — Вычислить инверсию матрицы 2X2
Матрица 2X2 имеет две строки и два столбца. Предположим, у нас есть квадратная матрица 2X2, как показано на рисунке ниже.
Шаг 1: Определите диапазон из 4 ячеек (поскольку у нас есть матрица 2X2) в том же листе Excel, который будет содержать обратную матрицу A. Здесь я выбрал ячейки A1: C5 в качестве диапазона для обратной матрицы A.
Это диапазоны, в которых будет вычисляться обратная матрица А.
Шаг 2: В ячейке B4 начните вводить формулу для обратной матрицы = MINV . Вы увидите диапазон формул, связанных с ключевым словом. Дважды щелкните мышью, чтобы выбрать МИНВЕРС из них, чтобы можно было вычислить инверсию матрицы А. Обязательно выбрать все ячейки, в которых будет вычисляться ваша инверсия.
Шаг 3: Укажите аргумент массива для функции MINVERSE как B1: C2 и закройте скобки, чтобы завершить формулу. Обратите внимание, что массив, который мы предоставляем в качестве аргумента функции MINVERSE, состоит из ячеек, которые имеют значения для исходной матрицы A.
Шаг 4: Чтобы увидеть результат формулы каждый раз, когда нам нужно нажать клавишу Enter. Но в этом случае вам нужно нажать клавиши Ctrl + Shift + Enter, чтобы формула была преобразована в формулу массива, которая выглядит следующим образом (= MINVERSE (B1: C2)) и работает вместе со всеми ячейками, связанными с инверсией A.
Вы можете видеть по ячейкам B1: C2 матрица, обратная к исходной матрице A.
Мы также можем проверить, правильно ли перехвачено обратное, полученное через функцию MINVERSE, или нет. Способ проверить это — умножить матрицы A и A -1 . Умножение должно привести к единичной матрице.
Мы можем добиться умножения матриц с помощью функции MMULT в Excel. Это умножает матрицы. Смотрите вывод в массиве ячеек B1: C5.
Пример № 2 — Вычислить инверсию матрицы 4X4
Шаг 1: Введите матрицу 4X4 в ячейки A1: E4, как показано на скриншоте ниже. Это матрица, для которой нам нужно вычислить обратную матрицу.
Шаг 2: Выберите ячейки от A6 до E9. Это ячейки, в которых мы будем вычислять обратную матрицу 4X4 с именем A.
Шаг 3: Сохраняя все выбранные ячейки, в ячейке B6 начните вводить формулу для обратной матрицы как = MINV . В списке формул, связанных с ключевым словом, дважды щелкните мышью, чтобы выбрать MINVERSE.
Шаг 4: Используйте ссылку на массив B1: E4 в качестве аргумента массива для этой функции и закройте скобки, чтобы завершить формулу.
Шаг 5: Вместо того чтобы нажимать клавишу Enter, как обычно, одновременно нажмите клавиши Ctrl + Shift + Enter, чтобы вычислить обратные значения для всех ячеек в B1: E4. Если вы этого не сделаете, формула не будет преобразована в формулу массива и будет применена только к текущей ячейке, и если вы попытаетесь перетащить ее для других ячеек, это приведет к ошибке.
Вот как мы можем вычислить обратную матрицу в Excel, используя функцию MINVERSE. Мы также можем проверить с помощью функции MMLUT, правильно ли вычислено обратное или нет.
Выберите диапазоны от B1 до E9, где мы можем проверить, является ли умножение этих двух матриц одинаковой или нет.
Это идет как идентичная матрица. Поэтому мы можем сказать, что обратное, которое мы захватили, правильно захвачено. Это из этой статьи. Давайте завернем вещи с некоторыми пунктами, которые будут помнить.
То, что нужно запомнить
- Если в данной матрице есть пустая ячейка или нечисловое значение, MINVERSE выдаст вам #VALUE! ошибка.
- В полученной матрице, если вы выберете несколько дополнительных ячеек, вы получите # N / A error.
- Если данная матрица является особой матрицей (для которой не существует обратной), вы получите #NUM! ошибка.
- Рекомендуется использовать MINVERSE в качестве формулы массива. В противном случае вы можете получить странные результаты по всем клеткам. Например, получение ошибок значений при перетаскивании формулы по строкам.
- Если вы не хотите, чтобы она использовалась в качестве формулы массива, вам нужно ввести одну и ту же формулу во все ячейки, чтобы получить результат.
Рекомендуемые статьи
Это руководство по обратной матрице в Excel. Здесь мы обсуждаем Как создать Обратную Матрицу в Excel вместе с практическими примерами и загружаемым шаблоном Excel. Вы также можете просмотреть наши другие предлагаемые статьи —
- Как использовать Excel IF и функцию?
- Примеры контрольного списка в Excel
- Вставка символа Delta в Excel
- Введение в модель данных в Excel
Нахождение обратной матрицы в Excel
Excel обладает мощным инструментарием, позволяющим выполнять множество математических, статистических, логических и прочих задач. В программе также можно выполнить такое действие, как нахождение обратной матрицы. Ниже мы на практическом примере рассмотрим, как именно это сделать.
Примечание: Найти обратную матрицу можно только при условии, что исходная является квадратной (количество столбцов и строк одинаковое). К тому же, ее определитель не должен равняться цифре 0.
Этап 1. Вычисляем определитель
В программе данное действие выполняется с помощью функции МОПРЕД.
- Переходим в свободную ячейку, в которой планируем производить расчеты, после чего кликаем по кнопке “Вставить функцию” (fx) слева от строки формул.



Этап 2. Находим обратную матрицу
Итак, после того, как мы вычислили, что определитель матрицы не равен нулю, можно приступить к нахождению обратной.
- Встаем в ячейку, которая станет самым верхним левым элементом новой обратной матрицы. Заходим в окно Вставки функции, нажав на соответствующую кнопку.
- В категории “Математические” выбираем функцию “МОБР”, после чего щелкаем по кнопке OK.
- Аналогично заполнению значения аргумента “Массив” для функции МОПРЕД, рассмотренной в первом разделе, указываем координаты первичной матрицы, после чего нажимаем OK.



Заключение
Нахождение обратной матрицы – не такая распространенная математическая задача, как, например, сложение, вычитание, умножение, деление, расчеты с процентами и т.д. Но, если все же возникнет такая потребность, вовсе необязательно делать это вручную на листке бумаги, ведь Эксель позволяет быстро и безошибочно справиться с этой задачей.
Как сделать проверку обратной матрицы в excel?
Приложение Excel выполняет целый ряд вычислений, связанных с матричными данными. Программа обрабатывает их, как диапазон ячеек, применяя к ним формулы массива. Одно из таких действий – это нахождение обратной матрицы. Давайте выясним, что представляет собой алгоритм данной процедуры.
Выполнение расчетов
Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.
Расчет определителя
Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.
- Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.
- Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
- Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».
- Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.
Расчет обратной матрицы
Теперь можно преступить к непосредственному расчету обратной матрицы.
- Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
- В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».
- В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».
- Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
- Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.
На этом расчет можно считать завершенным.
Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.
Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
8 июня 2013 Автор: Бакытжан
Нахождение обратной матрицы всегда вызывало большие затруднения у учащихся, так как это был очень трудоемкий процесс. И вот такое задание вполне по силам EXCEL.
Прежде всего, уясним одно правило: Матрица имеет обратную только тогда, когда ее определитель не равен нулю. А вот и задание: найдите матрицу, обратную к матрице А, где
Вычислять определитель этой матрицы мы умеем. Я его уже вычислил.
Он оказался равен -4, а это значит, что у нашей матрицы есть обратная (если бы определитель оказался равен нулю, то мы сказали бы что матрица не имеет обратную и немедленно прекратили все вычисления). Теперь отметим ячейку, с которой начнем записывать ответ. Я отметил ячейку E1. Нажимаем Формулы, затем Математические и в появившемся окне находим МОБР
После нажатия появляется вот такое окно, в котором надо вписать адреса ячеек, в которых находятся элементы матрицы в Массив
У нас элементы записаны в ячейки начиная с А1 и заканчивая в С3 , поэтому так и записываем (смотрите картинку)
Если все сделали правильно, то автоматически заполнится место, обведенное красным и запишется ответ, который обведен черным. В таком виде ответ трудно переваривать и поэтому нажимаем ОК. В ячейке, которую мы застолбили под ответ, появилось число 3, Это только первый элемент полученной обратной матрицы.
Чтобы виден был весь ответ, выполняем следующие действия: Начиная с ячейки Е1 выделяем три строчки и три столбца (именно столько было у исходной матрицы и столько же будет у обратной)
нажимаем клавишу F2, а затем на одновременно на три клавиши Ctrl+Shift+Enter.
В выделенном месте появляются, теперь уже все, элементы обратной матрицы. Если Вы сохраните этот документ, то в следующий раз можете воспользоваться плодами своего труда. Так, меняя элементы исходной матрицы, Вы автоматически получаете для нее же обратную матрицу.
На этом все. Крепких вам знаний.
Рубрика: EXCEL в помощь, Статьи.
Метки: EXCEL, ИКТ, матрица, обратная матрица
Навигация по записям
Как вычислить определитель при помощи MS EXCEL
В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.
Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.
Формулы массива
Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).
Порядок применения формулы массива:
- Выделить диапазон, где должен появиться результат действия формулы.
- Ввести формулу (как и положено, со знака «=»).
- Нажать сочетание кнопок Ctrl + Shift + Ввод.
В строке формул отобразится формула массива в фигурных скобках.
Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.
Решение матриц в Excel
С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.
Транспонирование
Транспонировать матрицу – поменять строки и столбцы местами.
Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.


- 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
- 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.
Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.
Сложение
Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.
В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.
Умножение матриц в Excel
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).
Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.
В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.
Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.
Обратная матрица в Excel
Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).
Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.
Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:
Нахождение определителя матрицы
Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.
Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).
Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.
Подробно рассмотрим особенности вычисления обратной матрицы в Excel и примеры использования функции МОБР.
В первую очередь освежим в памяти, что обратная матрица — это матрица (записывается как A-1), при умножении которой на исходную матрицу (A) дает единичную матрицу (E), другими словами выполняется формула:
Из определения следует важное свойство, что обратная матрица определена только для квадратных (т.е. число строк и столбцов совпадает) и невырожденных матриц (т.е. определитель отличен от нуля).
Как найти обратную матрицу в Excel?
В отличие от транспонированной матрицы, вычислить обратную матрицу технически несколько сложнее.
Посчитать обратную матрицу можно через построение матриц алгебраических дополнений и определителя исходной матрицы.
Однако сложность вычисления по данному алгоритму имеет квадратичную зависимость от порядка матрицы.
К примеру, для обращения квадратной матрицы 3-го порядка нам необходимо будет дополнительно сделать 9 матриц алгебраических дополнений, транспонировать итоговую созданную матрицу и поэлементно разделить на определитель начальной матрицы, что затрудняет возможность подобного расчета в Excel.
Поэтому воспользуемся стандартной функцией МОБР, которая позволит найти обратную матрицу:
Функция МОБР
Синтаксис и описание функции МОБР в Excel:
МОБР(массив)
Возвращает обратную матрицу (матрица хранится в массиве).
- Массив (обязательный аргумент) — числовой массив, содержащий матрицу с одинаковым числом столбцов и строк.
Рассмотрим расчет обратной матрицы посредством функции МОБР на конкретном примере.
Предположим у нас имеется следующая квадратная матрица 3-го порядка:
Выделяем диапазон пустых ячеек E2:G4, куда мы в дальнейшем поместим обратную матрицу.
Не снимая выделения ячеек вводим формулу =МОБР(A2:C4) и нажимаем комбинацию клавиш Ctrl + Shift + Ввод для расчета формулы массива по данному диапазону:
При работе с функцией МОБР могут возникнуть следующие ошибки:
- В том случае, когда исходная матрица является вырожденной (определитель равен нулю), то функция вернет ошибку #ЧИСЛО!;
- Если число строк и столбцов в матрице не совпадает, то функция возвратит ошибку #ЗНАЧ!;
- Функция также вернет ошибку #ЗНАЧ!, если хотя бы один из элементов матрицы является пустым или записан в текстовом виде.
|
Lyakysha Пользователь Сообщений: 29 |
Помогите пожалуйста. При выполнении кода: Sub MInverse() выдает ошибку: Run time error ‘1004’: Невозможно получить свойство MInverse класса В чем проблема? |
|
Lyakysha Пользователь Сообщений: 29 |
{quote}{login=Lyakysha}{date=27.08.2011 01:35}{thema=Application.WorksheetFunction.MInverse выдает ошибку}{post}Помогите пожалуйста. При выполнении кода: Sub MInverse() выдает ошибку: Run time error ‘1004’: Невозможно получить свойство MInverse класса В чем проблема? Разобрался сам, почему-то заработало вот в таком виде: Dim A() As Variant Ещё бы знать почему?:) |
|
ZVI Пользователь Сообщений: 4328 |
Из справки по Excel-функции МОБР(): Объявление ReDim A(2, 2) равносильно ReDim A(0 To 2, 0 To 2) — матрица 3×3. В примере1 вектор A(0, …) заполнен пустыми значениями Empty, что является источником ошибки. Кроме того, там есть еще одна ошибка: |
|
Lyakysha Пользователь Сообщений: 29 |
#4 27.08.2011 05:44:25 {quote}{login=ZVI}{date=27.08.2011 03:52}{thema=}{post}Из справки по Excel-функции МОБР(): Объявление ReDim A(2, 2) равносильно ReDim A(0 To 2, 0 To 2) — матрица 3×3. В примере1 вектор A(0, …) заполнен пустыми значениями Empty, что является источником ошибки. Кроме того, там есть еще одна ошибка: |
Функция МОБР возвращает обратную матрицу для матрицы, хранящейся в массиве.
Описание функции МОБР
Возвращает обратную матрицу для матрицы, хранящейся в массиве.
Синтаксис
=МОБР(массив)Аргументы
массив
Обязательный аргумент. Числовой массив с равным количеством строк и столбцов.
Замечания
- Массив может быть задан как диапазон ячеек, например A1:C3 как массив констант, например {1;2;3: 4;5;6: 7;8;9} или как имя диапазона или массива.
- Если хотя бы одна из ячеек массива пуста или содержит текст, функция МОБР возвращает значение ошибки #ЗНАЧ!.
- Функция МОБР также возвращает значение ошибки #ЗНАЧ!, если число строк в массиве не равно числу столбцов.
- Формулы, которые возвращают массивы, должны быть введены как формулы массива.
- Обратные матрицы, как и определители, обычно используются для решения систем уравнений с несколькими неизвестными. Произведение матрицы на ее обратную — это единичная матрица, т. е. квадратный массив, у которого диагональные элементы равны 1, а все остальные — 0.
- В качестве примера вычисления обратной матрицы, рассмотрим массив из двух строк и двух столбцов A1:B2, который содержит буквы a, b, c и d, представляющие любые четыре числа. В таблице приведена обратная матрица для массива A1:B2.
Столбец A Столбец B Строка 1 d/(a*d-b*c) b/(b*c-a*d) Строка 2 c/(b*c-a*d) a/(a*d-b*c) - Функция МОБР производит вычисления с точностью до 16 значащих цифр, что может привести к незначительным ошибкам округления.
- Некоторые квадратные матрицы не могут быть обращены: в таких случаях функция МОБР возвращает значение ошибки #ЧИСЛО!. Определитель такой матрицы равен 0.
Примеры
Для правильной работы формулу нужно ввести в приложении Excel как формулу массива, с помощью клавиш Ctrl+Shift+Enter.
Пример1Пример2
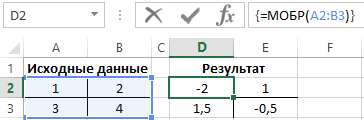
Исходная матрица:
Для нахождения обратной необходимо в одну из ячеек ввести формулу и потом выделить количество ячеек, которое соответсвует первоначальному (для нахождения обратной матрицы количество строк и столбцов должно совпадать) поставить курсор в строку формул и нажать Ctrl+Shift+Enter.
Результат:
Полностью заполненное решение нахождения обратной матрицы выглядит следующим образом:

И скрин с формулами: