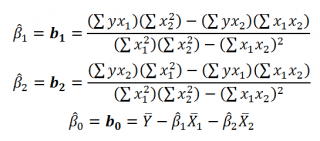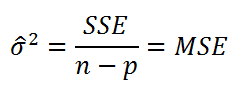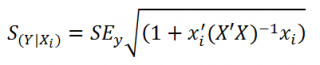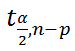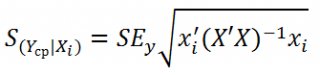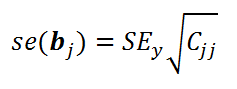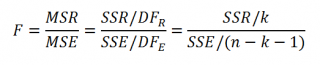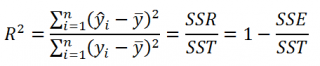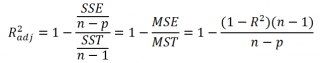Рассмотрим использование
MS
EXCEL
для прогнозирования переменной
Y
на основании нескольких переменных Х, т.е. множественную регрессию.
Перед прочтением этой статьи рекомендуется освежить в памяти
простую линейную регрессию
– прогнозирование на основе значений только одного фактора.
Disclaimer
: Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей
Множественного регрессионного анализа.
Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения
Регрессии
– плохая идея.
Статья про
Множественный регрессионный анализ
получилась большая, поэтому ниже для удобства приведены ее разделы:
- Оценка неизвестных параметров
- Диаграмма рассеяния
-
Вычисление прогнозных значений Y
(отдельное наблюдение и среднее значение) и построение доверительных интервалов
- Стандартные ошибки и доверительные интервалы для коэффициентов регрессии
- Проверка гипотез
- Генерация данных для множественной регрессии с помощью заданного тренда
- Коэффициент детерминации
Прогнозирование единственной переменной Y на основании значений 2-х или более переменных Х называется
множественной регрессией
.
Множественная линейная регрессионная модель
(Multiple Linear Regression Model)
имеет вид Y=β
0
+β
1
*X
1
+β
2
*X
2
+…+β
k
*X
k
+ε. В этом случае переменная Y зависит от k поясняющих переменных Х, т.е.
регрессоров
. ε —
случайная ошибка
. Модель является линейной относительно неизвестных параметров β.
Оценка неизвестных параметров
В этой статье рассмотрим модель с 2-мя регрессорами. Сначала введем необходимые обозначения и понятия множественной регрессии.
Для описания зависимости Y от 2-х переменных
линейная модель
имеет вид:
Y=β
0
+β
1
*X
1
+β
2
*X
2
+ε.
Параметры этой модели β
i
нам неизвестны, но их можно оценить, используя случайную выборку (измеренные значения переменной Y от заданных Х). Оценки параметров модели (β
0
, β
1
, β
2
) обычно вычисляются
методом наименьших квадратов (МНК)
, который минимизирует сумму квадратов ошибок прогнозирования (критерий минимизации в англоязычной литературе обозначают как SSE – Sum of Squared Errors).
Соответствующие оценки параметров будем обозначать как
b
0
,
b
1
и
b
2
.
Ошибка ε имеет случайную природу и имеет свою функцию распределения со
средним значением
=0 и
дисперсией σ
2
.
Оценки
b
1
и
b
2
называются
коэффициентами регрессии
, они определяют влияние соответствующей переменной X, когда все остальные независимые переменные остаются
неизменными
.
Сдвиг (intercept)
или
постоянный
член
b
0
, определяет прогнозируемое значение Y, когда все поясняющие переменные Х равны 0 (часто
сдвиг
не имеет физического смысла в рамках модели и обусловлен лишь математическими вычислениями
МНК
).
Вычислив оценки, полученные методом
МНК,
позволяют прогнозировать значения переменной Y:
Y=
b
0
+
b
1
*X
1
+
b
2
*X
2
Примечание
: Для случая 2-х регрессоров, все спрогнозированные значения переменной Y будут лежать в плоскости (в
плоскости регрессии
).
В качестве примера рассмотрим технологический процесс изготовления нити:
Инженер, на основе имеющегося опыта, предположил, что
прочность нити
Y зависит от
концентрации исходного раствора
(Х
1
) и
температуры реакции
(Х
2
), и соответствует модели линейной регрессии. Для нахождения комбинации переменных Х, при которых Y принимает максимальное значение, необходимо определить коэффициенты регрессии, сделав выборку.
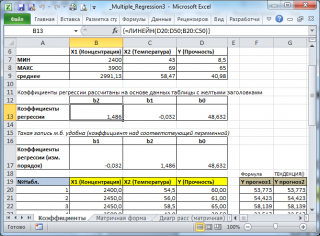
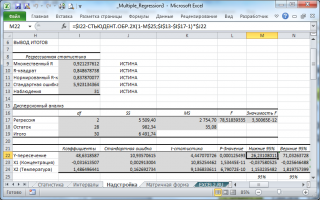
В MS EXCEL
коэффициенты множественной регрессии
удобнее всего вычислить с помощью функции
ЛИНЕЙН()
. Это сделано в
файле примера на листе Коэффициенты
. Чтобы вычислить оценки:
-
выделите 3 ячейки в одной строке (т.к. мы рассматриваем случай 2-х регрессоров, то будут вычислены 2
коэффициента регрессии
+
величина сдвига
= 3 значения, для вывода которых понадобится 3 ячейки). Пусть это будет диапазон
С8:Е8
; -
в
Строке формул
введите =
ЛИНЕЙН(D20:D50;B20:C50)
. Предполагается, что в столбце
В
содержатся прогнозируемые значения Y (в нашей модели это Прочность нити), в столбцах
С
и
D
содержатся значения контролируемых параметров Х (Х1 – Концентрация в столбце С и Х2 – Температура в столбце D). -
нажмите
CTRL
+
SHIFT
+
ENTER
(т.к. этоформула массива
).
В левой ячейке будет рассчитано значение
коэффициента регрессии
b
2
для переменной Х2, в средней ячейке — значение
коэффициента регрессии
b
1
для переменной Х1, в правой –
сдвиг
. Обратите внимание, что порядок вывода
коэффициентов
регрессии
обратный по отношению к расположению столбцов с данными соответствующих переменных Х (вычисленный коэффициент
b
2
располагается
левее
по отношению к
b
1
, тогда как значения переменной Х2 располагаются
правее
значений переменной Х1). Это может привести к путанице, поэтому лучше разместить коэффициенты над соответствующими столбцами с данными, как это сделано в строке 17
файла примера
.
Примечание
: В принципе без функции
ЛИНЕЙН()
можно обойтись, записав альтернативные формулы. Для этого в
файле примера на листе Коэффициенты
в столбцах
I
:
K
вычислены отклонения значений переменных Х
1i
, Х
2i
, Y
i
от их средних значений
, т.е.:
Далее коэффициенты регрессии рассчитываются по следующим формулам (эти формулы справедливы только при прогнозировании по 2-м независимым переменным Х):
При прогнозировании по 3-м и более независимым переменным Х формулы для вычисления
коэффициентов регрессии
значительно усложняются, поэтому следует использовать матричный подход.
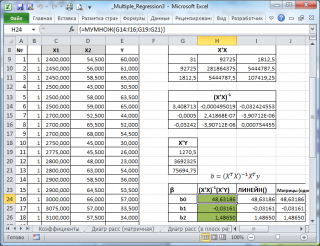
В
файле примера на листе Матричная форма
выполнены расчеты
коэффициентов регрессии
с помощью матричного подхода.
Расчет можно произвести как пошагово, так и одной
формулой массива
:
=МУМНОЖ(МОБР(МУМНОЖ(ТРАНСП(B9:D33);(B9:D33)));МУМНОЖ(ТРАНСП(B9:D33);(E9:E33)))
Коэффициенты регрессии
(вектор
b
)
в этом случае вычисляются по формуле
b
=(X
T
X)
-1
(X
T
Y) или в другом виде записи
b
=(X
’
X)
-1
(X
’
Y)
Под Х подразумевается матрица, состоящая из столбцов значений переменной Х с дополнительным столбцом единиц, а под Y – вектор-столбец значений Y.
Символ
Т
или ‘ – это
транспонирование матрицы
, а обозначение
-1
говорит о
вычислении обратной матрицы
.
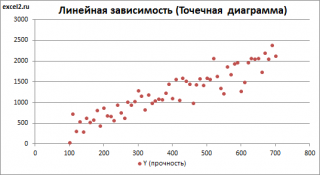
Диаграмма рассеяния
В случае
простой линейной регрессии
(один регрессор, т.е. одна переменная Х) для визуализации связи между прогнозируемым значением Y и переменной Х строят
диаграмму рассеяния
(двумерную).
В случае
множественной
линейной регрессии
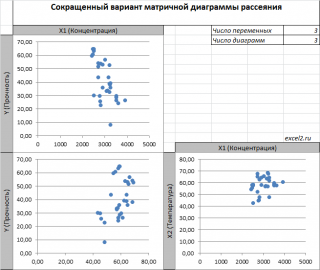
двумерную диаграмму рассеяния можно построить только для анализа влияния каждого отдельного регрессора на Y (при этом остальные Х не меняются), т.е. так называемую Матричную диаграмму рассеивания (См.
файл примера лист Диагр расс (матричная)
).
К сожалению, такую диаграмму трудно интерпретировать.
Более того, матричная диаграмма может вводить в заблуждение (см.
Introduction
to
linear
regression
analysis
/
D
.
C
.
Montgomery
,
E
.
A
.
Peck
,
G
.
G
.
Vining
, раздел 3.2.5
), демонстрируя наличие или отсутствие линейной взаимосвязи между отдельным регрессором X
i
и Y.
Для случая с 2-мя регрессорами можно предложить альтернативный вид матричной
диаграммы рассеяния
. В стандартной диаграмме рассеяния строятся проекции на координатные плоскости Х1;Х2, Y;X1 и Y;X2. Однако, если взглянуть на точки относительно
плоскости регрессии
, то картину, на мой взгляд, будет проще интерпретировать.
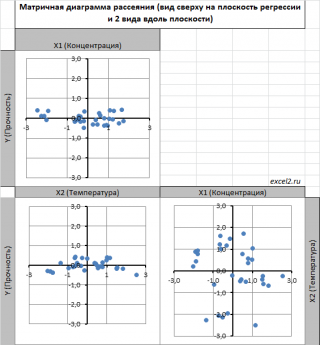
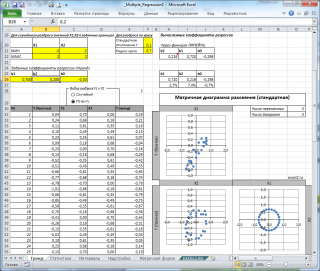
Сравним две матричные диаграммы рассеяния (см.
файл примера на листе «Диагр расс (в плоск регрессии)»
, построенные для одних и тех же наблюдений. Первая – стандартная,
вторая представляет собой вид сверху на плоскость регрессии и 2 вида вдоль плоскости.
На второй диаграмме становится очевидно, что разброс точек относительно плоскости регрессии совсем не большой и поэтому, скорее всего, построенная модель является полезной, а выбранные 2 переменные Х позволяют прогнозировать Y (конечно, для подтверждения этой гипотезы нужно
провести процедуру F-теста
).
Несколько слов о построении альтернативной матричной диаграммы рассеяния:
-
Перед построением необходимо нормировать значения наблюдений (для каждой переменной вычесть
среднее
и разделить на
стандартное отклонение
). В этом случае практически все точки на диаграммах будут находится в диапазоне +/-3 (по аналогии со
стандартным нормальным распределением
, 99% значений которого лежат в пределах +/-3 сигма). В этом случае, на диаграмме можно фиксировать мин/макс значений осей, чтобы EXCEL автоматически не модифицировал масштаб осей при изменении данных (это не всегда удобно);
-
Теперь координаты точек необходимо рассчитать в системе отсчета относительно плоскости регрессии (в которой плоскость Оху’ совпадает с плоскостью регрессии). Для этого необходимо найти
матрицу вращения
, например, через вращение приводящее к совмещению нормали к плоскости регрессии и вектора оси Z (0;0;1);
-
Новые координаты позволяют построить альтернативную матричную диаграмму. Кроме того, для удобства можно вращать систему координат вокруг новой оси Z, чтобы нагляднее представить себе распределение точек относительно плоскости регрессии (для этого использована Полоса прокрутки в ячейках
Q
31:
S
31
).
Вычисление прогнозных значений Y (отдельное наблюдение и среднее значение) и построение доверительных интервалов
После того, как нами были найдены тем или иным способом коэффициенты регрессии можно приступать к вычислению прогнозных значений Y на основе заданных значений переменных Х.
Уравнение прогнозирования или уравнение регрессии в случае 2-х независимых переменных (регрессоров) записывается в виде:
Y=
b
0
+
b
1
*
Х
1
+
b
2
*
Х
2
Примечание:
В MS EXCEL
прогнозное значение Y для заданных Х
1
и Х
2
можно также предсказать с помощью функции
ТЕНДЕНЦИЯ()
. При этом 2-й аргумент будет ссылкой на столбцы, содержащие все значения переменных Х
1
и Х
2
, а 3-й аргумент функции должен быть ссылкой на диапазон ячеек, содержащий 2 значения Х (Х
1i
и Х
2i
) для выбранного наблюдения i (см.
файл примера, лист Коэффициенты, столбец G
). Функция
ПРЕДСКАЗ()
, использованная нами в простой регрессии, не работает в случае
множественной регрессии
.
Найдя прогнозное значение Y, мы, таким образом, вычислим его точечную оценку. Понятно, что фактическое значение Y, полученное при наблюдении, будет, скорее всего, отличаться от этой оценки. Чтобы ответить на вопрос о том, на сколько хорошо мы можем предсказывать новые значения Y, нам потребуется построить
доверительный интервал
этой оценки, т.е. диапазон в котором с определенной заданной вероятностью, скажем 95%, мы ожидаем новое значение Y.
Доверительные интервалы
построим при фиксированном Х для:
- нового наблюдения Y;
- среднего значения Y (интервал будет уже, чем для отдельного нового наблюдения)
Как и в случае
простой линейной регрессии
, для построения
доверительных интервалов
нам потребуется сначала вычислить
стандартную ошибку модели
(standard error of the model)
, которая приблизительно показывает насколько велика ошибка предсказания значений переменной Y на основании значений переменных Х.
Для вычисления
стандартной ошибки
оценивают
дисперсию
ошибки ε, т.е. сигма^2
(ее часто обозначают как
MS
Е либо
MSres
)
. Затем, вычислив из полученной оценки квадратный корень, получим
Стандартную ошибку регрессии (часто обозначают как
SEy
или
sey
).
где SSE – сумма квадратов значений ошибок модели ei=yi — ŷi (
Sum of Squared Errors
). MSE означает Mean Square of Errors (среднее квадратов ошибок, точнее остатков).
Величина n-p – это количество
степеней свободы
(
df
–
degrees
of
freedom
), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y, р – количество оцениваемых параметров модели). В случае
простой множественной регрессии
с 2-мя регрессорами
число степеней свободы
равно n-3, т.к. при построении
плоскости регрессии
было оценено 3 параметра модели
b
(т.е. на это было «потрачено» 3
степени свободы
).
В MS EXCEL
стандартную ошибку
SEy можно вычислить формулы (см.
файл примера, лист Статистика
):
=
ИНДЕКС(ЛИНЕЙН($E$13:$E$43;$C$13:$D$43;;ИСТИНА);3;2)
Стандартная ошибка
нового наблюдения Y при заданных значениях Х (вектор Хi) вычисляется по формуле:
x
i
— вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.
Соответствующий доверительный интервал вычисляется по формуле:
где α (альфа) –
уровень значимости
(обычно принимают равным 0,05=5%)
р – количество оцениваемых параметров модели (в нашем случае = 3)
n-p – число степеней свободы
–
квантиль
распределения Стьюдента
(задает количество
стандартных ошибок
, в +/- диапазоне которых вероятность обнаружить новое наблюдение равно 1-альфа). Т.е. если
квантиль
равен 2, то диапазон шириной +/- 2
стандартных ошибок
относительно прогнозного значения Y будет с вероятностью 95% содержать новое наблюдение Y (для каждого заданного Хi). В MS EXCEL вычисления квантиля производят по формуле =
СТЬЮДЕНТ.ОБР.2Х(0,05;n-p)
, подробнее см.
в статье про распределение Стьюдента
.
– прогнозное значение Yi вычисляемое по формуле Yi=
b
0+
b
1*
Х1i+
b
2*
Х2i (точечная оценка).
Стандартная ошибка
среднего значения Y при заданных значениях Х (вектор Хi) будет меньше, чем стандартная ошибка отдельного наблюдения. Вычисления производятся по формуле:
x
i
— вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.
Соответствующий
доверительный интервал
вычисляется по формуле:
Прогнозное значение Yi (точечная оценка) используется тоже, что и для отдельного наблюдения.
Стандартные ошибки и доверительные интервалы для коэффициентов регрессии
В разделе
Оценка неизвестных параметров
мы получили точечные оценки
коэффициентов регрессии
. Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со
средним значением
и
дисперсией
. Но, чтобы перейти от
точечных оценок
к
интервальным
, необходимо вычислить соответствующие
стандартные ошибки
(т.е.
стандартные отклонения
)
коэффициентов регрессии
.
Стандартная ошибка коэффициента регрессии
b
j
(обозначается
se
(
b
j
)
) вычисляется на основании
стандартной ошибки
по следующей формуле:
где C
jj
является диагональным элементом матрицы (X
’
X)
-1
. Для коэффициента сдвига
b
0
индекс j=1 (верхний левый элемент), для
b
1
индекс j=2,
b
2
индекс j=3 (нижний правый элемент).
SEy –
стандартная ошибка регрессии
(см.
выше
).
В MS EXCEL
стандартные ошибки коэффициентов регрессии
можно вычислить с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН($E$13:$E$43;$C$13:$D$43;;ИСТИНА);2;j)
Примечание
: Подробнее о функции
ЛИНЕЙН()
см. статью
Функция MS EXCEL ЛИНЕЙН()
.
Применяя матричный подход
стандартные ошибки
можно вычислить и через обычные формулы (точнее через
формулу массива
, см.
файл примера лист Статистика
):
=
КОРЕНЬ(СУММКВРАЗН(E13:E43;F13:F43) /(n-p)) *КОРЕНЬ (ИНДЕКС (МОБР (МУМНОЖ(ТРАНСП(B13:D43);(B13:D43)));j;j))
При построении
двухстороннего доверительного интервала
для
коэффициента регрессии
его границы определяются следующим образом:
b
j
+/- t*Se(
b
j
)
где t – это
t-значение
, которое можно вычислить с помощью формулы =
СТЬЮДЕНТ.ОБР.2Х(0,05;n-p)
для
уровня значимости
0,05.
В результате получим, что найденный
доверительный интервал
с вероятностью 95% (1-0,05) накроет истинное значение
коэффициента регрессии
b
j
.
Здесь мы считаем, что
коэффициент регрессии
b
j
имеет
распределение Стьюдента
с n-p
степенями свободы
(n – количество наблюдений, т.е. пар Х и Y).
Проверка гипотез
Когда мы строим модель, мы предполагаем, что между Y и переменными X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X, возможен, когда все
коэффициенты регрессии
β
равны 0.
Чтобы убедиться, что вычисленная нами оценка
коэффициентов регрессии
не обусловлена лишь случайностью (они не случайно отличны от 0), используют
проверку гипотез
. В качестве
нулевой гипотезы
Н
0
принимают, что линейной связи нет, т.е. ВСЕ β=0. В качестве альтернативной гипотезы
Н
1
принимают, что ХОТЯ БЫ ОДИН коэффициент β <>0.
Процедура проверки значимости множественной регрессии, приведенная ниже, является обобщением
дисперсионного анализа
, использованного нами в случае
простой линейной регрессии (F-тест)
.
Если нулевая гипотеза справедлива, то
тестовая
F
-статистика
имеет
F-распределение
со степенями свободы
k
и
n
—
k
-1
, т.е. F
k, n-k-1
:
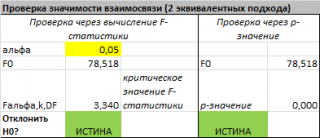
Проверку значимости регрессии можно также осуществить через вычисление
p
-значения
. В этом случае вычисляют вероятность того, что случайная величина F примет значение F
0
(это и есть
p-значение
), затем сравнивают p-значение с заданным
уровнем значимости α (альфа)
. Если
p-значение
больше уровня значимости
,
то нулевую гипотезу нет оснований отклонить, и регрессия незначима.
В MS EXCEL значение F
0
можно вычислить на основании значений выборки по вышеуказанной формуле или с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(E13:E43; C13:D43;;ИСТИНА);4;1)
В MS EXCEL для проверки гипотезы через
p
-значение
используйте формулу =F.РАСП.ПХ(F
0
;k;n-k-1)<
альфа
Если формула вернет ИСТИНА, то регрессия значима. Если формула вернет ЛОЖЬ, то у нас нет оснований отклонить нулевую гипотезу, т.е. «скорее всего» все коэффициенты регрессии равны 0 (см.
файл примера лист Статистика
, где показано эквивалентность обоих подходов проверки значимости регрессии).
В MS EXCEL критическое значение для заданного
уровня значимости
F
1-альфа, k, n-k-1
можно вычислить по формуле =
F.ОБР(1- альфа;k;n-k-1)
или =
F.ОБР.ПХ(альфа;k; n-k-1)
. Другими словами требуется вычислить
верхний альфа-
квантиль
F
-распределения
с соответствующими
степенями свободы
.
Таким образом, при значении статистики F
0
> F
1-альфа, k, n-k-1
мы имеем основание для отклонения нулевой гипотезы.
В программах статистики результаты процедуры
F
-теста
выводят с помощью стандартной таблицы
дисперсионного анализа
. В
файле примера такая таблица приведена на листе Надстройка
, которая построена на основе результатов, возвращаемых инструментом
Регрессия надстройки Пакета анализа MS EXCEL
.
Генерация данных для множественной регрессии с помощью заданного тренда
Иногда, бывает удобно сгенерировать значения наблюдений, имея заданный тренд.
Для решения этой задачи нам потребуется:
- задать значения регрессоров в нужном диапазоне (значения переменных Х);
-
задать коэффициенты регрессии (
b
); -
задать тренд (вычислить значения Y=
b
0
+
b
1
*
Х
1
+
b
2
*
Х
2
); - задать величину разброса Y вокруг тренда (варианты: случайный разброс в заданных границах или заданная фигура, например, круг)
Все вычисления выполнены в
файле примера, лист Тренд
для случая 2-х регрессоров. Там же построены
диаграммы рассеяния
.
Коэффициент детерминации
Коэффициент детерминации
R
2
показывает насколько полезна построенная нами
линейная регрессионная модель
.
По определению
коэффициент детерминации
R
2
равен:
R
2
=
Изменчивость объясненная моделью (
SSR
) / Общая изменчивость (
SST
).
Этот показатель можно вычислить с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(E13:E43;C13:D43;;ИСТИНА);3)
При добавлении в модель новой объясняющей переменной Х,
коэффициент детерминации
будет всегда расти. Поэтому, рост
коэффициента детерминации
не может служить основанием для вывода о том, что новая модель (с дополнительным регрессором) лучше прежней.
Более подходящей статистикой, которая лишена указанного недостатка, является
нормированный
коэффициент детерминации
(Adjusted R-squared):
где p – число независимых
регрессоров
(вычисления см.
файл примера лист Статистика
).
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а0 + а1х1 +…+акхк.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.
Download Article
Easily create a multiple regression model in your Excel spreadsheet
Download Article
Trying to create a multiple regression model in Excel? It’s pretty easy to do using the built-in data analysis tools. Multiple regression is a great way to examine how multiple independent variables explain the variation in a dependent variable. This wikiHow guide will show you how to run a multiple regression in Microsoft Excel on Windows or Mac.
Things You Should Know
- You’ll need to enable the Analysis ToolPak, a built-in add-in for Excel, before running a regression analysis.
- Make sure your data is arranged in adjacent columns with the first row being the headers.
- Click «Data Analysis» in the «Data» tab and select «Regression» to set up the analysis.
Steps
-
1
Enable the data analysis add-in (if needed). Whether you’re studying statistics or doing regression professionally, Excel is a great tool for running the analysis. Excel has a built-in data analysis add-in called «Analysis ToolPak.» You can check to see if it’s active by clicking the Data tab. If you don’t see the Data Analysis option, you will need to enable it:[1]
- Windows:
- Open the File tab (or press Alt+F) and select Options (Windows).
- Click Add-Ins on the left side of the window.
- Select Excel Add-ins next to «manage» and click Go.
- In the new window, check the box next to «Analysis ToolPak», then click OK. This will enable the built-in data analysis add-in.
- Mac:
- Click Tools and then Excel Add-ins.
- Check the box next to Analysis ToolPak and click OK.
- Note that you may need to click Browse to find the Analysis ToolPak.
- If the Data Analysis tool doesn’t appear in the Data tab, close and reopen Excel.
- Windows:
-
2
Enter your data or open your data file. Data must be arranged in immediately adjacent columns and labels should be in the first row of each column. This is a typical format for databases.
Advertisement
-
3
Click theData tab and click Data Analysis. This option is in the «Analysis» section near the far right of Data tab options.
- Another powerful tool is Excel’s Solver function, an optimization model feature.
-
4
Click Regression and then OK. This will open a new window for inputting the parameters of the regression model.
-
5
Input the dependent (Y) data range. To do so:
- Click the «Input Y Range» field.
- Highlight the column containing your dependent variable values.
- Click the Labels checkbox if your data has a header row.
-
6
Input the independent (X) data range. To do so:
- Click the «Input X Range» field.
- Highlight the column or columns containing your dependent variable values. This can include multiple columns if you have more than one independent variable.
- Note: The independent variable data columns must be adjacent to one another for the input to work.
-
7
Adjust the regression options (if needed). You can change the following parts of the analysis in the Regression window:
- The default confidence level is 95%. If you want to change this value, click the box next to Confidence Level and modify the adjacent value.
- Under «Output options,» select where you want the regression results to output.
- Select the desired options in the «Residuals» category. Graphical residual outputs are created by the Residual Plots and Line Fit Plots options.
-
8
Click OK and the analysis will be created. You’ll see the following information:
- Regression Statistics includes the correlation values, standard error, and number of observations.
- ANOVA is a table displaying the degrees of freedom, sum squares, mean squares, F value, and F significance. You can use this table to assess the statistical significance of the model.
- The confidence interval table shows the regression coefficient, standard error, significance, and confidence interval for each regression parameter (the intercept and the independent variable slopes).
Advertisement
Add New Question
-
Question
what is output range
Kyle Smith is a wikiHow Technology Writer, learning and sharing information about the latest technology. He has presented his research at multiple engineering conferences and is the writer and editor of hundreds of online electronics repair guides. Kyle received a BS in Industrial Engineering from Cal Poly, San Luis Obispo.
wikiHow Technology Writer
Expert Answer
The output range in the regression window is where the results of the analysis will appear. This can be in an existing sheet, a new sheet, or an entirely new workbook file.
-
Question
getting #NUM error p- values. What does it mean?
Kyle Smith is a wikiHow Technology Writer, learning and sharing information about the latest technology. He has presented his research at multiple engineering conferences and is the writer and editor of hundreds of online electronics repair guides. Kyle received a BS in Industrial Engineering from Cal Poly, San Luis Obispo.
wikiHow Technology Writer
Expert Answer
This could indicate that you don’t have enough observations to compute the significance of the model or its parameters. Try adding additional observations if this is the case.
-
Question
What is the formula of multiple regression used by Excel in the background?
Kyle Smith is a wikiHow Technology Writer, learning and sharing information about the latest technology. He has presented his research at multiple engineering conferences and is the writer and editor of hundreds of online electronics repair guides. Kyle received a BS in Industrial Engineering from Cal Poly, San Luis Obispo.
wikiHow Technology Writer
Expert Answer
Excel is using the linear regression formula y = m1x1 + m2x2 + … + b. It calculates the values using the least squares method.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
About This Article
Thanks to all authors for creating a page that has been read 807,255 times.
Is this article up to date?
Множественная линейная регрессия — это метод, который мы можем использовать для понимания взаимосвязи между двумя или более независимыми переменными и переменной отклика .
В этом руководстве объясняется, как выполнить множественную линейную регрессию в Excel.
Примечание. Если у вас есть только одна независимая переменная, вам следует вместо этого выполнить простую линейную регрессию .
Пример: множественная линейная регрессия в Excel
Предположим, мы хотим знать, влияет ли количество часов, потраченных на учебу, и количество сданных подготовительных экзаменов на балл, который студент получает на определенном вступительном экзамене в колледж.
Чтобы исследовать эту взаимосвязь, мы можем выполнить множественную линейную регрессию, используя часы обучения и подготовительные экзамены, взятые в качестве объясняющих переменных, и экзаменационный балл в качестве переменной ответа.
Выполните следующие шаги в Excel, чтобы провести множественную линейную регрессию.
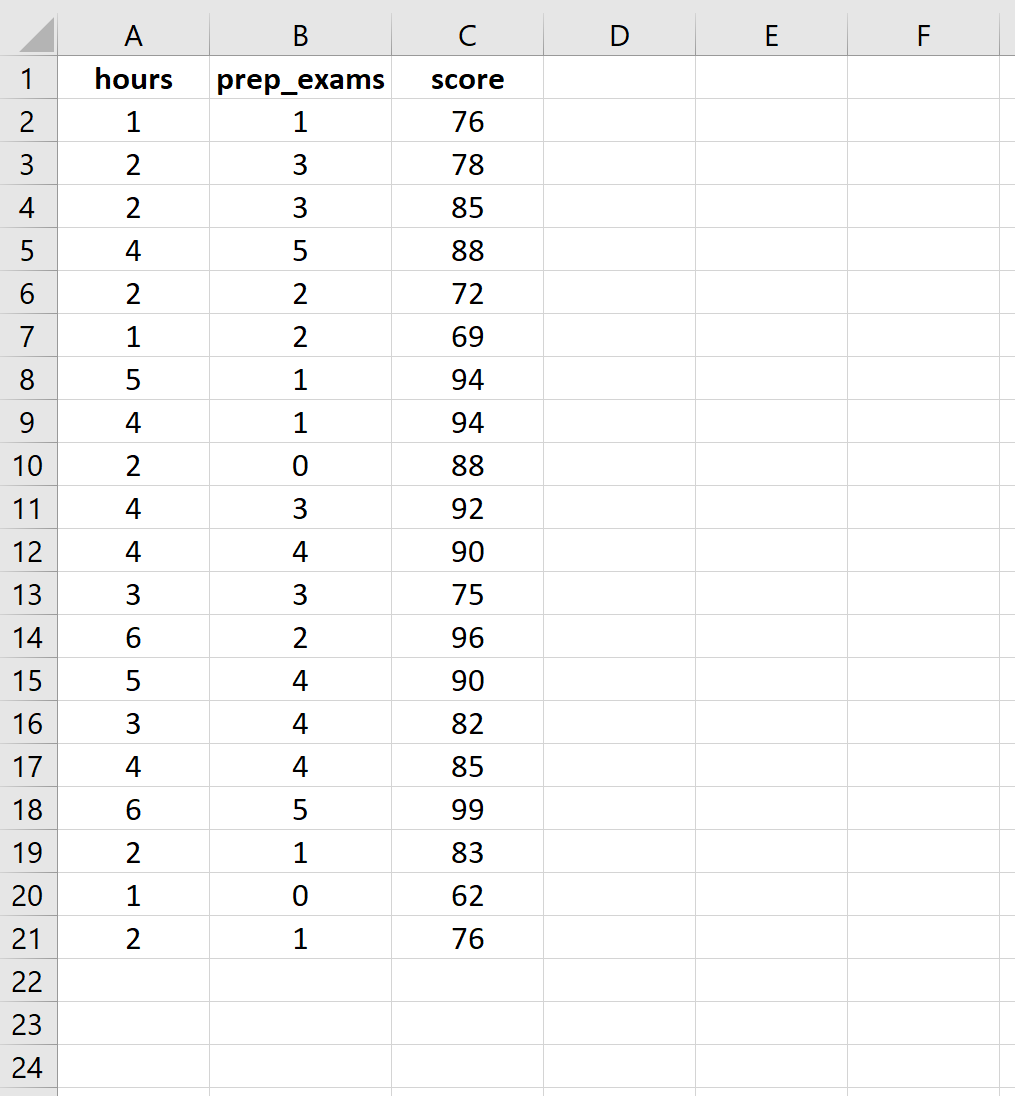
Шаг 1: Введите данные.
Введите следующие данные для количества часов обучения, сданных подготовительных экзаменов и результатов экзаменов, полученных для 20 студентов:
Шаг 2: Выполните множественную линейную регрессию.
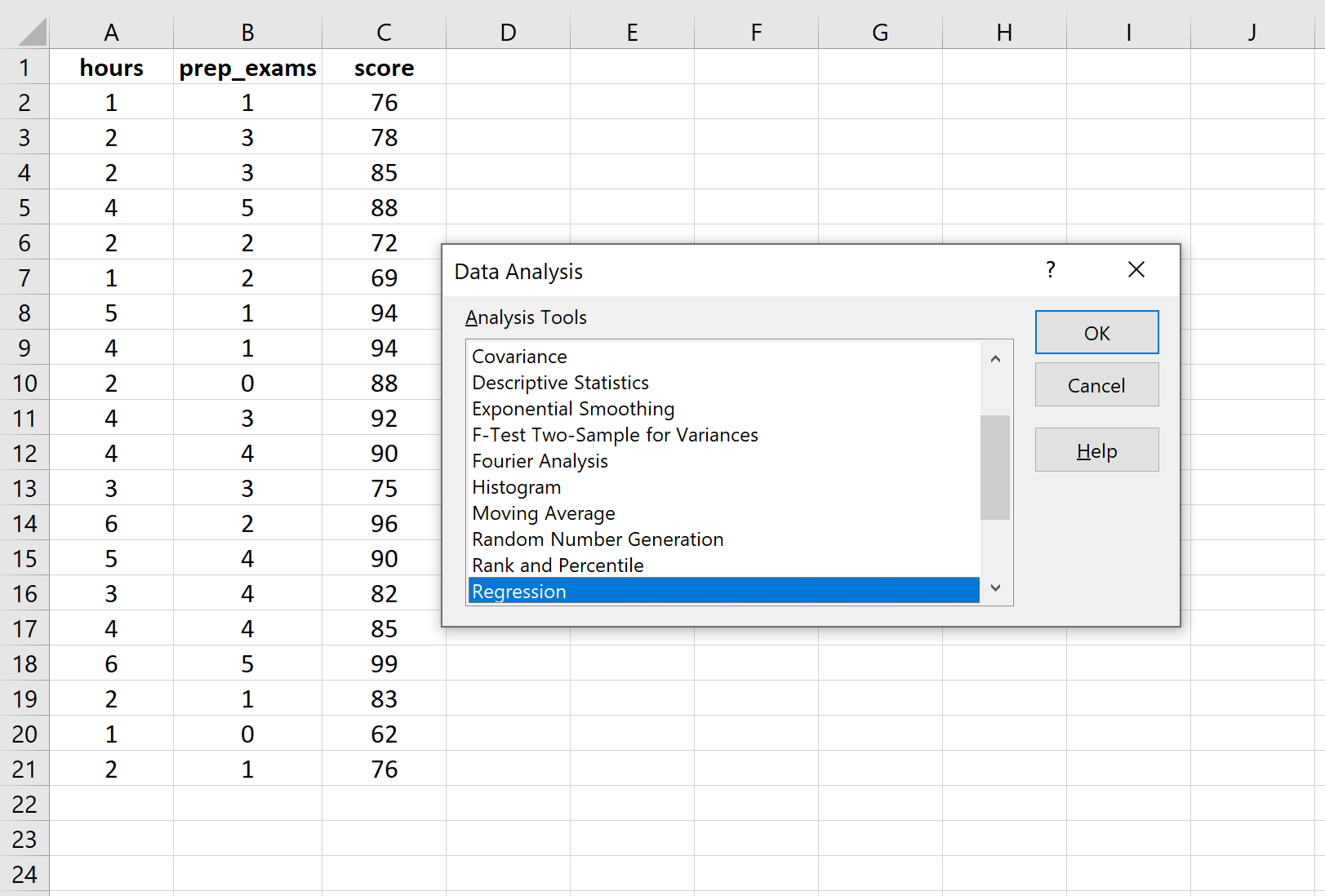
В верхней ленте Excel перейдите на вкладку « Данные » и нажмите « Анализ данных».Если вы не видите эту опцию, вам необходимо сначала установить бесплатный пакет инструментов анализа .
Как только вы нажмете « Анализ данных», появится новое окно. Выберите «Регрессия» и нажмите «ОК».
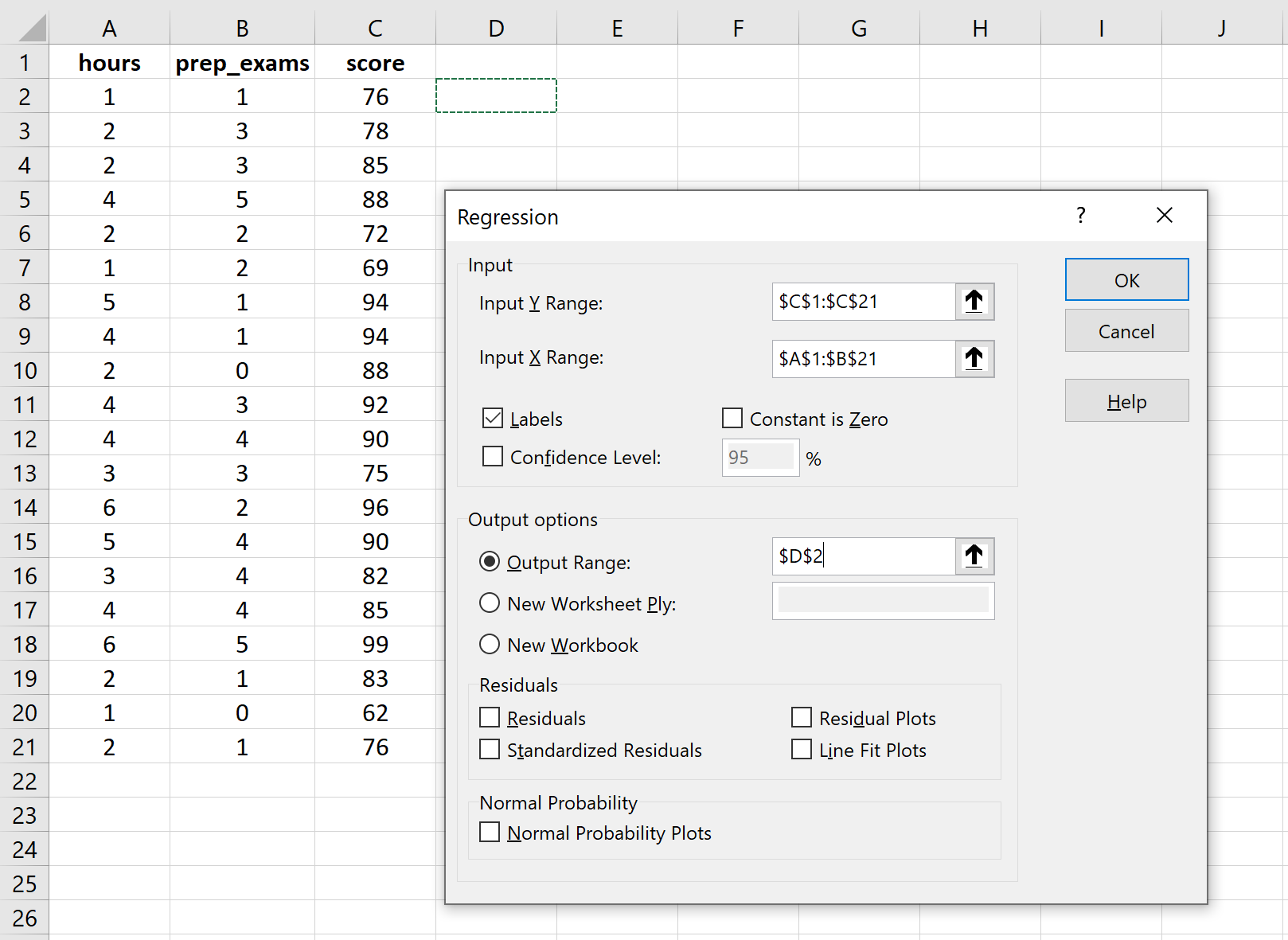
Для Input Y Range заполните массив значений для переменной ответа. Для Input X Range заполните массив значений для двух независимых переменных. Установите флажок рядом с Метки , чтобы Excel знал, что мы включили имена переменных во входные диапазоны. В поле Выходной диапазон выберите ячейку, в которой должны отображаться выходные данные регрессии. Затем нажмите ОК .
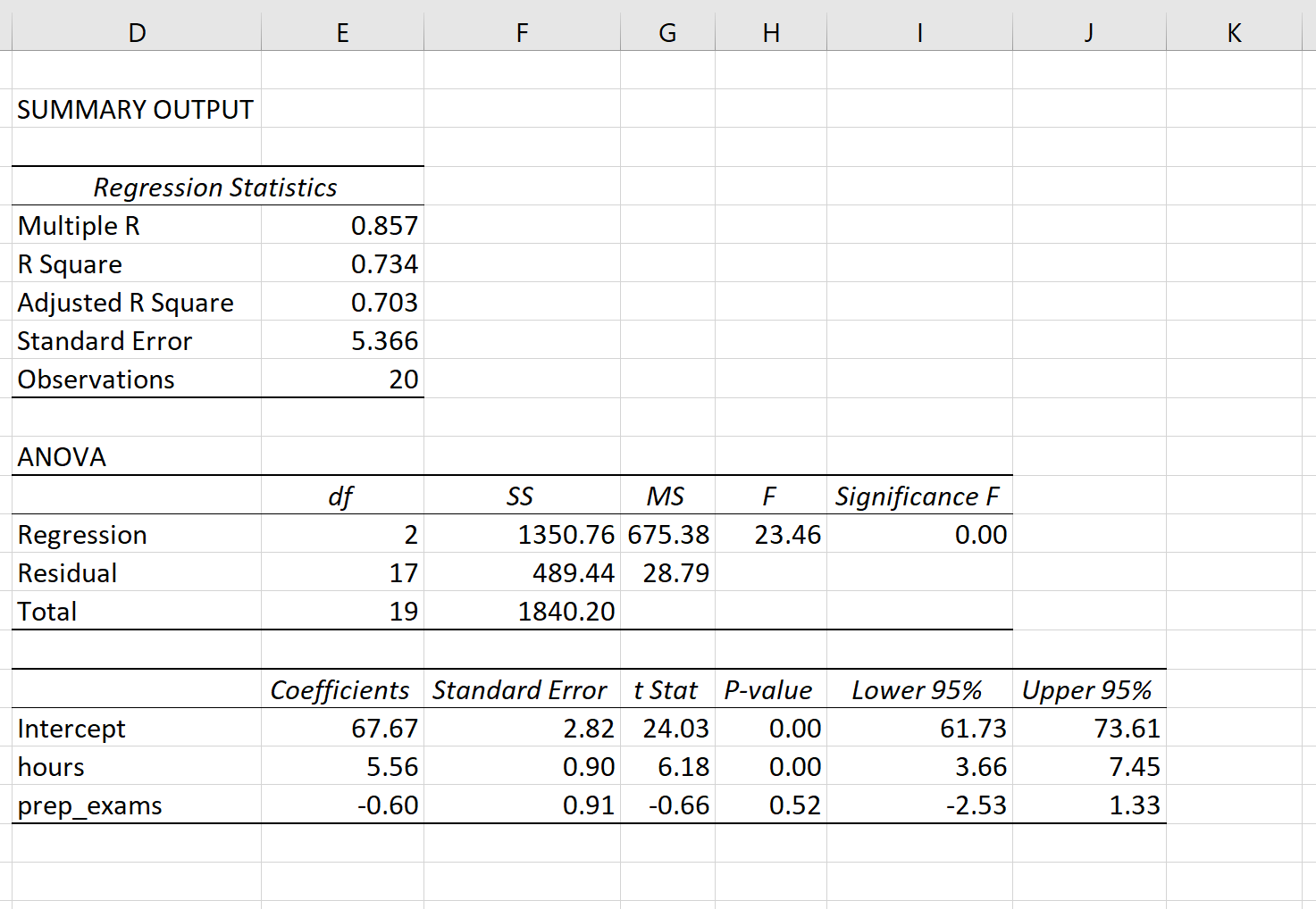
Автоматически появится следующий вывод:
Шаг 3: Интерпретируйте вывод.
Вот как интерпретировать наиболее релевантные числа в выводе:
R-квадрат: 0,734.Это известно как коэффициент детерминации. Это доля дисперсии переменной отклика, которая может быть объяснена объясняющими переменными. В этом примере 73,4% вариаций в экзаменационных баллах можно объяснить количеством часов обучения и количеством сданных подготовительных экзаменов.
Стандартная ошибка: 5,366.Это среднее расстояние, на которое наблюдаемые значения отходят от линии регрессии. В этом примере наблюдаемые значения отклоняются от линии регрессии в среднем на 5,366 единицы.
Ф: 23,46.Это общая F-статистика для регрессионной модели, рассчитанная как MS регрессии / остаточная MS.
Значение F: 0,0000.Это p-значение, связанное с общей статистикой F. Он говорит нам, является ли регрессионная модель в целом статистически значимой. Другими словами, он говорит нам, имеют ли объединенные две объясняющие переменные статистически значимую связь с переменной отклика. В этом случае p-значение меньше 0,05, что указывает на то, что независимые переменные количество часов обучения и сданных подготовительных экзаменов вместе имеют статистически значимую связь с экзаменационным баллом .
P-значения. Отдельные p-значения говорят нам, является ли каждая независимая переменная статистически значимой. Мы можем видеть, что изученные часы статистически значимы (p = 0,00), в то время как пройденные подготовительные экзамены (p = 0,52) не являются статистически значимыми при α = 0,05. Поскольку сданные подготовительные экзамены не являются статистически значимыми, мы можем принять решение удалить их из модели.
Коэффициенты: коэффициенты для каждой независимой переменной говорят нам о среднем ожидаемом изменении переменной отклика при условии, что другая независимая переменная остается постоянной. Например, ожидается, что за каждый дополнительный час, потраченный на учебу, средний экзаменационный балл увеличится на 5,56 при условии, что количество сданных подготовительных экзаменов останется неизменным.
Вот еще один способ подумать об этом: если учащийся А и учащийся Б сдают одинаковое количество подготовительных экзаменов, но учащийся А учится на один час больше, то ожидается, что учащийся А получит результат на 5,56 балла выше, чем учащийся Б.
Мы интерпретируем коэффициент для перехвата как означающий, что ожидаемая оценка экзамена для студента, который учится ноль часов и сдает нулевые подготовительные экзамены, составляет 67,67 .
Расчетное уравнение регрессии: мы можем использовать коэффициенты из выходных данных модели, чтобы создать следующее расчетное уравнение регрессии:
экзаменационный балл = 67,67 + 5,56*(часы) – 0,60*(подготовительные экзамены)
Мы можем использовать это оценочное уравнение регрессии, чтобы рассчитать ожидаемый балл экзамена для учащегося на основе количества часов, которые он изучает, и количества подготовительных экзаменов, которые он сдает. Например, студент, который занимается три часа и сдает один подготовительный экзамен, должен получить 83,75 балла:
экзаменационный балл = 67,67 + 5,56*(3) – 0,60*(1) = 83,75
Имейте в виду, что, поскольку пройденные подготовительные экзамены не были статистически значимыми (p = 0,52), мы можем решить удалить их, поскольку они не улучшают общую модель. В этом случае мы могли бы выполнить простую линейную регрессию, используя только часы изучения в качестве независимой переменной.
С результатами этого простого линейного регрессионного анализа можно ознакомиться здесь .
Дополнительные ресурсы
После выполнения множественной линейной регрессии есть несколько предположений, которые вы можете проверить, в том числе:
1. Тестирование на мультиколлинеарность с помощью VIF .
2. Тестирование на гетеродескедастичность с помощью теста Бреуша-Пагана .
3. Проверка нормальности с использованием графика QQ .
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
· линейной (у = а + bx);
· параболической (y = a + bx + cx 2);
· экспоненциальной (y = a * exp(bx));
· степенной (y = a*x^b);
· гиперболической (y = b/x + a);
· логарифмической (y = b * 1n(x) + a);
· показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а 0 + а 1 х 1 +…+а к х к.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
1. Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
2. Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
3. Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
1. Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
2. Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
3. После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Пакет MS Excel позволяет при построении уравнения линейной регрессии большую часть работы сделать очень быстро. Важно понять, как интерпретировать полученные результаты.
Для работы необходима надстройка Пакет анализа
, которую необходимо включить в пункте меню СервисНадстройки
В Excel 2007 для включения пакета анализа надо нажать перейти в блок Параметры Excel
, нажав кнопку в левом верхнем углу, а затем кнопку «Параметры Excel
» внизу окна:
Для построения модели регрессии необходимо выбрать пункт СервисАнализ данныхРегрессия
. (В Excel 2007 этот режим находится в блоке Данные/Анализ данных/ Регрессия
). Появится диалоговое окно, которое нужно заполнить:
1) Входной интервал Y
¾ содержит ссылку на ячейки, которые содержат значения результативного признака y
. Значения должны быть расположены в столбце;
2) Входной интервал X
¾ содержит ссылку на ячейки, которые содержат значения факторов . Значения должны быть расположены в столбцах;
3) Признак Метки
ставится, если первые ячейки содержат пояснительный текст (подписи данных);
4) Уровень надежности
¾ это доверительная вероятность, которая по умолчанию считается равной 95%. Если это значение не устраивает, то нужно включить этот признак и ввести требуемое значение;
5) Признак Константа-ноль
включается, если необходимо построить уравнение, в котором свободная переменная ;
6) Параметры вывода
определяют, куда должны быть помещены результаты. По умолчанию строит режим Новый рабочий лист
;
7) Блок Остатки
позволяет включать вывод остатков и построение их графиков.
В результате выводится информация, содержащая все необходимые сведения и сгруппированная в три блока: Регрессионная статистика
, Дисперсионный анализ
, Вывод остатка
. Рассмотрим их подробнее.
1. Регрессионная статистика
:
множественный R
определяется формулой (коэффициент корреляции Пирсона
);
R

);
Нормированный R
-квадрат вычисляется по формуле 
Стандартная ошибка S
вычисляется по формуле 
Наблюдения ¾ это количество данных n
.
2. Дисперсионный анализ
, строка Регрессия
:
Параметр df
равен m
(количество наборов факторов x
);
Параметр SS
определяется формулой ;
Параметр MS
определяется формулой ;
Статистика F
определяется формулой ;
Значимость F
. Если полученное число превышает , то принимается гипотеза (нет линейной взаимосвязи), иначе принимается гипотеза (есть линейная взаимосвязь).
3. Дисперсионный анализ
, строка Остаток
:
Параметр df
равен ;
Параметр SS
определяется формулой 
Параметр MS
определяется формулой .
4. Дисперсионный анализ
, строка Итого
содержит сумму первых двух столбцов.
5. Дисперсионный анализ
, строка Y-пересечение
содержит значение коэффициента , стандартной ошибки и t
-статистики .
P
-значение ¾ это значение уровней значимости, соответствующее вычисленным t
-статистикам. Определяется функцией СТЬЮДРАСП(t
-статистика; ). Если P
-значение превышает , то соответствующая переменная статистически незначима и ее можно исключить из модели.
Нижние 95%
и Верхние 95%
¾ это нижние и верхние границы 95-процентных доверительных интервалов для коэффициентов теоретического уравнения линейной регрессии. Если в блоке ввода данных значение доверительной вероятности было оставлено по умолчанию, то последние два столбца будут дублировать предыдущие. Если пользователь ввел свое значение доверительной вероятности, то последние два столбца содержат значения нижней и верхней границы для указанной доверительной вероятности.
6. Дисперсионный анализ
, строки содержат значения коэффициентов, стандартных ошибок, t
-статистик, P
-значений и доверительных интервалов для соответствующих .
7. Блок Вывод остатка
содержит значения предсказанного y
(в наших обозначениях это ) и остатки .
Метод линейной регрессии позволяет нам описывать прямую линию, максимально соответствующую ряду упорядоченных пар (x, y). Уравнение для прямой линии, известное как линейное уравнение, представлено ниже:
ŷ — ожидаемое значение у при заданном значении х,
x — независимая переменная,
a — отрезок на оси y для прямой линии,
b — наклон прямой линии.
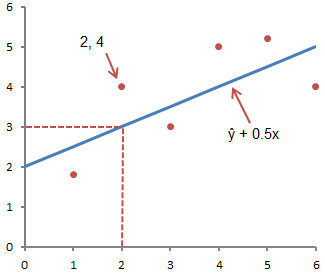
На рисунке ниже это понятие представлено графически:
На рисунке выше показана линия, описанная уравнением ŷ =2+0.5х. Отрезок на оси у — это точка пересечения линией оси у; в нашем случае а = 2. Наклон линии, b, отношение подъема линии к длине линии, имеет значение 0.5. Положительный наклон означает, что линия поднимается слева направо. Если b = 0, линия горизонтальна, а это значит, что между зависимой и независимой переменными нет никакой связи. Иными словами, изменение значения x не влияет на значение y.
Часто путают ŷ и у. На графике показаны 6 упорядоченных пар точек и линия, в соответствии с данным уравнением
На этом рисунке показана точка, соответствующая упорядоченной паре х = 2 и у = 4. Обратите внимание, что ожидаемое значение у в соответствии с линией при х
= 2 является ŷ. Мы можем подтвердить это с помощью следующего уравнения:
ŷ = 2 + 0.5х =2 +0.5(2) =3.
Значение у представляет собой фактическую точку, а значение ŷ — это ожидаемое значение у с использованием линейного уравнения при заданном значении х.
Следующий шаг — определить линейное уравнение, максимально соответствующее набору упорядоченных пар, об этом мы говорили в предыдущей статье, где определяли вид уравнения по .
Использование Excel для определения линейной регрессии
Для того, чтобы воспользоваться инструментом регрессионного анализа встроенного в Excel, необходимо активировать надстройку Пакет анализа
. Найти ее можно, перейдя по вкладке Файл –> Параметры
(2007+), в появившемся диалоговом окне Параметры
Excel
переходим во вкладку Надстройки.
В поле Управление
выбираем Надстройки
Excel
и щелкаем Перейти.
В появившемся окне ставим галочку напротив Пакет анализа,
жмем ОК.
Во вкладке Данные
в группе Анализ
появится новая кнопка Анализ данных.
Чтобы продемонстрировать работу надстройки, воспользуемся данными , где парень и девушка делят столик в ванной. Введите данные нашего примера с ванной в столбцы А и В чистого листа.
Перейдите во вкладку Данные,
в группе Анализ
щелкните Анализ данных.
В появившемся окне Анализ данных
выберите Регрессия
, как показано на рисунке, и щелкните ОК.
Установите необходимыe параметры регрессии в окне Регрессия
, как показано на рисунке:
Щелкните ОК.
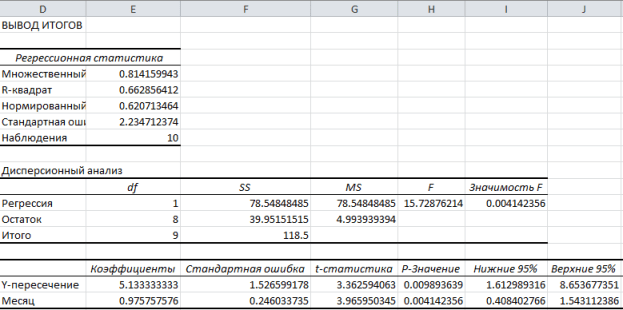
На рисунке ниже показаны полученные результаты:
Эти результаты соответствуют тем, которые мы получили путем самостоятельных вычислений в .
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx 2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а 0 + а 1 х 1 +…+а к х к.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача:
Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
Теперь стали видны и данные регрессионного анализа.
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости .
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами
как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН
.
Для этого:
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций
: в главном меню выберете Формулы / Вставить функцию
.
4) В окне Категория
выберете Статистические
, в окне функция — ЛИНЕЙН
. Щёлкните по кнопке ОК
как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
5) Заполните аргументы функции:
Известные значения у
Известные значения х
Константа
— логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика
— логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК
;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу
, а затем на комбинацию клавиш ++
.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Стандартная ошибка y | |
| F-статистика | |
| Регрессионная сумма квадратов
|
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
Означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х — среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.
По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: .
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее
, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия
можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа
. В главном меню последовательно выберите: Файл/Параметры/Надстройки
.
2) В раскрывающемся списке Управление
выберите пункт Надстройки Excel
и нажмите кнопку Перейти.
3) В окне Надстройки
установите флажок Пакет анализа
, а затем нажмите кнопку ОК
.
Если Пакет анализа
отсутствует в списке поля Доступные надстройки
, нажмите кнопку Обзор
, чтобы выполнить поиск.
Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да
, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия
, а затем нажмите кнопку ОК
.
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y
— диапазон, содержащий данные результативного признака;
Входной интервал X
— диапазон, содержащий данные факторного признака;
Метки
— флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа — ноль
— флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал
— достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист — можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК
.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как не превышает 8 — 10%.
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н 0 о статистически незначимом отличии показателей от нуля:
.
для числа степеней свободы
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ:
где 
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н 0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций
: в главном меню выберете Формулы / Вставить функцию
.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК
.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при с вероятностью 0,95 определяются выражением:
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. — М.: Финансы и статистика, 2003. — 192 с.: ил.