Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью линейной функции
y
=
a
x
+
b
.
Метод наименьших квадратов
(англ.
Ordinary
Least
Squares
,
OLS
) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров
регрессионных моделей
по выборочным данным.
Рассмотрим приближение функциями, зависящими только от одной переменной:
- Линейная: y=ax+b (эта статья)
-
Логарифмическая
: y=a*Ln(x)+b
-
Степенная
: y=a*x
m
-
Экспоненциальная
: y=a*EXP(b*x)+с
-
Квадратичная
: y=ax
2
+bx+c
Примечание
: Случаи приближения полиномом с 3-й до 6-й степени рассмотрены в этой статье. Приближение тригонометрическим полиномом рассмотрено здесь.
Линейная зависимость
Нас интересует связь 2-х переменных
х
и
y
. Имеется предположение, что
y
зависит от
х
по линейному закону
y
=
ax
+
b
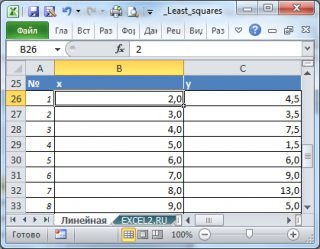
. Чтобы определить параметры этой взаимосвязи исследователь провел наблюдения: для каждого значения х
i
произведено измерение y
i
(см.
файл примера
). Соответственно, пусть имеется 20 пар значений (х
i
; y
i
).
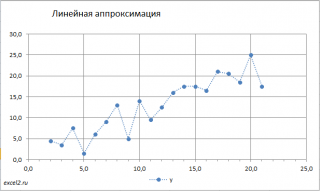
Для наглядности рекомендуется построить диаграмму рассеяния.
Примечание:
Если шаг изменения по
х
постоянен, то для построения
диаграммы рассеяния
можно использовать
тип График
, если нет, то необходимо использовать тип диаграммы
Точечная
.
Из диаграммы очевидно, что связь между переменными близка к линейной. Чтобы понять какая из множества прямых линий наиболее «правильно» описывает зависимость между переменными, необходимо определить критерий, по которому будут сравниваться линии.
В качестве такого критерия используем выражение:
где
ŷ
i
=
a
*
x
i
+
b
;
n – число пар значений (в нашем случае n=20)
Вышеуказанное выражение представляет собой сумму квадратов расстояний между наблюденными значениями y
i
и ŷ
i
и часто обозначается как SSE (
Sum
of
Squared
Errors
(
Residuals
), сумма квадратов ошибок (остатков)
)
.
Метод наименьших квадратов
заключается в подборе такой линии
ŷ
=
ax
+
b
, для которой вышеуказанное выражение принимает минимальное значение.
Примечание:
Любая линия в двухмерном пространстве однозначно определяется значениями 2-х параметров:
a
(наклон) и
b
(сдвиг).
Считается, что чем меньше сумма квадратов расстояний, тем соответствующая линия лучше аппроксимирует имеющиеся данные и может быть в дальнейшем использована для прогнозирования значений y от переменной х. Понятно, что даже если в действительности никакой взаимосвязи между переменными нет или связь нелинейная, то МНК все равно подберет «наилучшую» линию. Таким образом, МНК ничего не говорит о наличии реальной взаимосвязи переменных, метод просто позволяет подобрать такие параметры функции
a
и
b
, для которых вышеуказанное выражение минимально.
Проделав не очень сложные математические операции (подробнее см.
статью про квадратичную зависимость
), можно вычислить параметры
a
и
b
:
Как видно из формулы, параметр
a
представляет собой отношение ковариации и
дисперсии
, поэтому в MS EXCEL для вычисления параметра
а
можно использовать следующие формулы (см.
файл примера лист Линейная
):
=
КОВАР(B26:B45;C26:C45)/ ДИСП.Г(B26:B45)
или
=
КОВАРИАЦИЯ.В(B26:B45;C26:C45)/ДИСП.В(B26:B45)
Также для вычисления параметра
а
можно использовать формулу =
НАКЛОН(C26:C45;B26:B45)
. Для параметра
b
используйте формулу =
ОТРЕЗОК(C26:C45;B26:B45)
.
И наконец, функция
ЛИНЕЙН()
позволяет вычислить сразу оба параметра. Для ввода формулы
ЛИНЕЙН(C26:C45;B26:B45)
необходимо выделить в строке 2 ячейки и нажать
CTRL
+
SHIFT
+
ENTER
(см. статью про
формулы массива, возвращающими несколько значений
). В левой ячейке будет возвращено значение
а
, в правой –
b
.
Примечание
: Чтобы не связываться с вводом
формул массива
потребуется дополнительно использовать функцию
ИНДЕКС()
. Формула =
ИНДЕКС(ЛИНЕЙН(C26:C45;B26:B45);1)
или просто =
ЛИНЕЙН(C26:C45;B26:B45)
вернет параметр, отвечающий за наклон линии, т.е.
а
. Формула =
ИНДЕКС(ЛИНЕЙН(C26:C45;B26:B45);2)
вернет параметр, отвечающий за пересечение линии с осью Y, т.е.
b
.
Вычислив параметры, на
диаграмме рассеяния
можно построить соответствующую линию.
Инструмент диаграммы Линия тренда
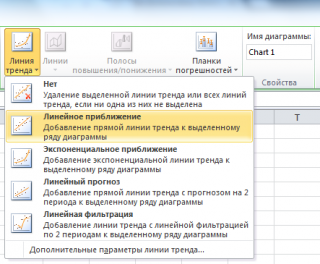
Еще одним способом построения прямой линии по методу наименьших квадратов является инструмент диаграммы
Линия тренда
. Для этого выделите диаграмму, в меню выберите
вкладку Макет
, в
группе Анализ
нажмите
Линия тренда
, затем
Линейное приближение
.
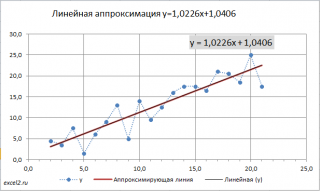
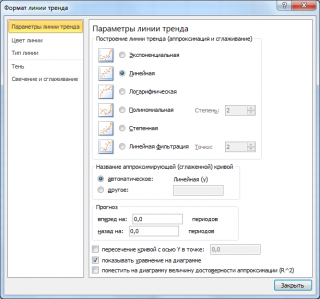
Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме.
Примечание
: Для того, чтобы параметры совпадали необходимо, чтобы тип у диаграммы был
Точечная, а не График
. Дело в том, что при построении диаграммы
График
значения по оси Х не могут быть заданы пользователем (пользователь может указать только подписи, которые не влияют на расположение точек). Вместо значений Х используется последовательность 1; 2; 3; … (для нумерации категорий). Поэтому, если строить
линию тренда
на диаграмме типа
График
, то вместо фактических значений Х будут использованы значения этой последовательности, что приведет к неверному результату (если, конечно, фактические значения Х не совпадают с последовательностью 1; 2; 3; …).
СОВЕТ
: Подробнее о построении диаграмм см. статьи
Основы построения диаграмм
и
Основные типы диаграмм
.
17 авг. 2022 г.
читать 2 мин
Метод наименьших квадратов — это метод, который мы можем использовать для поиска линии регрессии, которая лучше всего соответствует заданному набору данных.
В следующем видео представлено краткое объяснение этого метода:
Чтобы использовать метод наименьших квадратов для подбора линии регрессии в Excel, мы можем использовать функцию =ЛИНЕЙН() .
В следующем пошаговом примере показано, как использовать эту функцию на практике.
Шаг 1: Создайте набор данных
Во-первых, давайте создадим следующий набор данных в Excel:
Шаг 2: Используйте метод наименьших квадратов для подбора линии регрессии
Мы можем использовать функцию =LINEST(known_ys, known_xs) , чтобы использовать метод наименьших квадратов, чтобы подобрать линию регрессии к этому набору данных:
Как только мы нажмем ENTER , появятся коэффициенты регрессионной модели:
Шаг 3: интерпретируйте результаты
Используя коэффициенты из функции =LINEST() , мы можем написать следующую подобранную линию регрессии:
у = 11,55211 + 1,07949(х)
Мы можем использовать это уравнение для оценки значения y на основе значения x.
Например, если x = 10, то мы оценили бы, что y будет равно 22,347 :
у = 11,55211 + 1,07949(10) = 22,347
Шаг 4: Нанесите результаты на график
Наконец, мы можем использовать следующие шаги для построения набора данных вместе с подобранной линией регрессии:
- Выделите ячейки A2:B16 .
- Щелкните вкладку « Вставка » на верхней ленте. Затем щелкните первый параметр диаграммы под названием « Вставить точечную (X, Y)» или «Пузырьковую диаграмму » в группе «Диаграммы».
- После того, как диаграмма появится, нажмите знак плюс «+» в правом верхнем углу. В раскрывающемся меню установите флажок рядом с линией тренда , чтобы добавить на график подобранную линию регрессии.
Дополнительные ресурсы
Как выполнить множественную линейную регрессию в Excel
Как выполнить квадратичную регрессию в Excel
Как выполнить полиномиальную регрессию в Excel
Подбор кривой в Excel (с примерами)
Содержание
- Использование метода в Экселе
- Включение надстройки «Поиск решения»
- Условия задачи
- Решение
- Вопросы и ответы
Метод наименьших квадратов представляет собой математическую процедуру построения линейного уравнения, которое бы наиболее точно соответствовало набору двух рядов чисел. Целью применения данного способа является минимизация общей квадратичной ошибки. В программе Excel имеются инструменты, с помощью которых можно применять данный метод при вычислениях. Давайте разберемся, как это делается.
Использование метода в Экселе
Метод наименьших квадратов (МНК) является математическим описанием зависимости одной переменной от второй. Его можно использовать при прогнозировании.
Включение надстройки «Поиск решения»
Для того, чтобы использовать МНК в Экселе, нужно включить надстройку «Поиск решения», которая по умолчанию отключена.
- Переходим во вкладку «Файл».
- Кликаем по наименованию раздела «Параметры».
- В открывшемся окне останавливаем выбор на подразделе «Надстройки».
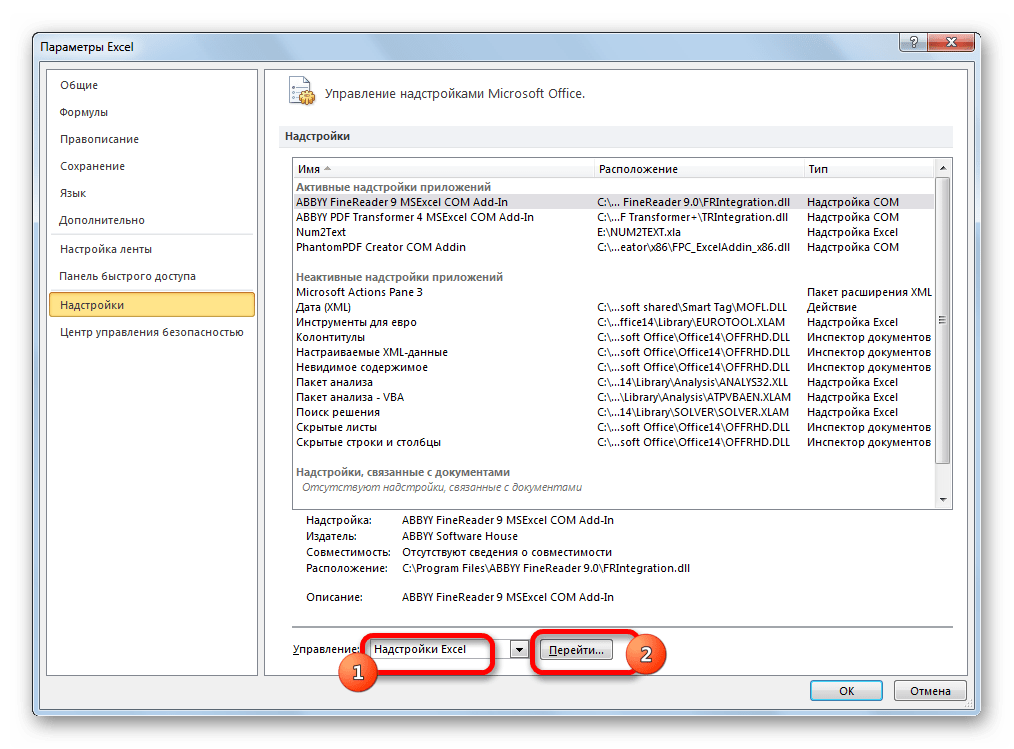
- В блоке «Управление», который расположен в нижней части окна, устанавливаем переключатель в позицию «Надстройки Excel» (если в нём выставлено другое значение) и жмем на кнопку «Перейти…».
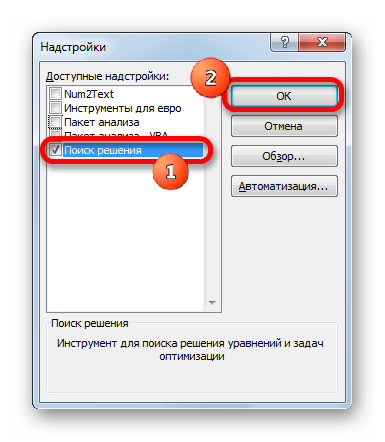
- Открывается небольшое окошко. Ставим в нём галочку около параметра «Поиск решения». Жмем на кнопку «OK».
Теперь функция Поиск решения в Excel активирована, а её инструменты появились на ленте.
Урок: Поиск решения в Экселе
Условия задачи
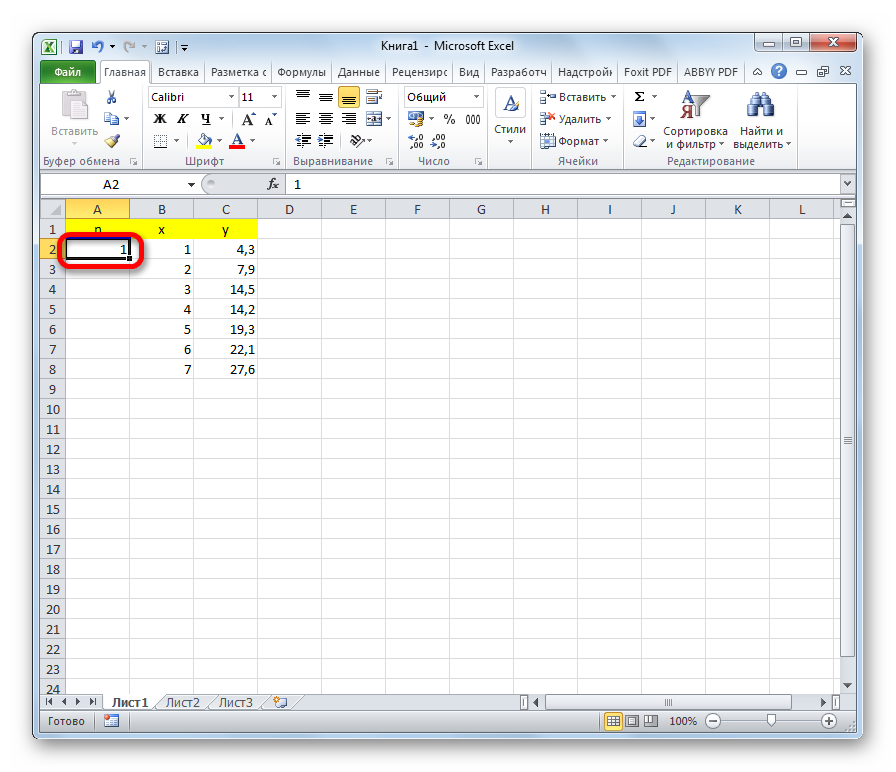
Опишем применение МНК на конкретном примере. Имеем два ряда чисел x и y, последовательность которых представлена на изображении ниже.
Наиболее точно данную зависимость может описать функция:
y=a+nx
При этом, известно что при x=0 y тоже равно 0. Поэтому данное уравнение можно описать зависимостью y=nx.
Нам предстоит найти минимальную сумму квадратов разности.
Решение
Перейдем к описанию непосредственного применения метода.
- Слева от первого значения x ставим цифру 1. Это будет приближенная величина первого значения коэффициента n.
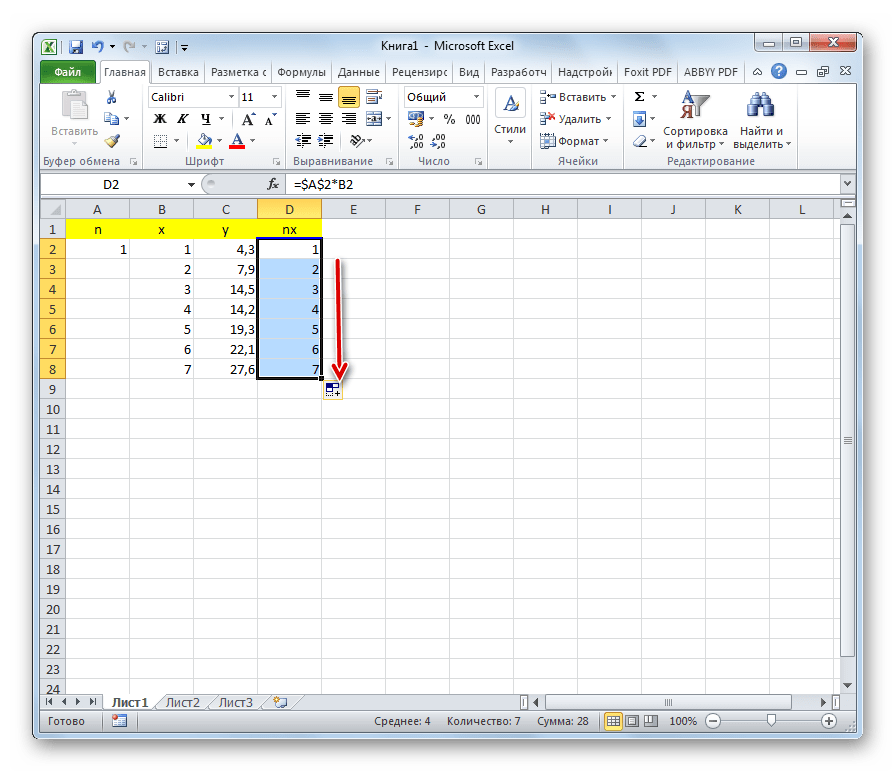
- Справа от столбца y добавляем ещё одну колонку – nx. В первую ячейку данного столбца записываем формулу умножения коэффициента n на ячейку первой переменной x. При этом, ссылку на поле с коэффициентом делаем абсолютной, так как это значение меняться не будет. Кликаем по кнопке Enter.
- Используя маркер заполнения, копируем данную формулу на весь диапазон таблицы в столбце ниже.
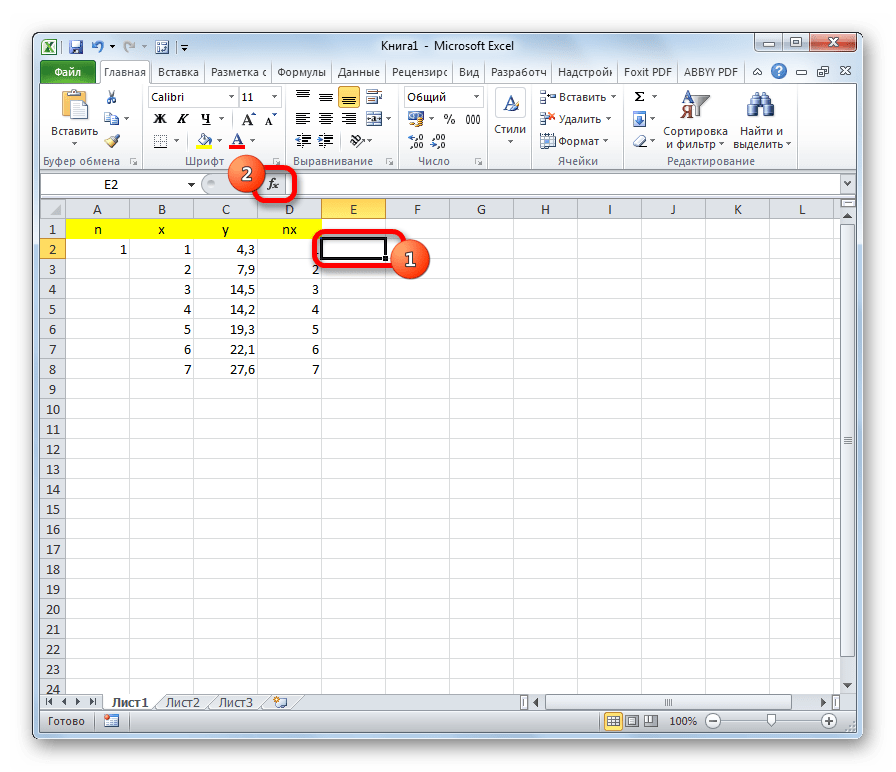
- В отдельной ячейке высчитываем сумму разностей квадратов значений y и nx. Для этого кликаем по кнопке «Вставить функцию».
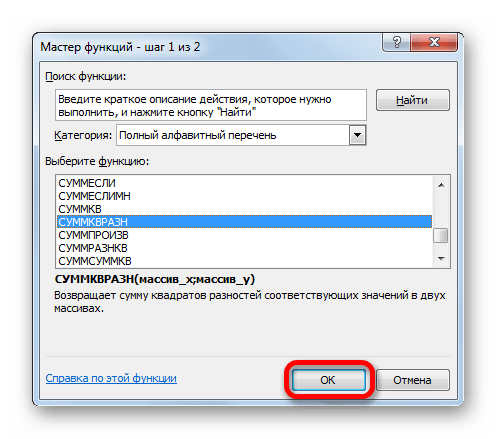
- В открывшемся «Мастере функций» ищем запись «СУММКВРАЗН». Выбираем её и жмем на кнопку «OK».
- Открывается окно аргументов. В поле «Массив_x» вводим диапазон ячеек столбца y. В поле «Массив_y» вводим диапазон ячеек столбца nx. Для того, чтобы ввести значения, просто устанавливаем курсор в поле и выделяем соответствующий диапазон на листе. После ввода жмем на кнопку «OK».
- Переходим во вкладку «Данные». На ленте в блоке инструментов «Анализ» жмем на кнопку «Поиск решения».
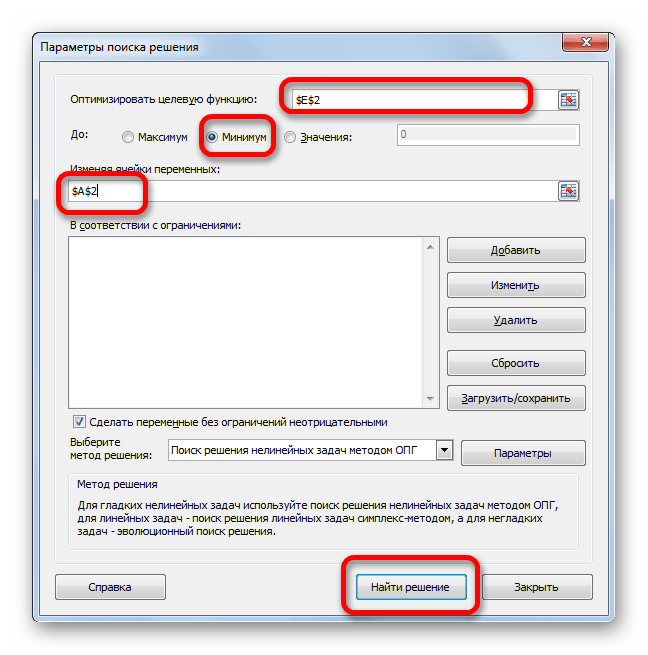
- Открывается окно параметров данного инструмента. В поле «Оптимизировать целевую функцию» указываем адрес ячейки с формулой «СУММКВРАЗН». В параметре «До» обязательно выставляем переключатель в позицию «Минимум». В поле «Изменяя ячейки» указываем адрес со значением коэффициента n. Жмем на кнопку «Найти решение».
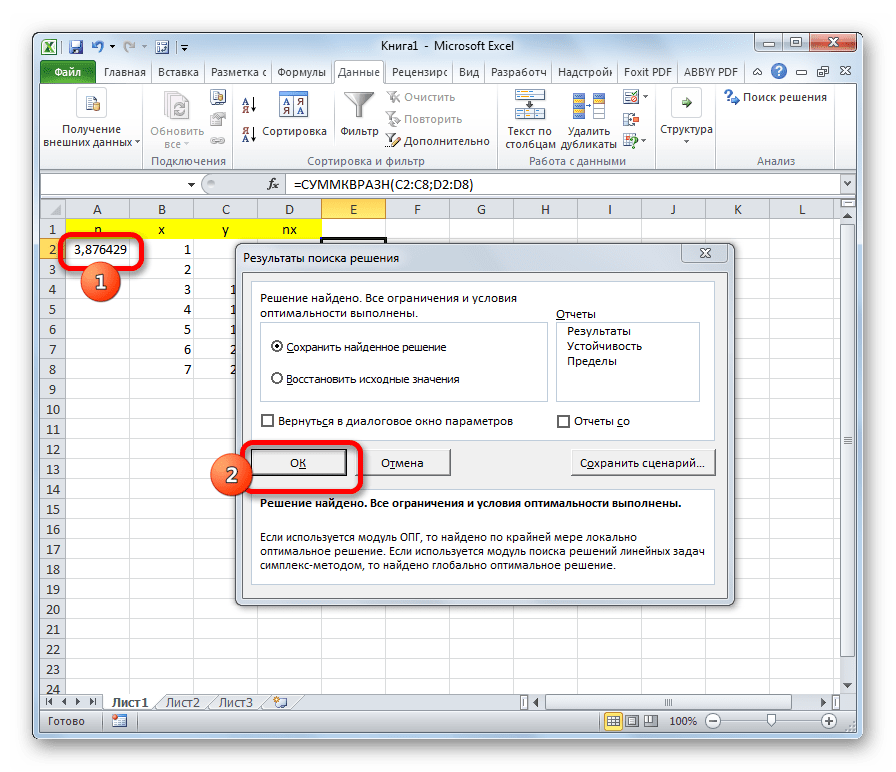
- Решение будет отображаться в ячейке коэффициента n. Именно это значение будет являться наименьшим квадратом функции. Если результат удовлетворяет пользователя, то следует нажать на кнопку «OK» в дополнительном окне.
Как видим, применение метода наименьших квадратов довольно сложная математическая процедура. Мы показали её в действии на простейшем примере, а существуют гораздо более сложные случаи. Впрочем, инструментарий Microsoft Excel призван максимально упростить производимые вычисления.
Еще статьи по данной теме:
Помогла ли Вам статья?
Программа Excel – мощный табличный редактор, позволяющий выполнять огромное количество различных операций и задач. В данной статье мы разберем, как можно применить метод наименьших квадратов (МНК), который используется для решения различных задач с минимизацией суммы квадратов отклонений некоторых функций от искомых переменных.
Содержание
- Подготовительный этап: активируем надстройку “Поиск Решения”
- Этап 1: исходные данные
- Этап 2: решаем задачу с применением МНК
- Заключение
Подготовительный этап: активируем надстройку “Поиск Решения”
Прежде, чем приступить к решению основной задачи, потребуется активировать надстройку “Поиск решения” в программе.
- Идем в меню “Файл”.
- В перечне слева выбираем пункт “Параметры”.
- В правой части подраздела “Надстройки” выбираем для параметра “Управление” вариант “Надстройки Excel” и жмем “Перейти”.
- Появится окно для выбора нужных надстроек. Устанавливаем галочку напротив пункта “Поиск решения” и щелкаем OK.
Этап 1: исходные данные
Давайте разберем применение метода наименьших квадратов, решив конкретный пример. Допустим, у нас есть два ряда числовых значений – X и Y.
Данная зависимость может быть описана уравнением ниже:
Y=A+NX
Также, мы знаем, что если X=0, то и Y=0. А значит, данное уравнение можно записать так:
Y=NX
Приступим к выполнению нашей задачи, которая заключается в нахождении суммы квадратов разности.
Этап 2: решаем задачу с применением МНК
- Столбцу, находящемся слева от X, задаем имя N пишем число “1” (примерное значение первого коэф. N) напротив первого значения ряда X.
- Столбцу с правой стороны от Y задаем название NX. Затем в самой верхней ячейке (напротив первых значений рядов X и Y) пишем формулу произведения коэф. N на соответствующее ему значение из столбца X. При этом адрес ячейки с коэффициентом нужно сделать абсолютным, чтобы он не менялся при копировании формулы. По готовности жмем Enter.
- Наводим указатель мыши на ячейку с полученным результатом. Как только появится черный плюсик (маркер заполнения), зажав левую кнопку мыши тянем его вниз до последней строки таблицы.
- Получаем результаты расчетов в каждой ячейке столбца NX.
- Теперь нужно посчитать сумму разностей квадратов значений Y и NX. Встаем в самую верхнюю ячейку столбца справа от NX (не считая шапки таблицы) и щелкаем по значку “Вставить функцию” (fx).
- В окне вставки функции выбираем категорию “Математические”, находим оператор “СУММКВРАЗН” и щелкаем OK.
- Теперь нужно заполнить аргументы функции:
- в поле “Массив_x” указываем координаты диапазона ячеек столбца Y (без шапки). Адреса ячеек можно указать как вручную, напечатав их с клавиатуры, так и путем выделения с помощью зажатой левой кнопки мыши в самой таблице.
- в поле “Массив_y” указываем диапазон ячеек столбца NX.
- жмем Enter, когда все готово.
- Переключаемся во вкладку “Данные”. В группе “Анализ” щелкаем по функции “Поиск решения”.
- Нам предстоит заполнить параметры поиска решения:
- в поле “Оптимизировать целевую функцию” следует указать ссылку на ячейку с функцией “СУММКВРАЗН”. Сделать это можно вручную или выбрав элемент в таблице.
- для опции “До” выбираем вариант – “Минимум”.
- в поле “Изменяя ячейки переменных” нужно указать координаты ячейки, в которой находится соответствующее значение коэф. N.
- по готовности нажимаем “Найти решение”.
- После выполнения функции появится окно с результатами поиска решения и произойдет замена значения в столбце N. Найденная величина является наименьшим квадратом функции. Нажимаем OK, если полученный результат удовлетворителен.
Заключение
Итак, мы только что разобрали на практическом примере, каким образом можно применить метод наименьших квадратов в Эксель. На практике могут встречаться более сложные задачи, однако, в целом логика действий схожа с той, что мы описали.
Содержание
- Постановка задачи на конкретном примере
- Наборы данных
- Графическая иллюстрация метода наименьших квадратов (мнк).
- Сглаживание ряда методом наименьших квадратов
- Суть метода
- Применение надстройки поиск решения
- Аппроксимация функции одной переменной методом наименьших квадратов с дополнительными условиями
- Оценка точности
- Вывод формул для нахождения коэффициентов.
- Как реализоавать метод наименьших квадратов в Excel
- Заключение
Постановка задачи на конкретном примере
Предположим, имеются два показателя X и Y. Причем Y зависит от X. Так как МНК интересует нас с точки зрения регрессионного анализа (в Excel его методы реализуются с помощью встроенных функций), то стоит сразу же перейти к рассмотрению конкретной задачи.
Итак, пусть X — торговая площадь продовольственного магазина, измеряемая в квадратных метрах, а Y — годовой товарооборот, определяемый в миллионах рублей.
Требуется сделать прогноз, какой товарооборот (Y) будет у магазина, если у него та или иная торговая площадь. Очевидно, что функция Y = f (X) возрастающая, так как гипермаркет продает больше товаров, чем ларек.
Наборы данных
Метод наименьших квадратов используется для обработки набора данных и прогнозирования будущих значений. Пусть у нас есть массивы данных X = {10, 12, 14, 16, 18, 20} и Y = {18, 22, 24, 26, 27, 28}, при этом значение Y зависит от X. Придадим этим массивам смысл. К примеру, массив X – это мощность паровой машины парохода, а Y — его ходовая скорость в узлах. Это означает, что при мощности энергетической установки в 10 тысяч лошадиных сил, пароход развивает скорость на уровне 18 морских миль в час, и так далее, так как каждое значение игрека соответствует своему иксу.
Эти данные можно представить в виде точек на декартовой плоскости, например как V1(X1, Y1), V2(X2, Y2) и так далее. Если соединить эти точки, то мы получим некую кривую, которую можем описать соответствующим уравнением y = f(x). Данное уравнение должно быть достаточно простым, но при этом максимально близко описывать полученную зависимость.
Получив кривую, мы можем продлить ее в любую сторону и узнать приблизительное значение игреков для любых иксов или наоборот. Например, аппроксимировав данные нашего примера, мы сможем узнать, какая мощность установки требуется для достижения скорости в 15 узлов. Или какую мы получим скорость, установив на борт установку мощностью в 22 тысячи лошадиных сил. Для того чтобы определить эту волшебную y = f(x), нам и необходим метод наименьших квадратов.
Графическая иллюстрация метода наименьших квадратов (мнк).
На графиках все прекрасно видно. Красная линия – это найденная прямая y = 0.165x+2.184, синяя линия – это 
Для чего это нужно, к чему все эти аппроксимации?
Я лично использую для решения задач сглаживания данных, задач интерполяции и экстраполяции (в исходном примере могли бы попросить найти занчение наблюдаемой величины y при x=3 или при x=6 по методу МНК). Но подробнее поговорим об этом позже в другом разделе сайта.
К началу страницы
Доказательство.
Чтобы при найденных а и b функция принимала наименьшее значение, необходимо чтобы в этой точке матрица квадратичной формы дифференциала второго порядка для функции 
Дифференциал второго порядка имеет вид:
То есть
Следовательно, матрица квадратичной формы имеет вид
причем значения элементов не зависят от а и b .
Покажем, что матрица положительно определенная. Для этого нужно, чтобы угловые миноры были положительными.
Угловой минор первого порядка 

Угловой минор второго порядка
Докажем, что 
-
Проверим справедливость неравенства для любого значения n, например для n=2.
Получили верное неравенство для любых несовпадающих значений
и
.
-
Предполагаем, что неравенство верное для n.
– верное.
-
Докажем, что неравенство верное для n+1.
То есть, нужно доказать, что
исходя из предположения что
– верное.
Поехали.
Выражение в фигурных скобках положительно по предположению пункта 2), а остальные слагаемые положительны, так как представляют собой квадраты чисел. Этим доказательство завершено.
Вывод : найденные значения а и b соответствуют наименьшему значению функции 
Сглаживание ряда методом наименьших квадратов
Задание.
1. Постройте прогноз численности наличного населения города Б на 2010-2011 гг., используя методы: скользящей средней, экспоненциального сглаживания, наименьших квадратов.
2. Постройте график фактического и расчетных показателей.
3. Рассчитайте ошибки полученных прогнозов при использовании каждого метода.
4. Сравните полученные результаты, сделайте вывод.
Решение.
1. Находим параметры уравнения методом наименьших квадратов. Линейное уравнение тренда имеет вид y = bt + a
Система уравнений МНК:
a0n + a1∑t = ∑y
a0∑t + a1∑t2 = ∑y•t
| t | y | t2 | y2 | t•y |
| 1 | 58.8 | 1 | 3457.44 | 58.8 |
| 2 | 58.7 | 4 | 3445.69 | 117.4 |
| 3 | 59 | 9 | 3481 | 177 |
| 4 | 59 | 16 | 3481 | 236 |
| 5 | 58.8 | 25 | 3457.44 | 294 |
| 6 | 58.3 | 36 | 3398.89 | 349.8 |
| 7 | 57.9 | 49 | 3352.41 | 405.3 |
| 8 | 57.5 | 64 | 3306.25 | 460 |
| 9 | 56.9 | 81 | 3237.61 | 512.1 |
| 45 | 524.9 | 285 | 30617.73 | 2610.4 |
Для наших данных система уравнений имеет вид:
9a0 + 45a1 = 524.9
45a0 + 285a1 = 2610.4
Из первого уравнения выражаем а0 и подставим во второе уравнение
Получаем a0 = -0.24, a1 = 59.5
Уравнение тренда:
y = -0.24 t + 59.5
Эмпирические коэффициенты тренда a и b являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Коэффициент тренда b = -0.24 показывает среднее изменение результативного показателя (в единицах измерения у) с изменением периода времени t на единицу его измерения. В данном примере с увеличением t на 1 единицу, y изменится в среднем на -0.24.
Ошибка аппроксимации.
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.
Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения тренда к исходным данным.
Поскольку ошибка меньше 7%, то данное уравнение можно использовать в качестве тренда.
Однофакторный дисперсионный анализ.
Средние значения
Дисперсия
Среднеквадратическое отклонение
Коэффициент эластичности.
Коэффициент эластичности представляет собой показатель силы связи фактора t с результатом у, показывающий, на сколько процентов изменится значение у при изменении значения фактора на 1%.
Коэффициент эластичности меньше 1. Следовательно, при изменении t на 1%, Y изменится менее чем на 1%. Другими словами – влияние t на Y не существенно.
Эмпирическое корреляционное отношение.
Эмпирическое корреляционное отношение вычисляется для всех форм связи и служит для измерение тесноты зависимости. Изменяется в пределах [0;1].
где (y-yt)² = 4.4-1.08 = 3.31
В отличие от линейного коэффициента корреляции он характеризует тесноту нелинейной связи и не характеризует ее направление. Изменяется в пределах [0;1].
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 0.3 0.5 0.7 0.9 Полученная величина свидетельствует о том, что изменение временного периода t существенно влияет на y.
Коэффициент детерминации.
т.е. в 75.39% случаев влияет на изменение данных. Другими словами – точность подбора уравнения тренда – высокая.
| t | y | y(t) | (y-ycp)2 | (y-y(t))2 | (t-tp)2 | (y-y(t)) : y |
| 1 | 58.8 | 59.26 | 0.23 | 0.21 | 16 | 0.00786 |
| 2 | 58.7 | 59.03 | 0.14 | 0.11 | 9 | 0.00557 |
| 3 | 59 | 58.79 | 0.46 | 0.0431 | 4 | 0.00352 |
| 4 | 59 | 58.56 | 0.46 | 0.2 | 1 | 0.0075 |
| 5 | 58.8 | 58.32 | 0.23 | 0.23 | 0 | 0.00813 |
| 6 | 58.3 | 58.09 | 0.0004 | 0.0452 | 1 | 0.00365 |
| 7 | 57.9 | 57.85 | 0.18 | 0.0022 | 4 | 0.000825 |
| 8 | 57.5 | 57.62 | 0.68 | 0.0137 | 9 | 0.00204 |
| 9 | 56.9 | 57.38 | 2.02 | 0.23 | 16 | 0.00847 |
| 45 | 524.9 | 524.9 | 4.4 | 1.08 | 60 | 0.0476 |
Интервальный прогноз.
Определим среднеквадратическую ошибку прогнозируемого показателя.
m = 1 – количество влияющих факторов в уравнении тренда.
Uy=yn+L±K
где
L – период упреждения; уn+L – точечный прогноз по модели на (n + L)-й момент времени; n – количество наблюдений во временном ряду; Sy – стандартная ошибка прогнозируемого показателя; Tтабл – табличное значение критерия Стьюдента для уровня значимости α и для числа степеней свободы, равного n-2.
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;α/2) = (7;0.025) = 2.365
Точечный прогноз, t = 10: y(10) = -0.24*10 + 59.5 = 57.15
57.15 – 1.08 = 56.07 ; 57.15 + 1.08 = 58.23
Интервальный прогноз:
t = 10: (56.07;58.23)
Точечный прогноз, t = 11: y(11) = -0.24*11 + 59.5 = 56.91
56.91 – 1.14 = 55.77 ; 56.91 + 1.14 = 58.05
Интервальный прогноз:
t = 11: (55.77;58.05)
2. Сглаживаем ряд методом скользящей средней. Одним из эмпирических методов является метод скользящей средней. Этот метод состоит в замене абсолютных уровней ряда динамики их средними арифметическими значениями за определенные интервалы. Выбираются эти интервалы способом скольжения: постепенно исключаются из интервала первые уровни и включаются последующие.
| t | y | ys | Формула |
| 1 | 58.8 | 58.75 | (58.8 + 58.7)/2 |
| 2 | 58.7 | 58.85 | (58.7 + 59)/2 |
| 3 | 59 | 59 | (59 + 59)/2 |
| 4 | 59 | 58.9 | (59 + 58.8)/2 |
| 5 | 58.8 | 58.55 | (58.8 + 58.3)/2 |
| 6 | 58.3 | 58.1 | (58.3 + 57.9)/2 |
| 7 | 57.9 | 57.7 | (57.9 + 57.5)/2 |
| 8 | 57.5 | 57.2 | (57.5 + 56.9)/2 |
| 9 | 56.9 | – | – |
Стандартная ошибка (погрешность) рассчитывается по формуле:
где i = (t-m-1, t)
3. Построим прогноз численности с использованием экспоненциального сглаживания. Важным методом стохастических прогнозов является метод экспоненциального сглаживания. Этот метод заключается в том, что ряд динамики сглаживается с помощью скользящей средней, в которой веса подчиняются экспоненциальному закону.
Эту среднюю называют экспоненциальной средней и обозначают St.
Она является характеристикой последних значений ряда динамики, которым присваивается наибольший вес.
Экспоненциальная средняя вычисляется по рекуррентной формуле:
St = α*Yt + (1- α)St-1
где St – значение экспоненциальной средней в момент t;
St-1 – значение экспоненциальной средней в момент (t = 1);
Что касается начального параметра S0, то в задачах его берут или равным значению первого уровня ряда у1, или равным средней арифметической нескольких первых членов ряда.
Yt – значение экспоненциального процесса в момент t;
α – вес t-ого значения ряда динамики (или параметр сглаживания).
Последовательное применение формулы дает возможность вычислить экспоненциальную среднюю через значения всех уровней данного ряда динамики.
Наиболее важной характеристикой в этой модели является α, по величине которой практически и осуществляется прогноз. Чем значение этого параметра ближе к 1, тем больше при прогнозе учитывается влияние последних уровней ряда динамики.
Если α близко к 0, то веса, по которым взвешиваются уровни ряда динамики убывают медленно, т.е. при прогнозе учитываются все прошлые уровни ряда.
В специальной литературе отмечается, что обычно на практике значение α находится в пределах от 0,1 до 0,3. Значение 0,5 почти никогда не превышается.
Экспоненциальное сглаживание применимо, прежде всего, при постоянном объеме потребления (α = 0,1 – 0,3). При более высоких значениях (0,3 – 0,5) метод подходит при изменении структуры потребления, например, с учетом сезонных колебаний.
В качестве S0 берем первое значение ряда, S0 = y1 = 58.8
| t | y | St | Формула |
| 1 | 58.8 | 58.8 | (1 – 0.1)*58.8 + 0.1*58.8 |
| 2 | 58.7 | 58.71 | (1 – 0.1)*58.7 + 0.1*58.8 |
| 3 | 59 | 58.97 | (1 – 0.1)*59 + 0.1*58.71 |
| 4 | 59 | 59 | (1 – 0.1)*59 + 0.1*58.97 |
| 5 | 58.8 | 58.82 | (1 – 0.1)*58.8 + 0.1*59 |
| 6 | 58.3 | 58.35 | (1 – 0.1)*58.3 + 0.1*58.82 |
| 7 | 57.9 | 57.95 | (1 – 0.1)*57.9 + 0.1*58.35 |
| 8 | 57.5 | 57.54 | (1 – 0.1)*57.5 + 0.1*57.95 |
| 9 | 56.9 | 56.96 | (1 – 0.1)*56.9 + 0.1*57.54 |
Прогнозирование данных с использованием экспоненциального сглаживания.
Методы прогнозирования под названием “сглаживание” учитывают эффекты выброса функции намного лучше, чем способы, использующие регрессивный анализ.
Базовое уравнение имеет следующий вид:
F(t+1) = F(t)(1 – α) + αY(t)
F(t) – это прогноз, сделанный в момент времени t; F(t+1) отражает прогноз во временной период, следующий непосредственно за моментом времени t
Стандартная ошибка (погрешность) рассчитывается по формуле:
где i = (t – 2, t)
Пример. Методом наименьших квадратов найти функции вида y=ax+b, y=ax²+bx+c, аппроксимирующие экспериментальную функцию y=f(x). В обоих случаях найти суммы квадратов невязок ∑bi². В декартовой системе координат построить экспериментальные точки и графики найденных функций y=ax+b,y=ax^2+bx+c.
Пример №5
Пример №6
Пример №3. Функция y=y(x) задана таблицей своих значений:
x: -2 -1 0 1 2
y: -0,8 -1,6 -1,3 0,4 3,2
Применяя метод наименьших квадратов, приблизить функцию многочленами 1-ой и 2-ой степеней. Для каждого приближения определить величину среднеквадратичной погрешности. Построить точечный график функции и графики многочленов.
Решение. Функция многочлена 2-ой степени имеет вид y = ax2+ bx + c.
1. Находим параметры уравнения методом наименьших квадратов. Система уравнений МНК:
a0n + a1∑x + a2∑x2= ∑y
a0∑x + a1∑x2+ a2∑x3= ∑yx
a0∑x2+ a1∑x3+ a2∑x4= ∑yx2
| x | y | x2 | y2 | x y | x3 | x4 | x2y |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| -2 | -0.8 | 4 | 0.64 | 1.6 | -8 | 16 | -3.2 |
| -1 | -1.6 | 1 | 2.56 | 1.6 | -1 | 1 | -1.6 |
| 0 | -1.3 | 0 | 1.69 | 0 | 0 | 0 | 0 |
| 1 | 0.4 | 1 | 0.16 | 0.4 | 1 | 1 | 0.4 |
| 2 | 3.2 | 4 | 10.24 | 6.4 | 8 | 16 | 12.8 |
| 0 | -0.1 | 10 | 15.29 | 10 | 0 | 34 | 8.4 |
Для наших данных система уравнений имеет вид
6a0+ 0a1+ 10a2= -0.1
0a0+ 10a1+ 0a2= 10
10a0+ 0a1+ 34a2= 8.4
Получаем a0= 0.494, a1= 1, a2= -0.84
Уравнение: y = 0.494x2+x-0.84
Суть метода
Данные таблицы можно изобразить на декартовой плоскости в виде точек M1 (x1, y1), … Mn (xn, yn). Теперь решение задачи сведется к подбору аппроксимирующей функции y = f (x), имеющей график, проходящий как можно ближе к точкам M1, M2, ..Mn.
Конечно, можно использовать многочлен высокой степени, но такой вариант не только труднореализуем, но и просто некорректен, так как не будет отражать основную тенденцию, которую и нужно обнаружить. Самым разумным решением является поиск прямой у = ax + b, которая лучше всего приближает экспериментальные данные, a точнее, коэффициентов – a и b.
Применение надстройки поиск решения
1. Если не включили надстройку «поиск решения», то возвращаемся к пункту Как включить надстройку «поискрешения» и включаем
2. В ячейку А1 введем значение «1». Эта единица будет первым приближением к реальному значению коэффициента (k) нашей функциональной зависимости y=kx.
3. В столбце B у нас расположились значения параметра X, в столбце C — значения параметра Y. В ячейках столбца D вводим формулу: «коэффициент k умножить на значение Х». Например, в ячейке D1 вводим «=A1*B1», в ячейке D2 вводим “=A1*B2” и т.д.
4. Мы считаем, что коэффициент к равен единице и функция f (x)=у=1*х – это первое приближение к нашему решению. Можем рассчитать сумму квадратов разностей между измеренными значениями величины Y и рассчитанными по формуле y=1*х . Можем все это сделать вручную, вбивая в формулу соответствующие ссылки на ячейки: “=(D2-C2)^2+(D3-C3)^2+(D4-C4)^2… и т.д. В конце концов ошибаемся и понимаем, что потеряли кучу времени. В Excel для расчета суммы квадратов разностей есть специальная формула, «СУММКВРАЗН», которая все за нас и сделает. Введем ее в ячейку А2 и зададим исходные данные: диапазон измеренных значений Y (столбец C) и диапазон рассчитанных значений Y (столбец D).
4. Сумму разностей квадратов рассчитали – теперь идем во вкладку «Данные» и выбираем «Поиск решения».
5. В появившемся меню в качестве изменяемой ячейки выбираем ячейку A1 (та, что с коэффициентом k).
6. В качестве целевой выбираем ячейку A2 и задаем условие «установить равной минимальному значению». Помним, что это ячейка, где у нас производится расчёт суммы квадратов разностей расчетного и измеренного значений, и сумма эта должна быть минимальной. Нажимаем «выполнить».
7. Коэффициент k подобран. Теперь можно убедиться, что рассчитанные значения теперь очень близки к измеренным.
Аппроксимация функции одной переменной методом наименьших квадратов с дополнительными условиями
Данный калькулятор использует метод наименьших квадратов (МНК) для аппроксимации функции одной переменной, аналогично калькулятору Аппроксимация функции одной переменной. Но, в отличии от указанного калькулятора, данный калькулятор поддерживает аппроксимацию функции с использованием ограничений на ее значения. То есть, можно задать условия равенства аппроксимирующей функции определенным значениям в определенных точках. Формулы аппроксимации будут выведены с учетом этих условий.
Используемый метод (метод множителей Лагранжа) накладывает ограничения на набор аппроксимирующих функций, так что этот калькулятор не поддерживает экспоненциальную аппроксимацию, аппроксимацию степенной функцией и показательную аппроксимацию. Одним словом поддерживается только линейная регрессия. Зато в него были добавлены аппроксимация полиномами 4-ой и 5-ой степени. Формулы и немного теории можно найти под калькулятором.
Если не ввести значения x, калькулятор будет считать, что значение x меняется начиная с 0 с шагом 1.
Оценка точности
При любой аппроксимации особую важность приобретает оценка ее точности. Обозначим через ei разность (отклонение) между функциональными и экспериментальными значениями для точки xi, т. е. ei = yi – f (xi).
Очевидно, что для оценки точности аппроксимации можно использовать сумму отклонений, т. е. при выборе прямой для приближенного представления зависимости X от Y нужно отдавать предпочтение той, у которой наименьшее значение суммы ei во всех рассматриваемых точках. Однако, не все так просто, так как наряду с положительными отклонениями практически будут присутствовать и отрицательные.
Решить вопрос можно, используя модули отклонений или их квадраты. Последний метод получил наиболее широкое распространение. Он используется во многих областях, включая регрессионный анализ (в Excel его реализация осуществляется с помощью двух встроенных функций), и давно доказал свою эффективность.
Вывод формул для нахождения коэффициентов.
Составляется и решается система из двух уравнений с двумя неизвестными. Находим частные производные функции 
Решаем полученную систему уравнений любым методом (например методом подстановки или методом Крамера) и получаем формулы для нахождения коэффициентов по методу наименьших квадратов (МНК).
При данных а и b функция 
Вот и весь метод наименьших квадратов. Формула для нахождения параметра a содержит суммы 



Пришло время вспомнить про исходый пример.
Решение.
В нашем примере n=5 . Заполняем таблицу для удобства вычисления сумм, которые входят в формулы искомых коэффициентов.
Значения в четвертой строке таблицы получены умножением значений 2-ой строки на значения 3-ей строки для каждого номера i .
Значения в пятой строке таблицы получены возведением в квадрат значений 2-ой строки для каждого номера i .
Значения последнего столбца таблицы – это суммы значений по строкам.
Используем формулы метода наименьших квадратов для нахождения коэффициентов а и b. Подставляем в них соответствующие значения из последнего столбца таблицы:
Следовательно, y = 0.165x+2.184 – искомая аппроксимирующая прямая.
Осталось выяснить какая из линий y = 0.165x+2.184 или 
Как реализоавать метод наименьших квадратов в Excel
В “Эксель” имеется функция для расчета значения по МНК. Она имеет следующий вид: «ТЕНДЕНЦИЯ» (известн. значения Y; известн. значения X; новые значения X; конст.). Применим формулу расчета МНК в Excel к нашей таблице.
Для этого в ячейку, в которой должен быть отображен результат расчета по методу наименьших квадратов в Excel, введем знак «=» и выберем функцию «ТЕНДЕНЦИЯ». В раскрывшемся окне заполним соответствующие поля, выделяя:
- диапазон известных значений для Y (в данном случае данные для товарооборота);
- диапазон x1, …xn, т. е. величины торговых площадей;
- и известные, и неизвестные значения x, для которого нужно выяснить размер товарооборота (информацию об их расположении на рабочем листе см. далее).
Кроме того, в формуле присутствует логическая переменная «Конст». Если ввести в соответствующее ей поле 1, то это будет означать, что следует осуществить вычисления, считая, что b = 0.
Если нужно узнать прогноз для более чем одного значения x, то после ввода формулы следует нажать не на «Ввод», а нужно набрать на клавиатуре комбинацию «Shift» + «Control»+ «Enter» («Ввод»).
Заключение
Метод наименьших квадратов — удобный метод для представления данных в виде функции. Благодаря такому представлению вы можете определить любое значение функции, оперируя небольшим набором данных или измерений.
Источники
- https://FB.ru/article/342215/metod-naimenshih-kvadratov-v-excel-regressionnyiy-analiz
- https://BBF.ru/calculators/69/
- http://www.cleverstudents.ru/articles/mnk.html
- https://math.semestr.ru/trend/least-square-method.php
- http://metallovedeniye.ru/analiz-dannyx-v-excel/metod-naimenshix-kvadratov-i-poisk-resheniya-v-excel.html
- https://planetcalc.ru/8735/?thanks=1

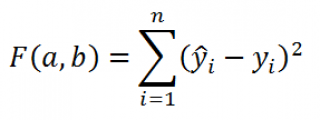
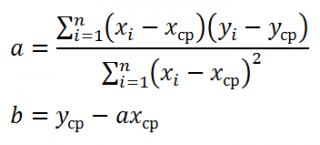


































 и
и  .
. исходя из предположения что
исходя из предположения что 


























