Microsoft excel в решении профессиональных задач

Введение

Программное приложение MS Excel — это отличный инструментальный набор, позволяющий обрабатывать и анализировать большие информационные объёмы и, помимо этого, дающий возможность осуществлять простые вычислительные операции. Основой этих впечатляющих достоинств программного пакета выступает использование сеточного набора ячеек, в которые записывается числовая и текстовая информация, а также данные в формульном формате. Необходимо занести данные в ячейки и осуществить их группировку в столбиках и строках. Далее появляется возможность выполнения различных вычислительных операций с информационными данными, возможность их сортировки и фильтрации, а также возможность размещения их в виде таблиц и формирования профессиональных диаграмм.

Создание книг

Документы в программе Excel называются книгами, состоящими из листового комплекта. В книгу может быть добавлено практически любое количество листов, а также есть возможность создания новой книги для сохранения информационных данных в виде отдельного файла. Чтобы осуществить такую операцию, следует выполнить такие процедуры:

1. Зайти во вкладку «Файл» и сделать выбор команды «Создать».
2. В разделе «Доступные шаблоны» осуществить выбор операции «Новая книга».

Далее, чтобы занести в книгу информацию, следует выполнить такие операции:

1. Выполнить щелчок указателем мыши по пустой ячейке, например, это может быть ячейка А1 на рисунке выше. Нумерация ячеек формируется на листе номерами столбиков и строчек. «А» считается столбцом номер один (а далее согласно английскому алфавиту), а число один является номером строки.
2. Занести в ячейку нужные информационные данные (цифровые или текстовые).
3. Чтобы перейти к следующей ячейке, необходимо нажать кнопку ВВОД или ТАБ.

«Решение профессиональных задач в пакете Excel» 👇

Операции с ячейками

Чтобы задать границы ячеек, над которыми будут выполняться действия, нужно осуществить следующие операции:

1. Выделить указателем мыши одну или группу ячеек, для которых требуется задать границы.
2. Зайти на главную вкладку и там найти раздел «Шрифт». Выполнить щелчок указателем мыши по стрелке вблизи кнопки «Границы» и сделать выбор необходимого стилистического оформления границ. На рисунке ниже изображено это окно:

Для заливки ячеек определённым цветом, нужно осуществить следующий порядок операций:

1. Выделить указателем мыши одну или комплект ячеек, которые требуется покрасить в определённый цвет.
2. В главной вкладке найти группу «Шрифт» и щёлкнуть на стрелку вблизи клавиши «Цвет заливки». Затем в группе «Цвета темы» или «Стандартные цвета» требуется сделать выбор требуемого цвета.

При необходимости оперативно просуммировать данные из определённых ячеек, можно воспользоваться операцией «Сумма». Для этого надо выполнить следующие действия:

1. Выбрать ячейку, расположенную ниже или правее от чисел, которые следует прибавить.
2. Зайти на главную вкладку и там найти раздел «Редактирование», где следует нажать кнопку «Авто сумма».

После этих действий будет выполнено суммирование требуемых чисел и результирующий итог будет занесён в указанную ранее ячейку.

Арифметическая операция определения суммы чисел — это лишь одна из большого набора математических операций в программе Excel. Например, можно задавать формулы, чтобы осуществить разные действия. В этом случае следует выполнить следующие действия:

• Выполнить задание ячейки, затем занести в неё символ «равно» (=). Он является признаком наличия формулы в данной ячейке.
• Занести в ячейку набор знаков операций и чисел, то есть, фактически записать формулу вычислений. Если требуется выполнить сложение, ставится знак «плюс» (+), если вычитание, то надо поставить «минус» (-). При выполнении умножения ставится знак «звезда» (*), а при выполнении операции деления ставится знак «наклонная черта» (/).
• Например, если ввести =4+6, =4-2, =4*6 или 10/5, далее нажать клавишу «Ввод», то произойдёт исполнение операции. При нажатии CTRL+ВВОД указатель будет оставлен в той же ячейке.

При необходимости отличать разные числовые виды, можно воспользоваться возможностью присваивать определённым группам разные форматы. К примеру, имеются форматы «дата», «проценты», «деньги». Чтобы задать требуемый информационный формат, следует осуществить такие операции:

1. Выделить числовые ячейки, которые нужно отформатировать.
2. Зайти на главную вкладку и щёлкнуть указателем мыши по стрелке в группе «Общий».
3. Выбрать требуемый числовой формат.

В случае отсутствия нужного формата в предложенном перечне, следует сделать выбор опции «Другие числовые форматы».

Для того, чтобы иметь возможность использования всего обширного инструментального и операционного набора программы Excel, следует оформить данные в табличном формате. Таблица позволяет оперативно фильтровать и сортировать данные. Для формирования данных в виде таблицы, следует исполнить следующие операции:

1. Выделить указателем мыши требуемые данные. Точнее надо щёлкнуть по первой из ячеек и далее осуществить выделение нужного участка, перетаскивая её до последней из требуемых ячеек. При необходимости выполнить выделение только клавиатурой, то требуется нажать клавишу SHIFT, а выделение выполнять клавишами со стрелками.
2. Нажать кнопку «Экспресс-анализ», которая расположена в нижнем углу справа в выбранном участке.
3. Зайти во вкладку «Таблицы» и сделать выбор указателем мыши кнопки «Таблица». Появится изображение будущей таблицы. В случае, когда нет ошибок и всё верно, нужно нажать кнопку «Таблица».
4. Щёлкнуть указателем мыши по стрелке в заглавии требуемого табличного столбика.
5. Чтобы отфильтровать информационные данные требуется снять флаг «Выделить всё» и выбрать данные, которые требуется отобразить в таблице.
6. Для выполнения сортировки данных, следует сделать выбор пункта «Сортировка от А до Я», или наоборот «Сортировка от Я до А».

Комитет образования и науки Курской области

Областное бюджетное профессиональное образовательное учреждение

«Рыльский аграрный техникум»

Индивидуальный проект

по предмету: «Информатика»

на тему: «Использование табличного процессора MS Excel в профессиональной деятельности»

Выполнила студентка

Толкачева Ирина Сергеевна,

очная форма, профессия

«Повар, кондитер»

Руководитель:

преподаватель Матюхина Ю.В.

Рыльск 2019г.

ОГЛАВЛЕНИЕ

Введение 3

1. Технология обработки числовых данных

1.1 Общая характеристика табличного процессора MS Excel 4

1.2. Вычисления в электронной таблице MS Excel 5

1.3. Надстройки MS Excel 7

2. Решение профессиональных задач средствами MS Excel

2.1. Калькуляция себестоимости готовой продукции 11

2.2. Решение задач оптимально планирования 13

Заключение 18

Библиографический список 19

Приложения 20

ВВЕДЕНИЕ

Современный период развития общества характеризуется сильным влиянием на него компьютерных технологий, проникающих во все сферы человеческой деятельности. Поэтому обязательным компонентом подготовки любого специалиста является умение использовать компьютер для решения профессиональных задач. Будущие специалисты должны обладать системой знаний и умений, позволяющих грамотно использовать компьютерные технологии в своей профессиональной деятельности.

Выпускникам по профессии «Повар, кондитер» необходимо уметь составлять калькуляционные карты, технологические карты, производить расчет количества продуктов для приготовления блюд, осуществлять оптимальное планирование выпуска продукции и решать другие вычислительные задачи.

Цель проекта – рассмотреть возможности табличных процессоров для решения профессиональных задач повара, кондитера.

Задачи:

• Изучить теоретический материал о вычислительных возможностях табличных процессоров;

• Разработать ассортимент блюд, рассчитать и составить технологические карты;

• Создать калькуляционные карты с автоматическим расчетом себестоимости блюд и цены продажи блюда;

• Познакомиться с использование электронной таблицы для решения задач оптимального планирования.

Объект исследования – табличный процессор. Предмет исследования – программа MS Excel.

1. ТЕХНОЛОГИЯ ОБРАБОТКИ ЧИСЛОВЫХ ДАННЫХ

1.1 Общая характеристика табличного процессора MS Excel

Табличный процессор Microsoft Excel представляет собой электронную таблицу, которая предназначена не только для составления таблиц различной степени сложности, но и для ведения различного рода отчетности (бухгалтерской, складской и др.). Помимо этого Microsoft Excel позволяет легко производить различные расчеты, строить графики и диаграммы, вести базы данных.

Microsoft Excel предназначен для работы с электронными таблицами (Sheets), позволяющими собирать, анализировать и представлять в удобном виде количественную и текстовую информацию.

Электронная таблица – самая распространенная и мощная технология для профессиональной работы с данными. В ячейках таблицы могут быть записаны данные различных типов: текст, даты, числа, формулы и др. Главное достоинство электронной таблицы – возможность мгновенного автоматического пересчета всех данных, связанных формульными зависимостями, при изменении значения любого компонента таблицы.

Основные возможности электронных таблиц:

1. Проведение однотипных сложных расчётов над большими наборами данных.

2. Автоматизация итоговых вычислений.

3. Решение задач путём подбора значений параметров.

4. Обработка (статистический анализ) результатов экспериментов.

5. Проведение поиска оптимальных значений параметров (решение оптимизационных задач).

6. Подготовка табличных документов.

7. Построение диаграмм по имеющимся данным.

8. Создание и анализ баз данных (списков).

Программа обработки электронных таблиц MS Excel обеспечивает пользователя богатым набором возможностей создания и изменения таблиц, которые могут содержать числа, текст, даты, денежные единицы, графику, а также математические и иные формулы для выполнения вычислений. Ввод данных в таблицы, их форматирование и выполнение различного рода вычислений в значительной степени автоматизированы. Предусмотрены средства представления числовых данных в виде диаграмм, создания, сортировки и фильтрации списков, статистического анализа данных и решения оптимизационных задач.

Кроме специфических инструментов, характерных для работы с электронными таблицами, MS Excel обладает стандартным для приложений Windows набором файловых операций, имеет доступ к буферу обмена и механизмам отмены и возврата.

Документы MS Excel записываются в файлы, имеющие расширение .xlsx. Кроме того, MS Excel может работать с электронными таблицами и диаграммами, созданными в других распространенных пакетах (например, Lotus 1-2-3), а также преобразовывать создаваемые им файлы для использования их другими программами.

1. Вычисления в электронной таблице MS Excel

Вычисления в таблицах программы Excel осуществляются при помощи формул. Формулой в Excel называется последовательность символов, начинающаяся со знака равенства “=“. В эту последовательность символов могут входить постоянные значения, ссылки на ячейки, имена, функции или операторы. Результатом работы формулы является новое значение, которое выводится как результат вычисления формулы по уже имеющимся данным.

Операторами обозначаются операции, которые следует выполнить над операндами формулы. В Microsoft Excel включено четыре вида операторов: арифметические, текстовые, операторы сравнения и операторы ссылок.

Арифметические операторы служат для выполнения арифметических операций, таких как сложение, вычитание, умножение. Операции выполняются над числами. Операторы сравнения используются для сравнения двух значений. Результатом сравнения является логическое значение: либо ИСТИНА, либо ЛОЖЬ. Текстовый оператор конкатенации (&) используется для объединения нескольких текстовых строк в одну строку. Операторы ссылки применяют для описания ссылок на диапазоны ячеек.

Формулы вычисляют значения в определенном порядке. Формула вычисляется слева направо, в соответствии с определенным порядком для каждого оператора в формуле. Для того чтобы изменить порядок выполнения, заключите часть формулы, которая должна выполняться первой, в скобки.

Для выполнения табличных вычислений нужны формулы. Поскольку некоторые формулы и их комбинации встречаются очень часто, то программа Excel предлагает более 200 заранее запрограммированных формул, которые называются функциями.

Все функции разделены по категориям, чтобы в них было проще ориентироваться. Встроенный Конструктор функций помогает на всех этапах работы правильно применять функции. Он позволяет построить и вычислить большинство функций за два шага.

В программе имеется упорядоченный по алфавиту полный список всех функций, в котором можно легко найти функцию, если известно ее имя; в противном случае следует производить поиск по категориям. Многие функции различаются очень незначительно, поэтому при поиске по категориям полезно воспользоваться краткими описаниями функций, которые предлагает Конструктор функций. Функция оперирует некоторыми данными, которые называются ее аргументами. Аргумент функции может занимать одну ячейку или размещаться в целой группе ячеек. Конструктор функций оказывает помощь в задании любых типов аргументов.

Функции в Excel используются для выполнения стандартных вычислений в рабочих книгах. Значения, которые используются для вычисления функций, называются аргументами. Значения, возвращаемые функциями в качестве ответа, называются результатами. Помимо встроенных функций вы можете использовать в вычислениях пользовательские функции, которые создаются при помощи средств Excel. Чтобы использовать функцию, нужно ввести ее как часть формулы в ячейку рабочего листа.

Последовательность, в которой должны располагаться используемые в формуле символы, называется синтаксисом функции. Все функции используют одинаковые основные правила синтаксиса. Аргументы функции записываются в круглых скобках сразу за названием функции и отделяются друг от друга символом точка с запятой “;”. В качестве аргументов можно использовать числа, текст, логические значения, массивы, значения ошибок или ссылки. Аргументы могут быть как константами, так и формулами.

В свою очередь формулы могут содержать другие функции. Функции, являющиеся аргументом другой функции, называются вложенными. В формулах Excel можно использовать до семи уровней вложенности функций. Задаваемые входные параметры должны иметь допустимые для данного аргумента значения. Некоторые функции могут иметь необязательные аргументы, которые могут отсутствовать при вычислении значения функции.

1. Надстройки MS Excel

Надстройки — это программы, входящие в состав Microsoft Excel и расширяющие его возможности.

Рассмотрим надстройки Подбор параметра и Поиск решения.

Команда Подбор параметра меню Сервис позволяет определить неизвестное значение (параметр), которое будет давать желаемый результат. Технология использования команды следующая:

1. решить нужную задачу с каким-либо начальным значением параметра;

2. выбрать команду Подбор параметра меню Сервис;

3. в окне диалога Подбор параметра в поле Установить в ячейке задать абсолютную ссылку на ячейку, содержащую расчетную формулу, а в поле Значение — то значение, которое следует получить в качестве результата формулы;

4. в поле Изменяя значение ячейки ввести ссылку на ячейку с параметром;

5. нажать кнопку ОК или клавишу Enter, на экране появится окно диалога Результат подбора параметра;

6. для сохранения найденного значения нажать кнопку ОК. Для восстановления значения, которое было в ячейке с параметром до использования команды Подбор параметра нажать кнопку Отмена.

При подборе параметра Excel использует итерационный процесс. Он проверяет для изменяемой ячейки одно значение за другим, пока не получит нужное решение.

Если задача подбора параметра занимает много времени, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы просмотреть результаты последовательных итераций.

По умолчанию команда Подбор параметра прекращает вычисления, когда выполняется 100 итераций, или при получении результата, который находится в пределах 0,001 от заданного целевого значения. Если нужна большая точность, можно изменить используемые по умолчанию параметры на вкладке Вычисления команды Параметры меню Сервис.

Команда Подбор параметра находит только одно решение, даже если задача имеет несколько решений.

Поиск решений может применяться для решения задач, которые включают много изменяемых ячеек, и помогает найти комбинацию переменных, которые максимизируют или минимизируют значение в целевой ячейке. Он также позволяет задать одно или несколько ограничений условий, которые должны выполняться при поиске решений. Для запуска этого инструмента следует выполнить команду Поиск решения меню Сервис.

В диалоговом окне Поиск решения в поле Установить целевую ячейку задается цель, которую должен достичь поиск решения. Целевая ячейка может быть задана ссылкой или именем. Поиск решения может находить конкретное значение целевой функции. В этом случае, задав только изменяемую ячейку без указания ограничений, можно использовать Поиск решения вместо команды Подбор параметра.

Цель поиска решений может не задаваться. Тогда поле Установить целевую ячейку следует оставить пустым, нажать кнопку Параметры и установить флажок Показывать результаты итераций. Поиск решения будет перебирать комбинации изменяемых ячеек, которые удовлетворяют заданным ограничениям. Пользователь может выбрать нужное решение, но оно необязательно будет оптимальным.

В поле Изменяя ячейки следует задать ячейки с переменными. Можно указать ссылки на ячейки или их имена. Если ячейки находятся в несмежных диапазонах, их следует разделять точкой с запятой. Вместо ввода ячеек можно нажать кнопку Предположить, и поиск решения сам предложит изменяемые ячейки, исходя из заданной целевой функции. Поле Изменяя ячейки нельзя оставить пустым, и указанные в нем ячейки обязательно должны влиять на значение целевой ячейки.

Последний шаг определения поиска решений — задание ограничений. Он не является обязательным. Чтобы задать ограничения, следует в окне Поиск решения нажать кнопку Добавить и заполнить окно диалога Добавление ограничений. Ограничение состоит из трех компонентов: ссылки на ячейку, оператора сравнения и значения ограничения. В левой части от оператора сравнения кроме ссылки на ячейку может также задаваться ссылка на диапазон. В правой части может задаваться диапазон (той же размерности, что и в левой части), ссылка на ячейку или константное значение.

После заполнения диалогового окна Поиск решения следует нажать кнопку Выполнить. При нахождении оптимального решения на экран выводится диалоговое окно Результаты поиска решения. Значения, отображаемые в рабочем листе, представляют собой оптимальное решение задачи. Можно либо оставить эти значения на листе, если установить переключатель Сохранить найденное решение и нажать кнопку ОК, либо восстановить исходные значения, если нажать кнопку Отмена или установить переключатель Восстановить исходные значения и нажать кнопку ОК. Можно также сохранить найденные значения в качестве сценария.

Поиск решений может решить не каждую предложенную задачу. Если оптимальное решение не найдено, в окне диалога Результаты поиска решений выводится сообщение о неуспешном завершении.

2. Решение профессиональных задач средствами MS Excel

2.1. Калькуляция себестоимости готовой продукции

Задача калькуляции себестоимости готовой продукции является одной из важнейших в сфере финансового и управленческого учета предприятия. Достоверная информация о фактической себестоимости выпуска, нормативных и фактических затратах товарно-материальных ресурсов дает возможность менеджменту компании принимать адекватные управленческие решения в сфере ценообразования готовой продукции тем самым, обеспечивая прибыльную деятельность предприятия.

Помимо выполнения главной задачи ценообразования калькуляция себестоимости также обеспечивает контроль движения основных позиций товарно-материальных запасов предприятия.

Вопрос калькуляции себестоимости готовой продукции является особо актуальным для предприятий общественного питания: кафе, ресторанов, баров и т.д.

Расчет отпускных цен на готовые блюда предприятий общепита производят на основе специальных калькуляционных карточек формы ОП-1 для каждого вида продукции. Калькуляцию составляют в расчете на одно или сто блюд. Чтобы наиболее точно определить цены реализации, рекомендуется производить калькуляцию на сто блюд.

Расчет продажных цен производится на каждое блюдо. Перед составлением калькуляции необходимо иметь ассортиментный перечень блюд, состав и нормы ингредиентов по списку рецептур или технологическим картам, закупочные цены на продукты.

Калькуляция производится в следующем порядке:

1. Определяется перечень блюд, на которые составляется калькуляция.

2. На основании сборника рецептур и технологических карт устанавливаются нормы вложений всех ингредиентов в готовое блюдо.

3. Определяются закупочные цены на сырье и ингредиенты.

4. Производится расчет стоимости сырьевого набора блюд путем умножения количества сырья на продажную цену и суммированием по всем позициям номенклатуры ингредиентов.

5. Сырьевая стоимость одного блюда получается путем деления общей суммы на 100.

6. Цена продажи готового блюда исчисляется путем увеличения сырьевой стоимости на величину торговой наценки (в %), устанавливаемой приказом руководителя предприятия общепита.

Наиболее оптимальным вариантом организации системы калькуляции является внедрение автоматизированной системы финансового учета, связывающей воедино все материально-финансовые потоки заведения.

Например, к таким системам можно отнести MS Excel. На первом этапе определяем ассортимент блюд из рубленного мяса. Затем составляем технологические карты для каждого блюда в соответствии с нормативами по Сборнику рецептур, выполняем расчет сырья на 100 порций по формулам. После чего оформляем калькуляционные карты блюда, выполнив необходимые расчеты себестоимости и продажной цены.

Разработанная в проекте система таблиц калькуляции блюд может быть использована:

1. при изучении теоретического материала и подготовке к практическим и лабораторным работам по профессиональным модулям

2. при подготовке выпускной квалификационной работы;

3. на предприятиях общественного питания.

2.2. Решение задач оптимально планирования

Постановка задачи планирования выглядит следующим образом:

• Имеются некоторые плановые показатели.

• Имеются некоторые ресурсы, за счет которых эти плановые показатели могут быть достигнуты. Эти ресурсы практически всегда ограничены.

• Имеется определенная стратегическая цель, зависящая от плановых показателей, на которую следует ориентировать планирование.

Нужно определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели. Это и будет оптимальным планом.

Рассмотрим пример: Кондитерский цех готовит пирожки и пирожные. В силу ограниченности емкости склада за день можно приготовить в совокупности не более 700 изделий. Рабочий день в кондитерском цехе длится 8 часов. Если выпускать только пирожные, за день можно произвести не более 250 штук, пирожков же можно произвести 1000, если при этом не выпускать пирожных. Стоимость пирожного вдвое выше, чем пирожка. Требуется составить дневной план производства, обеспечивающий кондитерскому цеху наибольшую выручку.

Чтобы составить дневной план производства, составим математическую модель задачи.

Плановыми показателями являются:

• х — дневной план выпуска пирожков;

• у — дневной план выпуска пирожных.

Ресурсы производства это:

• длительность рабочего дня — 8 часов;

• вместимость складского помещения — 700 мест.

Предполагается для простоты, что другие ресурсы (сырье, электроэнергия и пр.) не ограничены. Формализацию цели (достижение максимальной выручки цеха) мы обсудим позже.

Получим соотношения, следующие из условий ограниченности времени работы цеха и вместимости склада, т. е. суммарного числа изделий.

Из постановки задачи следует, что на изготовление одного пирожного затрачивается в 4 раза больше времени, чем на выпечку одного пирожка. Если обозначить время изготовления пирожка как t мин, то время изготовления пирожного будет равно 41 мин. Значит, суммарное время на изготовление х пирожков и у пирожных равно

tx + 4ty = (х + 4y)t.

Но это время не может быть больше длительности рабочего дня. Отсюда следует неравенство:

(х + 4y)t ≤ 8 • 60,

или

(х + 4y)t ≤ 480.

Легко посчитать t — время изготовления одного пирожка. Поскольку за рабочий день их может быть изготовлено 1000 штук, на один пирожок тратится 480/1000 = 0,48 мин. Подставляя это значение в неравенство, получим:

(х + 4у) • 0,48 ≤ 480. 

Отсюда

х + 4у ≤ 1000.

Ограничение на общее число изделий дает совершенно очевидное неравенство:

х + у ≤ 700.

К двум полученным неравенствам следует добавить условия положительности значений величин х и у (не может быть отрицательного числа пирожков и пирожных). В итоге получим систему неравенств:

А теперь перейдем к формализации стратегической цели: получению максимальной выручки. Выручка — это стоимость всей проданной продукции. Пусть цена одного пирожка — r рублей. По условию задачи, цена пирожного в два раза больше, т. е. 2r рублей. Отсюда стоимость всей произведенной за день продукции равна

rх + 2rу = r(х + 2у).

Целью производства является получение максимальной выручки. Будем рассматривать записанное выражение как функцию от х, у:

F(x, у) = r(х + 2у).

Она называется целевой функцией.

Поскольку значение r — константа, максимальное значение F(x, у) будет достигнуто при максимальной величине выражения (х + 2у). Поэтому в качестве целевой функции можно принять

f(x, у) = х + 2у. (2)

Следовательно, получение оптимального плана свелось к следующей математической задаче:

Требуется найти значения плановых показателей х и у, удовлетворяющих данной системе неравенств (1) и придающих максимальное значение целевой функции (2). 

Итак, математическая модель задачи оптимального планирования для кондитерского цеха построена.

Реализуем поиск оптимального решения для задачи планирования работы кондитерского цеха в MS Excel.

Подготовим электронную таблицу:

	A	B	C	D
1	Оптимальное планирование
2	Плановые показатели	X (пирожки)	Y (пирожные)
3
4	Ограничения
5		левая часть	знак	правая часть
6	время производства	=B3+4*C3		1000
7	общее количество	= B3+C3		700
8	положительность Х	=B3	=	0
9	положительность Y	=C3	=	0
10	Целевая функция	= B3+2*C3

Воспользуемся программой оптимизации «Поиск решения».

Для этого выполним команду Сервис — Поиск решения (если такой команды нет, то ее можно добавить Сервис — Настройки — установить флажок Поиск решения)

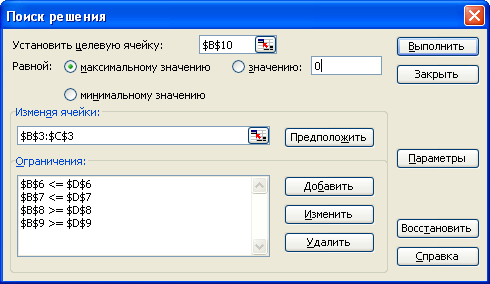
В диалоговом окне Поиск решения укажем:

1. адрес ячейки с целевой функцией, установить переключатель максимальное значение

2. в поле «изменяя ячейки» адреса ячеек, содержащих плановые показатели

3. в поле «ограничения», пользуясь кнопкой Добавить указать все имеющиеся ограничения

4. т.к. задача является линейной, то щелкнуть по кнопке Параметры и в открывшимся диалоговом окне установить флажок Линейная модель.

5. для получения решения щелкнуть по кнопке Выполнить.

В результате применения инструмента Поиск решения получен следующий оптимальный план дневного производства кондитерского цеха: нужно выпускать 600 пирожков и 100 пирожных.

ЗАКЛЮЧЕНИЕ

Табличный процессор – это прикладная программа, предназначенная для организации табличных вычислений на компьютере.

Вычислительная таблица, которая создаётся с помощью табличного процессора, называется электронной таблицей.

Одним из самых популярных табличных процессоров сегодня является MS Excel, входящий в состав MicrosoftOffice.

В данной работе были изучены основные характеристики табличного процессора MS Excel, раскрыты его основные функции, вычислительные возможности, надстройки. А также во второй главе рассмотрели возможности табличных процессоров для решения профессиональных задач повара, кондитера.

Таким образом, для решения ряда профессиональных задач целесообразно использовать многочисленные возможности табличных процессоров. Знание табличного процессора облегчит наш труд по созданию и заполнению калькуляционных карт и тех документов, где необходимы расчеты для осуществления профессиональной деятельности.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Информатика и ИКТ: учебник для нач. и сред. проф. образования/ М.С. Цветкова, Л.С. Великович. – 3-е изд., стер. – М.: Издательский центр «Академия», 2012. – 352 с.: ил.

2. Информатика. 11-й класс/ И.Г. Семакин, Е.К. Хеннер. – 2-е изд. – М.: БИНОМ. Лаборатория знаний, 2005. – 139 с.: ил.

3. Информатика и информационные технологии. Учебник для 10-11 классов/ Н.Д. Угринович. — М.: БИНОМ. Лаборатория знаний, 2003. – 512 с.: ил.

4. http://www.studfiles.ru/preview/5999270/

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

1. Количество изделий нам пока неизвестно. Это переменные.
2. В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
3. Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
4. Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.



Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

Заполнение аргументов:

1. Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
2. Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
3. Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
4. Тип – 0.
5. БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)^кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)¹⁶ = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.

Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

1. Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
2. Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
3. Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

1. Делаем таблицу со значениями матрицы А.
2. Выделяем на этом же листе область для обратной матрицы.
3. Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
4. В поле аргумента «Массив» вписываем диапазон матрицы А.
5. Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Скачать примеры

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

Приложение 5
Карточка 5. Выбор программы
MS Excel. 
Microsoft Excel является широко распространенной компьютерной программой, с 
помощью которой производятся расчеты, составляются таблицы и диаграммы, 
вычисляются простые и сложные функции.
Эта программа входит в пакет Microsoft Office. Электронная таблица является 
основным средством, которая используется для обработки и анализа цифровой 
информации с помощью средств вычислительной техники, Особенность программы 
заключается в том, что она позволяет осуществлять сложные расчеты. То есть в процессе 
вычисления одновременно можно оперировать данными, которые располагаются в разных 
зонах электронной таблицы и при этом связаны определенной зависимостью. Выполнение 
таких расчетов осуществляется благодаря возможности введения различных формул в 
ячейки таблицы. После выполнения вычисления результат будет отображаться в ячейке с 
формулой. В доступном диапазоне формул находятся разные функции – от сложения и 
вычитания до вычислений, связанных с финансами или статистикой.
Excel может применяться при выполнении финансовых расчетов, учете и контроле 
кадрового состава той или иной организации, в построении и обновлении графиков, 
которые основаны на введенных числах, что делает эту программу популярной среди 
бухгалтеров и экономистов. При этом программа отличается понятным интерфейсом и 
удобством использования.
Microsoft Word.
Является одной из самых востребованных программ современности, из 
используемых в офисной работе. Будучи текстовым редактором, она позволяет 
существенно облегчить работу по написанию текстов. Ведение корреспонденции, 
обработка текста, создание деловой и официальной переписки – все это стало проще 
проводить благодаря Microsoft Word. Выгодными особенностями программы являются ее 
функциональность и простота использования, благодаря чему даже неопытный 
пользователь способен легко разобраться в ней.
Microsoft Word обеспечивает простое и удобное форматирование текстового файла 
за счет продуманных инструментов и понятного интерфейса. Благодаря широкому спектру
функций текстовый процессор Microsoft Word напоминает настольную издательскую 
систему. Среди функциональных возможностей программы можно отметить:
­ наличие целого ряда шрифтов разного размера и начертания символов;
­ наличие способов выделения текста;
­ возможность установить параметры абзацев, междустрочные интервалы;
­  возможность проведения автоматической проверки правописания, подбора 
синонимов; 
­ автоматическая нумерация страниц и переносы слов на новую строку;
­ возможность создания таблиц и гипертекста со ссылками и многое другое.
Таким образом, программа Microsoft Word – это самый удобный вариант для 
создания текста и его последующего форматирования с возможностью гибкой настройки 
шрифта, стиля написания, оформления самой страницы.
Microsoft Access.
Относится к системам управления базами данных, ориентированными на рядовых 
потребителей. Она позволяет, не прибегая к программированию, с легкостью выполнять 
основные операции с базой данной: создание, редактирование и обработка данных. Microsoft Access является частью пакета Microsoft Office и входит в комплект его 
поставки.
Работает с данными, которые можно выстроить в иерархическую 
последовательность. Верхний уровень иерархии содержит основные объекты Access:
­ таблицы ­ главный тип объекта, поскольку все остальные вариации объектов ­ это
производные от таблицы. Основные составляющие таблицы ­ поля и записи, они 
определяют свойства элементов таблицы;
­ формы ­ вспомогательные объекты, от использования которых можно отказаться.
Они формируются, чтобы создать дополнительные удобства пользователю в плане 
просмотра, ввода и редактирования данных;
­ запросы ­ результаты обращения пользователя к БД с целью поиска данных, 
удаления, добавления и обновления записей. Результаты поиска (выборки) подаются в 
табличном виде;
­ отчеты ­ документы, предназначенные для вывода на печать, сформированные на 
информации, которая содержится в таблицах и запросах;
­ схема ­ описание архитектуры связей многотабличной базы данных;
­ макросы и модули ­ объекты повышенной сложности, при обыденной работе 
могут не использоваться.
Среди особенностей Access стоит отметить наличие VBA ­ встроенного языка 
программирования, посредством которого приложение может дополняться 
подпрограммами пользователей. Тем самым существенно расширяются возможности 
исходного варианта утилиты, обеспечивается удобство работы.

Министерство образования и науки РБ

Государственное автономное образовательное учреждение

 среднего профессионального образования

 «Техникум строительства и городского хозяйства»

Тема исследовательской работы:

Использование табличного процессора MS Excel и математического моделирования для решения профессиональных задач специалистами сервиса домашнего и коммунального хозяйства

Автор: Рябухина Анна,

студентка гр.СДиКХ-14

Руководители: Амшеева М.Р.,

преподаватель математики

Петрова Л.Ф.,

преподаватель информатики и ИКТ

Улан-Удэ, 2015

Содержание

1. Введение
2. Моделирование и его основные этапы
3. Математическое моделирование
4. Компьютерное моделирование в табличном процессоре Excel
5. Заключение
6. Литература

Введение

На современном этапе экономического, политического и социального развития Российской Федерации, стране все больше требуются высококвалифицированные специалисты, которые смогут решать стоящие перед ними профессиональные задачи на достаточно высоком уровне, применяя при этом достижения мировой науки и технического прогресса.

Уровень профессионализма   будущих специалистов   определяется не только совокупностью профессиональных знаний, умений применять стандартные и типовые методы и способы выполнения профессиональных задач,   но и способностью организовывать собственную деятельность, выбирая при этом  наиболее рациональные методы и способы решения профессиональных задач с использованием  информационно-коммуникационных технологий.

Применение ИКТ и математических знаний в профессиональной деятельности позволит будущему специалисту в области домашнего и коммунального хозяйства решать профессиональные задачи на более высоком уровне.

Одной из профессиональной задач, стоящих перед специалистами ЖКХ,  является планирование, организация и обеспечение контроля объемов, качества и сроков выполнения  ремонтных работ домовладений и жилищного фонда.

Специалист сервиса домашнего и коммунального хозяйства должен уметь составить  смету расходов по текущему и капитальному ремонту домовладений и жилищного фонда.

 Но если будущий специалист научится использовать табличный  процессор MS Excel и математическое моделирование,  то он сможет оптимизировать  выполнение  своих профессиональных задач.

Цель работы: разработка компьютерной модели, позволяющей рассчитывать  расход материала  в зависимости от размеров помещения и стоимость   материалов на данный момент времени.

Задачи исследования:

1. составить модель расчета площади ремонтируемой поверхности, применяя знания из геометрии;
2. отобрать необходимые  расчетные данные для организации ремонта в комнате, квартире;
3. составить    математическую модель расчетов количества и стоимости  материалов для ремонта;  
4.  изучить  методы моделирования в программе Ехсеl;
5. составить модель расчетов в программе Ехсеl.

Объект исследования: математическое моделирование в среде Excel.

Предмет исследования: разработка компьютерной модели, позволяющей решать производственные задачи.

Ожидаемые результаты:

• обрабатывать, анализировать, обобщать полученную информацию,
• производить необходимые расчеты,
• планировать и решать профессиональные задачи,
• применять  математическое моделирование для решения ситуационных задач

Методы исследования:

Эмпирического уровня

1. опрос работников ЖКХ

Теоретического уровня

1. изучение и анализ литературы по  геометрии  и информатике;
2. абстрагирование и формализация условия  профессиональной задачи

Экспериментально-теоретического уровня

1. моделирование  профессиональной задачи

План работы над темой исследования

1. Изучить и проанализировать литературу по теме исследования
2. Провести опрос работников ЖКХ
3. Проанализировать результаты опроса и сделать выводы
4. Изучить математические методы решения профессиональной задачи
5. Изучить методы математического моделирования
6. Составить математическую модель задачи
7. Изучить методы моделирования в программе Exсel
8. Составить компьютерную модель профессиональной задачи
9. Оформить  исследовательскую работу на компьютере
10. Оформить результаты работы в Power Point
11. Подготовиться к защите исследовательской работы.

Моделирование и его основные этапы

Microsoft Excel — одна из самых загадочных и интересных программ в пакете MS Office. Интересна она многочисленными средствами автоматизации работы, оформления документов и богатыми вычислительными возможностями. Загадочность ее состоит в том, что большинство пользователей применяют лишь малую толику того, что может дать им Excel. Это тем более удивительно, что спектр возможностей программы практически безграничен: от создания простых таблиц, построения диаграмм и графиков до решения сложных вычислительных задач и моделирования различных процессов.

С середины XX века в самых различных областях человеческой деятельности стали широко применять математические методы и ЭВМ. Возникли такие новые дисциплины, как «математическая экономика», «математическая химия», «математическая лингвистика» и т.д., изучающие математические модели соответствующих объектов и явлений, а также методы исследования этих моделей.

Под моделью (от лат. modulus — мера, образец, норма) понимают такой материальный или мысленно представляемый объект, который в процессе познания (изучения) замещает объект — оригинал, сохраняя некоторые важные для данного исследования типичные черты. Процесс построения и использования модели, называется моделированием.

Основные этапы моделирования

Процесс разработки моделей и их исследование на компьютере можно разделить на несколько основных этапов.

На первом этапе исследования объекта или процесса обычно строится описательная информационная модель. Такая модель выделяет существенные, с точки зрения целей проводимого исследования, параметры объекта, а несущественными параметрами пренебрегает.

На втором этапе создается формализованная модель, т.е. описательная информационная модель записывается с помощью какого-либо формального языка. В такой модели с помощью формул, уравнений, неравенств и т.д. фиксируются формальные соотношения между начальными и конечными значениями свойств объектов, а также накладываются ограничения на допустимые значения этих свойств.

На третьем этапе необходимо формализованную информационную модель преобразовать в компьютерную модель, т.е. выразить ее на понятном для компьютера языке. Существуют два принципиально различных пути построения компьютерной модели:

       построение алгоритма решения задачи и его кодирование на одном из языков программирования;

       построение компьютерной модели с использованием одного из приложений (электронных таблиц, СУБД и т.д.).

Четвертый этап исследования информационной модели состоит в проведении компьютерного эксперимента. Если компьютерная модель существует в виде программы на одном из языков программирования, ее нужно запустить на выполнение и получить результаты.

Если компьютерная модель исследуется в приложении, например, в электронных таблицах, можно провести сортировку или поиск данных, построить диаграмму или график и т.д.

Пятый этап состоит в анализе полученных результатов и корректировке исследуемой модели. В случае различия результатов, полученных при исследовании информационной модели, с измеряемыми параметрами реальных объектов, можно сделать вывод, что на предыдущих этапах построения модели были допущены ошибки или неточности.

Постановка задачи
План создания модели
			Построение математической модели
Создание модели
			Компьютерная реализация модели
Проверка адекватности модели
Решение задачи  и интерпретация результата		Проведение вычислительного эксперимента и интерпретация результата

Схема. Основные этапы моделирования

Был проведен опрос среди работников ЖКХ.  В  опросе участвовали 10 человек, им были предложены следующие вопросы:

1.  Для выполнения  ремонтных работ домовладений и жилищного фонда вы приглашаете к сотрудничеству фирмы  или обходитесь своими силами?
2. Смету расходов составляете с  использованием компьютерных программ или  нет?
3. Использование компьютерной программы, позволяющей рассчитывать количество и стоимость необходимых материалов облегчило бы вашу работу?
4. Можете ли вы самостоятельно разработать программу для подсчета материалов и их стоимости для организации ремонта любой площади?

Результаты опроса:

 Вопрос № 1:

Вопрос № 2:

Вопрос № 3:

Вопрос № 4:

Вывод:

1. Использование компьютерной программы, позволяющей рассчитывать количество и стоимость необходимых материалов несомненно облегчило бы работу специалистов ЖКХ.
2. Готовой программы (калькулятора) для подсчета материалов,  их стоимости для проведения  ремонта нет, а сами они затрудняются составить такую программу.
3.  Необходимо создать такую компьютерную модель, которая позволит автоматизировать расчеты и меняя значения исходных данных, можно  будет проследить за изменением получаемых результатов и из множества вариантов решения задачи выбрать наиболее подходящий.

Математическое моделирование

Для того чтобы составить формализованную модель расчета площади ремонтируемой поверхности:

1) представим  комнату  в виде прямоугольного параллелепипеда, который является ее геометрической  моделью;

2) для того чтобы рассчитать площадь стен и потолка комнаты, используем формулу нахождения площади боковой поверхности и площади основания прямоугольного параллелепипеда: S = Pосн Н + Sосн = (2а + 2b)Н + аb, где Pосн – периметр основания (комнаты), Н – высота параллелепипеда (высота комнаты)

S =  2а Н+ 2bН + аb

 где а – длина основания (комнаты), b – ширина основания (комнаты);

3) из формулы исключим площадь площадь окон и дверей:

S = 2а Н+ 2bН + аb – n Sок – Sдв = 2а Н+ 2bН + аb – n сd – к r,

S = 2а Н+ 2bН + аb – n сd – к r

где n – количество окон, с,d – размеры окна, к, r – размеры двери

Виды ремонта:

1) шпатлевка потолка и стен;

2) покраска потолка и стен;

3) покрытие пола ламинатом.

Необходимые расчетные данные:

• Расход шпатлевки на 1 м2   — 1,2 кг
• Расход водоэмульсионной краски на 1 м2 – 0,2 кг

Составим математическую модель расчетов количества и стоимости  материалов для шпатлевания:

(2а Н+ 2bН + аb – n ×сd – к r)×1,2×m, где m – стоимость 1 кг шпатлевки 

   Математическую модель расчетов количества и стоимости  материалов для окрашивания водоэмульсионной краской:

(2а Н+ 2bН + аb – n×сd – к ×r)×0,2×t, где  t – стоимость 1 кг в/э краски

Математическую модель расчетов количества и стоимости  материалов  для покрытия ламинатом:

аb⋅р, где р – стоимость 1 м2 ламината

Математическую модель расчетов количества и стоимости  материалов  для ремонта комнаты:

(2а Н+ 2bН + аb – n ×сd – к ×r)×1,2 ×m + (2а Н+ 2bН + аb – n×сd – к ×r)×0,2×t + аb×р

Компьютерное моделирование   в табличном процессоре Excel

Объединяем ячейки А1-Н1 и вводим текст: Расчет ремонта комнаты (шпатлевка и покраска потолка и стен,  настил ламината). Объединяем ячейки А3-Е3 и вводим текст: Исходные данные.

Вводим исходные данные:  в ячейки В5-В7 – длину, ширину, высоту соответственно. В ячейки  В9-В11 – длину, ширину и количество окон, а в ячейки В13- В14 – длину, ширину двери.  В ячейку Е5 вводим расход шпатлевки на 1 м2  в кг,  в  ячейку Е6 вводим стоимость 1 кг шпатлевки в руб., в  ячейку Е7 вводим расход водоэмульсионной краски на 1 м2  в кг,  в  ячейку Е8 вводим стоимость 1 кг в/э краски в руб,  а в ячейку Е9 вводим стоимость  1 м2 ламината.

Находим промежуточные результаты: В ячейке В17 вычисляем площадь потолка по формуле: В5*В6 (длину умножаем на ширину). В ячейке В18 вычисляем площадь  стен  по формуле: 2*(B5*B7+B6*B7)  (длину умножаем на высоту, ширину умножаем на высоту, все это складываем и умножаем на 2).  В ячейке В19 вычисляем площадь окон по формуле: В9*В10*В11 (длину умножаем на ширину и умножаем на количество окон). В ячейке В20 вычисляем площадь двери: В13*В14. В ячейке В21 вычисляем ремонтируемую площадь по формуле: B17+B18-B19-B20 (площадь потолка плюс площадь стен минус площадь окон и минус площадь двери).  В ячейке В22 вычисляем площадь пола: В5*В6.

 Далее вычисляем расход материалов:  В ячейке Е17 получаем расход шпатлевки по формуле: B21*E5 (ремонтируемую площадь умножаем на расход шпатлевки на 1 м2).  В ячейке Е18 находим расход водоэмульсионной краски по формуле: B21*E7 (ремонтируемую площадь умножаем на расход водоэмульсионной краски на 1 м2).  В ячейке Е19 вводим площадь пола.

Вычисляем стоимость материалов:

• шпатлевка  — E17*E6 (расход шпатлевки умножаем на стоимость 1 кг шпатлевки)
• в/краска — E18*E8 (расход в/э краски умножаем на стоимость 1 кг краски
• ламинат E19*E9 (площадь пола умножаем на стоимость 1 м2 ламината).

Общую стоимость материалов вычисляем  с помощью функции: СУММ(G17:G19), т.е. суммируем стоимость шпатлевки, в/краски и ламината.

Заключение

         В настоящее время получило всеобщее признание то, что успех развития многих областей науки и техники существенно зависит от развития многих направлений математики, информатики. Математика и информатика становятся средством решения проблем организации производства, поисков оптимальных решений.  

          Программа Microsoft Excel – одна из наиболее практически значимых, востребованных.  Электронные таблицы не только позволяют автоматизировать расчеты, но и являются эффективным средством моделирования различных вариантов и ситуаций. Меняя значения исходных данных, можно проследить за изменением получаемых результатов и из множества вариантов решения задачи выбрать наиболее подходящий.

При выполнении работы я научилась решать конкретную практическую задачу математическими методами, планировать ее решение, проводить исследовательскую работу.

В ходе работы над темой я научилась создавать формализованную модель расчета площади ремонтируемой поверхности, применяя знания из геометрии. Для создания  математической модели расчетов количества и стоимости  материалов  для ремонта комнаты я определилась с видами ремонта, которые я хотела произвести и, соответственно, с необходимыми расчетными данными, и включила их в расчетную формулу. Выполняя данную работу, я, в очередной раз,  убедилась в необходимости математических знаний в нашей жизни.

При составлении компьютерной модели расчета расходов  и стоимости материалов освоила методы моделирования в среде Excel. В этой модели я смогу выполнять необходимые расчеты для ремонта, в зависимости от размеров помещения, стоимости материалов, видов ремонта.

Теперь я смогу смоделировать решение других профессиональных задач и планировать свою индивидуальную деятельность.

Литература

1. Атанасян Л.С. и др. Геометрия 10 — 11, М.: Просвещение, 2010
2. Угринович Н.Д. Информатика и информационные технологии, 10-11 класс. М.: – Бином Лаборатория знаний, 2007.
3. Семакин И.Г., Хеннер Е.К., Информатика и ИКТ. Базовый уровень. М.: – Бином Лаборатория знаний, 2011.
4. http://www.consultant.ru/document/cons_doc_LAW_167387/?frame=1
5. http://vegosm.ru/catalog/section.php?SECTION_ID=6571
6. http://vegosm.ru/catalog/section.php?SECTION_ID=6514
7. http://vegosm.ru/catalog/section.php?SECTION_ID=6524